Torsional Stick–Slip Modeling and Mitigation in Horizontal Wells Considering Non-Newtonian Drilling Fluid Damping and BHA Configuration

Abstract

Stick–slip vibration leads to accelerated wear of drilling tools and downhole tool failures, particularly in long horizontal sections. Existing drill-string dynamics models and control or digital-twin frameworks have significantly improved our understanding and mitigation of stick–slip, but most of them adopt simplified Newtonian or linear viscous damping and low-degree-of-freedom representations of the drill-string–fluid–BHA system, which can under-represent the influence of non-Newtonian oil-based drilling fluids and detailed BHA design in long horizontal wells. In this study, an n-degree-of-freedom torsional stick–slip vibration model for horizontal wells is developed that explicitly incorporates Herschel–Bulkley non-Newtonian rheological damping of the drilling fluid, distributed friction between the horizontal section and drill string, and bit–rock interaction. The model is implemented in a computational program and calibrated and validated against stick–slip field measurements from four shale-gas horizontal wells in the Luzhou area, showing good agreement in stick–slip frequency and peak angular velocity. Using the Stick–Slip Index (SSI) as a quantitative metric, the influences of rotary table speed, weight on bit (WOB), and bottom-hole assembly (BHA) configuration on stick–slip vibration in a representative case well are systematically analyzed. The results indicate that increasing rotary speed from 64 to 144 r/min progressively reduces stick–slip severity and eliminates it at 144 r/min, reducing WOB from 150 to 60 kN weakens and eventually removes stick–slip at the expense of penetration rate, drill collar length has a non-monotonic impact on SSI with potential high-frequency vibrations at longer lengths, and increasing heavy-weight drill pipe (HWDP) length from 47 to 107 m consistently intensifies stick–slip. Based on these simulations, SSI-based stick–slip severity charts are constructed to provide quantitative guidance for drilling parameter optimization and BHA configuration in field operations.

1. Introduction

Horizontal-well technology, as a core method for enhancing hydrocarbon recovery, has played a pivotal role in the global development of unconventional oil and gas resources. According to statistics from the International Energy Agency (IEA), as of 2023, over 80% of global shale-gas production relies on horizontal wells combined with hydraulic fracturing technology. Major development areas, including the Permian Basin in the United States and the Sichuan South Shale Gas Field in China, predominantly adopt horizontal wells as their foundational architecture [1,2,3,4]. By significantly increasing reservoir contact area (5–10 times greater than vertical wells), horizontal wells markedly improve single-well productivity and economic efficiency. Stick–slip vibration is a self-excited oscillation phenomenon arising from the coupled tribological and dynamic interactions within the drill-string–rock–wellbore system during rotary motion. Its essence lies in a nonlinear dynamic process dominated by alternating static friction (stick) and kinetic friction (slip). In recent years, as horizontal wells have extended into ultra-deep and ultra-long horizontal sections, the frequency and severity of stick–slip vibrations have become increasingly pronounced [5,6,7].

Research on the dynamic mechanisms and control strategies of drill-string stick–slip vibration has evolved into a multidimensional framework, with domestic and international scholars uncovering its complex nonlinear nature through theoretical modeling, numerical simulations, and field experiments. In dynamic modeling, Yigit et al. [8] pioneered a coupled torsional–bending vibration model for drill strings, demonstrating that wellhead torque regulation effectively suppresses stick–slip effects. Divenyi et al. [9] further accounted for drill bit–formation contact heterogeneity to develop an axial–torsional-coupled model, precisely characterizing the interaction between stick–slip vibration and bit-bounce phenomena. Sarker et al. [10] introduced a 3D multibond graph approach to construct axial/lateral–torsional-coupled dynamic models for horizontal wells, systematically revealing the multidirectional coupled response characteristics of drill strings in complex wellbores. Based on the analysis of downhole triaxial acceleration field experimental data, Zhang et al. [11] established a coupled axial–lateral–torsional finite element model (FEM) for the drill string.

Regarding environmental factors and damping mechanisms, Omojuwa et al. [12] confirmed a positive correlation between drilling-fluid damping coefficients and vibration-suppression efficiency through torsional vibration analysis in viscous damping environments. Moharrami et al. [13] employed Rayleigh viscous damping to simulate drilling-fluid energy dissipation, establishing a five-degree-of-freedom (5-DoF) lumped parameter model validated by field trials for engineering applicability. Moraes [6] integrated factors such as wellbore contact and drilling-fluid damping to propose a 4-DoF lumped model, elucidating the differential impacts of drill pipe length on normal drilling and abnormal vibrations.

In mechanism analysis and parameter optimization, Chen et al. [14] classified stick–slip vibration excitation sources into rock-cutting and wellbore-friction nonlinear mechanisms based on field-data mining. Liu et al. [15] systematically decoupled the interactions among drilling parameters, formation properties, and tool configurations, proposing targeted vibration suppression strategies. Tian et al. [16] discovered through axial–torsional coupling dynamics that high-rotary-speed–low-WOB combinations significantly reduce stick–slip vibration intensity. Zhang et al. [17] derived a critical WOB criterion for stick–slip stability from an energy-conservation perspective, providing theoretical guidance for parameter optimization. Additionally, Jia et al. [18] quantified the impact of bit friction–cutting coupling effects using dimensionless equations and lumped parameter models. Luo et al. [19] developed a deep-well axial–torsional coupling model, validated with field data from a 5200 m well, demonstrating high-precision predictive capabilities.

In addition, recent research has further refined drill-string dynamic modeling by integrating fluid–structure interaction, three-dimensional coupling, and intelligent control. A series of works have established fluid–structure-coupled models in which the drill string is treated as an elastic beam conveying internal flow and interacting with the surrounding drilling fluid, revealing that flow-induced damping and added mass significantly modify the bifurcation behavior and vibration regimes of the system. Recent examples include nonlinear dynamic analyses of drill-string systems with fluid–structure interaction, lateral contact, and support constraints, as well as whirling dynamics models that couple beam vibrations with the Navier–Stokes equations of the drilling fluid, as reported by Wang et al. [20]. In parallel, Guo et al. [21] developed a three-dimensional nonlinear finite element-based reduced-order model combined with model predictive control to prevent stick–slip, further highlighting the potential of advanced dynamic models for active vibration mitigation. Furthermore, several studies have analyzed fully coupled axial–torsional–lateral vibrations under stochastic excitations and complex wellbore constraints, and have mapped out safe operating windows for multidirectional drill-string motions.

With the rapid development of drilling digitalization, digital twins and machine-learning techniques have also been introduced for stick–slip diagnosis and mitigation. Physics-guided or hybrid machine-learning models, such as those proposed by Sheth et al. [22] and Elahifar and Hosseini [23], have been trained on field data to predict stick–slip severity, downhole torque, or safe ranges of rotary speed and WOB, thereby enabling ahead-of-bit risk assessment and proactive parameter adjustment. Digital-twin frameworks, exemplified by the drilling digital twin of Gandikota et al. [24], further couple fast time-domain drill-string solvers with real-time surface and downhole measurements to forecast drilling dysfunctions online and support closed-loop control of drilling parameters. In addition, machine learning-based vibration pattern-recognition methods have been developed to automatically classify stick–slip, whirling, and other drill-string vibration modes from multi-channel acceleration signals and to trigger mitigation actions in real time [25,26].

Despite the abovementioned advances, several gaps still exist for horizontal wells with ultra-long lateral sections. First, most fluid–structure interaction or triaxial coupling models focus on vertical or slightly deviated wells, and rarely consider the combined influence of distributed drill-string–formation friction in the horizontal section and the non-Newtonian rheological damping of oil-based drilling fluids on torsional stick–slip, within a model that can be readily parameterized by field data. Second, digital-twin- and machine-learning-based solutions mainly target real-time monitoring and closed-loop control; they typically require high-bandwidth measurements, proprietary software, and large volumes of offset-well data, thus limiting their direct application to pre-drill parameter design and BHA configuration for new horizontal wells. Therefore, there is still a need for a physically transparent and computationally efficient horizontal-well model that simultaneously integrates drilling-fluid rheology, BHA layout, WOB, and rotary table speed, and that can be used to construct practical stick–slip severity maps for field operations. To address this need, this study establishes a horizontal-well drill-string–bit–formation dynamic model that comprehensively incorporates drilling-fluid rheological parameters, bottom-hole assembly (BHA), WOB, and rotary table speed. By simulating the non-Newtonian rheological damping between the drill string and drilling fluid, friction in the horizontal section between the drill string and wellbore, and bit–formation interactions, this work investigates the decoupled and coupled effects of these three nonlinear factors on drill-string vibrations. The goal is to unveil the triggering mechanisms of stick–slip vibrations in horizontal wells, analyze influencing factors, and propose mitigation strategies.

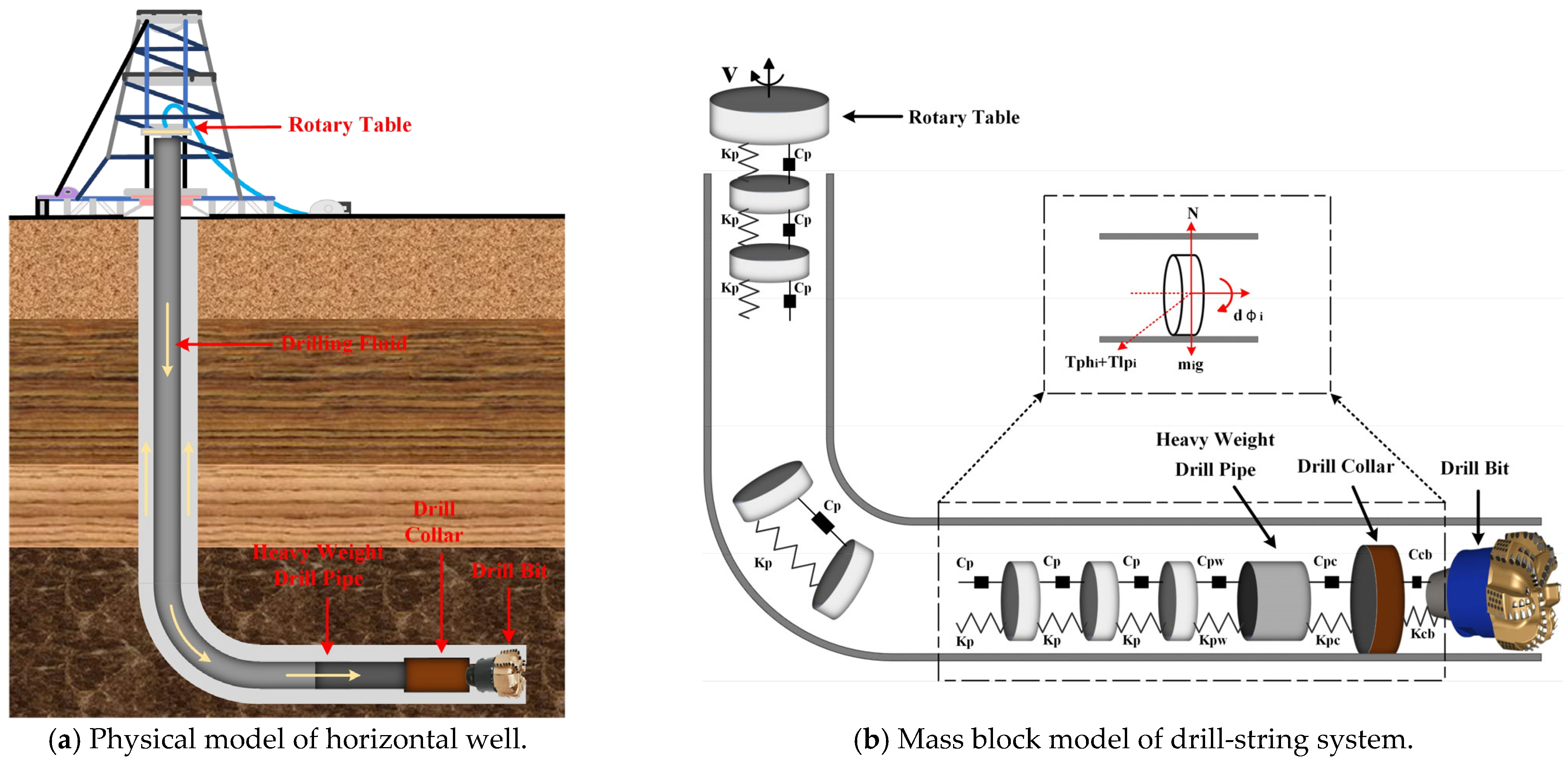
2. Stick–Slip Vibration Model of Horizontal-Well Drill-String System

2.1. Establishment of Stick–Slip Vibration Model

For the horizontal well drill-string system shown in Figure 1a, the drill string in the horizontal section frequently encounters friction against the wellbore. Many factors influence the system’s vibration during this process, including BHA, drill-bit type, wellbore structure, formation characteristics, drilling-fluid parameters, and operational parameters. The current work focuses on studying the stick–slip effect produced by drill tools during horizontal drilling, optimizing and designing suitable drilling parameters, and proposing strategies for preventing and controlling stick–slip vibration, with the goal of shortening drilling cycles and reducing drilling costs. The assumptions included in the developed analysis model for stick–slip vibration in horizontal-well drill strings are as follows.

(1)

The influence of lateral vibration on torsional vibration is disregarded.

(2)

The effect of an oil-based drilling fluid on the drill string is equivalent to a non-Newtonian rheological damping force.

(3)

The drill bit, drill collars, heavyweight drill pipe (HWDP), and drill pipe are considered N mass blocks with concentrated inertia, connected by springs and dampers.

(4)

The friction between the drill bit and the rock is represented by a concentrated friction torque.

It should be noted that, under these assumptions, the present model focuses on torsional dynamics and does not introduce lateral deformation as an independent degree of freedom. The influence of lateral contact in the horizontal section is represented by the normal reaction force and the corresponding friction torque projected onto the torsional direction, while higher-order lateral vibration modes and whirling or impact behavior cannot be captured in detail. For long horizontal sections, this simplification may lead to an underestimation of local torque peaks and cannot be used to evaluate lateral vibration indices. Therefore, the proposed model is mainly applicable to torsion-dominated horizontal wells with relatively smooth trajectories, where the primary objective is to assess bit stick–slip severity and to optimize drilling parameters and BHA configuration. For wells in which strong axial–lateral–torsional coupling and severe whirling are expected, a fully coupled tri-axial dynamic model should be adopted, which will be considered in future work.

On the basis of these assumptions, a multi-DoF mass block model of the drill-string system is established as shown in Figure 1b. Through force analysis, the dynamic differential equations of the drill-string system can be obtained.

Non-horizontal drill pipes:

$$\left\{\begin{array}{l}{J}_p{\stackrel{..}{\phi }}_1=K_p\left(Vt-{\phi }_1\right)+C_p\left(V-{\stackrel{.}{\phi }}_1\right)-K_p\left({\phi }_1-{\phi }_2\right)-C_p\left({\stackrel{.}{\phi }}_1-{\stackrel{.}{\phi }}_2\right)-C_{lp1}{\stackrel{.}{\phi }}_1\\ J_p{\stackrel{..}{\phi }}_2=K_p\left({\phi }_1-{\phi }_2\right)+C_p\left({\stackrel{.}{\phi }}_1-{\stackrel{.}{\phi }}_2\right)-K_p\left({\phi }_2-{\phi }_3\right)-C_p\left({\stackrel{.}{\phi }}_2-{\stackrel{.}{\phi }}_3\right)-C_{lp2}{\stackrel{.}{\phi }}_2\\ \dots \dots \\ J_p{\stackrel{..}{\phi }}_i=K_p\left({\phi }_{i-1}-{\phi }_i\right)+C_p\left({\stackrel{.}{\phi }}_{i-1}-{\stackrel{.}{\phi }}_i\right)-K_p\left({\phi }_i-{\phi }_{i+1}\right)-C_p\left({\stackrel{.}{\phi }}_i-{\stackrel{.}{\phi }}_{i+1}\right)-C_{lpi}{\stackrel{.}{\phi }}_i\end{array}\right.$$

(1)

Horizontal drill pipes:

$$\left\{\begin{array}{l}{J}_p{\stackrel{..}{\phi }}_1=K_p\left({\phi }_i-{\phi }_1\right)+C_p\left({\stackrel{.}{\phi }}_i-{\stackrel{.}{\phi }}_1\right)-K_p\left({\phi }_1-{\phi }_2\right)-C_p\left({\stackrel{.}{\phi }}_1-{\stackrel{.}{\phi }}_2\right)-C_{lp1}{\stackrel{.}{\phi }}_1-T_{hp1}\\ \dots \dots \\ J_p{\stackrel{..}{\phi }}_{j-1}=K_p\left({\phi }_{j-2}-{\phi }_{j-1}\right)+C_p\left({\stackrel{.}{\phi }}_{j-2}-{\stackrel{.}{\phi }}_{j-1}\right)-K_p\left({\phi }_{j-1}-{\phi }_j\right)-C_p\left({\stackrel{.}{\phi }}_{j-1}-{\stackrel{.}{\phi }}_j\right)-C_{lpj-1}{\stackrel{.}{\phi }}_{j-1}-T_{hpj-1}\\ J_p{\stackrel{..}{\phi }}_j=K_p\left({\phi }_{j-1}-{\phi }_j\right)+C_p\left({\stackrel{.}{\phi }}_{j-1}-{\stackrel{.}{\phi }}_j\right)-K_{pw}\left({\phi }_j-{\phi }_{j+1}\right)-C_{pw}\left({\stackrel{.}{\phi }}_j-{\stackrel{.}{\phi }}_{j+1}\right)-C_{lpj}{\stackrel{.}{\phi }}_j-T_{hpj}\end{array}\right.$$

(2)

HWDPs:

$$\left\{\begin{array}{l}{J}_{pw}{\stackrel{..}{\phi }}_1=K_{pw}\left({\phi }_j-{\phi }_1\right)+C_{pw}\left({\stackrel{.}{\phi }}_j-{\stackrel{.}{\phi }}_1\right)-K_{pw}\left({\phi }_1-{\phi }_2\right)-C_{pw}\left({\stackrel{.}{\phi }}_1-{\stackrel{.}{\phi }}_2\right)-C_{lpw1}{\stackrel{.}{\phi }}_1-T_{hpw1}\\ \dots \dots \\ J_{pw}{\stackrel{..}{\phi }}_{m-1}=K_{pw}\left({\phi }_{m-2}-{\phi }_{m-1}\right)+C_{pw}\left({\stackrel{.}{\phi }}_{m-2}-{\stackrel{.}{\phi }}_{m-1}\right)-K_{pw}\left({\phi }_{m-1}-{\phi }_m\right)-C_{pw}\left({\stackrel{.}{\phi }}_{m-1}-{\stackrel{.}{\phi }}_m\right)-C_{lpwm-1}{\stackrel{.}{\phi }}_{m-1}-T_{hpwm-1}\\ J_{pw}{\stackrel{..}{\phi }}_m=K_{pw}\left({\phi }_{m-1}-{\phi }_m\right)+C_{pw}\left({\stackrel{.}{\phi }}_{m-1}-{\stackrel{.}{\phi }}_m\right)-K_{pc}\left({\phi }_m-{\phi }_{m+1}\right)-C_{pc}\left({\stackrel{.}{\phi }}_m-{\stackrel{.}{\phi }}_{m+1}\right)-C_{lpwm}{\stackrel{.}{\phi }}_m-T_{hpwm}\end{array}\right.$$

(3)

Drill collars:

$$\left\{\begin{array}{l}{J}_c{\stackrel{..}{\phi }}_1=K_{pc}\left({\phi }_p-{\phi }_1\right)+C_{pc}\left({\stackrel{.}{\phi }}_p-{\stackrel{.}{\phi }}_1\right)-K_{pc}\left({\phi }_1-{\phi }_2\right)-C_{pc}\left({\stackrel{.}{\phi }}_1-{\stackrel{.}{\phi }}_2\right)-C_{lpc1}{\stackrel{.}{\phi }}_1-T_{hpc1}\\ \dots \dots \\ J_c{\stackrel{..}{\phi }}_{n-1}=K_{pc}\left({\phi }_{n-2}-{\phi }_{n-1}\right)+C_{pc}\left({\stackrel{.}{\phi }}_{n-2}-{\stackrel{.}{\phi }}_{n-1}\right)-K_{pc}\left({\phi }_{n-1}-{\phi }_n\right)-C_{pc}\left({\stackrel{.}{\phi }}_{n-1}-{\stackrel{.}{\phi }}_n\right)-C_{lpcn-1}{\stackrel{.}{\phi }}_{n-1}-T_{hpcn-1}\\ J_c{\stackrel{..}{\phi }}_n=K_{pc}\left({\phi }_{n-1}-{\phi }_n\right)+C_{pc}\left({\stackrel{.}{\phi }}_{n-1}-{\stackrel{.}{\phi }}_n\right)-K_{cb}\left({\phi }_n-{\phi }_b\right)-C_{cb}\left({\stackrel{.}{\phi }}_n-{\stackrel{.}{\phi }}_b\right)-C_{lpcn}{\stackrel{.}{\phi }}_n-T_{hpcn}\end{array}\right.$$

(4)

Drill bit:

$$J_b{\stackrel{..}{\phi }}_b=K_{cb}\left({\phi }_n-{\phi }_b\right)+C_{cb}\left({\stackrel{.}{\phi }}_n-{\stackrel{.}{\phi }}_b\right)-T_{fb}-C_{lb}{\stackrel{.}{\phi }}_b$$

(5)

The subscripts $p$, $pw$, $c$, and $b$ represent the drill pipe, HWDP, drill collars, and drill bit, respectively.

Simplifying the above equations,

$$\mathit{J}\stackrel{..}{\phi }+\mathit{C}\stackrel{.}{\phi }+\mathit{K}\phi =\mathit{T}$$

(6)

where

$$\mathit{J}=diag{\left(J_p,\dots ,J_p,J_{pw},\dots ,J_{pw},J_c,\dots J_c,J_b\right)}^T\in R^{{\left(1+i+j+p+q\right)}^2}$$

(7)

$$\mathit{C}=\left|\begin{array}{cccccccc}-C_p& 2C_p+C_{lp1}& -C_p& 0& \dots & 0& 0& 0\\ 0& -C_p& 2C_p+C_{lp2}& -C_p& \dots & 0& 0& 0\\ 0& 0& -C_p& 2C_p+C_{lp3}& \dots & 0& 0& 0\\ \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots \\ 0& 0& 0& 0& \dots & 2C_{pc}+C_{lpcq-1}& -C_{pc}& 0\\ 0& 0& 0& 0& \dots & -C_{pc}& C_{pc}+C_{cb}+C_{lpcq}& -C_{cb}\\ 0& 0& 0& 0& \dots & 0& -C_{cb}& C_{cb}+C_{lb}\end{array}\right|$$

(8)

$$\mathit{K}=\left|\begin{array}{cccccccc}-K_p& 2K_p& -K_p& 0& \dots & 0& 0& 0\\ 0& -K_p& 2K_p& -K_p& \dots & 0& 0& 0\\ 0& 0& -K_p& 2K_p& \dots & 0& 0& 0\\ \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots \\ 0& 0& 0& 0& \dots & 2K_{pc}& -K_{pc}& 0\\ 0& 0& 0& 0& \dots & -K_{pc}& K_{pc}+K_{cb}& -K_{cb}\\ 0& 0& 0& 0& \dots & 0& -K_{cb}& K_{cb}\end{array}\right|$$

(9)

$$\mathit{T}={\left(0,\dots ,0,T_{ph1},\dots ,T_{phj},T_{pwh1},\dots ,T_{pwhp},T_{pch1},\dots T_{pchq},T_{fb}\right)}^T$$

(10)

2.1.1. Friction Torque

This study employs the Karnopp friction model [27] to simulate the nonlinear torque, $T_{fb}$, and the same model is used to calculate the nonlinear torque between the horizontal section of the drill string and the formation. The expression for the nonlinear torque is as follows:

$$T_{fb}=\left\{\begin{array}{ll}{T}_r& if\left|{\stackrel{.}{\phi }}_{\mathrm{b}}\right|\le \Delta \nu and\left|T_r\right|<T_{sb}\\ T_{sb}sgn\left({\stackrel{.}{\phi }}_{\mathrm{b}}\right)& if\left|{\stackrel{.}{\phi }}_{\mathrm{b}}\right|\le \Delta \nu and\left|T_r\right|\ge T_{sb}\\ \left[T_{cb}+\left(T_{sb}-T_{cb}\right)e^{-\xi \left|{\stackrel{.}{\phi }}_{\mathrm{b}}\right|}\right]sgn\left({\stackrel{.}{\phi }}_{\mathrm{b}}\right)& if\left|{\stackrel{.}{\phi }}_{\mathrm{b}}\right|>\Delta \nu \end{array}\right.$$

(11)

$$\left\{\begin{array}{c}{T}_{sb}={\mu }_{sb}\cdot \mathrm{WOB}\cdot R_b\\ T_{cb}={\mu }_{cb}\cdot \mathrm{WOB}\cdot R_b\end{array}\right.$$

(12)

2.1.2. Drill-String System Parameters

The calculation methods for the parameters of the drilling system [28] are as follows.

(1)

Drill-string stiffness coefficient, K:

$$K={\displaystyle \frac{G}{32}}{\displaystyle \frac{\pi }{L}}\left(d_o^4-d_i^4\right)$$

(13)

(2)

Drill-string damping coefficient, C:

$$C=c_l{\displaystyle \frac{L}{3}}$$

(14)

(3)

Moment of inertia, J:

$$J={\displaystyle \frac{\rho \pi L}{32}}\left(d_o^4-d_i^4\right)$$

(15)

2.1.3. Drilling-Fluid Damping

Dushaishi et al. [29] validated, through comparative experimental and theoretical studies, that the Herschel–Bulkley non-Newtonian rheological (HBNR) damping model can accurately characterize the complex rheological behavior of drilling fluids under actual drilling conditions. By introducing yield stress and power-law behavior, this model more precisely simulates the nonlinear viscosity response of drilling fluids under multi-scenario operations such as annular flow and drill-string rotation, particularly suitable for describing high-performance drilling-fluid systems containing polymer additives or solid particles.

The HBNR damping expression is given by the following [30]:

$$C_l=A_f\left({\displaystyle \frac{{\tau }_{Hy}}{\dot{\phi }}}+k{\displaystyle \frac{{\dot{\phi }}^{n-1}}{\mathsf{\Delta }n}}\right)$$

(16)

In the equation,

$${\tau }_{Hy}=0.511{\theta }_3$$

(17)

$$n=3.26\lg \left[\left({\theta }_{200}-{\theta }_3\right)/\left({\theta }_{100}-{\theta }_3\right)\right]$$

(18)

$$k=0.511\left({\theta }_{100}-{\theta }_3\right)/170.2\mathrm{n}$$

(19)

2.1.4. Stick–Slip Vibration Grade

To measure the severity of stick–slip vibration, the current study adopts the drill-string stick–slip vibration-level evaluation criteria and recommendations provided by Schlumberger for different stick–slip vibration grades (

Table 1. Standard of stick–slip vibration level.

SSI	Stick–Slip Level	Color	Guidance/Recommendation
<0.5	Low	Green	Can drill normally
0.5–1.0	Medium	Yellow	For continuous operation over 25 h, risk of failure is medium
1.0–1.5	High	Orange	For continuous operation over 12 h, risk of failure is high
>1.5	Severe	Red	For continuous operation over 0.5 h, risk of failure is severe

). The expression for the stick–slip vibration index (SSI) [31] is as follows:

$$SSI={\displaystyle \frac{{\stackrel{.}{\phi }}_{b\max }-{\stackrel{.}{\phi }}_{b\min }}{2V}}$$

(20)

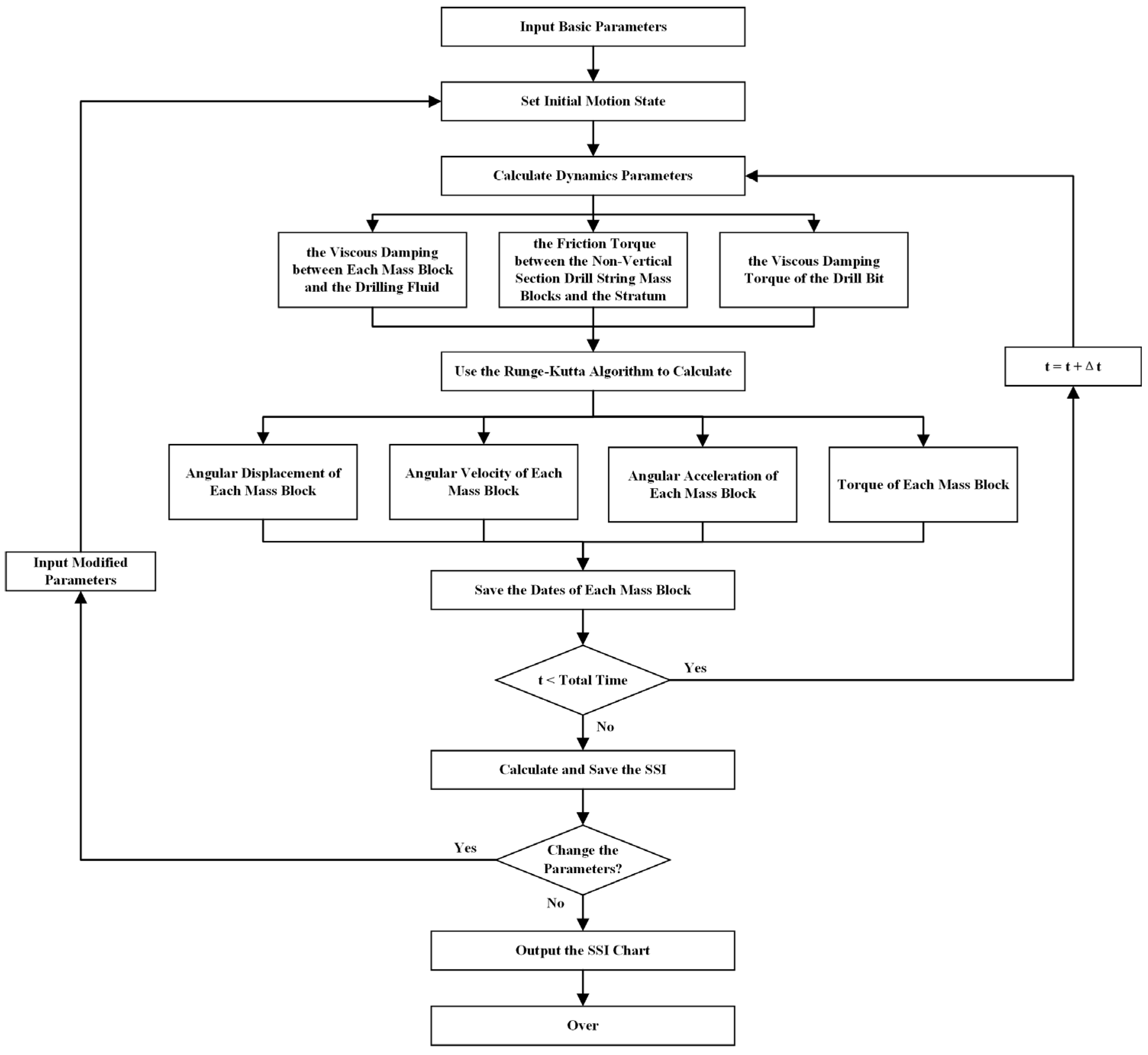
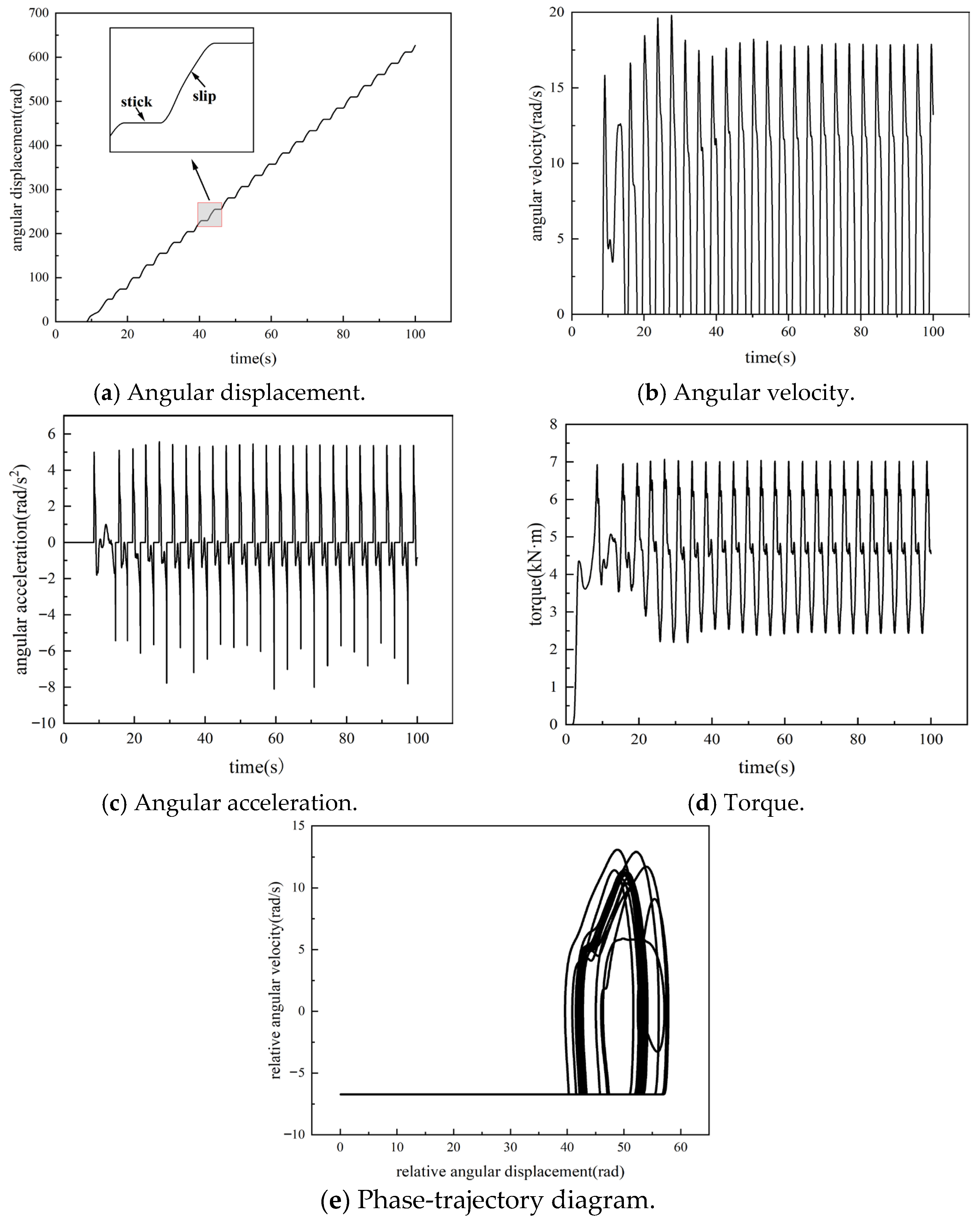
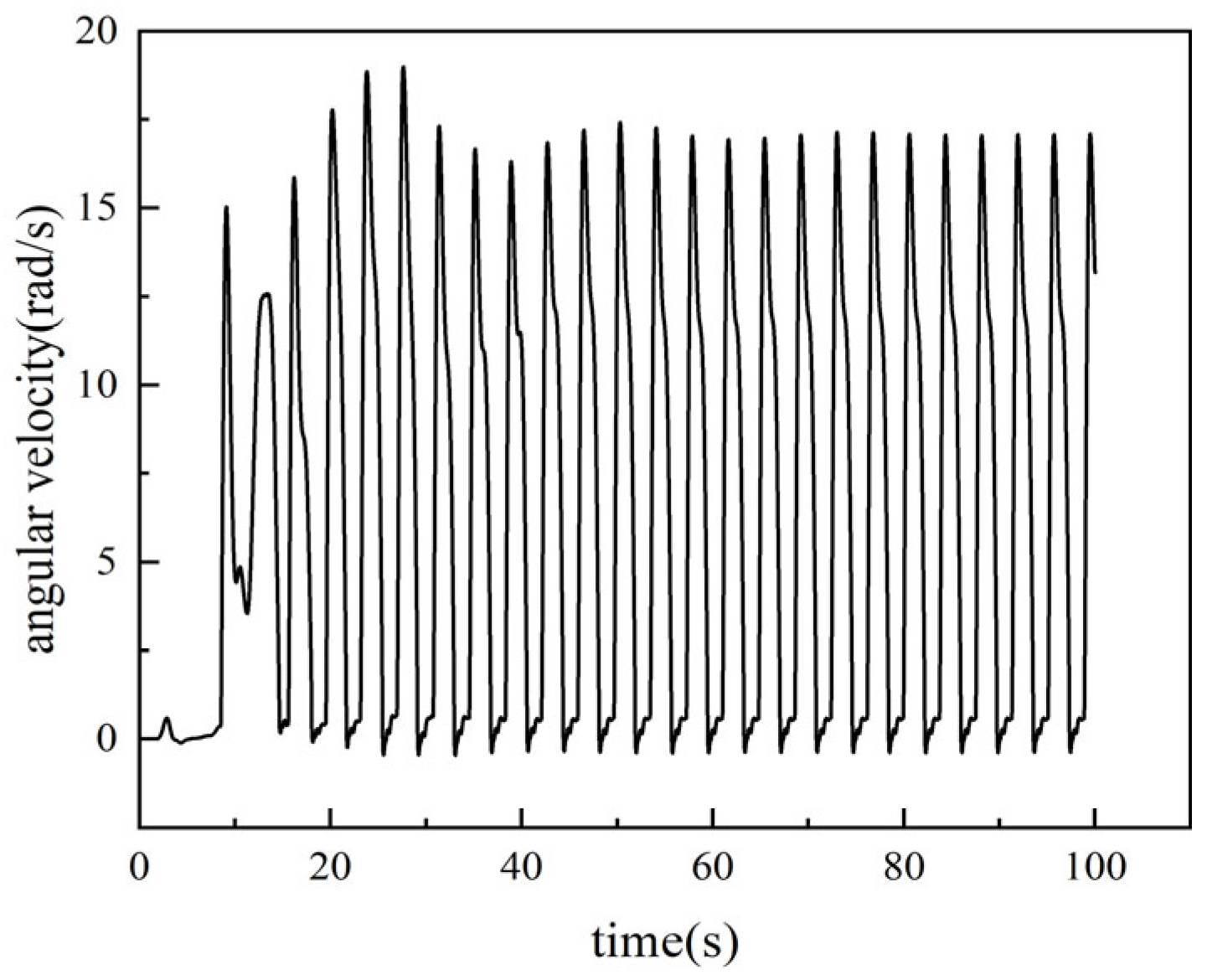
2.2. Solution of the Stick–Slip Vibration Model

This study employs the fourth- and fifth-order Runge–Kutta algorithms to solve the dynamic equations. The major process is illustrated in Figure 2 (where t represents time, and Δt represents the time step).

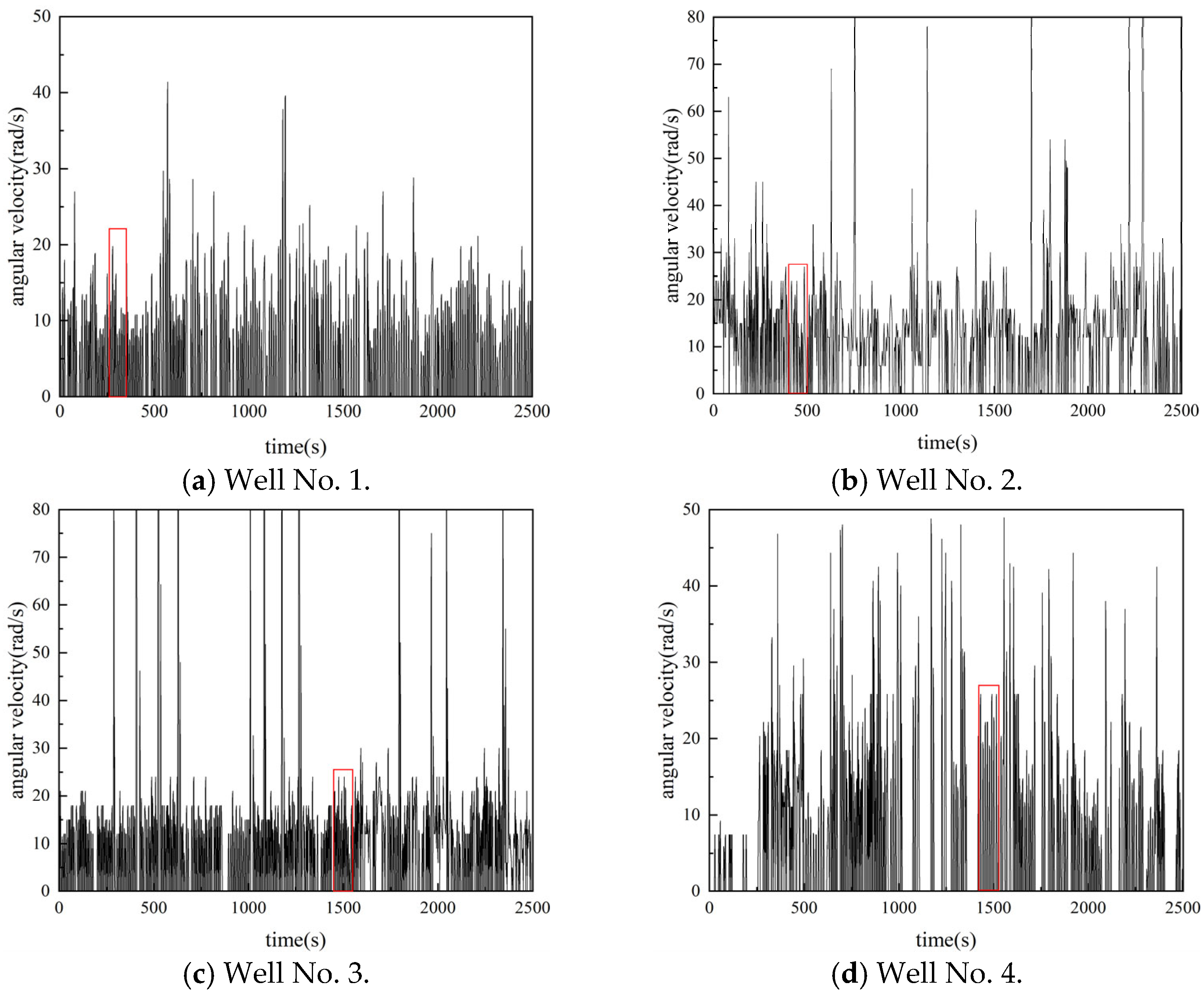
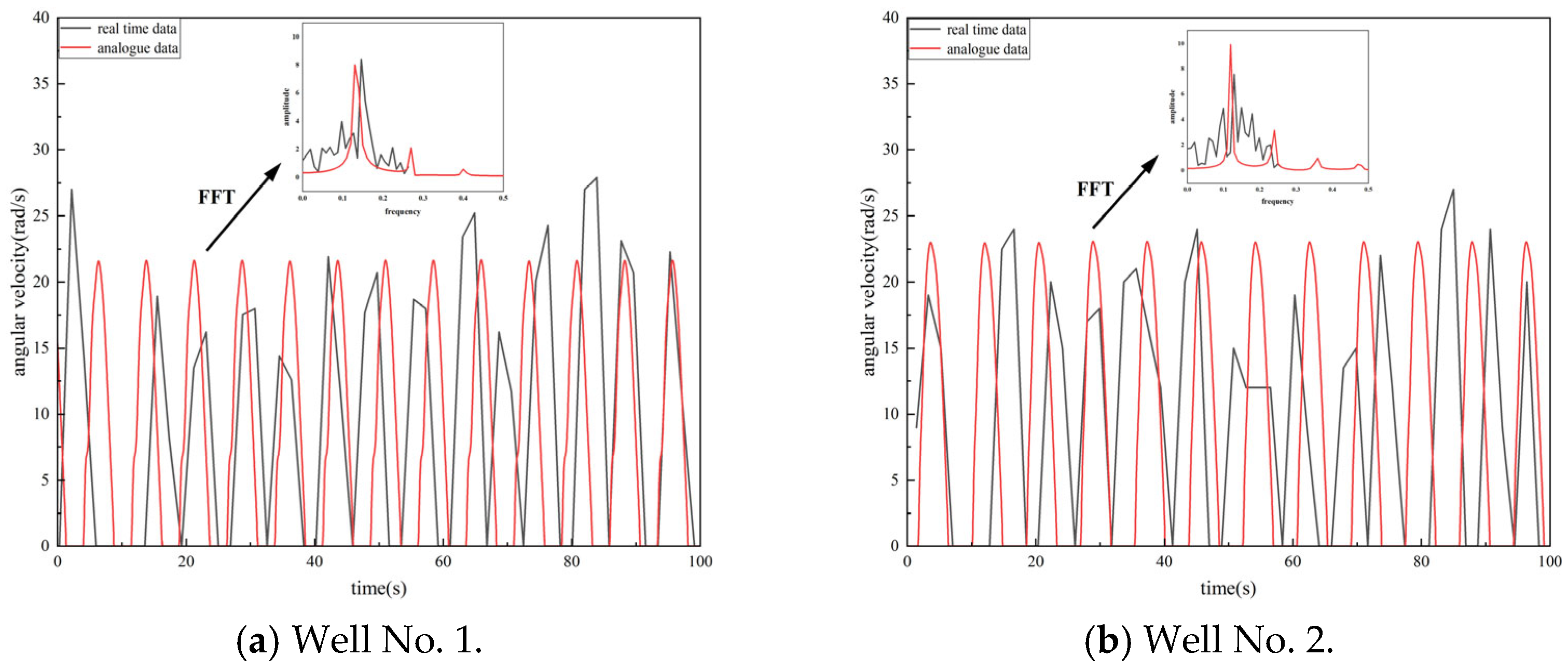
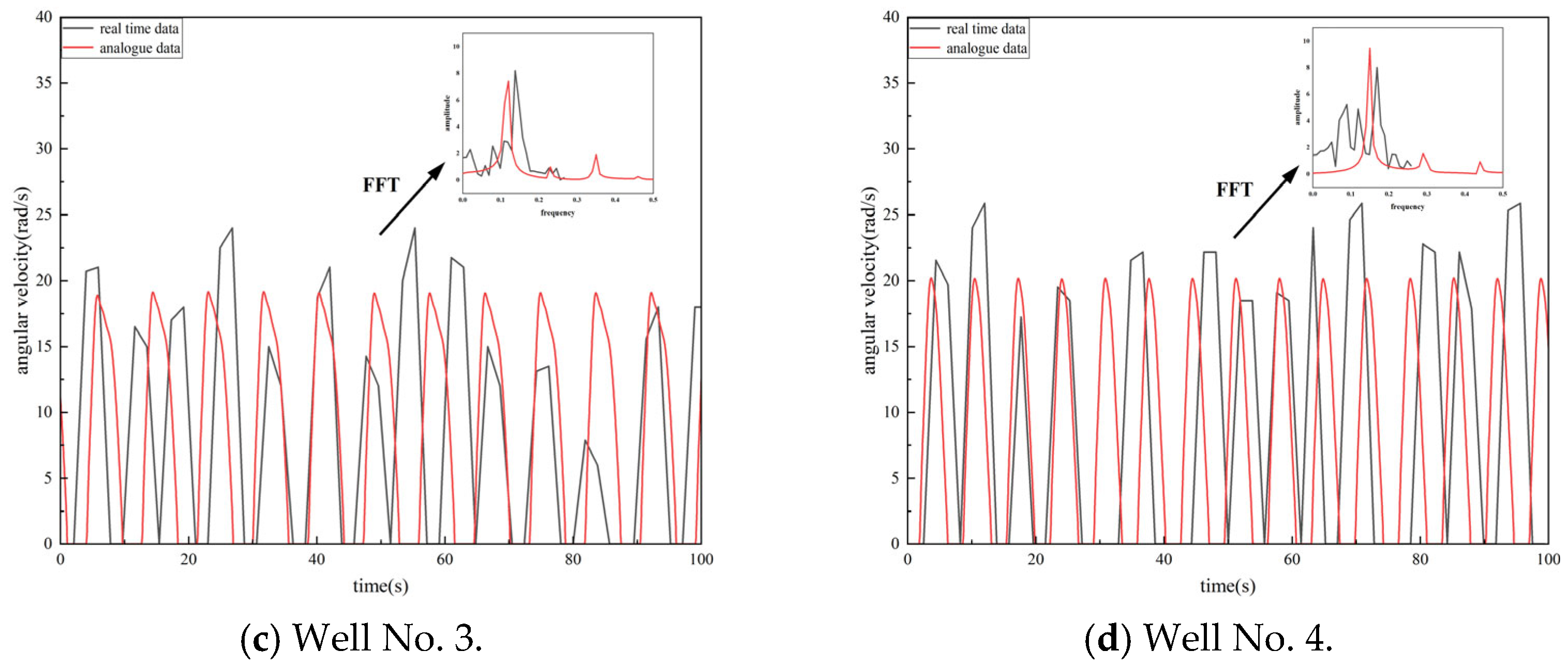
2.3. Verification of the Stick–Slip Vibration Model

Based on the dynamic model established in the preceding sections, numerical simulations were conducted for four shale-gas horizontal wells in a block of Luzhou City, whose key basic drilling parameters are summarized in

Table 2. Basic drilling parameters of horizontal wells.

Serial Number	Test Well Depth (m)	Kick-Off Point (m)	WOB (kN)	Rotary Table Speed (r/min)	Rotational Viscometer Reading
					at 3 rpm	at 100 rpm	at 200 rpm
1	3815	3700	74	72	3	30	53
2	4750	3548	132	91	6	32	58
3	5195	3617	79	80	6	32	57
4	3910	3720	73	59	7	40	62

. These simulations were implemented via the the MATLAB 2023a platform, followed by a comparative analysis with field-measured stick–slip vibration data. In the simulation parameter settings, the total duration was set to 100 s to ensure steady-state system response, and the time step was optimized to 0.001 s to balance computational efficiency and high-frequency dynamic resolution. Numerical integration was performed using the variable-step ODE45 solver, with dynamic and static friction coefficients set to 0.5 and 0.8, respectively. The angular-velocity variations over time during drilling in the four wells were measured, as shown in Figure 3.

A stable segment of stick–slip vibration (within the red box) from the measured angular-velocity–time plot was selected, enlarged, and compared with simulation results. Fourier-transform analysis was performed on both measured and simulated data, as shown in Figure 4. As illustrated in the figures, the simulated results exhibit high consistency with the measured data in terms of frequency and amplitude. The vibration peak amplitude is approximately 2.5 times the rotary table speed, which is consistent with the measured data. To further quantify the agreement between the simulations and the field measurements,

Table 3. Quantitative comparison between measured and simulated bit responses.

Well	Dominant Frequency (Hz)		Error (%)	Amplitude		Error (%)
	Measured Date	Simulated Date		Measured Date	Simulated Date
Well No. 1	0.161	0.148	8.07	8.19	8.05	8.05
Well No. 2	0.140	0.132	5.71	8.12	9.77	16.88
Well No. 3	0.148	0.129	12.84	8.01	7.89	1.50
Well No. 4	0.184	0.169	8.15	7.98	9.23	15.66

lists the dominant frequency and amplitude of the bit angular velocity after Fourier transform for the four horizontal wells. The relative errors of the dominant frequency are all within about 12.84%, and those of the amplitude are within about 16.88%. These results indicate that the proposed model not only reproduces the overall waveform and spectral characteristics of bit stick–slip, but also reasonably captures its main frequency and intensity.

3. Analysis of Factors That Affect Stick–Slip Vibration in the Horizontal-Well Drill-String System

The wellbore structure data for the case wells are provided in

Table 4. Wellbore structure data.

Drilling Sequence	Casing Name	Well Depth (m)	Borehole Size (mm)	Casing O.D.	Casing Down Depth	Casing Roof Depth	Casing I.D.
First Spud	Conductor Pipe	148.60	660.40	508.00	148.19	0.00	485.70
Second Spud	Surface Casing	967.00	444.50	339.70	966.70	0.00	315.32
Third Spud	Intermediate Casing	2525.00	311.20	244.50	2524.10	1346.91	220.50
Third Spud	Intermediate Casing	2525.00	311.20	250.83	1346.91	0.00	220.51

. The drill-string system length selected for this section is 5820 m, with the corresponding BHA, drilling, and drilling-fluid parameters presented in

Table 5. BHA chart.

Name of Drilling Tools × Specification	O.D. (mm)	I.D. (mm)	Length (m)
PDC Bit × Z516	215.90		0.24
Rotary Steerable Tool	172.00		4.27
Stabilizer Joint	172.00		0.82
MWD Hang-Off Sub	172.00	60.00	4.41
Nonmagnetic Drill Collar	171.50	57.20	7
Screen Sub	172.00	75.00	0.95
Sloped HWDP × S135I	127.00	76.20	28.68
Sloped HWDP × S135I	127.00	76.20	18.88
Drill Pipe × S135s	127.00	108.60	5774.87

and

Table 6. Drilling and drilling-fluid parameters.

Parameter	Well Depth	Kick-Off Point	Rotary Table Speed	WOB	Rotational Viscometer Reading			Dynamic Friction Coefficient	Static Friction Coefficient
					at 3 rpm	at 100 rpm	at 200 rpm
Value	5820 m	3306 m	64 r/min	90 kN	7	41	69	0.5	0.8

.

Numerical simulations were conducted on the target case well using the MATLAB platform, and the time-domain dynamic response of the drill-string system was obtained as shown in Figure 5. As shown in the figure, the drill-bit angular displacement exhibits typical periodic step-like changes, while the angular velocity demonstrates intermittent pulsing characteristics, alternating between “slip” and “stick” states. The stick-phase duration is approximately 2.8 s, with a vibration peak velocity of 17 rad/s, equivalent to 2.5 times the rotary table speed. The angular-acceleration curve and torque curve oscillate intensely within the ranges of −9 to 6 rad/s² and 2 to 7 kN·m, respectively. The negative spikes correspond to kinetic energy dissipation at the end of the slip phase, whereas positive fluctuations reflect the conversion of elastic potential energy to kinetic energy during the late stick phase [17]. The phase-trajectory plot displays a closed limit cycle, confirming that the system operates in a self-excited vibrational state.

Combining the drill bit angular-velocity–time graph (Figure 5b) and the drill collar angular-velocity–time graph (Figure 6), a slight reversal phenomenon occurs when the drill collar’s angular velocity decays to 0 rad/s, followed by the next slip state. This phenomenon is due to the high stiffness of the drill collar and its large contact area with the drilling fluid. When the drill string undergoes torsional vibration, the formation does not provide a sufficiently large reactive torque, causing its angular displacement to be relatively advanced and leading to a reversal phenomenon.

Subsequent analysis of the influencing factors will be based on this case well.

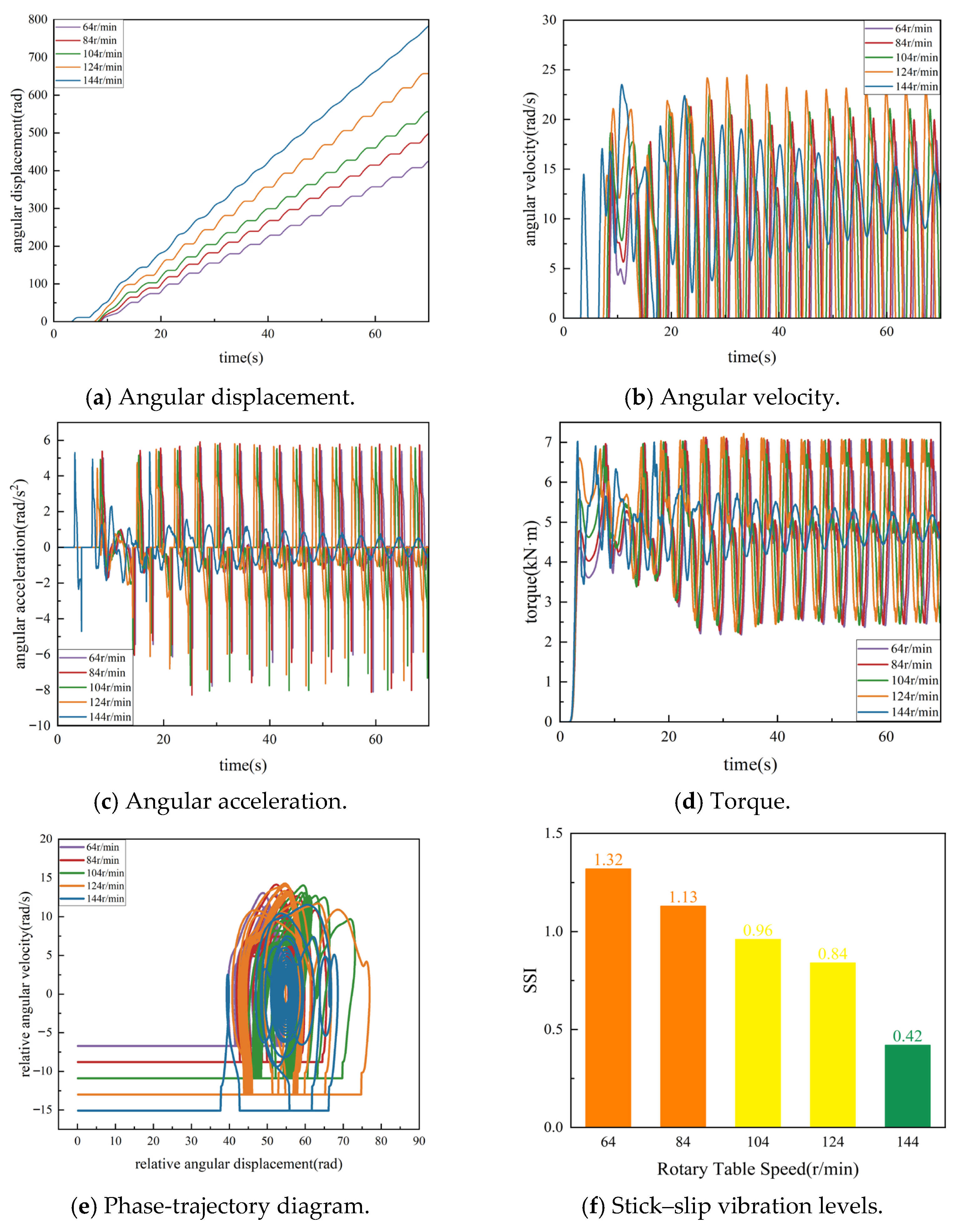
3.1. Effect of Rotary Table Speed

The rotational speeds of the rotary table studied in this section are 64, 84, 104, 124, and 144 r/min. The simulation results are presented in Figure 7.

As illustrated in the figure, when the rotary table speed reaches 144 rpm, the stick–slip vibration disappears. The angular-displacement–time curve approximates a straight line with a stable slope, while the angular velocity, angular acceleration, and torque exhibit harmonic-like oscillations that gradually attenuate and stabilize. The phase-trajectory plot shows the limit cycle gradually contracting and diminishing, indicating the drill-string system transitions to a steady state. When the rotary table speed is within 64–124 rpm, the drill bit exhibits significant stick–slip vibration. The angular displacement displays periodic step-like changes, and as the rotary speed decreases, the stick-phase duration increases from 1.9 s to 2.8 s. Although the energy input to the drill-string system decreases with lower rotary speeds, oscillation ranges of angular acceleration and bit torque show no significant reduction, implying intensified stick–slip vibration. This demonstrates that increasing the rotary table speed suppresses stick–slip vibration [15]. The rationale is that higher rotary speeds enhance energy input, enabling the horizontal drill string and bit to overcome frictional torque with the formation, thereby shortening the stick-phase duration, improving cutting efficiency, and mitigating or eliminating stick–slip vibration. However, Kamel [32] found that excessive rotary speeds may induce severe bit bounce, causing significant damage to the drill bit. Therefore, moderately increasing the rotary table speed is recommended to suppress stick–slip vibration during drilling operations.

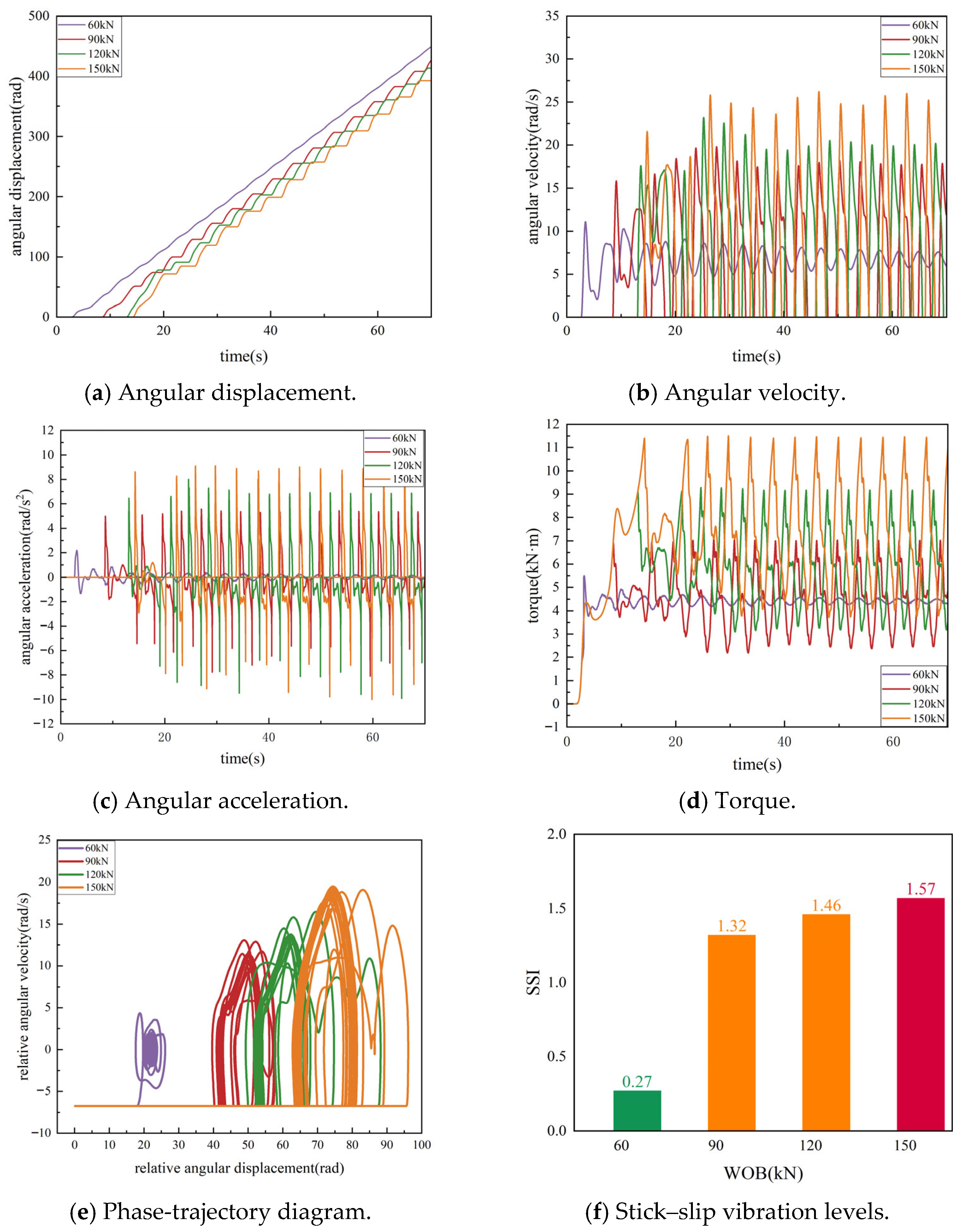
3.2. Effect of WOB

This section analyzes the WOB values of 60, 90, 120, and 150 kN. The simulation results are presented in Figure 8.

The figures show that when drilling pressure ranges from 90 kN to 150 kN, the drill bit shows stable stick–slip vibration during drilling. As the WOB increases, the drill bit starts more slowly, stick duration increases from 2.8 s to 4.5 s, and the angular displacement of the drill bit significantly decreases within the same time frame, reducing the cutting efficiency of the drill bit. Notably, the fluctuation peaks and amplitudes of the drill bit’s angular velocity, angular acceleration, and torque increase significantly. The phase-trajectory plot indicates a rightward shift and expansion of the limit cycle, reflecting intensified dynamic instability in the system. When the WOB is 60 kN, stick–slip vibration is eliminated. This finding indicates that increasing the WOB intensifies the stick–slip vibration [18]. The reason for this phenomenon is as follows: an increase in WOB leads to increased friction, prolonging the duration of stickiness and increasing the amount of energy released instantaneously when the drill bit enters the “slip” phase.

It should be emphasized that the WOB range of 60–150 kN considered in this paper is based on the drilling program and offset wells of the same shale-gas block, and it represents the practical operating window for the 8½ in PDC bit in this formation. In field practice, a WOB lower than about 60 kN is seldom used, because the bit aggressiveness becomes too weak and the mechanical rate of penetration decreases sharply, whereas a WOB higher than about 150 kN approaches the mechanical and torque limits of the drill string and surface equipment. Within this realistic window, the calculated SSI decreases monotonically as the WOB is reduced and approaches zero when the WOB is reduced to approximately 60 kN, indicating that a low WOB is an effective means of suppressing stick–slip for the present well. However, such a low WOB inevitably reduces the depth of cut and ROP. Therefore, for shale formations similar to the case well, WOB values in the lower part of the operational window (around 60 kN) are recommended when vibration control and tool safety are prioritized, while a higher WOB within the allowable range can be selected when a higher ROP is required, with the understanding that the risk of torsional stick–slip will increase.

3.3. Effect of BHA

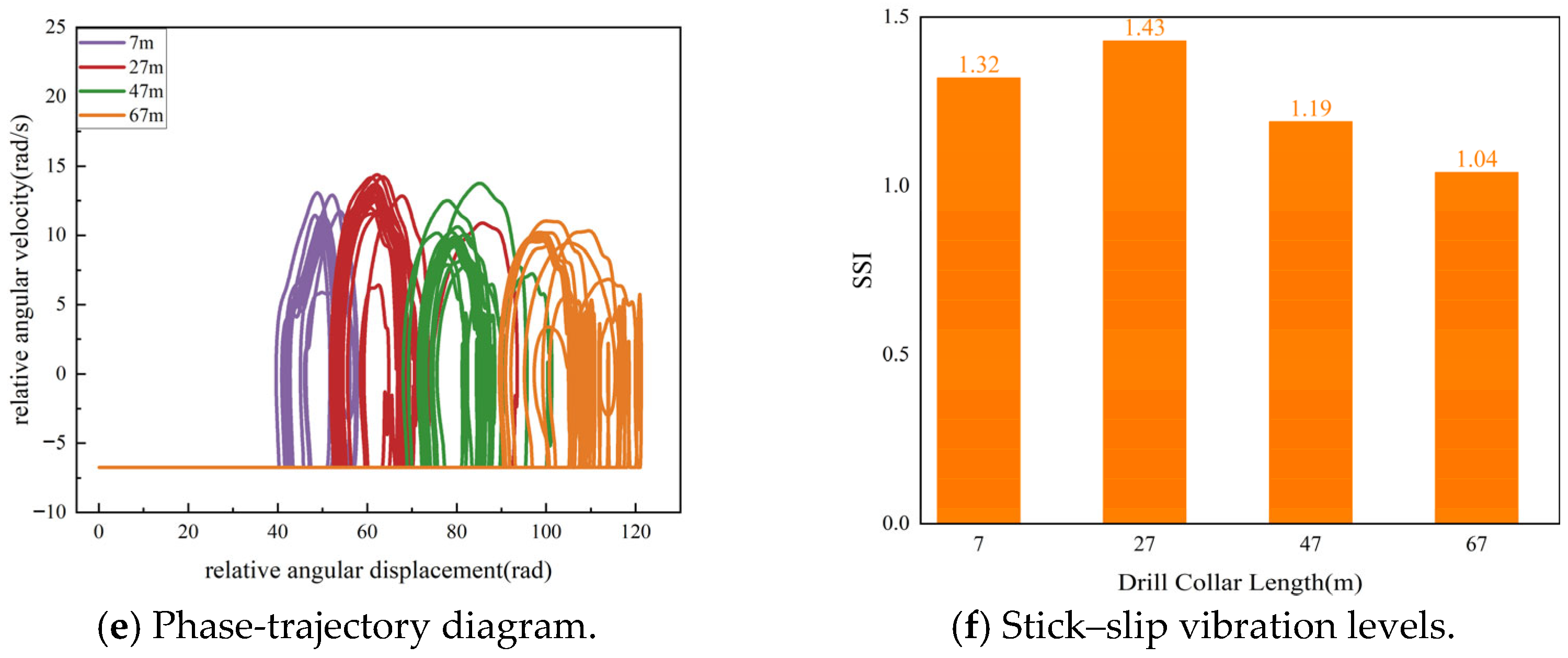
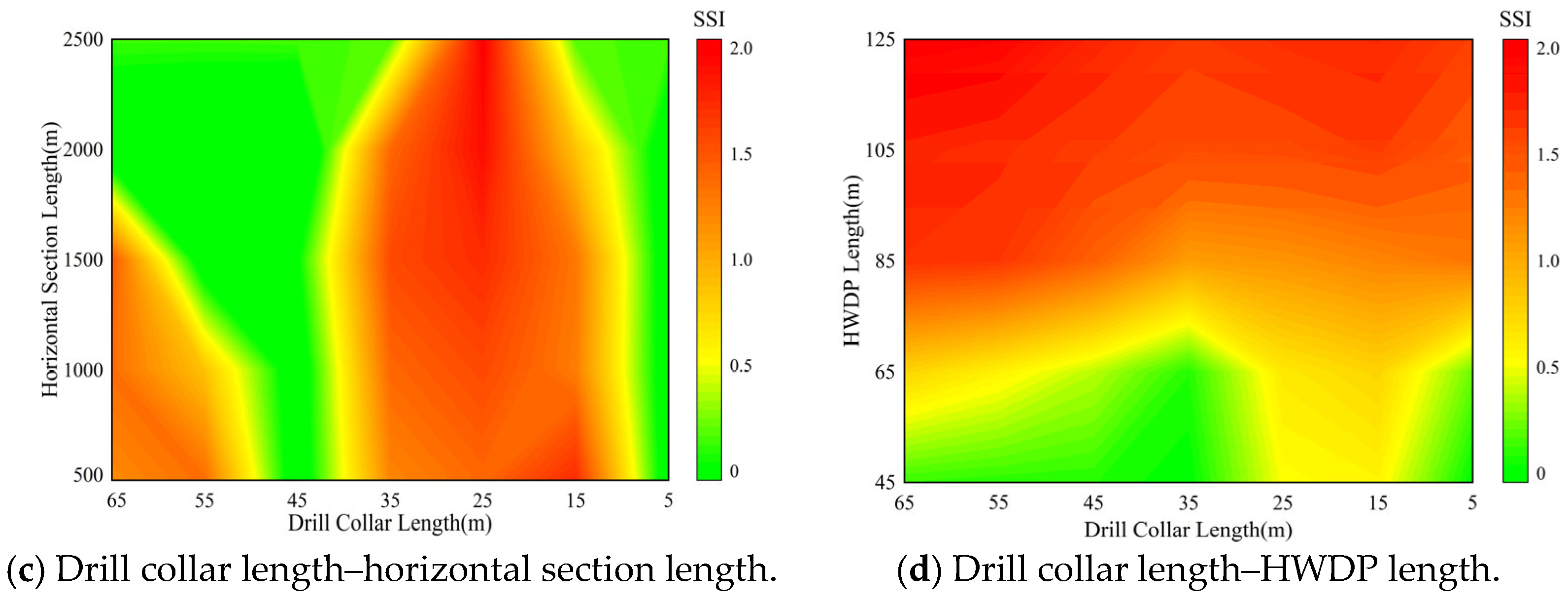
3.3.1. Drill Collar Length

Drill collars are characterized by their rigidity, wall thickness, and strength, making them resistant to bending under pressure. They provide WOB to the drill bit and enhance the rigidity of the drill string, enduring loads, such as bending, twisting, internal pressure, and vibrations, during use [33,34]. Drill collars’ outer diameter is frequently larger than that of drill pipes and HWDPs, leading to more frequent friction with the formation in horizontal wells. This section focuses on how the length of drill collars affects the stick–slip vibration response of the drill bit by considering only changes in the length of the drill collars. The studied drill collar lengths are 7, 27, 47, and 67 m, with the simulation results shown in Figure 9.

The figures indicate that with drill collar lengths of 7–67 m, the drill bit experiences stable stick–slip vibrations during drilling. When the drill collar length increases from 7 m to 27 m, the drill bit starts more slowly, and the peak fluctuations of angular velocity, angular acceleration, and torque increase, raising the stick–slip vibration level. This result is attributed to the increased length of the drill collars producing more friction with the formation, longer stick durations, and increased energy release when the drill bit enters the “slip” phase. When the drill collar length increases from 27 m to 67 m, the drill bit starts more slowly, and the peak fluctuation of angular velocity decreases. However, the peak fluctuations of angular acceleration and torque increase, lowering the stick–slip vibration level, because the increased length of the drill collars enhances the stiffness of BHA, facilitating torque transmission to the drill bit, extending slip duration, and improving cutting efficiency. Notably, when the length of the drill collar is 67 m, the drill bit experiences high-frequency vibrations during drilling, because the longer drill collar length not only increases the stiffness of BHA but also results in significant friction with the formation. This finding indicates that configuring drill collar length appropriately based on actual conditions is necessary to suppress stick–slip vibration effectively. Simultaneously, avoiding excessively long drill collars that can lead to high-frequency vibrations is crucial for effectively extending the life of the drill bit and reducing the risk of drill-string failure.

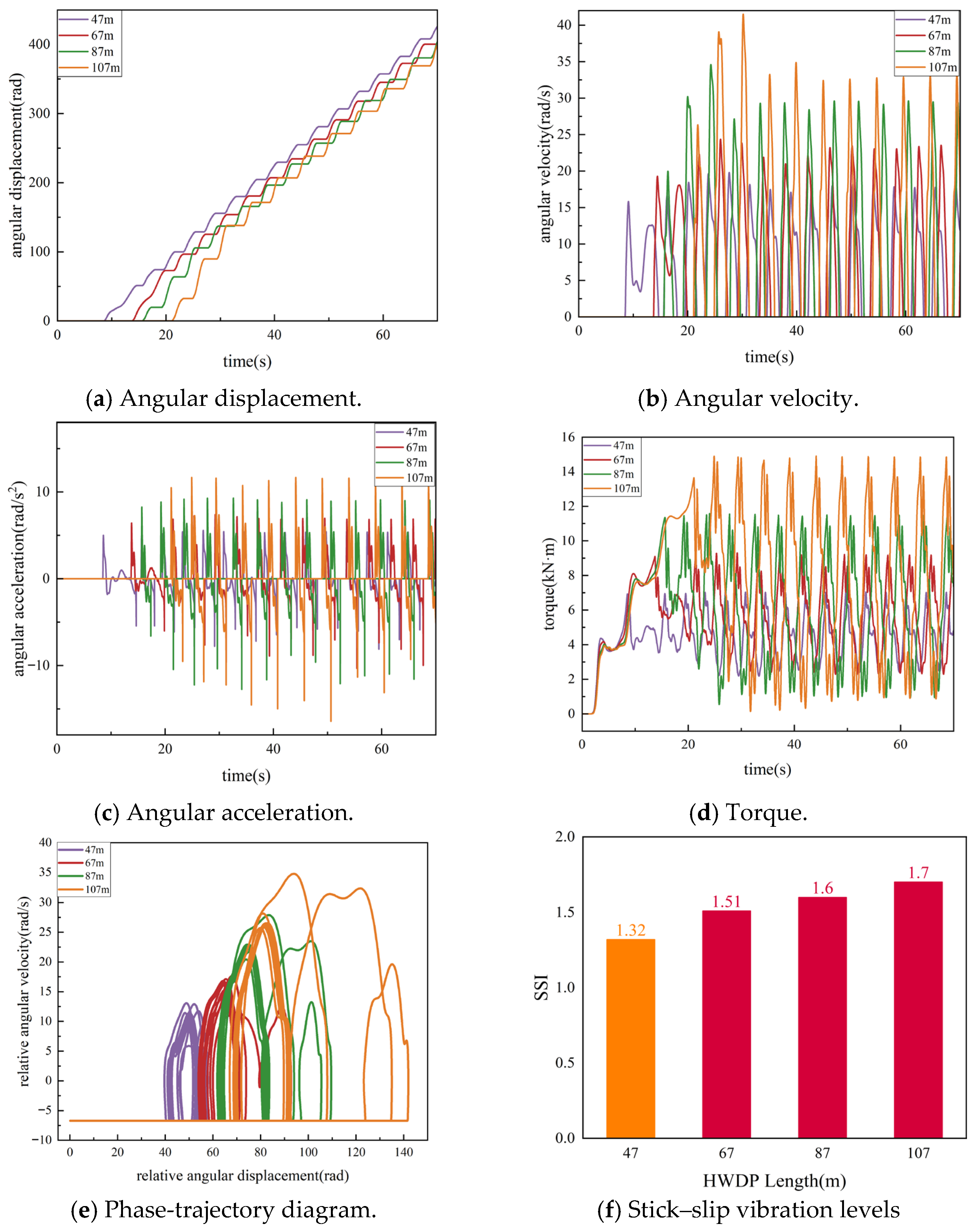
3.3.2. HWDP Length

HWDP serves as a transitional drill-string segment between the regular drill pipe and the drill collar, effectively alleviating stress concentration in the transition section between the drill collar and drill pipe, and providing WOB and rotational inertia. This section focuses on how the length of HWDPs affects the stick–slip vibration response of the drill bit, with changes limited to the length of HWDP. The studied drill collar lengths are 47, 67, 87, and 107 m. The simulation results are shown in Figure 10.

The figures show that with HWDP lengths of 47–107 m, the drill bit experiences stable stick–slip vibrations during drilling. As the HWDP length increases, the drill bit starts more slowly, the duration of stickiness increases from 2.8 s to 4.1 s, and the stick–slip vibration level increases. Notably, the peak fluctuations and amplitudes in the drill bit’s angular velocity, angular acceleration, and torque significantly increase, with the torque fluctuation range expanding from 2–7 kN·m to 0.5–15 kN·m, which will lead to damage to the drill bit and drill string. The phase-trajectory plot shows a rightward shift and expansion of the limit cycle. This indicates that increasing the length of HWDP intensifies stick–slip vibration. The underlying mechanism is as follows: In horizontal wells, increasing the length of HWDP significantly amplifies the rotational inertia of the drill string and its friction with the wellbore. A high-inertia system demands greater torque to initiate rotation, causing the accumulation of elastic potential energy to far exceed that of standard drill strings. When the stored energy exceeds the static friction threshold and transitions into the slip phase, the kinetic energy release becomes more violent, resulting in larger angular velocity transients and a marked increase in stick–slip vibration amplitude.

4. Stick–Slip Vibration-Mitigation Method

Building on the preceding analysis, this section leverages the SSI to propose specific recommendations for suppressing stick–slip vibrations in the case well, focusing on two key aspects: optimizing drilling parameters and refining BHA configurations.

(1)

Improving Drilling Parameters

Figure 11a,b display the stick–slip vibration-level charts under different drilling parameters for various horizontal section lengths of the case well. The drilling parameters can be optimized on the basis of these charts and the stick–slip vibration-level standards (Table 1).

(2)

Optimizing BHA Configuration

Figure 11c,d show the stick–slip vibration-level charts under different BHA configurations for different horizontal section lengths of the case well. BHA configuration can be optimized on the basis of these charts and the stick–slip vibration-level standards (Table 1).

In addition, the stick–slip vibration generated by the drill-string system during drilling can be suppressed by increasing the number of cutter blades on the drill bit [19,35] and using drilling tools, such as torsional impactors [16,36]. From the perspective of field application, the SSI-based stick–slip severity charts are intended to serve as a practical decision-support tool rather than a strictly predictive control law. In the pre-drill planning stage, they can be used to select suitable combinations of rotary table speed, WOB, and BHA configuration for a given horizontal section, so that the planned operating points fall in the mild or moderate stick–slip regions. During drilling operations, the charts are combined with real-time monitoring of surface parameters (rotary speed, torque, WOB, hook load, and standpipe pressure) and, where available, downhole measurements of bit rotational speed and torque. These measurements allow the driller to judge whether the current operating point is approaching the severe stick–slip region and to adjust the rotary speed and WOB accordingly. Due to inevitable uncertainties in formation properties, drilling-fluid rheology, friction factors, and sensor noise, the boundaries between the severity regions should be interpreted as approximate, and the charts are mainly used to indicate trends (e.g., how changes in rotary speed or WOB move the operating point across the severity map). In this context, the role of the operator is to define safe operating windows based on the charts, to implement parameter adjustments when monitored stick–slip indicators exceed tolerable levels, and to refine BHA design for subsequent runs if severe stick–slip cannot be eliminated.

5. Conclusions

This study establishes a torsional stick–slip vibration model for horizontal wells that explicitly considers drilling-fluid rheology, drill-string–formation friction in the horizontal section, and detailed BHA segmentation. By incorporating Herschel–Bulkley non-Newtonian damping, a Karnopp-type friction law at the bit–rock and drill-string–formation interfaces, and an n-DOF drill-string–BHA–bit representation, the model reproduces the measured stick–slip responses of four shale-gas horizontal wells in Southern Sichuan and enables systematic parameter studies. The main findings are as follows:

(1)

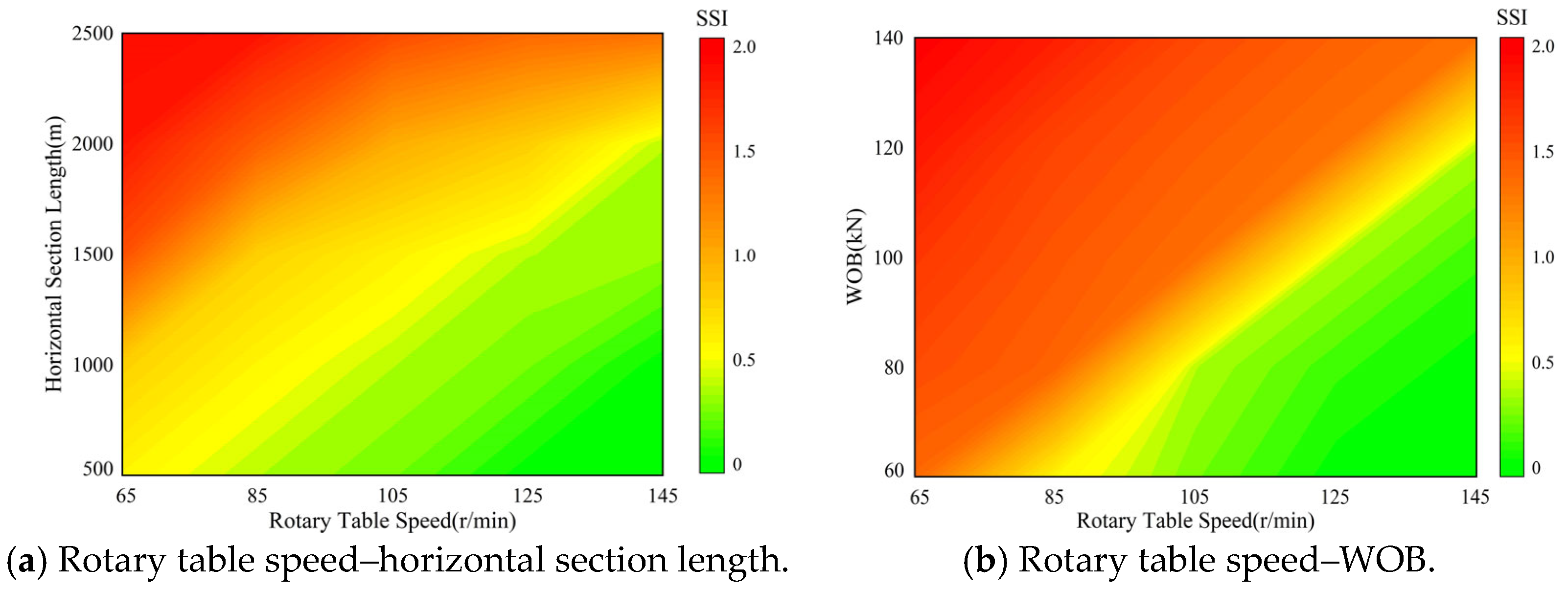
Rotary table speed has a dominant influence on torsional stick–slip. Low rotary speeds lead to long stick durations, large oscillations of bit angular velocity and torque, and a high Stick–Slip Index (SSI), whereas increasing the rotary speed within a suitable range effectively weakens stick–slip. However, excessively high speed may induce severe bit bounce, suggesting that an optimal speed window should be selected rather than simply maximizing speed.

(2)

For the case of horizontal well analyzed in this study, the WOB mainly affects stick–slip through the bit–rock interaction. The simulation results show that when WOB is reduced to about 60 kN, the torsional stick–slip vibration at the bit can be effectively eliminated and the SSI approaches zero, indicating that lowering the WOB is an efficient way to suppress stick–slip in this operating condition. However, such a low WOB also reduces the depth of cut and mechanical rate of penetration, implying that, in field practice, a compromise must be made between stick–slip mitigation and drilling efficiency when selecting the WOB.

(3)

BHA configuration, particularly drill collar and HWDP lengths, significantly affects the distribution of torsional stiffness and inertia along the string. Appropriately increasing the drill collar and HWDP length improves the rigidity of the lower BHA, smooths the bit rotational response, and reduces SSI, whereas unreasonable configurations may intensify torsional transients. By combining the SSI with the proposed model, stick–slip severity maps are constructed for different combinations of rotary speed, WOB, BHA parameters, and horizontal section length, providing a simple and practical tool for parameter and BHA optimization in horizontal wells.

Despite these contributions, the present model still has limitations. It focuses on torsional dynamics and represents the influence of lateral contact through equivalent friction torques, without explicitly modeling tri-axial coupling and whirling. Future work will extend the model toward fully coupled axial–lateral–torsional dynamics with fluid–structure interaction, refine bit–rock and friction models based on laboratory and field tests, and explore integration of the present physics-based model into digital-twin or data-driven frameworks for real-time diagnosis and active control of stick–slip in horizontal wells.