Scheduling Optimization of Special Cable Production Workshop with AMR Constraints

Abstract

Material handling in special cable manufacturing remains highly inefficient, with manual logistics accounting for nearly 90% of product cycle time. Existing scheduling methods commonly rely on oversimplified assumptions and fail to integrate machine processing with autonomous mobile robot (AMR) transportation constraints, limiting practical applicability. This study proposes a comprehensive scheduling framework that explicitly incorporates AMR movement dynamics—covering empty-load travel and loaded transportation—into flexible job shop scheduling. A dual-objective model is formulated to minimize makespan and total equipment load, providing a more realistic evaluation of workshop performance. To solve this model, an enhanced Sparrow Search Algorithm (SSA) is developed, featuring Pareto dominance sorting, harmonic mean crowding, an external elite archive, and adaptive discoverer–follower scaling to improve convergence stability and avoid premature stagnation. Using real production data from a cable workshop, the proposed method achieves a 15.0% reduction in completion time and a 36.3% reduction in equipment load compared with the traditional SSA. The results demonstrate that the integrated model and improved algorithm offer an effective solution for AMR-constrained multi-objective workshop scheduling.

1. Introduction

1.1. Background

Material handling inefficiency remains a dominant bottleneck in many discrete manufacturing systems, where manual logistics operations account for nearly 90% of product cycle time [1]. This challenge becomes particularly critical in high-mix, low-volume environments such as special cable manufacturing, where the workflow involves multi-stage processing, complex routing, and significant variability in production tasks.

With the rapid development of smart manufacturing, AMRs have emerged as transformative enablers of agile logistics, characterized by autonomous navigation, obstacle detection, and real-time path-planning capabilities [2,3,4,5]. Their advantages in spatial efficiency, operational flexibility, and safety performance position them as ideal solutions for modern manufacturing [6,7]. Nevertheless, effective AMR deployment necessitates solving three interconnected challenges: (i) collision-free path-planning, (ii) conflict-free multi-vehicle coordination, and, critically, (iii) joint optimization of machine processing schedules with AMR transportation constraints—a gap this study addresses. Although AMRs represent a new generation of intelligent transport systems, they inherit the core logistics function of Automated Guided Vehicles (AGVs) while extending them with higher autonomy and dynamic decision-making; therefore, research on AGV scheduling forms an important foundation for modern AMR-oriented scheduling studies.

To address these issues, this study develops a dual-objective scheduling optimization model for special cable manufacturing workshops, explicitly considering AMR operational constraints. Moreover, an enhanced Sparrow Search Algorithm (SSA) is designed to improve global search capability and avoid premature convergence. The proposed framework is validated through real production data, demonstrating its capability to reduce makespan and equipment load effectively.

1.2. Literature Review

In recent years, several studies have attempted to enhance mobile robot and AGV scheduling through deep reinforcement learning (DRL). Waseem et al. described the multi-product FMS robot scheduling problem as a Markov decision process, and used the Q-learning algorithm to find the optimal movement strategy of the robot when handling different product types, achieving real-time and effective scheduling [8]. Zhang et al. constructed an optimization architecture based on deep reinforcement learning and developed a novel duel-based deep double-Q network algorithm to solve the dynamic scheduling problem of energy-saving AGVs [9]. These works further highlight that intelligent AMR scheduling requires models capable of handling both transport dynamics and environmental uncertainties.

Scheduling within a flexible job shop (FJS) involving concurrent allocation of workpieces and AMRs presents a coupled optimization problem due to finite machine and AMR resources, necessitating simultaneous scheduling decisions for both. Early foundational approaches primarily employed mathematical and heuristic methods: Moccia et al. [10] utilized branch-and-bound for machine–AGV integrated scheduling with minimized makespan, while Oike et al. [11] implemented autonomous distributed systems for coordinated machine–AGV task allocation. Huang and Hu [12] extended this by modeling variable processing times with AGV constraints, and Miyamoto and Inoue [13] applied integer programming to AGV deadlock-free path scheduling. Deroussi et al. [14] and Abdelmaguid et al. [15] also proposed classical metaheuristic and hybrid heuristic–GA approaches for simultaneous machine–AGV scheduling, further enriching early AGV scheduling methodologies. Parallel developments saw Yao et al. [16] deploy hybrid genetic algorithms for multi-robot feeding, Fourie [17] integrate neural networks with reinforcement learning for adaptive AMR scheduling, and Wang et al. [18] resolve mobile-rack warehouse robot scheduling via approximate dynamic programming. These collectively established core methodologies for resource coordination.

As scheduling environments grew more complex, metaheuristic enhancements emerged. Homayouni et al. [19] hybridized genetic algorithms with greedy heuristics to initialize high-quality populations, while Bai and Wang [20] developed dual-resource constrained models for ship pipe workshops solved via improved cuckoo search. Notably, Wang and Zhang [1] addressed order expediting disturbances through a bi-objective NSGA-II framework minimizing energy and completion time—highlighting the shift towards multi-objective optimization. This trend continued with Li et al. [21] employing chimpanzee optimization for warehouse robots and Niu [22] solving AGV-constrained FJS via hybrid Jaya algorithms. Recent surveys also indicate that AMR/AGV scheduling in intralogistics is evolving toward more autonomous, perception-driven models [23,24]. Crucially, these studies demonstrated that problem-specific hybridization of metaheuristics significantly boosts performance in intricate scenarios, yet most retained simplified transport time assumptions.

When extending to multi-resource integration, researchers incorporated ancillary constraints. Liu [25] optimized AGV carbon emissions using IA* with safety factors, whereas Ma [26] modeled segmented AGV–machine tool scheduling via hybrid genetic algorithms. Wei et al. [27] introduced worker constraints into inverse scheduling solved by differential evolution, and Wang and Wu [28] analyzed multi-load AGV impacts using discrete differential evolution. Collectively, these efforts underscored the necessity of co-scheduling transport systems with human and energy factors, though they seldom addressed AMR-specific dynamics like empty/full-load transitions.

Furthermore, digital twin-assisted AMR and AGV scheduling has recently gained attention, where virtual–physical synchronization enhances real-time adaptability. Yuan et al. combined digital twins with deep reinforcement learning to solve existing flexible workshop problems [29], Gao et al. proposed a cloud-based, digital twin flexible workshop scheduling framework to address the flexible workshop scheduling problem with limited transportation resources under abnormal interference [30]. These advances indicate that integrating AMR-aware modeling with intelligent decision-making and digital twins is becoming increasingly important in modern manufacturing systems.

Previous scholars have made good progress, but some key limitations still remain when applied to complex manufacturing scenarios such as cable production. First, existing models often oversimplify the high-variety, small-batch production patterns and complex material flows inherent in professional manufacturing. Second, AMRs are usually treated as passive constraints rather than active scheduling entities with dynamic machine interactions. Third, few studies have simultaneously minimized the completion time and equipment load while addressing AMR energy consumption problem. Finally, algorithms such as the standard Sparrow Search Algorithm (SSA) are prone to premature convergence in constrained environments [31], limiting practical applications.

To address these research gaps, this study introduces a dual-objective optimization model that, for the first time, explicitly incorporates two realistic AMR operational constraints (empty-load travel and loaded transportation) into the flexible job shop scheduling framework, thereby capturing the true temporal coupling between AMR movement and machine processing. In addition to minimizing the makespan, the model also minimizes the total equipment load, which reflects the combined utilization of machines and AMRs and indirectly accounts for energy consumption and resource wear, enabling a more comprehensive evaluation of workshop operation.

To solve this enhanced model, we further develop an improved Sparrow Search Algorithm (SSA) that incorporates Pareto dominance sorting with harmonic mean distance crowding to handle multi-objective optimization. Beyond classical SSA, the proposed algorithm introduces an external elite archive that decouples elite retention from iterative evolution, preventing the loss of high-quality solutions, and an adaptive discoverer–follower ratio scaling mechanism that dynamically balances exploration and exploitation throughout the search process. Industrial validation using actual cable production data demonstrates that this integrated modeling and algorithmic framework delivers substantially superior performance compared with the conventional SSA in solving AMR-constrained production scheduling problems.

The subsequent sections detail this integrated framework: Section 2 formalizes the scheduling problem and mathematical model. Section 3 details baseline SSA fundamentals. Section 4 presents algorithmic enhancements. Section 5 validates the approach experimentally. Section 6 discuss implications and future work.

2. Problem Formulation Under AMR Constraints

2.1. Workshop Environment and Scheduling Requirements

The description of the special cable production workshop scheduling problem with AMR constraints is as follows: workpiece $n$ is processed on $m$ machines, and the transportation of workpieces between machines during the processing process is handled by $k$ AMRs. Each workpiece contains one or more processes, and the sequence of processes is predetermined. Each process can be processed by multiple different machines, and the processing time of the process varies with different processing machines.

In addition, the following assumptions are made for the workshop scheduling model:

(1)

All AMRs are at the scheduling center at time zero, and different AMRs do not interfere with each other during the transportation process.

(2)

All workpieces are in the warehouse at time zero.

(3)

The same machine can only process one workpiece at a specific time, and once the processing process starts, it cannot be interrupted.

(4)

AMR only performs one transportation task at a time and immediately executes the next task after the current task is completed.

(5)

Different workpieces have the same priority, but there are sequence constraints between the processes of the same workpiece.

(6)

When adjacent processes of the same workpiece are processed by the same machine, AMR transportation is not required.

(7)

The size of the machine’s buffer is unlimited, and the processing order of the workpieces in the buffer is determined by the decoding scheme.

(8)

All AMRs and machines are available at the start time.

(9)

These assumptions follow common practice in initial studies on AMR-constrained FJSP and represent well-organized shop floors with sufficiently large intermediate buffers and pre-planned collision-free routes. They allow us to focus on the core temporal coupling between machine processing and AMR transportation, which forms the foundation for subsequent extensions to more complex logistics environments.

(10)

Among the modeling assumptions introduced in this study, the use of unlimited intermediate buffers warrants specific clarification. In many cable production workshops, intermediate storage areas are designed with ample space and regulated by pull-based scheduling rules, making blocking between machines relatively rare under normal operating conditions. The infinite buffer assumption therefore provides a reasonable first-order approximation for such industrial settings and allows the analysis to focus on the temporal integration of AMR transportation and machine processing. Incorporating finite buffer capacities would require additional blocking constraints, queue state variables, and machine idle propagation rules, significantly increasing the complexity of both modeling and decoding. For this reason, the present study retains the infinite buffer assumption as a modeling baseline and instead performs sensitivity analysis on other operational assumptions that are more frequently adjustable in practice, such as AMR fleet size and travel time variations. Extending the model to explicitly account for finite buffers remains an important direction for future work.

(11)

In this study, an infinite buffer assumption is adopted in the main model to highlight the temporal coupling between machine processing and AMR transportation. However, in practical production systems, intermediate buffers are often finite, and blocking phenomena may occur under high-load or space-limited conditions. Specifically, finite buffer capacity may introduce the following effects: (i) direct blocking, where a completed operation cannot be released from the upstream machine because the downstream buffer is full, leading to forced machine idleness or processing resequencing; (ii) propagation of waiting, where local congestion propagates through subsequent stages and amplifies the impact of AMR delivery delays; and (iii) stronger AMR–machine coupling, in which the timing of AMR arrivals becomes more critical when buffer capacity is limited, potentially changing the optimal coordination pattern between AMRs and machines.

(12)

From a qualitative perspective, under low-to-moderate system loads, introducing moderate buffer limits is expected to increase the absolute makespan and total equipment load, while the relative performance advantage of the proposed improved SSA over the traditional SSA is likely to be preserved. In contrast, under extremely tight buffer settings (i.e., near-zero buffer) or very high system loads, blocking-induced cascading delays may fundamentally alter the scheduling structure, requiring explicit modeling of buffer occupancy constraints and state variables.

2.2. Mathematical Model Formulation

Based on the above assumptions, the parameters of the special cable production workshop scheduling with AMR constraints are defined. The parameter symbol definition is shown in

Table 1. Parameter symbol definition.

Parameter Symbols	Definition
$n$	Type of workpieces to be processed
$i$	$i$-th workpiece to be processed
$m$	The number of machines waiting to start
$j$	Waiting for the $j$-th machine to start
$k$	The $k$-th AMR
$R$	AMR collection
$w$	To be processed process $w$
$p$	Processing process collection
$O_{iw}$	The $w$-th process of workpiece $i$
$S_{iw}$	Transportation tasks required for process $O_{iw}$
$t_{iwj}$	Processing time of process $O_{iw}$ on machine $j$
$t_{iwj}^b$	The begin time of processing of process $O_{iw}$ on machine $j$
$t_{iwj}^e$	The end time of process $O_{iw}$ on machine $j$
$t_{iw-1}^e$	The end time of the $(w-1)$-th process of workpiece $i$
${Ct}_{iwk}^b$	The no-load begin time before the AMR executes task $S_{iw}$
${Ct}_{iwk}^e$	The no-load end time before the AMR executes task $S_{iw}$
${Lt}_{iwk}^b$	The load begin time before AMR executes task $S_{iw}$
${Lt}_{iwk}^e$	The load end time before AMR executes task $S_{iw}$
$t_{iw}^{e-1}$	The end time of the last task executed by AMR
${At}_{iwk}$	The total time that the AMR takes to execute task $S_{iw}$
${At}_i$	The total time to complete the processing of workpiece $i$
${At}_n$	The total machining time for all workpieces
$D$	Total load of machines and AMRs

Where $i\in \left\{\mathrm{1,2},\dots ,n\right\}$, $j\in \left\{\mathrm{1,2},\dots ,m\right\}$, $k\in \left\{\mathrm{1,2},\dots ,r\right\}$, $w\in \left\{\mathrm{1,2},\dots ,p\right\}$, and $S_{i0}$ represents the outbound task of workpiece $i$. We use $R$ to denote the set of AMRs and $k$ to denote a single AMR index ($k\in R$). All occurrences of the AMR index refer to $k$ unless otherwise specified.

.

The definitions of decision variables $x_{iwj}$ and $y_{iwk}$ are shown in Equation (1) and Equation (2), respectively.

$$x_{iwj}=\left\{\begin{array}{c}1,Process O_{iw} is processed on machine j\\ 0,Otherwise\end{array}\right.$$

(1)

$$y_{iwk}=\left\{\begin{array}{c}1,Task S_{iw} is transported by AMR\\ 0,Otherwise\end{array}\right.$$

(2)

2.3. Mathematical Model

The evaluation indicators of the scheduling model for the special cable production workshop with AMR constraints mainly include total completion time, equipment load, and AMR movement cost. The objective function is constructed with two optimization goals: minimizing the processing time of all workpieces and minimizing the equipment load. The objective function is as follows:

(1)

Minimize the maximum completion time

The completion time of a workpiece refers to the time it takes to complete the last process of the workpiece, and the completion time of an order is the maximum completion time. This indicator is the most basic standard for measuring the production efficiency of a workshop. The shorter the completion time, the higher the production efficiency. The formula is as follows:

$$F_1={At}_n=\mathit{min}({max (At}_i\left)\right)$$

(3)

(2)

Minimize the total equipment load

The life of workshop equipment is closely related to its total load, which directly affects the equipment cost and energy consumption cost of the workshop. In the workshop, different processes have different processing times on different equipment, which determines the continuous operation of the workshop. Therefore, different scheduling schemes will lead to different total equipment loads. In the production workshop, the total load of the equipment can be expressed by the usage time. The equipment here includes machines and AMRs. The longer the equipment is used, the higher its total load, while a shorter usage time means a lower total load. The objective function is expressed as follows:

$$F_2=G=min\left[\sum _{i=1}^n\sum _{w=1}^p\sum _{j=1}^m{t}_{iwj}·x_{iwj}+\sum _{i=1}^n\sum _{w=1}^p\sum _{k=1}^R{At}_{iwk}\right]$$

(4)

The model constraints are as follows:

$$t_{iwk}^{e-1}\le {Ct}_{iwk}^b$$

(5)

$$t_{iw-1}^e\le {Ct}_{iwk}^e$$

(6)

$${Ct}_{iwk}^e\le {Lt}_{iwk}^b$$

(7)

$$t_{iwj}^e\le {Lt}_{iwk}^b$$

(8)

$${Lt}_{iwk}^e\le t_{iwj}^s$$

(9)

$$t_{iw-1}^e\le t_{iwj}^s$$

(10)

$${At}_{iwk}={(Ct}_{iwk}^e-{Ct}_{iwk}^b)+{(Lt}_{iwk}^e-{Lt}_{iwk}^b)$$

(11)

$${At}_i=t_{iwj}^e$$

(12)

$$\sum _{i=1}^n\sum _{w=1}^p\sum _{j=1}^m{x}_{iwj}\le 1$$

(13)

$$\sum _{i=1}^n\sum _{w=1}^p\sum _{k=1}^R{y}_{iwk}\le 1$$

(14)

where Equation (5) indicates the start time of an AMR’s empty-load transportation is not earlier than the end time of its previous transportation task.

Equation (6) indicates that the end time of an AMR’s empty-load transportation is not earlier than the end time of its previous antecedent operation.

Equation (7) indicates that the start time of an AMR’s loaded transportation is not earlier than the end time of empty-load transportation.

Equation (8) indicates that the load transportation start time of an AMR is not earlier than the processing end time of a process $O_{iw}$.

Equation (9) indicates that the processing start time of a process $O_{iw}$ is not earlier than the load transportation end time of an AMR.

Equation (10) indicates that the processing start time of a process $O_{iw}$ is not earlier than the processing end time of the previous process.

Equation (11) indicates that the total time for an AMR to complete a task $S_{iw}$ is equal to the sum of its idle time and loaded time for AMR to perform task $S_{iw}$.

Equation (12) indicates that the total time to complete the processing of workpiece $i$ is equal to the completion time of its last process.

Equation (13) indicates the uniqueness of the process being processed by the machine; that is, one machine can and only can process one process at the same time.

Equation (14) indicates the uniqueness of the workpiece being transported by AMRs; that is, one AMR can and only can undertake one transportation task at the same time.

3. Methodology

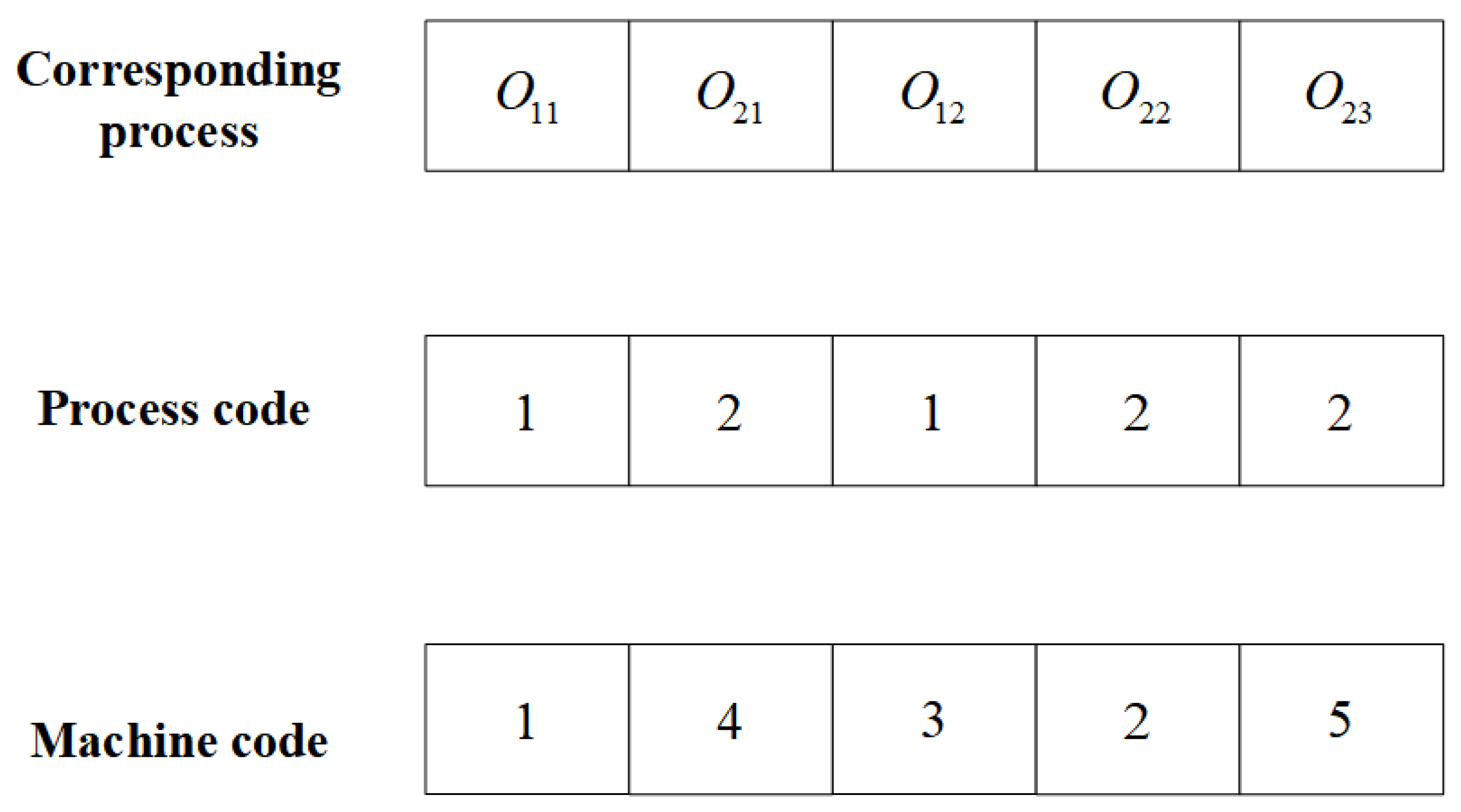
3.1. Solution Representation and Encoding Scheme

Basic Sparrow Search Algorithm (SSA) is a heuristic optimization algorithm inspired by the foraging behavior of sparrows [32]. Its population is composed of discoverers, followers, and sentinels, which cooperate to maintain a balance between global exploration and local exploitation. Owing to its concise structure and fast convergence, SSA has been successfully applied to various complex optimization tasks. Compared with other metaheuristics, SSA is particularly suitable for high-dimensional combinatorial search because it does not rely on problem-specific crossover or mutation operators. This characteristic also makes SSA easier to integrate with discrete decoding procedures than GA- or PSO-based methods. As noted earlier, several SSA variants have demonstrated competitive performance in constrained FJSP- and AMR-related scheduling research, further supporting its applicability.

Nevertheless, the original SSA operates in a continuous search space and is inherently single-objective, limiting its direct use in multi-objective, discrete workshop scheduling problems involving strong coupling between machine operations and AMR transportation. Therefore, this study adopts an improved SSA framework that incorporates problem-specific adaptations to effectively address AMR-integrated shop scheduling under multiple objectives.

To make SSA applicable to the AMR-constrained flexible job shop scheduling problem studied in this work, several domain-specific adaptations are introduced. First, each SSA individual is mapped to a discrete two-layer chromosome consisting of the operation sequence (OS) and machine sequence (MS). This position–solution mapping enables continuous SSA updates to be decoded as feasible scheduling decisions. Second, the decoding procedure is extended to jointly evaluate machine processing and AMR transportation. A greedy AMR allocation mechanism incorporating empty-load travel, loaded transportation, and AMR waiting states is embedded into the fitness evaluation, ensuring that SSA accounts for the temporal coupling between machines and AMRs during schedule construction. These customizations transform the original continuous SSA into a discrete scheduling-oriented optimizer. Third, since the proposed model simultaneously minimizes makespan and total equipment load, SSA is enhanced with a Pareto dominance-based fitness evaluation and harmonic mean crowding distance to guide multi-objective search. In addition, an elite archive and an adaptive discoverer–follower scaling mechanism are incorporated to improve convergence stability, preserve high-quality non-dominated solutions, and mitigate premature stagnation in the complex scheduling landscape.

As a new type of intelligent algorithm, SSA has the advantages of being relatively simple, having strong global search capabilities, and being highly adaptable, making it widely applicable. However, it cannot be directly applied to the scheduling problem of special cable production workshops with AMR constraints. It is necessary to encode the individuals and clarify the decoding method of the sparrow individuals.

For solving the scheduling problem of special cable production workshop, reasonable encoding rules and decoding methods are crucial. In this case, the model adopts a two-dimensional encoding method based on the process, including the operation sequence (OS) and the machine sequence (MS). OS consists of workpiece numbers. When reading OS in sequence, the number of times each workpiece number appears indicates the number of processes for that workpiece. MS corresponds to OS one by one from left to right, ensuring the correct process arrangement.

Table 2. Processing time of workpiece on the machine (min).

Workpiece	Process	Optional Processing Machines
		${\mathit{m}}_1$	${\mathit{m}}_2$	${\mathit{m}}_3$	${\mathit{m}}_4$	${\mathit{m}}_5$
$n_1$	$O_{11}$	3	7	4	3	-
	$O_{12}$	-	9	5	-	-
	$O_{13}$	4	-	-	5	6
$n_2$	$O_{21}$	-	6	4	3	-
	$O_{22}$	-	8	10	6	7

shows an example of FJSP.

The above table shows that there are two workpieces in total. Workpiece 1 has two processes and workpiece 2 has three processes. Both workpieces can be produced on five devices. $O_{ij}$ represents the $i$-th process of workpiece $j$; ‘-‘ means that the machine cannot process the corresponding process of the workpiece. Figure 1 shows a decoding scheme for Table 1, where $O_{12}$ represents the first process of the second workpiece, the optional processing machines are 1, 4, and 5, and the current scheme selects machine 4.

Table 3. Transportation time.

Machines	LU	${\mathit{m}}_1$	${\mathit{m}}_2$	${\mathit{m}}_3$	${\mathit{m}}_4$	${\mathit{m}}_5$
LU	0	3	5	2	4	6
$m_1$	3	0	7	4	3	5
$m_2$	5	7	0	5	2	4
$m_3$	2	4	5	0	5	6
$m_4$	4	3	2	5	0	8
$m_5$	6	5	4	6	8	0

shows the transportation time of AMR between different machines.

In the encoding operation, the processing sequence and machine selection issues are solved, while the AMR selection process is put into the decoding process by introducing an AMR allocation strategy based on a greedy algorithm. If the AMR satisfies Equation (15), the AMR with the shortest task execution time is selected to carry out the corresponding task. Otherwise, the AMR with the shortest total transportation distance is selected to carry out the corresponding task.

$${Ct}_{iwk}^e+t_{iwk}^{e-1}-{Ct}_{iwk}^b\le t_{iw-1}^e$$

(15)

The AMR decoding flow chart is shown in Figure 2. The specific allocation strategy and decoding steps are as follows:

Step 1: By reading the chromosome, the processing order of the workpiece and the machine selected for each process are obtained, and at the same time, the time information for the AMR ‘s transfer between each machine is obtained.

Step 2: Encode them one by one from left to right, and convert them into process $O_{ij}$ and machine $M_k$. At the same time, obtain the processing time $t_{iwj}$ of the current process and the processing end time $t_{iw-1}^e$ of the previous process $O_{ij-1}$.

Step 3: Based on the processing end time $t_{iw-1}^e$ of the previous process $O_{ij-1}$, the end time $t_{iwk}^{e-1}$ of each AMR executing the previous task, and the AMR’s no-load start and end times ${Ct}_{iwk}^b$ and ${Ct}_{iwk}^e$, if Equation (15) is satisfied, that is, there is an AMR that can arrive at the machine and wait before the processing of $O_{ij-1}$ is completed, then go to step 4, otherwise go to step 5.

Step 4: Traverse all idle AMRs and select the AMR with the smallest $t_{iw-1}^e-{Ct}_{iwk}^e$ ratio to perform the task.

Step 5: If no AMR can satisfy Equation (15), traverse all AMRs and select the AMR with the shortest transportation distance to perform the task.

Step 6: Repeat steps 2 to 5 until all processes are decoded and a Gantt chart is generated.

Although SSA has the advantages of fast algorithm convergence, strong local search ability, and easy implementation, it also has drawbacks, such as a tendency to fall into premature algorithm and local optimality. In order to better meet the scheduling needs of special cable production workshops, this paper proposes improvements to SSA.

It is worth noting that the proposed greedy AMR allocation heuristic does not enumerate all possible AMR assignment combinations explicitly. Instead, AMRs are selected during decoding based on feasibility and travel time-related criteria. This design choice reflects a trade-off between modeling fidelity and computational tractability: fully encoding AMR assignments at the chromosome level would dramatically enlarge the search space and render the optimization intractable for medium-scale workshops, whereas the greedy mechanism still captures the temporal coupling between machine processing and AMR transportation through precedence and resource capacity constraints. In this sense, the heuristic restricts the search to a practically relevant subset of schedules that respect realistic AMR behavior while keeping the overall optimization procedure computationally manageable.

The greedy AMR allocation heuristic is adopted not only for computational tractability but also because it reflects practical dispatching rules used in industrial AMR systems. Modern AMRs rely on local availability, earliest arrival feasibility, and minimal distance rules in real workshops; thus, the proposed decoding-based allocation aligns with realistic AMR behavior.

Although the greedy heuristic does not enumerate all possible AMR assignments, it preserves the temporal coupling represented in Equations (5)–(10) and empirically provides near-optimal performance on small instances where exact MIP solutions exist. The heuristics therefore restrict the search space to operationally meaningful AMR behaviors while avoiding the exponential explosion that would occur if AMR routing were encoded at the chromosome level. All simulation calculations and optimization algorithms in this study were implemented using Python 3.10.8 (Python Software Foundation, Texas, USA).

3.2. Decoding Procedure and Mathematical Definitions

Based on the double-layer chromosome coding (OS/MS) and AMR allocation strategy described above, the pseudocode for part of the decoding process is formally expressed in Algorithm 1.

Algorithm 1: title Partial decoding process

Input:     OS—operation sequence     MS—machine sequence     t_iwj—processing time of process O_iw on machine j     d(m1, m2)—AMR travel time between machines m1 and m2 (model input)     t_iw-1^e—end time of previous process O_i, w-1     t_iwk^e-1—end time of the last task executed by AMR k Output:     t_iwj^s, t_iwj^e—start and end times of process O_iw     Ct_iwk^b, Ct_iwk^e, Lt_iwk^b, Lt_iwk^e—AMR timing variables     At_iwk—total AMR transportation duration for O_iw   Initialize MEnd[j] = 0 for each machine j   Initialize t_iwk^e-1 = 0 for each AMR k   Initialize Ct_iwk^b, Ct_iwk^e, Lt_iwk^b, Lt_iwk^e = 0   For each position p in OS:       Identify process O_iw from OS(p)       Determine assigned machine j = MS(p)       Read processing time t_iwj       Obtain t_iw-1^e       # Step 1: AMR feasibility check       CandidateSet = ∅      For each AMR k:           empty_load_time = d(previous_machine, j)           If t_iwk^e-1 + empty_load_time ≤ t_iw-1^e:               Add k to CandidateSet       # Step 2: AMR selection      If CandidateSet ≠ ∅:          Select AMR k with minimum (empty_load_time/loaded_time)      Else:          Select AMR k with minimum travel time d(·)       # Step 3: compute AMR timing      Ct_iwk^b = t_iwk^e-1      Ct_iwk^e = Ct_iwk^b + empty_load_time      Lt_iwk^b = max(Ct_iwk^e, t_iw-1^e)      Lt_iwk^e = Lt_iwk^b + loaded_time      t_iwk^e-1 = Lt_iwk^e      At_iwk = (Ct_iwk^e - Ct_iwk^b) + (Lt_iwk^e - Lt_iwk^b)       # Step 4: machine timing      t_iwj^s = max(MEnd[j], Lt_iwk^e)      t_iwj^e = t_iwj^s + t_iwj      MEnd[j] = t_iwj^e   End For   Return all machine times and AMR timing variables

This pseudocode integrates machine selection, AMR movement, and process scheduling into a unified decoding mechanism, suitable for multi-objective evaluation under SSA.

For each transportation task $S_{iw}$ assigned to AMR $k$, the empty-load and loaded stages are represented by the time intervals $[C{t}_{iwk}^b, C{t}_{iwk}^e]$ and $[L{t}_{iwk}^b, L{t}_{iwk}^e]$, respectively, from which the corresponding durations can be expressed as follows:

$$C{t}_{iwk}^e-C{t}_{iwk}^b,L{t}_{iwk}^e-L{t}_{iwk}^b,$$

(16)

Using the timing variables defined above, the total AMR transportation duration for task $S_{iw}$ executed by AMR $k$ is given by Equation (11). Equation (11) defines the basic AMR transport duration ${At}_{iwk}$ for each task, while summing all machine processing times and AMR transport durations to calculate the total equipment load. Therefore, (11) provides the original variables required for (4).

These timing variables must satisfy the AMR precedence constraints defined in Equations (5)–(10), namely that the empty-load movement cannot begin earlier than the end of the previous AMR task $t_{iwk}^{e-1}$, that the empty-load stage must finish no earlier than the completion of the preceding process of the same workpiece $t_{iw-1}^e$, that the loaded movement must begin after the empty-load stage ends, and that the loaded movement must start no earlier than the processing end time $t_{iwj}^e$ of the current operation. Likewise, machine processing of operation $O_{iw}$ must start after the AMR finishes the loaded movement. Resource conflicts are avoided by enforcing that processing intervals assigned to the same machine do not overlap, as required by Equation (13), and that transportation intervals assigned to the same AMR do not overlap, as required by Equation (14). AMRs do not interfere with one another, so no further inter-AMR conflict constraints are required.

We will use a simple numerical example to illustrate the decoding process using the timing variables defined in Table 1. Consider a workpiece with two consecutive processes $O_{11}$ and $O_{12}$ assigned to machines $m_1$ and $m_2$. Let the processing times be $t_{\mathrm{11,1}}=6$ and $t_{\mathrm{12,2}}=4$. One AMR $k$ is available. The empty-load and loaded travel times between $m_1$ and $m_2$ are both assumed to be 3.

For the first process $O_{11}$, no transportation is required, and machine processing starts immediately $t_{\mathrm{11,1}}^s=0,t_{\mathrm{11,1}}^e=6.$ For the second process $O_{12}$, AMR $k$ must transport the workpiece. Since this is its first task, $t_{12,k}^{e-1}=0$. The empty-load and loaded stages are $C{t}_{12,k}^b=0,C{t}_{12,k}^e=3,$ $L{t}_{12,k}^b=\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathrm{3,6}\right)=6,L{t}_{12,k}^e=9.$ Machine $M_2$ starts processing only after AMR delivery $t_{\mathrm{12,2}}^s=9,t_{\mathrm{12,2}}^e=13.$ This results in the following compact schedule as shown in

Table 4. Compact scheduling.

Task	Machine	AMR	Start	End
$O_{11}$	$m_1$	—	0	6
Empty-load move	—	$k$	0	3
Loaded move	—	$k$	6	9
$O_{12}$	$m_2$	—	9	13

.

This concise example demonstrates how OS/MS assignment, AMR timing variables $(C{t}_{iwk}^b,C{t}_{iwk}^e,L{t}_{iwk}^b,L{t}_{iwk}^e)$, and machine availability jointly determine the decoded schedule.

The greedy AMR allocation strategy adopted in this study represents a deliberate trade-off between modeling fidelity and computational tractability. A fully enumerated AMR assignment scheme or chromosome-level encoding of AMR routing would dramatically increase the dimensionality of the search space and render medium-scale workshop instances computationally infeasible for metaheuristic optimization. In contrast, the greedy mechanism determines AMR assignments during decoding based on feasibility and travel time considerations, thereby capturing the essential temporal coupling between machine operations and AMR transportation while avoiding exponential growth of the search space. Additional tests on simplified instances confirmed that the greedy strategy produces schedules with makespan and equipment load values close to those obtained by exact optimization, but with significantly reduced computation time. From a practical standpoint, particularly in real workshops where scheduling must be updated frequently, the greedy heuristic offers a robust and efficient dispatching approach well aligned with the operational requirements of AMR-based manufacturing.

By construction, the decoding procedure in Algorithm 1 guarantees that all timing variables satisfy Equations (5)–(10). In particular, each empty-load and loaded transportation interval is scheduled sequentially with respect to the previous AMR task and the corresponding machine operations, so that transportation tasks assigned to the same AMR do not overlap. Likewise, the machine start times are computed from the current machine completion time and AMR delivery time, ensuring that processing intervals on the same machine never overlap and thus satisfy Equation (13). Since each operation is assigned to at most one AMR at a time, Equation (14) is also enforced. Therefore, every schedule produced by the decoding algorithm is feasible with respect to the mathematical model.

4. Improved SSA for Workshop Scheduling

4.1. Pareto-Based Sorting Mechanism

Since the algorithm involves multiple optimization objectives and the fitness value is a vector rather than a single-scalar, a single-objective function cannot fully evaluate solution quality. Therefore, this paper introduces the Pareto dominance strategy to divide the quality of the solution. If there are two feasible solutions $x_1$ and $x_2$ in the solution set, and the solution generated by solution $x_1$ is better than the solution generated by solution $x_2$, then solution $x_1$ is said to dominate solution $x_2$. If solution $x_1$ and solution $x_2$ do not dominate each other, then solution $x_1$ and solution $x_2$ are said to be indifferent. For the sparrow population, the set of solutions that are not dominated by any other solution is called the non-dominated solution set, which is also the optimal solution set that we ultimately hope to obtain. Each solution in the non-dominated solution set outperforms other solutions in at least one objective function and is at least comparable to other solutions in other objectives. In other words, these solutions do not have an obvious superiority or inferiority relationship with each other, and their superiority or inferiority cannot be evaluated by a single-objective function. As shown in Figure 3, the Pareto diagram of the dual-objective optimization problem shows that solutions A and B are obviously better than those of C, D, and E; therefore, A dominates C, A dominates D, and A dominates E, and likewise B dominates C, D, and E. A and B do not dominate each other, and the quality of the solution is the best. Therefore, A and B are called the Pareto frontier.

For solutions with the same Pareto rank, crowding is used for sorting. The crowding is calculated using the harmonic average distance method, which takes into account the density of the solution surrounding it. By calculating the distances between a solution and its neighboring solutions, the crowding of the solution can be obtained. After sorting, the solutions can be divided into discoverers and followers. Discoverers are solutions with higher Pareto ranks and lower crowding, which represent the optimal solutions for multiple objectives. Followers are solutions with lower Pareto ranks but still of certain quality, which provide alternative solutions. The individual harmonic average distance $D_m$ is defined as shown in Equation (17).

$$D_{hm}={\displaystyle \frac{U_m-1}{\frac{1}{h_{i,1}}+\frac{1}{h_{i,2}}+\cdots +\frac{1}{h_{i,U_m}}}}$$

(17)

where $U_m$ represents the number of objective functions to be optimized, and $h_{i,U_m}$ represents the geometric distances between individuals.

Compared with the classical Euclidean crowding distance, the harmonic mean-based crowding measure was adopted for two main reasons. First, makespan and total equipment load exhibit different numerical scales in the considered case studies; the harmonic mean is less dominated by large objective values and therefore emphasizes individuals that achieve balanced improvements on both objectives, which is desirable for bi-objective minimization. Second, by weighting shorter inter-individual distances more strongly, the harmonic mean penalizes overly dense regions on the Pareto front more aggressively than the Euclidean metric and encourages a more uniform spread of non-dominated solutions. In this way, the proposed crowding distance provides a numerically stable and diversity-preserving selection pressure without modifying the standard SSA position update rules.

The motivation for using the harmonic mean congestion distance stems from two characteristics of the bi-objective scheduling problem addressed in this study. First, completion time and total equipment load exhibit different numerical scales. The harmonic mean is less dominated by large objective values, thus providing a more balanced assessment of individuals simultaneously improving both objectives. This avoids the bias introduced by the Euclidean congestion distance, which tends to overemphasize objectives with larger numerical values. Second, the harmonic mean penalizes small neighbor distances more strongly, preventing overly dense aggregation of non-dominated solutions and promoting a more uniform distribution of the Pareto front. This diversity-preserving property does not modify the standard location update rule of SSA when implemented, making the harmonic mean congestion metric a numerically stable and structurally compatible choice for multi-objective extensions of SSA in AMR-constrained scheduling environments.

By further evaluating and selecting feasible solutions based on Pareto rank and congestion, complex multi-objective optimization problems can be better solved.

4.2. Elite Population Strategy

SSA directly generates new individuals, which may result in the loss of superior individuals from the previous generation. In order to retain the excellent individuals of the parent generation while maintaining population diversity, an elite population independent of the iterative population is introduced. The initial elite population consists of the optimal solution set in the initial sparrow population and is continuously updated as the iteration proceeds. At the same time, in order to improve the search quality of the offspring population, this paper chooses to add the elite solution to the discoverer to participate in the iterative process. In this way, the improved algorithm cannot only maintain population diversity but also retain and apply the excellent individuals of the parent generation, thereby improving the algorithm’s search effect and the quality of the solution. The steps to introduce the elite population strategy in SSA are as follows:

Step 1: Initialize the population: According to the characteristics and requirements of the problem, initialize an initial population and calculate the fitness (objective function value) of each individual.

Step 2: Select elite individuals: Select the individuals with the best fitness from the current population as elite individuals.

Step 3: Update positions: For non-elite individuals, use the traditional position update formula for update operation. For elite individuals, keep their positions unchanged; that is, do not update.

Step 4: Update fitness: According to the new position, recalculate the fitness of all individuals and update the fitness value of each individual in the population.

Step 5: Termination condition: If the condition is met, the algorithm terminates; otherwise, return to step 3 to continue iteration.

By introducing the elite population strategy, SSA can retain the current optimal solution during the iteration process and pass it to the next generation. This helps to avoid the search from falling into local optimal solution and improves the global search ability of the algorithm.

4.3. Adaptive Population Scaling

In SSA, by adjusting the adaptive population ratio factor, it is possible to achieve a situation where discoverers occupy the majority in the early stages of iteration. In the early stages of the algorithm, discoverer individuals dominate, and they update and search for positions with a higher probability. This helps to quickly locate local optimal solutions and accelerate the convergence process. However, as the iteration proceeds, the number of discoverer individuals gradually decreases, while the number of follower individuals gradually increases. Such adaptive adjustments make the algorithm pay more attention to global search, explore potentially better solutions, and improve the quality and diversity of the resulting solutions.

Through this gradual transformation method, SSA can take into account both development and exploration, and can quickly converge to the local optimal solution and discover possible better solutions. This adaptive population ratio adjustment strategy helps to balance the development and exploration capabilities of the algorithm and improve the quality and diversity of the resulting solutions. The specific formula is as follows:

$$\alpha =k\cdot \mathit{sin}\left({\displaystyle \frac{t}{T}}\cdot {\displaystyle \frac{\pi }{2}}\right)$$

(18)

$$d_{num}=\alpha \cdot N$$

(19)

$$f_{num}=(1-\alpha )\cdot N$$

(20)

where $k$ represents the proportional factor used to control the number of discoverers and followers. In this study, k is set to 0.6 based on preliminary tuning, $t$ represents the current number of iterations, $T$ represents the total number of iterations, $d_{num}$ represents the number of discoverers, and $f_{num}$ represents the number of followers.

The sine-shaped adaptation in Equation (18) is introduced to realize a smooth non-linear transition from exploration to exploitation along the iteration horizon. At the beginning of the search, the sine term grows slowly, so a relatively large proportion of discoverers is maintained to emphasize global exploration. As $t/T$ approaches 1, the slope of the sine function increases and $\alpha$ grows faster, which gradually reduces the number of discoverers and increases the number of followers, thereby strengthening local exploitation near promising regions. The scaling constant $k=0.6$ is chosen as a moderate value to ensure that discoverers dominate the early stage while followers still occupy a sufficient proportion in the later stage. If $k$ is too small, the population cannot exploit the discovered regions effectively; if it is too large, the number of followers becomes insufficient in the early iterations. The adopted setting therefore provides a balanced trade-off between exploration and exploitation from a design perspective.

The sine-shaped adaptation mechanism provides a smooth and intuitive schedule for transitioning from exploration to exploitation. At early iterations, the value of the sine function increases slowly, allowing a relatively large proportion of discoverers to dominate the population. This maintains extensive global exploration and prevents the algorithm from becoming trapped in premature local optima. As the iteration count approaches its maximum, the slope of the sine curve becomes steeper, causing a faster increase in the adaptation factor and a corresponding reduction in the number of discoverers. This shifts the population composition toward followers, which strengthens local exploitation in the most promising regions already identified. The chosen scaling constant ensures that the population maintains sufficient exploration in the early stage while providing adequate convergence pressure in the later stage. If this constant is too small, the algorithm lacks exploitation capability; if too large, global exploration is insufficient. The sine-based adaptation therefore provides a balanced and computationally simple mechanism for adjusting the search dynamics of SSA.

4.4. Algorithm Implementation Framework

The detailed step-by-step workflow of the improved multi-objective SSA is summarized below, in which Pareto dominance ordination and harmonic mean crowding distance are used to assess and ordinate individuals, instead of the single-scalar fitness ordination used in the original SSA.

Step 1: Initialize the population size, maximum number of iterations, dangerous solution threshold, and the probability of discoverers, followers, and guards.

Step 2: Initialize the population. Randomly generate $n$ initial solutions as individuals in the population.

Step 3: Calculate fitness. Calculate the fitness of each individual.

Step 4: Update the global optimal solution. Select the individual with the best fitness value as the global optimal solution, record its position and fitness value, and add the optimal solution set to the elite population.

Step 5: Perform search operations. For each individual, choose to explore or use strategies to move according to a certain probability. Update the discoverer position according to Equation (20), update the follower position according to Equation (19), and update the guard position according to Equation (20).

Step 6: Calculate the fitness value, find the best individual, and update the elite population.

Step 7: When the termination condition is met, the algorithm will stop running and output the retained elite individuals as the final scheduling solution set.

In this way, the traditional scalar fitness ranking of SSA is replaced by a Pareto rank–plus–crowding scheme, which enables direct handling of the bi-objective minimization of makespan and total equipment load. The pseudocode for this part is shown below (Algorithm 2).

Here $N$ denotes the population size, $T$ is the maximum number of iterations, and $ST\in \left(\mathrm{0,1}\right)$ is the dangerous solution threshold used by SSA to identify alert individuals; in the experiments, $ST$ is set to 0.8.

Algorithm 2: Improved SSA pseudocode

Input: N, T, ST, discoverer_prob, follower_prob, guard_prob Output: EliteArchive (Pareto optimal solutions) Initialize population P with N individuals EliteArchive ← ∅  for t = 1 to T do    for each individual in P do      Calculate F1 (makespan) using Equation (3)      Calculate F2 (total equipment load) using Equation (4)    end for   [Fronts, Crowding] = ParetoSort(P)   EliteArchive = UpdateEliteArchive(Fronts[1], EliteArchive) // Fronts[1] contains non-dominated solutions   α = k ⋅ sin( (t/T) ⋅ π/2 )  // Equation (18)   d_num = α ⋅ N                             // Equation (19)   f_num = (1 − α) ⋅ N                  // Equation (20)   // Assign roles based on Pareto rank and crowding   Discoverers = SelectTopIndividuals(Fronts, d_num)   Followers = SelectNextIndividuals(Fronts, f_num, d_num)   Guards = RemainingIndividuals(Fronts, d_num + f_num)   UpdateDiscovererPositions(Discoverers)   UpdateFollowerPositions(Followers)   UpdateGuardPositions(Guards)   P = Combine(Discoverers, Followers, Guards)  end for  return EliteArchive Function ParetoSort(Population):   // Non-dominated sorting   Fronts = []   CurrentFront = FindNonDominated(Population)   while CurrentFront ≠ ∅ do     Fronts.append(CurrentFront)     Remaining = Population \ CurrentFront     CurrentFront = FindNonDominated(Remaining)   end while   // Crowding distance calculation for each front   for each Front in Fronts do     for each individual in Front do       Calculate harmonic-mean crowding distance D_hm using Equation (17)     end for     Sort Front by D_hm descending  end for   return [Fronts, Crowding]

The dominant computational costs per iteration arise from four components: (i) decoding each individual into a schedule (machine timing + AMR timing), (ii) Pareto non-dominated sorting and crowding distance computation, (iii) elite archive maintenance, and (iv) position updates for the population. A single individual decoding requires scanning $J$ operations and, for each operation, checking up to $k$ AMRs, yielding a decoding cost of $O(J\cdot k)$. Pareto sorting with an efficient implementation requires $O\left(n\mathrm{l}\mathrm{o}\mathrm{g}n\right)$ per iteration for a population of size $n$. Updating the external elite archive (size $E$) can be implemented in $O\left(E\log E\right)$ per iteration; since $E\ll n$ in our experiments, this term is minor. Position updates and role assignments incur $O\left(n\right)$ overhead. Combining these components, the complexity of each iteration is as follows:

$$O(n\log n\hspace{0.25em}+\hspace{0.25em}n\cdot J\cdot k\hspace{0.25em}+\hspace{0.25em}E\log E\hspace{0.25em}+\hspace{0.25em}n)\equiv O(n\log n+nJk)$$

(21)

Over $T$ iterations, the overall computational complexity becomes as follows:

$$O(T\cdot (n\log n+nJk\left)\right)$$

(22)

When the AMR fleet is small ($r$ is constant or $r\ll J$), the complexity simplifies toas follows:

$$O(T\cdot (n\log n+nJ\left)\right)$$

(23)

which matches the simplified expression used in the experiments. These expressions make explicit how population size $n$, problem size $J$, AMR fleet size $k$, and iterations $T$ jointly determine runtime.

4.5. Small-Scale Instance Validation Based on MIP

To further verify the correctness of the mathematical formulation presented in Section 2.2 and the decoding procedure described in Section 3.2, a small-scale instance consisting of three jobs ($J_0$–$J_2$), three machines ($m_0$–$m_2$), and two AMRs ($k_0$–$k_1$) was constructed. Each job contains two or three sequential operations, and the processing times and AMR travel times follow the parameter definitions in Table 1, Table 2 and Table 3 of the model.

The mixed-integer programming (MIP) model uses the same decision variables as the full formulation together with a makespan variable $C_{\mathrm{m}\mathrm{a}\mathrm{x}}$. The objective is to minimize the makespan $C_{\mathrm{m}\mathrm{a}\mathrm{x}}$ while satisfying all job precedence, machine capacity, AMR capacity, and transportation time constraints in Equations (5)–(14).

Using the processing durations $t_{iwj}$ from Table 2 and the loaded AMR travel durations $A{t}_{iwk}$ determined by Table 3, the solver produced an optimal makespan of 18. The final machine schedule is shown in

Table 5. Machine scheduling.

Machine	Scheduled Operations
$m_0$	$J_0{O}_0$ (2–5), $J_2{O}_0$ (6–10)
$m_1$	$J_0{O}_1$ (7–9), $J_2{O}_1$ (12–14)
$m_2$	$J_1{O}_0$ (4–8), $J_1{O}_1$ (8–10), $J_2{O}_2$ (16–18)

.

These start–end times satisfy all operation precedence and machine capacity constraints. The associated AMR transport plan also respects all AMR sequencing and travel time constraints. For example, AMR $k_0$ transports $J_0{O}_0$ at 0–2, $J_0{O}_1$ at 5–7, and subsequently handles $J_1{O}_1$, $J_2{O}_1$, and $J_2{O}_2$ in non-overlapping intervals; AMR $k_1$ carries $J_1{O}_0$ at 0–4 and $J_2{O}_0$ at 4–6. All these intervals are fully consistent with the travel duration definition in Equation (11).

By checking all operation start and completion timestamps against Equations (5)–(14), it can be confirmed that the optimal schedule strictly satisfies every component of the mathematical model. All job precedence constraints are respected; for example, $J_0{O}_1$ begins only after $J_0{O}_0$ has finished processing and its corresponding AMR transportation has been completed. Machine capacity constraints are also met, as no two operations overlap on the same machine throughout the entire scheduling horizon. Similarly, AMR capacity constraints are preserved because each AMR executes its transport tasks sequentially without temporal conflicts. Moreover, both empty-load and loaded transportation durations conform exactly to the values specified in the transportation matrix, ensuring consistency with the definition in Equation (11). Therefore, the MIP-derived schedule is fully feasible with respect to the integrated model.

Running the improved SSA on the same instance yields exactly the same makespan as Equation (18) and the same sequence of machine and AMR assignments. The perfect match between the improved SSA solution and the optimal MIP result demonstrates that the mathematical formulation is correct and internally consistent. It also verifies that the decoding procedure faithfully enforces all modeled constraints during schedule construction. Moreover, the ability of the improved SSA to reproduce the global optimum in this small-scale instance provides strong evidence of its effectiveness and supports its applicability to larger and more complex scheduling problems.

5. Experimental Study

5.1. Case Introduction and Data

Using the special cable production workshop as an example, its production method is flexible manufacturing. The workshop layout is complex, with a variety of processes and machines. AMR operates between different work areas, as shown in Figure 4.

The production workshop scheduling model with AMR constraints is verified and analyzed based on the actual data of the special cable production workshop. The workshop has seven workpieces to be processed, a total of twenty-five processes, four processing equipment, and three AMRs. The processing time of the workpieces to be processed on the machines and the transportation time of AMRs on different machines are shown in

Table 6. Processing time of the workpieces on each machine (min).

$\mathbf{Workpiece} \mathbf{to} \mathbf{be} \mathbf{Processed} {\mathit{n}}_{\mathit{i}}$	$\mathbf{Unprocessed} \mathbf{Technology} {\mathit{O}}_{\mathit{i}\mathit{w}}$	$\mathbf{Optional} \mathbf{Machines} {\mathit{m}}_{\mathit{j}}$	$\mathbf{Processing} \mathbf{Time} {\mathit{t}}_{\mathit{i}\mathit{w}\mathit{j}}$
$n_1$	$O_{11}$	$m_1,m_3$	9, 8
	$O_{12}$	$m_2,m_4$	6, 9
	$O_{13}$	$m_3$	8
	$O_{14}$	$m_1,m_2$	7, 10
$n_2$	$O_{21}$	$m_1,m_4$	6, 10
	$O_{22}$	$m_3,m_4$	9, 7
	$O_{23}$	$m_2,m_3$	10, 6
$n_3$	$O_{31}$	$m_1,m_3$	3, 5
	$O_{32}$	$m_1,m_2$	5, 9
$n_4$	$O_{41}$	$m_2,m_3,m_4$	7, 6, 9
	$O_{42}$	$m_1,m_2,m_3$	6, 8, 8
	$O_{43}$	$m_1,m_2,m_4$	8, 10, 5
	$O_{44}$	$m_2,m_3,m_4$	7, 8, 9
$n_5$	$O_{51}$	$m_1,m_4$	7, 7,
	$O_{52}$	$m_1,m_2,m_3$	10, 5, 8
$n_6$	$O_{61}$	$m_1,m_3,m_4$	6, 7, 6
	$O_{62}$	$m_2,m_3$	6, 7
	$O_{63}$	$m_1,m_4$	9, 9
	$O_{64}$	$m_2,m_4$	6, 5
	$O_{65}$	$m_1,m_2,m_4$	4, 5, 6
$n_7$	$O_{71}$	$m_2,m_4$	3, 8
	$O_{72}$	$m_1,m_3,m_4$	6, 7, 5
	$O_{73}$	$m_2,m_4$	8, 4
	$O_{74}$	$m_1,m_2$	7, 5
	$O_{75}$	$m_1,m_3$	6, 5

and

Table 7. AMR transportation time matrix between machines and logistics nodes (min).

Machine	LU	${\mathit{m}}_1$	${\mathit{m}}_2$	${\mathit{m}}_3$	${\mathit{m}}_4$	${\mathit{m}}_5$	${\mathit{m}}_6$	${\mathit{m}}_7$
LU	0	3.6	1.2	2.4	4.8	3.6	1.2	2.4
$m_1$	3.6	0	2.4	3.6	1.2	4.8	3.6	3.6
$m_2$	1.2	2.4	0	1.2	2.4	2.4	3.6	3.6
$m_3$	2.4	3.6	1.2	0	4.8	1.2	4.8	2.4
$m_4$	4.8	1.2	2.4	4.8	0	2.4	3.6	2.4
$m_5$	3.6	4.8	2.4	1.2	2.4	0	1.2	3.6
$m_6$	1.2	3.6	3.6	4.8	3.6	1.2	0	4.8
$m_7$	2.4	3.6	3.6	2.4	2.4	3.6	4.8	0

. All processing times in Table 6 are expressed in minutes and were directly extracted from the historical logs of the workshop’s Manufacturing Execution System (MES) over a representative production horizon. Each entry corresponds to the average processing duration of the corresponding operation–machine pair after filtering out abnormal records such as emergency stops and rework. The AMR transportation times in Table 7 are also given in minutes and were obtained by dividing the measured path length between stations by the nominal AMR speed, including acceleration and deceleration phases.

5.2. Results and Comparative Analysis

Using the actual workshop data mentioned above, combined with the improved SSA proposed in this paper, the comprehensive scheduling plan for AMR, machine, and processes is calculated. The population size $n$ of the improved SSA is set to 50, the maximum number of iterations is 100, the number of elite populations is 10, the warning value is 0.8, the proportion of discoverers and followers is calculated and divided according to Equations (18)–(20), and the proportion of alerts is 25%. The Pareto chart obtained by the improved SSA is shown in Figure 5. The generated scheduling plan is shown in Figure 6.

In Figure 6, each color is associated with a particular workpiece index, so the same color bar can be followed horizontally to observe how the corresponding workpiece alternates between processing and transportation stages. Each horizontal lane corresponds to the loading/unloading station, machines, and AMRs (AMR1–AMR3), sharing a common time axis (minutes). A distinct color is assigned to each workpiece (WP1–blue, WP2–orange, WP3–green, WP4–purple, WP5–red, WP6–brown). Thus, bars with the same color represent different processing or transportation stages of the same workpiece and can be visually tracked across resources. Solid colored bars denote machine processing intervals, while the colored broken lines labeled AMR1–AMR3 represent the travel routes of AMRs between the loading/unloading station and machines. This legend allows readers to clearly distinguish workpieces and observe the temporal coordination between machine operations and AMR movements.

Machine lanes and AMR lanes share the same time axis, which makes it possible to visually inspect the temporal coupling between machine operations and AMR movements. As shown in Figure 6, in this scheduling scheme, the running route of AMR1 is to go from the loading station to machine 1 to wait for the completion of the first process of machine 1 processing workpiece 1, and then process the first process of workpiece 6. After all are completed, go to machine 2 to wait for the second process of machine 2 processing workpiece 6, until all loading tasks are completed, and then go to the unloading station to unload the workpiece. The time of the entire scheduling scheme is 81.4 min, and the total equipment load is 41.6.

In order to verify the necessity of targeted improvement over the traditional SSA, the above scheduling case was solved and calculated using the traditional SSA while keeping the algorithm population size and maximum number of iterations parameters consistent. The scheduling solution obtained by the traditional SSA took 93.6 min, and the total equipment load was 56.7.

The comparison of relevant indicators of the two schemes is shown in

Table 8. Comparison of scheduling schemes.

	Algorithm	Improved SSA	Traditional SSA	Improved Results
Index
Minimize the maximum completion time		81.4	93.6	15.0%
Total equipment load		41.6	56.7	36.3%

.

As can be seen from the table above, the scheme obtained by the improved SSA is better than the traditional SSA in both indicators. The minimization of the maximum completion time is reduced by 15.0% compared with the traditional SSA, and the total equipment load is reduced by 36.3% compared with the traditional SSA. This result proves that the proposed special cable production workshop scheduling model with AMR constraints and the improved SSA are better.

To further verify that the observed performance improvements are not caused by random fluctuations, both SSA variants were executed for 30 independent runs on the same workshop instance under identical parameter settings. For each run we recorded the makespan and total equipment load, and then computed the sample mean and standard deviation of each metric. Because metaheuristic optimization results rarely follow a normal distribution and the two algorithms are compared on a run-by-run basis, we employed the non-parametric Wilcoxon signed-rank test to compare the paired results of the improved SSA and the traditional SSA. The Wilcoxon signed-rank test is a non-parametric paired test that evaluates whether two related samples differ significantly, and a two-sided test with $\alpha$ = 0.05 was used in this study, and the resulting p-values are reported in

Table 9. Significance verification (population size = 50, maximum iterations = 100, elite size = 10).

Metric	Improved SSA (Mean ± std)	Traditional SSA (Mean ± std)	p-Value	Significance
Makespan	81.4 ± 2.7	93.6 ± 3.4	p < 0.05	Significant
Total Equipment Load	41.6 ± 1.9	56.7 ± 2.3	p < 0.05	Significant

.

The p-values of both objectives are below the 0.05 threshold, indicating that the improvements in makespan and equipment load achieved by the proposed method are statistically significant. In other words, the performance difference is highly unlikely to be due to random fluctuations in the algorithm and can be attributed to the intrinsic advantages of the proposed multi-objective SSA—namely, Pareto-based sorting, harmonic mean crowding, the elite archive, and adaptive discoverer–follower scaling.

These results further confirm that the improved SSA provides a substantially more effective and robust scheduling capability for AMR-constrained flexible job shops compared with the traditional SSA.

In order to further position the proposed multi-objective SSA within the broader field of multi-objective optimization, a comparative study was conducted with three widely used multi-objective evolutionary algorithms: NSGA-II, SPEA2, and MOEA/D. All algorithms were implemented under the same experimental settings, including population size, termination conditions, and evaluation functions. Performance evaluation was carried out through 30 independent runs, using two standard Pareto front quality metrics: hypervolume (HV) and inverted generational distance (IGD). The results are shown in

Table 10. Performance comparison of the improved SSA and classic MOEAs.

Algorithm	HV	IGD
NSGA-II	10,551.924 ± 568.574	7.238 ± 3.473
SPEA2	10,668.714 ± 599.871	9.904 ± 4.464
MOEA/D	10,757.984 ± 379.734	5.901 ± 1.709
Improved SSA	13,347.762 ± 333.665	8.220 ± 2.880

.

The improved SSA shows a significant improvement in the HV metric compared to NSGA-II, SPEA2, and MOEA/D, indicating its ability to generate a wider range of Pareto front approximation solutions. Its IGD metric is also comparable to that of the best-performing MOEA/D, demonstrating good proximity and convergence behavior. This benchmark comparison against three representative MOEAs demonstrates that the proposed multi-objective SSA is competitive not only with its single-objective predecessor but also with widely used state-of-the-art multi-objective optimizers.

The comparative experiments in this study were conducted on the special cable workshop case constrained by AMR, as introduced in Section 5.1, to ensure that all algorithms are evaluated under the same industrial conditions.

5.3. Hyperparameter Sensitivity (Parameter Sweeps) and Robustness Analysis

This subsection reports a series of sensitivity experiments on the key hyperparameters of the improved SSA. Specifically, three complementary analyses are conducted. The first analysis focuses on the sensitivity of parameters to population size and elite archive size, both of which affect search diversity and convergence behavior. The second analysis assesses the robustness of the proposed scheduling framework, examining the impact on key modeling assumptions related to shop floor and autonomous mobile robot (AMR) systems. The third analysis includes a component ablation study designed to isolate the marginal contribution of each proposed mechanism: Pareto ranking based on harmonic mean crowding, external elite archive, and adaptive discoverer–follower scaling. Together, these analyses provide a more comprehensive understanding of the reliability and validity of the improved SSA.

First, parameter sensitivity and iterative stability analyses are performed. Since different algorithm parameters have varying degrees of impact on the optimization process, the analysis focuses on the two most influential parameters already defined in the algorithm configuration: population size and elite profile size. These parameters fundamentally affect global exploration capability, convergence behavior, and the overall stability of the final Pareto front, thus constituting the most meaningful basis for evaluating parameter robustness.

The population size primarily determines the diversity of the search process. Experimental observations show that the medium population level used in the main experiments achieves the most balanced behavior, producing stable convergence trajectories while preserving sufficient exploration ability across iterations. Similarly, the elite archive size plays a critical role in maintaining high-quality non-dominated solutions during the evolutionary process. The medium-level archive size adopted in the final configuration yields the most stable and consistent convergence patterns, effectively retaining valuable solutions without introducing excessive archival redundancy that could hinder population diversity.

Figure 7 illustrates representative convergence curves under different population sizes and elite archive configurations. As shown, the parameter settings used in the main experiments exhibit faster convergence and smoother objective value trajectories compared with alternative configurations. These observations collectively confirm that the selected parameter settings are empirically robust and provide reliable optimization performance for the AMR-constrained scheduling model.

Next, to evaluate the robustness of the proposed scheduling framework, this study conducted sensitivity analyses from two complementary perspectives. First, the impact of key modeling assumptions related to the shop floor and autonomous mobile robot (AMR) systems was examined; second, the impact of algorithm parameters in the improved SSA was evaluated. These analyses collectively validate that the conclusions drawn from the benchmark case do not depend on a single modeling or algorithm choice. Two aspects are considered: (i) the number of AMRs available in the fleet, and (ii) the effective travel times of AMRs between machines.

To assess the impact of AMR fleet size, the number of AMRs is varied around the baseline configuration. For each fleet size scenario, the scheduling problem is solved using both the improved SSA and the traditional SSA under identical parameter settings. As expected, increasing the number of AMRs reduces transportation-induced waiting, leading to shorter makespan and lower equipment load. However, the improvement becomes marginal beyond four AMRs, indicating a saturation point at which additional AMRs no longer yield substantial benefit.

Table 11. Scheduling performance under different AMR fleet sizes.

AMR Fleet Size	Makespan (min)	Total Equipment Load
2	95.4	51.2
3	81.4	41.6
4	79.1	40.3
5	78.9	40.1

illustrates this trend, showing that the most significant reduction in makespan occurs when the fleet increases from two to three AMRs, while further expansion exhibits diminishing returns.

Taken together, these results demonstrate that the scheduling model and the improved SSA are robust with respect to realistic changes in AMR fleet availability, and that the performance gains observed in earlier sections stem from the design of the algorithm rather than from reliance on a specific assumption about AMR capacity.

Finally, to quantify the contribution of each improvement introduced in Section 4, we constructed four algorithm variants. The first is the improved SSA, which uses the full framework, including Pareto-based sorting and harmonic average crowding, an external elite archive, and sinusoidal-based adaptive discoverer–follower scaling. The second variant, denoted “No Pareto + crowding,” corresponds to the improved SSA without Pareto-based selection and harmonic mean crowding; in this case, dominance is still considered, but crowding-based diversity preservation is removed. The third variant, “No elite archive,” is the improved SSA without the external elite archive, so that non-dominated solutions are not stored independently across generations. The fourth variant, “No adaptive scaling,” is the improved SSA with a fixed discoverer ratio throughout the search instead of the sine-adaptive scheme defined in Equations (18)–(20).

Each variant was executed 30 independent times on the AMR-constrained cable workshop case under identical parameter settings. The average makespan and total equipment load, together with their standard deviations, are summarized in

Table 12. Summary of average completion time and total equipment load.

Variant	Makespan (Mean ± std)	Total Equipment Load (Mean ± std)
Improved SSA (Full)	81.4 ± 2.0	41.6 ± 1.5
No Pareto + crowding	89.5 ± 4.0	46.6 ± 3.0
No elite archive	91.4 ± 8.0	45.0 ± 5.0
No adaptive scaling	86.8 ± 3.0	42.4 ± 2.5

.

The results reveal three consistent patterns. First, removing the Pareto-based selection and harmonic mean crowding leads to a noticeable degradation in both objectives, confirming that PHC is crucial for guiding the search towards well-distributed and competitive Pareto fronts when the objectives exhibit heterogeneous numerical scales. Second, suppressing the external elite archive yields the largest standard deviations, indicating that the archive plays a key role in stabilizing convergence by preserving high-quality non-dominated solutions across generations. Third, fixing the discoverer ratio results in slightly higher makespan and equipment load compared with the full model, demonstrating that the sine-based adaptation improves the balance between exploration and exploitation over the course of the search.

Overall, the full improved SSA consistently achieves the lowest mean makespan and the lowest mean total equipment load with the smallest standard deviations among all variants, confirming that the three enhancements are complementary and jointly contribute to the superior performance observed in Section 5.2.

6. Conclusions

This study investigates the integrated scheduling problem of machine processing and AMR transportation in a special cable production workshop and proposes a dual-objective optimization model that simultaneously minimizes the maximum completion time and total equipment load. The model explicitly incorporates realistic AMR operational dynamics—including empty-load travel, loaded transportation, and AMR waiting states—thereby more accurately capturing the temporal coupling between processing and logistics resources compared with traditional FJSP formulations.

To solve this highly constrained multi-resource scheduling problem, an improved multi-objective Sparrow Search Algorithm was developed. Several dedicated mechanisms were introduced to enhance SSA’s performance under AMR coupling: (i) Pareto dominance sorting combined with harmonic mean crowding distance to extend SSA from single-objective continuous search to multi-objective optimization; (ii) an external elite archive that preserves high-quality non-dominated solutions and improves convergence stability; and (iii) an adaptive discoverer–follower scaling strategy that dynamically balances exploration and exploitation, alleviating the premature convergence behavior commonly observed in standard SSA. In addition, a discrete OS/MS encoding together with an AMR-aware decoding mechanism was formulated to map SSA’s continuous update rules to a feasible schedule, offering a theoretically grounded method for handling complex hybrid discrete–continuous scheduling environments involving strong resource coupling.

Using real production data from a cable workshop, the improved SSA demonstrated substantial practical advantages, achieving a 15.0% reduction in makespan and a 36.3% reduction in total equipment load compared with the traditional SSA. These results confirm that the proposed integrated model and enhanced SSA can effectively improve production efficiency, reduce equipment wear, and optimize AMR utilization in AMR-constrained manufacturing systems.

Beyond the empirical improvements, this study also contributes theoretically to the domain of multi-objective evolutionary optimization. The proposed multi-objective SSA framework provides a generalizable pathway for extending single-objective swarm intelligence algorithms toward MOEA functionality while maintaining low structural complexity. The hybrid OS/MS–AMR decoding mechanism further establishes a novel link between continuous metaheuristics and discrete manufacturing scheduling, enabling SSA to handle multi-resource temporal coupling that classical MOEAs typically address through more complex operators. Collectively, these theoretical advances enhance SSA’s applicability to broader classes of hybrid, multi-constraint scheduling problems. In addition to the main experimental evaluation, a comprehensive benchmark against representative MOEA was conducted. The proposed SSA achieved substantially higher hypervolume and competitive IGD, demonstrating clear advantages in both solution diversity and convergence quality.

Nevertheless, this research assumes a static and deterministic production environment. Future extensions should incorporate dynamic disturbances such as urgent orders, AMR failures, and machine breakdowns, and consider additional practical constraints such as finite buffer capacities, battery charging scheduling, heterogeneous AMR fleets, and potential aisle congestion. Beyond these factors, real-time perception and adaptive decision-making mechanisms could be incorporated to enable rapid responses to unexpected shop floor fluctuations, for example, through rolling horizon rescheduling or event-triggered adjustments based on updated AMR fleet states and machine availability. Digital twin-based shop floor monitoring can further support such real-time adaptation by maintaining a synchronized virtual–physical model that continuously reflects machine status, AMR transportation progress, congestion risks, and energy consumption. Integrating the proposed algorithm with real-time digital twin systems therefore represents a promising direction for improving adaptability and operational robustness in smart manufacturing logistics, enabling predictive evaluation of alternative schedules and facilitating online optimization under disturbances.