Modeling of Medical Waste Generation in Dental Clinics Affiliated to the Provincial Health Directorate in Kastamonu: PLS and Gradient Boosting Approaches

Abstract

Effective medical waste planning relies on the reliable estimation of waste volumes. As operational factors diversify, traditional linear regressions often fail to capture the underlying structure, whereas latent variable–based and ensemble approaches can better represent this complexity. In this study, fine-tuned Partial Least Squares (PLS), scikit-learn–based Gradient Boosting regression (GBR), and a baseline Ordinary Least Squares (OLS) model were compared for estimating medical waste generation using 48 months (2021–2024) of approximate data from Dental Clinics affiliated with the Provincial Health Directorate in Kastamonu. The model inputs were the monthly procedure counts for endodontics, treatment, prosthetics, periodontology, orthodontics, pedodontics, and surgery. Performance was evaluated using Root Mean Square Error (RMSE), Mean Absolute Error (MAE) and R-squared (R²). All models produced accurate predictions; however, PLS provided the strongest fit (R² = 0.979; MAE = 30.488; RMSE = 37.043), outperforming GBR (R² = 0.962; MAE = 36.544; RMSE = 48.990) and the OLS baseline (R² = 0.927; MAE = 41.762; RMSE = 59.013). The findings demonstrate that modern, data-driven waste-management planning is feasible in healthcare institutions and highlight PLS as a robust option, particularly under conditions of small sample size and collinearity.

1. Introduction

Medical waste generated in healthcare services is a critical source not only for hospital staff but also for public and environmental health due to factors such as infection risk, toxicity, and chemical and biological hazards. Failure to properly separate, transport, or dispose of waste can lead to global health problems such as water, air, and soil pollution, increased risk of hospital-acquired outbreaks, and antibiotic resistance. These risks and waste volumes are particularly pronounced in healthcare units where single-use materials are commonly used, such as dental clinics. From a cost perspective, waste disposal, sterilization, transportation, and regulatory compliance expenses place a significant burden on hospital budgets. Incorrectly estimated waste quantities can lead to either allocating excessive resources and increasing costs or creating environmentally and health-risky situations due to capacity shortages.

There are numerous studies in the literature on estimating medical waste production, but most of them focus on projecting annual waste quantities at the level of general hospitals or cities. For example, in the study titled “Prediction of medical waste generation using SVR, GM (1,1) and ARIMA models” conducted in Istanbul, data from 1995 to 2017 were used to estimate Istanbul’s annual medical waste production for the 2018–2023 period. The ARIMA (0,1,2) model was found to be superior to other models in terms of both RMSE and R². The same study also evaluated Support Vector Regression (SVR), Grey Model, and linear regression, but these models were found to be weaker than the ARIMA model in capturing nonlinear fluctuations and trends [1]. Altın et al. (2023) predicted medical waste production at a private hospital in Antalya using kernel-based SVM and deep learning methods; this study is noteworthy as a step down from the city level to the clinic/procedure level [2]. The study, titled “Simulation Design of Dental Practice Medical Waste Management Using Dynamic System Model Approach” was conducted in the city of Pekanbaru, analyzed the amount of medical waste generated from dental clinics using dynamic system simulation; the effects on environmental costs and waste volumes were determined through waste reduction scenarios (education, cooperation, etc.) [3]. Systematic reviews offering a broader perspective are also available; Mitsika and Chanioti (2024) reviewed studies on dental solid waste, highlighting issues such as the lack of methodological standards and differences in measurement units and classification methods [4]. Furthermore, the study “Medical waste management in a mid-populated Turkish city and development of medical waste prediction model,” conducted in a medium-sized Turkish city, focused on estimating waste production rates in hospitals using regression analysis and developed models that will provide forecasts for regional planning [5].

Since ARIMA is one of the key forecasting approaches commonly used in medical waste studies, a brief methodological explanation is provided below to clarify its structure and relevance. Autoregressive Integrated Moving Average (ARIMA) models constitute one of the most widely used time-series forecasting techniques in environmental and healthcare waste research. An ARIMA (p,d,q) structure incorporates three components: an autoregressive term (AR), which models the dependence of the current value on its past observations; an integration term (I), which applies differencing to achieve stationarity; and a moving-average term (MA), which captures the dependence on past forecast errors. This flexible combination enables ARIMA models to capture trends, short-term fluctuations and serial correlations in monthly waste data [6,7]. Previous applications in Türkiye—for instance the ARIMA (0,1,2) model used for Istanbul’s medical-waste forecasting—have shown that ARIMA can outperform several machine-learning approaches when long historical series and clear temporal patterns are present [1]. However, ARIMA models are limited in their ability to incorporate multiple operational predictors (e.g., procedure types), which is why regression-based or latent-variable approaches may provide additional explanatory value in clinic-level analyses such as the present study.

Although traditional linear regression models are widely used in healthcare waste analyses, the following limitations of these models are frequently observed: high correlation between variables (multicollinearity), the absence of variable interactions and nonlinear relationships in the model, non-constant variance of error terms (heteroscedasticity), and the inability to model seasonal or operational imbalances. For example, in the Istanbul study, the linear regression model performed worse than time series models such as ARIMA in capturing trends [1]. In dynamic system simulation (Pekanbaru study), it was found that operational changes and policy interventions significantly affected the model output, and therefore, methods that include nonlinearity and interactions between variables were more appropriate [3]. This literature indicates a growing need for nonlinear methods, latent variables, and model flexibility in medical waste prediction models.

Accurate short-term forecasting of healthcare waste enables concrete operational decisions: right-sizing container capacity, scheduling on-site storage and off-site transport, procurement planning and documentation for regulatory compliance. Global guidance underscores that suboptimal segregation and overflow elevate occupational exposure and environmental risk; predictive planning, therefore, reduces both cost and risk by matching capacity to expected loads. Dental settings deserve specific attention because their waste streams may include hazardous fractions (e.g., sharps, chemical residues, legacy amalgam) with distinct handling requirements [8]. Recent applications show that data-driven and machine-learning approaches can materially improve waste forecasts relative to ad hoc or purely descriptive methods, supporting facility-level planning [9,10].

The aim of this study is to compare Partial Least Squares (PLS) and scikit-learn-based Gradient Boosting regression models for estimating medical waste production using data on the number of procedures performed at dental clinics affiliated with the Provincial Health Directorate in Kastamonu. This clinic environment, where single-use materials are commonly used and waste is classified as domestic and medical, allows for the examination of the effect of dental procedure types on waste production at the procedure level. Performance criteria such as MAE, RMSE, and R² used in the analyses enable the simultaneous evaluation of both the margin of error and the power of fit of the models. Comparisons of PLS and Gradient Boosting using procedure types specific to dental hospitals are quite limited in the literature; therefore, this research provides a unique and up-to-date contribution to the field. Furthermore, the increase in single-use equipment brought about by the COVID-19 period has increased uncertainties in waste volume, and this study includes data obtained during such a period, further enhancing its timeliness.

In this context, while current studies primarily provide waste estimation at the hospital/city level using SVM/DL, penalized regressions, or voting ensembles, applications directly comparing tree-based ensembles with PLS at the procedure level in dental clinics are limited. This study fills the gap by comparing PLS–GBR–OLS using 48 months of clinic-procedure data and provides reliable short-term predictions for operational decision support.

2. Materials and Methods

2.1. Dataset

This study was conducted in dental clinics affiliated with the Provincial Health Directorate in Kastamonu. The hospital primarily provides outpatient services and regularly accepts patients in all basic dental medicine branches, including endodontics, periodontology, orthodontics, pedodontics, prosthetic treatment, conservative treatment, and surgical procedures. The choice of study area was influenced by the widespread use of disposable materials in dental clinics and the resulting high variability in medical waste quantities. Furthermore, it is believed that findings obtained from private healthcare institutions in densely populated areas such as city centers will contribute to medical waste management planning at both the local and national levels.

Kastamonu is a provincial city located in the Western Black Sea Region of Türkiye, characterized by a continental climate and an elevation of approximately 900 m. The province has a population of about 389,000, with nearly 126,000 residents living in the central district. Health services in the city are supported by a developing medical infrastructure that includes the Kastamonu Training and Research Hospital—affiliated with Kastamonu University—along with a Physical Therapy and Rehabilitation Center, a dedicated Oral and Dental Health Center and multiple family health units. The physician-to-population ratio, approximately one doctor per 874 residents, suggests moderate healthcare coverage compared with other regions. Overall, Kastamonu represents a mid-sized regional center with growing healthcare capacity, supported by ongoing investments in public health and university–hospital integration [11].

According to the World Health Organization’s guide for the safe management of waste from healthcare services, chemical/radioactive (hazardous healthcare waste), handling equipment, solvents and drugs, which are considered medical waste, are not included in this study because they are not used in these dental hospitals. Materials that come into contact with blood, such as gloves, glassware, metals and body (biometrics), etc., were included in the study [8,12].

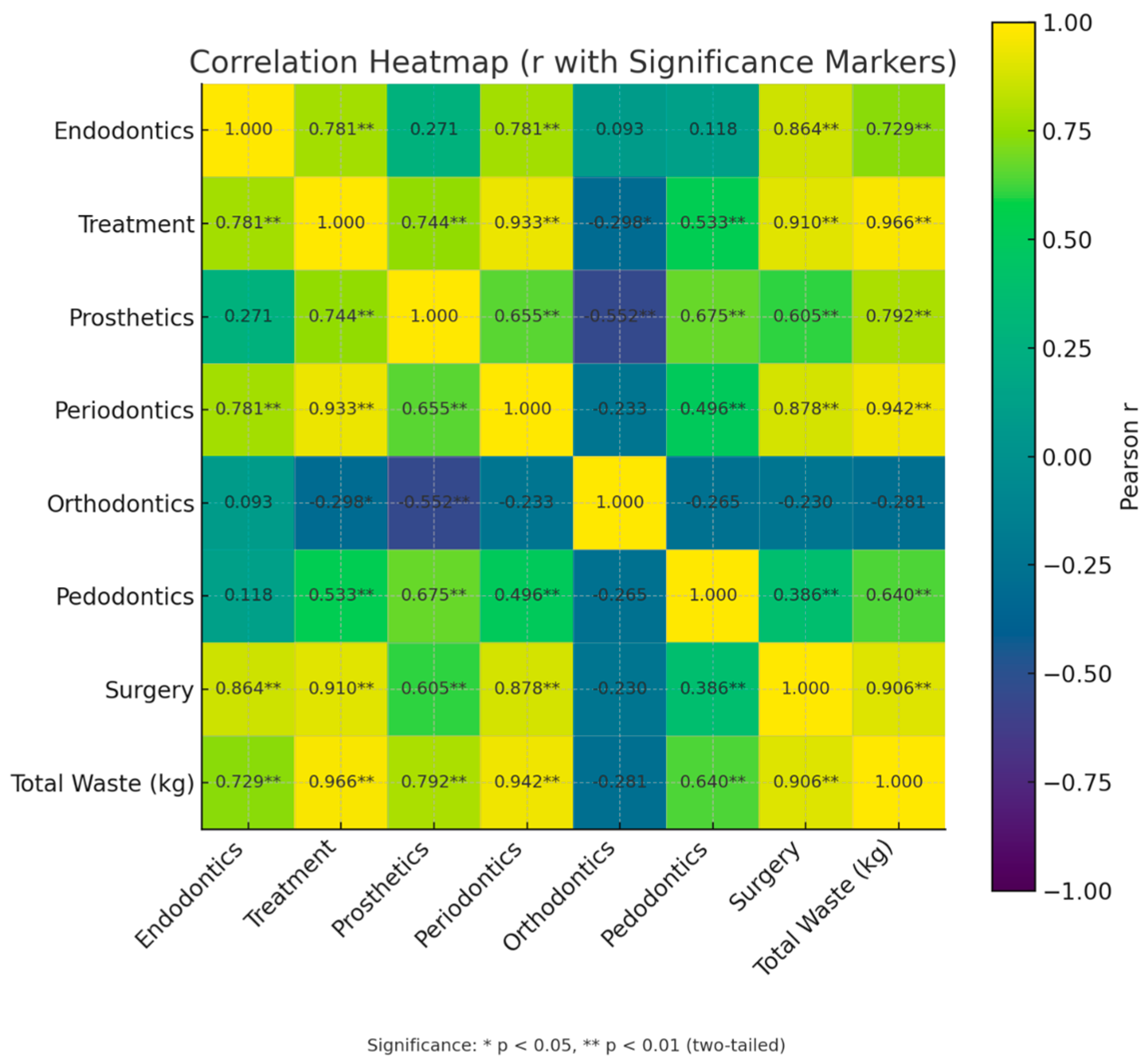
The dataset was approximately values created by matching the hospital’s transaction records with medical waste measurements collected by an authorized company in coordination with the municipality. The dependent variable in the study is the amount of medical waste produced monthly at the hospital (kg). Waste was classified as domestic and medical, and only the medical waste amounts were included in the model. The independent variables were separated according to the types of procedures performed at the hospital: endodontics, treatment, prosthetics, periodontology, orthodontics, pedodontics, and surgical procedures. These procedure data were obtained from the hospital information management systems.

The data collection period covers the 48-month period from January 2021 to December 2024. During this period, a regular time series consisting of 48 observations was obtained. The data are complete, and all variables have been recorded as continuous quantitative values. In the data preprocessing stage, measurement units were standardized, and variables were normalized to improve model fit prior to analysis.

Special COVID-19 management measures in Kastamonu (e.g., lockdowns, clinic restrictions) were implemented until August 2022, after which most restrictions were lifted and standard clinic operations resumed [13,14].

This comprehensive four-year dataset provides a strong foundation for demonstrating the impact of dental clinic-specific procedures on medical waste generation. However, as the results are specific to the dental hospitals studied, generalizability is limited to similar clinical settings.

2.2. Methods

In this study, considering the high correlation among independent variables and the presence of nonlinear interactions, both Partial Least Squares (PLS) regression, a classical latent variable approach model, and Gradient Boosting Regression (GBR), a robust ensemble-based method, were preferred for estimating the amount of medical waste.

Partial Least Squares (PLS) regression is an effective method, particularly when there are a large number of variables and high multicollinearity among these variables. PLS transforms the information in the independent variable (X) matrix into latent components, ensuring that these components are selected in a way that maximizes both the variance among the variables in X and the covariance with the dependent variable (Y). This feature of PLS, defined by Wold, alleviates the unstable coefficient estimates and high variance problems that arise in classical multiple linear regression (MLR) due to multicollinearity [15]. The use of PLS in studies involving multiple observations in health or environmental fields has been shown to increase the model’s generalization power and support interpretability. For example, the study titled “An adjusted partial least squares regression framework” demonstrated that PLS provides an appropriate modeling framework for data with multicollinear structures and high-dimensional mixtures [16].

The parameters used for PLS in this study are as follows: 2 components, an iteration limit of 500, and normalization of data by “scaling” (scale features and target). These settings were chosen to prevent the model from having an excessive number of latent components and to prevent overfitting.

Gradient Boosting Regression (GBR) is a powerful ensemble method in which weak learners, such as decision trees, are trained sequentially to reduce errors by focusing on the residuals of the previous model. Each new tree attempts to improve upon the errors of the previous stage; model flexibility and generalization ability are balanced through the appropriate selection of hyperparameters such as learning rate, number of trees, and max depth [17]. Especially in prediction problems arising from health or environmental processes, the nonlinear effects of GBRT, interactions between variables, and its ability to better handle noisy datasets have been frequently highlighted in the literature. For example, in a study published by Shehab et al. in 2024, the GBRT + optimization algorithm was used together with municipal solid waste to improve the model’s RMSE, MAE, and R² values [18].

The parameter settings specified for GBR in this study are as follows: 100 trees (number of trees = 100), learning rate = 0.10, maximum tree depth = 3, minimum number of samples during subsetting = 2, and use of the entire training data (fraction of training instances = 1.00). These settings aim to reduce the risk of overfitting by keeping the learning rate low.

Cross-validation was applied during the model evaluation and hyperparameter optimization process. In addition to splitting the data into training and test sets (e.g., 70% training/30% test), k-fold validation or repeated random sampling methods can be used to ensure the consistency of model performance; in this study, repeated test-train splits with random sampling were used. These methods prevent models from overfitting to the training dataset, thereby enhancing their generalization ability. In the literature, it is standard practice to evaluate model fit using metrics such as MAE, RMSE, and R² in many prediction studies, while testing parametric settings using GridSearch or similar hyperparameter optimization algorithms [9].

In this study, to make the comparison transparent, a basic linear regression (OLS) model was evaluated as an additional baseline comparison. OLS estimates the linear relationship between the target variable and multiple explanatory variables by minimizing the sum of residual squares using the least squares criterion; under classical assumptions (linear specification of the model, error terms with zero mean and independent/identically distributed with constant variance, absence of multicollinearity, etc.), it provides BLUE (Best Linear Unbiased Estimator) estimates with unbiasedness and minimum variance properties. This framework is one of the most established reference lines in applied statistics and machine learning literature.

One of the important practical limitations of OLS is high multicollinearity among explanatory variables. Strong collinearity can increase the variance of coefficient estimates, destabilize sign and magnitude interpretations and negatively affect the model’s generalization performance; therefore, it is necessary to pay attention to collinearity diagnostics (correlation matrix, VIF, etc.) when interpreting OLS results. This tendency to increase coefficient uncertainty is amplified when combined with small sample sizes [19].

Hyperparameter tuning for GBR was performed using grid search with 5-fold cross-validation on the training set. The grid included learning_rate ∈ {0.01, 0.05, 0.1}, n_estimators ∈ {50, 100, 200} and max_depth ∈ {2, 3, 4}. For PLS, the number of components was selected by cross-validation in the training set, considering components ∈ {1, 2, 3, 4} and 2 components were selected as optimal. Final performance metrics were computed on the held-out test set. All model training and evaluation were repeated across 10 random train/test splits and averaged to report robust metrics [20].

As a baseline model, we also trained an Ordinary Least Squares (OLS) linear regression under the same preprocessing and cross-validation scheme. OLS performance was evaluated using the same metrics (R², MAE, RMSE, MAPE) to enable a direct comparison with PLS and GBR [21].

To visually summarize the methodological approach, a workflow diagram was constructed to illustrate the sequence from data acquisition to preprocessing and model training. The diagram outlines the complete pipeline, including dataset preparation, normalization, train–test splitting, and the implementation of the Gradient Boosting Regression (GBR) and Partial Least Squares (PLS) models used for prediction. The workflow is presented in Figure 1.

Figure 1 presents the workflow of the data processing and modeling procedure used in this study, including preprocessing steps and the implementation of Gradient Boosting Regression (GBR) and Partial Least Squares (PLS) models.

Generative AI tools were used only for language editing and figure creation. ChatGPT-5.1 assisted in grammar and text refinement, and the Napkin AI Desktop/Web Version application was used to produce figures. All outputs were reviewed and edited by the authors, who take full responsibility for the final content.

2.3. Evaluation Criteria

In this study, mean-based error metrics and an explanatory power metric were used together to evaluate the accuracy and explanatory power of the models: MSE, RMSE, MAE, MAPE, and R². The reason for preferring multiple metrics is to capture error characteristics (extreme value sensitivity, percentage-based error perception, explained variance, etc.) that cannot be captured by a single metric. The literature shows that different metrics are complementary, especially in regression and forecasting studies, and can sometimes produce different rankings [22].

MSE (Mean Squared Error) penalizes large errors more heavily because it squares the prediction errors. Thus, it is useful in situations where large deviations are operationally critical; however, since the error unit is the square of the target variable, it can be more difficult to interpret and is highly sensitive to outliers. These characteristics of MSE are considered standard in energy-environment and atmospheric modeling literature [22].

RMSE (Root Mean Squared Error) provides the error magnitude directly in the units of the target variable, as it is the square root of MSE; in the case of healthcare waste, it facilitates reading the average deviation in “kg.” It has been shown that RMSE is advantageous in representing performance when the error distribution is approximately Gaussian and there is sufficient sampling; it also provides the triangle inequality as a distance measure. Therefore, it is one of the successful metrics in many environmental/predictive studies [23].

MAE (Mean Absolute Error) is more “robust” against outliers because it averages errors based on their absolute values and presents the “typical” error magnitude in a straightforward manner. Some studies argue that MAE is more suitable than RMSE for evaluating average performance; in practice, it is recommended to report both together [24].

MAPE (Mean Absolute Percentage Error) provides an intuitive interpretation for managers and policymakers because it expresses error as a percentage; it also allows for the comparison of series at different scales. However, it has been emphasized that it can become undefined/misleading when actual values are zero or very close to zero; therefore, it must be used with caution. Alternatives to percentage-based errors (e.g., MASE, MAAPE) have also been proposed in response to these limitations [25].

R² (Coefficient of Determination) indicates how much of the total variance in the dependent variable is explained by the model; it is highly interpretable and useful for comparing different models contextually. However, it can be misleading in nonlinear models or when used inappropriately; therefore, it is recommended that R² not be viewed as proof of “model validity” on its own, but rather be reported alongside other metrics [26].

In terms of suitability for comparison; RMSE and MSE are meaningful in planning with the goal of “minimizing worst errors” by giving more weight to large errors; MAE more fairly reflects typical errors in clinical data containing outliers; MAPE provides a percentage perception in managerial communication and cost-sensitive comparisons but is sensitive to small share values; R² summarizes the explanatory power of the model but should be complemented with error metrics, especially in nonlinear contexts [23]. Therefore, in our study, all of these metrics are reported together to achieve a more comprehensive evaluation.

3. Results

3.1. Descriptive Statistics

The dataset consists of 48 months of observations from January 2021 to December 2024, with all variables recorded continuously and quantitatively. Monthly numbers of endodontic, therapeutic, prosthetic, periodontal, orthodontic, pediatric, and surgical procedures were evaluated together with the approximate total amount of medical waste (kg) for the same period. Within the scope of descriptive statistics, the mean, standard deviation, and observed minimum–maximum values were reported for each variable; these summaries provided a basic reference in terms of showing the central tendency and spread of the data distribution (

Table 1. Descriptive statistics for monthly transaction counts and Total Medical Waste (kg).

Variable	Mean	Std	Min	Max
Endodontics	425.52	159.31	85	722
Treatment	926.15	406.01	115	1509
Prosthetics	1286.4	1336.18	0	4079
Periodontics	322.04	175.56	12	632
Orthodontics	9.92	2.73	2	13
Pedodontics	248.67	279.58	18	1020
Surgery	2048.4	699.77	780	3139
Total Waste (kg)	589.79	247.96	155	963

).

The descriptive statistics presented in Table 1 reveal that monthly transaction volumes and total medical waste showed significant variability during the January 2021–December 2024 period. The average total medical waste was ≈589.8 kg, ranging from 155 to 963 kg, indicating significant fluctuations throughout the period. Among procedures, surgery had the highest average (≈2.048) and a wide spread (SD ≈ 700), while prosthetics also had a high average (≈1.286) and a standard deviation exceeding the average (SD ≈ 1.336), suggesting pronounced seasonal peaks. Treatment (≈926) and periodontology (≈322) were at a medium level, while pedodontics (≈249) was observed with high variability (min 18, max 1.020). Orthodontics exhibits a low and stable volume compared to other branches (mean ≈ 9.9, SD ≈ 2.7, min 2, max 13).

On the other hand, Pearson correlation coefficients were calculated to observe the initial relationships between input variables and waste quantity. This preliminary analysis contributes to justifying the modeling strategy by revealing the direction and magnitude of linear relationships between variables. The correlation matrix was evaluated using a two-tailed test approach, with significance levels indicated as “*” for p < 0.05 and “**” for p < 0.01. These findings form the basis for interpreting the PLS and Gradient Boosting results in the subsequent modeling section.

The Pearson correlations in Figure 2 show a very strong relationship between total medical waste and monthly treatment (r = 0.966, p < 0.01) and periodontology (r = 0.942, p < 0.01) volumes; strong with surgery (r = 0.915, p < 0.01), prosthetics (r = 0.792, p < 0.01), and endodontics (r = 0.729, p < 0.01); and moderately strong with pediatric dentistry (r = 0.607, p < 0.01). The relationship between orthodontics and total waste is weak and statistically borderline/insignificant (r = −0.281, p = 0.053). The input variables are also highly correlated with each other, showing strong collinearity patterns such as treatment–periodontology (r = 0.933), treatment–prosthodontics (r = 0.744), surgery–endodontics (r = 0.864), and surgery–treatment (r = 0.910). while orthodontics is negatively correlated with many variables (e.g., prosthetics with r = −0.552, p < 0.01). This table shows that waste production is particularly driven by high-volume and concurrently increasing procedures and that, due to multicollinearity between variables, latent component approaches such as PLS and flexible methods such as GBR are methodologically supported.

3.2. Model Performance Comparison

In this section, PLS, scikit-learn–based Gradient Boosting (GBR) and a baseline Ordinary Least Squares (OLS) model were compared under the same data preprocessing and validation scheme. The evaluation was performed using a 70% training/30% test split and 10 stratified random folds; the averages of R², MAE and RMSE values for each model across the folds were reported. In the interpretation, higher R² and lower MAE/RMSE indicate better performance; thus, the most suitable model can be selected by considering both error tolerance and adaptability in clinical planning.

Table 2. PLS and Gradient Boosting regression performance comparison.

	R2	MSE	MAPE	MAE	RMSE
PLS	0.979	1372.202	0.055	30.488	37.043
Gradient Boosting (GBR)	0.962	2399.988	0.072	36.544	48.990
OLS	0.927	3481.650	0.086	41.762	59.013

shows that PLS outperforms GBR in all metrics: PLS achieves higher explanatory power (R² = 0.979 vs. 0.962) and provides clear advantages in error metrics (lower MSE, RMSE and MAE), with a similar improvement in relative error (MAPE). Both PLS and GBR also outperform the OLS baseline across all measures, which is consistent with the expectation that high inter-variable collinearity and limited sample size undermine OLS stability and predictive accuracy. This pattern suggests that the latent component structure of PLS captures the dominant linear dependencies more effectively in this setting, while shallow-tree GBR is competitive but would likely benefit from richer temporal features and nonlinearity-aware tuning. Consequently, PLS appears more reliable for point estimates for planning purposes in this data and validation scheme; however, GBR’s performance may improve when time effects and potential nonlinearities are explicitly incorporated, whereas OLS remains a useful but weaker baseline for benchmarking. As a visual counterpart to Table 2, Figure 3 highlights the overlap at key turning points by comparing the observed series with the PLS and GBR estimates.

Figure 3 shows the actual waste series alongside the predictions of the two models for the period 2021–2024, revealing that both models generally successfully track the underlying trends, seasonal fluctuations and sudden turning points. The PLS curve follows the actual series a bit more closely at peaks and troughs (e.g., during periods of large jumps and sudden drops), while Gradient Boosting can exhibit small delays by drawing a slightly smoother profile in places. The overall picture shows that PLS offers a relatively tighter fit at extreme values, while Gradient Boosting provides stable tracking over time.

4. Discussion

In this study, we compared two approaches for predicting the approximate amount of medical waste based on monthly procedure volumes in dental clinics affiliated with the Provincial Health Directorate in Kastamonu and demonstrated that PLS provided higher accuracy and lower error compared to GBR. Our findings are consistent with the literature, which shows that regression and machine learning models developed for waste volume/waste cost in healthcare facilities are becoming increasingly widespread. For example, predictive models developed for waste volume and management costs in Greek public hospitals have shown that accurate predictions provide direct input for cost planning. Similarly, studies predicting solid waste production in hospitals have reported that contemporary ML methods are used alongside classical regressions, and that different models may be superior depending on the data context. In this vein, more recent comparative studies emphasize that ML approaches (including tree-based models) provide higher accuracy than traditional models in most conditions for problems such as waste/solid waste production, but that data structure and sample size are critical determinants [27,28].

The superiority of PLS in our data is consistent with the method’s ability to make sound predictions under small/medium sample sizes and high collinearity. In the PLS-SEM literature, it has long been reported that PLS’s component-based structure allows model construction even with small samples and provides stable coefficients for highly correlated attributes. Furthermore, it has been demonstrated that the effect of multicollinearity increases, particularly in small samples; in this case, dimension reduction and component extraction (a fundamental feature of PLS) that considers the response variable (Y) offer advantages over classical methods. Recent methodological reviews also emphasize that PLS is a more robust alternative to MLR and PCA in terms of multicollinearity. In this context, it is expected that PLS will produce lower errors in our dataset, where strong linear relationships are observed between the process variables [29].

On the other hand, GBR is powerful in capturing nonlinear relationships and interactions with successively constructed decision trees; its ability to explain nonlinear effects in areas such as environmental and transportation demand has been demonstrated in numerous studies. However, realizing this power in practice is usually possible with larger samples, richer feature sets (calendar/seasonality, material type details, supply/workflow indicators, etc.), and careful hyperparameter tuning. In our context, the prominence of PLS under conditions of 48 monthly observations and high collinearity may also be related to the lack of feature diversity to feed GBR’s “nonlinear signal”; GBR’s performance can be improved by systematically exploring data enrichment (time effects, holiday/pandemic dummies, interaction terms) and settings such as learning rate–tree depth [30].

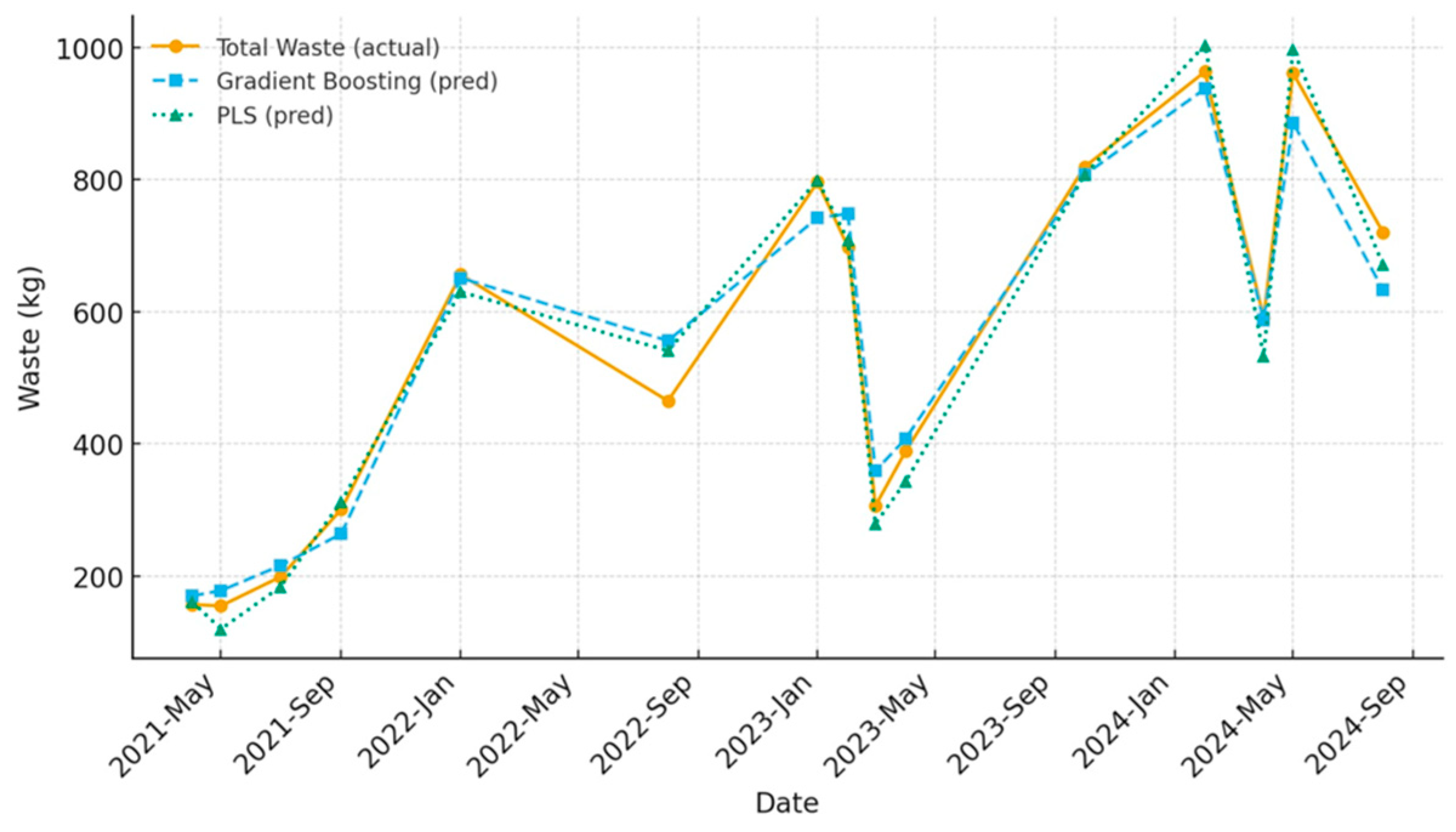
In this study, OLS lagged behind PLS and GBR as expected: R² = 0.927 for OLS, R² = 0.979 for PLS and R² = 0.962 for GBR were obtained in the test set. Under conditions of high multicollinearity and small sample sizes, the variance of OLS coefficients may increase (instability, wide confidence intervals), leading to a decrease in prediction accuracy; this phenomenon has been demonstrated in detail in comprehensive studies [31]. In contrast, PLS reduces collinearity by reflecting predictors onto latent components and can produce stable/prediction-focused solutions in small-n environments; the superiority observed here is consistent with this literature [32]. On the other hand, GBR achieved higher fit than OLS as it is an ensemble method capable of capturing nonlinear interactions and threshold effects; however, it lagged behind PLS when data scope and complexity were limited—this behavior is also consistent with the fundamental theoretical framework underlying gradient boosting [20].

Although the R² values reported in the literature for health/medical waste estimation vary in context and scale, they are concentrated in the range of 0.70–0.96; ANN/MLR comparisons and voting/GBM approaches on the Istanbul dataset have reported strong accuracies. High fits (e.g., R² ≈ 0.96) have also been observed in penalized regression applications [2,9,33,34]. Within this reference framework, the PLS result in our study (R² = 0.979; RMSE = 37 kg) corresponds to the upper range; GBR remains competitive, while OLS lags behind as expected under small sample size/collinearity.

More accurate waste estimates directly impact capacity and resource planning in the collection–storage–transport–disposal chain; inaccurate estimates lead to environmental risks due to excess disposal/safety costs or insufficient capacity. The literature shows that effective management both reduces costs and lowers the risk of environmental pollution; it also emphasizes that transparent monitoring and forecasting infrastructures must inform corporate decisions for fair/sustainable waste management. In dental-specific planning studies, findings indicate that appropriate location and route decisions are decisive for total cost and population risk; therefore, reliable predictions at the clinic level should be considered alongside logistics optimization at the district/city level. In this context, the low error values obtained in our study produce planning inputs that are applicable in terms of both cost control and the reduction in environmental/sanitary risks.

More accurate waste estimates rationalize capacity and resource allocation in the collection–temporary storage–transport–disposal chain; conversely, inaccurate estimates can increase unnecessary disposal/logistics costs while exacerbating environmental and health risks due to insufficient capacity. Guidelines and recent studies on the safe management of healthcare facility waste emphasize that accurate forecasting is the key input for successful management and that proper planning reduces risks and improves performance. Furthermore, evidence syntheses show that implemented interventions have led to meaningful improvements in waste volume and management cost indicators. In dentistry specifically, sustainable practices (reducing waste and single-use dependency, resource efficiency) should be addressed alongside monitoring and forecasting infrastructure that supports institutional decisions; when reliable clinical-level forecasts are integrated with transportation models that optimize city-scale route/location decisions, they create a leverage effect on total cost and population risk. In this context, the low error values obtained in our study provide operational planning inputs that can be directly used for both cost control and environmental risk reduction [35].

For limitations and future work, time effects (seasonality, holiday/pandemic waves) have not been explicitly included in the model; incorporating these effects could enhance the utility of flexible models such as GBR. Furthermore, single-center data limits generalizability; comparisons that more systematically test the conditional superiority of methods such as PLS and GBR/XGBoost using multi-center/multi-year data would be appropriate for future studies.

5. Conclusions

This study demonstrates that medical waste production can be reliably predicted using estimation models developed based on 48 months of data (2021–2024) from dental clinics affiliated with the Provincial Health Directorate in Kastamonu. Both Partial Least Squares (PLS) and Gradient Boosting (GBR) produced successful results in the criteria used (R², MAE, RMSE); however, PLS provided the best fit under conditions of high collinearity between variables and limited samples (R² = 0.979; RMSE = 37.0 kg; MAE = 30.5 kg). For benchmarking, a baseline Ordinary Least Squares (OLS) model was also evaluated and yielded comparatively lower accuracy (R² = 0.927; RMSE = 59.0 kg; MAE = 41.8 kg), which is consistent with expectations under small-sample, high-collinearity settings. Taken together, these findings indicate that PLS is a practical and robust option for clinical applications in data structures with high correlations related to dental procedures, while GBR remains competitive, and OLS provides a useful but weaker baseline.

The results obtained show that data-driven waste management planning in healthcare facilities is both feasible and beneficial. Accurate predictions contribute to improving capacity planning in collection, temporary storage, transportation, and disposal processes, reducing unnecessary costs, and lowering environmental/health risks. With the integration of models into hospital information management systems, monthly or even weekly operational decisions (vehicle/route planning, container size and number, staff shifts, supply planning) can be managed in a more evidence-based manner.

To strengthen the practical significance of the model outputs, we qualitatively assessed the marginal contribution per unit activity for each treatment type. To this end, we obtained a ranking at the kg/100 procedure level by tracking the change in the estimate in counterfactual scenarios where we increased the number of relevant procedures by +100 while holding other inputs constant. Resampling-based averages showed that procedures with higher material usage and/or more invasive procedures produced relatively more waste per unit, while more conservative procedures contributed less; this pattern was consistent across PLS and GBR models.

The single-center nature of the study and the fact that time effects (seasonality, holiday/pandemic waves) are not explicitly included in the model are key limitations. Future research should test external validity with multi-center data, add calendar/logistical variables and cost indicators, measure uncertainty (prediction intervals), and expand the methodological comparison with time series or more advanced ensemble approaches (e.g., XGBoost, CatBoost). Nevertheless, the current findings clearly demonstrate that PLS is a robust and applicable method for planning medical waste management in dental clinics and can provide reliable predictions to support organizational decisions.