Experimental and Numerical Replication of Thermal Conditions in High-Pressure Die-Casting Process
Abstract
1. Introduction
2. Literature Review
2.1. Analytical and Inverse Methods for IHTC Estimation
2.2. Influence of HPDC Process Parameters on IHTC
2.3. Vacuum-Assisted HPDC Effects on Quality
2.4. IHTC Behavior in Squeeze Casting
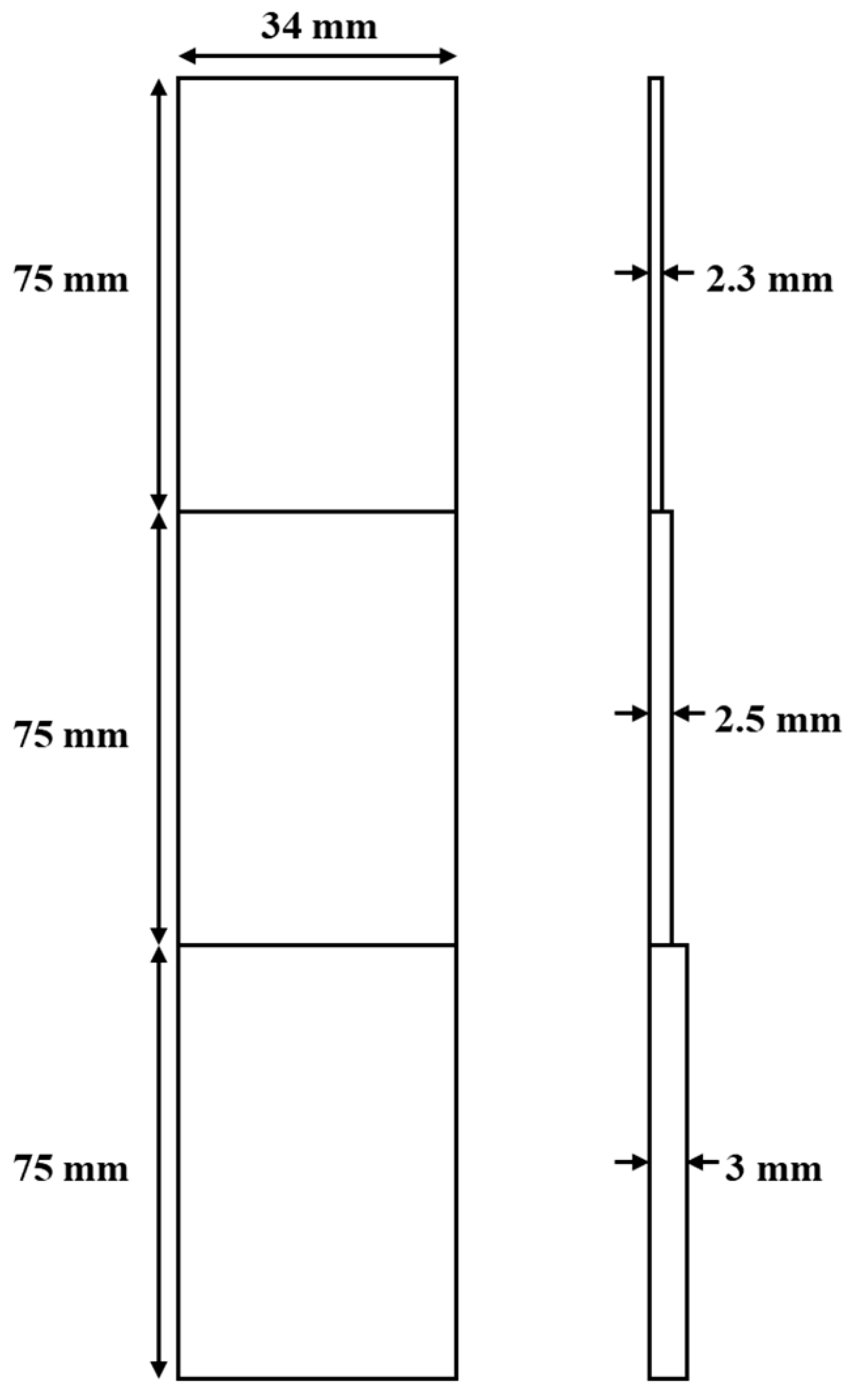
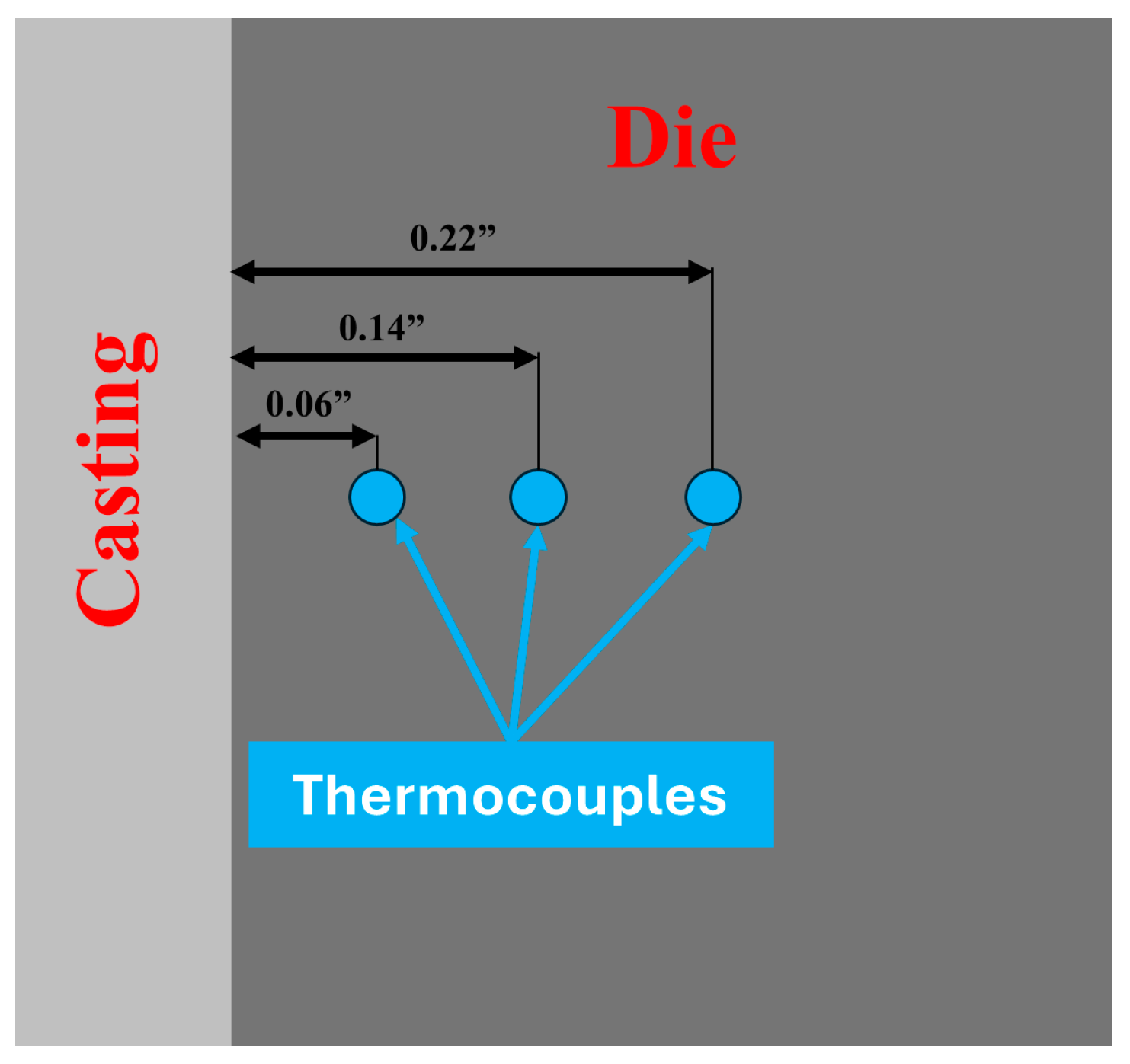
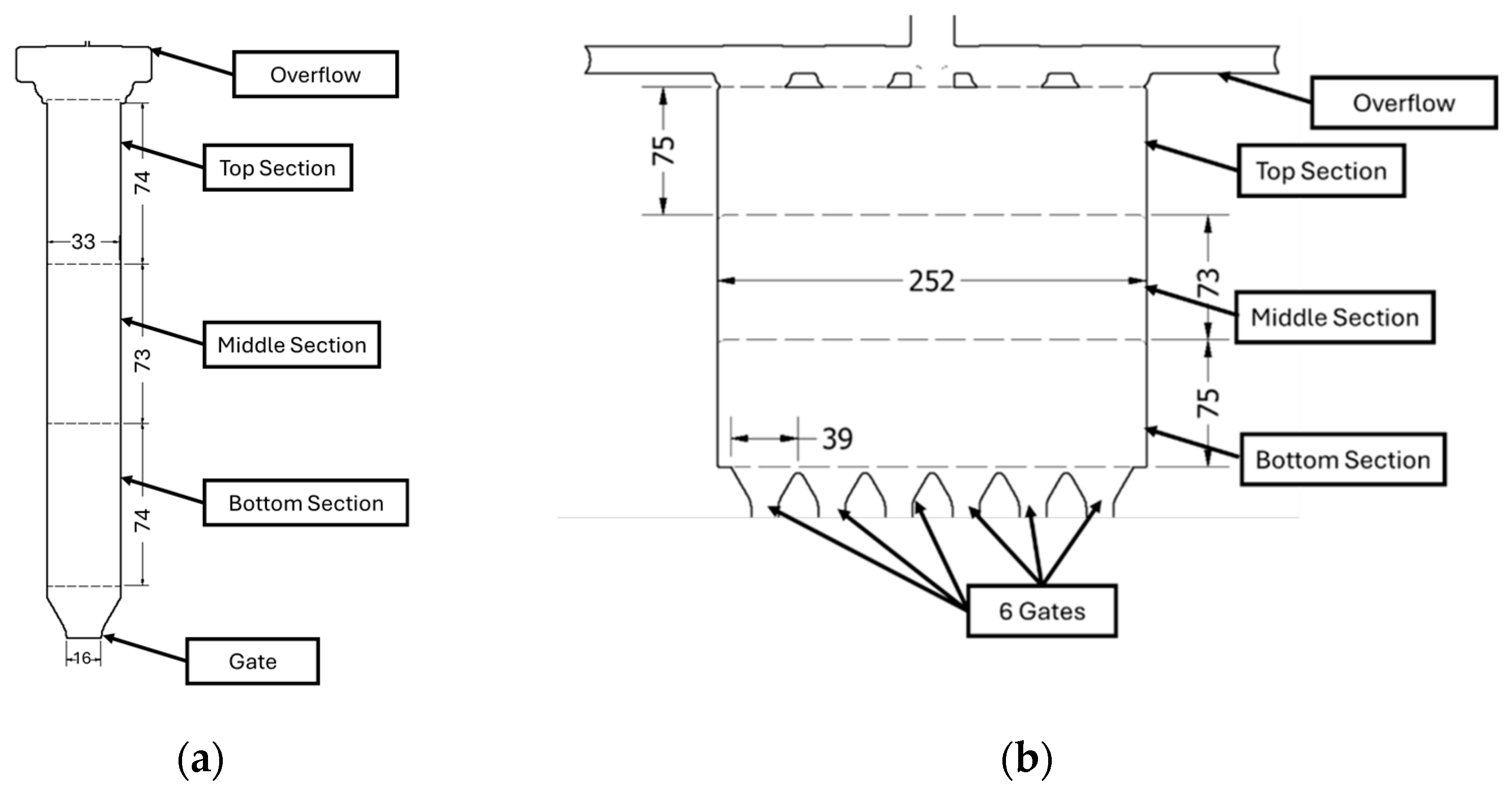
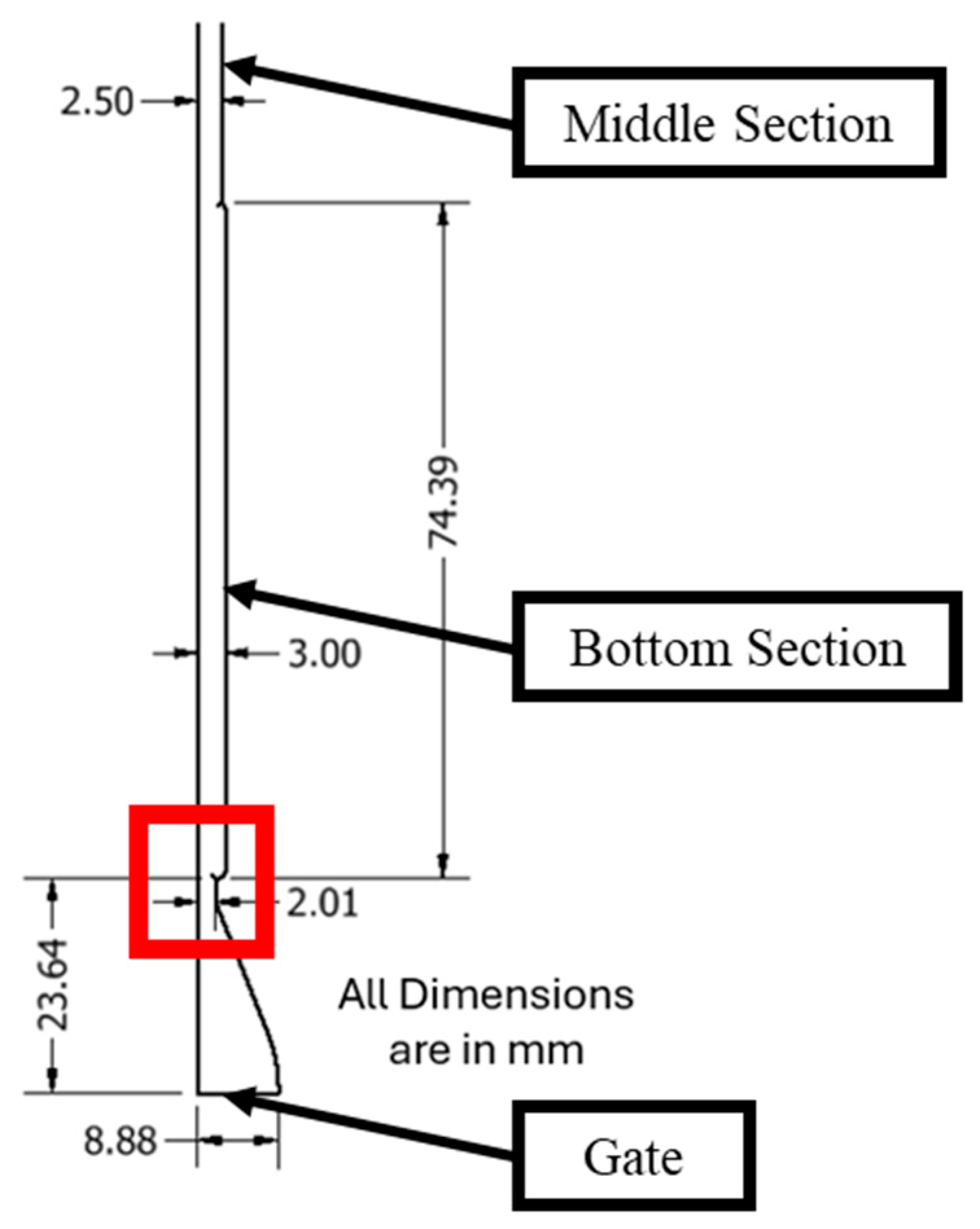
3. Experimental and Methodology
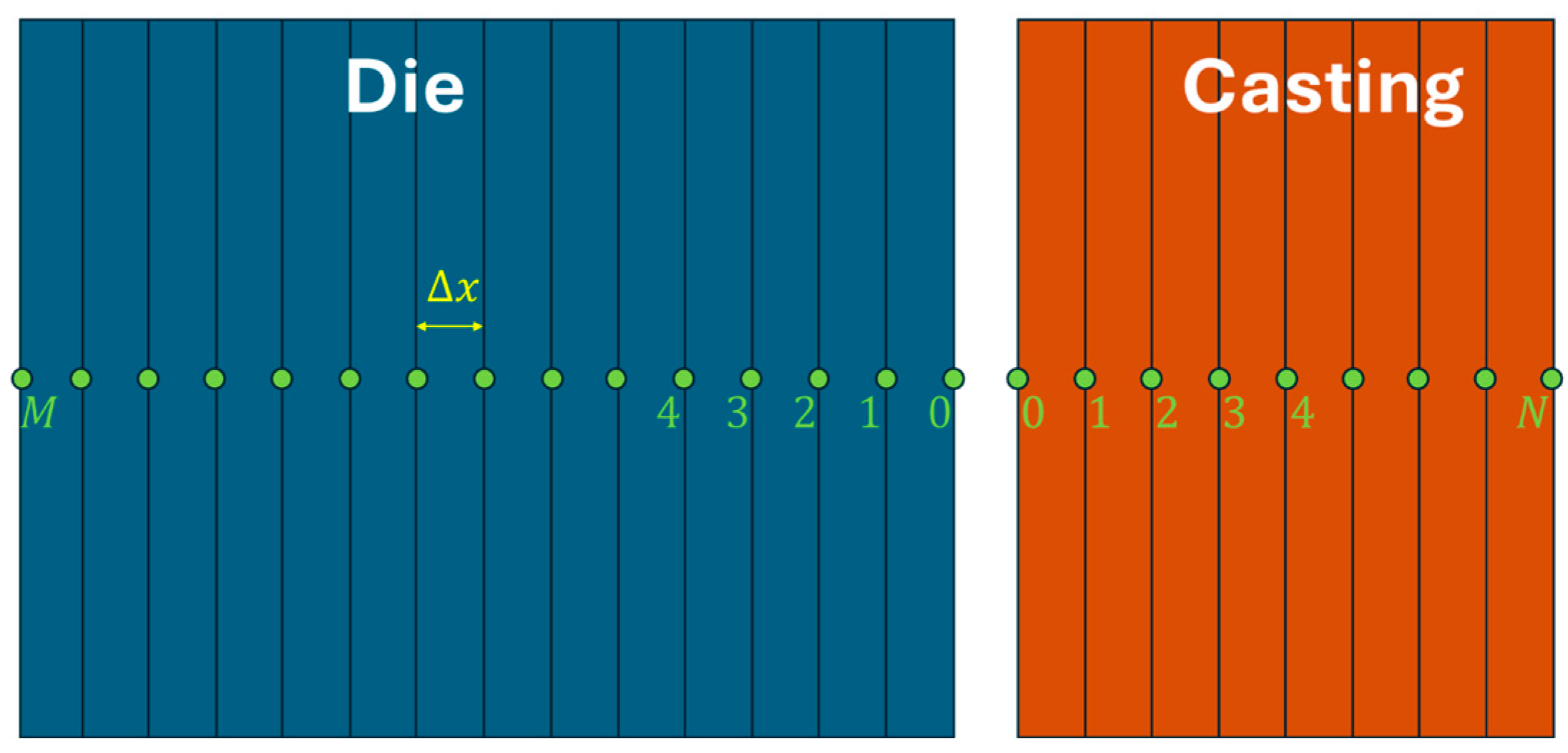
4. Mathematical Modeling
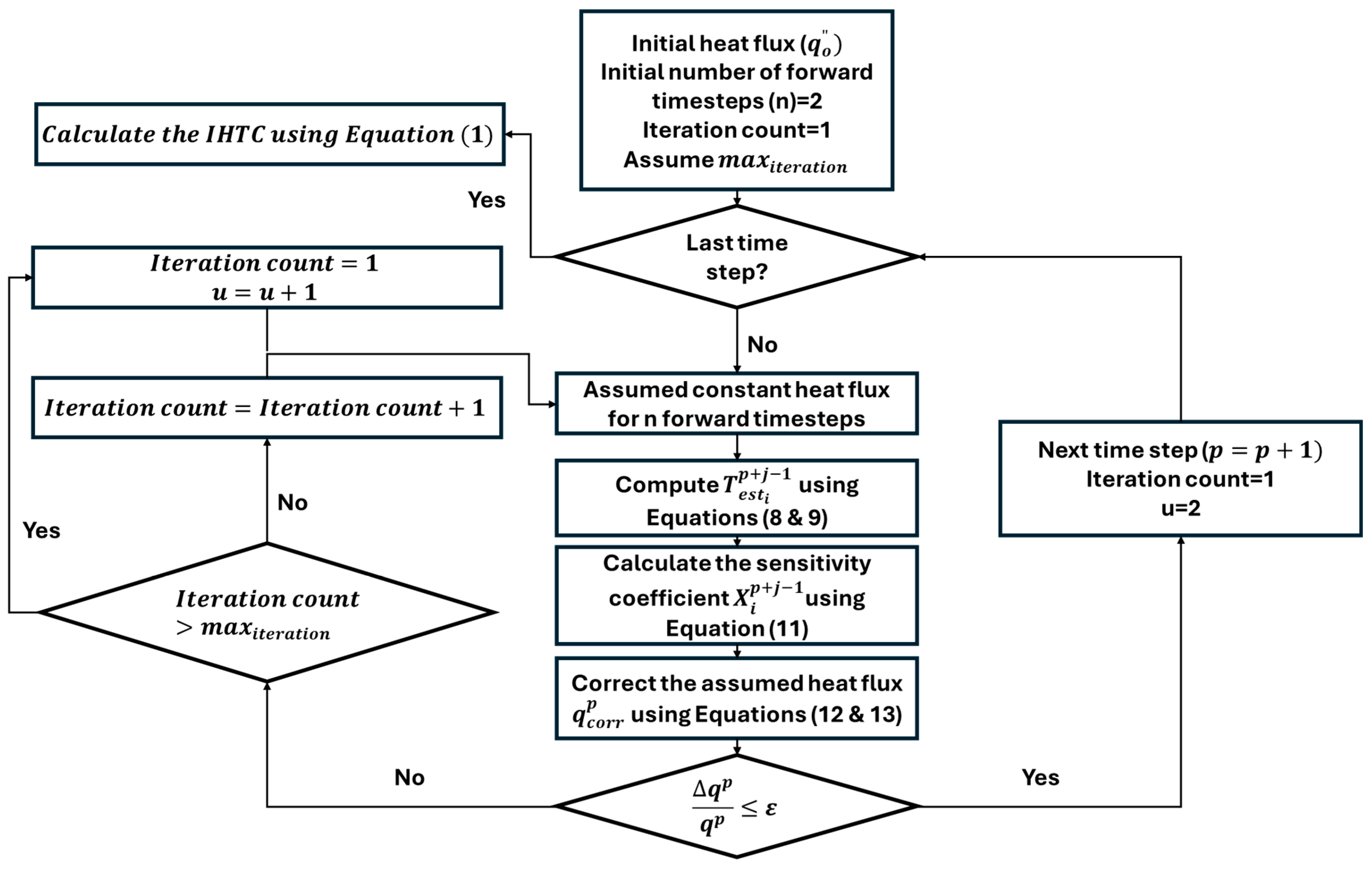
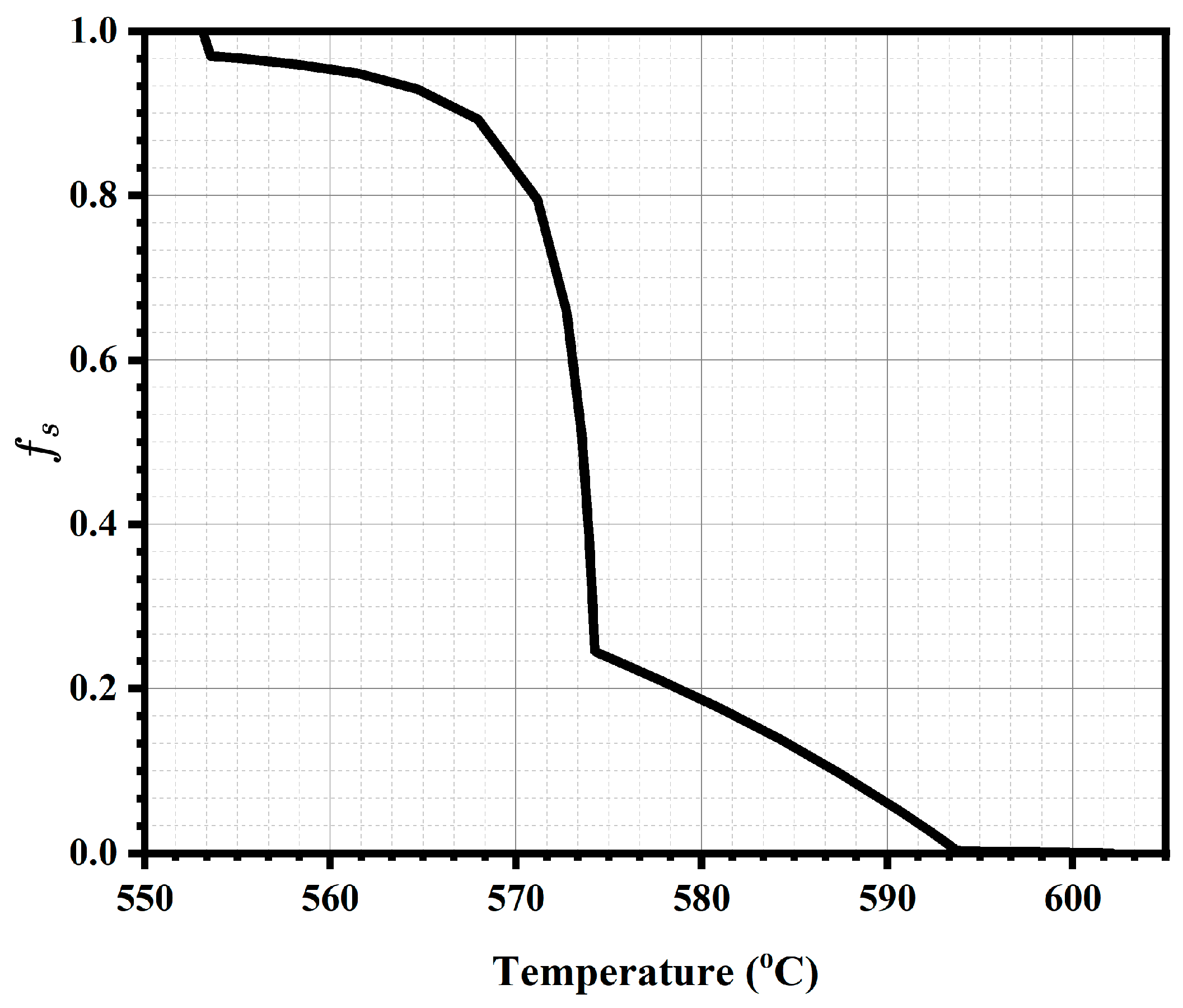
4.1. Inverse Heat Transfer Approach for Solidification Analysis
4.2. Thermal Modeling of the Casting
- , : casting temperature at the current and next time steps, respectively.
- : transient heat flux from the casting to the die at time [.
- : time increment [s].
- : density of the metal [].
- : specific heat capacity of the metal [].
- : Latent heat of fusion [].
- : is the solid fraction.
- : is half of the thickness of the casting.
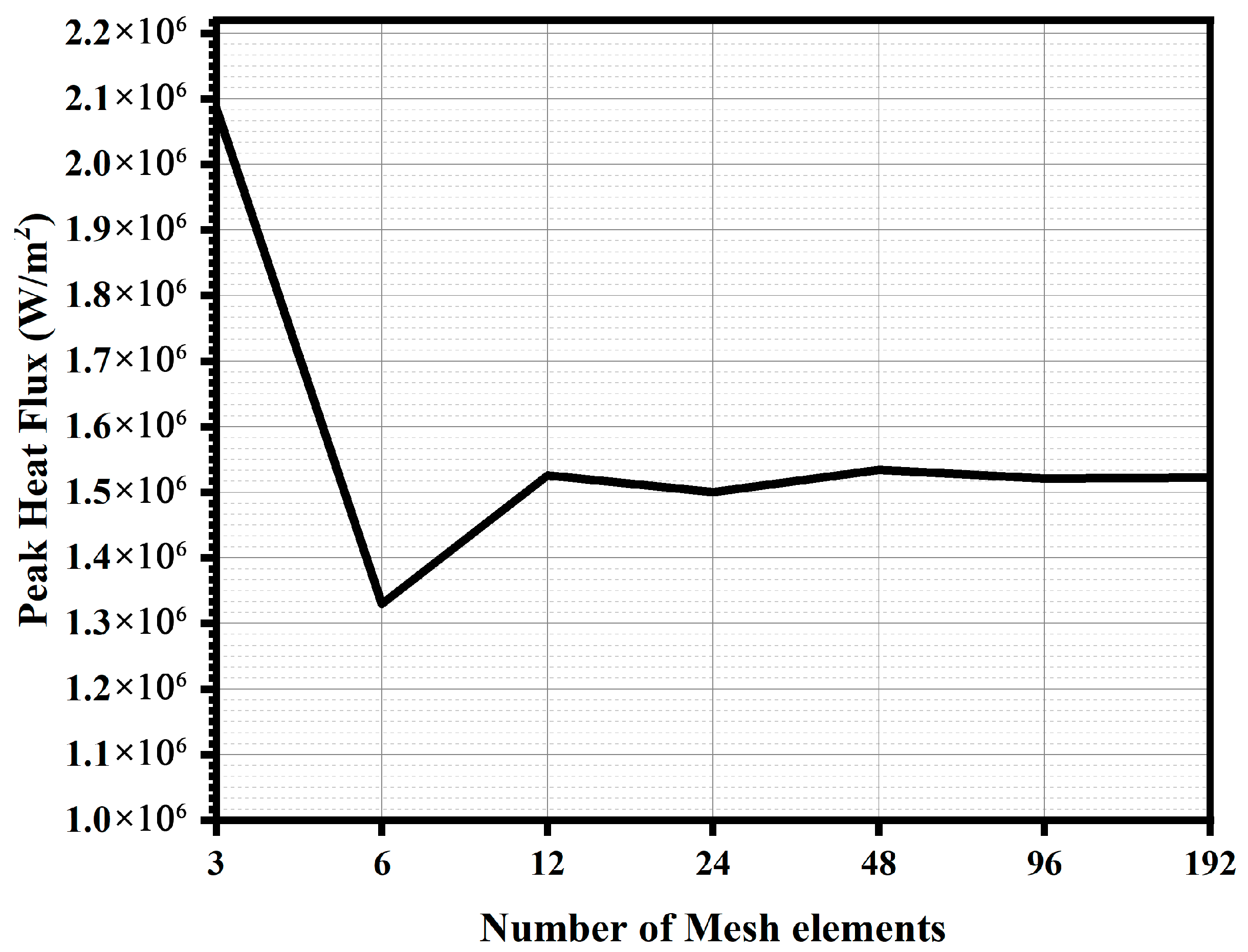
5. Mesh Independence Study
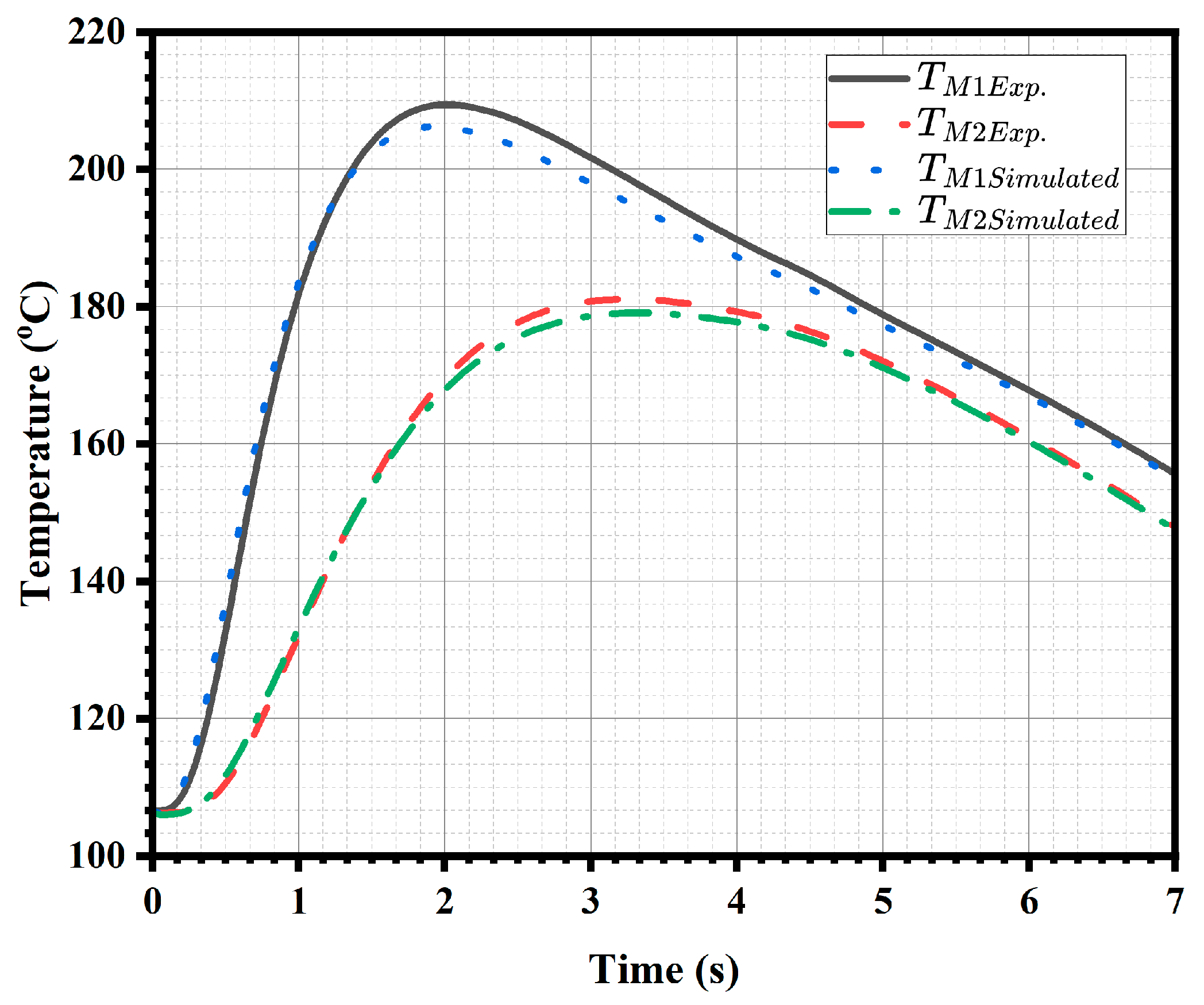
6. Forward Simulation Validation
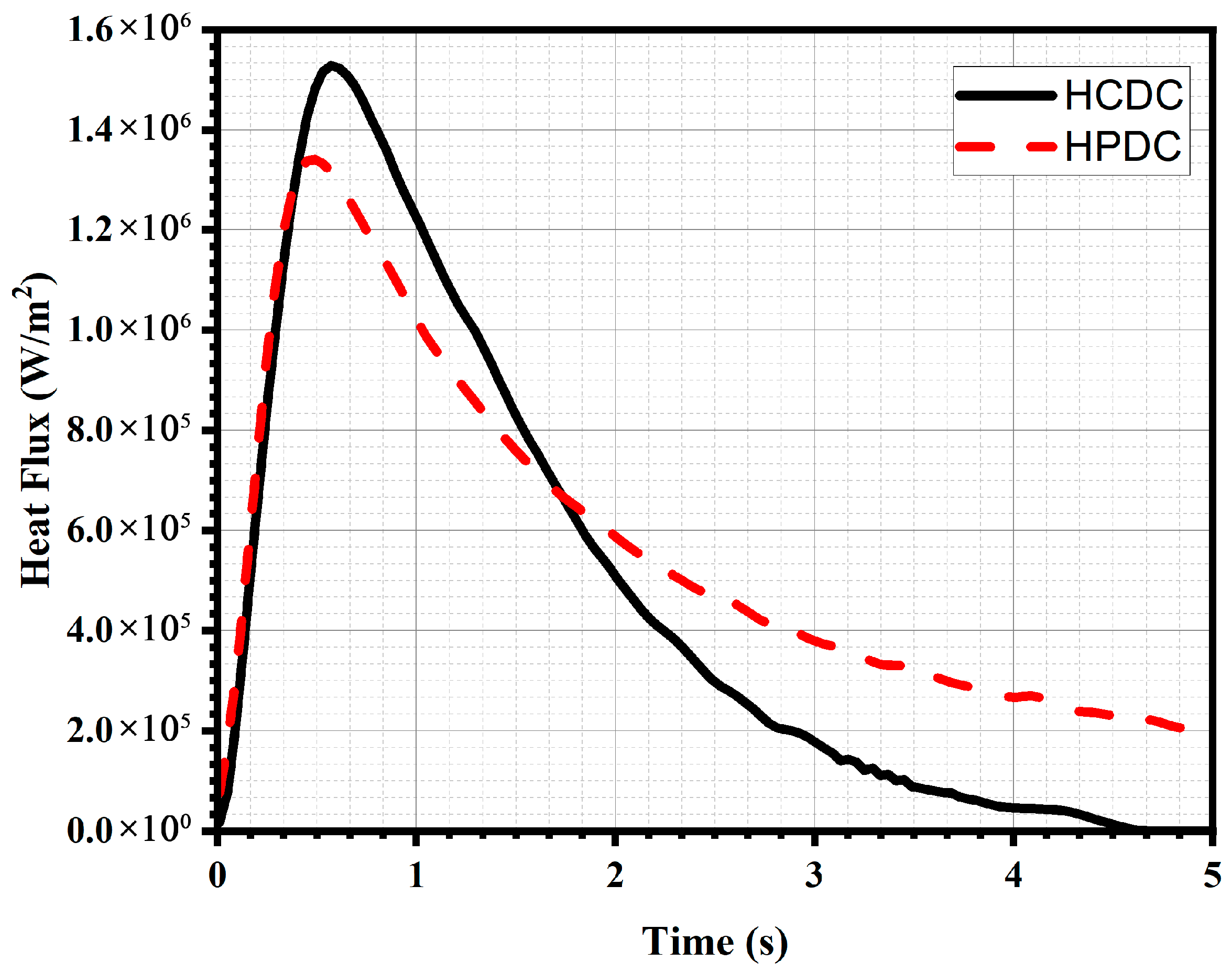
7. Experimental Results: HCDC vs. Industrial HPDC
8. Results and Discussion
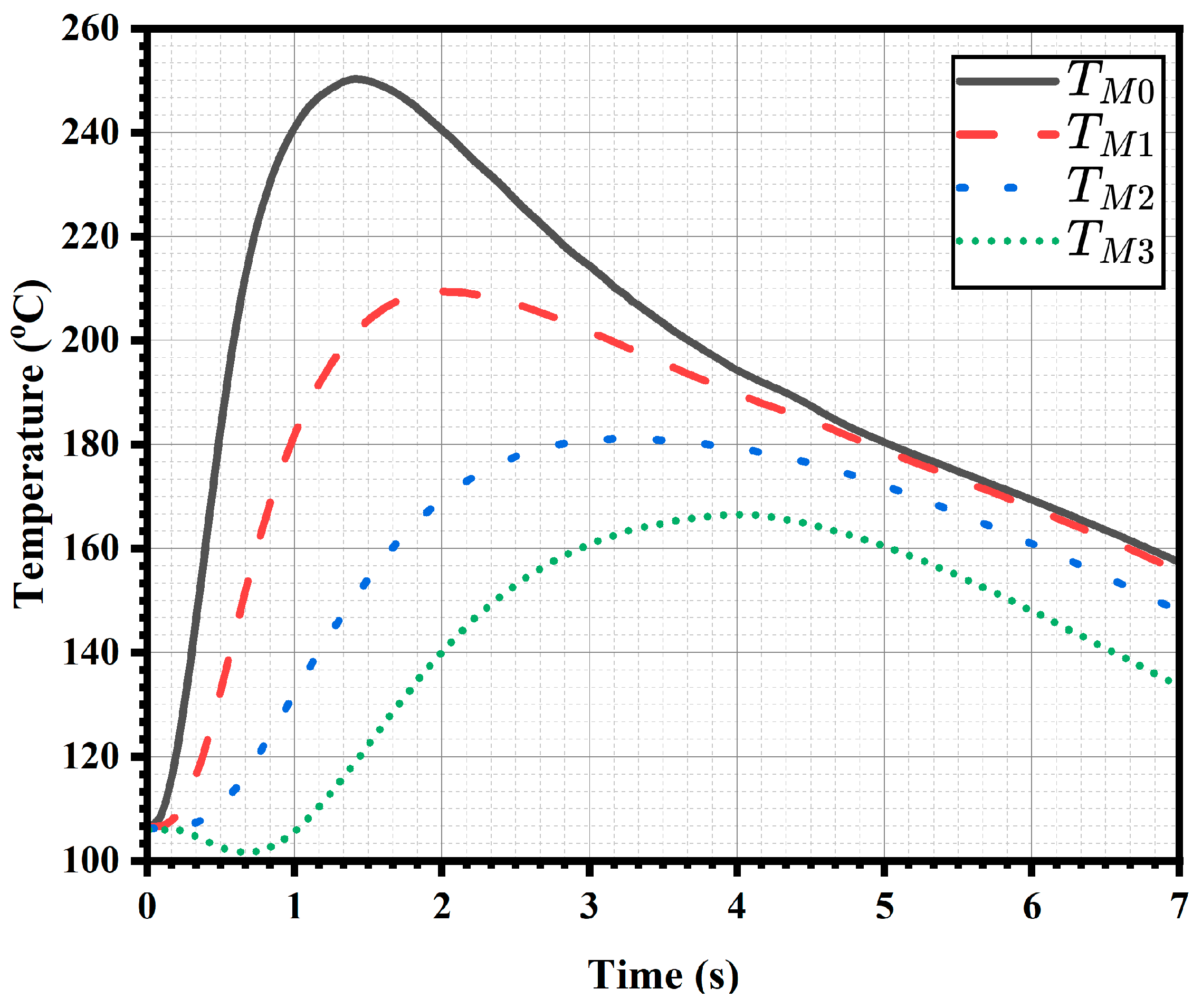
8.1. Die Temperature vs. Time
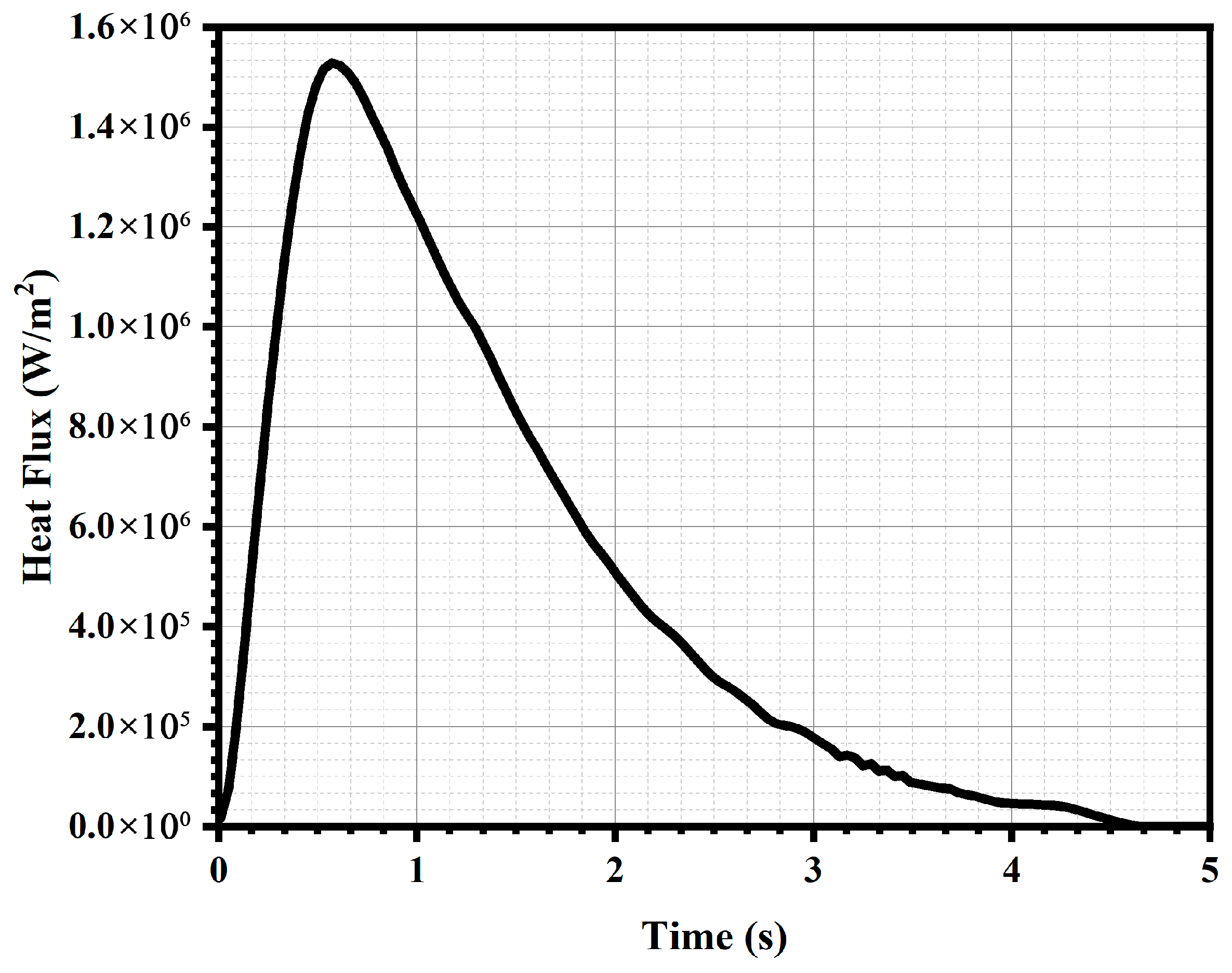
8.2. Heat Flux vs. Time
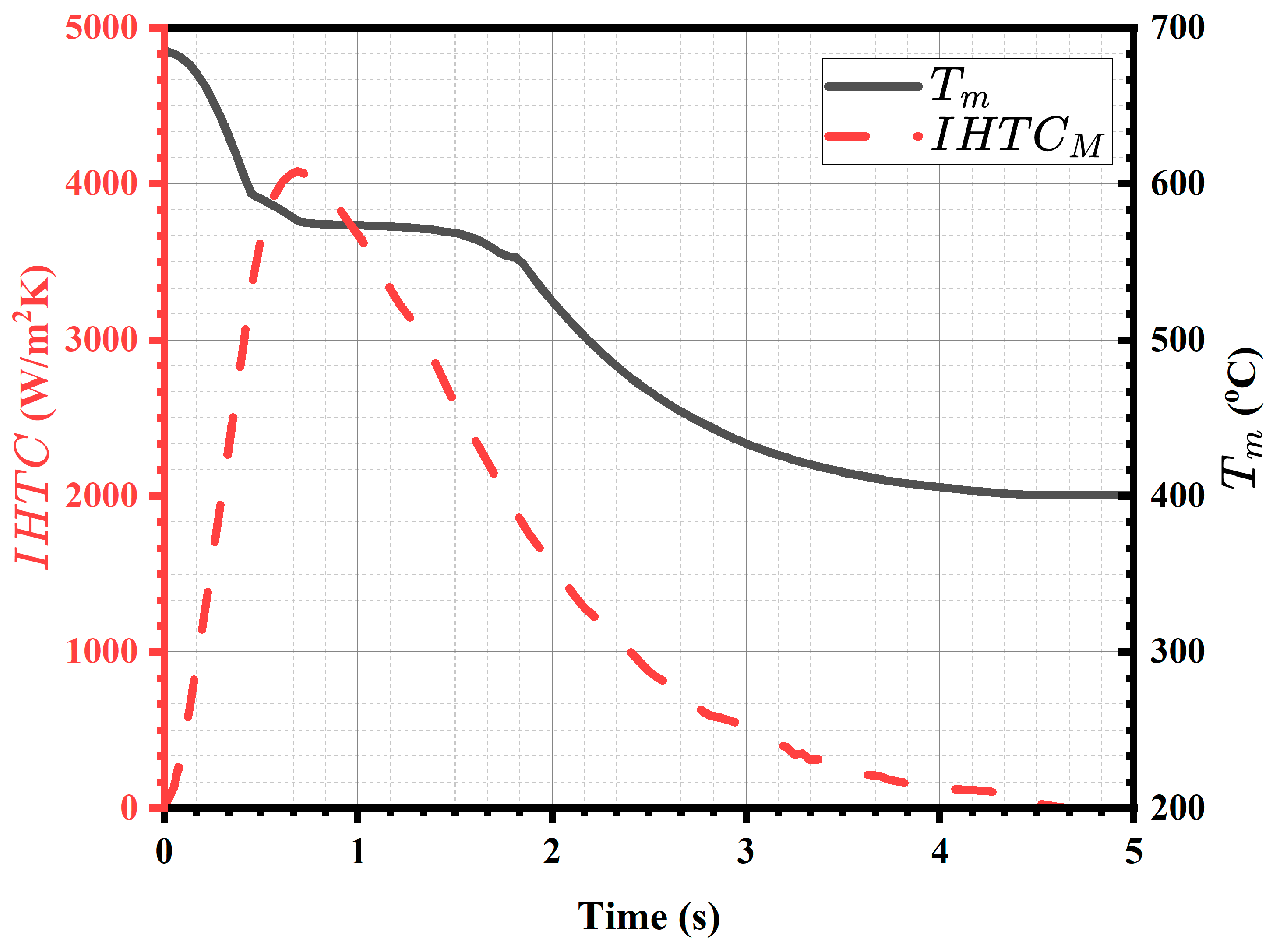
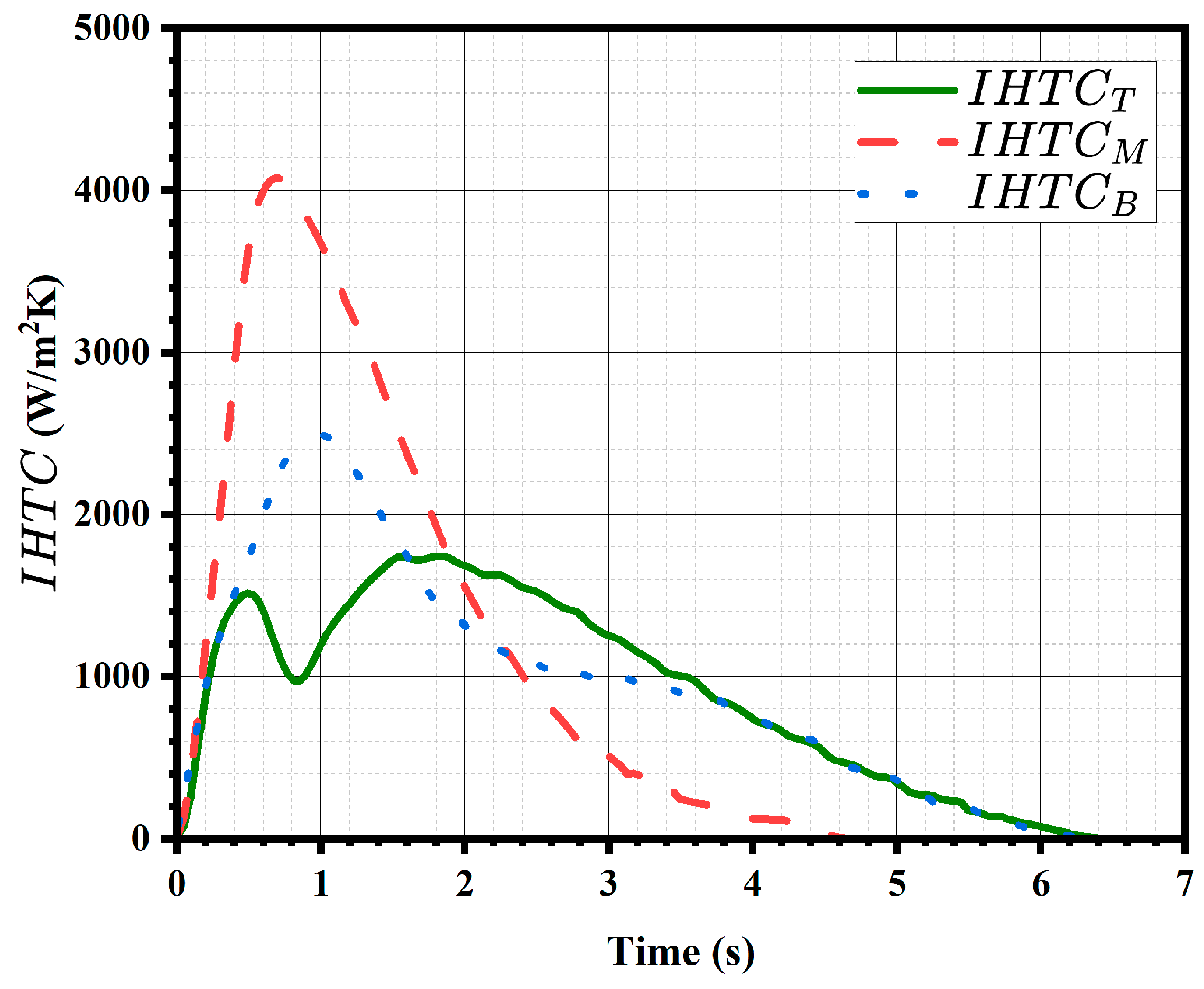
8.3. IHTC and Metal Temperature vs. Time
8.4. Effect of Thickness on the IHTC
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | ||
| Bi | Biot Number | |
| ) | ||
| Fo | Fourier Number | |
| ) | ||
| The timestep number | ||
| T | Temperature (°C) | |
| Number of forward timesteps | ||
| Sensitivity coefficient at the ith thermocouple | ||
| Greek symbols | ||
| The convergence criterion for the inverse method | ||
| Subscript | ||
| B | Bottom | |
| cs | Casting Surface | |
| ds | Die Surface | |
| est | Estimated | |
| Exp. | Experimental | |
| M | Middle | |
| s | Solid | |
| T | Top | |
| Acronyms | ||
| ANNR | Artificial Neural Network Regression | |
| DTR | Decision Tree Regression | |
| ESCs | Entrapped Surface Coatings | |
| ESGs | Entrapped Solid Grains | |
| FDM | Finite Difference Method | |
| FFT | Fast Fourier Transform | |
| FWHM | Full Width at Half | |
| HCDC | Hot Chamber Die Casting | |
| HPDC | High-Pressure Die Casting | |
| IHCP | Inverse Heat Conduction Problem | |
| IHTC | Interfacial Heat Transfer Coefficient | |
| MLR | Multiple Linear Regression | |
| VAM | Virtual Adjunct Method | |
| VPDC | Vacuum-Assisted High-Pressure Die Casting | |
References
- Merchán, M.; Egizabal, P.; García de Cortázar, M.; Irazustabarrena, A.; Galarraga, H. Development of an Innovative Low Pressure Die Casting Process for Aluminum Powertrain and Structural Components. Adv. Eng. Mater. 2019, 21, 1800105. [Google Scholar] [CrossRef]
- Dash, S.; Li, D.; Zeng, X.; Chen, D. Heterogeneous microstructure and deformation behavior of an automotive grade aluminum alloy. J. Alloys Compd. 2021, 870, 159413. [Google Scholar] [CrossRef]
- Collot, J. Review of new process technologies in the aluminum die-casting industry. Mater. Manuf. Process. 2001, 16, 595–617. [Google Scholar] [CrossRef]
- Wang, L.; Makhlouf, M.; Apelian, D. Aluminium die casting alloys: Alloy composition, microstructure, and properties-performance relationships. Int. Mater. Rev. 1995, 40, 221–238. [Google Scholar] [CrossRef]
- Dong, X.; Youssef, H.; Zhang, Y.; Wang, S.; Ji, S. High performance Al/TiB2 composites fabricated by nanoparticle reinforcement and cutting-edge super vacuum assisted die casting process. Compos. Part B Eng. 2019, 177, 107453. [Google Scholar] [CrossRef]
- Kawajiri, K.; Kobayashi, M.; Sakamoto, K. Lightweight materials equal lightweight greenhouse gas emissions?: A historical analysis of greenhouse gases of vehicle material substitution. J. Clean. Prod. 2020, 253, 119805. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Najm, S.M. Current trends in metallic materials for body panels and structural members used in the automotive industry. Materials 2024, 17, 590. [Google Scholar] [CrossRef]
- Soo, V.K.; Peeters, J.; Paraskevas, D.; Compston, P.; Doolan, M.; Duflou, J.R. Sustainable aluminium recycling of end-of-life products: A joining techniques perspective. J. Clean. Prod. 2018, 178, 119–132. [Google Scholar] [CrossRef]
- The Average Weight of Passenger Cars in Europe Has Increased Significantly Since 2020. Available online: https://www.inovev.com/index.php/en/market-analyses/category-blog/19969-2023-30-2 (accessed on 20 September 2025).
- Aluminum Content in Passenger Vehicles (Europe). Available online: https://european-aluminium.eu/wp-content/uploads/2023/05/23-05-02Aluminum-Content-in-Cars_Public-Summary.pdf (accessed on 20 September 2025).
- Aluminium Usage in Cars Surges as Automotive Industry Shifts Towards Electrification. Available online: https://aluminiumtoday.com/news/aluminium-usage-in-cars-surges-as-automotive-industry-shifts-towards-electrification (accessed on 20 September 2025).
- Baser, T.A.; Umay, E.; Akıncı, V. New trends in aluminum die casting alloys for automotive applications. Eurasia Proc. Sci. Technol. Eng. Math. 2022, 21, 79–87. [Google Scholar] [CrossRef]
- Koru, M.; Serçe, O. Experimental and Theoretical Investigation of Heat Transfer in Vacuum Assisted High Pressure Die Casting (HPDC) Process. Int. J. Met. 2024, 18, 3013–3027. [Google Scholar] [CrossRef]
- Nelson, C. Nature of heat transfer at the die face. In Proceedings of the 6th SDCE International Die Casting Congress, Cleveland, OH, USA, 16–19 November 1970. [Google Scholar]
- Lee, S.; Han, D.; Kang, S.; Kim, N. Method of predicting shrinkage defects and deriving process conditions in HPDC (high-pressure die-casting) for electric vehicle motor housings. Int. J. Met. 2024, 18, 1262–1272. [Google Scholar] [CrossRef]
- İpek, O.; Koru, M. Yüksek basınçlı döküm prosesinde kalıp sıcaklığına bağlı olarak döküm-kalıp ara yüzeyinde oluşan termal temas direncinin belirlenmesi. Isı Bilim. Tek. Derg. 2011, 31, 45–57. [Google Scholar]
- Dour, G.; Dargusch, M.; Davidson, C.; Nef, A. Development of a non-intrusive heat transfer coefficient gauge and its application to high pressure die casting: Effect of the process parameters. J. Mater. Process. Technol. 2005, 169, 223–233. [Google Scholar] [CrossRef]
- Chen, Z. Skin solidification during high pressure die casting of Al–11Si–2Cu–1Fe alloy. Mater. Sci. Eng. A 2003, 348, 145–153. [Google Scholar] [CrossRef]
- Garcia, A.; Prates, M. Mathematical model for the unidirectional solidification of metals: I. Cooled molds. Metall. Trans. B 1978, 9, 449–457. [Google Scholar] [CrossRef]
- Garcia, A.; Clyne, T.; Prates, M. Mathematical model for the unidirectional solidification of metals: II. Massive molds. Metall. Trans. B 1979, 10, 85–92. [Google Scholar] [CrossRef]
- Dargusch, M.; Hamasaiid, A.; Dour, G. An inverse model to determine the heat transfer coefficient and its evolution with time during solidification of light alloys. Int. J. Nonlinear Sci. Numer. Simul. 2008, 9, 275–282. [Google Scholar] [CrossRef]
- Long, A.; Thornhill, D.; Armstrong, C.; Watson, D. Determination of the heat transfer coefficient at the metal–die interface for high pressure die cast AlSi9Cu3Fe. Appl. Therm. Eng. 2011, 31, 3996–4006. [Google Scholar] [CrossRef]
- Guo, Z.-P.; Xiong, S.-M.; Liu, B.-C.; Li, M.; Allison, J. Effect of process parameters, casting thickness, and alloys on the interfacial heat-transfer coefficient in the high-pressure die-casting process. Metall. Mater. Trans. A 2008, 39, 2896–2905. [Google Scholar] [CrossRef]
- Hamasaiid, A.; Dour, G.; Dargusch, M.; Loulou, T.; Davidson, C.; Savage, G. Heat-transfer coefficient and in-cavity pressure at the casting-die interface during high-pressure die casting of the magnesium alloy AZ91D. Metall. Mater. Trans. A 2008, 39, 853–864. [Google Scholar] [CrossRef]
- Guo, Z.; Xiong, S.; Liu, B.; Mei, L.; Allison, J. Determination of the heat transfer coefficient at metal–die interface of high pressure die casting process of AM50 alloy. Int. J. Heat Mass Transf. 2008, 51, 6032–6038. [Google Scholar] [CrossRef]
- Yu, W.; Cao, Y.; Li, X.; Guo, Z.; Xiong, S. Determination of interfacial heat transfer behavior at the metal/shot sleeve of high pressure die casting process of AZ91D alloy. J. Mater. Sci. Technol. 2017, 33, 52–58. [Google Scholar] [CrossRef]
- Yang, H.-M.; Yu, W.-B.; Cao, Y.-Y.; Li, X.-B.; Guo, Z.-P.; Xiong, S.-M. Effect of different processing parameters on interfacial heat-transfer behavior in high-pressure die-casting process. Trans. Nonferrous Met. Soc. China 2018, 28, 2599–2606. [Google Scholar] [CrossRef]
- Sharifi, P.; Jamali, J.; Sadayappan, K.; Wood, J. Grain size distribution and interfacial heat transfer coefficient during solidification of magnesium alloys using high pressure die casting process. J. Mater. Sci. Technol. 2018, 34, 324–334. [Google Scholar] [CrossRef]
- Kan, M. Determination of the casting-mold interface heat transfer coefficient for numerically die-casting process depending on different mold temperatures. J. Mech. Sci. Technol. 2023, 37, 427–433. [Google Scholar] [CrossRef]
- Yalçin, B.; Koru, M.; Ipek, O.; Özgür, A.E. Effect of injection parameters and vacuum on the strength and porosity amount of die-casted A380 alloy. Int. J. Met. 2017, 11, 195–206. [Google Scholar] [CrossRef]
- Koru, M.; Serçe, O. The effects of thermal and dynamical parameters and vacuum application on porosity in high-pressure die casting of A383 Al-alloy. Int. J. Met. 2018, 12, 797–813. [Google Scholar] [CrossRef]
- Szalva, P.; Orbulov, I.N. The effect of vacuum on the mechanical properties of die cast aluminum AlSi9Cu3 (Fe) alloy. Int. J. Met. 2019, 13, 853–864. [Google Scholar] [CrossRef]
- Aksoy, B.; Koru, M. Estimation of casting mold interfacial heat transfer coefficient in pressure die casting process by artificial intelligence methods. Arab. J. Sci. Eng. 2020, 45, 8969–8980. [Google Scholar] [CrossRef]
- Kan, M.; Ipek, O.; Koru, M. An investigation into the effect of vacuum conditions on the filling analysis of the pressure casting process. Int. J. Met. 2023, 17, 430–446. [Google Scholar] [CrossRef]
- Aweda, J.O.; Adeyemi, M.B. Experimental determination of heat transfer coefficients during squeeze casting of aluminium. J. Mater. Process. Technol. 2009, 209, 1477–1483. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, L.; Sun, Z.; Hu, H.; Nie, X.; Tjong, J. Interfacial heat transfer in squeeze casting of magnesium alloy AM60 with variation of applied pressures and casting wall-thicknesses. Heat Mass Transf. 2016, 52, 2303–2315. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, L.; Hu, H.; Nie, X.; Tjong, J. Interfacial heat transfer of squeeze casting of wrought aluminum alloy 5083 with variation in wall thicknesses. Adv. Mater. Process. Technol. 2017, 3, 407–417. [Google Scholar] [CrossRef]
- Wang, F.; Wang, X.; Wu, K.; Han, Z. (Eds.) Study on the Effect of Die Coating Thickness on the Interfacial Heat Transfer Coefficient in Squeeze Casting of Aluminum Alloy. In TMS 2018 147th Annual Meeting & Exhibition Supplemental Proceedings; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Khawale, V.R.; Alshamrani, A.; Palanisamy, S.; Haldar, B.; Ramamurthy, S.; John, J.M.H.; Krishnamoorthy, S.; Sharma, M.; Alrasheedi, N.H. Analysis of interfacial heat transfer coefficients in squeeze casting of AA6061 aluminum alloy with H13 steel die: Impact of section thickness on thermal behavior. Therm. Sci. 2024, 28 Pt A, 223–232. [Google Scholar] [CrossRef]
- Teamah, A.; Teamah, A.; Hamed, M.; Shankar, S. (Eds.) On Replicating the Thermal Conditions in High Pressure Die Casting Processes. Available online: https://journals.library.torontomu.ca/index.php/ictea/article/view/2665 (accessed on 20 September 2025).
- Beals, R.; Niu, X.; Brown, Z. Development of advanced aluminum alloy for structural castings. In Light Metals 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 73–82. [Google Scholar] [CrossRef]
- Available online: https://thermtest.com/thermal-resources/materials-database (accessed on 20 September 2025).
- Sun, Z.; Hu, H.; Niu, X. Determination of heat transfer coefficients by extrapolation and numerical inverse methods in squeeze casting of magnesium alloy AM60. J. Mater. Process. Technol. 2011, 211, 1432–1440. [Google Scholar] [CrossRef]

| Thermal conductivity () () | |
| Specific heat () () | |
| Density () |
| Al | Si (%) | Mn (%) | Mg (%) | Fe (%) | Ti (%) | Sr (%) | Cu (%) | Cr (%) | P (%) |
|---|---|---|---|---|---|---|---|---|---|
| Balance | 10.35 | 0.56 | 0.29 | 0.186 | 0.07 | 0.022 | 0.02 | 0.01 | 0.001 |
| Thermal conductivity () | |
| Specific heat liquid () | |
| Specific heat Solid () | |
| Density liquid () | |
| Density Solid () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teamah, A.M.; Teamah, A.M.; Hamed, M.S.; Shankar, S. Experimental and Numerical Replication of Thermal Conditions in High-Pressure Die-Casting Process. Processes 2025, 13, 3815. https://doi.org/10.3390/pr13123815
Teamah AM, Teamah AM, Hamed MS, Shankar S. Experimental and Numerical Replication of Thermal Conditions in High-Pressure Die-Casting Process. Processes. 2025; 13(12):3815. https://doi.org/10.3390/pr13123815
Chicago/Turabian StyleTeamah, Abdelfatah M., Ahmed M. Teamah, Mohamed S. Hamed, and Sumanth Shankar. 2025. "Experimental and Numerical Replication of Thermal Conditions in High-Pressure Die-Casting Process" Processes 13, no. 12: 3815. https://doi.org/10.3390/pr13123815
APA StyleTeamah, A. M., Teamah, A. M., Hamed, M. S., & Shankar, S. (2025). Experimental and Numerical Replication of Thermal Conditions in High-Pressure Die-Casting Process. Processes, 13(12), 3815. https://doi.org/10.3390/pr13123815






