Heat Extraction Optimization of Well Clusters for Hydrothermal Reservoir Development
Abstract
1. Introduction
2. Materials and Methods
3. Model Description
- (1)
- Chemical interactions between reservoir rock and injected fluids are excluded;
- (2)
- Thermally induced stress variations are considered negligible;
- (3)
- Single-phase flow conditions governed by Darcy’s law are maintained throughout the extraction process;
- (4)
- Tiny cracks in the reservoir are not considered;
- (5)
- The wellbore geometry was reduced to a one-dimensional representation.
3.1. Governing Equation
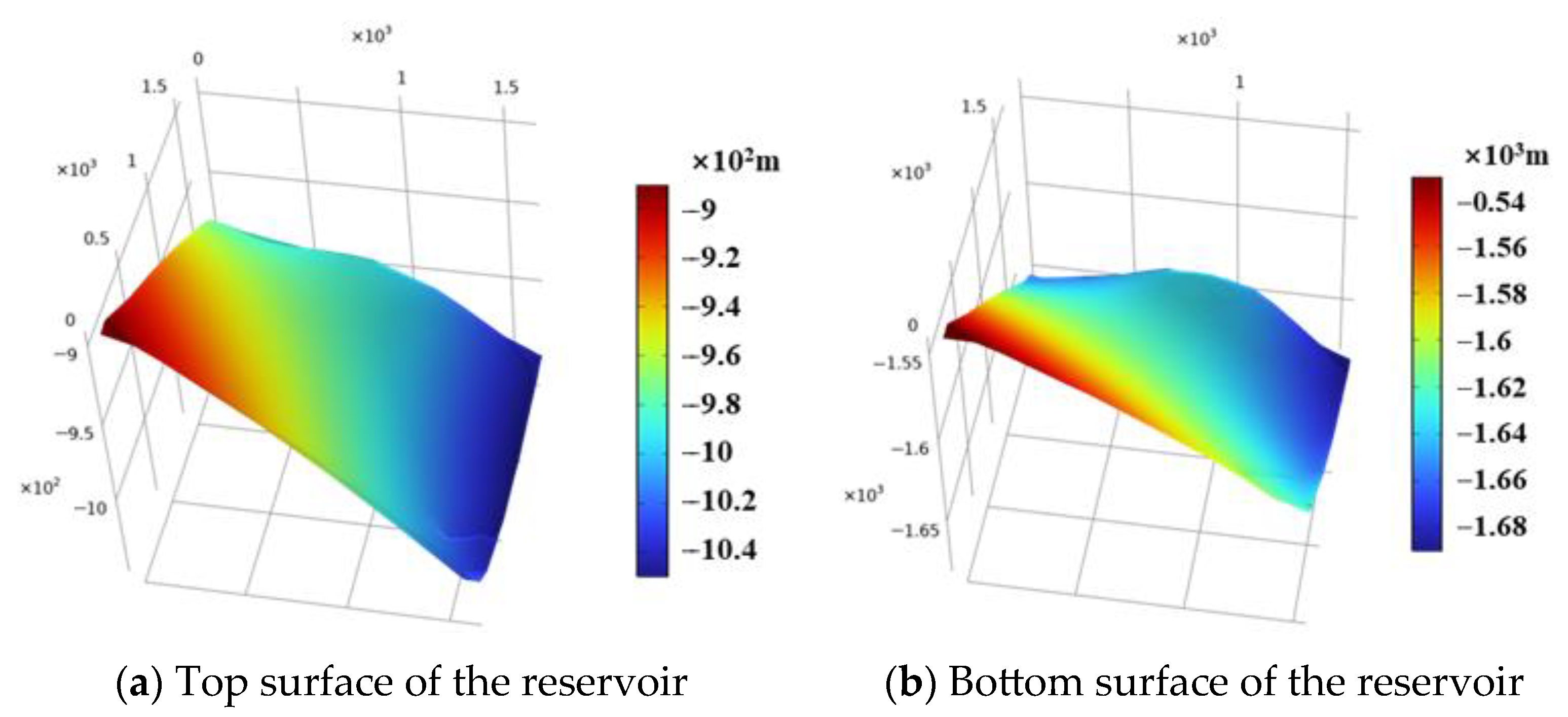
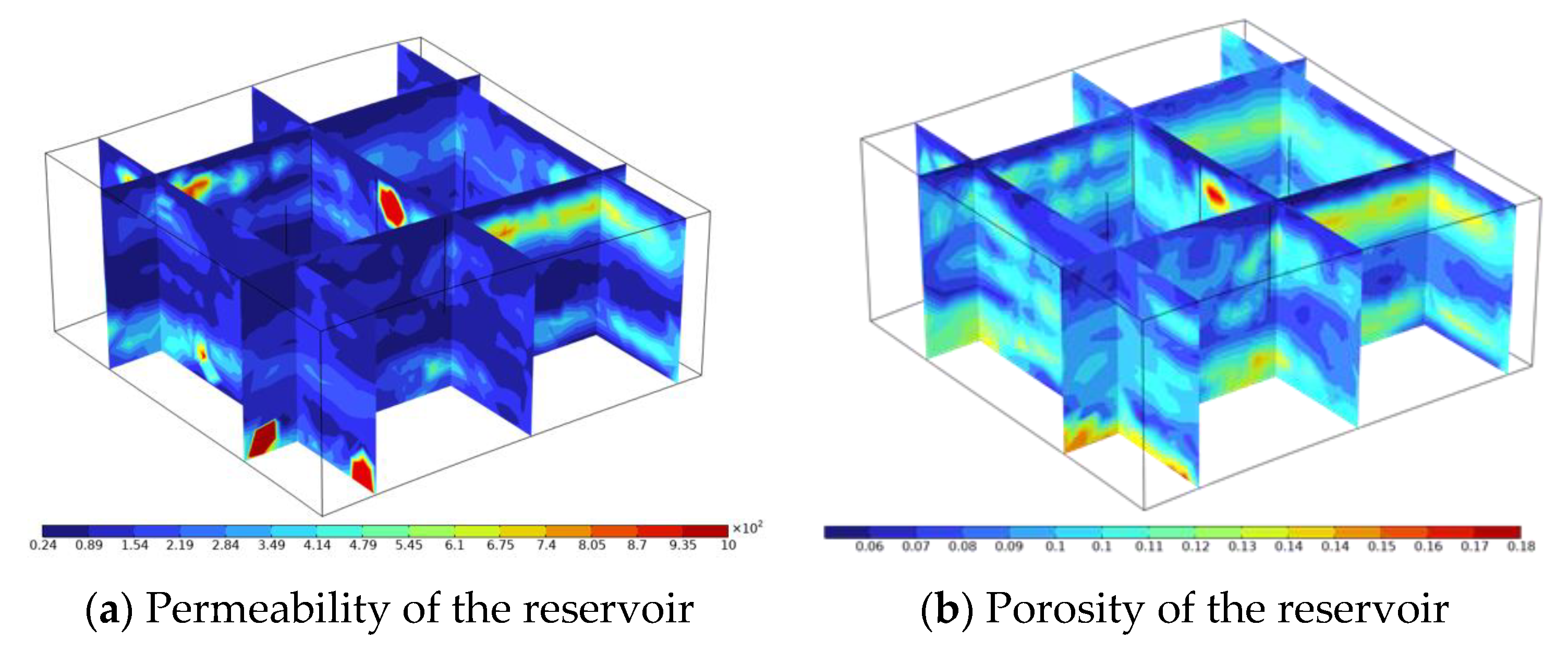
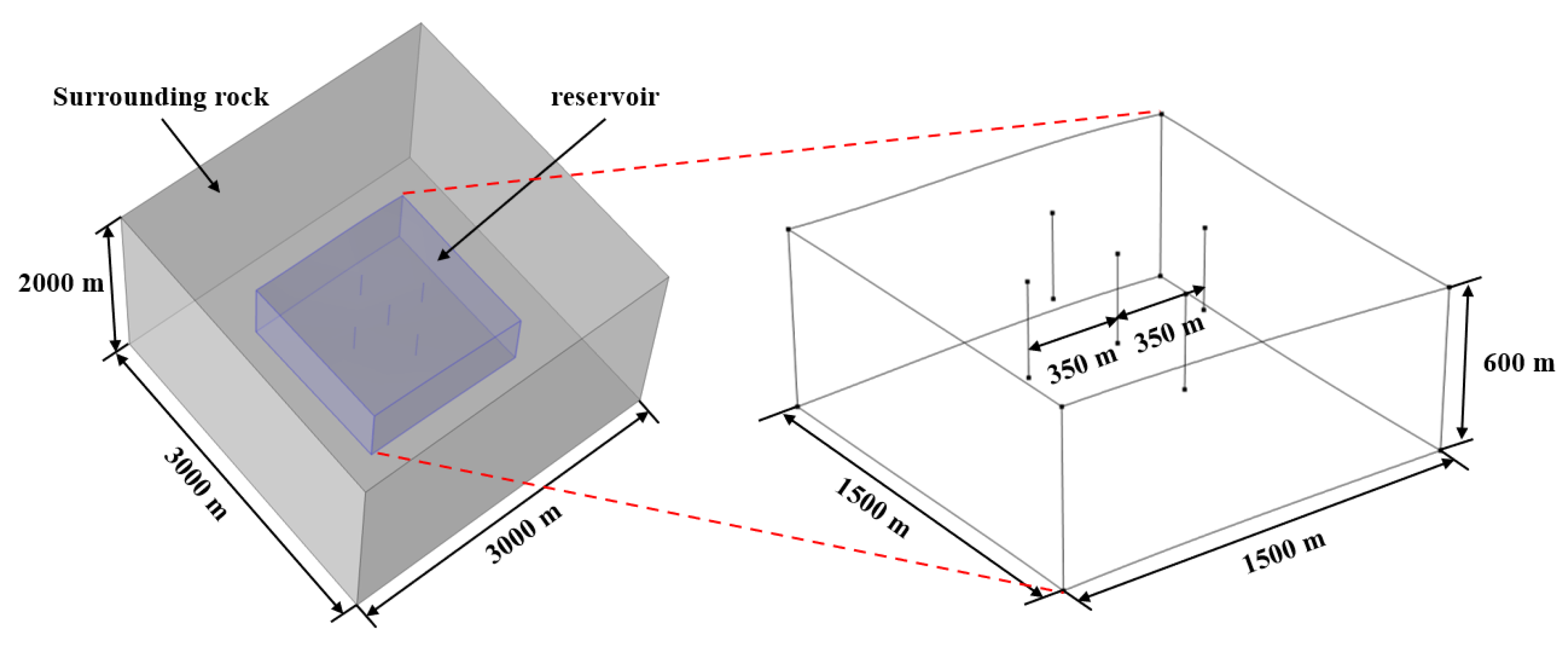
3.2. Geometric Model and Condition Settings
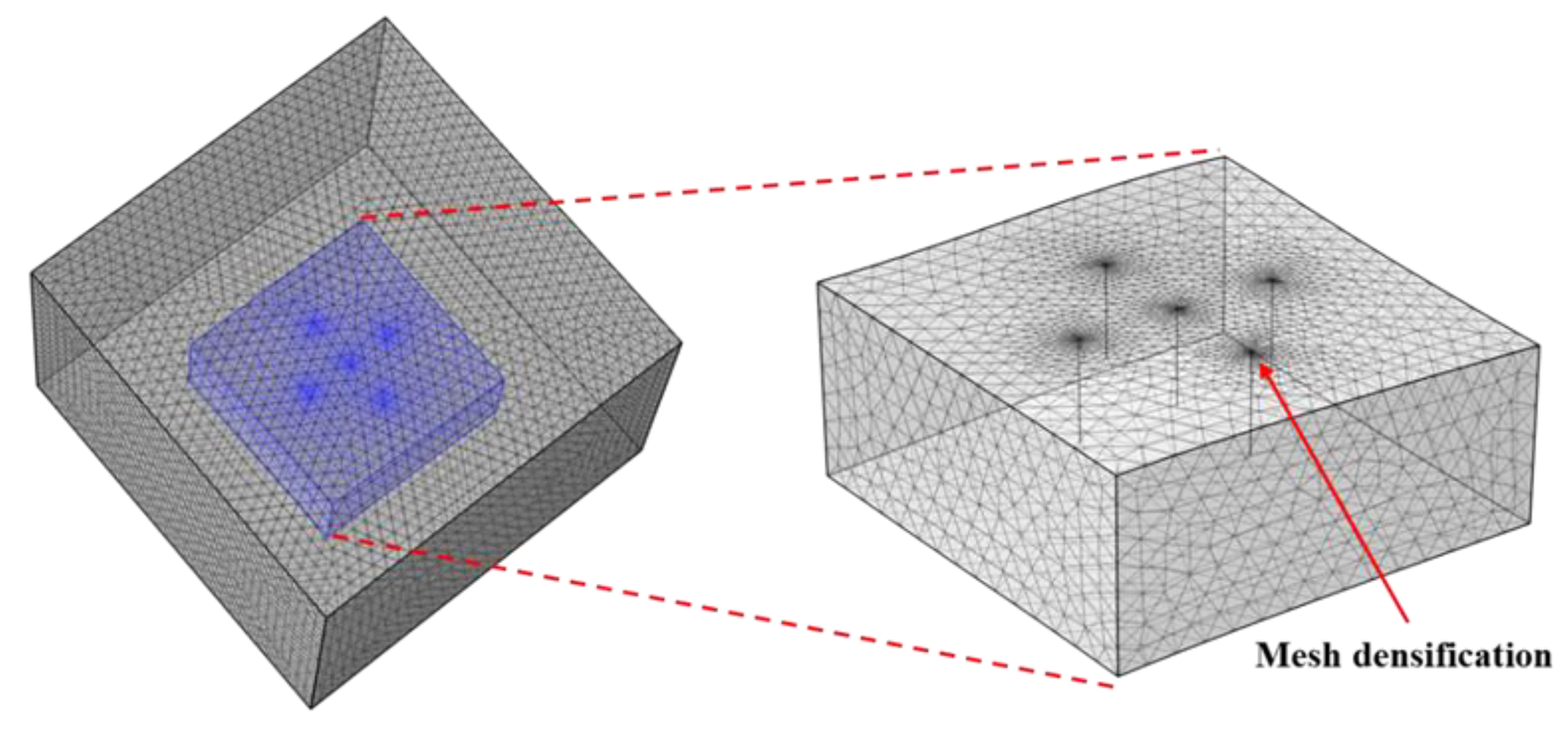
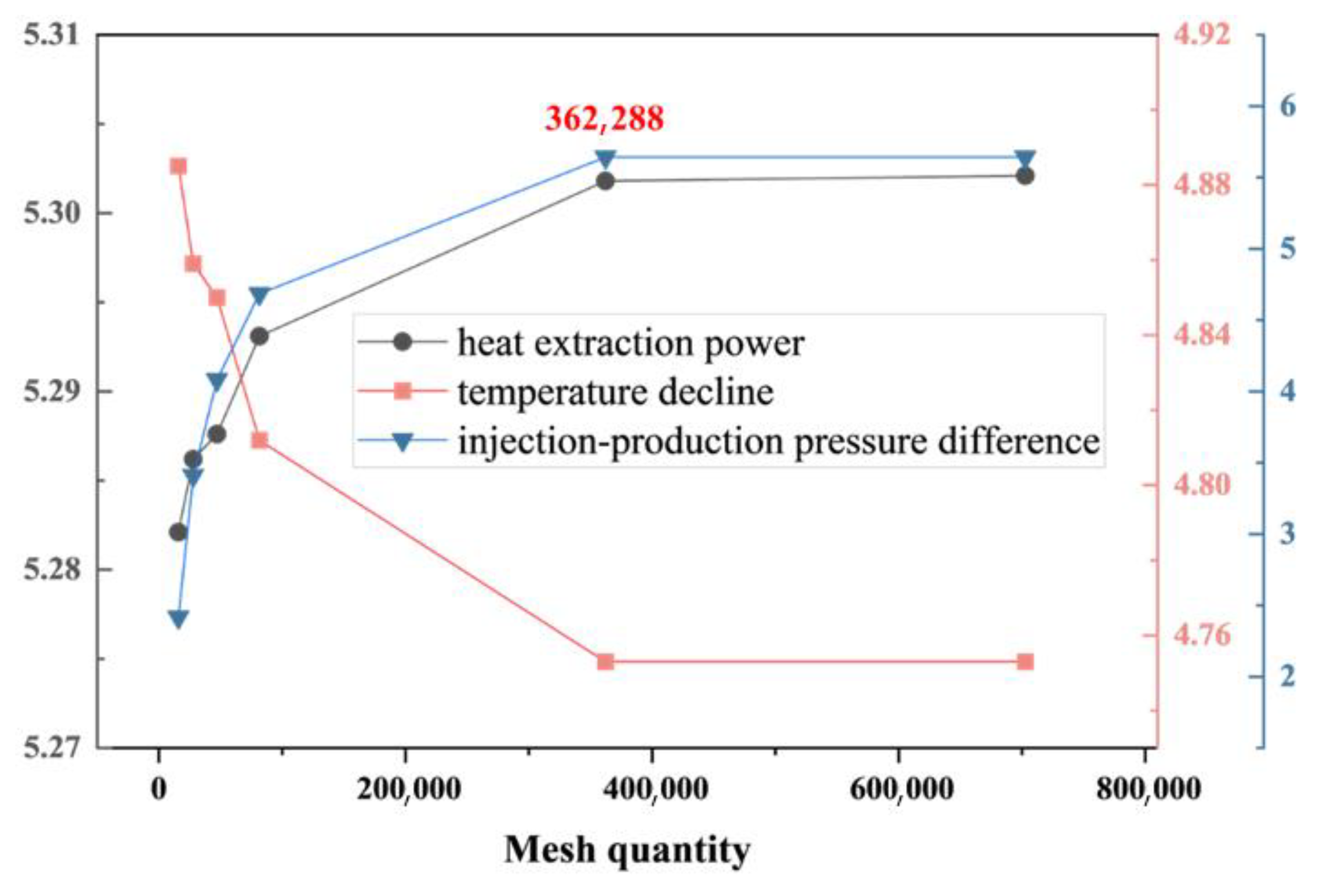
3.3. Verification of Grid Independence
3.4. Governing Equation
3.5. Numerical Simulation Software and Solver Settings
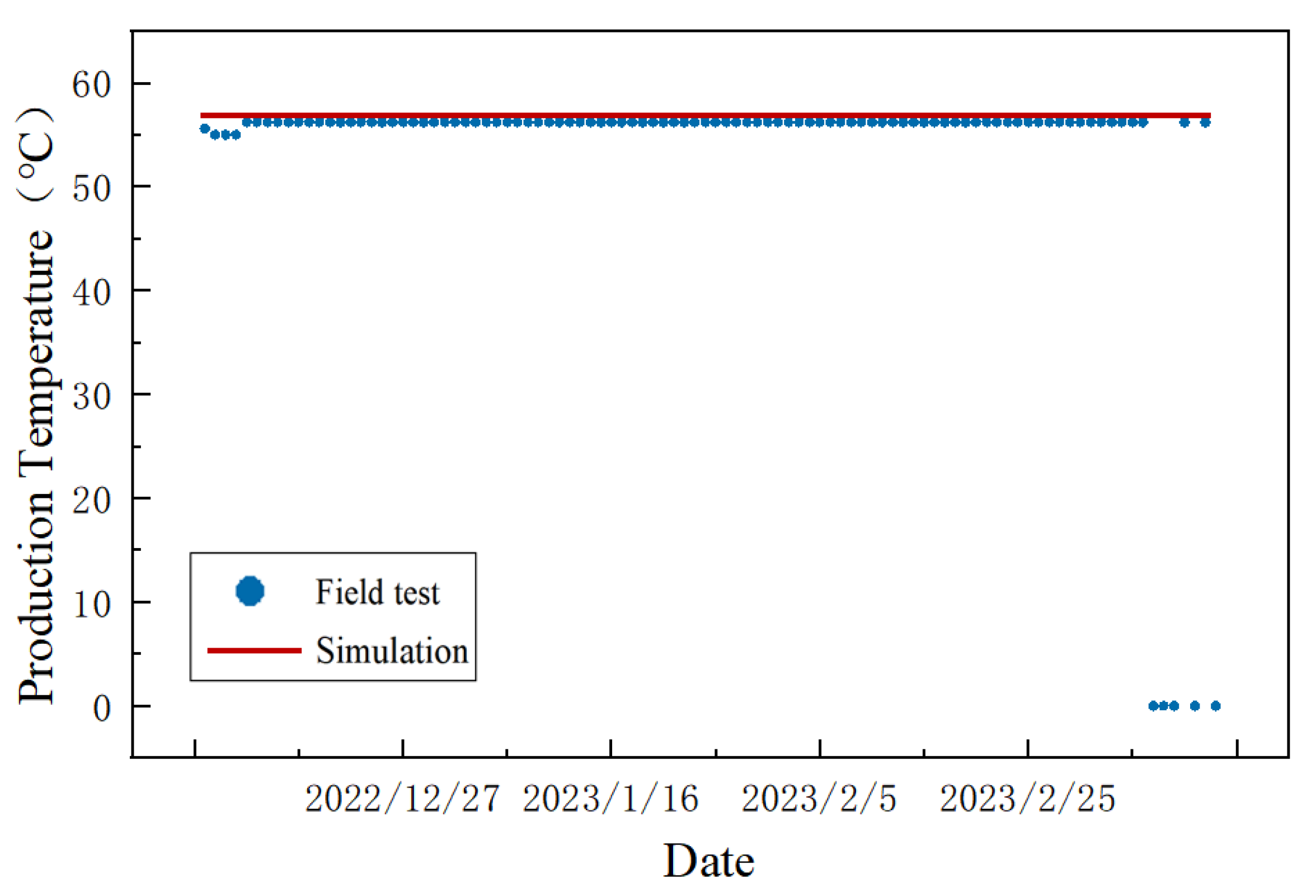
3.6. Model Validation
4. Results and Discussions
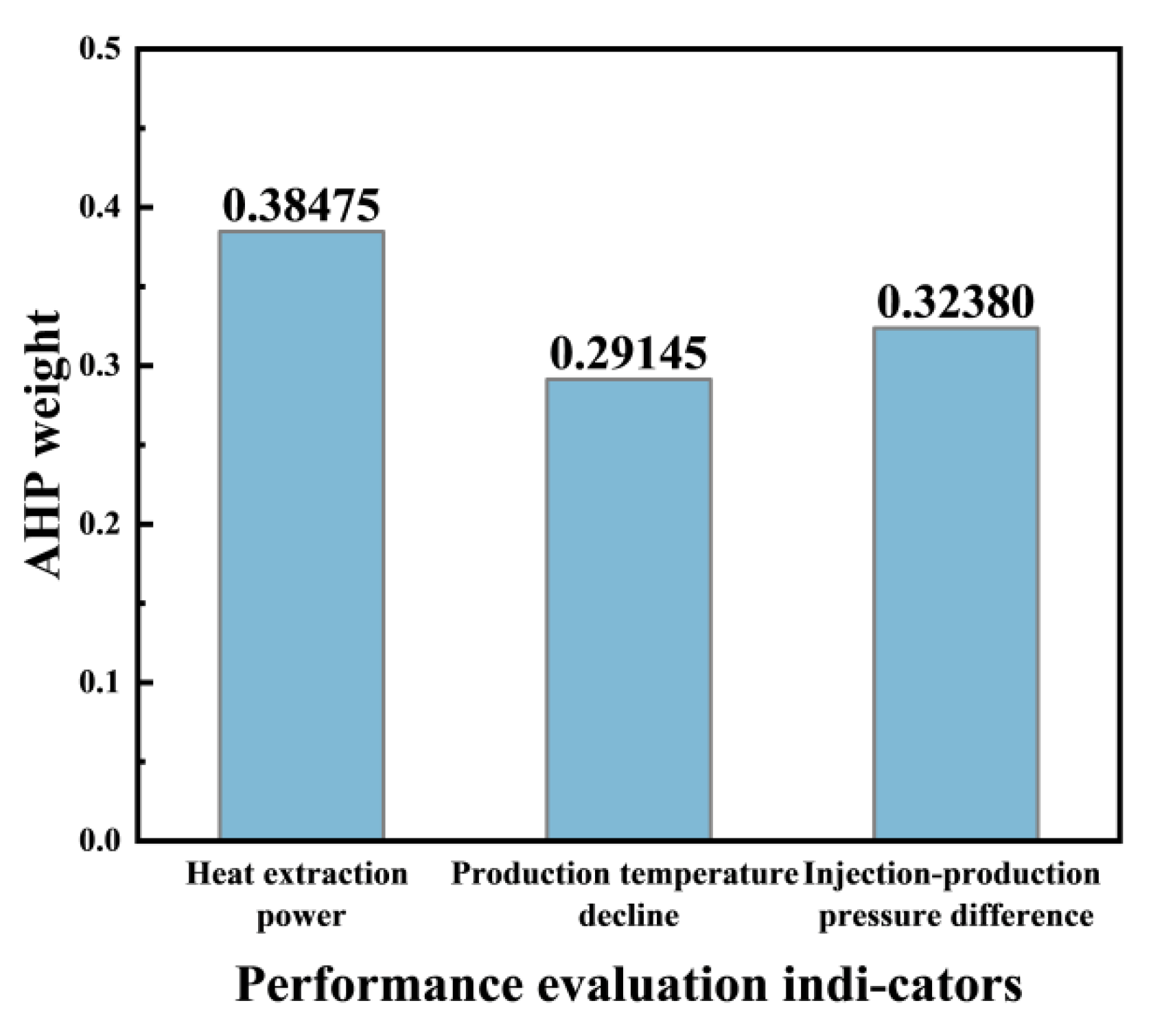
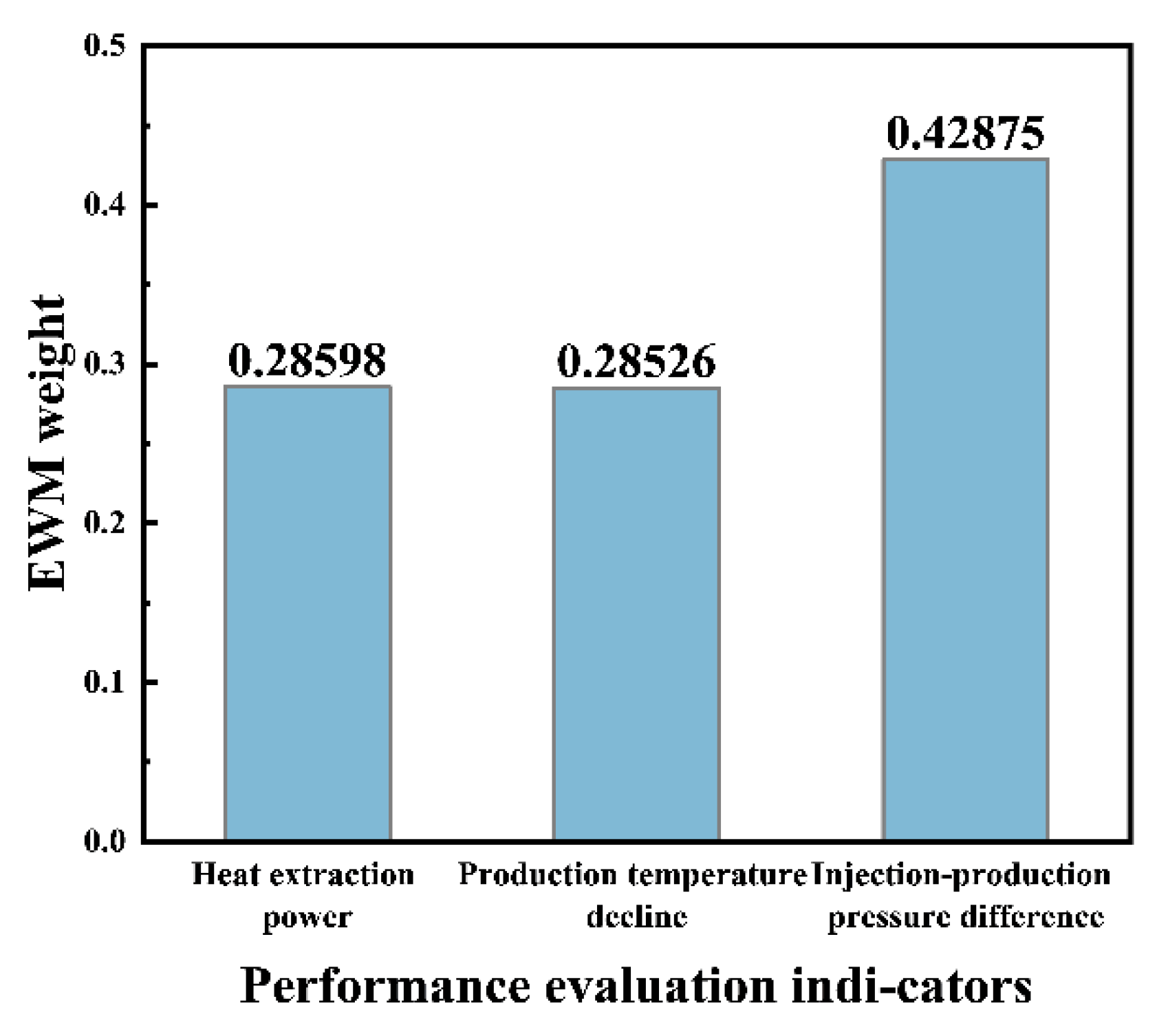
4.1. Performance Evaluation Indicators
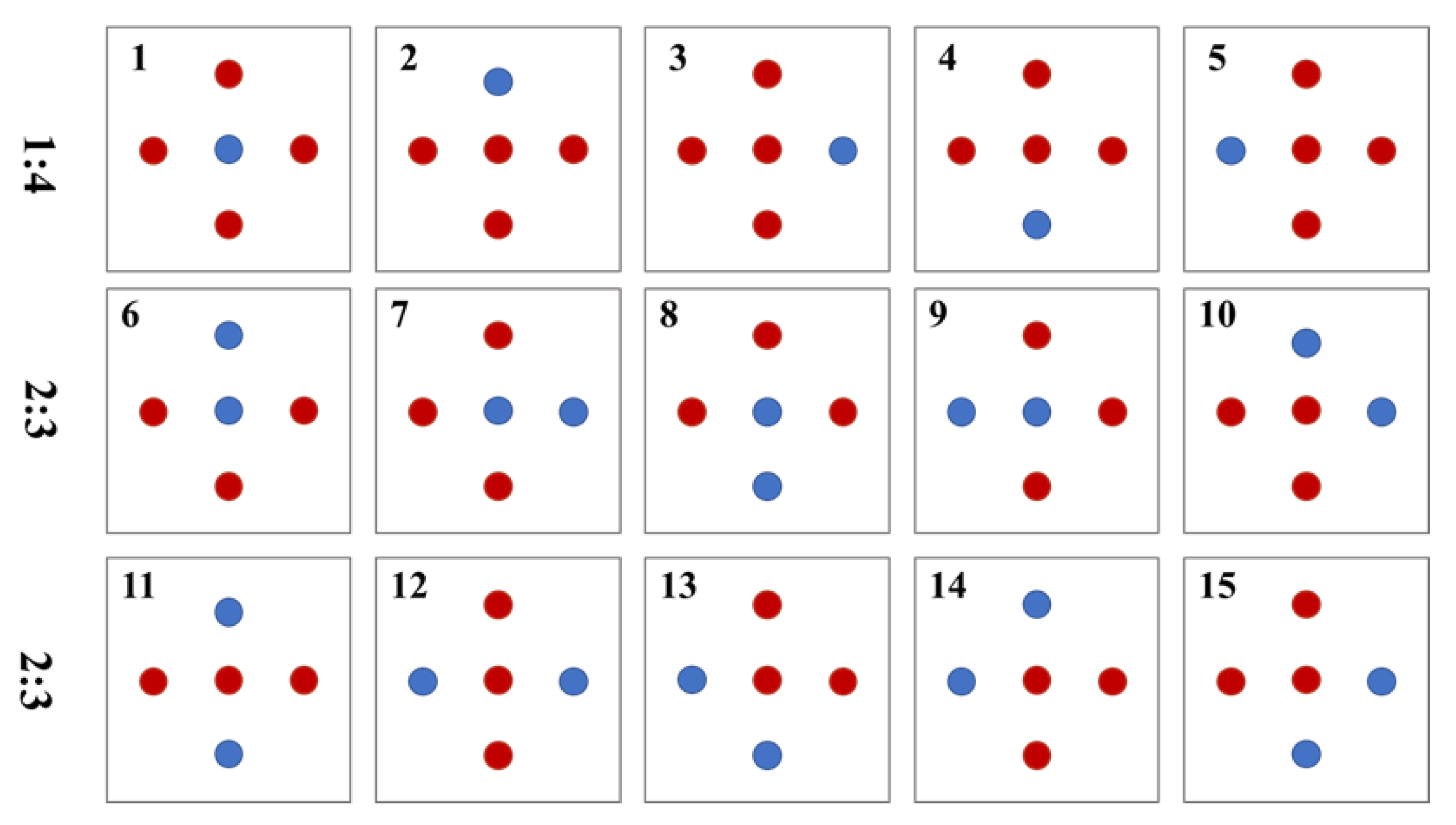
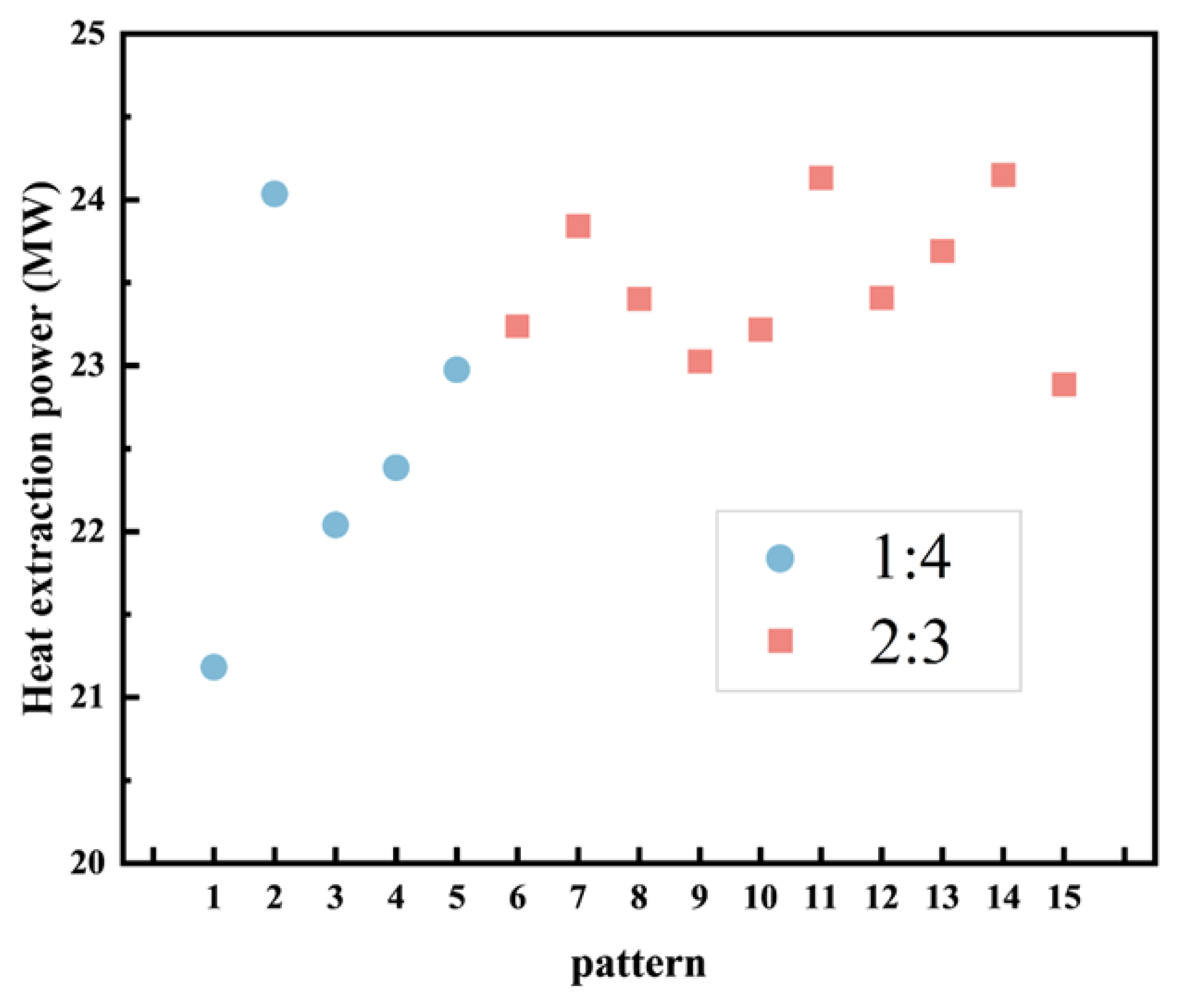
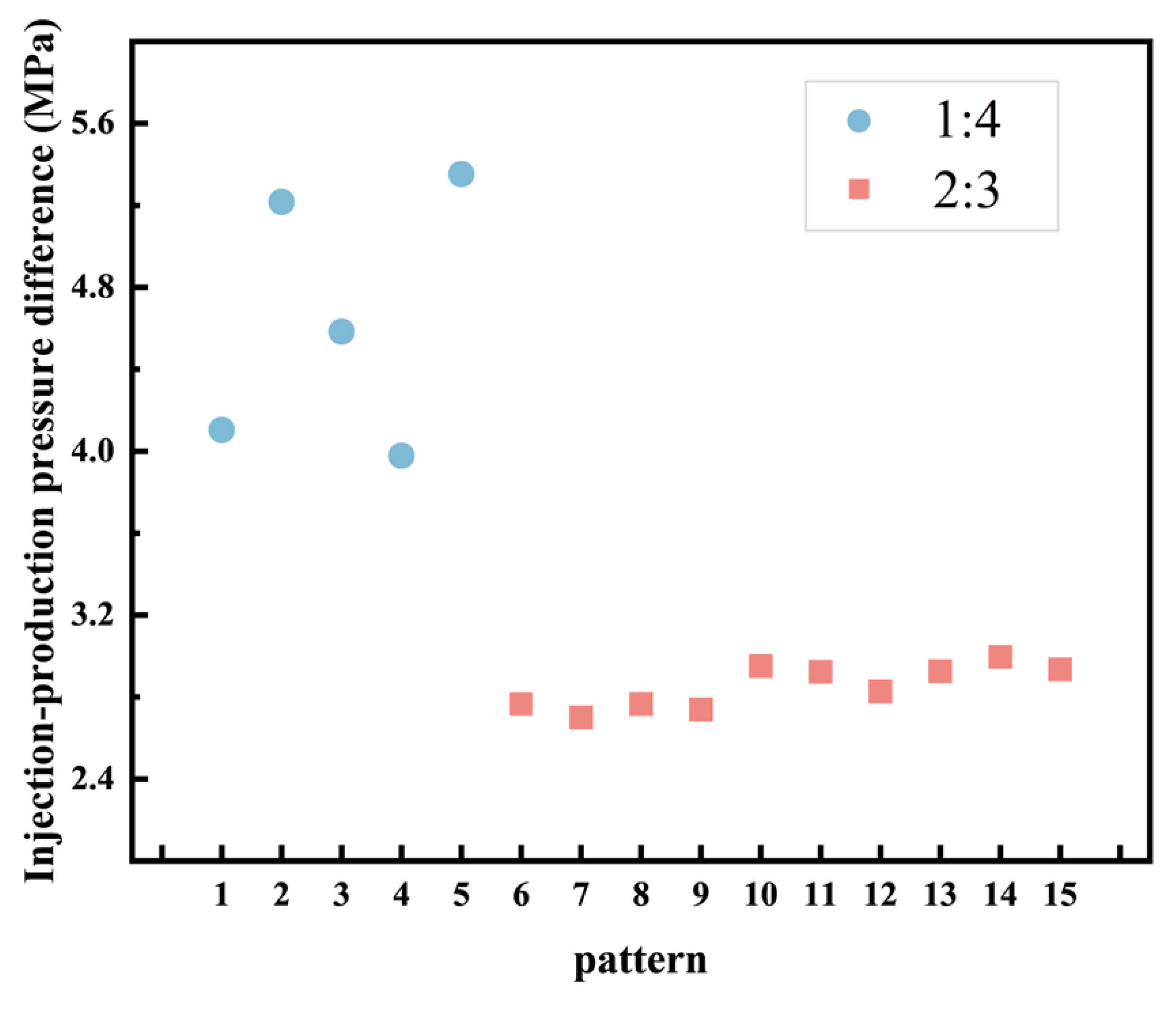
4.2. Performance of 15 Patterns
4.3. Multi-Attribute Decision
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bertani, R.J.G. Geothermal power generation in the world 2010–2014 update report. Geothermics 2016, 60, 31–43. [Google Scholar] [CrossRef]
- Wang, G.; Liu, Y.; Zhu, X.; Zhang, W. Current Status and Development Trends of Geothermal Resources in China. Earth Sci. Front. 2020, 27, 1–9. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, W.; Lin, W.; Liu, F.; Zhu, X.; Liu, Y.; Li, J. Research on formation mode and development potential of geothermal resources in Beijing-Tianjin-Hebei region. Geol. China 2017, 44, 1074–1085. [Google Scholar] [CrossRef]
- Wu, A.; Ma, F.; Wang, G.; Liu, J.; Hu, Q.; Miao, Q. A study of deep-seated karst geothermal reservoir exploration and huge capacity geothermal well parameters in Xiongan New Area. Acta Geosci. Sin. 2018, 39, 523–532. [Google Scholar] [CrossRef]
- Wang, F.; Cai, W.; Wang, M.; Gao, Y.; Liu, J.; Wang, Z.; Xu, J. Research Status and Prospect of Geothermal Heating Technology. J. Refrig. 2021, 42, 14–22. [Google Scholar] [CrossRef]
- Xiao, J.; Ji, H.; Hua, N.; Fang, C.; Li, H.; Ma, P. Sedimentary Facies Characteristics and Evolution of the Ordovician in the Dongpu Area, Bohai Bay Basin. Lithol. Reserv. 2016, 28, 78–87. [Google Scholar] [CrossRef]
- Wang, X.; Mao, X.; Mao, X.; Li, K. Characteristics and classification of the geothermal gradient in the Beijing–Tianjin–Hebei Plain, China. Math. Geosci. 2020, 52, 783–800. [Google Scholar] [CrossRef]
- Guo, X.; He, S.; Liu, K.; Shi, Z.; Bachir, S. Modelling the petroleum generation and migration of the third member of the Shahejie Formation (Es3) in the Banqiao Depression of Bohai Bay Basin, Eastern China. J. Asian Earth Sci. 2011, 40, 287–302. [Google Scholar] [CrossRef]
- Qiu, N.; Zuo, Y.; Zhou, X.; Li, C. Geothermal regime of the Bohai offshore area, Bohai Bay basin, North China. Energy Explor. Exploit. 2010, 28, 327–350. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, J. Prospects for Geothermal Energy Utilization in Oilfields of the Bohai Rim and Beijing-Tianjin Region. Acta Sci. Nat. Univ. Pekin. (Nat. Sci. Ed.) 2012, 36, 182–185. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Zhou, M.; Song, X.; Shi, Y.; Yi, J.; Zhao, J.; Zhou, Y. Thermal performance of an aquifer thermal energy storage system: Insights from novel multilateral wells. Energy 2024, 294, 130915. [Google Scholar] [CrossRef]
- Pandey, S.; Chaudhuri, A.; Kelkar, S. A coupled thermo-hydro-mechanical modeling of fracture aperture alteration and reservoir deformation during heat extraction from a geothermal reservoir. Geothermics 2017, 65, 17–31. [Google Scholar] [CrossRef]
- Xu, F.; Ma, T.; Tang, Y.; Song, X.; Shi, Y. Evaluation of heat extraction performance for vertical multi-fractures in enhanced geothermal system. Energy Sources Part A Recovery Util. Environ. Eff. 2025, 47, 9215–9236. [Google Scholar] [CrossRef]
- Liu, G.; Wang, G.; Zhao, Z.; Ma, F. A new well pattern of cluster-layout for deep geothermal reservoirs: Case study from the Dezhou geothermal field, China. Renew. Energy 2020, 155, 484–499. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, Z.; Peng, J.; Zhou, M.; Song, X.; Cui, Q.; Fan, M. CO2 storage characteristics and migration patterns under different abandoned oil and gas well types. Energy 2024, 292, 130545. [Google Scholar] [CrossRef]
- Kane, E.; Leeuwenburgh, O.; Joosten, G.; Daniilidis, A.; Bruhn, D. Flexible well patterns and cashflow optimisation on large-scale geothermal field development. Renew. Energy 2025, 243, 122494. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, Z.; Liu, G.; Xu, H. A robust optimization approach of well placement for doublet in heterogeneous geothermal reservoirs using random forest technique and genetic algorithm. Energy 2022, 254, 124427. [Google Scholar] [CrossRef]
- Cai, X.; Liu, Z.; Xu, K.; Li, B.; Zhong, X.; Yang, M. Numerical simulation study of an Enhanced Geothermal System with a five-spot pattern horizontal well based on thermal-fluid-solid coupling. Appl. Therm. Eng. 2025, 258, 124649. [Google Scholar] [CrossRef]
- Hou, X.; Chen, C.; Zhong, X.; Nie, S.; Wang, Y.; Tu, G. Numerical simulation study of closed-loop geothermal system well pattern optimisation and production potential. Appl. Therm. Eng. 2023, 231, 120864. [Google Scholar] [CrossRef]
- Gudala, M.; Govindarajan, S.K.; Yan, B.; Sun, S. Numerical investigations of the PUGA geothermal reservoir with multistage hydraulic fractures and well patterns using fully coupled thermo-hydro-geomechanical modeling. Energy 2022, 253, 124173. [Google Scholar] [CrossRef]
- Cui, Q.; Shi, Y.; Yang, Z.; Song, X.; Peng, J.; Liu, Q.; Fan, M.; Wang, L. An integrated system of CO2 geological sequestration and aquifer thermal energy storage: Storage characteristics and applicability analysis. Energy Convers. Manag. 2024, 318, 118876. [Google Scholar] [CrossRef]
- Franek, J.; Zmeškal, Z. A model of strategic decision making using decomposition SWOT-ANP method. In Proceedings of the Financial Management of Firms and Financial Institutions 9th International Scientific Conference Proceedings (Part I–III), Ostrava, Czech Republic, 9–10 September 2013; VŠB–Technical University of Ostrava: Ostrava, Czech Republic, 2013; pp. 172–180. [Google Scholar]

| Items | Value |
|---|---|
| Density of rock, kg/m3 | 2800 |
| Porosity of surrounding rocks, - | 0.05 |
| Permeability of surrounding rocks, mD | 5 |
| Heat capacity of rock, J/(kg·K) | 1100 |
| Thermal conductivity of reservoirs, W/(m·K)) | 4 |
| Thermal conductivity of surrounding, W/(m·K)) | 3 |
| Reinjection ratio | 100% |
| Production rate, m3/h | 126/168 |
| Injection temperature, °C | 15 |
| Well spacing | 350 |
| Performance Evaluation Indicators | Heat Extraction Power | Production Temperature Decline | Injection–Production Pressure Difference |
|---|---|---|---|
| AHP weight | 38.475% | 29.145% | 32.380% |
| EWM weight | 28.598% | 28.526% | 42.875% |
| Comprehensive weight | 33.42% | 29.05% | 37.53% |
| Pattern | Positive Ideal Solution Distance (D+) | Negative Ideal Distance (D−) | Comprehensive Score Index | Rank |
|---|---|---|---|---|
| 1 | 0.854076877 | 0.288970441 | 0.252807068 | 15 |
| 2 | 0.583132119 | 0.766576085 | 0.567956898 | 11 |
| 3 | 0.704751865 | 0.295407336 | 0.295360314 | 14 |
| 4 | 0.558781122 | 0.447681791 | 0.444807042 | 12 |
| 5 | 0.689883411 | 0.473173885 | 0.406836264 | 13 |
| 6 | 0.236075339 | 0.814727216 | 0.775338062 | 7 |
| 7 | 0.070599154 | 0.946419877 | 0.930582268 | 3 |
| 8 | 0.202262975 | 0.83809144 | 0.805582624 | 6 |
| 9 | 0.303728031 | 0.775314349 | 0.718520758 | 9 |
| 10 | 0.240002554 | 0.787058407 | 0.766321023 | 8 |
| 11 | 0.05100757 | 0.967360739 | 0.949912453 | 1 |
| 12 | 0.195205893 | 0.834546631 | 0.810434169 | 5 |
| 13 | 0.143802737 | 0.863194984 | 0.857196561 | 4 |
| 14 | 0.069352906 | 0.959080935 | 0.932564543 | 2 |
| 15 | 0.335093424 | 0.724020408 | 0.683609624 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yi, J.; Wang, G.; Wei, Q.; Li, S.; Cui, Q.; Zhao, J. Heat Extraction Optimization of Well Clusters for Hydrothermal Reservoir Development. Processes 2025, 13, 3791. https://doi.org/10.3390/pr13123791
Li X, Yi J, Wang G, Wei Q, Li S, Cui Q, Zhao J. Heat Extraction Optimization of Well Clusters for Hydrothermal Reservoir Development. Processes. 2025; 13(12):3791. https://doi.org/10.3390/pr13123791
Chicago/Turabian StyleLi, Xiangchun, Junlin Yi, Gaosheng Wang, Qian Wei, Shuang Li, Qiliang Cui, and Jialin Zhao. 2025. "Heat Extraction Optimization of Well Clusters for Hydrothermal Reservoir Development" Processes 13, no. 12: 3791. https://doi.org/10.3390/pr13123791
APA StyleLi, X., Yi, J., Wang, G., Wei, Q., Li, S., Cui, Q., & Zhao, J. (2025). Heat Extraction Optimization of Well Clusters for Hydrothermal Reservoir Development. Processes, 13(12), 3791. https://doi.org/10.3390/pr13123791






