Parameter Optimization of Wet Stirred Media Milling Using an Intelligent Algorithm-Based Stressing Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
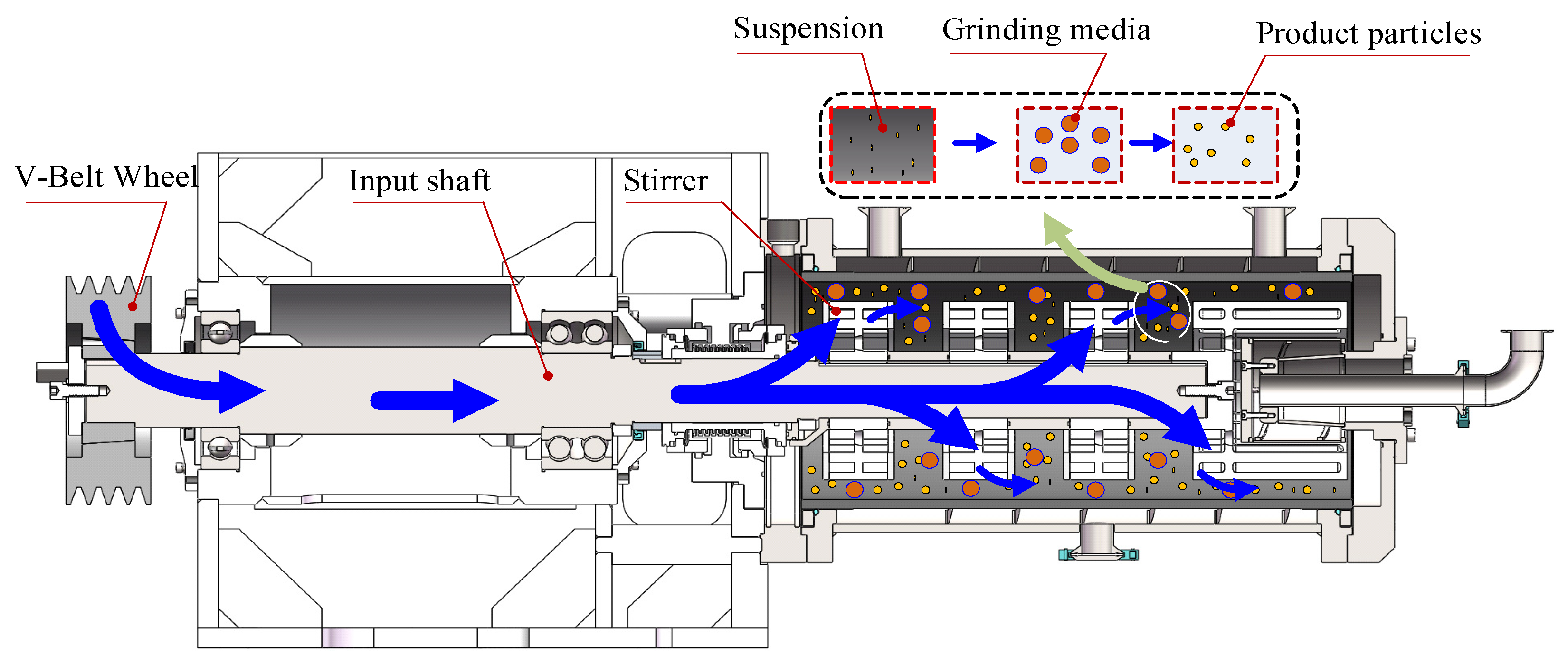
2.2.1. Energy Dissipation Mechanism in WSMM
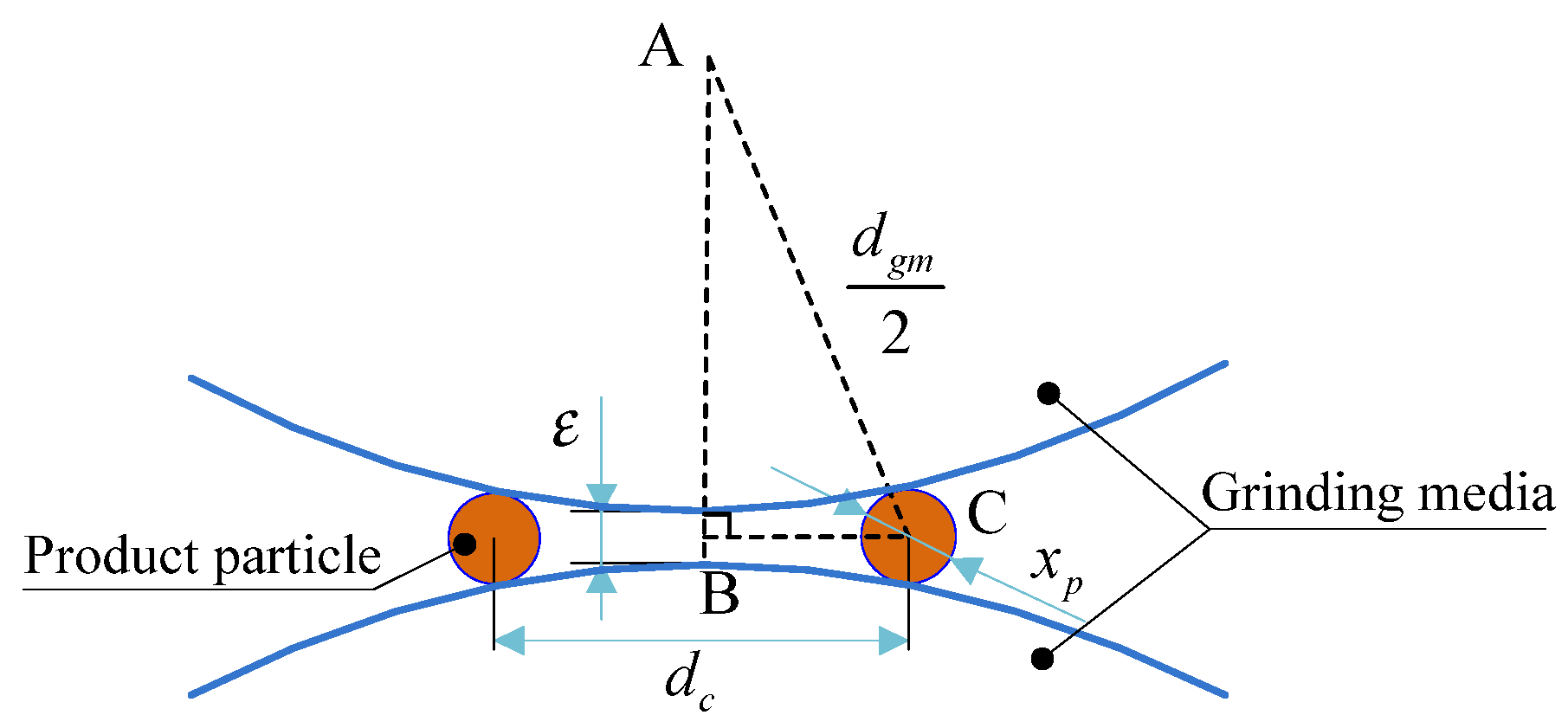
2.2.2. Parameter Optimization Using the Stressing Model
2.2.3. Optimization Strategy Using the Intelligent Algorithm
3. Results
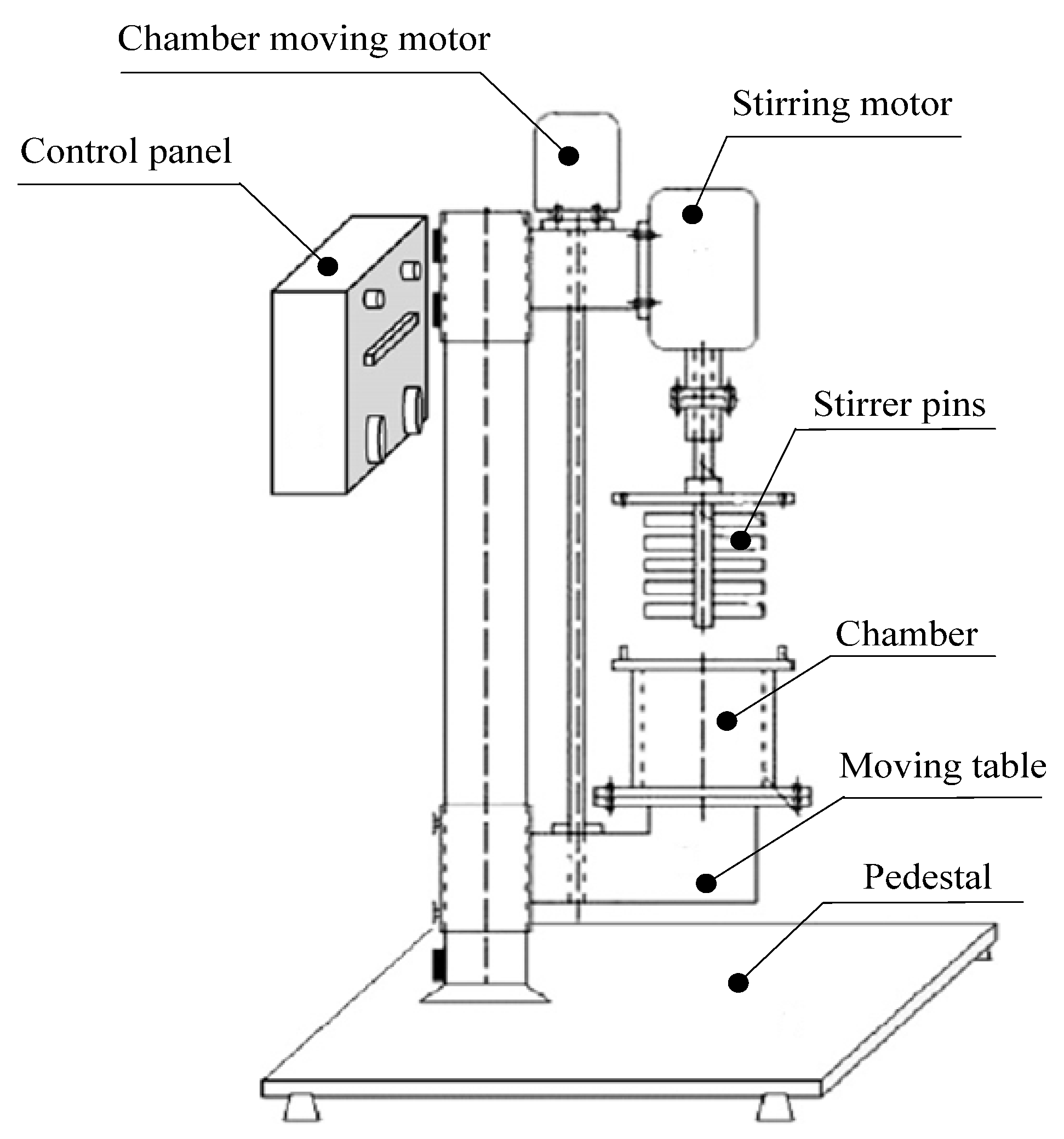
3.1. Application on Pin-Type Vertical Stirred Mill
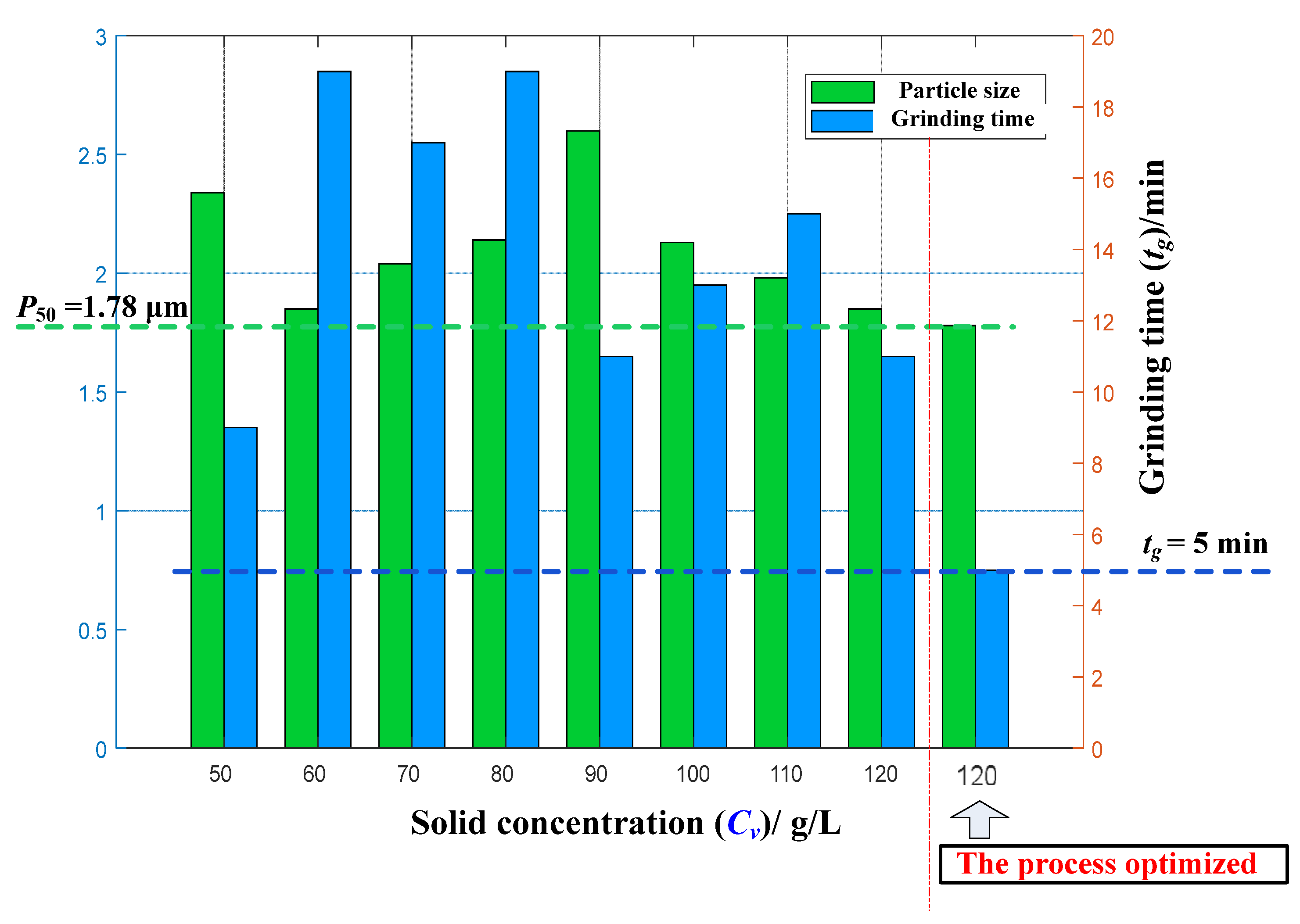
3.2. Application on Pin-Type Horizontal Stirred Mill
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Altun, O.; Toprak, A.; Altun, D.; Altun, D.; Bilgili, E. Assessment of different energy-based breakage distribution functions in population balance model of an industrial scale continuously operated wet stirred media mill. Miner. Eng. 2024, 218, 109054. [Google Scholar] [CrossRef]
- Siewert, C.; Moog, R.; Alex, R.; Kretzer, P.; Rothenhäusler, B. Process and scaling parameters for wet media milling in early phase drug development: A knowledge based approach. Eur. J. Pharm. Sci. 2018, 115, 126–131. [Google Scholar] [CrossRef]
- Guo, W.; Gao, P.; Tang, Z.; Han, Y.; Meng, X. Effect of grinding media properties and stirrer tip speed on the grinding efficiency of a stirred mill. Powder Technol. 2021, 382, 556–565. [Google Scholar] [CrossRef]
- Flach, F.; Breitung-Faes, S.; Kwade, A. Model based process optimization of nanosuspension preparation via wet stirred media milling. Powder Technol. 2018, 331, 146–154. [Google Scholar] [CrossRef]
- Kwade, A. A stressing model for the description and optimization of grinding processes. Chem. Eng. Technol. Ind. Chem.-Plant Equip.-Process Eng.-Biotechnol. 2003, 26, 199–205. [Google Scholar] [CrossRef]
- Kwade, A. Mill selection and process optimization using a physical grinding model. Int. J. Miner. Process. 2004, 74, S93–S101. [Google Scholar] [CrossRef]
- Alamprese, C.; Datei, L.; Semeraro, Q. Optimization of processing parameters of a ball mill refiner for chocolate. J. Food Eng. 2007, 83, 629–636. [Google Scholar] [CrossRef]
- Hou, T.H.; Su, C.H.; Liu, W.L. Parameters optimization of a nano-particle wet milling process using the Taguchi method, response surface method and genetic algorithm. Powder Technol. 2007, 173, 153–162. [Google Scholar] [CrossRef]
- Celep, O.; Aslan, N.; Alp, İ.; Taşdemir, G. Optimization of some parameters of stirred mill for ultra-fine grinding of refractory Au/Ag ores. Powder Technol. 2011, 208, 121–127. [Google Scholar] [CrossRef]
- Mäntynen, A.; Zakharov, A.; Jämsä-Jounela, S.L.; Graeffe, M. Optimization of grinding parameters in the production of colorant paste. Powder Technol. 2012, 217, 216–222. [Google Scholar] [CrossRef]
- Breitung-Faes, S.; Kwade, A. Use of an enhanced stress model for the optimization of wet stirred media milling processes. Chem. Eng. Technol. 2014, 37, 819–826. [Google Scholar] [CrossRef]
- Montalescot, V.; Rinaldi, T.; Touchard, R.; Jubeau, S.; Frappart, M.; Jaouen, P.; Bourseau, P.; Marchal, L. Optimization of bead milling parameters for the cell disruption of microalgae: Process modeling and application to Porphyridium cruentum and Nannochloropsis oculata. Bioresour. Technol. 2015, 196, 339–346. [Google Scholar] [CrossRef]
- Nekkanti, V.; Marwah, A.; Pillai, R. Media milling process optimization for manufacture of drug nanoparticles using design of experiments (DOE). Drug Dev. Ind. Pharm. 2015, 41, 124–130. [Google Scholar] [CrossRef] [PubMed]
- Brunaugh, A.; Smyth, H. Process optimization and particle engineering of micronized drug powders via milling. Drug Deliv. Transl. Res. 2018, 8, 1740–1750. [Google Scholar] [CrossRef] [PubMed]
- Katircioglu-Bayel, D. Impact of operating parameters on the breakage process of talc. Min. Metall. Explor. 2020, 37, 1717–1727. [Google Scholar] [CrossRef]
- Santosh, T.; Soni, R.K.; Eswaraiah, C.; Rao, D.; Venugopal, R. Optimization of stirred mill parameters for fine grinding of PGE bearing chromite ore. Part. Sci. Technol. 2020, 39, 663–675. [Google Scholar] [CrossRef]
- Katircioglu-Bayel, D. Optimization of operating parameters on dry grinding of calcite in a stirred media mill using the Box-Behnken design. Minerals 2020, 10, 251. [Google Scholar] [CrossRef]
- Amini, R.K.; Kitamura, Y.; Islam, M.Z.; Kokawa, M.; Eseese, V.F. Impact of micro wet milling process on pomegranate peel phenolics extraction using multi-response optimization. J. Food Meas. Charact. 2021, 15, 2865–2876. [Google Scholar] [CrossRef]
- Guner, G.; Mehaj, M.; Seetharaman, N.; Elashri, S.; Yao, H.F.; Clancy, D.J.; Bilgili, E. Do mixtures of beads with different sizes improve wet stirred media milling of drug suspensions? Pharmaceutics 2023, 15, 2213. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, Y.; Sobhy, A. Prediction and optimization of tower mill grinding power consumption based on GA-BP neural network. Physicochem. Probl. Miner. Process. 2023, 59, 172096. [Google Scholar] [CrossRef]
- BAHETI, V.; ABBASI, R.; MILITKY, J. Optimisation of ball milling parameters for refinement of waste jute fibres to nano/micro scale in dry conditions. J. Text. Eng. 2013, 59, 87–92. [Google Scholar] [CrossRef]
- Gbadeyan, O.J.; Sithole, B.; Adali, S.; Bright, G. Process optimization of nano-calcium carbonate produced from snail shell using supermasscollider. Part. Sci. Technol. 2024, 42, 659–667. [Google Scholar] [CrossRef]
- Guo, K.; Chen, H.; Liu, Q.; Guo, W.; Li, Y.; Xing, Y.; Gui, X. Optimizing the process parameters in stirred-media mills using mathematical modeling. Part. Sci. Technol. 2025, 43, 217–228. [Google Scholar] [CrossRef]
- Bilgili, E.; Guner, G. Mechanistic modeling of wet stirred media milling for production of drug nanosuspensions. AAPS PharmSciTech 2020, 22, 2. [Google Scholar] [CrossRef] [PubMed]
- Coello, C.C. Evolutionary multi-objective optimization: A historical view of the field. IEEE Comput. Intell. Mag. 2006, 1, 28–36. [Google Scholar] [CrossRef]
- Romeis, S.; Schmidt, J.; Peukert, W. Mechanochemical aspects in wet stirred media milling. Int. J. Miner. Process. 2016, 156, 24–31. [Google Scholar] [CrossRef]
- Becker, M.; Kwade, A.; Schwedes, J. Stress intensity in stirred media mills and its effect on specific energy requirement. Int. J. Miner. Process. 2001, 61, 189–208. [Google Scholar] [CrossRef]
- Kwade, A.; Schwedes, J. Breaking characteristics of different materials and their effect on stress intensity and stress number in stirred media mills. Powder Technol. 2002, 122, 109–121. [Google Scholar] [CrossRef]
- Kwade, A. Determination of the most important grinding mechanism in stirred media mills by calculating stress intensity and stress number. Powder Technol. 1999, 105, 382–388. [Google Scholar] [CrossRef]
- Zohrehvandi, M.; Zohrehvandi, S.; Khalilzadeh, M.; Amiri, M.; Jolai, F.; Zavadskas, E.K.; Antucheviciene, J. A multi-objective mathematical programming model for project-scheduling optimization considering customer satisfaction in construction projects. Mathematics 2024, 12, 211. [Google Scholar] [CrossRef]
- Pereira, J.L.J.; Oliver, G.A.; Francisco, M.B.; Cunha Jr, S.S.; Gomes, G.F. A review of multi-objective optimization: Methods and algorithms in mechanical engineering problems. Arch. Comput. Methods Eng. 2022, 29, 2285–2308. [Google Scholar] [CrossRef]
- He, K.; Jia, M.; Sun, F.; Yang, Q.; Wu, B.; Li, X.; Meng, C. Simulation of grinding media motion and collisions in wet-operated accelerator-mill using DEM coupled with CFD. Minerals 2022, 12, 341. [Google Scholar] [CrossRef]



| Process Parameters | Mill Type | Optimization Approaches | Object/Response | Ref. |
|---|---|---|---|---|
| Stirrer tip speed Grinding media size | Lab scale disc mill | Stress model Micro hydrodynamic model | Particle sizes Specific energy input | [4,14] |
| Stirrer tip speed Grinding media size Grinding media density | Lab scale disc mill | Stress model | Average stress energy Specific energy input | [5,6,11] |
| Media filling ratio Grinding media size Stirrer speed Grinding time Feed size Solid concentration | Vertical-type stirred media mill | Box–Behnken statistical design | Product particle size Surface area Energy consumption | [15,16] |
| Bead size Filling ratio Flow rate | Dyno®-mill | Stress intensities and stress number | Cell destruction kinetics Specific energy | [12] |
| Rotational speed Solid-to-solvent ratio Ethanol-to-water ratio | Micro wet milling | Response surface methodology | Total phenolic content Total anthocyanin content | [18] |
| Refining time Agitator shaft speed Bead volume | Stirred media mill | Response surface regression Central composite design | Electricity consumption Particle size Iron content Refining time Process yield | [7,13] |
| Tinting paste viscosity Bead charge Grinding bead size Rotor velocity Recycle flow rate | DCP-UPERFLOW® high-performance agitated media mill | Pareto-optimal solutions | Tinting strength Grinding power | [10] |
| Milling time Flow velocity Agitator rotation Weight ratio Bead filling ratio | Vertical milling machine | Taguchi method Response surface method Genetic algorithm | Mean grain size Variance of grain size | [8,9] |
| Zirconia bead sizes Bead loading | Wet stirred media milling | Microhydrodynamic model augmented with a decision tree | Solution flow rate Gas flow rate Solution concentration | [19] |
| Stirrer speed Grinding time Media filling ratio Solid mass fraction | Stirred media mill | Three-level Box–Behnken design | Mean grain size | [17] |
| Grinding concentration Screw speed Medium filling rate Material–ball ratio | Tower mill | BP neural network optimized by the GA | Grinding power consumption | [20] |
| Milling time Milling speed Ball to material ratio ball size | High energy planetary ball mill | A three-level Box-Behnken design combining a response surface methodology | Particle size and sticking of material to mill | [21] |
| Microparticle loading Number of runs | Supermasscolloider wet milling | Response surface design method | Particle size | [22] |
| Element | CaCO2 | MgO | Al2O3 | Fe2O3 | Insoluble Matter | Loss on Ignition |
|---|---|---|---|---|---|---|
| Content (%) | 98.5 | 0.8 | 0.1 | 0.05 | 0.2 | 0.35 |
| Element | SiO2 | Fe2O3 | Cu | Ba | Sb | Zn | Sr | Tot. S | Pb | Tot. C | Loss on Ignition |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Content (%) | 52.15 | 1.28 | 0.04 | 17.10 | 1.64 | 1.50 | 0.31 | 6.89 | 0.43 | 0.05 | 4.60 |
| Run | Coded Level | Actual Level | P80 (μm) | |||||
|---|---|---|---|---|---|---|---|---|
| v1 | v2 | v3 | dgm/mm | nsr/rpm | φgm/% | Observed | Predicted | |
| 1 | −1 | 1 | 0 | 1 | 750 | 70 | 4.35 | 4.32 |
| 2 | 0 | −1 | −1 | 3 | 250 | 60 | 9.23 | 9.26 |
| 3 | 0 | 0 | 0 | 3 | 500 | 70 | 5.61 | 5.73 |
| 4 | 0 | 0 | 0 | 3 | 500 | 70 | 5.75 | 5.73 |
| 5 | −1 | −1 | 0 | 1 | 250 | 70 | 9.79 | 9.86 |
| 6 | 0 | 1 | −1 | 3 | 750 | 60 | 5.17 | 5.08 |
| 7 | 1 | 0 | 1 | 5 | 500 | 80 | 8.05 | 7.66 |
| 8 | −1 | 0 | −1 | 1 | 500 | 60 | 6.80 | 6.78 |
| 9 | −1 | 0 | 1 | 1 | 500 | 80 | 5.22 | 4.82 |
| 10 | 0 | −1 | 1 | 3 | 250 | 80 | 7.68 | 8.68 |
| 11 | 1 | −1 | 0 | 5 | 250 | 70 | 10.41 | 11.00 |
| 12 | 1 | 0 | −1 | 5 | 500 | 60 | 7.92 | 7.90 |
| 13 | 0 | 0 | 0 | 3 | 500 | 70 | 5.83 | 5.73 |
| 14 | 1 | 1 | 0 | 5 | 750 | 70 | 6.66 | 7.14 |
| 15 | 0 | 1 | 1 | 3 | 750 | 80 | 4.64 | 3.46 |
| No. | Actual Level of Variables | Observed Results | |||
|---|---|---|---|---|---|
| nsr/rpm | tg/min | xp/μm | Cv/g/L | P50/μm | |
| 1 | 1200 | 9 | 16 | 90 | 3.19 |
| 2 | 700 | 7 | 20 | 120 | 16.82 |
| 3 | 800 | 9 | 8 | 110 | 4.24 |
| 4 | 700 | 17 | 10 | 60 | 3.66 |
| 5 | 1300 | 9 | 17 | 60 | 2.55 |
| 6 | 700 | 5 | 22 | 80 | 17.17 |
| 7 | 1200 | 7 | 17 | 50 | 3.56 |
| 8 | 900 | 13 | 32 | 90 | 5.30 |
| 9 | 800 | 11 | 32 | 80 | 9.58 |
| 10 | 1300 | 5 | 16 | 100 | 4.36 |
| 11 | 1000 | 15 | 32 | 100 | 2.66 |
| 12 | 800 | 13 | 22 | 120 | 6.84 |
| 13 | 800 | 21 | 14 | 90 | 3.75 |
| 14 | 1100 | 9 | 14 | 120 | 4.12 |
| 15 | 1000 | 11 | 22 | 110 | 5.44 |
| 16 | 1000 | 17 | 16 | 70 | 2.04 |
| 17 | 1300 | 11 | 10 | 120 | 1.85 |
| 18 | 800 | 15 | 20 | 70 | 3.91 |
| 19 | 1000 | 5 | 10 | 90 | 2.66 |
| 20 | 800 | 19 | 16 | 50 | 3.32 |
| 21 | 1200 | 21 | 22 | 70 | 2.55 |
| 22 | 1200 | 13 | 11 | 100 | 2.13 |
| 23 | 1200 | 15 | 10 | 110 | 1.98 |
| 24 | 900 | 11 | 20 | 50 | 4.40 |
| 25 | 1000 | 19 | 14 | 80 | 2.14 |
| 26 | 1000 | 21 | 17 | 120 | 2.46 |
| 27 | 900 | 9 | 10 | 80 | 3.85 |
| 28 | 1100 | 19 | 22 | 60 | 1.85 |
| 29 | 700 | 19 | 8 | 100 | 2.83 |
| 30 | 700 | 21 | 11 | 110 | 4.34 |
| 31 | 1100 | 5 | 17 | 70 | 5.97 |
| 32 | 1100 | 21 | 20 | 100 | 2.41 |
| 33 | 900 | 21 | 16 | 60 | 2.36 |
| 34 | 800 | 5 | 11 | 60 | 3.98 |
| 35 | 900 | 19 | 17 | 110 | 3.56 |
| 36 | 1100 | 11 | 11 | 90 | 2.60 |
| 37 | 1300 | 17 | 22 | 50 | 3.40 |
| 38 | 700 | 9 | 32 | 70 | 11.69 |
| 39 | 900 | 17 | 14 | 100 | 2.63 |
| 40 | 700 | 13 | 14 | 50 | 4.48 |
| 41 | 900 | 5 | 8 | 120 | 3.67 |
| 42 | 1000 | 13 | 20 | 60 | 4.43 |
| 43 | 1200 | 17 | 20 | 80 | 3.55 |
| 44 | 1200 | 11 | 8 | 60 | 2.18 |
| 45 | 900 | 7 | 11 | 70 | 3.79 |
| 46 | 1100 | 7 | 16 | 80 | 2.88 |
| 47 | 1300 | 7 | 14 | 110 | 2.76 |
| 48 | 700 | 15 | 17 | 90 | 9.52 |
| 49 | 1000 | 9 | 11 | 50 | 2.34 |
| 50 | 800 | 7 | 10 | 100 | 5.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, K.; Wu, B.; Sun, F.; Li, X.; Xi, C. Parameter Optimization of Wet Stirred Media Milling Using an Intelligent Algorithm-Based Stressing Model. Processes 2025, 13, 3785. https://doi.org/10.3390/pr13123785
He K, Wu B, Sun F, Li X, Xi C. Parameter Optimization of Wet Stirred Media Milling Using an Intelligent Algorithm-Based Stressing Model. Processes. 2025; 13(12):3785. https://doi.org/10.3390/pr13123785
Chicago/Turabian StyleHe, Kang, Bo Wu, Fei Sun, Xiaobiao Li, and Chengcai Xi. 2025. "Parameter Optimization of Wet Stirred Media Milling Using an Intelligent Algorithm-Based Stressing Model" Processes 13, no. 12: 3785. https://doi.org/10.3390/pr13123785
APA StyleHe, K., Wu, B., Sun, F., Li, X., & Xi, C. (2025). Parameter Optimization of Wet Stirred Media Milling Using an Intelligent Algorithm-Based Stressing Model. Processes, 13(12), 3785. https://doi.org/10.3390/pr13123785





