Multi-Objective Optimization of Supercritical Water Oxidation for Radioactive Organic Anion Exchange Resin Wastewater Using GPR–NSGA-II

Abstract

Radioactive organic anion exchange resins present a significant challenge in nuclear power plant waste disposal due to their volatility, instability, and biotoxicity. Based on experimental degradation data from the supercritical water oxidation (SCWO) of organic anion exchange resin waste liquids from the nuclear industry, this study conducted correlation analysis, cluster analysis, and Sobol sensitivity analysis of key process parameters. The results indicate that temperature is the primary factor influencing chemical oxygen demand (COD) and total nitrogen (TN) removal, while oxidant dosage exhibits a notable synergistic effect on nitrogen transformation. A Gaussian Process Regression–Non-Dominated Sorting Genetic Algorithm II (GPR–NSGA-II) multi-objective optimization model was developed to balance COD/TN removal rate and treatment cost. The optimal operating conditions were identified as a temperature of 472.2 °C, an oxidant stoichiometric ratio (OR) of 136%, an initial COD concentration of 73,124 mg·L⁻¹, and a residence time of 3.8 min. Under these conditions, COD and TN removal efficiencies reached 99.63% and 32.92%, respectively, with a treatment cost of 128.16 USD·t⁻¹. The proposed GPR–NSGA-II optimization strategy provides a methodological foundation for process design and economic assessment of SCWO in treating radioactive organic resin waste liquids and can be extended to other studies involving high-concentration, refractory organic wastewater treatment.

1. Introduction

The disposal of radioactive waste in the nuclear power industry has emerged as a critical issue requiring immediate attention. During nuclear reactor operation, the purification of circulating cooling water generates radioactive organic resin waste, characterized by high organic content, chemical recalcitrance, and intense radioactivity [1]. Improper treatment and disposal of this waste pose serious threats to environmental safety and human health. Conventional disposal methods, including incineration, solidification, and plasma melting, are constrained by high energy consumption, risks of secondary pollution, and limited long-term stability. In contrast, supercritical water oxidation (SCWO) enables the complete mineralization of organic compounds within a short reaction time and facilitates the solid-phase enrichment and stabilization of radionuclides [2]. As such, SCWO is considered a promising green technology for the treatment of radioactive organic waste [3,4]. However, the SCWO process faces problems such as the complexity of its reaction mechanism and the interaction of key parameters when treating organic matter, which bring huge challenges to process optimization.

In recent years, SCWO technology has made significant progress in the treatment of waste resins and organic liquid wastes. However, several technical challenges remain. Kim et al. [5] improved a commercial SCWO system for the treatment of ion exchange resins (IERs) from thermal and nuclear power plants. They effectively employed a fluidized bed reactor to achieve precise separation of mixed resins into cationic and anionic categories, which helped prevent the formation of ammonium sulfate salts and subsequent equipment corrosion. The addition of nitromethane during the treatment of anion resins significantly reduced total nitrogen (TN) concentrations in the effluent and eliminated NO_x emissions. Leybros et al. [6] investigated the decomposition behavior of IERs under supercritical water conditions to deepen the understanding of their decomposition pathways. They identified degradation intermediates such as formaldehyde, methylamine, and sulfur- and nitrogen-containing species, clarifying their roles in the reaction mechanisms. Jiang et al. [7] discussed various kinetic modeling approaches, including empirical, semi-empirical, and detailed chemical kinetic models (DCKMs). However, none of these models could fully describe the reaction mechanisms because DCKM is limited to elementary reactions only. Moreover, DCKM cannot be validated at high temperatures and pressures due to the difficulty in obtaining reliable reaction rate constants.

To date, most kinetic investigations of SCWO have relied on simple model compounds, leaving a research gap in developing kinetic models for complex mixtures of organic resins and organic liquid wastes [8,9]. Although the optimal treatment temperature for the degradation of waste resins and organic liquids in SCWO is relatively low, the removal efficiency of ammonia nitrogen (NH₃–N) remains unsatisfactory, and the overall reaction process is still difficult to maintain [10]. SCWO has been implemented in various reactor configurations, such as tubular and tank-type systems; however, these reactors face major engineering challenges, particularly clogging and corrosion, which hinder industrial application [11].

Several attempts have been made to optimize SCWO processes. Li et al. [12] optimized the SCWO process for the treatment of nuclear waste extraction solvents using response surface methodology (RSM) and achieved a total organic carbon (TOC) removal efficiency of 99.25%. Nevertheless, the high operational costs and corrosion resulting from salt deposition remain persistent issues. Transpiring-wall reactors (TWRs) have been proposed to mitigate these problems, as water films generated along the inner wall can prevent corrosion and salt deposition. However, the optimization of TWRs still requires extensive validation [13]. SCWO can achieve degradation efficiencies of up to 99% for radioactive organic wastes; however, the distribution, migration, and transformation behaviors of radionuclides remain poorly understood. Despite its high treatment efficiency, the industrial adoption of SCWO remains challenging because most experimental studies rely on single-factor or orthogonal tests to obtain model parameters without considering the interactions among variables [14].

In summary, current SCWO research on the degradation of waste resins and organic liquid wastes exhibits three major limitations. First, the microscopic mechanisms, radical reaction pathways, and evolution of intermediate products in complex organics remain unclear. Second, comprehensive kinetic models applicable to multi-component waste systems are still lacking. Third, optimization studies have been limited to laboratory-scale parameter adjustments, without multi-objective or techno-economic considerations necessary for industrial-scale implementation.

To address the aforementioned gaps, machine learning and multi-objective optimization provide an optimization strategy for optimizing key parameters of the SCWO process. Gaussian Process Regression (GPR) is a widely adopted probabilistic method for quantifying prediction uncertainty. Bradford et al. [15] reviewed the significant advantages of GPR in constructing high-accuracy force fields and predicting atomic properties. When integrated with Bayesian methods, GPR leverages its predictive capabilities to optimize chemical reaction parameters rapidly, achieving performance several times faster than traditional methods [16]. The Nondominated Sorting Genetic Algorithm II (NSGA-II) is a well-established technique for multi-objective optimization in chemical engineering and energy systems. For instance, Wolday et al. [17] used the GRNN-NSGA-II optimization model to optimize the methanol synthesis process. After optimization, the resource utilization rate was increased by 7.05%, and the energy consumption and carbon dioxide emissions were reduced. In addition, combining NSGA-II with the TOPSIS decision method has been proven to be an effective strategy for multi-objective optimization of combined cooling, heating, and power (CCHP) systems, which can improve energy efficiency, economic benefits, and environmental impact in a balanced way.

Artificial neural networks (ANNs) have also been employed in wastewater treatment. Dantas et al. [18] conducted a comprehensive review of this application. The backpropagation algorithm demonstrated excellent predictive accuracy for effluent parameters such as chemical oxygen demand (COD), biochemical oxygen demand (BOD), and total nitrogen (TN), with R² values exceeding 0.95. In the context of wastewater treatment plant control, the integration of machine learning and multi-objective optimization has exhibited superior performance over traditional control strategies in optimizing effluent quality, operational cost, and greenhouse gas emissions [19]. Additionally, Veli Şimşek et al. [20] used bio-based composite adsorbents to remove textile dyes and combined them with ANN to optimize key operating parameters. After optimization, the maximum removal rate of RR120 (Reactive Red 120) can exceed 94.75%. These data-driven modeling and optimization strategies highlight their strong potential in enhancing the treatment of complex organic pollutants.

In this study, a multi-objective optimization model was developed by combining GPR and NSGA-II to optimize SCWO process parameters and assess economic performance using experimental data from the SCWO of anion exchange resin. Correlation, cluster, and sensitivity analyses were conducted to explore the interactions among key parameters, while multiple regression models were used to predict the removal rates of COD and TN. Based on this framework, the GPR–NSGA-II algorithm achieved a multi-objective balance, maximizing the removal rates of COD and TN while minimizing treatment costs.

2. Experimental Setup and Method

2.1. Materials and Experimental Procedure

Considering the safety and compliance of nuclear testing, this study used fresh strongly basic anion exchange resin (ZGA NR170) as a simulant for radioactive waste resin. The rationale for this alternative approach has been fully validated. Wang et al. [21] studied the degradation mechanism of mixed ion exchange resins through supercritical water gasification experiments. The results showed that the degradation mechanism of mixed ion exchange resins was mainly determined by the polymer skeleton and functional groups of the resin and was not related to the types of ions adsorbed. To ensure reproducibility of the experimental process, ZGA NR170 was vacuum-dried at 72 °C, and the particle size after screening was controlled to be below 90 μm. As shown in Figure 1, the experimental process includes three stages: sample preparation, reaction, and product detection. Experiments were conducted using a sand bath fluidized bed and a microreactor. The heating temperature range was 50–600 °C, the heating medium was Al₂O₃, the maximum air flow rate was 85 L·min⁻¹, and the heating power was 1.5 kW.

To further investigate the interactive effects of key parameters during the supercritical water oxidation of anion exchange resin, this study conducted single-factor and randomized experiments on these key parameters. The single-factor parameters included temperature (400–500 °C), oxidant stoichiometry (80–150%), initial COD concentration (2 × 10⁴–1.2 × 10⁵ mg·L⁻¹), and residence time (1–10 min). Six experimental points were evenly spaced within the parameter range, resulting in a total of 24 experimental groups. A randomized set of experiments also included 30 experimental groups within the same parameter range. All experimental results were measured using a Spectroquant NOVA 60 water quality analyzer (Merck, Germany) and a 752 UV–visible spectrophotometer (Shanghai Jinghua Instrument Co., Ltd., Shanghai, China) for COD and TN, respectively.

The COD removal rate R_COD is used to represent the degradation effect of organic matter in waste resin:

$$R_{\mathrm{COD}}(\%)={\displaystyle \frac{{[\mathrm{COD}]}_i-{[\mathrm{COD}]}_r}{{[\mathrm{COD}]}_i}}\times 100$$

(1)

The TN removal rate R_TN is used to represent the degradation effect of organic matter in waste resin:

$$R_{\mathrm{TN}}(\%)={\displaystyle \frac{{[\mathrm{TN}]}_i-{[\mathrm{TN}]}_r}{{[\mathrm{TN}]}_i}}\times 100$$

(2)

Here, [COD]_i and [TN]_i are the initial concentrations of COD and TN in the spent ion exchange resin material, respectively, in mg·L⁻¹; [COD]_r and [TN]_r are the mass concentrations of COD and TN in the reaction product, respectively, in mg·L⁻¹.

The amount of oxidant added during the reaction is expressed by the oxidant stoichiometry (OS), defined as [O₂]_sto:

$${\left[{\mathrm{O}}_2\right]}_{sto}={\displaystyle \frac{{{[\mathrm{O}}_2]}_i}{{\left[\mathrm{COD}\right]}_i}}\times 100$$

(3)

Here, [O₂]_i is the initial oxidant concentration, mg·L⁻¹; [COD]_i is the mass concentration of the oxidant added to the system after the reaction, mg·L⁻¹.

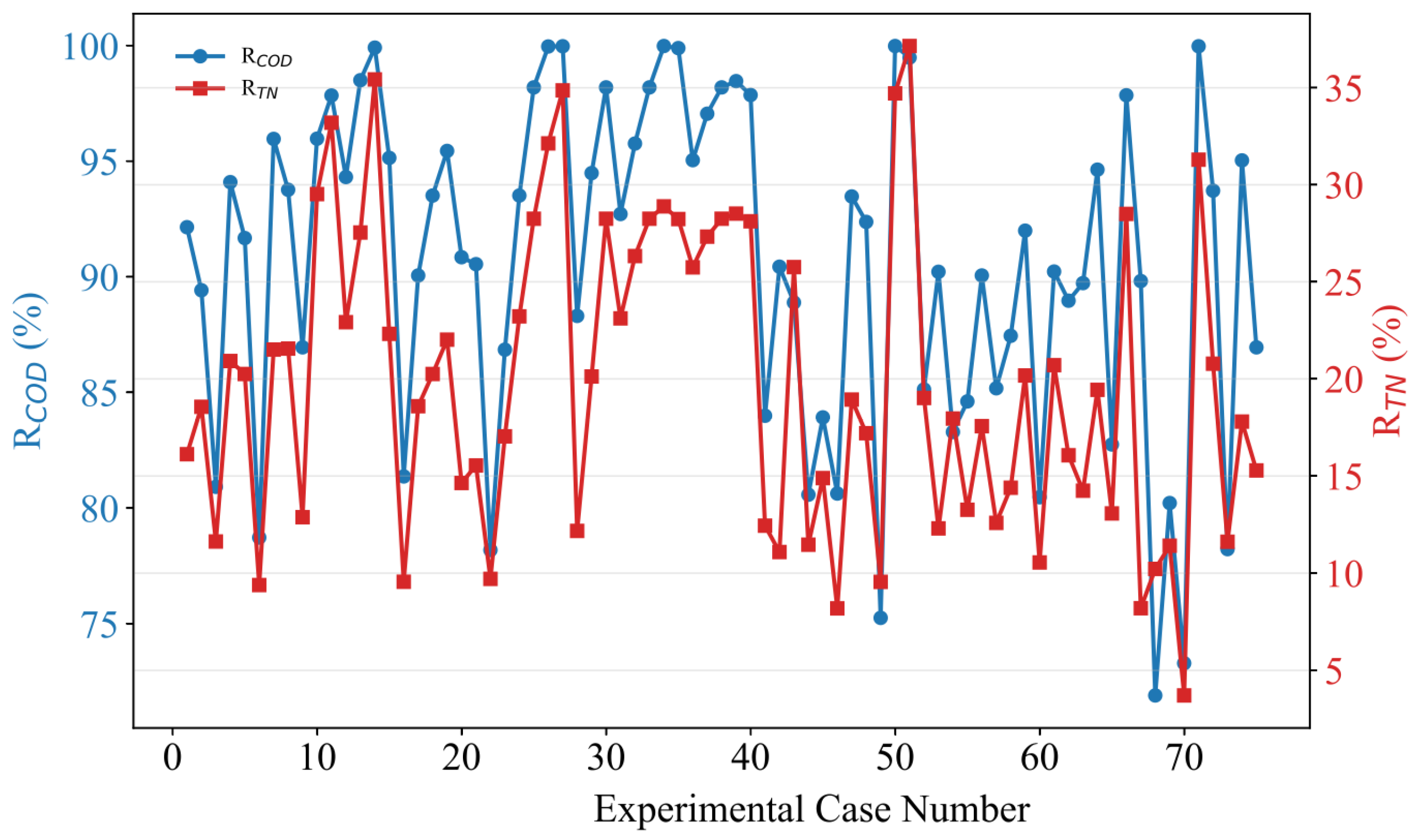
2.2. Experimental Data Preprocessing

The experimental data for supercritical water oxidation of anion exchange resins include 21 data sets from response surface experiments published in the literature [22], 24 data sets from single-factor experiments supplemented by this study, and 30 data sets from randomized parameter experiments within the same parameter range. All experiments utilized the same experimental platform and instrumentation, and the experimental data were replicated and validated, with outliers removed. The experimental distribution of COD and TN removal rates is shown in Figure 2.

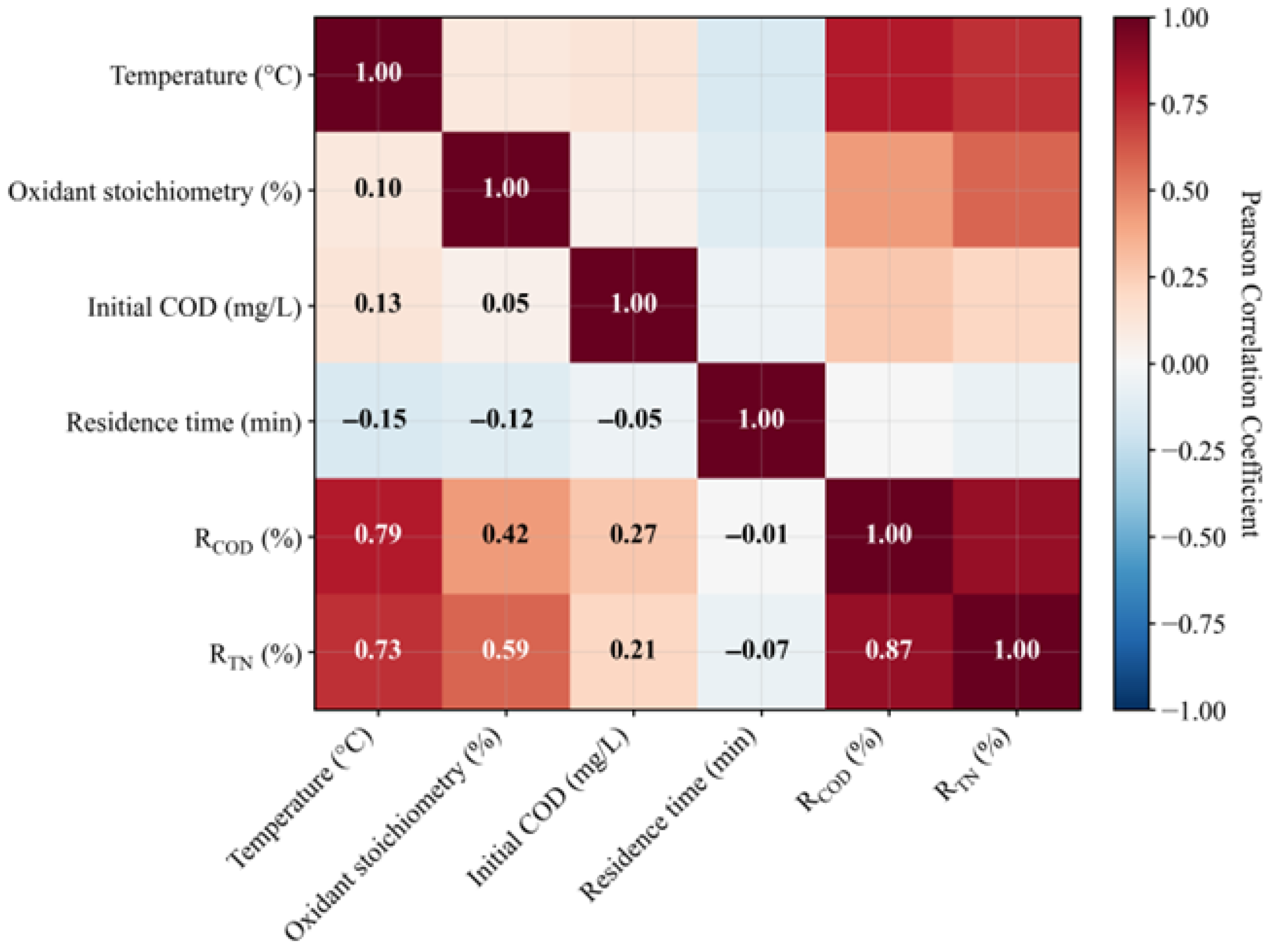
2.3. Correlation and Sensitivity Analysis Methods

This study conducted sensitivity, correlation, and cluster analyses using Python 3.11 on Windows 11. The libraries used included NumPy 1.26.4, Pandas 2.2.2, SciPy 1.13.1, scikit-learn 1.4.2, and SALib 1.5.1 [23]. Correlation and global sensitivity analyses were performed using experimental data from supercritical water oxidation of anion exchange resins combined with the GPR model. Pearson linear correlation coefficients and Spearman rank correlation coefficients for the response values (R_COD and R_TN) were calculated using the preprocessed experimental data from Section 2.2. The correlation matrix was calculated using the pandas.DataFrame.corr() function, and two-tailed significance tests were performed using scipy.stats.pearsonr and scipy.stats.spearmanr, respectively, at a significance level of p < 0.05 [24]. The proxy model used was the GPR model, which employed a radial basis function (RBF) kernel with an adaptive correlation distance (Automatic Relevance Determination, ARD) mechanism, combined with a constant kernel and a white noise kernel. The GPR model optimized hyperparameters using maximum likelihood estimation, with 5 optimization restarts and a fixed random seed of 42 to ensure reproducibility.

Based on this, a global sensitivity analysis was conducted using the Sobol variance decomposition method to quantitatively calculate the main effects (S₁) and total effects (S_t) of key parameters in the supercritical water oxidation anion exchange resin process [25]. The GPR model was combined with the SALib tool to generate a Saltelli sampling matrix with 6144 points. Furthermore, this study used 1000 bootstrap resampling of the training data with replacement to assess the uncertainty of the sensitivity indicators [26]. The GPR model was retrained and the Sobol analysis was repeated each time [27]. The final results were calculated using the 2.5–97.5% percentile to define the 95% confidence interval, and the mean value of each input parameter was used as the central estimate.

To further reveal the nonlinear influence mechanism of key parameters on COD and TN removal efficiency in the supercritical water oxidation anion exchange resin process, a GPR surrogate model was used to calculate partial dependencies. This study performed 1000 bootstrap resampling for each input variable to assess the robustness of the partial dependence results and model uncertainty. The results were constructed with 2.5–97.5% percentile intervals (95% confidence bands) based on these replicates. The K-means clustering algorithm (k = 3) was applied for unsupervised classification of treatment performance, and clustering effectiveness was assessed using the silhouette co-efficient [28].

2.4. Predictive Modeling Methods

In order to establish the mapping relationship between key parameters such as temperature, oxidant stoichiometric ratio, initial COD concentration, and residence time and R_COD and R_TN, this paper adopted a variety of machine learning regression models for modeling and prediction. The prediction models used include Linear Regression (LR) [29], Random Forest (RF) [30], Extreme Gradient Boosting (XGBoost) [31], Support Vector Regression (SVR) [32], Gaussian Process Regression (GPR) [33], and the small-sample modeling framework TabPFN (Tabular Prior-Data Fitted Networks) [34]. Since the number of samples is only 75, the leave-one-out cross-validation (LOOCV) method is used to evaluate the generalization and stability of the prediction results.

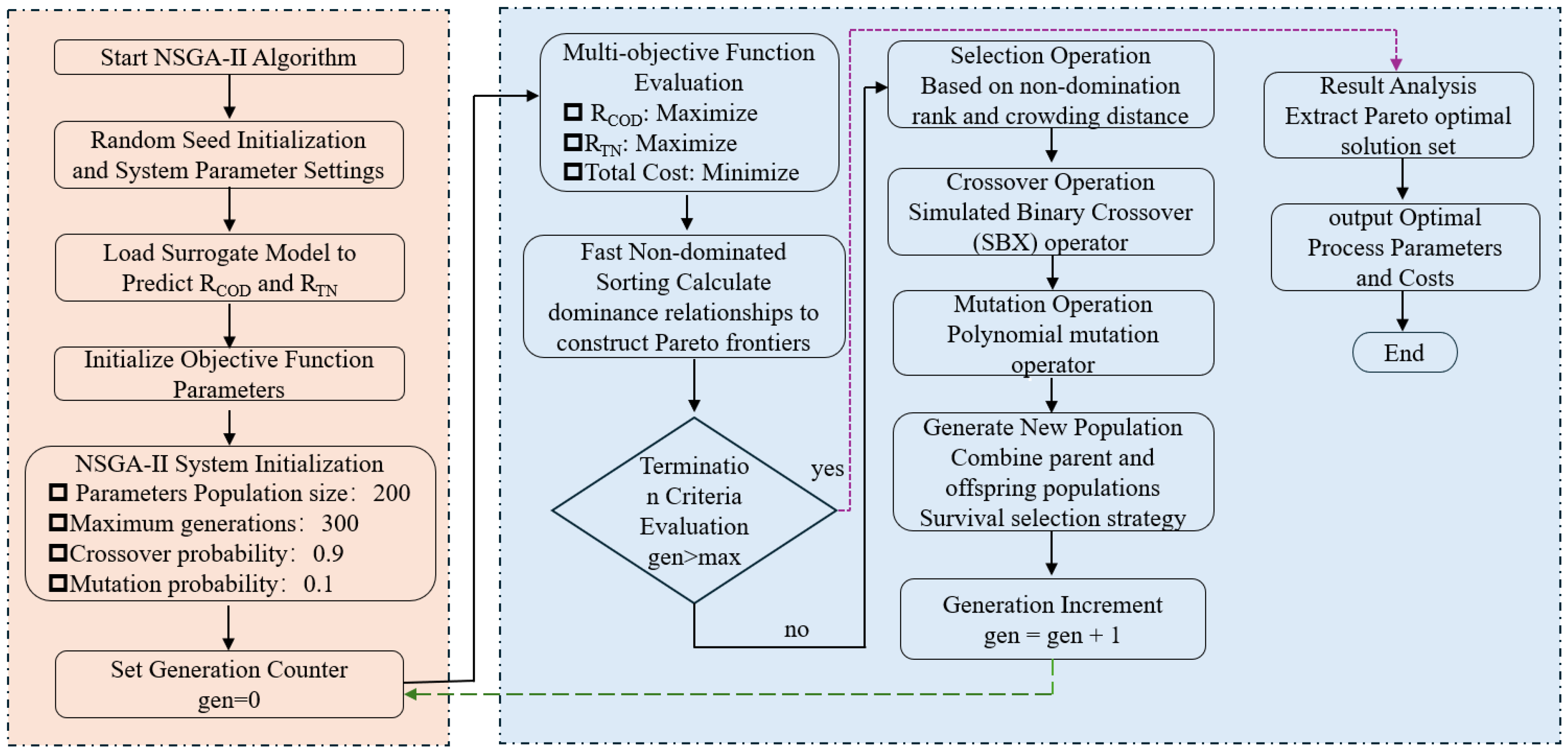
2.5. SCWO Process Optimization

An NSGA-II algorithm was developed to identify the optimal process parameters for treating anion exchange resin waste liquid via supercritical water oxidation. The algorithm simultaneously optimizes three objectives: R_COD, R_TN, and the total treatment cost (C_total). The decision variable vector X = [T, [O₂]_sto, COD_i, t] represents the reaction temperature (T, °C), oxidant stoichiometry (%), initial COD concentration (COD_i, mg·L⁻¹), and residence time (t, min). The constraints for the decision variables are defined as follows:

$$Operating constraints:\left\{\begin{array}{l}450 °\mathrm{C}\le T\le 490 °\mathrm{C},\\ 110\%\le {[\mathrm{O}}_2{]}_{\mathrm{sto}}\le 150\%,\\ 5.0\times {10}^4 \mathrm{mg}\cdot {\mathrm{L}}^{-1}\le {\mathrm{COD}}_i\le 8.0\times {10}^4 \mathrm{mg}\cdot {\mathrm{L}}^{-1},\\ 2 \min \le t\le 5 \min ,\\ R_{\mathrm{COD}}\ge 99.5\%.\end{array}\right.$$

Figure 3 presents the NSGA-II multi-objective optimization workflow based on the GPR surrogate model. The GPR model was constructed using experimental data to predict the response relationships of R_COD, R_TN, and $C_{\mathrm{total}}$. The GPR model employed a radial basis function (RBF) kernel with a length scale of 1.0 and a noise term ($\alpha$) of ${10}^{-4}$. Optimal hyperparameters were identified through five-fold cross-validation. The NSGA-II algorithm was configured with a population size of 100, 200 iterations, a crossover probability of 0.9, and a mutation probability of 0.1. The algorithm begins by randomly generating an initial population within the design space and uses the GPR model to predict the objective function values for each individual. Superior individuals are selected using fast non-dominated sorting and crowding distance calculation, followed by crossover and mutation operations to generate a new generation. This iterative process continues until convergence of the objective function, ultimately producing a set of Pareto-optimal solutions [35,36].

The cost model in this study is based on assumptions derived from conventional industrial wastewater treatment, adjusted to account for the alkaline and highly corrosive nature of nuclear waste liquids, while excluding the specific protective costs associated with radioactive nuclear waste [37,38]. The cost components primarily include energy consumption, oxidant usage, equipment investment, maintenance expenses, labor costs, utility charges, waste disposal fees, and special adjustments for handling waste liquids. The total treatment cost, $C_{\mathrm{total}}$, is defined as

$$C_{\mathrm{total}}=C_{\mathrm{energy}}+C_{\mathrm{oxidant}}+C_{\mathrm{equipment}}+C_{\mathrm{maintenance}}+C_{\mathrm{labor}}+C_{\mathrm{utilities}}+C_{\mathrm{disposal}}+C_{\mathrm{scale}}+B_{\mathrm{revenue}}$$

(4)

Energy costs consist of two components, electricity consumption and natural gas consumption, while also accounting for the benefits of waste heat recovery:

$$C_{\mathrm{energy}}=C_{\mathrm{electricity}}+C_{\mathrm{gas}}-B_{\mathrm{heat}}$$

(5)

$$C_{\mathrm{electricity}}={\displaystyle \frac{P_{\mathrm{total}}\cdot H\cdot D\cdot P_{\mathrm{elec}}}{Q_{\mathrm{annual}}}}$$

(6)

$$P_{\mathrm{total}}=45\cdot {\left({\displaystyle \frac{Q_{\mathrm{tpd}}}{2.0}}\right)}^{0.6}\cdot \left[1+0.0018\cdot (T-400)\right]$$

(7)

where Q_tpd represents the processing scale (t·d⁻¹), T denotes the reaction temperature (°C), H indicates the daily operating hours, D signifies the annual operating days, and P_elec represents the electricity price.

Natural gas costs are

$$C_{\mathrm{gas}}={\displaystyle \frac{E_{\mathrm{heating}}\cdot P_{\mathrm{gas}}}{Q_{\mathrm{annual}}}}$$

(8)

where E_heating represents heating demand (kWh) and P_gas denotes the unit price of natural gas.

Waste heat recovery benefits:

$$B_{\mathrm{heat}}=\min \left[6.0,{\displaystyle \frac{{\mathrm{COD}}_i-9000}{8000}}\cdot 6.0\right]$$

(9)

The cost of oxidants considers the impact of oxygen consumption and recovery efficiency [39]. The oxidant cost is

$$C_{\mathrm{oxidant}}={\displaystyle \frac{{\mathrm{COD}}_i}{1000}}\cdot 1.9\cdot {\displaystyle \frac{{{[\mathrm{O}}_2]}_{\mathrm{sto}}}{100}}\cdot (1-{\eta }_{\mathrm{recovery}})\cdot {\displaystyle \frac{P_{{\mathrm{O}}_2}}{1000}}$$

(10)

Oxygen recovery efficiency ${\eta }_{recovery}$ is defined in stages as follows:

$${\eta }_{\mathrm{recovery}}=\left\{\begin{array}{c}0.78, T>470 °\mathrm{C}, {{[\mathrm{O}}_2]}_{\mathrm{sto}}>130\%\\ 0.73, T>460 °\mathrm{C}, {{[\mathrm{O}}_2]}_{\mathrm{sto}}>120\%\\ 0.68, T>450 °\mathrm{C}\\ 0.63, \mathrm{Other} \mathrm{conditions}\end{array}\right.$$

Equipment investment costs are calculated using a piecewise function, fully accounting for economies of scale [40]. The equipment investment cost is

$$C_{\mathrm{equipment}}={\displaystyle \frac{C_{\mathrm{base}}\cdot f_{\mathrm{temp}}\cdot f_{\mathrm{pressure}}\cdot \left(r+\frac{1}{L}\right)}{Q_{\mathrm{annual}}}}$$

(11)

Considering corrosion and radiation, the depreciation period is set to L = 10. The base equipment cost C_base is a piecewise function:

$$C_{\mathrm{base}}=\left\{\begin{array}{c}135000\cdot {\left({\displaystyle \frac{Q_{\mathrm{tpd}}}{2.0}}\right)}^{0.6},Q_{\mathrm{tpd}}\le 5\\ 380000\cdot {\left({\displaystyle \frac{Q_{\mathrm{tpd}}}{10}}\right)}^{0.55},5<Q_{\mathrm{tpd}}\le {20}^{\leftarrow }\\ 950000\cdot {\left({\displaystyle \frac{Q_{\mathrm{tpd}}}{50}}\right)}^{0.5},Q_{\mathrm{tpd}}>20\end{array}\right.$$

(12)

The correction factors and parameters are as follows:

$$f_{\mathrm{temp}}=1+{\displaystyle \frac{T-410}{350}},\hspace{1em}{f}_{\mathrm{pressure}}=1.08,\hspace{1em}r=0.06,\hspace{1em}L=10$$

(13)

Other costs include maintenance costs, labor costs, and utility costs, as detailed below:

$$C_{\mathrm{maintenance}}=0.30\cdot C_{\mathrm{equipment}}$$

(14)

$$C_{\mathrm{labor}}={\displaystyle \frac{(N_{\mathrm{op}}\cdot S_{\mathrm{op}}+N_{\mathrm{eng}}\cdot S_{\mathrm{eng}})\cdot 1.08}{Q_{\mathrm{annual}}}}$$

(15)

The staffing configuration is as follows:

$$C_{\mathrm{utilities}}={\displaystyle \frac{(V_{\mathrm{cool}}\cdot P_{\mathrm{cool}}+V_{\mathrm{proc}}\cdot P_{\mathrm{proc}})\cdot D}{Q_{\mathrm{annual}}}}$$

(16)

$$\left\{\begin{array}{c}{V}_{\mathrm{cool}}=14\cdot {\displaystyle \frac{Q_{\mathrm{tpd}}}{2.0}}\cdot f_{\mathrm{cool}}\\ V_{\mathrm{proc}}=1.8\cdot {\displaystyle \frac{Q_{\mathrm{tpd}}}{2.0}}\end{array}\right.$$

(17)

$$f_{\mathrm{cool}}=\left\{\begin{array}{c}1.2, Conditions for self\text{-}sustained combustion\\ 0.8, Conditions for non\text{-}self\text{-}sustained combustion\end{array}\right.$$

(18)

Here, f_cool represents the cooling water correction factor. Based on empirical estimates, the cooling load increases by approximately 20% under self-sustaining combustion conditions and decreases by approximately 20% under non-self-sustaining conditions. Therefore, the values are set to 1.2 and 0.8 [41].

Waste disposal costs include the disposal of reaction residues and nitrogen-containing waste, with costs as follows:

$$C_{\mathrm{disposal}}={\displaystyle \frac{0.09\cdot Q_{\mathrm{tpd}}\cdot 140\cdot D}{Q_{\mathrm{annual}}}}$$

(19)

During the treatment of anion exchange resin waste liquid via supercritical water oxidation, the system can maintain stable operation without continuous external heating when the chemical energy released from the organic matter in the waste liquid is sufficient to compensate for heat losses and the temperature increase required by the reaction [42,43]. Based on the typical organic composition and calorific value analysis of nuclear waste liquid, this study proposes the following criteria for self-sustaining combustion:

$$\mathrm{Autothermal}=\left\{\begin{array}{c}\mathrm{yes},{ \mathrm{if} \mathrm{COD}}_i>9000 \mathrm{mg}\cdot {\mathrm{L}}^{-1},T>435 °\mathrm{C}, \\ \mathrm{no}, \mathrm{Other} \mathrm{circumstances}.\end{array}\right.$$

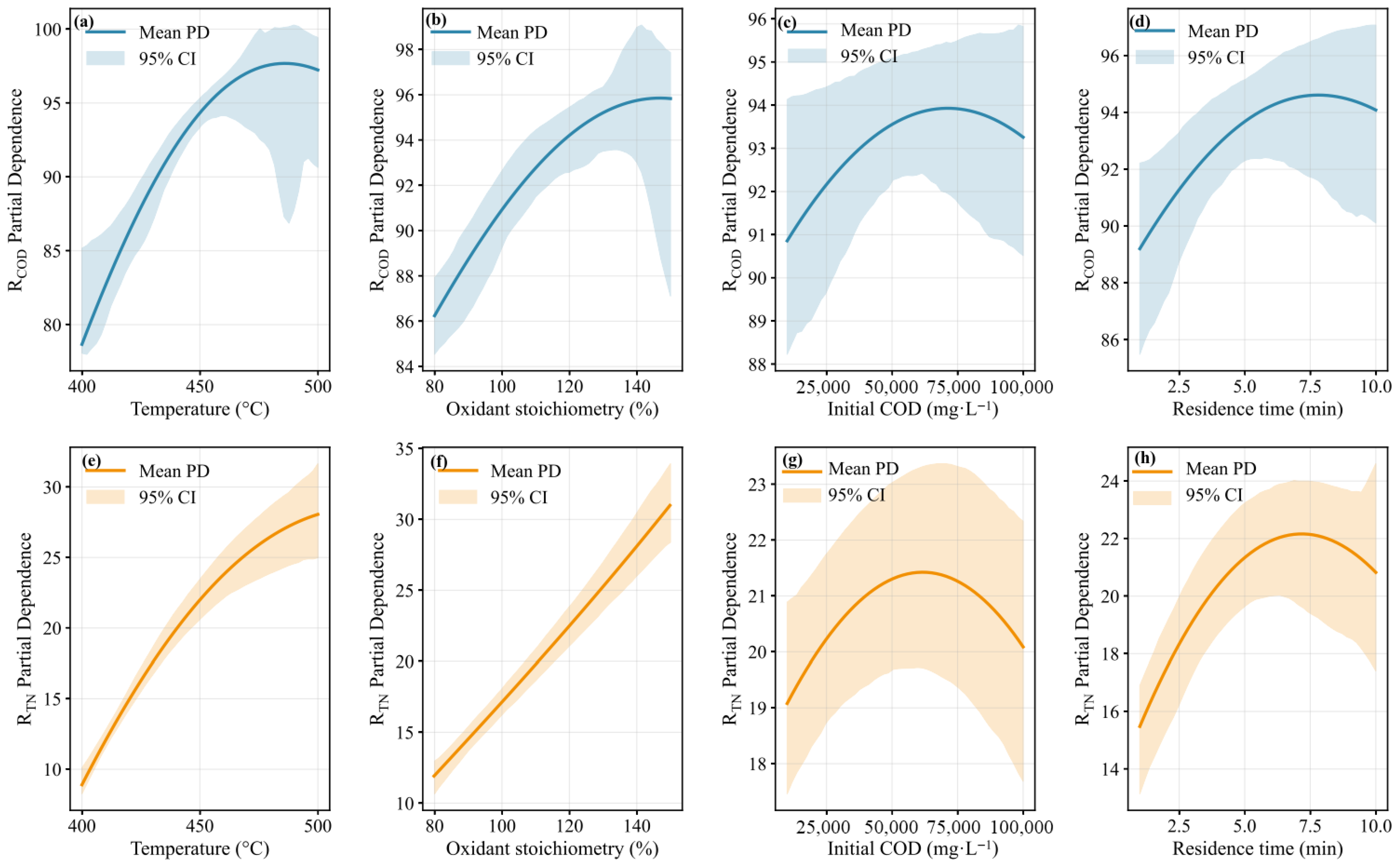
3. Results and Discussion

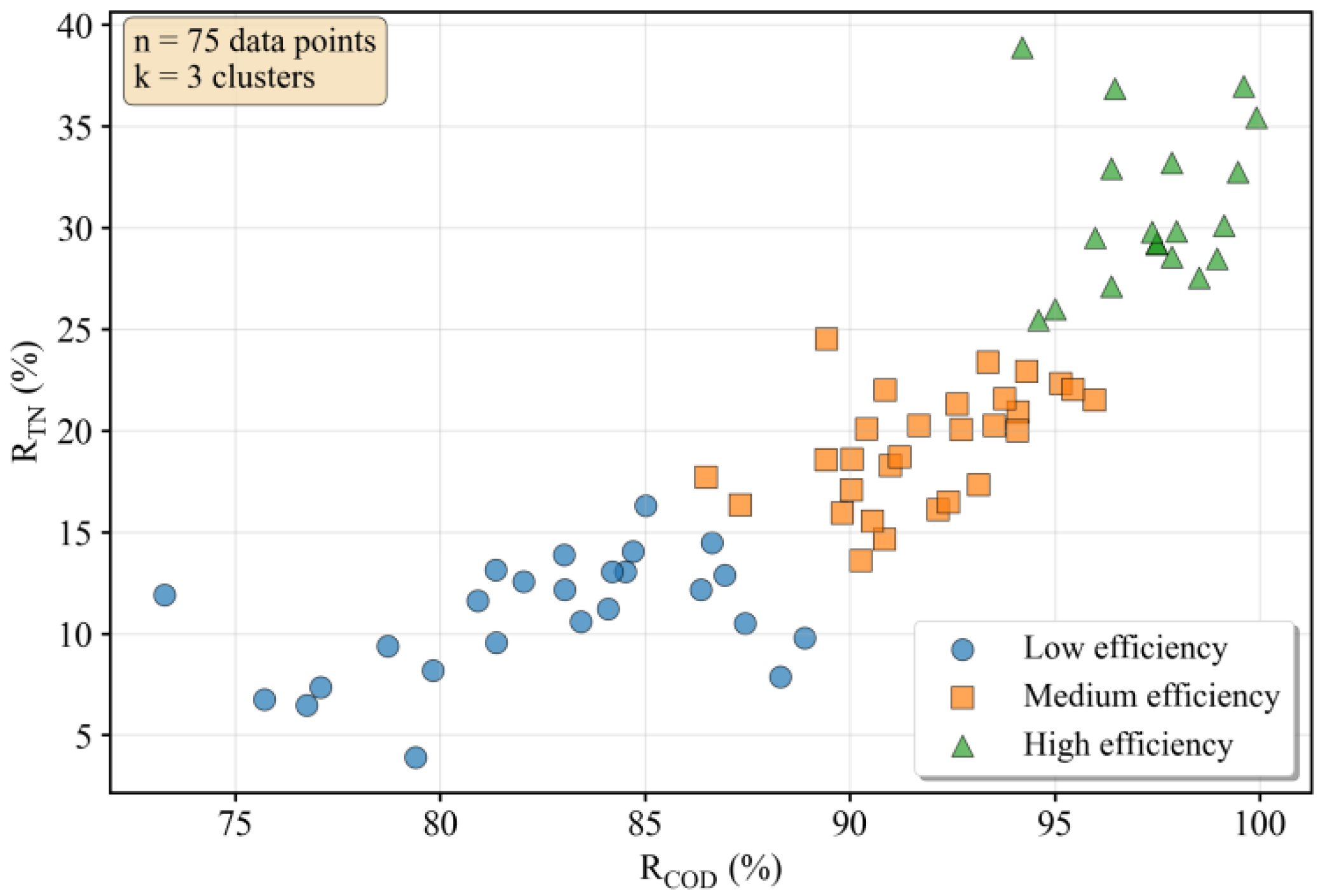
3.1. Correlation and Cluster Analysis

Figure 4 shows the relationship between the process parameters and COD and TN removal efficiencies during the SCWO of radioactive anion resin. It reveals that temperature is the most significant factor influencing both R_COD and R_TN during SCWO treatment of this resin, with correlation coefficients of 0.79 and 0.73, respectively. Increasing the process temperature of the SCWO enhances the oxidative degradation of organic compounds and the conversion and removal of nitrogen. In the waste resin SCWO organic matter degradation system, a higher temperature increases radical reactions, oxidation kinetics, and mass transfer rates. The oxidant stoichiometry positively correlates with R_COD and R_TN, with correlation coefficients of 0.42 and 0.59, respectively. A moderate increase in the oxidant stoichiometry improves the oxidizing property of the reaction system, which then promotes organic matter oxidation and further ammonia nitrogen or organic nitrogen removal. However, the oxidant stoichiometry has a more pronounced influence on R_TN than on R_COD. This is fundamentally due to the different reaction pathways for organic carbon oxidation and organic nitrogen oxidation. The oxidation process of organic matter in a reaction system under supercritical conditions is primarily controlled by reaction kinetics and free radical supply rate. However, when the oxidant is in stoichiometric excess, the free radical concentration in the reaction system reaches saturation, and increasing the oxidant concentration has limited effect on improving R_COD. In contrast, the TN removal process is primarily limited by the deep oxidation reaction of ammonia nitrogen (NH₃-N), following the reaction pathway R–NH₃ → NH₃ → NO₂⁻/NO₃⁻/N₂. When the oxidant is insufficient, the reaction system tends to remain in the NH₃ phase. Increasing the oxidant supply can further promote NH₃ oxidation.

Initial COD concentration is weakly correlated with both R_COD and R_TN, with correlation coefficients of 0.27 and 0.21, respectively. The SCWO reaction system for organic matter degradation in waste resin is in a supercritical state, where the free radical concentration is high. The organic matter oxidation rate is primarily influenced by the oxidant concentration and the free radical generation rate, not by the organic matter concentration. When the initial COD concentration increases while the oxidant ratio remains constant, the molar ratio of free radicals to organic matter decreases, allowing the system to rapidly reach a quasi-steady-state free radical concentration equilibrium. The final system reaction rate does not change significantly, and the sensitivity of R_COD and R_TN to the initial COD concentration is weakly correlated. Correlation analysis of the SCWO process parameters and the COD and TN removal performance indicates that temperature is the main factor, oxidant dosage is the secondary factor, and the influent concentration and residence time have relatively little effect. This trend is consistent with the results of Xu et al. [44] in an SCWO experimental study of strong acid ion exchange resin.

Figure 5 shows the K-means cluster analysis of the supercritical water oxidation performance of waste resin based on 75 sets of data. The K-means clustering results indicate a positive correlation between R_COD and R_TN during the supercritical water oxidation of anion resin, demonstrating significant synchronization between organic matter oxidation and nitrogen removal. During the engineering design of supercritical water oxidation of anion resin, it is not necessary to set separate operating conditions for organic matter and nitrogen removal; optimization can be achieved by controlling the same key parameters. In the low-efficiency, medium-efficiency, and high-efficiency zones, non-linear responses may be observed. By optimizing the temperature or oxidant ratio in the medium-efficiency zone, R_COD and R_TN can be improved by a significant margin. This method improves energy efficiency and reduces surplus oxidant consumption.

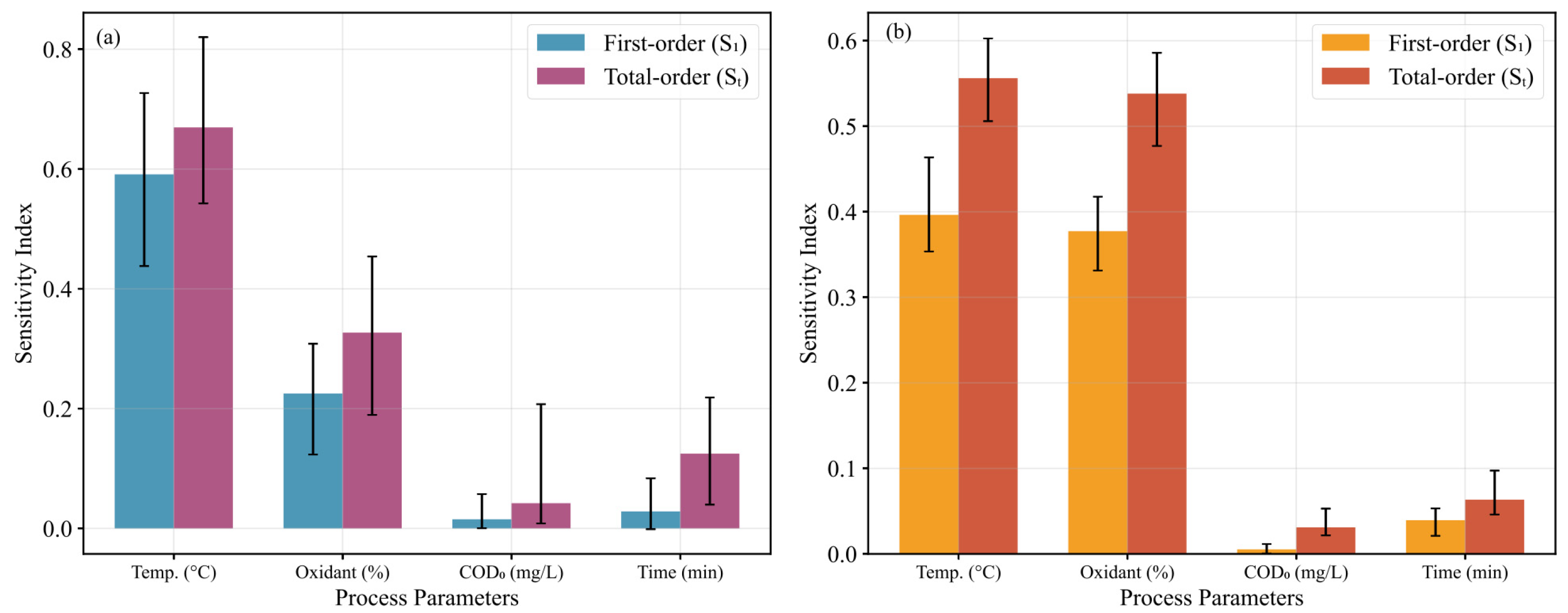
3.2. Parameter Sensitivity Analysis

In this study, GPR and Sobol global sensitivity analysis were adopted to fully assess the effect of key process parameters on COD and TN removal rate during SCWO processes of anion resin, as shown in Figure 6a,b. The first-order sensitivity (S₁) and total effect sensitivity (S_t) of the reaction temperature were 0.591 and 0.670, respectively, indicating that the oxidation of organic matters is mainly influenced by thermal effects and free radical generation rates. The first-order sensitivity and total effect sensitivity of the oxidant coefficient were 0.225 and 0.327, respectively, indicating that the oxidant coefficient in the reaction system works synergistically to maintain oxidation equilibrium and support free radical chain reactions. The low S₁ and S_t of the initial COD concentration and residence time indicate that the reaction system is near equilibrium. Increasing the initial COD concentration and extending the reaction time have limited effects on COD and TN removal rates.

In practical engineering, temperature and the oxidant stoichiometry should be the core control factors. The temperature of the supercritical water oxidation of anion resin is the primary factor that determines the oxidation rate of organic matter, and the oxidant supply is the key synergistic variable. Both of them show a significant interactive effect. This analytical conclusion is consistent with the results of Scheitlin C.G. et al. [45] in their SCWO study of ion exchange resin. When the oxidant equivalent increased from 1.0 to 2.0, the TOC removal rate increased by about 10–15%, verifying the synergistic enhancement effect of the oxidant under high-temperature conditions. In addition, Chiang S.Y.D. et al. [46] showed in their SCWO experiment on waste adsorption media that when the reaction temperature exceeded 500 °C, the fragmentation rate of nitrogen-containing and sulfur-containing functional groups was significantly accelerated, further supporting the mechanistic explanation proposed in this study that the increase in temperature promotes the generation of hydroxyl radicals, thereby enhancing TN removal.

This study, based on GPR, investigated the independent influence of process parameters on the model’s predicted response during the supercritical water oxidation of anionic resins. Figure 7a–h illustrate this, with the shaded areas representing the 95% confidence intervals. Overall, R_COD and R_TN respond significantly to temperature and oxidation coefficient, while initial COD concentration and residence time show weaker responses. R_COD and R_TN rise significantly and rapidly as the reaction temperature rises from 400 °C to 450 °C and then plateau around 470 °C. R_TN shows a linear relationship with temperature, with a narrow 95% confidence interval, meaning that the GPR model for temperature has a strong predictive stability for this parameter. This further validates that the process temperature is the most significant factor affecting the oxidation of organic pollutants and has a long-lasting effect on nitrogen oxidation. The oxidant stoichiometry can significantly improve the removal of R_COD and R_TN in the range of 80–100%, but it tends to be flat in other areas beyond this range. This suggests that moderate oxidation coefficients enhance free radical chain reactions in the reaction system, while excess oxidation has limited effects on R_COD. However, during supercritical water oxidation of anionic resin, R_TN exhibited a stronger dependence on the oxidation coefficient, a trend consistent with Sobol’s results. Initial COD concentration had a weak effect on R_COD and R_TN, with only a slight increase within the 4 × 10⁴ to 6 × 10⁴ mg·L⁻¹ range and wide confidence intervals. Residence time shows a limited and non-monotonic influence, mainly increasing slightly at short times and stabilizing thereafter.

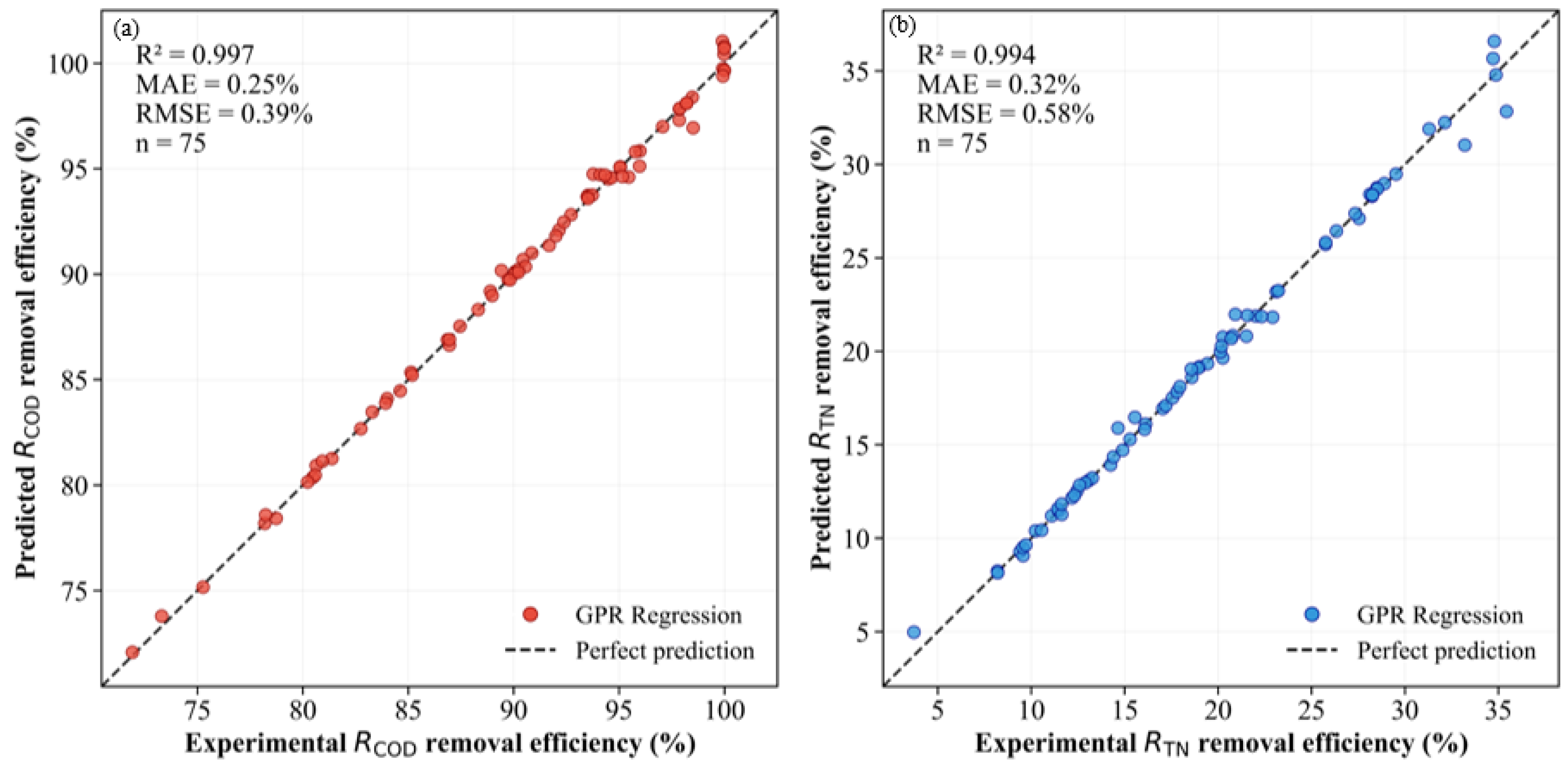
3.3. Model Performance Analysis

3.3.1. Single-Target Prediction Performance

To compare the performance of different machine learning models in predicting COD and TN removal rates in the supercritical water oxidation anion resin process, this study selected six typical regression models: LR, RF, XGBoost, SVR, TabPFN, and GPR.

Table 1. Comparative Analysis of Six Machine Learning Models for Predicting COD and TN Removal rate.

Model	R2 (COD)	MAE (%)	RMSE (%)	R2 (TN)	MAE (%)	RMSE (%)	Remarks
LR	0.786	2.53	3.04	0.857	2.35	2.94	performs poorly
RF	0.962	0.86	1.29	0.859	0.89	1.57	exhibits good stability
XGBoost	0.980	0.37	0.94	0.972	0.46	1.30	shows large prediction bias in the high-TN region
SVR	0.985	0.43	0.80	0.990	0.36	0.78	achieves the best performance on small samples
TabPFN	0.964	0.92	1.24	0.995	0.33	0.56	provides excellent fitting in the low-value region
GPR	0.983	0.53	0.76	0.980	0.90	1.17	possesses the capability of uncertainty quantification

shows the training accuracy of each model in predicting COD and TN removal rates. The R² values for COD and TN predictions were 0.786 and 0.857 for LR; 0.962 and 0.859 for RF; 0.980 and 0.972 for XGBoost; 0.985 and 0.990 for SVR; 0.964 and 0.995 for TabPFN; and 0.983 and 0.980 for GPR, respectively.

3.3.2. Multi-Objective Prediction Performance

In this study, the GPR model was selected for multi-objective prediction of COD and TN removal rates during the supercritical water oxidation anion resin process. Figure 8 shows the performance evaluation of the GPR model for simultaneous prediction of COD and TN removal rates, with experimental results and predictions compared in Figure 8a and Figure 8b, respectively. The GPR model predicted COD and TN removal rates with R² coefficients of determination (R²) of 0.997 and 0.994, respectively. MAEs were recorded at 0.25% and 0.32%, while the RMSEs were 0.39% and 0.58%, correspondingly. These findings suggest that no significant systematic bias exists, and the GPR model is accurate and reliable in reporting its predictions.

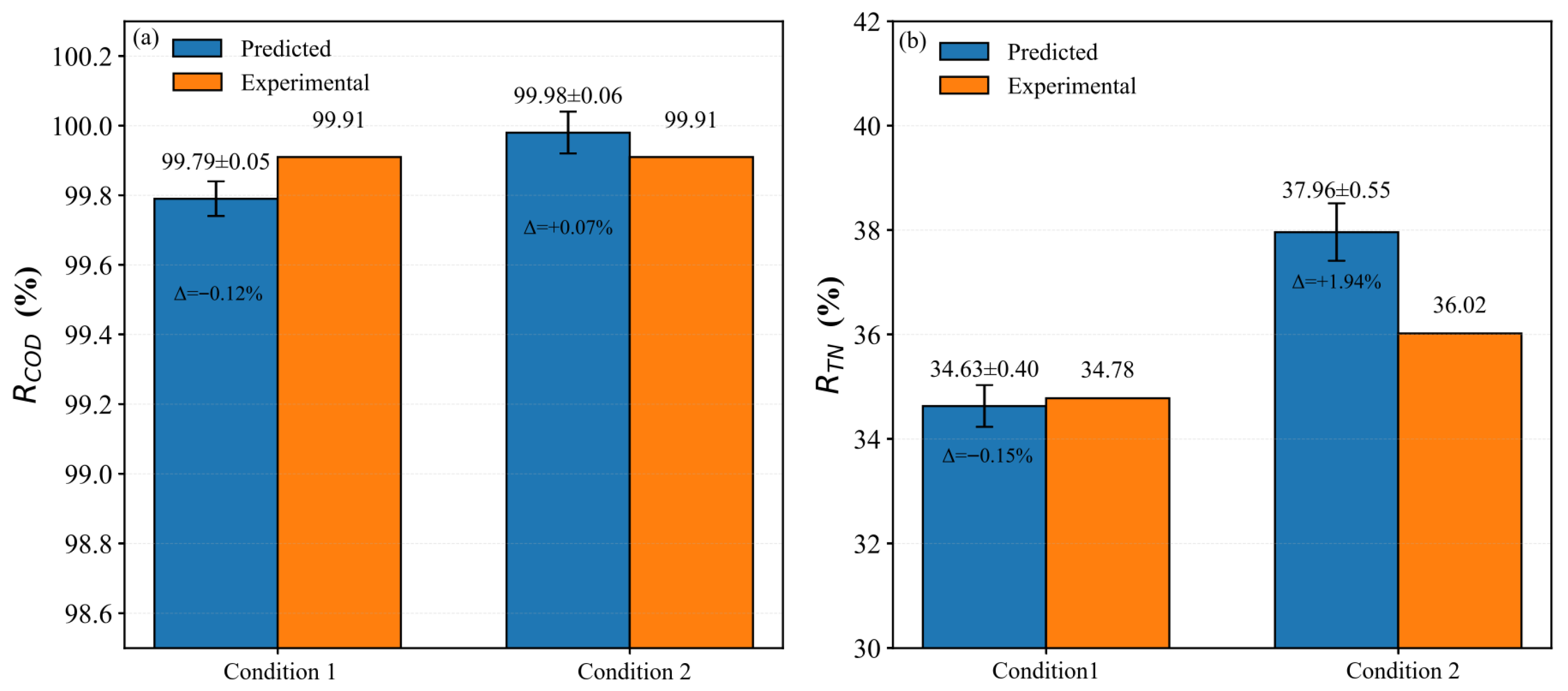
3.3.3. Experimental Validation of the GPR Model

Experimental findings obtained from two typical operating scenarios, presented in Figure 9, were used for the validation of the accuracy of GPR model predictions, which were predicted independently. Condition 1: Temperature of 470 °C, oxidant stoichiometry of 145%, initial chemical oxygen demand concentration of 58,054 mg·L⁻¹, and a residence time of 4.5 min. Condition 2: Temperature of 478 °C, oxide stoichiometric of 146%, initial chemical oxygen demand concentration of 77,310 mg·L⁻¹, and a residence time of 3.9 min. Although both experiments and model predictions differed from the GPR model’s predictions on R_COD by less than 1%, the model’s ability to predict small-scale measurements was still impressive. On the other hand, the R_TN values demonstrated slightly lower measured values than the predicted values; this probably has to do with the possibility of nitrogen reaction in the SCWO system being more complex than suspected. The validation results further prove that the GPR model is the most promising, with accuracy and generalizability in estimating COD and TN removal percentages using supercritical water oxidation of anion resin.

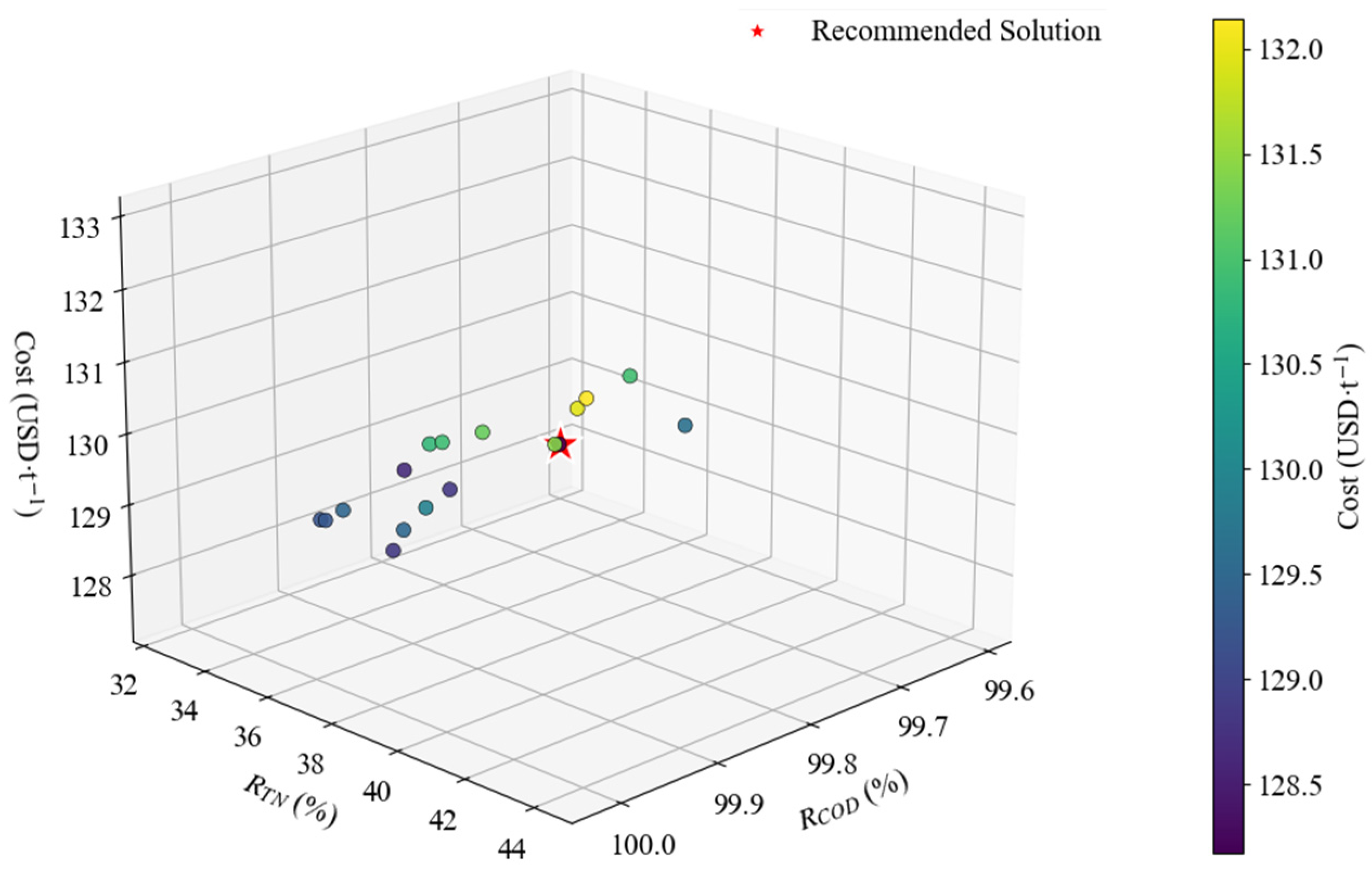
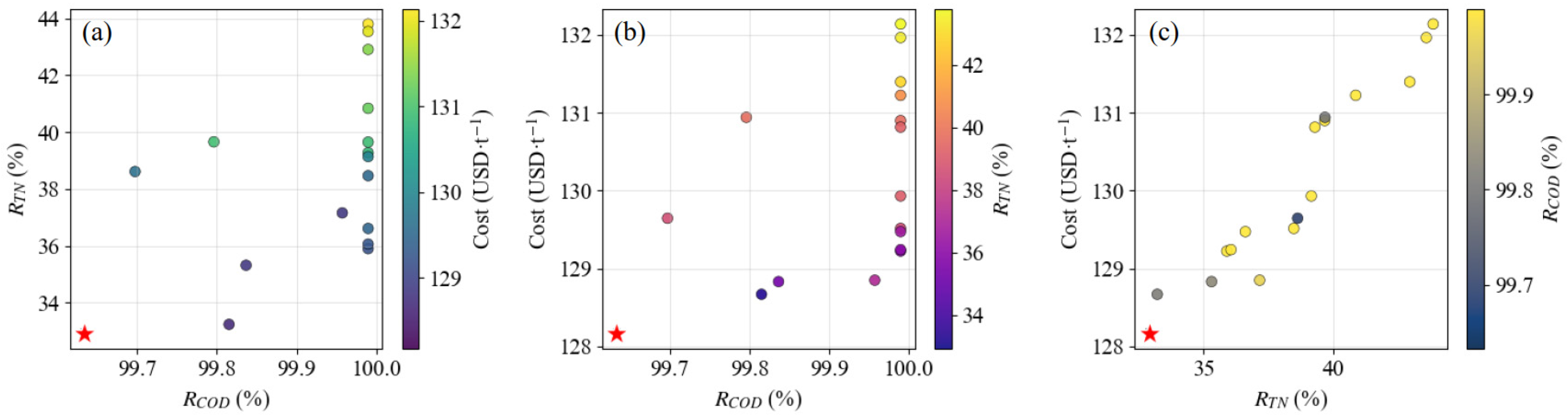
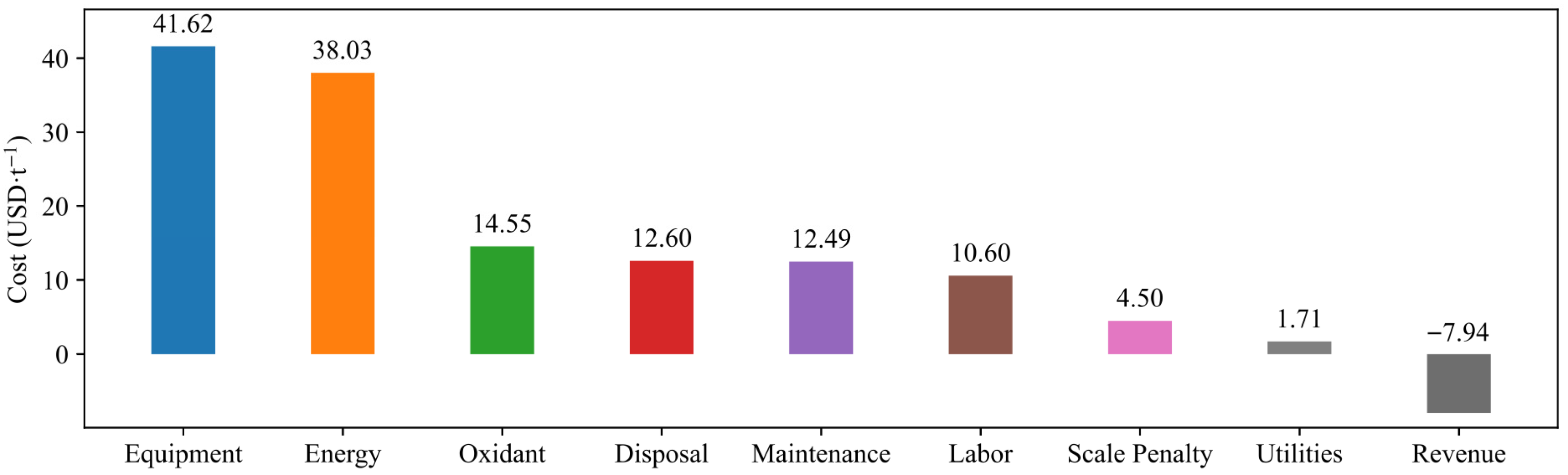
3.4. Process Parameter Optimization and Economic Analysis

Figure 10 illustrates the multi-objective optimization of the supercritical water oxidation of anion resin system designed with the GPR-NSGA-II model. The objective functions are maximizing COD removal rate, maximizing TN removal rate, and minimizing unit treatment cost; the corresponding weights are 0.5, 0.25, and 0.25, respectively. All Pareto solutions meet the constraints, with R_COD ranging from 99.50% to 99.99%, R_TN ranging from 32.13% to 36.0%, and costs ranging from 128.0 to 132.0 USD·t⁻¹. Although the cost differences between different solutions on the Pareto front are relatively small, there are still significant distribution differences in COD and TN removal performance, indicating a smoothing effect on economic performance in the high-efficiency range.

Figure 11 shows the two-dimensional projection of the Pareto frontier and the recommended solution obtained by the GPR-NSGA-II multi-objective optimization. As shown in Figure 11, R_TN increases with increasing R_COD, but the corresponding treatment cost also increases. The optimal parameters recommended for the supercritical water oxidation anion resin process are a temperature of 472.2 °C, an oxidant stoichiometry of 136%, an initial COD concentration of 73,124 mg·L⁻¹, and a residence time of 3.8 min. The performance indicators for R_COD, R_TN, and cost are 99.63%, 32.92%, and 128.16 USD/t⁻¹, respectively. These process parameters ensure extremely high COD removal while still achieving good TN removal and remaining within a reasonable economic cost range.

Figure 12 illustrates the cost analysis of an SCWO system with a treatment capacity of 2.0 t·d⁻¹ through optimal operating conditions. The cumulative operational cost of the SCWO system per ton of waste incinerated is 136.10 USD·t⁻¹, which, when accounting for the corresponding revenue from the byproduct recovery, results in a net cost of 128.16 USD·t⁻¹. The highest cost is the equipment investment, which accounts for 41.62 USD·t⁻¹ (approximately 31% of the total cost). This result is based on a 10-year equipment lifespan and a 6% annualized interest rate. Energy costs are 38.03 USD·t⁻¹, primarily from electricity consumption. Oxidant costs are 14.55 USD·t⁻¹. The net oxygen consumption is effectively controlled, considering a 75% oxygen recovery rate. Waste disposal and maintenance costs are 12.60 USD·t⁻¹ and 12.49 USD·t⁻¹, respectively; labor costs are 10.60 USD·t⁻¹. In addition, scale penalty and utility costs are 4.50 USD·t⁻¹ and 1.71 USD·t⁻¹, respectively. Heat recovery generates about 7.94 USD·t⁻¹ in revenue, mainly from waste heat utilization and a small amount of CO₂ recovery. Existing public studies have shown that unit treatment costs for SCWO systems generally range from 137 to 180 USD·t⁻¹ [47]. Li et al. studied the operating cost of a demonstration unit with a treatment capacity of 2.5 t·d⁻¹ and found it to be 83.1 USD·t⁻¹ [48]. Subsequent reviews and engineering evaluations have also reported a range of 70–150 USD·t⁻¹ [49]. The 128.16 USD·t⁻¹ obtained in this study is in the middle of this range, verifying the economic rationality and engineering feasibility of the model.

The cost results in Figure 12 are based on experimental results, engineering economic assumptions, and existing SCWO techno-economic studies. Energy consumption is calculated based on the actual electrical load measurements of the heating and pressurizing delivery units, combined with local industrial electricity prices [50]. Oxidant consumption is estimated based on stoichiometric oxygen demand, while considering an oxygen recovery efficiency of 60–80%, which is related to temperature and excess oxidant ratio [47]. The equipment is considered for a 10-year service life, with an annualized interest rate of 6%—which is consistent with the results of SCWO corrosion behavior and equipment life studies [51]. Utility, labor, maintenance, and waste disposal costs are based on small-scale SCWO engineering examples and then scaled up to a processing scale of 2.0 t·d⁻¹ [52]. In addition, the benefits of waste heat recovery and CO₂ recovery from the SCWO process are also considered [53]. The cost model of this study is constructed based on the parameters and engineering assumptions provided in the above literature, and its calculation results are consistent with the data reported in existing SCWO techno-economic studies.

4. Discussion

This study optimizes the degradation of nuclear industry anion exchange resins by supercritical water oxidation based on the GPR–NSGA-II model. This optimization model can predict the optimal operating parameters that balance COD removal, TN removal, and economic cost. However, the results need to be interpreted in conjunction with the reaction mechanism of SCWO degradation of anion exchange resins and engineering constraints to enhance the interpretability and engineering applicability of the results.

The oxidation of anion exchange resins under SCWO conditions consists of three stages: thermal decomposition, free radical oxidation, and complete mineralization. Under these conditions, the dielectric constant of water decreases significantly, making the originally hydrophobic resin backbone more easily dissolve or swell, thereby promoting the initial breakage of polymer chains and the thermal decomposition process [6]. High-temperature and high-pressure conditions can accelerate the chain breakage of the resin matrix and rapidly transform it into short-chain organic molecules. Short-chain organic molecules are more likely to react with free radicals such as ·OH and HO₂· under oxidant conditions, thus entering the oxidation stage [54]. Under SCWO conditions, the oxidation kinetics of nitrogen-containing groups are significantly lower than that of the carbon skeleton, with the conversion pathway being R–NH₃ → NH₃ → NO₂⁻/NO₃⁻/N₂. Although the oxidation of NH₃ is, in principle, sensitive to residence time, the experimental results in this study show that residence time exhibits only a weak effect within the investigated range [55]. Therefore, under conditions where COD is nearly completely degraded, TN removal is still mainly limited by the slow oxidation process of NH₃, exhibiting a low nitrogen conversion efficiency.

Sensitivity analysis shows that temperature is the most critical parameter affecting COD and TN degradation, consistent with the reaction kinetics where the free radical generation rate increases exponentially with temperature [56]. Based on the Pareto front solution obtained from the GPR–NSGA-II model, there is a significant trade-off between COD degradation rate, TN removal rate, and treatment cost. Increasing temperature accelerates the generation of free radicals such as ·OH and HO₂·, thereby improving COD and TN removal rates. Consistent with the sensitivity analysis, oxidant stoichiometry plays a secondary but notable role, especially for TN removal. However, high temperatures increase energy consumption and exacerbate equipment corrosion, leading to increased costs. Because TN oxidation kinetics are slow, improving TN removal requires higher parameter conditions, thus resulting in a more significant cost increase.

Considering that the high-temperature, high-pressure and high-salt characteristics of the SCWO system can easily cause equipment corrosion and salt scaling, the optimal operating conditions proposed in this study (472.2 °C, 25 MPa, initial COD 73,124 mg·L⁻¹, oxidant ratio 136%, residence time 3.8 min) achieve a balance between oxidation efficiency and material stability. On the one hand, this temperature is lower than the threshold for rapid corrosion of nickel-based alloys in oxidizing media (~500 °C) [57], which helps to reduce the high-temperature oxidation corrosion rate; on the other hand, the higher oxidant ratio promotes the complete oxidation of organic matter, reduces the generation of intermediate organic acids and chlorides, and inhibits acid corrosion from the source. The residence time is controlled within 4 min to avoid local oversaturation and deposition of salts.

In addition, literature studies have shown that radionuclides in radioactive resins (such as ¹³⁷Cs and ⁶⁰Co) are typically converted into thermally stable inorganic oxides or salts under SCWO conditions. These radionuclides become concentrated in the solid products, do not participate in organic oxidation reactions, and can be safely managed through solid–liquid separation and solidification technologies [58]. Therefore, radioactive components have a relatively small impact on the degradation mechanism of organic matrices. Supercritical water oxidation of nuclear industry anion exchange resins achieves efficient COD and TN degradation while maintaining closed, safe, and environmentally friendly post-disposal characteristics. Although the GPR–NSGA-II model demonstrates good predictive and process optimization capabilities, further validation under actual nuclear industry conditions is needed.

While the cost model in this study includes key components such as equipment investment, energy consumption, oxidant, and operation and maintenance costs, the economic cost model and experimental scheme still have certain assumptions and engineering limitations. The cost model does not fully consider additional expenditures related to radiation protection, regulatory compliance, and long-term solid waste management involved in radioactive waste treatment, thus potentially underestimating the total life-cycle cost of supercritical water oxidation of nuclear industry anion exchange resins. Furthermore, long-term continuous operation tests under real radioactive resin conditions are still needed to verify the predictive reliability and engineering applicability of the GPR–NSGA-II model under actual conditions, such as irradiation, accelerated corrosion, scale deposition, and material aging.

5. Conclusions

This study revealed the key parameters influencing the degradation of COD and TN in nuclear anion exchange resins through supercritical water oxidation and constructed a multi-objective optimization framework based on the GPR–NSGA-II model. The main conclusions are as follows:

(1)

The oxidant stoichiometry plays a key synergistic role in the nitrogen conversion process during the degradation of nuclear anion resins by supercritical water oxidation. The initial COD concentration and residence time have little effect on COD and TN removal rates. The interaction effect between temperature and oxidation coefficient is significant, which is consistent with the coupled characteristics of free radical generation and reaction kinetics.

(2)

All six machine learning models can effectively fit the pollutant removal efficiency of the SCWO system. Among these, SVR and GPR performed well in single-objective prediction (R² > 0.98), and the GPR model had extremely high accuracy in multi-objective prediction (R² > 0.99).

(3)

Based on the multi-objective optimization of GPR–NSGA-II, it was shown that the COD removal rate and TN removal rate under the optimal conditions were 99.63% and 32.92%, respectively, and the treatment cost was 128.16 USD·t⁻¹.

(4)

In practical engineering, improving the thermal management level of the SCWO system reactor and adopting a strategy of dynamically controlling the oxidant stoichiometry can simultaneously improve the removal rates of COD and TN. Reaction temperature and oxidant coefficient have the highest priority for control, while residence time and initial COD concentration are secondary control factors.