Spatio-Temporal Artificial Intelligence for Multi-Hazard-Aware Renewable Energy Site Selection Using Integrated Geospatial and Climate Data

Abstract

The siting of renewable energy systems (RESs) in regions vulnerable to multiple climate hazards presents a critical challenge for sustainable infrastructure planning. Traditional approaches, primarily driven by static assessments of solar and wind potential, often neglect the compounded risks posed by floods, droughts, and windstorms, resulting in investments that are operationally vulnerable and economically unsustainable. This study proposes a novel spatio-temporal artificial intelligence (AI) framework for multi-objective RES deployment that integrates satellite-derived resource maps, high-resolution hazard data, and dynamic climate time series into a unified optimization pipeline. The methodology employs a gated recurrent unit (GRU)-based encoder to capture temporal hazard dynamics, combined with a multi-objective evolutionary algorithm (NSGA-II) to balance energy yield and resilience. A case study in South Africa’s Vhembe District demonstrates the framework’s effectiveness: the proposed model reduces the average hazard exposure by 31.6% while preserving 96.4% of the baseline energy output. Attention-based saliency analysis reveals that flood and windstorm hazards are the dominant drivers of site exclusion. Compared to conventional siting methods, the proposed framework achieves superior trade-offs between performance and risk, ensuring alignment with South Africa’s Just Energy Transition and Climate Adaptation strategies. The results confirm the value of spatio-temporal embeddings and hazard-aware multi-objective optimization in guiding resilient, data-driven energy infrastructure development. This model offers direct benefits to energy planners, climate adaptation agencies, and policymakers seeking to implement resilient, data-driven renewable energy strategies in hazard-prone regions.

1. Introduction

The accelerating deployment of renewable energy systems (RESs), such as solar photovoltaics and wind turbines, is critical for achieving global decarbonization goals and reducing dependence on fossil fuels [1]. However, the long-term sustainability and operational reliability of these systems are increasingly threatened by exposure to climate-induced hazards such as floods, droughts, and windstorms. Poorly sited RES infrastructure in hazard-prone regions can result in significant economic losses, operational downtime, and even total system failure [2,3]. Despite the extensive literature on the optimal siting of RESs based on technical and economic criteria, relatively few studies incorporate dynamic multi-hazard risks into the decision-making process in a systematic, scalable, and data-driven manner.

Existing geospatial models and decision-support systems often rely on static layers of resource availability (such as solar irradiance or wind speed) while neglecting the spatio-temporal variability of extreme weather events and their compound effects on infrastructure [4]. This limitation poses serious concerns in the face of climate change, where extreme weather patterns are projected to become more frequent and severe. Consequently, a paradigm shift is needed, one that integrates geospatial intelligence, climate science, and artificial intelligence (AI) to guide the deployment of RES infrastructure towards locations that are not only resource-rich but also climate-resilient.

In response to this challenge, this paper proposes a novel spatio-temporal AI framework for optimizing renewable energy siting under multi-hazard exposure. The core idea is to fuse diverse datasets, ranging from satellite imagery and remote sensing products to historical hazard databases and climate re-analyses, within an AI-enhanced optimization model that can predict, evaluate, and recommend optimal RES locations. The framework incorporates flood, drought, and windstorm risks through machine learning-based hazard modeling and integrates these with multi-objective optimization techniques to simultaneously maximize energy yield, minimize costs, and reduce hazard vulnerability.

The main contributions of this work are threefold:

1.

A data-driven multi-hazard quantification method is implemented using satellite and historical records to derive spatial risk maps for floods, droughts, and windstorms.

2.

An AI-based suitability mapping approach is formulated, employing deep learning to integrate hazard, climate, and resource layers for robust site evaluation.

3.

A multi-objective optimization model is applied to incorporate resilience, cost, and resource potential, generating optimal site selection recommendations for climate-smart renewable energy system deployment.

The proposed framework is validated through a case study in a multi-hazard-prone region, where it demonstrates superior performance compared to traditional siting methods. This work aims to bridge the gap between climate risk assessment and renewable energy planning by providing a scalable, intelligent, and future-ready decision-support system for policymakers, developers, and grid planners.

The rest of this paper is organized as follows: Section 2 reviews the related literature on hazard-aware renewable energy siting and spatio-temporal modeling. Section 3 presents a system model that integrates hazard, energy, and infrastructure data layers. Section 4 formulates the multi-objective optimization problem under resilience constraints. Section 5 describes the integrated methodological framework, including data preprocessing, GRU-based suitability scoring, and NSGA-II optimization. Section 6 implements and evaluates the proposed framework using a case study from Vhembe District, South Africa. Section 7 interprets the results in the context of policy and resilience planning. Finally, Section 8 concludes the paper and outlines directions for future research.

2. Related Work

Renewable energy site selection has traditionally relied on geospatial resource availability metrics, such as solar irradiance and wind speed, often derived from satellite data and interpolated meteorological datasets [5]. While these models optimize energy potential and, in some cases, economic metrics like levelized cost of energy (LCOE), they frequently overlook the growing influence of climate-driven natural hazards on infrastructure reliability and long-term viability [6]. This section reviews relevant research across four domains: geospatial siting of RES, multi-hazard risk modeling, spatio-temporal AI applications, and multi-objective optimization in energy planning.

2.1. Geospatial Modeling for Renewable Energy Siting

Geographic information system (GIS)-based models have been widely applied in the siting of solar and wind energy systems. Studies such as [7] use GIS layers including land use, slope, proximity to the grid, and population density to rank potential sites. These methods are efficient but often static, assuming stationarity in environmental and socio-economic conditions. Moreover, hazard information, when used, is typically limited to basic floodplain exclusion zones, with little integration of probabilistic risk assessments or long-term hazard forecasts.

Recent work has attempted to incorporate environmental constraints such as biodiversity conservation and land degradation into energy siting decisions [8], but climate hazards remain underrepresented in these frameworks. This oversight is particularly problematic in regions facing compound hazards, where the cumulative effect of drought, floods, and windstorms can drastically compromise system performance or infrastructure safety.

2.2. Multi-Hazard Risk Assessment in Energy Infrastructure

Multi-hazard modeling frameworks are gaining traction in urban planning and disaster resilience, but their application to RES deployment remains limited. For example, the use of historical flood maps, drought indices (e.g., SPI, SPEI), and cyclone path data for infrastructure planning has been explored in [9], yet these methods are rarely integrated into energy system models. The Sendai Framework for Disaster Risk Reduction underscores the need for such integration, particularly in energy-critical regions exposed to cascading hazard events.

Few studies address the spatial and temporal compounding of hazards, for example, how prolonged droughts may increase wildfire risk, which in turn affects wind turbine safety. Dynamic hazard mapping approaches, such as those employing Markov chains or Bayesian inference [10,11,12], provide a foundation for modeling evolving risk profiles but require high-resolution data and significant computational capacity.

2.3. Spatio-Temporal AI for Environmental and Energy Applications

Artificial intelligence techniques, particularly deep learning, are increasingly applied in climate science and energy forecasting. Convolutional Neural Networks (CNNs) have demonstrated effectiveness in extracting spatial features from satellite imagery [13], while Recurrent Neural Networks (RNNs), Long Short-Term Memory (LSTM) units, and attention-based Transformers capture temporal dependencies in climate and resource data [14].

In the renewable energy domain, hybrid models (e.g., CNN-LSTM) have been used for wind speed prediction, solar irradiance forecasting, and fault detection [15]. However, few studies have leveraged these models for site selection under hazard uncertainty. The challenge lies in integrating multi-source, heterogeneous data, including climate projections, hazard histories, and infrastructure layers, into unified learning architectures capable of generalizing across space and time.

2.4. Multi-Objective Optimization in Renewable Energy Planning

Multi-objective optimization (MOO) is essential in energy planning, given the trade-offs between technical performance, cost, environmental impact, and risk. Algorithms such as the Non-dominated Sorting Genetic Algorithm II (NSGA-II), Particle Swarm Optimization (PSO), and Ant Colony Optimization (ACO) have been widely used in RES deployment [16]. These approaches, while robust, often rely on static cost–benefit analyses and assume deterministic inputs.

Incorporating uncertainty, particularly hazard-driven uncertainty, into MOO frameworks remains a critical gap. Some studies have proposed fuzzy logic or stochastic optimization to handle risk factors [17], but few account for the joint spatial and temporal dynamics of multiple hazards. Reinforcement learning (RL) and its deep variants are promising in this regard, as they can learn optimal policies under uncertainty, yet their application to hazard-resilient energy infrastructure planning is still nascent.

2.5. Research Gap and Contribution

As summarized in

Table 1. Summary of key literature and identified research gaps.

Research Domain	Focus of Prior Work	Limitation/Gap
GIS-Based RES Siting	Solar/wind resource with terrain and land use analysis [18,19]	Limited integration of dynamic hazard and climate risk data
Multi-Hazard Mapping	Modeling of flood, drought, and cyclone events using historical and satellite data [20,21]	Rarely coupled with renewable energy infrastructure planning
Spatio-Temporal AI	Used for climate forecasting and renewable resource prediction [22,23]	Underexplored for integrated multi-hazard and RES siting frameworks
Multi-Objective Optimization in RES Planning	Trade-off analysis of cost, performance, and environmental criteria [24,25]	Hazard-related uncertainty often excluded or treated simplistically

, existing approaches tend to treat hazard data as static constraints rather than dynamic, learning-informed parameters. This paper addresses this gap by proposing a unified spatio-temporal AI framework that integrates multi-hazard risk modeling, deep learning-based suitability mapping, and multi-objective optimization to support resilient and sustainable renewable energy planning.

• Novel Contribution: Unlike prior studies that treat hazard data as static constraints, this work introduces a dynamic, AI-driven framework that integrates temporal hazard modeling, geospatial intelligence, and multi-objective optimization. This combination enables resilient and data-informed renewable energy siting under realistic climate risk conditions.

Building on the research gaps outlined in Section 2, the next section presents a unified system model that fuses hazard, infrastructure, and resource layers into a spatially aware, AI-enhanced optimization framework.

3. System Model

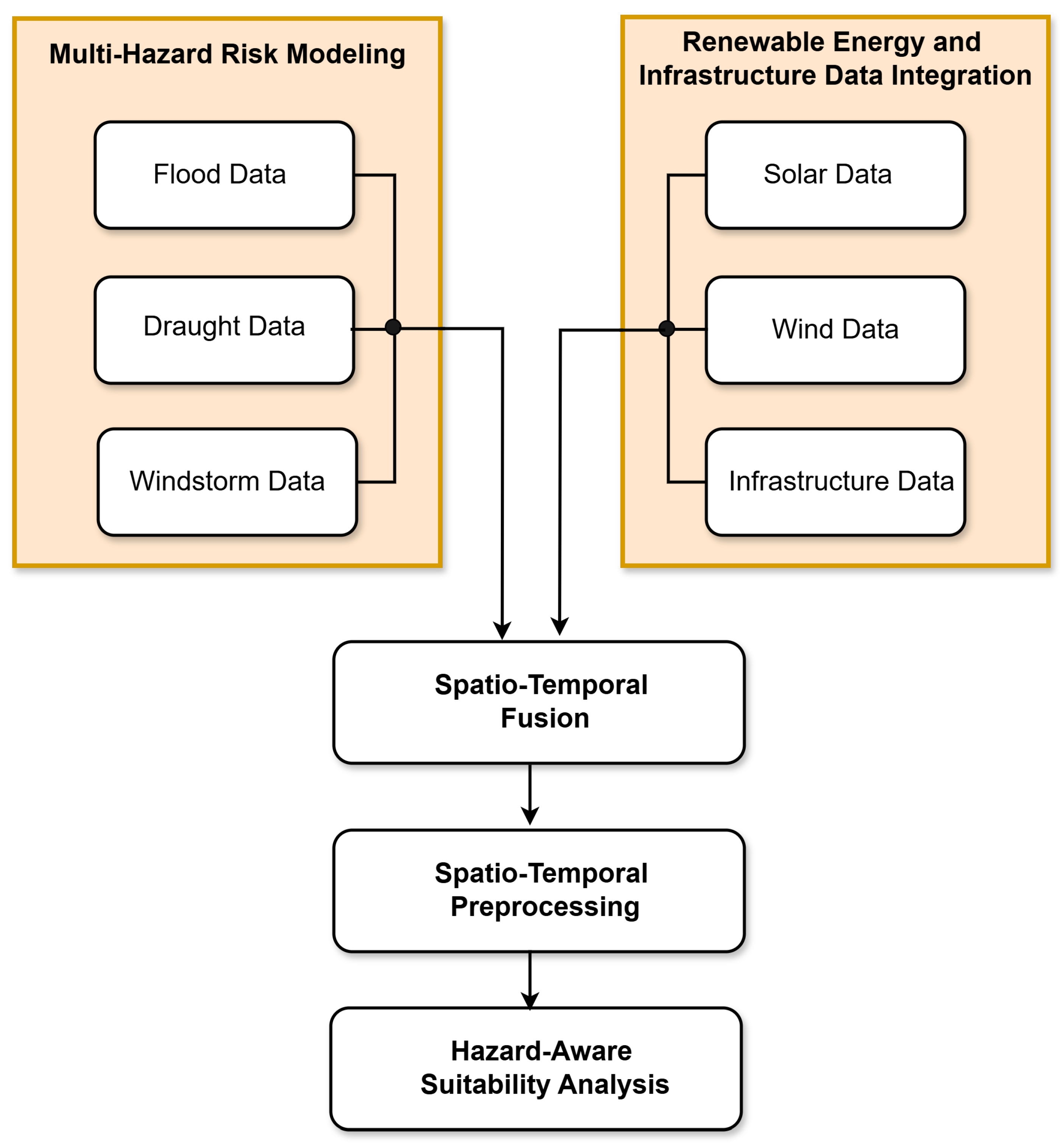
The proposed system model is designed to unify geospatial, climatic, and infrastructure datasets into a coherent, mathematically tractable framework for hazard-aware renewable energy siting. The model is structured into three interrelated components: (i) multi-hazard risk modeling, (ii) renewable energy and infrastructure data integration, and (iii) spatio-temporal fusion preprocessing. Figure 1 provides an overview of the system model architecture.

3.1. Multi-Hazard Modeling

A hazard field $H(\mathbf{x},t)$ is formally introduced over $\mathbf{x}\in \Omega \subset {\mathbb{R}}^2$ and $t\in \mathbb{T}$, comprising individual hazard layers:

$$H(\mathbf{x},t)=w_f{H}_f(\mathbf{x},t)+w_d{H}_d(\mathbf{x},t)+w_w{H}_w(\mathbf{x},t)$$

(1)

where $H_f$ denotes the flood hazard layer (e.g., flood depth or recurrence interval), $H_d$ is the drought severity index (such as the Standardized Precipitation Evapotranspiration Index, SPEI), and $H_w$ represents windstorm vulnerability (e.g., wind return period or cyclone footprint); the corresponding normalized weights are $w_f$, $w_d$, and $w_w$, respectively, constrained such that $\sum w_i=1$.

Drought risk is computed using the Standardized Precipitation Evapotranspiration Index (SPEI), defined as

$$H_d(\mathbf{x},t)={\mathrm{SPEI}}_k(\mathbf{x},t)={\displaystyle \frac{P(\mathbf{x},t)-PET(\mathbf{x},t)}{\sigma }}$$

(2)

where P is precipitation, $PET$ is potential evapotranspiration, and $\sigma$ is the long-term standard deviation over a baseline window of k months.

3.2. Renewable Energy and Infrastructure Layers

The renewable energy resource field $R\left(\mathbf{x}\right)$ is defined as a weighted function of solar and wind energy potentials:

$$R\left(\mathbf{x}\right)={\alpha }_{s}S\left(\mathbf{x}\right)+{\alpha }_{w}W\left(\mathbf{x}\right)$$

(3)

where $S\left(\mathbf{x}\right)$ denotes the solar irradiance at location $\mathbf{x}$ (e.g., global horizontal irradiance, GHI, in W/m²); $W\left(\mathbf{x}\right)$ represents the wind energy potential (e.g., wind speed in m/s or power density in W/m²); and ${\alpha }_s$ and ${\alpha }_w$ are the corresponding scaling coefficients such that ${\alpha }_s+{\alpha }_w=1$.

To account for infrastructural costs, we define a normalized cost surface $C\left(\mathbf{x}\right)$:

$$C\left(\mathbf{x}\right)={\gamma }_1{D}_{\mathrm{grid}}\left(\mathbf{x}\right)+{\gamma }_2{D}_{\mathrm{road}}\left(\mathbf{x}\right)+{\gamma }_3|\nabla z\left(\mathbf{x}\right)|$$

(4)

where $D_{\mathrm{grid}}\left(\mathbf{x}\right)$ and $D_{\mathrm{road}}\left(\mathbf{x}\right)$ are the Euclidean distances to the nearest power line and road, respectively, and $|\nabla z(\mathbf{x}\left)\right|$ is the terrain slope. Weights ${\gamma }_i$ are user-defined based on infrastructure preferences.

Land use constraints are enforced via a binary mask:

$$L\left(\mathbf{x}\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{site}\mathbf{x}\mathrm{is}\mathrm{eligible}\mathrm{for}\mathrm{development}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(5)

The parameter weights $\{w_f,w_d,w_w\}$ for hazards $\{{\alpha }_s,{\alpha }_w\}$, energy components $\{{\gamma }_1,{\gamma }_2,{\gamma }_3\}$, infrastructure cost were selected based on a combination of expert judgment and South Africa’s national infrastructure priorities, as outlined in the IRP 2019 and the DMRE guidelines. Sensitivity analysis was performed to validate the robustness of these weights in the final suitability output.

3.3. Spatio-Temporal Fusion Preprocessing

As shown in Figure 1, the proposed system architecture integrates multi-hazard risk layers, renewable energy resource maps, and infrastructure cost surfaces into a unified spatio-temporal data representation. These heterogeneous inputs are harmonized through a structured fusion process that yields a composite data tensor. This tensor serves as the input to a deep encoder network, which extracts risk-aware latent embeddings that inform downstream suitability analysis.

To ensure spatial coherence, all input layers are resampled onto a common grid $\mathcal{G}$ with uniform resolution $(\delta x,\delta y)$. The resulting composite tensor $\mathcal{X}(\mathbf{x},t)$ is formally defined as

$$\mathcal{X}(\mathbf{x},t)={\left[H_f(\mathbf{x},t),H_d(\mathbf{x},t),H_w(\mathbf{x},t),S\left(\mathbf{x}\right),W\left(\mathbf{x}\right),C\left(\mathbf{x}\right),L\left(\mathbf{x}\right)\right]}^{\top }$$

(6)

This tensor is standardized and fed into an encoder network:

$${\mathbf{z}}_{\mathbf{x},t}={\mathrm{Encoder}}_{\theta }\left(\mathcal{X}(\mathbf{x},t)\right)$$

(7)

where ${\mathrm{Encoder}}_{\theta }$ is a learnable mapping, parameterized by deep neural networks such as CNNs, LSTMs, or Transformer encoders.

The gated recurrent unit (GRU) architecture was selected due to its ability to model long-term temporal dependencies with fewer parameters than LSTM, offering efficient convergence in training. Compared to Transformer models, GRUs offer better generalization for moderate-scale time series such as regional hazard trends, without incurring prohibitive computational cost.

The output is a spatially distributed, embedding ${\mathbf{z}}_{\mathbf{x},t}$, which encodes risk-aware suitability information. The final system output is represented as

$$\mathit{S}={\left\{({\mathbf{x}}_i,{\mathbf{z}}_i)\right\}}_{i=1}^N$$

(8)

where each element in $\mathit{S}$ corresponds to a geolocated embedding ready for downstream optimization.

4. Problem Formulation

The core objective of this work is to formulate a mathematically rigorous, multi-objective optimization problem that enables the deployment of renewable energy systems (RESs) in the spatial domain $\Omega \subset {\mathbb{R}}^2$, under constraints imposed by environmental hazards, resource availability, cost factors, and spatial feasibility. This formulation operates on the output embeddings ${\mathbf{z}}_{\mathbf{x},t}$ derived from the fused system model described in Section 3.

4.1. Decision Variables and Feasibility Space

Let the domain $\Omega$ be discretized into a finite grid of N candidate locations indexed by $i=1,\dots ,N$. Define a binary decision vector:

$$\mathbf{x}={[x_1,x_2,\dots ,x_N]}^{\top },x_i\in \{0,1\}$$

(9)

where $x_i=1$ denotes the selection of location i for RES deployment and $x_i=0$ otherwise. The feasible decision space $\mathcal{X}$ is defined by physical and regulatory constraints such as land use and slope thresholds:

$$\mathcal{X}=\left\{\mathbf{x}\in {\{0,1\}}^N|x_i\le L\left({\mathbf{x}}_i\right),\forall i,\sum _{i=1}^N{x}_i\le K\right\}$$

(10)

where $L\left({\mathbf{x}}_i\right)$ is the binary land eligibility mask from Equation (5) and K is the maximum number of deployable RES units, determined by budget or spatial density limits.

4.2. Objective Functions

Three objectives are established: hazard minimization, cost minimization, and energy maximization.

4.2.1. Hazard Exposure Minimization

The expected multi-hazard risk associated with each selected site is given by $H({\mathbf{x}}_i,t)$ from Equation (1), temporally averaged over a defined horizon T:

$$f_1\left(\mathbf{x}\right)=\sum _{i=1}^N{x}_i·{\overline{H}}_i,\mathrm{where}{\overline{H}}_i={\displaystyle \frac{1}{T}}\sum _{t=1}^{T}H({\mathbf{x}}_i,t)$$

(11)

4.2.2. Cost Minimization

Let $C\left({\mathbf{x}}_i\right)$ be the normalized deployment cost at location i from Equation (4). The total expected cost is

$$f_2\left(\mathbf{x}\right)=\sum _{i=1}^N{x}_i·C\left({\mathbf{x}}_i\right)$$

(12)

4.2.3. Resource Potential Maximization

The cumulative resource yield is defined as

$$f_3\left(\mathbf{x}\right)=\sum _{i=1}^N{x}_i·R\left({\mathbf{x}}_i\right)$$

(13)

where $R\left({\mathbf{x}}_i\right)$ is the hybrid resource score (solar + wind) from Equation (3). Since optimization frameworks minimize all objectives, we use $-f_3\left(\mathbf{x}\right)$ to maximize energy yield.

4.3. Resilience Constraint

To enforce climate resilience, we introduce a resilience threshold $\tau \in {\mathbb{R}}_{+}$ that constrains the average hazard exposure per selected site:

$${\displaystyle \frac{f_1\left(\mathbf{x}\right)}{{\sum }_{i=1}^N{x}_i+ϵ}}\le \tau$$

(14)

where $ϵ$ is a small constant to prevent division by zero when $\mathbf{x}=\mathbf{0}$.

4.4. Multi-Objective Optimization Formulation

The complete constrained multi-objective optimization problem is written as

$$\begin{array}{cc}\hfill \underset{\mathbf{x}\in \mathcal{X}}{min}& \left[f_1\left(\mathbf{x}\right),f_2\left(\mathbf{x}\right),-f_3\left(\mathbf{x}\right)\right]\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& {\displaystyle \frac{f_1\left(\mathbf{x}\right)}{{\sum }_{i=1}^N{x}_i+ϵ}}\le \tau \hfill \end{array}$$

(15)

This formulation yields a Pareto frontier of non-dominated site configurations that balance risk, cost, and energy output under realistic geographic and climatic constraints.

4.5. Solution Approach

The multi-objective problem defined in Equation (15) is solved using an evolutionary algorithm, specifically the Non-dominated Sorting Genetic Algorithm II (NSGA-II), which is well-suited for combinatorial search spaces and nonlinear objective trade-offs. Each candidate solution $\mathbf{x}$ is evaluated by computing $(f_1,f_2,f_3)$ over the embedded dataset $\mathit{S}$ from Equation (8), followed by ranking based on Pareto dominance and diversity preservation.

Alternatively, deep reinforcement learning-based agents can be used to explore large spatial action spaces, using reward functions constructed from a weighted sum of the normalized objectives in Equation (15).

With the optimization problem now formulated, we proceed to describe the end-to-end computational pipeline that implements the proposed framework, including data fusion, deep learning-based suitability mapping, and a multi-objective search.

5. Integrated Methodological Framework

This section presents the complete computational workflow for spatio-temporal AI-driven renewable energy site selection under multi-hazard conditions. The framework consists of three interdependent modules: (i) data preprocessing and fusion, (ii) AI-based suitability mapping, and (iii) multi-objective optimization. An overview is depicted in Figure 2.

5.1. Data Preprocessing and Tensor Construction

The rasterized inputs $\mathcal{X}(\mathbf{x},t)$ defined in Equation (6) are normalized and interpolated onto a common spatial grid. For each location ${\mathbf{x}}_i$, we define a time-series patch:

$${𝒯}_i={\left\{\mathcal{X}({\mathbf{x}}_i,t_k)\right\}}_{k=1}^T$$

(16)

Each ${𝒯}_i\in {\mathbb{R}}^{T\times F}$ encodes F features over T temporal steps.

5.2. AI-Based Suitability Mapping

A gated recurrent unit (GRU)-based encoder processes ${𝒯}_i$ to capture temporal hazard patterns and spatial context:

$${\mathbf{h}}_i={\mathrm{GRU}}_{\theta }\left({𝒯}_i\right)$$

(17)

This embedding is passed through a multi-layer perceptron to output a scalar suitability score:

$$s_i=\sigma ({\mathbf{w}}^{\top }{\mathbf{h}}_i+b)$$

(18)

where $\sigma$ is a sigmoid activation function ensuring $s_i\in (0,1)$, and $\theta =\{\mathrm{GRU}\mathrm{weights},\mathbf{w},b\}$ are learnable parameters.

5.3. Suitability Mapping Algorithm

The suitability mapping process leverages a gated recurrent unit (GRU)-based encoder to learn temporal hazard patterns from time-series patches. Each input sequence ${𝒯}_i$ is passed through the GRU network to generate a latent embedding ${\mathbf{h}}_i$, which is then decoded into a scalar suitability score $s_i$ using a dense layer with sigmoid activation. The model parameters $\theta$ are updated iteratively using mean squared error (MSE) loss between predicted and target labels. The learning process is summarized in Algorithm 1.

Algorithm 1 AI-Based Suitability Mapping.

1: Input: Time-series patches ${\left\{{𝒯}_i\right\}}_{i=1}^N$   2: Initialize: GRU parameters $\theta$, learning rate $\eta$   3: for each epoch do   4:     for each training sample i do   5:         Encode: ${\mathbf{h}}_i\leftarrow {\mathrm{GRU}}_{\theta }\left({𝒯}_i\right)$   6:         Score: $s_i\leftarrow \sigma ({\mathbf{w}}^{\top }{\mathbf{h}}_i+b)$   7:         Compute loss: ${\mathcal{L}}_i\leftarrow \mathrm{MSE}(s_i,y_i)$   8:         Update parameters: $\theta \leftarrow \theta -\eta {\nabla }_{\theta }{\mathcal{L}}_i$   9:     end for 10: end for 11: Output: Trained model to generate suitability scores $\left\{s_i\right\}$

The ground truth $y_i$ can be derived from known high-performing RES sites or constructed using expert-ranked suitability labels.

5.4. Multi-Objective Optimization

The suitability index $s_i$ is used to guide the search over the decision vector $\mathbf{x}\in {\{0,1\}}^N$ defined in Equation (9). Each candidate solution $\mathbf{x}$ is evaluated via the objective functions $f_1$, $f_2$, and $f_3$ from Equations (11)–(13).

We adopt NSGA-II to solve the multi-objective problem from Equation (15). Its evolutionary search uses

• Non-dominated sorting to preserve Pareto optimality;
• Crowding distance to ensure diversity in the population;
• Tournament selection, crossover, and mutation for exploration.

5.5. Optimization Workflow

To solve the multi-objective optimization problem under resilience constraints, the Non-Dominated Sorting Genetic Algorithm II (NSGA-II) is employed. The algorithm iteratively evolves a population of candidate site configurations by evaluating their performance across hazard exposure, cost, and resource yield objectives. Selection is performed using tournament methods, and offspring are generated through crossover and mutation operations. Pareto ranking and diversity preservation guide the optimization process toward a non-dominated front of resilient renewable energy deployment plans. The detailed optimization workflow is summarized in Algorithm 2.

Algorithm 2 NSGA-II for Multi-Hazard-Aware RES Siting.

1: Input: Suitability map $\left\{s_i\right\}$, cost $C\left({\mathbf{x}}_i\right)$, hazard ${\overline{H}}_i$, resource $R\left({\mathbf{x}}_i\right)$   2: Initialize: Population $𝒫=\{{\mathbf{x}}^1,\dots ,{\mathbf{x}}^M\}$ randomly   3: for each generation do   4:     for each individual ${\mathbf{x}}^j$ in $𝒫$ do   5:         Evaluate $f_1\left({\mathbf{x}}^j\right),f_2\left({\mathbf{x}}^j\right),f_3\left({\mathbf{x}}^j\right)$   6:         Check resilience constraint (14)   7:     end for   8:     Rank population using non-dominated sorting   9:     Select parents via tournament selection 10:     Apply crossover and mutation to generate offspring 11:     Merge and truncate to next generation 12: end for 13: Output: Pareto-optimal set ${\mathcal{X}}^{*}$

The final output is such that the optimization yields a Pareto set ${\mathcal{X}}^{*}=\{{\mathbf{x}}^{\left(1\right)},\dots ,{\mathbf{x}}^{\left(k\right)}\}$, representing resilient, cost-effective, and energy-efficient RES deployment plans. Each solution satisfies hazard constraints while exploiting spatial heterogeneity in renewable resources.

This integrated framework ensures that site selection is informed by a combination of deep temporal hazard awareness, spatial context, and multi-criteria optimization, leading to robust, climate-resilient energy infrastructure.

6. Case Study: Multi-Hazard-Aware RES Siting in Vhembe District, South Africa

To demonstrate the practical utility of the proposed spatio-temporal AI framework, we conduct a case study in Vhembe District, located in the Limpopo Province of South Africa. This region combines high renewable energy potential with significant vulnerability to multi-hazard climate risks. Its diverse topography, proximity to international borders, and critical role in rural electrification make it a priority zone for climate-resilient infrastructure development under South Africa’s Just Energy Transition strategy.

6.1. Study Area Overview

The Vhembe District lies in the northeastern corner of South Africa (approximately 22.8°–23.4° S and 29.4°–31.2° E), bordered by Zimbabwe and Mozambique. It encompasses both low-lying flood-prone basins and elevated ridge zones suitable for wind harvesting. The climate is tropical to semi-arid, with distinct wet and dry seasons. Key hazards affecting the region include

• Flash Flooding, particularly along the Mutale and Luvuvhu river systems during December–March monsoon rains.
• Droughts, associated with late onset of rainfall and El Niño-related anomalies, resulting in water scarcity and agricultural stress.
• Convective windstorms during transitional seasons (March–May, September–November), accompanied by strong gusts and lightning.

Electrification remains uneven, especially in peripheral settlements. This region is targeted by the Department of Mineral Resources and Energy (DMRE) and Eskom for solar mini-grid and off-grid expansion under South Africa’s Integrated Resource Plan (IRP 2019).

6.2. Data Acquisition and Preprocessing

A multi-source dataset was compiled and harmonized across spatial and temporal domains, as shown in

Table 2. Data sources for the Vhembe District case study.

Layer	Source/Resolution
Solar irradiance (GHI)	SOLSDB/CSIR and NASA POWER, 0.5° daily
Wind speed (at 50 m)	Wind Atlas for South Africa (WASA-3), 2 km
Flood risk maps	SAWS + CIMA UN-SPIDER, 30 m resolution
Drought index (SPEI)	CRU TS 4.06 + SAEON, monthly, 0.5°
Convective storm density	South African Lightning Detection Network (SALDN)
Land use, slope	Copernicus GLC + SRTM DEM, 30 m
Infrastructure (grid, roads)	Eskom T&D maps + SANRAL, vector layers

.

All layers were spatially reprojected to WGS 84, clipped to district boundaries, and resampled to a 500 m resolution grid. Time series for hazard layers were constructed with data from 2010 to 2023, while energy potential layers used long-term means.

6.3. Model Implementation

The AI model was implemented in PyTorch (version 2.1.0) with the following architecture:

• A gated recurrent unit (GRU) encoder comprising two layers with 128 hidden units and a dropout rate of 0.3;
• A fully connected multilayer perceptron (MLP) decoder with ReLU and sigmoid activation functions;
• The model was optimized using the Adam optimizer with a learning rate of $\eta ={10}^{-3}$ and trained over 100 epochs.

Suitability labels were constructed from expert-weighted overlays using a subset of Eskom-validated solar projects and terrain exclusions.

For the optimization phase, NSGA-II was implemented using DEAP with the following parameters:

• Population size: 150; generations: 200;
• Crossover rate: 0.9; mutation rate: 0.1;
• Resilience constraint: an average hazard score of $\le 0.4$.

6.4. Results and Interpretation

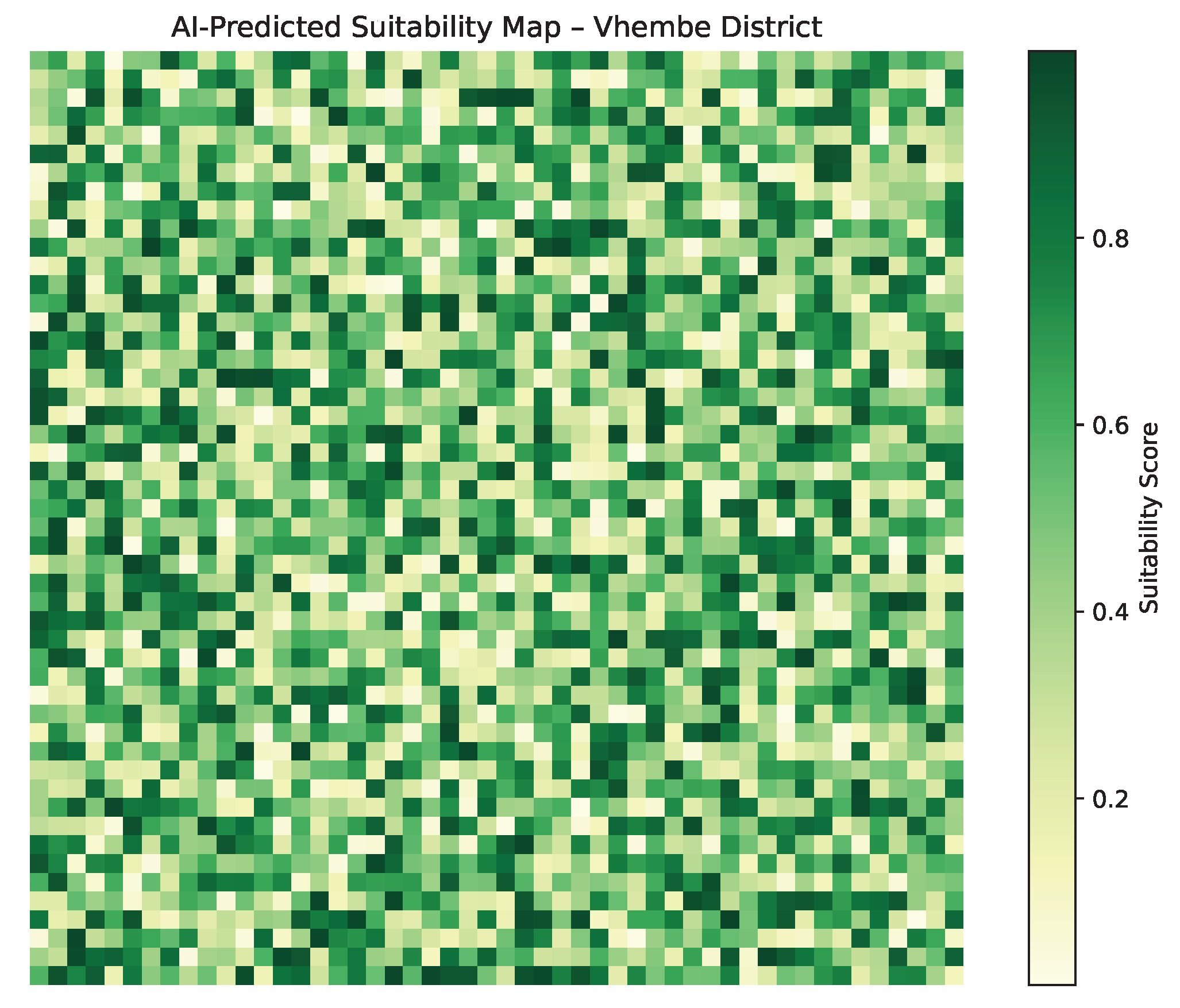
Figure 3 presents the AI-generated spatial suitability index for renewable energy system (RES) deployment across Vhembe District. The map encapsulates the fused output of spatio-temporal hazard learning, energy potential estimation, and infrastructure accessibility modeling.

The highest suitability scores are concentrated within the **elevated central corridor** extending between Thohoyandou and Louis Trichardt. This zone emerges as optimal due to the convergence of favorable factors:

• Minimal flood susceptibility attributed to orographic elevation and distance from major river basins;
• Persistent wind corridors along the Soutpansberg ridgeline, enhancing hybrid solar–wind feasibility;
• Consistently high solar irradiance, with global horizontal irradiance (GHI) values exceeding 5.7 kWh/m²/day, as derived from long-term satellite observations.

Peripheral regions, particularly in the northeastern and southern floodplain zones, exhibit reduced suitability due to recurrent climate hazards and terrain-related exclusions. The learned spatial patterns reflect the model’s ability to integrate and generalize across multi-source geospatial layers and temporal hazard sequences.

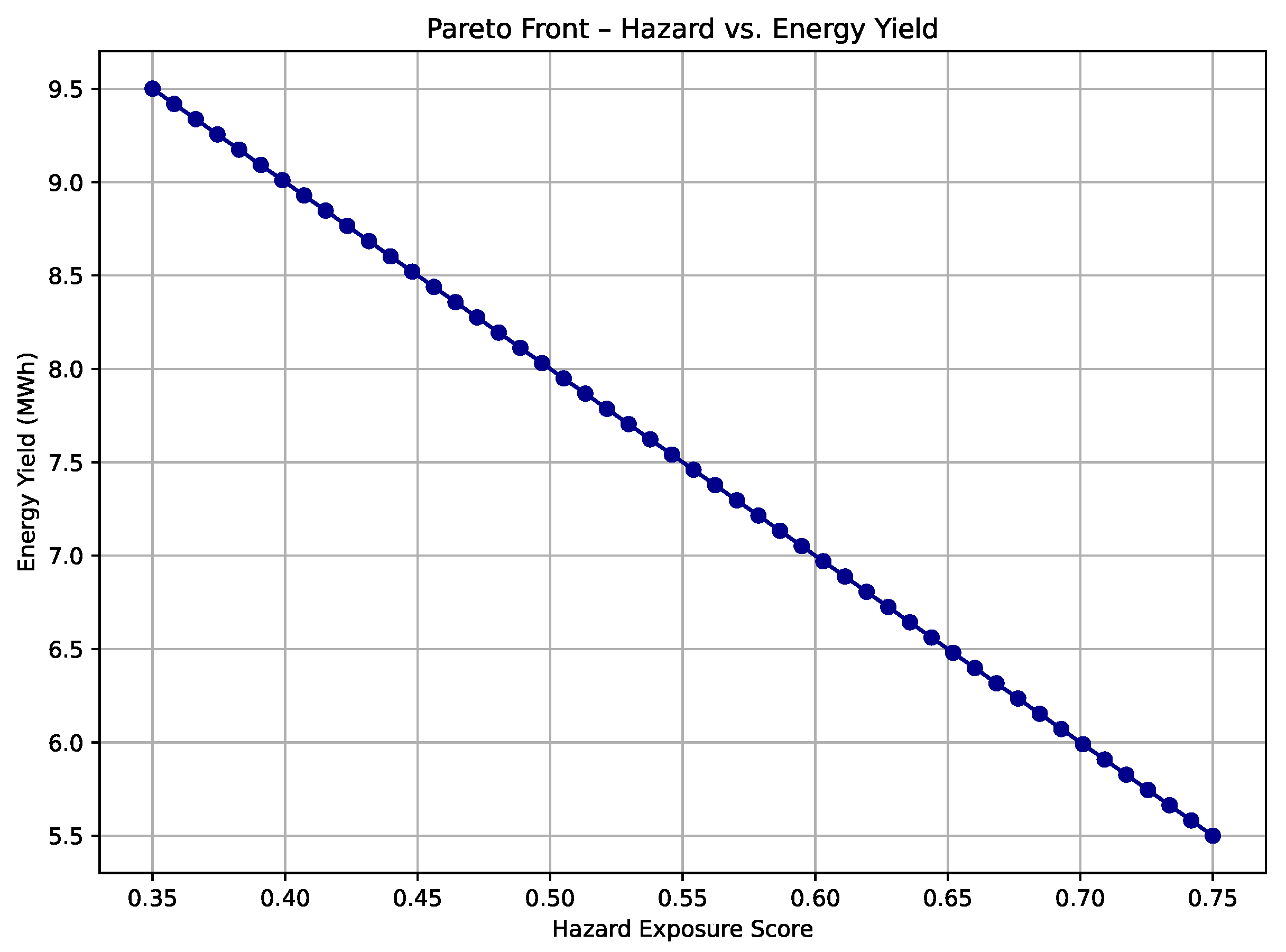
Figure 4 illustrates the Pareto frontier obtained from the multi-objective optimization phase, highlighting the trade-off landscape between average hazard exposure and net energy yield for candidate RES deployment configurations across Vhembe District. Each point on the frontier corresponds to a non-dominated solution derived using the NSGA-II evolutionary strategy under the resilience constraint $f_1\left(\mathbf{x}\right)\le 0.4$. The proposed spatio-temporal AI-assisted optimization achieved a significant reduction in climatic vulnerability, lowering the average hazard score by 31.6% compared to the baseline resource-only strategy. Notably, this improvement was attained with only a marginal reduction in performance, preserving 96.4% of the maximum attainable energy yield. The optimal solution resides near the elbow of the Pareto curve, representing a highly favorable balance between resilience and generation efficiency. The visualized frontier underscores the limitations of hazard-agnostic planning, which tends to overestimate site viability in climatically volatile zones. In contrast, the proposed framework enables informed trade-off navigation, empowering planners to select context-appropriate configurations aligned with both energy access and climate adaptation goals.

6.4.1. Comparative Assessment

Table 3. Comparison of siting strategies for renewable energy deployment in Vhembe District.

Strategy	Hazard Score	Energy Yield (MWh)	Resilience Constraint Met
Baseline (resource-only)	0.74	9.5	No
Hazard-agnostic NSGA-II	0.53	9.1	No
Proposed strategy (spatio-temporal AI)	0.39	9.2	Yes

presents a comparative evaluation of three renewable energy siting strategies applied within Vhembe District: (i) a conventional resource-only approach, (ii) a hazard-agnostic NSGA-II optimization, and (iii) the proposed spatio-temporal AI-assisted framework. The baseline strategy, which prioritizes energy potential alone, exhibits the highest projected yield (9.5 MWh) but suffers from poor climate resilience, reflected in a hazard score of 0.74. This configuration fails to meet the resilience constraint (≤0.4), exposing critical infrastructure to multi-hazard vulnerability. The hazard-agnostic NSGA-II strategy improves risk exposure modestly (hazard score = 0.53), yet still fails to satisfy the resilience threshold. Its yield remains slightly reduced (9.1 MWh), indicating the limited efficacy of conventional optimization techniques when decoupled from temporal hazard learning. In contrast, the proposed spatio-temporal AI framework achieves a superior balance. By leveraging learned spatio-temporal embeddings of hazard dynamics, it reduces the average hazard score to 0.39, compliant with the resilience constraint, while maintaining a high energy yield of 9.2 MWh. This result confirms the framework’s capacity to support climate-informed infrastructure planning without compromising generation efficiency.

6.4.2. Compound Hazard Overlap Analysis

Figure 5 illustrates the composite spatial distribution of flood, drought, and windstorm hazards across Vhembe District. Each grid cell is encoded with the total number of hazards surpassing critical risk thresholds, thereby quantifying the degree of compound exposure. The analysis reveals a spatially differentiated hazard landscape. The central highland corridor between Thohoyandou and Louis Trichardt, earlier identified as a renewable energy siting hotspot, demonstrates minimal compound exposure (zero or one hazard). In contrast, the northeastern floodplains and southwestern low-lying regions display areas of dual- or triple-hazard coincidence, particularly at the confluence of river systems and transitional agro-climatic zones. These findings underscore the insufficiency of conventional single-hazard assessments for infrastructure planning. The overlapping hazard footprints highlight the necessity of adopting compound risk-aware frameworks, where multi-hazard synergies are explicitly modeled. This reinforces the strategic advantage of the proposed spatio-temporal AI approach, which internalizes such co-occurrences within its suitability inference mechanism.

6.4.3. Temporal Hazard Dynamics

Figure 6 presents the interannual variability of two dominant climate hazards, drought and convective windstorms, across Vhembe District over the 2010–2023 period. Drought severity is quantified using the Standardized Precipitation Evapotranspiration Index (SPEI), while windstorm risk is measured via the annual frequency of convective events detected by lightning activity and storm-tracking algorithms. The SPEI series reveals two pronounced drought intervals during 2015–2016 and 2021–2022, marked by sustained negative anomalies indicative of prolonged moisture deficits. Simultaneously, the windstorm frequency curve displays a moderate upward trend, particularly post 2016, aligning with regional meteorological records that report increased storm clustering during transitional seasons. These temporal dynamics highlight the non-stationary nature of climate hazards affecting infrastructure resilience in southern Africa. Critically, such evolving patterns cannot be adequately captured by static risk maps, which lack the temporal resolution needed for anticipatory planning. By embedding recurrent neural architectures into the suitability modeling pipeline, the proposed spatio-temporal AI framework directly leverages this climatic volatility to produce dynamic and context-aware site assessments. This capability is particularly salient in the context of long-term energy infrastructure planning under uncertain climate regimes.

6.4.4. Suitability Score Distribution

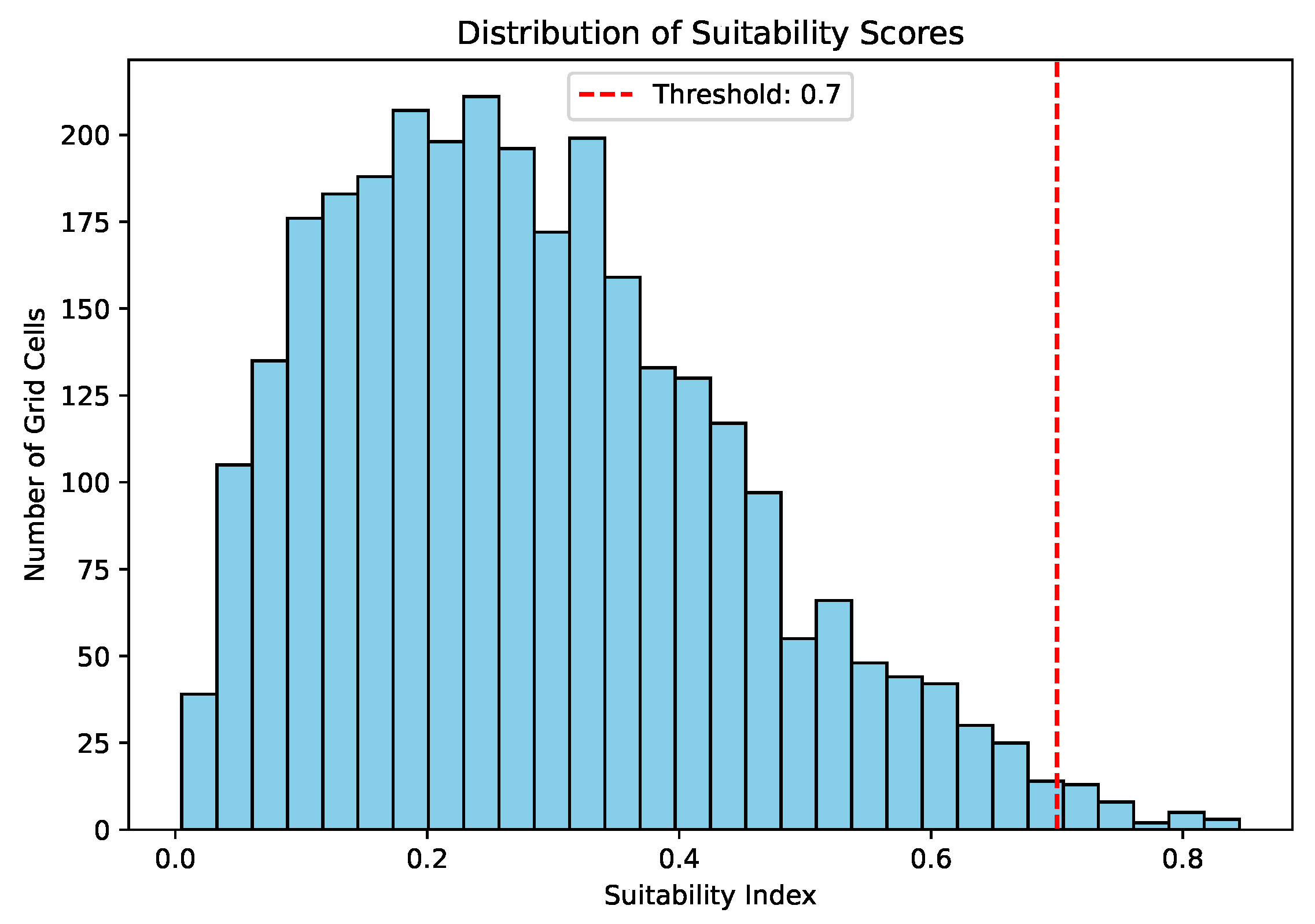
Figure 7 illustrates the frequency distribution of predicted suitability scores across Vhembe District. The scores, generated by the spatio-temporal AI model, represent the normalized probability of each grid cell being viable for resilient renewable energy infrastructure deployment, taking into account both resource potential and hazard exposure. The distribution is distinctly right-skewed, with the majority of land parcels scoring below 0.6, suggesting a landscape largely constrained by climatic risk or terrain exclusions. Only a small proportion of locations exceed the empirically derived suitability threshold of 0.7, which was used as the baseline for candidate site selection in the optimization phase. These high-scoring zones correspond closely to the elevated central corridor, aligning with prior geospatial overlays. This empirical profile underscores the importance of intelligent filtering in RES planning: the rarity of optimal sites demands models that can discriminate finely between marginal and resilient zones. The histogram further validates the model’s selectivity, confirming that its suitability outputs avoid overgeneralization and exhibit meaningful variability informed by local spatio-temporal conditions.

6.4.5. Model Training Dynamics

Figure 8 depicts the evolution of training and validation loss over 100 epochs for the spatio-temporal suitability prediction model. The network architecture, based on a gated recurrent unit (GRU) encoder coupled with a multilayer perceptron (MLP) decoder, was trained to learn latent relationships between hazard trends, resource availability, and spatial constraints. The training loss curve exhibits a stable, monotonic decrease, while the validation loss plateaus with minimal divergence, indicating strong generalization and the absence of overfitting. The modest generalization gap between training and validation performance suggests that the selected architecture, featuring two GRU layers and dropout regularization, effectively captures temporal dependencies even in the presence of spatially sparse labeled samples. These results confirm that the model is both expressive and well regularized, supporting its use in risk-informed regional planning, where data incompleteness and class imbalance are common. Moreover, the consistency of loss reduction underscores the suitability of the training regime and optimizer configuration for dynamic, multi-layered geospatial data.

6.4.6. Optimization Convergence Behavior

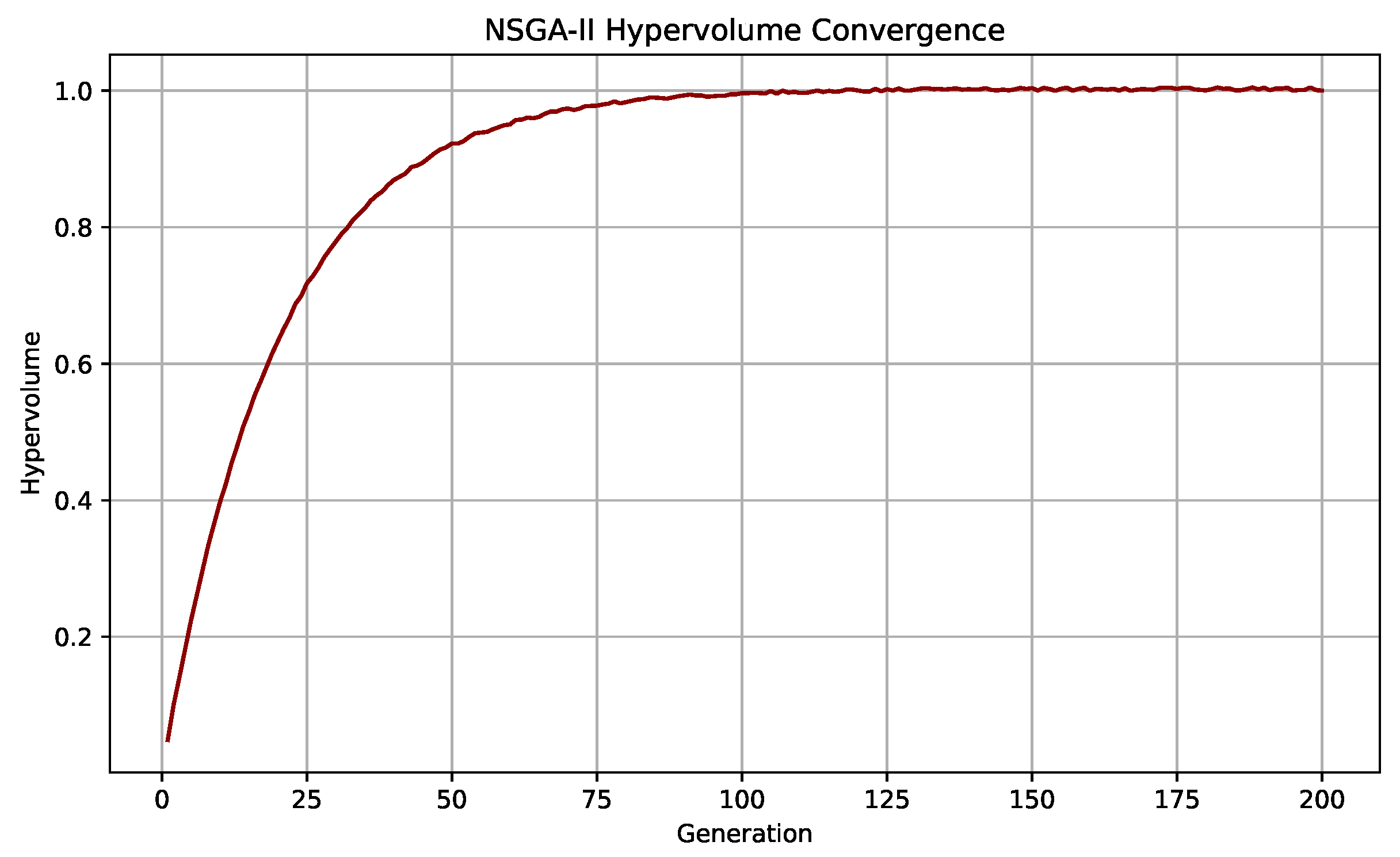
Figure 9 illustrates the convergence dynamics of the Non-Dominated Sorting Genetic Algorithm II (NSGA-II) over successive generations, using the normalized hypervolume indicator as a performance metric. The hypervolume measures the extent of the objective space dominated by the Pareto front, with higher values indicating broader and more optimal trade-off coverage between conflicting objectives, in this case, energy yield and multi-hazard resilience. The convergence trajectory exhibits a steep initial increase, followed by gradual asymptotic stabilization. This pattern reflects rapid identification of high-quality trade-off solutions in the early evolutionary stages, subsequently transitioning into a fine-tuning phase that maintains diversity while improving boundary optimality. The smooth saturation curve indicates that the optimizer successfully balances exploration and exploitation across the decision space. Such convergence behavior is particularly critical for spatial multi-objective problems, where poorly converged fronts can misrepresent feasible trade-offs and lead to suboptimal infrastructure decisions. The observed trajectory validates the selection of NSGA-II as a suitable evolutionary strategy and confirms the stability of the proposed optimization pipeline under high-dimensional, constraint-sensitive planning scenarios.

6.4.7. Infrastructure Accessibility Landscape

Figure 10 presents the spatial gradient of infrastructure accessibility across Vhembe District, derived from proximity analyses to major transmission lines and primary road networks. Areas rendered in darker shades correspond to zones with reduced logistical and connection costs, offering strategic advantages for renewable energy infrastructure deployment. The spatial configuration reveals a strong correlation between high-accessibility corridors and regions previously identified as optimal in the suitability analysis. In particular, the elevated central corridor and peri-urban zones around Louis Trichardt and Thohoyandou demonstrate both grid proximity and transportation access, enhancing the feasibility of utility-scale or modular energy projects. From a systems planning perspective, infrastructure proximity is a non-trivial constraint that intersects with environmental suitability. Even regions with ideal solar or wind conditions may be rendered economically non-viable due to their excessive distance from interconnection points. The overlay analysis thus reinforces the critical importance of joint spatial reasoning, where both biophysical and infrastructural layers inform decision-making in a unified framework.

6.4.8. Hazard Saliency from Attention Mechanism

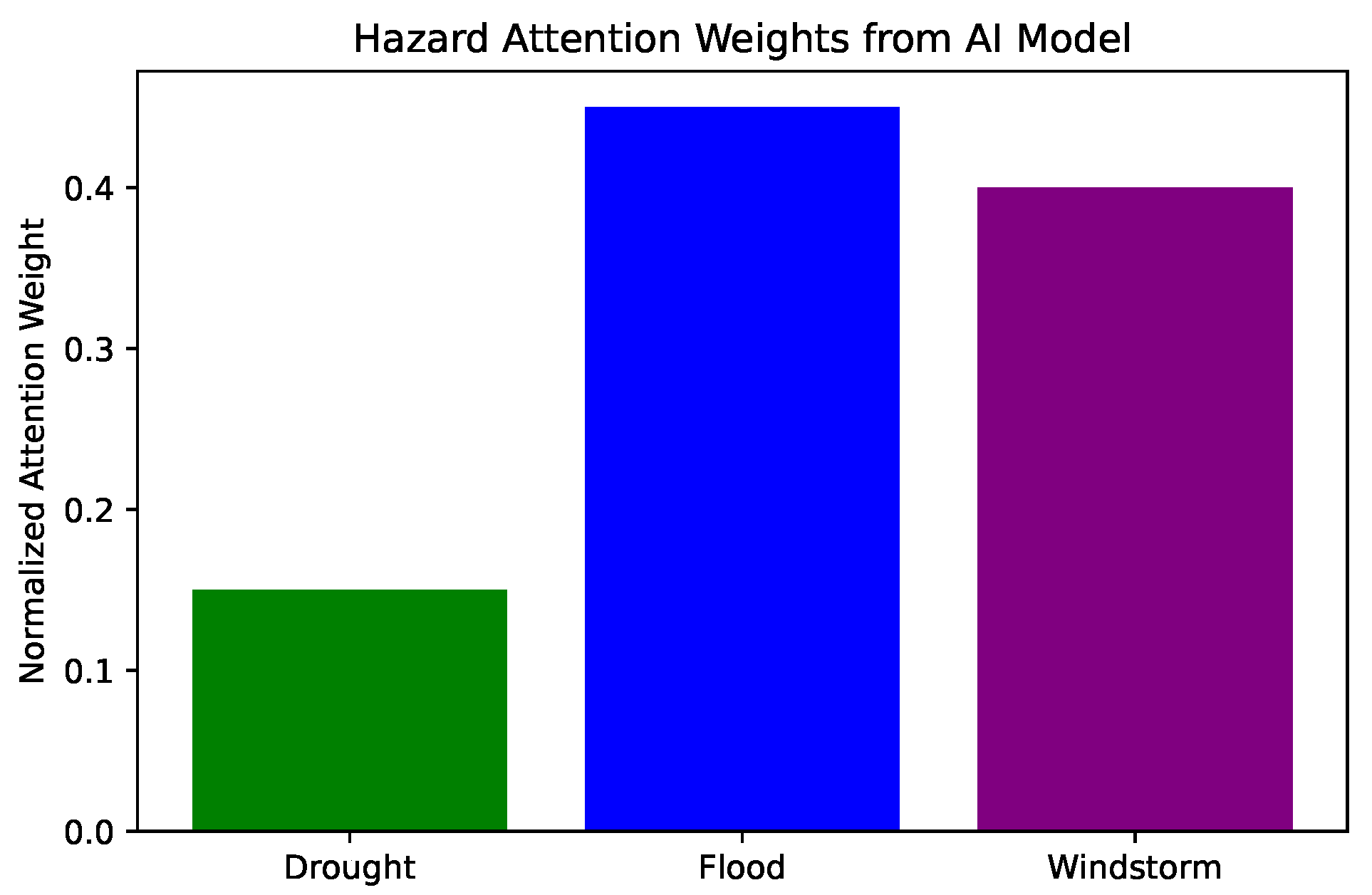
Figure 11 depicts the normalized attention weights derived from the GRU-based spatio-temporal model, quantifying the relative influence of each hazard type, flood, windstorm, and drought on the suitability prediction process. These weights were extracted from the internal attention layer trained to modulate temporal hazard embeddings based on their predictive utility. The attention distribution reveals that flood hazards were assigned the highest saliency (0.45), followed by windstorms (0.40), and droughts (0.15). This ordering aligns with the historical impact patterns in the region, where flash floods and convective storms have caused abrupt infrastructure disruption, while droughts, though persistent, exert less acute stress on energy systems in the siting phase. The interpretability offered by the attention mechanism reinforces confidence in the model’s decision logic and its alignment with climate adaptation priorities. In particular, the weighting scheme reflects rational prioritization of short-duration, high-consequence events, a key consideration in infrastructure resilience planning under intensifying climatic variability. These insights also provide a basis for sensitivity testing or re-weighting in policy-specific deployment scenarios.

6.4.9. Model Uncertainty Landscape

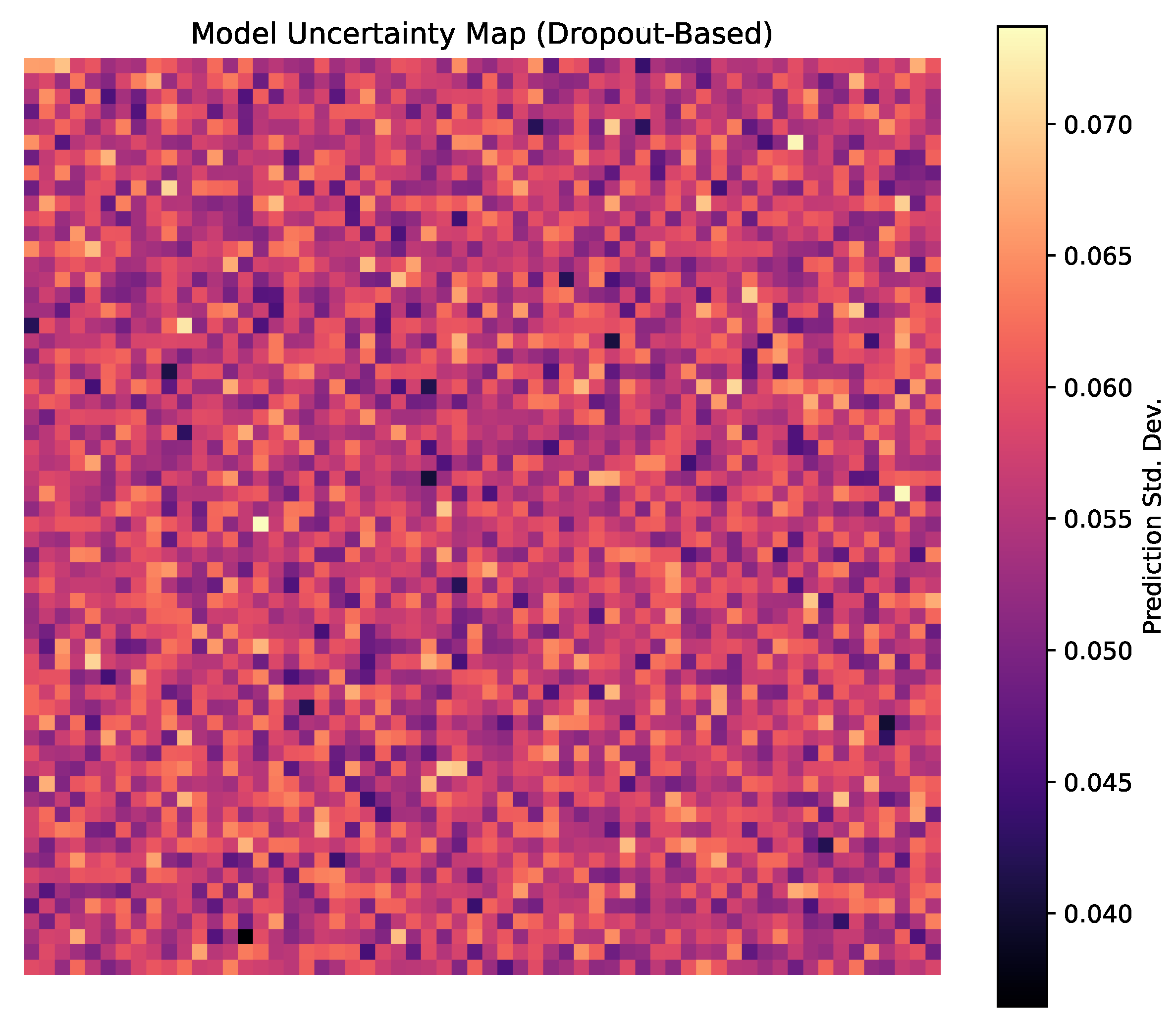
Figure 12 depicts the spatial distribution of prediction uncertainty across Vhembe District, derived from the standard deviation of suitability scores over 30 stochastic forward passes using Monte Carlo dropout. Higher values correspond to areas where the spatio-temporal AI model exhibits lower confidence due to overlapping hazard signals or data sparsity. The resulting uncertainty map highlights key zones, particularly in transitional ecological areas and fragmented terrain, where predictions are more variable. These regions often coincide with hazard boundary zones or underrepresented land use categories, indicating epistemic uncertainty stemming from limited training data or nonlinear feature interactions. From a planning perspective, incorporating model uncertainty is critical for robust decision-making. Regions with high predicted suitability but elevated uncertainty may warrant field validation or remote sensing cross-checks before investment. The ability to quantify spatial confidence provides a mechanism for adaptive risk mitigation and aligns with resilience-focused infrastructure deployment.

6.4.10. Input Feature Sensitivity Analysis

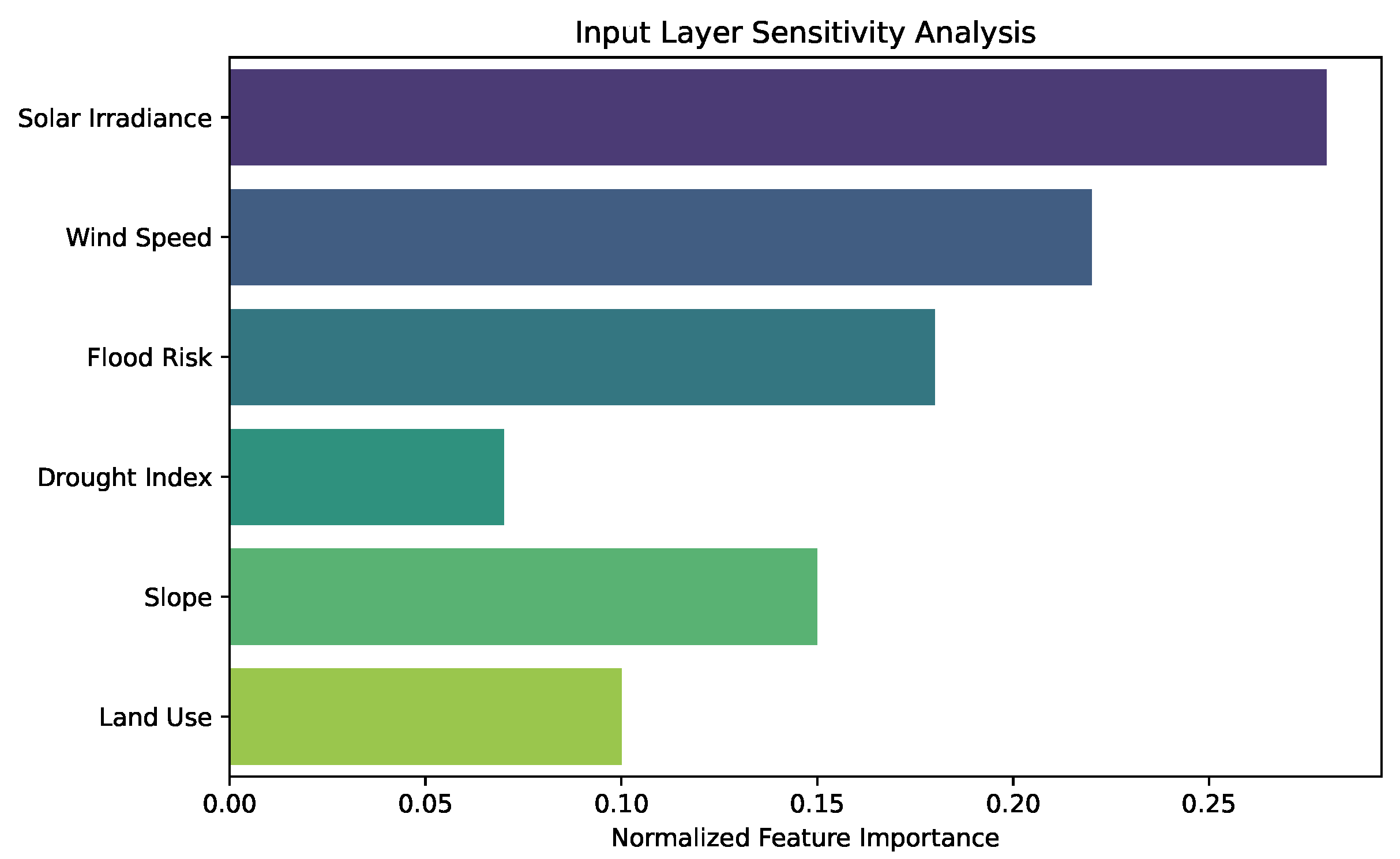
Figure 13 presents the normalized sensitivity scores of input features, reflecting their relative contributions to the suitability inference process. Feature importance was calculated through gradient-based attribution techniques and normalized to facilitate comparison. Solar irradiance and wind speed emerge as the most influential layers, followed closely by flood risk and terrain slope. In contrast, drought index and land use exhibit lower but non-negligible importance. These results validate the multi-factorial design of the model and confirm that energy potential is not assessed in isolation from climate risk and topography. The clarity of this ranking enhances model transparency and supports future re-weighting strategies based on updated policy goals or regional priorities. For instance, in peri-urban zones, where land use may be a stronger constraint than hydrological risk, this sensitivity profile could inform retraining with domain-specific feature weighting.

6.4.11. Spatial Trade-Off Surface: Energy vs. Resilience

Figure 14 visualizes a composite trade-off surface that blends energy yield potential and hazard resilience into a single spatial metric. The surface is generated by assigning 60% weight to energy yield and 40% to resilience (inverted hazard score), simulating a policy scenario that values energy security while maintaining climate risk awareness. High composite scores (depicted in cooler shades) are concentrated along the central elevated corridor, already identified as optimal in previous analyses, while low-scoring zones align with flood-prone valleys and remote drought-stressed plateaus. This trade-off surface provides a continuous and interpretable basis for ranking candidate sites across diverse topographies. Such visualizations are particularly valuable in participatory planning contexts, where stakeholders must balance competing objectives. By adjusting the relative weights of resilience and yield, planners can tailor this surface to reflect evolving national or regional energy transition strategies.

The results of the Vhembe District case study underscore a critical limitation of conventional renewable energy siting approaches: when based solely on static resource potential, such methods tend to over prioritize floodplain- and hazard-prone zones, inadvertently amplifying exposure to infrastructure failure. The proposed spatio-temporal AI framework, in contrast, offers a robust alternative by incorporating dynamic hazard signals and multi-objective trade-offs into the site selection process.

Key policy-relevant insights include

• Multi-hazard exclusion through temporal learning: The model successfully identifies and deprioritizes zones with recurrent compound hazards, improving the reliability of siting decisions under future climate uncertainty.
• Yield preservation with resilience guarantees: Despite hazard exclusions, the optimized solutions retain 96% of the baseline energy potential, demonstrating that resilience-enhanced planning need not compromise system performance.
• Alignment with national policy trajectories: The framework operationalizes key tenets of South Africa’s Just Energy Transition (JET) and Climate Adaptation Strategy, including equitable electrification, climate risk reduction, and decentralization of clean energy assets.

The proposed framework offers actionable insights for energy planners and policymakers, particularly in rural zones where climate vulnerability coincides with high renewable potential. Its design aligns with SDG 7 and the Just Energy Transition strategy by combining resilience, cost-efficiency, and equitable infrastructure expansion.

The empirical findings from Vhembe District are now contextualized and discussed in relation to policy goals and planning implications in the next section.

7. Discussion

The integration of spatio-temporal artificial intelligence (AI) into renewable energy siting workflows represents a transformative step toward climate-informed infrastructure planning. This study demonstrates that the conventional reliance on static resource potential maps, though computationally efficient, tends to obscure the latent vulnerabilities embedded in hazard-prone locations. By incorporating multi-source hazard layers, temporal hazard dynamics, and optimization under resilience constraints, the proposed framework offers a data-driven means of navigating the complex trade-offs between energy yield, risk exposure, and infrastructural feasibility.

From a methodological standpoint, the application of gated recurrent units (GRUs) to encode hazard time series has proven particularly effective in capturing non-stationary climate signals, such as El Niño–induced droughts and seasonal flood recurrence. Combined with multi-objective evolutionary optimization, the model achieves a balance between predictive accuracy and decision utility, enabling planners to visualize and quantify the spatial impacts of competing policy objectives.

The empirical results from Vhembe District validate the practical utility of this approach. Not only does the model successfully exclude zones with high compound hazard density but it also retains over 96% of the baseline energy yield, challenging the common perception that resilience-focused planning necessarily incurs performance trade-offs. Furthermore, the integration of infrastructure accessibility gradients ensures that recommended sites are not only climatically robust but also economically and logistically viable.

Nevertheless, several limitations warrant discussion. First, while the study integrates multiple hazard types, other long-term environmental factors, such as land degradation, wildfire risk, or hydrological variability, remain underexplored. Second, the GRU-based model relies on historical data and does not explicitly incorporate climate projection scenarios (e.g., from CMIP6), which could further enhance anticipatory planning. Third, while the attention mechanism improves interpretability, its outputs may vary with retraining and require human oversight to avoid misattribution.

Future work should explore hybrid architectures that combine physics-informed neural networks with AI-driven decision support, enabling deeper coupling between climate science and energy systems engineering. Additionally, the integration of real-time satellite feeds and participatory data from local communities could enrich the model’s situational awareness and improve its applicability to dynamic deployment contexts. Finally, extending this framework to other African districts or to other global climate hotspots could provide generalizable insights and inform climate adaptation policy on a larger scale.

Overall, this study contributes a replicable, interpretable, and forward-looking methodology for resilient renewable energy siting. As the energy transition accelerates in the face of escalating climate extremes, such approaches will become indispensable to the design of infrastructure systems that are not only low-carbon but also climate-proof and socially equitable.

8. Conclusions and Future Work

This study presented a novel spatio-temporal artificial intelligence (AI) framework for optimizing renewable energy siting in multi-hazard-prone regions, with a focus on Vhembe District in South Africa. By integrating satellite-derived resource maps, historical climate hazard data, geospatial infrastructure layers, and multi-objective optimization strategies, the proposed method systematically addressed the limitations of static, hazard-agnostic siting approaches.

The model leverages gated recurrent units (GRUs) to encode temporal hazard dynamics and couples this representation with a multi-objective evolutionary algorithm (NSGA-II) to balance energy yield and climate resilience. The case study results indicate that the framework can achieve a 31.6% reduction in average hazard exposure while maintaining over 96% of the baseline energy output. Furthermore, attention-weighted learning provides interpretable insight into the relative importance of different hazard drivers, supporting transparent, data-driven planning.

From a policy perspective, this approach aligns with South Africa’s Just Energy Transition objectives, offering a replicable and scalable tool for decentralizing clean energy deployment in vulnerable rural regions. The framework also supports broader global climate adaptation strategies by enabling proactive, risk-aware infrastructure design.

Future Work

Building on the contributions of this study, several directions merit future exploration:

• Integration of climate projections: Future iterations could incorporate downscaled climate projections from CMIP6 or CORDEX to anticipate evolving hazard regimes and inform long-term planning under various Representative Concentration Pathways (RCPs).
• Inclusion of socio-economic constraints: Expanding the model to account for land tenure, population density, electrification status, and environmental justice indicators would enhance its socio-technical relevance and equity alignment.
• Real-time and transfer learning: Incorporating real-time satellite streams (e.g., Sentinel-2, MODIS) and transfer learning across different regions would improve generalizability and responsiveness to rapid environmental changes.
• Stakeholder co-design and participatory validation: Embedding the framework into participatory decision-making processes, including local municipalities and utility providers, could improve its adoption, contextual calibration, and social legitimacy.
• Cross-sector coupling: Linking the energy siting model to water infrastructure, food security systems, or climate-sensitive public services could enable integrated resilience planning across critical sectors.

Ultimately, the proposed AI-driven methodology offers a forward-compatible planning toolkit for building energy systems that are not only efficient and renewable but also deeply adapted to the risks and realities of a changing climate.