Active–Reactive Coordination Optimal Dispatch of Active Distribution Network Considering Grid Balance Degree

Abstract

To address the impact of source-load uncertainty on voltage security and power flow distribution, this study proposes an active distribution network (ADN) active–reactive power coordinated optimal dispatch strategy that incorporates the grid balance degree (GBD). First, we analyzed GBD by defining it across three key dimensions: power flow, voltage, and network structure. We combined GBD with economic indicators to establish a pre-assessment indicators system to determine grid operational status. Second, to address source-load uncertainty, a dispatch model is established, incorporating a load factor penalty term into the optimal objective. Nonlinear terms in the model are linearized for efficient solution using the Gurobi solver. Finally, GBD is adjusted through measures such as load factor penalty threshold, voltage constraint upper/lower limits, and network restructuring. The optimal dispatch strategy is selected by comparing pre-assessment indicators of operational states across different dispatch schemes. Case studies demonstrate that compared to the baseline dispatch scheme, the proposed strategy achieves a 17.4% reduction in heavy load rates, a 5.7% decrease in power flow entropy, a 5.2% reduction in voltage peak-to-valley difference rates, and a 3% decrease in network losses. Although operating costs slightly increase by 0.56%, the operation reliability of the distribution network and power quality are further optimized. This fully demonstrates the gain value of GBD optimization and provides a reference for the optimization of ADN dispatch to achieve high operational reliability.

1. Introduction

With the introduction of the dual carbon goals, the installed capacity of distributed generation (DG) represented by wind and solar power has grown rapidly. How to effectively address the operational uncertainties of both generation and load [1,2,3] while ensuring high-quality operation of distribution grids presents dispatchers with a high degree of complexity. For instance, Europe recorded over 8600 grid voltage out-of-limit events in 2024—a more than 20-fold increase from 2015. Regions with high photovoltaic penetration, such as Bavaria, Germany, experienced approximately 3200 voltage out-of-limit incidents, posing severe challenges to distribution network operational reliability. Due to the relatively high R/X ratio of distribution feeder lines, node voltages are influenced by both active and reactive power. This necessitates coordinating active and reactive power to simultaneously meet voltage security and power balance requirements [4,5]. Optimized dispatch must balance multiple objectives: ensuring voltage stability while maintaining operational efficiency and reducing active/reactive power losses. Some of these optimal objectives are conflicting and mutually restrictive. Effectively balancing these optimal demands has become a pressing challenge for active distribution network (ADN) dispatch [6].

Currently, many studies [7,8] evaluate grid operational status by constructing load balance or power flow balance indicators. The authors of [9] propose a source-load power timing balance quantification method based on information entropy theory, measuring GBD through fluctuations in net load—defined as the difference between distribution network load and DG power—and incorporating this into optimal objectives. The authors of [10] define the heavy load rate indicator as a constraint for coordinated planning and operation of transmission grids, highlighting the importance of load rate balance for grid operation and dispatch. Balance in the power flow dimension reflects whether power transmission in distribution grids is distributed evenly and reasonably, preventing situations where some lines are overloaded while others are underloaded. A good balance can reduce network losses, improve node voltage levels, and enhance grid safety and stability. The authors of [11,12,13] propose incorporating voltage deviation into the objective function. By minimizing voltage deviation while ensuring compliance with voltage standards, node voltages fluctuate within a narrow range around the rated voltage, indicating good voltage balance. Currently, no studies have addressed grid structure-level balance. Such a balance reflects the equilibrium of the distribution network topology. High structural balance reduces network losses, elevates voltage levels, improves supply reliability, and enhances the integration of renewable energy. Therefore, defining GBD indicators is necessary to provide a multidimensional, intuitive representation of grid operational status.

In recent years, scholars have conducted extensive research on constructing operation status assessment indicator systems and optimal dispatch strategies for ADNs. The authors of [14] analyzed the impact of distributed renewable energy on grid operation across six dimensions, including safety and reliability. However, this study failed to deeply integrate assessment indicators with practical dispatch strategies, limiting its ability to provide quantitative dispatch support. Regarding specific indicator system development, the authors of [15] established ten quantitative assessment indicators aligned with dual-carbon goals; the authors of [16] developed a detailed 14-item indicator system tailored to the characteristics of ADNs—high penetration of distributed resources and flexible network structures—but both studies focused on static operational state assessment, failing to address the dynamic dispatch requirements of ADNs. In summary, existing research primarily evaluates grid operational status based on historical data and real-time measurements (e.g., node voltage and line current), enabling operational status early warning and equipment condition-based maintenance for ADNs. No dedicated status assessment indicator system exists to guide dispatchers in formulating dispatch strategies for ADNs. There is an urgent need to establish an assessment indicator system covering critical grid dimensions, providing service for dispatch with varying operational reliability requirements.

Given this, this paper proposes an ADN active–reactive power coordinated optimal dispatch model that considers GBD. The flowchart of the coordinated active and reactive power optimal dispatch for ADNs is shown in Figure 1. First, GBD is analyzed by defining it across three key dimensions—power flow, voltage, and network structure—while proposing measures to enhance GBD. Building upon this, an indicator system for pre-assessing distribution network operational status can be further developed by integrating GBD and economic efficiency indicators, enabling intuitive simulation of dispatch outcomes, and providing operational personnel with a scientific basis for selecting dispatch strategies. Next, it addresses source-load uncertainties by coordinating energy storage systems (ESS), reactive power compensation, and demand response (DR) resources to establish an optimal dispatch model. To handle the model’s complexity, nonlinear terms are linearized for efficient solution using the Gurobi solver. Measures to enhance GBD—such as adjusting load penalty lines, voltage upper/lower limit constraints, and network restructuring—enable optimized dispatch for ADNs with varying operational reliability requirements. Finally, pre-assessment indicators are calculated based on dispatch outcomes. Feedback from these indicators for different reliability levels enables operators to select appropriate dispatch schemes, realizing high-quality grid operation. Case studies demonstrate the effectiveness of the proposed optimal scheduling strategy and operational state pre-assessment indicator system, providing valuable reference for power operation personnel in formulating scheduling plans.

The structure of this paper is as follows: Section 2 establishes a multidimensional GBD indicator system; Section 3 constructs a pre-assessment indicator system to determine distribution network operational status; Section 4 develops an active power and reactive power optimal dispatch model for ADNs that incorporates GBD; Section 5 validates the effectiveness of the established model and assessment indicator system through case study analysis; Section 6 and Section 7 present conclusions and future work.

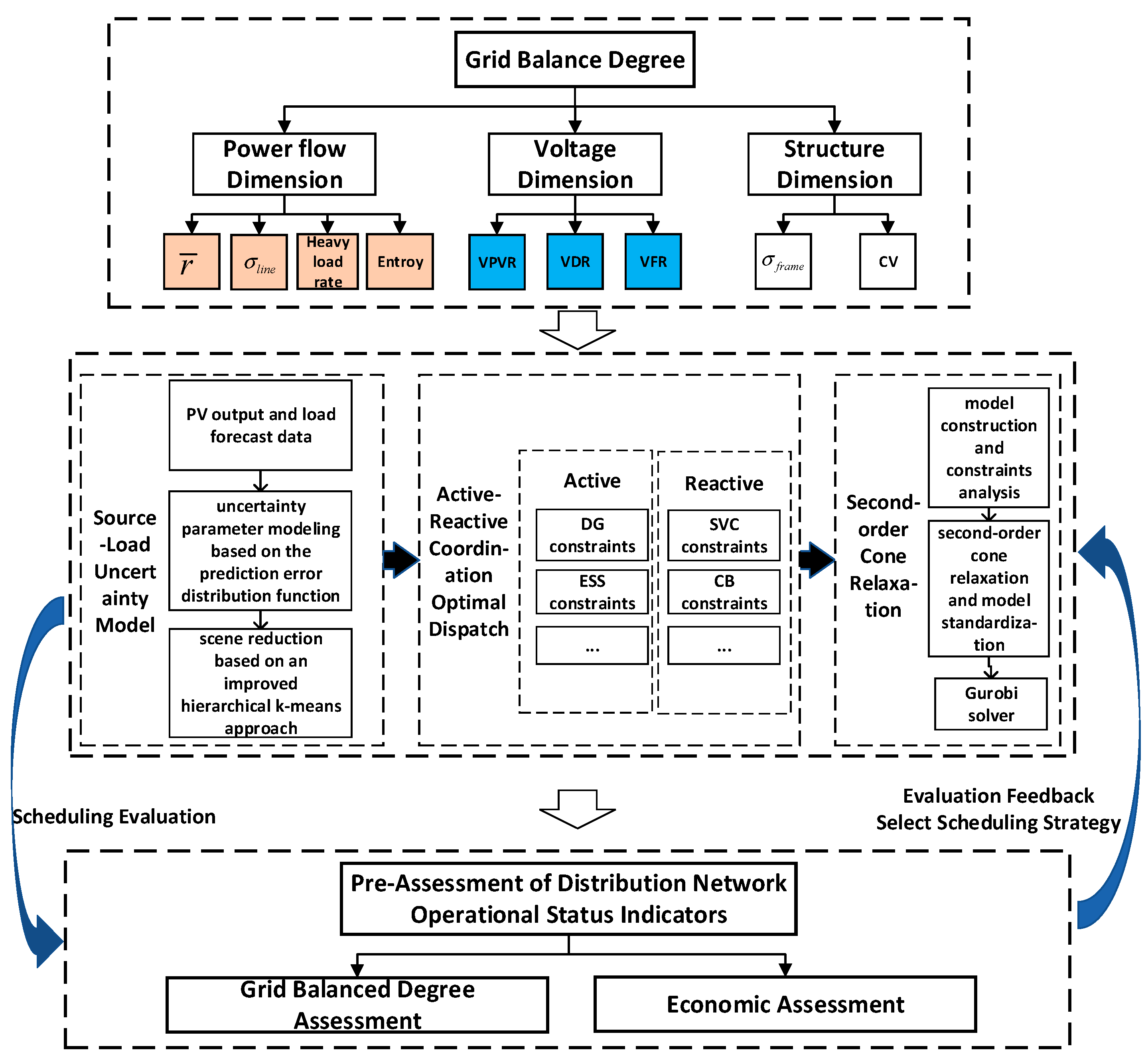
2. Multidimensional GBD Indicator System

GBD generally refers to the equilibrium of power flow or load within the grid. This paper selects nine key indicators across three dimensions—power flow, voltage, and network structure—from numerous indicators used to evaluate grid operational status. These indicators collectively redefine GBD and provide a comprehensive assessment of the distribution network equilibrium. High GBD ensures that the distribution network operation meets equilibrium requirements, thereby guaranteeing high operational reliability and quality. This helps reduce equipment failure rates, delay aging, and extend the service life of grid assets.

2.1. Power Flow Dimension GBD

GBD calculation indicators for the power flow dimension include power flow entropy, heavy load rate, average line load factor, and standard deviation of line load factor. Lower values of these indicators indicate a more balanced power flow distribution and higher operational reliability of the distribution network.

2.1.1. Power Flow Entropy

Power flow entropy can be used to analyze the intrinsic impact of power flow distribution equilibrium on the static (transient) stability of a system. Let k denote the branch number, $N_{branch}$ denote the total number of branches, $n_{i,t}$ denote the number of branches in the system at time $t$ whose load rates fall within the interval $\left(U_{i-1},U_i\right](U_i\in [0,1])$, M denote the number of intervals, and C denote a constant. Power flow entropy is defined as follows:

$$H_r=-C{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^M(\frac{n_{i,t}}{N_{branch}})}\log (\frac{n_{i,t}}{N_{branch}})}$$

(1)

The greater the power flow entropy, the more unbalanced the distribution of power flows across lines [17]. When the system experiences disturbances, heavily loaded lines are highly susceptible to overloading, worsening operational conditions. Conversely, other lines with lower load factors remain underutilized. Thus, power flow entropy reflects the overall distribution of power flow in distribution networks. However, even if the entire network exhibits a balanced load distribution, but all lines are within the heavy load range, the system remains unsafe—indicating that considering power flow entropy alone is insufficient. Additionally, heavy load rates and average load rates can be used to characterize the load distribution within the grid. Even when average load rates are identical, significant variations in the distribution of line load rates may exist: load rates across lines may either be close to the average level or differ substantially, necessitating the use of load rate standard deviation for identification. Comparing average load rates can indicate the degree of GBD. When average load rates are identical, the standard deviation of load rates must be used to further differentiate the level of GBD. Therefore, evaluating GBD in the power flow dimension of ADNs requires a comprehensive consideration of power flow entropy, heavy line load rates, average load rates, and the standard deviation of load rates.

2.1.2. Heavy Load Rate

The heavy load rate is a key indicator for measuring the load level of power system lines.

$$\begin{array}{l}{r}_{m,t}={\displaystyle \frac{\sqrt{P_{br,t}^2+Q_{br,t}^2}}{S_{br}^{\mathrm{rated}}}}\\ \mathrm{heavyloadrate}={\displaystyle \frac{{\displaystyle \sum _{\mathrm{t}=1}^T{N}_{r>\gamma ,t}}}{T\times N_{branch}}}\end{array}$$

(2)

where $P_{br,t}$ and $Q_{br,t}$ represent the active and reactive power of the branch, respectively; $S_{br}^{\mathrm{rated}}$ denotes the rated capacity of the branch; $r_{m,t}$ indicates the line load factor; and $N_{r>\gamma , t}$ represents the number of lines with a load factor greater than $\gamma$ at time $t$.

2.1.3. Average Load Factor

The average load factor $\overline{r}$ measures the overall load level of the power grid, indicating whether the system is experiencing “universal heavy load” or “excessive capacity redundancy”.

$$\overline{r}={\displaystyle \frac{1}{T\times N_{branch}}}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{m=1}^{N_{branch}}{r}_{m,t}}}$$

(3)

2.1.4. Standard Deviation of Load Factor

Load factor standard deviation ${\sigma }_{line}$ is used to evaluate the deviation of each line’s load factor from the average load factor, reflecting the risk of “localized overload.” A larger standard deviation indicates that some components’ load factors deviate significantly from the average, indicating the presence of “local weak points.”

$${\sigma }_{line}=\sqrt{{\displaystyle \frac{1}{T\times N_{branch}}}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{m=1}^{N_{branch}}{(r_{m,t}-\overline{r})}^2}}}$$

(4)

2.2. Voltage Dimension GBD

The voltage-related GBD calculation indicators include the peak-to-trough voltage difference rate, maximum voltage deviation rate, and voltage fluctuation rate. Lower values for these indicators indicate better voltage-related GBD, signifying that voltage deviations at each node remain within a narrow range and are relatively concentrated. This enhances voltage security by preventing localized overvoltage or undervoltage conditions.

2.2.1. Peak-to-Valley Voltage Ratio

The peak-to-valley voltage ratio (VPVR) measures the overall fluctuation range of voltage within a specific time period, indicating whether the system experiences “severe voltage fluctuations during that period”.

$$VPVR=\max ({\displaystyle \frac{V_{\max ,i}-V_{\min ,i}}{V_n}})\times 100\%$$

(5)

where $V_{\max ,i}$ and $V_{\min ,i}$ represent the maximum and minimum voltage at node $i$, respectively, and $V_n$ is the rated voltage.

2.2.2. Maximum Voltage Deviation Ratio

The maximum voltage deviation ratio (VDR) measures the maximum deviation between the actual voltage at each node and the rated voltage, indicating whether the system exhibits steady-state issues of “excessively high or low voltage”.

$$VDR={\displaystyle \frac{\max \left(\left|V_{\max }-V_n\right|,\left|V_{\min }-V_n\right|\right)}{V_n}}\times 100\%$$

(6)

2.2.3. Voltage Fluctuation Ratio

The voltage fluctuation ratio (VFR) is used to evaluate the severity of dynamic voltage variations within a given period T, indicating whether the system is subject to the dynamic risk of “instantaneous voltage surges and dips”.

$$\begin{array}{l}{\mu }_V={\displaystyle \frac{1}{T\times N_{bus}}}{\displaystyle \sum _{i=1}^{N_{bus}}{\displaystyle \sum _{t=1}^T{V}_{i,t}}}\\ {\sigma }_V=\sqrt{{\displaystyle \frac{1}{T\times N_{bus}}}{\displaystyle \sum _{i=1}^{N_{bus}}{\displaystyle \sum _{t=1}^T{(V_{i,t}-{\mu }_V)}^2}}}\\ VF{R}_{std}={\displaystyle \frac{{\sigma }_V}{{\mu }_V}}\times 100\%\end{array}$$

(7)

where $V_{i,t}$ represents the voltage at node $i$, $N_{bus}$ denotes the total number of nodes, ${\mu }_V$ is the average voltage over period T, and ${\sigma }_V$ is the voltage standard deviation.

2.3. Structure Dimension GBD

A balanced grid structure facilitates flexible operational adjustments. During maintenance or load growth, it enables smooth load transfer from one line to another. A balanced grid serves as the foundation for integrating renewable energy and ensuring power quality. Structure Dimension GBD primarily reflects the equilibrium of distribution network topology, with calculation indicators including the degree standard deviation (${\sigma }_{frame}$) and coefficient of variation (CV). Let $k_i$ denote the degree of a distribution network node and $\mu$ the average degree. Lower values of ${\sigma }_{frame}$ and CV indicate greater proximity in node degrees, signifying improved GBD at the structural level.

$$\begin{array}{l}{k}_i={\displaystyle \sum _{i:j\to i}{a}_{ij}},\mu ={\displaystyle \frac{1}{N}}{\displaystyle \sum k_i}\\ {\sigma }_{frame}=\sqrt{{\displaystyle \frac{1}{N-1}}{\displaystyle \sum {(k_i-\mu )}^2}}\end{array}$$

(8)

$$CV={\displaystyle \frac{{\sigma }_{frame}}{\mu }}$$

(9)

2.4. Analysis of Dispatch Methods Used to Improve GBD

Measures to enhance GBD from three aspects—power flow, voltage, and network structure—include the following:

(a)

Optimal Dispatch Objective Function: The objective function incorporates a load factor penalty term. By setting heavy load factor penalty, it reduces the number of heavily loaded lines, thereby achieving a more balanced distribution of power flow across the ADN.

(b)

Optimized Scheduling Constraints: This refers to adjusting (reducing) the upper and lower limits of voltage within the optimized scheduling constraints to ensure node voltages remain near their rated values and are more evenly distributed.

(c)

Grid Reconfiguration: From a structural perspective, altering the operational configuration of the power grid by changing switch states (closing or opening loops) to optimize power flow distribution and voltage levels.

3. Indicator System for Pre-Assessment of ADN Operational Status

The GBD is closely related to the operational reliability of the power grid. The better the GBD, the higher the active and reactive power margins, the greater the operational reliability, and the better the grid’s operational quality. As shown in Figure 1, this study establishes a pre-assessment indicator system to determine grid operational status by integrating GBD and economic indicators. GBD indicators are detailed in Section 2.1, Section 2.2 and Section 2.3, while economic indicators focus on operational costs and network losses. These indicators complement each other to provide an intuitive simulation of post-dispatch grid operational reliability levels and corresponding control costs, facilitating the selection of optimal dispatch plans by operational personnel. The economic assessment indicator for ADN operational state pre-assessment is system operating cost $f_1$, encompassing dispatch operation costs for all resources and line network losses. A lower value indicates greater economic efficiency.

$$f_1=f_{buy}+f_{\mathrm{CG}}+f_{ESS}+f_{wp}+f_{DR}+f_{rp}+f_{loss}$$

(10)

$$\left\{\begin{array}{l}{f}_{buy}={\displaystyle \sum _{t=1}^T{C}_0{P}_{Grid,t}}\\ f_{\mathrm{CG}}={\displaystyle \sum _{t=1}^T{C}_1{P}_{\mathrm{CG},t}}\\ f_{ESS}={\displaystyle \sum _{t=1}^T{C}_2\left|P_{ESS,t}\right|+W\left|P_{ESS,t}\right|}\\ f_{wp}={\displaystyle \sum _{t=1}^T{C}_3\left(P_{\mathrm{wp},t}\right)}\\ f_{DR}={\displaystyle \sum _{t=1}^T{k}_{\mathrm{DR},i}{P}_{DR,i,t}}\\ f_{rp}={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{t=1}^T{C}_{SVC}{Q}_{SVC,i,t}+{\displaystyle \sum _{t=1}^T{C}_{CB}{n}_{CB,t}}}}\\ f_{loss}=b{P}_{loss}={\displaystyle \frac{1}{2}}b\times {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{j=1}^N{\displaystyle \sum _{i=1}^N\left(I_{ij,t}^2·r_{ij}\right)}}}\end{array}\right.$$

(11)

where $f_{buy}$, $f_{CG}$, $f_{ESS}$, $f_{wp}$, $f_{DR}$, $f_{rp}$, and $f_{loss}$ denote the grid’s electricity purchasing cost, controllable distributed generation cost, ESS cost, distributed energy cost, customer interruption compensation cost, reactive power compensation cost, and network loss cost, respectively; $P_{\mathrm{CG},t}$ and $C_1$ represent the controllable distributed generation output active power and generation cost coefficient, respectively. $C_2$ and $W$ represent the ESS operating cost coefficient and the lifetime depreciation cost coefficient, respectively; $P_{wp,t}$ and $C_3$ denote the output active power and cost coefficient of the DG units, respectively. $k_{\mathrm{DR},i,t}$ and $P_{DR,i,t}$ are the cost coefficient and dispatched amount of type-$i$ DR resources. $Q_{SVC,i,\mathrm{t}}$ and $C_{SVC}$ denote the reactive power output and cost coefficient of the SVC, respectively; $n_{CB,t}$ and $C_{CB}$ denote the number of switched-in capacitor bank units and their cost coefficient, respectively; b is the network loss cost coefficient. $I_{ij,t}$ represents the current amplitude of line $ij$, while $r_{ij}$ and $x_{ij}$ denote the resistance and reactance of line $ij$.

4. Active and Reactive Power Optimal Dispatch Considering GBD

4.1. Objective Function

When constructing an ADN dispatch model, DR, wind power, photovoltaic power, interruptible loads, controllable distributed generation, ESS, Capacitor bank (CB), static var compensator (SVC) and DG are treated as dispatch resources. These resources are coordinated to minimize the sum of system operating costs $f_1$ and load factor penalties $f_{loading}$, establishing an optimal objective that ensures stable system voltage, balanced power flow distribution, and enhanced GBD.

$$\begin{array}{l}\min f=f_1+a{f}_{loading}\\ f_{loading}=\beta {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_{branch}}\left(\frac{S_{i,t}}{S_{i,rated}}-\gamma \right)}}\end{array}$$

(12)

where $\gamma$ represents the load factor penalty threshold, and $\beta$ denotes the penalty coefficient. $T$ indicates the scheduling cycle (24 h); a = 1 signifies that the objective function incorporates load factor penalties; a = 0 indicates that load factor penalties are not considered.

4.2. Constraints

The constraint conditions for the ADN dispatch model specifically include DR resource constraints, distributed generation constraints, wind and solar constraints, ESS constraints, reactive power compensation constraints, load factor and voltage constraints, and power balance constraints.

4.2.1. DR Resource Constraints

DR resources are categorized into price-based and incentive-based types [18]. Price-based DR loads include the curtailable load (CL) and shiftable load (SL).

(1)

Price-Based DR

(i)

CL Feature Modeling

The change in reducible load $\Delta P_{CL,t}^e$ at time $t$ is

$$\Delta P_{CL,t}^e=P_{CL,t}^{e0}\left[{\displaystyle \sum _{j=1}^{24}{E}_{CL}}\left(t,j\right){\displaystyle \frac{{\rho }_j-{\rho }_j^0}{{\rho }_j^0}}\right]$$

(13)

where $P_{CL,t}^{e0}$ is the initial reducible load at time $t$, ${\rho }_j$ represents the electricity price at time $j$, and $E_{CL}\left(t,j\right)$ is the DR elasticity matrix for the CL price, whose elements $e_{t,j}$ are defined as

$$e_{t,j}={\displaystyle \frac{\Delta P_t^e/P_t^{e0}}{\Delta {\rho }_j/{\rho }_j^0}}$$

(14)

where $\Delta P_t^e$ is the load variation value; $P_t^{e0}$ and ${\rho }_j^0$ denote the initial load and initial electricity price at time $t$, respectively; $\Delta {\rho }_j$ represents the electricity price variation value.

(ii)

SL Feature Modeling

The change in reducible load $\Delta P_{SL,t}^e$ at time $t$ is

$$\Delta P_{SL,t}^e=P_{SL,t}^{e0}\left[{\displaystyle \sum _{j=1}^{24}{E}_{SL}}\left(t,j\right){\displaystyle \frac{{\rho }_j-{\rho }_j^0}{{\rho }_j^0}}\right]$$

(15)

where $P_{SL,t}^{e0}$ is the initial transferable load at time $t$; $E_{SL}\left(t,j\right)$ represents the price elasticity matrix for SL.

(2)

Incentive-Based DR Constraints

Incentive-based DR (IDR) involves power networks and users entering into advance agreements specifying compensation rates and the range of load that can be called upon, enabling direct control over load. Let $P_{IDR,t}$ denote the load called upon, which is less than the maximum invocable load $P_{IDR,t}^{\max }$.

$$0\le P_{IDR,t}\le P_{IDR,t}^{\max }$$

(16)

4.2.2. Controllable Distributed Generation

$$\left\{\begin{array}{l}{P}_{\mathrm{CG}}^{\min }\le P_{\mathrm{CG}, t}\le P_{\mathrm{CG}}^{\max }\\ \left|P_{\mathrm{CG},t}-P_{\mathrm{CG}, t-1}\right|\le R_{Lim}\end{array}\right.$$

(17)

$$Q_{CG}^{\min }\le Q_{\mathrm{CG},t}\le Q_{CG}^{\max }$$

(18)

where $P_{\mathrm{CG}}^{\max }$, $P_{\mathrm{CG}}^{\min }$, $Q_{CG}^{\max }$, and $Q_{CG}^{\min }$ represent the upper and lower limits of active power output and reactive power output for controllable distributed generation, respectively, while $R_{Lim}$ denotes its active power ramp rate.

4.2.3. ESS

ESS constraints include inverter-rated power constraints and rated charge/discharge power constraints.

$$\begin{array}{l}{P}_{ESS,t}=P_{disch,t}-P_{ch,t}\\ u_{ch,t}+u_{disch,t}\le 1\\ 0\le P_{disch,t}\le P_{disch,\max }·u_{disch,t}\\ 0\le P_{ch,t}\le P_{ch,\max }·u_{ch,t}\\ \left(SO{C}_t-SO{C}_{t-1}\right)E_{ESS}=P_{ch,t}·{\eta }_{ch}-(P_{disch,t}/{\eta }_{disch})\\ SO{C}_{min}\le SO{C}_t\le SO{C}_{max}\end{array}$$

(19)

where $P_{ESS,t}$ represents the net power exchange between the ESS and the grid at time $t$; $P_{disch,t}$ and $P_{ch,t}$ denote the discharge power and charge power of the ESS at time $t$, respectively; $P_{disch,\max }$ and $P_{ch,\max }$ represent the maximum discharge power and maximum charge power of the ESS, respectively; $u_{disch,t}$ and $u_{ch,t}$ are binary variables representing the discharge state variable and charge state variable of the ESS at time $t$, respectively, where 1 indicates activation and 0 indicates deactivation; $SO{C}_t$ denotes the state of charge (SOC) of the ESS device at time $t$; $E_{ESS}$ represents its rated capacity; $SO{C}_{max}$ and $SO{C}_{min}$ denote the upper and lower limits of its SOC, respectively; ${\eta }_{disch}$ and ${\eta }_{ch}$ denote the discharge efficiency and charge efficiency of the ESS, respectively.

4.2.4. Distributed Generation (DG) Model

$$\left\{\begin{array}{l}{P}_{wp,\min }⩽P_{wp,t}⩽P_{wp,\max }\\ {(P_{wp,t})}^2+{(Q_{wp,t})}^2⩽{(S_{wp,\max })}^2\\ -P_{wp,t}\tan \phi ⩽Q_{wp,t}⩽P_{wp,t}\tan \phi \end{array}\right.$$

(20)

where $P_{wp,t}$, $P_{wp.\max }$, and $P_{\mathrm{wp},\min }$ represent the active power output and its upper and lower limits for the wind-solar power generation unit; $S_{wp,\max }$ denotes the maximum apparent power, and $\phi$ indicates the power factor angle.

4.2.5. CB

$$\begin{array}{l}{Q}_{CB,t}=n_{CB,t}\times Q_{CB}^{Step}\\ 0\le n_{CB,t}\le N_{CB,t}^{\max }\\ \left|n_{CB,t}-n_{CB,t-1}\right|\le \Delta n_{CB}^{\max }\end{array}$$

(21)

where $Q_{CB,t}$ and $Q_{CB}^{step}$ represent the total reactive power output of the capacitor banks and the reactive power compensation amount per tap, respectively; $n_{CB,t}^{\max }$ denotes the total number, $\Delta n_{CB}^{\max }$ represents the maximum number of switching operations within an adjacent time period for a capacitor bank.

4.2.6. SVC

$$Q_{SVC,i}^{\min }\le Q_{SVC,i,t}\le Q_{SVC,i}^{\max }$$

(22)

where $Q_{SVC,i}^{\min }$ and $Q_{SVC,i}^{\max }$ represent the minimum and maximum reactive power compensation values of the $i$ th SVC.

4.2.7. Operational Safety Constraints for ADNs

(1)

Node voltage constraint

$$V_i^{\min }\le V_{i,t}\le V_i^{\max }$$

(23)

(2)

Transmission power constraint

$$S_i\le S_{i,rated}$$

(24)

where $V_i^{\max }$ and $V_i^{\min }$ represent the upper and lower limits of the bus voltage for node $i$, respectively, while $S_i$ and $S_{i,rated}$ denote the transmission power and rated power of branch $i$.

4.3. Approach to Solving the Scheduling Model Based on Second-Order Cone Relaxation

4.3.1. Branch Flow Model

The distflow branch-load flow equations are employed to solve the dispatch problem, as shown in Equations (25)–(30).

$$P_{ij,t}={\displaystyle \sum _{k:j\to k}{P}_{jk,t}}+r_{ij}{\left(I_{ij,t}\right)}^2+P_{j,t}$$

(25)

$$Q_{ij.t}={\displaystyle \sum _{k:j\to k}{Q}_{jk,t}}+x_{ij}{\left(I_{ij,t}\right)}^2+Q_{j,t}$$

(26)

$${\left(V_{j,t}\right)}^2={\left(V_{i,t}\right)}^2-2\left(r_{ij}{P}_{ij,t}+x_{ij}{Q}_{ij,t}\right)+\left(r_{ij}^2+x_{ij}^2\right){\left(I_{ij,t}\right)}^2$$

(27)

$${\left(I_{ij,t}\right)}^2={\displaystyle \frac{{\left(P_{ij,t}\right)}^2+{\left(Q_{ij,t}\right)}^2}{{\left(V_{i,t}\right)}^2}}$$

(28)

$$P_{j,t}=P_{Load,j,t}-P_{G,j,t}+P_{ESS,j,t}-P_{wp,j,t}-P_{Grid,j,t}-\Delta P_{CL,t}^e-\Delta P_{SL,t}^e-P_{IDR,t}$$

(29)

$$Q_{j,t}=Q_{Load,j,t}-Q_{G,j,t}-Q_{wp,j,t}-Q_{CB,j,t}-Q_{SVC,j,t}-Q_{Grid,j,t}$$

(30)

where $P_{ij,t}$ and $Q_{ij.t}$ represent the active power and reactive power flowing through branch $ij$, respectively; $P_{j,t}$ and $Q_{j,t}$ denote the injected active power and reactive power at node $j$, respectively; $k$ represents all downstream sub-nodes of node $j$ (excluding node $i$); $V_{j,t}$ denotes the voltage magnitude at node $j$; $P_{Load,j,t}$ and $Q_{Load,j,t}$ represent the active and reactive loads at node $j$, respectively; $P_{G\mathrm{r}id,j,t}$ and $Q_{G\mathrm{rid},j,t}$ denote the active and reactive power transmitted from the main network to node j, respectively.

4.3.2. Convex Relaxation Model

Employing second-order cone relaxation [19], auxiliary variables $v_{i,t}$ and $i_{ij,t}$ are defined to facilitate the solution. Using convex relaxation, the problem is relaxed into inequalities:

$$v_{i,t}={\left(V_{j,t}\right)}^2,i_{ij,t}={\left(I_{ij,t}\right)}^2$$

(31)

$$i_{ij,t}\ge {\displaystyle \frac{{P^2}_{ij,t}+{Q^2}_{ij,t}}{v_{i,t}}}$$

(32)

The authors of [20] demonstrate that although this transformation expands the search range for the solution, the relaxed optimal solution remains identical. Equation (32) is further relaxed into a second-order cone constraint form:

$${‖\begin{array}{c}2P_{ij,t}\\ 2Q_{ij,t}\\ i_{ij,t}-{\nu }_{i,t}\end{array}‖}_2⩽i_{ij,t}+{\nu }_{i,t}$$

(33)

The original model is equivalently transformed into a mixed-integer second-order cone program. After conversion, the number of complex constraints is significantly reduced, and the non-convex factors are solely discrete variables. This enables an efficient solution using Gurobi Optimizer version 10.0.3 solver, thereby ensuring the algorithm’s convergence and optimality. The decision variables can be calculated as follows: $P_{Grid,t},P_{CG,t},P_{ESS,t},P_{wp,t},P_{DR,i,t},Q_{SVC,i,t},n_{CB,t},Q_{Grid,t},Q_{CG,t},Q_{wp,t},P_{ij,t},Q_{ij,t},P_{j,t},$$Q_{j,t},V_{i,t}$.

4.3.3. The Solution Process

The solution process for the scheduling model based on second-order cone relaxation is as follows:

(1)

Model construction and constraint refinement: For the day-ahead forecast data of wind, solar, and load, employ scenario generation to convert the random and uncertain generation and load forecast models into deterministic scenarios for a solution, thereby transforming them into deterministic power data; define the active and reactive power coordination optimal objective function (including GBD and economic efficiency indicators). Identify all constraints, including distribution network power flow constraints, equipment operation constraints (e.g., adjustment range of ESS charging/discharging), voltage upper/lower limit constraints, and load factor constraints, to form a complete non-convex optimal model.

(2)

Second-order cone relaxation conversion: For non-convex terms in distribution network power flow equations (e.g., nonlinear relationships between node power/voltage and line impedance), employ second-order cone relaxation to convexify these constraints. This converts non-convex constraints into second-order cone constraints solvable using Gurobi, eliminating computational difficulties caused by nonlinearity while ensuring relaxation error remains within acceptable limits.

(3)

Model Standardization and Parameter Configuration: Standardize the transformed second-order cone programming model by defining decision variables (including power generation output, reactive power compensation, DR adjustment, node voltage, etc. for each time period), specifying variable types (continuous/discrete) and their valid ranges; configure Gurobi solver parameters, including accuracy thresholds, solver methods (default interior-point method), and constraint tolerances, to match model scale and computational efficiency requirements.

(4)

Invoke Gurobi Solver: Import the standardized model into the Gurobi solver and utilize the solver’s built-in algorithms to perform numerical optimization of the second-order cone programming model. Output the optimal values for decision variables (e.g., reactive power compensation device outputs) and the optimal value of the objective function (e.g., operating costs).

5. Case Study Analysis

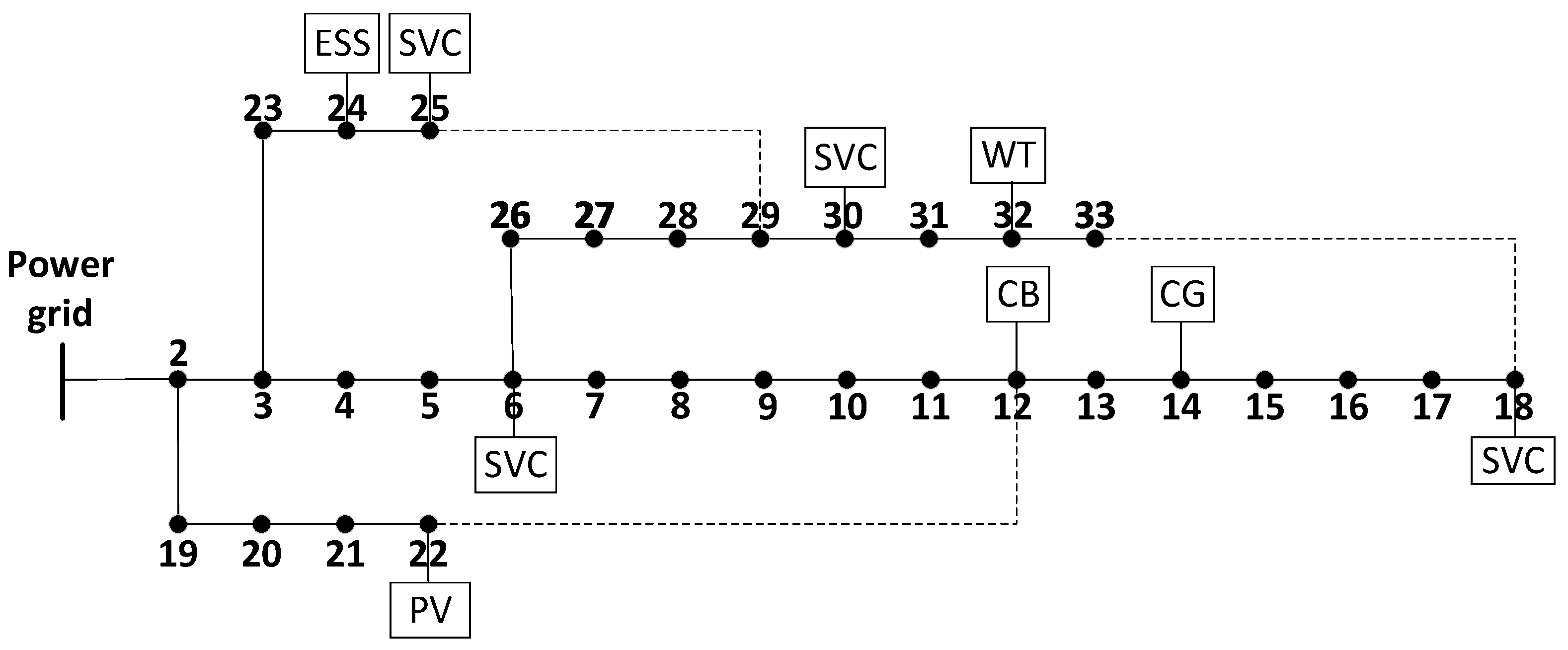
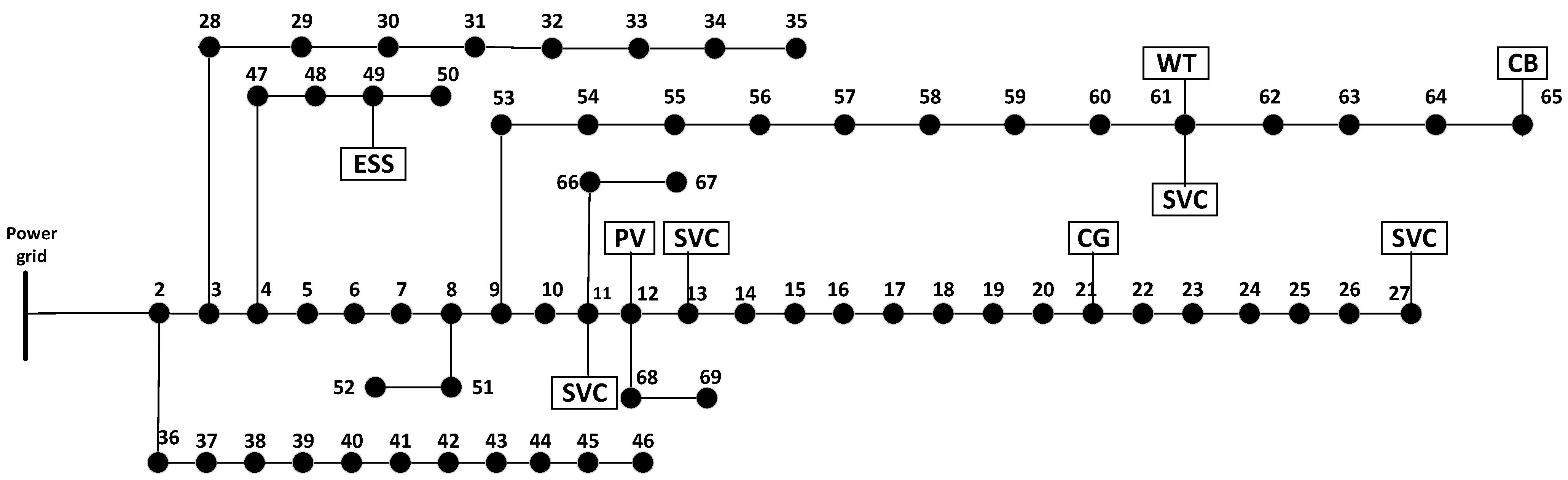
5.1. Case Configuration

To validate the efficacy of the proposed strategy, an ADN active–reactive power coordinated optimal dispatch model considering GBD was established using MATLAB R2022A software. A case study simulation was conducted on the IEEE 33-node system model with rated voltage $V_n=12.66 \mathrm{kV}$ and reference capacity $S_B=10 \mathrm{MVA}$. The CG was installed at node 14; PV and wind turbines are installed at nodes 22 and 32, respectively. The SVC units are installed at nodes 6, 18, 25, and 30; CB is installed at node 12, and the ESS is installed at node 24. The percentage caps for $P_{CL,t}^{e0}$, $P_{SL,t}^{e0}$, and $P_{IDR,t}^{\max }$ are 15%, 20%, and 15%, respectively. The parameters of the elastic electricity price matrix are shown in

Table 1. Elasticity of electricity price matrix parameters.

	Off-Peak Hours	Peak Hours	Regular Hours
Off-peak hours	−0.1	0.012	0.01
Peak hours	0.012	−0.1	0.016
Regular hours	0.01	0.016	−0.1

, and the time-of-use electricity price settings are shown in

Table 2. Setting of TOU price.

Peak-Valley Type	Electricity Rates (CNY/kW·h)	Time Period
Off-peak hours	0.35	1–7
Peak hours	0.68	8–9, 13–19, 23–24
Regular hours	1.09	10–12, 20–22

. The topology of the IEEE 33-node distribution network is shown in Figure 2. The cost parameters of the model are shown in

Table 3. Cost parameters.

Parameters	Value	Parameters	Value
Electricity Purchase Cost Factor $C_0$	0.78 ($\mathrm{CNY}/\mathrm{kW}·\mathrm{h}$)	IDR Call Cost $k_{DR,1}$	10 ($\mathrm{CNY}/\mathrm{kW}·\mathrm{h}$)
Cost of Controllable Distributed Generation $C_1$	3 ($\mathrm{CNY}/\mathrm{kW}·\mathrm{h}$)	SL Call Cost $k_{DR,2}$	3 ($\mathrm{CNY}/\mathrm{kW}·\mathrm{h}$)
ESS Operating Costs $C_2$	0.53 ($\mathrm{CNY}/\mathrm{kW}·\mathrm{h}$)	CL Call Cost $k_{DR,3}$	5 ($\mathrm{CNY}/\mathrm{kW}·\mathrm{h}$)
ESS Loss Cost $W$	0.05 ($\mathrm{CNY}/\mathrm{kW}·\mathrm{h}$)	Load Factor Penalty Coefficient $\beta$	1000
DG Cost Factor $C_3$	0.5 ($\mathrm{CNY}/\mathrm{kW}·\mathrm{h}$)	CB Cost $C_{CB}$	1 ($\mathrm{CNY}/\mathrm{kVar}·\mathrm{h}$)
Network Loss Cost Factor $b$	0.6 ($\mathrm{CNY}/\mathrm{kW}·\mathrm{h}$)	SVC Cost $C_{SVC}$	1 ($\mathrm{CNY}/\mathrm{kVar}·\mathrm{h}$)

, and the parameters of the dispatch resources are shown in

Table 4. Scheduling resource parameters.

Parameters	Value	Parameters	Value
$P_{\mathrm{CG}}^{\min }$ ($\mathrm{kW}$)	0	$P_{ch,\max }$ ($\mathrm{kW}$)	−800
$P_{\mathrm{CG}}^{\max }$ ($\mathrm{kW}$)	4000	${\eta }_{ch}$	0.9
$R_{Lim}$ ($\mathrm{k}\mathrm{W}/\mathrm{h}$)	3600	${\eta }_{disch}$	0.95
$Q_{CG}^{\min }$ ($\mathrm{kVar}$)	0	$SO{C}_{min}$	0.1
$Q_{CG}^{\max }$ ($\mathrm{kVar}$)	3000	$SO{C}_{max}$	0.9
$\cos \phi$	0.9	$E_{ESS}$ ($\mathrm{kW}·\mathrm{h}$)	4000
$Q_{SVC,i}^{\min }$ (kVar)	−3000	$Q_{CB}^{step}$ (kVar)	300
$Q_{SVC,i}^{\max }$ (kVar)	3000	$N_{CB,t}^{\max }$	6
$P_{disch,\max }$ (kW)	800	$\Delta n_{CB}^{\max }$	3

.

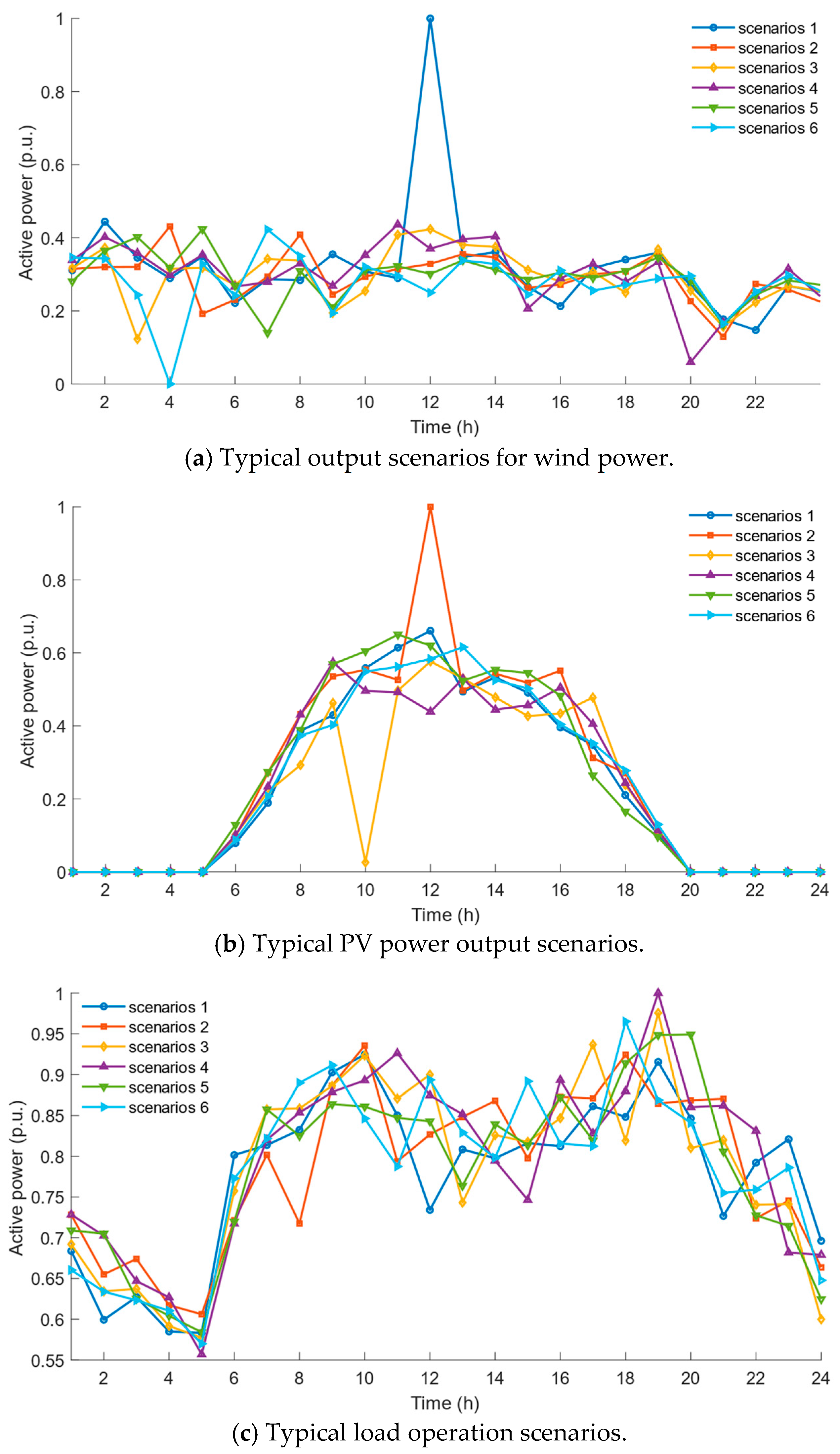
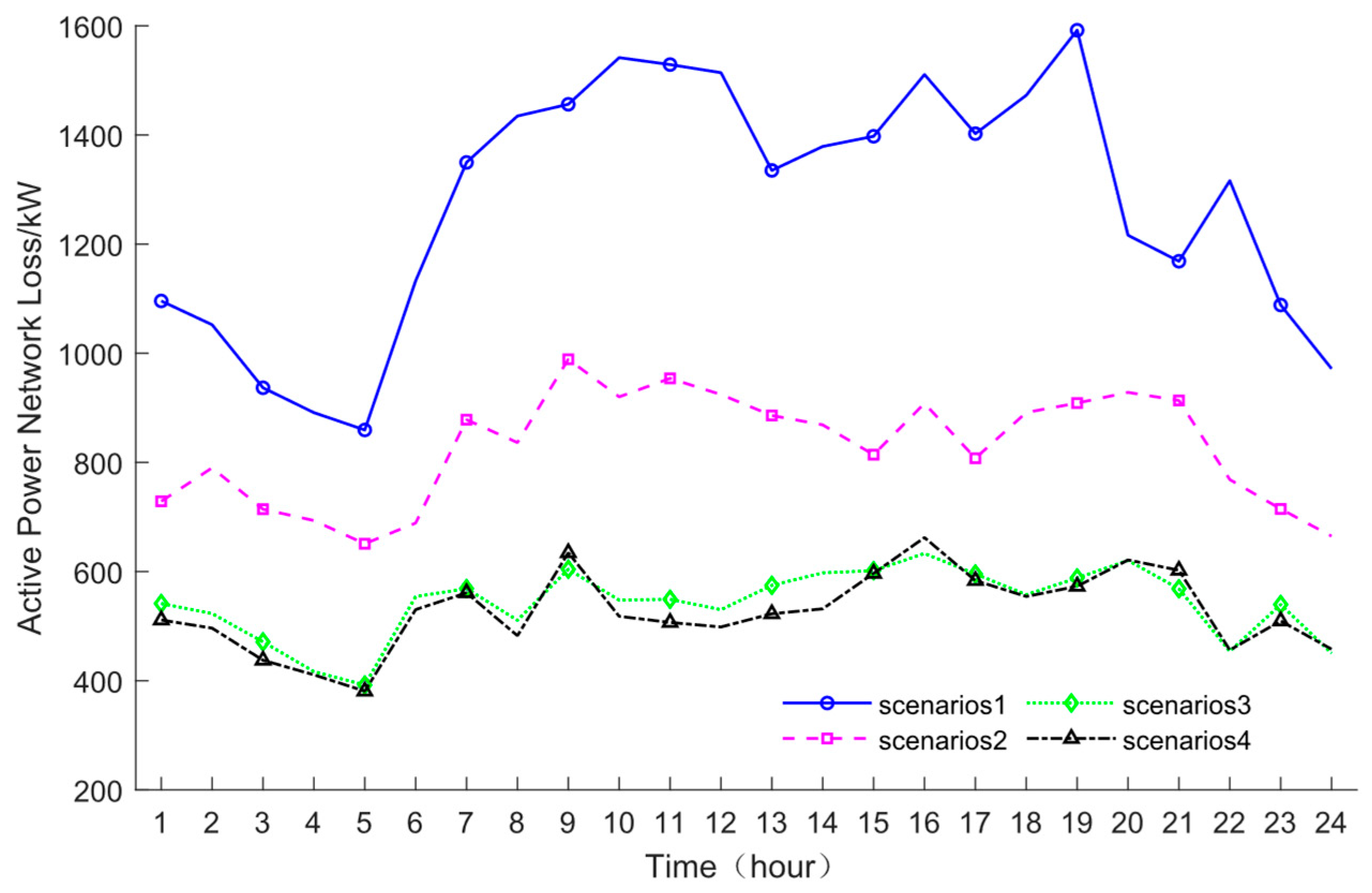
5.2. Generation and Analysis of Source Load Operation Scenarios Considering Uncertainty

According to [9], we can address source-load uncertainty by employing scenario generation to convert random and uncertain source-load prediction models into deterministic scenarios. We can use TLS (t-location-scale) distributions to predict wind and solar power generation and mean-zero normal distributions to forecast load. After generating 1000 scenarios each for load, wind power output, and solar power output via Latin Hypercube sampling, the hierarchical K-means clustering algorithm is applied for scenario reduction, consistently yielding 6 scenarios. The probabilities of each scenario are weighted accordingly, and the calculated results serve as the daily operational outputs for load and wind/solar generation. The probabilities for the six scenarios are shown in

Table 5. Typical daily output scenario probability.

Typical Scenarios	p	Typical Scenarios	p
1	0.001	4	0.386
2	0.012	5	0.512
3	0.034	6	0.055

, and the source-load prediction operational scenario set is illustrated in Figure 3.

5.3. Comparison of Scheduling Results for Different Strategies

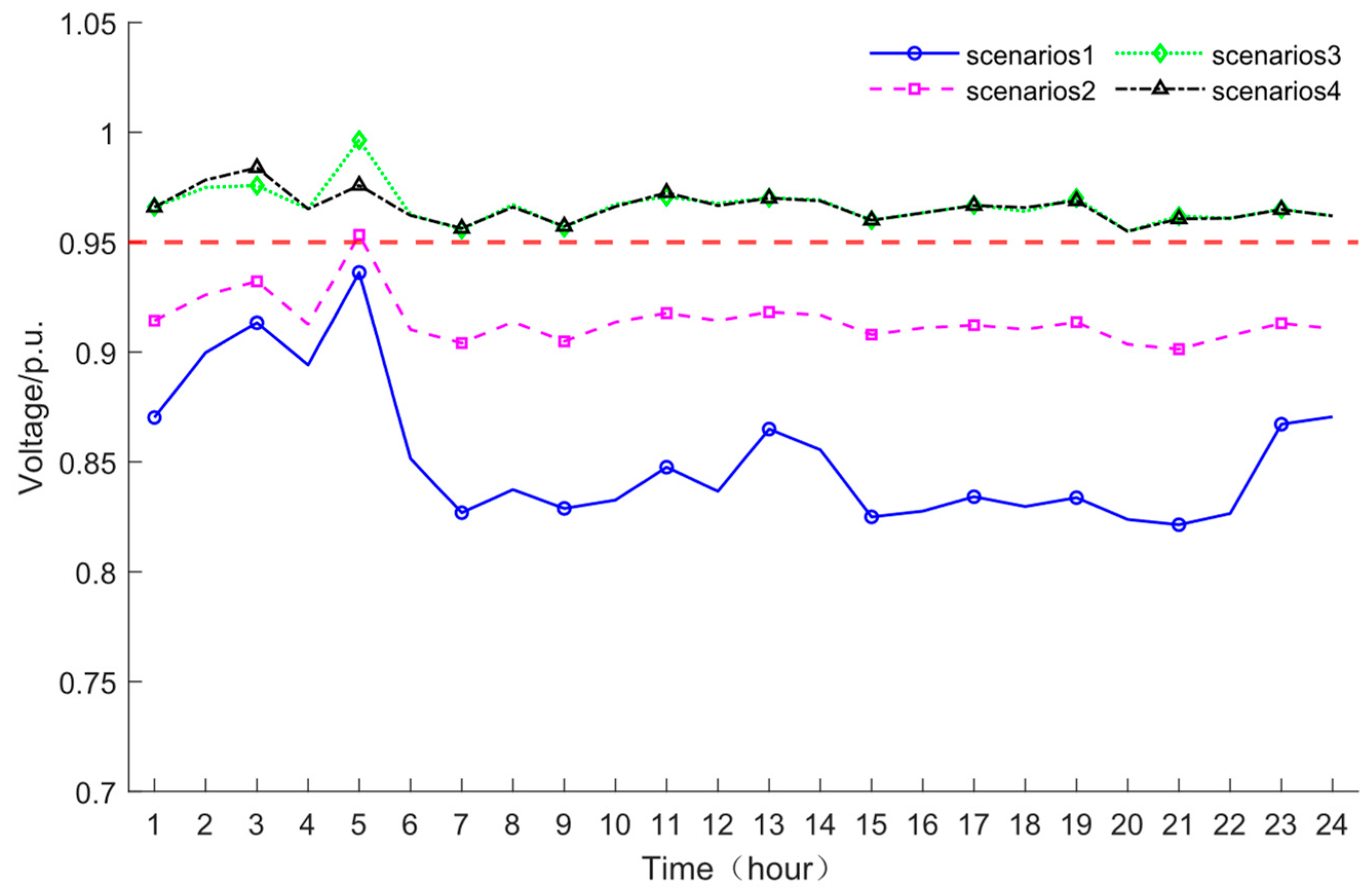
5.3.1. Analysis of Assessment Results for the Pre-Assessment Indicator System

To facilitate a comparison of scheduling outcomes across different strategies, four scheduling scenarios were established.

Scenario 1: Wind and solar generation plus load connected to the distribution grid (including ESS), a = 0, representing a simplified scenario with only baseload generation and ESS.

Scenario 2: Adds SVC and CB to Scenario 1, a = 0, representing an optimized scenario with supplementary reactive power resources.

Scenario 3: Integrates DR coordination into Scenario 2, a = 0, representing traditional economic dispatch serving as a baseline for evaluating subsequent GBD optimal effects.

Scenario 4: Building upon Scenario 3, the objective function incorporates GBD with a load factor penalty threshold set at 0.7, a = 1, representing the proposed optimal dispatch scheme in this paper.

Using the defined operational state pre-assessment indicator system, different operational scenarios were assessed. Results are shown in

Table 6. Calculation results of operational status pre-assessment indicators.

Scenario	Entropy	Heavy Load Rate	$\overline{\mathit{r}}$	${\mathit{\sigma }}_{\mathit{l}\mathit{i}\mathit{n}\mathit{e}}$	VDR	VPVR	VFR	Ploss /kW	${\mathit{f}}_1$/CNY
1	1.24	0.51	0.82	0.489	0.18	0.115	0.068	30,644	342,865
2	1.13	0.39	0.68	0.311	0.10	0.056	0.038	19,843	399,760
3	0.87	0.23	0.55	0.201	0.05	0.046	0.017	12,990	607,257
4	0.82	0.19	0.53	0.182	0.05	0.044	0.016	12,639	610,688

, while

Table 7. Resource scheduling cost (unit: CNY).

Scenario	${\mathit{f}}_{\mathit{b}\mathit{u}\mathit{y}}$	${\mathit{f}}_{\mathit{C}\mathit{G}}$	${\mathit{f}}_{\mathit{E}\mathit{S}\mathit{S}}$	${\mathit{f}}_{\mathit{w}\mathit{p}}$	${\mathit{f}}_{\mathit{r}\mathit{p}}$	${\mathit{f}}_{\mathit{D}\mathit{R}}$
1	181,414	92,170	835	50,059	0	0
2	168,267	110,331	835	50,060	58,361	0
3	147,894	165,654	835	46,278	148,586	90,215
4	150,451	168,699	835	43,951	148,849	90,321

presents the costs of dispatch resources.

(1)

Analysis of GBD Indicators in Power Flow and Voltage Dimensions

As shown in Table 6, from Scenario 1 to Scenario 4, power flow entropy decreased from 1.24 to 0.82, the heavy load rate dropped from 0.51 to 0.19, and the average load rate fell from 0.82 to 0.53. The maximum voltage deviation rate decreased from 0.18 (Scenario 1 relied solely on ESS, with node voltages unable to be controlled within 0.9) to 0.05. The peak-to-valley voltage difference rate decreased from 0.115 to 0.044, and the voltage fluctuation rate decreased from 0.068 to 0.016. These improvements indicate enhanced balance in both power flow and voltage dimensions, reduced dynamic voltage fluctuation range, mitigated load impact on voltage, and smoother voltage variations—reflecting increased operational reliability of the distribution network. These enhancements stem from the coordinated regulation of reactive power compensation devices, DR, and load factor penalty optimal strategies. Node 33, located at the distribution network’s end, exhibits typical voltage variations. Figure 4 displays its 24 h voltage changes across scenarios. As shown in Table 7 and Figure 4, Node 33’s voltage in Scenario 1 is the lowest with the greatest fluctuation—dropping to 0.82 at time 15 and peaking at 0.94 at time 5. In this scenario, only the ESS installed at Node 24 participates in regulation, yielding limited effectiveness and resulting in poor voltage stability. In Scenario 2, Node 33’s voltage significantly improved (0.90–0.95) with reduced fluctuations. All system node voltages were adjusted above 0.9, indicating that reactive power compensation effectively enhanced voltage levels. System operating costs increased, with SVC and CB deployment costs totaling CNY 58,361. In Scenario 3, node 33’s voltage further improved to 0.95–1.00. After incorporating DR, peak shaving and valley filling were achieved through reducible and transferable loads, optimizing load distribution, and reducing voltage fluctuations caused by significant load variations. This coordinated with SVC and CB to maintain voltage stability. The costs for activating reactive power compensation and DR increased the most, while the usage costs for wind and solar decreased due to their inherent variability. Scenario 4 features a node 33 voltage (0.95–0.98) similar to Scenario 3. By introducing a load factor penalty term and fine-tuning SVC, CB, and DR values, renewable energy usage is further reduced. This optimizes power flow distribution, lowers the average load factor, and improves voltage quality. Compared to Scenario 3 (the baseline dispatch scheme), the strategy proposed in Scenario 4 achieves a 17.4% reduction in heavy load rate, a 5.7% decrease in power flow entropy, and a 5.2% reduction in voltage peak-to-valley difference rate. With a slight increase of 0.56% in operating costs, it achieves a more stable and higher-quality power supply.

(2)

Economic Comparison

Figure 5 shows the active power losses of the ADN across 24 time periods for each scenario. As shown in Figure 5, Scenario 1 exhibits the highest losses across all periods (859.45–1591.97 kW), with only ESS participating in regulation; its effect is limited, and unreasonable power flow distribution leads to very high losses. Due to the application of SVC and CB, Scenario 2 effectively reduces power losses. Scenario 3 further reduces losses, with DR optimizing power flow through load adjustments to minimize losses. Scenario 4 achieves the lowest losses, where load factor penalties enhance GBD, reduce the number of heavily loaded lines, and further decrease losses. Table 6 shows that from Scenario 1 to Scenario 4, active power losses decrease from 30,644 kW to 12,639 kW (24 h cumulative); Operating costs increased from CNY 342,865 to CNY 610,688, primarily due to investments in improving operational reliability through reactive power compensation and DR, etc. The high cost stems from the relatively high cost coefficients of DR and reactive power compensation resources. Compared to Scenario 3 (the baseline dispatch plan), the strategy proposed in Scenario 4 results in a marginal 0.56% increase in operating costs while achieving a further 3% reduction in network losses. Despite the cost increase, GBD, system operational reliability, and power losses significantly improved. This dispatch strategy is particularly suitable for scenarios demanding high operational reliability.

5.3.2. Analysis of Measures to Improve GBD

(1)

Load Factor Penalty Threshold Sensitivity Analysis

For Scenario 4, the impact of different load factor penalty thresholds on the pre-assessment indicators of system operational status is discussed within the objective function of optimized dispatch. The indicators are shown in

Table 8. Effect of GBD on operational status pre-assessment indicators.

Scenario	Entropy	Heavy Load Rate	$\overline{\mathit{r}}$	${\mathit{\sigma }}_{\mathit{l}\mathit{i}\mathit{n}\mathit{e}}$	${\mathit{\sigma }}_{\mathit{f}\mathit{r}\mathit{a}\mathit{m}\mathit{e}}$	CV	VDR	VPVR	VFR	Ploss /kW	${\mathit{f}}_1$/CNY
4	0.82	0.19	0.53	0.182	0.496	0.256	0.05	0.044	0.016	12,639	610,688
5	0.85	0.21	0.53	0.186	0.496	0.256	0.05	0.048	0.016	12,774	609,493
6	0.86	0.22	0.54	0.190	0.496	0.256	0.05	0.047	0.016	12,856	609,268
7	0.86	0.23	0.54	0.192	0.496	0.256	0.05	0.047	0.016	12,925	608,529
8	0.86	0.23	0.55	0.195	0.496	0.256	0.05	0.048	0.017	12,958	607,981
9	0.87	0.23	0.55	0.198	0.496	0.256	0.05	0.048	0.017	13,002	607,973
10	0.77	0.17	0.53	0.176	0.496	0.256	0.07	0.070	0.025	13,409	536,321
11	0.98	0.22	0.51	0.217	0.496	0.256	0.03	0.042	0.012	12,872	764,723
12	0.82	0.19	0.53	0.182	0.496	0.256	0.05	0.042	0.016	12,641	609,149
13	0.76	0.15	0.53	0.182	0.496	0.256	0.05	0.045	0.016	12,620	611,019
14	0.79	0.16	0.52	0.194	0.415	0.196	0.05	0.024	0.014	11,878	551,136

, with $\gamma$ values for Scenarios 4 to 9 being 0.7, 0.75, 0.80, 0.85, 0.90, and 0.95, respectively. Its core function is to define the heavy line load constraint threshold. A lower value imposes stronger penalties for heavy loads, prompting the dispatch strategy to proactively engage generation, ESS, reactive power compensation, and DR resources to avoid heavy line load operation. Table 8 indicates that as $\gamma$ decreases, GBD indicators in both power flow and voltage dimensions improve, with network losses reduced by up to 363 kW. Concurrently, resource investments to lower heavy load rates increase costs by up to CNY 2715. When $\gamma$ is below 0.9, the average load factor and heavy load factor exhibit high sensitivity to its changes, while the load factor standard deviation (as the average load factors are the same, it is used to compare) shows extreme sensitivity to $\gamma$ variations. $\gamma$ settings can be adjusted based on specific dispatcher preferences. Table 8 indicates that pursuing economic efficiency warrants selecting a higher $\gamma$ value, whereas prioritizing operational reliability calls for a lower $\gamma$ value.

(2)

Setting Voltage Upper and Lower Limits in Constraints

For Scenario 4, we examine how different voltage upper and lower limits affect the pre-assessment indicators of system operating conditions. The indicators are shown in Table 8. The voltage constraints for Scenarios 10 to 13 are sequentially set to 0.93–1.05, 0.97–1.05, 0.95–1.03, and 0.95–1.01. Table 8 indicates that Scenario 13 requires precise coordination of reactive power regulation and load distribution within a narrow range to ensure voltage stability while preventing line imbalance. Consequently, its power flow indicators are optimal, its economic performance remains balanced, essentially matching Scenario 4. Scenario 10 has the least stringent constraints, requiring minimal resource investment to maintain voltage. It prioritizes balanced load distribution, yielding the second-best power flow indicators. However, reduced resource allocation leads to increased voltage fluctuations, making it the worst among the four scenarios. Network losses rise to 13,409 kW, while operating costs drop to CNY 536,321 (the lowest). Scenario 11 imposes moderately strict constraints but features a high voltage lower limit of 0.97. This requires concentrated resources to elevate terminal voltage, crowding out power flow optimization potential. Consequently, it achieves the best voltage performance but the worst power flow indicators. Sustained high-cost resource deployment elevates operating costs to CNY 764,723 (highest), with network losses slightly increasing to 12,872 kW. Scenario 12 (0.95–1.03) aligns its voltage constraints with Scenario 4’s control logic, yielding power flow, voltage, operating cost, and network loss indicators comparable to Scenario 4. In summary, voltage upper/lower limits must align with dispatch objectives. Pursuing optimal power flow: select 0.95–1.01 (balancing voltage stability and economy) or 0.93–1.05 (accepting voltage fluctuations); prioritizing voltage quality requires selection of 0.97–1.05 (accepting power flow imbalance and higher costs); pursuing multidimensional balance requires 0.95–1.03 and Scenario 4, offering the strongest adaptability. Voltage upper and lower limits not only define permissible node voltage fluctuations but also correlate voltage quality with resource dispatch intensity and influence power flow distribution balance through reactive power regulation priority and load allocation logic. Under strict constraints, resources must be prioritized to ensure voltage compliance, potentially degrading power flow indicators. Moderate constraints enable coordinated regulation of voltage and power flow.

(3)

Network Reconfiguration

To validate the effectiveness of the scheduling strategy, three pre-set backup interconnection lines in the IEEE 33-node system were activated (nodes 25–29, 33–18, and 22–12), as indicated by the dashed lines in Figure 2, designated as Scenario 14. As shown in Table 8, the standard deviation ${\sigma }_{frame}$ and coefficient of variation CV of the restructured grid are both lower than those of the pre-restructured grid. This indicates that the restructured grid has more closely matched node degrees, resulting in improved GBD. Compared to Scenario 4, Scenario 14 exhibits superior performance in both current and voltage dimension indicators (as the average load factors are not the same, there is no need to compare the load factor standard deviation), with a 9.8% reduction in operational costs. These optimizations fully demonstrate that the strategy can effectively adapt to optimal measures such as network restructuring. Through synergistic effects, it achieves comprehensive optimization of grid load, power flow, and voltage while enhancing economic efficiency. This further validates the effectiveness of network restructuring in ensuring the safe operation of ADNs and improving operational benefits.

5.3.3. Optimal Strategy Validation and Comparison

To validate the effectiveness of the proposed strategy in larger-scale systems, three comparative scenarios were established for the IEEE 69-node distribution system. Scenario 1 employs the strategy from Scenario 3 of the IEEE 33-node system, utilizing a conventional strategy that considers only operating costs as the performance assessment baseline. Scenario 2 adopts the strategy from Scenario 4 of the IEEE 33-node system, implementing the proposed optimal strategy that accounts for GBD. Scenario 3 shares identical resource allocation with Scenario 2 but employs a conventional strategy [13] that considers only comprehensive operating costs $f_1$ and voltage deviation. The objective function is

$$f=f_1+\beta {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_{bus}}\left|\frac{V_{i,t}-V_n}{V_n}\right|}}$$

(34)

where the voltage deviation coefficient $\beta$ = 1000.

The topology of the IEEE 69-node distribution network is shown in Figure 6. The wind and solar resources, load magnitudes, cost parameters, and resource parameters are identical to those of the IEEE 33-node system, with $V_n$ = 12.66 kV and $S_B$ = 10 MVA. Only the installation nodes for various equipment were adjusted. PV and wind turbines are installed at nodes 12 and 61, respectively; The SVC units are installed at nodes 11, 13, 27, and 61; CB is installed at node 65, and the ESS is installed at node 49. Using the operational state pre-assessment indicator system, these three operational scenarios were assessed, with the results shown in

Table 9. Pre-assessment indicators used to determine the operational status of the IEEE 69-node distribution network.

Scenario	Entropy	Heavy Load Rate	$\overline{\mathit{r}}$	${\mathit{\sigma }}_{\mathit{l}\mathit{i}\mathit{n}\mathit{e}}$	VDR	VPVR	VFR	Ploss /kW	${\mathit{f}}_1$ /CNY
1	0.84	0.46	0.66	0.189	0.10	0.111	0.039	21,659	515,709
2	0.76	0.27	0.60	0.168	0.10	0.104	0.034	15,921	577,857
3	0.95	0.40	0.64	0.213	0.10	0.104	0.032	18,452	537,405

.

As shown in Table 9, when comparing the three scenarios, Scenario 2 exhibits lower power flow and voltage indicators than Scenario 1, along with reduced network losses. However, its operational cost exceeds that of Scenario 1. This indicates that while incorporating the load factor penalty increases control costs, it enhances GBD in both power flow and voltage dimensions. Compared to Scenario 2, Scenario 3 exhibits higher power flow indicators. Its voltage fluctuation rate is slightly lower than 0.034 of Scenario 2, while other values remain identical. This demonstrates that optimizing solely for voltage deviation effectively controls dynamic voltage fluctuations, achieving similar voltage control performance to Scenario 2. However, its power flow balance is inferior to Scenario 2. The operating cost of Scenario 3 (CNY 537,405) is CNY 40,452 lower than that of Scenario 2, as it eliminates the need for dispatch resources required for GBD optimization. However, network losses are 2531 kW higher than Scenario 2, indicating significant losses; equipment may experience accelerated aging due to heavy loads, increasing hidden maintenance costs. Overall, compared to voltage-only optimization of Scenario 3, GBD of Scenario 2—though increasing short-term operational costs—achieves superior operational reliability in large-scale complex grids. This aligns with future high-quality grid operation requirements, further validating the core value of the GBD indicator. Moreover, this pre-assessment indicator system facilitates comparative analysis across three dimensions, enabling the simulation of dispatch effect and assisting dispatchers in selecting optimal dispatch plans.

6. Conclusions

To address uncertainties in generation and load, unbalanced power flow distribution, and peak load threats to voltage stability in ADNs, this study proposes an ADN active–reactive power coordinated optimal dispatch strategy that accounts for GBD. Key findings are as follows:

(1)

GBD is defined through three key dimensions: power flow (power flow entropy, heavy load factor, average load factor, and line load factor standard deviation), voltage (peak-to-valley voltage difference, maximum voltage deviation rate, and voltage fluctuation rate), and network structure (degree standard deviation and coefficient of variation), comprehensively reflecting grid operational reliability. Combining GBD and economic indicators, we propose a pre-assessment indicator system for ADN operation. This system visually displays the operational status and control costs of ADNs with varying GBD levels based on dispatch plans, addressing the current lack of specialized pre-assessment indicators tailored for dispatch planning that effectively demonstrate dispatch effects.

(2)

A coordinated active/reactive power optimal dispatch strategy incorporating GBD is proposed. Including load factor penalties in dispatch objectives, it guides balanced power flow distribution across lines, prevents heavy line load or overloading, and enhances GBD in the power flow dimension. Adjusting the voltage upper/lower limits modifies GBD in the voltage dimension. Network restructuring can adjust GBD at the structure level. Integrating reactive power compensation devices, ESS, and DR resources enhances GBD and the operational reliability of ADN; delays equipment aging; and extends the equipment lifespan. Combining the dispatch method with operational state pre-assessment indicators quantifies the costs and benefits of high-quality grid operation, enabling dispatchers to select scheduling schemes with varying reliability levels.

(3)

Based on the scheduling results of IEEE 33-node and 69-node systems, this study effectively validates the effectiveness of the GBD optimal strategy and its adaptability to larger-scale, more complex systems. Case studies demonstrate that the proposed method enhances system security and stability with a modest increase in operational costs, achieving comprehensive benefits including power flow balance, voltage stability, and reduced network losses. This demonstrates the core value and application potential of GBD as an optimal objective.

7. Limitations and Future Work

(1)

The validation scenarios focus on the IEEE standard node system. The sensitivity analysis and selection of relevant parameter thresholds require further verification and adaptation based on the specific engineering implementation scenarios of the scheduling strategy.

(2)

The DR modeling does not account for response deviations, user participation willingness, and satisfaction constraints in real-world scenarios. It assumes perfect response capability and availability, which differs from engineering practice. Subsequent research will consider these factors.