Bioinspired Fractal Design of (Reverse) Electrodialysis Stacks
Abstract
1. Introduction

2. Higher Power Density and Efficiency—Background
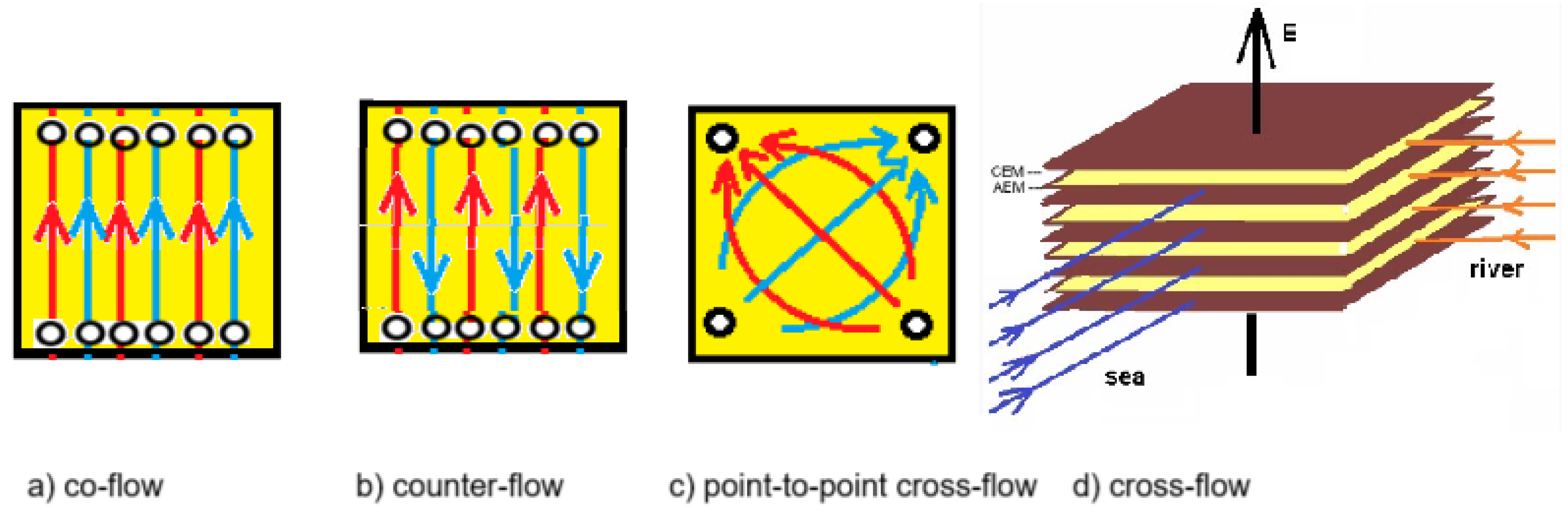
2.1. Stack Optimization
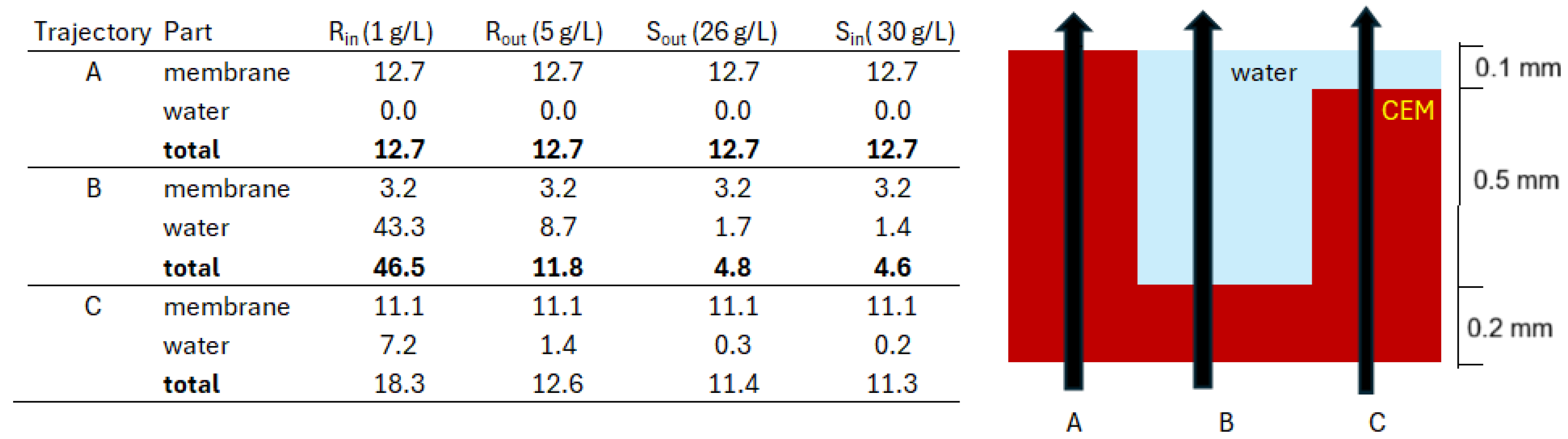
2.2. Classical Ion Exchange Membranes
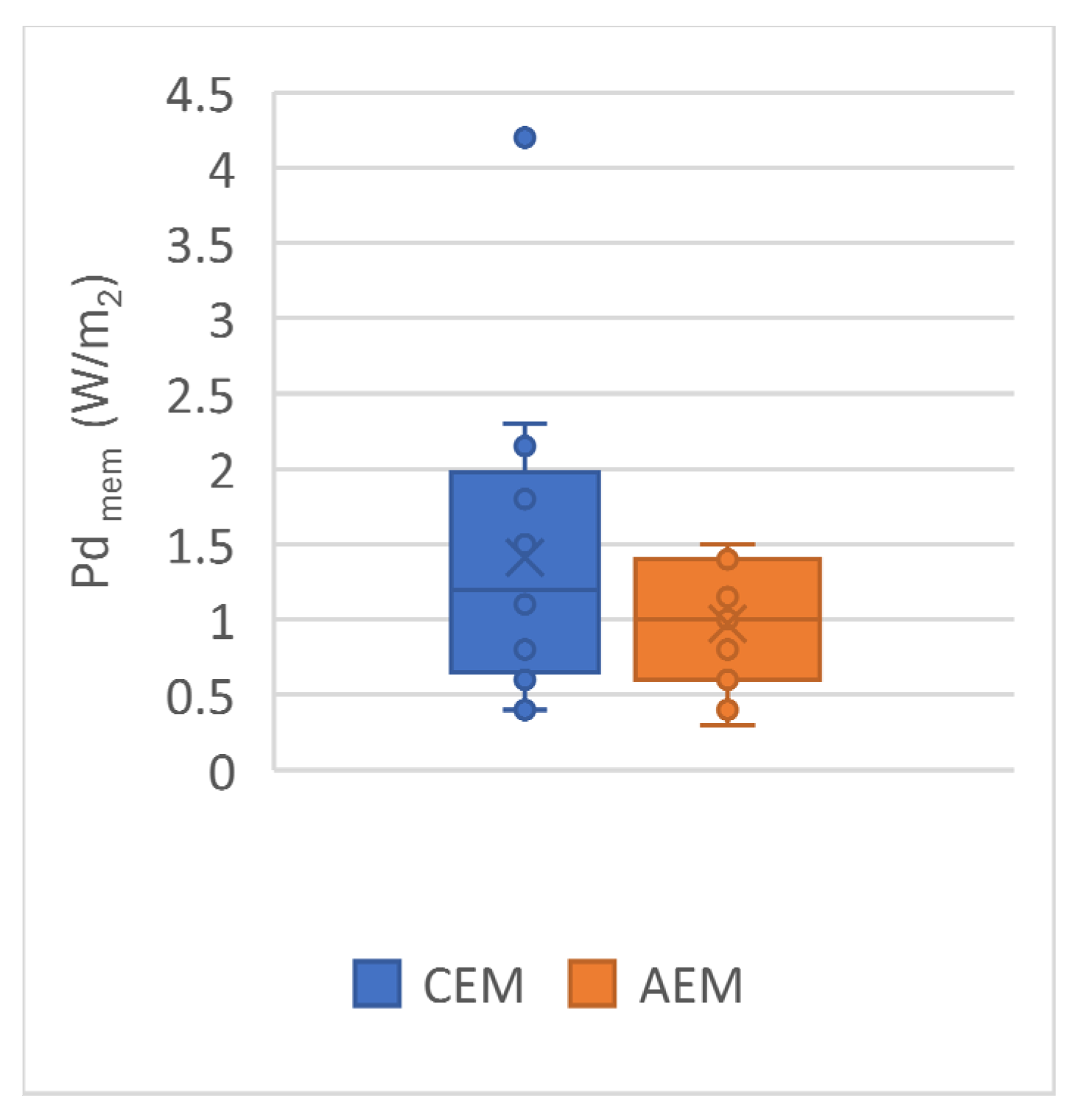
2.3. New Membranes
2.4. Profiled Membranes
3. Fractal Design—New Concepts
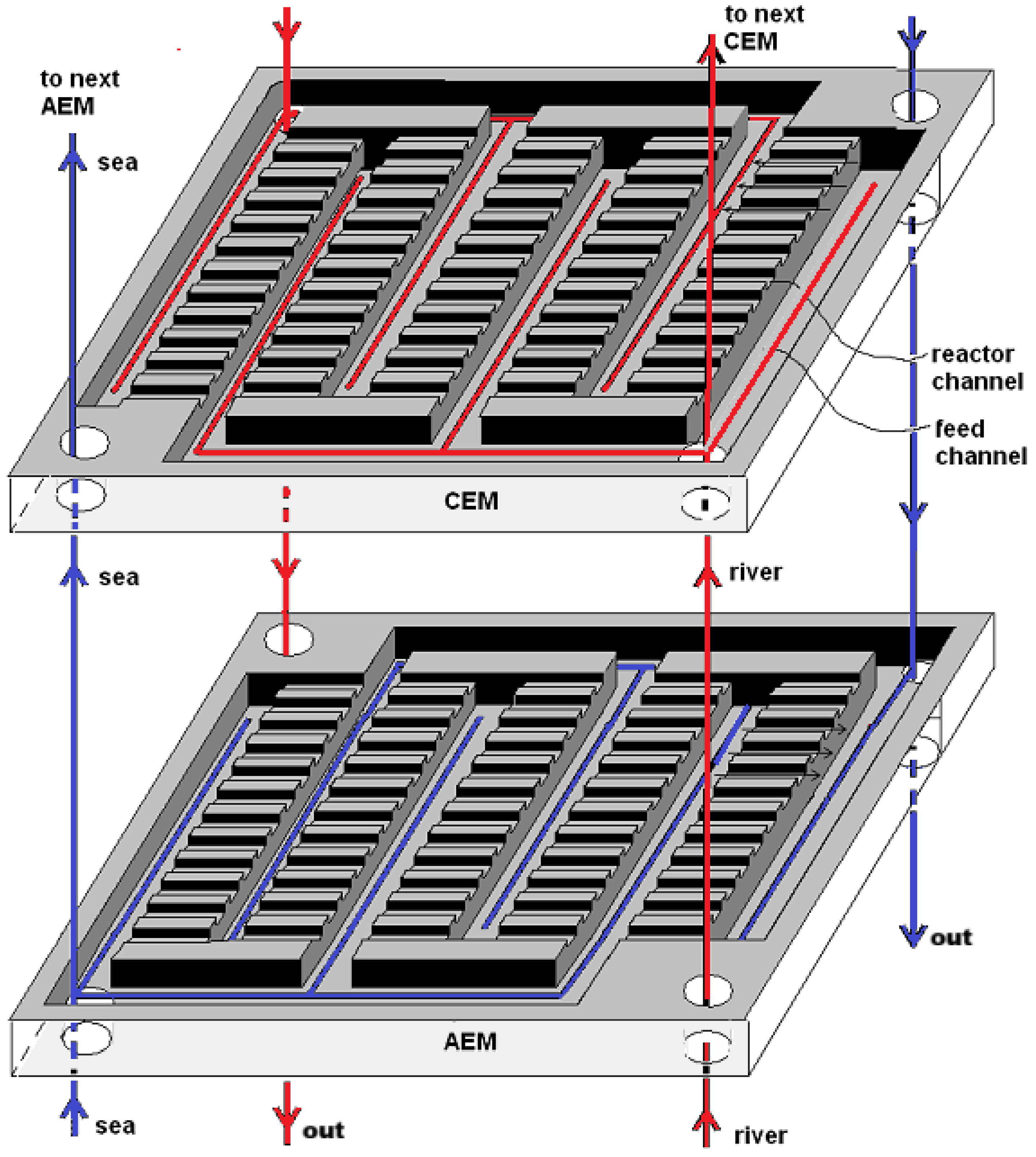
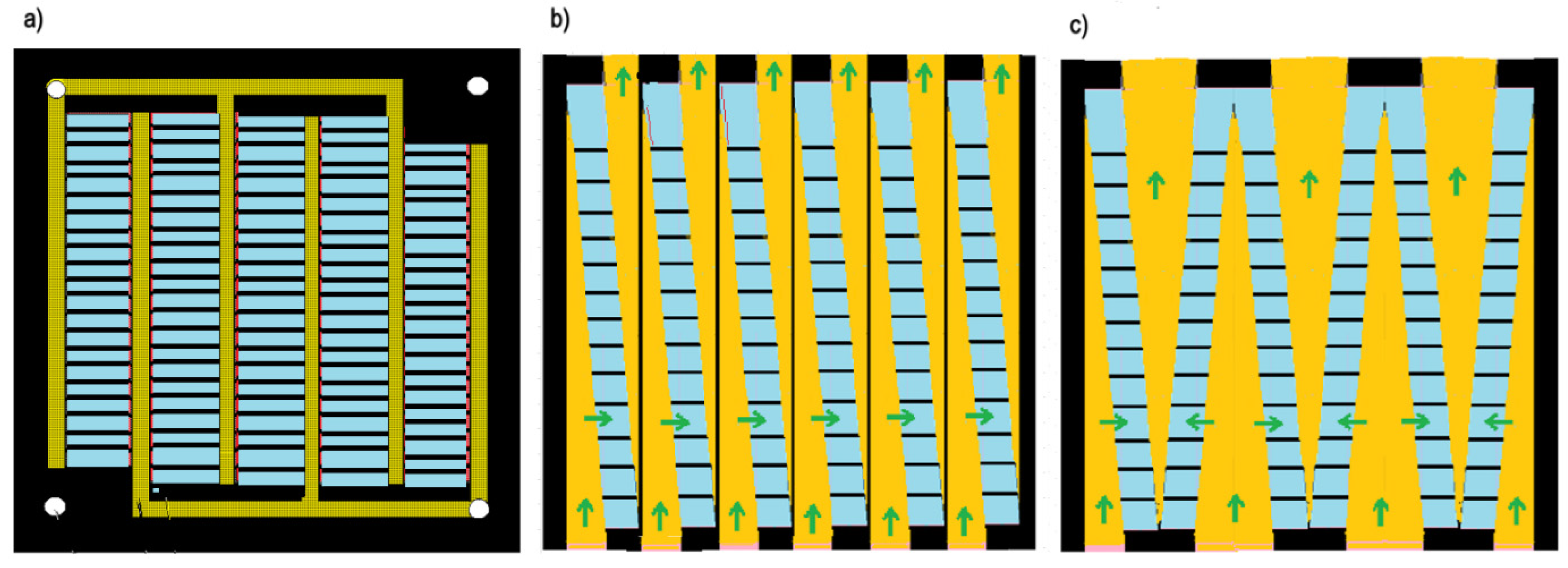
3.1. Fractal Profiled Membranes
| Ralex Membrane | IEC | Perm-Selectivity | Rarea | Swelling Degree | Thickness Dry | Thickness Wet |
|---|---|---|---|---|---|---|
| meq/g dry | % | Ω∙cm2 | % | μm | μm | |
| AMH-PES | 1.97 | 94.7 | 7.66 | 56 | 764 | |
| CMH-PES | 2.34 | 89.3 | 11.33 | 31 | 450 | 714 |
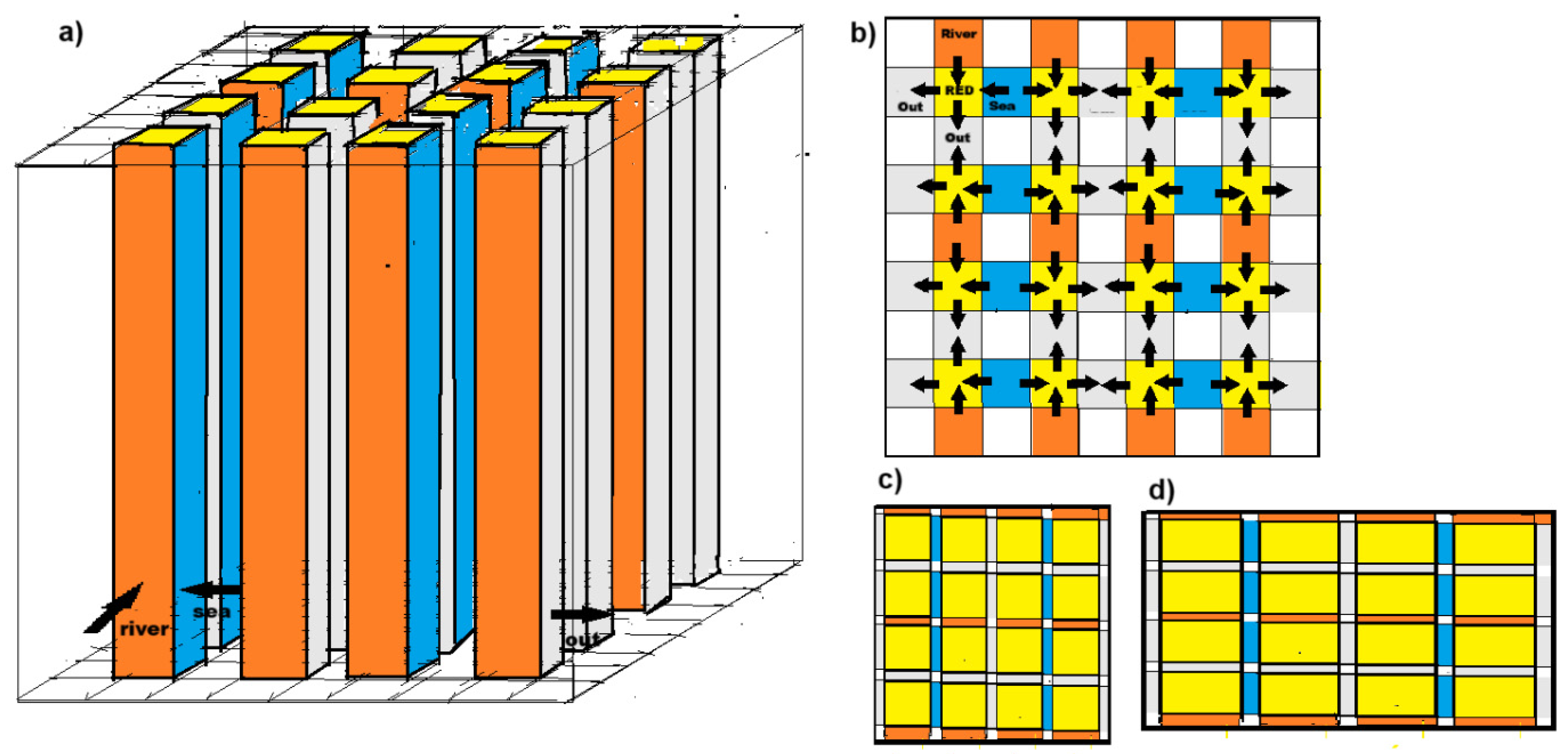
3.2. Fractal Stacks
4. Conclusions and Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AEM | Anion exchange membrane |
| CEM | Cation exchange membrane |
| CFD | Computational fluid dynamics |
| cRED | Capacitive RED |
| ED | Electrodialysis |
| HC | High-concentration feedwater |
| IEM | Ion exchange membrane |
| LC | Low-concentration feedwater |
| OCF | Overlapped cross filaments |
| RED | Reverse electrodialysis |
| SEE | Specific extractable energy |
| NPG | Nanopore power generation |
References
- Veerman, J. Harvesting salinity gradient energy by diffusion of Ions, liquid water, and water vapor. Processes 2025, 13, 554. [Google Scholar] [CrossRef]
- Clampitt, B.H.; Kiviat, F.E. Energy recovery from saline water by means of electrochemical cells. Science 1976, 194, 719–720. [Google Scholar] [CrossRef] [PubMed]
- Vermaas, D.A.; Bajracharya, S.B. Bastos Sales and M. Michel Saakes, Clean energy generation using capacitive electrodes in reverse electrodialysis. Energy Environ. Sci. 2013, 6, 643–651. [Google Scholar] [CrossRef]
- Wu, N.; Levant, M.; Brahmi, Y.; Tregouet, C.; Colin, A. Blue energy harvesting and divalent ions: Capacitive reverse electrodialysis cell with a single membrane opens a gateway to new application. Res. Sq. 2024. [Google Scholar] [CrossRef]
- Veerman, J.; Kunteng, D. Inorganic pseudo ion exchange membranes—Concepts and preliminary experiments. Appl. Sci. 2018, 8, 2142. [Google Scholar] [CrossRef]
- Veerman, J. Reverse electrodialysis: Co-and counterflow optimization of multistage configurations for maximum energy efficiency. Membranes 2020, 10, 206. [Google Scholar] [CrossRef]
- Veerman, J.; Hack, P.; Siebers, R. Blue energy from salinity gradients. J. Ocean Technol. 2023, 18, 26–36. [Google Scholar]
- Winter, A.G.; Wright, N.C. Spiral-Wound Electrodialysis Module. Patent US2019/0111393A1, 25 April 2019. [Google Scholar]
- Dow, Omexell, Spiral Wound Electrodeionization. Available online: https://www.lenntech.com/Data-sheets/DOW%20-EDI-210-L.pdf (accessed on 5 August 2025).
- Derkenne, T.; Colin, A.; Tregouet, C. Macroscopic access resistances hinders the measurement of ion-exchange-membrane performances for electrodialysis processes. ACS Appl. Energy Mater. 2024, 7, 6621–6629. [Google Scholar] [CrossRef]
- Vermaas, D.A.; Saakes, M.; Nijmeijer, K. Doubled power density from salinity gradients at reduced intermembrane distance. Environ. Sci. Technol. 2011, 45, 7089–7095. [Google Scholar] [CrossRef] [PubMed]
- Kaloc, J. Power Numbers in Grand Tours—VINGEGAARD and Pogačar Breaking Records. Available online: https://www.welovecycling.com/wide/2023/08/30/ (accessed on 29 May 2025).
- Veerman, J.; Saakes, M.; Metz, S.J.; Harmsen, G.J. Reverse electrodialysis: A validated process model for design and optimization. Chem. Eng. J. 2011, 166, 256–268. [Google Scholar] [CrossRef]
- Veerman, J. Reverse Electrodialysis—Design and Optimization by Modeling and Experimentation. Doctoral Thesis, University of Groningen, Groningen, The Netherlands, 2010. Available online: https://pure.rug.nl/ws/portalfiles/portal/2625515/13complete.pdf (accessed on 29 May 2025).
- Abidin, M.N.Z.; Nasef, M.M.; Veerman, J. Towards the development of new generation of ion exchange membranes for reverse electrodialysis: A review. Desalination 2022, 537, 115854. [Google Scholar] [CrossRef]
- Kim, D.-K.K.; Duan, C.; Chen, Y.-F.F.; Majumdar, A. Power generation from concentration gradient by reverse electrodialysis in ion-selective nanochannels. Microfluid. Nanofluidics 2010, 9, 1215–1224. [Google Scholar] [CrossRef]
- Siria, A.; Poncharal, P.; Biance, A.-L.; Fulcrand, R.; Blase, X.; Purcell, S.T.; Bocquet, L. Giant osmotic energy conversion measured in a single transmembrane boron nitride nanotube. Nature 2013, 494, 455–458. [Google Scholar] [CrossRef]
- Feng, J.; Graf, M.; Liu, K.; Ovchinnikov, D.; Dumcenco, D.; Heiranian, M.; Nandigana, V.; Aluru, N.R.; Kis, A.; Radenovic, A. Single-layer MoS2 nanopores as nanopower generators. Nature 2016, 536, 197–200. [Google Scholar] [CrossRef]
- Manikandan, D.; Karishma, S.; Kumar, M.; Nayak, P.K. Salinity gradient induced blue energy generation using two-dimensional membranes. npj 2D Mater. Appl. 2024, 8, 47. [Google Scholar] [CrossRef]
- Fan, F.R.; Wu, W. Emerging devices based on two-dimensional monolayer materials for energy harvesting. AAAS Res. 2019, 2019, 7367828. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Li, X.; Chu, X.; Zhang, B.; Zhang, J.; Hambsch, M.; Mannsfeld, S.C.; Borrelli, M.; Löffler, M.; Pohl, D.; et al. Giant blue energy harvesting in two-dimensional polymer membranes with spatially aligned charges. Adv. Mater. 2024, 36, 2310791. [Google Scholar] [CrossRef]
- Mai, V.-P.; Fauziah, A.R.; Gu, C.-R.; Yang, Z.-J.; Wu, K.C.-W.; Yeh, L.-H.; Yang, R.-J. Two-dimensional metal–organic framework nanocomposite membranes with shortened ion pathways for enhanced salinity gradient power harvesting. Chem. Eng. J. 2024, 484, 149649. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L.M.J.; Feng, Z.; Li, X.; Cao, M. Highly conductive anti-fouling anion exchange membranes for power generation by reverse electrodialysis. J. Power Sources 2024, 598, 234176. [Google Scholar] [CrossRef]
- Guo, Y.; Sun, X.; Ding, S.; Lu, J.; Wang, H.; Zhu, Y.; Jiang, L. Charge-gradient sulfonated poly (ether ether ketone) membrane with enhanced ion selectivity for osmotic energy conversion. ACS Nano 2024, 18, 7161–7169. [Google Scholar] [CrossRef]
- Li, J.; Li, C.; Dou, H.; Zhang, X.; Dai, Y.; Xia, F. PET-hydrogel heterogeneous membranes that eliminate concentration polarization for salinity gradient power generation. J. Membr. Sci. 2024, 698, 122644. [Google Scholar] [CrossRef]
- Qin, S.; Yang, G.; Wang, S.; Ma, Y.; Wang, Z.; Wang, L.; Liu, D.; Lei, W. Tunable surface charge of layered double hydroxide membranes enabling osmotic energy harvesting from anion transport. Small 2024, 20, e2400850. [Google Scholar] [CrossRef]
- Chen, C.; Meng, L.; Cao, L.; Zhang, D.; An, S.; Liu, L.; Wang, J.; Li, G.; Pan, T.; Shen, J.; et al. Phase engineering of zirconium MOFs enables efficient osmotic energy conversion: Structural evolution unveiled by direct imaging. J. Am. Chem. Soc. 2024, 146, 11855–11865. [Google Scholar] [CrossRef] [PubMed]
- Awati, A.; Yang, R.; Shi, T.; Zhou, S.; Zhang, X.; Zeng, H.; Lv, Y.; Liang, K.; Xie, L.; Zhu, D.; et al. Interfacial super-assembly of vacancy engineered ultrathin-nanosheets toward nanochannels for smart ion transport and salinity gradient power conversion. Angew. Chem. Int. Ed. 2024, 63, 202407491. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Wu, H. Dual-network fiber-hydrogel membrane for osmotic energy harvesting. Front. Chem. 2024, 12, 1401854. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, Q.; Yin, J.; Jia, P.; Lu, W.; Yao, Q.; Deng, M.; Gao, Y.; Liu, N. Enhancing osmotic energy harvesting through supramolecular design of oxygen-functionalized MXene with biomimetic ion channel. Adv. Funct. Mater. 2024, 34, 2404410. [Google Scholar] [CrossRef]
- Wang, S.; Shan, Z.; Ahmad, M.; Li, Z.; Sun, Z. Robust holey graphene oxide/cellulose nanofiber composites for sustainable and efficient osmotic energy conversion. ACS Appl. Nano Mater. 2024, 7, 14265–14274. [Google Scholar] [CrossRef]
- Wu, C.; Wang, J.; Wu, R.; Zeng, H.; Chen, X.; Yao, C.; Zhou, J.; Kong, X.-Y.W.L.; Jiang, L. Three-dimensional hydrogel membranes for boosting osmotic energy conversion: Spatial confinement and charge regulation induced by zirconium ion crosslinking. Nano Today 2024, 58, 102468. [Google Scholar]
- Gu, T.; Xu, J.; Zhu, F.; Ding, Z.; Luo, Y. Different hydrophilic bilayer membranes for efficient osmotic energy harvesting with high-concentration exfoliation. Appl. Clay Sci. 2024, 261, 107577. [Google Scholar] [CrossRef]
- Li, G.; Ma, W.; Zhou, J.; Wu, C.; Yao, C.; Zeng, H.; Wang, J. A composite hydrogel with porous and homogeneous structure for efficient osmotic energy conversion. Chin. Chem. Lett. 2024, 36, 110449. [Google Scholar] [CrossRef]
- Chuang, C.-H.; Peng, Y.-H.; Chang, C.-K.; Chang, P.-Y.; Kang, D.-Y.; Yeh, L.-H. Crystal orientation control in angstrom-scale channel membranes for significantly enhanced blue energy harvesting. Chem. Eng. J. 2024, 499, 155934. [Google Scholar] [CrossRef]
- Lin, C.; Jia, W.; Chang, L.; Ren, G.; Hu, S.; Sui, X.; Gao, L.; Sui, K.S.; Jiang, L. Anti-swelling 3D nanohydrogel for efficient osmotic energy conversion. Adv. Funct. Mater. 2025, 35, 2416425. [Google Scholar] [CrossRef]
- Zou, K.; Ling, H.; Wang, Q.; Zhu, C.; Zhang, Z.; Huang, D.; Li, K.; Wu, Y.; Xin, W.; Kong, X.-Y.; et al. Turing-type nanochannel membranes with extrinsic ion transport pathways for high-efficiency osmotic energy harvesting. Nat. Commun. 2024, 15, 10231. [Google Scholar] [CrossRef]
- Wu, C.; Wu, R.; Zeng, H.; Yao, C.; Zhou, J.; Li, G.; Wang, J. High-performance hydrogel membranes with superior environmental stability for harvesting osmotic energy. Chem. Eng. J. 2024, 499, 156681. [Google Scholar] [CrossRef]
- Wei, R.; Liu, X.; Cao, L.; Chen, C.; Chen, I.-C.; Li, Z.; Miao, J.; Lai, Z. Zeolite membrane with sub-nanofluidic channels for superior blue energy harvesting. Nat. Commun. 2024, 15, 10489. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Patel, S.Z.; Lin, S.; Elimelech, M. Nanopore-based power generation from salinity gradient: Why it is not viable. ACS Nano 2021, 15, 4093–4107. [Google Scholar] [CrossRef]
- Pawlowski, S.; Geraldes, V.; Crespo, J.G.; Velizarov, S. Computational fluid dynamics (CFD) assisted analysis of profiled membranes performance in reverse electrodialysis. J. Membr. Sci. 2016, 502, 179–190. [Google Scholar] [CrossRef]
- Vermaas, D.A.; Saakes, M.; Nijmeijer, K. Power generation using profiled membranes in reverse electrodialysis. J. Membr. Sci. 2011, 385, 234–242. [Google Scholar] [CrossRef]
- Pawlowski, S.; Rijnaarts, T.; Saakes, M.; Nijmeijer, K.; Crespo, J.G.; Velizarov, S. Improved fluid mixing and power density in reverse electrodialysis stacks with chevron-profiled membranes. J. Membr. Sci. 2017, 531, 111–121. [Google Scholar] [CrossRef]
- Güler, E.; Elizen, R.; Saakes, M.; Nijmeijer, K. Micro-structured membranes for electricity generation by reverse electrodialysis. J. Membr. Sci. 2014, 458, 136–148. [Google Scholar] [CrossRef]
- Loza, S.; Loza, N.; Kutenko, N.; Smyshlyaev, N. Profiled ion-exchange membranes for reverse and conventional electrodialysis. Membranes 2022, 12, 985. [Google Scholar] [CrossRef]
- Pawlowski, S.; Crespo, J.G.; Velizarov, S. Profiled ion exchange membranes: A comprehensible review. Int. J. Mol. Sci. 2019, 20, 165. [Google Scholar] [CrossRef]
- Tanaka, M.; Sugimoto, Y.; Higa, M. Power generation by reverse electrodialysis stack using profiled ion exchange membranes with novel concave-convex pattern. Salt Seawater Sci. Technol. 2024, 4, 22–23. [Google Scholar]
- Gurreri, L.; Santoro, F.; Battaglia, G.; Cipollina, A.; Tamburini, A.; Micale, G.; Ciofalo, M. Investigation of reverse electroDialysis units by multi-physical modelling. In Proceedings of the COMSOL Conference 2016 Munich, Munich, Germany, 12–14 October 2016. [Google Scholar]
- Gurreri, L.; Battaglia, G.T.A.; Cipollina, A.; Micale, G.; Ciofalo, M. Multi-physical modelling of reverse electrodialysis. Desalination 2017, 423, 52–64. [Google Scholar] [CrossRef]
- La Cerva, M.F.; Di Liberto, M.; Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G.; Ciofalo, M. Coupling CFD with a one-dimensional model to predict the performance of reverse electrodialysis stacks. J. Membr. Sci. 2017, 541, 595–610. [Google Scholar] [CrossRef]
- Jalili, Z.; Burheim, O.S.; Einarsrud, K.E. Computational Fluid Dynamics Modeling of the Resistivity and Power Density in Reverse Electrodialysis: A Parametric Study. Membranes 2020, 10, 209. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Pismenskaya, N.D.; Istoshin, A.G.; Zabolotsky, V.I.; Shudrenko, A.A. Description of mass transfer characteristics of ED and EDI apparatuses by using the similarity theory and compartmentation method. Chem. Eng. Process.—Process. Intensif. 2008, 47, 1118–1127. [Google Scholar] [CrossRef]
- Larchet, C.; Zabolotsky, V.I.; Nikonenko, P.N.V.V.; Tskhay, A.; Tastanov, K.; Pourcelly, G. Comparison of different ED stack conceptions when applied for drinking water production from brackish waters. Desalination 2008, 222, 489–496. [Google Scholar] [CrossRef]
- Seo, J.; Kusher, I.; Hickner, M.A. 3D Printing of micropatterned anion exchange membranes. ACS Appl. Mater. Interfaces 2016, 8, 16656–16663. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Geise, G.M.; Luo, X.; Hou, H.; Zhang, F.; Feng, Y.; Hickner, M.A.; Logan, B.E. Patterned ion exchange membranes for improved power production in microbial reverse electrodialysis cells. J. Power Sources 2014, 271, 437–443. [Google Scholar] [CrossRef]
- Gurreri, L.; Filingeri, A.; Ciofalo, M.; Cipollina, A.; Tedesco, M.; Tamburini, A.; Micale, G. Electrodialysis with asymmetrically profiled membranes: Influence of profiles geometry on desalination performance and limiting current phenomena. Desalination 2021, 506, 115001. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Macmillan: New York, NY, USA, 1983; ISBN 978-0-7167-1186-5. [Google Scholar]
- Coppens, M.O. Nature inspired chemical engineering learning from the fractal geometry of nature in sustainable chemical engineering. Fractal Geom. Appl. A Jubil. Benoit Mand. 2004, 72, 507–532. [Google Scholar]
- Veerman, J.; Metz, S.J. Membrane, Stack of Membranes for Use in an Electrode-Membrane Process, and Device and Method Therefore. Patent WO2011/002288A1, 6 January 2011. [Google Scholar]

| Spacer | Membrane | Pdnet (W/m2) | Pdnet (W/m2) | Pdnet (W/m2) |
|---|---|---|---|---|
| @ 0.01 m | @ 0.1 m | @ 1 m | ||
| empty | ideal | 60.2 | 19.0 | 6.0 |
| woven | ideal | 11.58 | 3.66 | 1.16 |
| empty | Qianqiu | 2.43 | 1.91 | 1.27 |
| woven | Qianqiu | 1.63 | 0.99 | 0.47 |
| Parameter | - | - | Maximized Pdnet | Maximized RPZ | ||||
|---|---|---|---|---|---|---|---|---|
| Path length | L (m) | m | 0.01 | 0.1 | 1 | 0.01 | 0.1 | 1 |
| Net power density | Pdnet | W/m2 | 1.63 | 0.99 | 0.47 | 1.05 | 0.74 | 0.38 |
| Net river water yield | Znet | kJ/m3 | 78 | 126 | 156 | 298 | 299 | 272 |
| Flow ratio sea/river water | ΦS/ΦR | - | 0.90 | 1.11 | 1.36 | 5.76 | 3.82 | 3.03 |
| Thickness sea water comp. | δS | μm | 194 | 503 | 1430 | 240 | 590 | 1500 |
| Thickness river water comp. | δR | μm | 96 | 240 | 672 | 54 | 175 | 553 |
| Authors | Ref. | Type | CHC/CLC | Pd (W/m2) | Membrane |
|---|---|---|---|---|---|
| Liu et al. | [21] | CEM | S/R | 48.4 | Propidium iodide-based two-dimensional polymer |
| Mai et al. | [22] | CEM | 50 | 6.48 | Metal–organic framework |
| Liu et al. | [23] | AEM | S/R | 1.47 | Modified cross-linked alginate hydrogels |
| Guo et al. | [24] | CEM | 50 | 9.2 | Sulfonated poly(ether ether) ketone membrane |
| Li et al. | [25] | CEM | 50 | 1.92 | PET–hydrogel heterogeneous membranes |
| Qin et al. | [26] | AEM | S/R | 2.31 | Layered double-hydroxide membranes |
| Chen et al. | [27] | CEM | 50 | 10.08 | Zirconium-based MOF |
| Awati et al. | [28] | CEM | S/R | 5.35 | VOLD/CNF-wrapped carbon nanotubes |
| Cao and Wu | [29] | CEM | 50 | 4.84 | Dual-Network Fiber–Hydrogel Membrane |
| Ren et al. | [30] | CEM | S/R | 21.7 | Oxygen-functionalized Mxene |
| Wang et al. | [31] | CEM | 500 | 1.25 | Hole-enriched graphene oxide and cellulose nanofibers |
| Wu et al. | [32] | CEM | 50 | 16.44 | Three-dimensional hydrogel |
| Gu et al. | [33] | CEM | - | 4.66 | Hydrophilic bilayers of vermiculite and Mxene |
| Li et al. | [34] | CEM | 50 | 13.73 | Composite hydrogel |
| Chuang et al. | [35] | CEM | S/R | 9.64 | MOF MIL-178 |
| Lin et al. | [36] | CEM | 500 | 48.5 | Anti-swelling nanohydrogel |
| Zou et al. | [37] | CEM | S/R | 7.7 | Turing-type nanochannels |
| Wu et al. | [38] | CEM | 50 | 30.94 | PASH hydrogel |
| Wei et al. | [39] | CEM | 50 | 21.27 | NaX zeolite |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veerman, J. Bioinspired Fractal Design of (Reverse) Electrodialysis Stacks. Processes 2025, 13, 3720. https://doi.org/10.3390/pr13113720
Veerman J. Bioinspired Fractal Design of (Reverse) Electrodialysis Stacks. Processes. 2025; 13(11):3720. https://doi.org/10.3390/pr13113720
Chicago/Turabian StyleVeerman, Joost. 2025. "Bioinspired Fractal Design of (Reverse) Electrodialysis Stacks" Processes 13, no. 11: 3720. https://doi.org/10.3390/pr13113720
APA StyleVeerman, J. (2025). Bioinspired Fractal Design of (Reverse) Electrodialysis Stacks. Processes, 13(11), 3720. https://doi.org/10.3390/pr13113720






