Two-Phase Stefan Problem for the Modeling of Particle Solidification in a Urea Prilling Tower
Abstract
1. Introduction
2. Problem Formulation
2.1. Assumptions
- The process is stationary.
- The urea droplets fall only in the vertical direction. There is no radial velocity.
- The effect of moisture on melting temperature is negligible due to the low moisture content of the droplets (less than 0.5%)
- The moisture content of the cooling air remains unchanged; only the temperature of the cooling air varies.
- Radiation heat transfer is not considered.
- The particles are considered to be perfectly spherical.
- The particles do not shrink during the solidification process due to the low water content and the low evaporation of urea liquid.
- The process is adiabatic because of the large thickness of the tower wall and the high thermal resistance of the concrete.
2.2. Momentum Transfer
2.3. Material Balance and Mass Transfer
2.4. Energy Balance and Heat Transfer
3. Solution Procedure and Model Parameters
3.1. Solution Procedure
3.2. Model Parameters
4. Results and Discussions
4.1. Validation of Numerical Scheme for Stefan Two-Phase Problem
4.2. Air Temperature Profiles
4.3. Moisture Content Profiles
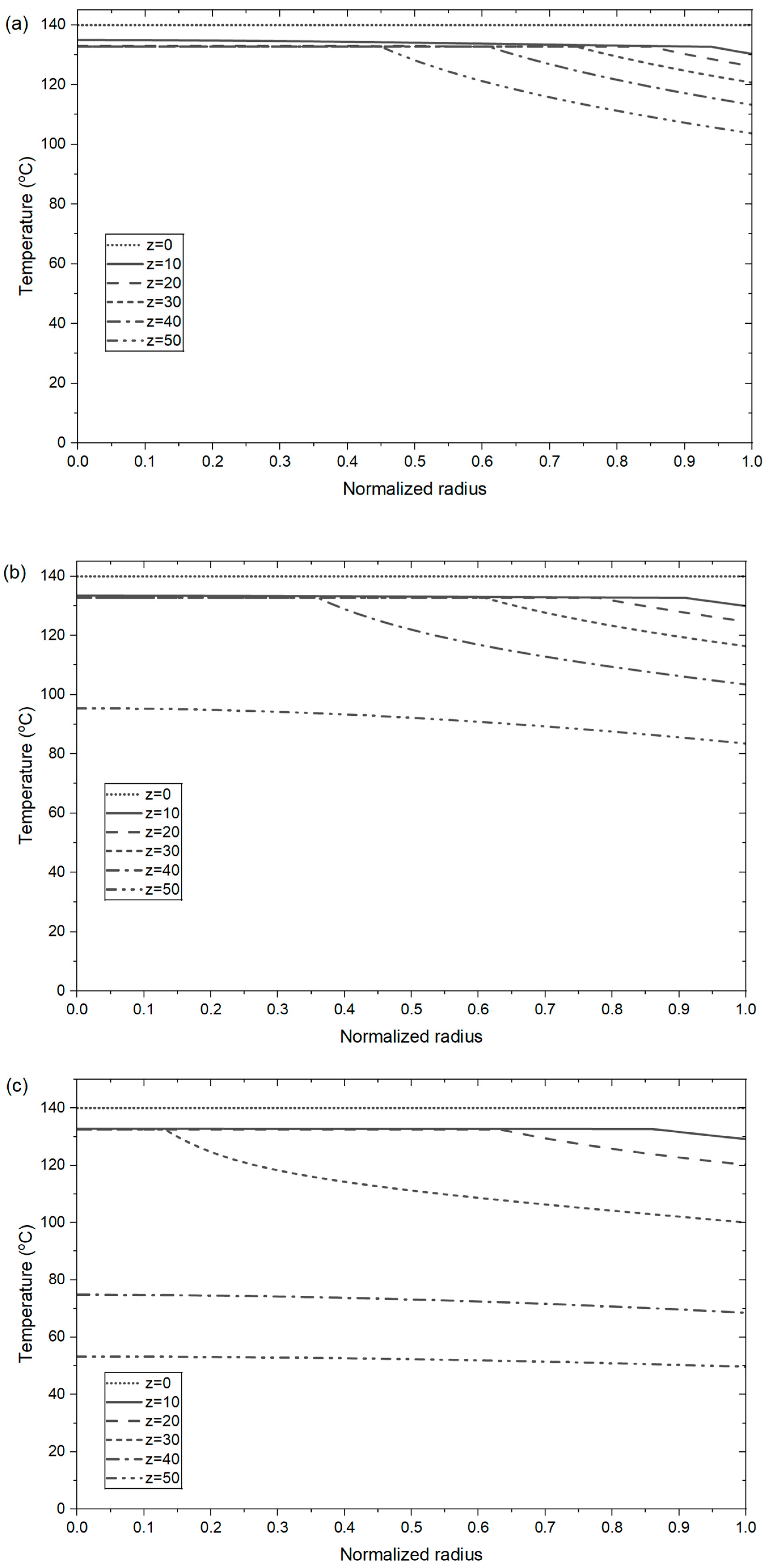
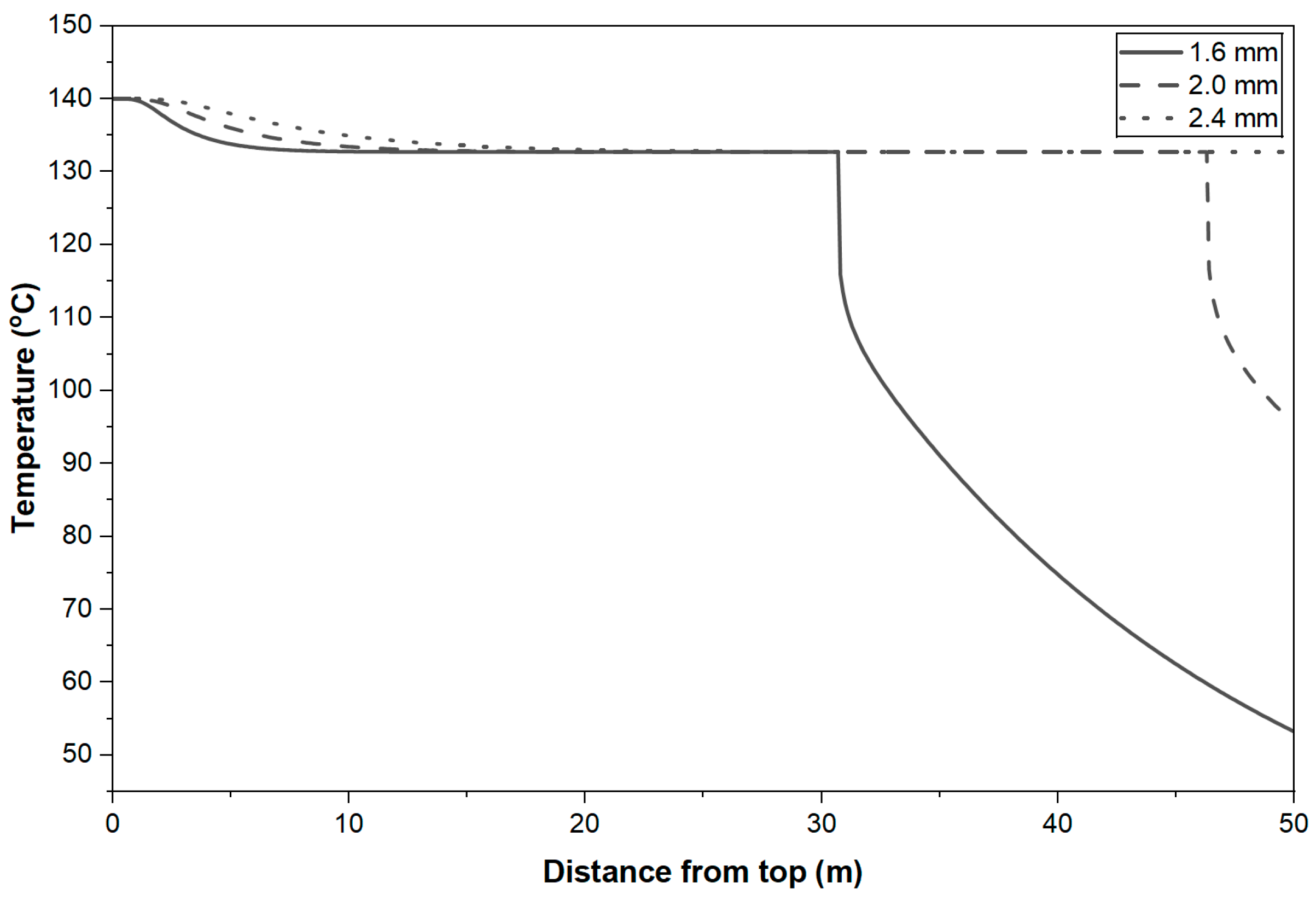
4.4. Temperature Profiles of the Prills
4.5. Velocity Profiles
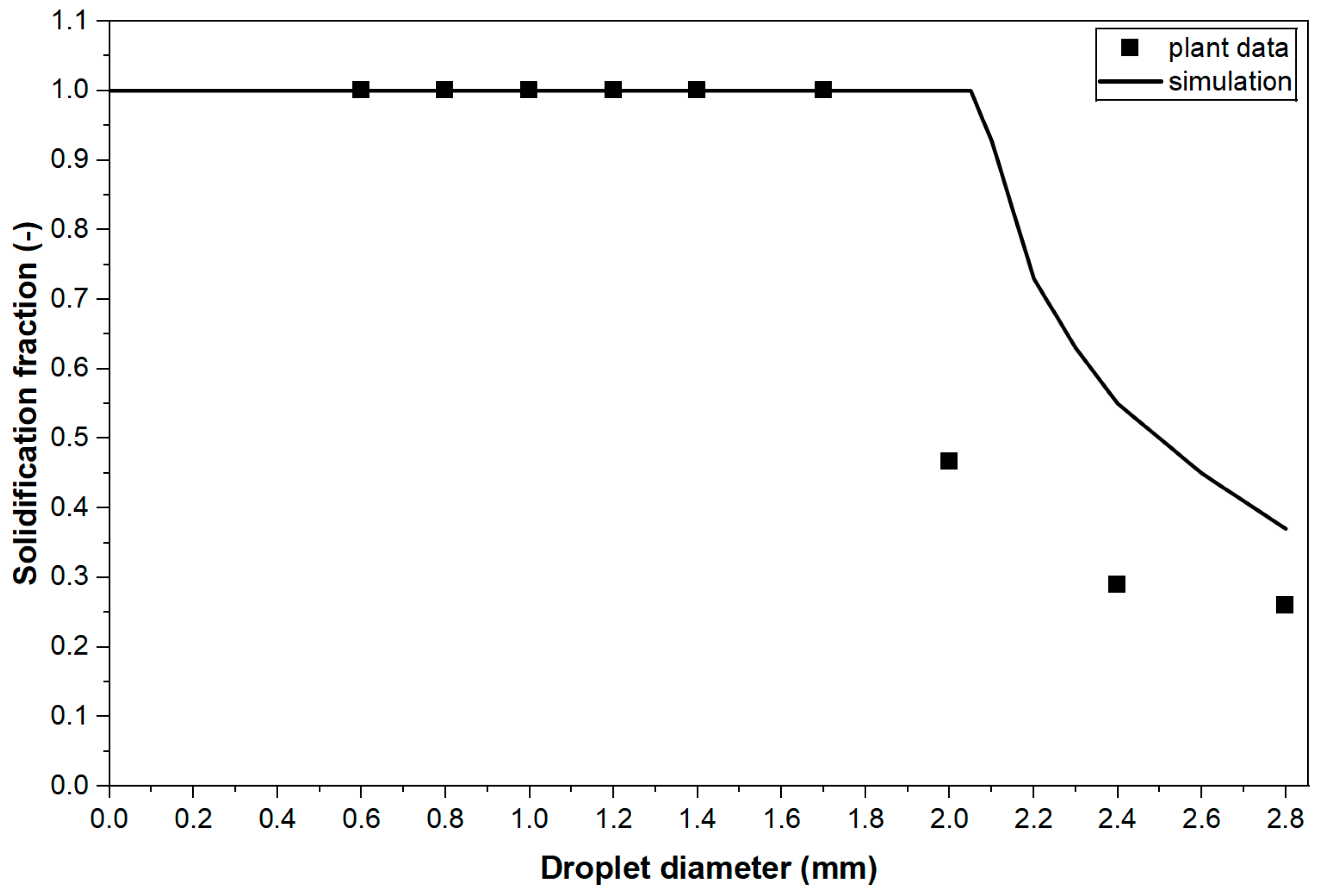
4.6. Solidification Ratio
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| cp,a | specific heat of air at constant pressure (J/kg·K) |
| cp,l | specific heat of melt urea at constant pressure (J/kg·K) |
| cp,s | specific heat of solid urea at constant pressure (J/kg·K) |
| CD | drag coefficient (dimensionless) |
| dp | particle diameter (m) |
| DM | diffusion coefficient of moisture through urea within particles (m2/s) |
| Dt | tower diameter (m) |
| f | local liquid fraction (mol liquid/mol liquid and solid) |
| g | gravitational acceleration (m/s2) |
| H | enthalpy (kJ/mol) |
| h | reduced enthalpy (K) |
| hmass | convective heat-transfer coefficient between air and particles (W/m2·K) |
| ka | thermal conductivity of air (W/m·K) |
| kl | thermal conductivity of melt urea (W/m·K) |
| ks | thermal conductivity of solid urea (W/m·K) |
| L | latent heat of freezing (kJ/mol) |
| M | local moisture content of particle (kg H2O/kg dry urea) |
| Ma | moisture content of the air (kg H2O/kg dry air) |
| M* | equilibrium moisture content (kg H2O/kg urea) |
| mp | mass of a particle (kg) |
| ṁp | mass flow rate of particles (kg/s) |
| ṁa | mass flow rate of air (kg/s) |
| Nu | Nusselt number (dimensionless) |
| P | pressure (atm) |
| Psat | saturated vapor pressure |
| Pr | Prandtl number (dimensionless) |
| Rep | Reynolds number of the particle (dimensionless) |
| Rp | particle radius (m) |
| RH | relative humidity of the air (%) |
| r | radial coordinate from particle center (m) |
| Sc | Schmidt number (dimensionless) |
| Sh | Sherwood number (dimensionless) |
| T | temperature of urea particle (K) |
| Ta | temperature of air (K) |
| Ti | temperature of urea feed (K) |
| Tm | melting temperature of urea (K) |
| Tp | temperature at the surface of the particle (K) |
| t | time taken when a particle falls to the position z from the top (s) |
| va | velocity of air (m/s) |
| vp | velocity of particle (m/s) |
| z | axial coordinate from top of the tower (m) |
| Z | tower height (m) |
| Greek letters | |
| μa | viscosity of air (kg/m3) |
| ρa | density of air (kg/m3) |
| ρl | density of melt urea (kg/m3) |
| ρs | density of solid urea (kg/m3) |
References
- Yahya, N. Urea Fertilizer: The Global Challenges and Their Impact to Our Sustainability. In Green Urea: For Future Sustainability; Springer: Singapore, 2018; pp. 1–21. [Google Scholar] [CrossRef]
- Skorupka, M.; Nosalewicz, A. Ammonia Volatilization from Fertilizer Urea—A New Challenge for Agriculture and Industry in View of Growing Global Demand for Food and Energy Crops. Agriculture 2021, 11, 822. [Google Scholar] [CrossRef]
- Xia, M.; Mao, C.; Gu, A.; Tountas, A.A.; Qiu, C.; Wood, T.E.; Li, Y.F.; Ulmer, U.; Xu, Y.; Viasus, C.J.; et al. Solar Urea: Towards a Sustainable Fertilizer Industry. Angew. Chem. Int. Ed. 2022, 61, e202110158. [Google Scholar] [CrossRef] [PubMed]
- Rahmanian, N.; Naderi, S.; Supuk, E.; Abbas, R.; Hassanpour, A. Urea Finishing Process: Prilling Versus Granulation. Procedia Eng. 2015, 102, 174–181. [Google Scholar] [CrossRef]
- Bakhtin, L.A.; Vagin, A.A.; Esipovich, L.Y.; Labutin, A.N. Heat-exchange calculations in prilling towers. Chem. Pet. Eng. 1978, 14, 994–999. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, C.; Zhou, Y. An Innovated Tower-fluidized Bed Prilling Process. Chin. J. Chem. Eng. 2007, 15, 424–428. [Google Scholar] [CrossRef]
- Ricardo, G.A.N.; Noriler, D.; Martignoni, W.P.; Meier, H.F. Application of Euler–Lagrange Approach to Predict the Droplet Solidification in a Prilling Tower. Ind. Eng. Chem. Res. 2015, 54, 9615–9626. [Google Scholar] [CrossRef]
- Alamdari, A.; Jahanmiri, A.; Rahmaniyan, N. Mathematical modelling of urea prilling process. Chem. Eng. Commun. 2000, 178, 185–198. [Google Scholar] [CrossRef]
- Rahmanian, N.; Homayoonfard, M.; Alamdari, A. Simulation of Urea Prilling Process: An Industrial Case Study. Chem. Eng. Commun. 2013, 200, 764–782. [Google Scholar] [CrossRef]
- Mehrez, A.; Ookawara, S.; Ali, A.H.H.; Suzuki, M. A Numerical Study on Cooling-Solidification Process of Urea Particles in Prilling Tower. J. Chem. Eng. Jpn. 2014, 47, 628–634. [Google Scholar] [CrossRef]
- Torkashvand, B.; Gilassi, S.; Moghadam, R. Analysis of Heat and Moisture Transfer During Drying of Urea Particles. Chem. Ind. Chem. Eng. Q. 2019, 25, 171–182. [Google Scholar] [CrossRef]
- McCue, S.W.; Wu, B.; Hill, J.M. Classical two-phase Stefan problem for spheres. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 2055–2076. [Google Scholar] [CrossRef]
- Ha, K.T.V.; Nguyen, T.-A.; Nguyen, Q.-L.; Dang, V.-V.; Dang, V.-H.; Van, H.-L.; Pham, L.-N.T. Two-Phase Stefan Problem for the Modeling of Urea Prilling Tower. Eng. Proc. 2023, 37, 122. [Google Scholar] [CrossRef]
- Brown, P.P.; Lawler, D.F. Sphere Drag and Settling Velocity Revisited. J. Environ. Eng. 2003, 129, 222–231. [Google Scholar] [CrossRef]
- Paláncz, B. A mathematical model for continuous fluidized bed drying. Chem. Eng. Sci. 1983, 38, 1045–1059. [Google Scholar] [CrossRef]
- McKenna, T.F.; Spitz, R.; Cokljat, D. Heat transfer from catalysts with computational fluid dynamics. AIChE J. 1999, 45, 2392–2410. [Google Scholar] [CrossRef]
- Caldwell, J.; Chan, C.-C. Numerical solutions of the stefan problem by the enthalpy method and the heat balance integral method. Numer. Heat Transf. Part B Fundam. 1998, 33, 99–117. [Google Scholar] [CrossRef]
- Meessen, J.H. Urea. In Ullmann’s Encyclopedia of Industrial Chemistry; VCH: Weinheim, Germany, 1985. [Google Scholar] [CrossRef]
- Serth, R.W.; Lestina, T.G. (Eds.) Appendix A—Thermophysical Properties of Materials. In Process Heat Transfer, 2nd ed.; Academic Press: Boston, MA, USA, 2014; pp. 555–580. [Google Scholar] [CrossRef]
- Hindmarsh, J.P.; Russell, A.B.; Chen, X.D. Experimental and numerical analysis of the temperature transition of a suspended freezing water droplet. Int. J. Heat Mass Transf. 2003, 46, 1199–1213. [Google Scholar] [CrossRef]
- Akhtar, S.; Xu, M.; Sasmito, A.P. Development and validation of an asymptotic solution for a two-phase Stefan problem in a droplet subjected to convective boundary condition. Int. J. Therm. Sci. 2021, 164, 106923. [Google Scholar] [CrossRef]




| Property | Notation | Value |
|---|---|---|
| Density of solid urea (kg/m3) | ρs | 1335 |
| Melting point of urea (°C) | Tm | 132 |
| Thermal conductivity of solid urea (W/(m·K)) | ks | 2.651 × 10−2 |
| Specific heat capacity of solid urea (J/(kg·K)) | cp,s | 1334 |
| Heat of fusion (kJ/kg) | L | 224 |
| Density of liquid urea (kg/m3) | ρl | 1247 |
| Thermal conductivity of liquid urea (W/(m·K)) | kl | 1.3 × 10−2 |
| Specific heat capacity of liquid urea (J/(kg·K)) | cp,l | 2250 |
| Particle (droplet) diameter range (mm) | 0.6–2.4 | 0.6–2.4 |
| Properties | Notation | Values |
|---|---|---|
| Density of air (kg/m3) | ρa | 1.166 |
| Viscosity of air (Pa·s) | μa | 1.87 × 10−5 |
| Specific heat capacity (kJ/(kg·K)) | cp,a | 1.005 |
| Thermal conductivity (W/(m·K)) | ka | 0.025 |
| Properties | Notation | Values |
|---|---|---|
| Tower height (m) | Z | 50 |
| Tower diameter (m) | Dt | 18 |
| Temperature of urea feed (°C) | Ti | 140 |
| Moisture content of urea feed (%wt) | Mi | 0.5 |
| Mass flow rate of urea (kg/s) | ṁp | 19 |
| Mass flow rate of air (kg/s) | ṁa | 128.6 |
| Relative humidity of air (%) | RH | 45 |
| Velocity of air (m/s) | va | 0.63 |
| Inlet air temperature (°C) | Ta,i | 30 |
| Pressure (atm) | P0 | 1 |
| Particle (droplet) diameter range (mm) | 0.6–2.4 | 0.6–2.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.-A.; Dang, V.-H.; Nguyen, Q.-L. Two-Phase Stefan Problem for the Modeling of Particle Solidification in a Urea Prilling Tower. Processes 2025, 13, 3717. https://doi.org/10.3390/pr13113717
Nguyen T-A, Dang V-H, Nguyen Q-L. Two-Phase Stefan Problem for the Modeling of Particle Solidification in a Urea Prilling Tower. Processes. 2025; 13(11):3717. https://doi.org/10.3390/pr13113717
Chicago/Turabian StyleNguyen, Tuan-Anh, Van-Han Dang, and Quoc-Lan Nguyen. 2025. "Two-Phase Stefan Problem for the Modeling of Particle Solidification in a Urea Prilling Tower" Processes 13, no. 11: 3717. https://doi.org/10.3390/pr13113717
APA StyleNguyen, T.-A., Dang, V.-H., & Nguyen, Q.-L. (2025). Two-Phase Stefan Problem for the Modeling of Particle Solidification in a Urea Prilling Tower. Processes, 13(11), 3717. https://doi.org/10.3390/pr13113717








