Coordinated Multi-Market Regulation Strategy for Hybrid Pumped Storage Power Plants Considering Contracts for Difference

Abstract

Compared with pure pumped storage, hybrid pumped storage plants (HPSPs) face more complex challenges in electricity markets, such as multi-time-scale decision-making and coupled market mechanisms. Existing mid- to long-term curve decomposition strategies often lead to deviations from actual spot prices and compressed bidding space, limiting profitability and sustainable development. To address this, this study introduces Contracts for Difference (CfDs) to enhance revenue and operational flexibility. A bi-level optimization model is developed for joint participation in spot and frequency regulation markets under CfDs: the upper level maximizes HPSP revenue through capacity allocation and bidding, while the lower level maximizes social welfare via joint energy and ancillary service market clearing. The model is solved using a commercial solver and NSGA-II. Simulations show that CfDs increase spot market revenue by 33.2% and improve bidding alignment with price fluctuations, demonstrating strong market adaptability.

1. Introduction

1.1. Concept and Motivation

Against the macroeconomic backdrop in which medium- and long-term planning serves as an essential instrument for guiding national economic and social development [1], China is accelerating the transformation of its energy system and the establishment of electricity market mechanisms. In 2025, the National Development and Reform Commission and the National Energy Administration jointly issued the Basic Rules for Electricity Market Metering and Settlement (NDRC Energy Regulation [2025] No. 976), marking the fundamental establishment of a unified national metering and settlement system. This provides institutional safeguards for the efficient operation of a multi-level electricity market [1,2]. With the large-scale integration of renewable energy units, the inherent volatility and intermittency of their output, coupled with the prevailing situation of high investment and low returns, have placed increasing demands on system flexibility and highlighted the urgent need for scalable and economically viable regulation resources. In this context, pumped storage power plants, as critical infrastructure for enhancing system flexibility, are experiencing significant development opportunities. According to Zhang et al. [3], the installed capacity of pumped storage is expected to reach 62 GW by 2025 and further expand to 120 GW by 2030. However, as high-quality sites for pure pumped storage plants become increasingly scarce, developing hybrid pumped storage power plants (HPSPs)—which combine conventional hydropower stations with pumped storage units—has emerged as a key strategy to overcome site constraints [4], enhance system flexibility, and support the efficient integration of renewable energy at scale [5].

HPSPs integrate the generation capabilities of conventional hydropower units with the storage capabilities of reversible units. Compared with pure pumped storage plants, they offer wider regulation ranges and longer regulation cycles, enabling more flexible participation in electricity market transactions across multiple time scales. This allows HPSPs to deliver low-cost, reliable flexibility services to the power system, offering considerable comprehensive benefits and development potential.

1.2. Literature Review

At present, numerous scholars have conducted in-depth studies on the optimal scheduling of HPSPs. For example, Zhang et al. [6] considered weekly time scales under extreme scenarios of sustained high and low output from wind and photovoltaic sources and demonstrated that HPSPs can effectively reduce the variance of residual load. Liu et al. [7] proposed a short-term peak-shaving optimization model for HPSPs retrofitted from cascade hydropower plants, showing that they significantly reduce the peak–valley difference in residual load compared with conventional cascaded plants. Guo et al. [8] analyzed changes in peak-shaving characteristics after retrofitting cascade hydropower plants into HPSPs in the Yellow River basin, emphasizing benefits for the coordinated development of basin-wide hydropower. Luo et al. [9] investigated the joint operation of HPSPs and wind power, constructing detailed models for both conventional and pumped storage units to provide insights into multi-energy coordinated scheduling. These studies primarily focus on satisfying grid load requirements and exploring short- to medium-term scheduling strategies. However, they have not fully addressed the competitive participation of HPSPs alongside other generation resources within the unified national electricity market.

From another perspective, extensive research has been conducted on the interrelationships among capacity configuration, market mechanisms, and capacity pricing. Li et al. [10] proposed an optimization method for the capacity allocation of wind–solar–hydro–storage systems based on coordination between capacity and spot markets, which effectively enhances reliable capacity and market revenues. Wang et al. [11] explored unit capacity optimization in retrofitted cascade HPSPs to improve peak-shaving performance. Zhang et al. [12] adopted a multi-energy complementary perspective, considering the coupling between water inflows and electricity generation, and proposed a two-stage decision-making method that coordinates operational optimization with capacity configuration under market rules. Ma et al. [13] introduced a combined scenario generation method that captures uncertainties in renewable generation and water inflows, identifying optimal capacity configuration through life-cycle comprehensive evaluation. Wang, et al. [14] further examined short-term multi-market participation of HPSPs in spot and ancillary service markets, developing optimization models under wet, normal, and dry hydrological scenarios. Nevertheless, these studies have mainly concentrated on planning and capacity decision-making stages, while research addressing post-construction market participation and bidding strategies remains limited.

Internationally, Birkeland and AlSkaif [15] and Fatras et al. [16] conducted comparative analyses of electricity market research in China and abroad, particularly contrasting the Nordic electricity market with that of China. Favaro et al. [17] proposed a neural network-constrained optimization model for pumped storage scheduling, which generates physically feasible day-ahead dispatch plans in energy and reserve markets. Dogan et al. [18] introduced a hybrid linear–nonlinear hydropower reservoir optimization model that improves initialization of nonlinear programming problems, significantly reducing iteration counts and computational time. While Wang Peng, Zhang Yushan, Ding et al. [19] established a multi-agent game-theoretic framework analyzing PSP participation in electricity markets and identified three distinct game relationships, it does not address bidding strategies specific to HPSPs acting as independent market entities. Abdolahi et al. [20] incorporated risk analysis into a congestion management model, enhancing the alignment of decisions with the risk preferences of practical system operators. Zhang et al. [21] investigated the synergistic effects of a hybrid clean energy storage strategy combining pumped storage and hydrogen storage in multi-market participation. These studies offer valuable methods for solving pumped storage scheduling models, but lack evaluation of the benefits and value of HPSPs—either independently or in conjunction with other resources—in supporting the operation of modern power systems.

Existing research on HPSPs still faces the following limitations.

(1) Most studies focus on short-term spot markets, neglecting the long-term regulation capability and extended regulation cycles enabled by large storage capacities, thereby underestimating the revenue potential of HPSPs in medium- and long-term markets.

(2) In spot markets, conventional pumped storage is typically regarded as a “regulator” and acts as a price taker during scheduling. In contrast, HPSPs can participate in mid- to long-term contracts to hedge against price volatility, and their influence on price formation should not be overlooked; however, related mechanisms have not been systematically examined.

(3) In joint operations with renewable energy, existing studies emphasize the overall benefits of the alliance but often disregard the individual economic performance of HPSPs as independent market participants.

1.3. Novelties and Contribution

In light of the above background and research gaps, this paper introduces mid- to long-term contracts for difference (CfDs) and investigates the operational and bidding strategies of HPSPs in day-ahead energy and frequency regulation markets under a full-capacity bidding framework in a high-penetration wind and solar environment.

The introduction of CfD establishes a financial linkage that naturally couples medium and long-term markets with spot electricity markets. The financial nature of CfD enables generators to lock in long-term price signals while retaining full physical operational flexibility in the spot market, thereby effectively addressing the prevalent research gap of focusing exclusively on short-term market operations [22]. Furthermore, the coordinated operation across medium/long-term and spot markets empowers plants to develop more strategic bidding behaviors based on the secured baseline revenue from CfD, overcoming the conventional simplification of treating them as price-takers. This integrated approach enhances bidding flexibility in the spot market and subsequently expands the plant’s capability to participate in ancillary service markets such as frequency regulation, enabling coordinated optimization across multiple temporal scales and market products, thereby significantly improving overall market competitiveness and profitability [23].

The main contributions of this paper are reflected in the following three aspects:

(1) Proposed Methodology

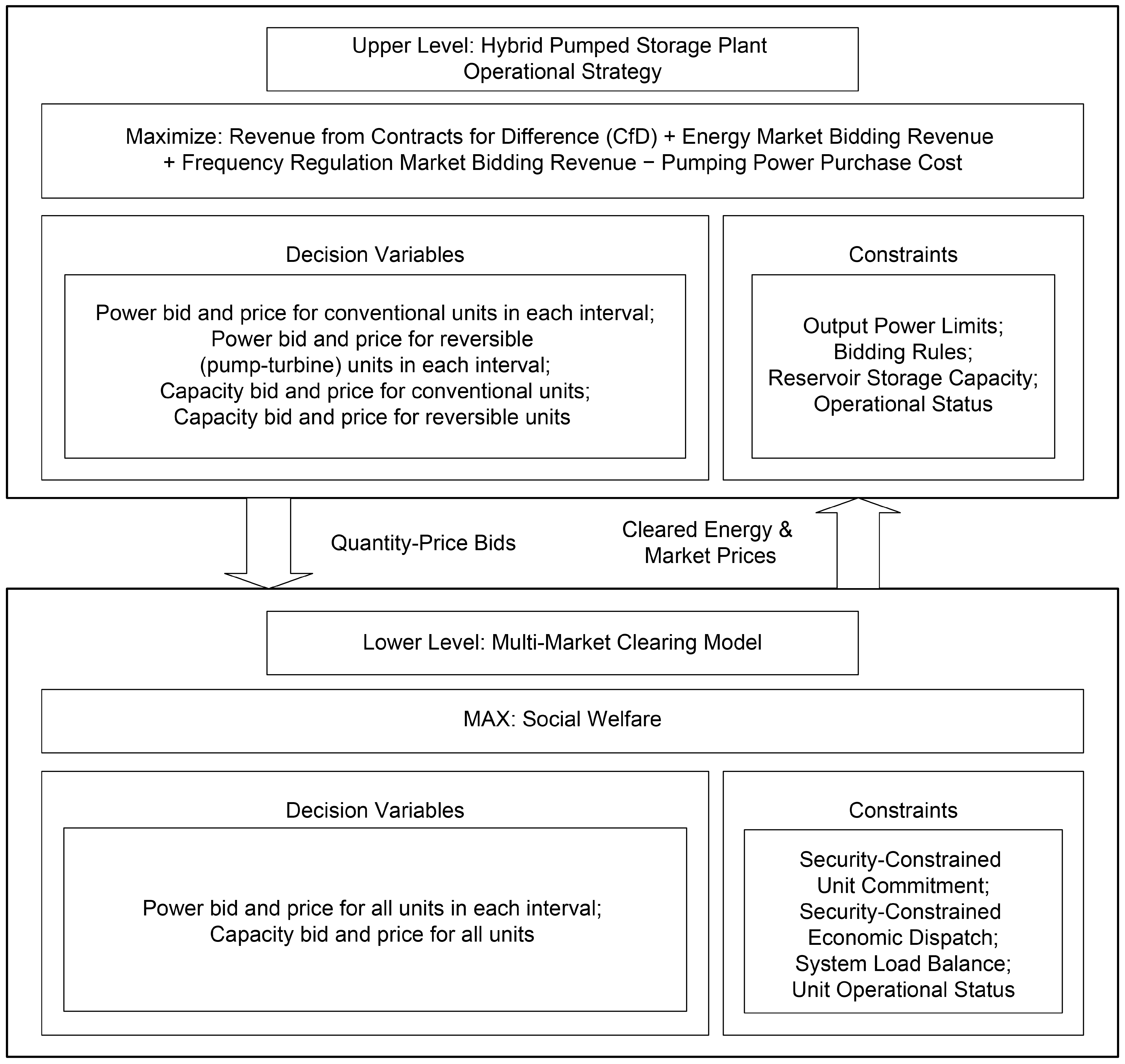
A novel bi-level optimization framework is developed to formulate the coordinated multi-market operation of HPSPs, explicitly incorporating mid- to long-term CfDs. The upper level maximizes plant revenue by integrating spatiotemporal coupling characteristics, short-term operational constraints, and non-decreasing stepwise bidding curves. The lower level minimizes total social cost through a joint clearing mechanism for spot energy and frequency regulation markets, incorporating CfDs settlement rules.

(2) Multi-Market Coupling Mechanism

The proposed model seamlessly integrates mid- to long-term, day-ahead energy, and frequency regulation markets under a full-capacity bidding framework. It effectively ad-dresses the coupling challenges between multiple market mechanisms and complex operational constraints, enabling HPSPs to optimize capacity allocation and bidding strategies across heterogeneous temporal scales and market products.

(3) Model Validation and Results

A hybrid solution strategy combining commercial solvers with genetic algorithms is implemented to efficiently solve the complex bi-level model. Case studies demonstrate the model’s effectiveness, quantifying how ancillary service participation enhances profitability. Results show significantly improved market performance, with bidding behaviors aligning closely with price dynamics, validating the model’s practical applicability.

1.4. Paper Organization

The paper is organized as follows. Section 2 establishes the multi-market framework, detailing the coordination mechanism between medium- and long-term CfDs and short-term markets. Section 3 formulates the bi-level optimization model, with the upper level focusing on HPSP revenue maximization and the lower level addressing social welfare optimization. Section 4 elaborates on the hybrid solution methodology, particularly the NSGA-II implementation and parameter configuration. Section 5 presents comprehensive case studies validating the model’s effectiveness and analyzing the economic impact of multi-market participation. Finally, Section 6 summarizes key findings and Section 7 suggests future research directions.

2. Operational Framework for Hybrid Pumped Storage in Multi-Market Participation

2.1. Market Framework

In medium- and long-term electricity markets, a CfD refers to a financial agreement in which the contracting parties settle at a predetermined fixed price for a future period, with the difference between the contract price and the spot market clearing price settled in cash, without physical delivery. Such contracts typically specify both the contracted quantity and price and serve as important financial instruments for hedging against spot market price volatility [24]. Under a centralized electricity market structure, CfDs are purely financial arrangements that do not affect actual dispatch but only influence the final settlement. A common form is the two-way CfD: when the market price exceeds the contract price, the generator returns the difference to the buyer; conversely, when the market price falls below the contract price, the buyer compensates the generator for the difference. This two-way settlement mechanism not only effectively mitigates risks associated with price volatility but also enhances contract flexibility and fairness, thereby fostering long-term and stable cooperation between generators and consumers [25].

In the spot market, if wind and photovoltaic power participate as independent entities, they face significant risks related to deviation penalties due to output inaccuracies [26]. To address this issue, when actual wind or solar generation exceeds day-ahead declared values, reversible units can absorb the surplus electricity through pumped storage, thereby shifting energy from off-peak to peak periods. This enables inter-temporal arbitrage and improves overall system economics. In the day-ahead energy market, both generation and load entities must submit full-volume bids, and the day-ahead generation and consumption schedules, as well as time-of-use prices, are determined through centralized optimization and market clearing, with all settlements based on the clearing prices [27]. According to market rules, generation enterprises must participate in the day-ahead market using non-decreasing stepwise bidding curves, as illustrated in Figure 1.

In the frequency regulation ancillary services market, trading is organized according to the system’s daily regulation requirements. This process determines both the awarded regulation capacity for each unit and the corresponding capacity and mileage prices [28]. The capacity price compensates for the opportunity cost of providing regulation services, while the mileage price reflects the unit’s actual regulation performance and dynamic response.

2.2. Bi-Level Multi-Market Regulation Model for Hybrid Pumped Storage

In a competitive electricity market environment, the decision-making behaviors of different market participants are mutually constrained and jointly determine the market clearing outcomes. Driven by revenue maximization, participants develop bidding strategies to increase their profits. This study focuses on HPSPs, investigating their strategies for market participation and profitability. When submitting bids for quantities and prices, HPSPs must consider both the bidding behaviors of other units and the market clearing mechanism of the trading center. The clearing process, in turn, determines the final dispatch by maximizing social welfare based on all participants’ responses.

On this basis, a bi-level optimization model is constructed, as illustrated in Figure 2. The upper level represents the bidding decision model for the HPSP, with the objective of maximizing revenue through capacity allocation. This model incorporates the marginal costs of energy production and ancillary services, competitor bidding strategies, and forecasts of market clearing prices, thereby generating optimized bidding schemes for both the spot and frequency regulation markets [29]. The lower level represents the joint clearing model for the energy and ancillary service markets, with the objective of minimizing total social costs. It determines the clearing results by considering unit commitment security constraints and economic operating conditions and executes market clearing based on submitted bids. Through iterative interaction between the upper and lower levels, a market equilibrium is ultimately achieved.

In this study, quantities such as generation, pumping, and regulation capacity are uniformly expressed in units of power to ensure consistency in modeling and analysis.

2.3. CFD-Based Competitive Bidding Models for HPSP

For the HPSPs, the energy volume secured through mid-term Contracts for CfDs establishes a fundamental and predictable revenue stream. While this contracted energy is physically delivered through the spot market clearing process, its financial settlement follows a distinct mechanism. The revenue from the CfD-covered energy is derived from the difference between the contracted strike price and the spot market clearing price, multiplied by the corresponding contracted energy volume. Simultaneously, the HPSP generates additional revenue through awarded energy obtained via optimized bidding strategies in the spot market [3]. This component represents the product of the cleared energy quantity and the spot market clearing price, primarily achieved through strategic arbitrage behaviors such as energy storage during low-price periods and generation during high-price periods. Consequently, the total revenue of the HPSP effectively combines these two complementary revenue streams: the financial settlement from CfDs and the physical arbitrage gains from the spot market [5].

In the lower-level market clearing model, CfDs function purely as financial instruments without modifying the physical operational parameters of generation units or system security constraints [7]. The market clearing process determines the spot price independently based on bidding curves submitted by all market participants, including the HPSP. This resulting clearing price is subsequently fed back to the upper-level model, where it serves as a key input for calculating the HPSP’s total profit, incorporating both the CfD-related financial settlements and spot market earnings.

2.4. Model Universality and Cross-Market Applicability Analysis

Although the proposed bi-level decision-making model is primarily developed within the context of China’s electricity market framework [30], its structural design and methodological principles offer considerable international applicability for the following reasons. First, China’s electricity market has incorporated institutional expertise from mature international markets, particularly in market clearing mechanisms that similarly prioritize social welfare maximization and employ integrated energy and frequency regulation ancillary service market clearing [31]. This alignment ensures compatibility between the proposed model’s clearing logic and that of most electricity markets worldwide. Second, in modeling the bidding strategies of the hybrid pumped storage plant, the study adopts reasonable simplifications regarding the behavior of other market participants [32]. These agents are modeled to follow fundamental economic principles rather than relying heavily on jurisdiction-specific rules, thereby enhancing the model’s adaptability to diverse regulatory environments [33]. Owing to these design features, the model retains its relevance for China’s specific conditions while demonstrating significant potential for extension to other electricity market contexts.

3. Mathematical Model

3.1. Upper-Level Operation Model of the Hybrid Pumped Storage Plant

The upper-level model represents the regulation model of the HPSP, with the objective of maximizing total revenue. In this study, the revenue of the HPSP comprises three components: (i) returns from fulfilling mid- to long-term CfDs; (ii) profits from bidding in the day-ahead spot market; and (iii) income from participation in the frequency regulation ancillary services market [26].

The objective function is given by:

$$MAX{\displaystyle \sum }_{t=1}^T\left[Q_{c,t}\left(P_{s,t}-P_c\right)+Q_{a,t}{P}_{s,t}+Q_{fcap,t}{P}_{fcap,t}+Q_{fmile,t}{P}_{fmile,t}\right],$$

(1)

where $Q_{c,t}$ is the contracted electricity under the CfD in period $t$; $P_{s,t}$ is the spot market clearing price in period $t$; $P_c$ is the agreed CfD price; $Q_{a,t}$ is the awarded electricity quantity of the HPSP in period $t$; $Q_{fcap,t}$ is the awarded frequency regulation capacity in period $t$; $P_{fcap,t}$ is the corresponding capacity price; $Q_{fmile,t}$ is the awarded frequency regulation mileage in period $t$; $P_{fmile,t}$ is the corresponding mileage price; and $T$ denotes the total number of periods.

Output Constraints:

$$P_{gen}^{min}\le P_{gen,t}\le P_{gen}^{max},$$

(2)

$$P_{pump}^{min}\le P_{pump,t}\le P_{pump}^{max},$$

(3)

where $P_{gen,t}$ is the generation output in period t, with lower and upper bounds $P_{gen}^{min} \mathrm{and} P_{gen}^{max}$ respectively. Similarly, $P_{pump,t}$ is the pumping output in period $t$, bounded by $P_{pump}^{min}$ and $P_{pump}^{max}$.

Bidding Output Constraints:

$$Q_{a,t}=P_{gen,t}-P_{pump,t},$$

(4)

$$Q_a^{min}\le Q_{a,t}\le Q_a^{mx},$$

(5)

where $Q_{a,t}$ is the awarded electricity of the HPSP in period t, representing net power output (generation minus pumping). The bounds $Q_a^{min}$ and $Q_a^{max}$ are determined by technical output limits.

Reservoir Storage Constraints:

$$V_t=V_{t-1}+{\eta }_p{P}_{pump,t}-{\displaystyle \frac{1}{{\eta }_g}}{P}_{gen,t},$$

(6)

$$V^{min}\le V_t\le V^{max},$$

(7)

where $V_t$ is the reservoir storage level at period t; $V_{t-1}$ is the storage at period t − 1; ${\eta }_p$ is the pumping efficiency; ${\eta }_g$ is the generation efficiency; and $V^{min}$ and $V^{max}$ are the minimum and maximum reservoir storage levels, respectively.

Operating-State Transition Constraints

Minimum generation duration constraint:

$$g_t-g_{t-1}\le s_t,$$

(8)

$${\displaystyle \sum }_{k=t}^{t+T_{gen}^{min}-1}{g}_k\ge T_{gen}^n\left(g_t-g_{t-1}\right).$$

(9)

Minimum pumping duration constraint:

$$p_t-p_{t-1}\le u_t,$$

(10)

$${\displaystyle \sum }_{kt}^{t+T_{pump}^{min}-1}{p}_k\ge T_{pump}^{min}\left(p_t-p_{t-1}\right).$$

(11)

Mutual exclusivity constraint:

$$g_t+p_t\le 1,$$

(12)

where $g_t$ is the generation state variable in period t ($g_t=1$ if generating, otherwise 0), $p_t$ is the pumping state variable ($p_t=1$ if pumping, otherwise 0), $s_t$ is the generation start-up variable, and $u_t$ is the pumping start-up variable. $T_{gen}^n$ and $T_{pump}^{min}$ denote the minimum continuous generation and pumping durations, respectively. These constraints ensure that the HPSP does not switch operating modes too frequently, thereby guaranteeing equipment safety and stability.

3.2. Lower-Level Joint Clearing Model for Multi-Market Participation

The lower-level model represents the joint clearing mechanism for the energy market and the frequency regulation ancillary services market, with the objective of maximizing total social welfare. Within this framework, CfD settlements are calculated based on the price difference between the contracted price and the spot market clearing price, and the associated settlement rules are embedded in the overall market operation mechanism. Based on the framework proposed in [34], this model adopts an integrated clearing approach that simultaneously determines the clearing quantities and prices for both the energy and frequency regulation markets within a unified optimization process. This approach facilitates efficient resource allocation and maximizes overall social welfare. In China’s electricity spot market, which has transitioned to formal operation in several provincial-level pilot programs (including but not limited to Shandong, Shanxi and Guangdong [35,36,37]), social welfare maximization is universally employed as the fundamental objective in their market clearing models.

Objective Function:

$$\min {\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{i=1}^N\left(Q_{s,i,t}{P}_{s,t}+Q_{fcap,i,t}{P}_{fcap,t}+Q_{fmile,i,t}{P}_{fmile,t}+C_{su,i}{y}_{i,t}+C_{sd,i}{z}_{i,t}\right),$$

(13)

where $Q_{s,i,t}$ is the awarded electricity quantity of unit i in the spot market during period t; $P_{s,t}$ is the spot market price in period t; $Q_{fcap,i,t}$ is the awarded frequency regulation capacity of unit i in period t; $P_{fcap,t}$ is the corresponding capacity price; $Q_{fmile,i,t}$ is the awarded frequency regulation mileage; $P_{fmile,t}$ is the mileage price; $C_{su,i}$ and $C_{sd,i}$ are the start-up and shutdown costs of unit i; and $y_{i,t}$ and $z_{i,t}$ are binary variables indicating the start-up and shutdown status of unit i in period t; T is the total number of periods and N is the total number of generating units.

System Power Balance Constraint:

$${\displaystyle \sum }_{i=1}^N{Q}_{s,i,t}=D_t,$$

(14)

where $D_t$ is the total system load demand in period t.

Unit Output Limits:

$$P_i^{min}{u}_{i,t}\le Q_{s,i,t}+Q_{fcap,i,t}+Q_{fmile,i,t}\le P_i^{max}{u}_{i,t},$$

(15)

where $P_i^{min}$ and $P_i^{max}$ are the minimum and maximum technical outputs of unit i, respectively, and $u_{i,t}$ is a binary variable indicating whether the unit is online in period t.

Ramping Constraints:

$$-R_{d,i}\le \left(Q_{s,i,t}+Q_{fcap,i,t}+Q_{fmile,i,t}\right)-\left(Q_{s,i,t-1}+Q_{fcap,i,t-1}+Q_{fmile,i,t-1}\right)\le R_{u,i},$$

(16)

where $R_{d,i}$ and $R_{u,i}$ represent the down- and up-ramp rates of unit i, respectively, i.e., the maximum permissible decrease or increase in output per time step.

Minimum Up/Down Time Constraints:

$${\displaystyle \sum }_{k=t-T_{u,i}+1}^t{y}_{i,k}\le u_{i,t},$$

(17)

$${\displaystyle \sum }_{k=t-T_{d,i}+1}^t{z}_{i,k}\le 1-u_{i,t},$$

(18)

where $T_{u,i}$ and $T_{d,i}$ represent the minimum up- and down-time requirements of unit i, ensuring continuous operation or shutdown for at least the specified number of periods.

Maximum Number of Start-ups and Shutdowns:

$${\displaystyle \sum }_{t=1}^T{y}_{it}\le N_{su,i},$$

(19)

$${\displaystyle \sum }_{t=1}^T{z}_{i,t}\le N_{sd,i},$$

(20)

where $N_{su,i}$ and $N_{sd,i}$ are the maximum allowable start-up and shutdown counts for unit $i$ within the scheduling horizon, respectively.

3.3. Model Complexity and Tractability Analysis

The proposed bilevel optimization model is classified as an NP-hard problem. Both levels constitute Mixed-Integer Linear Programming (MILP) problems due to the presence of binary decision variables. The upper-level model incorporates binary variables representing the operational states of the pumped storage unit, while the lower-level model involves binary variables for thermal unit commitment decisions. The interconnection between these two levels through market-clearing prices creates a computationally challenging bilevel MILP structure. According to established computational complexity theory [38], even simplified versions of single-level unit commitment problems have been proven NP-hard. In our formulation, the introduction of state transition constraints for the HPSP facility and minimum uptime/downtime constraints for conventional units significantly exacerbates the combinatorial complexity, making exact algorithms computationally prohibitive for practical-scale problems.

The model exhibits inherent non-convex characteristics originating from multiple sources. In the upper-level problem, the reservoir dynamics contain nonlinear terms and, while the state transition logic operating-state transition constraints introduces discrete nonlinearities. For the lower-level problem, the inclusion of start-up and shutdown costs in the lower-level objective function creates a fixed-cost structure that inherently leads to non-convexity. Furthermore, the minimum generation constraints combined with unit commitment logic form a non-convex and discontinuous feasible set. Although some nonlinearities can be addressed through linearization techniques using big-M methods, the fundamental non-convex nature of the original problem persists [39]. This non-convexity precludes the direct application of traditional convex optimization techniques and necessitates specialized global optimization approaches.

Given the NP-hard nature and non-convex structure of the problem, the selection of the NSGA-II multi-objective evolutionary algorithm is theoretically justified. NSGA-II operates based on Pareto dominance relationships without relying on convexity or differentiability assumptions of the objective functions, enabling effective handling of non-convex and nonlinear Pareto fronts [40]. The algorithm’s population-based approach with genetic operators (crossover and mutation) provides global exploration capability to escape local optima. Moreover, its constraint-handling mechanism through the constraint-domination principle can directly manage complex constraints such as reservoir capacity constraints and ramping constraints. While NSGA-II cannot guarantee global optimality, it has been demonstrated to provide high-quality approximate Pareto sets for practical engineering applications, particularly in power system optimization problems [41].

4. Model Solution Approach

The proposed bi-level model constitutes a multi-stage optimization problem incorporating complex hydroelectric and power system constraints. To solve this problem efficiently, a hybrid approach is adopted that integrates the Non-dominated Sorting Genetic Algorithm II (NSGA-II) with a commercial mathematical programming solver.

In solving this bi-level electricity market optimization problem, the NSGA-II algorithm demonstrates superior applicability compared to MOEA/D and SPEA2. Unlike the decomposition-based mechanism of MOEA/D, NSGA-II employs a non-dominated sorting approach that requires no predefined weight vectors, enabling more natural handling of the complex trade-offs between revenue and social costs while avoiding solution bias caused by improper weight settings [42]. Compared to SPEA2, NSGA-II features a fast non-dominated sorting mechanism with lower computational complexity, significantly enhancing solution efficiency while maintaining population diversity—a crucial advantage for computationally expensive bi-level optimization problems. Furthermore, the uniformly distributed Pareto front generated by NSGA-II’s crowding distance operator, combined with its robustness in handling complex constraints, makes it an ideal choice for solving such multi-objective electricity market problems [43].

Specifically, the NSGA-II algorithm is used to iteratively update the generation and pumping schedules, as well as the bidding strategies, of the HPSP, while the market clearing problem is solved using a commercial solver (e.g., CPLEX) to determine energy and ancillary service clearing prices and quantities.

By maintaining a diverse Pareto-optimal solution set, the method captures the trade-offs between the upper- and lower-level objectives. The application of an elitist strategy and fast non-dominated sorting ensures that the evolutionary process consistently advances toward high-quality solution regions. A crowding-distance operator is employed to preserve population diversity and prevent premature convergence. In addition, a two-layer chromosome encoding scheme is designed to directly represent the coupling between upper-level bidding strategies and lower-level unit commitment decisions. A constraint-repair mechanism is applied to efficiently manage complex operational constraints, such as ramping limits, minimum up/down times, and reservoir balance, thereby ensuring that the resulting schedules are both economically efficient and technically feasible within a finite number of iterations.

The solution procedure is as follows.

• Initialization of Outer-Level NSGA-II Parameters

Set the population size N = 100, maximum number of generations $G_{max}=300$, crossover probability $p_c=0.9$, and mutation probability $p_m=0.2$. Randomly generate the initial population, where each individual represents a bidding strategy of the HPSP: $[{p_t^{\mathrm{offer}},c_t^{\mathrm{offer}},s_t^{\mathrm{offer}}]}_{t=1}^{\mathrm{T}}$ including generation, pumping, and ancillary service offers over the entire scheduling horizon.

2.

Inner-Level Optimization (Social Cost Minimization)

For each individual in the outer population, fix the bidding strategy ($p_t^{\mathrm{offer}},c_t^{\mathrm{offer}}$) as boundary conditions, and solve the lower-level model using a MILP solver. The solution yields unit commitment and dispatch decisions $x_{i,t}$, $p_{i,t}$, spot market clearing prices ${\lambda }_t$, ancillary service prices ${\mu }_t$, and total social procurement cost C.

3.

Computation of Bi-Level Objective Values

The upper-level objective (HPSP revenue) is given by:

$$R_{\mathrm{HPS}}={\displaystyle \sum }_{t=1}^T\left({\lambda }_t{p}_t^{\mathrm{bid}}-{\lambda }_t{c}_t^{\mathrm{bid}}+{\mu }_t{s}_t^{\mathrm{bid}}\right).$$

(21)

The lower-level objective is the total social cost C.

Construct the bi-objective minimization vector:

$$F=\left(-R_{\mathrm{HPS}},C_{\mathrm{soc}}\right).$$

(22)

4.

Fast Non-Dominated Sorting

Perform fast non-dominated sorting on the population to identify Pareto dominance relationships and classify individuals into Pareto fronts, where Rank 1 corresponds to the best non-dominated front.

5.

Crowding Distance Calculation

For individuals in the same Pareto front, compute the normalized crowding distance in the objective space:

$$\mathrm{crowding}\left(i\right)={\displaystyle \sum }_{m=1}^2{\displaystyle \frac{\left|f_m\left(i+1\right)-f_m\left(i-1\right)\right|}{f_m^{\max }-f_m^{\min }}}.$$

(23)

6.

Selection

Apply binary tournament selection: randomly select two individuals and choose the one with the lower Rank; if both individuals have the same Rank, select the one with the greater crowding distance.

7.

Genetic Operators

Simulated Binary Crossover:

$${\beta }_k^{\mathrm{child}}=0.5\left[\left(1+{\beta }_q\right){\beta }_k^{\mathrm{p}1}+\left(1-{\beta }_q\right){\beta }_k^{\mathrm{p}2}\right].$$

(24)

Polynomial Mutation:

$${\beta }_k^{\prime }={\beta }_k+\left({\beta }_k^{\mathrm{U}}-{\beta }_k^{\mathrm{L}}\right){\overline{\delta }}_k.$$

(25)

8.

Elitist Preservation

Merge the parent and offspring populations (resulting in a total size of 2N), perform non-dominated sorting on all individuals, and construct the next generation by selecting individuals in order of increasing Rank. If multiple individuals share the same Rank, prioritize those with higher crowding distances.

9.

Termination Criterion

The algorithm terminates when either the maximum number of generations ($G_{max}$) is reached or the Pareto front converges, as indicated by a hypervolume change rate below ϵ. If neither condition is met, return to Step 2 and continue the evolutionary process.

5. Case Study and Numerical Analysis

5.1. Parameter Settings

To verify the effectiveness of the proposed model, a 24 h scheduling horizon is considered. The system load profile is proportionally scaled to match the total system generation capacity. An HPSP, along with nearby wind farms, photovoltaic (PV) plants, and thermal power plants, is selected as the case study system.

The HPSP reservoir has a total storage capacity of $2.0\times {10}^9{\mathrm{m}}^3$, with a normal water level of 355 m and a dead water level of 330 m. The station is equipped with conventional generating units with a total installed capacity of 500 MW and reversible units with a capacity of 300 MW. A bilateral long-term CfD is assumed, with a contracted electricity price of 450 CNY/MWh and a contracted energy quantity of 3840 MWh. These contractual parameters were determined based on historical CfD data from the normal water storage period of the plant, representing characteristic values for contract price and volume.

The system also includes three thermal power plants. Due to their relatively high generation costs, their bidding prices are set significantly higher than those of other market participants. To reflect cost structure heterogeneity, each thermal power plant submits energy bids equal to its installed capacity. Detailed parameters of the thermal units are presented in

Table 1. Parameters of the thermal power plant.

Power Plant Type	Installed Capacity (MW)	Ramp Rate (MW/h)	Minimum Bid Price ($/MWh)
Thermal Unit 1	1500	300	340
Thermal Unit 2	1000	200	340
Thermal Unit 2	800	100	300

.

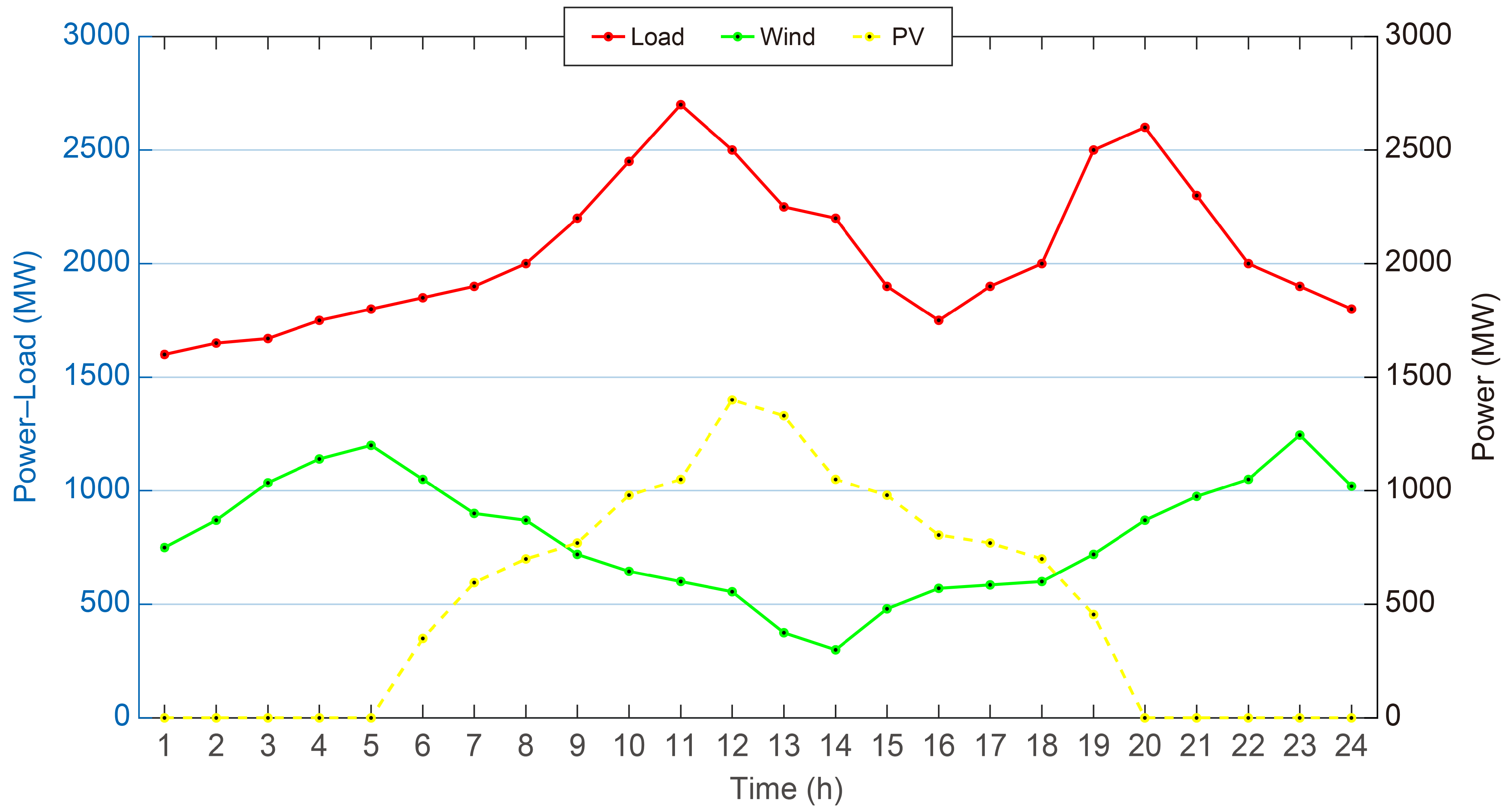
Additionally, one PV plant and one wind farm are connected to the system. Their stochastic output characteristics are shown in Figure 3. On the demand side, only power quantities are submitted, without price bids, and the declared power demand follows the forecasted load profile.

The spot market bidding curve is designed with reference to actual market conditions in a specific region. The bidding and offering rules for the frequency regulation market are summarized in

Table 2. Regulation market bidding rules.

	Eligible FR Capacity Ratio	Bid Price ($/MWh)	Clearing Price ($/MWh)
Coal-fired Unit	3–6%	(5, 15]	(5, 15]
Gas-fired Unit	10–20%	(5, 15]	(5, 15]
Conventional Hydro Unit	10–20%	(5, 15]	(5, 15]
Reversible Unit	10–20%	(5, 15]	(5, 15]

. For frequency regulation units that do not participate in market bidding, a default bid price of 6 CNY/MW is assumed.

5.2. Comparative Analysis of Algorithm Performance

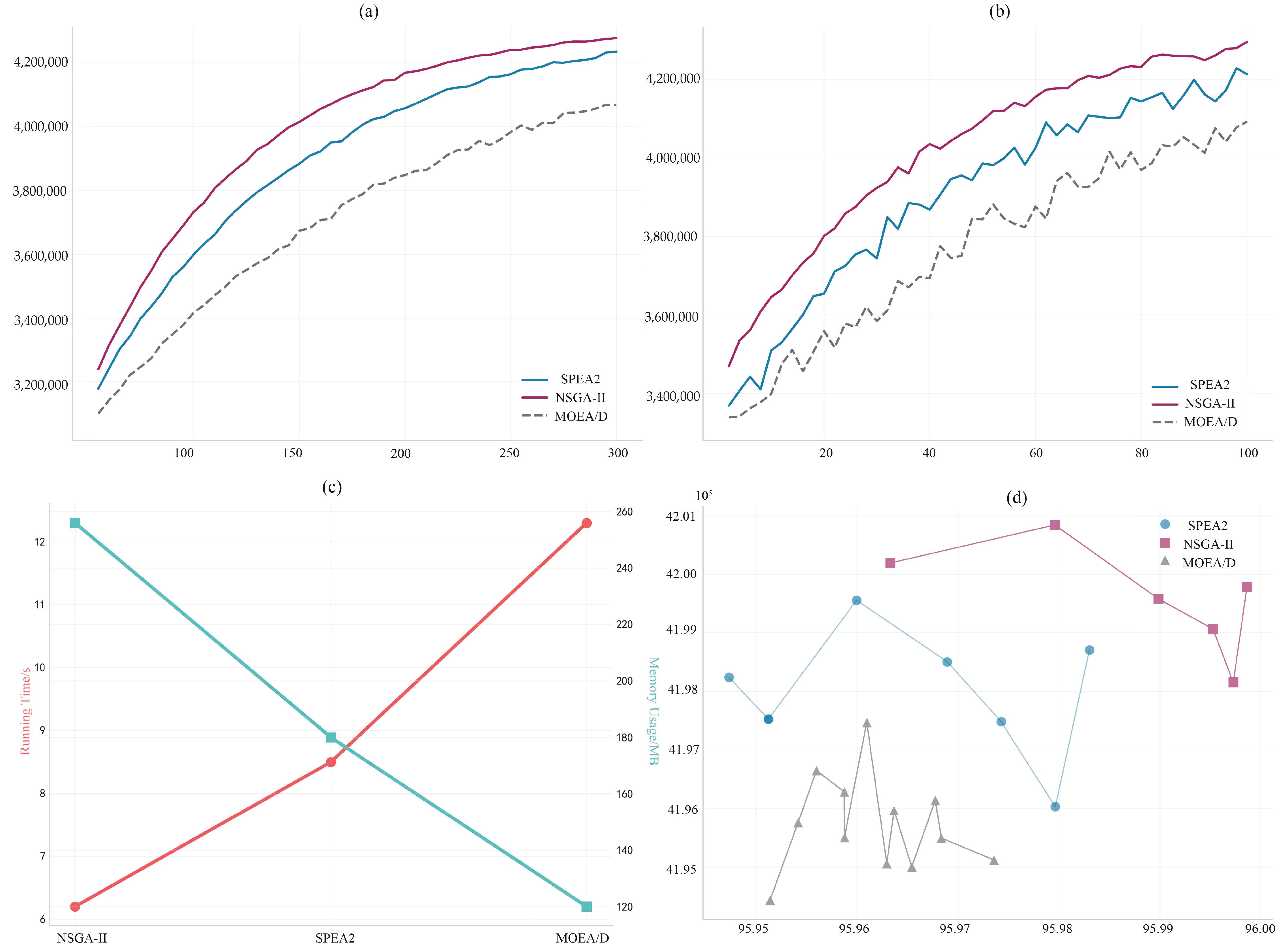
Figure 4 presents a comparative analysis of the performance metrics among three multi-objective evolutionary algorithms: MOEA/D, NSGA-II, and SPEA2. The results demonstrate that although NSGA-II requires the highest memory consumption, it achieves superior convergence speed and produces higher-quality Pareto-optimal solutions compared to the other two algorithms. These findings validate the rationality of selecting NSGA-II for solving the proposed bilevel optimization problem and offer valuable insights for algorithm design in addressing similar complex optimization challenges in the future.

5.3. Market Clearing Results of the Power Plant

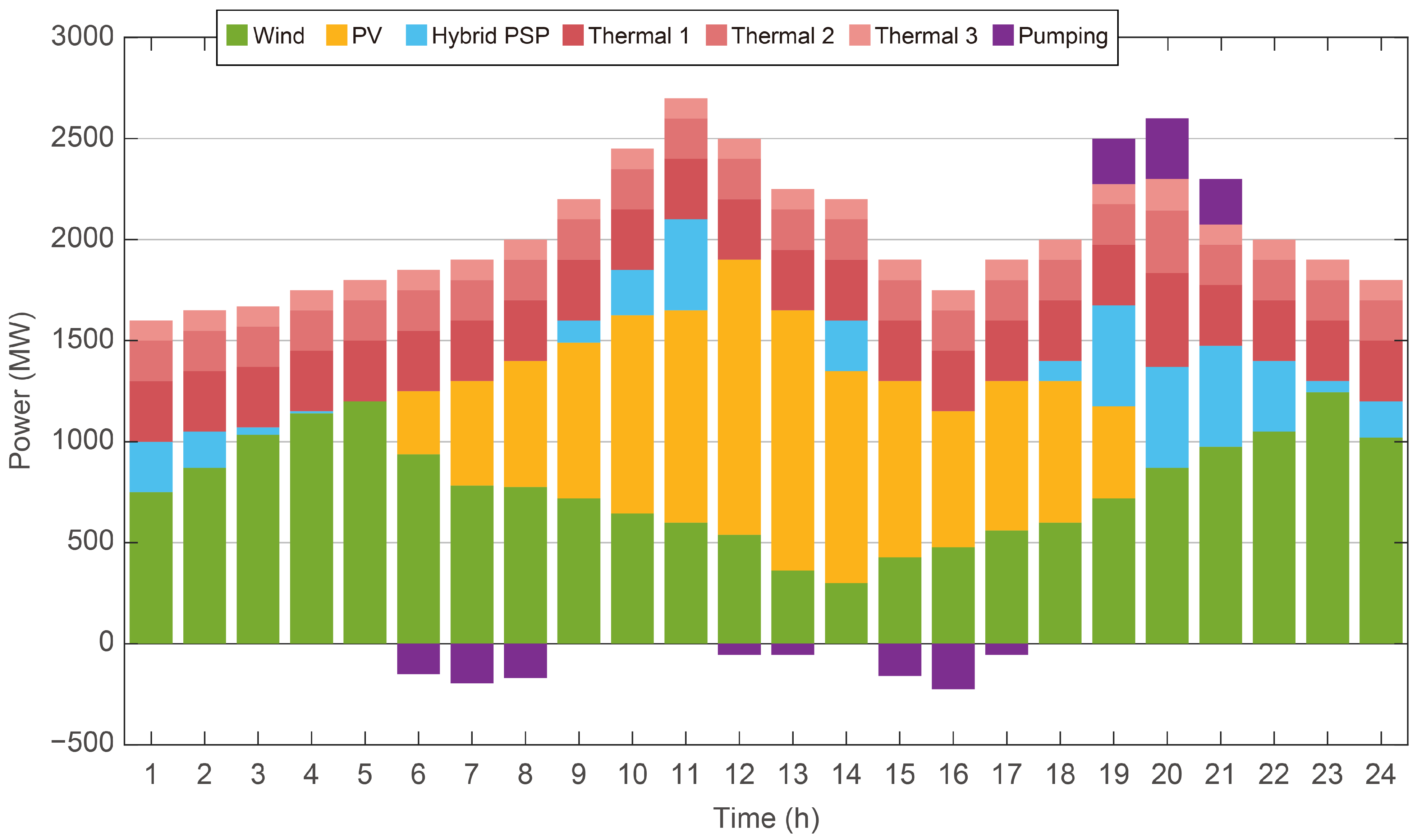
The awarded electricity quantities of different units in the spot and frequency regulation markets are shown in Figure 5. As illustrated, when wind and solar generation account for 63.17% of the total market share, thermal power units operate at their minimum output levels during 95.89% of the scheduling periods. From 01:00 to 05:00, as wind power output gradually increases, conventional hydropower units reduce their generation to prioritize the consumption of renewable energy. Between 06:00 and 08:00, PV generation begins, and although wind generation decreases slightly, the increase in load demand is insufficient to absorb the additional PV output. This results in excess supply and a decline in electricity prices, during which the reversible units shift to pumping mode, with an average pumping power of 170 MW. From 09:00 to 11:00, the rising demand cannot be fully met by thermal and renewable generation alone, requiring conventional hydropower units to increase their output. During the evening peak from 18:00 to 20:00, when demand reaches its highest level and PV generation phases out, the conventional units of the HPSP operate at full capacity. Meanwhile, the reversible units bid near their rated capacity and successfully clear the market during peak hours.

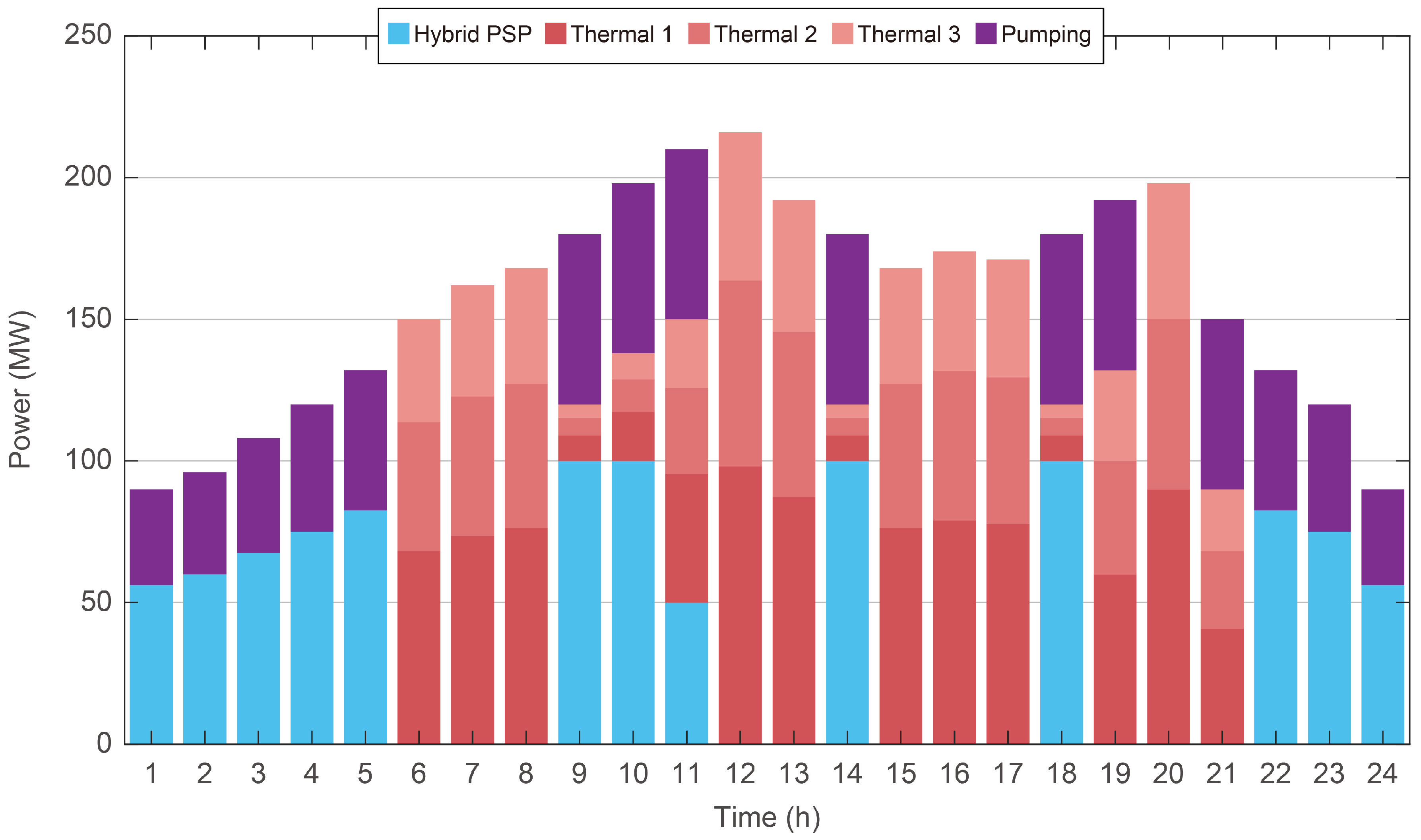
In the frequency regulation market, Figure 6 shows that hydropower units account for 46.54% of the total market share. Specifically, conventional hydropower units participate at their maximum declared capacity of 100 MW during 66.7% of the time periods, after fulfilling renewable energy absorption requirements. The reversible units also receive frequency regulation awards whenever they are not operating in pumping mode. The only exception occurs at 20:00, when both conventional and reversible units are fully committed in the spot market; under these conditions, frequency regulation is exclusively provided by thermal units.

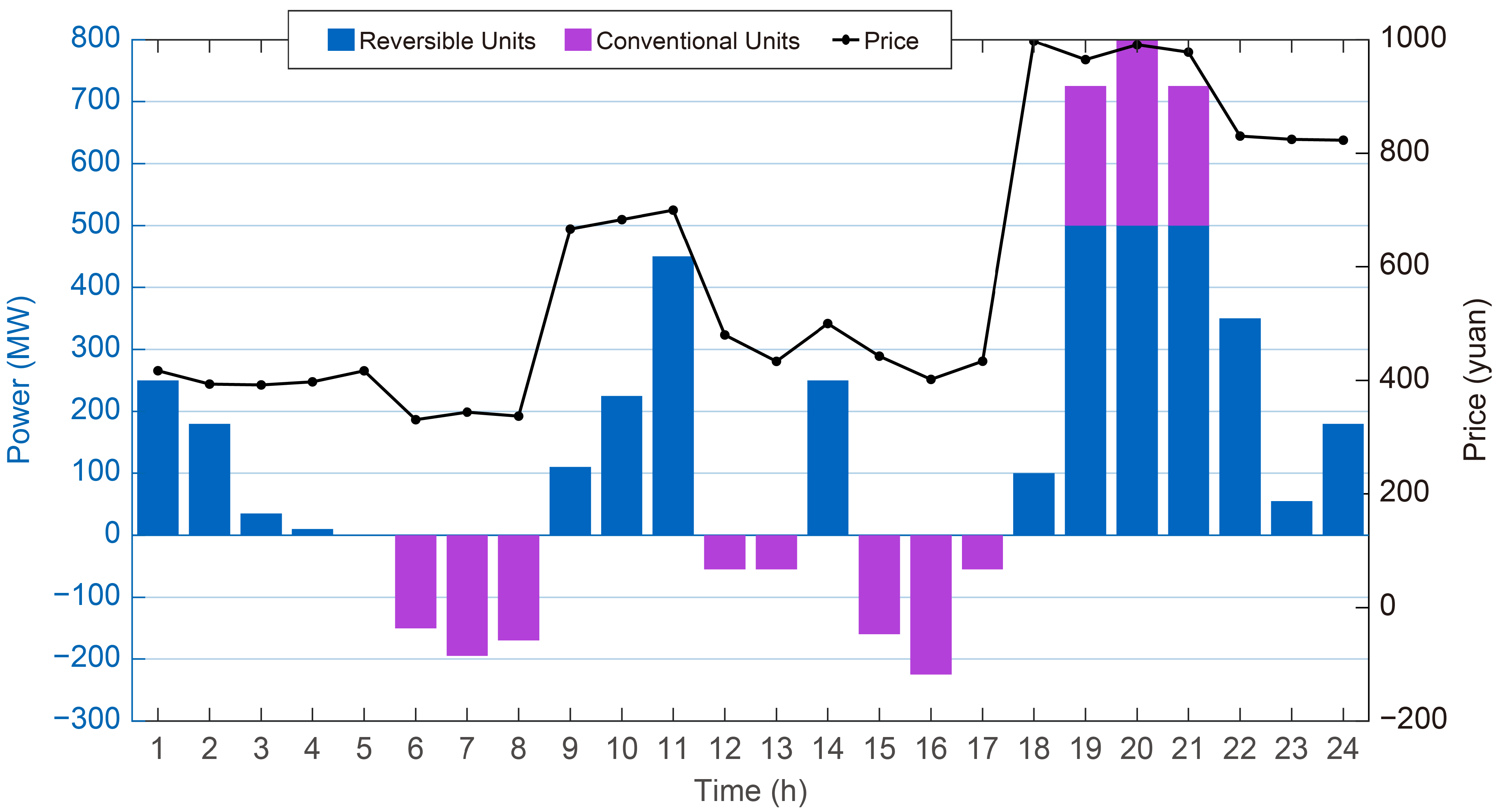
In the spot market, Figure 7 illustrates that the HPSP generally adopts a strategy of “pumping during low-price hours and generating during high-price hours.” Between 11:00 and 17:00, the HPSP adjusts its operation flexibly in response to real-time price fluctuations, maintaining a dispatch pattern closely aligned with the price trend. From 19:00 to 21:00, after the complete absorption of renewable energy and with thermal units operating at their minimum output levels, the remaining demand is met through a combination of thermal ramp-up and increased hydropower generation. Due to their lower bidding prices, hydropower units are prioritized in market clearing. During this period, both the conventional and reversible units of the HPSP operate at full generation capacity.

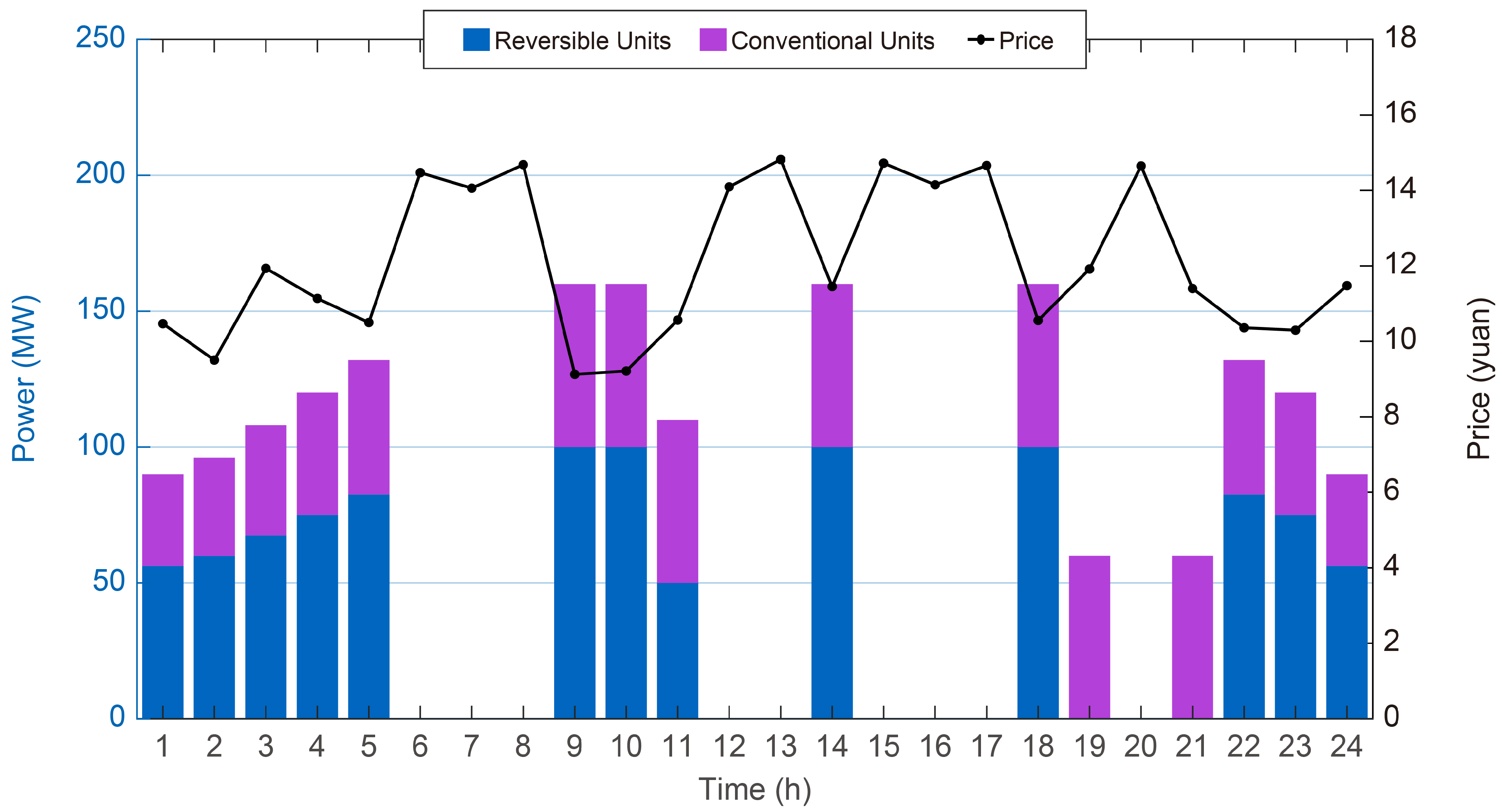
In the frequency regulation market, Figure 8 indicates that, due to operational constraints, the HPSP cannot provide frequency regulation services during pumping periods. As a result, such services are fully provided by thermal units, leading to relatively higher clearing prices. However, during generating periods, both conventional and reversible units of the HPSP capture a dominant share of the regulation market owing to their operational flexibility and lower regulation costs. Although their bidding prices are slightly above the default clearing value of 6 CNY/MW, they remain substantially lower than those of thermal units, highlighting their competitive advantage and economic efficiency.

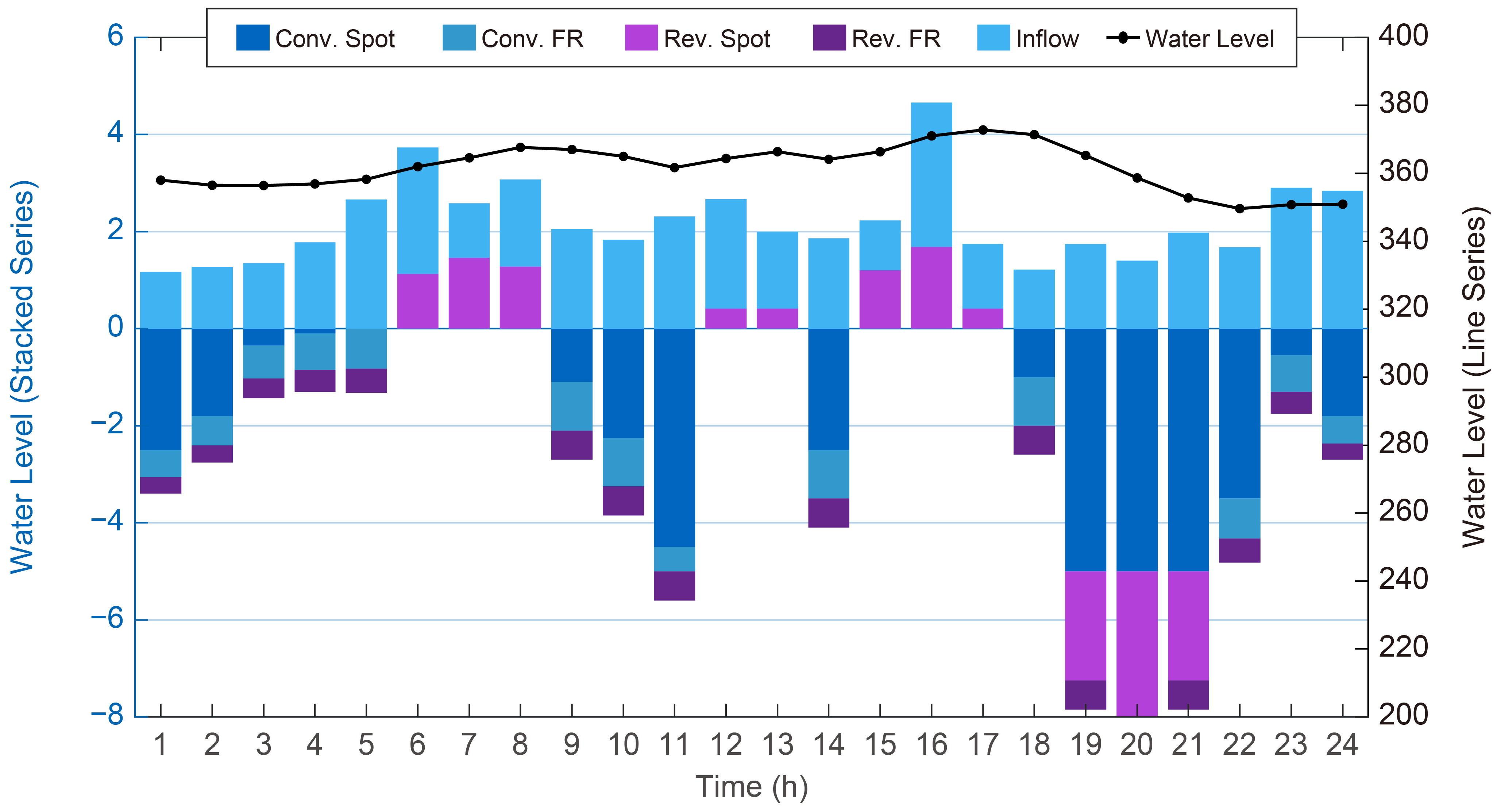
5.4. Reservoir Water Level Variations

As shown in Figure 9, the overall operational strategy of the HPSP is to pump water during periods of abundant renewable generation and low electricity prices, and to release water for generation during peak demand hours—thus achieving temporal energy shifting and value enhancement. Before 08:00, system demand remains low while wind and solar output continues to increase. During this time, the reversible units pump water in conjunction with natural inflows, raising the upper reservoir level to a first peak of approximately 367.6 m. From 09:00 to 11:00, as system demand rises, both conventional and reversible units generate simultaneously, causing the water level to decline to 361.2 m. During 12:00–14:00, the water level stabilizes around 365 m. Between 15:00 and 17:00, reduced demand allows the reversible units to resume pumping, pushing the reservoir level to a second peak of approximately 372.7 m. After 18:00, with PV generation ceasing and limited additional wind output, system demand reaches its evening peak. Both conventional and reversible units operate continuously, lowering the reservoir level to 354.5 m—only 0.97% below its initial level. This operational trajectory demonstrates the multi-timescale flexibility of the HPSP and underscores its critical role in supporting renewable energy integration.

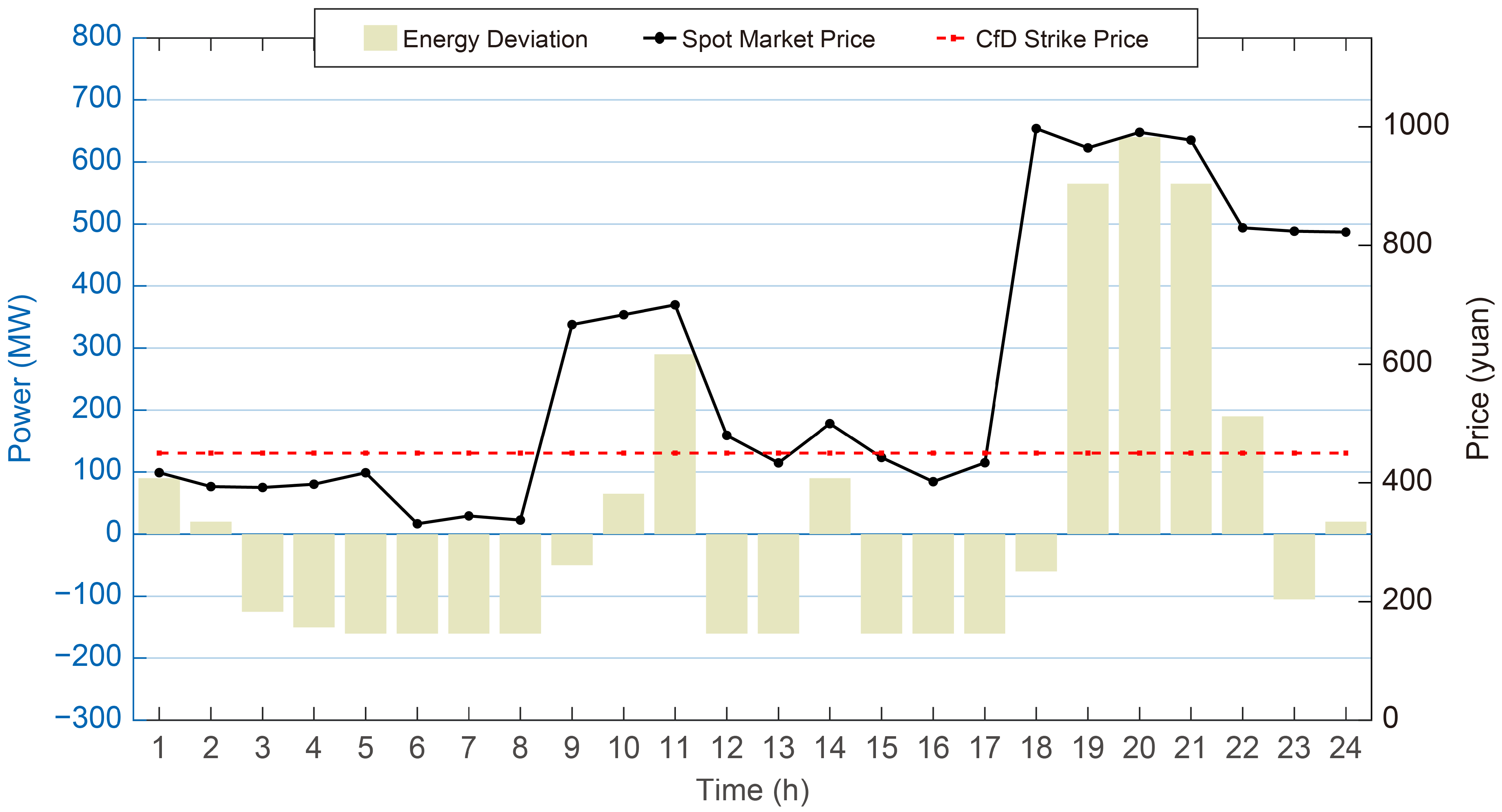
5.5. Contract for Difference Performance Analysis

As illustrated in Figure 10, the HPSP exhibits four typical CfD compliance states under varying operating conditions.

03:00–08:00: The spot price is lower than the CfD contract price, and the HPSP does not fulfill its contractual output. During this period, abundant renewable generation suppresses market prices. According to CfD settlement rules, the shortfall is treated as though the plant sold electricity at the contract price and repurchased the shortfall at the lower spot price—thereby earning a profit from the price differential.

09:00 and 12:00: Although spot prices exceed the contract price, the HPSP is unable to meet the contracted output. This situation typically arises during periods of load growth when renewable generation dominates but remains insufficient. In such cases, the shortfall results in financial losses, as electricity must be procured at higher spot prices and settled at the lower contract price.

01:00–02:00: The spot price is below the contract price, and the HPSP successfully fulfills its contractual obligations. With lower renewable output, hydropower generation supplies the required energy. Any surplus generation beyond the contracted quantity is sold at the prevailing, lower spot price.

19:00–22:00: The spot price exceeds the contract price, and the HPSP fully satisfies its contractual obligations. This period corresponds to the evening demand peak, characterized by diminished renewable output and heightened system flexibility requirements. Surplus energy is sold at high spot prices, resulting in substantial profits and demonstrating the market incentive of “more generation, more profit.”

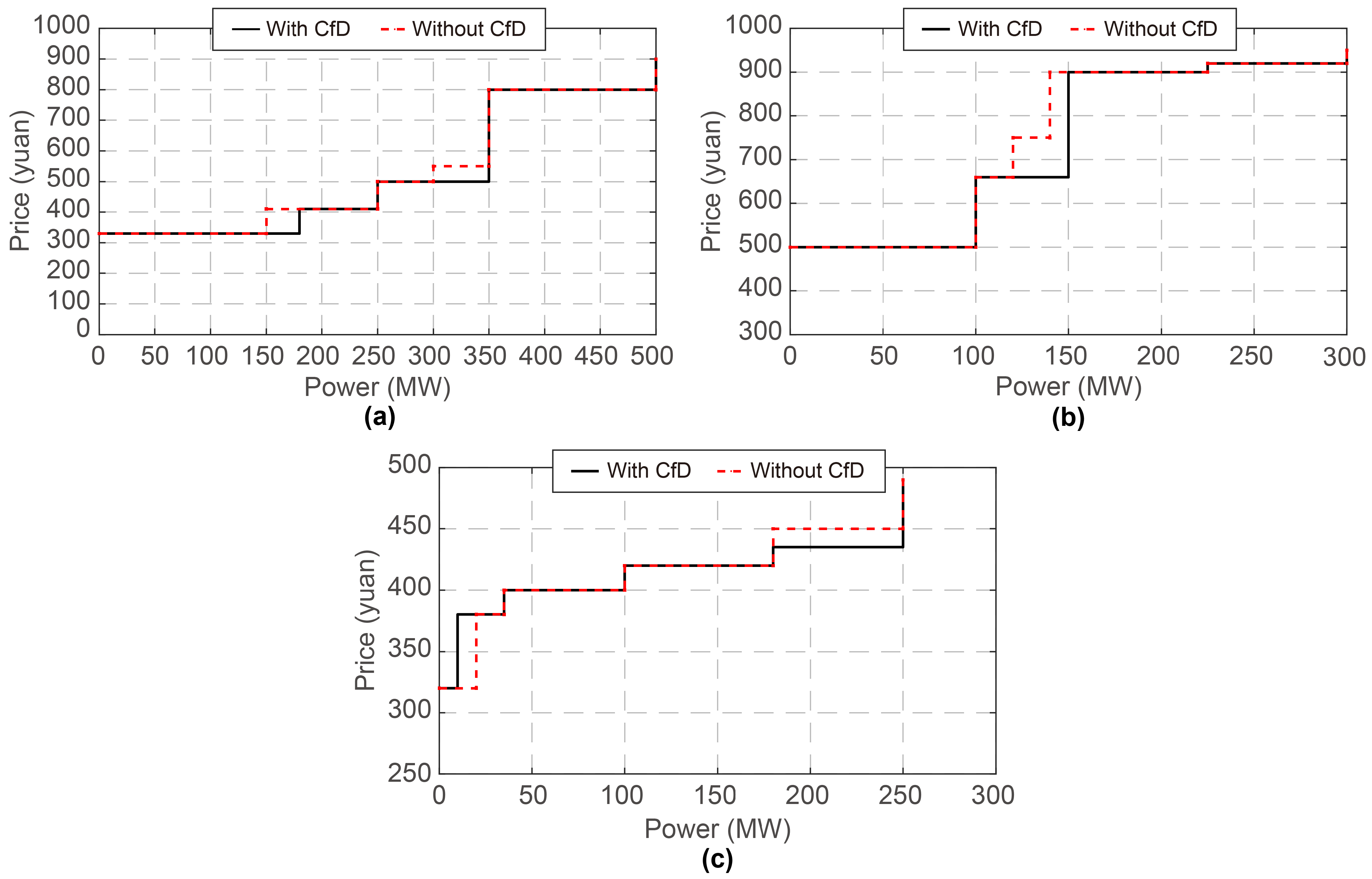
As illustrated in Figure 11, the number and placement of steps in the bidding curves vary, reflecting differences in both output levels and pricing strategies. Although all models aim to maximize overall utility, the resulting bidding behaviors differ significantly due to the distinct factors considered within each model. Notably, the day-ahead bidding model that incorporates CfD settlement rules has a substantial impact on bidding strategies.

Specifically, aside from pumped storage units—which avoid bidding during off-peak, low-price hours—conventional units exhibit distinct peak–valley bidding patterns depending on the presence of CfDs. For both conventional and pumped storage units, in the absence of CfDs, bidding strategies during peak periods tend to be more aggressive, as there is no contractual price guarantee and plants must rely more heavily on capturing peak–valley price spreads to generate revenue. In contrast, during off-peak periods, the bidding flexibility of conventional units is relatively constrained, resulting in flatter bidding curves.

5.6. Sensitivity Analysis of Revenue to Hydrology and Contract for Differences

Table 3. Hybrid pumped storage power plant income statement.

	Pumping	Spot Market	Frequency Regulation
With CfD	−409,466.12	4,296,200.17	17,870.40
Without CfD	−409,466.12	3,226,771.95	17,870.40

CfD: Contracts for difference.

summarizes the profitability of the HPSP under various market participation scenarios, including CfD, spot, and frequency regulation markets. Results indicate that the plant earns 3.2268 million CNY through participation in the spot market alone. When both CfD and spot market participation are considered, total revenue increases to 4.2962 million CNY. After deducting pumping costs of 0.4095 million CNY, the net revenue rises substantially—representing an improvement of approximately 33.2% compared with the spot-only scenario. Additionally, participation in the frequency regulation market contributes 0.0179 million CNY.

Table 4. Revenue Distribution Across Characteristic Water Periods.

Characteristic Water Period	Contract Revenue	Spot Market Revenue
Dry Season	1,700,000	200,000
Normal Season	1,566,000	4,296,200.17
Wet Season	1,400,000	5,500,000

Note: All calculations are based on a Contract for Difference (CfD) with 85% of total generation allocated to the contract at a strike price of 450 CNY/MW, serving as the benchmark scenario.

illustrates the adaptive bidding strategies employed by the HPSP across different hydrological periods. During the dry season, limited water inflow prompts a defensive strategy, where the plant significantly increases its mid- to long-term CfD allocation to secure stable revenue and mitigate market risks. Consequently, contract-based revenue reaches its peak while spot market earnings remain minimal. In contrast, the wet season, characterized by abundant water resources, facilitates an aggressive strategy. The plant reduces its contracted energy volume to enhance operational flexibility, enabling it to capitalize on high-price opportunities in the spot market and maximize spot revenue. A balanced approach is adopted during normal water storage periods, aiming to harmonize the stability of contracted revenue with the profit potential of the spot market. This study underscores the necessity for the plant to dynamically optimize its energy allocation based on hydrological forecasts to achieve maximum lifecycle profitability.

Table 5. Impact of CfD Energy Percentage on Revenue Distribution.

CfD Energy as % of Total	Contract Revenue	Spot Market Revenue
10%	184,235.29	25,777,201.02
40%	736,941.18	17,184,800.68
60%	1,105,411.76	11,456,533.79
85%	1,566,000.00	4,296,200.17
100%	1,842,352.94	0.00

Note: All calculations are based on a CfD strike price of 450 CNY/MW during the normal season.

and

Table 6. Impact of CfD Strike Price on Revenue.

CfD Strike Price (CNY/MW)	Contract Revenue	Spot Market Revenue
200	309,400.00	17,821,000.68
300	696,000.00	12,410,000.00
450	1,566,000.00	4,296,200.17
650	2,661,176.00	0.00
800	3,275,294.00	0.00

Note: All calculations are based on normal hydrological conditions with 85% of total generation allocated to CfDs.

reveal a significant trade-off between the proportion of CfD-committed energy and the revenue structure of the plant. As the share of contracted energy increases, the corresponding contract revenue grows linearly; however, this marginal gain is counterbalanced by an accelerated decline in spot market revenue. The underlying mechanism is that a higher CfD allocation reduces the flexible energy capacity available for arbitrage (e.g., pumping during low-price periods and generating during high-price periods), thereby constraining the plant’s ability to exploit real-time price fluctuations and capture excess profits. Thus, under given market conditions, an optimal CfD energy ratio exists that maximizes total revenue. Over-reliance on the certainty of contracted volumes may consequently lead to potential losses in overall profitability.

From a structural standpoint, the CfD and spot markets serve as the primary revenue sources, jointly accounting for over 99% of total income. This underscores the central role of the energy market in determining overall profitability. The pumping costs highlight the need for operational efficiency, while ancillary services—although contributing a smaller portion—offer supplementary value by enhancing system flexibility. Overall, the coordinated participation of HPSPs in “CfD + spot + ancillary service” markets not only maximizes economic returns but also provides a stable path toward cost recovery and sustainable operation. Therefore, it is recommended that HPSPs optimize pumping efficiency and strategically coordinate across multiple electricity markets to enhance profitability.

6. Conclusions

a. The proposed bi-level optimization model effectively demonstrates the feasibility and economic advantages of HPSPs participating in coordinated multi-market operations—including long-term contracts, spot markets, and frequency regulation—within a CfD framework. The model offers a robust theoretical foundation and decision-making support for maximizing HPSP revenues under complex market conditions.

b. Simulation results indicate that the integration of CfDs significantly enhances the revenue-generating potential of HPSPs in the spot market, with profits increasing by approximately 33.2% compared to the spot-only participation scenario. By securing contracted electricity volumes and prices, CfDs serve as effective financial instruments for hedging against spot price volatility and improving overall profit stability.

c. In power systems with high penetration of wind and solar generation, HPSPs demonstrate strong adaptability and operational flexibility. They can absorb surplus renewable energy during low-demand periods and release stored energy during peak hours, thereby contributing to system balance and supporting the secure, reliable operation of the grid.

7. Future Work

a. Future research should focus on incorporating multiple uncertainties—such as renewable energy output and electricity price volatility—into the decision-making framework. Advanced probabilistic modeling or robust optimization techniques could be employed to enhance the model’s applicability in real-world stochastic environments.

b. The current model may be extended to account for strategic interactions with other market participants. Integrating game-theoretic approaches would enable more realistic simulations of oligopolistic markets and strategic bidding behaviors.

c. Further studies could incorporate transmission-level constraints, such as nodal pricing and network congestion effects. This extension would improve the physical representation of market clearing and support regional coordination of HPSP operations.