Morphological Controlling Factors of Braided River Reservoir Based on Delft3D Sedimentary Numerical Simulation: Application to Ordos Basin, China

Abstract

To reveal the regulatory mechanisms and differences in sensitivity of hydrodynamic forces and sediment parameters to the sedimentary evolution of braided river channel bars, this study takes the Sulige Gas Field as a case study and conducts 21 sets of sedimentary numerical simulation experiments using the controlled variable method. The three parameters of discharge, slope gradient, and sediment grain size were fixed, while the target variable was adjusted iteratively. After the river reaches a steady state, quantitative statistics of the area and length-width ratio of 547 identified channel bars are carried out, and sensitivity evaluation is performed by combining principal component analysis and multiple linear regression. The results show that the sedimentary evolution of braided rivers follows a unified evolutionary law, the evolution of channel bars is synergistically regulated by parameter combinations. Under the action of single factors, an increase in discharge promotes the axial extension and scale expansion of channel bars; an increase in grain size enhances the morphological stability of channel bars; slope gradient controls the erosion-deposition balance through gravitational potential energy. The parameter sensitivity is ranked as slope gradient, discharge, sediment grain size.

1. Introduction

As widely distributed geomorphic units in terrestrial environments, braided rivers produce sedimentary features known as channel bars, which serve not only as preferential reservoir units for resources such as oil and gas but also as carriers of key historical information regarding fluvial sedimentary evolution [1,2,3]. Clarifying the developmental patterns of channel bar morphology is critical for explaining fluvial sedimentary processes and predicting sedimentary evolution; furthermore, as vital reservoir hosts for resources like oil and gas, the sedimentary morphology of channel bars directly influences key development parameters, including reservoir permeability and fluid migration efficiency. Conducting numerical simulation studies is therefore not only fundamental to fine-scale reservoir characterization but also aligns with practical demands for efficient resource utilization [4,5,6]. In recent years, qualitative or semi-quantitative investigations have been conducted via approaches such as natural river observations and simulation experiments [7,8,9,10,11,12,13,14]. However, existing numerical simulations of braided river sedimentation exhibit certain limitations [15,16], Li et al. (2023) developed a numerical model of sandy braided rivers based on Delft3D and verified the controlling effect of slope gradient on channel bar migration rates through 28 experimental sets. Nevertheless, their study employed only the “slope gradient-discharge” two-parameter system, failed to incorporate the synergistic influence of sediment grain size, and did not establish a quantitative functional relationship between channel bar area and the parameters [17]. Guo et al. (2025) performed sedimentation simulations of sandy braided rivers under varying discharge conditions and observed that high discharge enhances the overlapping frequency of channel bars. However, their analysis focused solely on the independent effect of discharge as a single factor, omitted the quantification of coupling weights for slope gradient and sediment grain size, and did not address the response patterns of morphological parameters [18]. Feng et al. (2025) derived a semi-empirical formula linking channel bar scale to hydrodynamic intensity through quantitative flume experiments; however, these experiments were conducted under ideal laboratory conditions and did not extend to multi-parameter dynamic evolution scenarios over geological time scales via numerical simulations [19].

Existing research on braided rivers primarily focuses on fluvial evolution mechanisms or the impacts of individual parameters on channel sandbodies [7,14,20], and has not systematically analyzed the synergistic regulatory relationships among discharge, slope gradient, and sediment grain size. This gap prevents the effective interpretation of the complete evolutionary process of sandbars under the combined action of multiple factors in natural channels. Additionally, quantitative functional relationships between topography, discharge, sediment grain size, and channel bar morphology remain unestablished, which constrains the accurate understanding of braided river sedimentary processes.

By virtue of its ability to construct reproducible models of complex sedimentary processes and achieve precise control over multiple variables, sedimentary numerical simulation technology has become a core approach to overcoming the limitations of traditional research methods and deeply analyzing the developmental mechanisms of braided river channel bars. Among various simulation tools, those based on physical principles include Delft3D software version 4.04.01, are most widely applied [21,22,23,24]. Delft3D software relies on a hydrodynamic simulation framework built on the Navier–Stokes equations, enabling it to accurately simulate the dynamic changes in fluvial sedimentation under different sedimentary conditions. It has demonstrated unique advantages in the quantitative study of fluvial geomorphology and sedimentary processes [14,17,18,20,25]. Given that the coupled driving effects of topography, hydrodynamics, and sediment grain size on channel bar morphology have not yet been systematically quantified and explained, this study employs Delft3D software to design multiple sets of simulation experiments covering different topographic gradients, discharges, and sediment grain sizes. The aim is to systematically explore the developmental patterns of braided river channel bars under the synergistic action of multiple factors, establish a predictive equation for the area of braided river channel bars, provide a scientific basis for establishing quantitative relationships between “topography-hydrodynamics-sediment properties” and channel bar morphology, and offer theoretical and data support for advancing the theory of braided river sedimentary dynamics.

2. Materials and Methods

2.1. Sedimentary Numerical Simulation Experimental Scheme

This study conducts research on the influencing factors of braided river channel bars based on sedimentary numerical simulation experiments and has designed 21 sets of simulation experiments to explore the coupled effects of topographic gradients, discharges, and sediment grain sizes on the morphological development of braided river channel bars. The value ranges of these factors basically cover the general conditions of natural braided rivers. This experiment aims to systematically reveal the action mechanisms of different influencing factors and the synergistic effects of multiple factors through the controlled variable method. The analysis and interpretation of the simulation results mainly include two aspects: first, investigating the planar morphological scale under different factor combinations, which is based on the visual delineation and quantitative analysis of channel bars in the simulation results; second, exploring the quantitative functional relationships between different factor combinations and channel bar scales. This analysis is mainly achieved by comparing the results of different simulation experiments and aims to separately test the sensitivity of model outputs to water discharge, topographic gradient, and sediment grain size.

2.2. Sedimentary Numerical Simulation Based on Delft3D

As a typical type of active channel system, braided rivers can be classified into two main categories, namely sandy braided rivers and gravelly braided rivers, based on the grain size characteristics of their sediment composition [19,26]. Focusing on the sandy braided river system, this study aims to reveal the factors influencing channel bar morphology through the targeted coupling of numerical simulations with the sedimentary context of the study area, building on the mature technology of the Delft3D sedimentary numerical simulation platform. With reference to the hydrodynamic and sedimentary parameters of modern natural sandy braided rivers, the study sets reasonable variable ranges and boundary conditions and systematically conducts sedimentary numerical simulation experiments.

2.2.1. Principles of Sedimentary Numerical Simulation

The Delft3D-FLOW module is the core tool used in this study to simulate the hydrodynamic and sedimentary processes of braided rivers. Its basic principle is to solve the reasonably simplified Navier–Stokes equations (N-S equations) using numerical methods [27] so as to reproduce the processes of flow movement, sediment transport, and riverbed evolution. Due to the characteristics of natural river systems such as large spatiotemporal scales, complex boundaries, and coupling of multiple physical processes, it is quite difficult to directly solve the three-dimensional N-S equations in their full form. Therefore, Delft3D introduces several basic assumptions when constructing the hydrodynamic model to balance computational efficiency and physical authenticity. These assumptions mainly include the shallow water assumption, which is suitable for water bodies where the horizontal scale is much larger than the vertical scale; the incompressible fluid assumption, which ignores changes in water density; the Boussinesq approximation, which considers density changes only in the buoyancy term; the hydrostatic pressure assumption, which ignores vertical acceleration and simplifies the vertical momentum equation to a hydrostatic equilibrium relationship; and the Reynolds-averaged method, which decomposes turbulent motion into time-averaged and fluctuating components with closure achieved via a turbulence model.

$$\begin{array}{l}{\displaystyle \frac{\partial u}{\partial t}}+u{\displaystyle \frac{\partial u}{\partial x}}+v{\displaystyle \frac{\partial u}{\partial y}}+g{\displaystyle \frac{{\partial z}_w}{\partial x}}+{\displaystyle \frac{gu\sqrt{u^2+v^2}}{C^{2}h}}-V\left({\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}\right)+F_x=0\\ {\displaystyle \frac{\partial v}{\partial t}}+u{\displaystyle \frac{\partial v}{\partial x}}+v{\displaystyle \frac{\partial v}{\partial y}}+g{\displaystyle \frac{{\partial z}_w}{\partial y}}+{\displaystyle \frac{gv\sqrt{u^2+v^2}}{C^{2}h}}-V\left({\displaystyle \frac{{\partial }^{2}v}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}v}{\partial y^2}}\right)+F_y=0\\ {\displaystyle \frac{\partial h}{\partial t}}+{\displaystyle \frac{\partial hu}{\partial x}}+{\displaystyle \frac{\partial hv}{\partial y}}=0\end{array}$$

Regarding the selection of coordinate systems, Delft3D-FLOW provides multiple options to adapt to the simulation of water bodies with different scales and types. This study adopts the orthogonal curvilinear coordinate system (ξ, η) for horizontal discretization. This co-ordinate system can generate body-fitted grids through the Delft3D-RGFGRID module, which better fits the irregular boundaries of natural rivers and effectively reduces the discretization errors caused by traditional rectangular grids at the boundaries. In the vertical direction, the model uses the σ coordinate for layering, which is defined as σ = (Z−ζ)/H. Here, Z represents the vertical physical coordinate, ζ denotes the water level, and H stands for the total water depth. The σ coordinate ranges from −1 to 0, enabling accurate fitting from the riverbed bottom (σ = −1) to the water surface (σ = 0). It is particularly suitable for simulating hydrodynamic and sediment processes in areas with significant changes in water depth.

On the basis of the aforementioned assumptions, Delft3D-FLOW mathematically describes the flow of water and sediment movement through a set of governing equations. The continuity equation ensures the mass conservation of water, while the momentum equations—based on the Reynolds-averaged N-S equations—describe the motion law of water flow under the combined action of pressure gradients, Coriolis forces, turbulent stresses, and bed friction.

For the sediment transport module, Delft3D classifies sediments into cohesive and non-cohesive categories based on their material properties and adopts different models for each type. For cohesive sediments, their transport is mainly dominated by suspension transport. The settling velocity is calculated using an empirical formula that accounts for the influence of salinity, while the erosion and deposition fluxes are described by the Partheniades–Krone formula. This model incorporates critical erosion and deposition shear stresses as the main criteria. For non-cohesive sediments, such as sandy sediments, the Van Rijn formula is used to calculate the settling velocity and near-bed reference concentration. This model is suitable for simulating the transport and exchange processes of medium-coarse sand particles in the form of bed load and suspended load [28].

In terms of numerical solution methods, Delft3D-FLOW adopts the finite difference method based on a staggered grid system. Within this grid system, scalar variables such as water level and concentration are defined at grid centers, while velocity variables are defined at grid interfaces. This setup helps improve numerical stability and simplify the handling of boundary conditions. For time integration, the alternating direction implicit (ADI) method is used, which involves dividing each time step into two half-steps. Implicit solving is performed alternately in the ξ and η directions for each half-step, while the other direction is handled explicitly. This method not only avoids the strict time-step constraints of fully explicit schemes but also offers higher computational efficiency than fully implicit methods, making it suitable for long-term and large-scale hydrodynamic-sedimentary coupled simulations.

To summarize, the numerical model established in this study has systematically achieved high-resolution and process-based simulation of the formation and evolution processes of channel bars in sandy braided rivers. This is accomplished by virtue of reasonable simplification of physical processes, adoption of the body-fitted orthogonal curvilinear grid and σ vertical coordinate, coupling of hydrodynamic-sediment transport-riverbed deformation modules, and application of the efficient and stable ADI algorithm. The model provides a reliable numerical experimental platform for exploring the response mechanisms of channel bar morphology to various environmental factors.

2.2.2. Boundary Conditions and Parameter Settings

The boundary conditions of the model mainly include grid resolution, flow conditions, and transport conditions. For channel bars in the braided rivers of the Sulige Gas Field, their lengths and widths mostly range from 100 to 850 m [29]. Accordingly, as shown in Figure 1, the model domain is set to 10 km in length and 1 km in width, with individual grids measuring 12.5 m along the long axis and 5 m along the short axis. This setup not only accurately captures subtle changes in channel bar boundaries but also avoids blurring of channel bar morphology caused by excessive grid coarseness [7,30]. Water inlets and outlets are, respectively, placed on both sides of the grid’s short axis: the water inlets are defined by discharge magnitude, while the water outlets are defined by water level changes. Meanwhile, the long-axis boundaries of the grid are set as non-erosive barriers to simulate the real scenario of braided rivers flowing within river valleys [31]. While accounting for the horizontal plane, the vertical direction of the model is divided into 3 layers based on the core geological characteristics of the sandy braided rivers in the Lower Member 8 of the He8 Formation in the Sulige Gas Field, namely “shallow water, low energy, and gentle slope.” Each layer has a uniform thickness, which fully covers the key vertical structures of the near-bottom layer, middle layer, and surface layer. Additionally, the model adopts a vertical σ-coordinate that automatically adapts to water depth changes through adjustments, enabling relative refinement of the near-bottom region. Combined with the setting of the near-bottom reference concentration in the Delft3D sediment module, this further eliminates the impact of layer thickness on sediment deposition calculations.

Figure 1. Grid setup.

Except for the three variables of topographic gradient, discharge, and sediment grain size, all other parameters in the experiments are set consistently to ensure a single variable in the experiments. Table 1 lists the other parameters as follows: The hydrodynamic module uses Manning’s equation to calculate riverbed roughness. In sediment simulation, the dry bulk densities of sand and mud are set to 1650 kg/m³ and 500 kg/m³ respectively. The main physical constant, gravitational acceleration, is set to a constant value of 9.81 m/s². Water density is set to the freshwater density of 1000 kg/m³. To accelerate the geomorphic evolution process and meet the requirements of the simulated event scale, the geomorphic evolution coefficient is set to 100. This coefficient speeds up the simulation while ensuring the simulation results do not become distorted. The total simulation duration is 30 days, and the computational time step is 0.5 min. If the time step is reduced to 0.25 min, the fineness of the simulation results increases by approximately 5%, while the computational load rises by roughly 53%. When the time step is increased to 1 min, however, the channel bar morphology in the simulation results becomes unstable and the fineness deteriorates.

Table 1. Basic parameter table of braided river sedimentary numerical simulation.

Parameters	Unit	Set Value
Grid Unit Size	m	5 × 12.5
Total Length of the River	km	10
River Width	km	1
Roughness Equation	-	Manning
Dry Bulk Density of Sand	kg/m3	1650
Dry Bulk Density of Mud	kg/m3	500
Horizontal Eddy Viscosity	m2/s	1
Horizontal Eddy Diffusivity	m2/s	0.1
Lower Limit of Sedimentary Thickness Change Recording	m	0.05
Gravitational Acceleration	m/s2	9.81
Water Density	kg/m3	1000
Simulation Duration	d	30
Geomorphic Evolution Coefficient	-	100
Time Step	min	0.5

2.2.3. Simulation Group Setup

The setup of simulation groups mainly involves establishing control groups based on three variables: topographic gradient, discharge, and sediment grain size. To ensure the simulation experiments have relevant practical basis, this study takes the He 8 Lower Submember Formation of the Sulige Gas Field in the Ordos Basin as a case study. This formation develops typical sandy braided rivers and has abundant drilling data and relevant geological materials, which can effectively support the acquisition of relevant parameters [18,32]. Based on the relevant analysis of the He 8 Lower Submember Formation of the Sulige Gas Field in the Ordos Basin, the ranges of the three variables are defined, and different simulation groups are set within these ranges. This provides data support for establishing a sedimentary numerical simulation knowledge base in this area.

The determination of the topographic gradient range mainly relies on recovering the paleoslope based on the formation thickness of the Sulige Gas Field. Based on the systematic collection and comprehensive investigation of existing geological data, this study re-covered and statistically analyzed the formation thickness of multiple wells in the Sulige area. By comparing the thickness difference in inter-well sedimentary formations (denoted as d2−d1) with their corresponding horizontal distance (S), the paleotopographic gradient of this area was estimated. The calculation results show that the paleogradient of the target interval in the Sulige Area during geological history was relatively gentle, with an average value of approximately 0.02°. This indicates that the area was once in a low-energy sedimentary environment with a weak topographic gradient. To characterize this result in detail, the formation recovery data of seven key wells in the area were statistically analyzed (Table 2). Each well provides information on the current formation thickness, sand-to-ground ratio of the Upper He Member and Lower He Member, as well as the paleothickness recovered through the sedimentary compensation principle. The paleothickness recovery results show that there is a certain spatial variability in the sedimentary preservation status of the area, with the recovered thickness ranging from 103 m to 157 m. Furthermore, four groups of well pairs were selected for topographic gradient calculation (Table 3). The results show that the gradient values between well pairs range from 0.0016° to 0.0176° [33].

Table 2. Statistical table of recovered formation thickness for partial wells in the Sulige Area.

Well Number	He 8 Upper (m)	He 8 Lower (m)	Current Thickness (m)	Sand-to-Formation Ratio (%)	Paleothickness (m)
W1	30.4	35	65.4	51.68196	137
W2	25.2	29.4	54.6	63.91941	103
W3	30.6	33	63.6	30.81761	157
W4	38.4	21.2	59.6	34.0604	144
W5	35.2	26.4	61.6	33.6039	148
W6	28.4	27.5	55.9	49.55277	119
W7	36.9	28.8	65.7	45.50989	145

Table 3. Gradient calculation table for the Sulige Area.

Well Number	d2 (m)	d1 (m)	Horizontal Distance S (km)	Gradient (°)
W1−W4	145	147	72.944	0.0016
W2−W7	119	141	75.402	0.0167
W3−W5	145	140	53.516	0.0054
W4−W6	103	139	117.303	0.0176

Structural restoration of the Lower Member 8 of the He8 Formation in the Sulige Gas Field during its sedimentary period shows that short-term slope gradient increases occurred in this area, reaching 15–20 times the peak value [33]. Based on the recovered slope gradient range and relevant studies, a total of three slope gradients (1 m/10 km, 3 m/10 km, and 5 m/10 km) were set, corresponding to slope values of 0.0057–0.0286°. This setup is basically consistent with the sedimentary characteristics of gentle slopes in the Sulige Area and also covers the typical gradient range of natural sandy braided rivers [34].

For each gradient value, each group is set with three different discharges and grain sizes. The discharge for each gradient is gradually increased, and after multiple adjustments, the water depth in the corresponding simulation results falls within the same range. This adjustment ensures that the comparison of discharges is reasonable, while the sediment grain sizes are set to 200 μm, 400 μm, and 800 μm.

The simulation experiments are divided into 7 groups (Group A to Group G), with each group including three experiments (Table 4). Specifically, for Groups A, C, and E, the discharge is gradually increased within each group, while the gradient and sediment grain size remain consistent across these three groups. For Groups B, D, and F, the sediment grain size is gradually increased within each group, while the topographic gradient and discharge are consistent across these three groups. Group G focuses solely on topographic gradient, with 3 gradient values set.

Table 4. Experimental group setup table.

Group	Number	Gradient (m/10 km)	Discharge (m3/s)	Median Grain Size of the Sandy Component (μm)
A	1	1	1420	200
	2	1	1500	200
	3	1	1680	200
B	4	1	1500	200
	5	1	1500	400
	6	1	1500	800
C	7	3	1300	200
	8	3	1500	200
	9	3	1880	200
D	10	3	1500	200
	11	3	1500	400
	12	3	1500	800
E	13	5	1420	200
	14	5	1880	200
	15	5	2350	200
F	16	5	1880	200
	17	5	1880	400
	18	5	1880	800
G	19	1	1500	200
	20	3	1500	200
	21	5	1500	200

3. Results

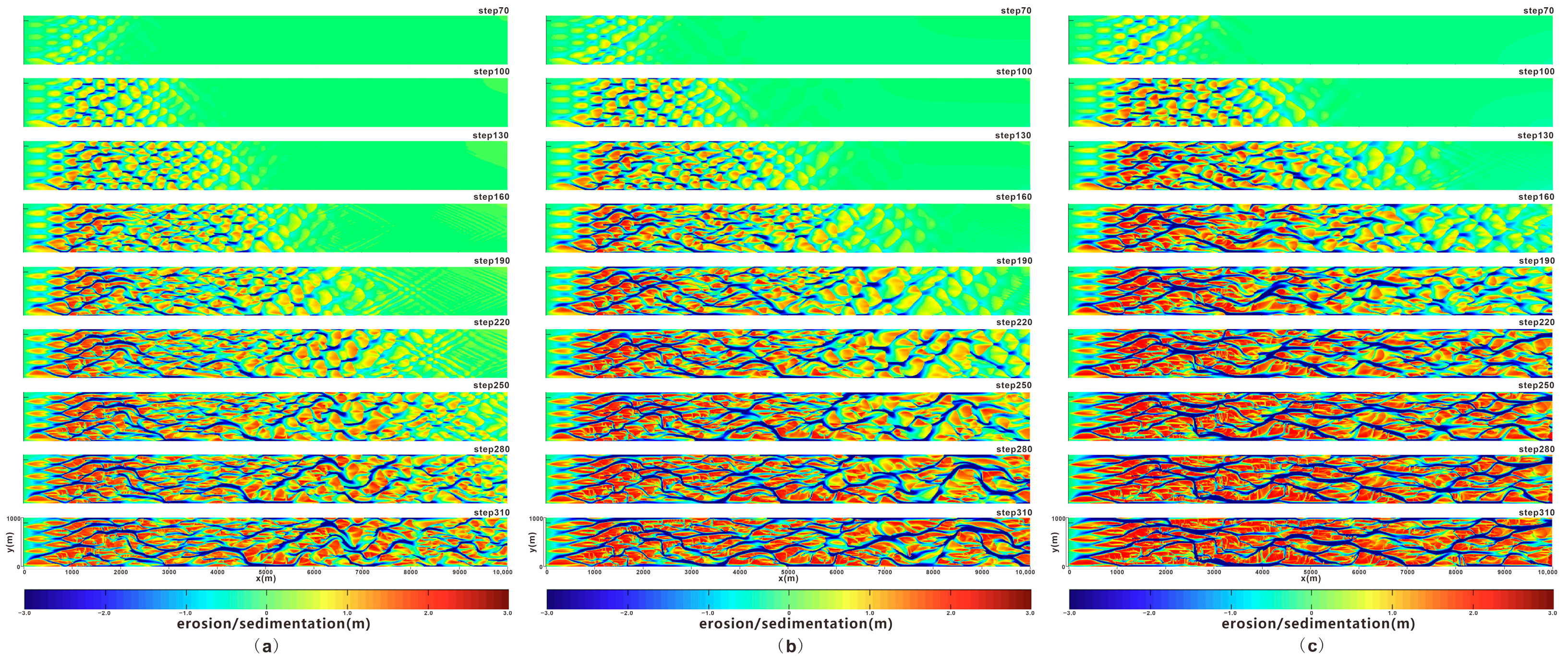
Simulation results in Figure 2 show that all braided rivers undergo the same stages of formation and evolution, which are summarized as follows:

Figure 2. Sedimentary evolution process of braided rivers in sedimentary numerical simulation. (a) embryonic form of channel bars; (b) rhombic-shaped bars; (c) tongue-shaped bars; (d) unit bars; (e) composite bars; (f) composite reworked bars.

(a) The water flow begins to advance forward, and channel bars start to take shape in their embryonic form, exhibiting characteristics of slight undulations and downstream migration, with the height of the undulations mostly less than 1 m.

(b) After a period of evolution, the bed sandbodies form rhombic-shaped sand bars, exhibiting continuous foreset structures. The bedform overall shows slight undulations against an otherwise gentle background, with elevation differences concentrated in the range of 1–2 m.

(c) As the water flow advances further, the morphology of the sand bars changes: the rhombic bars undergo migration and transformation, and the front ends of the bars become rounded due to forward resistance, forming tongue-shaped sand bars. These exhibit the response characteristics of first eroding the bed and then forming high-angle foreset bodies, with the maximum elevation approximately 2–3 m.

(d) The tongue-shaped bars continue to migrate and merge, assuming an overall oval-shaped morphology and developing into the most common channel bars in braided river deposits. These channel bars exhibit a distinct undulating wavy morphology, demonstrate the characteristics of migration and superimposition along the downstream direction, and have an elevation of approximately 4 m.

(e) Channel bars advance downstream, and multiple ones undergo composite splicing to form larger composite bars; small crevasses form on the upper parts of these composite bars, with their elevations mostly reaching more than 6 m.

(f) Composite bars undergo further transformation: water flow erodes the composite bar bodies, and crevasses gradually become more complex, which is evident on both the tops and edges of the bar bodies. Meanwhile, various accretionary bodies tend to stabilize, and the elevation reaches near its maximum value at this stage, approximately 7–8 m.

The six evolutionary stages identified in this study not only inherit the general laws of sandy braided river channel bar evolution and are highly consistent with the models presented in existing studies [3,13,19], but the morphological transformation characteristics of the first four stages in particular all align with the classic framework of sandy braided river channel bar evolution. Additionally, the experimental parameters strictly match the geological reality of the Lower Member 8 of the He8 Formation in the Sulige Gas Field, supplementing the detail gaps of existing models under low-energy gentle slope settings. In the final evolutionary stage, the channel bars exhibit minimal fluctuations in area, indicating that the channel morphology basically tends towards a stable state. This stable node not only confirms the integrity of sandbody evolution in low-energy gentle slope environments but also provides a key temporal basis for subsequent sandbody characterization in the study area. It can clarify the temporal boundary for stable sandbody development, enabling sandbody morphology depiction to closely align with the actual evolutionary process and avoiding deviations caused by the selection of transient evolutionary data.

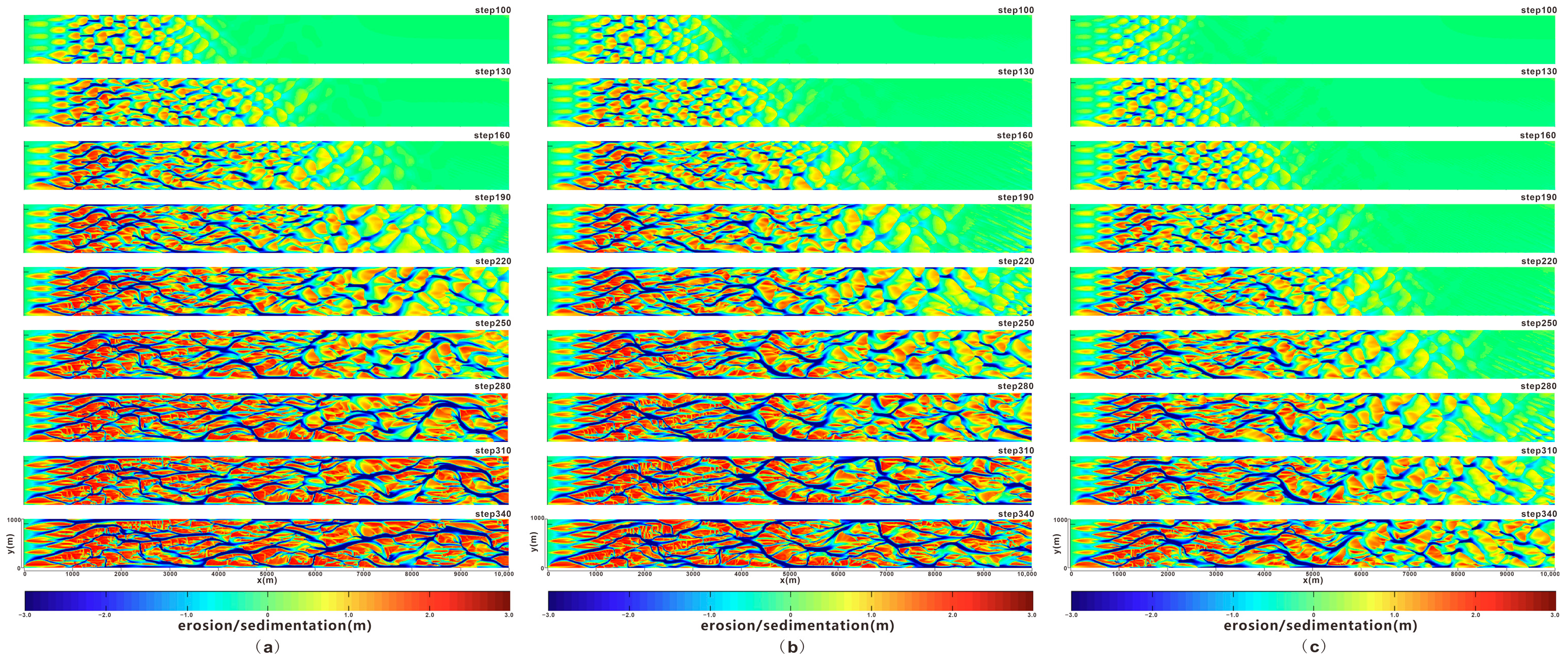
3.1. Single-Factor Analysis of Discharge

As a core characteristic parameter of hydrodynamics, discharge directly determines the efficiency of water flow in sediment transport and deposition and serves as a key driving factor for the scale expansion and morphological remodeling of channel bars. To eliminate interference from other parameters, this study takes Group C experiments as the research object and clarifies the regulatory laws of discharge by comparing the evolutionary dynamics of channel bars under different discharge conditions.

Results in Figure 3 show that within the same simulation time, under low discharge conditions, the differentiation process between channel bars and channels is gentle, with simple sandbody morphology and low remodeling frequency. As discharge increases, the hydrodynamic response to bed erosion-deposition is significantly enhanced, the rate of channel bar scale remodeling accelerates, and channel bifurcation begins to emerge. When high discharge is reached, channel bars undergo frequent migration and superimposition; moreover, after the river stabilizes, the developmental complexity of secondary landforms such as crevasses in the upper part of the bars increases significantly, forming a denser braided channel network. This result confirms the mechanism by which high discharge provides a material basis for the axial extension and scale expansion of channel bars by increasing the sediment transport flux.

Figure 3. Evolution diagram of single-factor analysis of discharge: (a) discharge: 1300 m³/s; (b) discharge: 1500 m³/s; (c) discharge: 1880 m³/s.

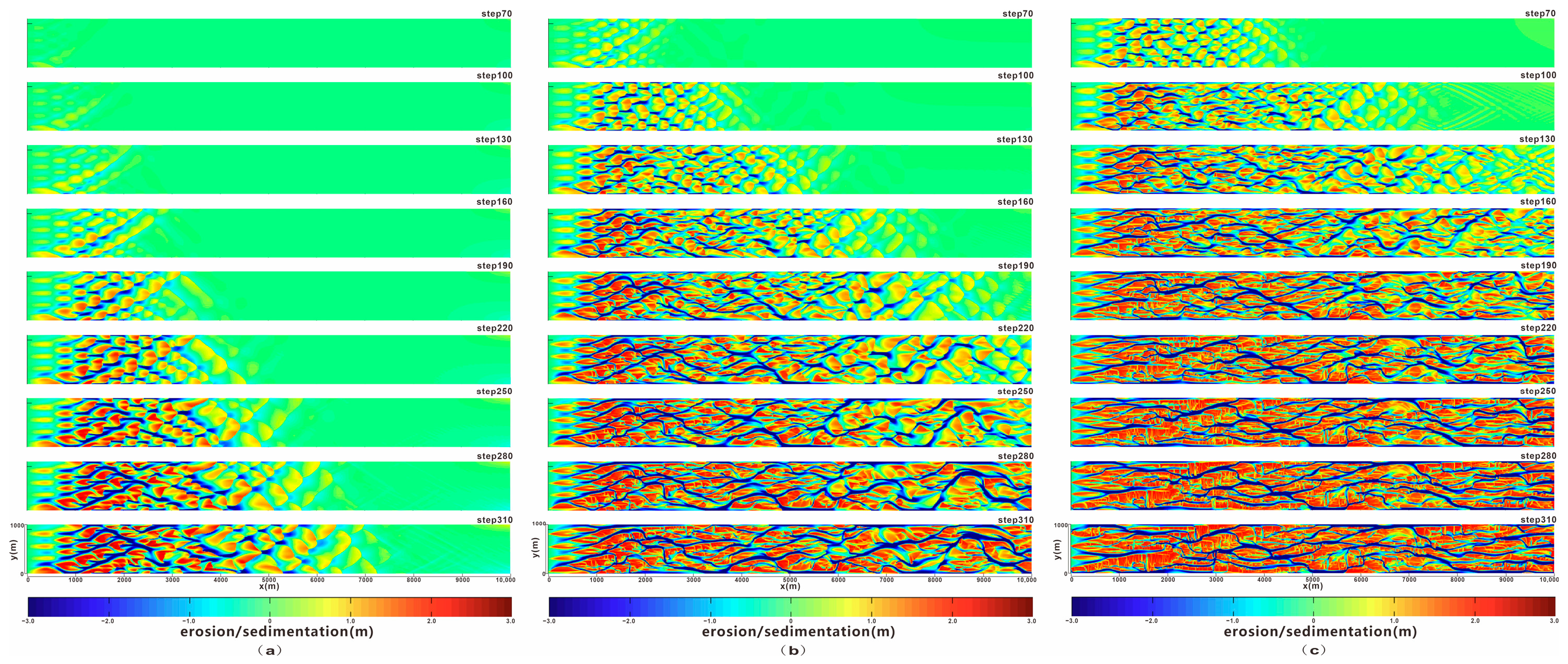
3.2. Single-Factor Analysis of Grain Size

Sediment grain size directly affects the morphological stability of channel bars by altering the critical shear stress for particle entrainment and the erosion resistance of particles. Focusing on the regulatory role of material properties, this study takes Group D experiments as the research object to clarify the influence of grain size on the evolutionary rhythm and stability of channel bars.

Experimental results in Figure 4 show that the transport-deposition responses of sandbodies differ significantly under different grain sizes. Fine-grained sediments are easily entrained and transported by water flow, resulting in a high frequency of erosion and disturbance on the bed, a fast channel bar remodeling rate, and a complex interweaving degree of the overall channel network. For medium-grained sediments, the transport difficulty increases; large-scale migration is only triggered when the hydrodynamic force reaches a certain intensity. At this point, the morphological stability of channel bars is significantly higher than that of fine-grained sediments, the evolutionary rhythm slows down, but well-defined braided channels can still develop. Coarse-grained sediments have the highest transport resistance; particle movement can only be initiated under stronger water flow conditions. This leads to slow formation and development of channel bars in the early stage, a low migration rate, and the formation time of secondary landforms such as channel bifurcations and crevasses is later than that of fine-grained and medium-grained sediments.

Figure 4. Evolution diagram of single-factor analysis of grain size: (a) grain size: 200 μm; (b) grain size: 400 μm; (c) grain size: 800 μm.

3.3. Single-Factor Analysis of Gradient

Topographic gradient directly determines the erosion-deposition balance of hydrodynamic force by regulating the gravitational potential energy of water flow and serves as a core factor affecting the scale and evolutionary complexity of channel bars. Taking Group G experiments as the research object, this study reveals the dominant constraining effect of gradient on channel bar morphology.

Simulation results show in Figure 5 that gradient exerts a significant controlling effect on the rate and complexity of sedimentary evolution. Under low gradient conditions, the gravitational potential energy of water flow is weak, and the erosion and transport capacity of hydrodynamic force on the bed is limited. The processes of channel bar formation and channel bifurcation are slow, and even in the later evolutionary stage, the overall geomorphic complexity remains low. Under medium gradient conditions, the potential energy of water flow increases significantly, and erosion-deposition rates accelerate simultaneously. The interweaving degree and evolutionary rate of the channel network increase substantially, and the superimposition frequency of channel bars is significantly higher than that under low gradient conditions. Under high gradient conditions, sediment transport and bed erosion are extremely active. Channel bars undergo frequent fragmentation and reorganization, while crevasses quickly cut through the bars and develop toward greater complexity, eventually forming braided river depositional configurations with the highest complexity.

Figure 5. Evolution diagram of single-factor analysis of gradient: (a) gradient: 1 m/10 km; (b) gradient: 3 m/10 km; (c) gradient: 5 m/10 km.

3.4. Quantitative Analysis

The determination of the scale of sandstone bodies in the simulation results is based on the measurement method of channel bars in modern braided rivers. Satellite images of the lower reaches of the modern braided Lena River are captured using the Google Earth web version (Figure 6). The scale of channel bars mainly refers to the channel bar length, channel bar width, and aspect ratio. Among these, the channel bar length refers to the extension scale of the channel bar along the main flow direction of the river; by identifying the two endpoints of the channel bar along the main flow direction, the straight-line distance between the two endpoints is measured and calculated using measurement tools. The channel bar width refers to the maximum lateral scale perpendicular to the main flow direction. On the basis of the already determined channel bar length, the position with the maximum width is selected as the typical section position for width measurement according to the channel bar morphology [35,36].

Figure 6. Schematic diagram of channel bar scale measurement method.

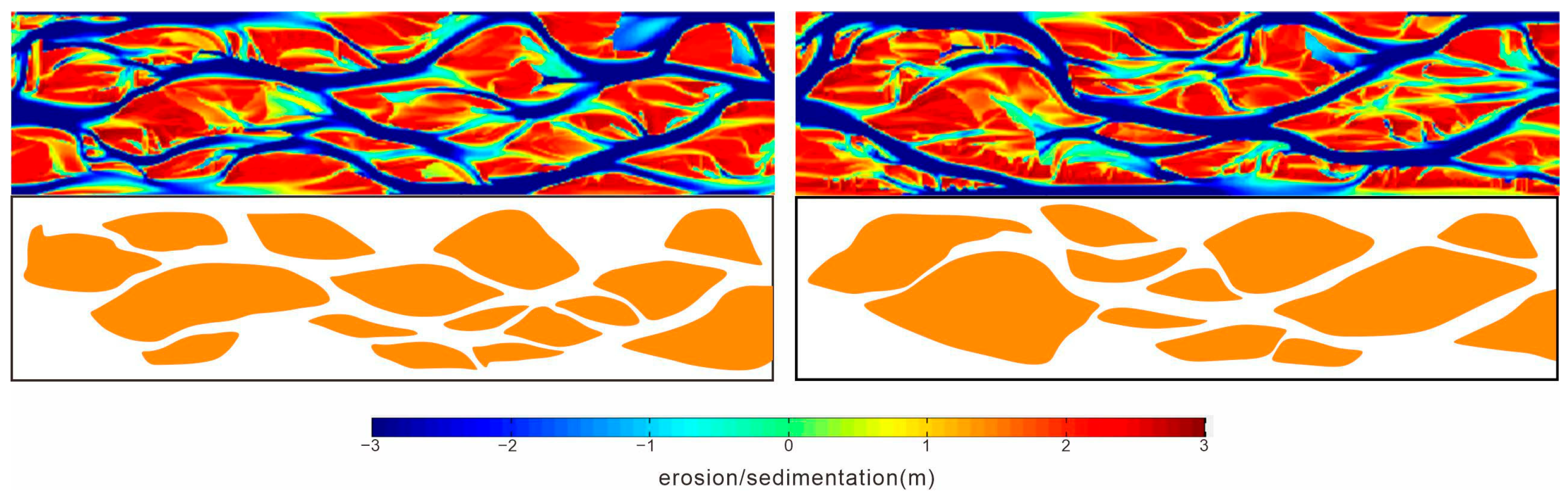
3.4.1. Channel Bar Scale Parameter Statistics

To accurately quantify the morphological characteristics of channel bars in braided rivers, after the river enters a stable state, taking Figure 7 as an example, at which point the height of the channel bar crests reaches or approaches the water level, this time point is estimated. Based on the aforementioned measurement method for channel bar scale, statistical analysis of morphological parameters is conducted on 547 channel bars identified in 21 groups of simulation experiments, with a focus on analyzing two key indicators: the area and aspect ratio of channel bars (Table 5 and Table 6).

Figure 7. Schematic diagram of channel bar depiction in simulation results.

Table 5. Statistical table of channel bar aspect ratio data.

Simulation Serial Number	Maximum Value	Minimum Value	Average Value
Run1	4.26	1.50	2.60
Run2	3.90	1.07	2.51
Run3	4.69	0.84	2.70
Run4	3.90	1.07	2.52
Run5	4.32	1.38	2.81
Run6	4.88	1.36	2.93
Run7	5.59	1.75	3.15
Run8	4.94	2.23	3.24
Run9	4.89	1.80	3.52
Run10	4.94	2.23	3.24
Run11	6.66	2.02	3.72
Run12	3.80	2.22	3.10
Run13	7.95	3.08	4.60
Run14	8.70	2.07	3.96
Run15	4.54	2.53	3.82
Run16	8.70	2.07	3.96
Run17	6.14	2.32	3.72
Run18	4.41	2.11	3.23
Run19	3.90	1.29	2.55
Run20	4.94	2.23	3.24
Run21	6.10	0.95	3.66

Table 6. Statistical table of channel bar area data.

Simulation Serial Number	Maximum Value (km2)	Minimum Value (km2)	Average Value (km2)
Run1	0.61	0.03	0.16
Run2	0.53	0.02	0.17
Run3	0.56	0.04	0.20
Run4	0.53	0.02	0.17
Run5	0.47	0.05	0.25
Run6	0.59	0.20	0.37
Run7	0.24	0.03	0.08
Run8	0.18	0.01	0.08
Run9	0.26	0.02	0.11
Run10	0.18	0.01	0.08
Run11	0.30	0.02	0.10
Run12	0.32	0.03	0.11
Run13	0.16	0.04	0.09
Run14	0.26	0.04	0.12
Run15	0.38	0.02	0.16
Run16	0.26	0.04	0.12
Run17	0.33	0.04	0.13
Run18	0.30	0.04	0.14
Run19	0.53	0.02	0.17
Run20	0.18	0.01	0.08
Run21	0.13	0.02	0.08

To verify the reliability of the simulation results, four modern braided rivers were captured using Google Earth software (Figure 8). Statistical measurements of parameters such as channel bar scale were conducted, with a total of 56 sets of length-width ratio data of channel bars accumulated. A fitting curve was also established, providing a basis for the reliability of the simulation results.

Figure 8. Satellite image of modern sedimentation in braided rivers: (a) Yarlung Zangbo River; (b) Ganges River; (c) Lena River; (d) Paraná River.

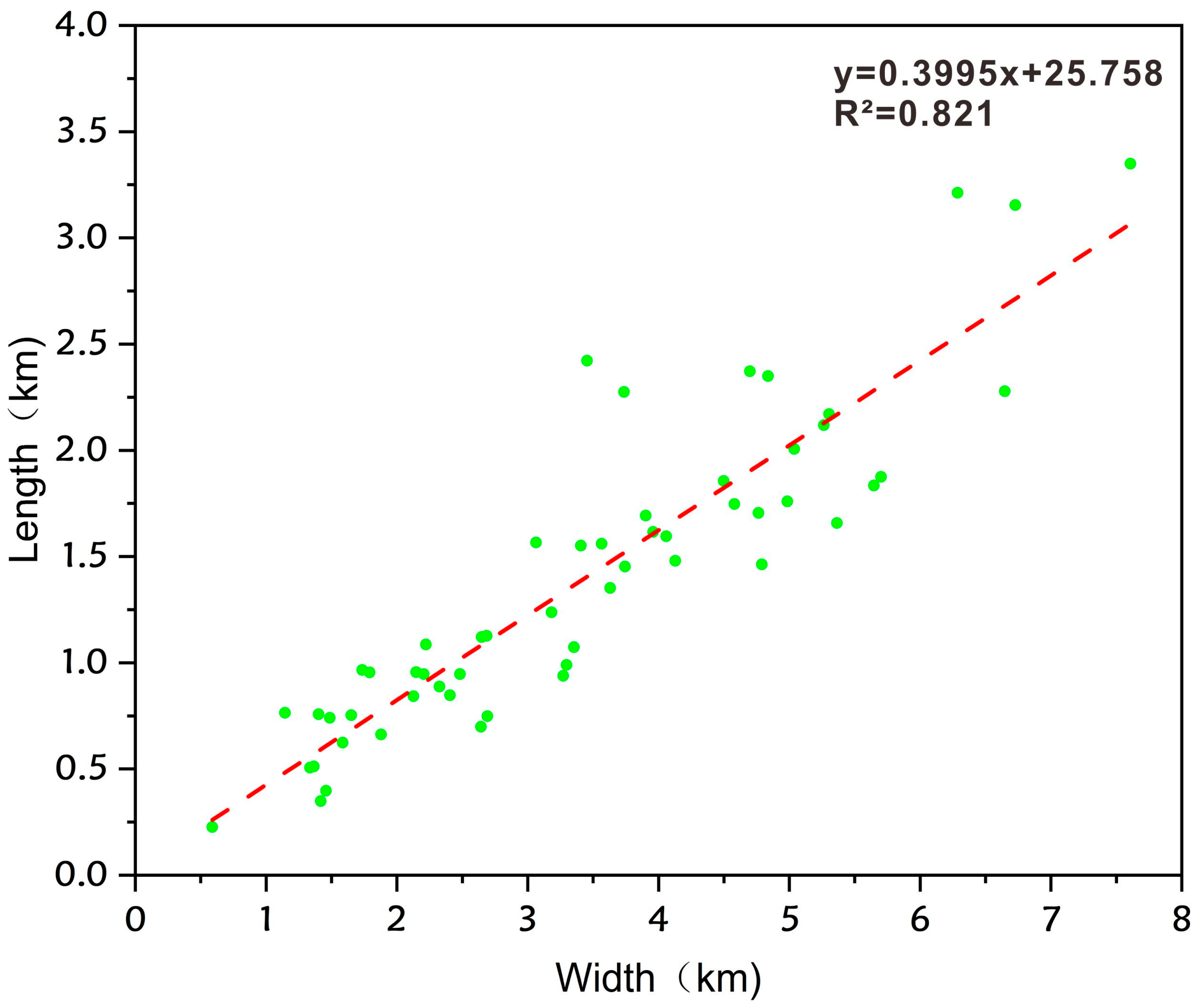
Typical modern sandy braided rivers were selected. Figure 9 shows the length-width relationship of channel bars, which was fitted as y = 0.3995x + 25.758 (R² = 0.821) after extracting its length/width parameters from satellite images. This high goodness of fit indicates that the length and width of channel bars in modern braided rivers have a strong linear correlation, and the fitting curve can effectively reflect the morphological laws of real channel bars. 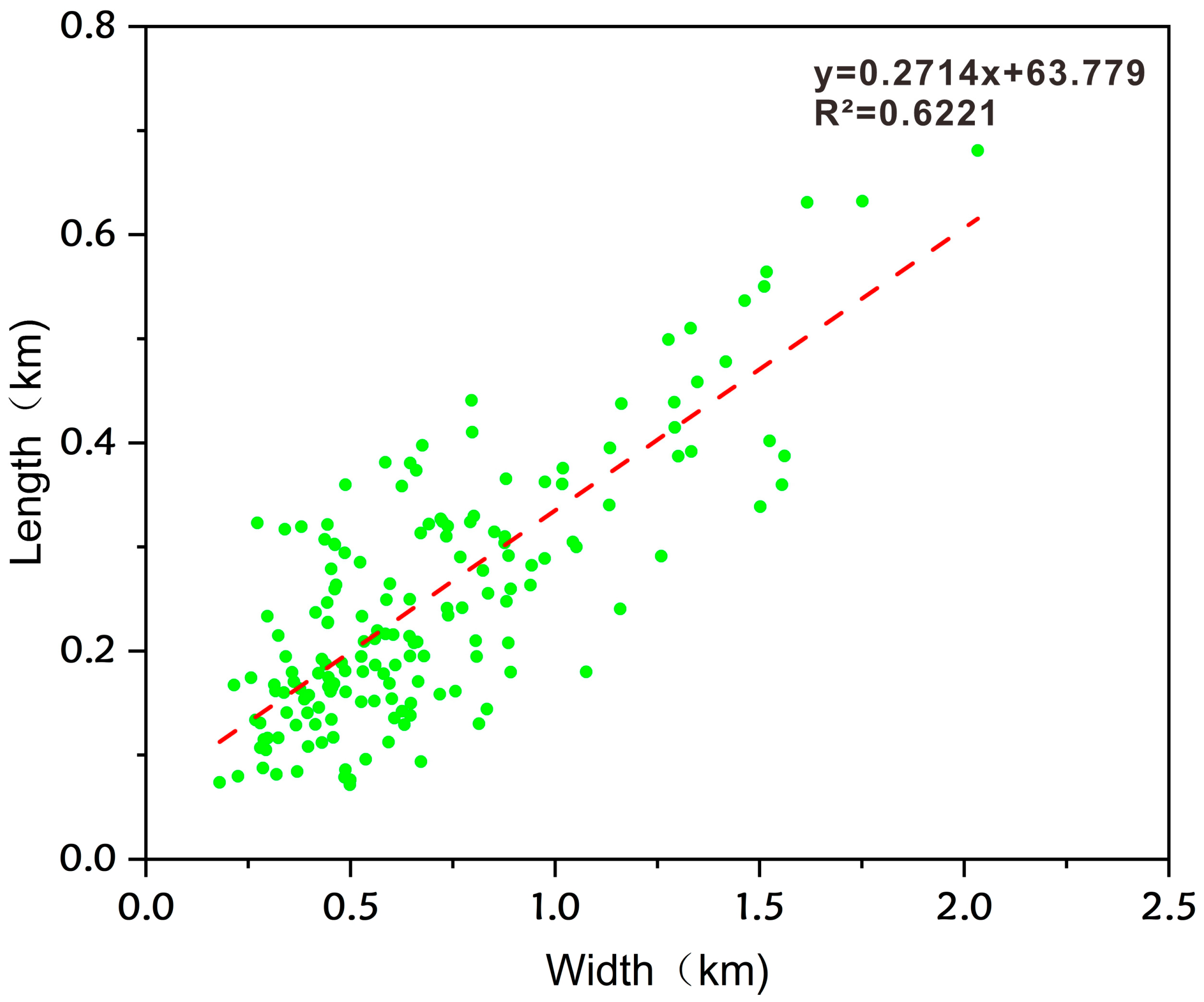Figure 10 presents the length-width relationship fitted based on the simulation results of this study, which is expressed as y = 0.2714x + 63.779 (R² = 0.6221). However, due to simplified boundary conditions such as straight channels and absence of vegetation, the R² is slightly lower than that of modern deposits. Nevertheless, the fitting trend is highly consistent with that of modern deposits: both show a linear law where length increases synchronously with increasing width. The error between the length/width value range of simulated channel bars and the proportional range of modern braided rivers is small. Although the simplification of boundary conditions reduces the goodness of fit, it does not undermine the significance of the linear trend. This further indicates that the simulation results reliably reflect the morphological evolution laws of channel bars in real braided rivers, providing a solid quantitative basis for subsequent sandbody characterization.

Figure 9. Fitting curve of length/width of channel bars in modern sedimentary braided rivers.

Figure 10. Fitting curve of length/width of braided river channel bars from simulation results.

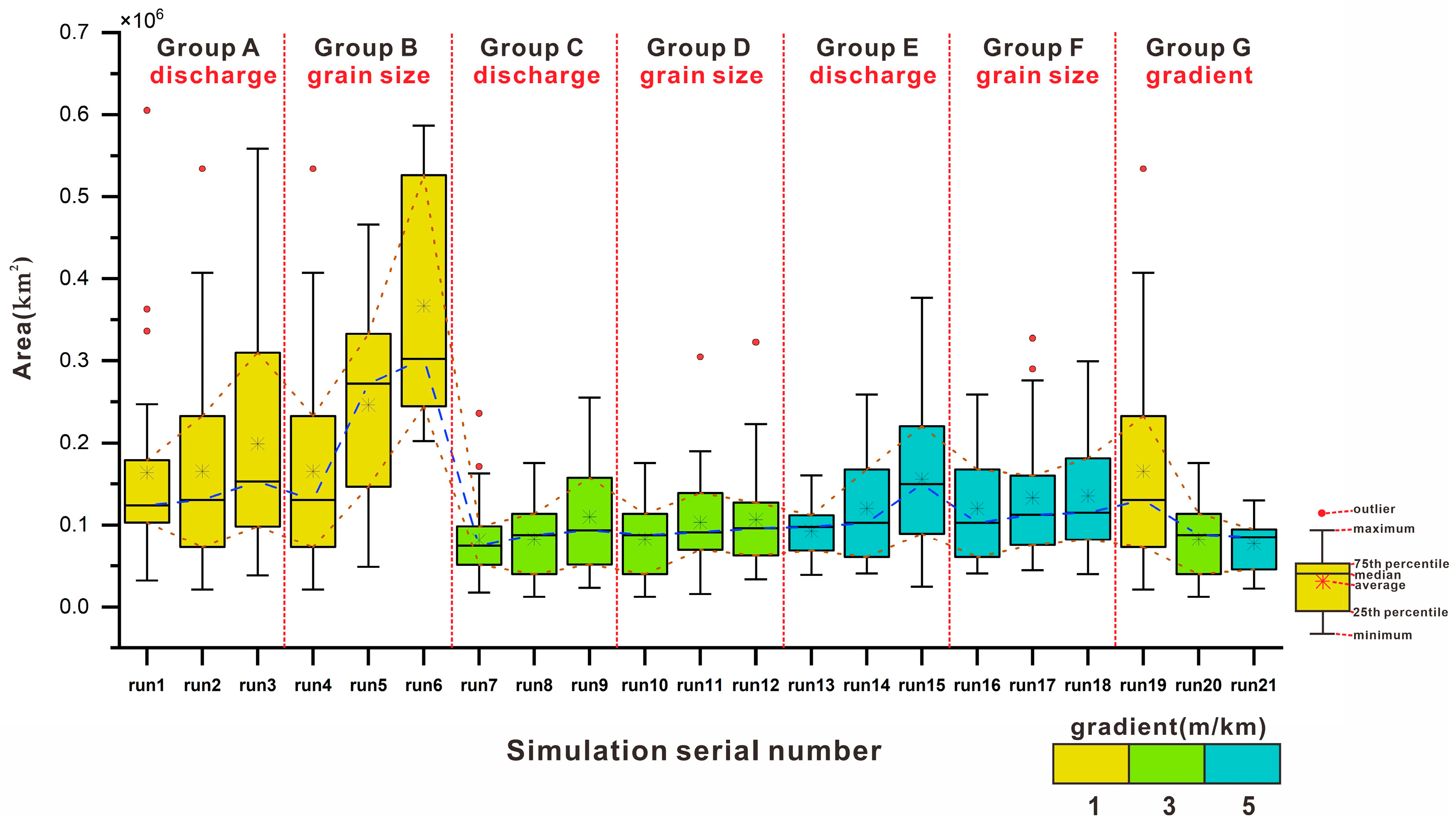
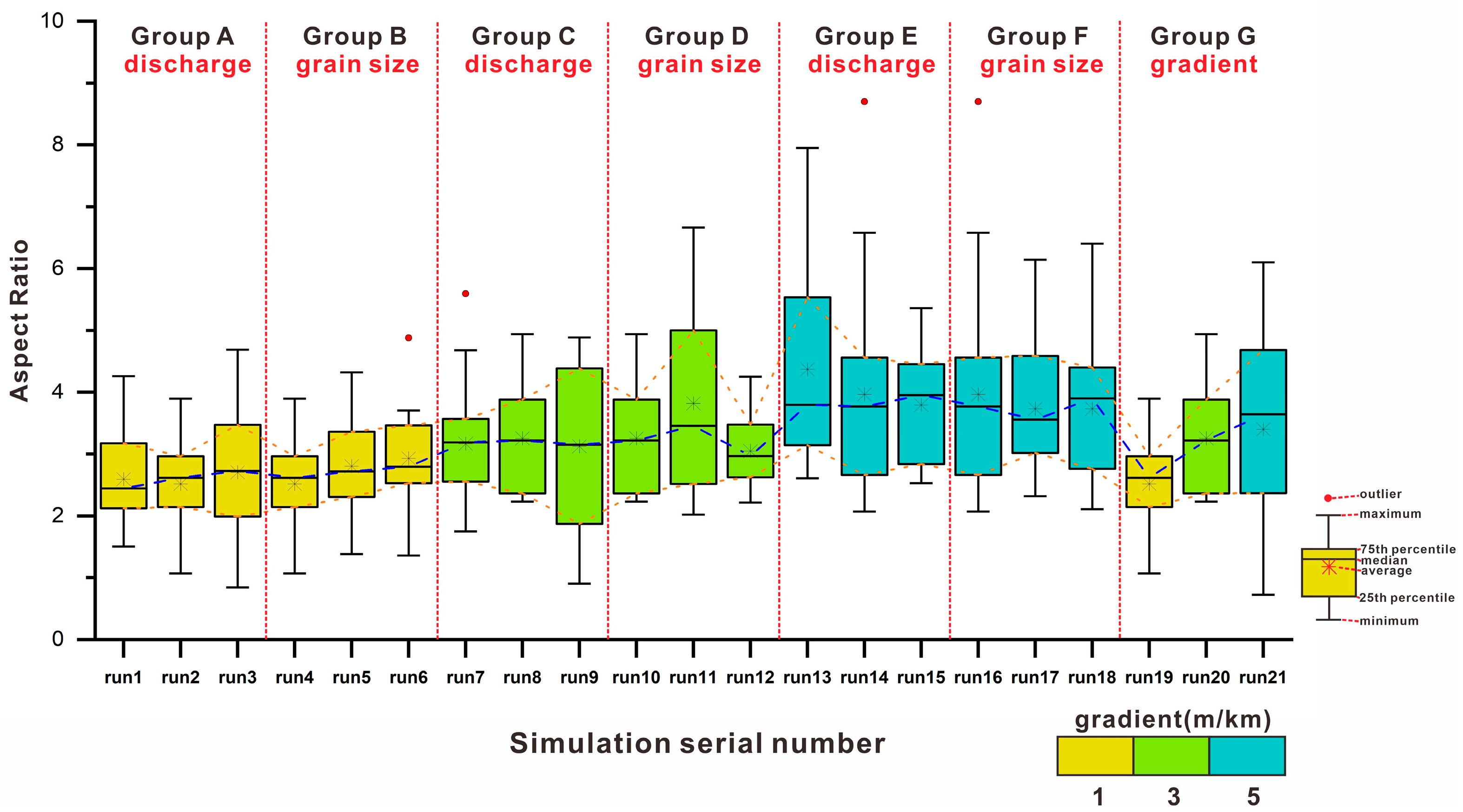
Based on the statistical results, the aspect ratio and area of channel bars show significant differences under different combinations of experimental parameters. To better demonstrate the relationships between three variables (gradient, discharge, and sediment grain size) and channel bar scale, box plots are created for the statistical data grouped by different categories (Figure 11 and Figure 12), so as to more clearly present the response law of the morphological scale of braided river channel bars.

Figure 11. Box plot of channel bar area for different groups.

Figure 12. Box plot of channel bar aspect ratio for different groups.

The variation in channel bar area is comprehensively regulated by discharge, gradient, and sediment grain size. When the gradient is fixed, the channel bar area shows a positive correlation with discharge and sediment grain size. It can be seen from the box plot that when the gradient is consistent, the increase in discharge and the coarsening of sediment grain size significantly expand both the median and distribution range of the channel bar area. This reflects that high discharge enhances the material cycle efficiency of sediment transport and deposition, while coarse-grained sediments are more likely to accumulate into large-scale channel bars due to their higher erosion resistance.

The variation in the channel bar aspect ratio more prominently highlights the controlling effect of the gradient: as the gradient increases, the channel bar aspect ratio also increases [37]. When the gradient is fixed, discharge and sediment grain size have a relatively weak impact on the channel bar aspect ratio, but they generally still show an increasing trend.

An analysis of the outliers in the box plot shows that all outliers correspond to specific dynamic sedimentary processes rather than random number deviations. Their occurrence is an objective reflection of the evolution of channel bars in natural braided rivers. For example, in the high-gradient group, strong hydrodynamic forces cause frequent fragmentation of channel bars, forming small-scale channel bars; meanwhile, enhanced erosion along the main flow direction leads to the aspect ratio of some narrow and elongated channel bars exceeding 6.0. Such outliers are consistent with the phenomenon of fragmented channel bars in high-gradient sections observed in field surveys of modern braided rivers, thus reflecting real geological processes. Alternatively, in high discharge-fine grain size combinations, instantaneous discharge peaks induce rapid sediment accumulation, forming oversized channel bars. In terms of the impact on core conclusions, outliers do not alter the core laws, and they account for only 4.2% of the total sample, which further verifies the reliability of the results.

3.4.2. Sensitivity Analysis of Channel Bar Area to Key Parameters

To quantitatively reveal the sensitivity differences in channel bar area to discharge, sediment grain size, and riverbed gradient, and clarify the influence weights of different parameters on the development scale of channel bars, Principal Component Analysis and Multiple Linear Regression Analysis are adopted to conduct a systematic study. Principal Component Analysis quantifies the cumulative explanatory power of each parameter on channel bar area by extracting the common variance of “discharge-sediment grain size-riverbed gradient”, while Multiple Linear Regression focuses on the linear correlation strength between parameters and channel bar area.

The results of Principal Component Analysis in Table 7 show that the cumulative variance contribution rate of discharge and riverbed gradient to channel bar area reaches 93.98%, while that of sediment grain size is only 6.02%. This difference mainly stems from the dominance of coupling between hydrodynamic conditions and sedimentary processes: discharge directly determines the “transport-deposition efficiency” of hydrodynamics on sediment, while riverbed gradient regulates the “erosion-accumulation balance” of water flow through gravity; the two together form the dynamic basis for the development of channel bar scale. In contrast, sediment grain size only exerts a secondary impact through particle accumulability, and its role is easily overshadowed by the dominant effect of hydrodynamics.

Table 7. Principal component loading matrix table.

	Discharge	Grain Size	Gradient
PC1	0.71	0.02	0.71
PC2	0	0.99	−0.03
PC3	0.71	−0.02	−0.71
Contribution Rate (%)	53.3	6.02	40.68

A multiple linear regression model including discharge, sediment grain size, and gradient was constructed (Table 8), and through standardized coefficients, t-tests, and p-values, an in-depth analysis of the significance level of the impact of each parameter on channel bar area was conducted.

Table 8. Standardized coefficients table.

		Unstandardized Coefficients		Standardized Coefficients
Model		B	Standard error	Beta	t	Significance
1	(Constant)	8184.113	46,379		0.176	0.86
	Discharge	166.873	30.569	0.237	5.459	<0.001
	Grain Size	68.694	34.645	0.079	1.983	0.048
	Gradient	−8,674,185	874,518	−0.43	−9.919	<0.001

From the results of the regression model, discharge, gradient, and sediment grain size all have a significant impact on channel bar area; however, the absolute values of the t-values for discharge and gradient are larger, and their significance levels are stronger than that of sediment grain size. To verify the influence weight of sediment grain size, a further residual analysis with the “grain size variable excluded” was conducted. 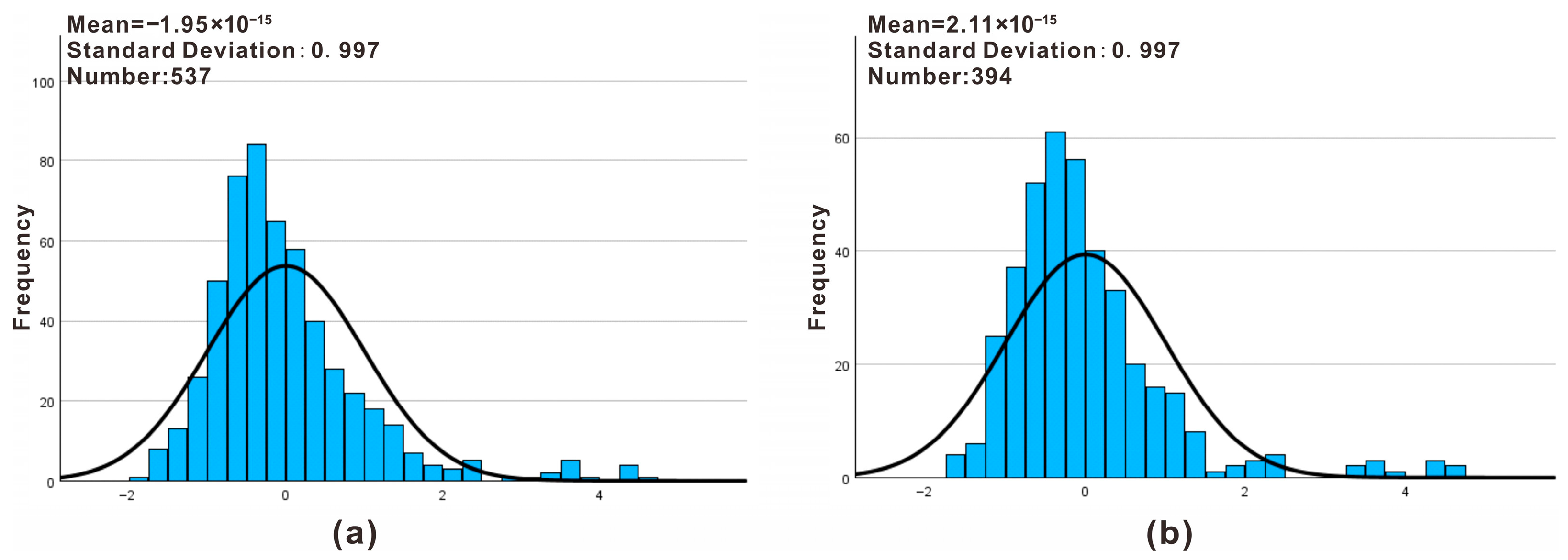By comparing the histograms of standardized residuals between the “grain size-included” and “grain size-excluded” scenarios (Figure 13), it was found that the normality of the residuals was not compromised after excluding grain size. This indicates that the contribution of grain size to the core explanatory power of the model is low, and its impact can be partially over-shadowed by the dominant role of discharge and gradient.

Figure 13. Histogram of standardized residuals: (a) grain size-included; (b) grain size-excluded.

Finally, based on the regression results with the “grain size variable excluded”, a regression equation between discharge, gradient, and channel bar area was established: Channel Bar Area (m²) = 29,556.03 + 170.92 × Discharge (m³/s) − 8,581,400.8 × Gradient (°).

The channel bar area prediction equation established in this study based on sedimentary numerical simulation has a core advantage: it establishes a quantitative link between paleoenvironmental parameters and sandbody morphology, addressing the limitation of traditional characterization that relies on subjective experience. In practical applications, paleoenvironmental parameters can be obtained from the geological data of the study area, and the theoretical area of channel bars can be derived using the equation. Meanwhile, the aspect ratio characteristics of channel bars can be inferred based on the sedimentary environment, providing a clear geological basis for sandbody characterization.

By synthesizing the Principal Component Contribution Rate, the significance of Multiple Regression, and the Marginal Effect, it can be clearly determined that the sensitivity of discharge, sediment grain size, and riverbed gradient to channel bar area in descending order is gradient > discharge > sediment grain size. The regulatory mechanisms and sensitivity differences in each parameter can be summarized as follows:

(1) Gradient exhibits the strongest sensitivity: By regulating the gravitational potential energy of water flow, gradient directly determines the “erosion-deposition balance” of hydrodynamic forces. When the gradient increases, the erosive capacity of water flow increases exponentially, making channel bars prone to frequent cutting and fragmentation and thus difficult to form large-scale contiguous morphologies; meanwhile, the 40.68% contribution rate of gradient in Principal Component Analysis (PCA) and the highest t-value in the regression model both support it as the primary constraining factor for channel bar area.

(2) Discharge exhibits the second-highest sensitivity: By enhancing the “sediment transport-deposition efficiency” of hydrodynamic forces, discharge provides the material basis for channel bar development. Under high discharge conditions, water flow can carry more sediment for transport, promoting the superposition and scale expansion of channel bars; the 53.3% contribution rate in Principal Component Analysis (PCA) also indicates that discharge is the core driving factor for the positive development of channel bar area.

(3) Sediment grain size exhibits the weakest sensitivity: Sediment grain size affects channel bar scale through the depositional capacity of particles, but this effect depends on the hydrodynamic context of discharge and gradient. When the dominant role of discharge or gradient is strong, the influence of grain size on channel bar area is overshadowed, so its overall regulatory capacity is limited.

This sensitivity law is mutually corroborated by the conclusions of previous single-factor experiments on discharge, gradient, and sediment grain size. It not only clarifies the regulatory weights of different parameters on channel bar area but also provides a theoretical basis and methodological support for the priority control of key parameters in subsequent braided river sedimentary numerical simulations.

4. Discussion

First, the evolutionary laws of the six stages of channel bars in braided rivers are a direct reflection of the synergistic effect of hydrodynamic force, sediment properties, and topographic conditions. They are not isolated morphological changes but rather the result of the dynamic coupling of various parameters. Under gentle slope settings, the gravitational potential energy of water flow is weak, resulting in a slow evolutionary rhythm of channel bars. For the superimposition and expansion of composite bars, this process relies not only on the increase in sediment transport flux brought by the rise in discharge but also on the erosion resistance support provided by sediment grain size.

Second, the laws of single-factor regulation and the results of sensitivity analysis together construct a hierarchical regulatory framework of “dynamics–material–topography”. Single-factor experiments confirm that discharge positively regulates the area of channel bars, gradient negatively constrains the scale of channel bars and positively affects their aspect ratio, and the coarsening of sediment grain size enhances the stability of channel bars. These three types of laws further receive quantitative support from the sensitivity ranking, which indicates that gradient is the core constraint on channel bar morphology, hydrodynamic force is the key driver of material supply, and sediment grain size only plays a secondary regulatory role under the dominance of these two factors.

Finally, the establishment of the channel bar area prediction equation serves as the practical application of all previous results. Based on sensitivity analysis, the equation constructed is “Channel bar area (m³) = 29,556.03 + 170.92 × Discharge (m³/s) – 8,581,400.8 × Gradient (°)”. Its core value lies in transforming the qualitative laws of the six evolutionary stages of channel bars and the quantitative analysis of single-factor and sensitivity into a practical tool. This equation provides an operable quantitative basis for sandbody scale prediction in fine reservoir characterization. Meanwhile, the regression equation can be applied to channel bar sandbody prediction in the Sulige Gas Field, addressing the limitation of characterization relying on subjective experience. By restoring paleogradient and paleodischarge based on drilling data in the study area, substituting them into the regression equation to calculate the theoretical area of channel bars in the target area, and combining the results of single-factor analysis to estimate the aspect ratio of channel bars in the target area, the sandbody characterization of “area + morphology” is ultimately achieved. Additionally, this scheme has universality, but the parameter range needs to be adjusted according to the geological background of the target area.

However, all simulations in this study have certain limitations: only several main factors were considered, including discharge, gradient, and sediment grain size. In modern rivers, however, the morphology of braided rivers and the scale of channel bars are jointly influenced by multiple factors. For instance, the role of vegetation in river development was not taken into account: vegetation can effectively resist water erosion, thereby hindering sandbody deposition. These multiple factors interact with each other and jointly regulate the sedimentary evolution of rivers. In addition, all river boundaries in the model are set as straight lines, while the boundaries of modern rivers are usually curved; river sinuosity may also affect sandbody deposition to a certain extent.

5. Conclusions

(1) This study reveals the evolutionary laws of the six stages of channel bars in braided rivers under gentle slope settings, fills the gaps in details of classic evolutionary models, and describes in detail the distinctive characteristics of each stage.

(2) The single-factor regulation laws are as follows: discharge and grain size show a positive correlation with channel bar area but have a relatively small impact on the channel bar aspect ratio; grain size has a significant correlation with channel bar stability; gradient shows a negative correlation with channel bar area and a certain positive correlation with the channel bar aspect ratio.

(3) Sensitivity analysis confirms that gradient and discharge are the dominant factors affecting channel bar area, with their cumulative explanatory power reaching 93.98%, while sediment grain size plays a secondary regulatory role.

(4) This study quantified the synergistic regulatory mechanism of gradient, discharge, and grain size on the morphology of channel bars; established a channel bar area prediction equation applicable to sandy braided rivers; and effectively provided a basis for the quantitative characterization of channel bar morphology.

(5) At present, breakthroughs have been made in sedimentary numerical simulation, but there are some issues worthy of consideration: (1) the research is based on numerical simulation under ideal conditions, and complex factors in natural rivers such as “periodic discharge variation” and “tectonic subsidence” cannot be reflected; (2) there are differences between the sedimentary numerical simulation parameters obtained from geological data and the actual situation, which affects the accuracy of simulation results; (3) this study did not design multi-functional utilization scenarios for late-stage reservoir development. Future research can be advanced in the following directions: (1) introduce dynamic discharge sequences during flood periods to enhance relevance to natural conditions; (2) combine Google Earth remote sensing data to perform calibration of simulation results with real rivers, so as to ensure maximum consistency with natural conditions; (3) based on the sedimentary numerical simulation model, further couple the fluid-rock interaction module to explore the adaptability of braided river reservoirs in scenarios such as late-stage reservoir development.