Predicting Oil Productivity of High Water Cut Fractured Horizontal Wells in Tight Oil Reservoirs Based on KAN
Abstract
1. Introduction
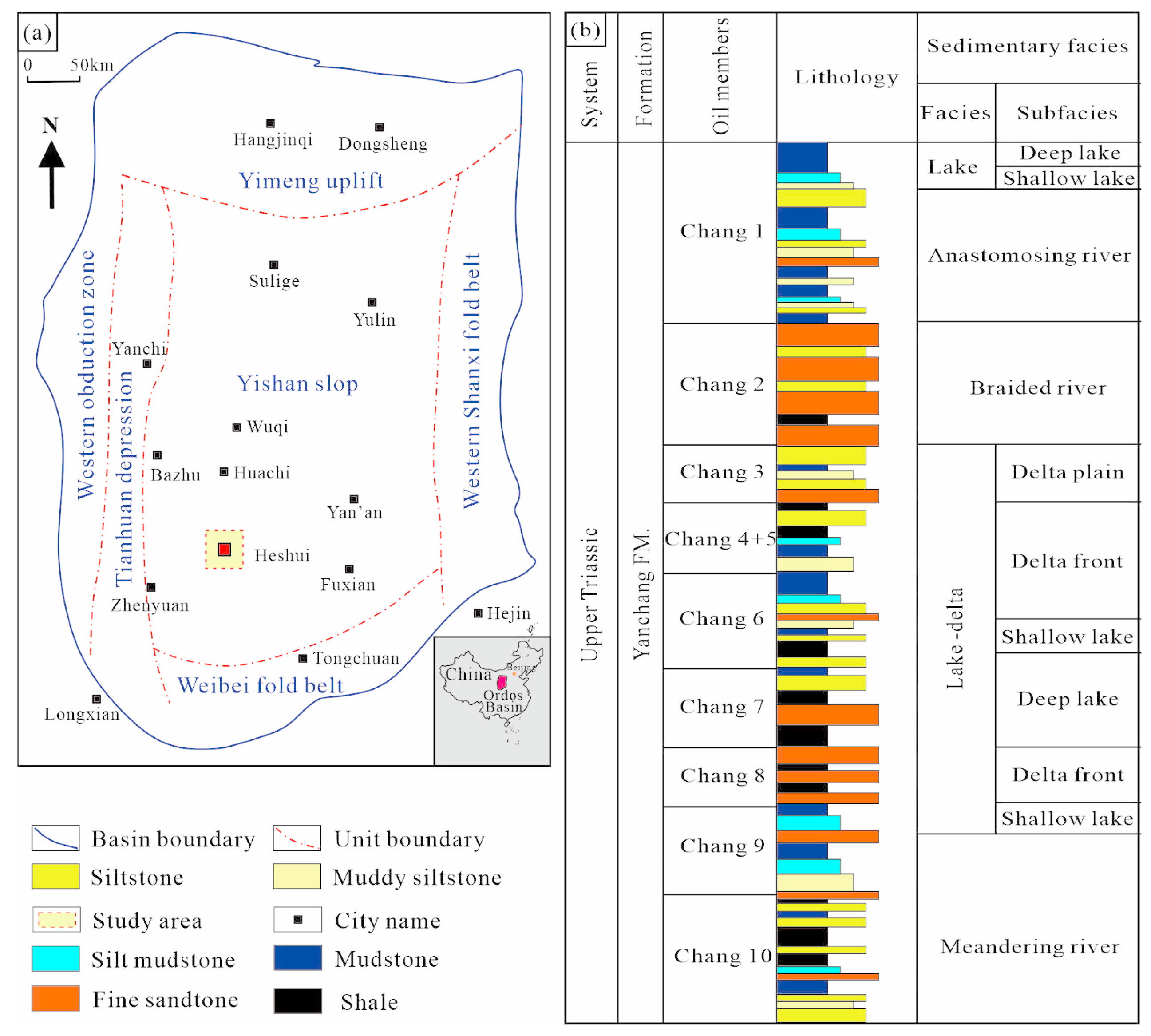
2. Geology Background and Data Characteristics
3. Deep Learning Productivity Prediction Method
3.1. Principle of KAN Deep Learning Algorithm
3.2. WOA-KAN Productivity Forecast Model
- Enclosure of prey
- 2.
- Hunting behavior
- 3.
- Searching for prey
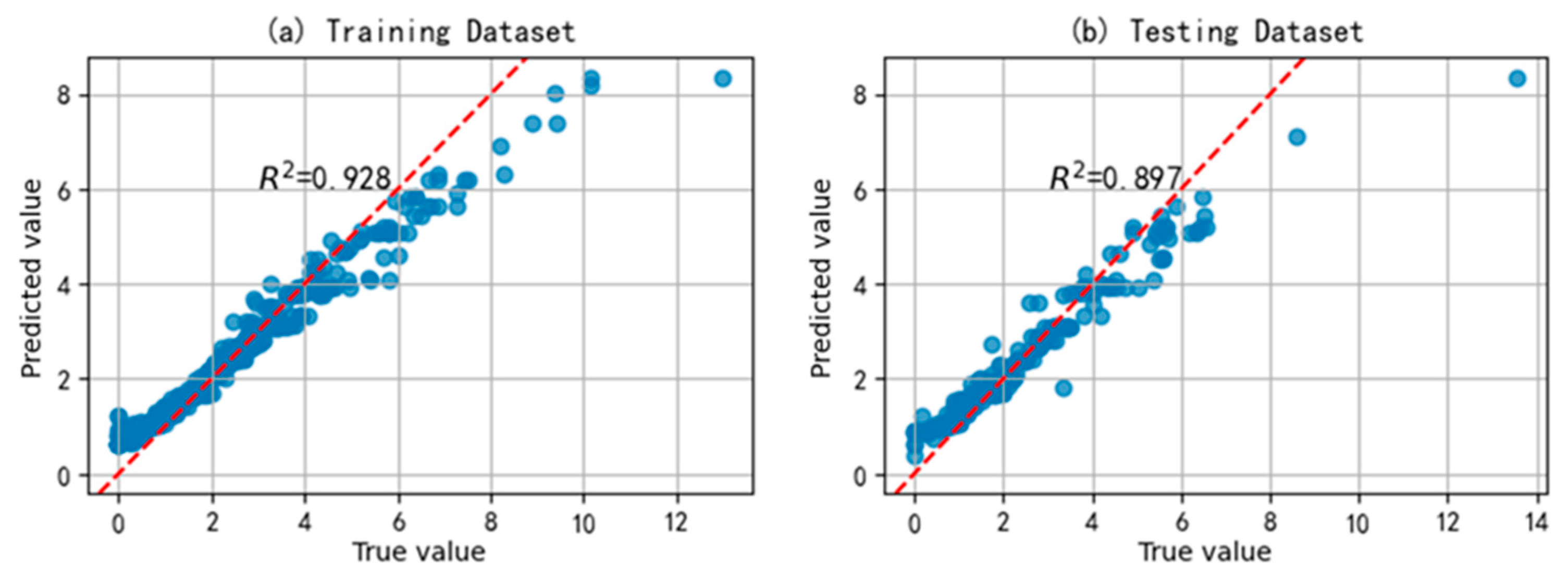
3.3. Model Evaluation
4. Productivity Forecast Results
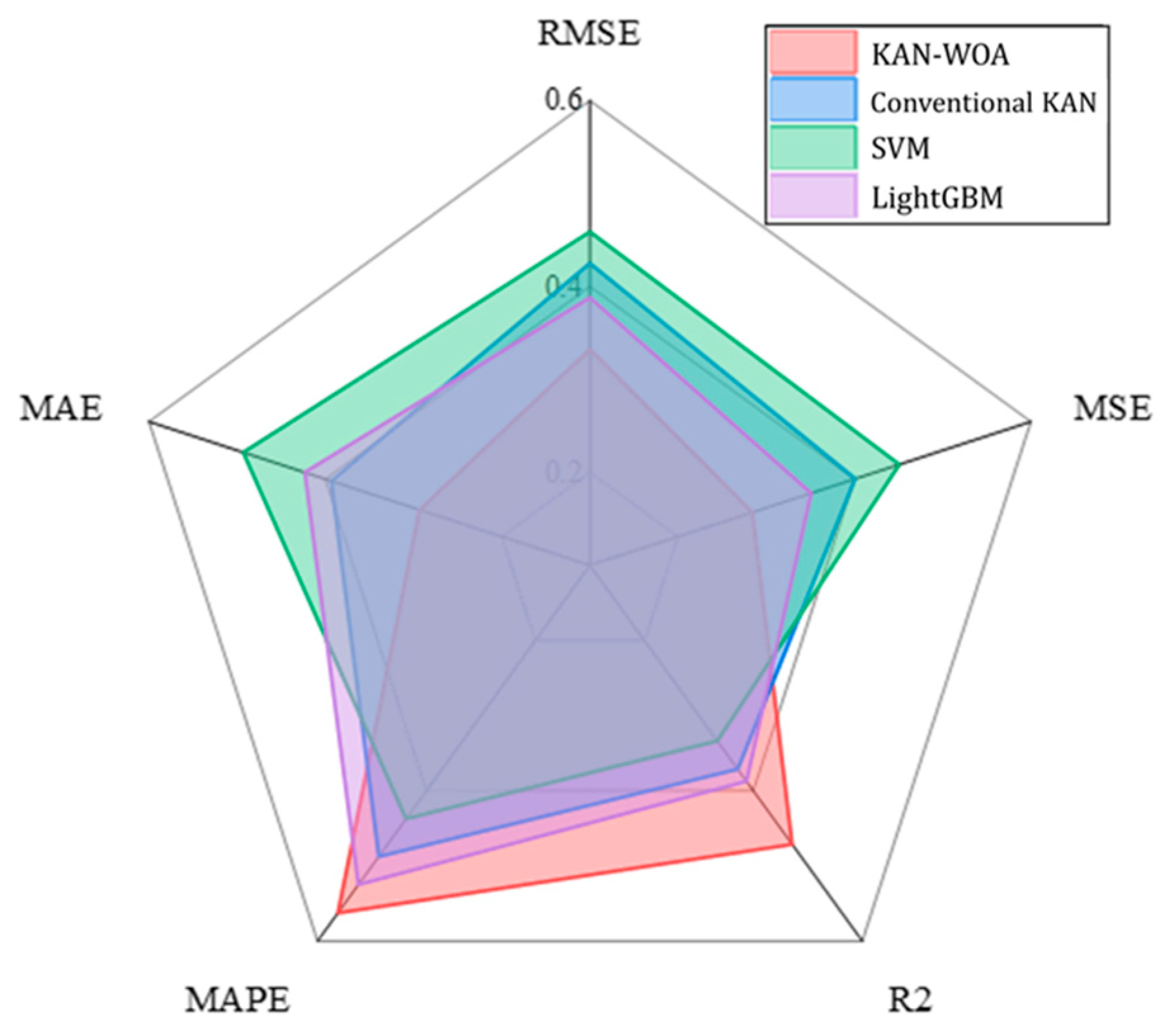
4.1. Comparison of Prediction Performance of Different Models
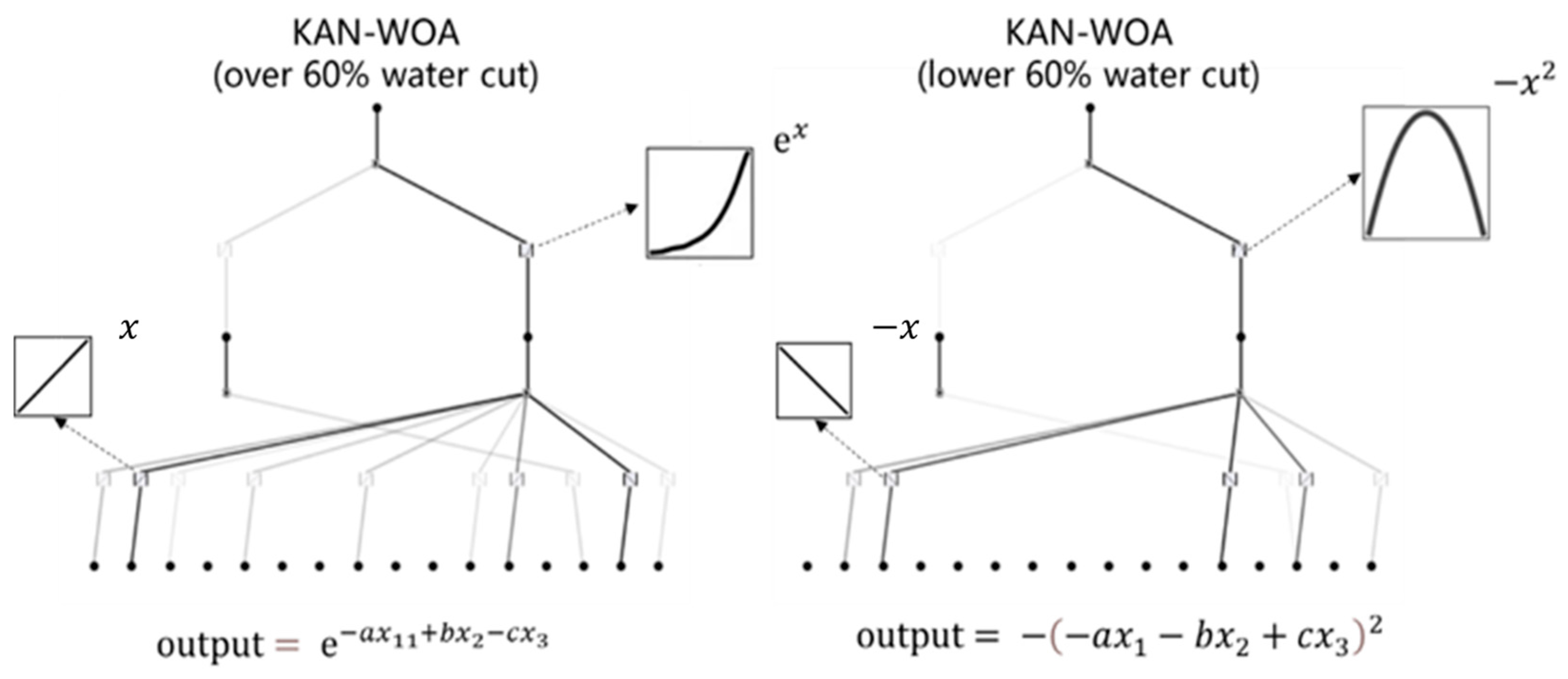
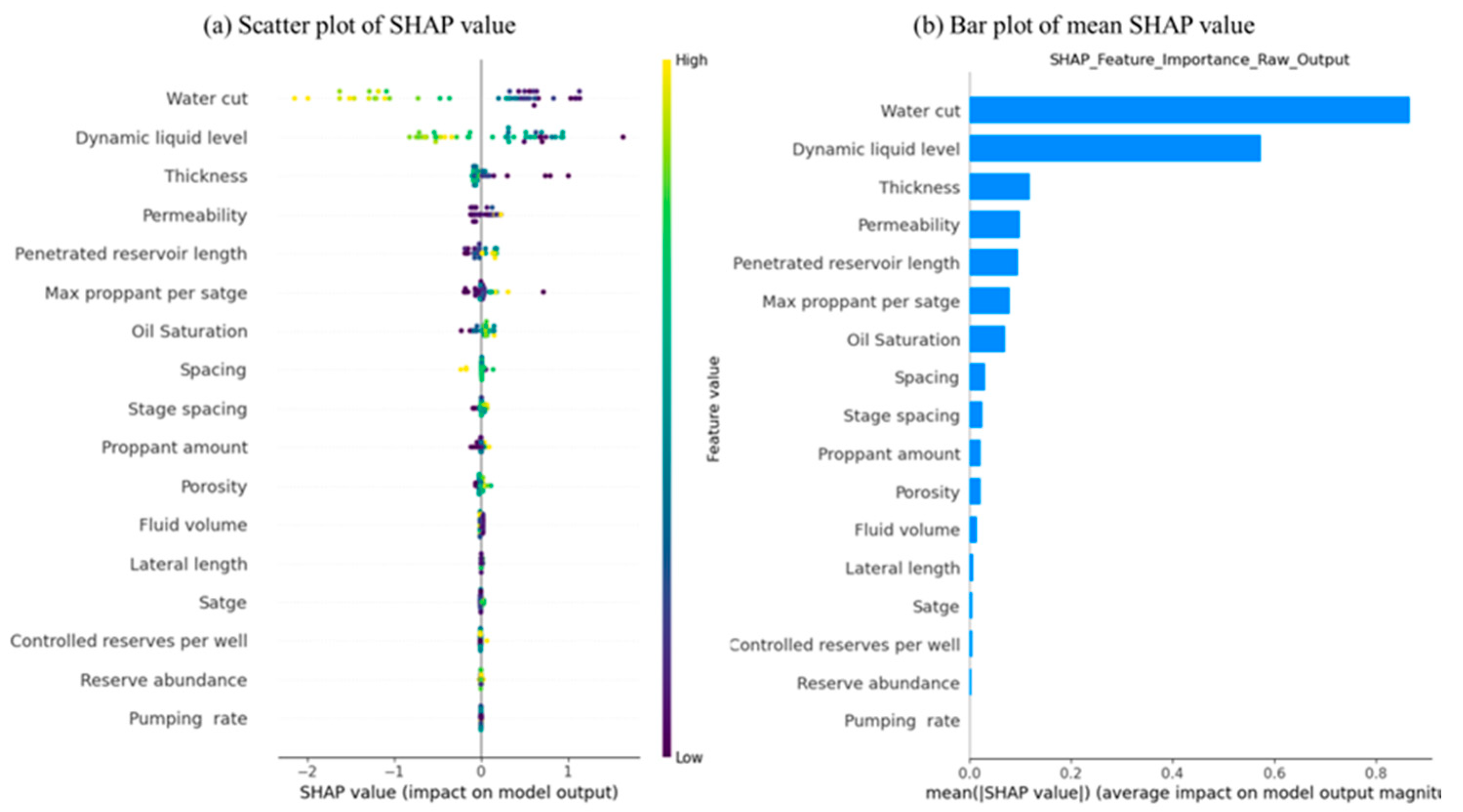
4.2. Explanatory Analysis of Factors Affecting KAN Productivity Combined with SHAP Value
5. Conclusions
- (1)
- The WOA algorithm was integrated with the KAN model and applied to the domain of oil well productivity prediction. By leveraging the global search capability of WOA, the selection of model hyperparameters was substantially optimized. Experimental results demonstrate that this approach not only enhances prediction accuracy but also improves computational efficiency. Compared with traditional parameter adjustment methods, WOA showed better stability and robustness when processing complex datasets, providing an efficient path for the construction of oil well productivity prediction models.
- (2)
- Based on the interpretability of the model itself, combined with the SHAP value and correlation heat map, the trend of productivity changes with influencing factors and the correlation between influencing factors and productivity were systematically analyzed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Geng, S.; Li, C.; Li, Y.; Zhai, S.; Xu, T.; Gong, Y.; Jing, M. Pressure transient analysis for multi-stage fractured horizontal wells considering threshold pressure gradient and stress sensitivity in tight sandstone gas reservoirs. Gas Sci. Eng. 2023, 116, 205030. [Google Scholar] [CrossRef]
- Liu, Z.-B.; Liu, H.-H. An effective method to predict oil recovery in high water cut stage. J. Hydrodyn. 2015, 27, 988–995. [Google Scholar] [CrossRef]
- Shen, A.; Liu, Y.; Wang, X.; Cai, B.; He, C.; Liang, S. The geological characteristics and exploration of continental tight oil: An investigation in China. J. Pet. Explor. Prod. Technol. 2019, 9, 1651–1658. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.; Li, J.; Zhang, Y.; Gao, L. Characteristics and causes of Mesozoic reservoirs with extra-low permeability and high water cut in northern Shaanxi. Pet. Explor. Dev. 2011, 38, 583–588. [Google Scholar] [CrossRef]
- Yang, H. Characteristics and resource prospects of tight oil and shale oil in Ordos Basin. Acta Pet. Sin. 2013, 34, 1–11. [Google Scholar]
- Wang, H.; Mu, L.; Shi, F.; Dou, H. Production prediction at ultra-high water cut stage via Recurrent Neural Network. Pet. Explor. Dev. 2020, 47, 1084–1090. [Google Scholar] [CrossRef]
- Aydin, G. Regression models for forecasting global oil production. Pet. Sci. Technol. 2015, 33, 1822–1828. [Google Scholar] [CrossRef]
- Sen, D.; Hamurcuoglu, K.I.; Ersoy, M.Z.; Tunç, K.M.M.; Günay, M.E. Forecasting long-term world annual natural gas production by machine learning. Resour. Policy 2023, 80, 103224. [Google Scholar] [CrossRef]
- Zhai, S.; Geng, S.; Li, C.; Gong, Y.; Jing, M.; Li, Y. Prediction of gas production potential based on machine learning in shale gas field: A case study. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 6581–6601. [Google Scholar] [CrossRef]
- Davtyan, A.; Rodin, A.; Muchnik, I.; Romashkin, A. Oil production forecast models based on sliding window regression. J. Pet. Sci. Eng. 2020, 195, 107916. [Google Scholar] [CrossRef]
- Ibrahim, N.M.; Alharbi, A.A.; Alzahrani, T.A.; Abdulkarim, A.M.; Alessa, I.A.; Hameed, A.M.; Albabtain, A.S.; Alqahtani, D.A.; Alsawwaf, M.K.; Almuqhim, A.A. Well performance classification and prediction: Deep learning and machine learning long term regression experiments on oil, gas, and water production. Sensors 2022, 22, 5326. [Google Scholar] [CrossRef] [PubMed]
- Luo, G.; Tian, Y.; Bychina, M.; Ehlig-Economides, C. Production Optimization Using Machine Learning in Bakken Shale. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018. [Google Scholar]
- Wang, S.; Chen, S. Insights to fracture stimulation design in unconventional reservoirs based on machine learning modeling. J. Pet. Sci. Eng. 2019, 174, 682–695. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, C.; Xu, C.; Wang, Z.; Li, F.; Shang, Y.; Zhang, S.; Li, X. Support vector machine-based initial productivity prediction for SRV of horizontal wells in tight oil reservoirs. China Offshore Oil Gas 2022, 34, 102–109. [Google Scholar]
- Suhag, A.; Ranjith, R.; Aminzadeh, F. Comparison of shale oil production forecasting using empirical methods and artificial neural networks. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov-arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar] [PubMed]
- Hu, Y.; Xin, X.; Yu, G.; Deng, W. Deep insight: An efficient hybrid model for oil well production forecasting using spatio-temporal convolutional networks and Kolmogorov–Arnold networks. Sci. Rep. 2025, 15, 8221. [Google Scholar] [CrossRef]
- Geng, S.; Zhai, S.; Li, C. Swin transformer based transfer learning model for predicting porous media permeability from 2D images. Comput. Geotech. 2024, 168, 106177. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J.; Khandelwal, M.; Yang, H.; Yang, P.; Li, C. Performance evaluation of hybrid WOA-XGBoost, GWO-XGBoost and BO-XGBoost models to predict blast-induced ground vibration. Eng. Comput. 2022, 38 (Suppl. S5), 4145–4162. [Google Scholar] [CrossRef]
- Zivkovic, M.; Bacanin, N.; Antonijevic, M.; Nikolic, B.; Kvascev, G.; Marjanovic, M.; Savanovic, N. Hybrid CNN and XGBoost model tuned by modified arithmetic optimization algorithm for COVID-19 early diagnostics from X-ray images. Electronics 2022, 11, 3798. [Google Scholar] [CrossRef]
- Ekanayake, I.; Palitha, S.; Gamage, S.; Meddage, D.; Wijesooriya, K.; Mohotti, D. Predicting adhesion strength of micropatterned surfaces using gradient boosting models and explainable artificial intelligence visualizations. Mater. Today Commun. 2023, 36, 106545. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, T.; Yang, H.; Qian, S.; Dong, Z.; Li, W.; Zou, L.; Liu, Z.; Wang, Z.; Zhang, T.; et al. Explainable Machine Learning-Based Method for Fracturing Prediction of Horizontal Shale Oil Wells. Processes 2023, 11, 2520. [Google Scholar] [CrossRef]
- Ma, X.; Hou, M.; Zhan, J.; Liu, Z. Interpretable Predictive Modeling of Tight Gas Well Productivity with SHAP and LIME Techniques. Energies 2023, 16, 3653. [Google Scholar] [CrossRef]
- Kim, H.-S.; Kim, H.-S.; Choi, S.-Y. Investigating the Impact of Agricultural, Financial, Economic, and Political Factors on Oil Forward Prices and Volatility: A SHAP Analysis. Energies 2024, 17, 1001. [Google Scholar] [CrossRef]
- Ma, Y.-Q.; Zhang, C.; Lu, Y.-C.; Kong, X.-Y.; Guo, Y.; Dong, Y.-X.; Chen, L.; Qi, R.; Xing, F.-C. Characteristics, main controlling factors and densification mechanisms of unconventional tight reservoirs in Triassic Yanchang Formation in southern Ordos Basin, China. Pet. Sci. 2024, 21, 3884–3898. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Cao, W.; Zhou, J.; Xu, Q.; Zhen, J.; Huang, X. Short-Term Forecasting and Uncertainty Analysis of Photovoltaic Power Based on the FCM-WOA-BILSTM Model. Front. Energy Res. 2022, 10, 926774. [Google Scholar] [CrossRef]
- Geng, S.; Zhai, S.; Ye, J.; Gao, Y.; Luo, H.; Li, C.; Liu, X.; Liu, S. Decoupling and predicting natural gas deviation factor using machine learning methods. Sci. Rep. 2024, 14, 21640. [Google Scholar] [CrossRef] [PubMed]
- Ekanayake, I.; Meddage, D.; Rathnayake, U. A novel approach to explain the black-box nature of machine learning in compressive strength predictions of concrete using Shapley additive explanations (SHAP). Case Stud. Constr. Mater. 2022, 16, e01059. [Google Scholar] [CrossRef]
- Mangalathu, S.; Hwang, S.-H.; Jeon, J.-S. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Eng. Struct. 2020, 219, 110927. [Google Scholar] [CrossRef]
- Jin, Y.; Guo, K.; Gao, X.; Li, Q. Tight Oil Well Productivity Prediction Model Based on Neural Network. Processes 2024, 12, 2088. [Google Scholar] [CrossRef]
- Zhao, K.; Du, P. A new production prediction model for multistage fractured horizontal well in tight oil reservoirs. Adv. Geo-Energy Res. 2020, 4, 152–161. [Google Scholar] [CrossRef]
- Gu, Z.; Eils, R.; Schlesner, M. Complex heatmaps reveal patterns and correlations in multidimensional genomic data. Bioinformatics 2016, 32, 2847–2849. [Google Scholar] [CrossRef] [PubMed]







| Variable | Value Before Z-Score | Value Before Z-Score | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Mean | Median | Std. | Max | Min | Mean | Median | Std. | |
| Spacing | 750 | 200 | 469.28 | 500 | 73.10 | 3.84 | −3.68 | 0 | 0.42 | 1 |
| Lateral Length | 2091 | 200 | 863.20 | 761 | 357.82 | 3.43 | −1.85 | −0.29 | ||
| Controlled Reserve Per Well | 49.94 | 2.62 | 19.04 | 18.03 | 8.41 | 3.67 | −1.95 | −0.12 | ||
| Penetrated Reservoir Length | 1889.90 | 36 | 712.69 | 641.27 | 328.22 | 3.59 | −2.06 | −0.22 | ||
| Permeability | 0.99 | 0.07 | 0.20 | 0.175 | 0.10 | 8.13 | −1.33 | −0.25 | ||
| Porosity | 16.90 | 6.63 | 10.20 | 10.2 | 1.07 | 6.28 | −3.35 | 0.00 | ||
| Oil Saturation | 72.89 | 41.25 | 56.20 | 56.39 | 4.75 | 3.51 | −3.15 | 0.04 | ||
| Thickness | 21.20 | 0.7 | 12.87 | 12.67 | 3.76 | 2.22 | −3.24 | −0.05 | ||
| Fracturing Stages | 33 | 4 | 11.60 | 10 | 4.67 | 4.58 | −1.63 | −0.34 | ||
| Stage Spacing | 238 | 60 | 64.97 | 64.845 | 29.84 | 5.80 | −2.18 | 0.00 | ||
| Proppant Amount | 5544.50 | 160 | 924.69 | 596.2 | 855.94 | 5.40 | −0.89 | −0.38 | ||
| Max Proppant Per Stage | 256.90 | 18.3 | 83.08 | 64.7 | 44.91 | 3.87 | −1.44 | −0.41 | ||
| Pumping Rate | 24.44 | 2 | 6.59 | 6 | 2.86 | 6.23 | −1.60 | −0.21 | ||
| Fluid Volume | 37,749.10 | 1521 | 7768.40 | 5336.6 | 5906.15 | 5.08 | −1.06 | −0.41 | ||
| Water Cut | 100 | 0 | 34.60 | 28.05 | 23.42 | 2.79 | −1.48 | −0.28 | ||
| Dynamic Liquid Level | 1436 | 179 | 1104.16 | 1160 | 209.10 | 1.59 | −4.42 | 0.27 | ||
| Oil Productivity | 13.57 | 0 | 2.67 | 2.23 | 1.92 | 5.67 | −1.39 | −0.23 | ||
| Parameter | Physical Meaning | Reference Range |
|---|---|---|
| width (width) | The number of nodes per layer of the model | 1–10 |
| grid (number of grid nodes) | The number of B-splines per spline activation function | 5–10 |
| K (degree) | The order of the B-spline function | 3–5 |
| steps (number of training rounds) | Control the training rounds of the model to avoid underfitting or overfitting | 10–200 |
| opt (optimizer type) | Optimize each model training to improve convergence speed | LBFGS, Adam |
| loss_fn (loss function) | Measuring model prediction error | MSE, CrossEntropy |
| lambda (L2 regularization term) | Control parameter size and improve model generalization ability | 0–0.1 |
| lamb_entropy (entropy regularization coefficient) | Control the complexity of the spline function to improve the accuracy of the model | 1–50 |
| Model | Parameters | Value |
|---|---|---|
| Network | Maximal depth | 4 |
| Maximal number of neurons per hidden layer | 5 | |
| Maximal grid value | 64 | |
| WOA | Population size | 30 |
| Max iteration | 50 | |
| Dimensions of the problem | 3 |
| KAN-WOA | Conventional KAN | SVM | LightGBM | |
|---|---|---|---|---|
| RMSE | 0.02326 | 0.0405 | 0.04589 | 0.03881 |
| MSE | 5.40935 × 10−4 | 0.00164 | 0.00211 | 0.00151 |
| R2 | 0.92 | 0.817 | 0.787 | 0.83 |
| MAPE | 0.97 | 0.91 | 0.87 | 0.94 |
| MAE | 0.03933 | 0.04933 | 0.05933 | 0.05233 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yi, T.; Zhou, D.; Zhang, H.; Zhang, Y.; Xue, R.; Zhu, Z.; Wen, Z. Predicting Oil Productivity of High Water Cut Fractured Horizontal Wells in Tight Oil Reservoirs Based on KAN. Processes 2025, 13, 3629. https://doi.org/10.3390/pr13113629
Zhang H, Yi T, Zhou D, Zhang H, Zhang Y, Xue R, Zhu Z, Wen Z. Predicting Oil Productivity of High Water Cut Fractured Horizontal Wells in Tight Oil Reservoirs Based on KAN. Processes. 2025; 13(11):3629. https://doi.org/10.3390/pr13113629
Chicago/Turabian StyleZhang, Hongjun, Tao Yi, Dalin Zhou, Hongbo Zhang, Yuyang Zhang, Rui Xue, Zhuyi Zhu, and Zhigang Wen. 2025. "Predicting Oil Productivity of High Water Cut Fractured Horizontal Wells in Tight Oil Reservoirs Based on KAN" Processes 13, no. 11: 3629. https://doi.org/10.3390/pr13113629
APA StyleZhang, H., Yi, T., Zhou, D., Zhang, H., Zhang, Y., Xue, R., Zhu, Z., & Wen, Z. (2025). Predicting Oil Productivity of High Water Cut Fractured Horizontal Wells in Tight Oil Reservoirs Based on KAN. Processes, 13(11), 3629. https://doi.org/10.3390/pr13113629





