Physical-Guided Dynamic Modeling of Ultra-Supercritical Boiler–Turbine Coordinated Control System Under Wet-Mode Operation
Abstract
1. Introduction
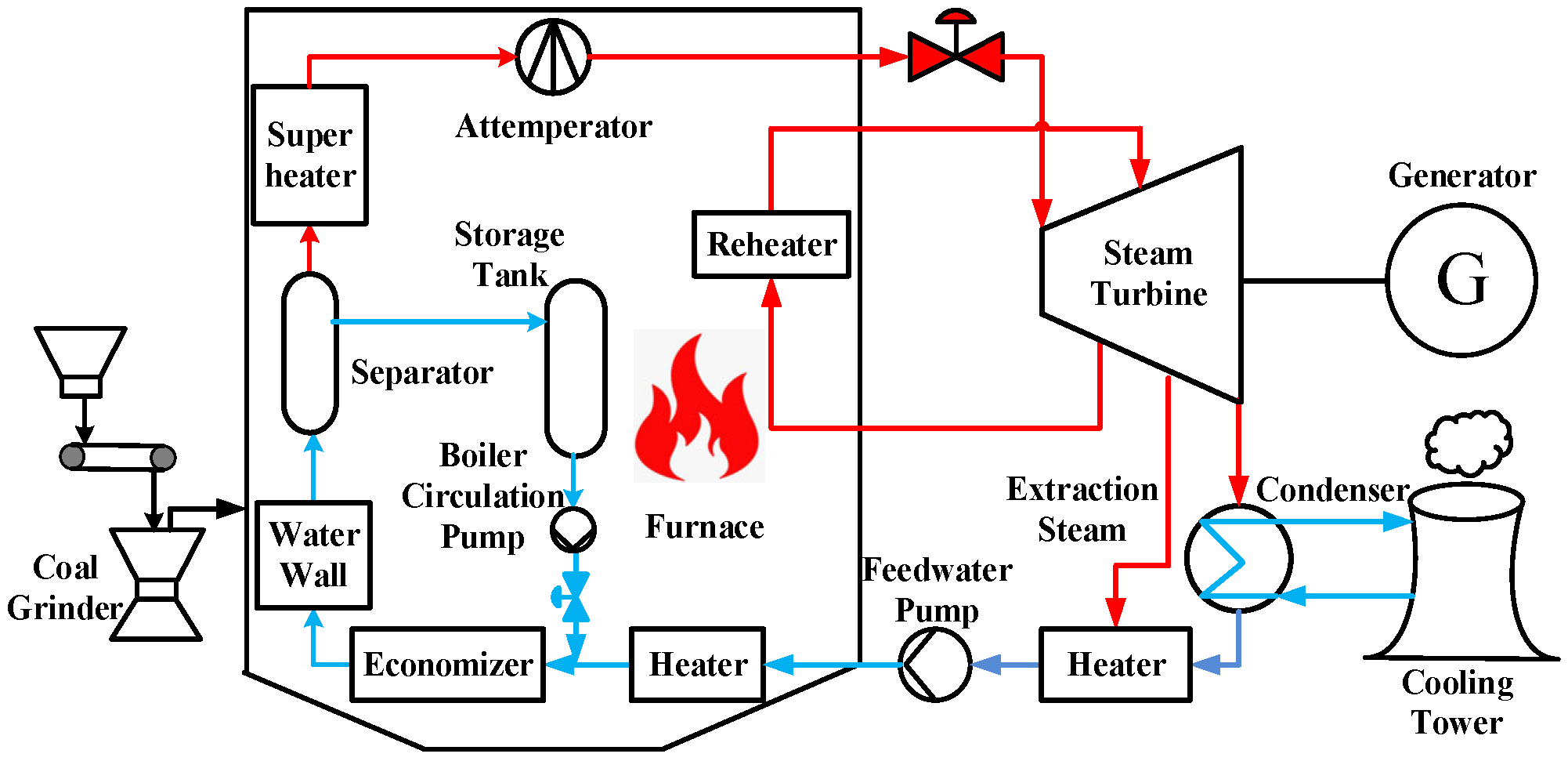
2. Description of BTCCS for OTB Coal-Fired Units Under Wet Conditions
2.1. Operational Process of BTCCS for OTB Coal-Fired Units Under Wet Conditions
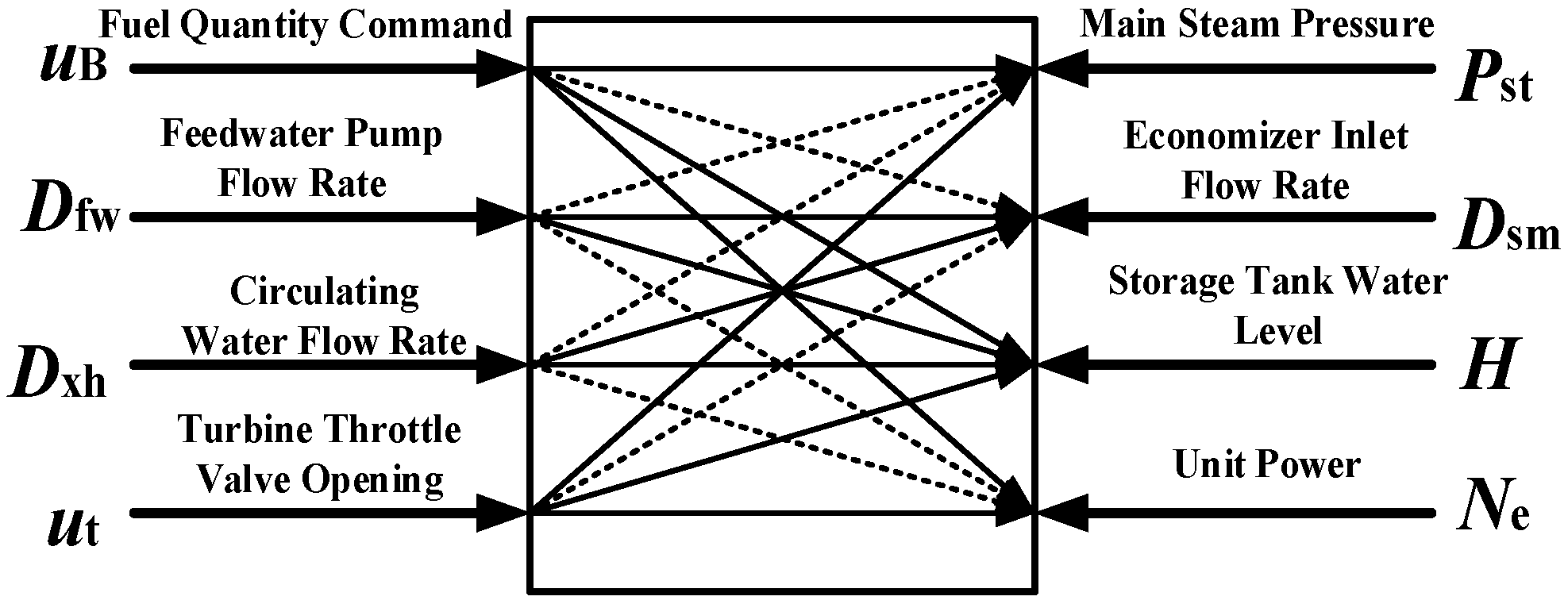
2.2. Control Model Variables of BTCCS for OTB Coal-Fired Units Under Wet Conditions
3. Dynamic Modeling of BTCCS for OTB Coal-Fired Units Under Wet Conditions
3.1. Dynamic Modeling of Pulverizing System
3.2. Dynamic Modeling of the Economizer and Water-Wall System
3.3. Dynamic Modeling of Water Storage Tank System
3.4. Dynamic Modeling of Superheater System
3.5. Dynamic Modeling of Steam Turbine System
3.6. Dynamic Model Structure of BTCCS for OTB Coal-Fired Units Under Wet Conditions
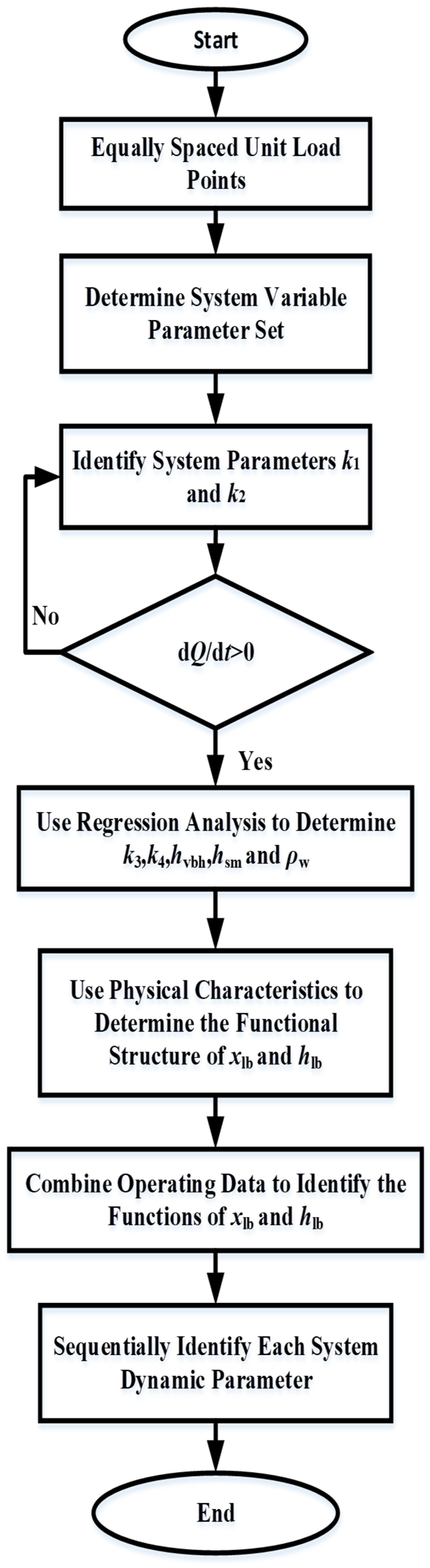
4. Parameter Identification
5. Model Validation
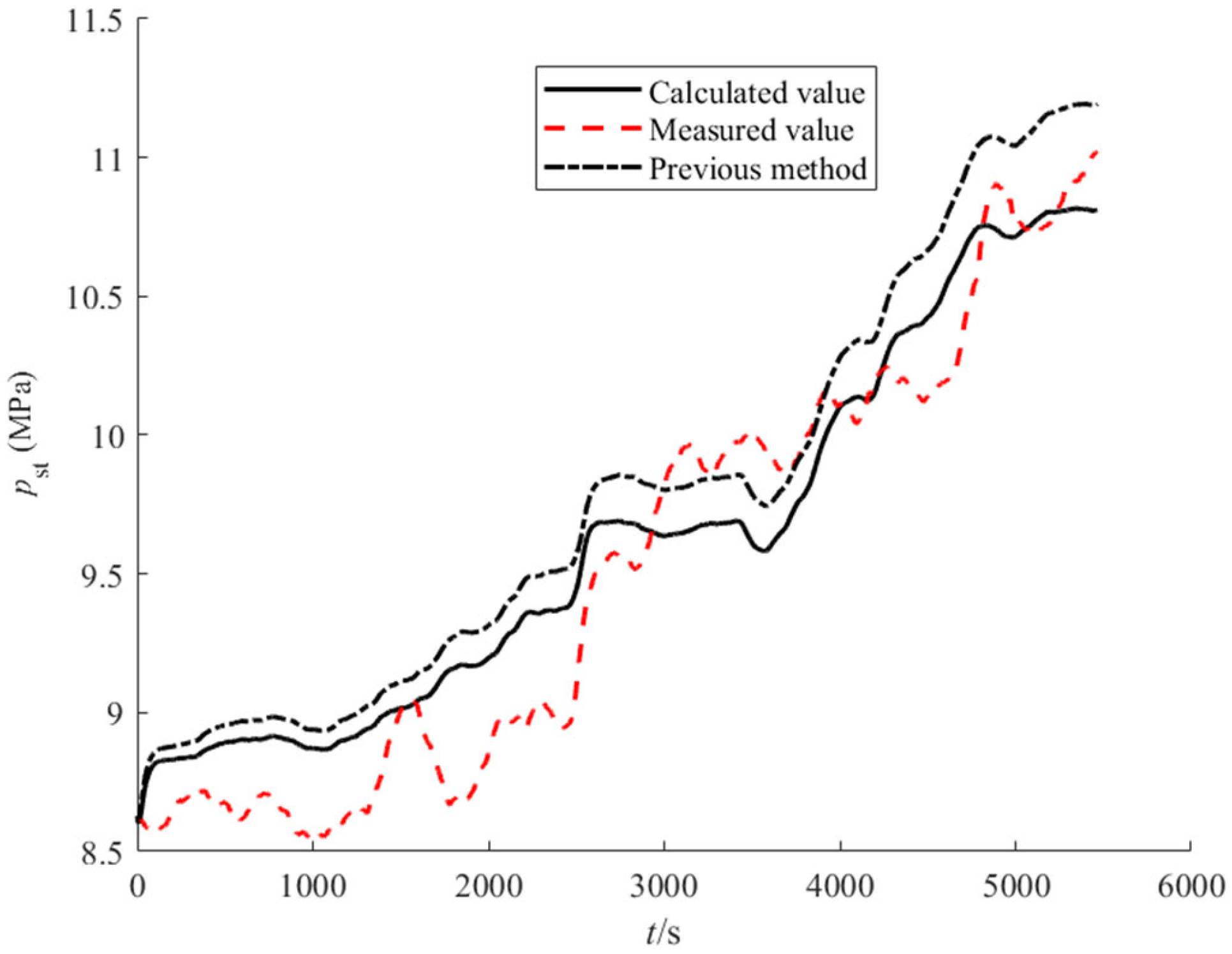
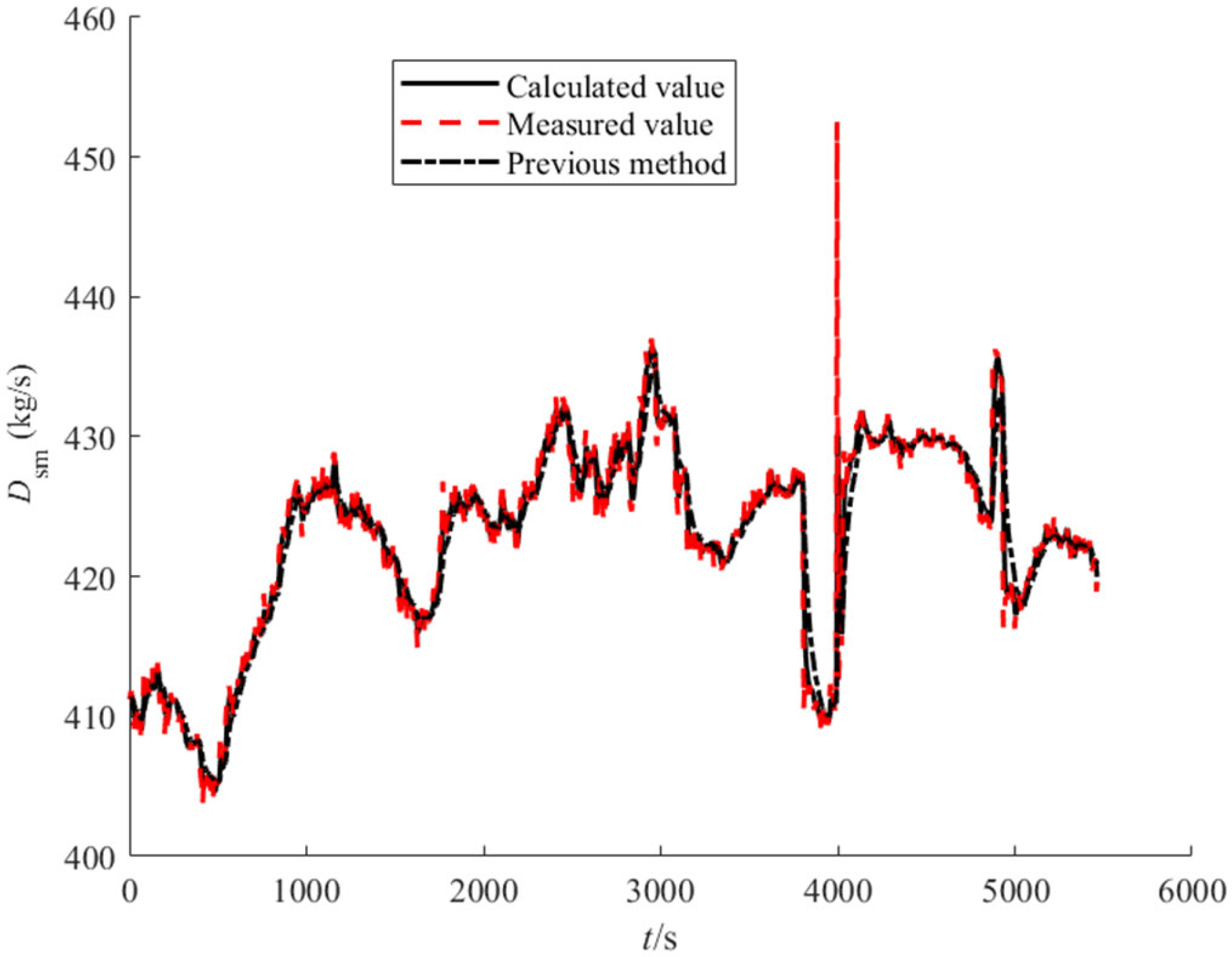
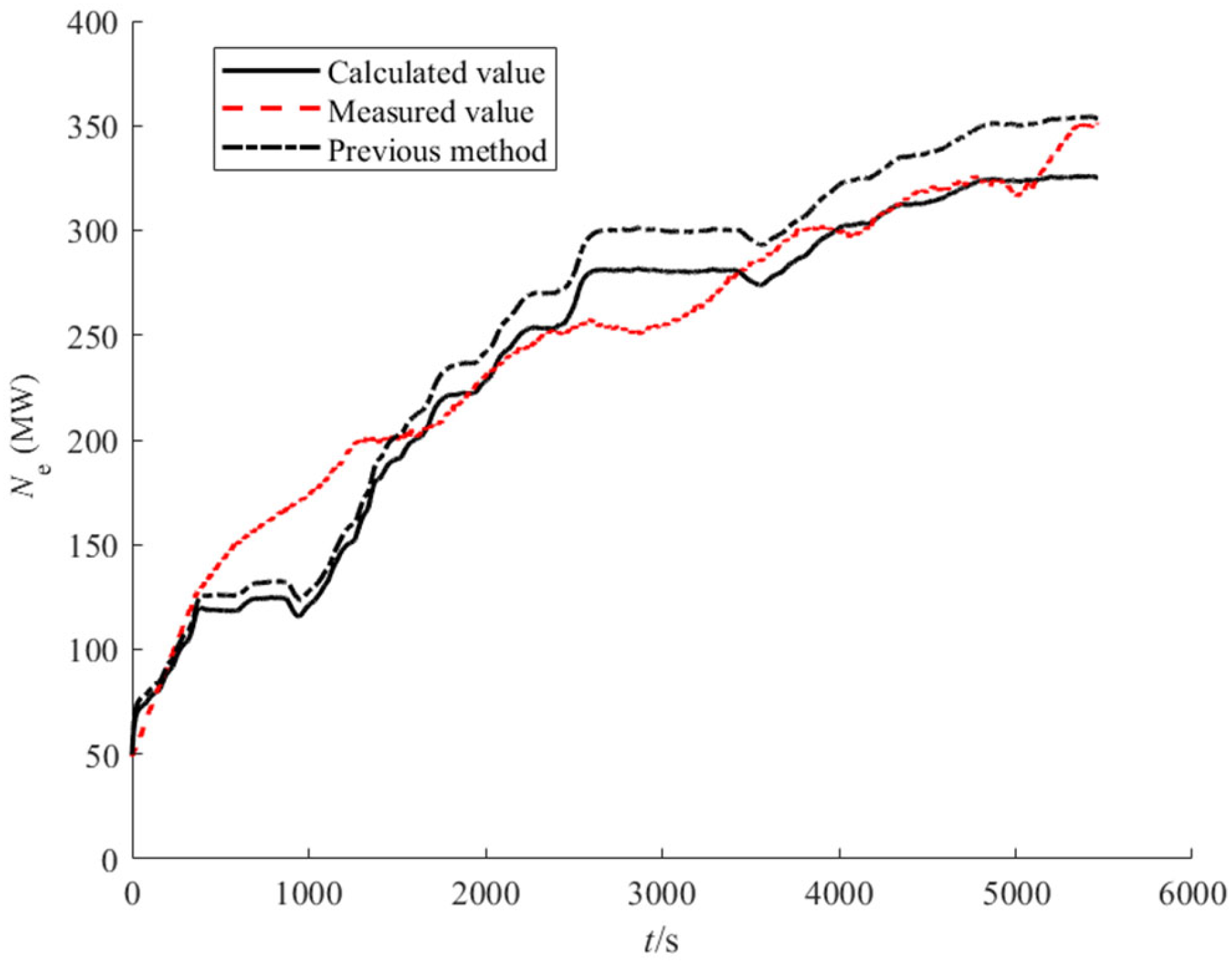
5.1. Model Dynamic Accuracy Validation
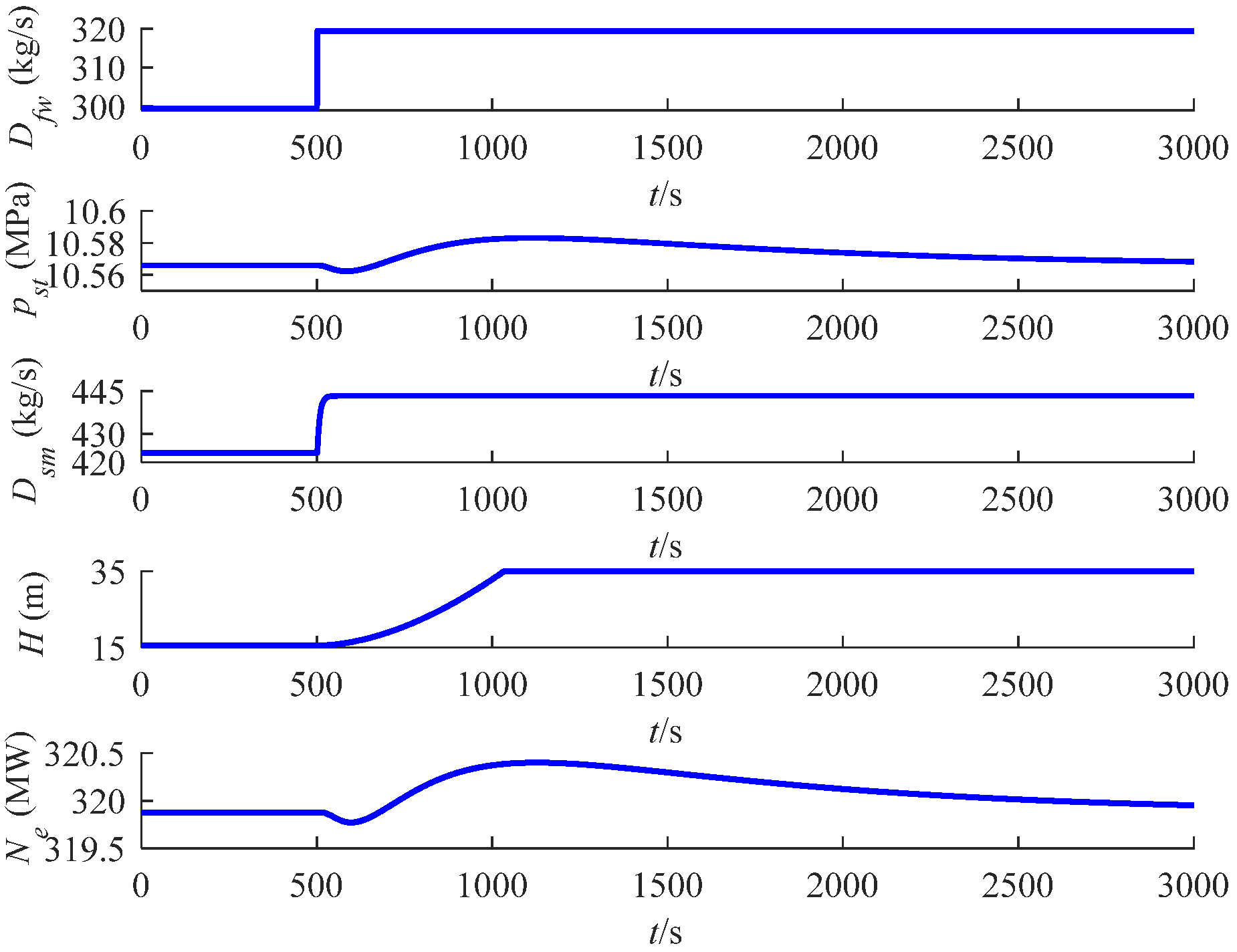
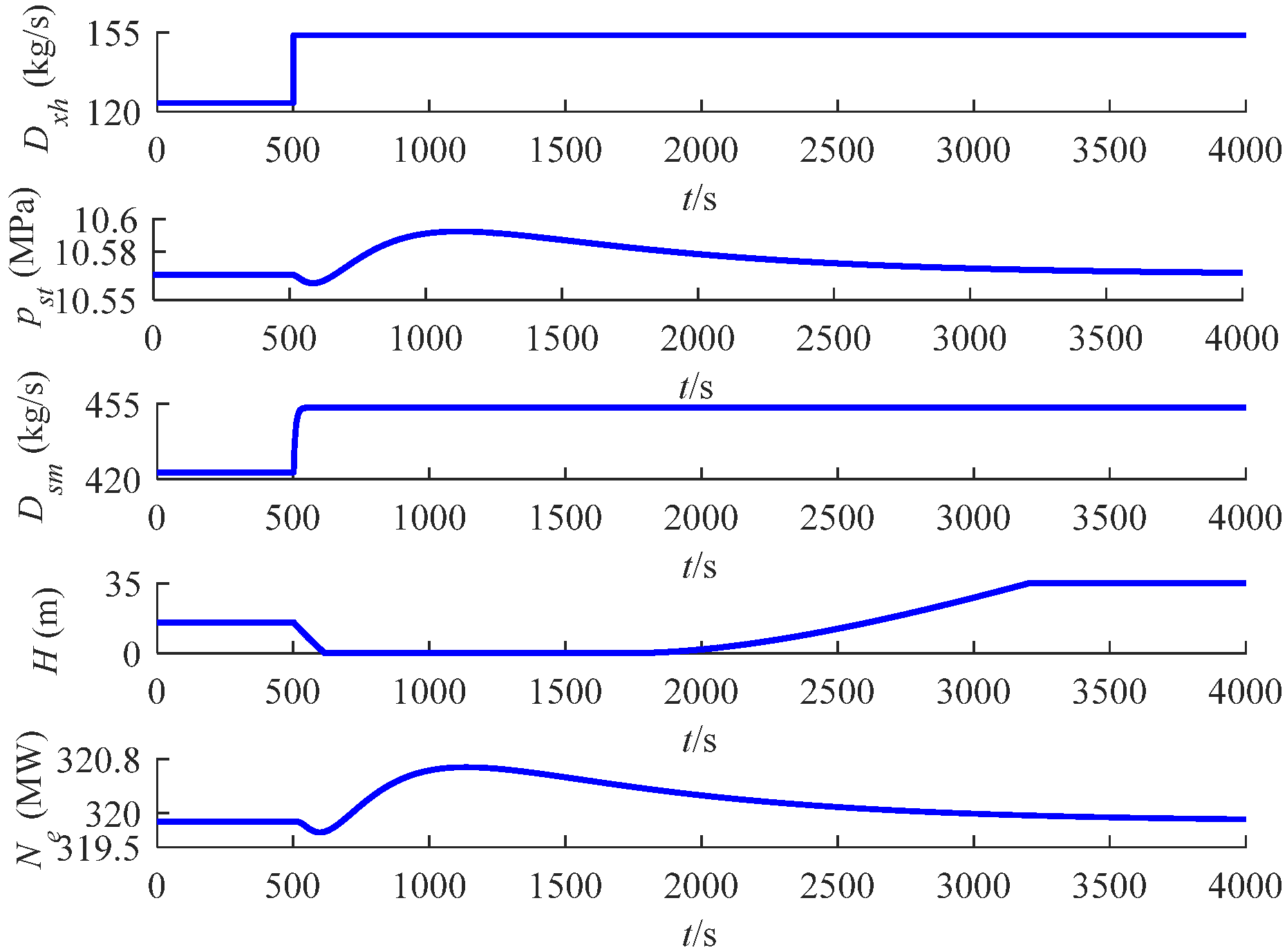
5.2. Model Dynamic Characterization and Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, C.L.; Wang, C.; Hou, Z.Y.; Wang, Z. Flexible peak shaving in coal-fired power plants: A comprehensive review of current challenges, recent advances, and future perspectives. Energy 2025, 327, 136446. [Google Scholar] [CrossRef]
- Sun, F.; Ji, J.X.; Zeng, G.; Li, J.L.; Wei, G.S. Employment of molten salt thermal energy storage coupled to coal-fired power unit for power grid peak shaving: A thermodynamic study. J. Energy Storage 2025, 131, 117503. [Google Scholar] [CrossRef]
- Esmaeili, M.; Moradi, H. Robust & nonlinear control of an ultra-supercritical coal fired once-through boiler-turbine unit in order to optimize the uncertain problem. Energy 2023, 282, 128312. [Google Scholar] [CrossRef]
- Gao, Z.; Lv, J.H.; Qv, X.F.; Ge, H. Research on Modeling of a Fully Loaded Ultra-supercritical Boiler-Turbine Coordination System. Power Equip. 2021, 35, 201–206. (In Chinese) [Google Scholar] [CrossRef]
- Wang, G.T.; Du, M.; Zhang, T.; Wu, Z. Research on Coordinated System Model and Control Strategy of Thermal Power Unit under Wet Operation. J. Eng. Therm. Energy Power 2022, 37, 25–32. (In Chinese) [Google Scholar] [CrossRef]
- Liu, Z.F.; Wang, C.Y.; Fan, M.Y.; Wang, Z.; Fang, F.; Liu, M.; Yan, J.J. Investigation on the allowable load ramping-up rate and wet-to-dry conversion time of a 660 MW supercritical coal-fired power plant with deep peak-shaving work conditions. Energy 2025, 314, 134200. [Google Scholar] [CrossRef]
- Hentschel, J.; Zindler, H.; Spliethoff, H. Modelling and transient simulation of a supercritical coal-fired power plant: Dynamic response to extended secondary control power output. Energy 2017, 137, 927–940. [Google Scholar] [CrossRef]
- Sarda, P.; Hedrick, E.; Reynolds, K.; Bhattacharyya, D.; Stephen, E.Z.; Omell, B. Development of a Dynamic Model and Control System for Load-Following Studies of Supercritical Pulverized Coal Power Plants. Processes 2018, 6, 226. [Google Scholar] [CrossRef]
- Liu, J.Z.; Yan, S.; Zeng, D.L.; Hu, Y.; Lv, Y. A dynamic model used for controller design of a coal fired once-through boiler-turbine unit. Energy 2015, 93, 2069–2078. [Google Scholar] [CrossRef]
- Liang, Q.J.; Liu, J.Z.; Xue, Y.G.; Yan, S.; Zeng, D.L. A Non-linear Model for Ultra-supercritical Power Unit and the Dynamic Characteristic Study. J. Chin. Soc. Power Eng. 2012, 32, 118–123. (In Chinese) [Google Scholar] [CrossRef]
- Qin, Z.M.; Liu, J.Z.; Zhang, L.Y.; Gu, J.J. A Simplified Nonlinear Dynamic Model for Once-through Boiler Units. J. Chin. Soc. Power Eng. 2013, 33, 955–961. (In Chinese) [Google Scholar]
- Yan, S.; Zeng, D.; Liu, J.; Liang, Q. A simplified non-linear model of a once-through boiler-turbine unit and its application. Proc. CSEE 2012, 32, 126–134. (In Chinese) [Google Scholar] [CrossRef]
- Niu, Y.G.; Du, M.; Ge, W.C.; Luo, H.H.; Zhou, G.P. A dynamic nonlinear model for a once-through boiler-turbine unit in low load. Appl. Therm. Eng. 2019, 161, 113880. [Google Scholar] [CrossRef]
- Tian, L.; Lian, H.; Liu, X.; Liu, J. Coupling Characteristics of Steam Pressure and Intermediate Point Temperature for Once-through Boiler. Proc. CSEE 2017, 37, 1142–1150. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, H.; Liu, C.K.; Liu, Z.W.; Hu, W.S. Temperature Control via Affine Nonlinear Systems for Intermediate Point of Supercritical Once-Through Boiler Units. Math. Probl. Eng. 2014, 2014, 873142. [Google Scholar] [CrossRef]
- Go, G.; Moon, U.C. A Water-Wall Model of Supercritical Once-Through Boilers Using Lumped Parameter Method. J. Electr. Eng. Technol. 2014, 9, 1900–1908. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, J.Z.; Zeng, D.L.; Hu, Y.; Zhu, Y.S.; Li, R.L. A dynamic mathematical model used for controller design of a supercritical once-through boiler-turbine unit in all load conditions. Appl. Therm. Eng. 2024, 248, 123139. [Google Scholar] [CrossRef]
- Tian, Z.; Yuan, J.Q.; Zhang, X.; Kong, L.; Wang, J.C. Modeling and sliding mode predictive control of the ultra-supercritical boiler-turbine system with uncertainties and input constraints. ISA Trans. 2018, 76, 43–56. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, J.-Z.; Zeng, D.-L.; Hu, Y.; Li, R.-L.; Zhu, Y.-S. A dynamic hybrid model of supercritical once-through boiler-turbine unit including recirculation mode and once-through mode. Energy 2024, 309, 132941. [Google Scholar] [CrossRef]
- Deng, K.J.; Yang, C.; Chen, H.; Zhou, N.N.; Huang, S.L. Start-Up and dynamic processes simulation of supercritical once-through boiler. Appl. Therm. Eng. 2017, 115, 937–946. [Google Scholar] [CrossRef]
- Zhang, H.F.; Gao, M.M.; Fan, H.H.; Zhang, K.P.; Zhang, J.H. A dynamic model for supercritical once-through circulating fluidized bed boiler-turbine units. Energy 2022, 241, 122914. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, Y.F.; Su, Z.G.; Wang, B. A dynamic mathematical model of an ultra-supercritical coal fired once-through boiler-turbine unit. Appl. Energy 2017, 189, 654–666. [Google Scholar] [CrossRef]
- Fan, H.; Su, Z.G.; Wang, P.H.; Lee, K.Y. A dynamic nonlinear model for a wide-load range operation of ultra-supercritical once-through boiler-turbine units. Energy 2021, 226, 120425. [Google Scholar] [CrossRef]
- Fan, H.; Su, Z.-G.; Wang, P.-H.; Lee, K.Y. A dynamic mathematical model for once-through boiler-turbine units with superheated steam temperature. Appl. Therm. Eng. 2020, 170, 114912. [Google Scholar] [CrossRef]
- Haddad, A.; Mohamed, O.; Zahlan, M.; Wang, J. Parameter identification of a highly promising cleaner coal power station. J. Clean. Prod. 2021, 326, 129323. [Google Scholar] [CrossRef]
- Taler, J.; Zima, W.; Ocłoń, P.; Gradziel, S.; Taler, D.; Cebula, A.; Jaremkiewicz, M.; Korzen, A.; Cisek, P.; Kaczmarski, K.; et al. Mathematical model of a supercritical power boiler for simulating rapid changes in boiler thermal loading. Energy 2019, 175, 580–592. [Google Scholar] [CrossRef]
- Ghaffari, A.; Chaibakhsh, A.; Lucas, C. Soft computing approach for modeling power plant with a once-through boiler. Eng. Appl. Artif. Intell. 2007, 20, 809–819. [Google Scholar] [CrossRef]
- Liu, X.J.; Kong, X.B.; Hou, G.L.; Wang, J.H. Modeling of a 1000 MW power plant ultra super-critical boiler system using fuzzy-neural network methods. Energy Convers. Manag. 2013, 65, 518–527. [Google Scholar] [CrossRef]
- Liu, X.J.; Zhang, H.; Niu, Y.G.; Zeng, D.L.; Liu, J.Z.; Kong, X.B.; Lee, K.Y. Modeling of an ultra-supercritical boiler-turbine system with stacked denoising auto-encoder and long short-term memory network. Inf. Sci. 2020, 525, 134–152. [Google Scholar] [CrossRef]
- Huang, C.Z.; Li, Z.Y. Data-driven modeling of ultra-supercritical unit coordinated control system by improved transformer network. Energy 2023, 266, 126473. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Tan, P.; He, Z.Q.; Zhang, C.; Fang, Q.Y.; Chen, G. Nonlinear model predictive control of USC boiler-turbine power units in flexible operations via input convex neural network. Energy 2022, 255, 124486. [Google Scholar] [CrossRef]
- Hou, G.L.; Du, H.; Yang, Y.; Huang, C.Z.; Zhang, J.H. Coordinated control system modelling of ultra-supercritical unit based on a new T-S fuzzy structure. ISA Trans. 2018, 74, 120–133. [Google Scholar] [CrossRef]
- Hou, G.L.; Gong, L.J.; Huang, C.Z.; Zhang, J.H. Novel fuzzy modeling and energy-saving predictive control of coordinated control system in 1000 MW ultra-supercritical unit. ISA Trans. 2019, 86, 48–61. [Google Scholar] [CrossRef]
- Hou, G.L.; Xiong, J.; Zhou, G.P.; Gong, L.J.; Huang, C.Z.; Wang, S.J. Coordinated control system modeling of ultra-supercritical unit based on a new fuzzy neural network. Energy 2021, 234, 121231. [Google Scholar] [CrossRef]
- Lee, K.Y.; Van Sickel, J.H.; Hoffman, J.A.; Jung, W.H.; Kim, S.H. Controller Design for a Large-Scale Ultrasupercritical Once-Through Boiler Power Plant. IEEE Trans. Energy Convers. 2010, 25, 1063–1070. [Google Scholar] [CrossRef]
- Dai, B.W.; Chang, Y.Q.; Xu, S.; Wang, F.L. Process Knowledge-Guided Optimization Control for Once-Through Boiler-Turbine Units Based on Multi-Agent Reinforcement Learning. ACS Omega 2025, 10, 14844–14857. [Google Scholar] [CrossRef]
- Huang, C.Z.; Sheng, X.X. Data-driven model identification of boiler-turbine coupled process in 1000 MW ultra-supercritical unit by improved bird swarm algorithm. Energy 2020, 205, 118009. [Google Scholar] [CrossRef]



| Project | Value |
|---|---|
| Unit load (MW) | 1000 |
| Superheated steam flow (t/h) | 3044 |
| Superheated steam temperature (°C) | 605 |
| Superheated steam pressure (MPa) | 27.46 |
| Feedwater temperature (°C) | 297 |
| Reheat steam flow (t/h) | 2544 |
| Reheater outlet steam temperature (°C) | 603 |
| Storage tank height (m) | 35 |
| Storage tank bottom diameter (m) | 0.61 |
| Ne (MW) | pst (MPa) | H (m) | Dsm (kg/s) | uB (kg/s) | Dfw (kg/s) | Dxh (kg/s) | ut | Dst (kg/s) | pm (MPa) | hst (kJ/kg) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.819 | 8.71 | 4.13 | 399.5 | 32.3 | 218.7 | 180.6 | 1 | 213.7 | 8.93 | 3283.9 |
| 50.42 | 8.62 | 12.62 | 411.38 | 35.9 | 249.1 | 162.3 | 1 | 243.1 | 8.91 | 3195.9 |
| 100.2 | 8.68 | 12.02 | 411.2 | 37.3 | 247.0 | 164.3 | 1 | 246 | 9.00 | 3200.5 |
| 150.5 | 8.62 | 4.44 | 411.5 | 38.2 | 251.7 | 159.8 | 1 | 249.5 | 8.95 | 3205.8 |
| 200.36 | 8.83 | 12.75 | 422.4 | 41.4 | 239.6 | 182.7 | 1 | 239.9 | 9.19 | 3263.4 |
| 251.3 | 8.97 | 12.7 | 431.0 | 45.6 | 263.4 | 167.6 | 1 | 262.6 | 9.49 | 3308.3 |
| 300.7 | 10.1 | 10.6 | 413.8 | 48.4 | 293.3 | 120.7 | 1 | 298.4 | 10.64 | 3252.7 |
| 350.4 | 11 | 12.5 | 421.7 | 50.3 | 316.5 | 105.2 | 1 | 315.8 | 11.55 | 3299.4 |
| Indicator | pst (MPa) | Dsm (kg/s) | H (m) | Ne (MW) | |
|---|---|---|---|---|---|
| Proposed method | MRE (%) | 2.31 | 0.14 | 1.86 | 7.42 |
| RMSE | 0.245 | 1.31 | 0.22 | 20.43 | |
| Previous method | MRE (%) | 3.15 | 0.28 | 9.3 | 10.02 |
| RMSE | 0.33 | 2.09 | 1.28 | 26.09 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, G.; Fan, H.; Peng, X.; Wang, Y.; Wang, Y.; He, Z.; Zhuang, K.; Chen, G.; Zhang, Z.; Sun, X.; et al. Physical-Guided Dynamic Modeling of Ultra-Supercritical Boiler–Turbine Coordinated Control System Under Wet-Mode Operation. Processes 2025, 13, 3625. https://doi.org/10.3390/pr13113625
Yin G, Fan H, Peng X, Wang Y, Wang Y, He Z, Zhuang K, Chen G, Zhang Z, Sun X, et al. Physical-Guided Dynamic Modeling of Ultra-Supercritical Boiler–Turbine Coordinated Control System Under Wet-Mode Operation. Processes. 2025; 13(11):3625. https://doi.org/10.3390/pr13113625
Chicago/Turabian StyleYin, Ge, He Fan, Xianyong Peng, Yongzhen Wang, Yuhan Wang, Zhiqian He, Ke Zhuang, Guoqing Chen, Zhenming Zhang, Xueli Sun, and et al. 2025. "Physical-Guided Dynamic Modeling of Ultra-Supercritical Boiler–Turbine Coordinated Control System Under Wet-Mode Operation" Processes 13, no. 11: 3625. https://doi.org/10.3390/pr13113625
APA StyleYin, G., Fan, H., Peng, X., Wang, Y., Wang, Y., He, Z., Zhuang, K., Chen, G., Zhang, Z., Sun, X., Sheng, W., Xu, M., Zhang, H., Lu, Y., & Zhou, H. (2025). Physical-Guided Dynamic Modeling of Ultra-Supercritical Boiler–Turbine Coordinated Control System Under Wet-Mode Operation. Processes, 13(11), 3625. https://doi.org/10.3390/pr13113625






