Optimization Method of Heat-Sealing Process for Pillow Packaging Machine

Abstract

Aiming at the problems of low production efficiency and high manual dependence in the heat-sealing process of the pillow packaging machine, the existing optimization methods of process parameters were improved, and an intelligent decision-making model of the longitudinal sealing heat-sealing process based on the radial basis function neural network and orthogonal least square method was proposed to realize the efficient and accurate optimization of heat-sealing process parameters. By analyzing the fracture yield strength of the composite, the target heat-sealing strength range was determined. The heat-sealing temperature, heat-sealing speed, and heat-sealing plate distance were selected as key process variables, and the actual production data were used to train the model to accurately construct the nonlinear mapping relationship between heat-sealing process parameters and heat-sealing strength. On this basis, the genetic algorithm optimization framework with the model predictive output as the fitness function is designed to realize the rapid search of the optimal combination of process parameters. The optimization results were introduced into the pillow packaging machine for a verification test. The measured heat-sealing strength was stable within the target range. The maximum error of the optimization group was less than 10%, and the average error was less than 5%, which was significantly better than the effect of manual experience. The experimental results show that the proposed method can effectively improve the efficiency and consistency of process optimization under the premise of ensuring the quality of heat-sealing, meet the requirements of automatic production for high precision and low consumption of the heat-sealing process optimization, and realize the comprehensive improvement of efficiency, accuracy, and intelligent level in the longitudinal heat-sealing process of the pillow packaging machine.

1. Introduction

As a part of the commodity itself, the packaging bag can not only avoid the damage of the commodity in the transportation process, but also directly affect the purchase behavior of consumers. It is a necessary condition for the commodity to enter the circulation field, and the packaging equipment is the main means to realize the commodity packaging [1]. Although the automatic packaging machine for prefabricated bags has made great progress, there are still some problems, such as low packaging accuracy, low packaging speed, and unstable heat-sealing quality [2,3]. As the most critical link in the packaging process, the heat-sealing process plays a decisive role in the packaging production. In the actual production and commodity transportation process, the damage of packaging bags also mostly occurs in the heat-sealing part [4,5]. Therefore, it is of great significance to study the heat-sealing device and heat-sealing process parameters for improving the overall quality of packaging products.

The heat-sealing quality of packaging bags mainly depends on the heat-sealing pressure, temperature, and time. When the heat-sealing time is fixed, the higher the frequency of sealing opening and closing, the higher the working efficiency, but the impact on the heat-sealing mechanism is increased, and the working life is reduced, which is the main reason restricting the improvement of the production efficiency of the packaging machine [6]. At the same time, due to the increase in the speed of the packaging machine, the heat-sealing residence time is shortened in the packaging process. In engineering practice, the shortage of heat-sealing residence time is often offset by increasing the heat-sealing temperature and pressure. However, too high heat-sealing temperature and pressure will scald the surface of the packaging bag material, and the heat-sealing quality of the packaging bag is extremely unstable at high speed [7]. The academic community generally believes that the heat-sealing between films is the diffusion of molecules in the molten film under the action of external pressure and temperature. After a certain time, the two heat-sealing surfaces are combined and cooled sufficiently to form a bond. The main factors affecting the heat-sealing performance of films are heat-sealing pressure, heat-sealing temperature, and heat-sealing time [8].

In the production process of the pillow packaging machine, there is a large waste of manpower in the longitudinal sealing and heat-sealing process. The main reason is the difficulty in selecting heat-sealing parameters. Mihindukulasuriya et al. [9] established a heat transfer model to elucidate the heat transfer of two-layer linear low-density polyethylene (LLDPE) film during the heat-sealing process, and validated the heat transfer model with experimental data on the membrane–membrane interface temperature, which can effectively predict the membrane–membrane interface temperature. Junior et al. [10] studied the effects of high-pressure treatment on the morphology, thermal properties, and mechanical properties of flexible packaging materials from a thermodynamic perspective under different process conditions. Aiyengar et al. [11] obtained a second-order model of heat-sealing strength using response surface methodology and replicated center composite statistical experiments by optimizing the heat-sealing strength of 18 µM thick, untreated, double-sided sealable biaxially oriented polypropylene film. Experiments have shown that residence time, temperature, and their interactions have significant effects. Yuan et al. [12] studied the effect of bar sealing parameters on the heat-sealing strength of oriented polypropylene (OPP)/metal cast polypropylene (MCPP) laminated films. Based on the results of parametric research, a window for the rod sealing process has been established. All drop points within the process window are a combination of pressure plate temperature and dwell time, resulting in an acceptable heat-seal. The above scholars have studied the factors affecting the heat-sealing strength of thin films from different perspectives, but have not simultaneously selected multiple key parameters that affect the heat-sealing strength of thin films.

With the development of finite element simulation technology, scholars use the simulation method to establish the heat-sealing parameters of packaging film. Jang [13] et al. studied the temperature distribution of the inner layer of the pet/al/cpp composite film by establishing the heat transfer model of the pet/al/cpp composite film and taking the heat-sealing time and the heat-sealing head width as variables, and finally determined that the heat-sealing quality of the composite film was the best when the heat-sealing time was 3S and the heat-sealing head width was 15 mm. Aghkand et al. [14] used COMSOL (5.6) software to analyze the heat transfer behavior of each layer of pa/pe (polyamide/polyethylene) composite film during the heat-sealing process, and measured the temperature distribution at the junction of the film interface by adding thermocouples at the contact interface of the two layers of composite film, and finally determined the heat-sealing temperature range of pa/pe composite film based on the finite element analysis results. Aghkand et al. [15] established the rheological model of pa/pe composite film in the heat-sealing process and studied the effects of heat-sealing temperature, heat-sealing time, heat-sealing pressure, and heat-sealing layer material thickness on the heat-sealing performance of multilayer polymer film by using the method of combining theory with experiment, and then optimized the heat-sealing parameters. Ilhan et al. [16] estimated that the minimum heat-sealing time required for the heat-sealing of bopp/ldpe composite film was 0.5 s by analyzing the heat transfer behavior of bopp/ldpe composite film with different thicknesses under different heat-sealing temperatures and pressures, and verified the correctness of the estimated heat-sealing time through a heat-sealing strength test. Ponnambalam et al. [17] studied the effects of heat-sealing residence time, heat-sealing temperature, heat-sealing pressure and the presence of pollutants on the heat-sealing performance of pet/al/pe (polyethylene terephthalate/aluminum/polyethylene) composite film, and concluded that when the heat-sealing temperature was greater than 240 °C and the heat-sealing residence time was greater than 1 s, the heat-sealing strength of the composite film would decrease. To sum up, the above research is only to optimize the heat-sealing parameters of composite film from the theoretical aspect, but there is no in-depth study on how to establish the optimal heat-sealing parameters under the given packaging speed in actual production. In this paper, combined with the heat-sealing device and process studied, under the condition that the heat-sealing time is known, the influence of different heat-sealing parameters on the heat-sealing quality of packaging film is further analyzed, and then the heat-sealing parameters in the actual production are determined.

The existing research work lacks the analysis of the actual production process, especially for the longitudinal sealing and heat-sealing process of the pillow packaging machine. Compared with the laboratory conditions, it is more difficult to apply the heat-sealing process to actual production, so many scholars have not carried out in-depth research on it. After using neural network genetic algorithm to optimize the parameters with reference to the directions of various disciplines [18,19], this topic proposes a parameter optimization strategy of RBF neural network (radial basis function neural network)—genetic algorithm for the automatic parameter optimization of longitudinal heat-sealing of pillow packaging machine, so as to realize the automatic optimization of longitudinal heat-sealing process parameters [20].

In this paper, the PET/Al/PE composite film was used as the object, and the longitudinal heat-sealing processing and heat-sealing strength of the composite film were measured through different process parameters. The relationship between process parameters and heat-sealing strength was established based on a radial basis function (RBF) neural network. After comprehensively considering the fitting accuracy and the amount of calculation, minimum orthogonal multiplication (OLS) is used to realize the iterative calculation of the RBF neural network. The optimization of longitudinal seal and heat-seal process parameters is realized by a genetic algorithm. Because the data types of heat-sealing distance, heat-sealing temperature, and heat-sealing speed are different, different methods are adopted to realize the coding of process parameters. The constraint conditions and target heat-sealing strength are established according to the actual working conditions and the characteristics of the composite membrane. The selection operator, crossover operator, and mutation operator are determined according to the coding method. The objective function of the genetic algorithm is established based on the RBF neural network, and the optimal process parameters are obtained through iterative optimization.

2. Processing Technology and Algorithm Applicability Analysis

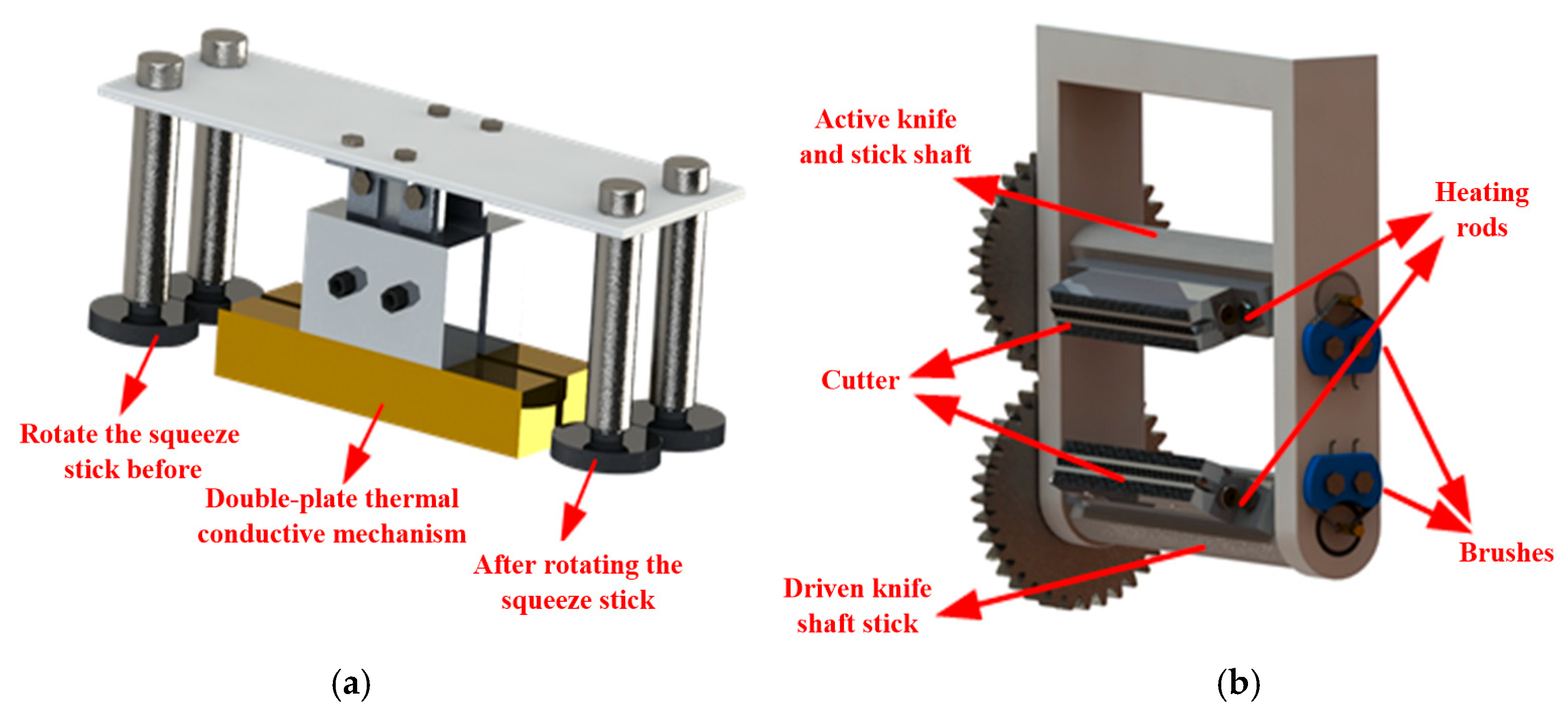
The two most important mechanisms of the pillow packaging machine are the longitudinal sealing mechanism and the transverse sealing mechanism, and both include the heat-sealing process. The longitudinal sealing mechanism adopts a double plate structure, as shown in Figure 1a. The front rotary extrusion roll rotates to drive the composite film forward, while ensuring that the composite film is in a tensioned state. The double plate mechanism controls the temperature between the two plates by means of electric heat generation to reach the heat-sealing temperature. Driven by the front extrusion roll, the composite membrane moves forward to make the inner membrane close. At the same time, when the composite film passes through the gap between the two plates, the high temperature between the two plates makes the composite film preheat and melt. The rear rotary extrusion roller compresses and fits the preheated composite film to further achieve the heat-sealing effect. As shown in Figure 1b, there are two cutter roller shafts in the transverse seal heat-seal wheel cutting mechanism, one of which is the driving shaft and the other is the driven shaft. The two shafts rotate synchronously. A heating rod is embedded in the cutter head, which is electrically heated by rotating the brush during rotation. When the composite film is sent into the mechanism, the high-temperature cutter head will conduct transverse heat-sealing on the composite film and cut the composite film at the same time. In the cutting process, the cutter has a forward traction force on the composite film, which helps the composite film move forward smoothly.

2.1. Process Parameter Analysis

The pillow packing machine adopts double plate heat-sealing, as shown in Figure 2. In Figure 2, 1 shows the heating plate heated by heat-seal; 2 is the heating wire, which controls the temperature of the heat-sealing plate according to the temperature controller to reach the heat-sealing temperature $T$; 3 is the heat-sealing distance $d$ control knob, which can adjust the distance according to the mechanical structure design, and the common parameters are 5 mm, 6 mm and 7 mm; 4 is the heat-sealing distance. During the processing, the composite film is heated by heating the double plate gap, and the heat-sealing distance $d$ will have an important impact on the heat transfer effect, which then affects the heat-sealing strength.

The main influencing factors of the composite film’s heat-sealing effect include heat-sealing time $\tau$ and heat-sealing temperature $T$, and the heat-sealing effect is evaluated by the heat-sealing strength $P$. In the longitudinal heat-sealing process of a pillow-type packaging machine, the heat-sealing time $\tau$ is also an important factor affecting the heat-sealing strength $P$, but the processing process of the pillow-type packaging machine adopts speed control, so the heat-sealing speed $v$ (packets/min) is used to replace the heat-sealing time $\tau$, and the relationship between the two is as follows:

$$\tau ={\displaystyle \frac{60L}{v{l}_o}}$$

(1)

where $L$ is the length of the heating plate, mm; $l_o$ is the standard film length of the prediction model, mm.

According to the formula, there is a certain relationship between the heat-sealing speed $v$ and the heat-sealing time $\tau$. The faster the heat-sealing speed, the shorter the heat-sealing time, and the corresponding heat-sealing strength will decrease. For other inputs with different film lengths, it is necessary to convert the heat-sealing speed according to the standard film length $l_o$ of the prediction model. The conversion process is as follows:

$$v={\displaystyle \frac{l_m}{l_o}}{v}_s$$

(2)

where $v_s$ represents the set speed under the film length $l_m$.

2.2. Heat-Seal Strength Analysis

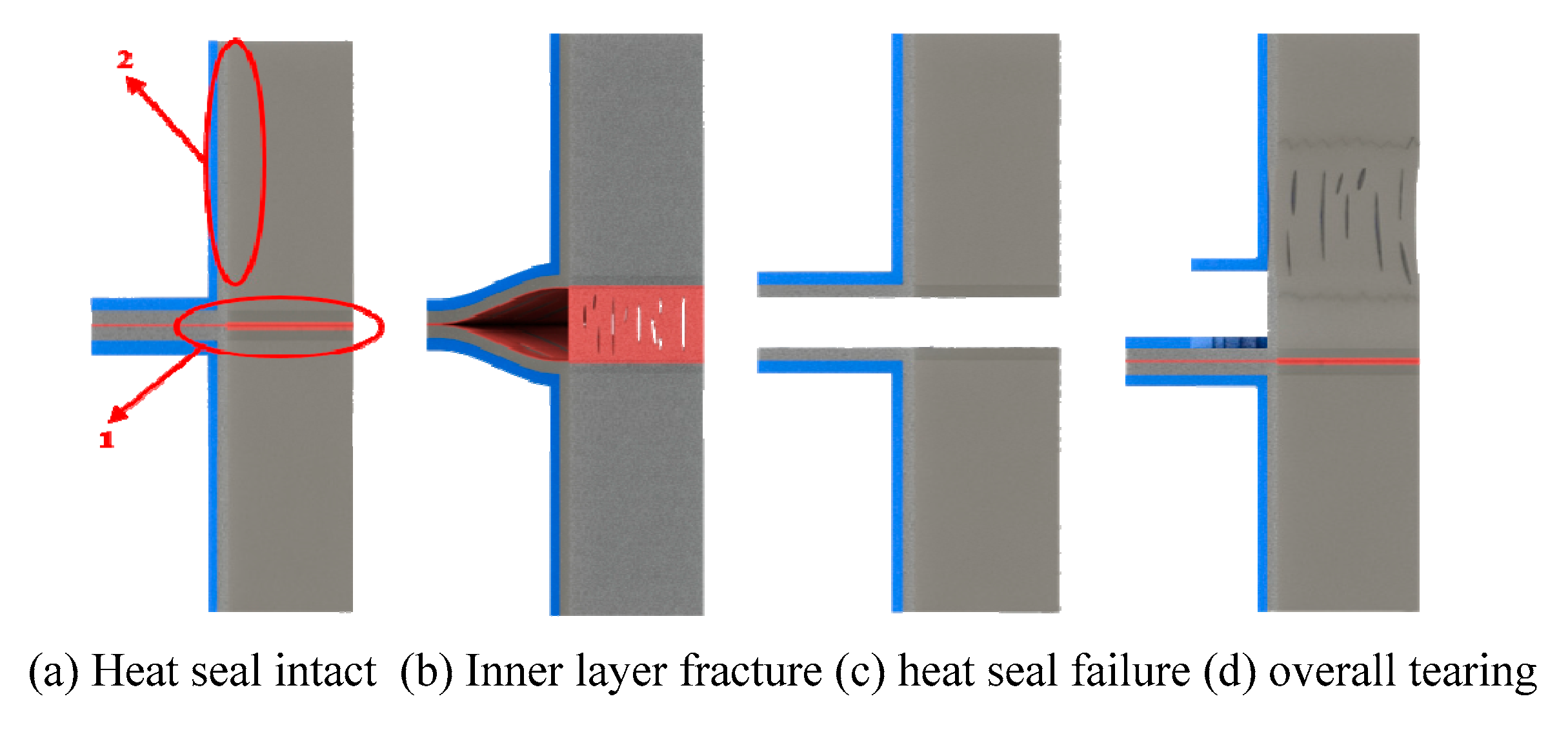
The heat-sealing strength is an important factor in determining the heat-sealing effect of composite film. It is usually obtained by measuring the yield stress of the composite film material at the time of sending fracture at the heat-seal using a tensile machine. After heat-sealing treatment of bopp/cpp composite membrane material, longitudinal tension will produce three different situations, as shown in Figure 3.

As shown in Figure 3a, the connection state of the composite film after heat-sealing is shown. One is the interlayer joint of the heat-sealing layer, and the other is the interlayer joint of the composite film; It is the fracture state of the inner layer of the composite film. When the heat-sealing strength is close to the bonding strength between the layers of the composite film, the interlayer fracture separation phenomenon occurs at the heat-sealing position of the composite film. At this time, the heat-sealing effect of the composite film is the best, as shown in Figure 3b; The state in Figure 3c is the heat-seal failure state. The heat-seal strength at the heat-seal of the composite film is low, and the bonding strength between the layers of the composite film is far greater than the heat-seal strength. Under this state, the heat-seal requirement cannot be met; When the heat-seal strength is greater than the fracture yield strength of the composite film, the overall tearing state occurs. At this time, the heat-seal strength at the heat-seal of the composite film is too large, and the heat-seal surface is distorted, and its toughness and appearance surface cannot meet the heat-seal requirements, as shown in Figure 3d. To sum up, the heat-sealing strength can greatly reflect the heat-sealing effect of composite membrane materials, and the target heat-sealing strength $P_a$ of bopp/cpp composite membrane is 27.67 N per 15 mm.

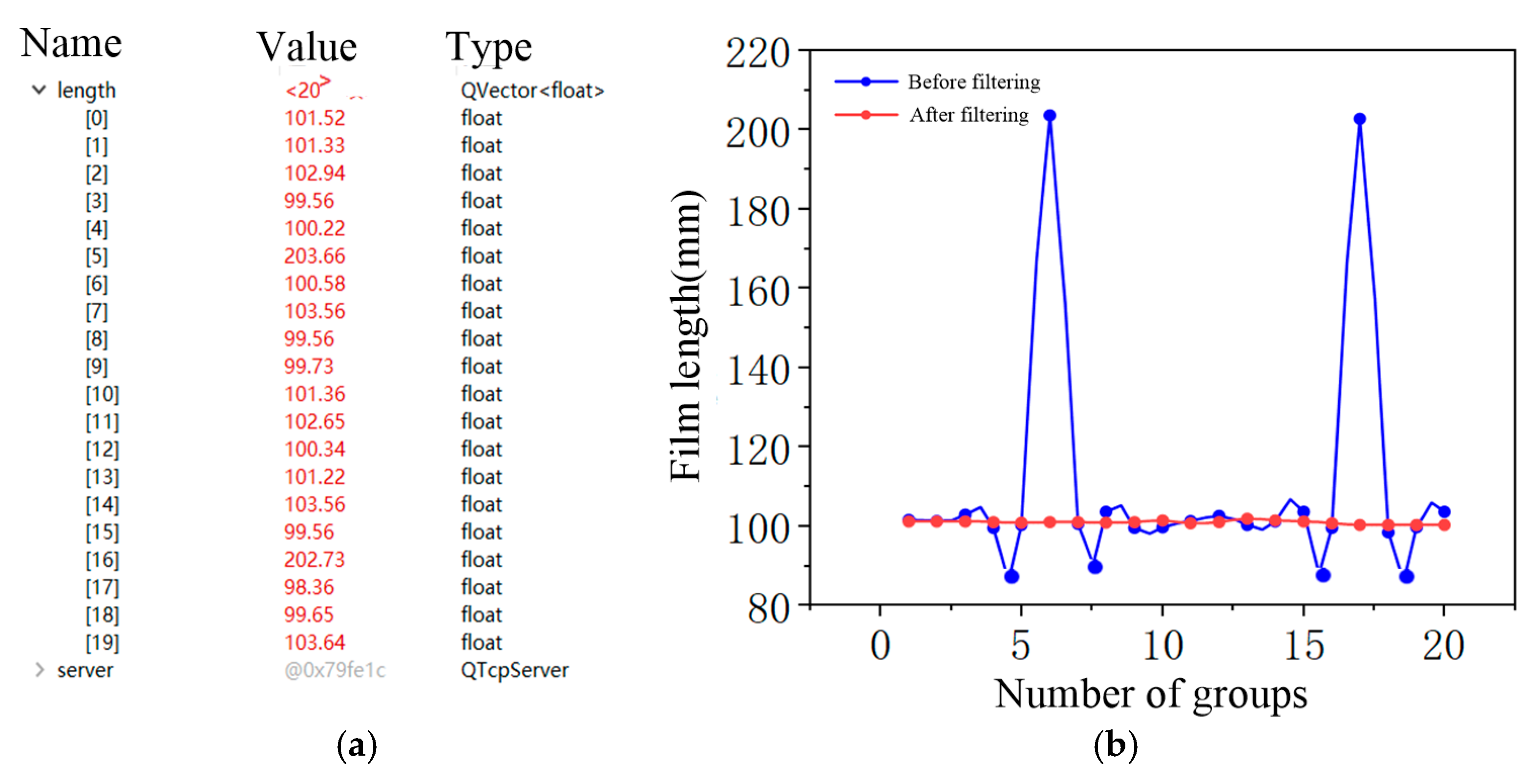
In this paper, the bopp/cpp composite film is longitudinally sealed and heat-sealed. Based on the standard qb/t 2358-1998, the cutting length is set to 15 mm. The tensile test is carried out on the products processed with the same process parameters, and the average value is taken as the heat-sealing strength in a group of 10. The measured results are shown in

Table 1. Processing data of the heat-sealing process.

Experiment No.	Influence Factor			Heat-Seal Strength (N/15 mm)
	Heat-Seal Distance (mm)	Heat-Sealing Temperature (℃)	Heat-Sealing Speed (Packages·min−1)
1	5	135	41.0	5.09
2	5	134	43.5	4.28
3	5	135	51.6	1.87
4	5	133	54.2	1.06
⋮	⋮	⋮	⋮	⋮
250	6	175	52.3	37.24
251	6	174	55.6	32.72
⋮	⋮	⋮	⋮	⋮
531	7	185	86.1	26.31
532	7	186	90.3	22.99
533	7	187	94.7	12.43
534	7	184	100.0	6.93

.

According to the test data, there is a nonlinear relationship between the heat-seal distance, heat-seal temperature, heat-seal speed, and heat-seal strength, and there is a complex coupling relationship between the force field and temperature field, so it is difficult to establish a general mathematical model. To solve this problem, this paper uses an RBF neural network training model to replace the mathematical model and optimizes it using the genetic algorithm. The design structure diagram of the decision method model is shown in Figure 4. Input the material yield strength to calculate the target heat-sealing strength, and set some process parameters as constraints according to the actual processing requirements. The RBF neural network regression model was established, and its accuracy was verified. The iterative population of the genetic algorithm is input into the regression model for fitness calculation. The optimal process parameters of heat-seal strength close to the target heat-seal strength were obtained by the genetic algorithm.

2.3. Implementation of RBF Neural Network Based on OLS

In the iterative calculation of the RBF neural network, the parameters to be confirmed include the expansion coefficient spread, the number of neurons in the hidden layer $p$, and the center vector ${\mathrm{C}}_i$ corresponding to each hidden layer. The width parameter spread is set manually, while the number of neurons $p$ and the center vector ${\mathrm{C}}_i$ are solved iteratively by orthogonal least squares (OLS).

It is necessary to input all training sets and calculate the radial basis function value with the center vector composed of all training sets:

$${(M_r)}_{ij}=\varphi (\gamma ‖X_i-X_j‖)$$

(3)

where (M_r)_ij represents the radial basis function value of X_j when $X_i$ is the center vector, and $M_r$ is the column pool to be selected.

The column vectors selected from the column pool to be selected are combined into a matrix $M_s$, which is called the selected column pool, and the corresponding output vector is $P_s$. If $M_s$ is a unit orthogonal matrix, the theoretical error calculated by the least square method is:

$$E(M_s)=P_s^T{P}_s-P_s^T{M}_s{(P_s^T{M}_s)}^T$$

(4)

At this time, if the k-th column vector $V_k$ is selected from the column pool to be selected $M_r$ and added to the selected column pool $M_s$, the error reduction is calculated as follows:

$$\mathsf{\Delta }E(k)=E(M_s)-E([M_s,V_k])={(P_s{V}_k)}^2$$

(5)

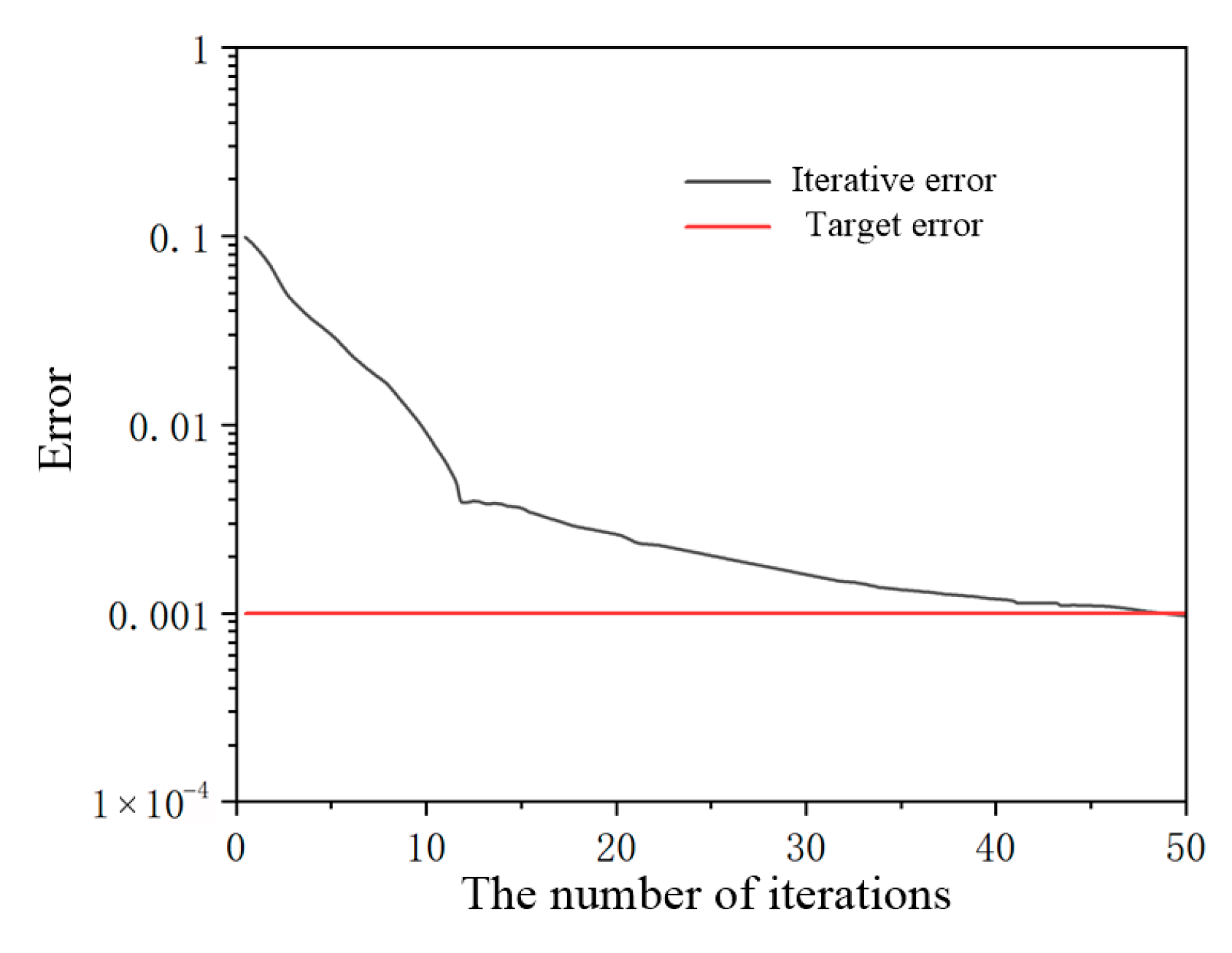
Column vector $V_k$ must be the one with the largest error reduction $\mathsf{\Delta }E$ among all column vectors $V$. At this time, add $X_k$ in the corresponding training set as the center vector. For most cases, $M_r$ and $M_s$ are not unit orthogonal matrices, but because the space represented by the two matrices after standard orthogonalization is the same, the corresponding error reduction $\mathsf{\Delta }E$ is the same. $M_r^{\prime }$ and $M_s^{\prime }$ are obtained by standard orthogonalization of $M_r$ and $M_s$. At this time, the column with the largest error reduction $\mathsf{\Delta }E$ in $M_r^{\prime }$ can be added to $M_s^{\prime }$, and the corresponding column in $M_r$ can be added to $M_s$. Through the above method, the center vector is continuously selected to add, and finally, the error meets the target requirements.

3. Optimization of Process Parameters Based on Genetic Algorithm

3.1. Fitness Function Design Based on Heat-Seal Strength Prediction Model

Fitness value is an important standard to judge the survival of the fittest in the population. The purpose is to select better individuals as parents for reproduction, so it is necessary to design the fitness function. At the beginning of the optimization process, the target heat-sealing strength $P_a$ will be obtained. The closer the individual heat-sealing strength is to the target heat-sealing strength $P_a$ in the iteration process, the better the fitness of the individual. Therefore, it is necessary to calculate the difference between the heat-sealing strength $P_s=(P_{s1},P_{s2},\dots ,P_{sn})$ and the target heat-sealing strength $P_a$ in the initial population, that is $\left|P_a-P_{si}\right|$, which is obtained through the regression model of the RBF network. The relationship obtained is as follows:

$$Diff(X)=\left|P_a-P(normal(X))\right|$$

(6)

where $Diff(X)$ is the difference between the calculated and the target heat-seal strength; $normal()$ is to normalize the parameters.

3.2. Encoding and Decoding of Heat-Sealing Process Parameters

The appropriate coding method is beneficial to the iterative calculation of the genetic algorithm. The heat-seal distance $d$ is a discrete variable, and there are only 5 mm, 6 mm, and 7 mm data after input into the fitness function. In order to speed up the subsequent operator calculation, symbol coding is adopted, which is coded into 001, 010, and 100 symbols. Because there is a unique mapping relationship between the two, the decoding process can find and decode according to the mapping relationship of the encoding.

The heat-sealing temperature $T$ is a positive integer, which is encoded by the gray code. Compared with binary coding, the coding values of two consecutive integers encoded by gray code are only different by one code point, so this coding method can greatly improve the local search ability of the genetic algorithm. First, the positive integer is converted into a two-level system, and each is numbered $B=b_n{b}_{n-1}\dots b_0$, and the gray code is also represented as $G=g_n{g}_{n-1}\dots g_0$, and the encoding method is as follows:

$$\left\{\begin{array}{l}{g}_i=b_i\oplus b_{i+1}\\ g_n=b_n\end{array}\right.$$

(7)

The decoding method is as follows:

$$\left\{\begin{array}{l}{b}_i=g_i\oplus b_{i+1}\\ b_n=g_n\end{array}\right.$$

(8)

The heat-sealing speed is a floating-point number. In order to ensure that the accuracy of data is not lost after coding, floating-point number coding is adopted.

After coding the data in the above way, it becomes the three-segment chromosome of the population individual in the genetic algorithm. In order to ensure the rapidity and accuracy of the iterative process, different operators are used to process the three different kinds of data.

3.3. Genetic Algorithm Operator Determination

In the iteration process of the genetic algorithm, it is necessary to select appropriate genetic operators, including the selection operator, crossover operator, and mutation operator. This optimization strategy adopts the roulette selection operator, which determines the probability $D_i$ of each individual is selected by calculating the fitness function value of each individual in the population. The calculation method is as follows:

$$D_i={\displaystyle \frac{1/Diff(X_{si})}{{\displaystyle \sum _{j=1}^{80}1/Diff(X_{si})}}}$$

(9)

Randomly select one of the individuals as the parent population according to the probability, and repeat the process until n individuals are selected as the parent population to calculate the crossover operator and mutation operator, and the same individual can be selected multiple times. The crossover operator is the main operation to generate new individuals in the genetic algorithm. It exchanges some chromosomes between two individuals with $D_c$ certain probability.

The heat-sealing distance is $d$ chromosome, and the genetic information of the two parents is directly exchanged; Heat-sealing temperature $T$ chromosome uses the way of double point crossover, randomly selects the information of two positions, and exchanges their positions; the heat-sealing speed SBX operator is used for chromosome $v$. Suppose that the heat-sealing speed $v$ of the two parents is $v_i$ and v_j, and the heat-sealing speed of the offspring is $v_k$ and $v_m$. The sbx operator is calculated as follows:

$$\left\{\begin{array}{l}{v}_k=0.5\times \left[(1+\beta )v_i+(1-\beta )v_j\right]\\ v_m=0.5\times \left[(1-\beta )v_i+(1+\beta )v_j\right]\end{array}\right.$$

(10)

where $\beta$ is the cross-distribution coefficient.

The mutation operator refers to the process of mutating a gene according to a certain pattern during the selection crossover, which can prevent the optimization process from falling into local optima. Mutation usually occurs with a lower probability because it carries the risk of damaging the individual performance of this operator. Set mutation probability $D_h$. For the heat-sealed distance $d$ chromosome, randomly select two of the bits for swapping; The heat-sealing temperature $T$ chromosome adopts an exchange mutation, which can cause significant changes in the heat-sealing temperature $T$ and avoid becoming stuck in local optimal solutions; Polynomial variation is used for heat-sealing speed $v$ chromosome. Assuming the unchanged heat-sealing speed is $v_e$, and after polynomial mutation, $v_o$ is obtained, the relationship between the two is as follows:

$$v_o=v_e+\lambda (v_u-v_d)$$

(11)

where $\lambda$ is the coefficient of variation distribution, calculated according to the following formula.

$$\left\{\begin{array}{l}\lambda ={(2\mu )}^{1/({\eta }^{\prime }+1)}\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \mu \le 0.5\\ \lambda =1-{(2(1-\mu ))}^{1/({\eta }^{\prime }+1)}\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \mu >0.5\end{array}\right.$$

(12)

where ${\eta }^{\prime }$ is the user-defined variation distribution index; $\mu$ is a random number belonging to [0, 1).

4. Processing Operation Test

4.1. Simulation Comparison of Training Results

After normalizing all the heat-seal strength test data, they were divided into 400 training sets and 105 test sets. 400 sets of training sets are input into the RBF neural network. The parameters of the neural network are set as follows: the width parameter is 0.21, the mean square error target is 0.001, and the maximum number of iterations is 100. Input the training set data into the neural network model for training, and the obtained iterative process curve is shown in Figure 5.

According to the curve change, the iteration error reached 0.003 in the 12th iteration, and the iteration error change was relatively small from the 12th iteration to the 50th iteration, reaching the target requirements after the 50th iteration.

The prediction effect of the same group of data is compared with the BP neural network, as shown in Figure 6. From the comparison results of the predicted values, the RBF neural network model has better prediction results than the BP neural network model, and the overall error is small. Although when the heat-seal strength is between 0 N per 15 mm and 16 N per 15 mm, there is a large relative error between the prediction set and the test set of the two models. For the subsequent iteration process of parameter optimization based on the genetic algorithm, in order to ensure the integrity of the calculation, the heat-seal strength within this range will also be involved in the calculation, but the heat-seal strength within this range is small. In order to ensure the quality of the heat-seal, the process parameters corresponding to the heat-seal strength within this range will not be selected and will be discarded after each iteration, so the prediction error of the heat-seal strength within 0 N per 15 mm to 16 N per 15 mm can be ignored.

The test set data and the prediction set data of the two models are brought into the formula to calculate the determination coefficient $R^2$.

$$R^2={\displaystyle \frac{{\left(l{\displaystyle \sum _{i=1}^l\overline{Y}Y-{\displaystyle \sum _{i=1}^l\overline{Y}{\displaystyle \sum _{i=1}^{l}Y}}}\right)}^2}{\left(l{\displaystyle \sum _{i=1}^l{\overline{Y}}^2-{\left({\displaystyle \sum _{i=1}^l\overline{Y}}\right)}^2}\right)\left(l{\displaystyle \sum _{i=1}^l{Y}^2-{\left({\displaystyle \sum _{i=1}^{l}Y}\right)}^2}\right)}}$$

(13)

where $Y$ represents test set data; $\overline{Y}$ represents forecast set data.

The results obtained are 0.9117 and 0.8710, respectively, indicating that the prediction model of heat-sealing strength fitted by the RBF neural network has better regression characteristics.

When the heat-seal strength is between 16 N per 15 mm and 50 N per 15 mm, the comparison results between the prediction set and the test set of the two models are shown in Figure 7a, and the prediction error of the RBF neural network model is basically less than that of the BP neural network. The error comparison between the RBF neural network model and the BP neural network model is shown in Figure 7b. It can be seen that when the heat-sealing strength is within the range of 16 N per 15 mm to 50 N per 15 mm, the error of the RBF neural network is basically less than that of the BP neural network model, and the jitter change in error is also small. It shows that the RBF neural network model has good stability for the prediction of heat-sealing strength. Within the range of heat-seal strength, the prediction error of the RBF neural network model is basically less than 5%, and the maximum error of an individual is less than 10%, which meets the actual processing requirements. By transplanting the trained model (i.e., the relationship shown) into the human–computer interaction system, the prediction of the heat-sealing strength of the composite film product can be realized.

4.2. Iterative Results of Process Parameter Optimization

Set three groups of experiments: the first group set the heat-sealing distance as 6 mm, the second group set the heat-sealing temperature as 180 °C, and the third group set the processing speed as 80.0 packets/min.

Table 2. Genetic algorithm parameters.

Parameter Name	Parameter Value	Parameter Name	Parameter Value
Crossover probability Dc	0.9	Upper limit of heat-seal temperature Td	185 °C
SBX cross distribution index $\eta$	20	Lower limit of heat-seal temperature Tu	135 °C
Mutation probability Dh	0.1	Upper limit of heat-sealing speed vd	100.00 bags/min
Polynomial variation distribution index ${\eta }^{\prime }$	20	Lower limit of heat-sealing speed vu	50.00 bags/min

for other algorithm parameter settings.

The iteration process is shown in Figure 8. Under three different parameter settings, the average fitness value of the population decreases rapidly when the number of iterations is 10 to 15. After the number of iterations is 15, the average heat-seal strength is gradually stable. When the number of iterations is about 20 to 30, it is basically stable, and the final iteration result converges.

Select the population with the minimum average fitness from the iterative population, and then select the individual with the minimum fitness from the population. The optimization results of process parameters are shown in

Table 3. Optimization results.

Input Parameter Selection	d = 6 mm	T = 180 °C	v = 80.0 Bags/min
Optimization results X = [d,T,v]	[6,175,67.0]	[7,180,73.0]	[5,183,80.0]

.

Verify the film length measurement. Figure 9a shows the film length data read through the debugging window, and Figure 9b shows the comparison between the read film length data and the filtered film length data.

4.3. Verification of Process Parameter Optimization Strategy

The pillow packaging machine used for processing and the experimental platform for measuring the heat-sealing strength are shown in Figure 10. Set the heat-sealing temperature through the temperature control module, set the heat-sealing distance through the mechanical mechanism knob, set the heat-sealing speed of the pillow packaging machine through the human–computer interaction system, and then send the processed products to the wdw-5kn microcomputer-controlled electronic tensile testing machine for heat-sealing strength test.

The three groups of optimal process parameters obtained by the optimization strategy of the RBF neural network genetic algorithm are brought into the pillow packaging machine for the heat-sealing processing of bopp/cpp composite film to eliminate the products with unexpected working conditions. 200 processed products are randomly selected from each case for the heat-sealing strength test. At the same time, two groups of control groups are set for each group of optimal process parameters. The same method is adopted for processing by manually adjusting two parameters other than the corresponding constrained process parameters. The process parameters for the final test are shown in

Table 4. Processing validation input parameters.

Constraint Condition	Optimization Group	Control Group 1	Control Group 2
Constraint condition d = 6 mm	[6,175,67.0]	[6,185,72.4]	[6,165,62.0]
Constraint condition T = 180 °C	[7,180,73.0]	[6,180,78.3]	[5,180,83.3]
Constraint condition v = 80.0 bags/min	[5,183,80.0]	[6,185,80.0]	[7,185,80.0]

.

The distribution of 20 groups of heat-sealing strength obtained by each process parameter is shown in Figure 11. Due to the influence of the double plate heat-sealing process, the distribution of heat-sealing strength of 9 groups of parameters is relatively scattered, but a roughly different distribution range can be seen. According to the formula in Section 4, the upper and lower limits of the heat-sealing strength are obtained. The upper limit is 1.1 times the target heat-sealing strength of 30.44 N per 15 mm, and the lower limit is 0.9 times the target heat-sealing strength of 24.90 N per 15 mm. Figure 11a,d,g show the distribution of heat-sealing strength of the heat-sealing part of bopp/cpp composite film after the optimal process parameters are input into the pillow packaging machine. Compared with the process parameters adjusted by the operators’ manual experience in Figure 11b,c,e,f,h,i, the heat-sealing strength corresponding to the optimal process parameters is within the upper and lower limits of the heat-sealing strength, while some of the heat-sealing strength corresponding to the manual parameters are beyond the upper and lower limits, which requires further manual adjustment. Therefore, the heat-sealing part of the product processed with the optimal process parameters can basically meet the actual production requirements.

The error results of various process parameters calculated at the same time are shown in

Table 5. Comparison of heat-seal strength error.

Process Parameters [d,T,v]	Maximum Error (%)	Mean Error (%)	Group
[6,175,67.0]	9.71	5.87	Optimization group
[6,185,72.4]	15.4	6.63	Control group
[6,165,62.0]	14.71	7.91	Control group
[7,180,73.0]	9.95	3.52	Optimization group
[6,180,78.3]	12.48	6.33	Control group
[5,180,83.3]	15.31	7.44	Control group
[5,183,80.0]	8.16	3.24	Optimization group
[6,185,80.0]	8.17	4.11	Control group
[7,185,80.0]	14.71	6.25	Control group

. The maximum error of the optimization group is not more than 10%, and the average error is not more than 5%, which is lower than the parameters selected by human experience.

It can be verified that the optimization strategy proposed in this paper can effectively reduce labor costs and improve decision-making efficiency. Each processed product extracted in the experiment is within the upper and lower limits of the target heat-sealing strength, which proves that the optimized process parameters obtained by this method have a high qualification rate in practical engineering. At the same time, compared with other manually selected process parameters, although most of the manually selected process parameters are within the required heat-sealing strength range, some products still exceed the specified range, and the distribution of products is more inclined towards the boundary.

5. Conclusions

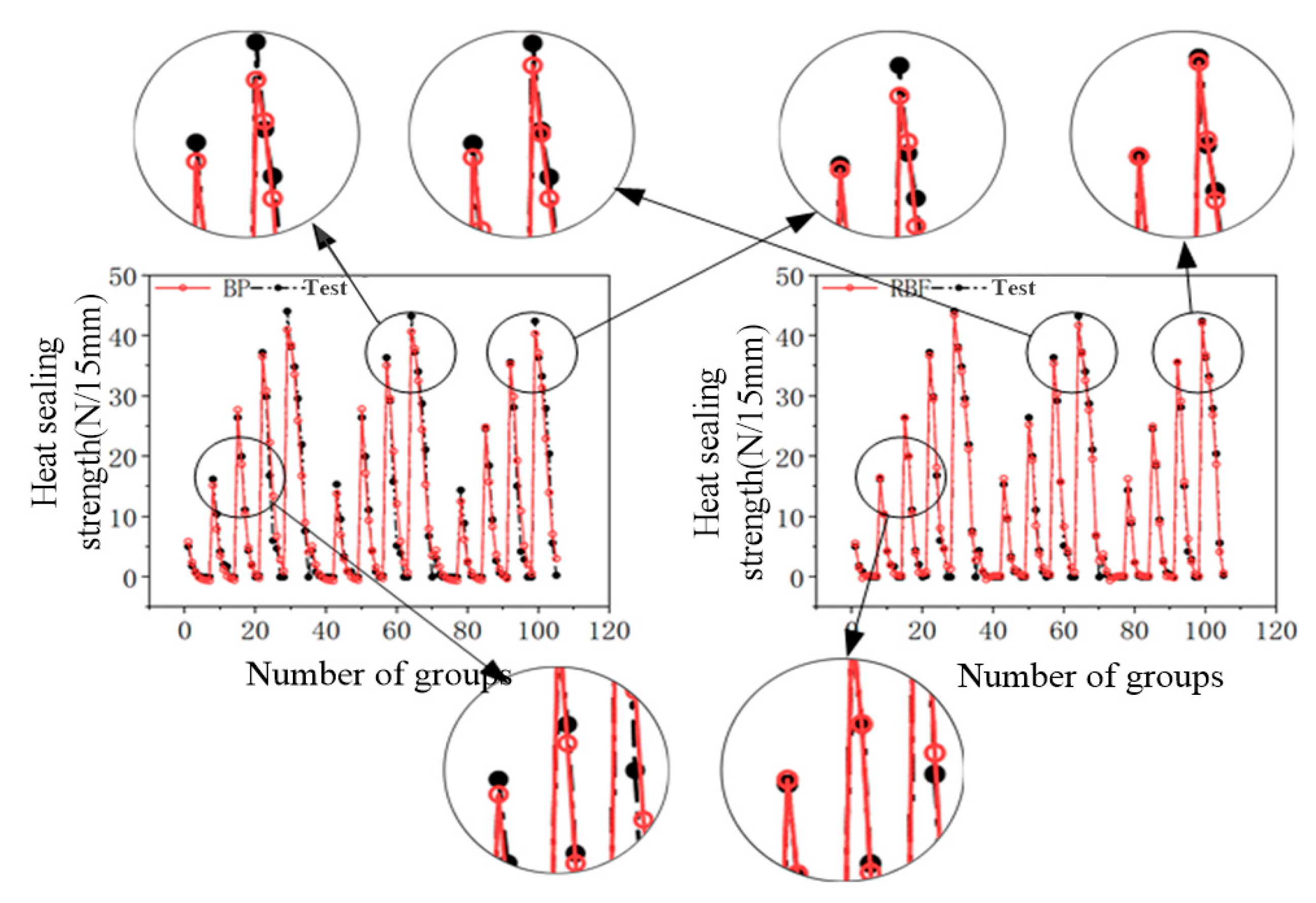
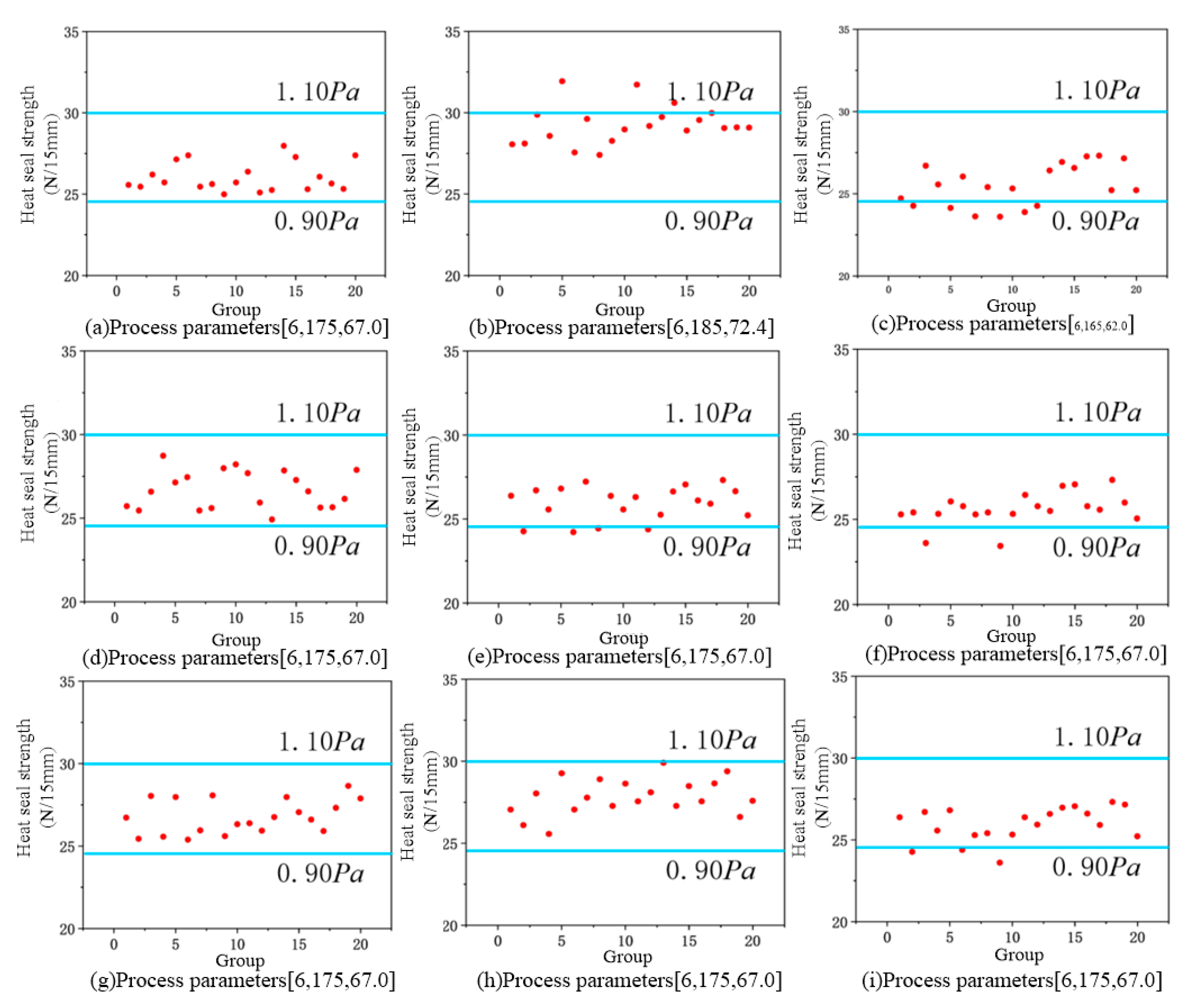
In order to improve the processing efficiency and reduce the labor cost of the pillow-type packaging machine through pre-parameter input, a process parameter decision method based on rbf-ols is constructed in this paper. The nonlinear relationship between different process parameters and heat-sealing strength was obtained from the experimental data, and an RBF network was used to predict the heat-sealing strength. The comparison of data sets shows that the regression model based on the RBF neural network has high accuracy and fast convergence, and the overall error of the effective part of the model is less than 5%, so the model can effectively predict the heat-seal strength. According to different input parameters, the fitness function is designed based on the RBF network, and the optimal process parameters are selected by the genetic algorithm. Finally, the optimal process parameters are obtained. The final results were brought into the actual processing process, and the results were measured. All 20 groups of products were within the processing requirements and met the processing requirements. The decision-making method proposed in this paper replaces the manual parameter selection, which effectively reduces the labor cost and improves the decision-making efficiency.

For different composite membrane materials, it is necessary to relearn the RBF neural network prediction model. In the future, other characteristics, such as composite membrane materials, can be considered to be added to the prediction model of the RBF neural network to increase its universality.