Prediction of Boil-Off Gas in Cryogenic Tanks with a Coupled Thermal Resistance and Thermodynamic Model
Abstract
1. Introduction
1.1. Modeling Approaches for BOG Prediction
1.2. Research Objective
2. Modeling of BOG in Cryogenic Storage Tanks
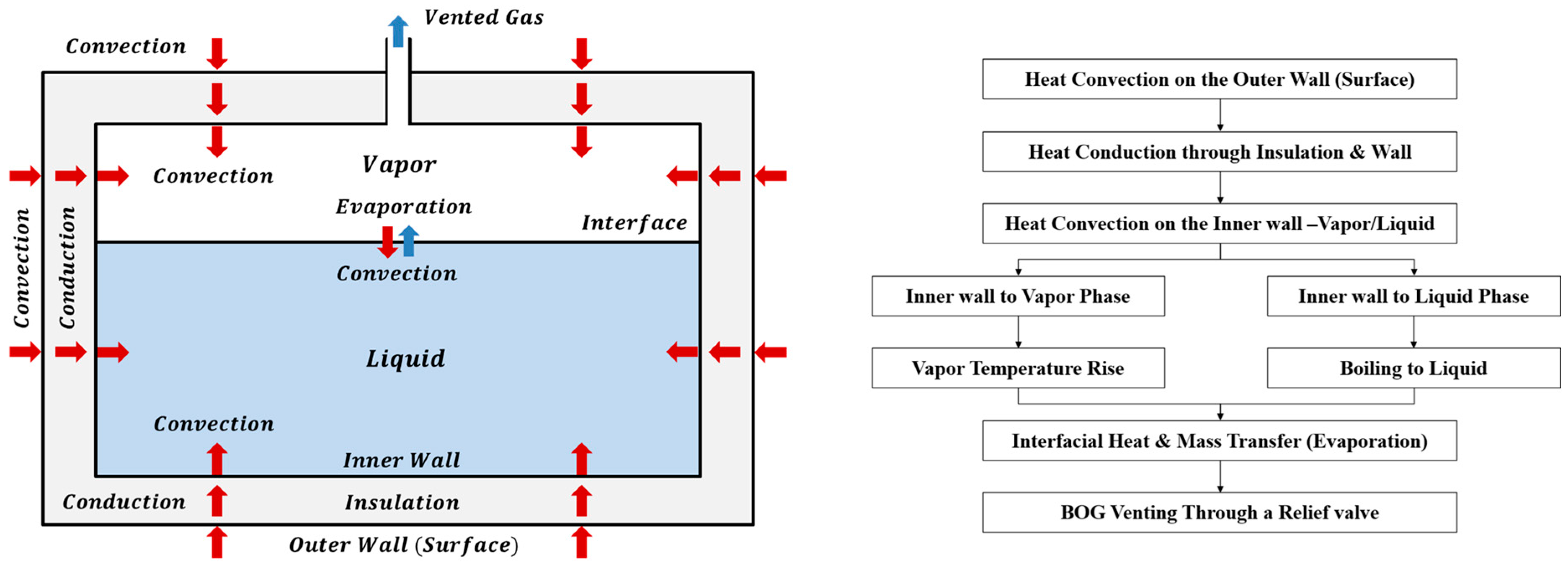
2.1. Physical Phenomena
- The vapor phase is superheated, while the liquid phase remains saturated.
- The tank operates under long-term storage with open-vent (vent-to-atmosphere) conditions; pressure is approximately ambient, and pressure-rise dynamics are neglected.
- The tank is assumed to be installed in an indoor environment; solar radiation is neglected.
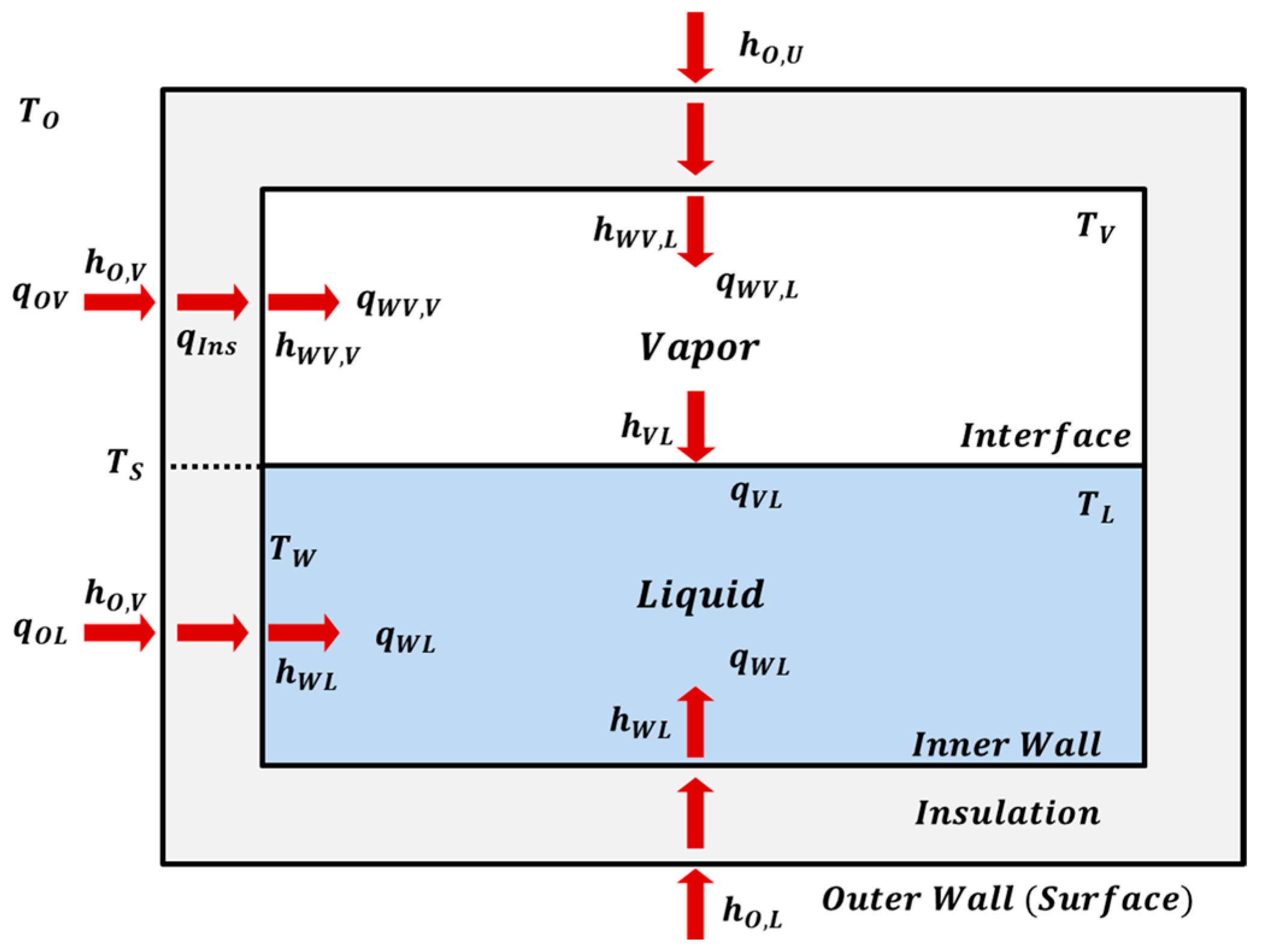
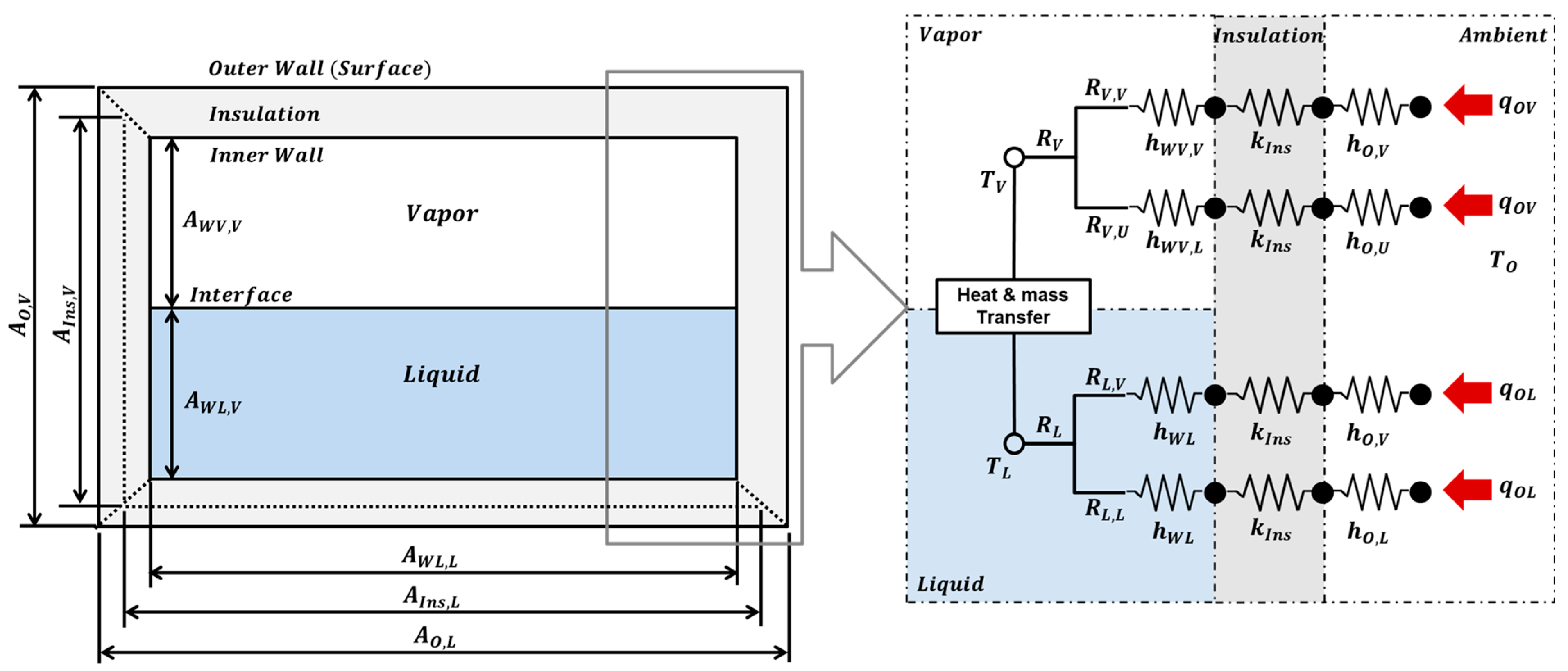
2.2. Heat-Transfer Pathways and Boundary Conditions
2.2.1. Convective HTCs of the Tank Outer Wall
2.2.2. Convective HTCs of the Tank Inner Wall
2.2.3. Convective HTCs of the Vapor-Liquid Interface
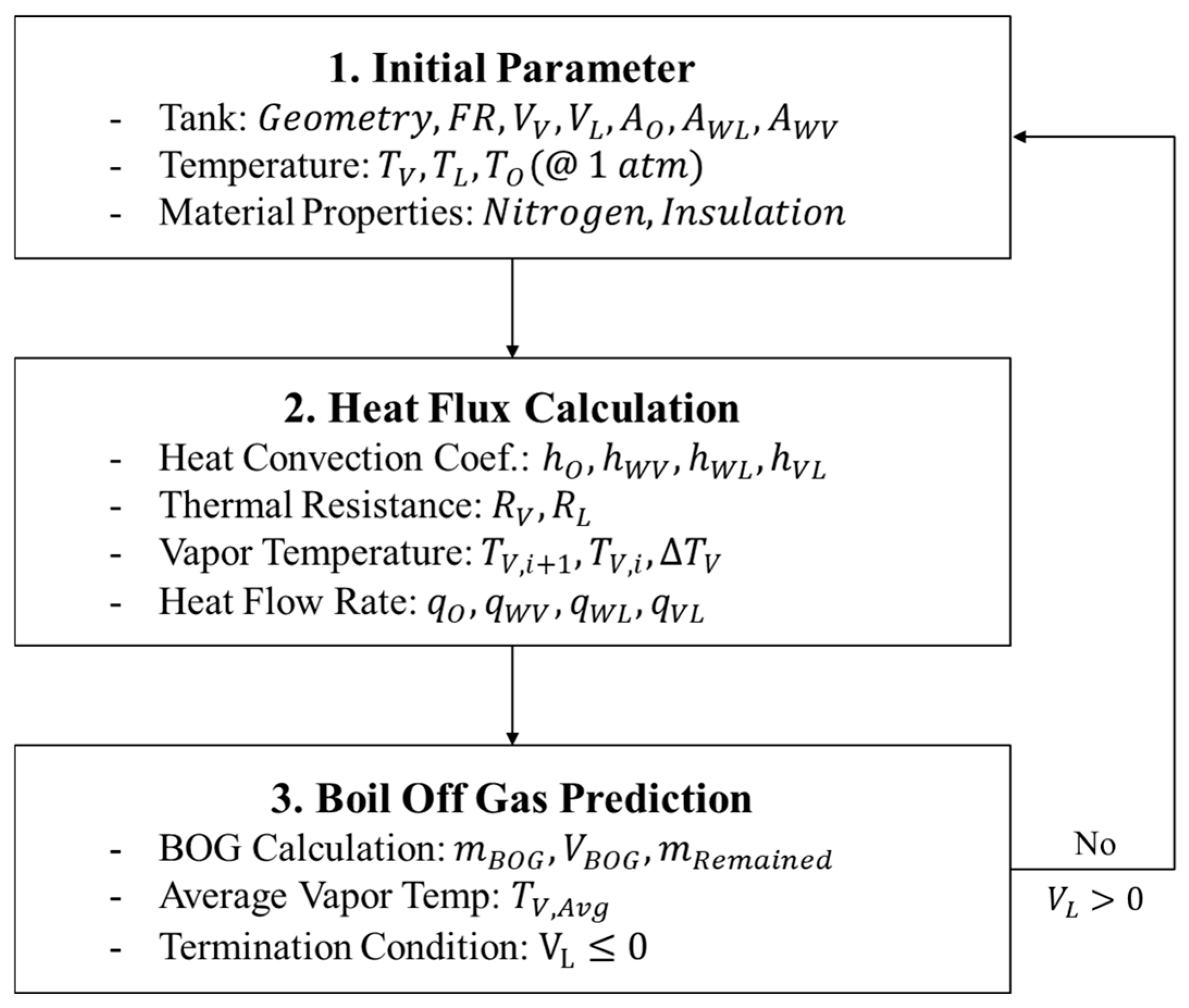
2.3. TDM-Based BOG Prediction Model
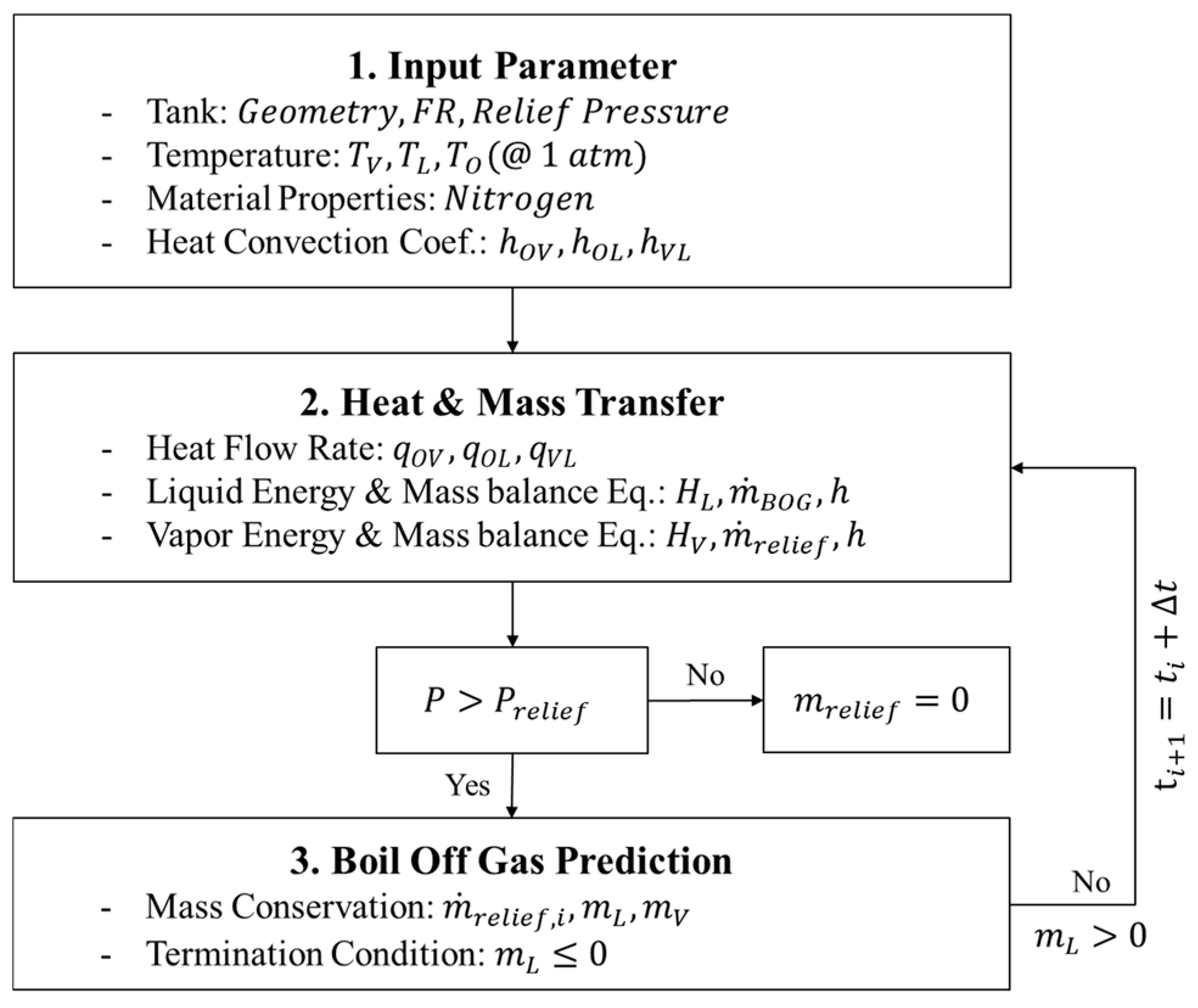
2.4. BOG Prediction Model Using BoilFAST
2.5. BOG Prediction Model Using SINDA/FLUINT
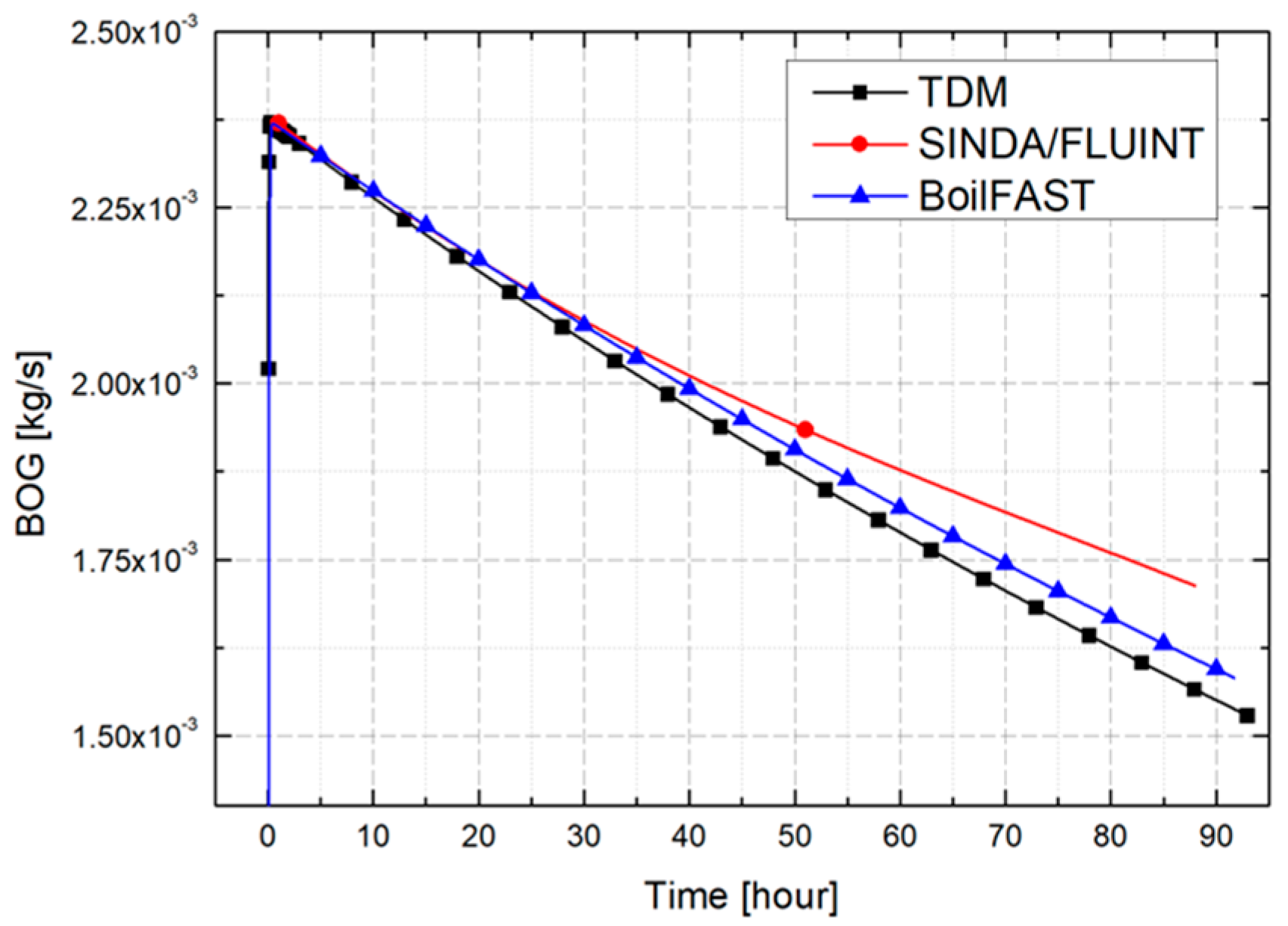
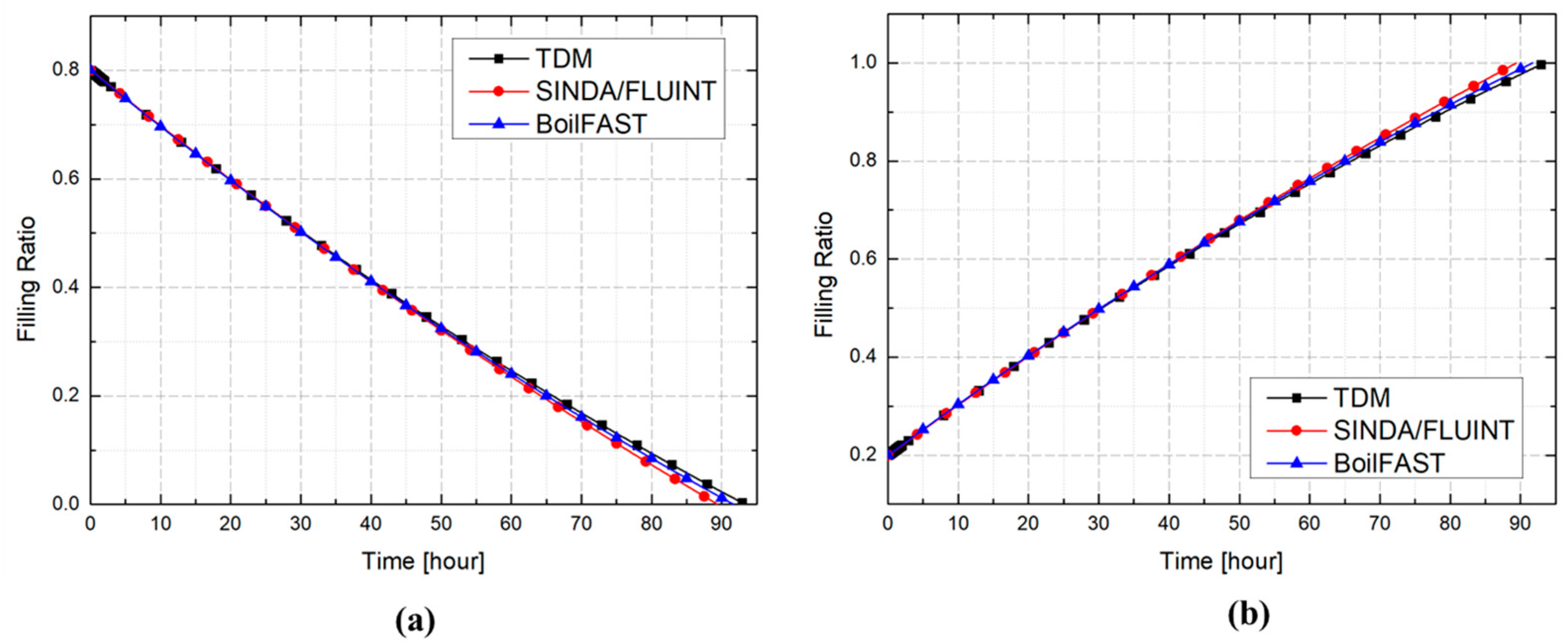
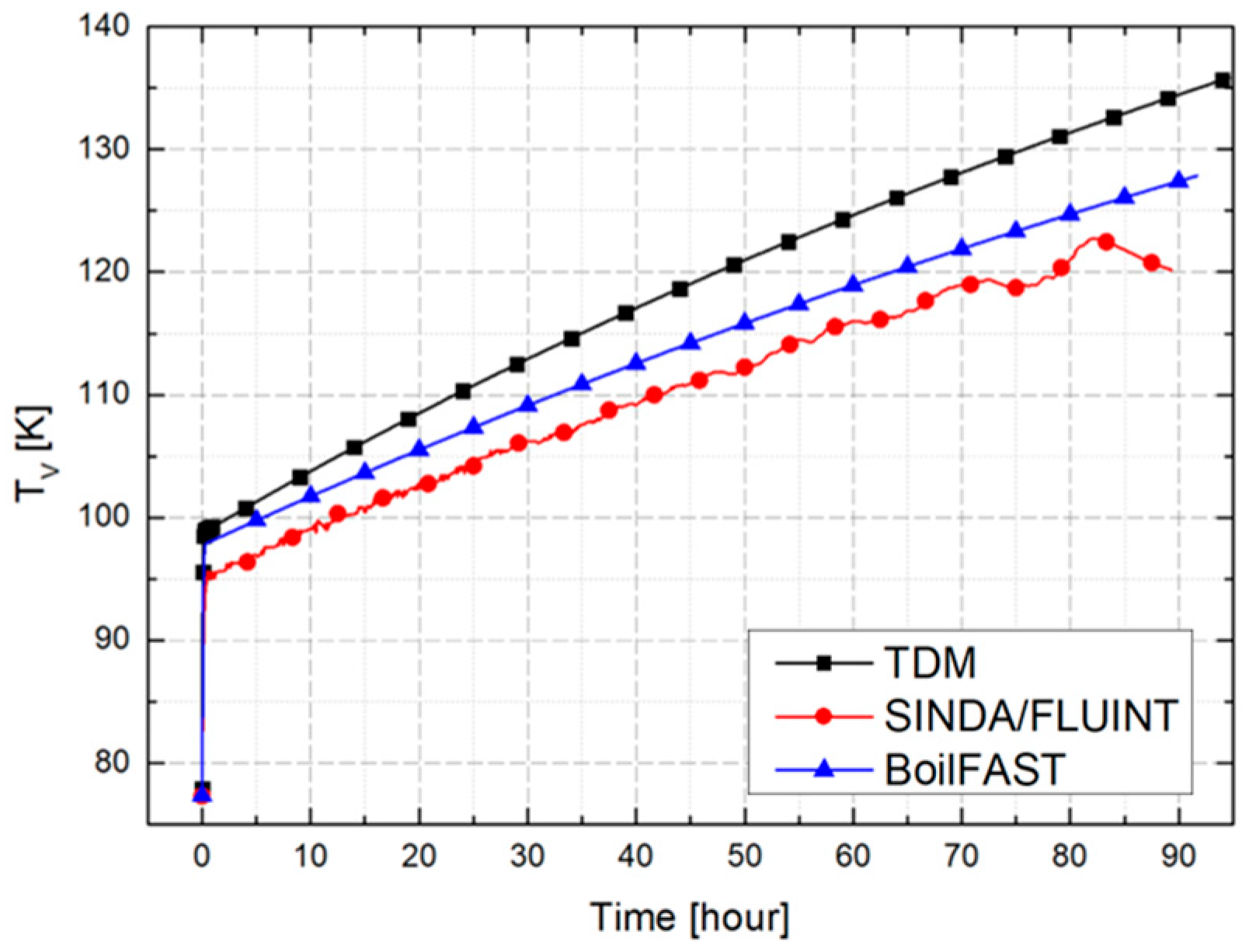
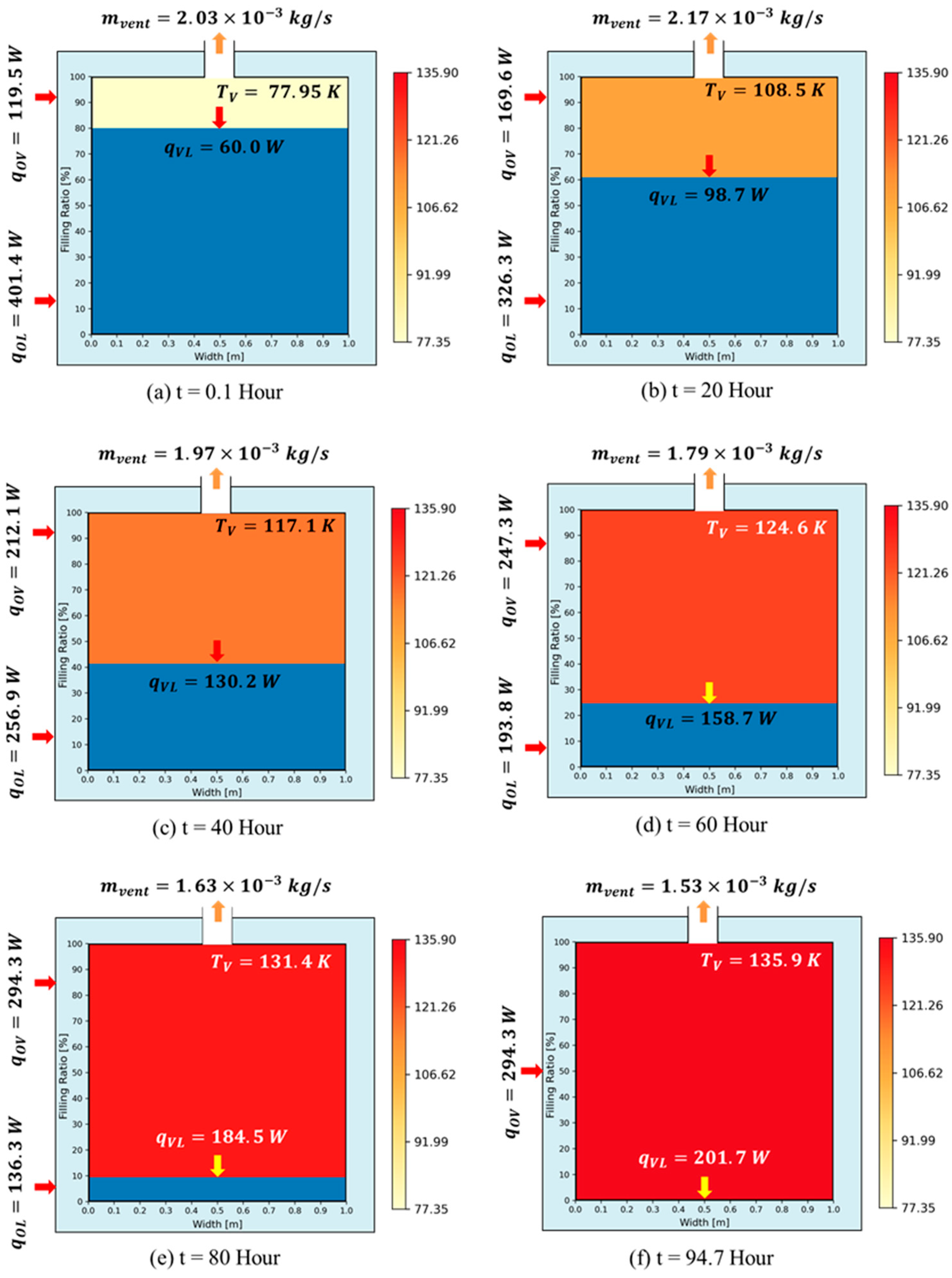
3. Validation and Comparative Analysis of BOG Prediction Models
3.1. Problem Definition
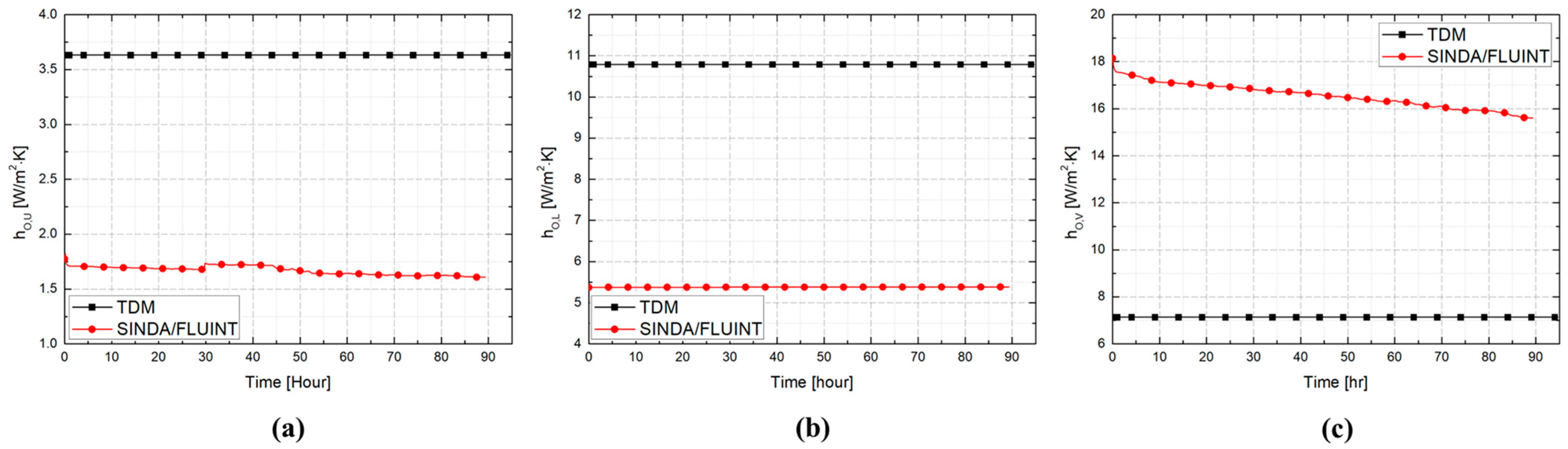
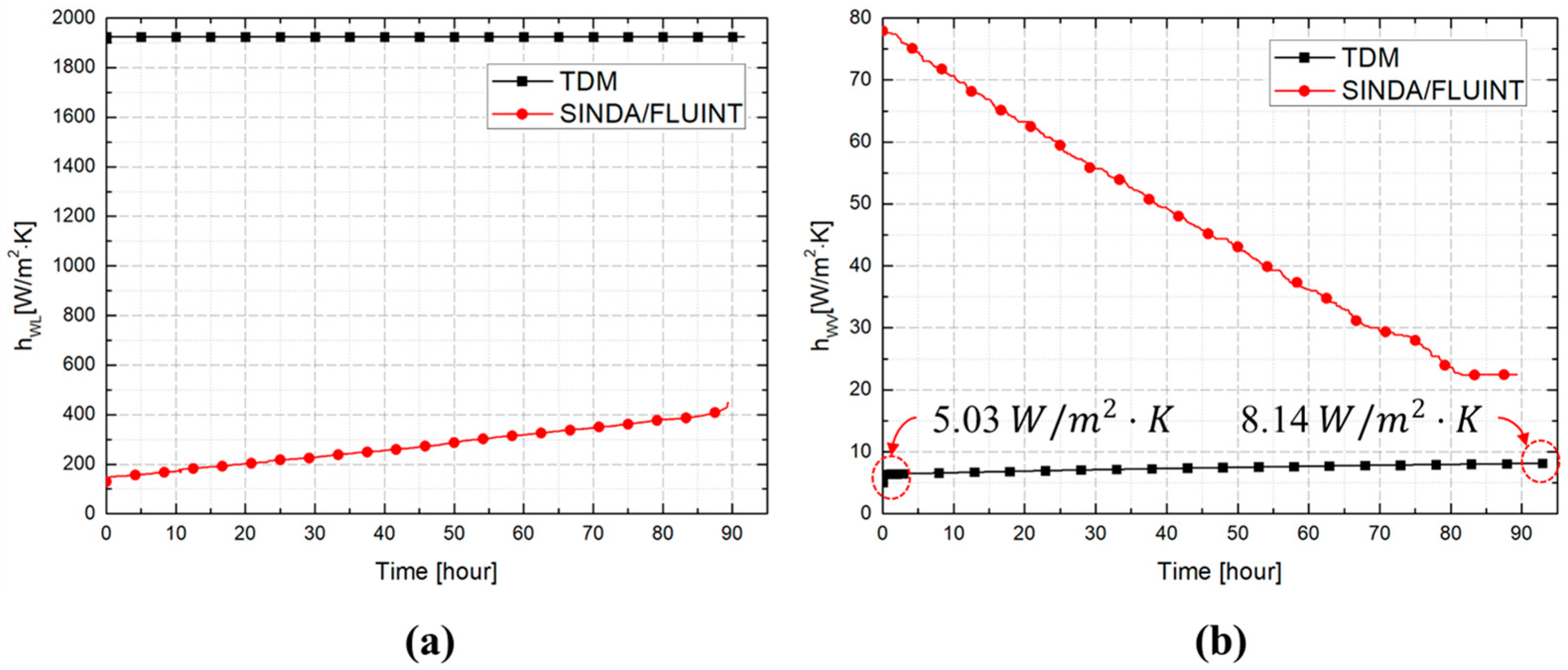
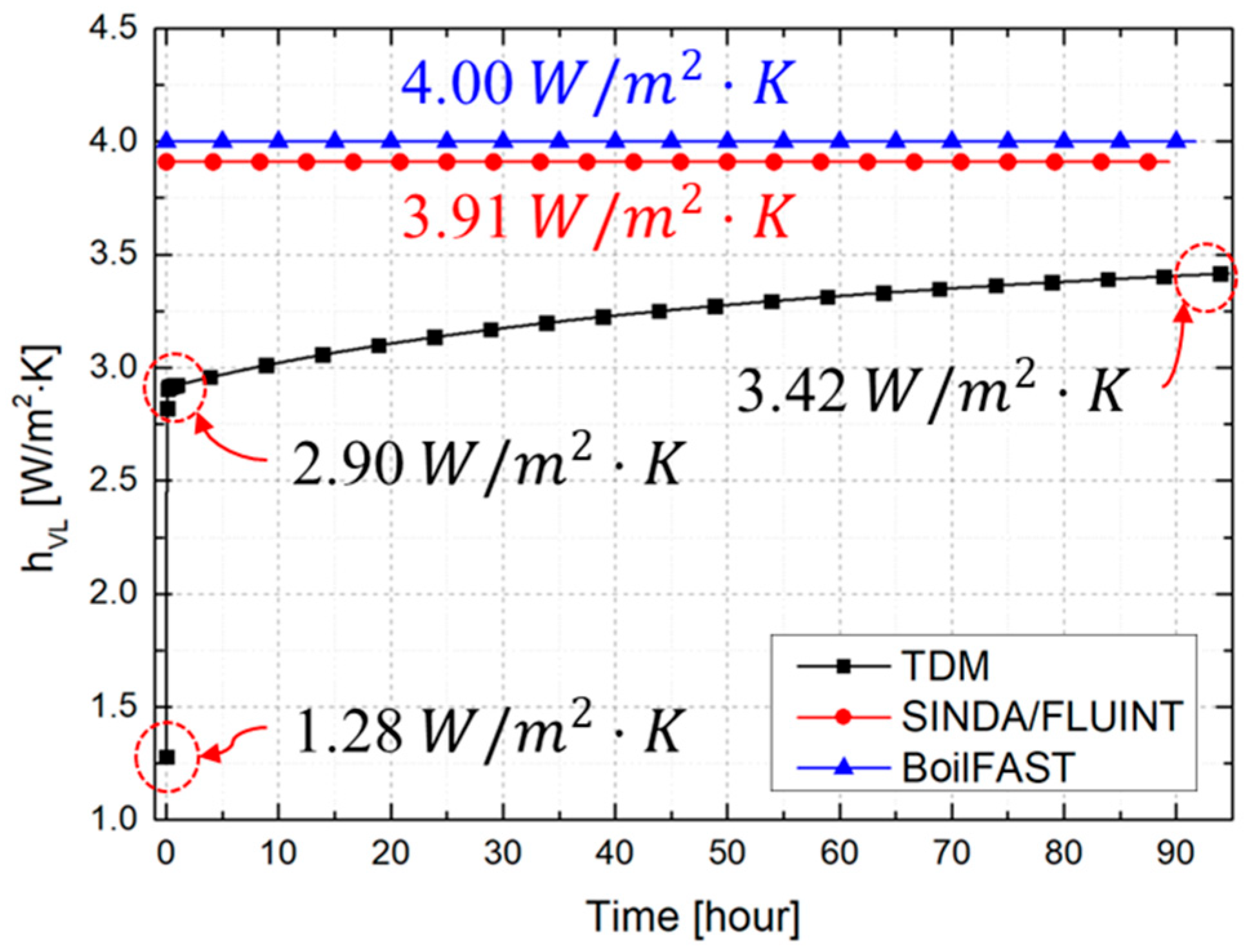
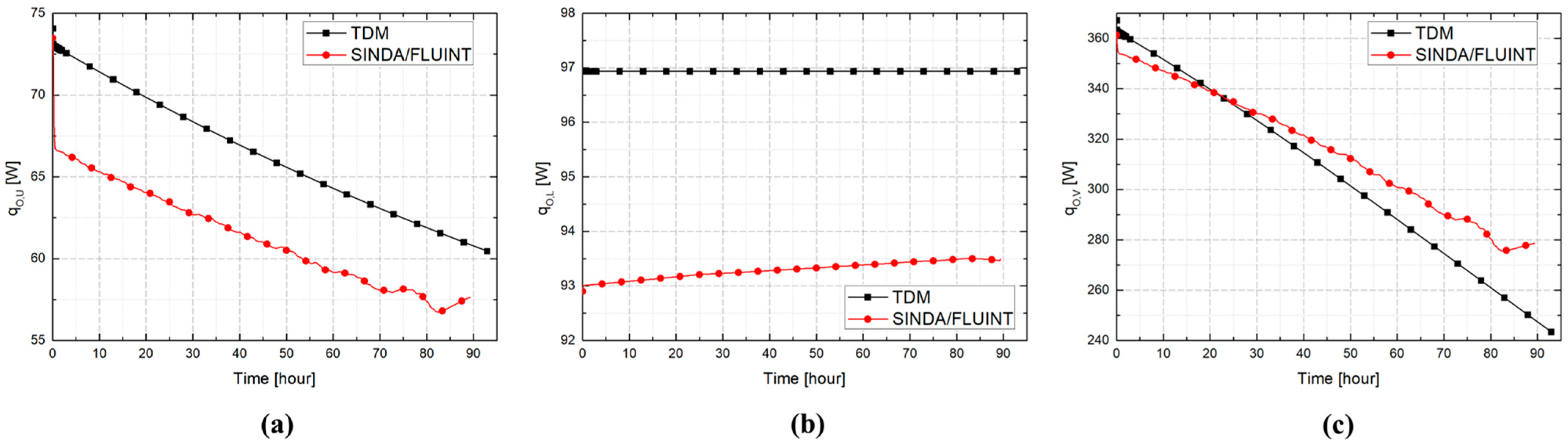
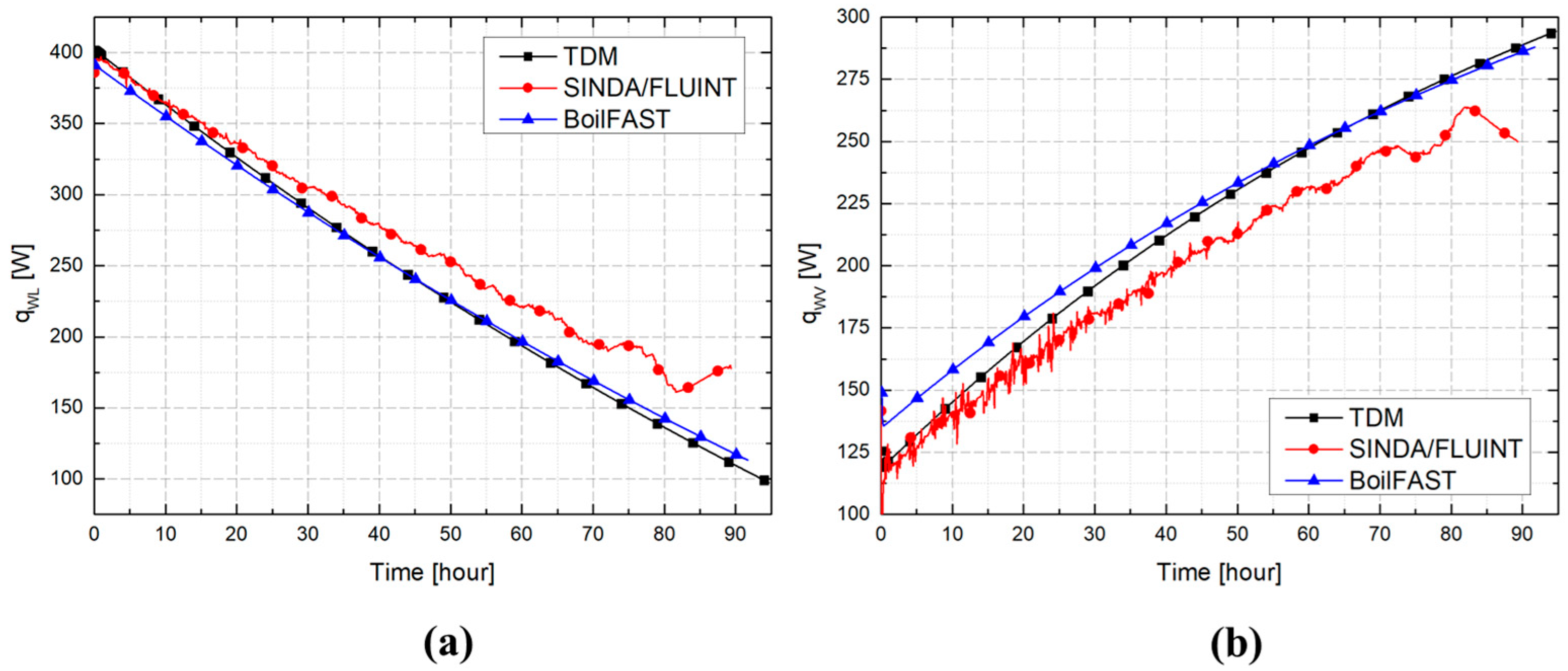
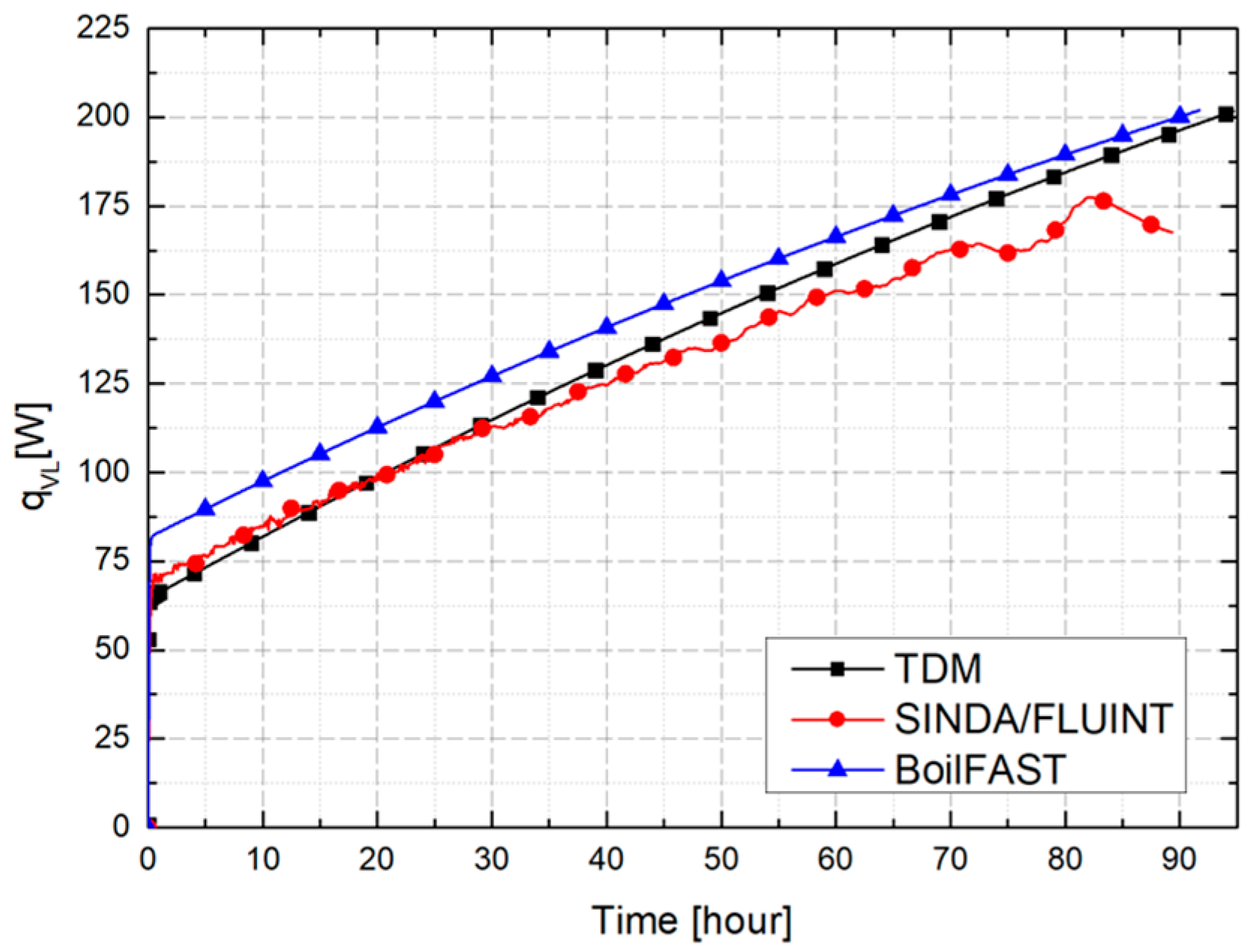
3.2. Comparative Performance of TDM, BoilFAST, and SINDA/FLUINT
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols and Variables | ||
| Symbol | Description | Unit |
| Area | ||
| Specific heat at constant pressure | ||
| Filling Ratio | % | |
| Grashof Number | – | |
| Gravitational acceleration | ||
| Entalpy | ||
| Convective Heat Transfer Coefficient | ||
| Latent heat of vaporization | ||
| Specific Entalpy | ||
| Characteristic length | ||
| k | Thermal conductivity | |
| Mass | ||
| Mass flow rate | ||
| Nusselt Number | – | |
| Pressure | ||
| Prandtl Number | – | |
| Heat (Energy) | ||
| Heat Flow Rate | ||
| Thermal Resistance | ||
| Rayleigh Number | – | |
| Reynolds Number | – | |
| Temperature | ||
| t | Time | |
| Time increment | ||
| Volume | ||
| Greek Letters | ||
| Symbol | Description | Unit |
| Thermal expansion coefficient | ||
| Kinematic viscosity | ||
| Dynamic viscosity | ||
| Density | ||
| Surface tension | ||
| Subscripts | ||
| Symbol | Description | |
| Average | ||
| Boil-Off Gas | ||
| Insulation | ||
| Interface Surface | ||
| Liquid Phase | ||
| Liquid Phase at Horizontal surface | ||
| Liquid Phase at Vertical surface | ||
| Laminar flow | ||
| Outside | ||
| Outside to Liquid Phase | ||
| Outside to Liquid for Horizontal surface | ||
| Outside to Liquid for Vertical surface | ||
| Outside to Vapor Phase | ||
| Outside to Vapor for Vertical surface | ||
| Outer wall for Lower surface | ||
| Outer wall for Upper surface | ||
| Outer wall for Vertical surface | ||
| s | Tank outer wall | |
| Vapor Phase | ||
| Vapor-Liquid Interface | ||
| Vapor Phase at Horizontal surface | ||
| Vapor Phase at Vertical surface | ||
| Inner Tank Wall | ||
| Wall to Liquid | ||
| Wall to Vapor | ||
| Wall to Vapor for Horizontal surface | ||
| Wall to Vapor for Vertical surface | ||
References
- Yin, L.; Ju, Y. Review on the design and optimization of BOG re-liquefaction process in LNG ship. Energy 2022, 244, 123065. [Google Scholar] [CrossRef]
- Ratnakar, R.R.; Sun, Z.; Balakotaiah, V. Effective thermal conductivity of insulation materials for cryogenic LH2 storage tanks: A review. Int. J. Hydrogen Energy 2023, 48, 7770–7793. [Google Scholar]
- Matveev, K.I.; Leachman, J.W. The Effect of Liquid Hydrogen Tank Size on Self-Pressurization and Constant-Pressure Venting. Hydrogen 2023, 4, 444–455. [Google Scholar] [CrossRef]
- Jeon, G.M.; Park, J.C.; Choi, S. Multiphase-thermal simulation on BOG/BOR estimation due to phase change in cryogenic liquid storage tanks. Appl. Therm. Eng. 2021, 184, 116264. [Google Scholar]
- Lin, Y.; Ye, C.; Yu, Y.; Bi, S. An approach to estimating the boil-off rate of LNG in type C independent tank for floating storage and regasification unit under different filling ratio. Appl. Therm. Eng. 2018, 135, 463–471. [Google Scholar] [CrossRef]
- Khan, M.S.; Qyyum, M.A.; Ali, W.; Wazwaz, A.; Ansari, K.B.; Lee, M. Energy saving through efficient BOG prediction and impact of static boil-off-rate in full containment-type LNG storage tank. Energies 2020, 13, 5578. [Google Scholar] [CrossRef]
- Migliore, C.; Tubilleja, C.; Vesovic, V. Weathering prediction model for stored liquefied natural gas (LNG). J. Nat. Gas Sci. Eng. 2015, 26, 570–580. [Google Scholar] [CrossRef]
- Seo, Y.M.; Noh, H.W.; Koo, T.H.; Ha, D.W.; Ko, R.K. Development of Numerical Analysis Model on Cryogenic Vessel for Safety Pressure Maintenance and Control of Liquid Hydrogen BOG. J. Hydrogen New Energy 2024, 35, 280–289. [Google Scholar] [CrossRef]
- Nam, T.; Yu, T.; Lim, Y. Thermodynamic Modeling and Analysis of Boil-off Gas Generation and Self-Pressurization in Liquefied Carbon Dioxide Tanks. J. Ocean Eng. Technol. 2024, 38, 257–268. [Google Scholar] [CrossRef]
- Kang, M.; Kim, J.; You, H.; Chang, D. Experimental investigation of thermal stratification in cryogenic tanks. Exp. Therm. Fluid Sci. 2018, 96, 371–382. [Google Scholar] [CrossRef]
- Yu, K.; Ge, Z.; Korpus, R. CFD predictions of FLNG BOG including the influence of Filling, Offloading, and Vessel motion. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2016. [Google Scholar]
- Huerta, F.; Vesovic, V. A realistic vapour phase heat transfer model for the weathering of LNG stored in large tanks. Energy 2019, 174, 280–291. [Google Scholar] [CrossRef]
- Ferrín, J.L.; Pérez-Pérez, L.J. Numerical simulation of natural convection and boil-off in a small size pressurized LNG storage tank. Comput. Chem. Eng. 2020, 138, 106840. [Google Scholar] [CrossRef]
- Sakowski, B.A.; Hauser, D.M.; Kassemi, M. SINDA/FLUINT and Thermal Desktop Multi-Node Settled and Unsettled Propellant Tank Modeling of Zero Boil Off Test. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar]
- Perez, F.; Al Ghafri, S.Z.S.; Gallagher, L.; Siahvashi, A.; Ryu, Y.; Kim, S.; Kim, S.G.; Johns, M.L.; May, E.F. Measurements of boil-off gas and stratification in cryogenic liquid nitrogen with implications for the storage and transport of liquefied natural gas. Energy 2021, 222, 119853. [Google Scholar] [CrossRef]
- Al Ghafri, S.Z.S.; Swanger, A.; Park, K.H.; Jusko, V.; Ryu, Y.; Kim, S.; Kim, S.G.; Zhang, D.; Seo, Y.; Johns, M.L.; et al. Advanced boil-off gas studies of liquefied natural gas used for the space and energy industries. Acta Astronaut. 2022, 190, 444–454. [Google Scholar] [CrossRef]
- Al Ghafri, S.Z.S.; Swanger, A.; Jusko, V.; Siahvashi, A.; Perez, F.; Johns, M.L.; May, E.F. Modelling of Liquid Hydrogen Boil-Off. Energies 2022, 15, 1149. [Google Scholar] [CrossRef]
- Majumdar, A.K.; LeClair, A.; Moore, R.; Schallhorn, P.A. Generalized Fluid System Simulation Program (GFSSP)-Version 6. In Proceedings of the 51st AIAA/SAE/ASEE Joint Propulsion Conference, Orlando, FL, USA, 27–29 July 2015. [Google Scholar]
- LeClair, A.; Hartwig, J.W.; Hauser, D.M.; Kassemi, M.; Diaz-Hyland, P.G.; Going, T.R. Modeling Cryogenic Chilldown of a Transfer Line with GFSSP. In Proceedings of the Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar]
- Bandyopadhyay, A.; Majumdar, A.K.; LeClair, A.; Valenzuela, J. Multi-Node Modeling of Cryogenic Tank Pressurization System Using Generalized Fluid System Simulation Program (GFSSP). In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar]
- Joseph, J.; Agrawal, G.; Agarwal, D.K.; Pisharady, J.C.; Kumar, S.S. Effect of insulation thickness on pressure evolution and thermal stratification in a cryogenic tank. Appl. Therm. Eng. 2017, 111, 1629–1639. [Google Scholar] [CrossRef]
- Schallhorn, P.; Campbell, D.; Chase, S.; Piquero, J.; Fortenberry, C.; Li, X.; Grob, L. Upper stage tank thermodynamic modeling using SINDA/FLUINT. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. [Google Scholar]
- Kashani, A.; Luchinskiy, D.G.; Ponizovskaya-Devine, E.; Khasin, M.; Timucin, D.; Sass, J.; Perotti, J.; Brown, B. Optimization of cryogenic chilldown and loading operation using SINDA/FLUINT. IOP Conf. Ser. Mater. Sci. Eng. 2015, 101, 012115. [Google Scholar] [CrossRef]
- Wang, H.R.; Wang, B.; Pan, Q.W.; Wu, Y.Z.; Jiang, L.; Wang, Z.H.; Gan, Z.H. Modeling and thermodynamic analysis of thermal performance in self-pressurized liquid hydrogen tanks. Int. J. Hydrogen Energy 2022, 47, 30530–30545. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Lee, J.H.; Kim, K.H.; Lim, C.H.; Lee, S.H. Coupled CFD modeling and thermal analysis of multi-layered insulation structures in liquid hydrogen storage tanks for various vapor-cooled shields. Case Stud. Therm. Eng. 2024, 63, 105317. [Google Scholar] [CrossRef]
- Lan, E.; Shi, S. Coupled modeling and simulation of tank self-pressurization and thermal stratification. Int. J. Heat Mass Transf. 2024, 232, 125885. [Google Scholar] [CrossRef]
- Zuo, Z.; Zhu, W.; Huang, Y.; Wang, L.; Tong, L. A review of cryogenic quasi-steady liquid-vapor phase change: Theories, models, and state-of-the-art applications. Int. J. Heat Mass Transf. 2023, 205, 123916. [Google Scholar] [CrossRef]
- McAdams, W.H. Heat Transmission, 3rd ed.; McGraw-Hill: New York, NY, USA, 1954. [Google Scholar]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Çengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer: Fundamentals and Applications, 5th ed.; McGraw-Hill: New York, NY, USA, 2015. [Google Scholar]
- Churchill, S.W.; Chu, H.H.S. Correlating equations for laminar and turbulent free convection from a vertical plate. Int. J. Heat Mass Transf. 1975, 18, 1323–1329. [Google Scholar] [CrossRef]
- Rohsenow, W.M. A method of correlating heat-transfer data for surface boiling of liquids. Trans. ASME 1952, 74, 969–975. [Google Scholar]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.I. Handbook of Heat Transfer, 3rd ed.; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties—REFPROP, Version 10.0. Available online: https://www.nist.gov/srd/refprop (accessed on 23 August 2025).
- Fluid Science and Resources. BoilFAST Software. The University of Western Australia. Available online: https://www.fsr.ecm.uwa.edu.au/software/boilfast/ (accessed on 23 August 2025).
- Cullimore and Ring Technologies, Inc. SINDA/FLUINT: Software for Thermal and Fluid Analysis. Available online: https://www.crtech.com/products/sindafluint (accessed on 23 August 2025).
- Cullimore, B.A. Optimization, data correlation, and parametric analysis features in SINDA/FLUINT version 4.0. SAE Trans. 1998, 107, 347–356. [Google Scholar]
- C&R Technologies, Inc. TD Suite Manual: For Thermal Desktop®, TD Direct®, and SINDA/FLUINT Version 6.3; C&R Technologies, Inc.: Boulder, CO, USA, 2022. [Google Scholar]
- Guyer, E.C. Handbook of Applied Thermal Design; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Goldstein, R.J.; Sparrow, E.M.; Jones, D.C. Natural Convection Mass Transfer Adjacent to Horizontal Plates. Int. J. Heat Mass Transf. 1973, 16, 1025–1035. [Google Scholar] [CrossRef]
- Raithby, G.D.; Hollands, K.G.T. A General Method of Obtaining Approximate Solutions to Laminar and Turbulent Free Convection Problems. Adv. Heat Transf. 1975, 11, 265–315. [Google Scholar]
- Kreith, F. Principles of Heat Transfer, 3rd ed.; Intext: New York, NY, USA, 1973. [Google Scholar]




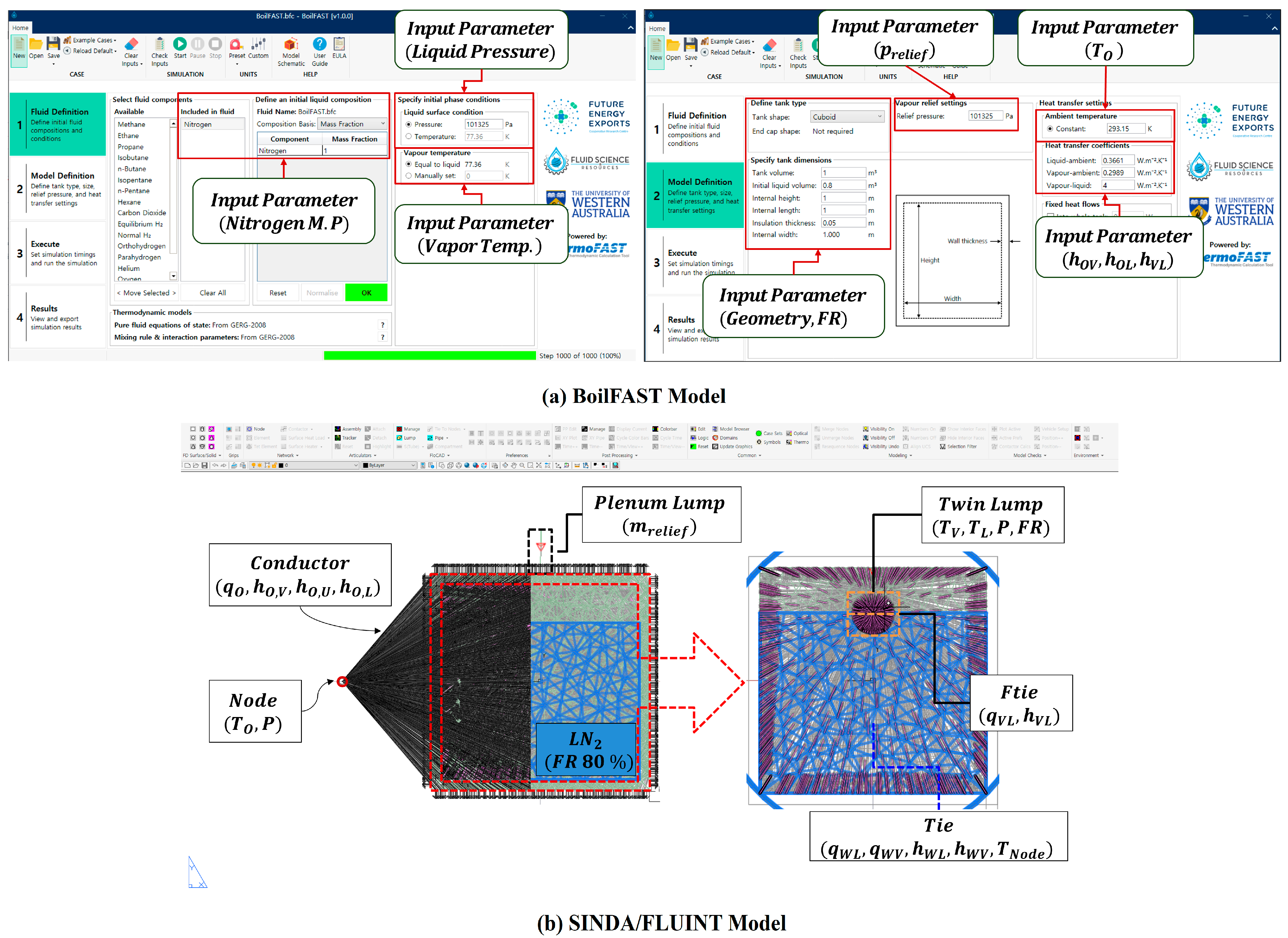


| Component | Connection Type | Variables |
|---|---|---|
| Conductor | Node to node | |
| Tie | Node to lump (twin lump) | |
| Ftie | Lump (vapor) to lump (liquid) | |
| Path | Lump (vapor) to lump (plenum) |
| Component | Outside-Tank Bottom Wall (hO,L) | Outside-Tank Side Wall (hO,V) | |
|---|---|---|---|
| HTC | |||
| Nusselt Number | |||
| Procedure | TDM Model | BoilFAST | SINDA/FLUINT |
|---|---|---|---|
| Model type | Lumped thermodynamic model | Semi-empirical lumped model | Finite-volume (node-based) transient solver |
| Heat-transfer mechanism | Heat transfer via time-varying thermal resistance | Constant wall-to-fluid heat flux | Full transient conduction through wall & insulation |
| HTC | Time-dependent, updated per time step | Fixed or averaged HTC under steady conditions | Locally computed, fully transient |
| Heat flux | Coupled with dynamic HTC and interface temperature | Prescribed constant input | Solved per node and time step |
| Boundary condition | Quasi-steady Outer wall; transient inner wall | Fixed ambient & wall temperature | Fully transient external & internal boundaries |
| Phase-change model | Thermodynamic equilibrium at vapor–liquid interface | Empirical boil-off correlation | Transient evaporation from local temperature gradients |
| Fidelity | Intermediate (Parametric studies) | Low (Quick sizing) | High (Detailed design) |
| Specification | Description | |
|---|---|---|
| Tank | Type | Rectangular cuboid tank |
| Thickness () | 0.0065 | |
| Thermal conductivity () | 16.2 | |
| Volume () | Gross | 1.331 |
| Net | 1.000 | |
| Insulation | Type | Expanded polystyrene (EPS) |
| Thickness () | 0.05 | |
| Thermal conductivity () | 0.021 | |
| Boundary Condition | Convective HTC (W/m2·K) | |||
|---|---|---|---|---|
| TDM | BoilFAST | SINDA/FLUINT | ||
| Ambient to surface () | To upper () | 3.632 (Equation (1)) | - | Temperature dependent (Equation (35)) |
| To lower () | 7.140 (Equation (2)) | - | Temperature dependent (Table 2) | |
| To vertical () | 10.790 (Equation (3)) | - | Temperature dependent (Table 2) | |
| Ambient to liquid () | - | 0.366 (Equation (27)) | - | |
| Ambient to vapor () | - | 0.299 (Equation (29)) | - | |
| Inner wall to vapor () | To lower () | Temperature dependent (Equation (7)) | - | Temperature dependent (Equation (38)) |
| To vertical () | Temperature Dependent (Equation (8)) | - | ||
| Inner wall to liquid () | 1924 (Equation (9)) | - | Temperature dependent (Rohsenow et al. [32]) | |
| Vapor to liquid () | Temperature dependent (Equation (11)) | 4.000 (Perez et al. [15]) | 3.908 (Equation (11)) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-S.; Lee, J.H. Prediction of Boil-Off Gas in Cryogenic Tanks with a Coupled Thermal Resistance and Thermodynamic Model. Processes 2025, 13, 3584. https://doi.org/10.3390/pr13113584
Kim M-S, Lee JH. Prediction of Boil-Off Gas in Cryogenic Tanks with a Coupled Thermal Resistance and Thermodynamic Model. Processes. 2025; 13(11):3584. https://doi.org/10.3390/pr13113584
Chicago/Turabian StyleKim, Min-Seok, and Jang Hyun Lee. 2025. "Prediction of Boil-Off Gas in Cryogenic Tanks with a Coupled Thermal Resistance and Thermodynamic Model" Processes 13, no. 11: 3584. https://doi.org/10.3390/pr13113584
APA StyleKim, M.-S., & Lee, J. H. (2025). Prediction of Boil-Off Gas in Cryogenic Tanks with a Coupled Thermal Resistance and Thermodynamic Model. Processes, 13(11), 3584. https://doi.org/10.3390/pr13113584








