Study on Borehole Trajectory Deviation Characteristics and Influencing Factors in Three-Soft Coal Seams
Abstract
1. Introduction
2. Engineering Overview of Drilling Area
2.1. Core Sampling in Drilling Area
2.2. Three-Dimensional Model of Drilling Area
3. Variation and Law of Borehole Deflection Trajectory
3.1. Variation Law of Borehole Deflection Angle
3.2. The Trajectory Equation of the Change in Borehole Inclination
4. Analysis of Influencing Factors of Drilling Trajectory Deflection
4.1. Classification of Influencing Factors
4.1.1. Geological Factors
4.1.2. Factors Affecting Equipment
4.1.3. Human Factors
4.2. AHP Analysis Model
4.2.1. Constructing the AHP Analysis Model
4.2.2. AHP Analysis Model Calculation Weight
- (1)
- Determine the judgment matrix of each level
- (a)
- The judgment matrix AZ of the criterion layer to the target layer Z:
- (b)
- The judgment matrix AU1 of the index layer to the criterion layer U1:
- (c)
- The judgment matrix AU2 of the index layer to the criterion layer U2:
- (d)
- The judgment matrix AU3 of the index layer to the criterion layer U3
- (2)
- Calculate the importance ranking
- (3)
- Consistency test
- (4)
- Calculate the composite weight of each layer element for the target layer
- (5)
- Total sort consistency ratio
5. Conclusions
- (1)
- Through on-site drilling and coring operations, the lithology and fragmentation characteristics of cores from each rock stratum were observed. A large volume of on-site data was collected via on-site monitoring, and trajectory data of gas drainage boreholes with inclination angles of 15°, 30°, 45°, 60°, 75°, and 90° were obtained. Analysis shows that the Δ value of borehole inclination variation changes with the borehole inclination angle, and the overall relationship presents a quadratic function. Specifically, when the borehole inclination angle is 15° or 90°, the Δ value is close to 0°; when the borehole inclination angle is 30° or 75°, the Δ value is close to 2.5°; and when the borehole inclination angle is 45° or 60°, the Δ value is close to 4.5°.
- (2)
- Through computer-based fitting, a function formula describing the relationship between the Δ value of borehole inclination variation and the borehole inclination angle was derived from the corresponding relationship graph: y = −0.00415x2 + 0.4379x − 6.7519 (where x represents the borehole inclination angle, and y represents the Δ value of inclination variation). Using this formula, it was determined that when the borehole inclination angle is 50°, the Δ value reaches its maximum (close to 5°), meaning the gas drainage borehole has the largest deviation. This formula can be used to predict and control the deviation magnitude, thereby reducing borehole deviation.
- (3)
- The influencing factors of borehole trajectory deviation primarily include geological factors, equipment factors, and human factors. Among these, geological factors are objective causes of borehole deviation, mainly manifested in variations in rock hardness, rock stratum dip angle, and rock anisotropy of the drilled formation; these factors exhibit low controllability. However, based on the AHP analysis model, it was determined that during cross-stratum drilling, geological factors are one of the primary causes of borehole deviation, and targeted control can still be implemented for key geological influencing factors.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, M.; Zheng, P.; Zheng, C.; Hu, Z.; Wang, J.; Dai, G. Numerical Analysis and Prediction of Coal Mine Methane Drainage Based on Gas-Solid Coupling Model. Teh. Vjesn. 2019, 26, 752–761. [Google Scholar] [CrossRef]
- Zhang, T.J.; Zhang, L.; Pan, H.Y.; Zhang, C. Stability of Gas Drainage Borehole Analysis on Rock Mechanics Parameters with Roadway of Complex Stress. Appl. Mech. Mater. 2015, 3753, 330–335. [Google Scholar] [CrossRef]
- Cleary, P.W.; Pereira, G.G.; Lemiale, V.; Piane, C.D.; Ben Clennell, M. Multiscale model for predicting shear zone structure and permeability in deforming rock. Comput. Part. Mech. 2016, 3, 179–199. [Google Scholar] [CrossRef]
- Zhou, C.; Gao, W.; Hu, C.J.; Chen, X.; Cui, S. Numerical study of related factors affecting mechanical properties of fractured rock mass and its sensitivity analysis. Comput. Part. Mech. 2022, 10, 369–386. [Google Scholar] [CrossRef]
- Zárate, F.; Cornejo, A.; Oñate, E. A three-dimensional FEM–DEM technique for predicting the evolution of fracture in geomaterials and concrete. Comput. Part. Mech. 2018, 5, 411–420. [Google Scholar] [CrossRef]
- Johnny, Q.; Qu, Q.D.; Hua, G. CFD simulations for longwall gas drainage design optimisation. Int. J. Min. Sci. Technol. 2017, 27, 777–782. [Google Scholar] [CrossRef]
- Fan, C.; Xu, H.; Wang, G.; Wang, J.; Liu, Z.; Cheng, Q. Determination of roof horizontal long drilling hole layout layer by dynamic porosity evolution law of coal and rock. Powder Technol. 2021, 394, 970–985. [Google Scholar] [CrossRef]
- Zhang, C.L.; Xu, J.; Peng, S.J.; Li, Q.; Yan, F. Experimental study of drainage radius considering borehole interaction based on 3D monitoring of gas pressure in coal. Fuel 2019, 239, 955–963. [Google Scholar] [CrossRef]
- Park, K.-W.; Choi, C.-S.; Park, B.-H.; Ji, S.-H. Numerical and experimental investigation of the hydrogeological evolution around a borehole due to stress redistribution in fractured rock. Tunn. Undergr. Space Technol. 2022, 124, 104461. [Google Scholar] [CrossRef]
- Zheng, Y.H.; Zhao, Z.G.; Wu, W.B.; Zhang, K.; Sun, X. Numerical simulation study on measuring coal stress by drilling parameters. Arab. J. Geosci. 2021, 14, 2110. [Google Scholar] [CrossRef]
- Zhao, H.B.; Li, J.Y.; Liu, Y.H.; Wang, Y.; Wang, T.; Cheng, H. Experimental and measured research on three-dimensional deformation law of gas drainage borehole in coal seam. Int. J. Min. Sci. Technol. 2020, 30, 397–403. [Google Scholar] [CrossRef]
- Wang, H.; Wang, E.Y.; Li, Z.G.; Shen, R.; Liu, X. Study and application of a new gas pressure inversion model in coal seam while drilling based on directional drilling technology. Fuel 2021, 306, 121679. [Google Scholar] [CrossRef]
- Chen, X.; Cao, W.H.; Gan, C.; Wu, M. A hybrid partial least squares regression-based real time pore pressure estimation method for complex geological drilling process. J. Pet. Sci. Eng. 2022, 210, 109771. [Google Scholar] [CrossRef]
- Duan, H.J.; Wang, Y.; Xiao, Q.; Wang, J.; Peng, D. Gas extraction technology and application of near horizontal high directional drilling. Energy Rep. 2022, 8 (Suppl. S4), 1326–1333. [Google Scholar] [CrossRef]
- Shang, Y.Q.; Wu, G.Y.; Liu, Q.Z.; Kong, D.; Li, Q. The Drainage Horizon Determination of High Directional Long Borehole and Gas Control Effect Analysis. Adv. Civ. Eng. 2021, 11, 3370170. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, L.; Kong, D.; Wang, Y.; Cheng, Z. Overlying strata failure mechanism and gas migration law in close distance outburst coal seams: A case study. Eng. Fail. Anal. 2023, 148, 107214. [Google Scholar] [CrossRef]
- Shang, Y.; Wang, Y.; Zhang, L.; Wu, G.; Kong, D.; Zhang, P.; Jia, T. Impact of Lower Protective Coal Seam Mining on Overlying Strata: Deformation, Pressure Relief, and Permeability Enhancement. Int. J. Geomech. 2024, 24, 04024178. [Google Scholar] [CrossRef]
- Hong, L.; Wei, W.; Liu, Y.W.; Ma, J.; Gao, H. An integrated drilling, protection and sealing technology for improving the gas drainage effect in soft coal seams. Energy Rep. 2020, 6, 2030–2043. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Q.Z.; Lou, Y.H.; Kong, D. Deviation Principles of Gas Drainage Drilling in Three-Soft Outburst Coal Seams. Geotech. Geol. Eng. 2022, 40, 3147–3168. [Google Scholar] [CrossRef]
- Xie, L.Q.; Jin, P.; Su, T.C.; Li, X.; Liang, Z. Numerical simulation of uniaxial compression tests on layered rock specimens using the discrete element method. Comput. Part. Mech. 2020, 7, 753–762. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, J. Gob-Side Entry Retaining Technology with Advanced Empty Hole Butterfly-Shaped Weakening in Three-Soft Coal Seam in China. Adv. Mater. Sci. Eng. 2020, 2020, 2476789. [Google Scholar] [CrossRef]
- Sun, X.Y.; Cheng, Z.H.; Chen, L.; Li, Z.; Wang, H.; Yin, S. Deflection Laws of Gas Drainage Boreholes in Interbedded Soft and Hard Seams: A Case Study at Xinzheng Coal Mine, China. Adv. Civ. Eng. 2021, 2021, 5533879. [Google Scholar] [CrossRef]

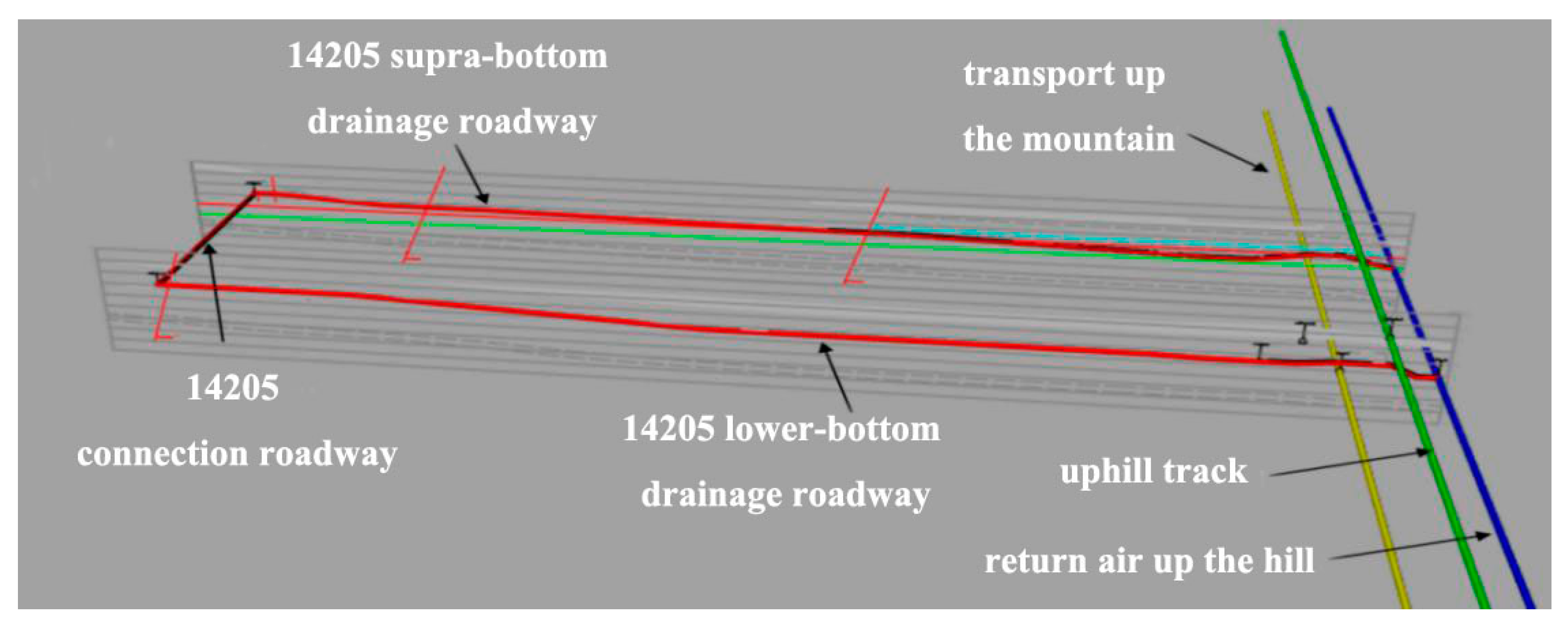
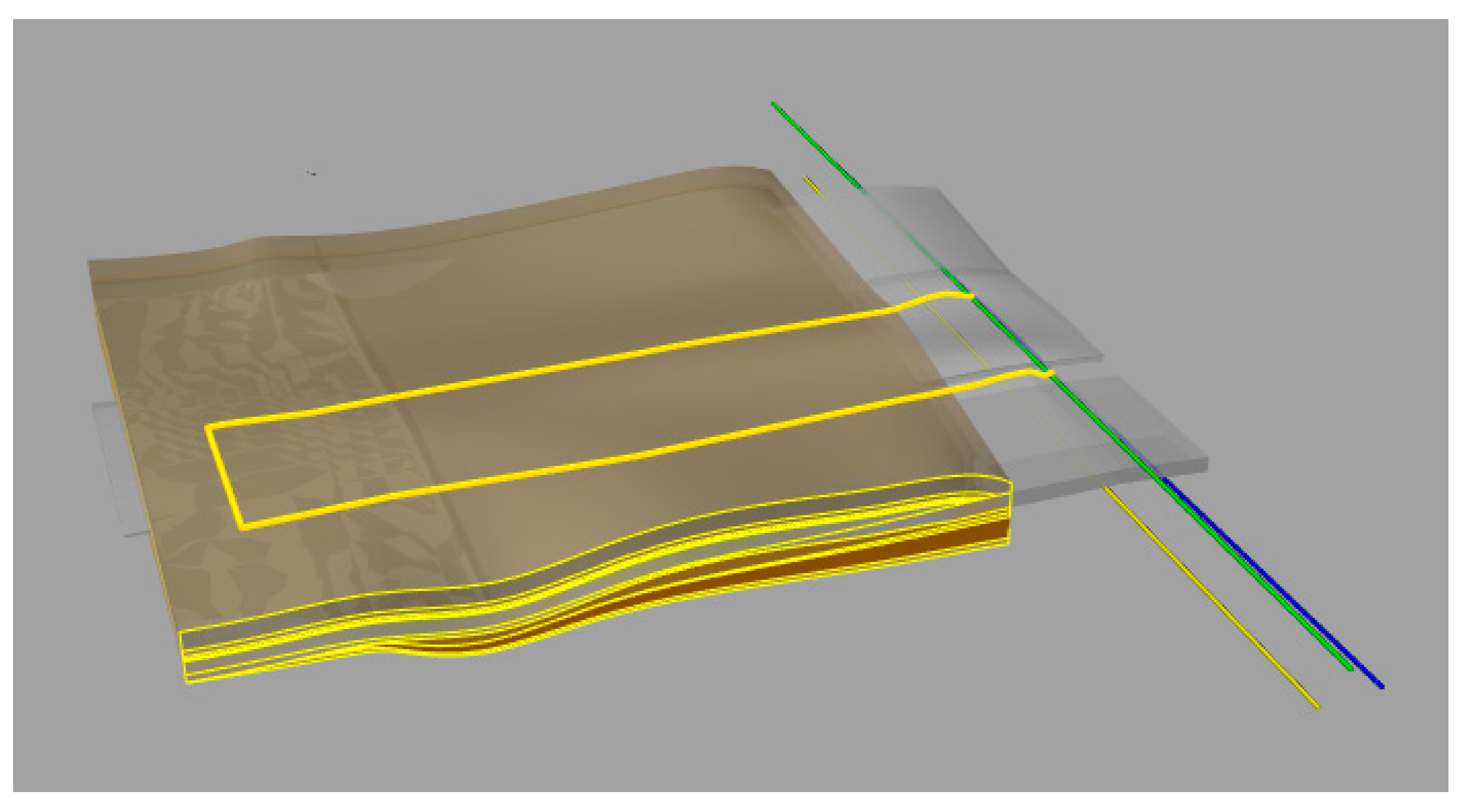
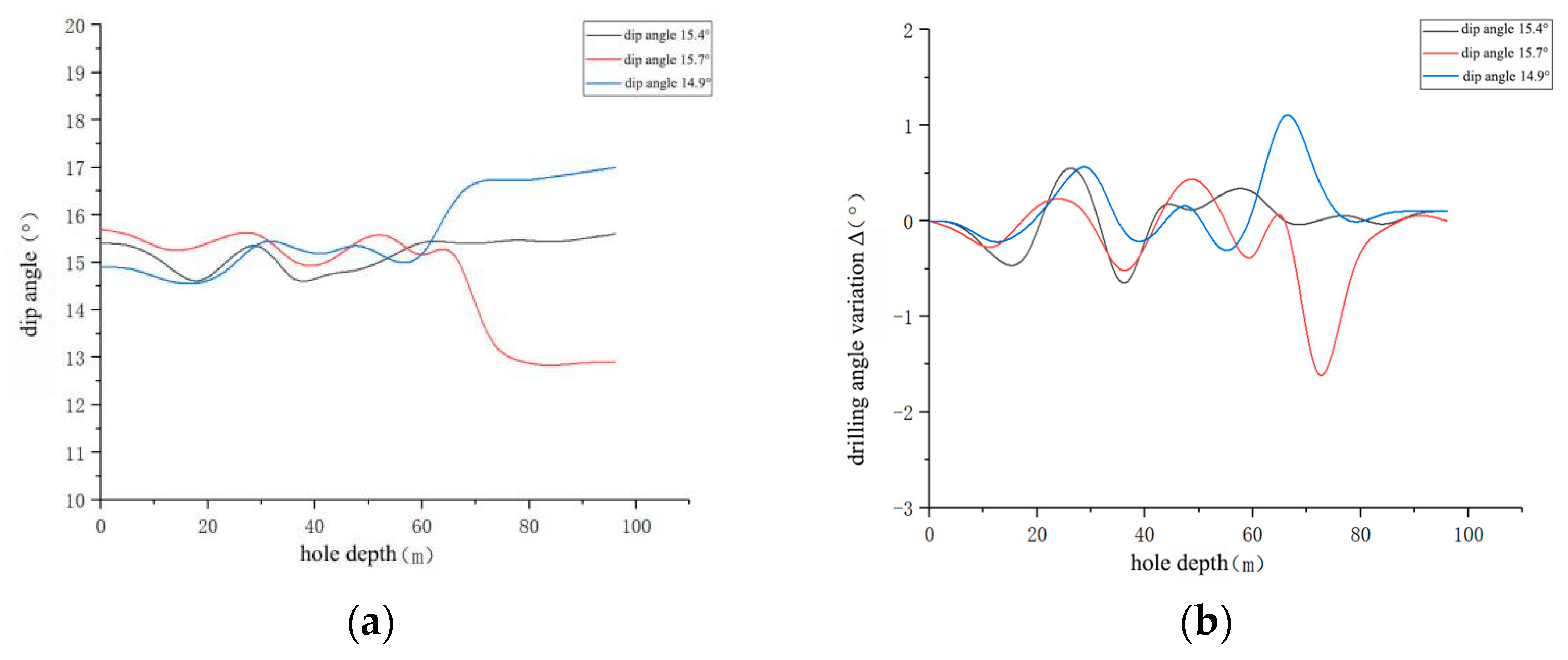

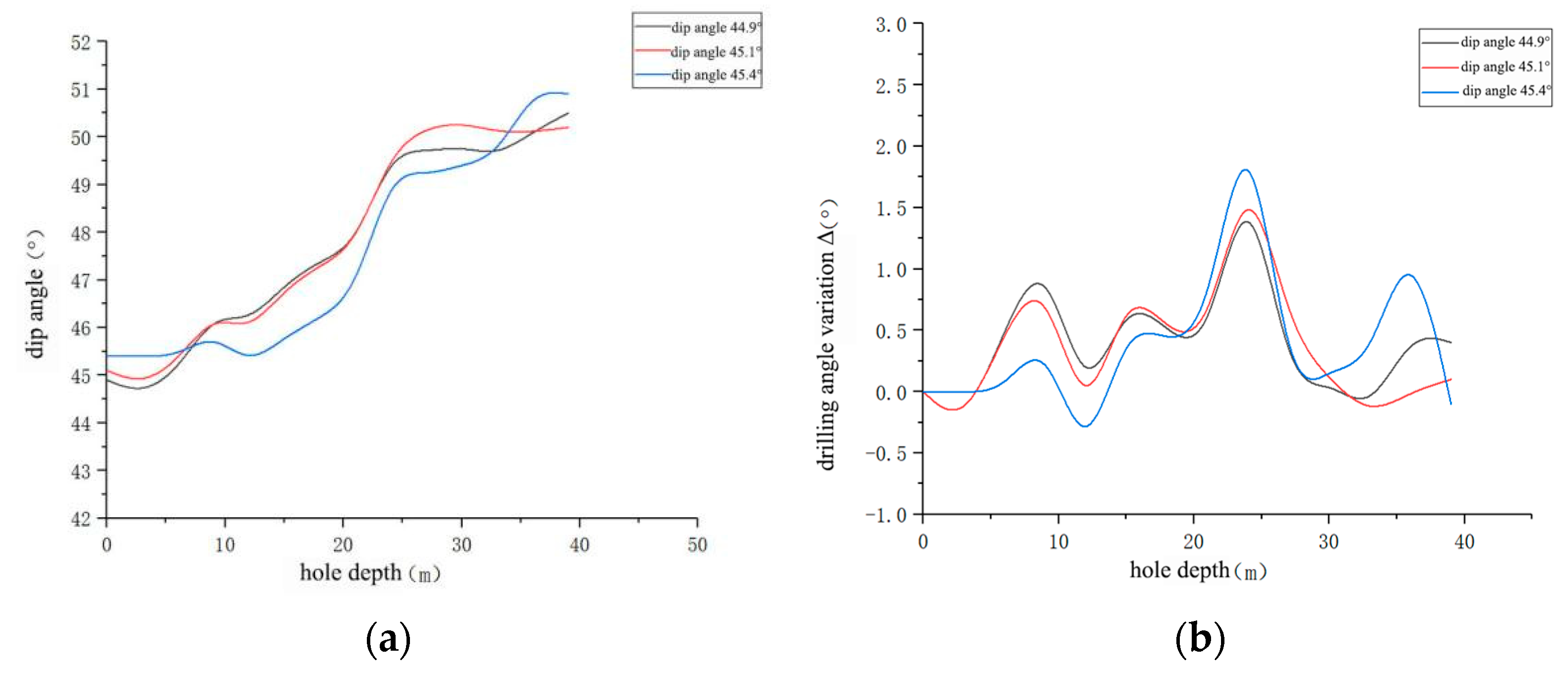
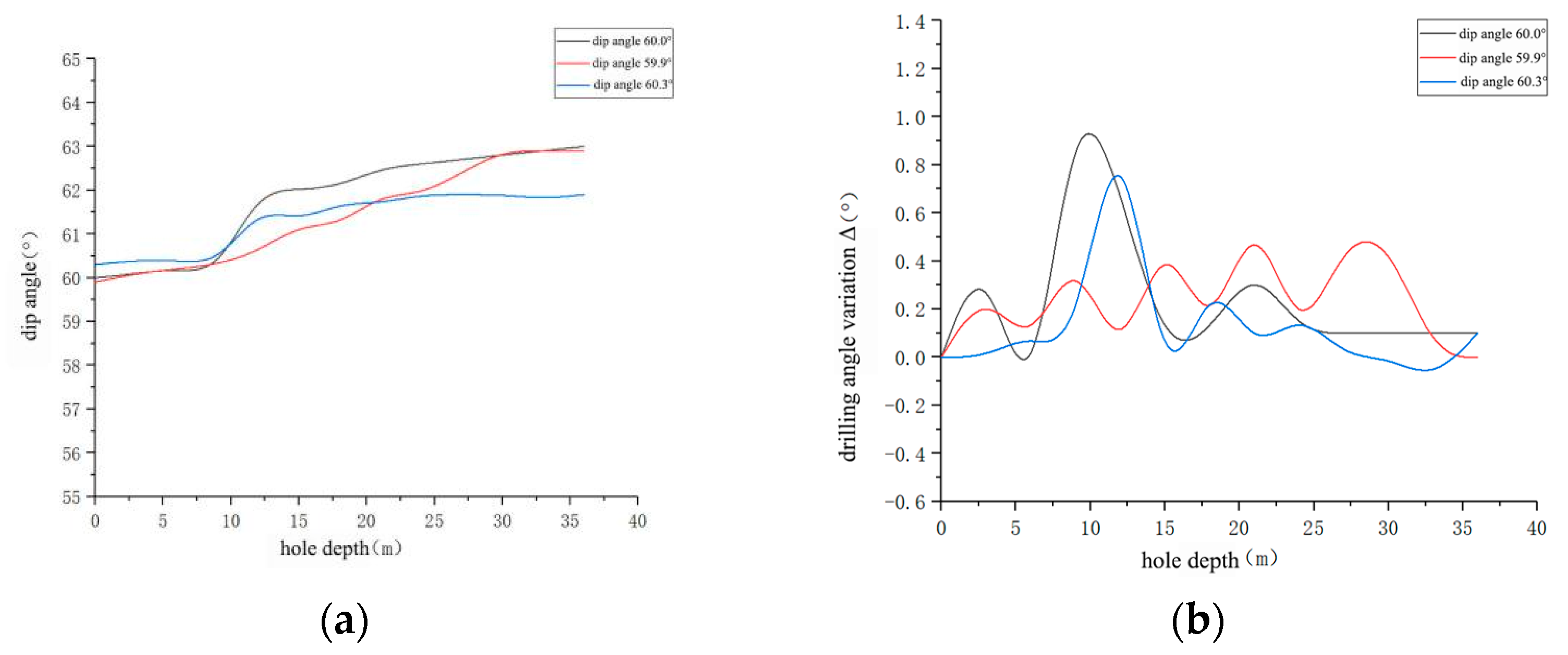
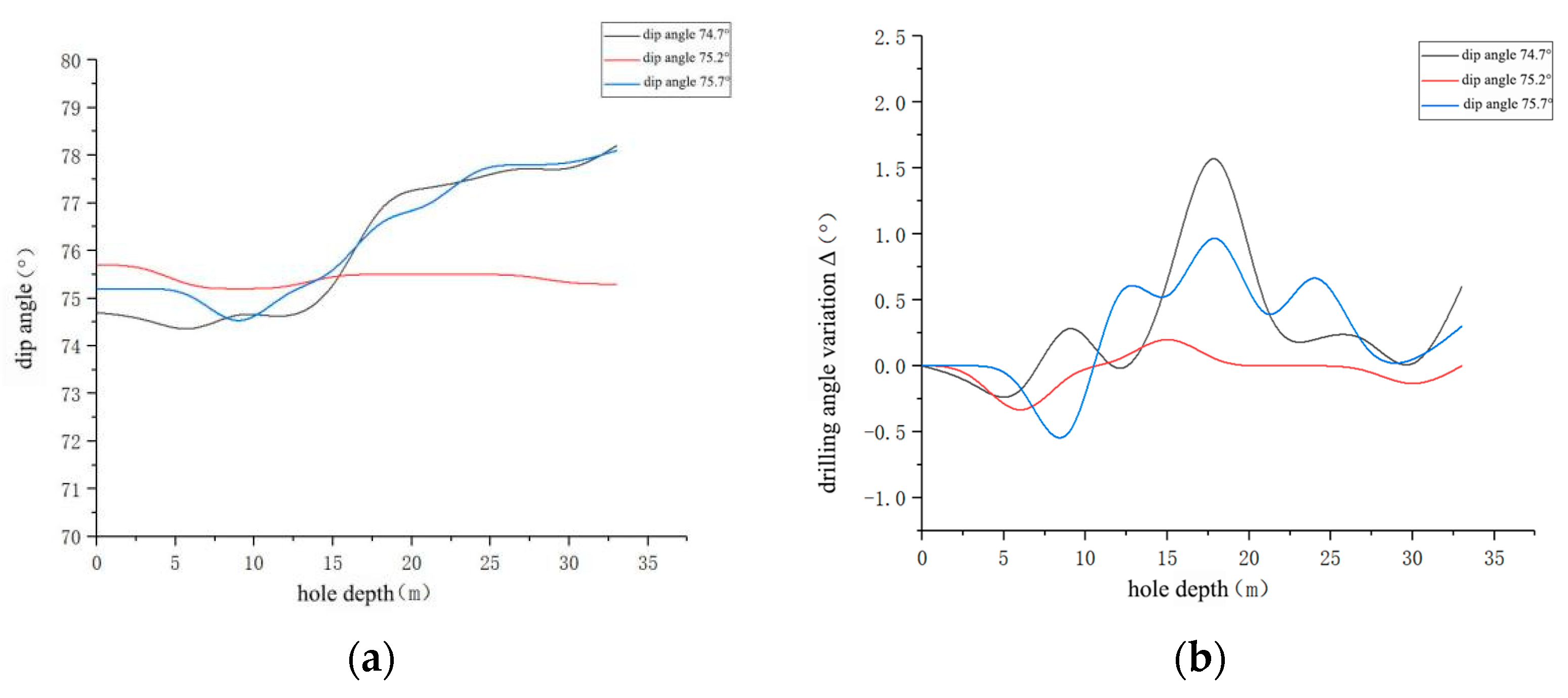
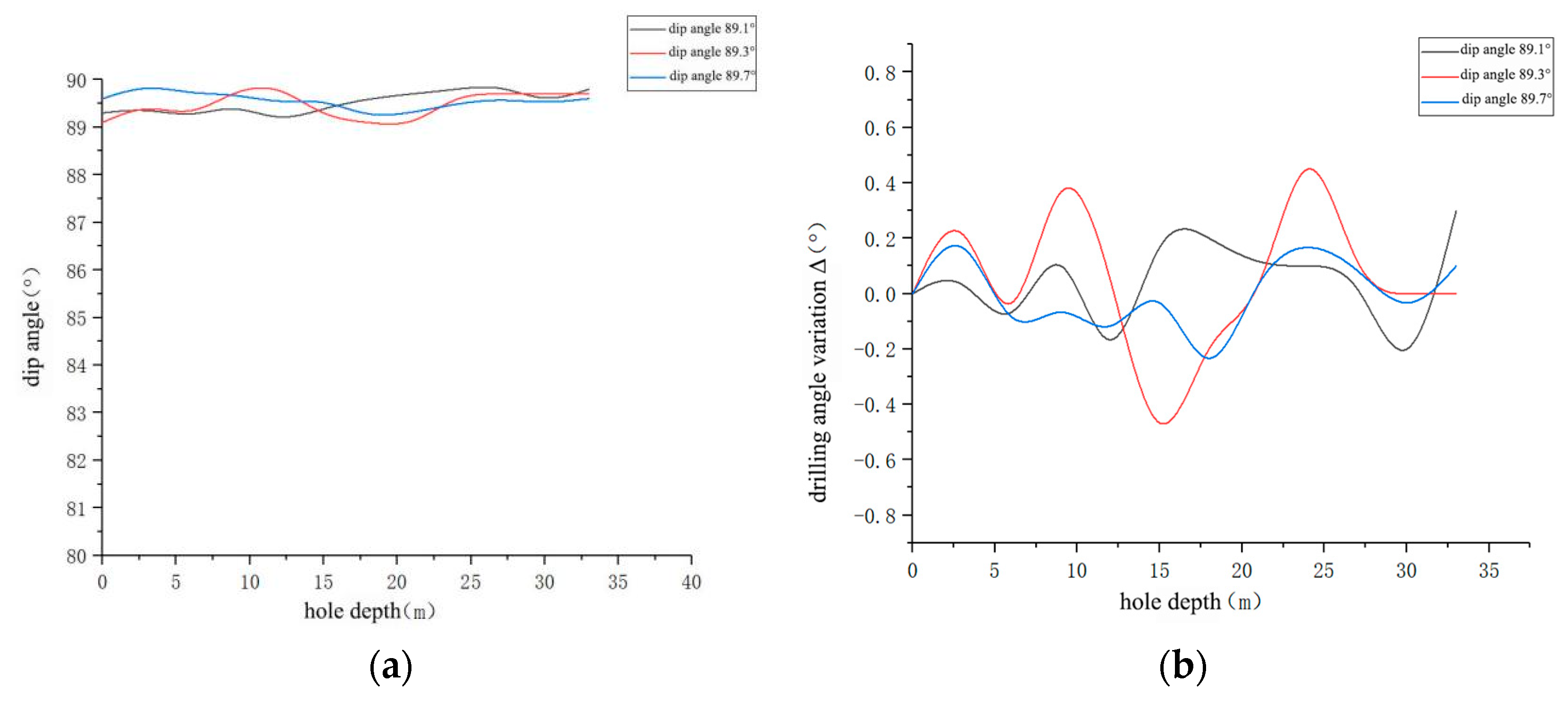

| Initial Borehole Inclination | Number of Variation Stages | Key Depth Intervals and Deflection Characteristics | Maximum Deflection Value | Average Deviation |
|---|---|---|---|---|
| 15° | 5 | 0–16 m: inclination decreases (decrease range ≤0.5°); 16–30 m: inclination increases (increase ≈1°); 30–60 m: inclination fluctuates (fluctuation range ≤1°); 60–65 m: inclination changes by ±2°; 65–95 m: inclination stabilizes (change range ≤0.5°) | ~2° | ~0° |
| 30° | 5 | 0–7 m: inclination decreases (decrease ≈0.5°); 7–16 m: inclination increases (increase ≈0.5°); 16–25 m: inclination decreases (fluctuation range ≤1°); 25–35 m: inclination gently increases (increase ≈0.5°); 35–45 m: inclination increases (increase ≈1.5°); 45–66 m: inclination stabilizes (change range ≤0.5°) | ~1.5° | ~0.5° |
| 45° | 5 | 0–4 m: inclination has no obvious change (change range ≤0.5°); 4–10 m: inclination increases (change range ≤1°); 10–20 m: inclination fluctuates (fluctuation range ≤1.5°); 20–25 m: inclination rises rapidly (increase ≈2.5°); 25–39 m: inclination stabilizes then gradually increases (change range ≤1°) | ~2.5° | ~1° |
| 60° | 3 | 0–9 m: inclination has no obvious change (change range ≤0.5°); 9–13 m: inclination rises rapidly (increase ≈2°); 13–36 m: inclination stabilizes (change range ≤0.5°) | ~2° | ~0.8° |
| 75° | 2–4 | 0–5 m: inclination decreases (change range ≤0.5°); 5–12 m: inclination fluctuates (fluctuation range ≤1°); 12–17 m: inclination increases (increase ≈2°); 17–33 m: inclination stabilizes (change range ≤0.5°) | ~2° | ~0.6° |
| 90° | 1 | 0–40 m: inclination has no obvious increase/decrease trend; 5–25 m: inclination shows slight fluctuation (fluctuation range ≤1°); overall inclination variation ≤1° | ≤1° | ~0.1° |
| Inclination Interval | Average Borehole Inclination | Average Borehole Inclination Angle Change Value (Δ) |
|---|---|---|
| 10~20° | 15.253 | −0.813 |
| 20~30° | 25.216 | 0.989 |
| 30~40° | 33.256 | 3.309 |
| 40~50° | 49.092 | 5.798 |
| 50~60° | 56.177 | 4.775 |
| 60~70° | 66.079 | 3.095 |
| 70~80° | 75.176 | 2.698 |
| 80~90° | 88.230 | −0.172 |
| Drilling Deflection Z | U1 | U2 | U3 | Weights |
|---|---|---|---|---|
| U1 | 1 | 2 | 5 | 0.606 |
| U2 | 1/2 | 1 | 2 | 0.265 |
| U3 | 1/5 | 1/2 | 1 | 0.129 |
| Geological Factors U1 | U11 | U12 | U13 | Weights |
|---|---|---|---|---|
| U11 | 1 | 1/6 | 1/2 | 0.11 |
| U12 | 6 | 1 | 3 | 0.67 |
| U13 | 2 | 1/3 | 1 | 0.22 |
| Technical Factors U2 | U21 | U22 | U23 | Weights |
|---|---|---|---|---|
| U21 | 1 | 1/2 | 1 | 0.25 |
| U22 | 2 | 1 | 1 | 0.5 |
| U23 | 1 | 1 | 1 | 0.25 |
| Human Factors U3 | U31 | U32 | U33 | U34 | Weights |
|---|---|---|---|---|---|
| U31 | 1 | 1 | 1/2 | 1/2 | 0.2 |
| U32 | 1 | 1 | 1/2 | 1/2 | 0.2 |
| U33 | 1 | 2 | 1 | 2 | 0.2 |
| U34 | 2 | 2 | 1/2 | 1 | 0.4 |
| Impact Factor | Total Sort | Wi |
|---|---|---|
| Soft and hard interlayer | 1 | 0.406 |
| bedding angle | 2 | 0.133 |
| Drilling tool structure | 3 | 0.133 |
| Anisotropy | 4 | 0.067 |
| Device installation | 5 | 0.066 |
| Drilling tool weight | 6 | 0.066 |
| ROP selection | 7 | 0.052 |
| Drilling method | 8 | 0.026 |
| Drilling parameters | 9 | 0.026 |
| WOB selection | 10 | 0.025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Shang, Y.; Li, Q.; He, L.; Wang, C. Study on Borehole Trajectory Deviation Characteristics and Influencing Factors in Three-Soft Coal Seams. Processes 2025, 13, 3566. https://doi.org/10.3390/pr13113566
Wang X, Shang Y, Li Q, He L, Wang C. Study on Borehole Trajectory Deviation Characteristics and Influencing Factors in Three-Soft Coal Seams. Processes. 2025; 13(11):3566. https://doi.org/10.3390/pr13113566
Chicago/Turabian StyleWang, Xiaodong, Yuqi Shang, Qingsong Li, Lu He, and Chunhua Wang. 2025. "Study on Borehole Trajectory Deviation Characteristics and Influencing Factors in Three-Soft Coal Seams" Processes 13, no. 11: 3566. https://doi.org/10.3390/pr13113566
APA StyleWang, X., Shang, Y., Li, Q., He, L., & Wang, C. (2025). Study on Borehole Trajectory Deviation Characteristics and Influencing Factors in Three-Soft Coal Seams. Processes, 13(11), 3566. https://doi.org/10.3390/pr13113566





