Robust THRO-Optimized PIDD2-TD Controller for Hybrid Power System Frequency Regulation
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Research Gaps
- Limited exploration of novel cascaded controller architectures: Most studies focus on single-stage controllers or well-established cascaded structures (e.g., PI-PID, PD-PI). The potential benefits of innovative combinations such as PIDD2-TD remain unexplored.
- Insufficient validation under diverse disturbance scenarios: While individual studies test specific disturbances (step loads and random variations), comprehensive evaluation under simultaneous RES fluctuations, multi-step changes, and random disturbances with parameter variations is lacking.
- Many studies employ established algorithms without systematic comparison against recently proposed meta-heuristics that might offer superior convergence characteristics and solution quality.
- Few studies comprehensively assess controller performance under parameter uncertainties and system configuration changes, limiting confidence in real-world applicability.
1.4. Main Contributions
- i.
- Enhancing the frequency stability of a two-region connected power grid with RESs by utilizing a first-of-its-kind regulator, known as PIDD2-TD.
- ii.
- Application of an innovative and recently reported optimization algorithm (i.e., THRO) for LFC design in order to optimally chose the gains of the proposed PIDD2-TD regulator.
- iii.
- iv.
- Evaluating the performance of various control methodologies provided in previous work, such as the PIDD2-PD regulator and PID-TID regulator, to confirm the efficacy of the presented PIDD2-TD regulator.
- v.
- Evaluating the suggested regulator’s performance and stability in the presence of a variety of disturbances, including RES fluctuations, step, multi-step, and random load fluctuations.
- vi.
- Evaluating the robustness of the suggested PIDD2-TD regulator against the system parameters’ variations.
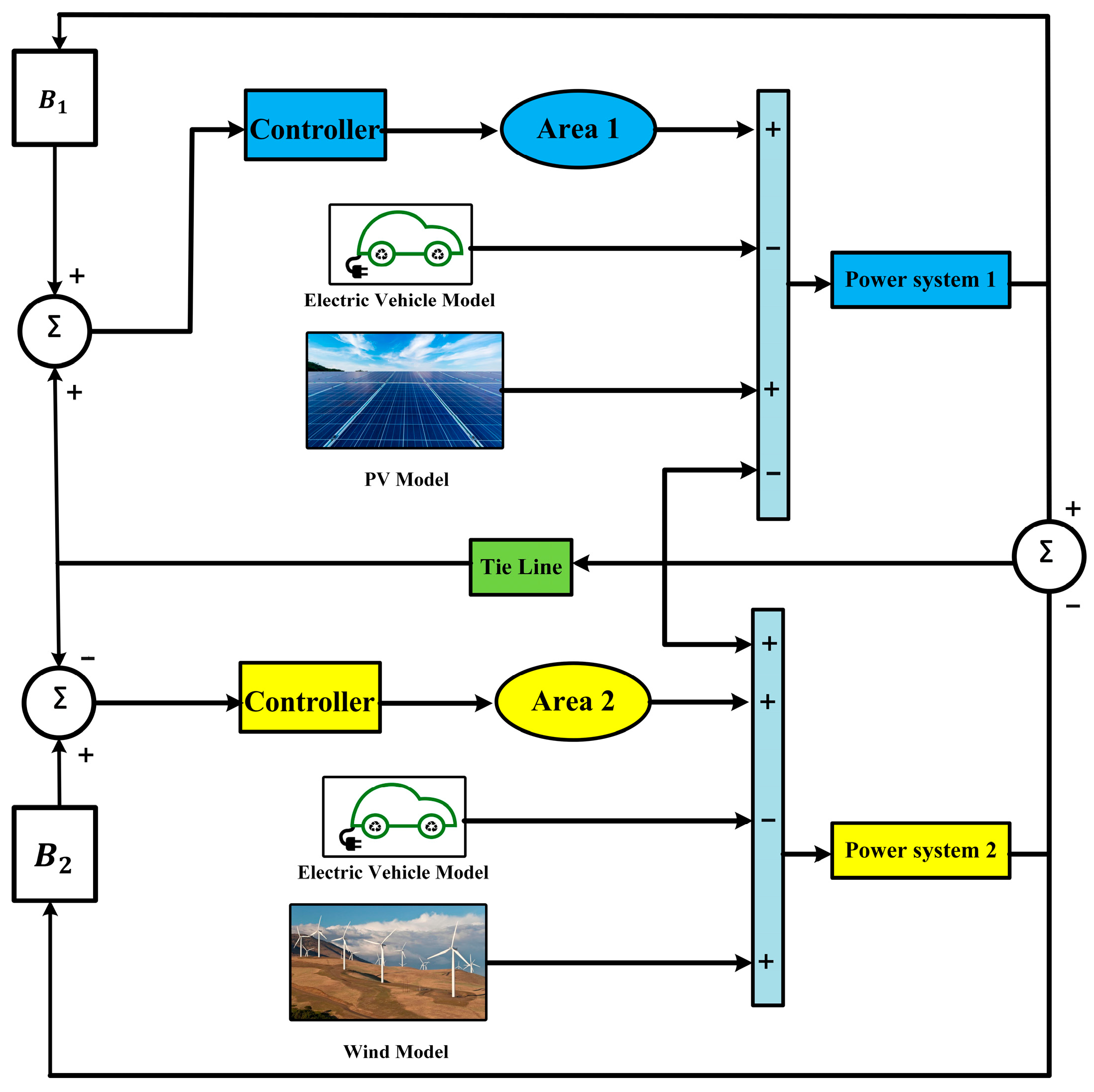
2. Dual-Area Hybrid Power Grid Architecture
2.1. Dynamic Subsystems Models
2.1.1. Thermal Power Plant
- Governor Dead Band (GDB)
- Steam Turbine Reheating Unit
2.1.2. Hydraulic Power Plant
- Hydraulic Governor
- Transient Droop Correction
- Penstock Hydraulic Turbine
2.1.3. Gas Power Plant
- Valve Positioner
- Speed Governor
- Compressor Discharger
- Compressor Discharge
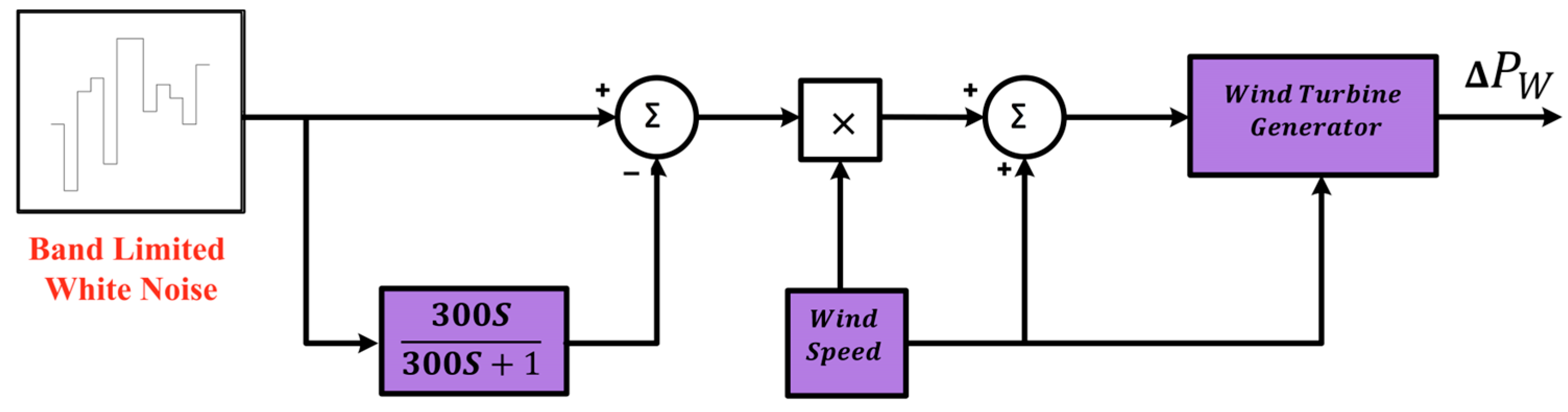
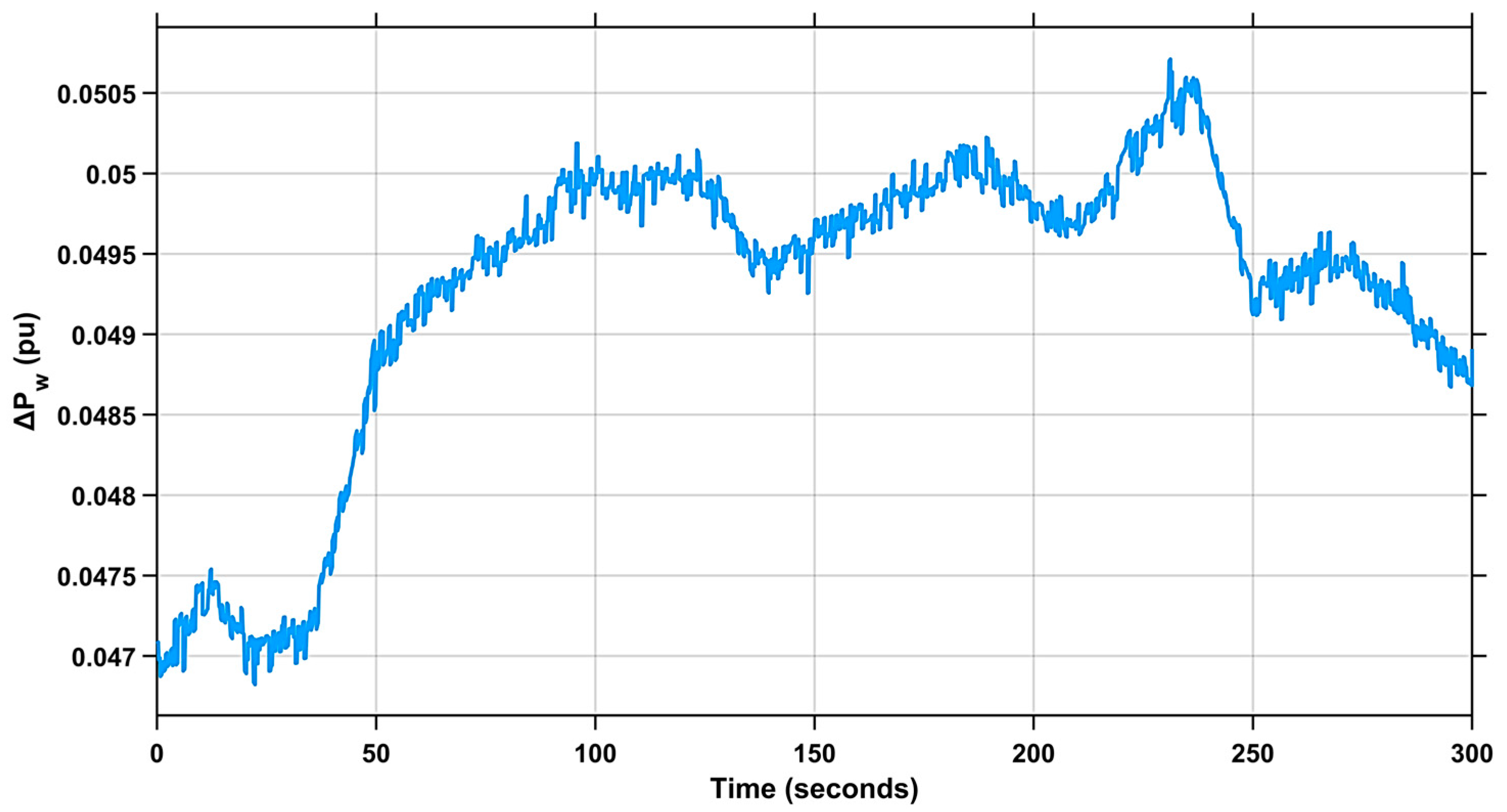
2.2. Wind Farm Modelling
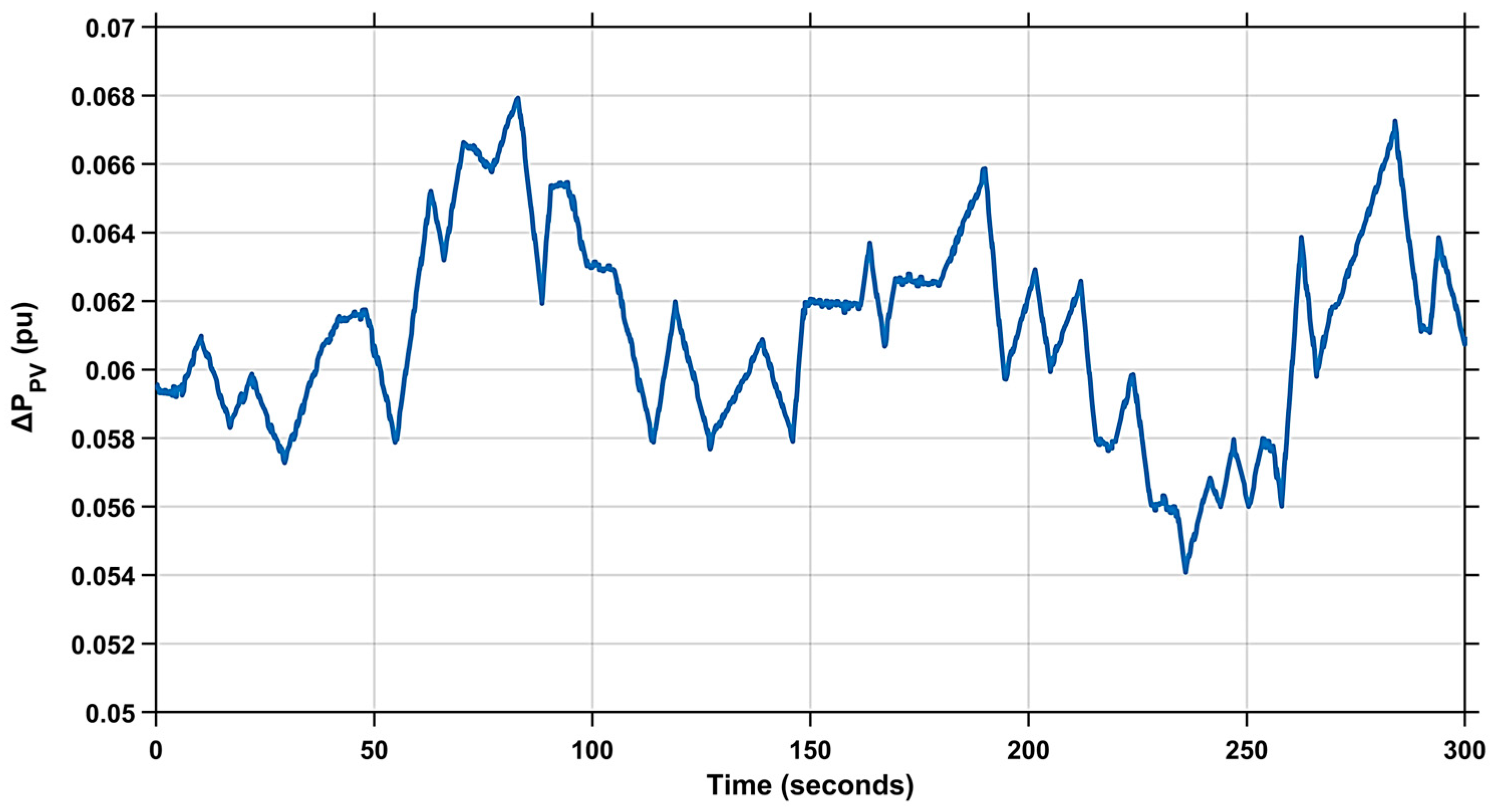
2.3. PV Farm Modelling
2.4. EVs Modelling
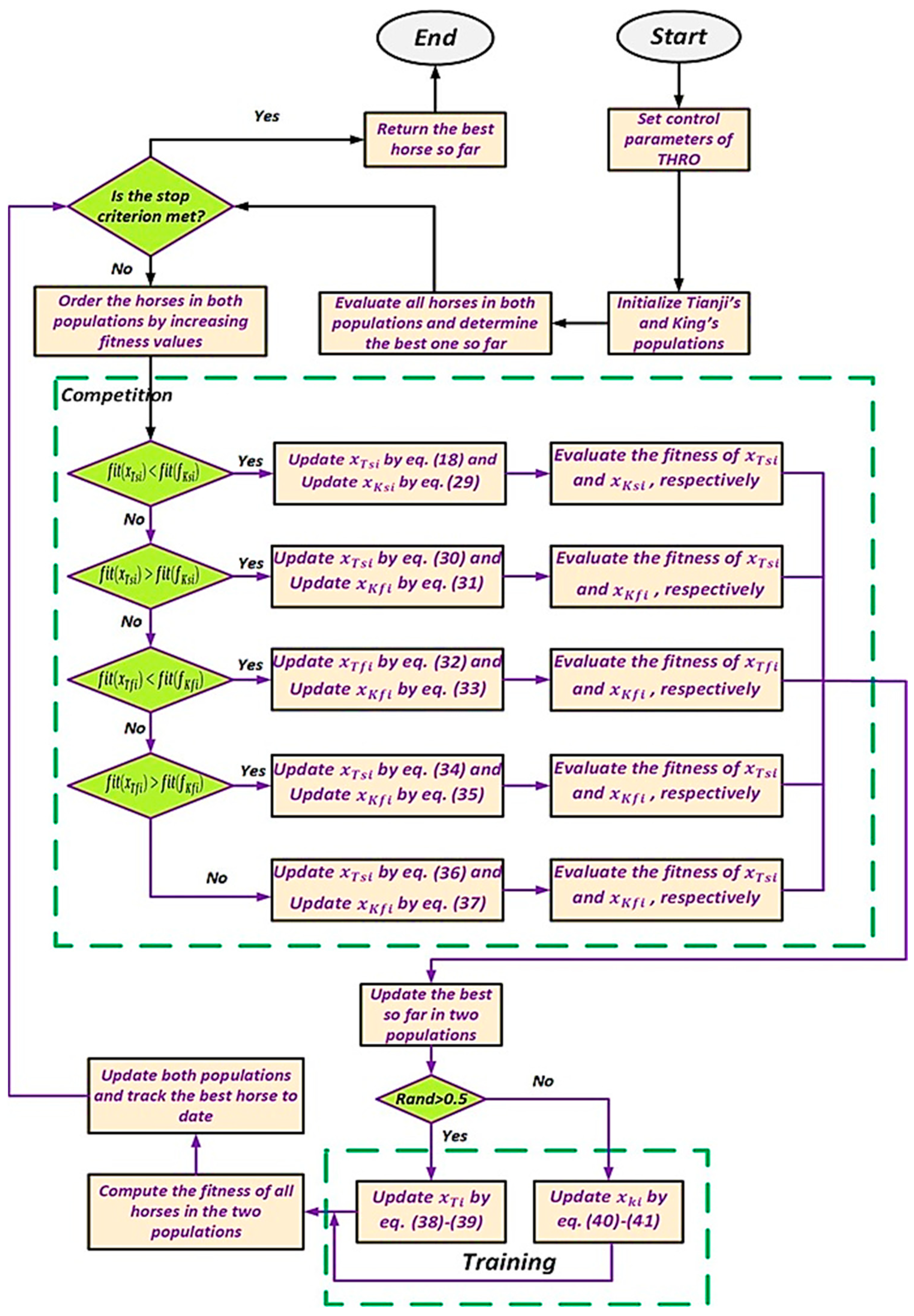
3. Tianji’s Horse Racing Optimizer
3.1. Initialization
3.2. Competition
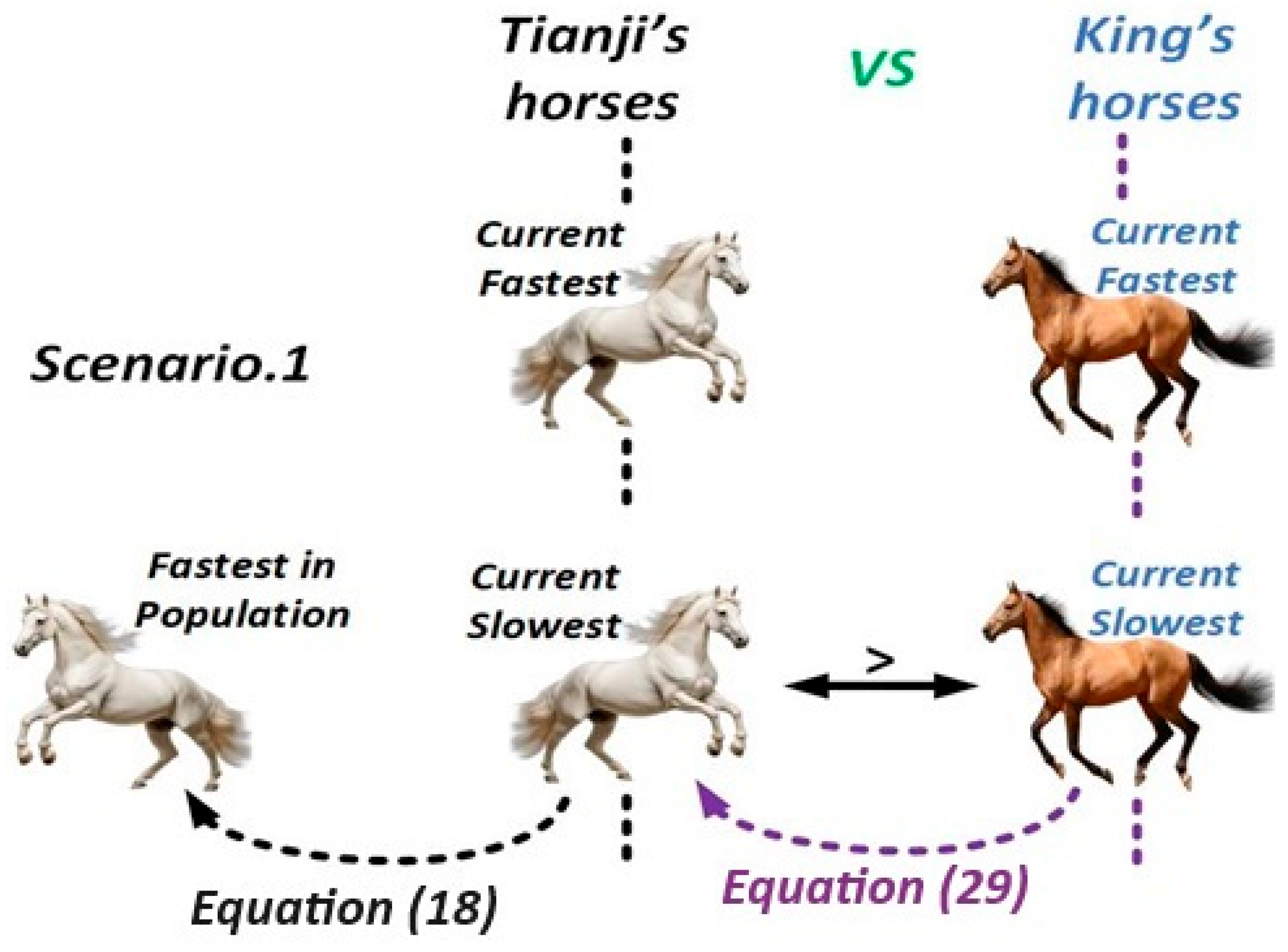
- Scenario 1: When the slowest current horse of Tianji outperforms the slowest horse of the king, it is selected in the race and secures a win for Tianji. To maintain this advantage, the algorithm updates Tianji’s slowest current horse based on the characteristics of the fastest horse of Tianji. During this update, the influence of Tianji’s top-performing horse and the overall quality gap between both populations are taken into account. The updated formulation for the slowest horse of Tianji is as follows:
- Population Renewal Control: α determines how many solutions are modified in each iteration. This ensures controlled population diversity while maintaining algorithmic stability.
- Adaptive Search Intensity: By incorporating the random component (rand), α introduces adaptive variation in the update process. Larger α values promote exploration by affecting more horses, while smaller values enhance exploitation by focusing on fewer, promising solutions.
- Quality Difference Amplification: In Equation (18), α acts as a weighting factor for the term , which represents the overall quality gap between Tianji’s and the king’s populations. This amplifies or dampens the influence of population quality differences on the slowest horse’s update, enabling strategic positioning in the search space.
- Strategic Competition Depth: α mirrors the tactical horse-matching strategy from the ancient legend, determining how deeply the competition affects the current population and thus controlling the balance between preserving good solutions and exploring new regions.
- Scenario 2: When the slowest current horse of Tianji is not faster than the slowest horse of the king, it is deliberately matched verses the fastest horse of the king. Even this results in a loss for Tianji in that round, and the strategy aims to sacrifice the weakest horse to offset the king’s strongest. In this case, knowing that the slowest one in the populations of Tianji is inferior to any horse in the king’s group, the strategy replaces the slowest horse of Tianji by referencing a selected horse from population of Tianji randomly. The replacement rule for Tianji’s slowest horse is as follows:
- Scenario 3: In the case where Tianji’s slowest horse equals the king’s slowest and his fastest horse outperforms the king’s fastest, Tianji selects his fastest horse to compete in the round and secures a win. To help Tianji’s horse keep this leading advantage, the algorithm updates the current fastest horse based on the top-performing horse within Tianji’s group. This update is defined in the following equation:
- Scenario 4: At the point where Tianji’s slowest horse matches the king’s slowest, but his fastest horse is not as fast as the king’s fastest, Tianji strategically uses his slowest horse to compete against the king’s strongest. Although this results in a loss, the goal is to offset the opponent’s best horse. Given that defeat in this round is inevitable, the algorithm updates Tianji’s current slowest horse by referencing any horse randomly taken from Tianji’s collection. The replacement is defined as per the following equation:
- Scenario 5: When the weakest horse in Tianji’s stable currently matches the speed of the king’s bottom-ranked horse and his fastest horse also matches the speed of the king’s fastest, Tianji chooses his slowest horse to compete against the king’s fastest, resulting in a loss. In this case, the algorithm applies the same update strategy as in Scenario 4. The update for the lowest-speed horse currently in Tianji’s team is given by the following:
3.3. Training
3.4. THRO Working Mechanism
- Case 1: The slowest horse in Tianji’s group is swapped with the fastest horse, whereas the king’s slowest horse is replaced in relation to Tianji’s slowest horse.
- Case 2: The slowest horse in Tianji’s lineup is replaced by a randomly picked horse from his population, while the king replaces his fastest horse based on his group’s fastest.
- Case 3: The fastest horse in Tianji’s lineup is replaced with the best-performing horse from his population, whereas the king’s fastest horse is replaced in relation to Tianji’s top-speed horse as of now.
- Cases 4 and 5: Tianji updates his current slowest horse by substituting it with a randomly picked horse from his group, whereas the king updates his fastest horse based on his population’s fastest.
3.5. Computational Complexity Examination
- The size of the population of the horse groups of Tianji and the king alike .
- The problem dimensionality .
- The high limit of iterations .
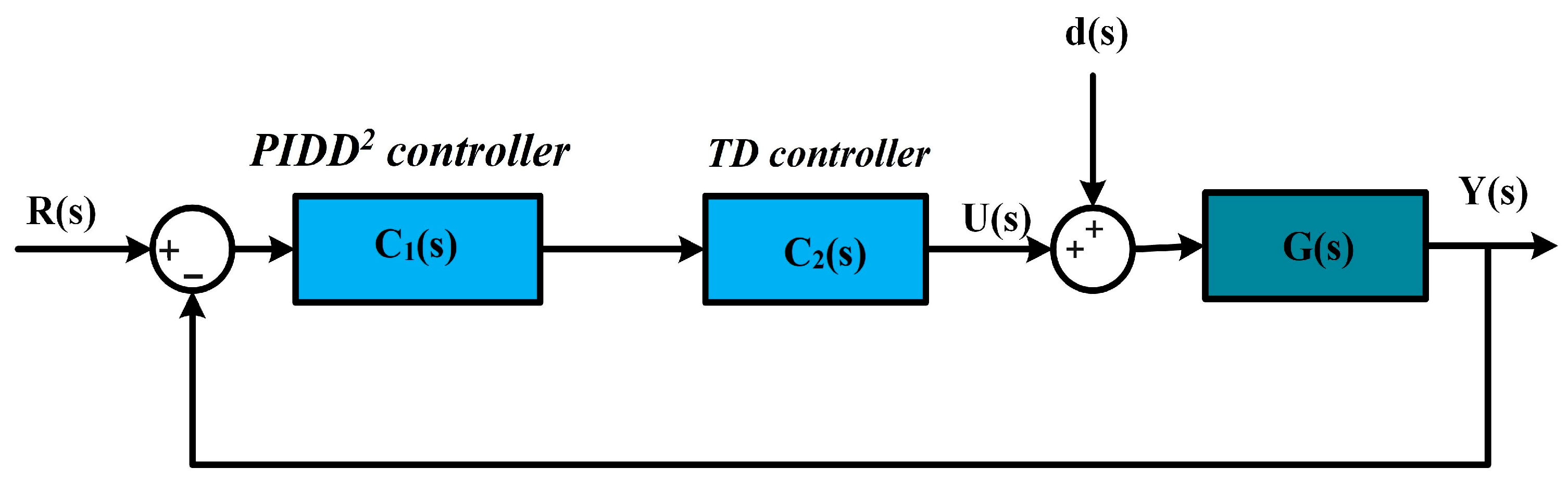
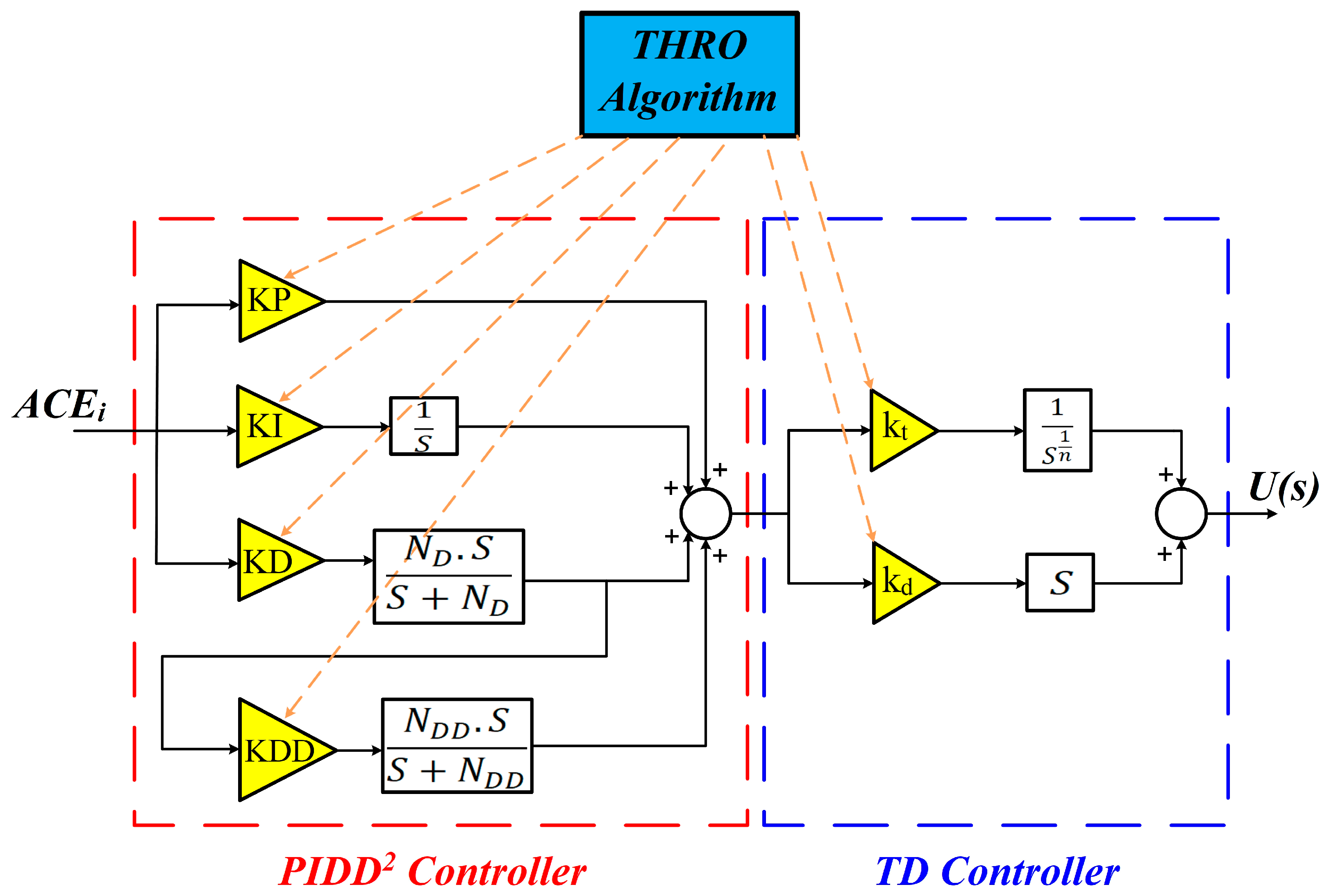
4. Problem Formulation and Controller Structure
5. Simulation Results and Discussion
5.1. Performance Analysis of the THRO Algorithm
5.2. Simulation Outcomes
- Case (1): Analysing the electricity grid’s dynamic response under the impact of step load disturbance (SLD).
- Case (2): Analysing the electricity grid’s dynamic response under the impact of multi-step load disturbance (MSLD).
- Case (3): Analysing the dynamic reaction of the power grid under the impact of random load disturbance (RLD).
- Case (4): Analysing the dynamic reaction of the power grid under penetration of renewable energy sources (RESs).
- Case (5): Sensitivity analysis.
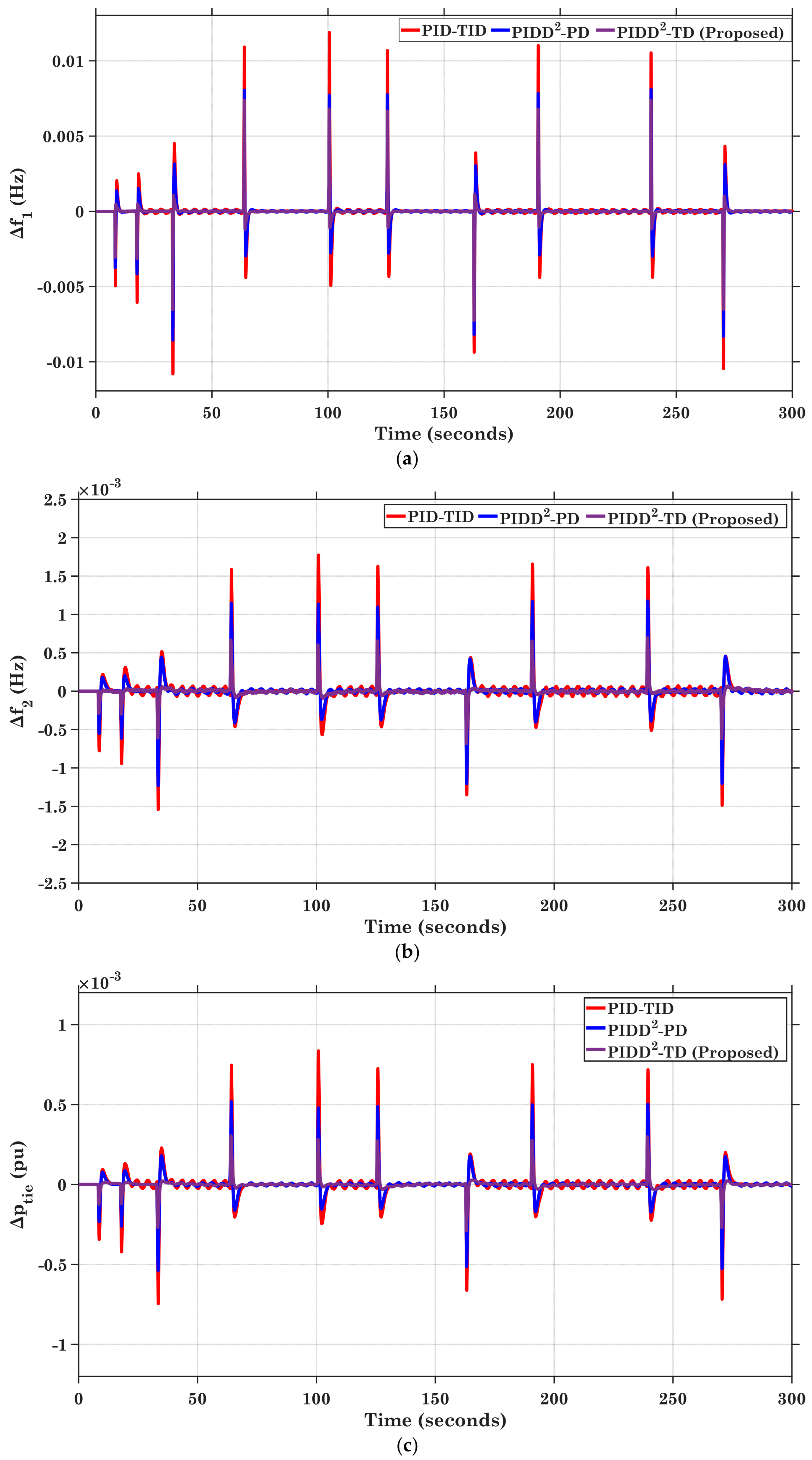
5.2.1. Case (1): Analysing the Electricity Grid’s Dynamic Response Under the Impact of SLD
5.2.2. Case (2): Analysing the Electricity Grid’s Dynamic Response Under the Impact of MSLD
5.2.3. Case (3): Analysing the Dynamic Reaction of the Power Grid Under the Impact of RLD
5.2.4. Case (4): Analysing the Dynamic Reaction of the Power Grid Under Penetration of RES
5.2.5. Case (5): Sensitivity Analysis
6. Conclusions
7. Limitations and Future Trends
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| EV | Electric vehicle | Δf1, Δf2 | Frequency variations |
| PV | Photovoltaic | ΔPtie | Fluctuation of tie-line power |
| TD | Tilt derivative | SLD | Step load disturbance |
| PIDD2 | Proportional–integral–derivative with second derivative | MSLD | Multi-step load disturbance |
| DOA | Dhole optimization algorithm | RLD | Random load disturbance |
| WUTP | Water uptake and transport in plants | SCA | Sine cosine algorithm |
| THRO | Tianji’s horse racing optimization | AGC | Automated generation control |
| RESs | Renewable energy sources | TCSC | Thyristor-controlled series capacitor |
| LFC | Load frequency control | WCA | Water cycle approach |
| V2G | Vehicle-to-grid | GDB | Governor deadband |
| ANNs | Artificial neural networks | GRC | Generation rate constraint |
| GA | Genetic algorithm | SOC | State of charge |
| CTDs | Communication time delays | ITSE | Integral time squared error |
| ICS | Imperialist competitive search | FF | Fitness function |
| FLC | Fuzzy logic controller | JSO | Jellyfish search optimization |
| CPSO | Chaotic particle swarm optimizer | PSO | Particle swarm optimization |
| PFA | Pathfinder algorithm | AI | Artificial intelligence |
Appendix A. The Studied Power System Parameters’ Values
| Parameter | Nominal Value | Parameter Definition |
| 0.08 s | Governor time constant | |
| 0.3 s | Gain of reheater steam turbine | |
| 10.2 s | The time constant of reheater steam turbine | |
| 0.3 s | Steam turbine time constant | |
| 0.2 s | Speed governor time constant of hydro turbine | |
| 4.9 s | Hydro turbine speed governor reset time | |
| 28.749 s | Time constant of the transient droop | |
| 1.1 s | Nominal string time of water in penstock | |
| 0.049 s | Gas turbine constant of valve positioner | |
| 1 | Gas turbine valve positioner | |
| 0.6 s | Governor lead time constant for a gas turbine | |
| 1.1 s | Governor lag time constant for a gas turbine | |
| 0.01 s | Delay in the combustion response time of a gas turbine | |
| 0.239 s | Gas turbine fuel time constant | |
| 0.2 s | Constant discharge volume-time for gas turbine compressor | |
| 68.965 | Power system gains | |
| 11.49 s | Power system time constants | |
| 0.0433 MW | Coefficient of synchronizing | |
| , | 1 | Gains of EVs |
| , | 0.28 s | Time constants of EVs |
| 0.431, 0.431 MW/Hz | Frequency bias coefficients | |
| 2.4 Hz/MW | Constant governor regulation of speed for thermal, hydro, and gas units | |
| , , | 0.2873, 0.138, 0.5747 | Participation factors for hydro, gas and thermal units |
| GRC with Hydro | -------- | 0.045 pu.MW/s and 0.06 pu.MW/s for both rising and decreasing rates, respectively |
| GRC with Thermal | -------- | The GRC for the thermal unit is set (0.0017 pu.MW/s) for rising and decreasing rates |
References
- Khudhair, M.; Ragab, M.; AboRas, K.M.; Abbasy, N.H. Robust Control of Frequency Variations for a Multi-Area Power System in Smart Grid Using a Newly Wild Horse Optimized Combination of PIDD2 and PD Controllers. Sustainability 2022, 14, 8223. [Google Scholar] [CrossRef]
- Hassan, M.; Aly, A.; Elmelegi, M.; Nasrat, L.; Watanabe, M.; Mohamed, E.A. Optimal Frequency Control of Multi-Area Hybrid Power System Using New Cascaded TID-PIλDμN Controller Incorporating Electric Vehicles. Fractal Fract. 2022, 6, 548. [Google Scholar] [CrossRef]
- Xiao, A.; Chen, H.; Wei, C.; Bai, X. Statistical Measure for Risk-Seeking Stochastic Wind Power Offering Strategies in Electricity Markets. J. Mod. Power Syst. Clean Energy 2021, 10, 1437–1442. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Murawwat, S.; Sibtain, D.; Shahid, K.; Javed, I.; Gui, Y. Modified Cascaded Controller Design Constructed on Fractional Operator ‘β’ to Mitigate Frequency Fluctuations for Sustainable Operation of Power Systems. Energies 2022, 15, 7814. [Google Scholar] [CrossRef]
- Zhang, P.; Daraz, A.; Malik, S.A.; Sun, C.; Basit, A.; Zhang, G. Multi-Resolution Based PID Controller for Frequency Regulation of a Hybrid Power System with Multiple Interconnected Systems. Front. Energy Res. 2023, 10, 1109063. [Google Scholar] [CrossRef]
- Khairalla, A.G.; Kotb, H.; AboRas, K.M.; Ragab, M.; ElRefaie, H.B.; Ghadi, Y.Y.; Yousef, A. Enhanced Control Strategy and Energy Management for a Photovoltaic System with Hybrid Energy Storage Based on Self-Adaptive Bonobo Optimization. Front. Energy Res. 2023, 11, 1283348. [Google Scholar] [CrossRef]
- Zaid, S.A.; Bakeer, A.; Magdy, G.; Albalawi, H.; Kassem, A.M.; El-Shimy, M.E.; AbdelMeguid, H.; Manqarah, B. A New Intelligent Fractional-Order Load Frequency Control for Interconnected Modern Power Systems with Virtual Inertia Control. Fractal Fract. 2023, 7, 62. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T.; Blaabjerg, F.; Dragičević, T. A New Load Frequency Control Strategy for Micro-Grids with Considering Electrical Vehicles. Electr. Power Syst. Res. 2017, 143, 585–598. [Google Scholar] [CrossRef]
- Margaris, D.; Papathanassiou, S.A.; Hatziargyriou, N.D.; Hansen, A.D.; Sørensen, P. Frequency Control in Autonomous Power Systems with High Wind Power Penetration. IEEE Trans. Sustain. Energy 2012, 3, 189–199. [Google Scholar] [CrossRef]
- Kerscher, S.; Arboleya, P. The Key Role of Aggregators in the Energy Transition Under the Latest European Regulatory Framework. Int. J. Electr. Power Energy Syst. 2022, 134, 107103. [Google Scholar] [CrossRef]
- Zhu, X.; Xia, M.; Chiang, H.D. Coordinated Sectional Droop Charging Control for EV Aggregator Enhancing Frequency Stability of Microgrid with High Penetration of Renewable Energy Sources. Appl. Energy 2018, 210, 936–943. [Google Scholar] [CrossRef]
- Maghami, M.R.; Thang, K.F.; Mutambara, A.G.; Firoozi, A.A.; Yaghoubi, E.; Jahromi, M.Z.; Yaghoubi, E. Optimized Planning of Electric Vehicle Charging Infrastructure for Grid Performance Improvement. Discov. Sustain. 2025, 6, 706. [Google Scholar] [CrossRef]
- Zheng, Y.; Shang, Y.; Shao, Z.; Jian, L. A Novel Real-Time Scheduling Strategy with Near-Linear Complexity for Integrating Large-Scale Electric Vehicles into Smart Grid. Appl. Energy 2018, 217, 1–13. [Google Scholar] [CrossRef]
- Liu, H.; Hu, Z.C.; Song, Y.H.; Lin, J. Decentralized Vehicle-to-Grid Control for Primary Frequency Regulation Considering Charging Demands. IEEE Trans. Power Syst. 2013, 28, 3480–3489. [Google Scholar] [CrossRef]
- Alharbi, M.; Ragab, M.; AboRas, K.M.; Kotb, H.; Dashtdar, M.; Shouran, M.; Elgamli, E. Innovative AVR-LFC Design for a Multi-Area Power System Using Hybrid Fractional-Order PI and PIDD2 Controllers Based on Dandelion Optimizer. Mathematics 2023, 11, 1387. [Google Scholar] [CrossRef]
- AboRas, K.M.; Ragab, M.; Shouran, M.; Alghamdi, S.; Kotb, H. Voltage and Frequency Regulation in Smart Grids via a Unique Fuzzy PIDD2 Controller Optimized by Gradient-Based Optimization Algorithm. Energy Rep. 2023, 9, 1201–1235. [Google Scholar] [CrossRef]
- Alghamdi, S.; Alqarni, M.; Hammad, M.R.; AboRas, K.M. First-of-Its-Kind Frequency Enhancement Methodology Based on an Optimized Combination of FLC and TFOIDFF Controllers Evaluated on EVs, SMES, and UPFC-Integrated Smart Grid. Fractal Fract. 2023, 7, 807. [Google Scholar] [CrossRef]
- Yogendra, A.; Narendra, K. BFOA-Scaled Fractional Order Fuzzy PID Controller Applied to AGC of Multi-Area Multi-Source Electric Power Generating Systems. Swarm Evol. Comput. 2017, 32, 202–218. [Google Scholar]
- Sahu, R.K.; Panda, S.; Biswal, A.; Sekhar, G.C. Design and Analysis of Tilt Integral Derivative Controller with Filter for Load Frequency Control of Multi-Area Interconnected Power Systems. ISA Trans. 2016, 61, 251–264. [Google Scholar] [CrossRef]
- Malik, S.; Suhag, S. A Novel SSA Tuned PI-TDF Control Scheme for Mitigation of Frequency Excursions in Hybrid Power System. Smart Sci. 2020, 8, 202–218. [Google Scholar] [CrossRef]
- Elmelegi, A.; Mohamed, E.A.; Aly, M.; Ahmed, E.M.; Mohamed, A.A.A.; Elbaksawi, O. Optimized Tilt Fractional Order Cooperative Controllers for Preserving Frequency Stability in Renewable Energy-Based Power Systems. IEEE Access 2021, 9, 8261–8277. [Google Scholar] [CrossRef]
- Arya, Y. A New Optimized Fuzzy FOPI-FOPD Controller for Automatic Generation Control of Electric Power Systems. J. Franklin Inst. 2019, 356, 5611–5629. [Google Scholar] [CrossRef]
- Paliwal, N.; Srivastava, L.; Pandit, M. Application of Grey Wolf Optimization Algorithm for Load Frequency Control in Multi-Source Single Area Power System. Evol. Intell. 2020, 15, 563–584. [Google Scholar] [CrossRef]
- Ayas, M.S.; Sahin, E. FOPID Controller with Fractional Filter for an Automatic Voltage Regulator. Comput. Electr. Eng. 2021, 90, 106895. [Google Scholar] [CrossRef]
- Zamani, A.-A.; Shafiee, M.; Sajadinia, M. Optimal Self-Tuning Fractional Order Fuzzy Load Frequency Control Considering Sustainable Energy Sources and Electric Vehicle. Int. J. Ambient Energy 2023, 44, 2170–2184. [Google Scholar] [CrossRef]
- Gong, X.; Yang, K.; Dong, X.; Jiang, X.; Liu, D.; Luo, Z. Fractional Order PID Optimal Control Method of Regional Load Frequency Containing Pumped Storage Plants. Energies 2023, 16, 1703. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Nivolianiti, E. Optimal Load Frequency Control of a Hybrid Electric Shipboard Microgrid Using Jellyfish Search Optimization Algorithm. Appl. Sci. 2023, 13, 6128. [Google Scholar] [CrossRef]
- Yousri, D.; Babu, T.S.; Fathy, A. Recent Methodology-Based Harris Hawks Optimizer for Designing Load Frequency Control Incorporated in Multi-Interconnected Renewable Energy Plants. Sustain. Energy Grids Netw. 2020, 22, 100352. [Google Scholar] [CrossRef]
- Daraz, A.; Malik, S.A.; Azar, A.T.; Aslam, S.; Alkhalifah, T.; Alturise, F. Optimized Fractional Order Integral-Tilt Derivative Controller for Frequency Regulation of Interconnected Diverse Renewable Energy Resources. IEEE Access 2022, 10, 43514–43527. [Google Scholar] [CrossRef]
- Oshnoei, A.; Khezri, R.; Muyeen, S.M.; Oshnoei, S.; Blaabjerg, F. Automatic Generation Control Incorporating Electric Vehicles. Electr. Power Compon. Syst. 2019, 47, 720–732. [Google Scholar] [CrossRef]
- Magdy, G.; Bakeer, A.; Nour, M.; Petlenkov, E. A New Virtual Synchronous Generator Design Based on the SMES System for Frequency Stability of Low-Inertia Power Grids. Energies 2020, 13, 5641. [Google Scholar] [CrossRef]
- Arya, Y. Impact of Ultra-Capacitor on Automatic Generation Control of Electric Energy Systems Using an Optimal FFOID Controller. Int. J. Energy Res. 2019, 43, 8765–8778. [Google Scholar] [CrossRef]
- Priyadarshani, S.; Subhashini, K.R.; Satapathy, J.K. Path Finder Algorithm Optimized Fractional Order Tilt-Integral-Derivative (FOTID) Controller for Automatic Generation Control of Multi-Source Power System. Microsyst. Technol. 2021, 27, 23–35. [Google Scholar] [CrossRef]
- Daraz, A.; Malik, S.A.; Basit, A.; Aslam, S.; Zhang, G. Modified FOPID Controller for Frequency Regulation of a Hybrid Interconnected System of Conventional and Renewable Energy Sources. Fractal Fract. 2023, 7, 89. [Google Scholar] [CrossRef]
- Arya, Y. Impact of Hydrogen Aqua Electrolyzer-Fuel Cell Units on Automatic Generation Control of Power Systems with a New Optimal Fuzzy TIDFII Controller. Renew. Energy 2019, 139, 468–482. [Google Scholar] [CrossRef]
- Mohamed, E.A.; Aly, M.; Watanabe, M. New Tilt Fractional-Order Integral Derivative with Fractional Filter (TFOIDFF) Controller with Artificial Hummingbird Optimizer for LFC in Renewable Energy Power Grids. Mathematics 2022, 10, 3006. [Google Scholar] [CrossRef]
- Khudhair, M.; Ragab, M.; AboRas, K.M.; Abbasy, N.H. A Newly Resilient Combination of PIDD2 and PD Controllers to Boost the Frequency Response in a Two-Area Hybrid Power System with Nonlinearities Using Wild Horse Optimizer. In Proceedings of the 2022 International Conference on Electrical, Computer and Energy Technologies (ICECET), Prague, Czech Republic, 20–22 July 2022; pp. 1–11. [Google Scholar]
- Latif, A.; Hussain, S.M.S.; Das, D.C.; Ustun, T.S. Optimum Synthesis of a BOA Optimized Novel Dual-Stage PI-(1+ID) Controller for Frequency Response of a Microgrid. Energies 2020, 13, 3446. [Google Scholar] [CrossRef]
- Arya, Y.; Kumar, N.; Dahiya, P.; Sharma, G.; Çelik, E.; Dhundhara, S.; Sharma, M. Cascade-IDN Controller Design for AGC of Thermal and Hydro-Thermal Power Systems Integrated with Renewable Energy Sources. IET Renew. Power Gener. 2021, 15, 504–520. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, Y.; Yin, S. Adaptive Fuzzy Fault-Tolerant Control for Markov Jump Systems with Additive and Multiplicative Actuator Faults. IEEE Trans. Fuzzy Syst. 2021, 29, 772–785. [Google Scholar] [CrossRef]
- Yang, H.; Yin, S.; Kaynak, O. Neural Network-Based Adaptive Fault-Tolerant Control for Markovian Jump Systems with Nonlinearity and Actuator Faults. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3687–3698. [Google Scholar] [CrossRef]
- Ginidi, A.; Elattar, E.; Shaheen, A.; Elsayed, A.; El-Sehiemy, R.; Dorrah, H. Optimal Power Flow Incorporating Thyristor-Controlled Series Capacitors Using the Gorilla Troops Algorithm. Int. Trans. Electr. Energy Syst. 2022, 2022, 8344749. [Google Scholar] [CrossRef]
- El-Ela, A.A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Diab, M.A.I.-G. Enhanced Coyote Optimizer-Based Cascaded Load Frequency Controllers in Multi-Area Power Systems with Renewable. Neural Comput. Appl. 2021, 33, 8459–8477. [Google Scholar] [CrossRef]
- Kalyan, C.N.S.; Goud, B.S.; Reddy, C.R.; Ramadan, H.S.; Bajaj, M.; Ali, Z.M. Water Cycle Algorithm Optimized Type II Fuzzy Controller for Load Frequency Control of a Multi-Area, Multi-Fuel System with Communication Time Delays. Energies 2021, 14, 5387. [Google Scholar] [CrossRef]
- Elkasem, M.H.A.; Khamies, M.; Magdy, G.; Taha, I.B.M.; Kamel, S. Frequency Stability of AC/DC Interconnected Power Systems with Wind Energy Using Arithmetic Optimization Algorithm-Based Fuzzy-PID Controller. Sustainability 2021, 13, 12095. [Google Scholar] [CrossRef]
- Gupta, D.K.; Soni, A.K.; Jha, A.V.; Mishra, S.K.; Appasani, B.; Srinivasulu, A.; Bizon, N.; Thounthong, P. Hybrid Gravitational–Firefly Algorithm-Based Load Frequency Control for Hydrothermal Two-Area System. Mathematics 2021, 9, 712. [Google Scholar] [CrossRef]
- Hossam-Eldin, A.; Negm, E.; Ragab, M.; AboRas, K.M. A Maiden Robust FPIDD2 Regulator for Frequency-Voltage Enhancement in a Hybrid Interconnected Power System Using Gradient-Based Optimizer. Alex. Eng. J. 2023, 65, 103–118. [Google Scholar] [CrossRef]
- Wang, C.; Du, H.; Zhang, Z.; Hu, G.; Mirjalili, S.; Khodadadi, N.; Hussien, A.G.; Liao, Y.; Zhao, W. Tianji’s Horse Racing Optimization (THRO): A New Metaheuristic Inspired by Ancient Wisdom and Its Engineering Optimization Applications. Artif. Intell. Rev. 2025, 58, 282. [Google Scholar] [CrossRef]
- Oveis, B.; Aghdasi, H.S.; Salehpour, P. Dhole Optimization Algorithm: A New Metaheuristic Algorithm for Solving Optimization Problems. Cluster Comput. 2025, 28, 430. [Google Scholar]
- Braik, M.; Al-Hiary, H. A Novel Meta-Heuristic Optimization Algorithm Inspired by Water Uptake and Transport in Plants. Neural Comput. Appl. 2025, 37, 13643–13724. [Google Scholar] [CrossRef]
- Pahadasingh, S. TLBO Based CC-PID-TID Controller for Load Frequency Control of Multi Area Power System. In Proceedings of the 2021 1st Odisha International Conference on Electrical Power Engineering, Communication and Computing Technology (ODICON), Bhubaneswar, India, 8–9 January 2021; pp. 1–7. [Google Scholar]
- Parmar, K.P.S.; Majhi, S.; Kothari, D.P. LFC of an Interconnected Power System with Thyristor Controlled Phase Shifter in the Tie Line. Int. J. Comput. Appl. 2012, 41, 27–30. [Google Scholar] [CrossRef]
- Morsali, J.; Zare, K.; Hagh, M.T. Comparative Performance Evaluation of Fractional Order Controllers in LFC of Two-Area Diverse-Unit Power System with Considering GDB and GRC Effects. J. Electr. Syst. Inf. Technol. 2018, 5, 708–722. [Google Scholar] [CrossRef]
- Kalyan, C.N.S.; Suresh, C.V. PIDD Controller for AGC of Nonlinear System with PEV Integration and AC-DC Links. In Proceedings of the 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 21–23 January 2021; pp. 1–6. [Google Scholar]
- Ahmed, M.; Magdy, G.; Khamies, M.; Kamel, S. Modified TID Controller for Load Frequency Control of a Two-Area Interconnected Diverse-Unit Power System. Int. J. Electr. Power Energy Syst. 2022, 135, 107528. [Google Scholar] [CrossRef]















| Coefficient | Value | Coefficient | Value |
|---|---|---|---|
| AREA 1 | ||||||||||||
| Controller | ||||||||||||
| PIDD2-PD | 49.066 | 50 | 10.733 | 0.104 | 100 | 366 | -- | -- | 38.475 | -- | 1.493 | 86.649 |
| PID-TID | 50 | 0 | 49.929 | -- | -- | -- | 49.999 | 2.674 | -- | 0 | 2.622 | -- |
| PIDD2-TD (Proposed) | 49.067 | 49.9593 | 2.889 | 0.121 | 495 | 498 | 50 | 8.9732 | -- | -- | 39.013 | -- |
| AREA 2 | ||||||||||||
| Controller | ||||||||||||
| PIDD2-PD | 48.627 | 0 | 10.705 | 0.3367 | 490 | 499 | -- | -- | 49.998 | -- | 0.559 | 150 |
| PID-TID | 35.835 | 0.002 | 6.215 | -- | -- | -- | 49.241 | 9.844 | -- | 9.477 | 34.938 | -- |
| PIDD2-TD (Proposed) | 48.627 | 0 | 49.991 | 0.005 | 459 | 102 | 50 | 8.349 | -- | -- | 5.614 | -- |
| Parameter | Lower Bound | Upper Bound | Parameter | Lower Bound | Upper Bound |
|---|---|---|---|---|---|
| 0 | 50 | 0 | 50 | ||
| 0 | 50 | 0 | 50 | ||
| 0 | 50 | 0 | 1 | ||
| 0 | 50 | 100 | 500 | ||
| 100 | 500 | 1 | 10 | ||
| 0 | 50 | 50 | 300 |
| Controller | Δf1 (Hz) | Δf2 (Hz) | ΔPtie (pu) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Max. OS | Max. US | Set-Time (s) | Max.OS | Max. US | Set-Time (s) | Max. OS | Max. US | Set- Time (s) | |
| PIDD2-TD (THRO) | 0.00048 | 0.003 | 1.7 | 0.00017 | 0.00054 | 4.6 | 0.00001 | 0.00012 | 3.4 |
| PID-TID (THRO) | 0.002 | 0.0037 | 2.3 | 0.00021 | 0.00078 | 5.9 | 0.00007 | 0.00023 | 4.8 |
| PIDD2-PD (THRO) | 0.0013 | 0.0045 | 1.9 | 0.00023 | 0.00054 | 5.7 | 0.00009 | 0.00023 | 6.8 |
| Controller | Δf1 (Hz) | Δf2 (Hz) | ΔPtie (pu) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Max. OS | MAX. US | Set-Time (s) | Max.OS | MAX. US | Set-Time (s) | Max. OS | MAX. US | Set- Time (s) | |
| PIDD2-TD (THRO) | 0.0047 | 0.0095 | 2.2 | 0.00044 | 0.0009 | 2.25 | 0.00019 | 0.00038 | 3.1 |
| PID-TID (THRO) | 0.0076 | 0.0136 | 3.2 | 0.00084 | 0.00209 | 4.2 | 0.00037 | 0.00066 | 5.1 |
| PIDD2-PD (THRO) | 0.0062 | 0.0106 | 2.6 | 0.00118 | 0.00156 | 4.8 | 0.00052 | 0.00095 | 4.6 |
| Controller | Δf1 (Hz) | Δf2 (Hz) | ΔPtie (pu) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Max. OS | MAX. US | Set-Time (s) | Max.OS | MAX. US | Set-Time (s) | Max. OS | MAX. US | Set- Time (s) | |
| PIDD2-TD (THRO) | 0.00725 | 0.0072 | 2.2 | 0.0006 | 0.00066 | 2.25 | 0.00019 | 0.00038 | 2.8 |
| PID-TID (THRO) | 0.01177 | 0.0085 | 2.9 | 0.00173 | 0.00153 | 4.4 | 0.00037 | 0.00066 | 4.9 |
| PIDD2-PD (THRO) | 0.00778 | 0.011 | 2.7 | 0.0011 | 0.0012 | 3.8 | 0.00052 | 0.00095 | 4.2 |
| Controller | Δf1 (Hz) | Δf2 (Hz) | ΔPtie (pu) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Max. OS | MAX. US | Set-Time (s) | Max.OS | MAX. US | Set-Time (s) | Max. OS | MAX. US | Set- Time (s) | |
| PIDD2-TD (THRO) | 0.00516 | 0.0013 | 4.1 | 0.017 | 0.00011 | 2.2 | 0.00037 | 0.0017 | 4.1 |
| PID-TID (THRO) | 0.018 | 0.0076 | 4.3 | 0.0497 | 0.015 | 4.8 | 0.00125 | 0.0058 | 4.4 |
| PIDD2-PD (THRO) | 0.0104 | 0.0038 | 5.2 | 0.0346 | 0.00025 | 4.2 | 0.00065 | 0.005 | 4.8 |
| Controller | Coefficient | % Alteration | Δf1 | Δf2 | ΔPtie | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Max.OS (Hz) | Max.US (Hz) | ST (s) | Max.OS (Hz) | Max.US (Hz) | ST (s) | Max.OS (Hz) | Max.US (Hz) | ST (s) | |||
| PIDD2-TD (proposed) | Normal | 0.00048 | 0.003 | 1.7 | 0.00017 | 0.00054 | 4.6 | 0.00001 | 0.00012 | 3.4 | |
| 0.00048 | 0.004 | 1.8 | 0.00019 | 0.0006 | 4.7 | 0.00001 | 0.00012 | 3.4 | |||
| 0.00048 | 0.003 | 1.7 | 0.00017 | 0.00054 | 4.7 | 0.00001 | 0.00012 | 3.5 | |||
| 0.00048 | 0.004 | 1.8 | 0.00017 | 0.0006 | 4.7 | 0.00001 | 0.00012 | 3.4 | |||
| 0.00048 | 0.004 | 1.7 | 0.00017 | 0.00054 | 4.6 | 0.00001 | 0.00018 | 3.6 | |||
| 0.00048 | 0.003 | 1.7 | 0.00019 | 0.00054 | 4.6 | 0.00001 | 0.00012 | 3.4 | |||
| 0.00048 | 0.003 | 1.8 | 0.00017 | 0.00054 | 4.6 | 0.00001 | 0.00012 | 3.4 | |||
| 0.00048 | 0.002 | 1.7 | 0.00015 | 0.00054 | 4.6 | 0.00001 | 0.00014 | 3.5 | |||
| 0.00048 | 0.003 | 1.7 | 0.00017 | 0.00051 | 4.6 | 0.00001 | 0.00012 | 3.4 | |||
| 0.00049 | 0.003 | 1.7 | 0.00015 | 0.00054 | 4.5 | 0.00001 | 0.00012 | 3.4 | |||
| 0.00048 | 0.003 | 1.7 | 0.00017 | 0.00054 | 4.6 | 0.00001 | 0.00012 | 3.3 | |||
| 0.00049 | 0.003 | 1.6 | 0.00017 | 0.00052 | 4.6 | 0.00001 | 0.00012 | 3.4 | |||
| 0.00048 | 0.002 | 1.7 | 0.00017 | 0.00054 | 4.5 | 0.00001 | 0.00012 | 3.2 | |||
| 0.00048 | 0.003 | 1.7 | 0.00019 | 0.00051 | 4.5 | 0.00001 | 0.00012 | 3.4 | |||
| 0.00048 | 0.003 | 1.6 | 0.00017 | 0.00054 | 4.6 | 0.00001 | 0.00012 | 3.3 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehri, M.H.; Megahed, A.I.; Hossam-Eldin, A.; Ibrahim, M.A.; AboRas, K.M. Robust THRO-Optimized PIDD2-TD Controller for Hybrid Power System Frequency Regulation. Processes 2025, 13, 3529. https://doi.org/10.3390/pr13113529
Alshehri MH, Megahed AI, Hossam-Eldin A, Ibrahim MA, AboRas KM. Robust THRO-Optimized PIDD2-TD Controller for Hybrid Power System Frequency Regulation. Processes. 2025; 13(11):3529. https://doi.org/10.3390/pr13113529
Chicago/Turabian StyleAlshehri, Mohammed Hamdan, Ashraf Ibrahim Megahed, Ahmed Hossam-Eldin, Moustafa Ahmed Ibrahim, and Kareem M. AboRas. 2025. "Robust THRO-Optimized PIDD2-TD Controller for Hybrid Power System Frequency Regulation" Processes 13, no. 11: 3529. https://doi.org/10.3390/pr13113529
APA StyleAlshehri, M. H., Megahed, A. I., Hossam-Eldin, A., Ibrahim, M. A., & AboRas, K. M. (2025). Robust THRO-Optimized PIDD2-TD Controller for Hybrid Power System Frequency Regulation. Processes, 13(11), 3529. https://doi.org/10.3390/pr13113529








