Tubing String Dynamics During Transient Start-Up and Shutdown in CO2 Flooding
Abstract
1. Introduction
2. Definition of Vibration Boundary Conditions for Tubing String During Start-Up and Shutdown Processes
2.1. Definition of Vibration Boundary Conditions During Start-Up Process
2.2. Definition of Vibration Boundary Conditions of Tubing String During Pump Stopping Process
- p0 is the initial pressure at pump shutdown (Pa);
- is the maximum pressure increment due to water hammer (Pa);
- T is the total pump shutdown time (s);
- is the pump shutdown coefficient (dimensionless);
- is the pressure relaxation time (s);
- a is the CO2 pressure wave velocity (m/s);
- v0 is the steady-state flow velocity before pump shutdown (m/s).
3. Analysis of Parameter Influence Inside the Tubing String During Start-Up Process
4. Analysis of the Influence of Injection Rate on Parameters Inside the Tubing String
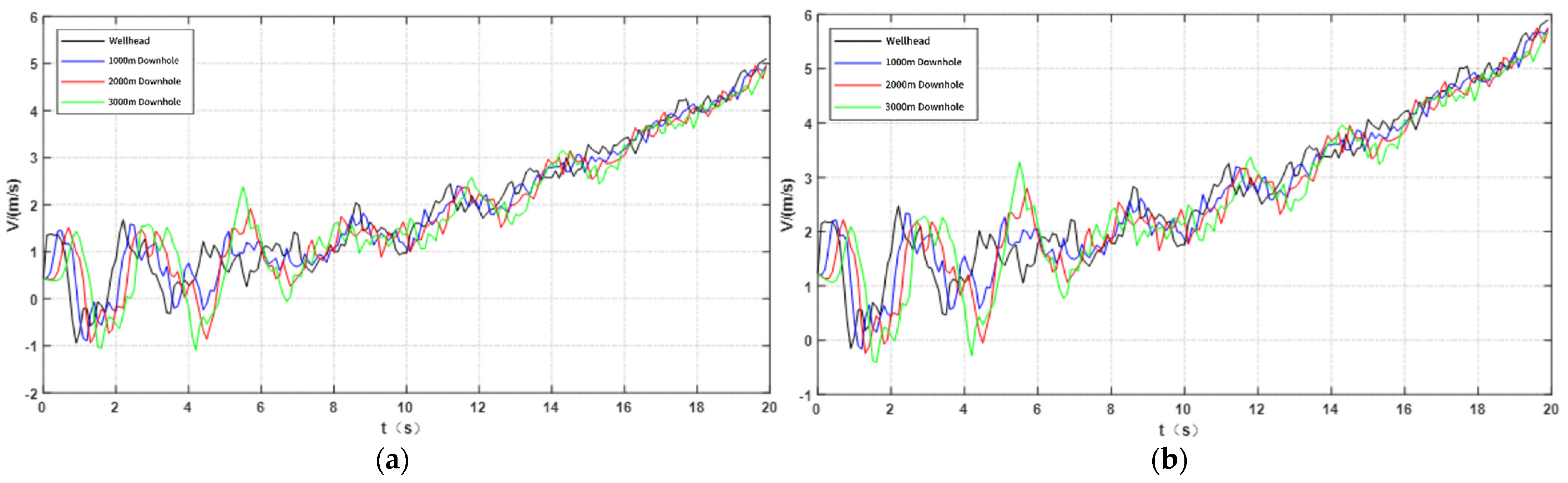
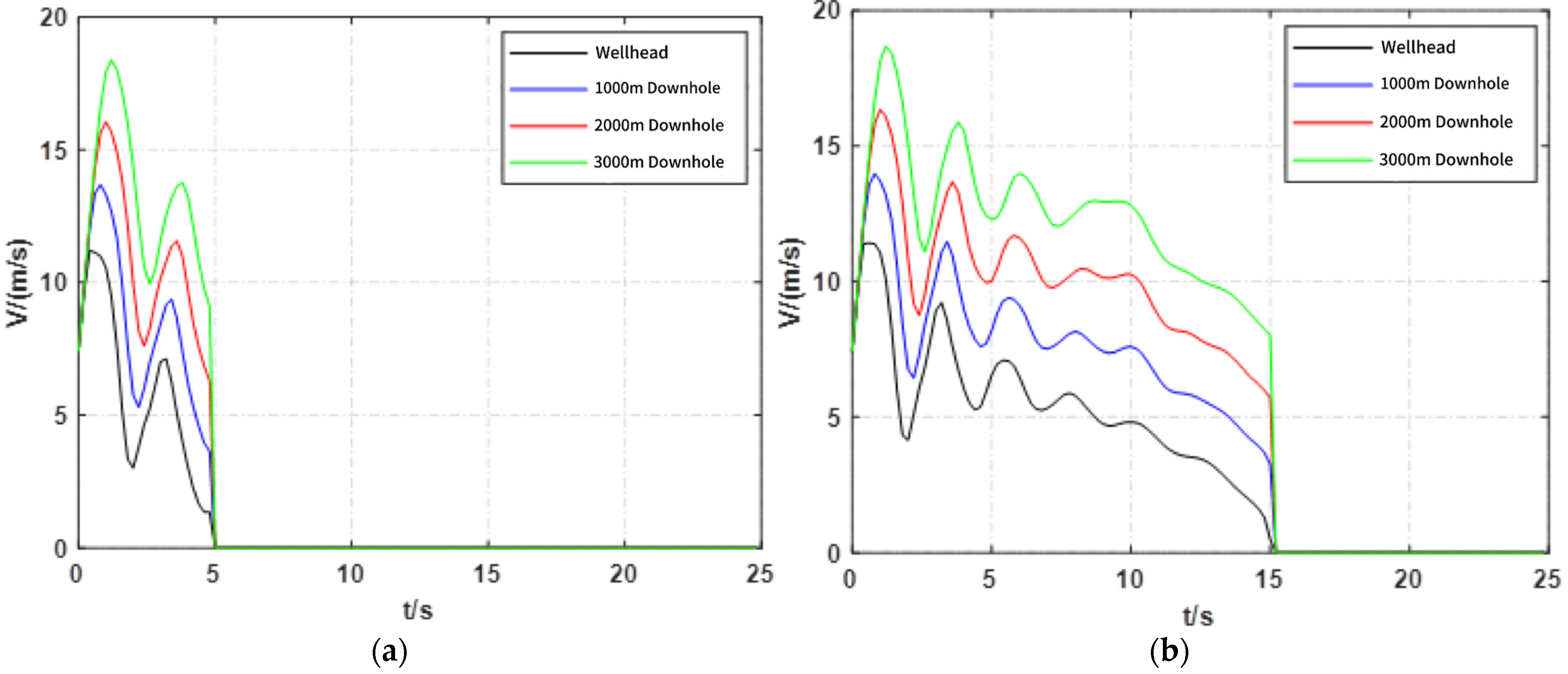
4.1. Influence of Injection Rate on Fluid Velocity in the Tube
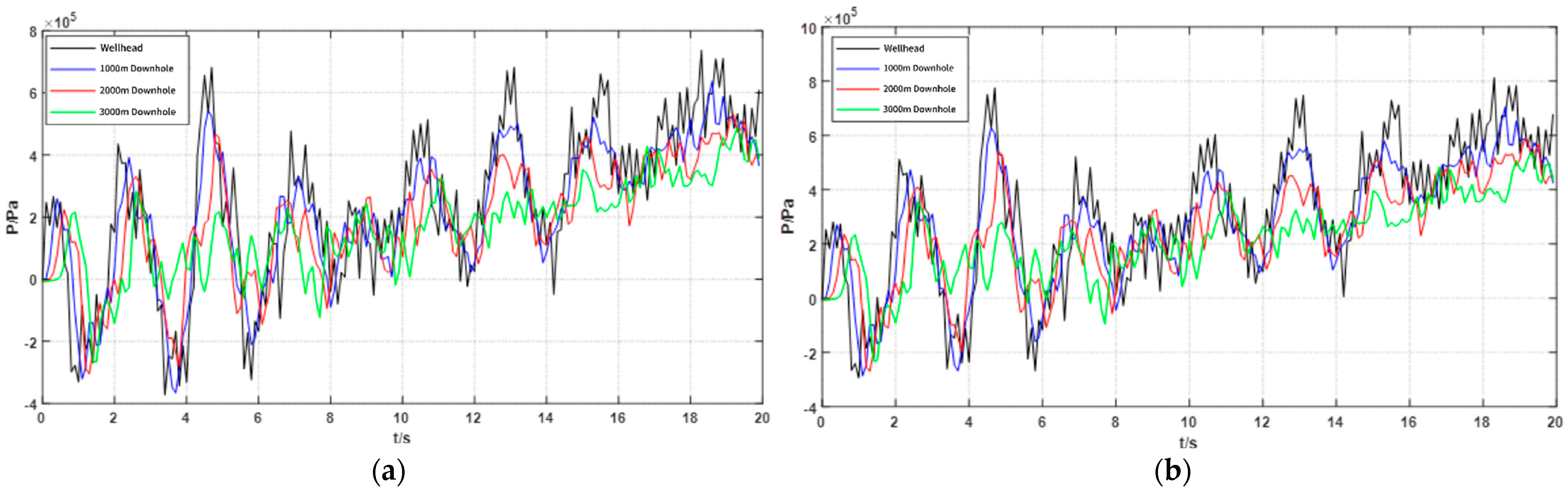
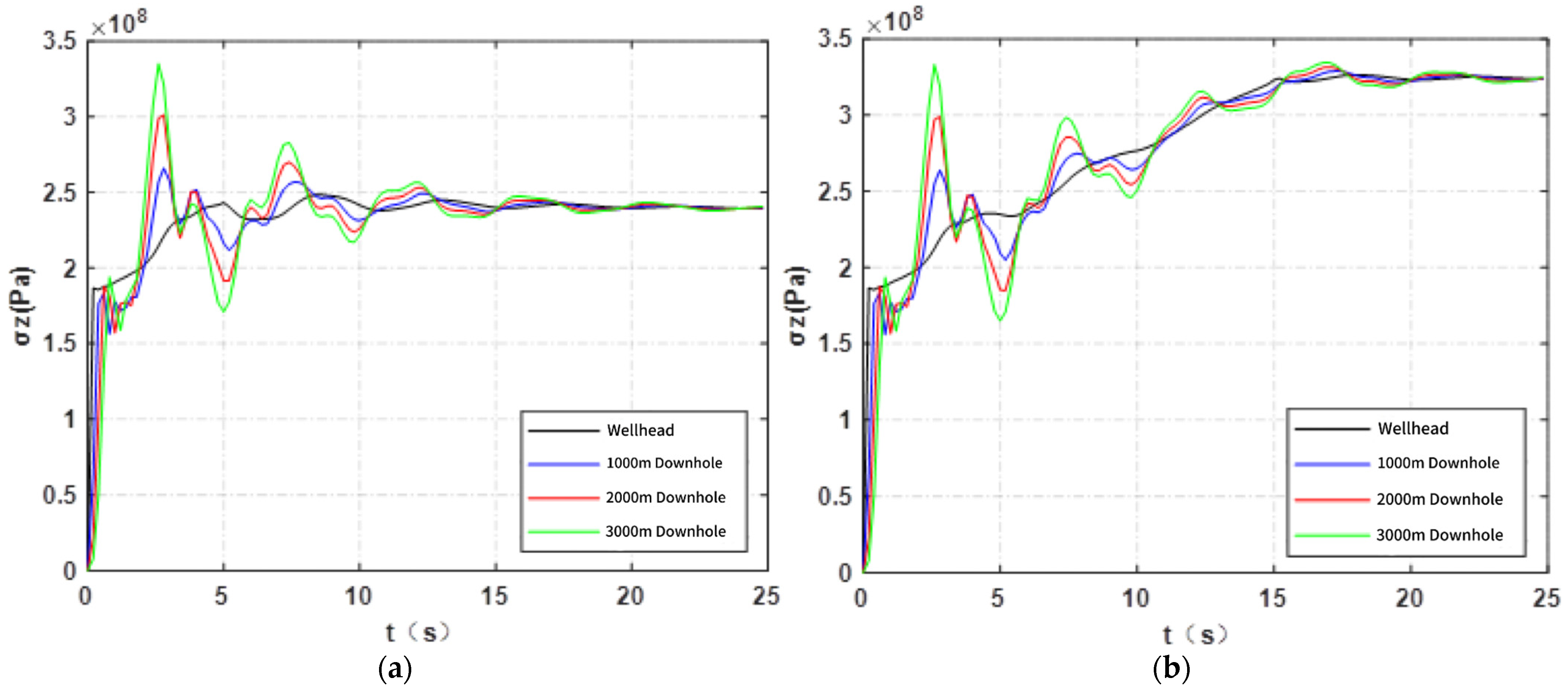
4.2. Influence of Injection Rate on Fluid Pressure in the Tube
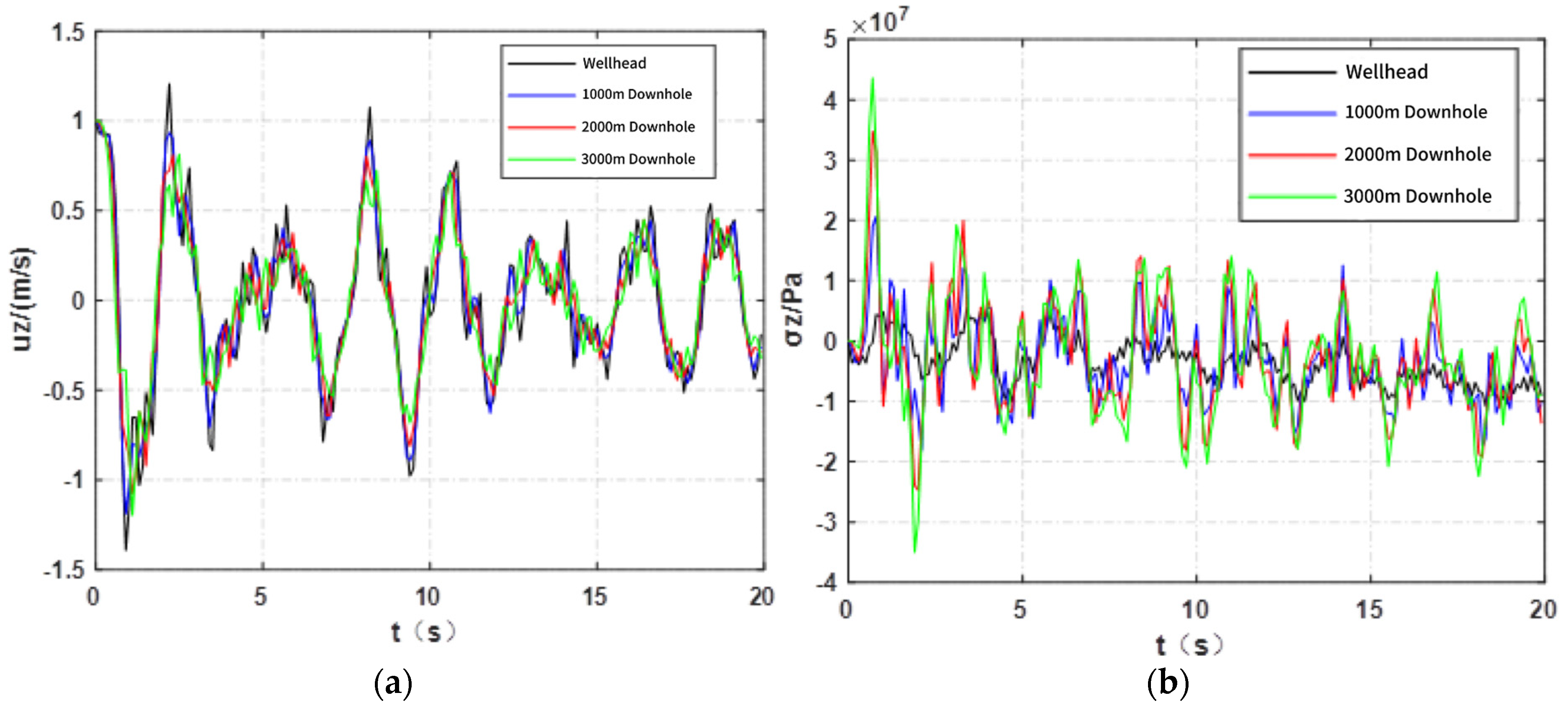
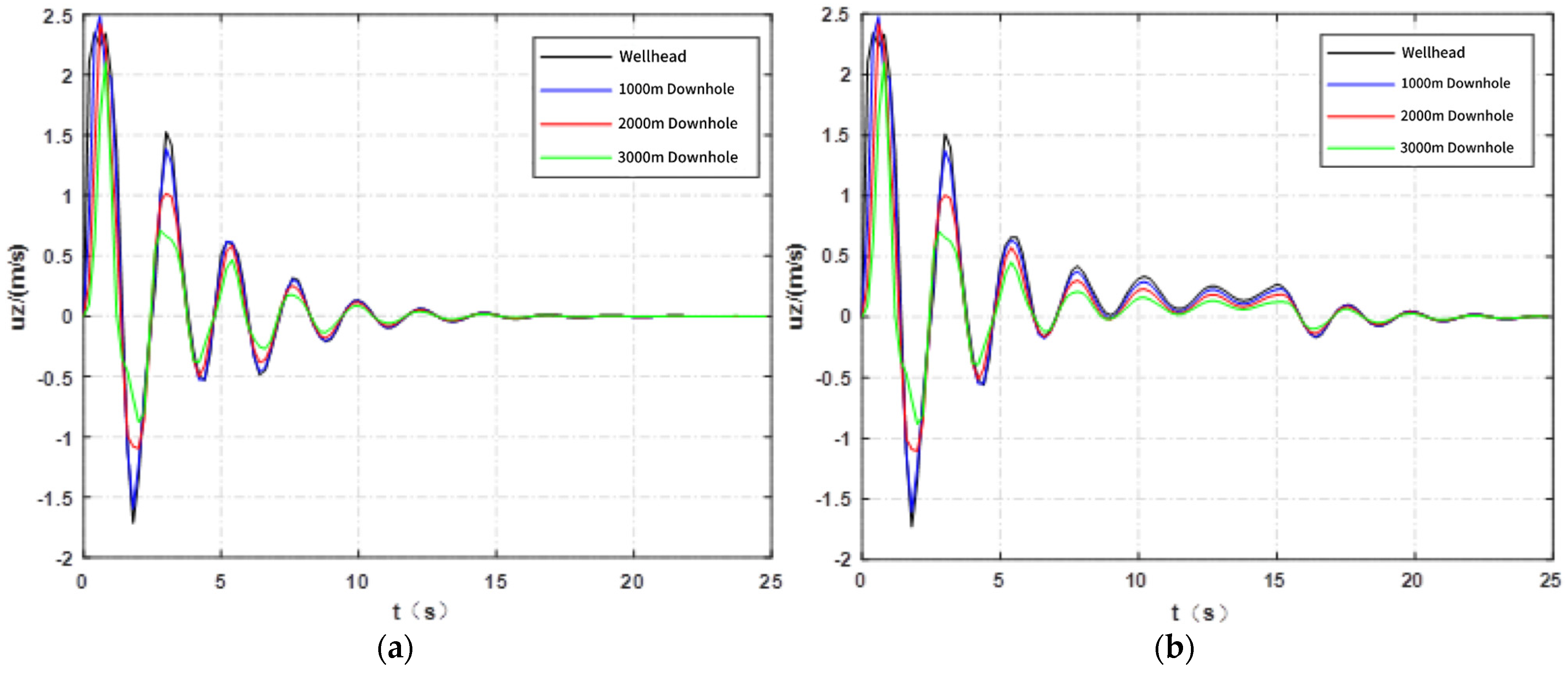
4.3. Influence of Injection Rate on Axial Vibration Velocity of Tubing String
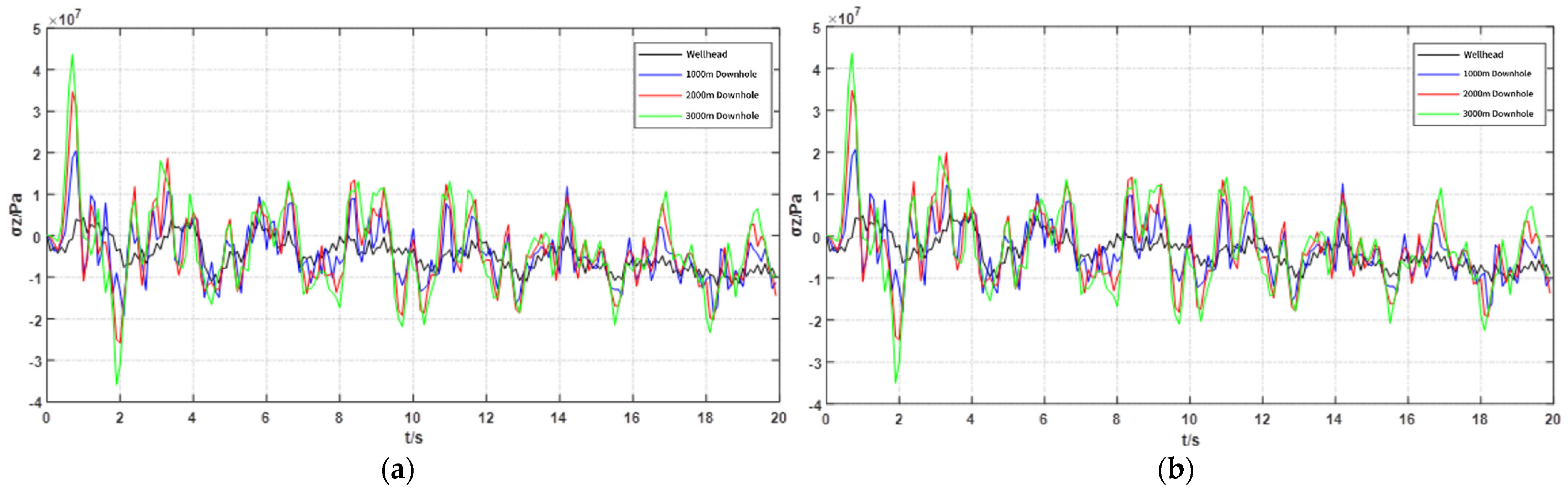
4.4. Influence of Injection Rate on Axial Additional Stress of Tubing String
5. Analysis of Parameter Influence Inside the Tubing String During Shutdown Process
5.1. Influence of Shutdown Time on Fluid Velocity
5.2. Influence of Shutdown Time on Fluid Pressure
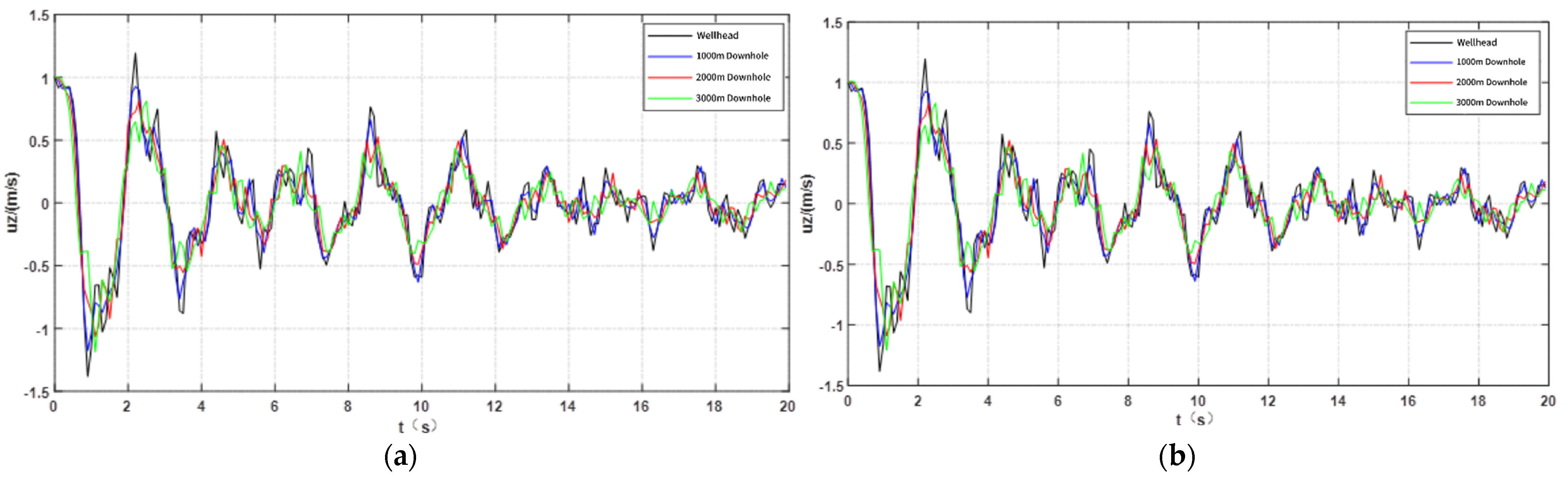
5.3. Influence of Shutdown Time on Axial Vibration Velocity of Tubing String
5.4. Influence of Shutdown Time on Axial Additional Stress of Tubing String
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, Z.; Jiang, N.C.; Wang, X.H.; Guan, X.W. Water Hammer and Its Prevention During Pump Shutdown, 2nd ed.; China Architecture & Building Press: Beijing, China, 2004. [Google Scholar]
- Xu, Z.G. Numerical Simulation and Visualization Technology of Pump Shutdown Water Hammer; Hunan University: Changsha, China, 2009. [Google Scholar] [CrossRef]
- Ding, J.D.; Lian, Z.H.; Ding, Y.R.; Zhang, Q.; Liu, J.W. Simulation Tests and Vibration Pattern Analysis of Injection and Production Tubing in Gas Storage Reservoirs. Pet. Tubing Instrum. 2019, 5, 30–34. [Google Scholar] [CrossRef]
- Wang, J.P. Analysis and Experimental Research on Fluid-Solid Coupling Vibration Characteristics of Gas Production Tubular; Xi’an Shiyou University: Xi’an, China, 2021. [Google Scholar] [CrossRef]
- Dou, Y.H.; Wang, L.Q.; Liu, J.C. Safety Analysis of Completion Tubing Vibration under Switching Well Conditions. Pet. Field Mach. 2015, 44, 11–15. [Google Scholar] [CrossRef]
- Zhu, F.; Ye, Y. Research on Water Hammer Protection Measures for Pump-Stopping in Long-Distance Water Transmission Projects. Water Conserv. Sci. Technol. Econ. 2021, 27, 1–6. [Google Scholar] [CrossRef]
- Xu, Z.X.; Wan, J.F.; Hong, Y.; Liu, H.M.; Yi, X.Z.; Diao, B.B.; Wang, Y.B. Analysis of three-dimensional nonlinear fluid-solid coupling vibration characteristics of coalbed methane abandoned well plugging string. Coal Geol. Explor. 2024, 52, 174–186. [Google Scholar] [CrossRef]
- Yang, W.W.; Li, H.; Lin, Y.; Ren, S.W.; Zhang, Z.L.; Xu, S.J.; Li, F.Q. Vibration mechanics analysis of a perforating string under the influence of multiple factors. J. Vib. Shock 2024, 43, 223–229. [Google Scholar] [CrossRef]
- Dou, Y.H.; Zhao, X.B.; Mi, H.X.; He, J.L.; Niu, Z.S.; Li, M.F. Mechanical performance analysis of downhole safety valve of completion string under typical working conditions. Oil Drill. Prod. Technol. 2023, 45, 184–189. [Google Scholar] [CrossRef]
- Zhang, C.Y. Staged Fracturing String Mechanics Analysis in Oil and Gas Development; Yanshan University: Qinhuangdao, China, 2021. [Google Scholar] [CrossRef]
- Gao, D.L.; Huang, W.J. Some research advances in downhole tubular mechanics and control methods. Adv. Mech. 2021, 51, 620–647. [Google Scholar] [CrossRef]
- Qin, A. Study on the Vibration Mechanism of Fluid-Solid Coupling of Tandem Double Wave Cone Cylinder; Wuhan University of Technology: Wuhan, China, 2021. [Google Scholar] [CrossRef]
- Yang, B.K. Characteristics Analysis of Multi-Dimensional Fluid-Structure Interactional Vibration in Completion String; Xi’an Shiyou University: Xi’an, China, 2020. [Google Scholar] [CrossRef]
- Ai, P.X. Fluid-Solid Coupling Vibration Characteristics and Experimental Study of Fracturing String Considering Friction Effect; Xi’an Shiyou University: Xi’an, China, 2020. [Google Scholar] [CrossRef]
- Cao, Y.P.; Guo, L.; Dou, Y.H. Influence of Fluid-Solid Interaction on the Vibration Characteristics of Tubing in Oil and Gas Well. Mach. Des. Manuf. 2019, 6, 84–87+91. [Google Scholar] [CrossRef]
- Cao, Y.P.; Huang, Y.X.; Yu, K.Q.; Dou, Y.H. Natural frequency analysis for fluid-solid coupling vibration of completion string based on ANSYS workbench. Well Test. 2018, 27, 1–7. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, H.H.; Zhang, L.P.; Yang, X.; Feng, G.Q. Analysis of fluid-structure interaction of completion string system in high pressure gas well. J. Vib. Shock 2011, 30, 202–207. [Google Scholar] [CrossRef]
- Fan, H.H.; Wang, Y.; Zhang, L.P.; Yang, X.; Yang, X.T.; Wei, F. A fluid-solid coupled oscillation model for completion string and its application in high pressure gas well. Acta Pet. Sin. 2011, 32, 547–550. [Google Scholar] [CrossRef]
- Beune, A.; Kuerten, J.; Heumen, M. CFD Analysis with Fluid-Structure Interaction of Opening High-Pressure Safety Valves. Comput. Fluids 2012, 64, 108–116. [Google Scholar] [CrossRef]
- Nerella, R.; Rathnam, E.V. Fluid Transients and Wave Propagation in Pressurized Conduits Due to Valve Closure. Procedia Eng. 2015, 127, 1158–1164. [Google Scholar] [CrossRef]
- Slipchuk, A.; Pukach, P.; Vovk, M.; Kunynets, A. On the Vibrational Characteristics of a Moving Wire via the KBM Asymptotic Method. Appl. Mech. 2025, 6, 31. [Google Scholar] [CrossRef]
- Archut, J.-L.; Kins, R.; Heider, Y.; Cloppenburg, F.; Markert, B.; Gries, T.; Corves, B. A Study of the Mechanical Response of Nonwovens Excited by Plate Vibration. Appl. Mech. 2022, 3, 496–516. [Google Scholar] [CrossRef]
- Giagopoulos, D.; Arailopoulos, A.; Chatziparasidis, I. Optimal Modeling of an Elevator Chassis under Crash Scenario Based on Characterization and Validation of the Hyperelastic Material of Its Shock Absorber System. Appl. Mech. 2022, 3, 227–243. [Google Scholar] [CrossRef]
- Prem, M.S.; Klanner, M.; Ellermann, K. Identification of Fractional Damping Parameters in Structural Dynamics Using Polynomial Chaos Expansion. Appl. Mech. 2021, 2, 956–975. [Google Scholar] [CrossRef]
- Sozinando, D.F.; Tchomeni, B.X.; Alugongo, A.A. Fluid Interaction Analysis for Rotor-Stator Contact in Response to Fluid Motion and Viscosity Effect. Appl. Mech. 2024, 5, 964–977. [Google Scholar] [CrossRef]
- Abdalla, M.A. The Combined Effects of the Minimum Miscibility Pressureand Injection Rate Variations on Recovery of CO2 Flooding in Sandstone Reservoir. J. Pet. Explor. Prod. Technol. 2022, 12, 108–116. [Google Scholar] [CrossRef]
- Zhang, Q.; Liao, T.; Lian, Z.H. Study on water hammer effect and tubing string vibration in high-pressure high-production gas wells. Geoenergy Sci. Eng. 2023, 229, 212147. [Google Scholar] [CrossRef]
- Guo, X.Q.; Liu, J.; He, Y.F. Nonlinear flow-induced vibration response characteristics of a tubing string in HPHT oil & gas well. Appl. Ocean Res. 2021, 102, 102468. [Google Scholar] [CrossRef]
- Mao, L.J.; Chen, X.W.; Fu, Q. Vibration characteristics and safety analysis of production string in high temperature, high pressure gas wells. Geoenergy Sci. Eng. 2024, 239, 212959. [Google Scholar] [CrossRef]
- Liu, J.; Zeng, L.L.; Cai, L. Experimental study on flow-induced vibration response characteristics of leaching tubing in salt cavern gas storage. Eng. Fail. Anal. 2022, 139, 106302. [Google Scholar] [CrossRef]
- Liu, J.; Zeng, L.L.; Guo, X.Q.; Dai, L.M.; Huang, X.; Cai, L. Nonlinear flow-induced vibration response characteristics of leaching tubing in salt cavern underground gas storage. J. Energy Storage 2021, 41, 102909. [Google Scholar] [CrossRef]
- Cao, Y.P.; Wang, J.P.; Dou, Y.H.; Hang, X.Y. Study on the Vibration Response Characteristics of Fracturing Tubing Under Water Hammer Excitation (English). Mach. Tools Hydraul. 2019, 47, 1–7. [Google Scholar] [CrossRef]
- Li, B. Research and Analysis on the Mechanism of Crack Propagation and Damage in Pile Heads Caused by High-Pressure Water Jet. Hunan Transp. Sci. Technol. 2025. Available online: https://link.cnki.net/urlid/43.1193.U.20250630.1147.002 (accessed on 10 September 2025).
- Wu, F.T. Technical Analysis of Water Hammer Protection Calculations in Water Supply Pipeline Construction Projects. Heilongjiang Water Conserv. Sci. Technol. 2025, 53, 119–122. [Google Scholar] [CrossRef]
- He, C.S.; Zeng, P.J.; Zeng, Y.; Wang, H.; Wan, X.B.; Han, D.D.; Feng, L.J.; He, J.Y. Testing and Adaptive Optimization of Key Parameters for Frequency Regulation of High-Ratio Hydropower Units. J. Irrig. Drain. Mach. Eng. 2025, 6, 716–723. [Google Scholar] [CrossRef]
- Xu, Q.; Du, G.Q.; Dong, M.Y. Discussion on the Impact of Water Hammer Phenomena on Pipelines Based on the Enping Block Case Study. Liaoning Chem. Ind. 2021, 50, 862–864. [Google Scholar] [CrossRef]
- Zhang, A.L. Hydraulic Design and Water Hammer Protection Calculations for the Water Supply Pipeline of a Medium-Sized Irrigation District in the Jingtai Mountainous Area of Gansu Province. Gansu Water Conserv. Hydropower Technol. 2019, 55, 28–32. [Google Scholar] [CrossRef]
- Huang, Y.X. Analysis of Fluid-Structure Interaction Vibration Characteristics of Tubing in Fracturing Conditions; Xi’an ShiYou University: Xi’an, China, 2018. [Google Scholar]
- Zhu, L. Research on Fluid-Structure Coupling Vibration Analysis and Fatigue Life Assessment Technology of Liquid-Filled Pipelines; National University of Defense Technology: Changsha, China, 2018. [Google Scholar] [CrossRef]
- Gaponenko, S. Mathematical Modeling of the Effect of Various Defects on the Parameters of Natural Vibrations of the Pipeline Under Operating Conditions. In Advances in Automation IV, RusAutoCon 2022, Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2023; pp. 136–146. [Google Scholar] [CrossRef]
- Samara, H.; Jaeger, P. Driving Mechanisms in CO2-Assisted Oil Recovery from Organic-Rich Shales. Energy Fuels 2021, 35, 710–720. [Google Scholar] [CrossRef]
- Lameh, M.; Al-Mohannadi, D.M.; Linke, P. Graphical Analysis of CO2 Emissions Reduction Strategies. Clean. Eng. Technol. 2020, 1, 100023. [Google Scholar] [CrossRef]
- Fu, Q.; Zhang, L.; Mao, L.J.; Hang, S.M. Study on the Temperature Field Distribution of Cold Water Pipes in Ocean Thermal Energy Conversion Power Generation. Mar. Eng. Equip. Technol. 2022, 9, 7–13. [Google Scholar] [CrossRef]
- Zhou, J. Research on the Protection of Offshore Oil Well Variable Frequency Drives Against External Power Supply Fluctuations. China Pet. Chem. Stand. Qual. 2023, 43, 134–135. [Google Scholar] [CrossRef]
- Zhu, Z.X.; Yu, K.; Jiao, G.; Hu, X.; Cao, D.H. Performance Analysis of a Reciprocating Throttling Positive Pulse Generator. Navig. Position. Timing 2022, 9, 156–162. [Google Scholar] [CrossRef]
- Mo, L.; Jia, D.P.; Mao, L.J.; Wang, G.R. Experimental Study on the Vibration Mechanism of Horizontal Well Completion Tubing under Different Gas Production Rates. J. Eng. Des. 2020, 27, 690–697. [Google Scholar] [CrossRef]
- Tang, Z.Q. Research on the Control of Wellbore Integrity in Horizontal Wells with Segmented Fracturing in Tight Oil Reservoirs; Southwest Petroleum University: Chengdu, China, 2018. [Google Scholar] [CrossRef]


| Year | Researchers/Teams (Region) | Research Content | Core Achievements |
|---|---|---|---|
| 2004 | Jin Zhui et al. (China) [1] | Theoretical study on shutdown water hammer protection | Proposed protective measures including gas injection valves and slow-closing check valves; published the monograph Shutdown Water Hammer and Its Protection |
| 2009 | Xu Zhigang (China) [2] | Visualization of shutdown numerical simulation | Developed a water hammer calculation program and an Excel-based visualization system using VC++ |
| 2012 | A. Beune et al. (International) [19] | FSI of high-pressure safety valves | Established a multi-grid Computational Fluid Dynamics (CFD) model; observed the valve closure oscillation phenomenon |
| 2015 | Dou Yihua et al. (China) [9] | Vibration of completion strings during well startup and shutdown | Identified the risk of plastic deformation caused by transient resonance; established an ABAQUS finite element model |
| 2015 | Ruben Nerella et al. (International) [20] | Pressure transients during valve closure | Quantitatively described the variation laws of pressure and flow rate in pipelines using the Method of Characteristics (MOC) model |
| 2019 | Ding Jiandong et al. (China) [3] | Vibration test of gas storage injection-production strings | Measured that the transient impact load is 5–15 times the static load |
| 2021 | Wang Jipeng (China) [4] | FSI experiment of gas production strings | Confirmed that sand and liquid inclusion increase vibration amplitude; the amplitude increases by more than 30% during well startup and shutdown |
| 2023 | Zhang et al. (International) [27] | Water hammer and vibration in high-pressure high-yield gas wells | Pointed out that transient pressure waves are the main inducement of vibration; established a pressure-vibration coupling model |
| Model Parameters | Numerical Value | Relevant Parameters | Numerical Value |
|---|---|---|---|
| Tubing string length | 3000 m. | Pumping displacement | 6–20 m3/h |
| Tubing string diameter | 88.9 mm | Pumping pressure | 20, 33.5, 40 MPa |
| Wall thickness Elasticity modulus Tubing string density Poisson’ratio | 6.45 mm 2.06 × 1011 Pa 7850 kg/m3 0.3 | Spatial step size Time step Output quantity | 30 m V, P. uz-бz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Li, J.; Chen, D.; Cao, Y.; Dou, Y.; Luo, X. Tubing String Dynamics During Transient Start-Up and Shutdown in CO2 Flooding. Processes 2025, 13, 3514. https://doi.org/10.3390/pr13113514
Wu X, Li J, Chen D, Cao Y, Dou Y, Luo X. Tubing String Dynamics During Transient Start-Up and Shutdown in CO2 Flooding. Processes. 2025; 13(11):3514. https://doi.org/10.3390/pr13113514
Chicago/Turabian StyleWu, Xiangyang, Jianxun Li, Dong Chen, Yinping Cao, Yihua Dou, and Xin Luo. 2025. "Tubing String Dynamics During Transient Start-Up and Shutdown in CO2 Flooding" Processes 13, no. 11: 3514. https://doi.org/10.3390/pr13113514
APA StyleWu, X., Li, J., Chen, D., Cao, Y., Dou, Y., & Luo, X. (2025). Tubing String Dynamics During Transient Start-Up and Shutdown in CO2 Flooding. Processes, 13(11), 3514. https://doi.org/10.3390/pr13113514





