Experimental Study on Proppant Transport and Distribution in Asymmetric Branched Fractures

Abstract

Hydraulic fracturing is a key technique for creating complex fractures in unconventional reservoirs to enhance energy recovery. Asymmetric branched fractures, as fundamental units, are widely observed in complex fracture networks. Effective proppant distribution within such structures is critical but remains poorly understood. To investigate this, a rough-walled slot with two branches was developed, where asymmetry was introduced by inserting plates with different geometries on one side. The results show that the structural asymmetry between the left and right branches can significantly induce non-uniform transport and irregular sand bed morphology. Reducing the height and width of branch fractures increases fluid velocity, limiting proppant settling within the branch. As the flow area decreases, the fluid velocity increases, driving more proppant through the branch toward the distal fracture region. Injection pressure increases as the flow area of the branch fracture decreases. At a height ratio of 0.25, sand plugging and ineffective proppant placement probably occur within the natural fracture. When the branch is located at the upper section, proppants hardly settle to form a bed, leading to closure of the fracture. The study provides new insights into optimizing proppant placement in complex fractures.

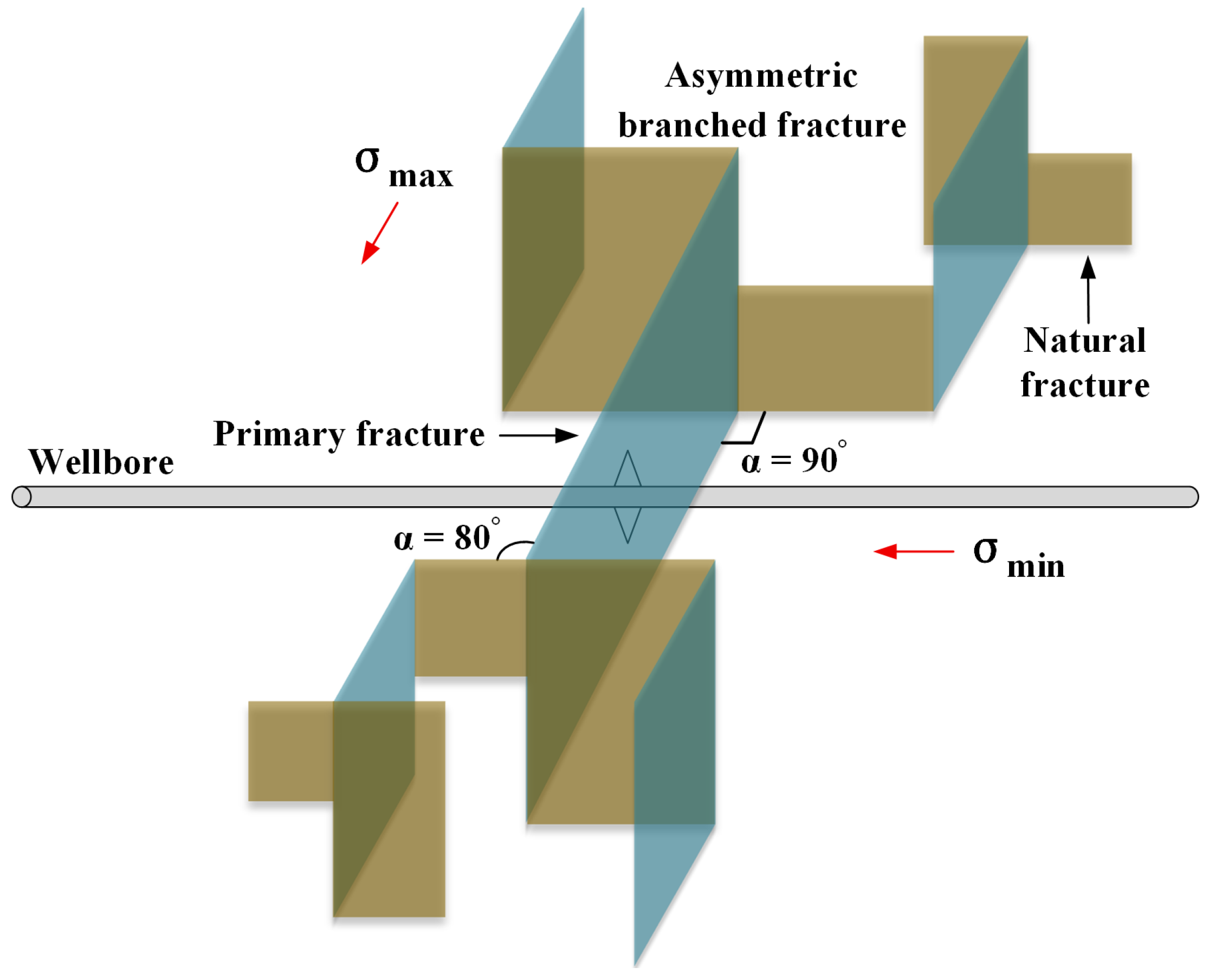
1. Introduction

Hydraulic fracturing is a key technique for creating complex fracture systems in unconventional oil and gas reservoirs, thereby enhancing energy recovery [1]. Due to in situ stress heterogeneity and natural cracks, asymmetric branched fractures are fundamental units in the system that commonly occur and play a crucial role in fluid flow [2,3]. Ensuring effective proppant distribution within such structures is essential to sustaining long-term fracture conductivity [4,5]. Hydraulic fracturing tends to generate complex fracture networks in unconventional reservoirs because of the presence of well-developed natural fractures, as shown in Figure 1. Due to the random geometry of natural fractures, asymmetric branched fractures are typically characterized by differences in height and width between the two branches, resulting in unequal cross-sectional areas [6]. Such asymmetry disrupts local flow dynamics, leading to non-uniform proppant placement, decreased fracture conductivity, and reduced contribution from affected zones [7]. However, there is currently little research on proppant distribution in such structures, and it remains poorly understood. An in-depth study of particle transport and distribution in asymmetric branched fractures become inevitably significant.

Proppant transport experiments provide an effective approach to visualizing and better understanding proppant transport across various fracture geometries, including planar [8], branched [9], and complex fracture networks [10]. Various straight smooth slots have been developed under dynamic and geometric similarity, without considering fluid leak off through the walls [11]. Model dimensions are generally under 3 m long, 0.5 m high, and 2–10 mm wide [12]. The injection parameters can be aligned with field conditions, including fluid velocity in the fracture, proppant mesh size, fluid type (slickwater or clear water), and sand concentration. Kern conducted pioneering experiments using a planar acrylic slot [13]. The sand quickly settled to the slot bottom and formed an initial bed. As more sand accumulated, the bed height would reach an equilibrium height. Then, sand transport was primarily dominated by fluidization and settling, progressively filling the fracture. The equilibrium height correlates power law with the fluid velocity, proppant properties, and proppant concentration [14]. The correlation evaluates fracturing design and treatment [15]. Attaching transparent plates with a certain level of surface roughness to the smooth walls allows for visualization and analysis of the influence of wall roughness on particle migration [16]. The roughness enhances particle–wall interactions by increasing collisions and friction, which alters particle trajectories, reduces their velocity, and may result in particles becoming trapped or deposited along the walls. The rough walls hinder particle transport, forming a higher sand bed that extends closer to the wellbore [17]. However, the planar slot has constant height and width along the flow direction, while the effects of changes in flow area on proppant transport remain largely unexplored.

Recent studies have introduced advanced models to explore proppant transport within complex fracture networks.

Table 1. Model structure and parameters for proppant transport.

Reference	Length (m)	Height (m)	Width (mm)	Inner Wall	Intersection Angle (°)	Liquid	Proppant
Sahai, Miskimins and Olson [18]	P = 1.2 S = 0.3	0.6	5.4	Smooth	90	Water	Sand
Tong and Mohanty [9]	P = 0.38 S = 0.19	0.076	2.0	Smooth	30, 60, 90	Water	Sand
Wen, Wang and Duan [19]	P = 0.6 S = 0.3 T = 0.6	0.4	10	Smooth	90	Water Guar gum	Ceramsite
Alotaibi and Miskimins [16]	P = 1.2 S = 0.3	0.6	5.4	Rough	90	Water	Sand

P = Primary fracture; S = Secondary fracture; T = Tertiary fracture.

lists transparent complex slots. Sahai developed a large, smooth fracture model consisting of one primary slot and two secondary slots [18]. They found that dune accumulation within the primary slot strongly affects proppant entry into the secondary slots. Two distinct mechanisms were identified: (1) when the pump rate exceeds a threshold (corresponding to a critical velocity in the primary slot), proppants are carried around the slot corner into the secondary slot; and (2) gravity-driven particles fall from the primary slot into the secondary slot, occurring regardless of the pump rate. Tong and Mohanty designed a complex model featuring a primary slot intersected by a secondary slot at angles ranging from 30° to 90° [9]. Their results showed that proppant placement in the secondary slot increases with decreasing intersection angle and increasing flow rate. Wen developed a slot to simulate complex fracture networks [19]. A vortex develops at the fracture intersection, which erodes the sand bed and reduces its height at the junction. These turning points can significantly decrease the propped area. Thus, proppant transport and distribution in complex fractures differ markedly from those in straight fractures. Nevertheless, most existing models assume constant fracture height and width, which limits their ability to capture the influence of geometric variability.

Existing experimental models for proppant transport generally assume constant fracture dimensions in the width and height directions. Moreover, experimental studies on asymmetric, branched fracture models are lacking, and the characteristics of proppant placement within such complex fracture geometries remain unclear. To address these gaps, this study is the first to experimentally investigate proppant transport in asymmetric, branched fractures. A rough-walled slot with two branches was developed, and plastic plates of varying heights and widths were placed on one side of the fracture to introduce controlled geometric asymmetry. The effects of fracture width, height, and branch position on proppant distribution are systematically analyzed, enabling a quantitative assessment of how fracture asymmetry influences proppant placement. The findings provide new insights into fracture-scale proppant distribution and offer guidance for optimizing hydraulic fracturing in naturally fractured reservoirs.

2. Materials and Methods

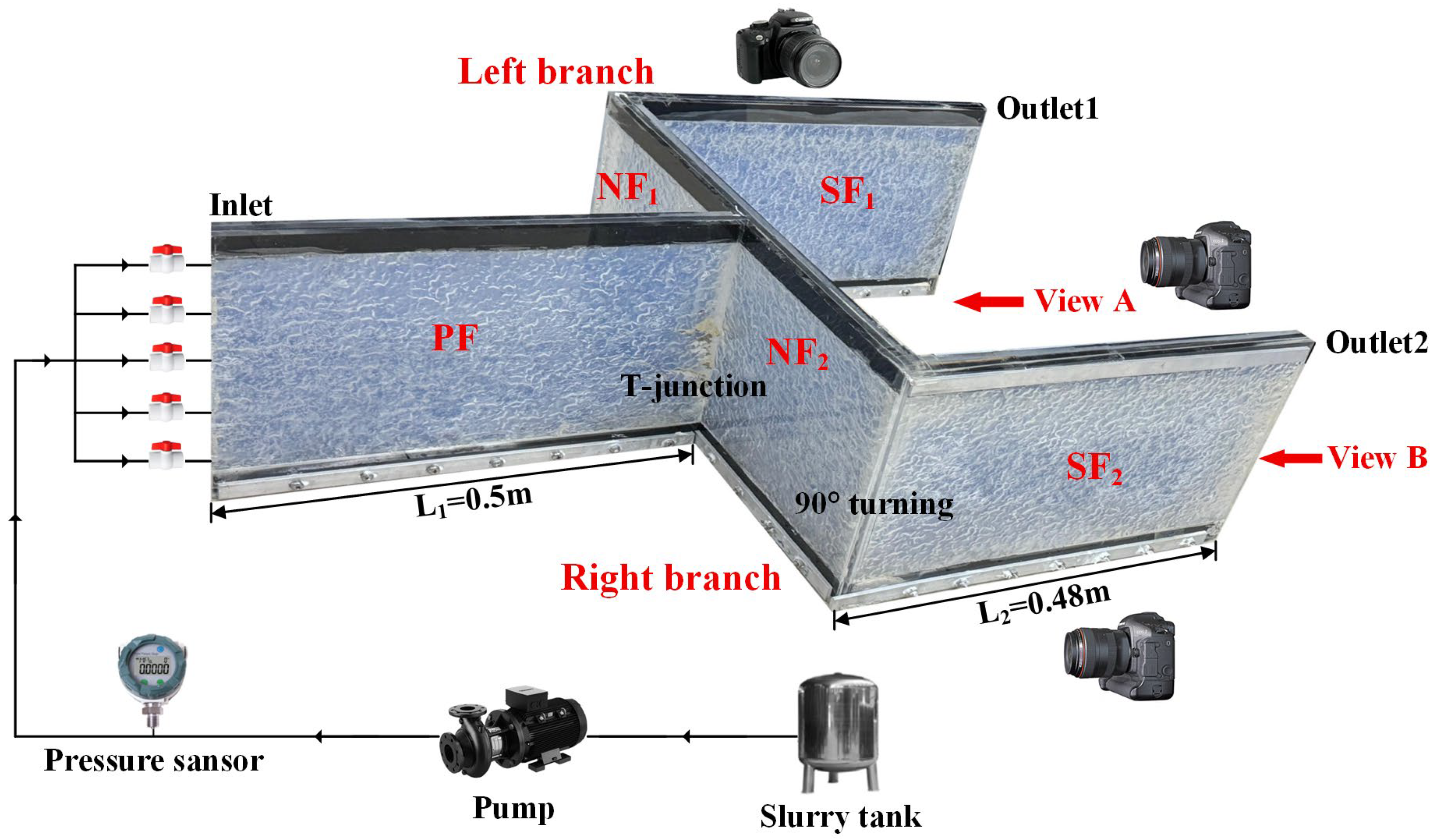
2.1. Experimental Apparatus

The T-shaped slot was constructed using acrylic sheets due to their favorable mechanical and optical properties. The sheets possess good toughness, allowing them to be bent multiple times to form the desired curvature without cracking. In addition, their high transparency enables clear observation of particle–fluid interactions during the experiments. The thickness of each acrylic sheet was 10 mm to ensure adequate strength and to prevent deformation under injection pressure conditions. Due to the difficulty of realizing fluid leak-off in transparent plates, proppant transport experiments based on flat models typically neglect the leak-off effect along the fracture walls. If leak-off were considered, the fluid velocity within the fracture would be reduced to some extent. Figure 2 shows the particle transport system. The slot is designed to simulate particle-fluid flow in an asymmetric fracture. A primary fracture (PF) intersects a natural fracture (NF) at 90°, continues to extend within it, and induces secondary fractures, also oriented at 90°. The left branch consists of NF₁ and SF₁, and the right branch consists of NF₂ and SF₂. Considering the limitations of pump capacity and the pressure tolerance of the acrylic plates, the slot height typically ranges from 0.1 to 0.6 m [10]. Both branches are of equal dimensions, each with an inner height of 0.27 m. In addition, due to the length constraint of the acrylic plates, the total internal length of the slot was kept within 3 m to facilitate assembly and ensure structural stability [18]. The PF has a length of 0.50 m, and the lengths of NF₁ and NF₂ are 0.3 m, and the secondary fractures SF₁ and SF₂ are each 0.48 m long.

The perforations on the casing had diameters ranging from 8 to 12 mm, with a perforation density of 16–20 holes per meter. Based on this standard, five 10 mm-diameter perforations were arranged along the inlet, spaced 50 mm apart. The slurry is injected from five holes into the slot. The outlet, located at the top-right corner, had an opening height of 0.07 m, and the overall height of the right boundary was 0.2 m. The outlet remained open throughout the experiments, and no backflow pressure was applied. Injection pressure is monitored by a pressure sensor installed at the inlet and displayed in real time by a pressure gauge. Three cameras are mounted perpendicular to the slots.

Figure 3a presents the NF at View A. Two red dashed lines mark the PF aperture. Roughness characteristics of the plates were replicated from natural rock surfaces, as documented in [20]. Two sets of rough panels were combined to form the fracture channel. A white opaque plastic plate of defined dimensions is inserted into the NF₂ to generate an asymmetric configuration. Varying the height and thickness of the panels allows the left and right branches to differ in size, resulting in a non-symmetrical fracture configuration. In Figure 3a, the panel height is 0.135 m, and the pathway height is 0.135 m. Figure 3b shows a local profile of Outlet2. The aperture ranges from 3.19 mm to 5.22 mm. The real fracture width typically varies between 1 and 6 mm, and the average width is 4 mm. The joint roughness coefficient (JRC), which quantifies the roughness of rock fracture surfaces and ranges from 0 to 20, was calculated as 11.5 for the rough plate using the empirical equation provided in the study [21]. A JRC value exceeding 10 is generally considered representative of rock fractures.

2.2. Experimental Materials

The slurry is prepared using 40/70 mesh sand and slickwater. In Figure 4, the average diameter of sands is 311 μm, and the size ranges from 0.106 mm to 0.43 mm. The bulk density of the sand is 1670 kg/m³, and the slickwater viscosity is 1.5 mPa·s. The parameters are consistent with the field condition [1].

2.3. Experimental Scheme

Table 2. Experimental scheme.

Case	Fracture Height (mm)	Panel Position	Fracture Weight (mm)	Height Ratio Hr	Width Ratio Wr
1	270	/	4	1	1
2	NF1 = 202.5	Bottom	4	0.75	1
3	NF1 = 135	Bottom	4	0.5	1
4	NF1 = 67.5	Bottom	4	0.25	1
5	NF1 = 202.5	Top	4	0.75	1
6	NF1 = 135	Top	4	0.5	1
7	NF1 = 67.5	Top	4	0.25	1
8	270	/	NF1 = 3	1	0.75
9	270	/	NF1 = 2	1	0.5
10	270	/	NF1 = 1	1	0.25

summarizes the experimental scheme. Case 1, with symmetric left and right branches, is the benchmark. In Cases 2–4 and 5–7, panels are inserted at the top and bottom of NF₁, respectively, creating flow pathways at the opposite sides. In Cases 8–9, a transparent panel is inserted into NF₁ to modify its width. The panel dimensions are 270 mm in height and 300 mm in length, with thicknesses of 3, 2, and 1 mm. The injection rate in the primary fracture (PF) is 2.93 m³/h, corresponding to an average flow velocity of 0.42 m/s. The velocity is within the typical range of fluid velocities (0.1–0.5 m/s) observed in real hydraulic fractures [16,18]. The sand volume fraction is a constant value of 3%.

2.4. Dimensionless Parameters

The proppant bed dimensions, including height and length, were nondimensionalized to facilitate analysis, as expressed in Equations (1) and (2).

$${\mathrm{r}}_{\mathrm{L}}={\displaystyle \frac{{\mathrm{L}}_{\mathrm{s}}}{\mathrm{L}}}$$

(1)

$${\mathrm{r}}_{\mathrm{H}}={\displaystyle \frac{{\mathrm{H}}_{\mathrm{s}}}{\mathrm{H}}}$$

(2)

where r_L is the normalized length; r_H is the normalized height; L_s is the sand bed length, m; H_s is the sand bed height, m; L is the fracture lenght, m; and H is the fracture height, m.

Equation (3) indicates the coverage of the proppant bed within the fracture.

$$\mathrm{C}\mathrm{R}={\displaystyle \frac{{\mathrm{A}}_{\mathrm{s}}}{\mathrm{A}}}\times 100\mathrm{\%}$$

(3)

where CR is the area coverage ratio; A is the cross-sectional area of the fracture, calculated along the length and height directions, m²; and A_s is the sand bed area, m².

3. Results and Analysis

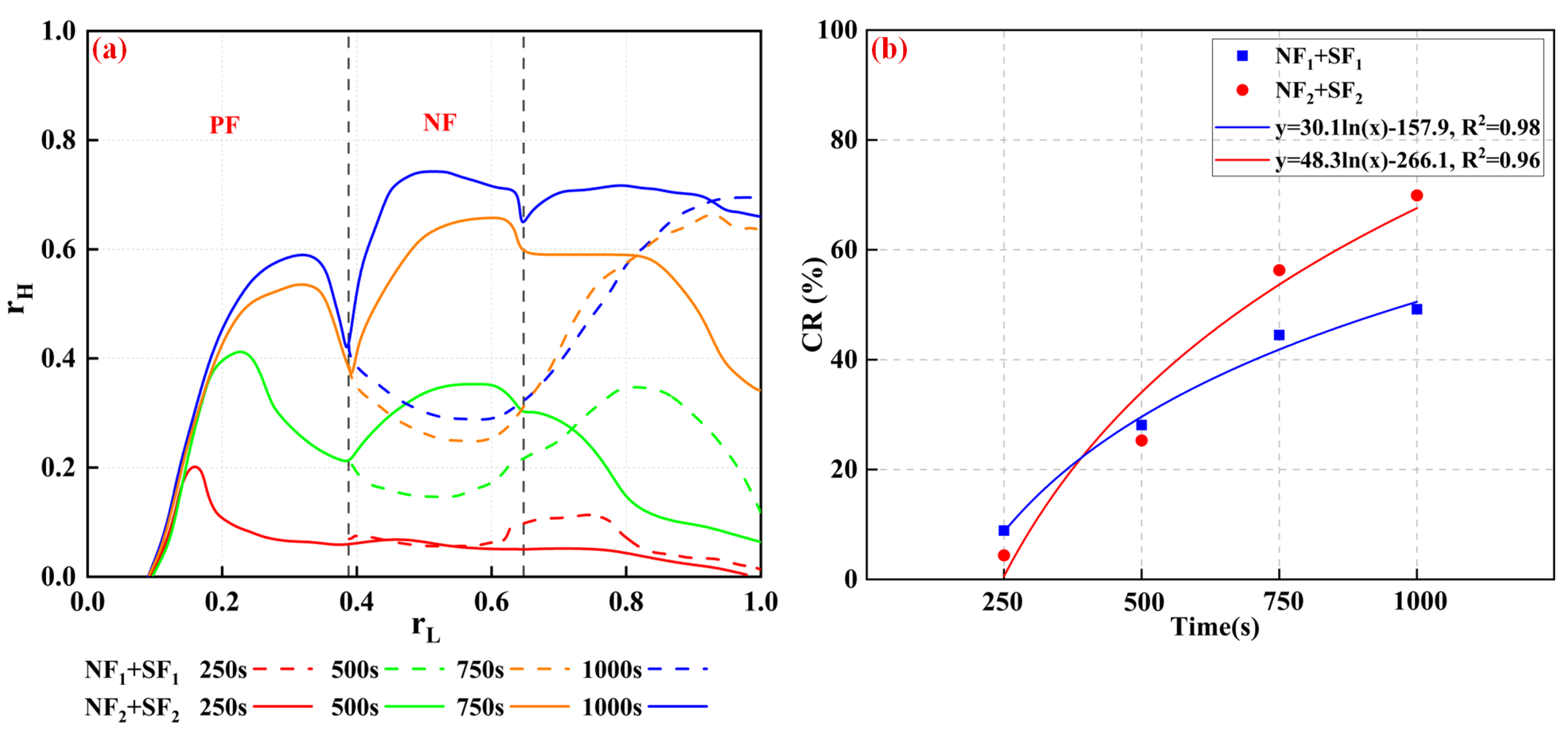
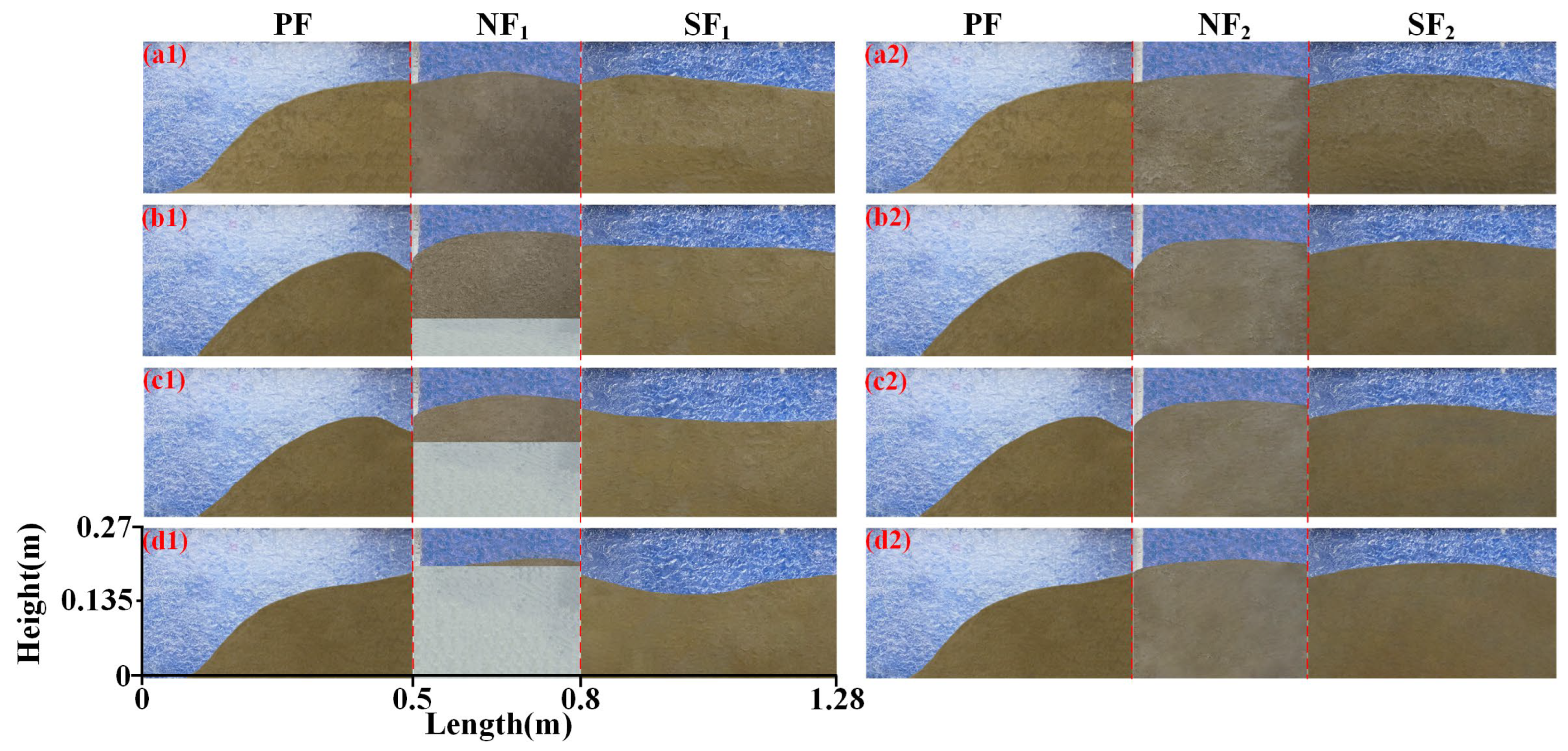
3.1. Proppant Distribution Evolution

Due to lithological influences, the height of the NF₁ is constrained to half of NF₂. Figure 5 shows the bed geometries in the slot at four moments for Case 3 in Table 2. At the initial stage, the asymmetric structure is found to have little influence on the sand bed morphology. The 40/70 mesh sands can pass through the T-junction and negotiate two 90° turns, depositing along the entire slot, while some particles remain suspended and exit directly through the outlet. During this process, strong collisions occur at the junction and turns. Frequent collisions with convex surfaces deflect sands, while impacts with concave regions lead to particle trapping and localized deposition, which is identical to the literature [17]. The trapped sands are later dispersed by the flowing fluid, facilitating the dynamic redistribution of proppants within the slot.

At 500 s, the asymmetric structure of the NF begins to impact the sand distribution. With no obstruction in NF₂, the lower fluid velocity facilitates sand settling, resulting in a taller sand bed. Sands undergo frequent collisions near the turns in NF₂ and SF₂, where changes in flow direction and velocity gradients enhance particle–wall interactions. These collisions promote particle deposition, leading to locally elevated sand beds around the 90° turn. As the height of NF₁ is reduced by half, the fluid entering NF₁ from the PF contracts due to the decreased cross- sectional area, resulting in an increase in fluid velocity. This acceleration enhances downward-directed shear stress, generating erosion that forms a downward-sloping sand bed in NF₁. When the flow moves from NF₁ into SF₁, it expands, causing a sudden reduction in velocity and turbulence near the bed surface. This expansion induces surface erosion and leads to the formation of an upward-sloping sand bed in SF₁.

At 1000 s, the beds reach equilibrium. In the left branch, the sand bed further reduces the flow area of NF₁. The resulting high-velocity erosion produces a lower equilibrium height and a more irregular bed morphology, with an upward-sloping bed formed in SF₁. In contrast, in the right branch, sands settle more readily, resulting in a higher and more uniform equilibrium sand bed. It proves that the significant influence of geometric asymmetry on local flow dynamics, particle–wall interactions, and proppant distribution patterns within branched fractures. Local vortices induced by flow separation and recirculation near the inner corners of the turning sections erode the sand bed surface, resulting in the formation of small pits. This phenomenon is consistent with the observations reported by Wen and Tong [9,19]. Qu Hai et al. further demonstrated through numerical simulations that vortices generated at the turning sections of narrow fractures can erode the sand bed surface, leading to the formation of small pits [22].

Figure 6a shows normalized profiles of sand beds at four moments. At equilibrium, the bed profile becomes the most regular, while small pits appear near the turns. In Figure 6b, the CR exhibits a logarithmic correlation with time, indicating a rapid early-stage increase that gradually levels off as equilibrium is approached. High flow velocity initially promotes rapid particle transport and deposition, resulting in a sharp rise in coverage ratio. As the particle bed develops, the flow area becomes constricted, leading to an increase in local fluid velocity and enhanced particle washout from the slot. Consequently, the coverage ratio gradually approaches a steady value. After 500 s, the coverage ratio in the right branch exceeds that in the left branch. At equilibrium, the difference in coverage ratio between the left and right branches is the largest. The reduced height of NF₁ decreases the coverage area in the left branch. Furthermore, suppose the injection time is insufficient and the sand bed has not yet reached equilibrium. In that case, the effective proppant coverage will be further reduced, which may significantly compromise the stimulation performance.

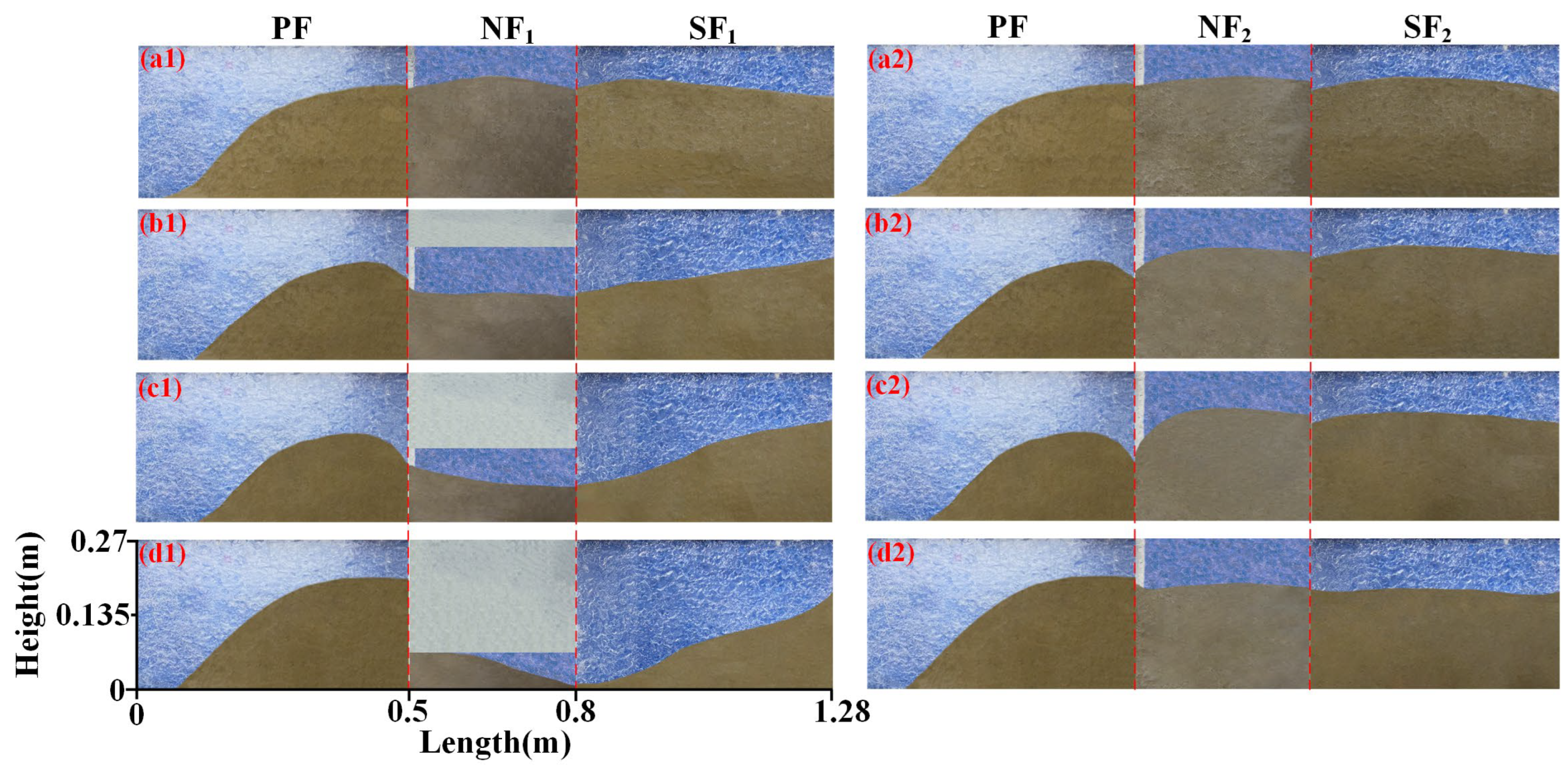
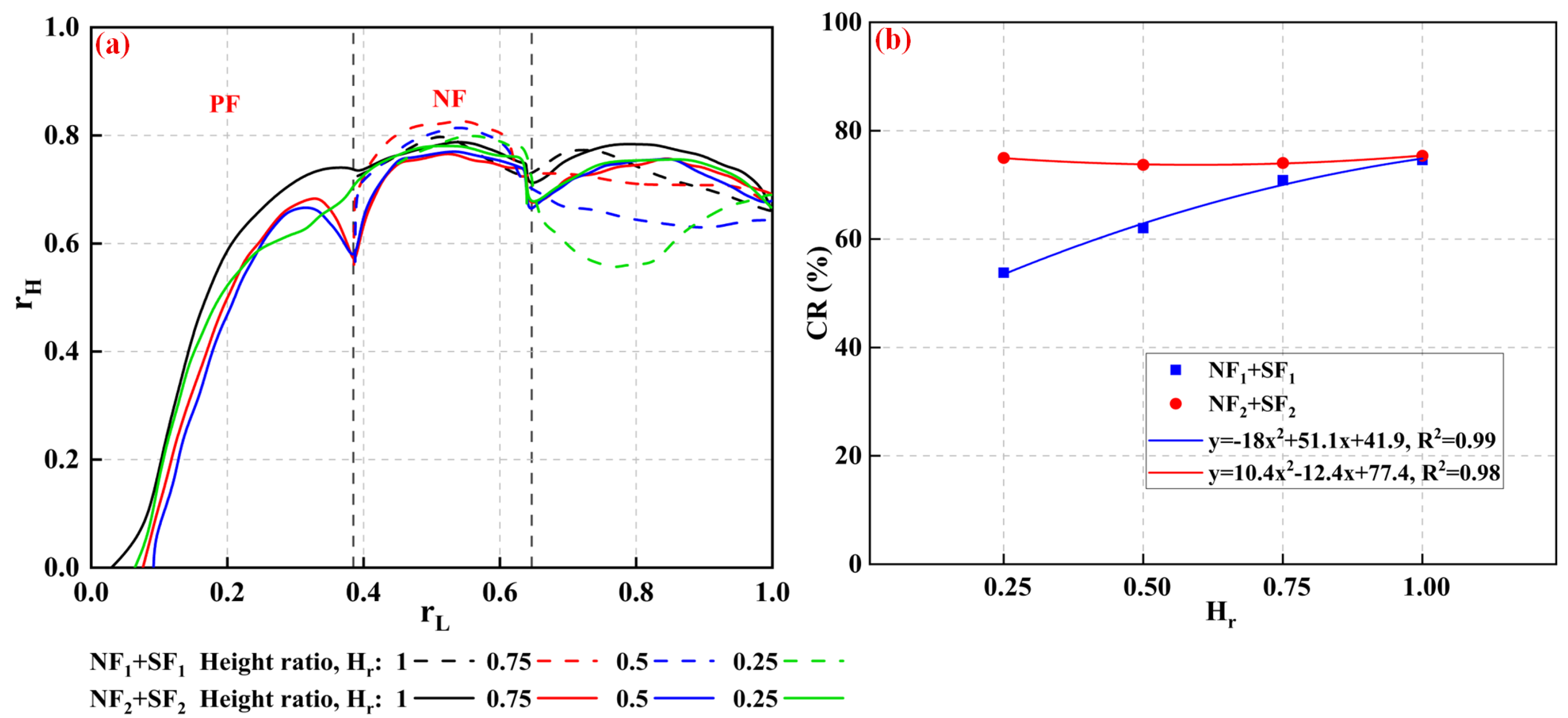
3.2. Proppant Distribution with NF₁ at the Bottom

When the upper section of the left branch experiences higher rock stress, the fracture tends to extend downward. In Figure 7, the NF₁ is at the bottom for Cases 1, 2 to 4 (Table 2). In Figure 7a, the structures of the two branches are identical, and the bed morphologies are also similar, with only small pits observed at the two 90° turns. The sand bed evolution is similar to the bed in the straight slot [7,23]. In Figure 7b, the height of NF₁ is 75% of that of NF₂. Even though NF₁ has a smaller height, it reduces sand bed height and coverage ratio and alters the bed profile. It indicates that the bed morphology is highly sensitive to fracture height. The lower height also increases local fluid velocity, intensifying bed erosion and further limiting proppant placement. In Figure 7d, the height of NF₁ decreases to 67.5 mm. Since NF₁ is positioned lower, when the sand bed height in PF exceeds that of NF₁, sand bridging occurs at the PF–NF₁ turn, forcing the slurry to flow entirely into the left branch. The increased fluid velocity in the left branch subsequently leads to a slight reduction in the bed equilibrium height. Besides, the small NF₁ causes the violent fluid flow in the right branch, and the sand bed in SF₁ develops a steeper slope and exhibits a lower coverage ratio. The sand bed around the turn between NF₁ and SF₁ is discontinuous. Thus, the discontinuous and small sand beds in the right branch cannot support the fracture effectively. The right branch becomes a weak link, and the fracture network connected to SF₁ can probably not contribute to production.

In Figure 8a, as the height ratio of NF₁ decreases from 1 to 0.25, the bed profile in the left branch becomes increasingly irregular. When CR = 0.25, sand plugging occurs in NF₁, causing the bed in the PF to shift closer to the inlet. In Figure 8b, this change in height ratio causes the CR of NF₁ to decrease from 73.8% to 35.1%, whereas the CR of NF₂ increases from 68.8% to 76.1%. The reduced height of NF₁ directs more sand toward NF₂, leading to an increased bed height in NF₂.

Figure 9 shows the liquid pressure at the inlet. A reduction in NF₁ height increases the fluid flow resistance, leading to higher pumping pressure. For a height ratio of 1, the pathway height remains unchanged, flow resistance is low, and the initial pressure is 35 kPa. When the height ratio is reduced to 0.25, the flow area is constricted, and the initial pressure rises to 42 kPa. As the sand bed gradually accumulates, the effective flow region in the slot decreases, causing a steady increase in liquid pressure. When the coverage ratio reaches 0.25, the injection pressure exhibits a sudden spike from 43.1 kPa to 44.8 kPa at 520 s due to sand bridging at NF₁. Due to the constant pump speed, the reduction in effective flow area resulted in a sudden increase in pressure. The phenomenon is identical to the injection pressure at the field [24].

3.3. Proppant Distribution with NF₁ at the Top

When the lower section of the left branch experiences higher rock stress, the fracture tends to extend upward. In Figure 10, the NF₁ is at the top for Cases 1, 5 to 7 (Table 2). The asymmetric structure primarily affects the sand distribution in the left branch. The sand bed exhibits minimal morphological differences in the right branch. In Figure 10b, the sand bed in NF₁ becomes slightly thinner, producing a modest asymmetry, while the overall coverage remains relatively extensive. In Figure 10c, the sand bed morphology begins to exhibit changes. The sand bed heights in PF and SF₁ decrease moderately, whereas those in NF₁ and NF₂ remain largely comparable. In Figure 10d, significant changes in sand bed morphology occur within the left branch. Owing to the limited flow area in NF₁, the flow velocity increases markedly, inhibiting sand deposition. A thin sand layer forms mainly near the 90° turn, likely resulting from deposition obstructed by the 90° turn. When the slurry flows from NF₁ into SF₁, the expansion of the flow area induces oblique erosion of the sand bed, forming a concave surface. Also, the sand bed height in SF₁ is reduced. Because of the lack of proppant support, NF₁ will rapidly close after the fracturing. In complex hydraulic fractures, branches like NF₁ serve as critical bridging links between upstream and downstream sections, governing local fracture connectivity. The result is identical to the literature [25]. Fracture coverage can be improved by reducing proppant transport capacity, for example, through lower injection rates, higher fluid viscosity, or larger proppant sizes.

In Figure 11a, when the H_r is less than 0.5, the bed height in SF₁ is significantly reduced. In Figure 11b, as the H_r of NF₁ decreases from 1 to 0.25, the CR of the left branch decreases from 74.5% to 53.8%, while the average CR of the right branch remains around 74.5%.

In Figure 12, as the NF₁ height decreases, the reduced flow area increases hydraulic resistance, thereby requiring a higher injection pressure. For the height ratio of 0.25, the initial pressure is 41.9 kPa, which is higher than the initial pressure of 35.8 kPa for the height ratio of 1. When H_r is 0.25, the sand bed reaches equilibrium at 1254 s. It is because the flow is turbulent, making it difficult for the sand to settle into the slot, thus requiring a longer injection time.

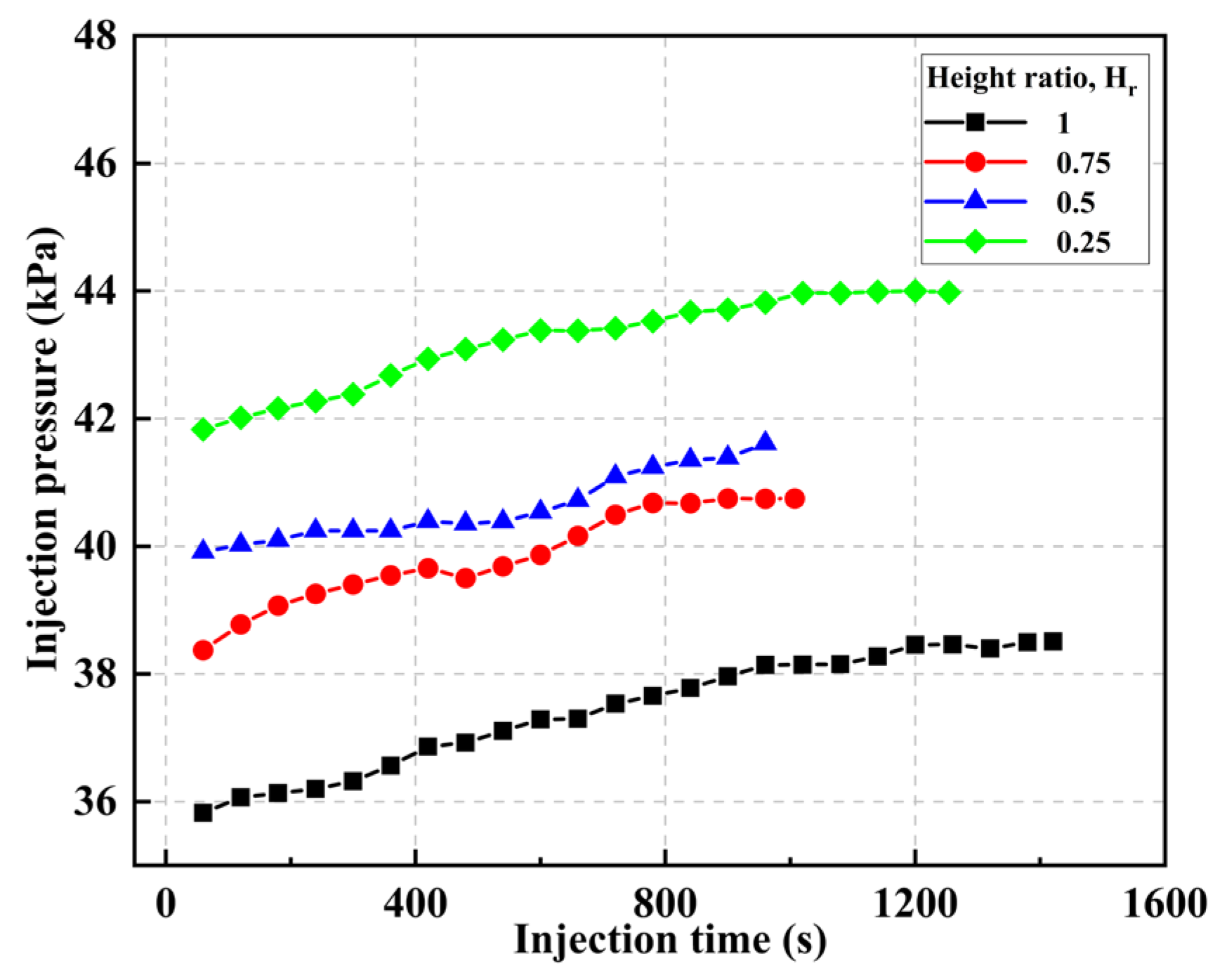
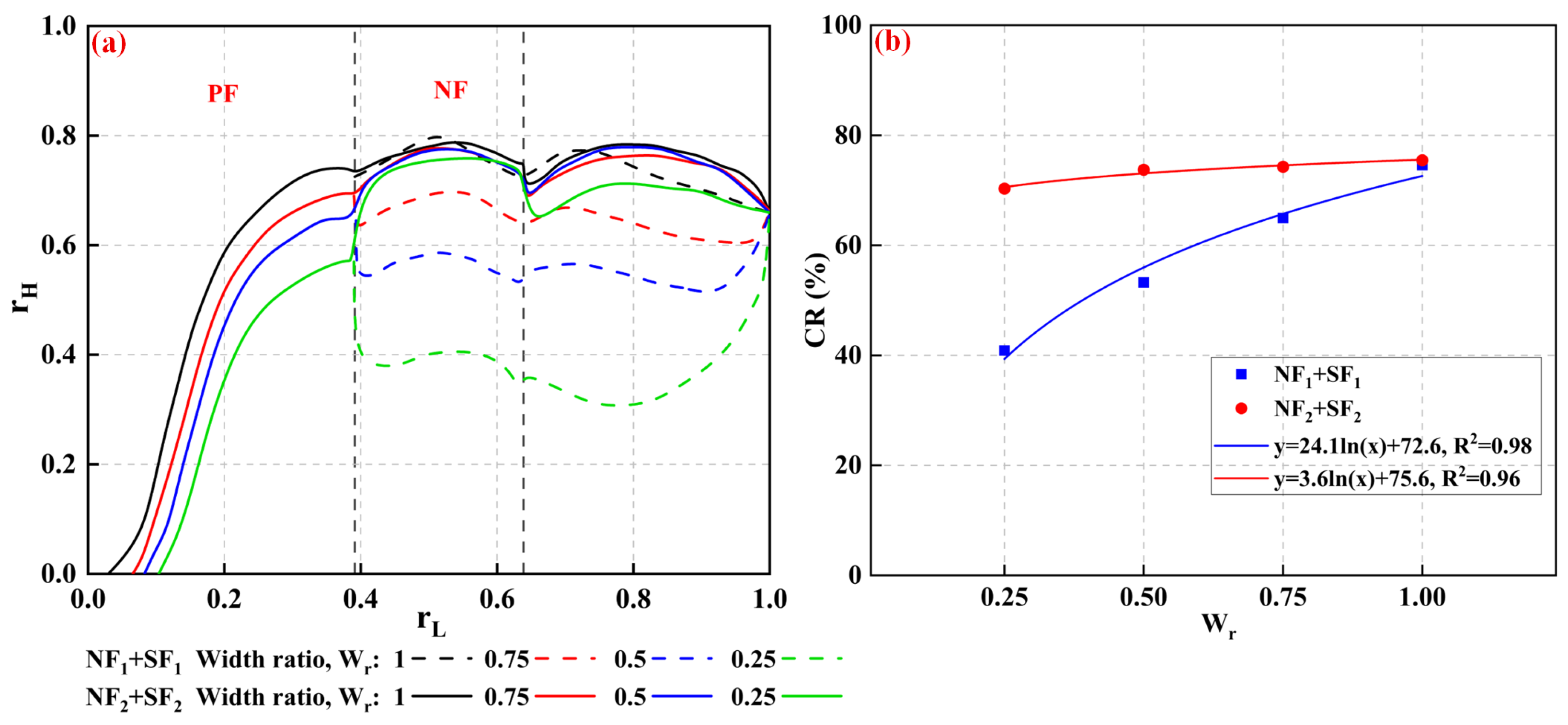
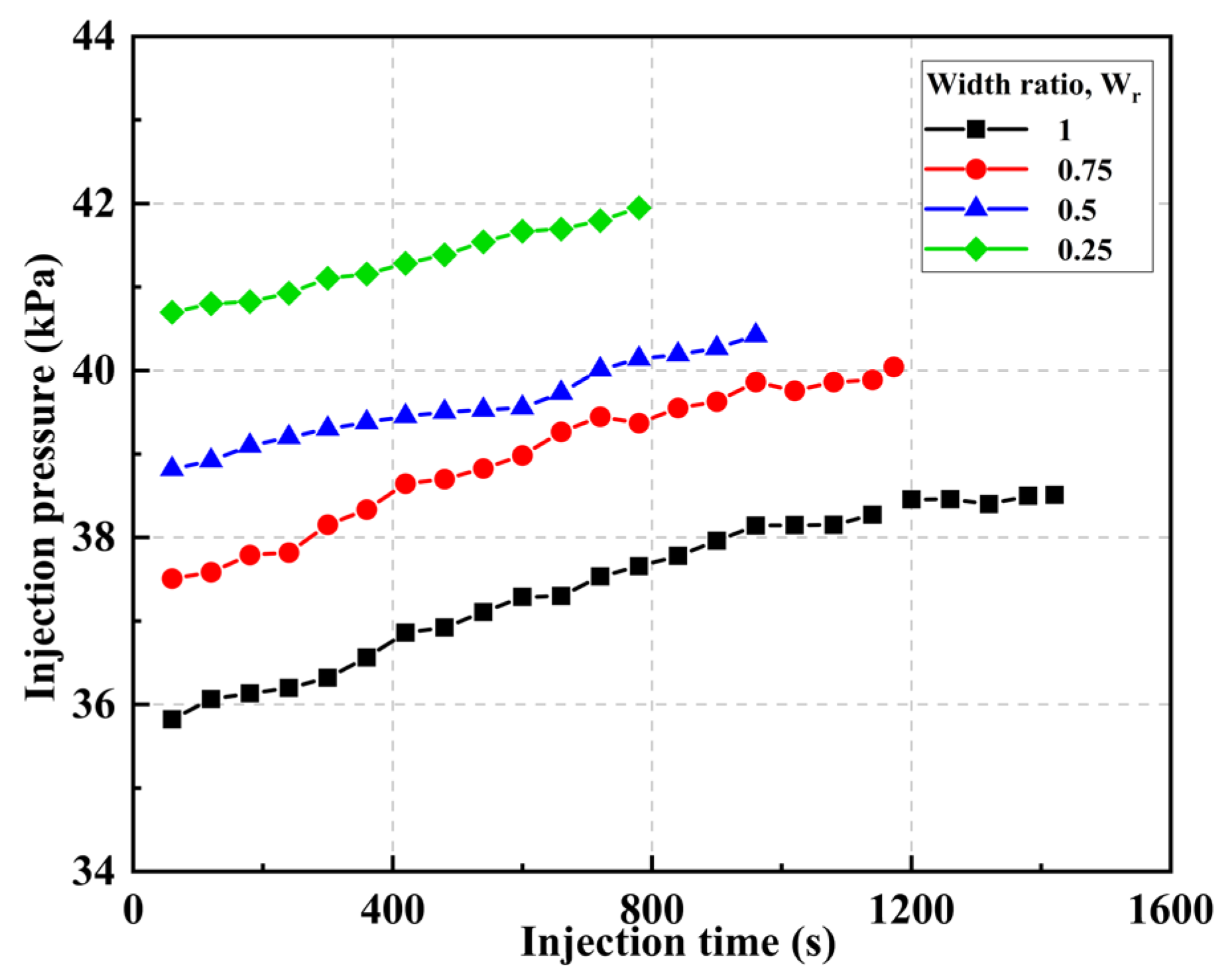
3.4. Effect of Branch Width

When the in situ stress is higher on one side, the fracture width becomes smaller, leading to asymmetric widths between the two branches. In Figure 13, the width of the NF decreases from 4 mm to 2 mm for Cases 1, 8 to 10 (Table 2). As the width of NF₁ decreases, the overall heights of the sand bed in the left branch and in PF both decrease, while the height of the sand bed in the right branch remains largely unchanged. Unlike height variations, changes in fracture width do not lead to irregular sand bed morphologies. It indicates that the effects of fluid contraction and expansion on sand bed morphology in the fracture width direction differ significantly from those in the height direction.

In Figure 14a, as the width of NF₁ decreases, the sand bed height in both the PF and the left branch is reduced, and when W_r is lower than 0.25, the sand bed height in the right branch decreases significantly. In Figure 14b, as the W_r decreases from 1 to 0.25, the CR of the left branch decreases from 74.5% to 40.8%, and the CR of the right branch decreases from 75.4% to 70.3%.

In Figure 15, as the NF width decreases, flow resistance increases due to the reduced flow area, resulting in higher fluid pressure at the injection point. For a width ratio of 1, the pressure rises from 35.9 kPa to 38.4 kPa, whereas for a width ratio of 0.25, it increases from 40.8 kPa to 42.2 kPa. Notably, the sand bed height in the model with a width ratio of 1 is higher than that in the model with a width ratio of 0.25. These results indicate that fracture width exerts a greater influence on injection pressure than sand bed height. When the width ratio is 0.25, the sand bed reaches equilibrium in the shortest time of 780 s due to the reduced coverage.

4. Limitations

Several limitations should be noted. The model is based on a laboratory scale, which differs significantly in size from actual fractures that can extend to hundreds of meters. The slot walls do not possess leak off capability, unlike fracture surfaces in the formation. In addition, the sand concentration was assumed to be constant. Therefore, the particle bed configuration in the model may differ from that in real fractures. In future work, numerical simulations will be combined to account for variations in fracture dimensions and injection parameters, enabling a more in-depth understanding of proppant transport mechanisms in asymmetric fractures.

5. Conclusions

Hydraulic fracturing in naturally fractured reservoirs often generates complex fracture networks, in which asymmetric structures are commonly present. This study is the first to experimentally investigate proppant transport in asymmetric, branched fractures. The effects of fracture width, height, and branch position on proppant distribution are systematically analyzed. Several new insights have been obtained for engineering applications.

• At a height ratio of 0.25, the branch is located in the lower section, and sand bridging is likely to occur once the sand bed in the primary fracture reaches a certain height. In naturally fractured reservoirs, it is recommended to increase the proportion of small-sized proppants (e.g., 70/140 or 200 mesh) to ensure smooth transport through narrow fractures and minimize the risk of premature bridging.
• When the branch is located at the upper section, proppants hardly settle to form a bed, leading to closure of the natural fracture. In the later stage of fracturing, lowering the injection rate could enhance particle accumulation in the natural fracture.
• A reduction in fracture width significantly increases the injection pressure while decreasing the sand bed area. In naturally fractured reservoirs, this leads to higher operational pressures during fracturing. Increasing fluid viscosity or reducing the injection rate decreases injection pressure and particle transport.
• The bed morphology within asymmetric branch fractures is more irregular than in regular slots, leading to a lower sand bed coverage ratio. The more complex slurry flow in asymmetric fractures can transport particles deeper into the fracture, further reducing coverage. In the later stage of fracturing, lowering the injection rate or using larger-sized proppant can enhance particle settling, improving overall coverage.