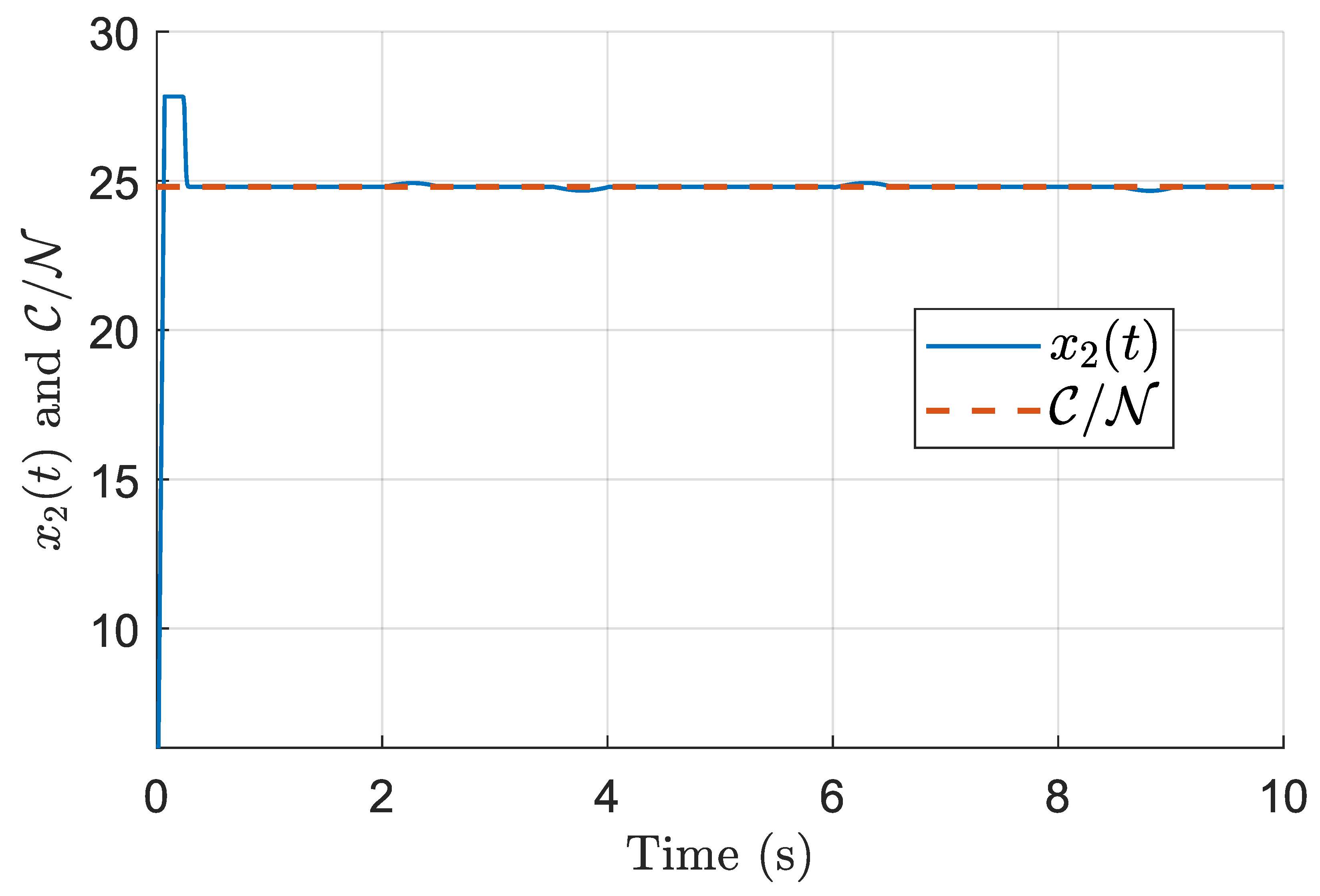A New Control Tracking Approach for the Congestion Problem of a TCP System Based on Nonlinear Sliding Mode Control

Abstract

In this paper, we propose two control approaches based on sliding mode control (SMC) to address the congestion problem in transmission control protocol (TCP) systems. First, a nonlinear sliding variable is introduced using a ${\mathcal{K}}_1$ function, which ensures robustness and finite-time convergence. Based on this sliding variable, a suitable switching controller is designed. Additionally, a continuous version of the controller is developed using the arctangent function to reduce chattering. Two simulation scenarios are presented to validate the effectiveness of the proposed control schemes in terms of congestion control and tracking performance.

1. Introduction

In control theory and process control, nonlinear control strategies are widely employed to achieve desired system performance under complex and uncertain conditions. Common nonlinear control approaches include backstepping techniques, model predictive control (MPC), sliding mode control (SMC), and Lyapunov-based methods. Among these, SMC offers several notable advantages, such as finite-time convergence, model order reduction through the use of sliding manifolds, and strong robustness against perturbations and uncertainties. Motivated by these strengths, this paper proposes a novel control scheme based on nonlinear sliding mode control.

Network congestion, particularly in communication systems governed by the transmission control protocol (TCP), continues to pose a major challenge [1]. Efficient TCP congestion control is essential to ensure optimal data flow while avoiding network overload. However, the TCP faces significant uncertainties arising from dynamic network conditions, such as bandwidth variations and packet loss [2,3]. These uncertainties necessitate the development of robust control strategies capable of adapting to such disturbances. In this context, sliding mode control emerges as an attractive solution, offering both simplicity and robustness, as demonstrated in numerous studies (see, e.g., [4,5,6]). This paper addresses these challenges by introducing a novel nonlinear sliding mode control framework tailored to TCP congestion control, aiming to enhance performance, robustness, and adaptability in dynamic network environments.

Recently, several variants of second-order sliding mode controllers have been proposed for diverse applications in TCP tracking control. For example, ref. [7] introduces a family of nonlinear controllers exhibiting fixed-time convergence. In the context of second-order TCP tracking systems, modifications of the second-order finite-time nested controller have been developed to allow adjustment of the closed-loop system’s settling time [2]. Although these approaches offer promising Lyapunov-based characterizations, the calculation of controller gains remains complex and challenging. The development of TCP tracking control methods within robust control frameworks continues to progress, offering significant improvements in achieving high-precision trajectory tracking while maintaining robustness in the presence of disturbances and uncertainties. In this paper, we introduce a novel nonlinear control strategy for TCP systems subject to disturbances. The sliding variable is designed using ${\mathcal{K}}_1$-type functions to ensure finite-time convergence of the system state to the origin. This ${\mathcal{K}}_1$-based sliding mode design not only guarantees finite-time stability but also enhances robustness against mismatched perturbations—an important feature for TCP systems where the first integrator is influenced by capacity constraints. This approach was recently presented in the Automatica journal [8,9], and here we extend it to address the tracking problem while rejecting perturbations in TCP systems. Furthermore, we propose alternative sliding surface design techniques inspired by this methodology. We also present a continuous version of the proposed controller and prove that the resulting closed-loop system satisfies the input-to-state stability (ISS) property, ensuring robust performance under dynamic disturbances. The main contributions and novelties of this work are as follows:

• Unlike existing TCP tracking controllers [1,2,3], we propose a simple nonlinear controller defined by only three parameters, significantly simplifying implementation without sacrificing performance.
• Singularities in the closed-loop system are avoided without the need for switching control laws or intricate sliding surface designs, representing a significant improvement over existing predefined-time controllers for second-order systems.
• Our controller design framework enables the development of a wide class of robust controllers for second-order systems, guaranteeing finite-time stability.
• We also present a continuous version of the proposed controller and establish the input-to-state stability (ISS) of the resulting closed-loop system, thereby ensuring robustness and stability under perturbations.

2. Related Work

Congestion control in transmission control protocol (TCP) networks has motivated extensive research on Active Queue Management (AQM) as a means to regulate queue lengths, reduce packet loss, and improve fairness. Early control-theoretic studies such as [10] modeled AQM as a feedback control problem, demonstrating how control principles can stabilize queue dynamics and enhance throughput. A broad survey in [11] further summarized advances in AQM-based TCP congestion control, identifying key challenges in terms of stability, responsiveness, and fairness under diverse network scenarios.

Robust control methodologies have been widely investigated to address uncertainties and time-varying network conditions. A variable structure control strategy for AQM with Explicit Congestion Notification (ECN) was introduced in [12], offering robustness against disturbances and system variations. Similarly, ref. [13] proposed robust AQM controllers for TCP networks, ensuring stability under parameter uncertainties. More recently, hybrid and adaptive methods have gained attention: ref. [14] presented a robust PID and recursive least squares (RLS) controller for TCP/AQM systems, while ref. [15] focused on an analytical design of proportional–integral AQM controllers with explicit stability criteria, offering improved guarantees of stability and performance.

Recent works have also examined AQM in specialized or heterogeneous environments. For instance, ref. [16] explored controlling TCP socket queueing delay to improve performance at the end-host level. In satellite communications, ref. [17] evaluated congestion control algorithms combined with traffic control policies in a Performance Enhancing Proxy (PEP)-based geosynchronous satellite scenario, highlighting the importance of AQM mechanisms tailored for high-latency links.

Parallel to robust and analytical designs, data-driven and artificial intelligence (AI) methods are being integrated into congestion control [18] compared traditional AQM with AI-enhanced strategies, showing that learning-based approaches can improve adaptability, congestion prediction, and decision-making. Complementing these developments, ref. [19] investigated queueing network topology inference using passive and active measurements, providing insights into how measurement-based intelligence can support congestion management in complex network topologies.

Overall, the literature illustrates a clear evolution of AQM research: from early control-theoretic modeling [10], through robust and adaptive controller design [12,13,14,15], to the integration of AI and data-driven techniques [18,19]. These complementary approaches reflect the ongoing effort to achieve stability, robustness, and adaptability in TCP congestion control across diverse networking environments. The related work section is comprehensive, yet a clearer positioning of this paper’s novelty compared to adaptive and AI-based TCP control approaches is needed. Several studies have addressed congestion control in TCP/AQM systems using adaptive and learning-based methods [20,21,22,23,24,25,26]. These approaches include adaptive finite-time sliding mode control [20], neural adaptive terminal sliding mode control [21], adaptive congestion tracking with input saturation [22], and funnel-based neural control [23,24]. Other works explore adaptive integral backstepping [25] and neuro-fuzzy control strategies [26]. Our contribution differs by introducing a novel ${\mathcal{K}}_1$-type sliding surface and developing both discontinuous and continuous sliding mode controllers. This ensures finite-time stability with low computational complexity and high scalability for large-scale TCP/IP networks, without requiring online optimization or extensive parameter tuning.

Recent research has also emphasized robust and finite-time control approaches for AQM, aiming to ensure stability and performance under uncertainties and time-varying network conditions. Robust control designs guarantee resilience against modeling errors and disturbances [12,13,14,15], while finite-time control strategies ensure that system states reach desired conditions within a prescribed time, improving responsiveness in congestion scenarios. Continuous-time control frameworks have been widely adopted for AQM due to their ability to model the natural dynamics of TCP systems and to facilitate rigorous stability analysis [10,11], making them a foundational tool for both theoretical developments and practical implementations.

Notation

Let a be a positive real number and x be a real number. In general, we use the notation ${⌈x⌋}^a$ with $a\in \mathbb{Q}$, which can be defined as follows:

$${⌈x⌋}^a={\left|x\right|}^{a}sgn\left(x\right).$$

For the special case where $a=0$, we have

$$sgn\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{x}{\left|x\right|}},\hfill & \mathrm{if}x\ne 0,\hfill \\ 0,\hfill & \mathrm{if}x=0.\hfill \end{array}\right.$$

We denote $sgn\left(x\right)$ as ${⌈x⌋}^0$. The derivative of ${⌈x⌋}^a$ with respect to x is given by

$${\displaystyle \frac{d{⌈x⌋}^a}{dx}}=a{\left|x\right|}^{a-1}.$$

Class ${\mathcal{K}}_1$ functions are strictly increasing, continuously differentiable functions that vanish at zero.

3. System Model

In this section, we describe the dynamic model of a TCP network, which is a nonlinear system that captures the network’s behavior over time. This model is used to understand the interactions between the various system parameters, such as the TCP receive window size, queue length, network capacity, and disturbances. The system’s dynamics can be expressed by the following equations [27]:

$$\begin{array}{cc}\hfill \dot{w}\left(t\right)& =d\left(t\right)+u\left(t\right),\hfill \\ \hfill \dot{q}\left(t\right)& ={\displaystyle \frac{\mathcal{N}\left(t\right)}{r\left(t\right)}}w\left(t\right)-\mathcal{C}\left(t\right),\hfill \\ \hfill r\left(t\right)& ={\displaystyle \frac{q\left(t\right)}{\mathcal{C}\left(t\right)}}+T_p,\hfill \end{array}$$

(1)

where the terms are defined as follows:

• $w\left(t\right)$: The TCP receive window size, which defines the amount of data that can be sent over the network. It is a dynamic parameter that regulates the sending and receiving of data to ensure stable network operation.
• $q\left(t\right)$: The number of packets in the system, also referred to as the queue length in the router.
• $u\left(t\right)$: The control input to the system, which influences the system’s behavior.
• $d\left(t\right)$: Disturbances or external factors affecting the system’s performance, such as network congestion or packet loss.
• $\mathcal{N}\left(t\right)$: The number of TCP connections active in the system at time t.
• $r\left(t\right)$: The signal propagation delay, which is the time it takes for data to travel from the sender to the receiver.
• $T_p$: The round-trip time (RTT) of the system, which accounts for the total delay, including both the sending and receiving times.
• $\mathcal{C}\left(t\right)$: The available link capacity, which limits the rate at which data can be sent through the network.

The rate of TCP source $\gamma \left(t\right)$ can be defined based on the window size and signal propagation delay as follows, inspired by the work of Ariba et al. [27]:

$$\begin{array}{c}\hfill \gamma \left(t\right)={\displaystyle \frac{w\left(t\right)}{r\left(t\right)}}\end{array}$$

(2)

The derivative of this rate with respect to time is given by

$$\begin{array}{c}\hfill \dot{\gamma }\left(t\right)={\displaystyle \frac{\dot{w}\left(t\right)r\left(t\right)-w\left(t\right)\dot{r}\left(t\right)}{r^2\left(t\right)}}\end{array}$$

(3)

Using the system model Equations (1), we can express the relationship between the network variables in the following manner:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{q}\left(t\right)=\mathcal{N}\left(t\right)\gamma \left(t\right)-\mathcal{C}\left(t\right)\hfill \\ \dot{\gamma }\left(t\right)={\displaystyle \frac{1}{q\left(t\right)+T_p\mathcal{C}\left(t\right)}}\left[\mathcal{C}\left(t\right)-\mathcal{N}\left(t\right){\gamma }^2\left(t\right)+\mathcal{C}\left(t\right)u\left(t\right)+\mathcal{C}\left(t\right)d\left(t\right)\right]\hfill \end{array}\right.\end{array}$$

(4)

For simplicity, we introduce new state variables: let $x_1\left(t\right)=q\left(t\right)$ and $x_2\left(t\right)=\gamma \left(t\right)$, where $x_1\left(t\right)$ represents the queue length and $x_2\left(t\right)$ represents the TCP rate. The system then becomes

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_1\left(t\right)=\mathcal{N}\left(t\right)x_2\left(t\right)-\mathcal{C}\left(t\right)\hfill \\ {\dot{x}}_2\left(t\right)=f\left(x\left(t\right)\right)+g\left(x\left(t\right)\right)u\left(t\right)+g\left(x\left(t\right)\right)d\left(t\right)\hfill \\ y\left(t\right)=x_1\left(t\right)\hfill \end{array}\right.\end{array}$$

(5)

Here, $x\left(t\right)={\left(x_1{x}_2\right)}^{\top }\in {\mathbb{R}}^2$ is the state vector of the system and $y\left(t\right)$ is the system’s output, which represents the queue length $x_1\left(t\right)$. The functions $f\left(x\right(t\left)\right)$ and $g\left(x\right(t\left)\right)$ are nonlinear functions of the state, defined as follows:

$$f\left(x\left(t\right)\right)={\displaystyle \frac{1}{x_1\left(t\right)+T_p\mathcal{C}\left(t\right)}}\left(x_1\left(t\right)\mathcal{C}\left(t\right)-\mathcal{N}\left(t\right)x_2^2\left(t\right)\right)$$

and

$$g\left(x\left(t\right)\right)={\displaystyle \frac{\mathcal{C}\left(t\right)}{x_1\left(t\right)+T_p\mathcal{C}\left(t\right)}}$$

Assumption 1.

We assume that the perturbation term in the system (5), i.e., $g\left(x\right(t\left)\right)d\left(t\right)$, is bounded by some constant Δ, such that $\left|g\right(x\left(t\right)\left)d\right(t\left)\right|<\Delta$. This assumption ensures that the disturbances do not grow unbounded and are manageable by the system.

The control objective in this model is twofold:

• The queue length $x_1\left(t\right)$ should follow a reference value $q_{\mathrm{ref}}\left(t\right)$; that is, we aim to drive $x_1\left(t\right)\to q_{\mathrm{ref}}$.
• The system must reject both matched perturbations (those proportional to $g\left(x\right(t\left)\right)d\left(t\right)$) and mismatched perturbations (those associated with $\mathcal{C}\left(t\right)$).

To track the queue length, we define the tracking error as follows.

$$\begin{array}{c}\hfill e\left(t\right)=x_1\left(t\right)-q_{\mathrm{ref}}\left(t\right),\end{array}$$

(6)

where $e\left(t\right)$ represents the deviation of the queue length from its reference value. The derivative of the tracking error is given by

$$\begin{array}{c}\hfill \dot{e}\left(t\right)=\mathcal{N}\left(t\right)x_2\left(t\right)-\mathcal{C}\left(t\right)-{\dot{q}}_{\mathrm{ref}}\left(t\right),\end{array}$$

(7)

where ${\dot{q}}_{\mathrm{ref}}\left(t\right)$ is the time derivative of the length of the reference queue. The control design will focus on minimizing this tracking error while rejecting disturbances $g\left(x\right(t\left)\right)d\left(t\right)$ and ensuring robustness against disturbances related to the network capacity $\mathcal{C}\left(t\right)$.

This model and control strategy offer a powerful framework for understanding and managing the dynamic behavior of TCP networks under varying conditions, with practical applications to optimize network throughput and stability.

In this paper, the following problem is considered.

Control Problem

The primary objective of this paper is to design a feedback control law:

$$u\left(t\right)=\kappa \left(s\right(t\left)\right),$$

(8)

where s denotes a sliding surface such that, for all initial conditions $x_0\in D_0$, the tracking error $e\left(t\right)$ converges to zero within a finite time T, despite the presence of uncertainties. Here, T denotes the settling time of the system.

Problem 1.

The key challenge is to ensure the global finite-time stability of the origin as an equilibrium point of the normal form (5), while maintaining robustness against uncertainties. Addressing this problem is essential for achieving the overarching control objective: stabilizing the origin of the controlled system (5) as an asymptotically stable equilibrium point, regardless of uncertainties.

Within the framework of classical sliding mode control, the system output $y\left(t\right)$ is referred to as the sliding variable, and the feedback control law $\kappa \left(s\right)$ is typically designed as a linear combination of the system states.

4. Preliminaries

We consider a dynamical system described by

$$\dot{x}=f(t,x),t\ge 0,x\left(0\right)=x_0,$$

(9)

where x is an n-dimensional state vector, residing in ${\mathbb{R}}^n$. The function $f:{\mathbb{R}}_{\ge 0}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ is presumed to be locally bounded uniformly with respect to time. When f is locally measurable but discontinuous with respect to x, solutions are interpreted under the framework of Filippov [28]. Specifically, $x(t,x_0)$ is considered a valid solution if it is absolutely continuous and fulfills almost everywhere the set-valued differential equation

$$\dot{x}\in K\left[f\right](t,x)=co\bigcap _{\epsilon >0}\bigcap _{\mu \left(N\right)=0}f(t,B(x,\epsilon )\setminus N),$$

(10)

where $K\left[f\right](t,x)$ gives a compact, convex, upper semi-continuous map, $co$ indicates the convex hull operator, $B(x,\epsilon )$ defines a ball of radius $\epsilon$ about x in ${\mathbb{R}}^n$, and $\mu$ is the Lebesgue measure. The intersections span all zero-measure sets N and all positive epsilon values.

Definition 1

([29,30]). Suppose the origin represents an equilibrium point of the system (9). The system (9) is then classified as Globally Uniformly Finite-Time Stable (FTS) provided it possesses the following properties:

• Lyapunov Stability: A class-$\mathcal{K}$ function, α, exists such that the solution norm satisfies $\left|\right|x(t,x_0)\left|\right|\le \alpha \left(\right||x_0\left|\right|)$ for all $t\ge 0$ and any initial condition $x_0\in {\mathbb{R}}^n$.
• Finite-Time Attractiveness: A locally bounded function $T:{\mathbb{R}}^n\setminus \left\{0\right\}\to {\mathbb{R}}_{>0}$ is present such that the solution becomes zero for any $t>T\left(x_0\right)$, for all initial conditions $x_0\in {\mathbb{R}}^n$

Class ${\mathcal{K}}_1$ Functions

Drawing inspiration from the foundational work [31], the concept of class ${\mathcal{K}}_1$ functions are introduced, which play a crucial role in our subsequent analysis.

Definition 2

(Class ${\mathcal{K}}_1$ Functions). A continuous scalar function $\mathcal{H}:{\mathbb{R}}_{\ge 0}\to [0,1)$ is defined to be a member of the class ${\mathcal{K}}_1$, denoted $\mathcal{H}\in {\mathcal{K}}_1$, if it possesses the following properties:

• Strict Monotonicity: The function $\mathcal{H}$ is strictly monotonically increasing on its domain.
• Zero Initial Value: It satisfies the condition $\mathcal{H}\left(0\right)=0$.
• Asymptotic Limit: As its argument r approaches infinity, the function asymptotically approaches 1; i.e., ${lim}_{\sigma \to \infty }\mathcal{H}\left(\sigma \right)=1$.

Remark 1.

If a function $\mathcal{H}\in {\mathcal{K}}_1$ is also differentiable, we classify it as a differentiable class ${\mathcal{K}}_1$ function. In this case, there exists a positive function $\varpi :{\mathbb{R}}_{\ge 0}\to {\mathbb{R}}_{>0}$ such that the derivative of $\mathcal{H}$ is given by ${\mathcal{H}}^{\prime }\left(\sigma \right)=\varpi \left(\sigma \right)>0$. Consequently, $\mathcal{H}$ can be represented in an integral form as $\mathcal{H}\left(\sigma \right)={\int }_0^r\varpi \left(z\right)dz$. Since ${lim}_{\sigma \to \infty }\mathcal{H}\left(\sigma \right)=1$, the function ϖ must satisfy the normalization condition ${\int }_0^{\infty }\varpi \left(z\right)dz=1$. This allows us to interpret ϖ and $\mathcal{H}$ as a probability density function and a cumulative distribution function, respectively, for a positive random variable.

Proposition 1

([31]). Every function belonging to class ${\mathcal{K}}_1$ is inherently a bijective mapping, implying that it is both injective (one-to-one) and surjective (onto).

Proof. 

Consider a function $\mathcal{H}\in {\mathcal{K}}_1$. The injectivity of $\mathcal{H}$ is a direct consequence of its continuous and strictly monotonically increasing nature. Furthermore, since $\mathcal{H}\left(0\right)=0$ and given the continuity, strict monotonicity, and asymptotic limit ${lim}_{r\to \infty }\mathcal{H}\left(\sigma \right)=1$, its image is precisely the interval $[0,1)$, i.e., $\mathcal{H}\left({\mathbb{R}}_{\ge 0}\right)=[0,1)$, making the function surjective. As it is both injective and surjective, we conclude that $\mathcal{H}$ is a bijective function. □

The bijective nature of class ${\mathcal{K}}_1$ functions ensures that the inverse mapping exists, a property that is used in subsequent designs.

The following are examples that demonstrate a number of valid functions that satisfy the criteria for belonging to class ${\mathcal{K}}_1$.

Example 1.

Examples of valid class ${\mathcal{K}}_1$ functions are as follows:

• $\mathcal{H}\left(\sigma \right)=erf\left(\sigma \right)$;
• $\mathcal{H}\left(\sigma \right)=1-exp(-\sigma )$;
• $\mathcal{H}\left(\sigma \right)=tanh\left(\sigma \right)$;
• $\mathcal{H}\left(\sigma \right)={\displaystyle \frac{2}{\pi }}arctan\left(\sigma \right)$;
• $\mathcal{H}\left(\sigma \right)={\displaystyle \frac{\sigma }{\sigma +\alpha }}$, where $\alpha >0$;
• $\mathcal{H}\left(\sigma \right)=P(\alpha ,\sigma )={\displaystyle \frac{\gamma (\alpha ,\sigma )}{\Gamma \left(\alpha \right)}}$, with $\Gamma \left(\alpha \right)$ representing the gamma function defined as $\Gamma \left(\alpha \right)={\int }_0^{\infty }{t}^{\alpha -1}{e}^{-t}dt$ and $\gamma (\alpha ,\sigma )$ representing the incomplete gamma function, defined by $\gamma (\alpha ,\sigma )={\int }_0^{\sigma }{t}^{\alpha -1}{e}^{-t}dt$.
• $\mathcal{H}\left(\sigma \right)=I(\alpha ,\beta ,{\displaystyle \frac{\sigma }{\sigma +1}})$, where $\alpha >0$ and $\beta >0$. Here, $b(\alpha ,\beta ,\sigma )={\int }_0^r{t}^{\alpha -1}{(1-t)}^{\beta -1}dt$ and $I(\alpha ,\beta ,\sigma )={\displaystyle \frac{b(\alpha ,\beta ,r)}{B(\alpha ,\beta )}}$ denote the incomplete beta function and the regularized incomplete beta function, respectively. The beta function is denoted by $B(\alpha ,\beta )$ and these functions are defined for all $\sigma \in [0,1]$ [31].

5. Finite-Time Control Design for TCP System

Building upon prior work in [8,9], a family of sliding variables is introduced to design a controller for the TCP system that ensures finite-time stability of the closed-loop system, even under perturbations. The sliding variable $s\left(t\right)$ is defined as follows [8,9]:

$$\begin{array}{c}\hfill s\left(t\right)=\dot{e}\left(t\right)+{⌈{⌈\dot{e}\left(t\right)⌋}^a+\lambda \mathcal{H}\left(e\left(t\right)\right)⌋}^{{\displaystyle \frac{1}{a}}},\end{array}$$

(11)

where a and $\lambda$ are positive design parameters with the constraint that $a>1$. The function $\mathcal{H}\left(e\right)$ belongs to the class ${\mathcal{K}}_1$ and satisfies the following conditions:

$\mathcal{H}\left(0\right)=0,\mathcal{H}\left(e\right)>0\mathrm{for}e\ge 0,|{\mathcal{H}}^{\prime }\left(e\right)|\le {\mathcal{H}}^{+}\mathrm{for}\mathrm{all}e\in \mathbb{R},{\mathcal{H}}^{\prime }\left(0\right)>0,$ where ${\mathcal{H}}^{+}$ is a positive constant bounding the derivative of $\mathcal{H}\left(e\right)$. This sliding variable $s\left(t\right)$ combines a derivative term, a nonlinear term involving the sliding surface, and a damping term $\mathcal{H}\left(e\right(t\left)\right)$ that helps stabilize the system’s error dynamics.

The control input u is designed using the sliding variable $s\left(t\right)$ as follows:

$$\begin{array}{c}\hfill u\left(t\right)=-{\displaystyle \frac{1}{g\left(x\right(t\left)\right)}}\left(-\mathcal{N}{\ddot{q}}_{\mathrm{ref}}+f\left(x\left(t\right)\right)+K{\lceil s\left(t\right)\rfloor }^0\right),\end{array}$$

(12)

where $g\left(x\right)$ and $f\left(x\right)$ are system-dependent functions that satisfy certain stability conditions and K is a positive gain parameter to be determined based on the stability analysis.

Remark 2.

In Equation (12), the control input $u\left(t\right)$ consists of three main contributions: (i) $-\mathcal{N}{\ddot{q}}_{\mathrm{ref}}$ acts as a feedforward term to compensate for the desired reference acceleration; (ii) $f\left(x\right(t\left)\right)$ represents the system dynamics and nonlinearities to be canceled; and (iii) $K{\lceil s\left(t\right)\rfloor }^0$ is the discontinuous sliding control term ensuring finite-time convergence to the sliding surface and robustness against matched perturbations. The division by $g\left(x\right(t\left)\right)$ normalizes the control action according to the system’s gain structure.

The central result of this section is the following theorem, which guarantees the finite-time stability of the system under the proposed control law.

Theorem 1.

Consider the TCP system in the form of (5) with tracking error dynamics given by (6). Let the sliding variable $s\left(t\right)$ be defined as in (11), with parameters $a>1$, $\lambda >0$, and $\mathcal{H}:\mathbb{R}\to {\mathbb{R}}^{+}$ of class ${\mathcal{K}}_1$ satisfying

$$\mathcal{H}\left(0\right)=0,\mathcal{H}\left(e\right)>0\forall e\ne 0,|{\mathcal{H}}^{\prime }\left(e\right)|\le {\mathcal{H}}^{+},{\mathcal{H}}^{\prime }\left(0\right)>0.$$

Let $f\left(x\right)$ and $g\left(x\right)$ satisfy the conditions ensuring well-posedness and boundedness of the closed-loop system. If the control input is designed as in (12), and the control parameters satisfy

$$a>1,\lambda >0,K\ge {\displaystyle \frac{\lambda {\mathcal{H}}^{+}+a\Delta }{a}},$$

where $\Delta >0$ is a known bound on $|\dot{e}\left(t\right)|$, then the closed-loop system is Globally Uniformly Finite-Time Stable (GUFTS). That is, the tracking error $e\left(t\right)$ and its derivative $\dot{e}\left(t\right)$ converge to zero in finite time, and the settling time is bounded by

$$T\le {\displaystyle \frac{2V{\left(0\right)}^{1/2}}{\eta }},\eta =K-{\displaystyle \frac{\lambda {\mathcal{H}}^{+}+a\Delta }{a}}>0.$$

Proof. 

Consider the Lyapunov candidate function

$$V\left(t\right)={\displaystyle \frac{1}{2}}{s}^2\left(t\right),$$

where $s\left(t\right)$ is the sliding variable defined in (11). Clearly, $V\left(t\right)\ge 0$ and $V\left(t\right)=0$ if and only if $s\left(t\right)=0$.

Differentiating $V\left(t\right)$ gives

$$\dot{V}\left(t\right)=s\left(t\right)\dot{s}\left(t\right).$$

From (11), we have

$$s\left(t\right)=\dot{e}\left(t\right)+{⌈{⌈\dot{e}\left(t\right)⌋}^a+\lambda \mathcal{H}\left(e\left(t\right)\right)⌋}^{{\displaystyle \frac{1}{a}}}.$$

Differentiating yields

$$\dot{s}\left(t\right)=\ddot{e}\left(t\right)+{\displaystyle \frac{1}{a}}{⌈\dot{e}\left(t\right)⌋}^{a-1}\ddot{e}\left(t\right)+{\displaystyle \frac{\lambda }{a}}{\mathcal{H}}^{\prime }\left(e\left(t\right)\right)\dot{e}\left(t\right).$$

From the tracking error dynamics (6) and the control law (12),

$$\ddot{e}\left(t\right)=f\left(x\left(t\right)\right)+g\left(x\left(t\right)\right)u\left(t\right)-{\ddot{q}}_{\mathrm{ref}}.$$

Substituting $u\left(t\right)$ from (12) gives

$$\ddot{e}\left(t\right)=-K{⌈s\left(t\right)⌋}^0.$$

Thus,

$$\dot{s}\left(t\right)=-K{⌈s\left(t\right)⌋}^0-{\displaystyle \frac{K}{a}}{⌈\dot{e}\left(t\right)⌋}^{a-1}{⌈s\left(t\right)⌋}^0+{\displaystyle \frac{\lambda }{a}}{\mathcal{H}}^{\prime }\left(e\left(t\right)\right)\dot{e}\left(t\right).$$

Substituting into $\dot{V}\left(t\right)$ yields

$$\dot{V}\left(t\right)=-K\left|s\left(t\right)\right|-{\displaystyle \frac{K}{a}}{⌈\dot{e}\left(t\right)⌋}^{a-1}\left|s\left(t\right)\right|+{\displaystyle \frac{\lambda }{a}}{\mathcal{H}}^{\prime }\left(e\left(t\right)\right)\dot{e}\left(t\right)s\left(t\right).$$

Applying the bound $|{\mathcal{H}}^{\prime }\left(e\right)|\le {\mathcal{H}}^{+}$ and $|\dot{e}\left(t\right)|\le \Delta$,

$$\dot{V}\left(t\right)\le -K\left|s\left(t\right)\right|+{\displaystyle \frac{\lambda }{a}}{\mathcal{H}}^{+}\Delta \left|s\left(t\right)\right|.$$

Define

$$\eta :=K-{\displaystyle \frac{\lambda {\mathcal{H}}^{+}+a\Delta }{a}}.$$

The parameter condition $K\ge {\displaystyle \frac{\lambda {\mathcal{H}}^{+}+a\Delta }{a}}$ ensures $\eta >0$; hence,

$$\dot{V}\left(t\right)\le -\eta \left|s\left(t\right)\right|.$$

Since $\left|s\left(t\right)\right|=\sqrt{2V\left(t\right)}$, it follows that

$$\dot{V}\left(t\right)\le -\eta \sqrt{2V\left(t\right)}.$$

Integrating this differential inequality yields finite-time convergence:

$$V\left(t\right)=0,\forall t\ge T,$$

with the settling time bound

$$T\le {\displaystyle \frac{2V{\left(0\right)}^{1/2}}{\eta }}.$$

Thus, $s\left(t\right)\to 0$ in finite time. From $s\left(t\right)=0$ and (11), we have

$$\dot{e}\left(t\right)=-{⌈\lambda \mathcal{H}\left(e\right(t\left)\right)⌋}^{1/a}.$$

Since $\mathcal{H}\left(e\right)>0$ for $e\ne 0$ and $\mathcal{H}\left(0\right)=0$, $\dot{e}\left(t\right)$ drives $e\left(t\right)$ to zero in finite time. Thus, both $e\left(t\right)$ and $\dot{e}\left(t\right)$ converge to zero in finite time.

Therefore, the closed-loop system is Globally Uniformly Finite-Time Stable. □

The proposed finite-time control design ensures robustness and fast convergence for TCP systems. By introducing a simple nonlinear control law based on sliding mode techniques, we can guarantee that the system will stabilize in a finite amount of time. The conditions on the design parameters a, $\lambda$, and K are crucial for ensuring finite-time stability and avoiding unwanted oscillations or instability in the system.

The controller’s effectiveness is independent of external disturbances, which makes it particularly suitable for applications requiring robustness to perturbations. In conclusion, the finite-time control law presented here ensures fast convergence and robust performance in the presence of perturbations, making it an effective solution for TCP system control. Some guidelines are provided below in order to tune the parameters of controller (12).

• Select $\mathcal{H}\in {\mathcal{K}}_1$ satisfying system requirements.
• Define sliding variable $s\left(t\right)$ incorporating $\mathcal{H}\left(e\right(t\left)\right)$.
• Derive $\dot{s}\left(t\right)$ using system dynamics.
• Choose control law $u\left(t\right)$ to satisfy the sliding condition.
• Prove finite-time convergence using Lyapunov analysis.
• Tune parameters $(\lambda ,K,a)$ for desired performance.

6. Continuous Control Design for TCP System

Depending on the limitations of the system actuators, it is reasonable to consider a continuous version of the proposed discontinuous controller. The following theorem proposes a continuous version of the proposed control.

Theorem 2.

Consider the TCP system in the form of (5) with tracking error $e\left(t\right)=q\left(t\right)-q_{\mathrm{ref}}\left(t\right)$ and sliding variable $s\left(t\right)$ defined in (11). Assume the following:

1. 

The functions $f\left(x\right)$ and $g\left(x\right)$ are such that $g\left(x\right)$ is uniformly bounded away from zero; i.e., $0<g_{min}\le g\left(x\right)\le g_{max}$ for all x;

2. 

The perturbation/uncertainty term is bounded by $|\Delta (t\left)\right|\le \Delta$;

3. 

The function $\mathcal{H}(·)$ satisfies $\mathcal{H}\left(0\right)=0$, $|{\mathcal{H}}^{\prime }\left(e\right)|\le {\mathcal{H}}^{+}$ for all e, and $a>1,\lambda >0$.

Let the continuous control law be given by

$$\begin{array}{c}\hfill u\left(t\right)=-{\displaystyle \frac{1}{g\left(x\right(t\left)\right)}}\left(-\mathcal{N}{\ddot{q}}_{\mathrm{ref}}+f\left(x\left(t\right)\right)+k_1\mathrm{sat}(s\left(t\right)/\epsilon )\right),\end{array}$$

(13)

with gain $k_1>0$, saturation level $\epsilon >0$, and

$$\mathrm{sat}\left(\xi \right)=\left\{\begin{array}{cc}sign\left(\xi \right),\hfill & \left|\xi \right|>1,\hfill \\ \xi ,\hfill & \left|\xi \right|\le 1.\hfill \end{array}\right.$$

Suppose there exists a constant $c>0$ (depending on a and bounds on $\dot{e}$) such that

$$1+{\psi }_{\dot{e}}(e,\dot{e})\le c,\left|{\psi }_e(e,\dot{e})\right|\le {\displaystyle \frac{\lambda {\mathcal{H}}^{+}}{a}},$$

where $\psi (e,\dot{e}):={⌈{\lceil \dot{e}\rceil }^a+\lambda \mathcal{H}\left(e\right)⌋}^{1/a}-\dot{e}$ (as in the decomposition $s=\dot{e}+\psi$). If the gain $k_1$ satisfies

$$k_{1}c>c\Delta +{\displaystyle \frac{\lambda {\mathcal{H}}^{+}}{a}}\Delta ,$$

then the closed-loop system under (13) is input-to-state stable (ISS) with respect to the boundary layer parameter $\epsilon >0$. Moreover, the sliding variable $s\left(t\right)$ and the tracking error $e\left(t\right)$ converge to a neighborhood of the origin whose radius is $\mathcal{O}\left(\epsilon \right)$; specifically the Lyapunov function $V=\frac{1}{2}{s}^2$ satisfies the differential inequality

$$\dot{V}\le -\eta \sqrt{2V}+k_{1}c\epsilon ,$$

with $\eta :=k_{1}c-c\Delta -\frac{\lambda {\mathcal{H}}^{+}}{a}\Delta >0$. Hence the ultimate bound on $\left|s\right|$ is proportional to ε and can be made arbitrarily small by reducing ε.

Proof. 

Let the Lyapunov candidate be

$$V\left(t\right)=\frac{1}{2}{s}^2\left(t\right),$$

so $\left|s\right|=\sqrt{2V}$. Differentiate V:

$$\dot{V}=s\dot{s}.$$

From (11) write $s=\dot{e}+\psi (e,\dot{e})$ and differentiate:

$$\dot{s}=\ddot{e}+{\psi }_{\dot{e}}(e,\dot{e})\ddot{e}+{\psi }_e(e,\dot{e})\dot{e}.$$

By the tracking error dynamics and control law (13), we have (after canceling reference acceleration terms as in the derivation for (12))

$$\ddot{e}=-k_1\mathrm{sat}\left(\frac{s}{\epsilon }\right)+\Delta \left(t\right),$$

where $|\Delta (t\left)\right|\le \Delta$ captures model mismatch and perturbations.

Substitute $\ddot{e}$ into $\dot{s}$:

$$\dot{s}=-(1+{\psi }_{\dot{e}})k_1\mathrm{sat}\left(\frac{s}{\epsilon }\right)+(1+{\psi }_{\dot{e}})\Delta \left(t\right)+{\psi }_e\dot{e}.$$

Hence

$$\dot{V}=s\dot{s}=-(1+{\psi }_{\dot{e}})k_{1}s\mathrm{sat}\left(\frac{s}{\epsilon }\right)+(1+{\psi }_{\dot{e}})\Delta \left(t\right)s+{\psi }_e\dot{e}s.$$

We now use two bounds. First, for any $s\in \mathbb{R}$ and $\epsilon >0$

$$s\mathrm{sat}\left(\frac{s}{\epsilon }\right)\ge \left|s\right|-\epsilon .$$

(14)

(Indeed, if $\left|s\right|>\epsilon$ the left-hand side equals $\left|s\right|$; if $\left|s\right|\le \epsilon$ the left-hand side equals $s^2/\epsilon \ge 0$, while $\left|s\right|-\epsilon \le 0$.) Using (14) we obtain

$$-(1+{\psi }_{\dot{e}})k_{1}s\mathrm{sat}\left(\frac{s}{\epsilon }\right)\le -(1+{\psi }_{\dot{e}})k_1\left(\right|s|-\epsilon ).$$

Second, by hypothesis there exists $c>0$ such that $1+{\psi }_{\dot{e}}\le c$ and $|{\psi }_e|\le \frac{\lambda {\mathcal{H}}^{+}}{a}$. Also $|\Delta (t\left)\right|\le \Delta$ and $|\dot{e}|\le \Delta$ (use the assumed bound on the error derivative). Thus

$$(1+{\psi }_{\dot{e}})\Delta \left(t\right)s\le c\Delta \left|s\right|,{\psi }_e\dot{e}s\le {\displaystyle \frac{\lambda {\mathcal{H}}^{+}}{a}}\Delta \left|s\right|.$$

Collecting terms yields

$$\dot{V}\le -k_1(1+{\psi }_{\dot{e}})\left|s\right|+k_1(1+{\psi }_{\dot{e}})\epsilon +c\Delta \left|s\right|+{\displaystyle \frac{\lambda {\mathcal{H}}^{+}}{a}}\Delta \left|s\right|.$$

Using $1+{\psi }_{\dot{e}}\le c$ we further bound

$$\dot{V}\le -k_{1}c\left|s\right|+k_{1}c\epsilon +c\Delta \left|s\right|+{\displaystyle \frac{\lambda {\mathcal{H}}^{+}}{a}}\Delta \left|s\right|.$$

Rearranging yields

$$\dot{V}\le -\left(k_{1}c-c\Delta -{\displaystyle \frac{\lambda {\mathcal{H}}^{+}}{a}}\Delta \right)\left|s\right|+k_{1}c\epsilon .$$

Define

$$\eta :=k_{1}c-c\Delta -{\displaystyle \frac{\lambda {\mathcal{H}}^{+}}{a}}\Delta .$$

By the condition in the theorem, $\eta >0$. Since $\left|s\right|=\sqrt{2V}$ we obtain the differential inequality

$$\dot{V}\le -\eta \sqrt{2V}+k_{1}c\epsilon .$$

This inequality establishes ISS with respect to the input $\epsilon$: when V is large the negative term $-\eta \sqrt{2V}$ dominates, forcing V to decrease; in steady state the two terms balance and the ultimate value $V_{\infty }$ is determined by

$$\eta \sqrt{2V_{\infty }}\le k_{1}c\epsilon ⟹{\left|s\right|}_{\infty }\le {\displaystyle \frac{k_{1}c}{\eta }}\epsilon .$$

Therefore $s\left(t\right)$ converges to an $\mathcal{O}\left(\epsilon \right)$-neighborhood of zero and the tracking error $e\left(t\right)$ (through the relation enforced by s) converges to a neighborhood of the origin whose size scales with $\epsilon$. By decreasing $\epsilon$ the ultimate bound can be made arbitrarily small (at the price of increased control activity).

Hence the closed-loop system is ISS with respect to the boundary layer parameter $\epsilon$, which completes the proof. □

Remark 3.

• The continuous controller provides weaker stabilization compared to the sliding-mode controller, ensuring only input-to-state stability.
• Tuning$\epsilon$may require trial-and-error and offline computations.

Remark 4.

The proposed control approach is suitable for large-scale systems since it relies solely on analytical system equations without requiring online optimization or solving complex constraints. This significantly reduces computational complexity and makes the method inherently scalable. However, while the algorithmic simplicity is advantageous, a deeper analysis of computational cost in very large-scale or high-dimensional systems would strengthen the discussion, particularly regarding memory usage, communication overhead, and real-time implementation constraints.

7. Simulation Results

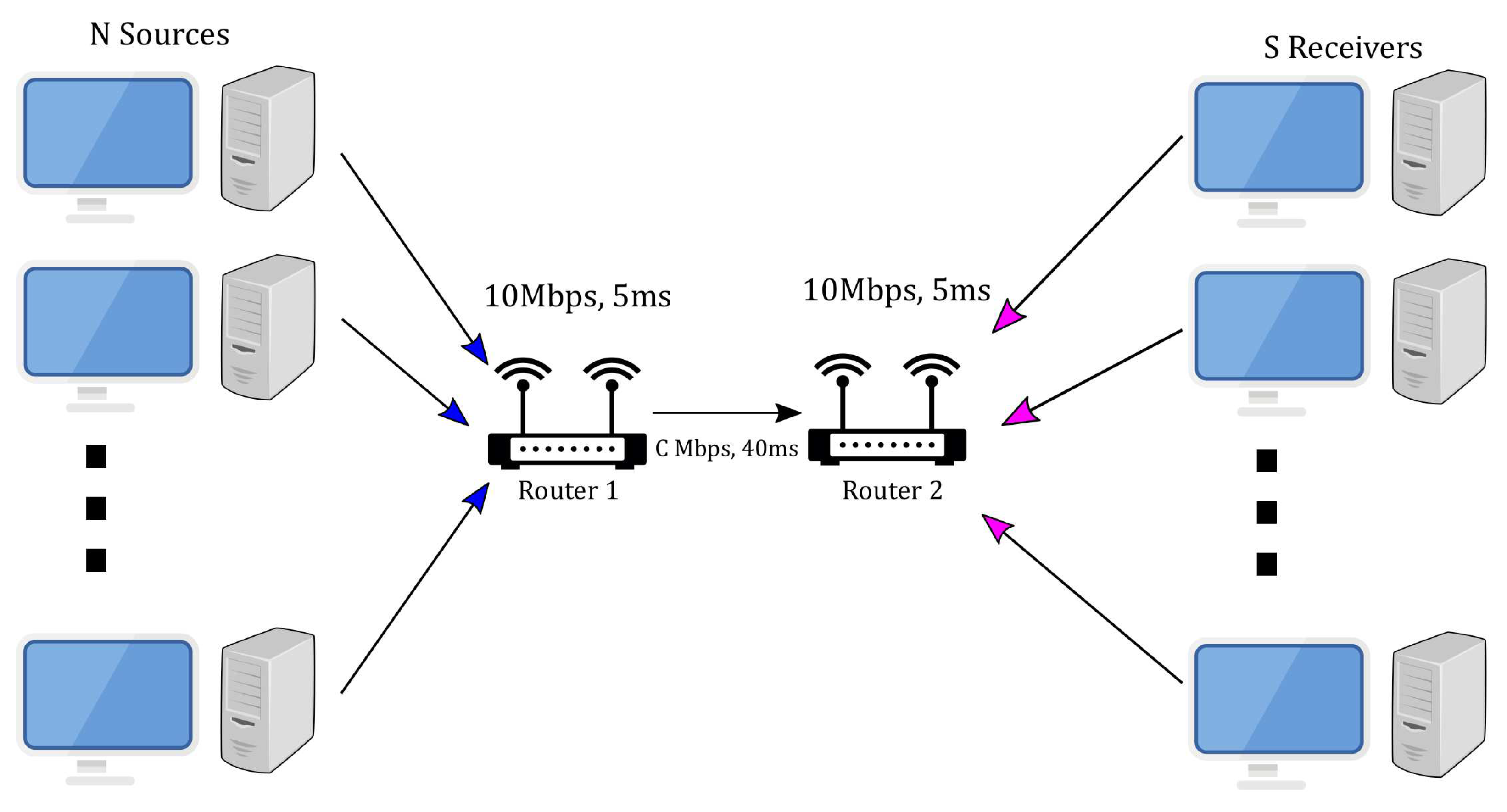
To assess the efficacy of the proposed active window management technique, we employ simulations using MATLAB. These simulations are conducted using a single-bottleneck dumbbell network topology, visualized in Figure 1. In this configuration, a bottleneck router serves as a shared resource for $\mathcal{N}$ concurrent TCP flow sessions. This allows us to evaluate the performance and robustness of the designed controllers under realistic network conditions. The developed control strategy and model are implemented in MATLAB, employing the Euler method with a time step of $T_s={10}^{-3}$ s. This numerical integration approach was chosen for its simplicity and efficiency in simulating the system dynamics while maintaining sufficient accuracy for the control design evaluation.

The parameters for our TCP/AWM network system, initially defined in (5), are configured as follows: We set the number of TCP flow sessions, $\mathcal{N}$, to 50. The bottleneck router’s capacity, $\mathcal{C}$, is specified at 1250 packets per second. The propagation delay, ${\mathcal{T}}_p$, is set to 0.15 s. The initial state, $x_0$, is chosen as the column vector ${[105,0]}^{\top }$. 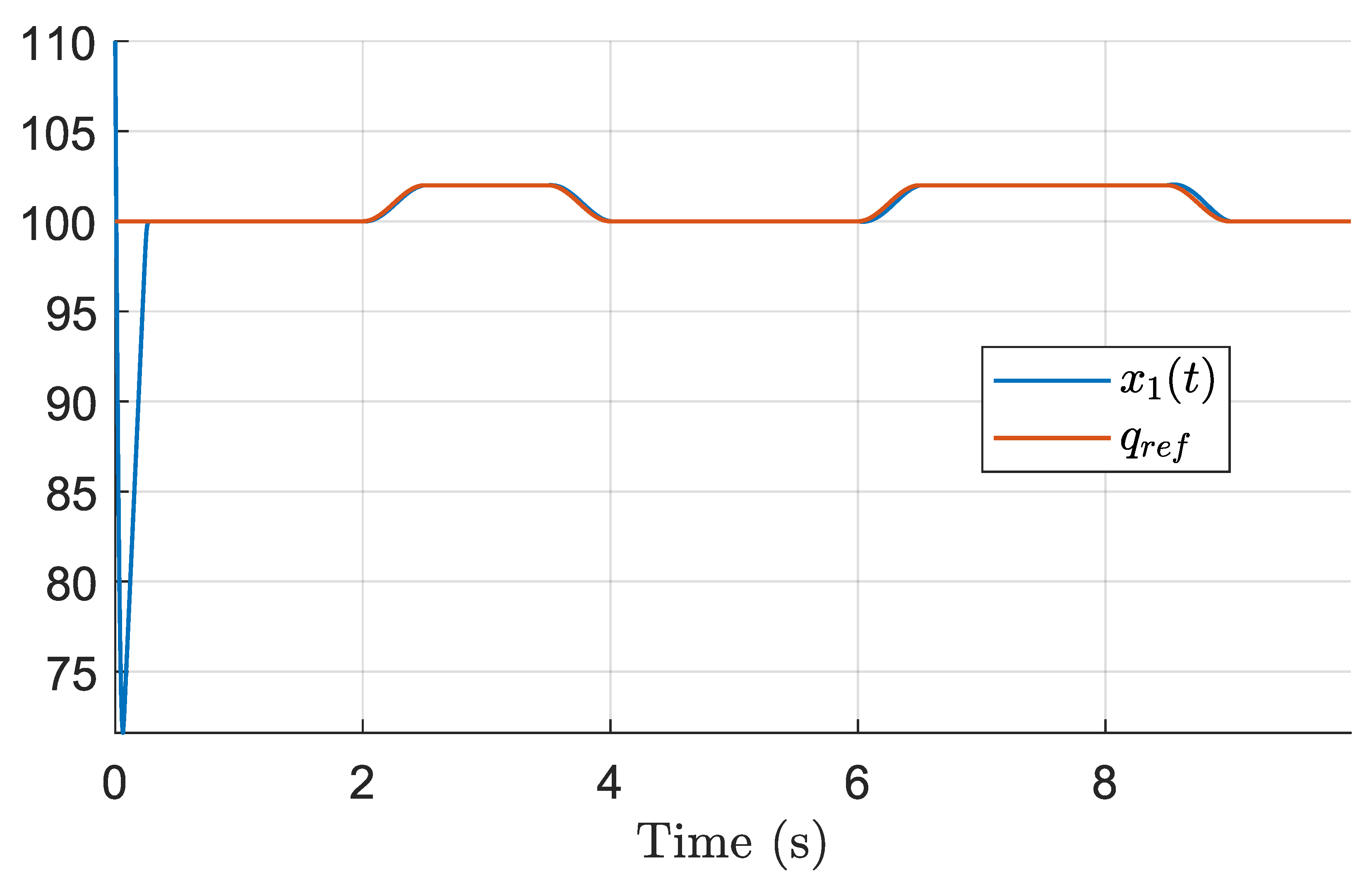A time-varying reference queue length, $q_{\mathrm{ref}}\left(t\right)$, is employed. This dynamic reference provides a testbed for the controller to demonstrate tracking capabilities under changing conditions.

The specific values for the control parameters are established as follows: $\lambda =70$, $a={\displaystyle \frac{11}{10}}$, and $K=200$. To further emulate the real-world complexities, an external disturbance is introduced into the simulation; this disturbance is defined as $d\left(t\right)=0.1sin\left(6t\right)+0.01cos\left(\pi t\right)+0.1$ packets per second. This component is employed to rigorously evaluate the controllers’ resilience to external influences.

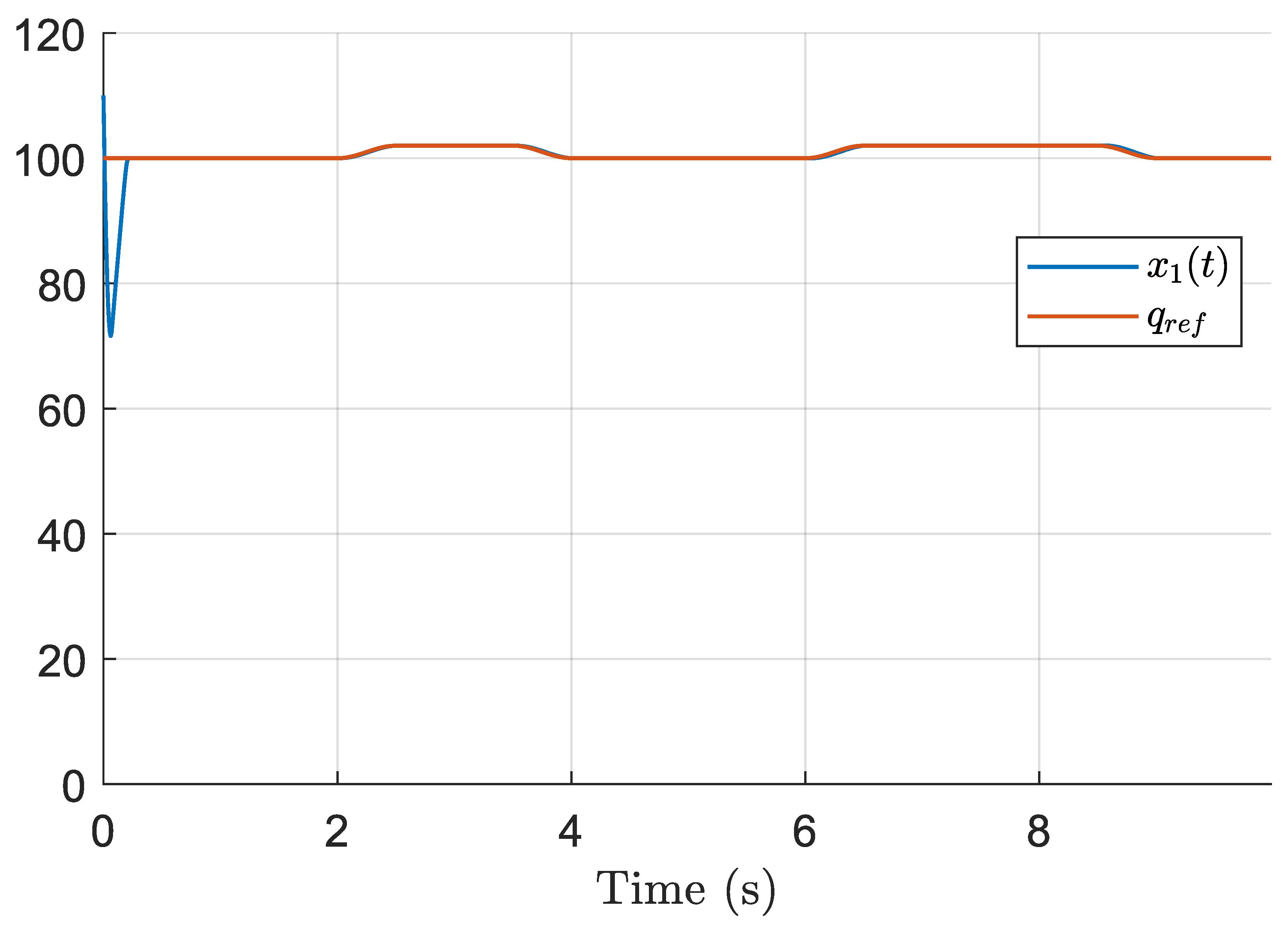
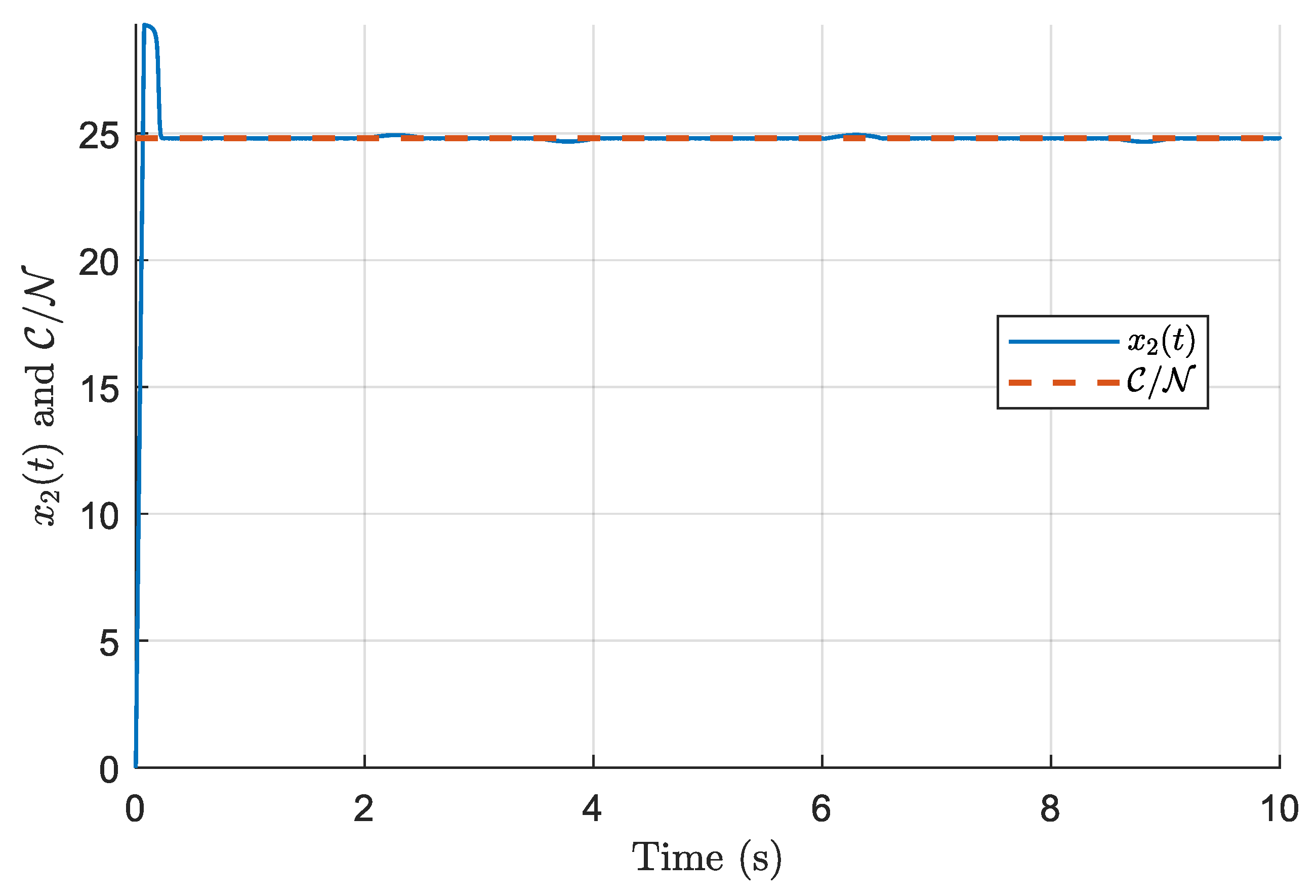
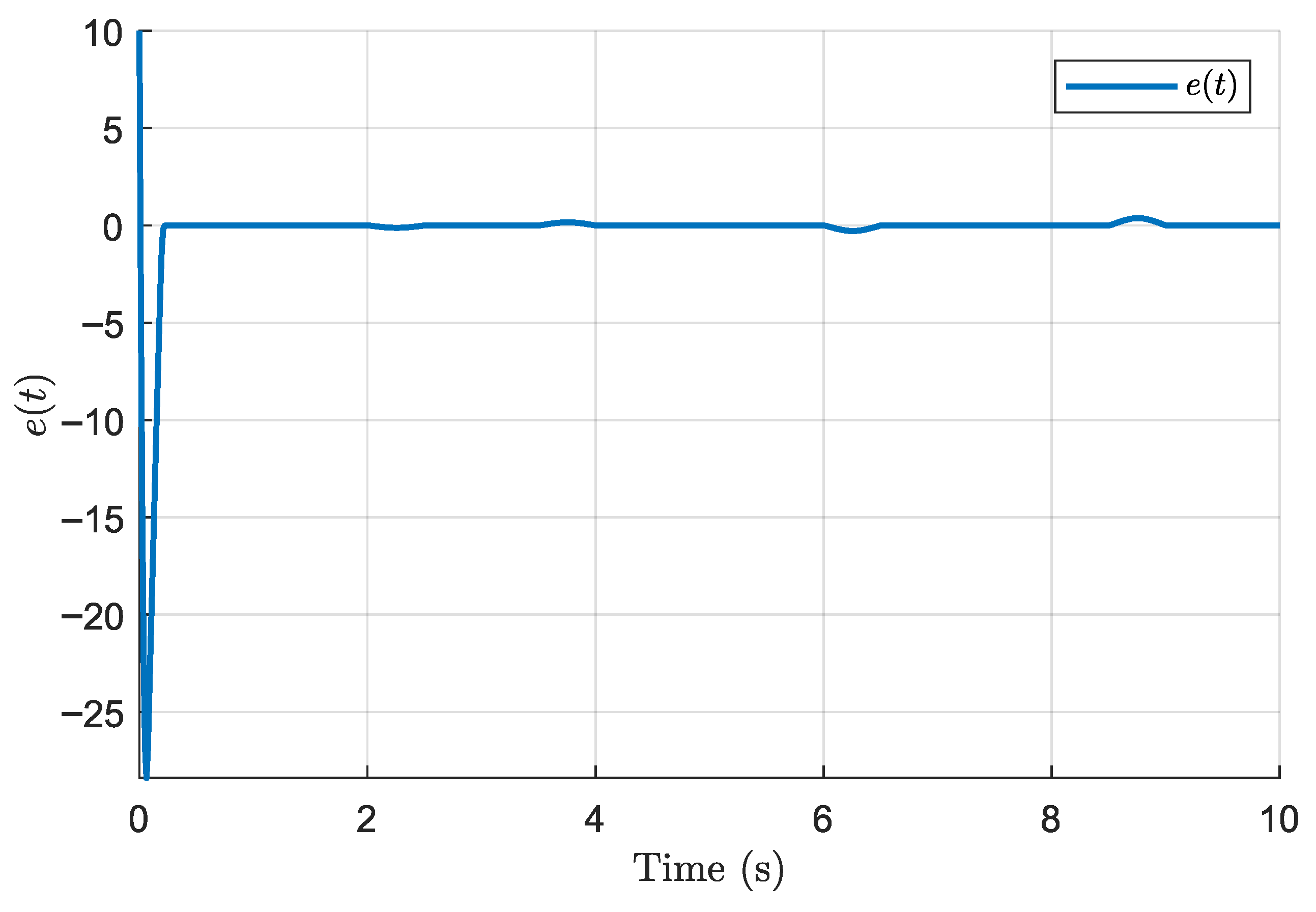
7.1. Finite-Time Discontinuous Controller (Theorem 1)

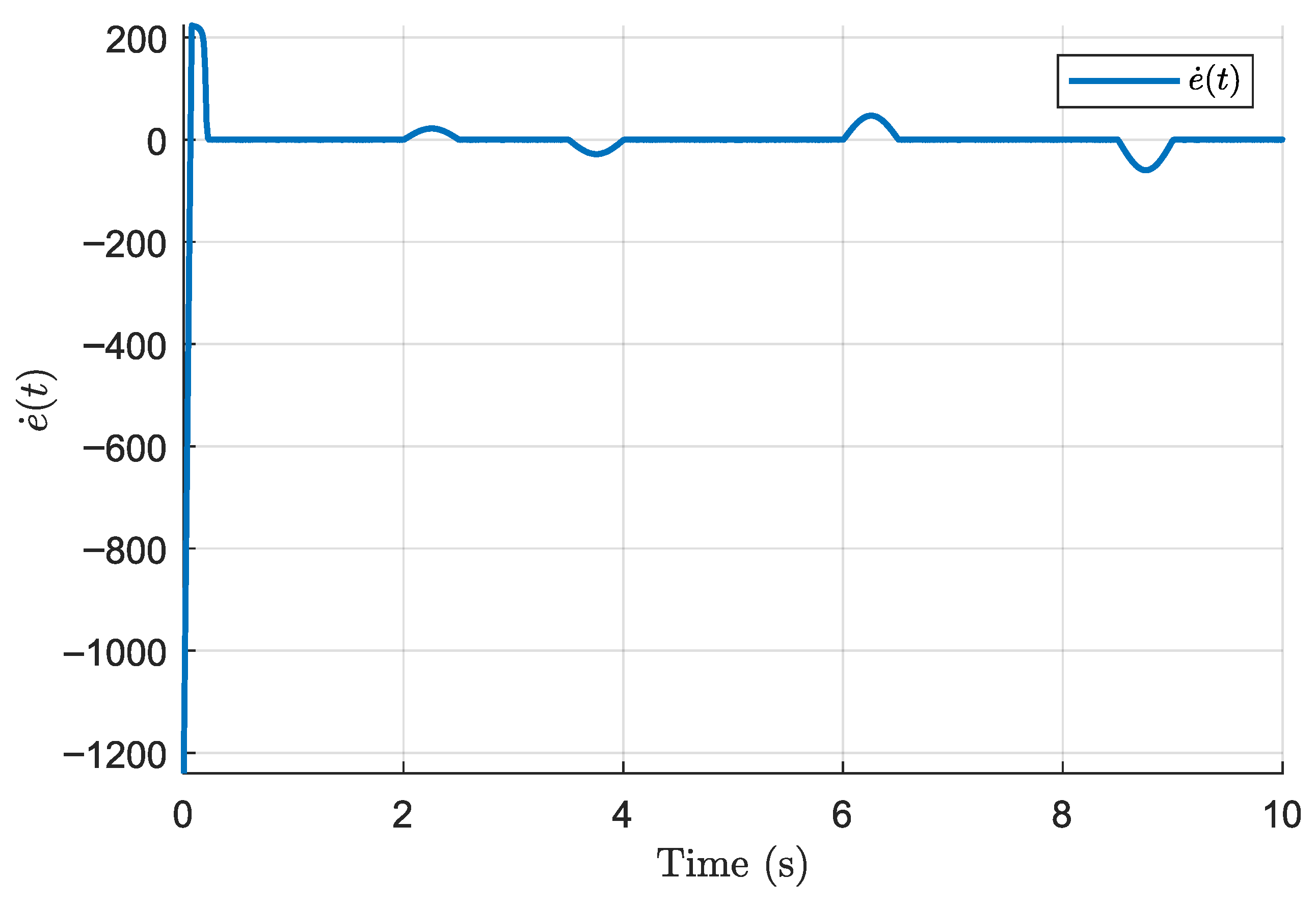
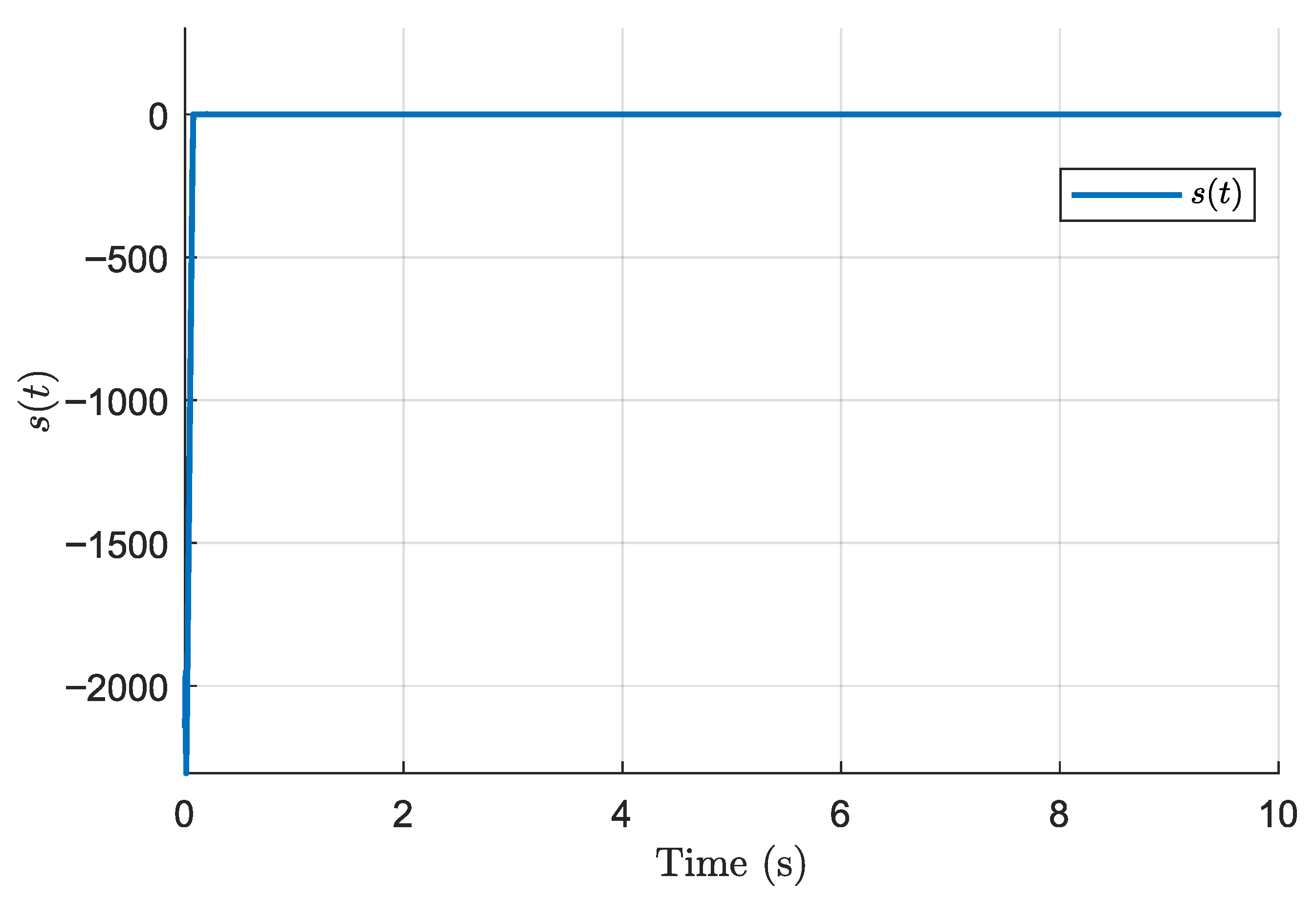
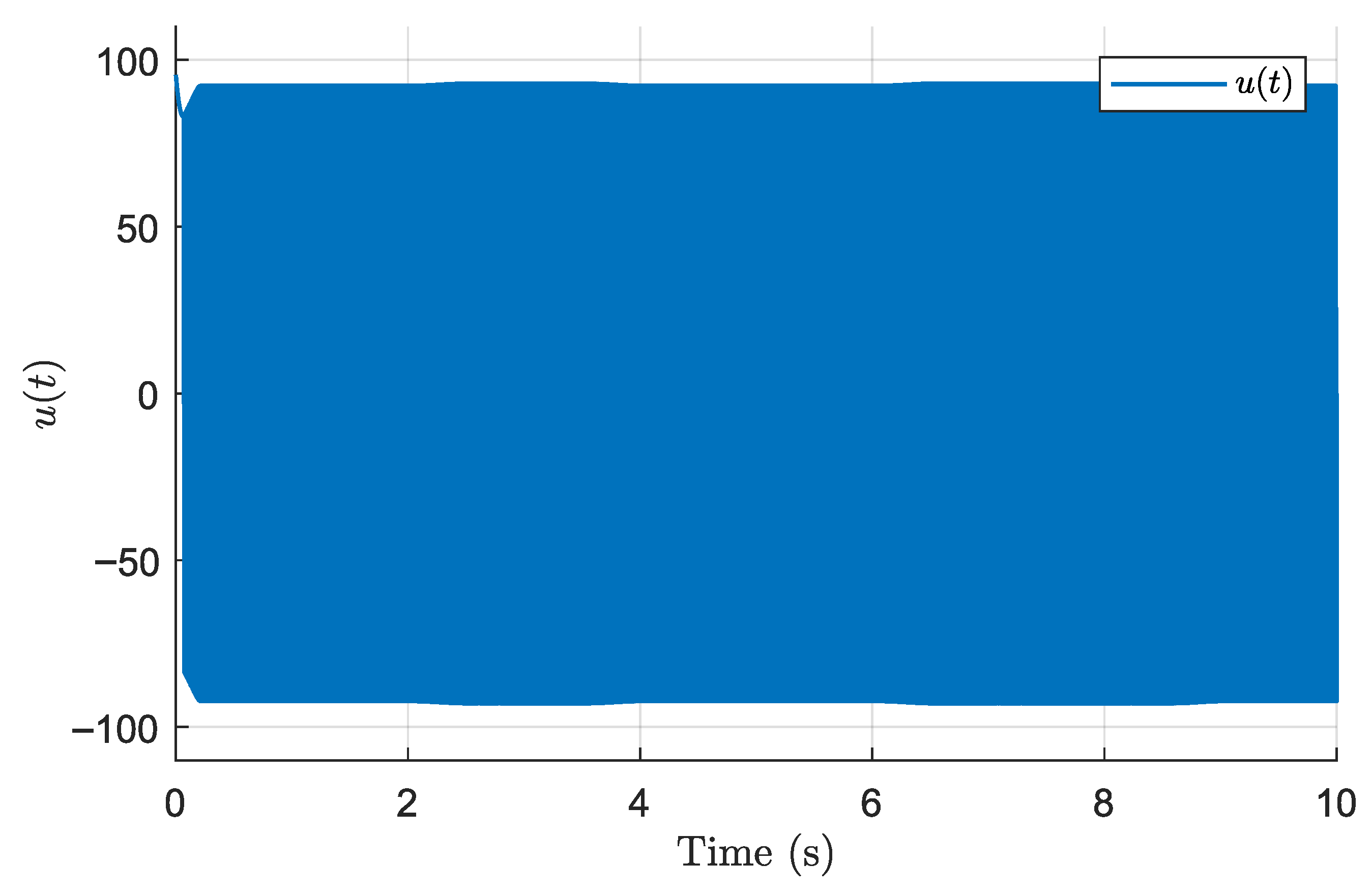
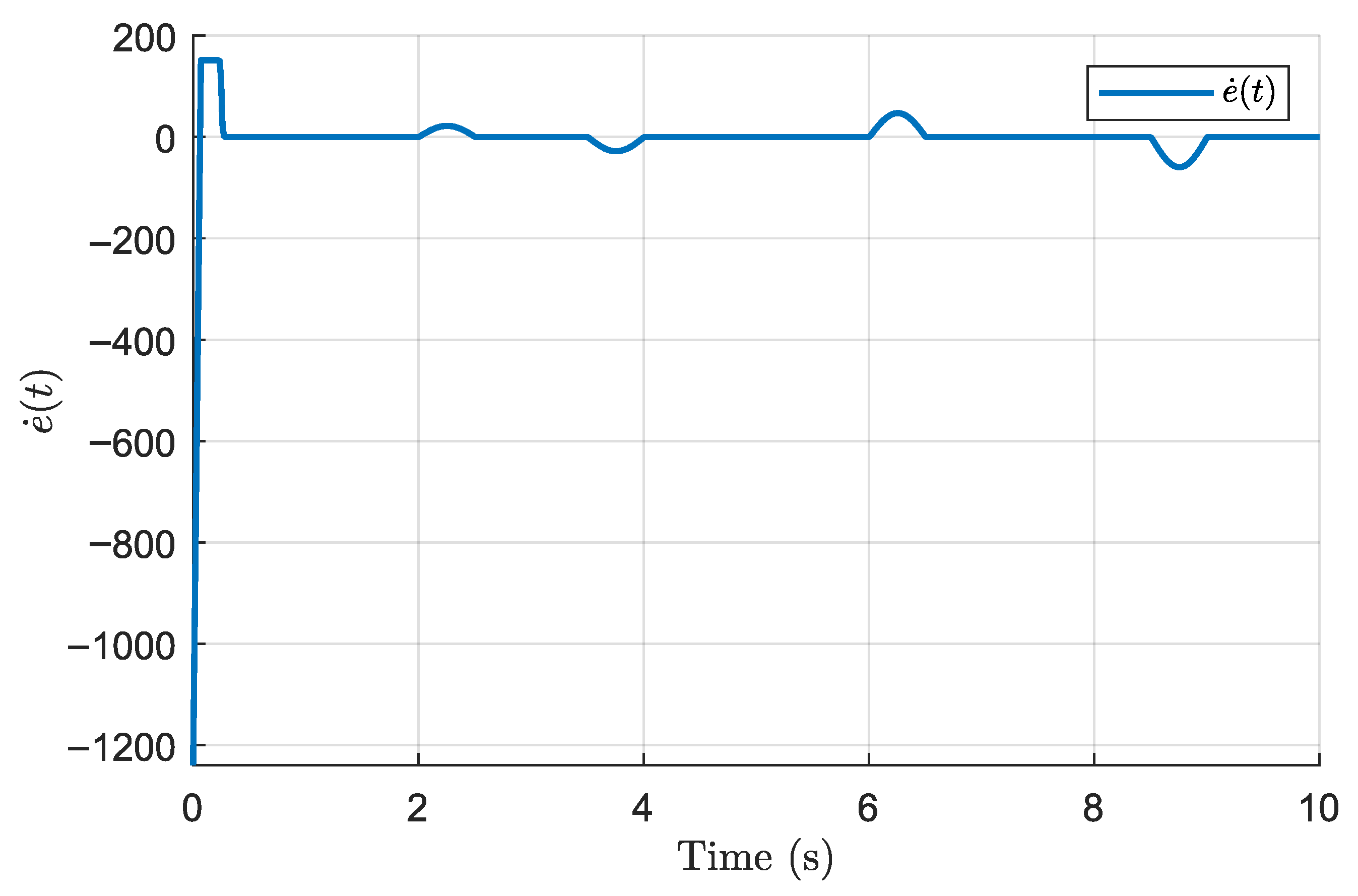
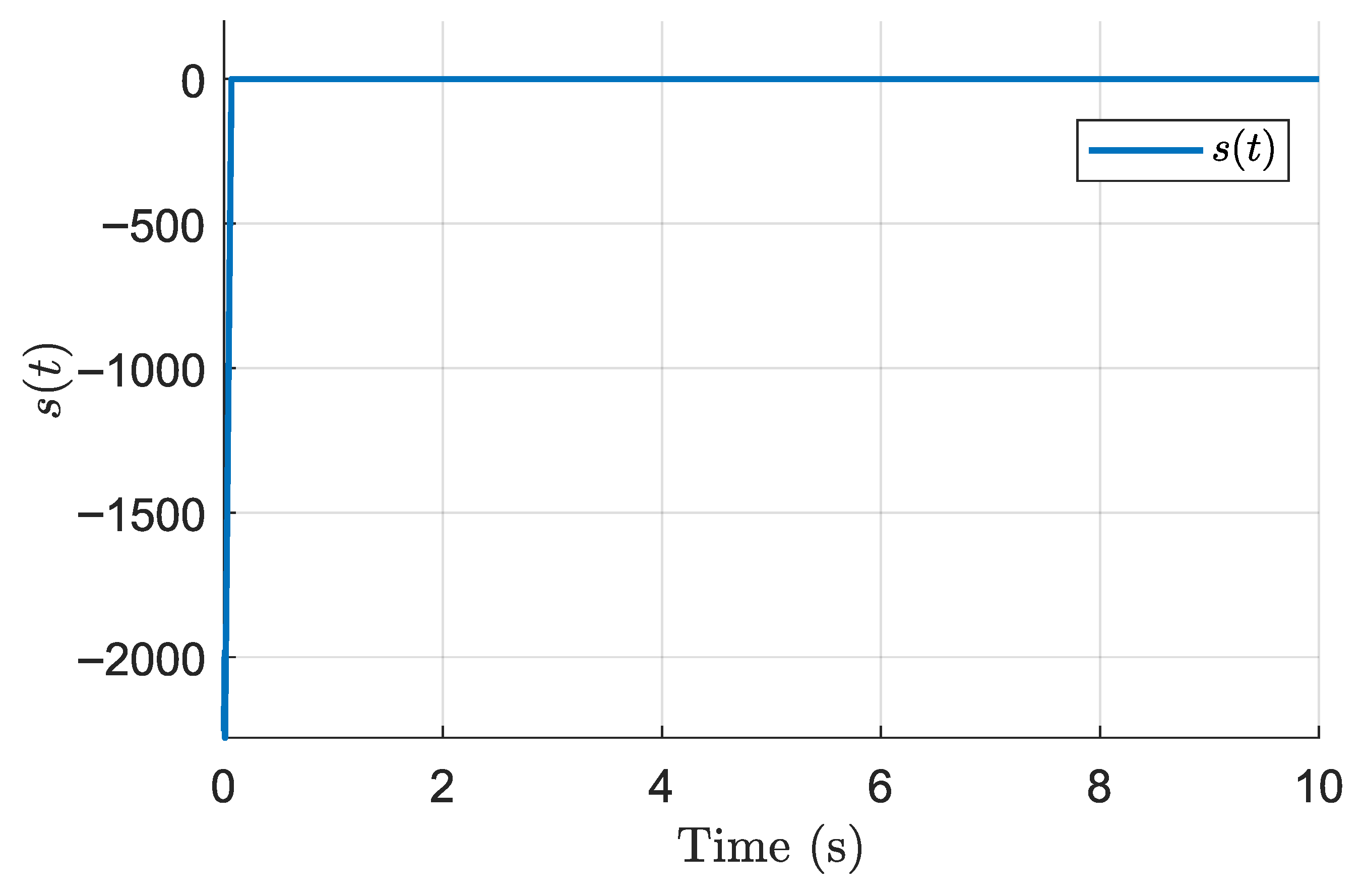
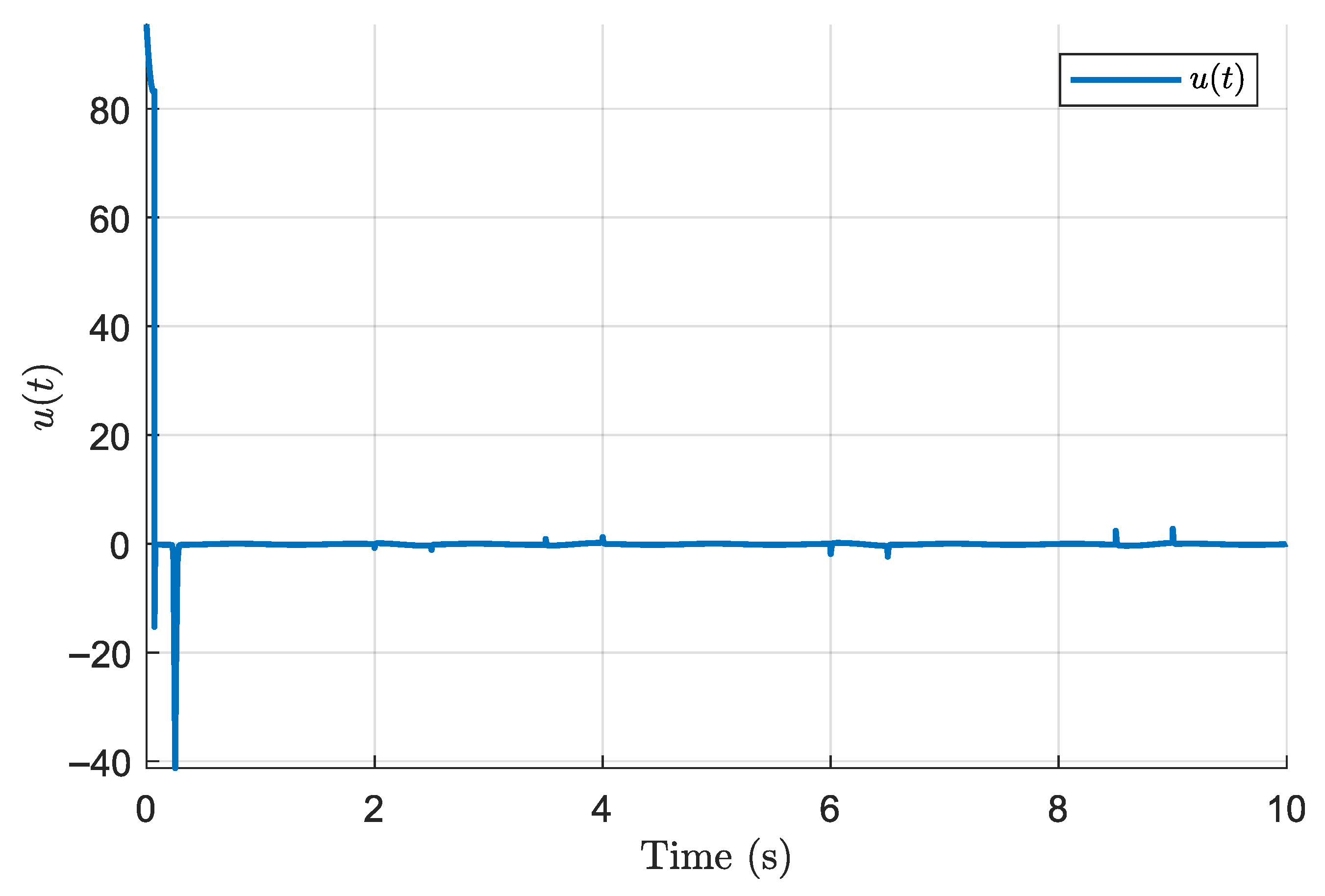
Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 illustrate the performance of the finite-time discontinuous controller derived from Theorem 1. This controller guarantees finite-time convergence of the tracking error and robustness to matched uncertainties. However, due to the discontinuous nature of the control law, some chattering is observed, which is a known effect of discontinuous sliding mode control.

7.2. Continuous Controller (Theorem 2)

Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 demonstrate the performance of the continuous controller derived from Theorem 2. The continuous control law ensures chatter reduction while still guaranteeing robust performance and input-to-state stability (ISS). Although the convergence rate is not strictly finite-time as in Theorem 1, this controller provides smoother control action and improved robustness against disturbances.

Compared to classical PID controllers, which generally cannot compensate effectively for the perturbations considered in this simulation, the proposed control schemes demonstrate superior robustness. In particular, the first controller achieves finite-time convergence, ensuring that congestion tracking errors vanish within a bounded time regardless of initial conditions, a property unattainable by standard PID designs. The second controller emphasizes smoothness, reducing abrupt control actions and enhancing practical implementability. For adaptive control approaches such as those in [20], while they can handle uncertainties, the control inputs often suffer from chattering phenomena that may degrade system performance and cause wear in actuators. Moreover, the simulation results presented here are informative, but they would be strengthened by explicit comparisons against baseline controllers such as classical PID or existing adaptive AQM methods to more clearly quantify the advantages in terms of convergence speed, robustness, and control smoothness.

8. Conclusions

In this paper, we addressed the congestion control problem in TCP networks by proposing two novel sliding mode controllers. A new sliding surface using a ${\mathcal{K}}_1$-type function was introduced to better suit nonlinear TCP systems.

The first controller uses a discontinuous law ensuring finite-time stability, but with chattering. The second is a continuous version reducing chattering while preserving robustness through input-to-state stability (ISS).

Simulations confirmed the fast convergence of the discontinuous controller and the smoother action of the continuous one.

The proposed controllers are practical for real TCP/IP networks, as they require no complex optimization and are scalable for large systems. Future work will extend this approach to complex network topologies and heavy traffic conditions, including practical case studies to assess performance and robustness in realistic environments.