Abstract
Biobanks rely on ultra-low-temperature (ULT) storage for irreplaceable specimens, where precise 3D temperature field reconstruction is critical to preserve integrity. This is the first study to apply geostatistical methods to ULT field reconstruction in cryogenic biobanking systems. We address critical gaps in sparse-sensor environments where conventional interpolation fails due to vertical thermal stratification and non-stationary trends. Our physics-informed universal kriging framework introduces (1) the first domain-specific adaptation of universal kriging for 3D cryogenic temperature field reconstruction; (2) eight novel lag-binning methods explicitly designed for sparse, anisotropic sensor networks; and (3) a leave-one-out cross-validation-driven framework that automatically selects the optimal combination of trend model, binning strategy, logistic weighting, and variogram model fitting. Validated on real data collected from a 3000 L operating cryogenic chest freezer, the method achieves sub-degree accuracy by isolating physics-guided vertical trends (quadratic detrending dominant) and stabilising variogram estimation under sparsity. Unlike static approaches, our framework dynamically adapts to thermal regimes without manual tuning, enabling centimetre-scale virtual sensing. This work establishes geostatistics as a foundational tool for cryogenic thermal monitoring, with direct engineering applications in biobank quality control and predictive analytics.
1. Introduction
Biological specimens preserved in ultra-low-temperature (ULT) environments represent irreplaceable resources for biomedical research, clinical diagnostics, and future therapeutic development. From rare disease tissue samples to genetically engineered cell lines and cryopreserved reproductive materials, these biological assets often embody decades of scientific investment and possess intrinsic value that cannot be replicated [1,2,3]. The integrity of these specimens fundamentally depends on thermal stability throughout their preservation lifecycle, where even transient temperature excursions beyond narrow operational bounds can compromise cellular viability, alter molecular structures, and invalidate years of research [4,5].
Cryogenic storage systems face an inherent paradox: while thermal field characterisation is essential for system design, monitoring, and optimisation, the physical constraints of biobanking environments severely limit sensor deployment. Biological storage compartments must maximise specimen capacity, creating spatially sparse and geometrically constrained sensor networks that make it difficult to detect the actual thermal topography within storage chambers.
The geostatistical community has long grappled with challenges analogous to those encountered in terrestrial and atmospheric sciences, particularly in the realm of spatial interpolation, where the objective is to achieve statistically optimal predictions. At the heart of geostatistics lies the construction of predictive models—exemplified by variograms—grounded in the principle of spatial autocorrelation, whereby measurements at known locations are leveraged to estimate values at unobserved sites. This foundational paradigm extends naturally to the reconstruction of ultra-low-temperature (ULT) fields: thermal distributions in cryogenic environments exhibit marked spatial continuity, enabling inference of the full temperature field across a storage volume from discrete sensor readings.
While established geostatistical techniques—most notably, kriging—offer a rigorous, theory-driven framework for spatial prediction from sparse and irregularly distributed observations, their direct application to ULT environments is fundamentally limited by a misalignment between classical assumptions and the physical realities of cryogenic systems. Conventional methods such as ordinary kriging rest on assumptions of spatial stationarity and isotropic covariance structures. However, ULT domains are characterised by pronounced anisotropy—vertical correlation lengths often being orders of magnitude shorter than horizontal ones due to stratified convection—and by strong non-stationary trends arising from phase-change phenomena, boundary-layer effects, and thermal stratification [6]. These intrinsic complexities are further amplified under conditions of sparse and geometrically irregular sensor deployment, where traditional interpolation schemes—including inverse distance weighting and radial basis functions—may prove inadequate in capturing fine-scale spatial heterogeneity, resulting in substantial reconstruction inaccuracies.
Critically, the non-stationary nature of cryogenic temperature fields—distinct from many canonical geostatistical applications—demands the explicit modelling of deterministic drift components that reflect underlying physical processes. This challenge underscores the need for adaptive geostatistical frameworks that seamlessly integrate first-principles physical knowledge with advanced spatial statistical methodologies. It is precisely this gap that our approach, rooted in universal kriging, seeks to bridge by incorporating physics-informed trend models into the spatial prediction process, thereby enhancing fidelity, interpretability, and robustness in the reconstruction of ultra-low-temperature fields.
To overcome these limitations, we introduce a physics-informed universal kriging framework that fundamentally rethinks spatial interpolation for cryogenic environments. Our approach integrates three key innovations: (1) adaptive lag-binning strategies optimised for sparse, anisotropic sensor networks—including dynamic programming formulations that balance spatial coherence with statistical reliability; (2) physics-guided detrending that isolates non-stationary thermal trends using domain-specific functional forms; and (3) logistic-weighted variogram estimation that prioritises physically meaningful spatial correlations. Crucially, a leave-one-out cross-validation (LOOCV) workflow autonomously selects optimal configurations across operational phases, enabling robust reconstruction without manual tuning. Validated against cryogenic storage systems, this framework achieves notable improvement in 3D temperature field reconstruction under the sparse sensing constraints inherent to biobanking.
The remainder of this paper is organised as follows: Section 2 critically reviews relevant literature on cryogenic temperature reconstruction and geostatistical methodologies, identifying specific gaps our work addresses. Section 3 details our physics-informed universal kriging framework, including mathematical formulations of the adaptive components. Section 4 describes the experimental validation using data from a representative cryogenic storage system under multiple operational scenarios. Section 5 reports results demonstrating the superiority of our approach across diverse thermal conditions. Finally, Section 6 discusses practical implications for biobanking applications and outlines future research directions.
2. Related Works
2.1. Cryogenic Temperature Field Reconstruction Challenges
Accurate reconstruction of three-dimensional temperature fields in cryogenic environments faces unique challenges due to extreme conditions, strong vertical gradients, and sparse sensor placement constraints. These factors create “gappy data” conditions that severely test standard interpolation techniques [7]. In cryogenic storage systems for aerospace, quantum computing, and bio-specimen preservation, precise spatial temperature knowledge is critical for structural integrity and insulation performance [8].
The primary challenge stems from vertical temperature gradients in cryogenic tanks, arising from stratification effects, heat leakage, and phase-change phenomena [9]. These gradients produce significant spatial variability over short distances, particularly during transient operational phases. The high cost and physical constraints of sensor deployment result in sparse and unevenly distributed measurements, making high-fidelity reconstruction exceptionally challenging [10]. Ferrando et al. [11] demonstrated similar challenges in meteorological applications, noting that, “despite the difficulties due to the sparse distribution of data and considerable orographic effect, simplified physical models can produce reliable maps,” highlighting the need for specialised interpolation approaches for vertically stratified systems. In terms of sparsity, recent physics-based machine learning advances highlight the value of embedding physical knowledge in spatial imputation. Yao et al. [12] proposed a Physics-Informed Recurrent Feature Reasoning (PI-RFR) method for reconstructing missing Antarctic climate data, where deep learning model initialisation with climate model (E3SM) patterns enabled 38–74% accuracy gains over kriging/IDW at high missing rates. However, the author also notes that kriging still has the advantage of providing uncertainty, while 3D temperature data are not involved.
2.2. Kriging for Spatial Interpolation
Kriging, also known as Gaussian process regression [13], has demonstrated statistical superiority over alternative interpolation methods. Zimmerman et al. [14] experimentally confirmed that “the two Kriging methods were substantially superior to inverse distance weighting methods across all surface types, sampling patterns, noise levels, and correlation structures”. This advantage stems from kriging’s ability to handle spatially incomplete data effectively, with Gunes et al. [7] establishing that “for insufficient temporal resolution, large spatial gappiness, or flow fields with black zones, Kriging interpolation is more effective”.
For temperature applications specifically, Wu and Li [15] demonstrated residual kriging’s effectiveness, noting that decomposing observations into “a surface trend plus a residual value is better than interpolating directly on observed data.” Similarly, Li et al. [16] developed a space-time regression-kriging model that reduced MAE and RMSE by ~60% compared to pure time forecasting.
However, standard kriging implementations face limitations in cryogenic environments due to non-stationary spatial correlation structures. Yang and Zhu [17] established that kriging performance critically depends on measurement error magnitude, with “the bias of the plug-in Kriging predictor becoming non-negligible when [error variance] is close to 1/2”. Parrott et al. [18] provided early evidence of kriging’s statistical optimality in 3D medical imaging, noting it “quantifies interpolation error,” but assumed isotropy that does not address cryogenic directional gradients.
2.3. Domain-Specific Kriging Adaptations
Domain-specific adaptations have emerged to address specialised interpolation challenges. Thaokar and Rabin [8] developed a temperature reconstruction framework for cryosurgery that “combines hardware development and mathematical techniques for real-time temperature field reconstruction”.
For sparse data applications, Li et al. [19] addressed magnetic map interpolation by developing a method that “uses the third power of lag distance to fit magnetic anomaly trends,” introducing “a hyperparameter λ to control the balance between second and third powers of lag distance,” improving accuracy by 30–50% over traditional models. Similarly, Yu et al. [20] proposed a “regional search Kriging interpolation method” that “divides the triangle search area,” improving prediction accuracy by over 20%.
Cui et al. [21] systematically evaluated eight interpolation methods for geological modelling, demonstrating that “optimal methods vary significantly based on data sparsity and spatial characteristics”. Ng and Hughes [22] developed “Continuous Part Kriging” for ice-flow fields, noting its “smoothing effect is evidenced by the smoothness of reconstructed fields,” providing valuable insights for the handling of sparse data in directional fields.
2.4. Lag-Binning Improvements
Lag binning critically impacts kriging performance in sparse data applications. Yang and Zhu [17] established theoretical foundations, showing that “variance function estimation deteriorates as measurement error increases,” underscoring the need for adaptive binning strategies.
Jia et al. [23] proposed a kriging algorithm using constraint particle swarm optimisation that “improves precision by setting weight coefficients and limiting search scope”. Li et al. [19] demonstrated that “the spherical variogram relates to the third power of lag distance,” introducing domain-specific adaptations that addressed under-fitting in sparse variogram graphs.
Li et al. [24] addressed 3D temperature field reconstruction using kriging, noting it “accurately reflects temperature change trends”, with “time reduced by 99% compared to CFD simulation,” but focused on parameter optimisation rather than fundamental binning challenges. Ferrando et al. [11] emphasised that for real-time applications, “the interpolator should be fast and automatically adjustable to different network configurations,” a requirement directly applicable to cryogenic monitoring.
2.5. Research Gap and Contribution
Existing approaches fail to address cryogenic-specific challenges:
Vertical stratification dominance—Unlike magnetic fields [19] or geological layers [21], cryogenic temperature fields display logarithmic correlation decay primarily in the vertical direction.
Phase-dependent spatial correlation—Cryogenic systems exhibit fundamentally different spatial correlation structures across operational phases, requiring adaptive interpolation approaches.
Asymmetric sensor distribution—As demonstrated by Yu et al. [20], asymmetric distributions require specialised search strategies not addressed for cryogenic vertical sensor concentration.
Our work bridges this gap by introducing adaptive lag-binning strategies specifically designed for cryogenic temperature fields. Unlike previous approaches treating binning as static, our dynamic framework optimises configurations based on evolving spatial correlation across operational phases. The log-hybrid binning strategy aligns with logarithmic correlation decay in cryogenic systems, while dynamic programming (DP)-based methods preserve structural discontinuities. This phase-specific adaptation addresses Yang and Zhu’s [17] concerns about measurement error impact, ensuring consistent performance across thermal conditions.
By integrating these innovations within a comprehensive LOOCV-driven framework, our approach achieves higher accuracy while maintaining computational efficiency for real-time monitoring. Unlike Li et al. [24], who focused on parameter optimisation for fixed binning, we address the fundamental challenge of lag binning under cryogenic-specific conditions, meeting Ferrando et al.’s [11] requirement for “fast and automatically adjustable” interpolators while specifically addressing vertical stratification challenges.
3. Experimental Methodology
This study presents a geostatistical framework using universal kriging to reconstruct spatial ultra-low-temperature fields, integrating three core components—adaptive lag binning, detrending, and weighted empirical variogram estimation—to improve interpolation accuracy in cryogenic systems with sparse sensor data and non-uniform spatial correlation; to address classical equal-distance binning’s limitation of unstable semivariance estimates at large lags, it proposes adaptive strategies (including distribution-aware methods like quantile-based/logarithmic, greedy binning with residual handling, and dynamic programming optimising bin homogeneity and statistical reliability) for robust variogram estimation; evaluates candidate trend models via goodness-of-fit metrics to ensure residual stationarity; uses leave-one-out cross-validation (LOOCV) to systematically explore the full parameter space (binning strategies, trend functions, variogram models, and distance weighting schemes) and identify configurations minimising reconstruction error; and, by combining geostatistical best practices with domain-specific adaptations, enables high-fidelity 3D thermal mapping to support accurate monitoring and analysis of cryogenic storage and transport systems.
3.1. Adaptive Lag-Binning Strategies for Robust Empirical Variogram Calculation
Accurate variogram estimation is foundational to geostatistical modelling—especially in environments with sparse sensors or localised heterogeneity (e.g., cryogenic storage systems, which often have limited sensor numbers and coverage)—as it underpins analysis of spatial correlation structures. The first core step in empirical variogram calculation is lag binning, grouping pairwise distances into intervals to compute averaged semivariance estimates; however, traditional equal-distance binning frequently results in bins with too few point pairs (notably at larger lags), causing unstable, highly variable estimates. To address this, we propose eight adaptive lag-binning strategies that dynamically adjust bin widths based on distance distributions, ensuring sufficient sample sizes per bin while preserving sensitivity to spatial structure. To contextualise these advancements, we first review foundational methods, using the classical equal-distance approach as a reference for comparison.
3.1.1. The Baseline Algorithm: Equal-Distance Binning
Equal-distance binning serves as a foundational approach in empirical variogram estimation, where lag distances are partitioned into intervals of uniform width. Given a minimum lag distance (), maximum lag distance (), and a user-defined number of bins (), the bin edges () are defined as follows:
This method ensures that the spatial lag domain is evenly sampled, providing a uniform basis for semivariance calculation.
While this approach is computationally simple and widely adopted in geostatistical practice, it exhibits notable limitations in the context of cryogenic temperature field reconstruction:
Sparse Data Sensitivity—In sensor networks with limited spatial coverage, fixed-width bins often contain insufficient point pairs at larger lags. This results in unstable semivariance estimates with high sampling variability.
Resolution–Representativeness Trade-off—Excessively narrow bins exacerbate data sparsity problems, while overly broad bins obscure critical spatial correlation structures.
These inherent limitations motivate the development of adaptive binning strategies that dynamically optimise bin boundaries according to the underlying distance distribution characteristics.
3.1.2. Distribution-Adaptive Binning Strategies: Quantile-Based and Logarithmic-Based
To overcome fixed-width binning’s limitations in sparse cryogenic environments, we introduce distribution-adaptive lag-binning methods that dynamically adjust interval widths based on the empirical distribution of pairwise distances—balancing the critical dual objectives of statistical reliability (sufficient point pairs per bin) and spatial representativeness (capturing meaningful spatial correlation variations) for sparse cryogenic sensor networks—and present two primary adaptive frameworks (quantile-based and logarithmic binning) that improve equal-distance methods by aligning bin boundaries with intrinsic distance distribution features, enhanced via hybrid implementations integrating clustering for robust boundary selection in heterogeneous sensor placements. The following subsections detail these approaches’ algorithmic design and domain-specific advantages for cryogenic temperature field reconstruction.
- (1)
- Quantile-Based Binning and Cluster-Enhanced Hybridisation
To address the limitations of fixed-width binning—particularly unstable semivariance estimates in data-scarce regimes, we first introduce pure quantile-based binning, a distribution-aware strategy that partitions lag distances according to the quantiles of the empirical pairwise distance distribution. This method ensures that each bin contains approximately the same number of point pairs, enhancing statistical reliability at the cost of potentially uneven bin widths.
Let be the set of all pairwise distances between sensor locations, where and denotes the total number of sensor locations. The quantile-based binning method partitions the lag space by mapping equal probability intervals from the cumulative distribution of distances back to the original distance domain. Formally, given a target number of bins (), the bin boundaries () are defined as follows:
where denotes the empirical quantile function computed from and represents the cumulative probability corresponding to the -th bin boundary. This formulation results in bin edges that partition the distance space into bins, each containing approximately the same number of point pairs. This ensures improved statistical reliability of semivariance estimation, especially under sparse sampling conditions.
Despite its advantages in stabilising bin counts, pure quantile binning may still merge distances that span natural discontinuities in the distribution, potentially leading to artificial averaging across regions with distinct spatial correlation characteristics.
To overcome this limitation, we propose a cluster-enhanced hybrid quantile binning strategy that integrates quantile partitioning with k-means clustering for boundary refinement. This method improves boundary placement by incorporating structural information from the distance distribution.
The method proceeds in two stages:
- Initial Quantile Partitioning—Compute initial bin boundaries using the quantile-based method described above. This ensures a minimum count of point pairs per bin and provides a statistically stable starting point.
- Boundary Refinement via Clustering—Refine bin boundaries using k-means clustering in an augmented feature space defined as follows:
The constant term acts as a regulator to prevent boundary collapse and encourages spatial coherence in cluster formation. After clustering with , final bin boundaries are determined by computing the midpoints between adjacent cluster centroids ():
This hybrid approach preserves the statistical robustness of quantile binning while improving alignment with natural groupings in the distance distribution. By refining bin boundaries to respect local density variations, the method enhances the representativeness of each bin with respect to spatial correlation characteristics.
This adaptive strategy demonstrates particular efficacy in systems with irregular sensor placement, as is common in cryogenic storage, effectively bridging the gap between statistical stability and structural sensitivity. It offers a more meaningful partitioning of the lag domain for empirical variogram estimation in ultra-low-temperature fields.
While quantile-foundation methods improve binning consistency, they implicitly assume relatively homogeneous distance distributions. In systems exhibiting significant sensor spacing variation—particularly cryogenic systems with stratified temperature gradients—logarithmic distance scaling offers distinct advantages in capturing multi-scale correlation structures. This motivates the development of our adaptive logarithmic binning strategy, which we describe in the following section.
- (2)
- Logarithmic-Based Binning and Threshold-Controlled Hybridisation
In sensor networks characterised by spatial heterogeneity, particularly cryogenic storage systems with stratified thermal gradients, we propose a logarithmic distance scaling approach that effectively captures multi-scale spatial correlation structures. This method employs a logarithmic transformation of lag distances to accommodate sensor configurations with variable spatial resolution, inherently aligning with the exponential decay typical of spatial correlation functions in cryogenic environments.
In pure logarithmic binning, the lag space is partitioned using geometric progression:
where represents the -th bin boundary.
This formulation yields exponentially increasing bin widths at larger lags, which simultaneously enhances resolution at fine scales while enabling stable semivariance estimation in sparse regions.
While pure logarithmic binning effectively captures multi-scale correlation patterns, it may still merge distances across abrupt structural transitions. To address this limitation while preserving multi-scale sensitivity, we propose a log-hybrid binning strategy that dynamically integrates adaptive thresholding with density-guided merging. The core innovation lies in a tuneable threshold of , which governs the transition from logarithmic spacing to structurally aware merging. To ensure both statistical stability and structural sensitivity, the merging process is guided by two complementary principles. First, each bin must contain at least point pairs to support reliable semivariance estimation—a requirement that ensures a sufficient sample size for meaningful statistical inference. Second, adjacent bins with large relative differences in their distance ranges, measured against the global scale, i.e., , should generally not be merged unless necessary to maintain statistical validity.
These two criteria are combined into a formal merging rule:
Here, denotes the number of point pairs in bin , and is a user-specified lower bound on the number of pairs required per bin to ensure statistical reliability. The quantity of represents the maximum distance in bin , while captures the overall spatial extent of the sensor network.
This mechanism ensures that extreme lag bins are merged based on both statistical sufficiency and spatial coherence, enhancing robustness in data-scarce regions.
To enable fine-grained exploration of local distance distributions, we first generate an over-discretised logarithmic grid by dividing the distance range into intervals, where is the target number of final bins and is a resolution enhancement factor. This ensures sufficient granularity for subsequent merging steps.
To prevent numerical instability due to zero-distance pairs (e.g., duplicate sensor locations), we apply a small regularisation term of to all distances before binning.
The threshold () plays a critical role in balancing local precision and global consistency. It adapts the binning logic to the observed distance distribution and sampling density. A lower prioritises fine-scale detail, while a higher enhances robustness in sparse regions.
Empirically, this adaptive strategy demonstrates particular efficacy in ultra-low-temperature systems with uneven sensor placement or sharp thermal discontinuities. By regulating resolution based on local data characteristics, the log-hybrid method provides a principled yet flexible foundation for robust empirical variogram estimation under sparse sampling conditions.
3.1.3. Operations Research-Inspired Approaches
The fundamental and distribution-adaptive binning methods for empirical variogram estimation help but do not fully address the trade-off between bin homogeneity and statistical reliability. To fix this, we introduce optimisation-driven techniques that treat lag binning as a structured decision problem, using algorithms to optimise bin configurations. These methods leverage operations research and numerical optimisation to balance minimizing within-bin distance variation and ensuring sufficient pair counts for stable semivariance estimation—shifting from heuristic partitioning to formal optimisation (principled algorithms over empirical rules). Our two key approaches—greedy binning with residual handling and dynamic programming-based partitioning—offer distinct advantages in computational efficiency and structural sensitivity.
- (1)
- Greedy Binning with Residual Merging
The greedy binning algorithm presents a computationally efficient strategy for constructing lag bins that satisfy minimum pair-count requirements while preserving sensitivity to the local structure of the distance distribution. This approach follows a deterministic, threshold-driven procedure that iteratively groups point pairs into bins until a minimum sample size per bin is achieved. It is designed to ensure both computational efficiency and robustness to numerical precision issues.
The greedy binning algorithm operates on the sorted list of non-zero pairwise distances (), which was previously defined. Starting from the smallest distance, the algorithm accumulates consecutive distances into a bin until the number of point pairs reaches the minimum required count (). Once this threshold is met, the current bin is closed, and the process continues with the next unassigned distance.
The greedy binning algorithm iteratively accumulates distances into bins until each contains at least point pairs. The resulting bin boundaries are defined such that
where is the total number of bins formed.
To handle floating-point precision issues and ensure numerical stability, a small tolerance () is applied during distance comparisons. If the final bin contains fewer than point pairs, it is deterministically merged with the preceding bin to avoid unstable semivariance estimates—a common issue in sparse sensor networks.
This greedy approach operates in time complexity and demonstrates high numerical stability, making it particularly suitable for large-scale or real-time variogram estimation.
- (2)
- Dynamic Programming-Based Binning Methods
Whereas greedy and distribution-adaptive strategies offer practical heuristics for stable variogram estimation, they often lack formal guarantees regarding bin homogeneity and global optimality. To overcome these limitations, we turn to optimisation theory, introducing dynamic programming (DP)-based binning as a methodologically rigorous alternative that redefines lag binning not as a heuristic grouping task but as a structured decision problem with quantifiable objectives. This approach shifts the focus from local rules to global cost minimisation, enabling the construction of bins that explicitly trade off statistical reliability (via minimum pair counts) against spatial coherence (via distance range or variance). By formulating binning as a recursive optimisation process, we ensure that each interval contributes meaningfully to the overall stability of semivariance estimates—particularly important when reconstructing ultra-low-temperature fields with sparse and uneven sensor coverage.
We propose three distinct DP formulations that differ in their cost functions and sensitivity to spatial structure:
- DP with Range Minimisation (Basic Formulation)
- DP with Adjusted Range Cost (Hybrid Objective)
- DP with Variance Minimisation (Statistical Precision)
The formulations differ in cost evaluation but share a common algorithmic framework: a monotonic queue is used to maintain optimal partition indices, enabling near-linear time complexity with proper bin-width constraints. Unlike heuristic binning strategies, which rely on randomisation or local rules, DP-based binning follows a strict, recursive optimisation logic that guarantees identical results for the same input data (sorted distances), cost function, and minimum pair count. The algorithm proceeds in four deterministic steps: (1) sort all non-zero pairwise distances in ascending order; (2) precompute cost metrics (range/variance) for all possible bin intervals; (3) use a monotonic queue to track optimal partition indices; (4) backtrack to construct bin boundaries. This eliminates variability across runs, ensuring the clustering of distance pairs is 100% repeatable for a given dataset. The DP binning workflow is schematic in its determinism: (1) Input—sorted pairwise distances, cost function (range/variance), and minimum pair count. (2) Precompute—cost metrics for all possible intervals [i, j] in the sorted list. (3) Optimise—use a monotonic queue to track the minimum cost for partitioning the first k distances. (4) Backtrack—starting from the final distance, select the optimal previous partition to build bin boundaries. Every step relies solely on predefined rules—no randomness—ensuring the same bins are generated every time.
DP Binning with Range Minimisation
This formulation aims to minimise the sum of bin ranges by recursively computing the optimal partition using a monotonic queue to reduce redundant comparisons. It defines the bin cost as the simple distance range:
where and represent the smallest and largest distances in the candidate bin and is the minimum required number of point pairs per bin.
The DP state () stores the minimum total cost for partitioning the first distances:
where and depend on the maximum and minimum bin sizes derived from and user-defined multipliers. To ensure efficiency, indices () are maintained in a monotonic queue where, decreases.
This strategy excels in spatially continuous temperature fields, where abrupt range increases can highlight structural discontinuities. However, it may produce bins that barely meet the requirement, leading to marginally stable semivariance estimates.
DP Binning with Adjusted Range Cost
As an enhancement of the range minimisation formulation, this method introduces a penalty-based cost function to discourage small or marginally valid bins. The adjusted bin cost is defined as follows:
The denominator acts as a size-aware stabiliser, increasing the cost for bins that contain exactly pairs or show weak internal homogeneity.
The recurrence remains similar, i.e.,
but the cost function now enforces stronger statistical regularisation, particularly at short lags, where distance density is high but sampling is uneven.
This formulation improves short-range accuracy and numerical robustness, making it well-suited for gradient-sensitive cryogenic applications where bin reliability directly affects model fitting stability.
DP Binning with Variance Minimisation
The most statistically rigorous approach is to directly minimise within-bin distance variance, which better reflects heterogeneity than absolute range alone. This is achieved by maintaining a prefix sum of and squared prefix sum of , enabling efficient variance calculation for any interval :
The DP recurrence is expressed as follows:
which is solved iteratively using precomputed sums.
This method shows superior performance in environments with abrupt spatial heterogeneity, where variance of distances within a bin is a more informative measure than range. It is especially well-suited for ultra-low-temperature fields where short-range precision in semivariance estimation is critical for capturing subtle thermal gradients.
This completes our presentation of adaptive lag-binning strategies, which address the challenge of stable semivariance estimation under sparse and heterogeneous spatial sampling. While binning ensures reliable distance grouping, accurate variogram computation also depends on appropriate preprocessing of the observed values. The following section introduces a range of detrending approaches that remove large-scale spatial trends, enabling more precise characterisation of local spatial dependence in ultra-low-temperature fields.
3.2. Trend Modeling
In ultra-low-temperature and cryogenic environments, spatial temperature fields often exhibit significant trends due to thermal stratification, geometric asymmetry, and boundary conditions. These global patterns must be accounted for before performing geostatistical interpolation to ensure stationarity of residuals and improve local estimation accuracy. To address this, we implement a physics-guided trend decomposition module that supports multiple functional forms, enabling flexible adaptation to different thermal profiles.
The spatial temperature distribution (, where denotes a three-dimensional coordinate vector in real space), is decomposed into two components: a deterministic trend component (), which captures large, predictable patterns, and a stationary residual (), which captures small, spatially correlated fluctuations (the “noise” around the trend). Mathematically, this decomposition is expressed as follows:
Given that vertical stratification dominates spatial variation in deep cryogenic cooling processes, the trend function () is assumed to depend only on the vertical coordinate (). A set of candidate trend models is considered, each parameterised as follows:
where is a small constant added to avoid singularities in logarithmic computations.
Each model is fitted using nonlinear least squares regression, with bounded parameter constraints to prevent numerical instabilities during optimisation. To ensure numerical stability, avoid ill conditioning during model fitting, and accelerate convergence across all models, the vertical coordinate () is normalised as .
All five trend models are evaluated independently, and their corresponding residuals are used as input for empirical variogram calculation and subsequent universal kriging interpolation. This multi-model approach enables robustness across diverse thermal states, particularly in transient cooling phases where the dominant trend may evolve over time.
By explicitly separating large-scale trends from local variations, the detrending step enhances the stationarity of the residual field, allowing the kriging process to focus on capturing fine-scale spatial variability. This significantly improves the accuracy and reliability of deep cryogenic temperature field reconstruction.
3.3. Computational Implementation
All geostatistical algorithms (Section 3.1 and Section 3.2) and data processing workflows were implemented in Python 3.11, using open-source libraries for efficiency, reproducibility, and alignment with geostatistical best practices. Key dependencies included the following:
- PyKrige 1.7.2 [25]: Core framework for universal kriging, including variogram estimation (e.g., adaptive lag binning) and spatial prediction;
- NumPy 2.0.1: Foundation for numerical operations (e.g., coordinate storage and distance calculations);
- Pandas 2.2.2: Manages structured data (e.g., reading time-series temperature data and storing optimisation results);
- SciPy 1.14.0: Supports trend fitting (nonlinear regression) and spatial distance calculations (e.g., pdist for point-pair distances);
- Joblib 1.4.2: Parallelizes batch processing (e.g., LOOCV for parameter optimisation) to reduce runtime by ~60%.
Core methodological components were implemented via custom scripts:
- binning_methods_latest.py: Adaptive lag binning (equal, greedy, logarithmic, dynamic programming);
- detrend_latest.py: Physics-guided trend decomposition (linear, quadratic, and exponential models);
- empirical_variogram_latest.py: Empirical variogram calculation with weighting schemes.
LOOCV and batch time-point processing were parallelized using joblib.Parallel, distributing tasks across all CPU cores for efficiency.
All scripts are archived in a public GitHub repository (https://github.com/Curtis-Tang/CryoKriging, accessed on 24 September 2025) to ensures full reproducibility of results.
4. Setup
The experimental configuration was designed to reflect real-world constraints commonly encountered in cryogenic storage systems, including sparse sensor placement, spatial heterogeneity, and transient thermal conditions.
The experiment was conducted in a 3000 L chest freezer (YN-3000 Shanghai Origincell Biological Cryo Equipment Co., Ltd., Shanghai, China), representing a typical large-scale bio-specimen storage system. The internal dimensions of the chamber are approximately 2470 mm (length) × 905 mm (width) × 1335 mm (height), forming a rectangular thermal enclosure suitable for studying spatial temperature distribution under various operating conditions.
A total of 48 temperature sensors were strategically placed throughout the chamber to capture the three-dimensional thermal field. These sensors were arranged across three horizontal planes at different heights (Z = 1335 mm, 692 mm, and 230 mm), with each plane containing 15 to 18 sensors distributed to represent both edge and central regions. All sensors were factory-calibrated Class-B PT1000 resistance thermometers.
Due to the limitations of the measurement system, all sensors were connected via wires to an external data acquisition unit. This setup introduced potential disturbances in local thermal fields due to cable heat conduction and minor convection; however, the configuration allowed for reliable long-term monitoring of transient thermal states. Temperature readings were recorded at 20 s intervals throughout all operational phases, providing high temporal resolution for tracking of thermal evolution.
Measurements were conducted under three representative operational stages to evaluate the framework’s performance across diverse spatial correlation structures:
Cooling-down phase: Starting from ambient temperature, the chamber was cooled to the target ultra-low temperature (−84 °C). A total of 929 time points of data were collected.
Steady-state operating phase: Once the target temperature was reached, the system eventually stabilised into a steady state characterised by minor fluctuations and stable thermal stratification. A total of 290 time points of data were collected.
Warm-up phase: After cooling, the system was allowed to warm naturally, simulating a power failure scenario. A total of 671 time points of data were collected.
These three stages provide comprehensive coverage of typical thermal behaviours in cryogenic systems, making them ideal for validating spatial interpolation techniques.
5. Results and Discussion
This section evaluates the performance and robustness of the proposed adaptive lag-binning strategies and universal kriging framework for cryogenic temperature field reconstruction. We first present visualisations of bin edges and centres to demonstrate how the adaptive methods address the limitations of classical equal-width binning, particularly in sparse and heterogeneous sensor networks. These plots highlight the distribution-aware design of quantile-based, logarithmic, and optimisation-driven binning techniques, emphasising their ability to stabilise semivariance estimates while preserving sensitivity to spatial correlation structures. Subsequent sensitivity analysis systematically examines the impact of binning strategies, detrending models, and variogram parameterisations on interpolation accuracy, validated against inverse distance weighting (IDW) baselines. Results are analysed across three operational phases—cooling, steady state, and warm-up—to assess adaptability to dynamic thermal conditions. By analysing binning efficacy through reconstruction error metrics and theoretical model consistency, we demonstrate how the framework integrates statistical rigor with cryogenic-specific physical principles, achieving high-fidelity spatial mapping, even under sparse sensor conditions and dynamic thermal gradients.
5.1. Binning Method Comparison: Structural and Statistical
Accurate empirical variogram estimation in cryogenic temperature fields hinges on lag-binning strategies that reconcile statistical reliability (sufficient point pairs per bin) with spatial resolution (capturing local correlation structures). Classical equal-width binning often fails to balance these requirements, producing unstable semivariance estimates in sparse sensor networks. Here, we compare eight adaptive binning methods—including distribution-aware quantile partitioning, logarithmic scaling, and optimisation-driven methods—to demonstrate their efficacy in stabilising semivariance estimates while preserving critical spatial features. Figure 1 and Figure 2 jointly evaluate these strategies, validating their distinct patterns in balancing structural fidelity and statistical reliability.

Figure 1.
Structural comparison of adaptive lag-binning strategies.
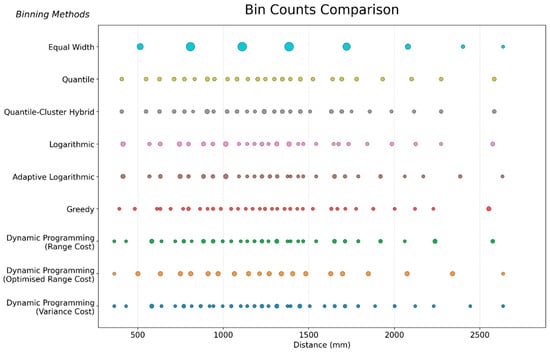
Figure 2.
Statistical reliability of binning methods.
The equal-width approach produces uniformly spaced bin edges that fail to adapt to the empirical distance distribution. This rigidity manifests in starkly uneven pair counts, with bins at larger lags (>2000 mm) containing as few as 31 pairs, barely meeting the minimum point-pair threshold of 30, while mid-range bins hold over 200 pairs. Such imbalance amplifies sampling noise in semivariance estimates.
In contrast, distribution-aware methods like quantile-based binning enforce statistical reliability by aligning bin widths with the cumulative distance distribution. The quantile-cluster hybrid strategy, for instance, partitions the lag space into intervals containing 30–61 pairs, ensuring stable estimates, even in sparse regions. However, this comes at the cost of irregular edge spacing, which compresses bins in dense Figure 1 regions and expands them where distances are sparse. The hybrid model’s integration of k-means clustering further refines boundary placement features that preserve structural discontinuities in the sensor network’s spatial configuration.
Colour coding highlights method families, with grid lines anchoring comparisons to physical distance scales. Collectively, the visualization validates the fact that adaptive strategies dynamically align binning with data density, avoiding the pitfalls of fixed-width approaches.
Logarithmic strategies such as the log-hybrid method refine this balance by prioritising short-range precision. At larger lags, geometric bin expansion merges distant pairs into broader intervals, avoiding undersized bins while suppressing noise. This dual-scale approach mirrors the exponential decay of spatial correlation in ultra-low-temperature fields, as evidenced by tightly clustered centres at mid-range distances.
Optimisation-driven methods, particularly dynamic programming (DP), achieve global homogeneity by minimising internal bin variance. DP with optimised range cost, for example, merges bins only when necessary to maintain statistical validity. Its runtime (0.0040 s) remains competitive with heuristic methods, while its edge transitions at structural discontinuities preserve critical spatial features. The greedy algorithm, though faster (0.0010 s), sacrifices some resolution by aggressively merging undersized bins, as evident in its final bin containing 61 pairs as a compensatory adjustment for sparse data.
Statistical reliability emerges as a unifying theme across adaptive strategies. Quantile methods enforce balanced pair counts, logarithmic approaches prioritise short-range density, and DP methods optimise homogeneity. These adaptations directly address the instability of classical binning, as seen in the absence of critically undersized bins (<30 pairs) in all adaptive results. Structurally, the methods diverge in their sensitivity to local distance distributions: quantile strategies emphasise uniformity, logarithmic methods favour multi-scale resolution, and DP approaches optimise global coherence.
These observations underscore the core advantage of adaptive strategies: they ensure sufficient pair counts per bin (statistical reliability) while preserving sensitivity to local distance distributions (spatial resolution). This dual focus directly addresses the instability of classical binning in sparse networks, as emphasised in the methodology.
5.2. Sensitivity Analysis
To rigorously evaluate the robustness of our adaptive kriging framework’s performance across different thermal conditions, we conducted systematic sensitivity analyses using leave-one-out cross-validation (LOOCV). This analysis serves three essential purposes: first, establishing reliable performance baselines against conventional methods to contextualise the framework’s improvements; second, identifying which framework components most affect accuracy under specific conditions; and third, validating the fact that physics-guided parameter selection outperforms fixed configurations in cryogenic environments. We begin with inverse distance weighting (IDW) as our baseline method, since its parameter behaviour directly reflects spatial correlation patterns in temperature fields. Our comprehensive parameter search across all combinations reveals distinct methodological preferences for each operational phase, suggesting that cryogenic temperature fields exhibit fundamentally different spatial structures depending on thermal dynamics. The following analysis documents these observed patterns and explores potential physical explanations for why certain configurations perform better under specific thermal conditions, providing evidence that supports our framework’s adaptive design philosophy.
5.2.1. IDW Baseline Performance Analysis
To establish a robust reference for evaluating our framework, we first conducted exhaustive LOOCV experiments using IDW interpolation across three operational conditions: steady-state, cool-down, and warm-up phases. We chose mean squared error (MSE) as the primary metric because it uniquely penalizes large temperature errors—critical for cryogenic applications where deviations can easily compromise specimen integrity—while aligning with the squared-error cost function optimised in our LOOCV process. The systematic grid search evaluates power exponents from −10.0 to 10.0 with 0.1 increments to capture both conventional distance-decay (positive exponents) and inverse-decay (negative exponents) behaviours, alongside neighbour counts from 1 to 16 to resolve spatial influences across local-to-regional scales.
Table 1 below summarises the optimal IDW configurations, revealing distinct spatial correlation characteristics and providing critical insights for subsequent kriging configuration research. For readability and interpretation, we selected the root mean square error (RMSE) to present the baseline performance.

Table 1.
Optimal IDW configuration across operational phases.
The comparative analysis of IDW performance across operational phases revealed distinct spatial characteristics that align with the physical dynamics of cryogenic systems. During the steady-state phase, moderate predictability (RMSE = 1.179 °C) with a negative power exponent (−0.6) indicated stable thermal stratification where intermediate distances dominated spatial correlation. In contrast, the cool-down phase exhibited higher uncertainty (RMSE = 1.370 °C, 16% greater than steady state) with near-uniform weighting (power = −0.1), reflecting transient thermal gradients that equally engage local and regional patterns. The warm-up phase demonstrated superior predictability (RMSE = 0.936 °C) with strong local dependence (power = 5.5) and expanded neighbour utilisation (4 points), consistent with natural convection-driven homogenization. This systematic variation in optimal configurations directly informs our adaptive framework’s design, demonstrating that dynamic parameter selection through LOOCV is essential to capture the cryogenic system’s evolving spatial correlation structure across operational regimes.
5.2.2. Phase-Specific Method Preferences: Frequency Analysis
To evaluate the framework’s adaptability to dynamic thermal environments, we analysed the frequency of optimal kriging configurations across 24,948 parameter combinations for every time step during cool-down, steady-state, and warm-up phases. This approach identifies methodological choices that consistently outperform others under specific physical conditions, revealing how adaptive strategies align with features of the cryogenic environment. The optimal configurations will be marked with a star.
- (1)
- Binning Strategy Preferences: Structural vs. Statistical Trade-Offs
- Cool-Down Phase:
As shown in Figure 3, the adaptive logarithmic binning strategy dominated over the other methods (24.5%, 200,692 selections), exceeding traditional equal-width binning (5.3%, 43,311) by 362%. The dynamic programming-based methods followed closely: optimised range cost (146,226, 17.9%), basic range cost (90,001, 11.0%), and variance cost (86,829, 10.6%). The pure logarithmic method (87,865, 10.7%) also demonstrated strong efficacy, while quantile-based, greedy, and equal-distance approaches trailed substantially (<10% of wins). Crucially, all adaptive binning methods offer the chance to surpass the IDW baseline, but logarithmic and DP-based strategies achieved this more frequently than alternatives.
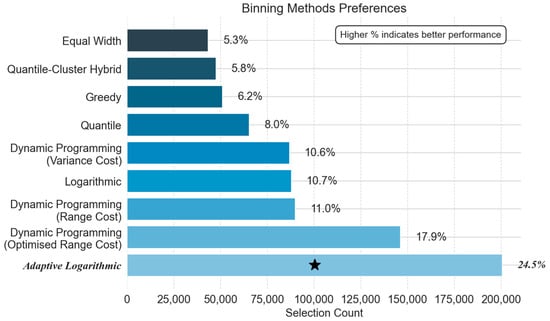
Figure 3.
Binning method preferences: cool-down.
- Steady-State Phase:
During steady-state operation, dynamic programming with range optimisation emerged as the dominant strategy (46,125 selections, 28.1%), shows in Figure 4, surpassing adaptive logarithmic binning (32,789, 20.0%) by 40.6%. This represents a critical phase-dependent reversal from the cool-down phase. The pure logarithmic method (16,495, 10.1%) and DP with range minimisation (18,378, 11.2%) maintained secondary efficacy, while DP with variance minimisation (11,574, 7.1%) dropped below 10%. The quantile-based binning method (11,542, 7.0%), its k-mean hybrid (10,254, 6.3%), the greedy method (10,035, 6.1%), and equal-distance binning (6804, 4.2%) tended to underperform.
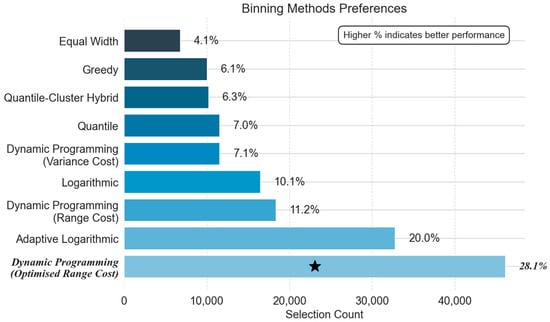
Figure 4.
Binning methods preferences: steady state.
- Warm-up Phase:
As shown in Figure 5, adaptive logarithmic binning achieved major dominance (632,082 selections, 28.9%), outperforming all other methods combined during the warm-up stage. This represents a dramatic intensification of its cool-down phase advantage. The pure logarithmic method (21,3162, 10.7%), the two quantile variants (212,908 and 212,822, both 9.7%), the two DP methods with basic minimisation, and the greedy method (210,885, 210,315, and 210,264, all 9.6%) exhibited near-identical secondary efficacy, while DP range optimisation—the steady-state champion—collapsed to 4.3% (93,111), which is the lowest among adaptive methods. Crucially, the adaptive logarithmic method’s 28.9% win rate exceeded equal-distance binning (9.7%) by 227%, confirming logarithmic scaling’s unique suitability for reconstructing rapidly evolving thermal fronts during heating transients.
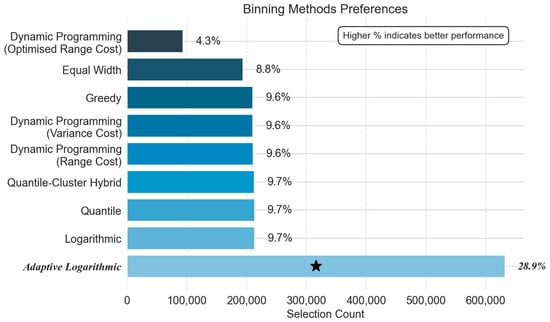
Figure 5.
Binning method preferences: warm-up.
- (2)
- Detrending Method Preferences
Detrending model efficacy proved remarkably consistent across all operational phases. Figure 6 (cool-down), Figure 7 (steady state), and Figure 8 (warm-Up) collectively reveal a striking truth: nonlinear detrending is the framework’s indispensable cornerstone. Linear detrending and no-trend removal, in contrast, resulted in significant inaccuracies.
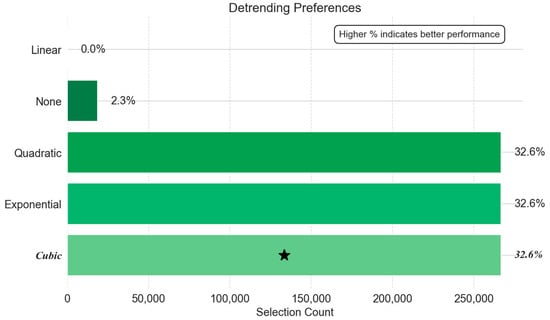
Figure 6.
Detrending preferences: cool-down.
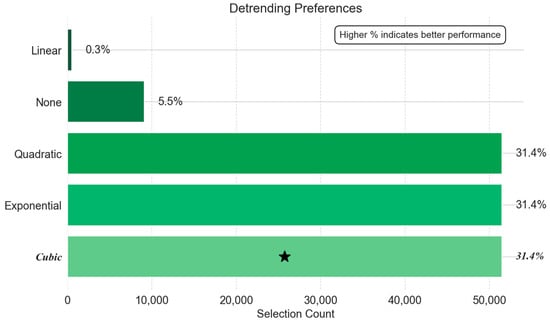
Figure 7.
Detrending preferences: steady state.
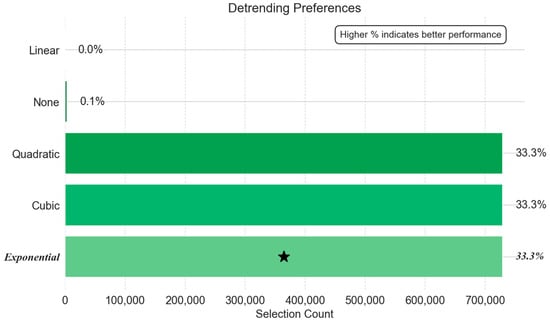
Figure 8.
Detrending preferences: warm-up.
Considering quadratic detrending is the most energy-efficient method, it achieves optimal efficiency–accuracy balance. Unlike binning strategy selection, which requires phase-aware adaptation, detrending model choice is invariant: quadratic detrending should be the default for all operational conditions, reserving cubic/exponential detrending for specialised cases with extreme nonlinearities. This insight transforms detrending from a preprocessing step into a design principle for cryogenic monitoring systems.
- (3)
- Weighting Scheme Preferences: Spatial Sensitivity Control
Contrary to expectations, the choice of distance weighting scheme had a minimal impact on reconstruction accuracy across all operational phases. Figure 9 (cool-down phase) shows logistic weighting with a centre/slope ratio of 0.7/5.0 achieved 118,702 selections (14.5%), but this barely exceeded the unweighted baseline (118,488, 14.5%) by 0.2%. In steady-state operation (Figure 10), logistic 0.5/10.0 led with 24,877 selections (15.2%), while the unweighted configuration trailed at 22,793 (14.1%). During warm-up (Figure 11), the unweighted configuration dominated (314,098, 15.2%) over logistic variants (312,100–312,992). Even the worst-performing scheme (logistic 0.7/10.0: 312,100 in warm-up) trailed the best by around 0.6%—orders of magnitude smaller than binning method differences.
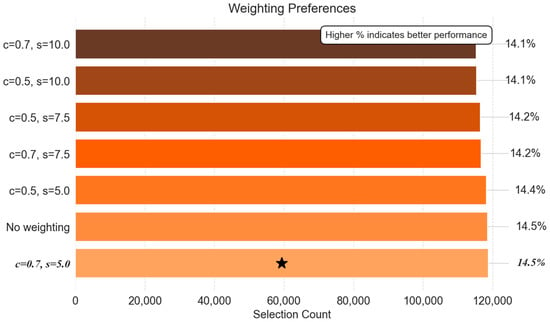
Figure 9.
Weighting scheme preferences: cool-down.
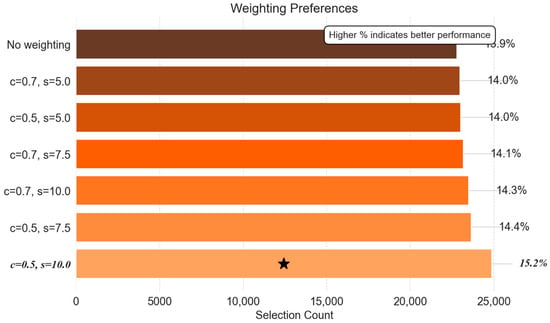
Figure 10.
Weighting scheme preferences: steady state.
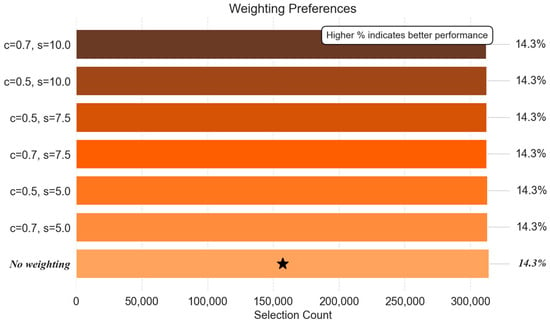
Figure 11.
Weighting scheme preferences: warm-up.
This striking insensitivity to weighting suggests that our adaptive binning and detrending components already capture the dominant spatial correlation structures. The logistic function’s distance decay control—designed to suppress boundary effects—adds negligible value when variogram estimation is already stabilised by logarithmic-based or DP-based binning methods. Notably, the performance of unweighted baselines indicates that equal weighting of point pairs preserves sufficient spatial information when bins are optimally configured. This simplifies deployment: operators can safely omit weighting without sacrificing accuracy, reducing computational overhead.
- (4)
- Theoretical Variogram Model Preferences: Bridging Statistical and Physical Models
The choice of theoretical variogram model exhibited strong phase dependency, with exponential and power models dominating transients while linear and Gaussian variants performed moderately in steady-state phase. This aligns with the physical nature of cryogenic thermal fields: unbounded models (power and linear models) excel during transients with evolving spatial correlations, while bounded models (Gaussian and exponential models) capture stable gradients. Crucially, the framework’s dynamic model selection—implemented via PyKrige [25]—avoids the pitfalls of static assumptions, adapting to the spatial structure of each operational regime.
- Cooling-Down Phase:
During cool-down, as shown in Figure 12, the power modelled decisively (251,232 selections, 30.7%), outperforming Gaussian (215,177, 26.3%) and linear (196,398, 24.0%) models by 16.8–27.9%. Spherical and hole-effect models did not show enough advantages, likely due to their bounded sill assumptions, making them invalid when spatial correlation evolves rapidly in transient systems.
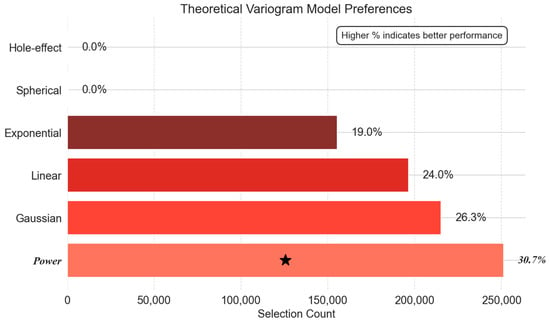
Figure 12.
Theoretical variogram model preferences: cool-down.
- Steady-State Phase:
In the steady-state phase, as shown in Figure 13, the power model retained dominance (122,710, 74.8%) but with reduced margin, while linear (21,765, 13.3%) and Gaussian (19,365, 11.8%) models gained secondary traction. This shift reflects the system’s transition to stable, diffusive heat transfer where linear trends and Gaussian smoothness assumptions become valid. The near-complete collapse of spherical and hole-effect models confirms their inapplicability to equilibrium cryogenic fields.
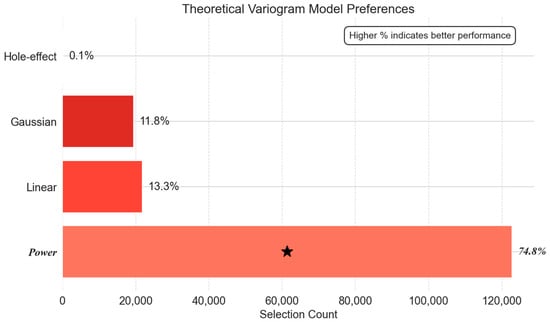
Figure 13.
Theoretical variogram model preferences: steady state.
- Warm-Up Phase:
As shown in Figure 14, warm-up saw a significant shift: the exponential model dominated (854,756 selections, 39.0%), surpassing the power model (549,683, 25.1%) by 55.5%. The linear model (495,993, 22.7%) remained competitive, but the Gaussian and hole-effect models collapsed to near zero, proving their inadequacy for non-stationary warming dynamics.
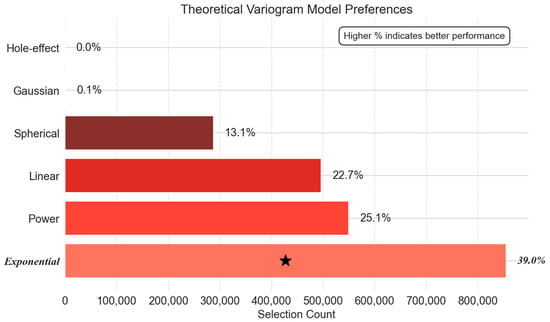
Figure 14.
Theoretical variogram model preferences: warm-up.
The phase-dependent dominance of theoretical variogram models underscores the necessity of adaptive framework design in cryogenic systems. The power model exhibited consistent dominance during cool-down and steady-state phases, while the exponential model surged during warm-up. These findings underscore our framework’s core strength: it eliminates the need for static, user-defined assumptions and automatically aligns with the physics of each operational regime. This adaptive approach not only improves accuracy but also simplifies deployment in real-world cryogenic systems, where operational phases shift unpredictably and manual retuning is impractical.
5.3. Interpolation Error Comparison and Statistical Significance
To validate our framework’s performance against conventional inverse distance weighting (IDW), we conducted leave-one-out cross-validation (LOOCV) to calculate the mean prediction error (accuracy) and standard error of the mean (SEM) (consistency of errors). We then used paired t-tests to assess whether differences between methods were statistically meaningful.
Cool-Down: Kriging’s mean error (−0.0013 °C, SEM = 0.0213 °C) was slightly more accurate than IDW’s (0.0060 °C, SEM = 0.0193 °C), but differences were not significant (p = 0.6601, ns).
Steady State: Kriging’s mean error (−0.0026 °C, SEM = 0.0149 °C) was closer to zero than IDW’s (−0.0099 °C, SEM = 0.0141 °C), but again, no significant difference was observed (p = 0.5229, ns).
Warm-Up: Kriging outperformed IDW dramatically, with a mean error of 0.0014 °C (SEM = 0.0127 °C) vs. IDW’s −0.0127 °C (SEM = 0.0128 °C). This difference was highly significant (p < 0.001, ***).
As shown in Figure 15, low SEM values (≤0.022 °C) across all phases confirm that our framework’s predictions are consistent—critical for cryogenic applications where stable accuracy protects specimens. Additionally, the significant warm-up result, shown as “***”, validates our framework’s core strength: phase-aware adaptation (e.g., logarithmic binning for rapid warming) outperforms IDW’s fixed parameters in dynamic environments. Meanwhile, non-significant (ns) results in the cool-down/steady-state phases show that kriging matches IDW’s best performance in static, stratified conditions—without manual tuning.
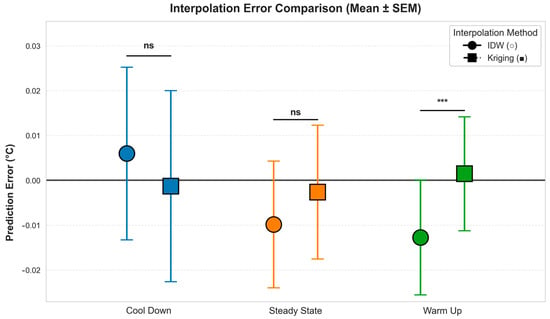
Figure 15.
Interpolation error comparison (Mean ± SEM).
5.4. Summary of Key Findings
The analysis in this chapter reveals critical insights about the adaptability and performance of our physics-informed kriging framework, with implications for cryogenic temperature field reconstruction:
Adaptive lag binning is critical. Adaptive strategies (logarithmic scaling and dynamic programming (DP)-based partitioning) outperform classical equal-width binning by balancing statistical reliability (sufficient point pairs per bin) and spatial resolution (capturing local correlation). Logarithmic binning dominates transient phases (cool-down and warm-up), owing to its ability to handle evolving thermal fronts, while DP-based binning (e.g., range optimisation) excels in steady-state conditions (stable stratification demands global homogeneity).
Nonlinear detrending is indispensable. Nonlinear models (especially quadratic models) are mandatory for isolating residuals in vertically stratified cryogenic environments. Linear detrending or no trend removal fails catastrophically, confirming physics-guided detrending as a foundational design principle. This confirms that the introduction of a drift term (deterministic trend component) is a key improvement of universal kriging over ordinary kriging. Ordinary kriging assumes spatial stationarity (no large-scale trends), which fails catastrophically in cryogenic systems where vertical stratification dominates. Linear detrending or no trend removal also produces unreliable results, underscoring physics-guided detrending as a foundational design principle for cryogenic applications.
With respect to phase-dependent variogram models, the power model is consistently favoured during cool-down and steady-state phases, while the exponential model emerges as the dominant choice during warm-up. The choice of theoretical variogram model exhibited strong phase dependency, with distinct models outperforming others due to their statistical adaptability to the evolving spatial correlation structures of each operational phase. This phase-aware dominance underscores the framework’s ability to select models that best match the statistical behaviour of the data—rather than relying on static assumptions—ensuring robust performance across dynamic regimes.
Weighting schemes have minimal impact. Optimised binning/detrending already capture dominant spatial structures, and weighting-scheme differences (e.g., logistic vs. unweighted) have negligible effects on accuracy. This simplifies deployment (equal weighting is sufficient).
In terms of framework robustness, the LOOCV-driven adaptive approach matches or outperforms conventional methods (e.g., IDW) across all phases, maintaining sub-degree Celsius accuracy without manual tuning. This addresses a critical gap in cryogenic monitoring, where operational regimes shift unpredictably.
These findings validate the fact that integrating geostatistical innovations with domain-specific physics is essential for reliable thermal mapping in sparse-sensor cryogenic systems.
6. Conclusions
This study presents a physics-informed universal kriging framework tailored for high-fidelity reconstruction of 3D cryogenic temperature fields, addressing critical challenges in sparse sensor networks and non-stationary thermal trends. By integrating adaptive lag binning, physics-guided detrending, and logistic-weighted variogram estimation with LOOCV-driven parameter optimisation, the proposed method achieves robust spatial interpolation across transient and steady-state operational phases of ultra-low-temperature systems. The core contributions lie in three innovations.
Hybrid lag-binning strategy: This strategy combines logarithmic scaling, dynamic programming (DP), and quantile-based partitioning to stabilise semivariance estimation under sparse data. Adaptive logarithmic binning excels during transients (e.g., warm-up phases), while DP-based methods dominate in steady-state conditions, ensuring optimal balance between statistical reliability and spatial resolution.
Physics-guided detrending: Nonlinear trend models (quadratic, cubic, exponential) isolate spatial residuals, ensuring stationarity in vertically stratified cryogenic environments. Quadratic detrending emerged as the default choice across all phases, offering the best trade-off between accuracy and computational efficiency.
Logistic-weighted variogram framework: The proposed framework prioritises spatial consistency while mitigating noise from irregular sensor distributions. However, sensitivity analyses revealed that weighting scheme selection had a minimal impact on reconstruction accuracy (differences <0.6% across phases), suggesting that optimised binning and detrending already capture dominant spatial structures. This simplifies deployment, as equal weighting of point pairs preserves sufficient spatial information when bins are adaptively configured.
Experimental validation using a 48-sensor cryogenic chest freezer demonstrated the framework could provide advantages over conventional methods like inverse distance weighting (IDW). During transient phases (cool-down and warm-up), adaptive logarithmic binning and power/exponential variogram models dominated. In steady-state conditions, DP-based binning and quadratic detrending emerged as optimal choices, reflecting stable stratification patterns. Notably, the LOOCV-driven adaptability minimised manual parameter tuning, enabling seamless transitions and adaptation to the system’s evolving spatial structure while maintaining sub-degree Celsius accuracy.
These advancements help address the critical need for reliable thermal mapping in biobanking and cryopreservation, where specimen integrity hinges on precise temperature monitoring despite spatially constrained sensor networks. The framework’s ability to decompose complex thermal fields into interpretable trends and residuals further enhances its utility for uncertainty quantification and system diagnostics.
This work advances cryogenic thermal management by providing a scalable, automated solution that harmonises geostatistical theory with domain-specific physics. Future efforts could explore three key directions: (1) real-time IoT sensor integration for dynamic data streaming; (2) hybridisation with computational fluid dynamics (CFD) and finite element analysis (FEA) to incorporate heat transfer modes (conduction, convection, and radiation)—overcoming current limitations of purely statistical interpolation by modelling complex cryogenic chamber geometries, boundary conditions (e.g., heat leakage and fan airflow), and material properties (e.g., insulation, specimen racks); and (3) fusion with machine learning for predictive analytics, transforming reactive monitoring into proactive thermal management. Integrating CFD/FEA would enable more accurate boundary condition coupling and multi-physics validation, providing high-fidelity reference fields to refine our geostatistical framework. However, this requires the solution of practical challenges, including simplifying intricate internal structures (e.g., densely packed specimens) for computational efficiency, aligning sensor data with CFD mesh resolutions, and calibrating models to real-world operational data.
By helping to resolve the misalignment between classical geostatistics and cryogenic realities, this framework could set a foundation for next-generation monitoring systems in ultra-low-temperature applications, ensuring the integrity of temperature-sensitive biological specimens critical to biomedical research and clinical therapies.
Author Contributions
Conceptualisation, J.T., Y.C., B.L., and J.W.; methodology, J.T. and J.W.; software, J.T.; formal analysis, J.T.; investigation, J.T., Y.C., and J.C.; data curation, Y.C. and J.C.; writing—original draft preparation, J.T. and Y.C.; writing—review and editing, Y.C. and J.W.; visualization, J.T.; supervision, B.L.; project administration, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received financial support from the Pudong New Area Postdoctoral Research Innovation Fund.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors gratefully acknowledge Yao Shiqi for the skilled installation of instrumentation, which was essential to this study. We acknowledge the use of large language model (LLM) DeepSeek-R1-0528, which assisted in structuring the initial experimental protocol framework. We also utilised Qwen3-235B-a22B to support code development and polishing of the English language expression of the manuscript. The authors retain full responsibility for the scientific rigor, validity, and integrity of the study, including critical evaluation and revision of all AI-generated outputs.
Conflicts of Interest
Authors Jiecheng Tang, Yisha Chen, Jie Cao and Jianxin Wang were employed by the company Shanghai Origincell Biological Cryo Equipment Co., Ltd. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The company had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Hirtzlin, I.; Dubreuil, C.; Préaubert, N.; Duchier, J.; Jansen, B.; Simon, J.; Lobato De Faria, P.; Perez-Lezaun, A.; Visser, B.; Williams, G.D.; et al. An empirical survey on biobanking of human genetic material and data in six EU countries. Eur. J. Hum. Genet. EJHG 2003, 11, 475–488. [Google Scholar] [CrossRef] [PubMed]
- Saleh, J.; Mercier, B.; Xi, W. Bioengineering methods for organoid systems. Biol. Cell 2021, 113, 475–491. [Google Scholar] [CrossRef] [PubMed]
- Watson, P.H.; Nussbeck, S.Y.; Carter, C.; O’Donoghue, S.; Cheah, S.; Matzke, L.A.; Barnes, R.O.; Bartlett, J.; Carpenter, J.; Grizzle, W.E.; et al. A framework for biobank sustainability. Biopreserv. Biobank. 2014, 12, 60–68. [Google Scholar] [CrossRef]
- Babel, M.; Mamilos, A.; Seitz, S.; Niedermair, T.; Weber, F.; Anzeneder, T.; Ortmann, O.; Dietmaier, W.; Brochhausen, C. Compared DNA and RNA quality of breast cancer biobanking samples after long-term storage protocols in −80 °C and liquid nitrogen. Sci. Rep. 2020, 10, 14404. [Google Scholar] [CrossRef]
- Shabihkhani, M.; Lucey, G.M.; Wei, B.; Mareninov, S.; Lou, J.J.; Vinters, H.V.; Singer, E.J.; Cloughesy, T.F.; Yong, W.H. The procurement, storage, and quality assurance of frozen blood and tissue biospecimens in pathology, biorepository, and biobank settings. Clin. Biochem. 2014, 47, 258–266. [Google Scholar] [CrossRef] [PubMed]
- Weikert, J.; Mehrländer, A.; Baber, R. Keep cool! Observed temperature variations at different process stages of the biobanking workflow—Examples from the Leipzig medical biobank. J. Lab. Med. 2023, 47, 69–80. [Google Scholar] [CrossRef]
- Gunes, H.; Sirisup, S.; Karniadakis, G.E. Gappy data: To Krig or not to Krig? J. Comput. Phys. 2006, 212, 358–382. [Google Scholar] [CrossRef]
- Thaokar, C.; Rabin, Y. Temperature field reconstruction for minimally invasive cryosurgery with application to wireless implantable temperature sensors and/or medical imaging. Cryobiology 2012, 65, 270–277. [Google Scholar] [CrossRef]
- Powell, S.; Molinolo, A.; Masmila, E.; Kaushal, S. Real-Time Temperature Mapping in Ultra-Low Freezers as a Standard Quality Assessment. Biopreserv. Biobank. 2019, 17, 139–142. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, C.; Ji, H. A temperature field reconstruction method for spacecraft leading edge structure with optimized sensor array. J. Intell. Mater. Syst. Struct. 2021, 32, 2024–2038. [Google Scholar] [CrossRef]
- Ferrando, I.; De Rosa, P.; Federici, B.; Sguerso, D. Spatial interpolation techniques for a near real-time mapping of pressure and temperature data. PeerJ Prepr. 2016, 4, e2223v2. [Google Scholar] [CrossRef]
- Yao, Z.; Zhang, T.; Wu, L.; Wang, X.; Huang, J. Physics-Informed Deep Learning for Reconstruction of Spatial Missing Climate Information in the Antarctic. Atmosphere 2023, 14, 658. [Google Scholar] [CrossRef]
- Xiong, S. The Reconstruction Approach: From Interpolation to Regression. Technometrics 2021, 63, 225–235. [Google Scholar] [CrossRef]
- Zimmerman, D.; Pavlik, C.; Ruggles, A.; Armstrong, M.P. An Experimental Comparison of Ordinary and Universal Kriging and Inverse Distance Weighting. Math. Geol. 1999, 31, 375–390. [Google Scholar] [CrossRef]
- Wu, T.; Li, Y. Spatial interpolation of temperature in the United States using residual kriging. Appl. Geogr. 2013, 44, 112–120. [Google Scholar] [CrossRef]
- Li, S.; Griffith, D.A.; Shu, H. Temperature prediction based on a space-time regression-kriging model. J. Appl. Stat. 2020, 47, 1168–1190. [Google Scholar] [CrossRef]
- Yang, S.; Zhu, Z. Variance estimation and kriging prediction for a class of non-stationary spatial models. Stat. Sin. 2015, 25, 135–149. [Google Scholar] [CrossRef]
- Parrott, R.W.; Stytz, M.R.; Amburn, P.; Robinson, D. Statistically optimal interslice value interpolation in 3D medical imaging: Theory and implementation. In Proceedings of the Fifth Annual IEEE Symposium on Computer-Based Medical Systems, Durham, NC, USA, 14–17 June 1992; pp. 276–283. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.; Pan, M.; Chen, D.; Yu, Z.; Xu, Y.; Ding, Z.; Liu, X.; Wan, K.; Dai, W. Enhancing Precision in Magnetic Map Interpolation for Regions with Sparse Data. Appl. Sci. 2024, 14, 756. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, K.; Wu, J. Research on spatial interpolation of pile defects based on improved Kriging method. J. Ground Improv. 2023, 5, 376–382. [Google Scholar] [CrossRef]
- Cui, M.; Hou, E.; Lu, T.; Hou, P.; Feng, D. Study on Spatial Interpolation Methods for High Precision 3D Geological Modeling of Coal Mining Faces. Appl. Sci. 2025, 15, 2959. [Google Scholar] [CrossRef]
- Ng, F.; Hughes, A. Reconstructing ice-flow fields from streamlined subglacial bedforms: A kriging approach. Earth Surf. Process. Landf. 2018, 44, 861–876. [Google Scholar] [CrossRef]
- Jia, Y.; Deng, S.W.; Yao, X.M.; Cai, Y.F. Kriging interpolation algorithm based on constraint particle swarm optimization. J. Chengdu Univ. Technol. (Sci. Technol. Ed.) 2015, 42, 104–109. [Google Scholar] [CrossRef]
- Li, K.; Li, X.; Pang, C.; Zeng, X. Fast Reconstruction and Optimization of 3D Temperature Field Based-on Kriging Interpolation. In Proceedings of the 2021 3rd International Symposium on Smart and Healthy Cities (ISHC), Toronto, ON, Canada, 28–29 December 2021; pp. 198–203. [Google Scholar] [CrossRef]
- Murphy, B.; Yurchak, R.; Müller, S. GeoStat-Framework/PyKrige: v1.7.2, Version 1.7.2; Zenodo: Geneva, Switzerland, 2024.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).