Genesis of Meniscus Dynamic Distortions (MDDs) in a Medium Slab Mold Driven by Unstable Upward Flows
Abstract
1. Introduction
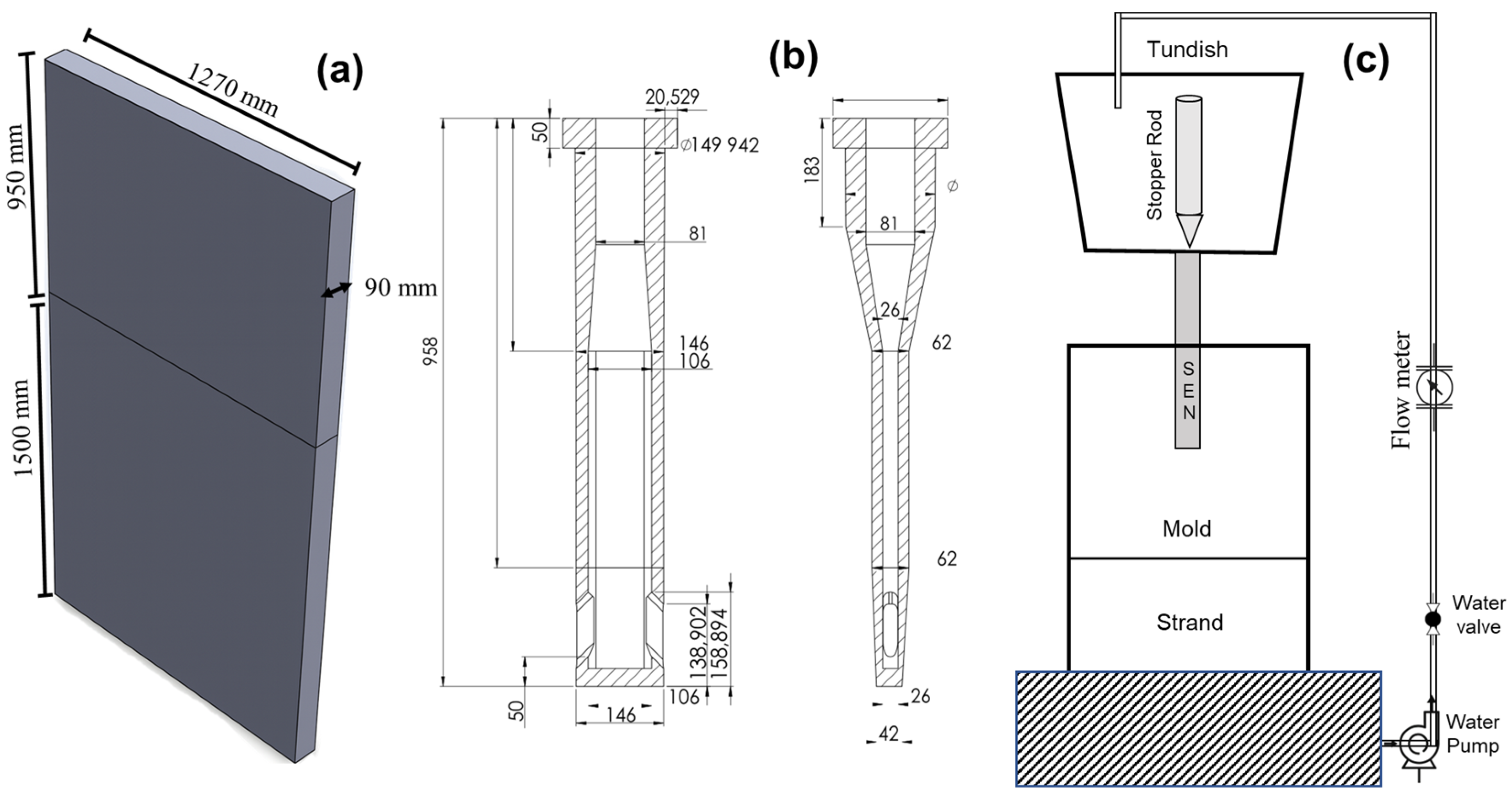
2. Materials and Methods
2.1. Experimental Procedure
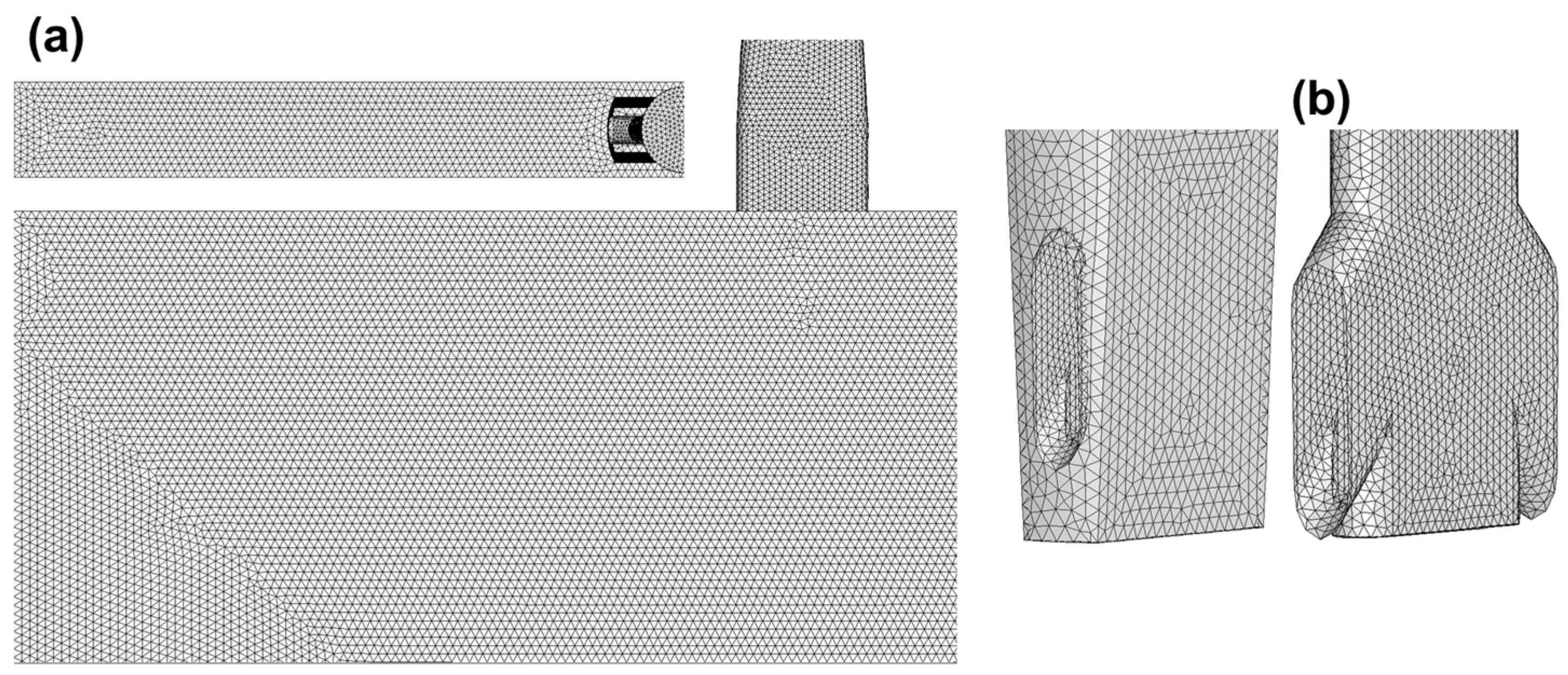
2.2. Mathematical Model
2.2.1. Basic Assumptions
The Volume of Volume (VOF)
Boundary Conditions and Numerical Details
3. Results and Discussion
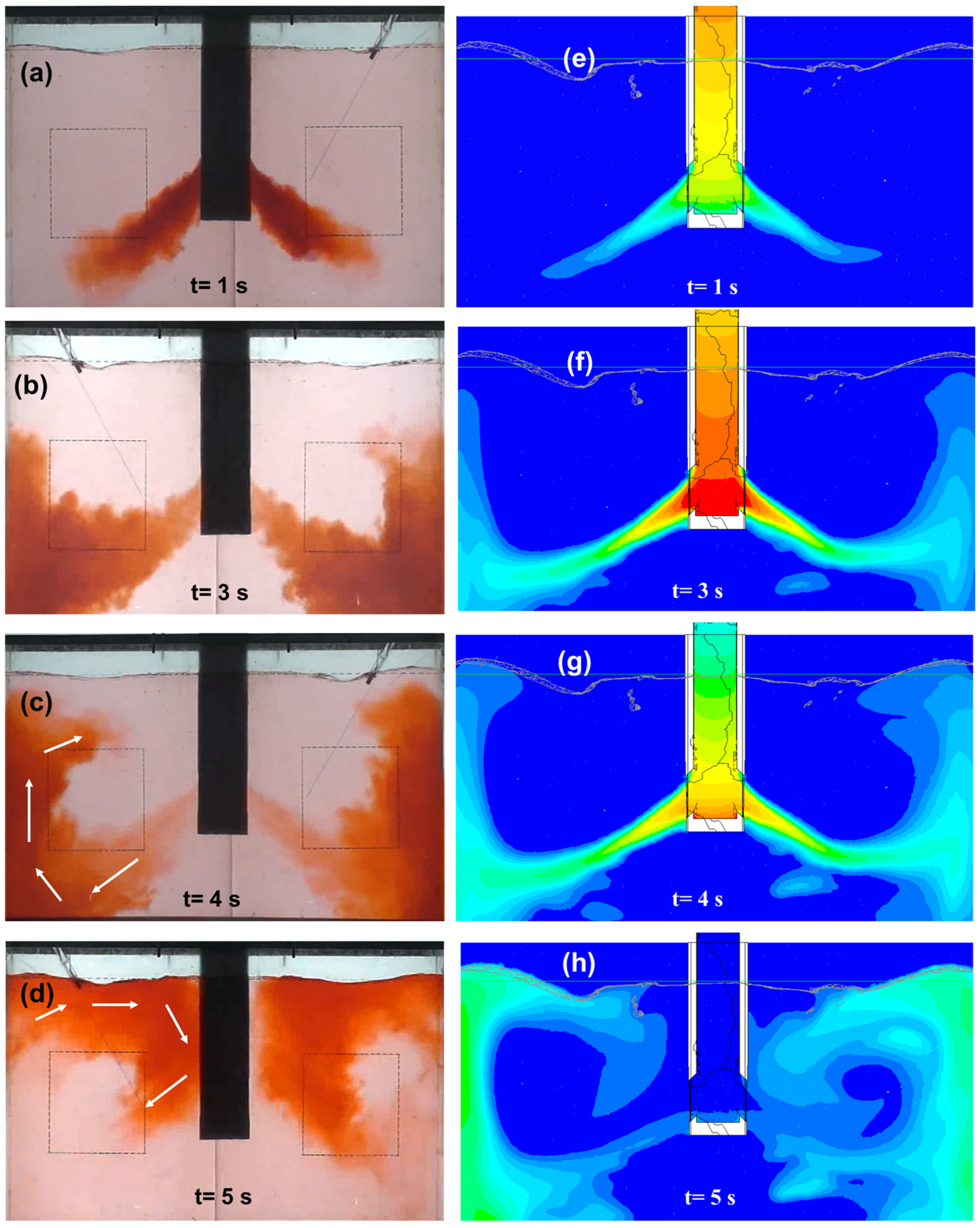
3.1. Model Validation
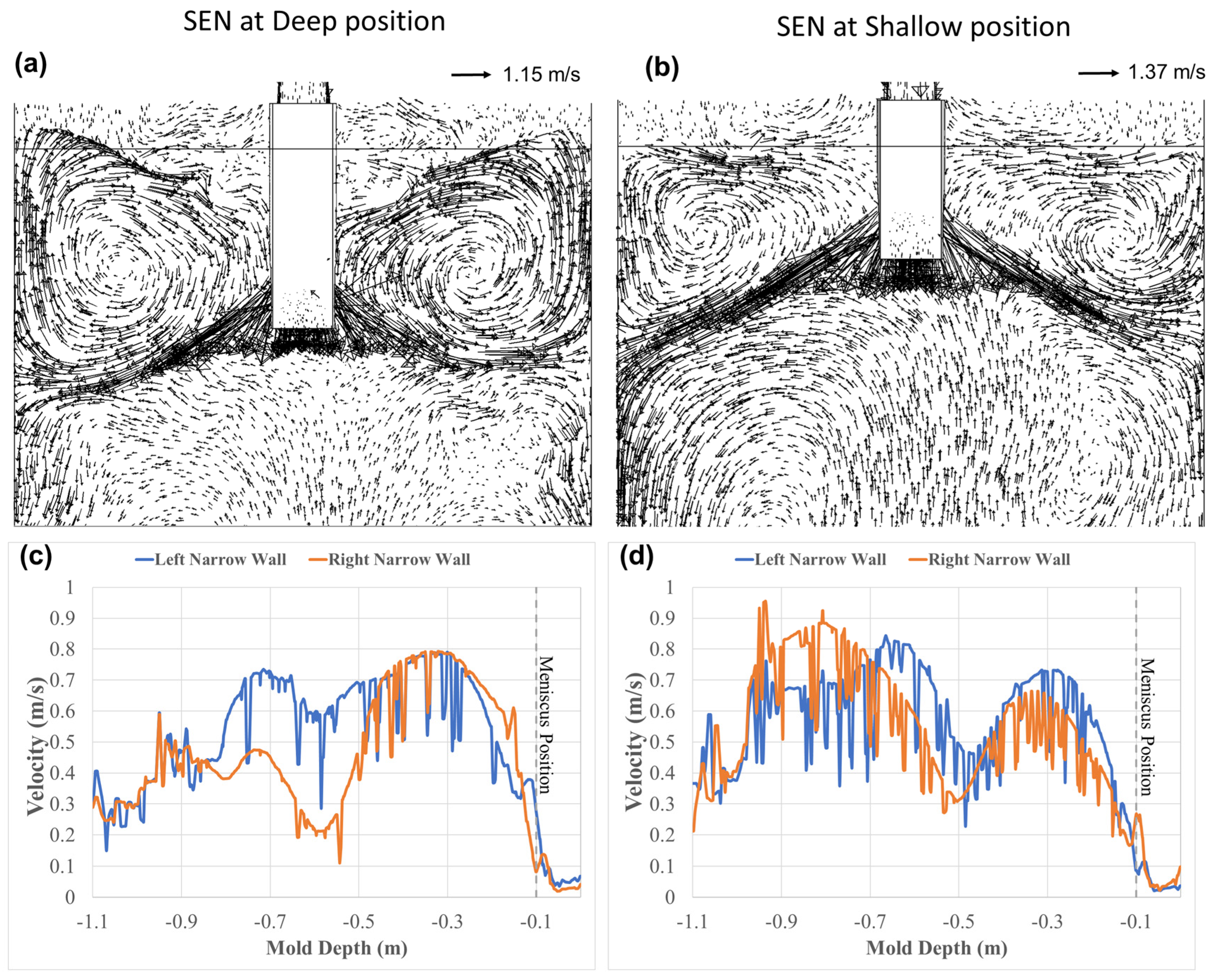
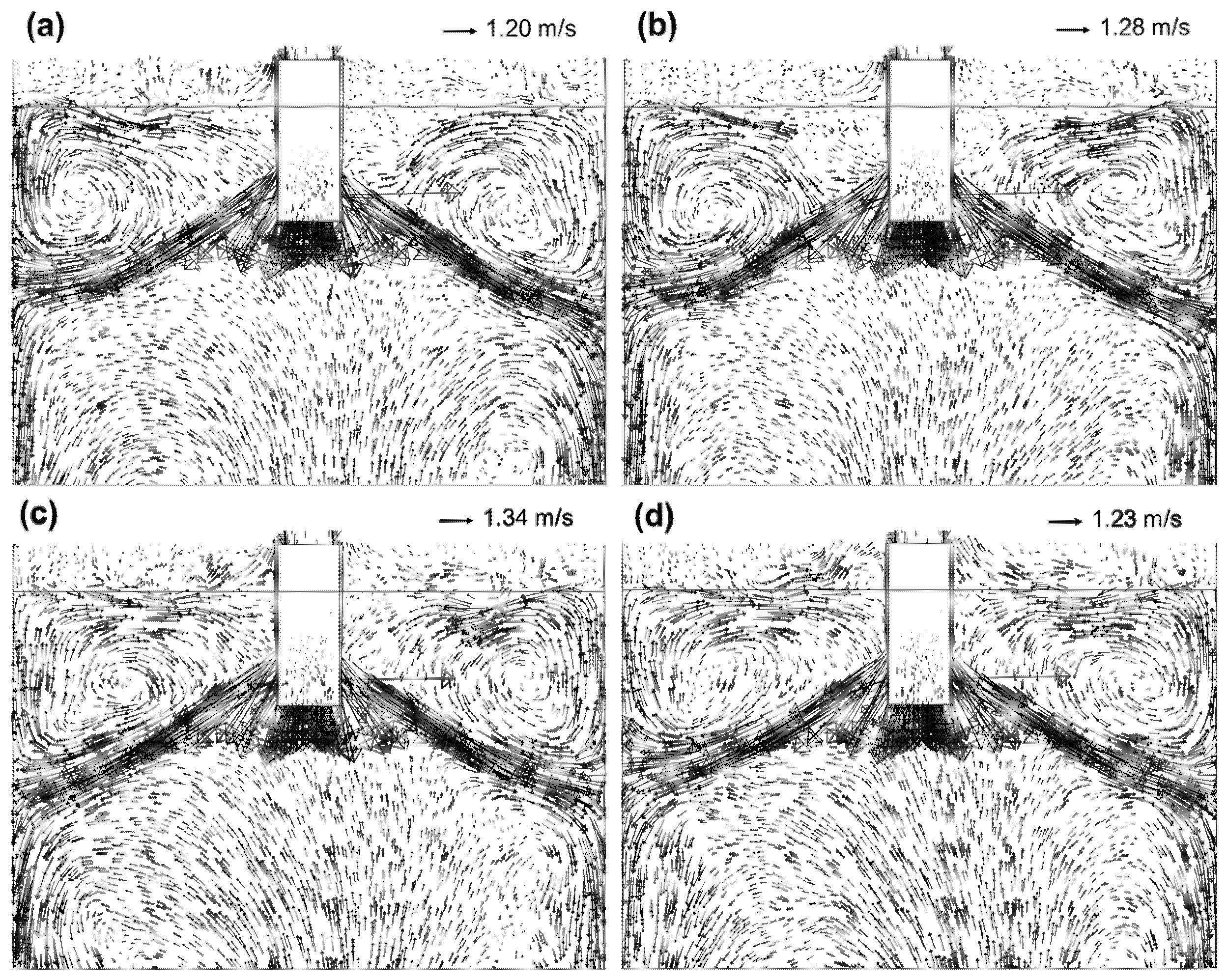
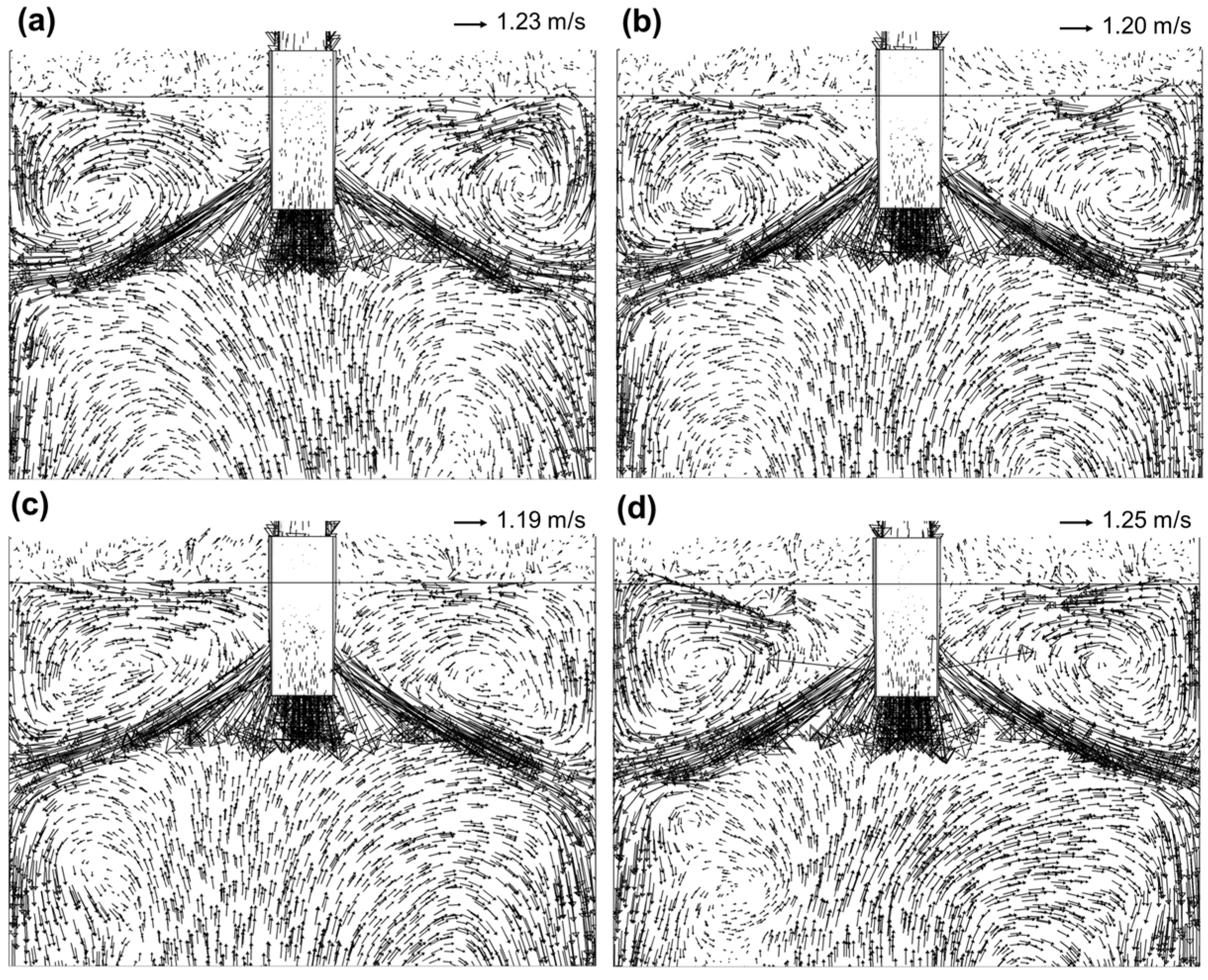
3.2. Fluid Flow Characteristics in a Quasisteady State Considering Both SEN Immersions
3.3. Study of the Fluid Dynamics Involved in the Transient Meniscus Instability
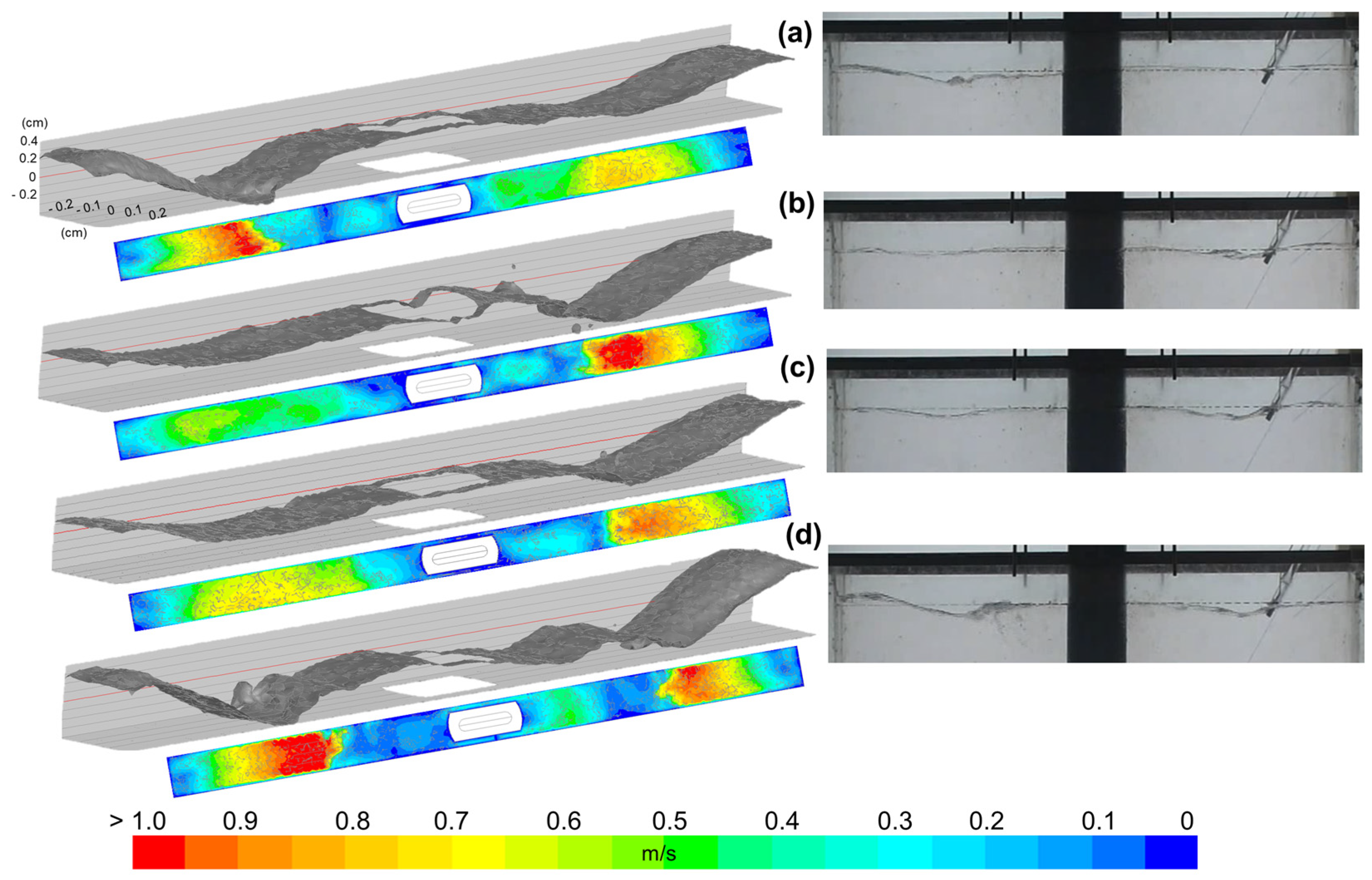
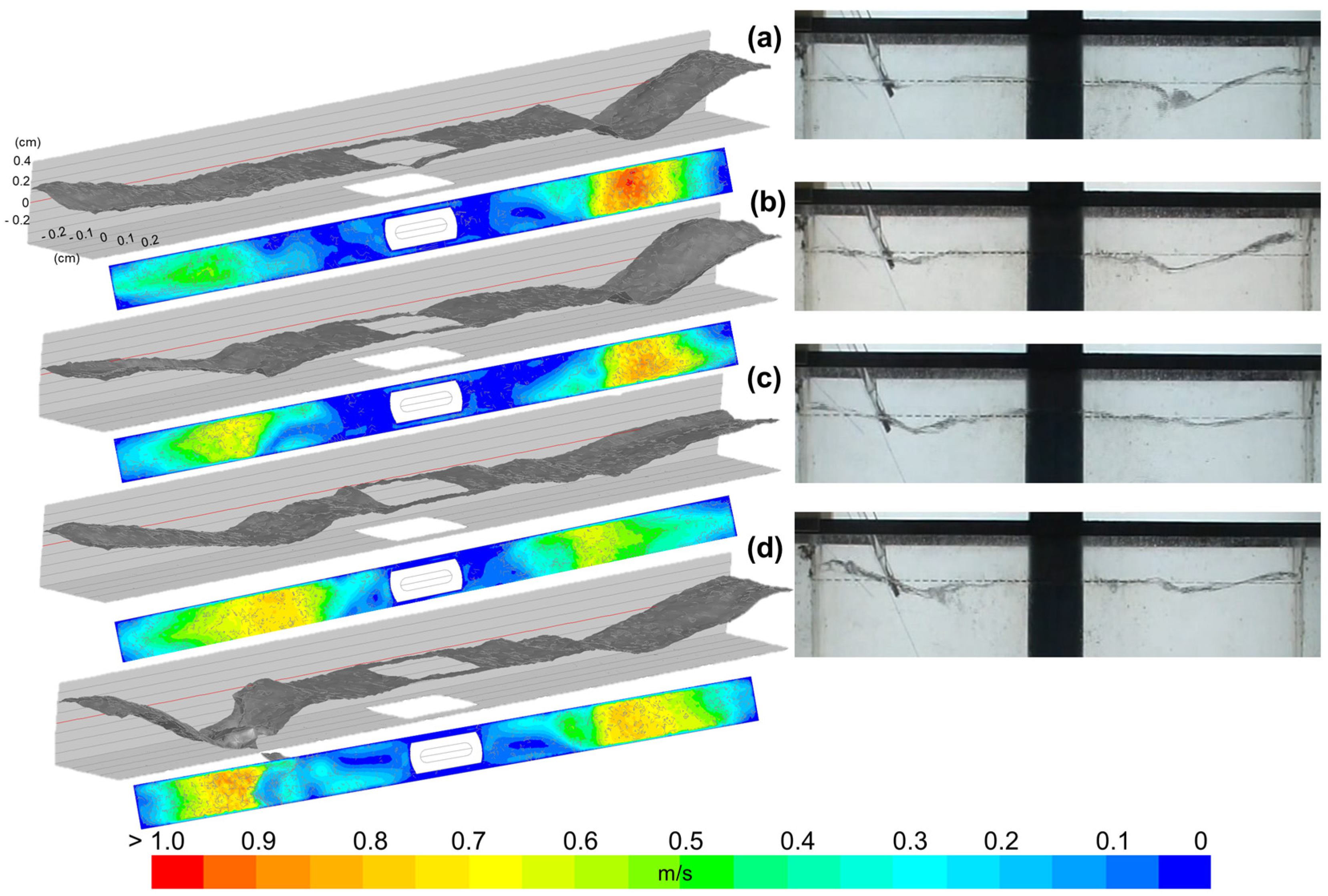
3.4. Analysis of the Meniscus Deformations
3.5. Future Work
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DD | Dynamic Distortion |
| MDD | Meniscus Dynamic Distortion |
| VOF | Volume of Fluid |
| SEN | Submerged Entry Nozzle |
| KHI | Kelvin–Helmholtz instability |
References
- Li, X.; Li, B.; Liu, Z.; Niu, R.; Liu, Y.; Zhao, C.; Huang, C.; Qiao, H.; Yuan, T. Large Eddy Simulation of Multi-phase flow and slag Entrapment in a Continuous Casting Mold. Metals 2019, 9, 7. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B.; Tsukihashi, F. Instability and Periodicity of Asymmetrical Flow in a Funnel Thin Slab Casting Mold. ISIJ Inter. 2015, 55, 805–813. [Google Scholar] [CrossRef]
- Morales, R.D.; Garcia-Hernandez, S. Turbulent instabilities in a thin slab mold. In TMS, Jim Evans Honorary Symposium; Wiley: Hoboken, NJ, USA, 2010; pp. 87–94. [Google Scholar]
- Torres-Alonso, E.; Morales, R.D.; Garcia-Hernandez, S.; Palafox-Ramos, J. Cyclic Turbulent Instabilities in a Thin Slab Mold. Part I: Physical Model. Metall. Mater. Trans. B 2010, 41B, 583–597. [Google Scholar] [CrossRef]
- Torres-Alonso, E.; Morales, R.D.; Garcia-Hernandez, S. Cyclic Turbulent Instabilities in a Thin Slab Mold. Part II: Mathematical Model. Metall. Mater. Trans. B 2010, 41B, 675–690. [Google Scholar] [CrossRef]
- Torres-Alonso, E.; Morales, R.D.; Demedices, L.G.; Najera, A.; Palafox-Ramos, J. Flow Dynamics in Thin Slab Molds Driven by Sustainable Oscillating Jets from the Feeding SEN. ISIJ Inter. 2007, 47, 679–688. [Google Scholar] [CrossRef]
- Park, H.S.; Nam, H.; Yoon, J.K. Numerical Analysis of Fluid Flow and Heat Transfer in the Parallel Type Mold of a Thin Slab Caster. ISIJ Inter. 2001, 41, 974–980. [Google Scholar] [CrossRef]
- Shen, B.Z.; Shen, H.F.; Liu, B.C. Water Modelling of Level Fluctuation in thin Slab Continuous Casting Mould. Ironmak. Steelmak. 2009, 36, 33–38. [Google Scholar] [CrossRef]
- Shen, B.; Shen, H.; Liu, B. Instability of Fluid Flow and Level Fluctuation in Continuous Thin Slab Casting Mould. ISIJ Inter. 2007, 47, 427–432. [Google Scholar] [CrossRef]
- Hajari, A.; Meratian, M. Surface Turbulence in a Physical Model of a Steel Thin Slab Continuous Caster. Int. J. Miner. Metall. Mater. 2010, 17, 697–703. [Google Scholar] [CrossRef]
- Jeon, Y.J.; Sung, H.J.; Lee, S. Flow Oscillations and Meniscus Fluctuations in a Funnel-Type Water Mold Model. Metall. Mater. Trans. B 2010, 41B, 121–130. [Google Scholar] [CrossRef]
- Morales, R.D.; Tang, Y.; Nitzl, G.; Eglsaeer, C.; Hackl, G. Design of a Submerged Entry Nozzle for Thin Slab Molds Operating at High Casting Speeds. ISIJ Inter. 2012, 52, 1607–1615. [Google Scholar] [CrossRef]
- Xiao, P.; Wang, R.; Zhu, L.; Chen, C. Influence of Submerged Entry Nozzle Offset on the Flow Field in a Continuous Casting Mold. Metals 2025, 15, 575. [Google Scholar] [CrossRef]
- Garcia-Hernandez, S.; Gonzalez-Guzman, C.H.; Morales, R.D.; Barreto, J. de J.; Gutierrez, E.; Calderon-Ramos, I. Modeling Study of EMBr Effects on the Detrimental Dynamic Distortion Phenomenon in a Funnel Thin Slab Mold. Crystals 2020, 10, 958. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Z.; Li, B. Combined Effects of EMBr and SEMS on Melt Flow and Solidification in a Thin Slab Continuous Caster. Metals 2021, 11, 948. [Google Scholar] [CrossRef]
- Vakhrushev, A.; Kharicha, A.; Karimi-Sibaki, E.; Wu, M.; Ludwig, A.; Nitzl, G.; Hackl, G.; Watzinger, J. Modeling Asymmetric Flow in the Thin-Slab Casting Mold Under Electromagnetic Brake. Steel Res. Inter. 2022, 93, 2200088. [Google Scholar] [CrossRef]
- Vakhrushev, A.; Kharicha, A.; Liu, Z.; Wu, M.; Ludwig, A.; Nitzl, G.; Tang, Y.; Hackl, G.; Watzinger, J. Optimizing the Flow Conditions in the Thin-Slab Casting Mold Using Electromagnetic Brake. In Proceedings of the 8th International Conference on Modeling and Simulation of Metallurgical Processes in Steelmaking, Toronto, ON, Canada, 13–15 August 2019; pp. 615–619. [Google Scholar] [CrossRef]
- Gutierrez-Montiel, Y.S.; Morales, R.D. Control of Meniscus Stability in Medium Thickness-straight Walls Slab Mould. ISIJ Inter. 2013, 53, 230–239. [Google Scholar] [CrossRef]
- Xuan, M.; Chen, M. Optimal Design of the Submerged Entry Nozzle for Thin Slab Continuous Casting Molds. Metals 2021, 11, 1223. [Google Scholar] [CrossRef]
- Hai-qi, Y.; Miao-Yong, Z.; Jun, W. Interfacial Fluctuation Behavior of Steel/Slag in a Medium-Thin Slab Continuous Mold With Argon Gas Injection. J. Iron Steel Res. Int. 2010, 17, 5–11. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, X.; Zhang, J.; Wang, W. Effect of SEN Structure on the Mold Level Fluctuation and Heat Transfer for a Medium Thin Slab Caster. Metallurgy 2008, 15, 120–124. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: London, UK, 2000; p. 358. [Google Scholar]
- Poirier, D.R.; Geiger, G.H. Transport Phenomena in Materials Processing; Springer: Cham, Switzerland, 1994; p. 39. [Google Scholar]
- ANSYS Inc. FLUENT 12.0, User’s Guide; Centerra Resource Park: Cavendish Court, Lebanon, 2009. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comp. Meth Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comp. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Liovic, P.; Liow, J.L.; Rudman, M.A. Volume of Fluid (VOF) Method for the Simulation of Metallurgical Flows. ISIJ Int. 2001, 41, 225–233. [Google Scholar] [CrossRef]
- Barati, H.; Wu, M.; Kharicha, A.; Ludwig, A. Role of Solidification in Submerged Entry Nozzle Clogging during Continuous Casting of Steel. Steel Res. Int. 2020, 91, 2000230. [Google Scholar] [CrossRef]
- Lee, W.; Kim, J.G.; Jung, J.; Huh, K.Y. Prediction of Nozzle Clogging through Fluid–Structure Interaction in the Continuous Steel Casting Process. Steel Res. Inter. 2021, 92, 2000549. [Google Scholar] [CrossRef]
- Bai, H.; Ni, P.; Ersson, M.; Zhang, T.; Jönsson, P.G. Effect of swirling flow tundish submerged entry nozzle outlet design on multiphase flow and heat transfer in mould. Ironmak. Steelmak. 2019, 46, 911–920. [Google Scholar] [CrossRef]
- Xu, L.; Pei, Q.-W.; Han, Z.-F.; Yang, S.; Wang, J.-Y.; Yao, Y.-T. Modeling study on melt flow, heat transfer, and inclusion motion in the funnel-shaped molds for two thin-slab casters. Processes 2022, 10, 2738. [Google Scholar] [CrossRef]
- Hibbeler, L.C.; Thomas, B.G. Mold slag entrainment mechanisms in continuous casting molds. Iron Steel Technol. 2013, 10, 121–136. [Google Scholar]
- Lopez, A.; Gutierrez, E.; Garcia-Hernandez, S.; Morales, R.D.; Barreto, J.d.J. A Numerical Analysis of the Fluid Flow in a Slab Mold Considering a SEN with Real Clogging and with Symmetrical Reductions. Crystals 2025, 15, 777. [Google Scholar] [CrossRef]
- Ramos-Cardona, E.; Calderon-Ramos, I.; Morales, R.D.; Servin-Castañeda, R.; Perez-Alvarado, A.; Arreola-Villa, S.A.; Mendez-Gordillo, A.R.; Garcia-Hernandez, S. Internal SEN Design and Its Influence on Fluid Dynamics in Slab Molds: A Combined Numerical and Experimental Analysis. Metals 2025, 15, 1043. [Google Scholar] [CrossRef]
- Liu, J.Q.; Yang, J.; Ma, C.; Guo, Y.; He, W.Y.; Zhao, C.L.; Jiang, R.B.; Guo, Y.T. Effect of mold width on flow field in a slab continuous-casting mold with high-temperature velocity measurement and numerical simulation. Metals 2021, 11, 1943. [Google Scholar] [CrossRef]
- Wang, X.H.; Wang, X.H.; Zhang, J.M.; Jing, C.L. Water modeling study on the meniscus dynamic distortion of molten steel level in a CSP thin slab casting mould. J. Univ. Sci. Technol. Beijing 2009, 31, 234–239. [Google Scholar] [CrossRef]







| Phase | Parameter | Value |
|---|---|---|
| Air [14] | Density (kg/m3) | 1.225 |
| Viscosity (kg/m·s) | 1.7894 × 10−5 | |
| Steel [14] | Density (kg/m3) | 7100 |
| Viscosity (kg/m·s) | 0.0064 | |
| Air–Steel [14] | Interphase tension (N/m) | 1.6 |
| SEN Position * | Deep (mm) | 396 |
| Shallow (mm) | 245 | |
| Casting velocity ** (m/min) | 3.62 | |
| Thickness of the air phase ** (mm) | 50 |
| SEN Immersion | Meniscus Side | Meniscus Deformation | Mathematical Model | Physical Model |
|---|---|---|---|---|
| Deep | Left | Max (mm) | 30 | 29 |
| Min (mm) | −38 | −33 | ||
| Right | Max (mm) | 31 | 28 | |
| Min (mm) | −30 | −27 | ||
| Shallow | Left | Max (mm) | 30 | 34 |
| Min (mm) | −35 | −38 | ||
| Right | Max (mm) | 32 | 35 | |
| Min (mm) | −29 | −29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tello-Cabrera, E.D.; García-Hernández, S.; Gutierrez, E.; Morales Dávila, R.; Barreto, J.d.J.; Servín-Castañeda, R. Genesis of Meniscus Dynamic Distortions (MDDs) in a Medium Slab Mold Driven by Unstable Upward Flows. Processes 2025, 13, 3425. https://doi.org/10.3390/pr13113425
Tello-Cabrera ED, García-Hernández S, Gutierrez E, Morales Dávila R, Barreto JdJ, Servín-Castañeda R. Genesis of Meniscus Dynamic Distortions (MDDs) in a Medium Slab Mold Driven by Unstable Upward Flows. Processes. 2025; 13(11):3425. https://doi.org/10.3390/pr13113425
Chicago/Turabian StyleTello-Cabrera, Eriwiht Dominic, Saúl García-Hernández, Enif Gutierrez, Rodolfo Morales Dávila, Jose de Jesus Barreto, and Rumualdo Servín-Castañeda. 2025. "Genesis of Meniscus Dynamic Distortions (MDDs) in a Medium Slab Mold Driven by Unstable Upward Flows" Processes 13, no. 11: 3425. https://doi.org/10.3390/pr13113425
APA StyleTello-Cabrera, E. D., García-Hernández, S., Gutierrez, E., Morales Dávila, R., Barreto, J. d. J., & Servín-Castañeda, R. (2025). Genesis of Meniscus Dynamic Distortions (MDDs) in a Medium Slab Mold Driven by Unstable Upward Flows. Processes, 13(11), 3425. https://doi.org/10.3390/pr13113425







