Numerical Study on a PV/T Using Microchannel Heat Pipe
Abstract
1. Introduction
2. Description of the Microchannel Heat Pipe PV/T Model
2.1. Establishment of the Microchannel Heat Pipe Model
- (1)
- Assume steady-state conditions.
- (2)
- The vapor-liquid interface temperature is close to saturation, and the flow was confirmed to be turbulent based on calculated Reynolds numbers exceeding 2100 under typical operating conditions.
- (3)
- Consider convective heat loss through the microchannel heat pipe surface, Convective heat loss from external surfaces was calculated using the Churchill-Chu correlation for natural convection from horizontal cylinders, with the heat transfer coefficient ranging from 8 to 12 W/m2·K under typical conditions [17].
- (4)
- Assume that the thermal properties of all materials are isotropic and constant.
2.2. Establishment of the PV/T Model
- (1)
- Assume that the conversion efficiency of the solar cell at 298.15 K is 13.5%, and the temperature coefficient is 0.0045 K−1 [20].
- (2)
- Assume steady-state conditions.
- (3)
- Consider heat losses from convection and radiation on the upper and lower surfaces of the photovoltaic module.
- (4)
- Assume that the thermal properties of all materials are isotropic and constant.
- (5)
- Regarding radiative heat losses, the front and back surfaces of the photovoltaic panel face the sky and ground, respectively.
3. Mathematical Model
3.1. Mathematical Model of Fluid Heat Transfer Process
3.2. Mathematical Model of the PV/T Model
4. Results and Discussions
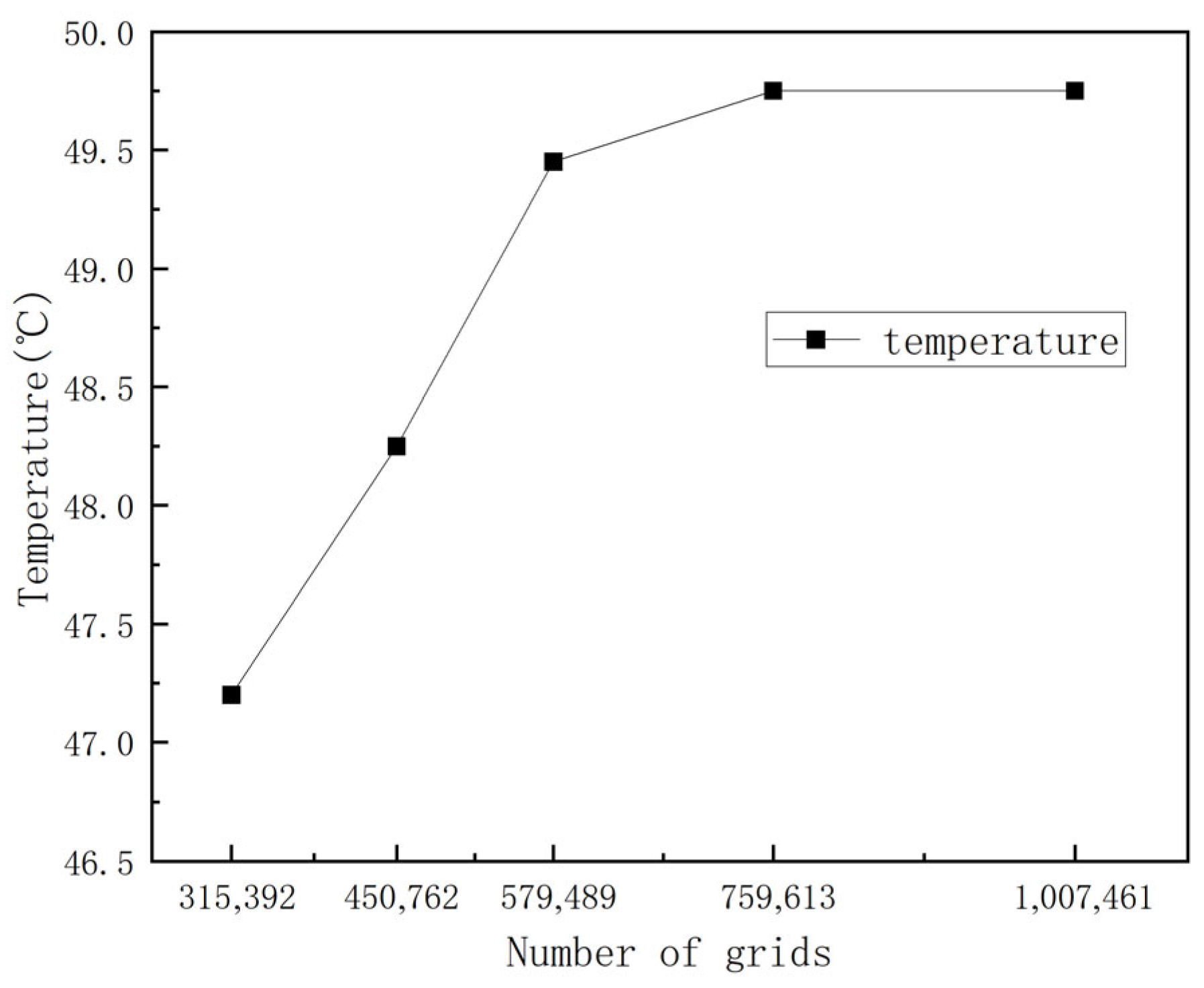
4.1. Grid Independence Verification and Model Verification
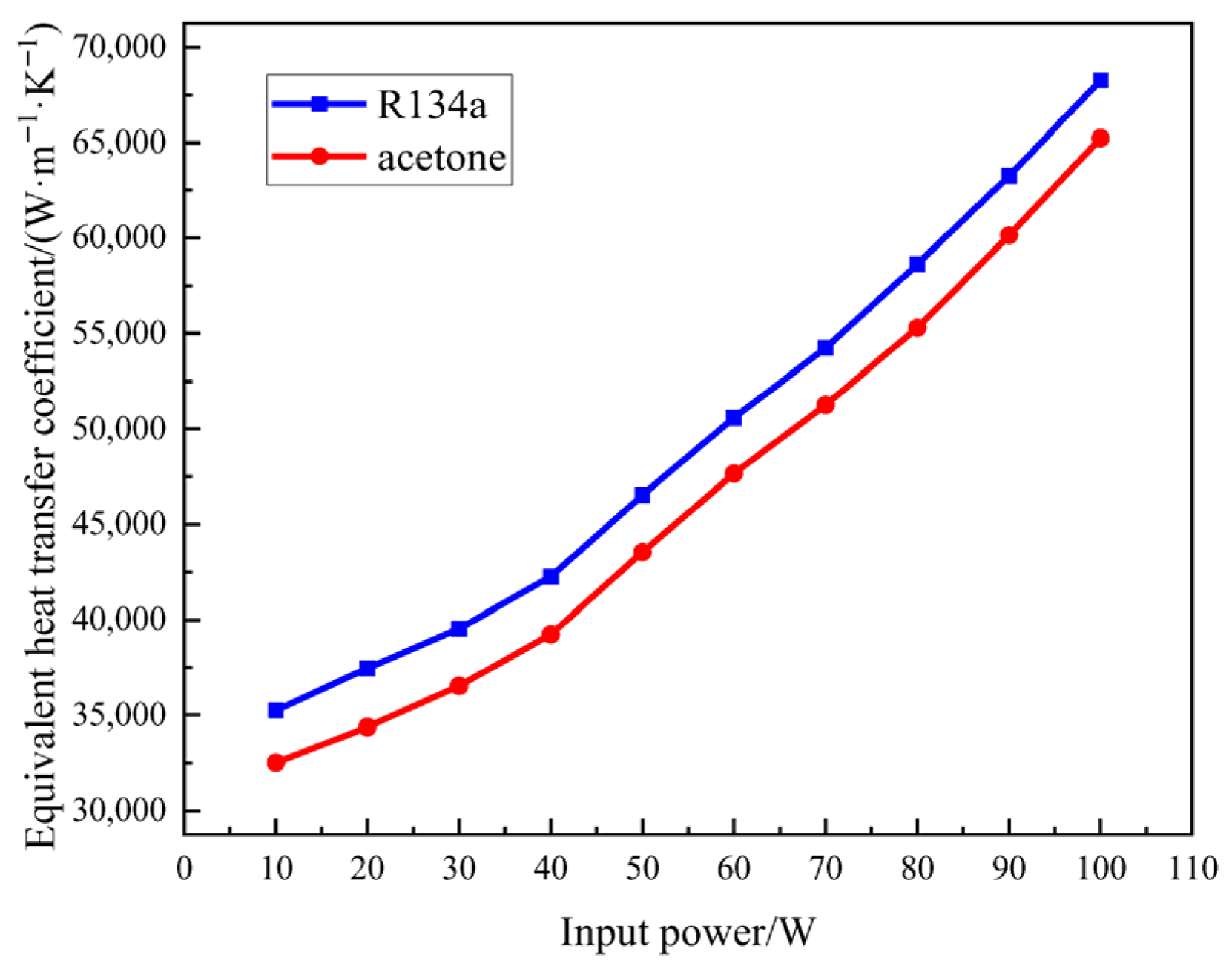
4.2. Selection of Working Fluid and Physical Properties
4.3. Performance Study of Microchannel Heat Pipe
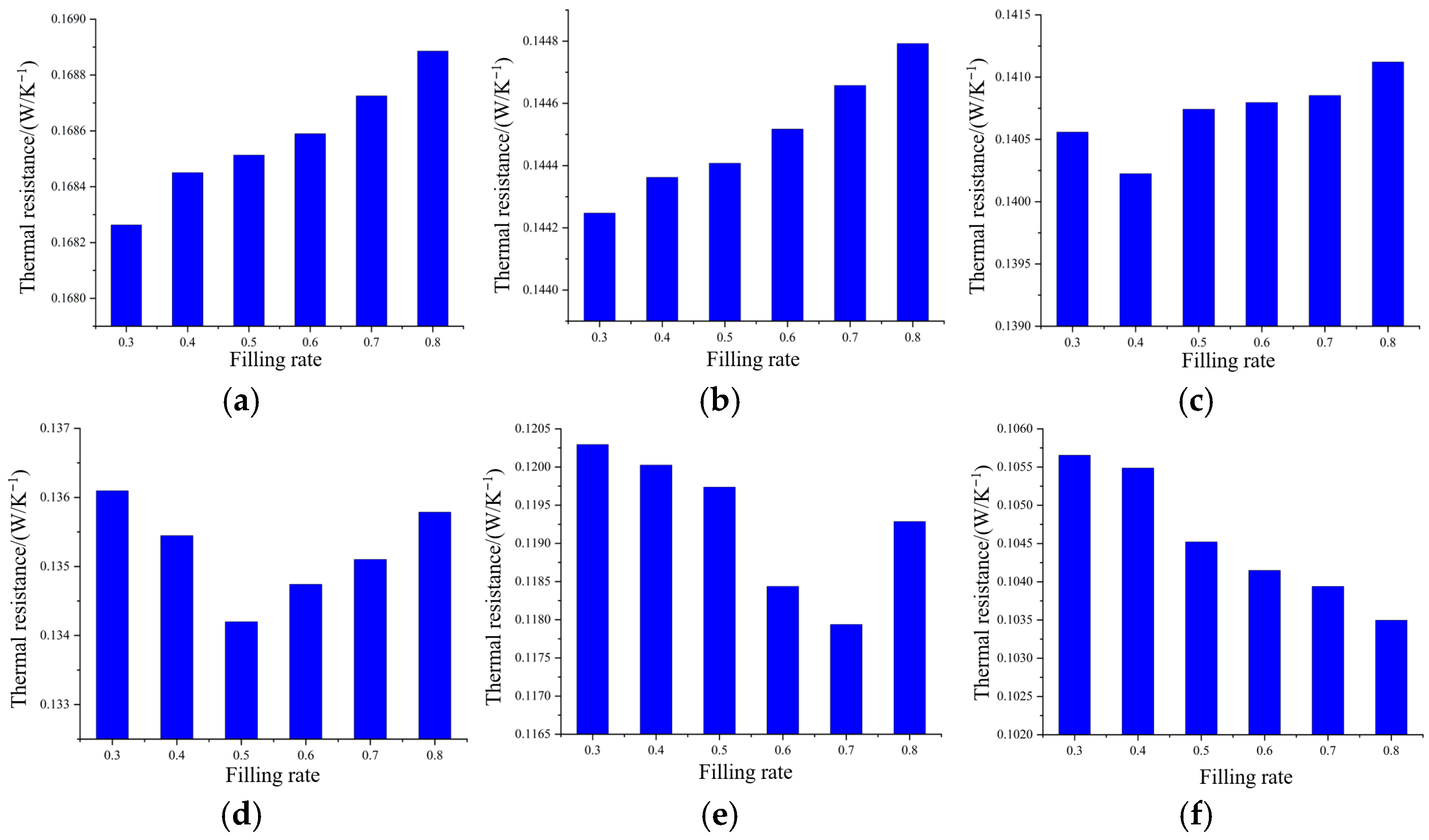
4.3.1. Heat Transfer Characteristics of Microchannel Heat Pipes at Different Fill Rates
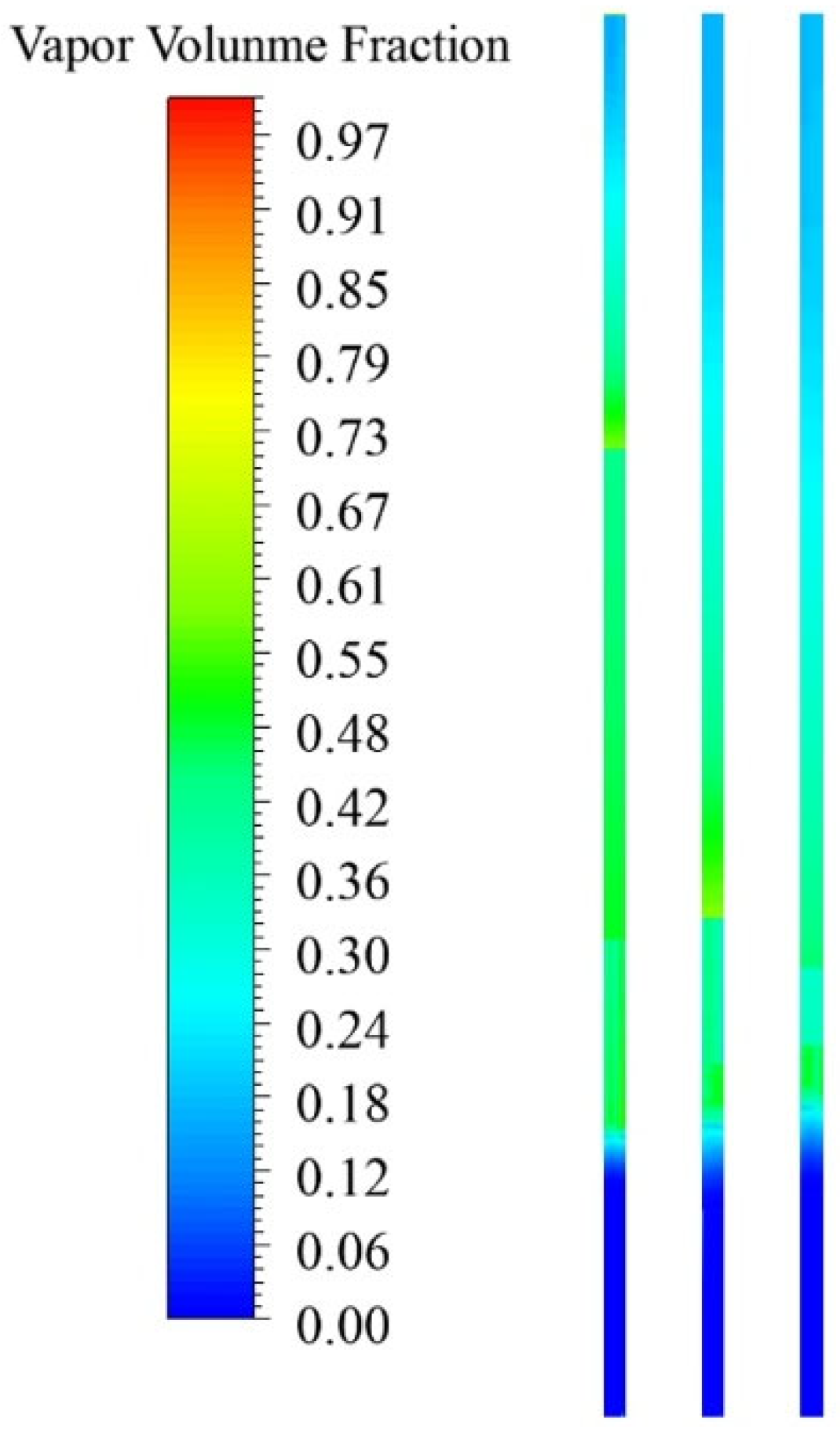
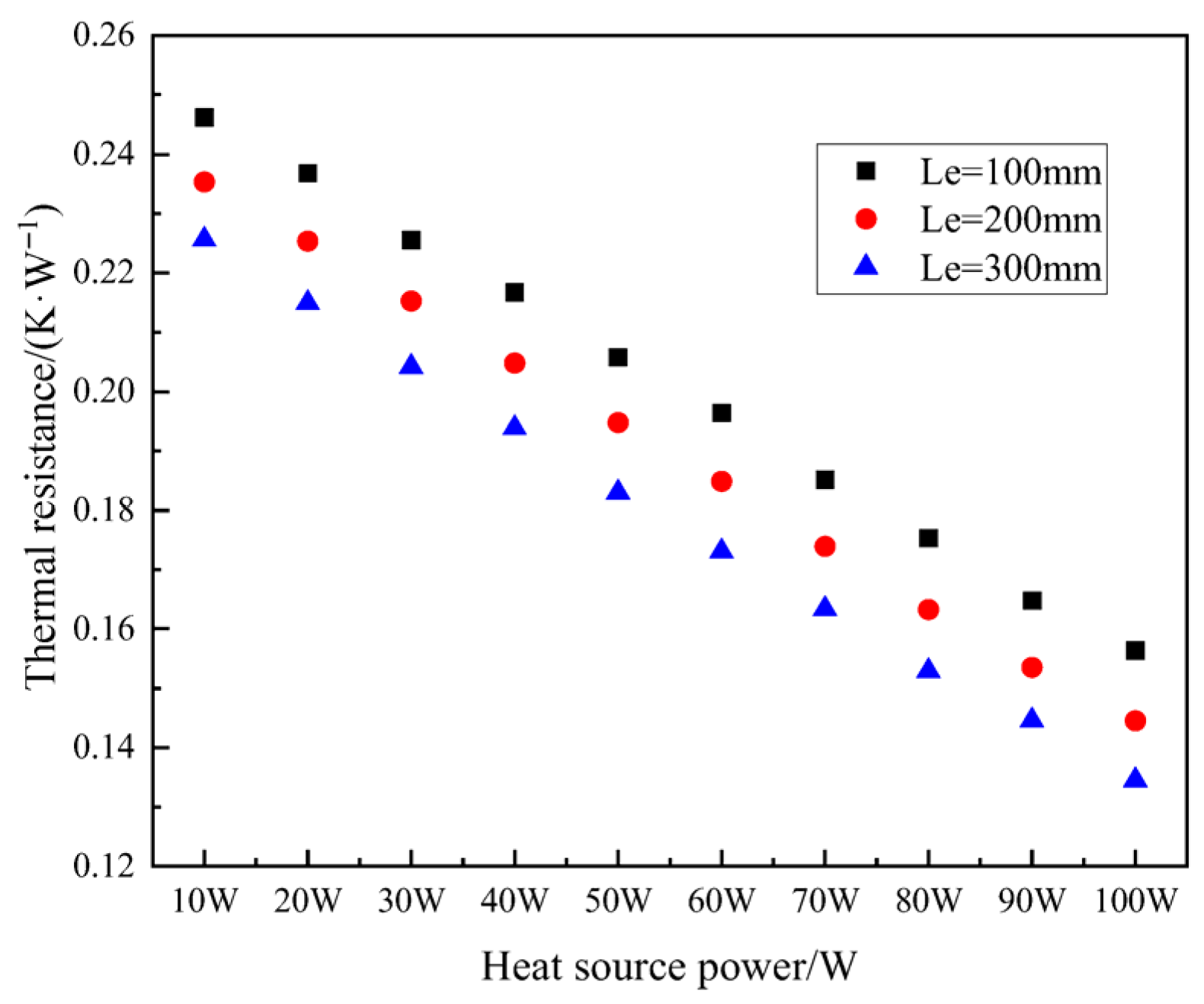
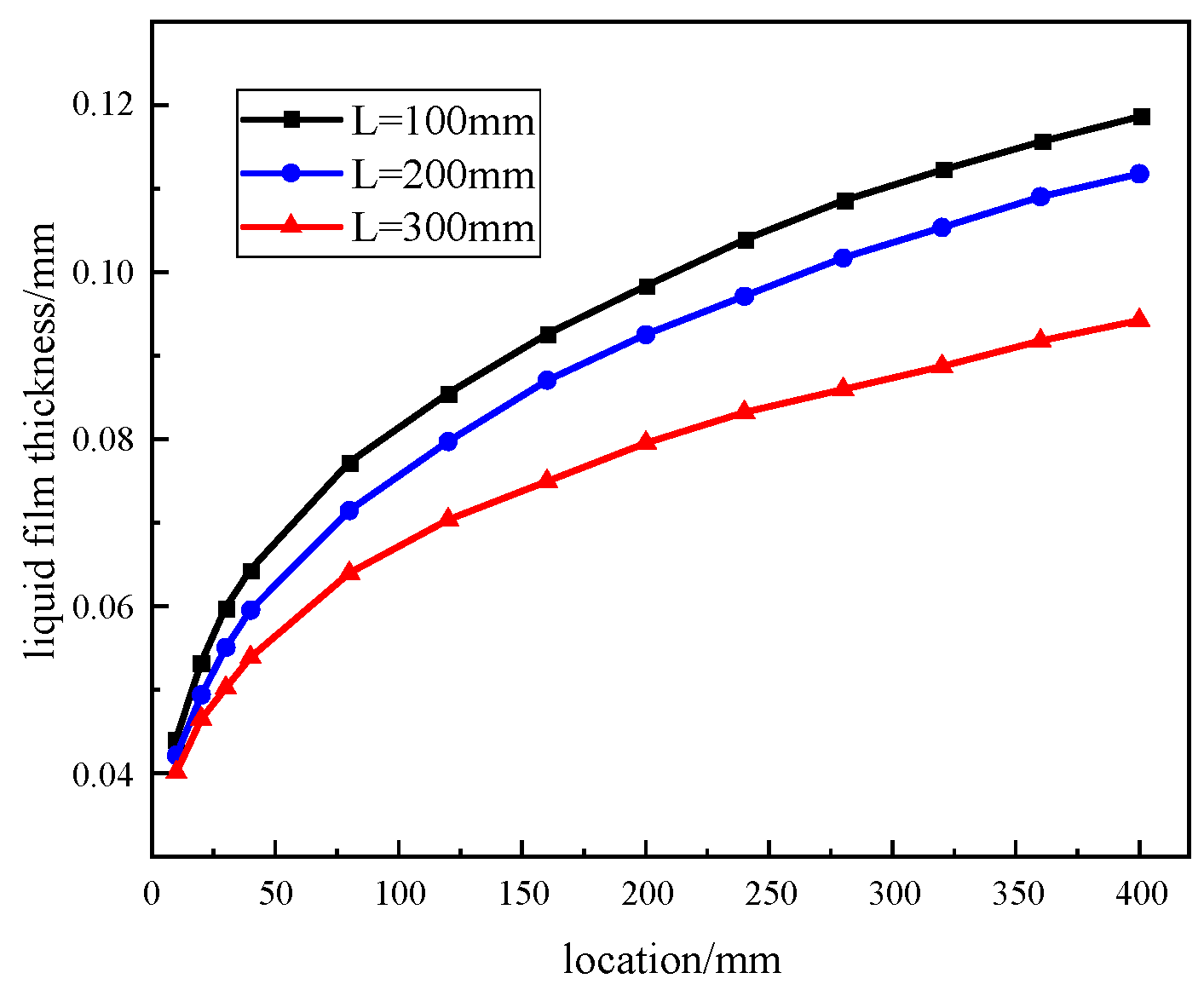
4.3.2. The Effect of Condensation Section Length on Heat Pipe Performance
4.4. Performance Study of Microchannel Heat Pipe PV/T
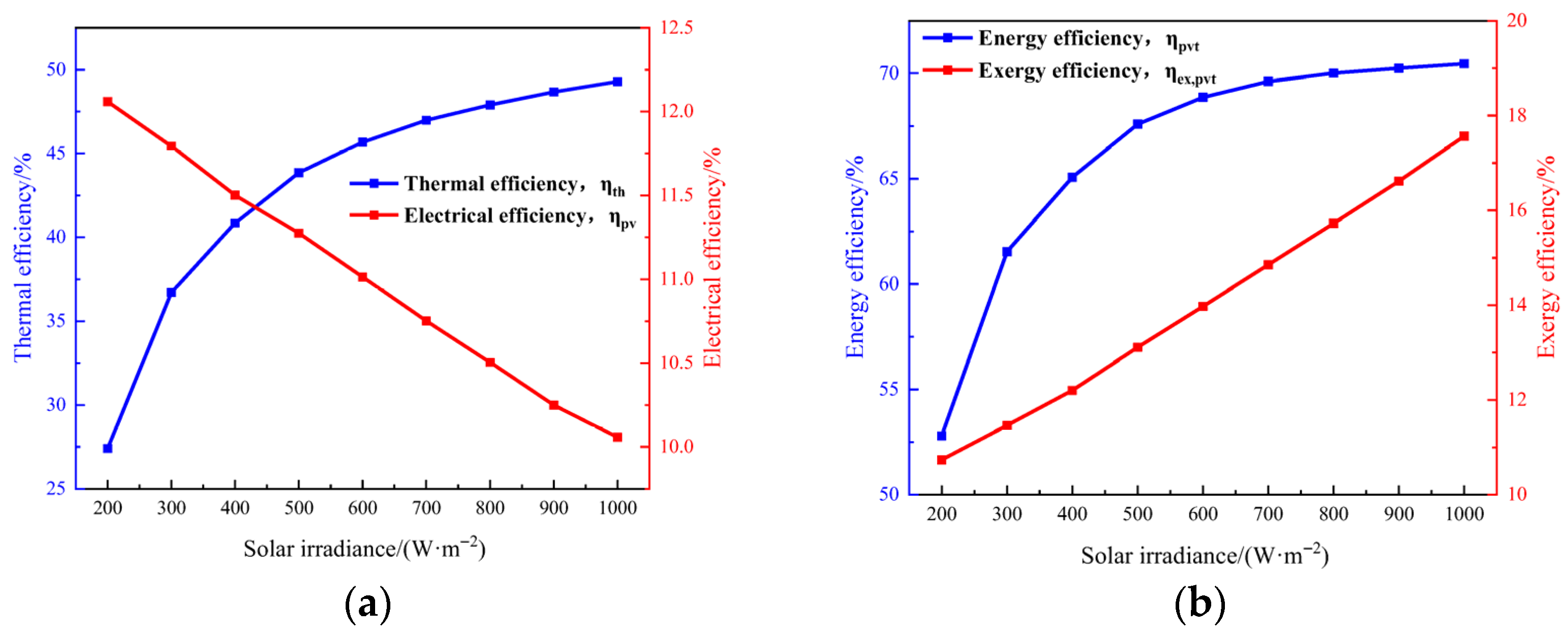
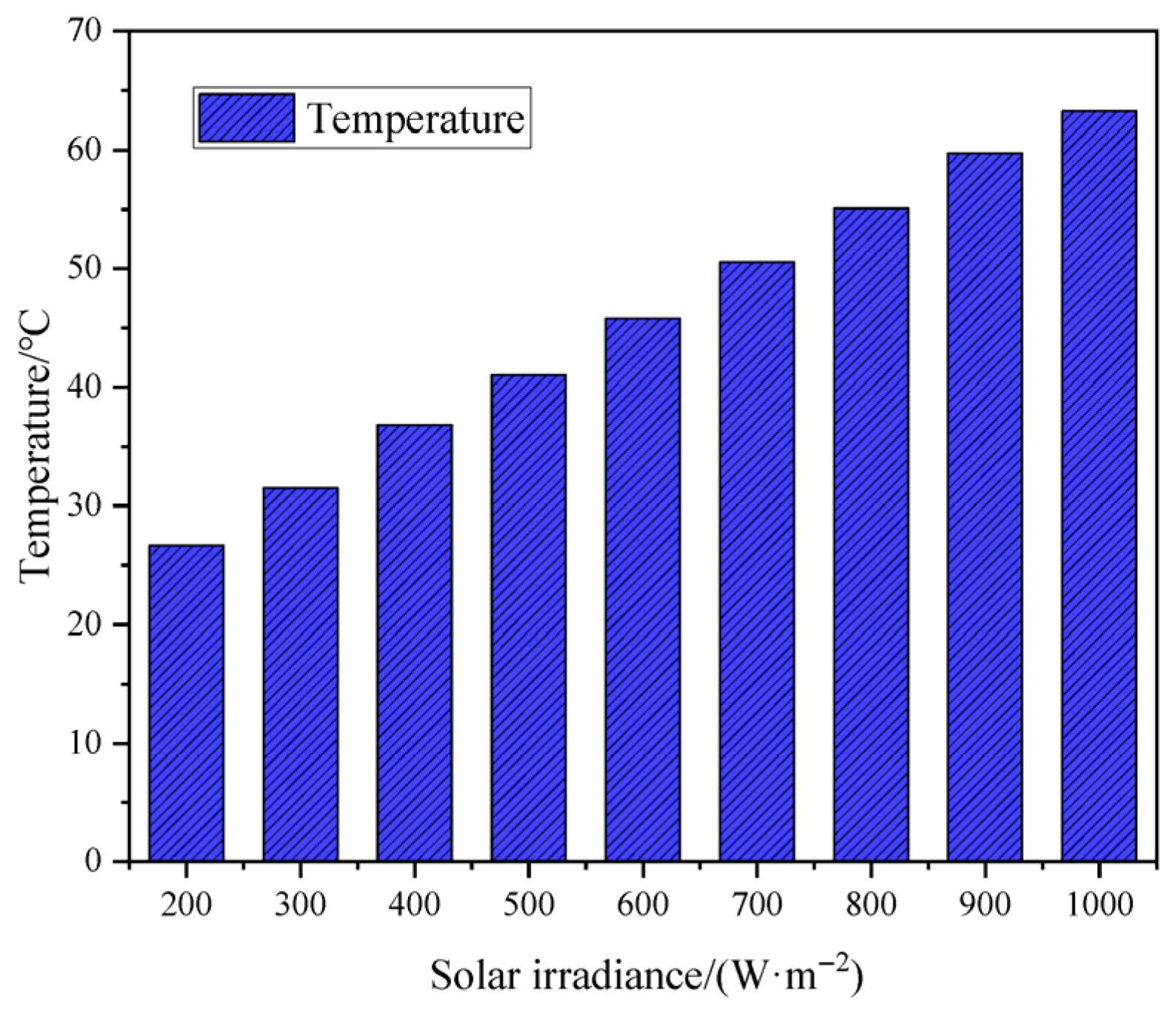
4.4.1. Effect of Solar Irradiance on PV/T Systems
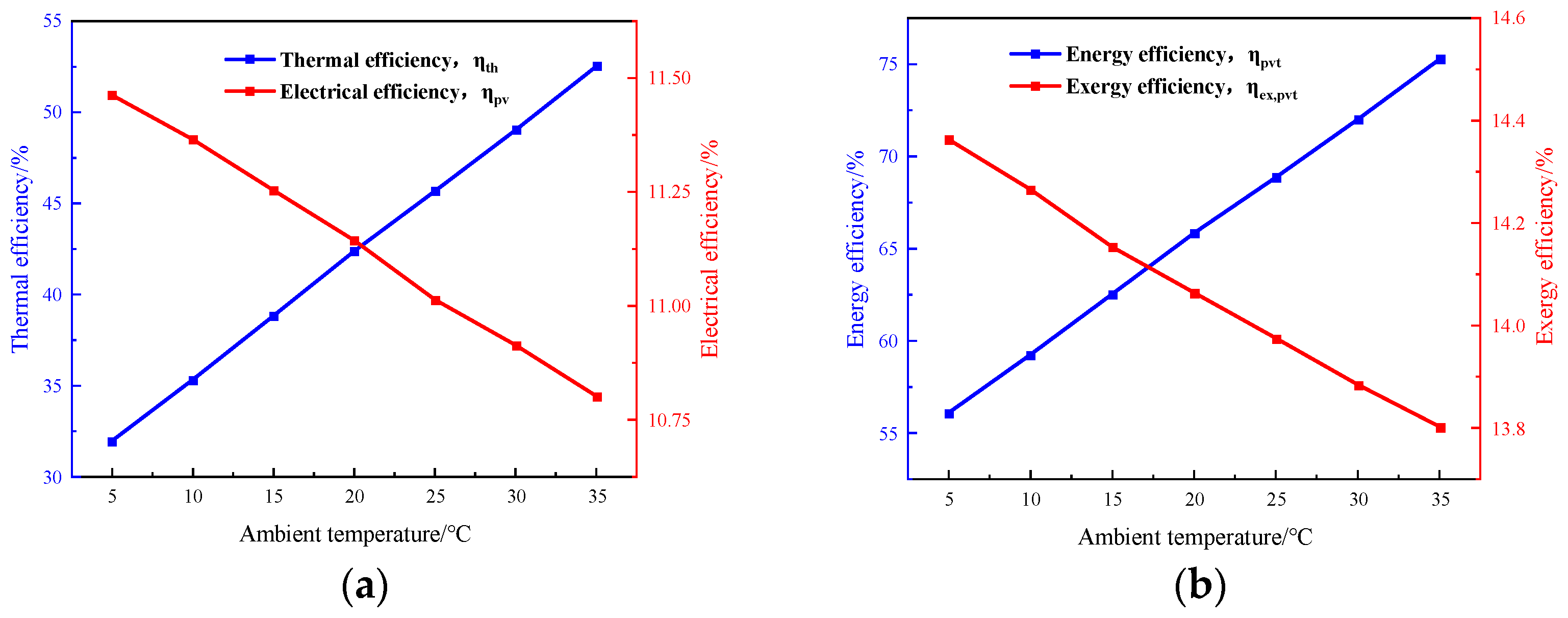
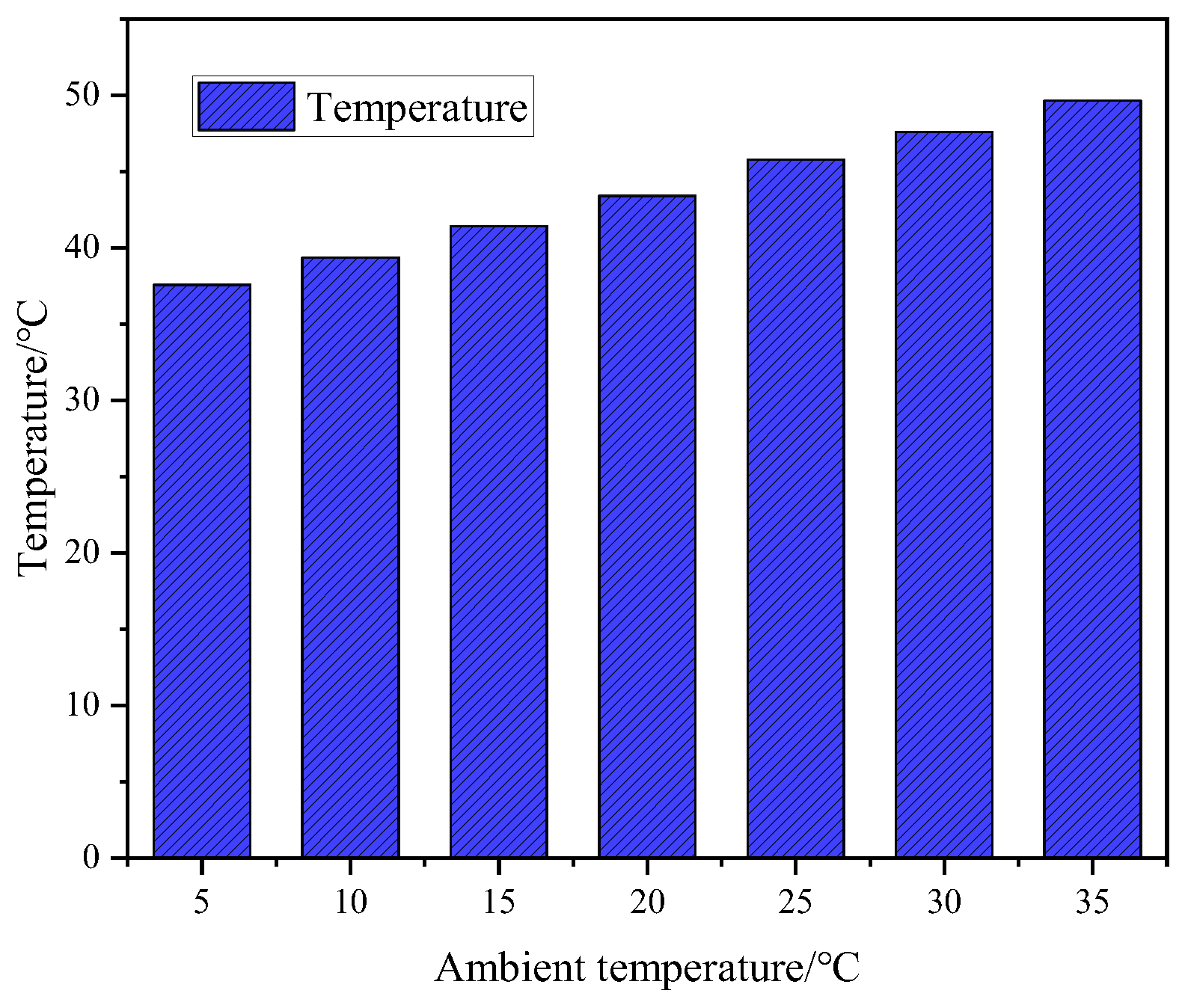
4.4.2. Effect of Ambient Temperature on PV/T Systems
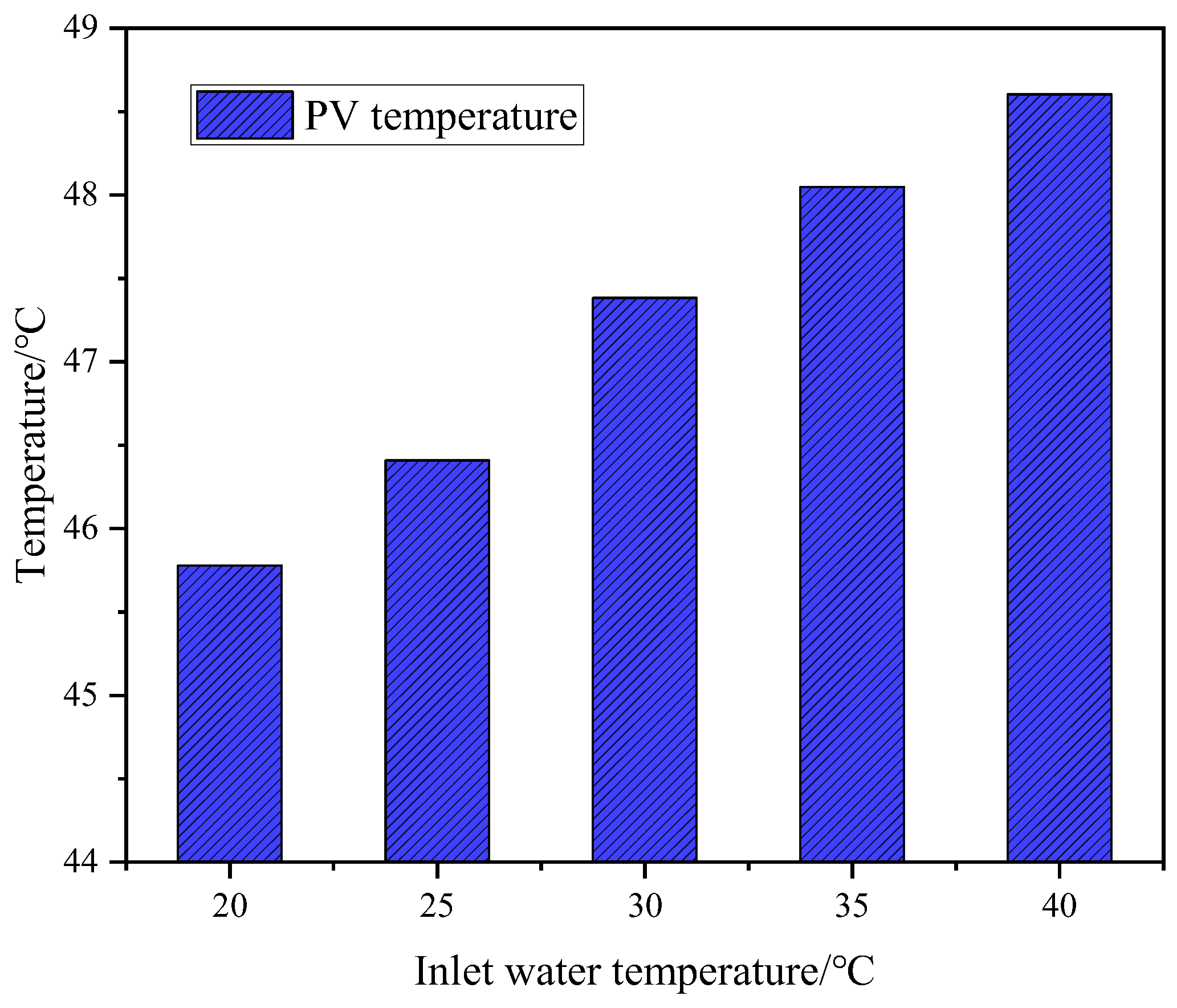
4.4.3. Effect of Inlet Water Temperature on PV/T Systems
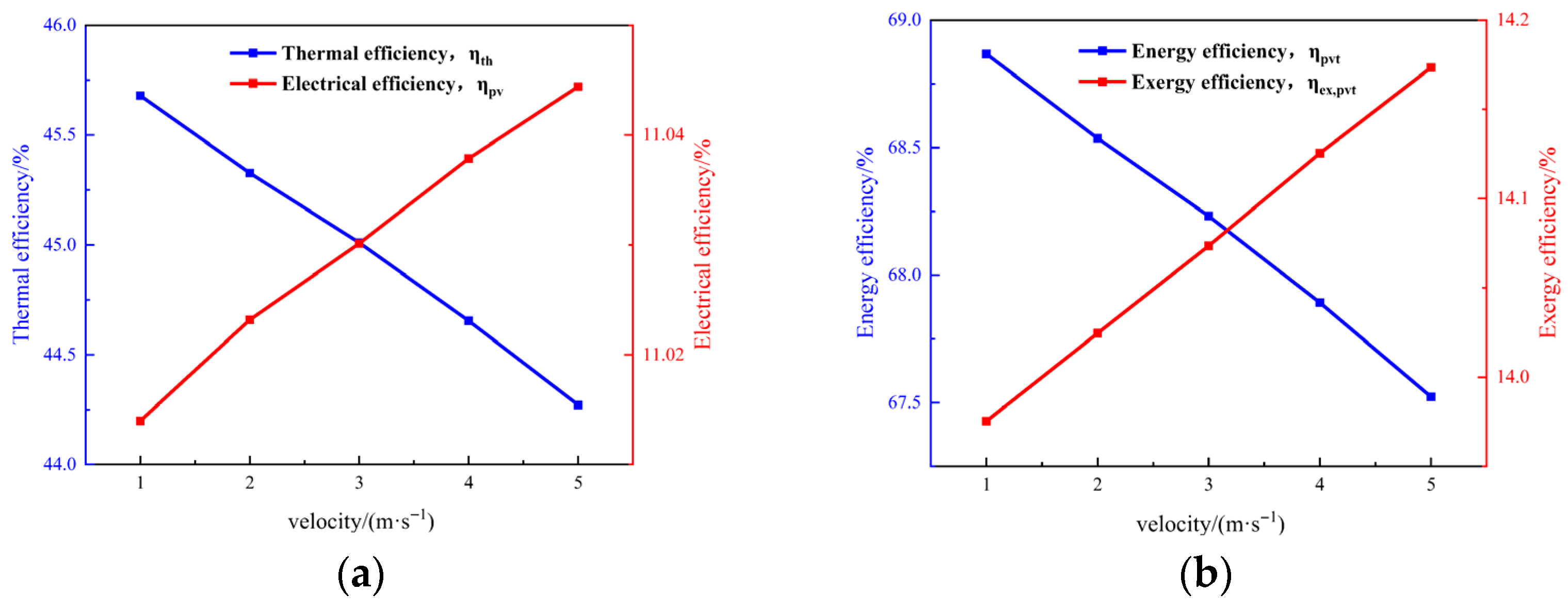
4.4.4. Effect of Wind Speed on PV/T Systems
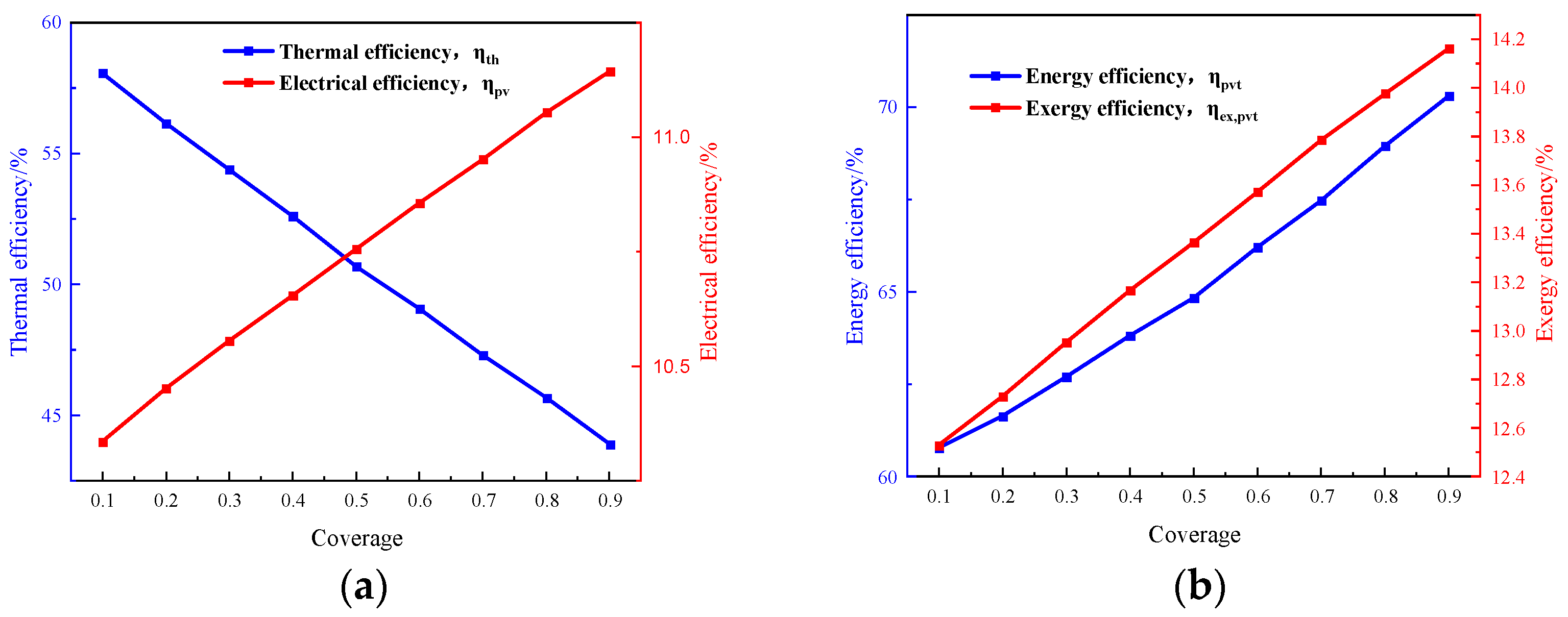
4.4.5. Analysis of the Impact of Photovoltaic Cell Coverage on Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Roman Letters | |
| Symbol | Meaning |
| A | Area |
| Ac | Collector area |
| Ai | Area of the i-th layer |
| ALV | Interfacial area density between liquid and vapor |
| cp | Specific heat capacity |
| D | Diameter (Sauter mean diameter) |
| E | Total energy per unit mass |
| Ex | Exergy |
| Exel | Electrical exergy |
| Exin | Input exergy (solar radiation) |
| Exth | Thermal exergy |
| G | Solar irradiance |
| g | Gravitational acceleration vector |
| h | Convective heat transfer coefficient |
| hfg | Latent heat of vaporization |
| k | Turbulent kinetic energy |
| L | Length |
| Le | Length of evaporation section |
| Lc | Length of condensation section |
| La | Length of adiabatic (insulation) section |
| mdot | Mass flow rate |
| mdot,gl | Net mass flow rate through the Gas–Liquid interface |
| M | Molar mass |
| n | Unit normal vector |
| P | Pressure |
| Psat | Saturation pressure |
| Q | Heat source power |
| q | Heat flux |
| R | Thermal resistance |
| Rg | Gas constant |
| S | Source term (general) |
| Sm | Mass source term |
| Sv | Momentum source term |
| SE | Energy source term |
| T | Temperature |
| Tamb | Ambient temperature |
| Tavg | Average temperature |
| Tcell | PV cell temperature |
| Tin | Inlet water temperature |
| Tout | Outlet water temperature |
| Tref | Reference temperature (298.15 K) |
| Tsat | Saturation temperature |
| Tsky | Sky temperature |
| Tsun | Solar surface temperature (5760 K) |
| t | Time |
| U | Overall heat transfer coefficient |
| v | Velocity vector |
| u | Wind speed |
| V | Volume |
| Wdot | Power generation per unit volume |
| Greek Letters | |
| α | Volume fraction |
| αL | Liquid phase volume fraction |
| αV | Vapor phase volume fraction |
| β | Time relaxation factor (phase change) |
| βe | Evaporation time relaxation factor |
| βc | Condensation time relaxation factor |
| ε | Turbulent dissipation rate |
| η | Efficiency (general) |
| η0 | Reference PV efficiency at Tref |
| ηel | Electrical efficiency |
| ηex | Exergy efficiency |
| ηex,el | Electrical exergy efficiency |
| ηex,th | Thermal exergy efficiency |
| ηex,pv | Electrical exergy efficiency |
| ηex,pvt | Exergy efficiency |
| ηth | Thermal efficiency |
| ηpv | Electrical efficiency |
| ηpvt | Energy efficiency |
| ηpower | Average thermal-to-electric conversion efficiency (38%) |
| κ | Thermal conductivity |
| λ | Absorption coefficient |
| μ | Dynamic viscosity |
| μt | Turbulent viscosity |
| ρ | Density |
| ρm | Mixture density |
| σ | Surface tension coefficient |
| σe | C_2ε Empirical constants in k-ε model |
| τ | Shear stress |
| φ | PV coverage ratio (PV cell area/Collector area) |
| ψ | Reflectance |
| Subscripts and Superscripts | |
| e | Evaporation/Evaporator |
| c | Condensation/Condenser |
| L | Liquid phase |
| V | Vapor phase |
| gl | Gas–Liquid interface |
| m | Mixture |
| sat | Saturation state |
| ref | Reference condition |
| i | i-th layer (in PV model) |
| el | Electrical |
| th | Thermal |
| in | Inlet |
| out | Outlet |
| amb | Ambient |
| sky | Sky |
| sun | Sun |
| cell | Photovoltaic Cell |
| gen | Generation |
References
- Shahsavar, A.; Arıcı, M. Energy and exergy analysis and optimization of a novel heating, cooling, and electricity generation system composed of PVT-heat pipe system and thermal wheel. Renew. Energy 2023, 203, 394–406. [Google Scholar] [CrossRef]
- Li, R.; Zhai, P.; Li, J.; Liu, X. Experimental study and performance enhancement of micro heat pipe PV/T system. Energy Built Environ. 2025, 6, 718–729. [Google Scholar] [CrossRef]
- Li, C.; Wang, H.; Zhao, Y.; Li, P.; Zhao, L. Investigation of the heat transfer perfor-mance of micro heat pipe arrays with long evaporation sections for thermal management in PV/T systems. Appl. Therm. Eng. 2025, 280, 128394. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Q.; Li, J.; Novakovic, V. Annual Optimal Performance Anal-ysis of Micro Heat Pipe PV/T under Different Angles in Northwest China. J. Therm. Sci. 2025, 34, 400–412. [Google Scholar] [CrossRef]
- Cotter, T.P. Principles and Prospects for Micro Heat Pips; International Heat Pipe Conference; Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 1984; Volume 48, p. 101860. [Google Scholar]
- Launay, S.; Sartre, V.; Lallemand, M. Experimental study on silicon micro-heat pipe arrays. Appl. Therm. Eng. 2004, 24, 233–243. [Google Scholar] [CrossRef]
- Peterson, G.P.; Duncan, A.B.; Weichold, M.H. Experimental Investigation of Micro Heat Pipes Fabricated in Silicon Wafers. J. Heat Transf. 1993, 115, 751–756. [Google Scholar] [CrossRef]
- Modjinou, M.; Ji, J.; Li, J.; Yuan, W.; Zhou, F. A numerical and experimental study of micro channel heat pipe solar photovoltaics thermal system. Appl. Energy 2017, 206, 708722. [Google Scholar] [CrossRef]
- Diallo, T.M.; Yu, M.; Zhou, J.; Zhao, X.; Shittu, S.; Li, G.; Ji, J.; Hardy, D. Energy performance analysis of a novel solar PVT loop heat pipe employing a microchannel heat pipe evaporator and a PCM triple heat exchanger. Energy 2019, 167, 866–888. [Google Scholar] [CrossRef]
- Ren, X.; Yu, M.; Zhao, X.; Li, J.; Zheng, S.; Chen, F.; Wang, Z.; Zhou, J.; Pei, G.; Ji, J. Assessment of the cost reduction potential of a novel loop-heat-pipe solar photovoltaic/thermal system by employing the distributed parameter model. Energy 2020, 190, 116338. [Google Scholar] [CrossRef]
- Yu, F.; Ji, T.; Liu, X.; Zhang, C. Experimental Study on the Influence of Liquid Filling Ratio on Heat Transfer Characteristics of Small Gravity Heat Pipes. J. Eng. Thermophys. 2018, 39, 2749–2754. [Google Scholar]
- Noie, S.H.; Sarmasti Emami, M.R.; Khoshnoodi, M. Effect of Inclination Angle and Filling Ratio on Thermal Performance of a Two-Phase Closed Thermosyphon under Normal Op-erating Conditions. Heat Transf. Eng. 2007, 28, 365–371. [Google Scholar] [CrossRef]
- Fazeli, K.; Vafai, K. Analysis of optimized combined microchannel and heat pipes for elec-tronics cooling. Int. J. Heat Mass Transf. 2024, 219, 124842. [Google Scholar] [CrossRef]
- Zheng, G.; Deng, D.; Shen, Y.; Huang, Y.; Wu, H. Multi-objective optimization of Ω-shaped reentrant microchannels by numerical simulation and genetic algorithm. Heat Mass Transf. 2025, 61, 96. [Google Scholar] [CrossRef]
- Wen, X.; Ji, J.; Li, Z.; Song, Z.; Yao, T. Performance characterization of a PV/T system employing mi-cro-channel heat pipes and thermoelectric generators: An experimental and numerical study. Energy 2023, 264, 126182. [Google Scholar] [CrossRef]
- Yang, Z.; Song, J.; Zhang, G.; Sun, X.; Cheng, S.; Zhang, X.; Jiang, Y. Unraveling the promotion for SO2 and H2O resistance of transition metal-doped CeO2-TiO2 catalysts in NH3-SCR reaction: A DFT study. J. Hazard. Mater. 2025, 489, 137563. [Google Scholar] [CrossRef] [PubMed]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: New, York, NY, USA, 2013; pp. 565–567. [Google Scholar]
- Faghri, A. Heat pipe science and technology. Fuel Energy Abstr. 1995, 36, 285. [Google Scholar] [CrossRef]
- Peterson, G.P. An Introduction to Heat Pipes: Modeling, Testing, and Applications; John Wiley & Sons: New, York, NY, USA, 1994. [Google Scholar]
- Green, M.A.; Dunlop, E.D.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Siefer, G.; Hinken, D.; Rauer, M.; Hohl-Ebinger, J.; Hao, X. Solar cell efficiency tables (Version 63). Prog. Photovolt. Res. Appl. 2024, 32, 3–13. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Pergamon: Oxford, UK, 1983; pp. 96–116. [Google Scholar]
- Knudsen, M.; Partington, J.R. The Kinetic.Theory of Gases. Some Modern Aspects. J. Phys. Chem. 1952, 39, 307. [Google Scholar] [CrossRef]
- Tanasawa, I. Advances in condensation heat transfer. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1991; Volume 21, pp. 55–139. [Google Scholar]
- De Schepper, S.C.K.; Heynderickx, G.J.; Marin, G.B. Modeling the evaporation of a hydrocarbon feedstock in the convection section of a steam cracker. Comput. Chem. Eng. 2009, 33, 122–132. [Google Scholar] [CrossRef]
- Shittu, S.; Li, G.; Zhao, X.; Akhlaghi, Y.G.; Ma, X.; Yu, M. Comparative study of a concentrated photovoltaic thermoelectric system with and without flat plate heat pipe. Energy Convers. Manag. 2019, 193, 1–14. [Google Scholar] [CrossRef]
- Joshi, A.S.; Tiwari, A.; Tiwari, G.N.; Dincer, I.; Reddy, B.V. Performance evaluation of a hybrid photovoltaic thermal (PV/T)(glass-to-glass) system. Int. J. Therm. Sci. 2009, 48, 154–164. [Google Scholar] [CrossRef]
- Lee, J.H.; Hwang, S.G.; Lee, G.H. Efficiency Improvement of a Photovoltaic Thermal (PVT) System Using Nanofluids. Energies 2019, 12, 3063. [Google Scholar] [CrossRef]
- Gholampour, M.; Ameri, M. Energy and exergy analyses of Photovoltaic/Thermal flat transpired collectors: Experimental and theoretical study. Appl. Energy 2016, 164, 837–856. [Google Scholar] [CrossRef]
- Jeter, S.M. Maximum conversion efficiency for the utilization of direct solar radiation. Sol. Energy 1981, 26, 231–236. [Google Scholar] [CrossRef]
- Ren, X.; Li, J.; Zhao, X.; Cao, J.; Pei, G.; Ji, J. Parametric Analysis of a Novel Photovoltaic/Thermal System Using Amorphous Silicon Cells and Micro-Channel Loop Heat Pipes. Heat Transf. Eng. 2022, 43, 1149–1170. [Google Scholar] [CrossRef]
- Zhou, J.C.; Zhang, Z.; Liu, H.J.; Yi, Q. Temperature distribution and back sheet role of polycrystalline silicon photovoltaic modules. Appl. Therm. Eng. 2017, 111, 1296–1303. [Google Scholar] [CrossRef]
- Zhou, J.; Yi, Q.; Wang, Y.; Ye, Z. Temperature distribution of photovoltaic module based on finite element simulation. Sol. Energy 2015, 111, 97–103. [Google Scholar] [CrossRef]
- Cecelski, C.E.; Harris, K.J.; Goodman, C.A.; Kimes, W.A.; Liu, Q.; Miller, W.R.; Carney, J. Certification of NIST Gas Mixture Standard Reference Materials: NIST SP 260-222; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022; Volume 260. [Google Scholar]
- Fadhl, B.; Wrobel, L.C.; Jouhara, H. CFD modelling of a two-phase closed thermosyphon charged with R134a and R404a. Appl. Therm. Eng. 2015, 78, 482–490. [Google Scholar] [CrossRef]



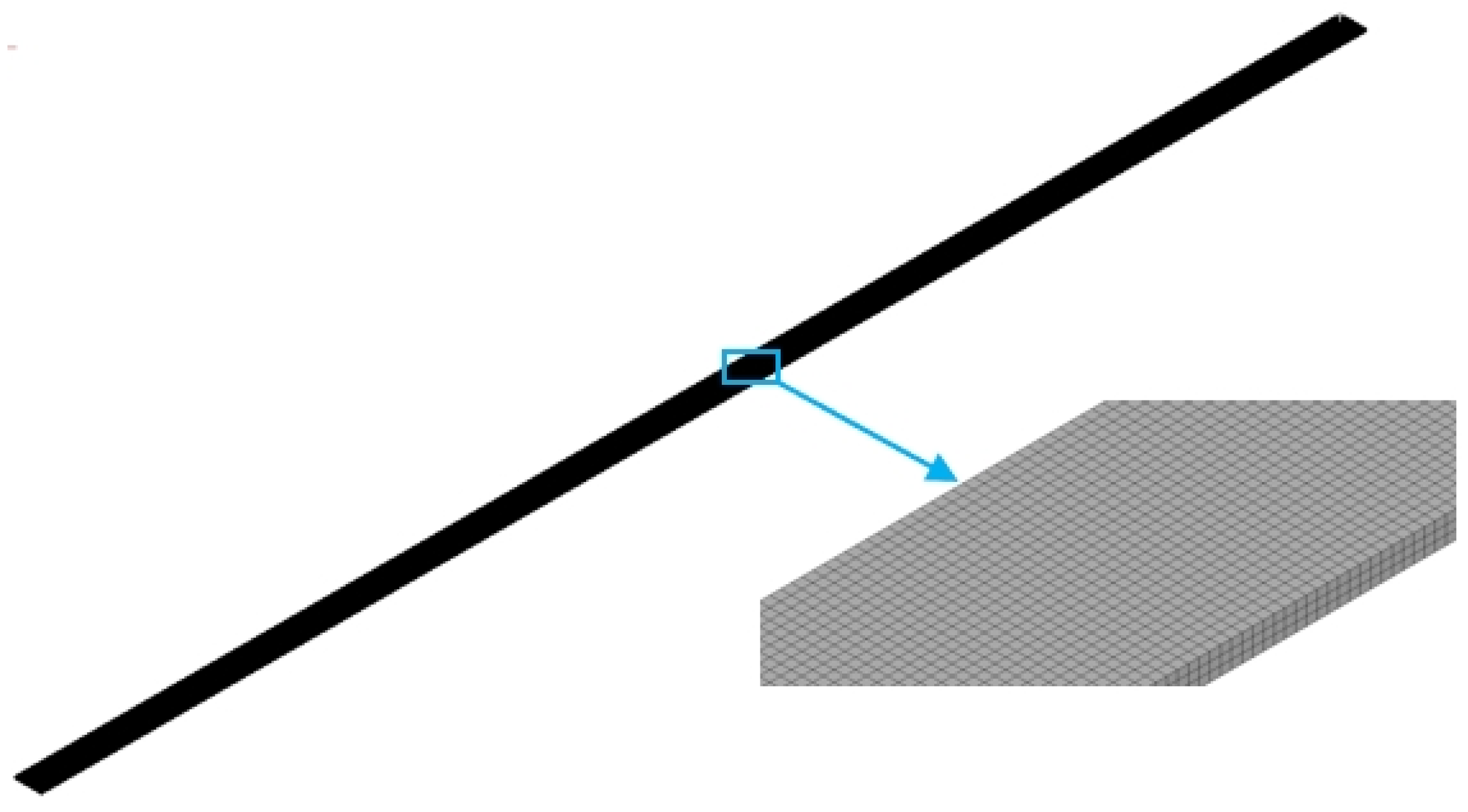

| Model Settings | Heat Pipe Wall | Working Fluid | Model | Solver | Flow Model | Solution Method |
|---|---|---|---|---|---|---|
| Materials | aluminum | R134a/acetone | Mixture | Pressure solver | k-e model | Quick |
| Transmission Volume | Phase Transition Process | Phase Transition Criterion | Phase | Source Term Expression |
|---|---|---|---|---|
| Quality | Evaporation | liquid phase | ||
| gas phase | ||||
| Condensation | liquid phase | |||
| gas phase | ||||
| Energy | Evaporation | |||
| Condensation |
| Physical Parameters | R134a | Acetone | Unit |
|---|---|---|---|
| liquid density | 1147.4 | 797.2 | kg·m−3 |
| gas density | 32.25 | 2.12 | kg·m−3 |
| Specific heat capacity of liquid | 1.4246 | 2.1625 | kJ·kg−1·K−1 |
| Specific heat capacity of gas | 1.0316 | 1.45237 | kJ·kg−1·K−1 |
| liquid phase thermal conductivity | 0.081134 | 0.177702 | W·m−1·k−1 |
| gas phase thermal conductivity | 0.013825 | 0.0096338 | W·m−1·k−1 |
| liquid viscosity | 1.9489 × 10−4 | 3.31 × 10−4 | kg·m−1·s−1 |
| gas phase viscosity | 1.1693 × 10−5 | 7.25 × 10−6 | kg·m−1·s−1 |
| Molecular weight | 102.03 | 58.0791 | kg·kmol−1 |
| critical temperature | 374.21 | 508.65 | K |
| critical pressure | 40,593 | 4720 | kPa |
| Part | Evaporation Section | Thermal Insulation Section | Condensation Section |
|---|---|---|---|
| Length/mm | 600 | 300 | 100 |
| 600 | 200 | 200 | |
| 600 | 100 | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Fu, H.; Li, H.; Pan, C.; Sun, Z.; Ren, X. Numerical Study on a PV/T Using Microchannel Heat Pipe. Processes 2025, 13, 3402. https://doi.org/10.3390/pr13113402
Huang H, Fu H, Li H, Pan C, Sun Z, Ren X. Numerical Study on a PV/T Using Microchannel Heat Pipe. Processes. 2025; 13(11):3402. https://doi.org/10.3390/pr13113402
Chicago/Turabian StyleHuang, Hu, Hao Fu, Huashan Li, Chenghang Pan, Zongyu Sun, and Xiao Ren. 2025. "Numerical Study on a PV/T Using Microchannel Heat Pipe" Processes 13, no. 11: 3402. https://doi.org/10.3390/pr13113402
APA StyleHuang, H., Fu, H., Li, H., Pan, C., Sun, Z., & Ren, X. (2025). Numerical Study on a PV/T Using Microchannel Heat Pipe. Processes, 13(11), 3402. https://doi.org/10.3390/pr13113402





