Optimal Control of MSWI Processes Using an RBF-IPOA Strategy for Enhanced Combustion Efficiency and NOX Reduction
Abstract
1. Introduction
2. MSWI Process and Process Characteristic Analysis
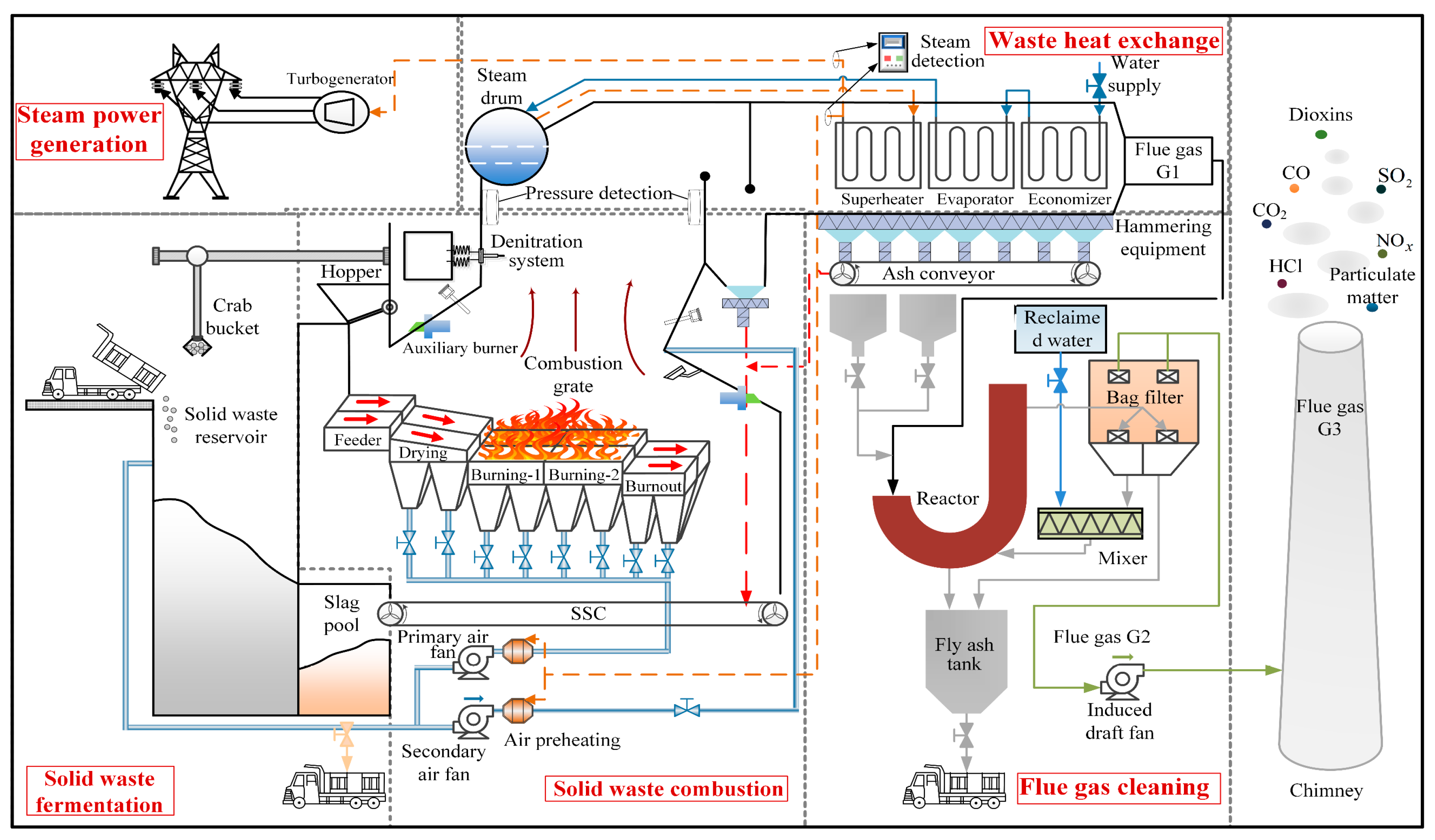
2.1. Process Description
2.2. Analysis of Factors Influencing Combustion Efficiency and NOX Emissions in the MSWI
3. Optimal Control Method for the MSWI Process Based on IWOA-RBF-IPOA
3.1. Definition of Optimal Control for the MSWI Process
- Maximize Combustion Efficiency : Ensure the complete destruction of waste and maximize energy recovery, which is intrinsically linked to maintaining a high CO2/CO ratio in the flue gas.
- Minimize Environmental Impact : Suppress the formation of regulated pollutants, most notably NOX, to levels strictly below the mandated emission limits.
- Ensure Operational Feasibility and Safety: Maintain all process variables within safe operating limits and, critically, ensure that CO emissions remain below the regulatory threshold ([CO] ≤ [CO]max) to prevent incomplete combustion and the potential formation of toxic by-products.
3.2. Control Objectives
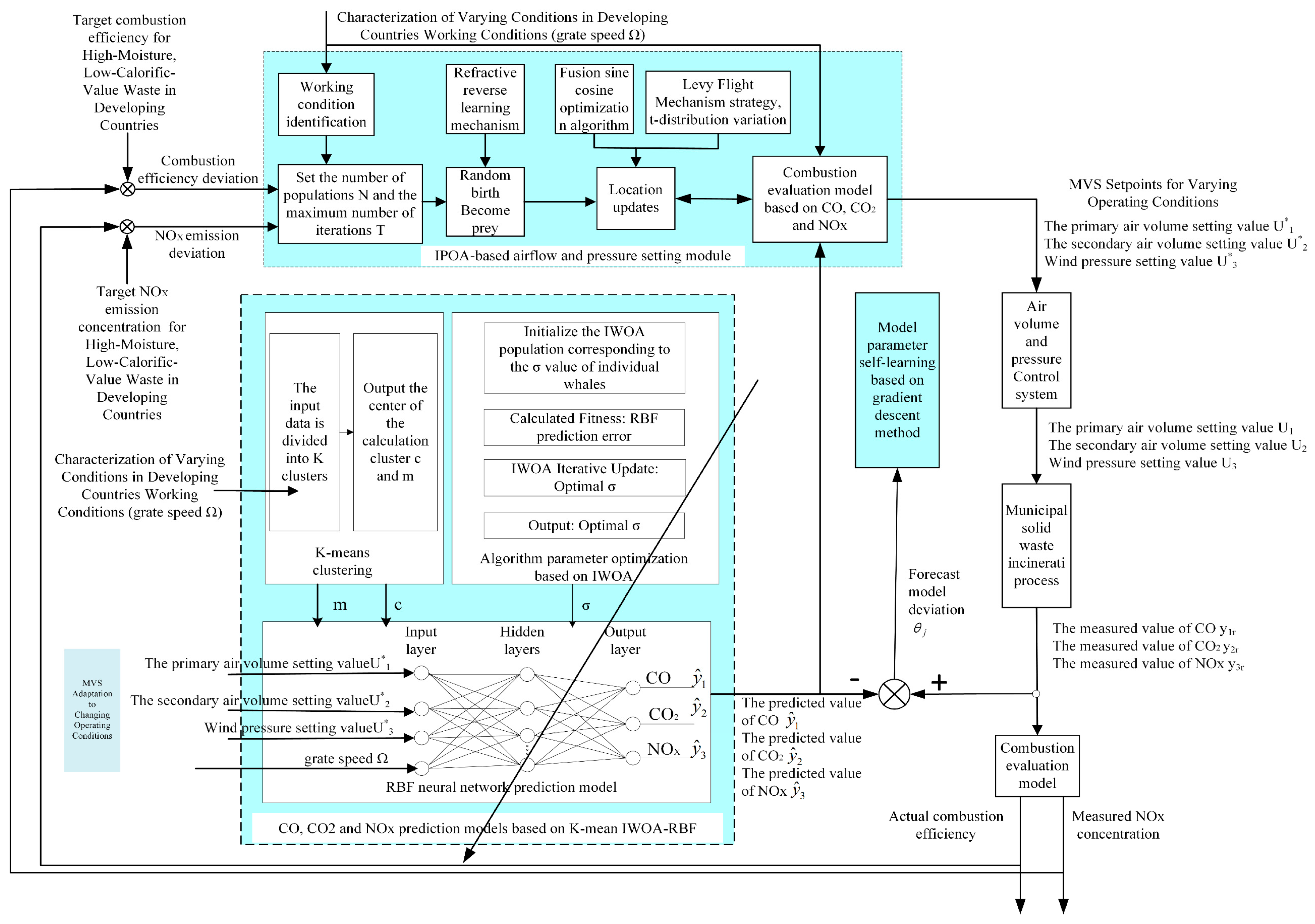
3.3. Control Strategy
Specificity of the MSWI Process and Control Objectives
3.4. Control Algorithms
3.4.1. Prediction Models Based on IWOA-RBF for CO, CO2, NOX
RBF Network Structure
Determination of Hidden Layer Node Number m and Centers C Using K-Means Clustering Algorithm
| Algorithm 1: K-Means Clustering Pseudocode |
| 1: Begin K-Means algorithm 2: Input datasets V and number of clusters K 3: Determine maximum iterations T and convergence threshold ε 4: Randomly initialize cluster centers C = {c1, c2, …, cₖ} 5: For t = 1 : T: 6: Phase 1: Data point assignment 7: For i = 1 : n: 8: For j = 1 : K: 9: Calculate distance using Formula (10) 10: End 11: Determine minimum distance using Formula (11) 12: Assign input data to the nearest cluster center 13: End 14: Phase 2: Cluster center update 15: For j = 1 : K: 16: Calculate new center using Formula (12) 17: End 18: Check convergence condition using Formula (13) 19: If converged: 20: Break 21: Else: ) 23: End 24: End 25: Output clustering result C = {C1, C2, …, Cₖ} 26: End K-Means algorithm |
Determination of Neuron Widths Based on IWOA
- (1)
- Limitations of the Standard WOA for the Optimization Problem
- (2)
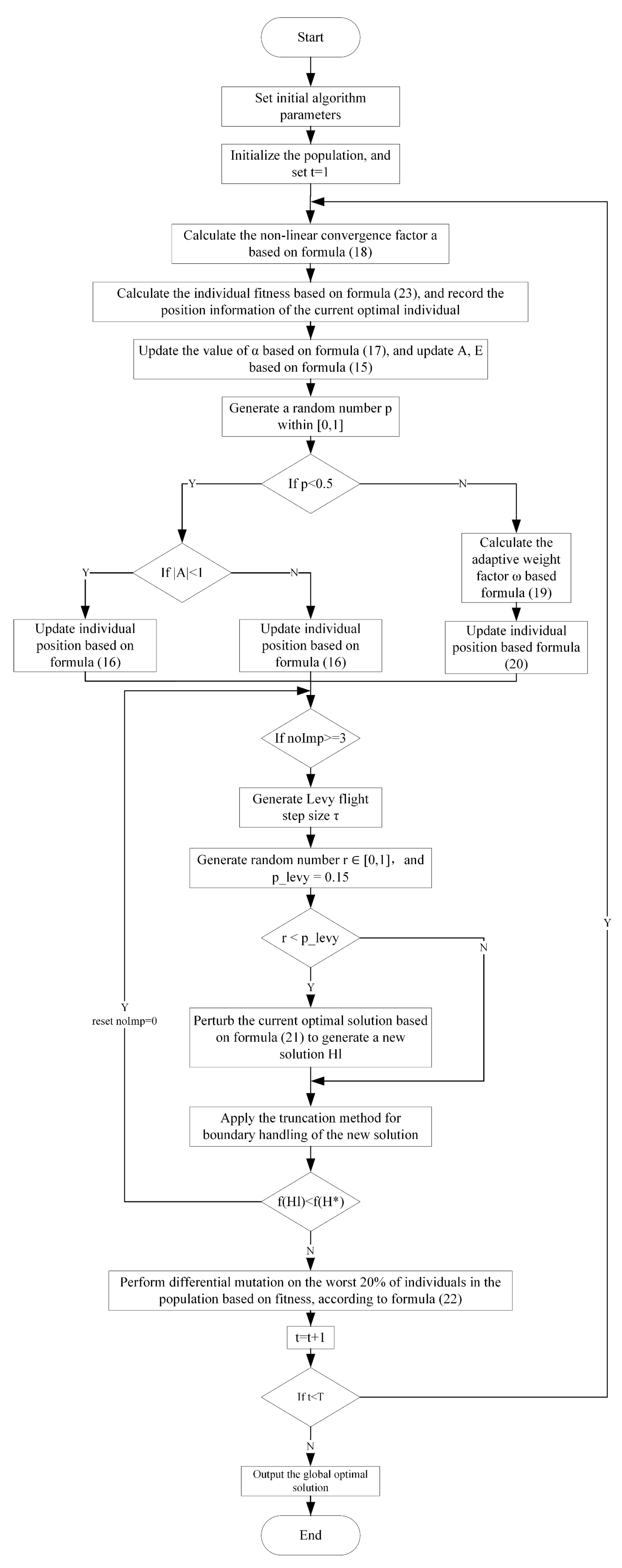
- IWOA Improvement Strategies for Combustion Condition Optimization
- (i)
- Nonlinear Convergence Factor Adjustment Strategy
- (ii)
- Adaptive Spiral Weight Mechanism
- (iii)
- Levy Flight Disturbance Strategy
- (iv)
- Differential Mutation Operation
| Algorithm 2: IWOA Pseudocode |
| 1: procedure IWOA_RBF_TUNING 2: Define inputs: Training data {H, Q}, RBF centers C, Population size N, Max iterations T, p_levy 3: Define output: Optimal width parameters σ= {σ1, σ2, …, σm} 4: Initialize whale population Hi(0)= {σ1, σ2, …, σm} 5: Calculate fitness f(Hi(0)) for each individual using Formula (23) 6: Determine current best individual H* 7: for t = 1 : T : 8: Update convergence factor a using Formula (18) 9: Update spiral weight ω using Formula (19) 10: Assuming (15) refers to the formulas for A and E 11: for Hi : 12: if p < 0.5 : 13: if |A| < 1 : 14: Perform encircling prey using Formula (16) 15: else 16: Perform random search using Formula (16) 17: end if 18: else 19: Perform spiral update using Formula (20) 20: end if 21: Apply Levy flight disturbance using Formula (21) with probability p_levy 22: Calculate new fitness f(Hi(t)) using Formula (23) 23: end for 24: Perform differential mutation on the worst 20% individuals using Formula (22) 25: Update the best individual H* 26: end for 27: return σ* = H* 28: end |
3.4.2. IPOA-Based Optimization Method for Air Volume and Pressure
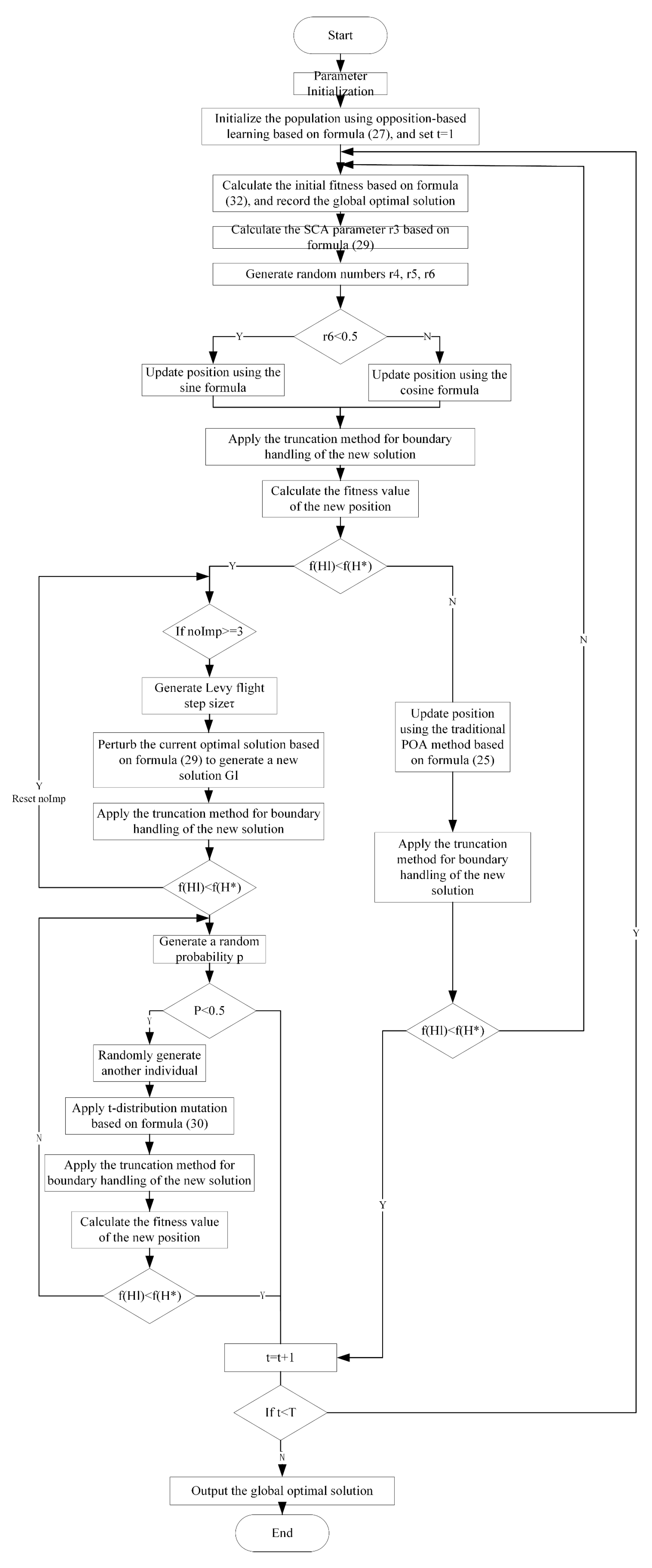
Limitations of the Traditional POA
Improvement Strategies for POA
3.5. Implementation Steps of the Air Volume and Pressure Optimization Control Algorithm
4. Experimental Design and Result Analysis
4.1. Experiment of the K-Means and IWOA-RBF-Based Prediction Models for CO, CO2, NOX
4.1.1. Data Description
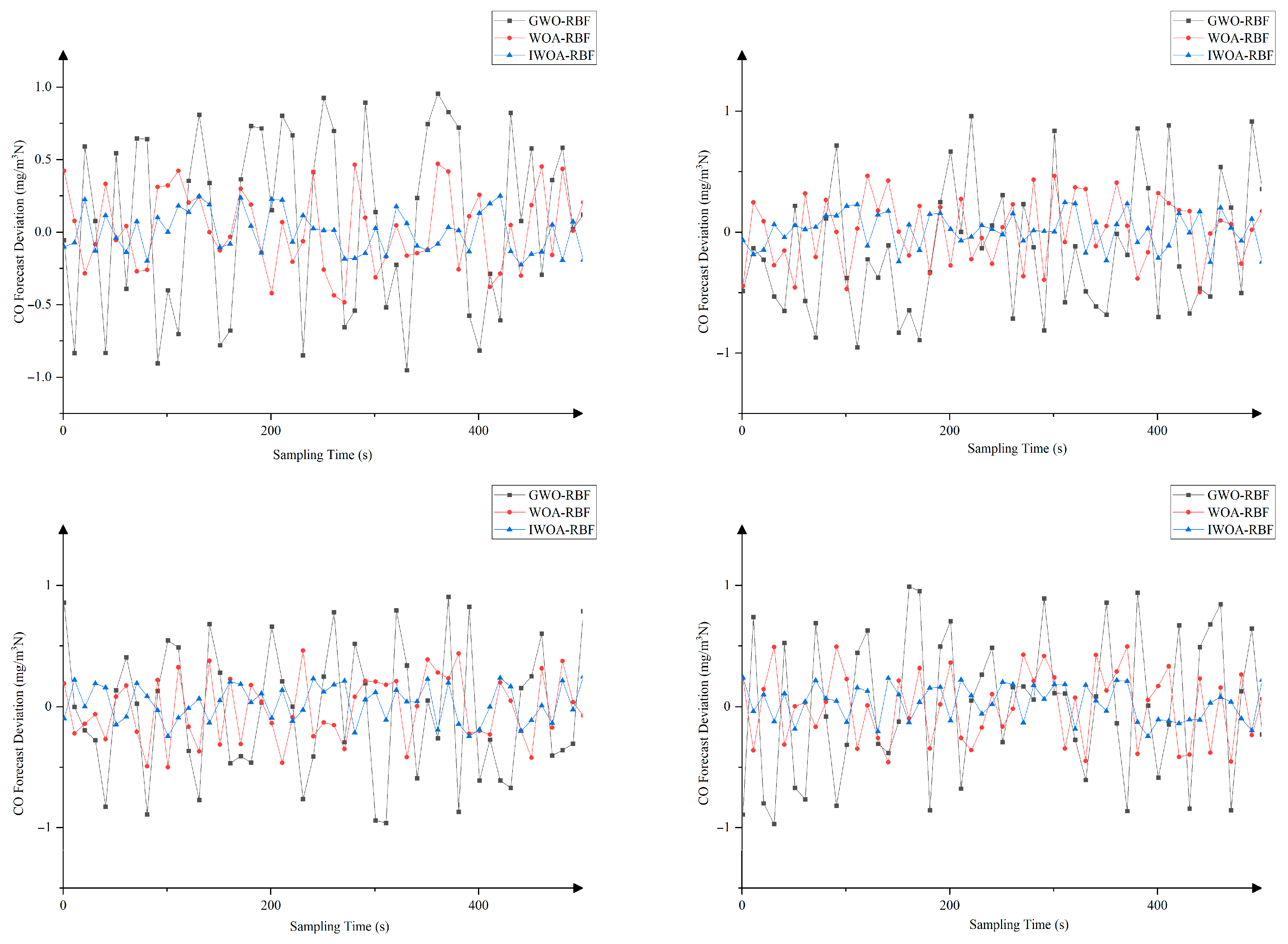
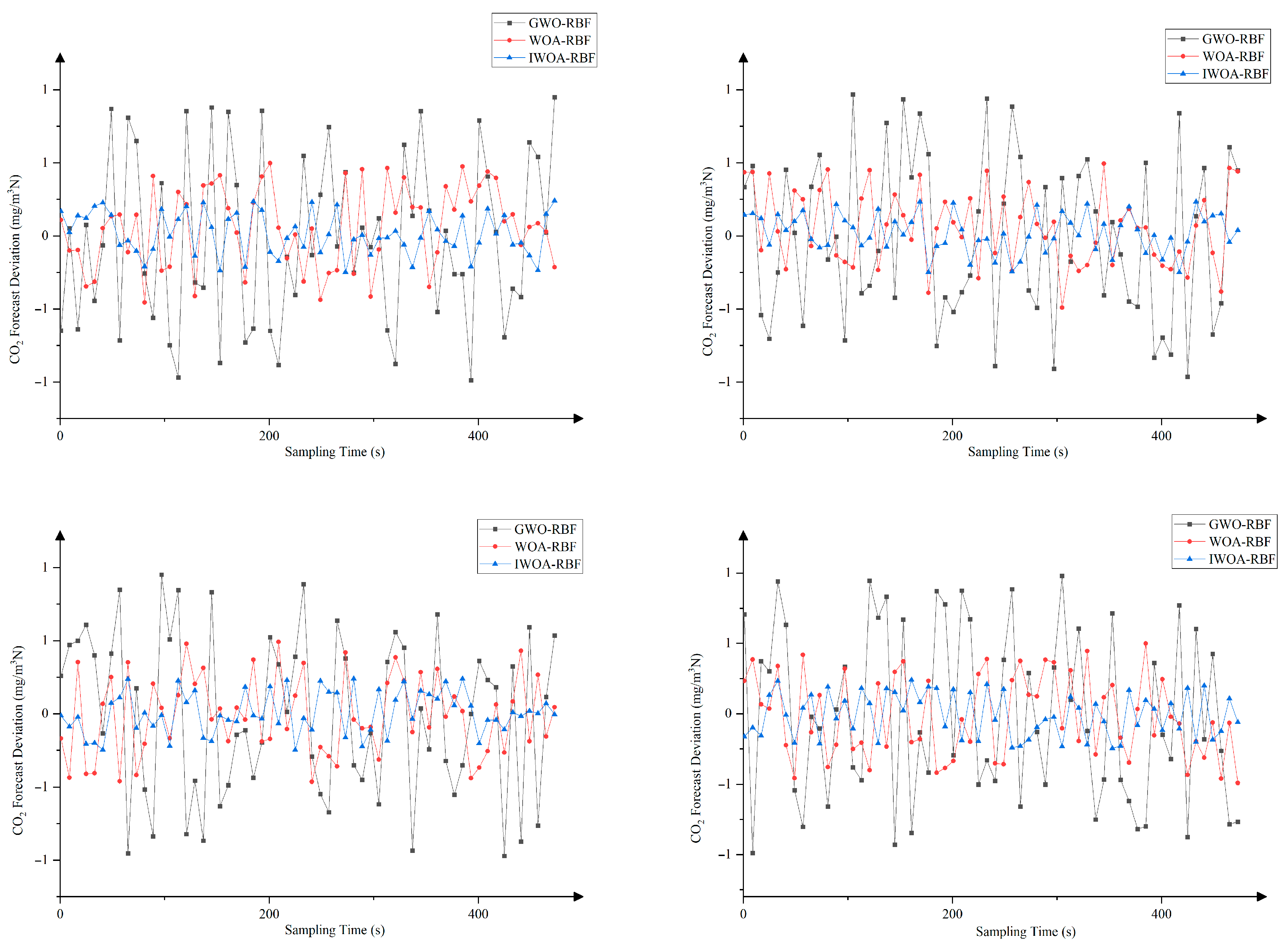
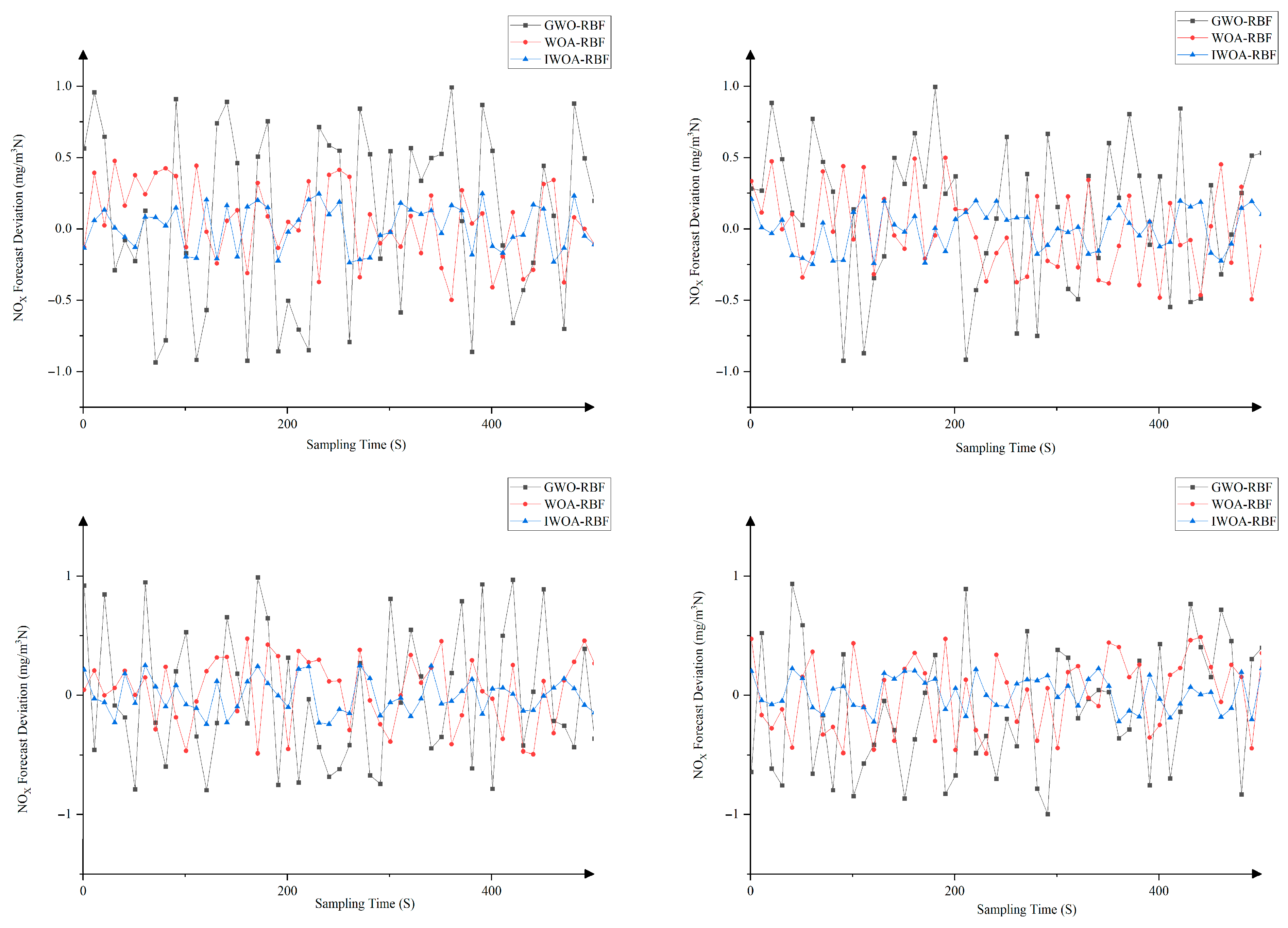
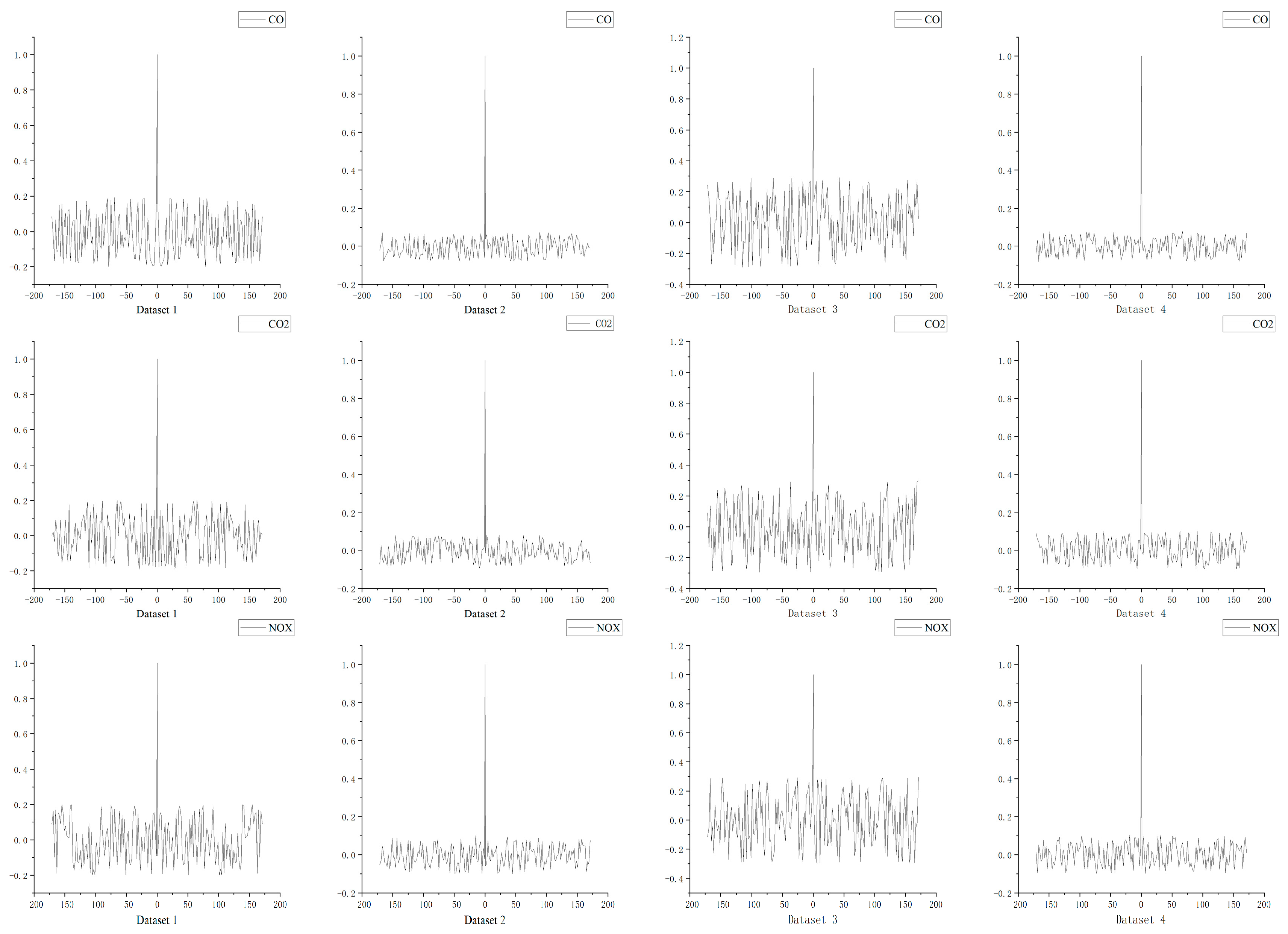
4.1.2. Experimental Results and Analysis
4.2. Experiment of the Optimal Control
4.2.1. Data Description
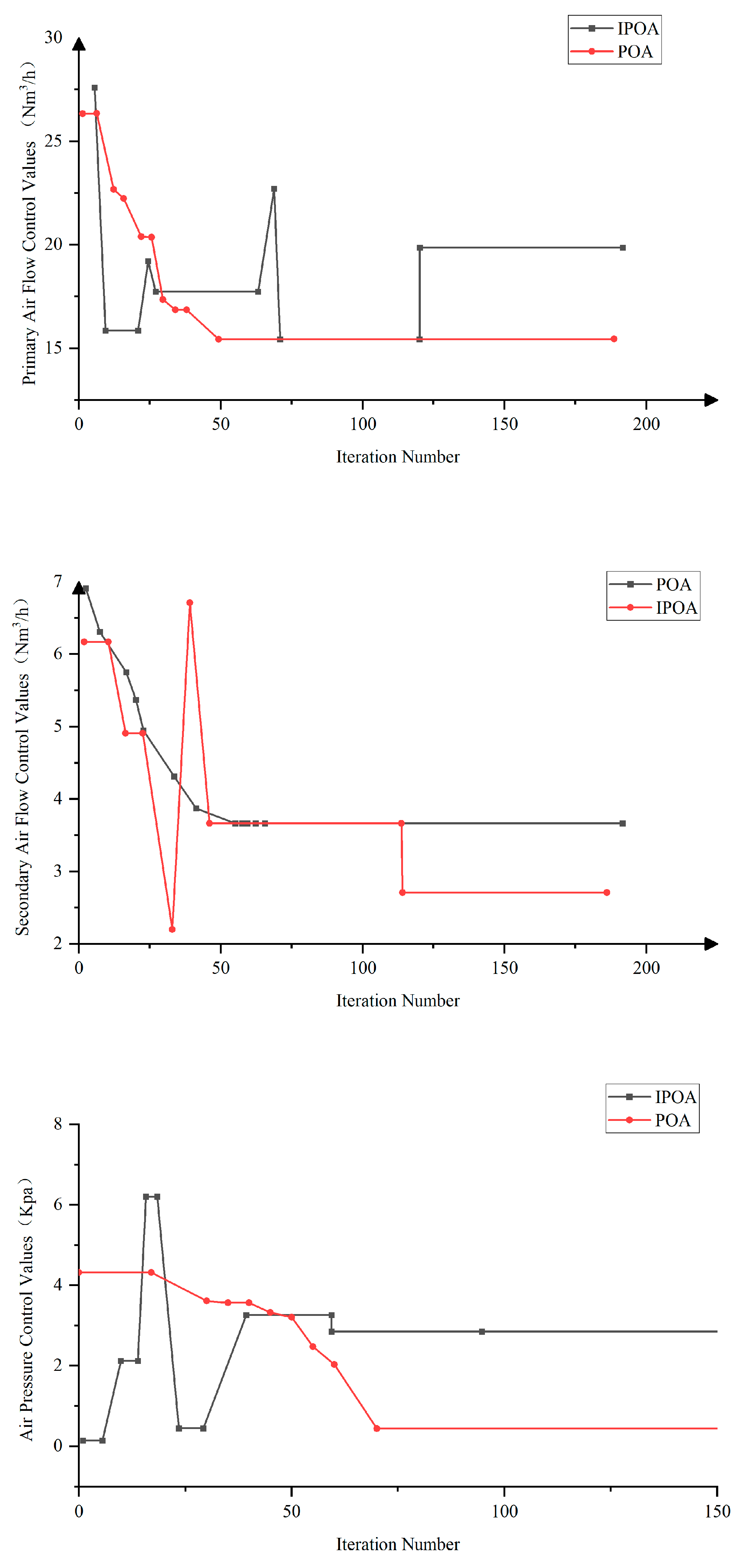
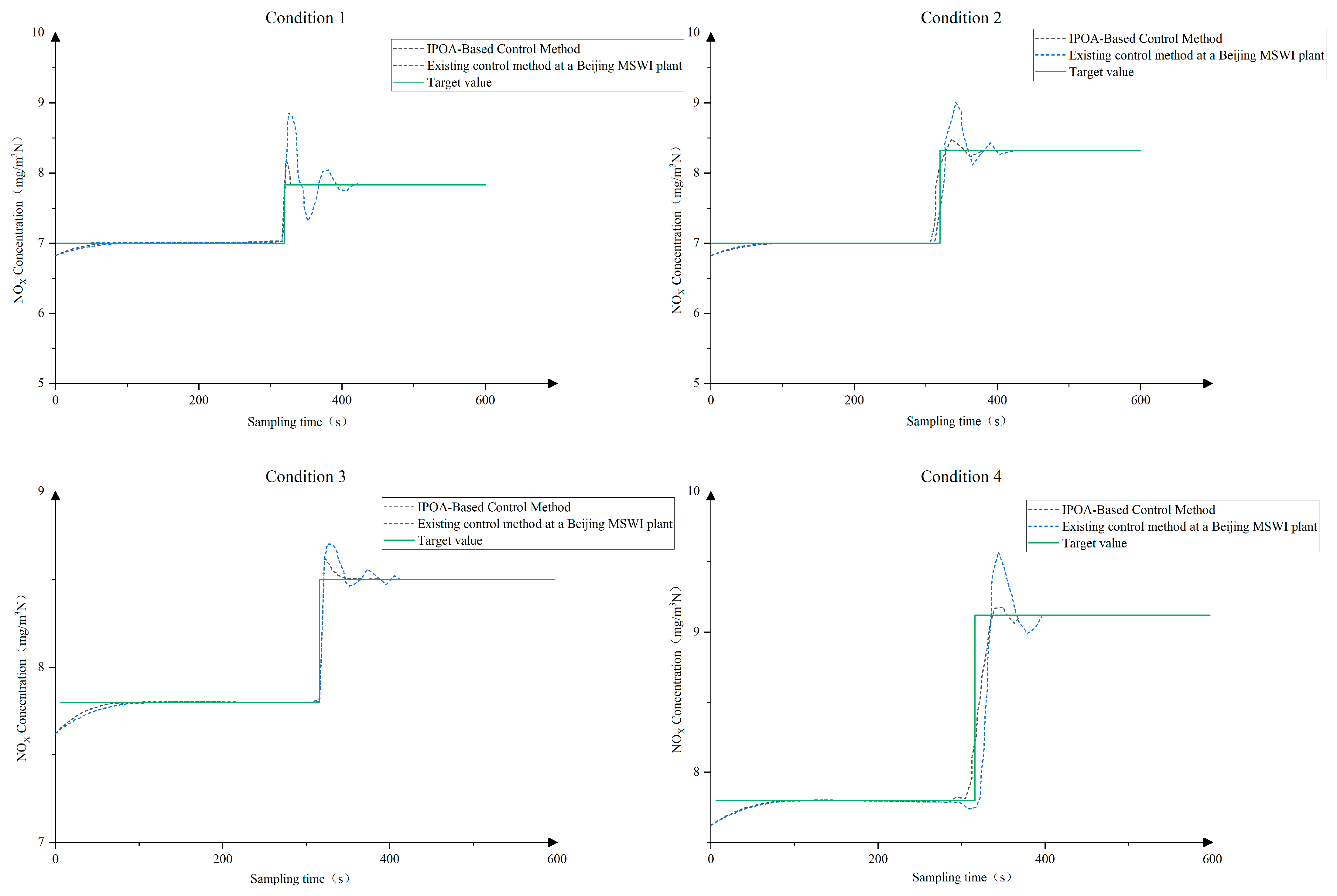
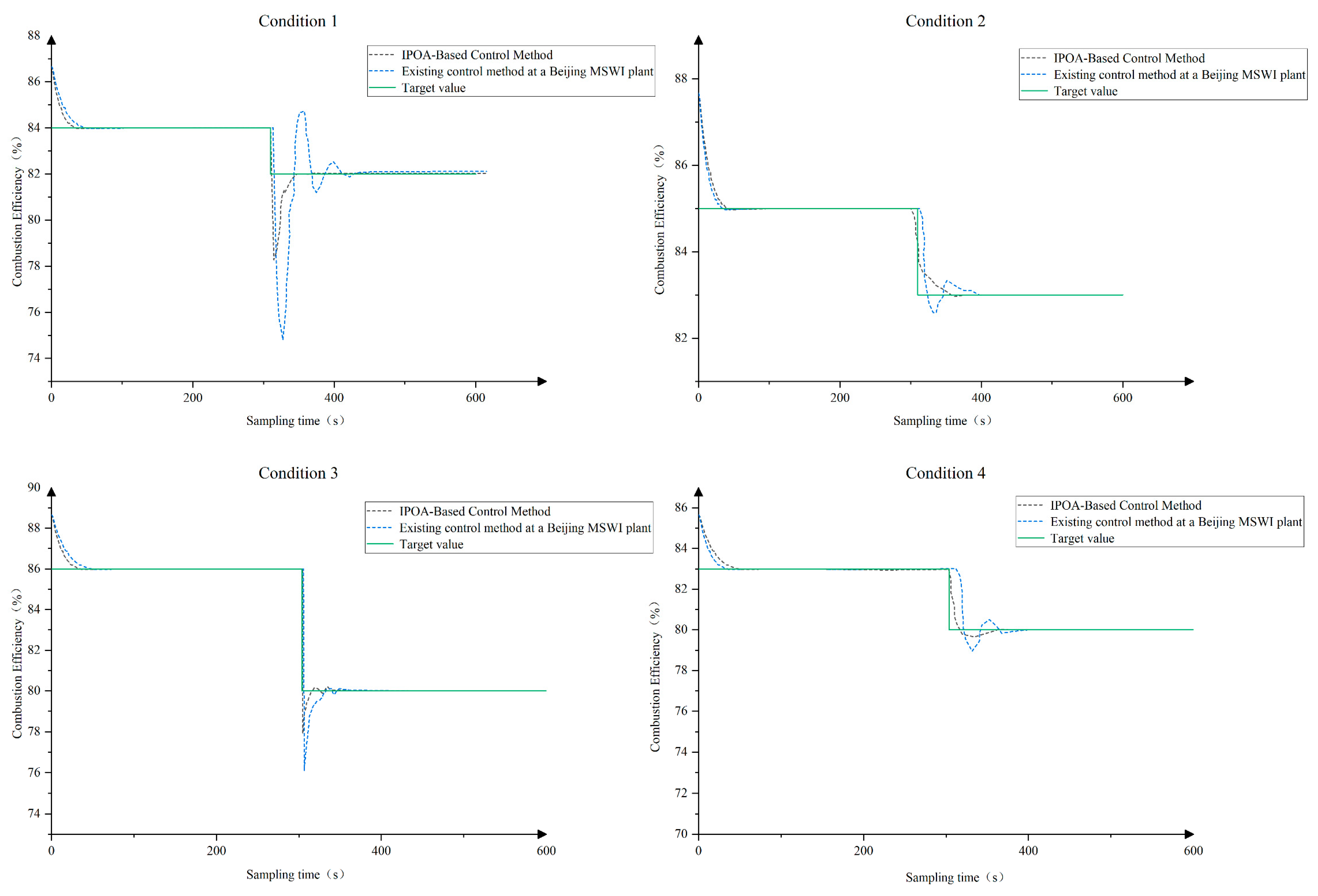
4.2.2. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| U | Input vector of the neural network |
| Primary air flow | |
| Secondary air flow | |
| Air pressure | |
| σ | Neuron width |
| the predicted values for CO | |
| the predicted values for CO2 | |
| the predicted values for NOX | |
| Primary air flow setting | |
| Secondary air flow setting | |
| Air pressure setting | |
| The lower limits for the primary air flow | |
| The upper limits for the primary air flow | |
| The lower limits for the secondary air flow | |
| The upper limits for the secondary air flow | |
| The lower limits for the air pressure | |
| The upper limits for the air pressure | |
| The lower limits for the operating condition parameter | |
| The upper limits for the operating condition parameter | |
| The combustion efficiency | |
| NOX emission concentration | |
| Y | The output of the network |
| Gaussian RBF | |
| The gradient descent algorithm | |
| The measured CO values | |
| The measured CO2 values | |
| The measured NOX values | |
| The Euclidean distance | |
| The i-th data point | |
| The i-th cluster center | |
| The j-th feature value | |
| The j-th feature value | |
| The minimum distance | |
| The new center point of the j-th cluster | |
| The center point used for the j-th cluster | |
| Convergence threshold | |
| The state at the next time step | |
| The position vector of the current best search agent | |
| The distance between the current individual and the best solution | |
| A constant | |
| A random number | |
| Random numbers | |
| Random numbers | |
| T | The maximum number of iterations |
| t | The current iteration number |
| a | The nonlinear convergence factor |
| Levy flight | |
| Parameter controlling | |
| A step size parameter controlling the magnitude of the update | |
| Randomly selected individuals | |
| Randomly selected individuals | |
| Q | Training data |
| N | Population size |
| The position of the i-th individual in the j-th dimension | |
| The lower bounds of the j-th dimension variable | |
| The upper bounds of the j-th dimension variable | |
| The new position after the exploration phase | |
| The position of the prey | |
| The fitness values of the prey | |
| The current individual | |
| The new position after the exploitation phase | |
| C | Center of the RBF |
| m | Number of hidden layer nodes |
| An adjustment exponent | |
| ωj | Connection weight from j-th hidden neuron to output |
| K | Number of candidate clusters |
| Z | Sample data |
| α | Adaptive parameter |
| β | Learning rate |
| A | Coefficient matrix in the whale algorithm formula |
| E | Coefficient matrix in the whale algorithm formula |
| p | Random number (typically in [0, 1])/Probability |
| R | A constant |
| The original opposite solution | |
| A random number | |
| A random number | |
| A random number | |
| q | A constant |
| The state at the next time step | |
| The current global best solution | |
| Random individuals from the population |
References
- Qiao, J.-F.; Guo, Z.-H.; Tang, J. Dioxin emission concentration measurement approaches for municipal solid wastes incineration process: A survey. Acta Autom. Sin. 2020, 46, 1063–1089. [Google Scholar] [CrossRef]
- dos Santos, I.F.S.; Mensah, J.H.R.; Gonçalves, A.T.T.; Barros, R.M. Incineration of municipal solid waste in Brazil: An analysis of the economically viable energy potential. Renew. Energy 2020, 149, 1386–1394. [Google Scholar] [CrossRef]
- Li, H.J.; Tan, D. Dynamic control of pollution of municipal solid waste incineration. Kybernetes 2025, 54, 727–748. [Google Scholar] [CrossRef]
- Margallo, M.; Taddei, M.B.M.; Hernández-Pellón, A.; Aldaco, R.; Irabien, Á. Environmental sustainability assessment of the management of municipal solid waste incineration residues: A review of the current situation. Clean Technol. Environ. Policy 2015, 17, 1333–1353. [Google Scholar] [CrossRef]
- Sun, J.; Meng, X.; Qiao, J. Data-driven optimal control for municipal solid waste incineration process. IEEE Trans. Ind. Inform. 2023, 19, 11444–11454. [Google Scholar] [CrossRef]
- Bose, D.; Ghanta, K.C.; Hens, A. CFD-based investigation of NOx removal from industrial waste gas by selective catalytic reduction (SCR) and selective non-catalytic reduction (SNCR) process using NH3. Int. J. Chem. React. Eng. 2025, 23, 701–713. [Google Scholar] [CrossRef]
- Wang, T.; Tang, J.; Xia, H.; Yang, C.; Yu, W.; Qiao, J. Data-driven multi-objective intelligent optimal control of municipal solid waste incineration process. Eng. Appl. Artif. Intell. 2024, 137, 109157. [Google Scholar] [CrossRef]
- Beylot, A.; Hochar, A.; Michel, P.; Descat, M.; Ménard, Y.; Villeneuve, J. Municipal solid waste incineration in France: An overview of air pollution control techniques, emissions, and energy efficiency. J. Ind. Ecol. 2018, 22, 1016–1026. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Kawai, K.; Nakakubo, T. Drivers and constraints of waste-to-energy incineration for sustainable municipal solid waste management in developing countries. J. Mater. Cycles Waste Manag. 2021, 23, 1688–1697. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Liu, Q.; Luo, H.; Li, B.; Cheng, J.; Huang, Y. Emission characteristics and impact factors of air pollutants from municipal solid waste incineration in Shanghai, China. J. Environ. Manag. 2022, 310, 114732. [Google Scholar] [CrossRef]
- Khan, S.; Anjum, R.; Raza, S.T.; Bazai, N.A.; Ihtisham, M. Technologies for municipal solid waste management: Current status, challenges, and future perspectives. Chemosphere 2022, 288, 132403. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.-W.; Zhang, S.; Hai, J.; Lei, M. Status and perspectives of municipal solid waste incineration in China: A comparison with developed regions. Waste Manag. 2017, 69, 170–186. [Google Scholar] [CrossRef]
- Qiao, J.-F.; Meng, X.; Tang, Y.-T. Perspectives on Intelligent Optimized Control of Municipal Solid Waste Incineration Process under Dual Carbon Target. Bull. Natl. Nat. Sci. Found. China 2024, 38, 593–602. [Google Scholar] [CrossRef]
- Tang, J.; Tian, H.; Wang, T. A review of model predictive control for the municipal solid waste incineration process. Sustainability 2024, 16, 7650. [Google Scholar] [CrossRef]
- Hu, Q.-X.; Long, J.-S.; Wang, S.-K.; He, J.-J.; Bai, L.; Du, H.-L.; Huang, Q.-X. A novel time-span input neural network for accurate municipal solid waste incineration boiler steam temperature prediction. J. Zhejiang Univ. A 2021, 22, 777–791. [Google Scholar] [CrossRef]
- Yan, A.; Wang, R.; Guo, J.; Tang, J. A knowledge transfer online stochastic configuration network-based prediction model for furnace temperature in a municipal solid waste incineration process. Expert Syst. Appl. 2024, 243, 122733. [Google Scholar] [CrossRef]
- Bunsan, S.; Chen, W.-Y.; Chen, H.-W.; Chuang, Y.H.; Grisdanurak, N. Modeling the dioxin emission of a municipal solid waste incinerator using neural networks. Chemosphere 2013, 92, 258–264. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zhao, H.; Zhang, Y. Nonlinear system modeling using self-organizing fuzzy neural networks for industrial applications. Appl. Intell. 2020, 50, 1657–1672. [Google Scholar] [CrossRef]
- Pian, J.; Liu, J.; Tang, J.; Hou, J. Intelligent Control of the Main Steam Flow Rate for the Municipal Solid Waste Incineration Process. Sustainability 2025, 17, 6036. [Google Scholar] [CrossRef]
- Tao, J.; Li, Z.; Chen, C.; Liang, R.; Wu, S.; Lin, F.; Cheng, Z.; Yan, B.; Chen, G. Intelligent technologies powering clean incineration of municipal solid waste: A system review. Sci. Total. Environ. 2024, 935, 173082. [Google Scholar] [CrossRef]
- Wen, C.; Lin, X.; Ying, Y.; Ma, Y.; Yu, H.; Li, X.; Yan, J. Dioxin emission prediction from a full-scale municipal solid waste incinerator: Deep learning model in time-series input. Waste Manag. 2023, 170, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Zhu, Y.; Liu, X.; Fu, L.; Guo, Q. Bayesian-Based NIMBY Crisis Transformation Path Discovery for Municipal Solid Waste Incineration in China. Sustainability 2019, 11, 2364. [Google Scholar] [CrossRef]
- Tang, J.; Wang, T.; Xia, H.; Cui, C. An overview of artificial intelligence application for optimal control of municipal solid waste incineration process. Sustainability 2024, 16, 2042. [Google Scholar] [CrossRef]
- Cui, Y.; Meng, X.; Qiao, J. Multi-condition operational optimization with adaptive knowledge transfer for municipal solid waste incineration process. Expert Syst. Appl. 2023, 238, 121783. [Google Scholar] [CrossRef]
- Huang, W.; Ding, H.; Qiao, J. Large-scale and knowledge-based dynamic multiobjective optimization for MSWI process using adaptive competitive swarm optimization. IEEE Trans. Syst. Man Cybern. Syst. 2023, 54, 379–390. [Google Scholar] [CrossRef]
- He, J.; Xiong, C.; Li, Z.; Mei, R.; Zhao, X.; Wu, H. Research on aerial radioactive hotspot detecting based on an improved pelican optimization algorithm. J. Radioanal. Nucl. Chem. 2025, 334, 4159–4170. [Google Scholar] [CrossRef]
- Feng, H.; Song, Q.; Ma, S.; Ma, W.; Yin, C.; Cao, D.; Yu, H. A new adaptive sliding mode controller based on the RBF neural network for an electro-hydraulic servo system. ISA Trans. 2022, 129, 472–484. [Google Scholar] [CrossRef]
- Magnanelli, E.; Tranås, O.L.; Carlsson, P.; Mosby, J.; Becidan, M. Dynamic modeling of municipal solid waste incineration. Energy 2020, 209, 118426. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Liao, L. Near-optimal control of nonlinear dynamical systems: A brief survey. Annu. Rev. Control. 2019, 47, 71–80. [Google Scholar] [CrossRef]
- Xu, B.; Yuan, L.; Yu, H. RBF Neural Network-Based Anti-Disturbance Trajectory Tracking Control for Wafer Transfer Robot Under Variable Payload Conditions. Appl. Sci. 2025, 15, 9193. [Google Scholar] [CrossRef]
- Chai, Y.; Chang, X.; Ren, S. Beluga Whale Optimization with Improved Multi-Strategy Integration Problem. Comput. Eng. Appl. 2025, 61, 76–93. [Google Scholar] [CrossRef]
- Wang, X.; Bai, Y. A Study on Comparison of Recognition Abilities Between Improved BP Network and RBF Network. J. Shangluo Univ. 2025, 39, 39–46. [Google Scholar] [CrossRef]
- Ahmad, Z.; Li, J.; Mahmood, T. Adaptive Hyperparameter Fine-Tuning for Boosting the Robustness and Quality of the Particle Swarm Optimization Algorithm for Non-Linear RBF Neural Network Modelling and Its Applications. Mathematics 2023, 11, 242. [Google Scholar] [CrossRef]
- Li, Y.; Gao, W.; Ying, S. RBF-Assisted Hybrid Neural Network for Solving Partial Differential Equations. Mathematics 2024, 12, 1617. [Google Scholar] [CrossRef]
- Huang, K.Q.; Xu, J. Path planning of mobile robot based on multi-strategy improved whale optimization algorithm. Sens. Microsyst. 2025, 44, 121–125. [Google Scholar] [CrossRef]
- Wang, S.Y.; He, F.Y.; He, T. Contact force tracking algorithm of robotic arm based on adaptive weight WOA. J. Hubei Univ. Technol. 2025, 40, 5–10. [Google Scholar]
- Wen, X.; He, M.; Zhang, J.; Zhou, K.; Cai, Y.; Zhang, F. Research on ultra-short-term power forecasting of photovoltaic clusters based on K-means clustering. Power Syst. Prot. Control 2025, 53, 165–172. [Google Scholar] [CrossRef]
- Cheng, C.N.; Feng, S.L.; Mo, L.P. Harmony search algorithm based on sine cosine optimization operator and Levy flight mechanism. J. Data Acquis. Process. 2023, 38, 690–703. [Google Scholar] [CrossRef]
- Wang, T. Trajectory Optimization and Control of Polishing Robot Based on Improved Whale Optimization Algorithm. Ph.D. Dissertation, North University of China, Taiyuan, China, 2021. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.J.; Zhao, T.Z.; Li, C.H.; Jie, J.; Shi, H.Q.; Yang, H. Improved pelican optimization algorithm integrating multi-strategy. Control Eng. China 2025, 32, 1184–1197+1206. [Google Scholar] [CrossRef]
- Huang, X.Y.; Luo, H. An arithmetic optimization algorithm integrating sine-cosine strategy. Comput. Eng. Sci. 2023, 45, 1320–1330. [Google Scholar]
- Barua, S.; Merabet, A. Lévy Arithmetic Algorithm: An enhanced metaheuristic algorithm and its application to engineering optimization. Expert Syst. Appl. 2024, 241, 122335. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Q.; Ma, L.; Zhang, Z. Sparrow Search Algorithm with Adaptive t Distribution for Multi-Objective Low-Carbon Multimodal Transportation Planning Problem with Fuzzy Demand and Fuzzy Time. Expert Syst. Appl. 2024, 238, 122042. [Google Scholar] [CrossRef]
| Parameter | Positive Impacts on Combustion Efficiency and Emissions | Negative Impacts on Combustion Efficiency and Emissions |
|---|---|---|
| Primary Air Volume | Enhances combustion efficiency | Reduces furnace temperature, increases NOX formation |
| Secondary Air Volume | Promotes complete combustion and gas mixing; improves efficiency | Excessive amounts increase NOX formation |
| Air Pressure | Increases flow velocity and efficiency | Excessive pressure may lead to high temperatures, promoting NOX production |
| Grate Speed | Controls waste residence time within the furnace | Too low speeds lead to over-combustion and higher NOX emissions |
| Category | Symbol | Description |
|---|---|---|
| Inputs (Manipulated Variables) | Primary Air Flow | |
| Secondary Air Flow | ||
| Air Pressure | ||
| Input (Disturbance) | Grate Speed | |
| Outputs (Predicted Flue Gas Components) | CO Concentration | |
| CO2 Concentration | ||
| NOX Concentration |
| WOA Element | Neuron Width Optimization |
|---|---|
| Whale Individual | Data Feasible solution for parameters |
| Whale Population | Set of candidate solutions for parameters |
| Best Whale (Global Best) | Optimal solution for parameters |
| Whale Preying | Optimization process |
| Bubble-net Attack | Local fine search near the optimal solution |
| Ocean | Solution range for parameters |
| Pelican Hunting Behavior | Finding Air Volume and Pressure Setting |
|---|---|
| Prey | Air volume and pressure setting |
| Pelican preying | Optimization process |
| Prey’s position | Optimal solution for air volume and pressure |
| Pond | Solution space |
| Parameter | Range | Value |
|---|---|---|
| l | −1–1 | −0.06 |
| p | 0–1 | 0.74 |
| r1 | 0–1 | 0.25 |
| r2 | 0–1 | 0.37 |
| a | 0–2 | 0.12 |
| 0–2 | 1.5 | |
| same | 1 | |
| same | 3 | |
| same | 0.01 |
| Parameter | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
|---|---|---|---|---|---|---|---|---|
| U1 | 0.5213 | 0.3487 | 0.4751 | 0.5743 | 0.6582 | 0.8452 | 0.4763 | 0.2987 |
| U2 | 0.5375 | 0.3742 | 0.4632 | 0.5894 | 0.6712 | 0.8743 | 0.4712 | 0.3648 |
| U3 | 0.5845 | 0.3851 | 0.4633 | 0.5134 | 0.6841 | 0.8762 | 0.4796 | 0.3546 |
| U4 | 0.5341 | 0.3647 | 0.4637 | 0.5979 | 0.6458 | 0.8553 | 0.4683 | 0.2873 |
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Width Value | 0.253 | 0.249 | 0.231 | 0.273 | 0.296 | 0.272 | 0.252 | 0.263 |
| Dataset | GWO-RBF | WOA-RBF | IWOA-RBF |
|---|---|---|---|
| 1 | 0.51592 | 0.39232 | 0.30213 |
| 2 | 0.52831 | 0.39334 | 0.29882 |
| 3 | 0.51367 | 0.40223 | 0.28776 |
| 4 | 0.51258 | 0.39872 | 0.29776 |
| Dataset | GWO-RBF | WOA-RBF | IWOA-RBF |
|---|---|---|---|
| 1 | 0.52342 | 0.38146 | 0.29857 |
| 2 | 0.51611 | 0.39273 | 0.29334 |
| 3 | 0.52421 | 0.39346 | 0.28184 |
| 4 | 0.51269 | 0.40231 | 0.29921 |
| Dataset | GWO-RBF | WOA-RBF | IWOA-RBF |
|---|---|---|---|
| 1 | 0.51425 | 0.37523 | 0.29249 |
| 2 | 0.51317 | 0.38231 | 0.28716 |
| 3 | 0.52182 | 0.38312 | 0.28825 |
| 4 | 0.51759 | 0.39115 | 0.29147 |
| Dataset | GWO-RBF | WOA-RBF | IWOA-RBF |
|---|---|---|---|
| 1 | 0.47465 | 0.32358 | 0.23312 |
| 2 | 0.46892 | 0.33361 | 0.23421 |
| 3 | 0.47332 | 0.34189 | 0.22892 |
| 4 | 0.47158 | 0.34442 | 0.23322 |
| Dataset | GWO-RBF | WOA-RBF | IWOA-RBF |
|---|---|---|---|
| 1 | 0.46632 | 0.31872 | 0.22981 |
| 2 | 0.46553 | 0.32963 | 0.23258 |
| 3 | 0.47261 | 0.33411 | 0.22787 |
| 4 | 0.46238 | 0.33818 | 0.23848 |
| Dataset | GWO-RBF | WOA-RBF | IWOA-RBF |
|---|---|---|---|
| 1 | 0.45251 | 0.30963 | 0.21245 |
| 2 | 0.46125 | 0.31236 | 0.21381 |
| 3 | 0.45637 | 0.31355 | 0.20848 |
| 4 | 0.45385 | 0.30861 | 0.21239 |
| Parameter Symbol | Value |
|---|---|
| Rand | 1 |
| q | 1 |
| r3 | 1 |
| r4 | 1 |
| r5 | 0.5 |
| r6 | 1 |
| 0.01 | |
| 1.5 |
| Operating Condition | Grate Speed (m/h) |
|---|---|
| 1 | 5 |
| 2 | 6 |
| 3 | 7 |
| 4 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pian, J.; Deng, P.; Tang, J. Optimal Control of MSWI Processes Using an RBF-IPOA Strategy for Enhanced Combustion Efficiency and NOX Reduction. Processes 2025, 13, 3350. https://doi.org/10.3390/pr13103350
Pian J, Deng P, Tang J. Optimal Control of MSWI Processes Using an RBF-IPOA Strategy for Enhanced Combustion Efficiency and NOX Reduction. Processes. 2025; 13(10):3350. https://doi.org/10.3390/pr13103350
Chicago/Turabian StylePian, Jinxiang, Peng Deng, and Jian Tang. 2025. "Optimal Control of MSWI Processes Using an RBF-IPOA Strategy for Enhanced Combustion Efficiency and NOX Reduction" Processes 13, no. 10: 3350. https://doi.org/10.3390/pr13103350
APA StylePian, J., Deng, P., & Tang, J. (2025). Optimal Control of MSWI Processes Using an RBF-IPOA Strategy for Enhanced Combustion Efficiency and NOX Reduction. Processes, 13(10), 3350. https://doi.org/10.3390/pr13103350







