Two-Step Statistical and Physical–Mechanical Optimization of Electric Arc Spraying Parameters for Enhanced Coating Adhesion
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Equipment
2.3. Experimental Design and Parameter Ranges
2.4. Conducting the Experiments
2.5. Mathematical Modeling
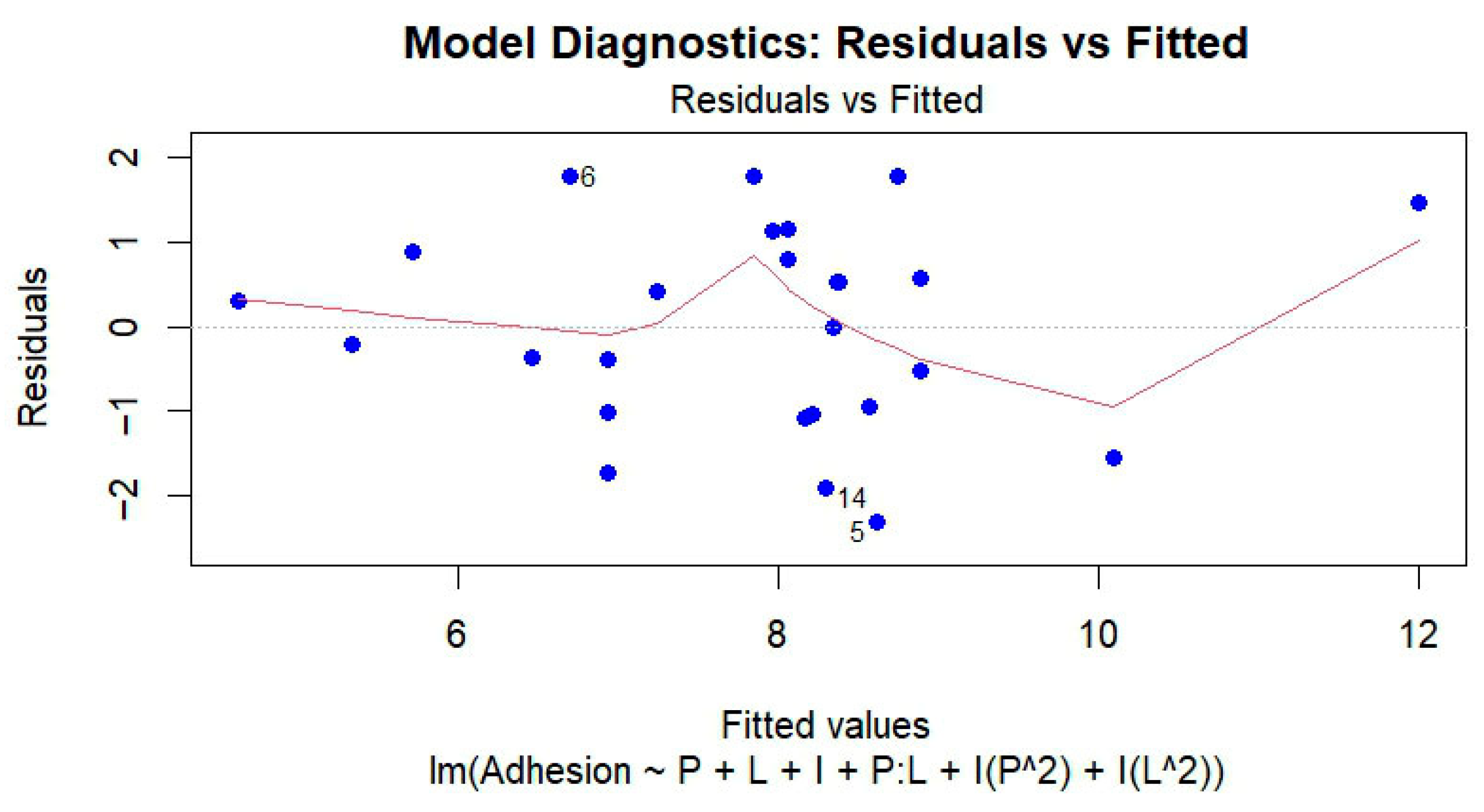
2.6. Diagnostics, Validation, and Data Processing
3. Results
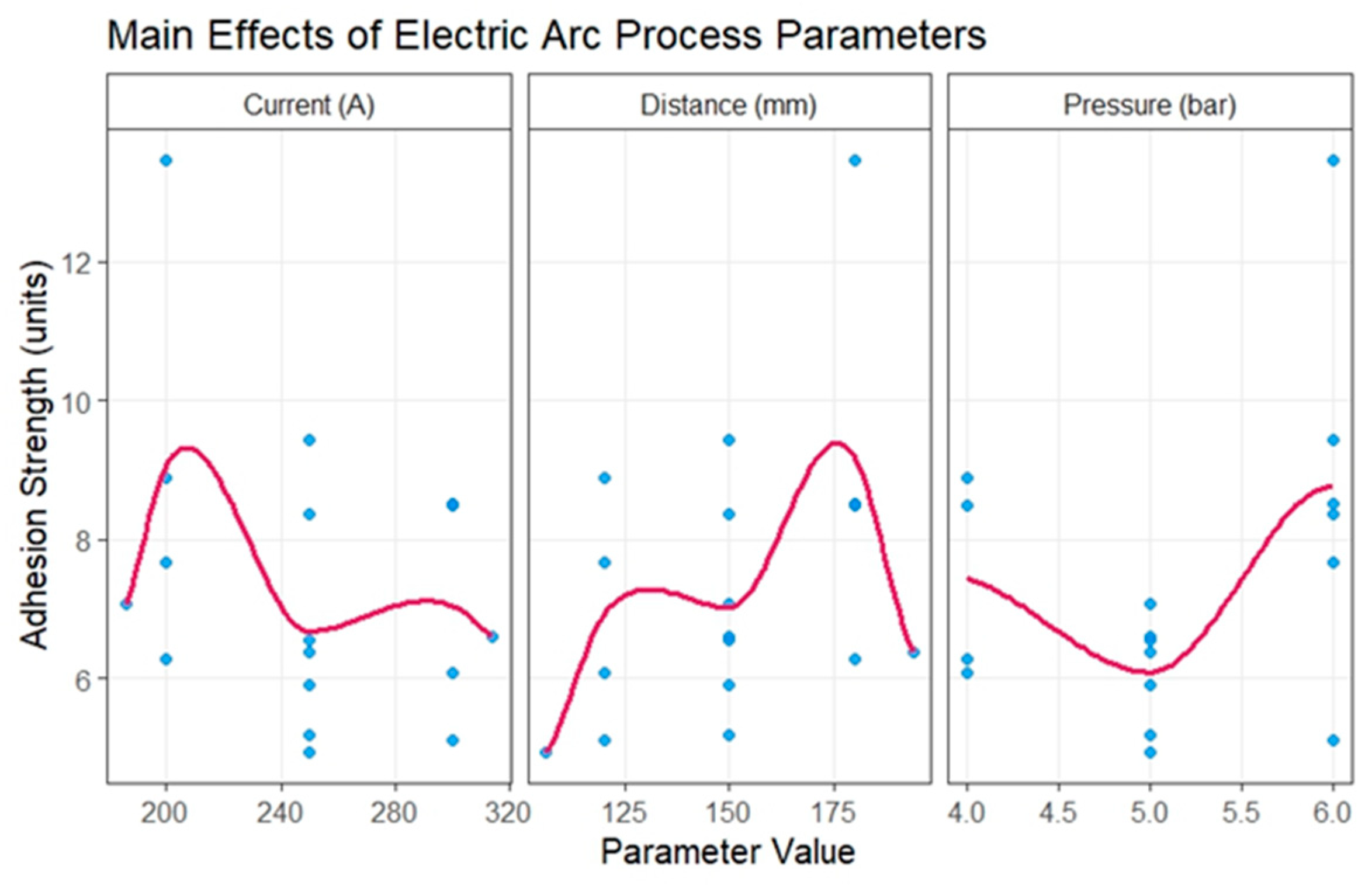
3.1. Main Effects of Individual Factors (P, L, I)
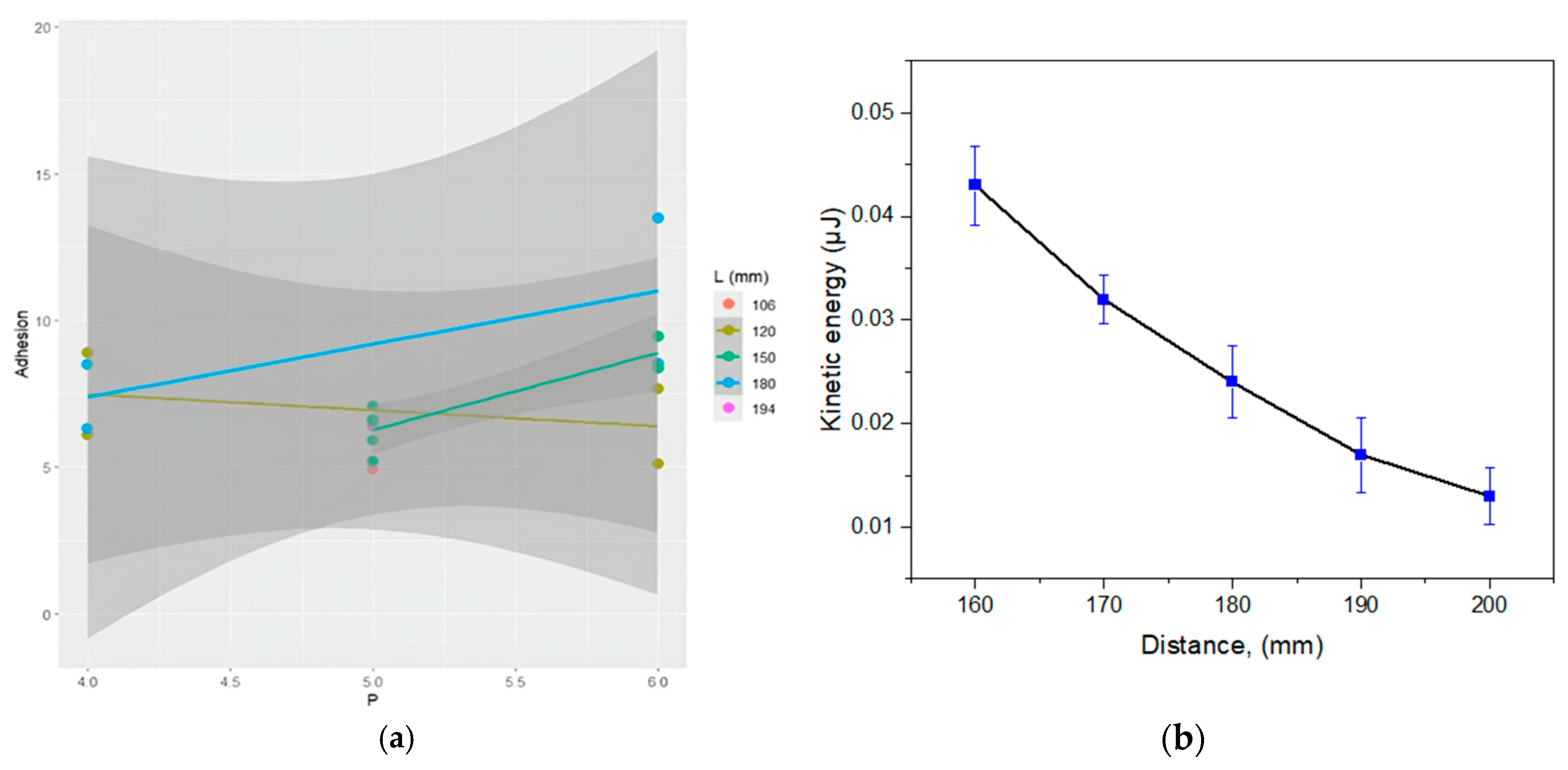
3.2. Effect of Stand-Off Distance (L) and Physical Rationale
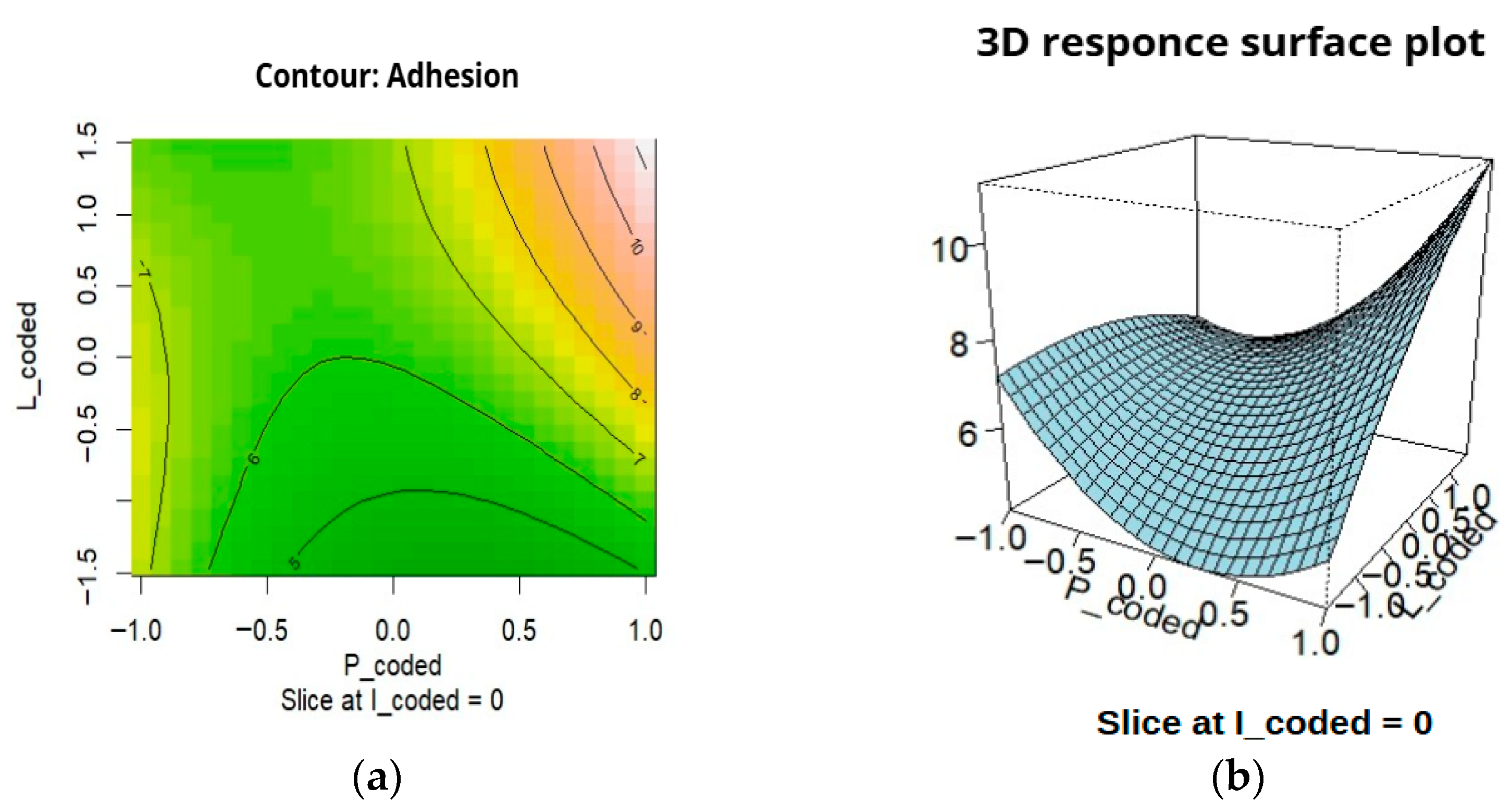
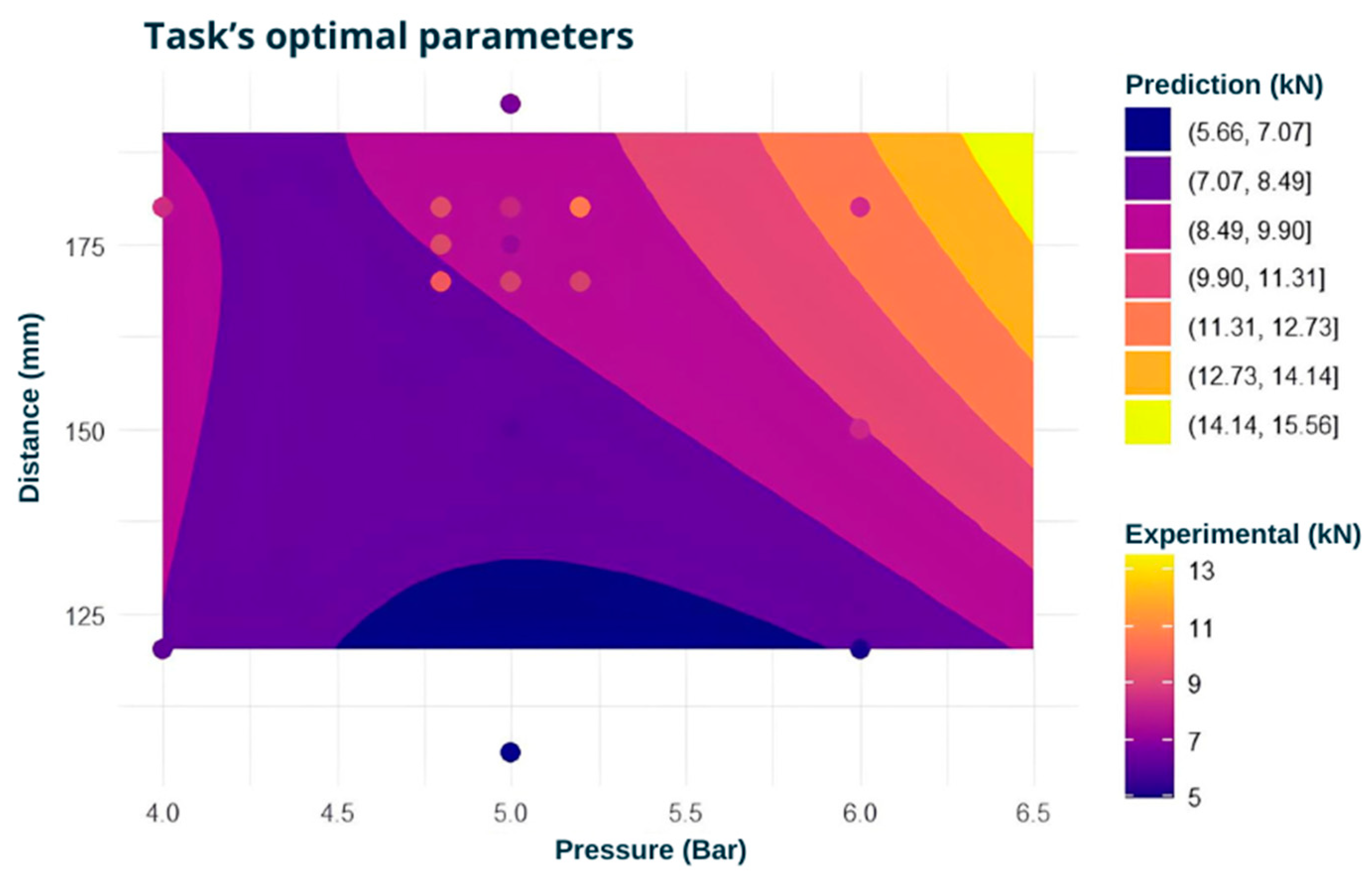
3.3. Interaction Between Pressure and Distance (P × L): Response Surface Analysis
3.4. Validation and Reliability of the Model
3.5. Comparison with Experiment
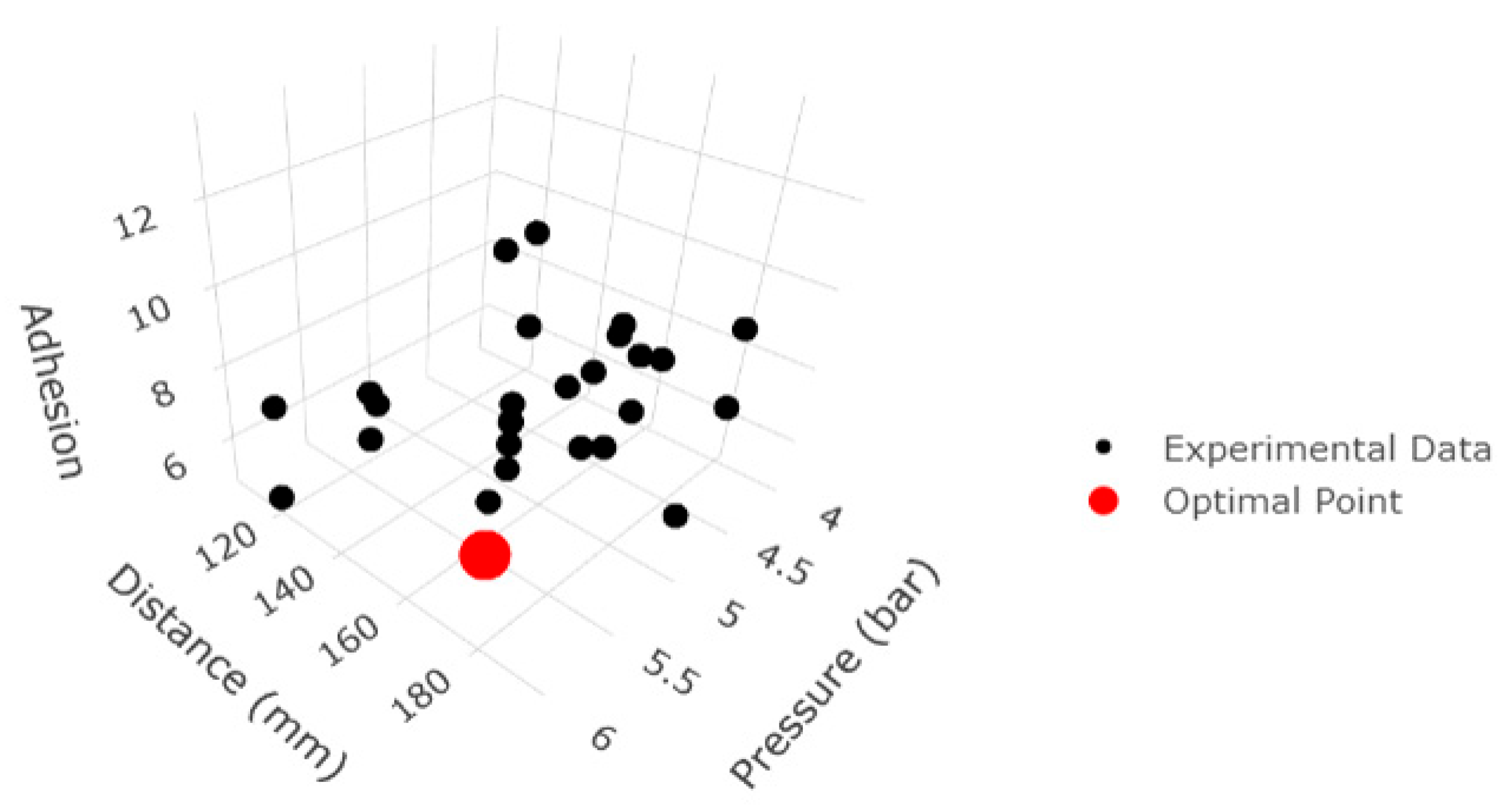
3.6. Spatial Representation of the Optimum
3.7. Summary Generalization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mozetič, M. Surface Modification to Improve Properties of Materials. Materials 2019, 12, 441. [Google Scholar] [CrossRef]
- Maksakova, O.V.; Pogrebnjak, A.D.; Buranich, V.V.; Ivashchenko, V.I.; Baimoldanova, L.S.; Rokosz, K.; Raaen, S.; Malovana, N. Theoretical and experimental investigation of multiplayer (TiAlSiY)N/CrN coating before and after gold ions implantation. High Temp. Mater. Process. Int. Q. High-Technol. Plasma Process. 2021, 25, 57–70. [Google Scholar] [CrossRef]
- Rakhadilov, B.; Bayandinova, M.; Kussainov, R.; Maulit, A. Electrolyte-plasma surface hardening of hollow steel applicator needles for point injection of liquid mineral fertilizers. AIMS Mater. Sci. 2024, 11, 295–308. [Google Scholar] [CrossRef]
- Molbossynov, Y.; Rakhadilov, B.; Magazov, N.; Apsezhanova, A.; Kussainov, A. Impact of gas pressure and spray distance on coating formation in electric arc metallization. Phys. Sci. Technol. 2025, 12, 14–26. [Google Scholar] [CrossRef]
- Skakov, M.; Bayandinova, M.; Kozhakhmetov, Y.; Tuyakbaev, B. Microstructure and Corrosion Resistance of Composite Based on Ultra-High Molecular Weight Polyethylene in Acidic Media. Coatings 2025, 15, 89. [Google Scholar] [CrossRef]
- Horner, A.L.; Hall, A.C.; McCloskey, J.F. The effect of process parameters on Twin Wire Arc spray pattern shape. Coatings 2015, 5, 115–123. [Google Scholar] [CrossRef]
- Rakhadilov, B.; Buitkenov, D.; Apsezhanova, A.; Kakimzhanov, D.; Nabioldina, A.; Magazov, N. Selection of Optimal Process Parameters for Arc Metallization. Coatings 2025, 15, 300. [Google Scholar] [CrossRef]
- Ružbarský, J.; Panda, A. Plasma and Thermal Spraying; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Palani, P.K.; Murugan, N. Selection of parameters of pulsed current gas metal arc welding. J. Mater. Process. Technol. 2006, 172, 1–10. [Google Scholar] [CrossRef]
- Carlsson, L.S.; Samuelsson, P.B.; Jönsson, P.G. Predicting the electrical energy consumption of electric arc furnaces using statistical modeling. Metals 2019, 9, 959. [Google Scholar] [CrossRef]
- Royanov, V.; Zakharova, I.; Lavrova, E. Development of properties of spray flow and nature of pressure distribution in electric arc metalization. Bocmoчнo-Еврoпейский журнал передoвых технoлoгий 2017, 6, 41–49. [Google Scholar] [CrossRef][Green Version]
- Rakhadilov, B.; Muktanova, N.; Kengesbekov, A.; Magazov, N. Use of Computational Fluid Dynamics (CFD) Methods to Analyze Combustion Chamber Processes at HVOF Spraying and Their Comparison with Experimental Data. Modelling 2025, 6, 4. [Google Scholar] [CrossRef]
- Skakov, M.K.; Ocheredko, I.A.; Bayandinova, M.B.; Tuyakbaev, B.T. The impact of technological parameters of the torch to physical and chemical properties of a gas-thermal burner for spraying ultra-high molecular weight polyethylene. Phys. Sci. Technol. 2022, 9, 59–68. [Google Scholar] [CrossRef]
- Darabi, A.; Azarmi, F. Investigation on relationship between microstructural characteristics and mechanical properties of wire-arc-sprayed Zn-Al coating. J. Therm. Spray Technol. 2020, 29, 297–307. [Google Scholar] [CrossRef]
- Gedzevicius, I.; Valiulis, A.V. Analysis of wire arc spraying process variables on coatings properties. J. Mater. Process. Technol. 2006, 175, 206–211. [Google Scholar] [CrossRef]
- Yurdgülü, H.I.; Sadeler, R.; Koç, B. Optimization of multiple outputs of electric arc spray coating parameters for EN AW 7020-T6. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2025, 09544089251317383. [Google Scholar] [CrossRef]
- Davis, J.R. Handbook of Thermal Spray Technology; ASM International: Almere, The Netherlands, 2004; p. 131. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; Wiley: Hoboken, NJ, USA, 2017; p. 735. [Google Scholar]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Fukumoto, M.; Nishioka, E.; Nishiyama, T. New criterion for splashing in flattening of thermal sprayed particles onto flat substrate surface. Surf. Coat. Technol. 2002, 161, 103–110. [Google Scholar] [CrossRef]
- Zhou, J.; Jiang, J.; Deng, L.; Huang, J.; Yuan, J.; Cao, X. Influence of bond coat on thermal shock resistance and thermal ablation resistance for polymer matrix composites. Front. Mater. 2021, 8, 672617. [Google Scholar] [CrossRef]
- Ndumia, J.N.; Kang, M.; Gbenontin, B.V.; Lin, J.; Liu, J.; Li, H.; Nyambura, S.M. Optimizing parameters of arc-sprayed Fe-based coatings using the response surface methodology. J. Therm. Spray Technol. 2023, 32, 2202–2220. [Google Scholar] [CrossRef]
- Das, B.K.; Jha, D.N.; Sahu, S.K.; Yadav, A.K.; Raman, R.K.; Kartikeyan, M. Analysis of Variance (ANOVA) and Design of Experiments. In Concept Building in Fisheries Data Analysis; Springer: Singapore, 2022; pp. 119–136. [Google Scholar]
- Rakhadilov, B.; Muktanova, N.; Seitkhanova, A.; Kakimzhanov, D.; Dautbekov, M. Investigation of the Influence of the Oxygen Flow Rate on the Mechanical, Structural and Operational Properties of 86WC-10Co-4Cr Coatings, as Determined Using the High-Velocity Oxyfuel Spraying Method. Coatings 2024, 14, 1275. [Google Scholar] [CrossRef]
- Boinovich, L.B.; Domantovsky, A.G.; Emelyanenko, A.M.; Emelyanenko, K.A. Synergism of Arc Spraying, Laser Processing, and Hydrophobization for Long-Lasting Corrosion Protection of MA8 Magnesium Alloy. Adv. Eng. Mater. 2025, 27, 2401708. [Google Scholar] [CrossRef]
- Ellinas, K.; Dimitrakellis, P.; Sarkiris, P.; Gogolides, E. A Review of Fabrication Methods, Properties and Applications of Superhydrophobic Metals. Processes 2021, 9, 666. [Google Scholar] [CrossRef]
- GOST 14959-2016; Spring Nonalloy and Alloy Steel Product. Specifications. Standartinform: Moscow, Russia, 2016.
- Branch, B.; Ionita, A.; Clements, B.E.; Montgomery, D.S.; Jensen, B.J.; Patterson, B.; Dattelbaum, D.M. Controlling shockwave dynamics using architecture in periodic porous materials. J. Appl. Phys. 2017, 121, 13. [Google Scholar] [CrossRef]
- Rakhadilov, B.; Magazov, N.; Kakimzhanov, D.; Apsezhanova, A.; Molbossynov, Y.; Kengesbekov, A. Influence of Spraying Process Parameters on the Characteristics of Steel Coatings Produced by Arc Spraying Method. Coatings 2024, 14, 1145. [Google Scholar] [CrossRef]
- Bae, G.; Xiong, Y.; Kumar, S.; Kang, K.; Lee, C. General aspects of interface bonding in kinetic sprayed coatings. Acta Mater. 2008, 56, 4858–4868. [Google Scholar] [CrossRef]
- Mahendru, P.; Tembely, M.; Dolatabadi, A. Artificial intelligence models for analyzing thermally sprayed functional coatings. J. Therm. Spray Technol. 2023, 32, 388–400. [Google Scholar] [CrossRef]
- Strokovsky, E.A. Lectures on the Fundamentals of Kinematics of Elementary Processes. In University Book; University Book Publishing House: Moscow, Russia, 2010; 298p. (In Russian) [Google Scholar]
- Venkatachalapathy, V.; Katiyar, N.K.; Matthews, A.; Endrino, J.L.; Goel, S. A Guiding Framework for Process Parameter Optimisation of Thermal Spraying. Coatings 2023, 13, 713. [Google Scholar] [CrossRef]
| № | I (A) | P (Bar) | L (mm) | Comment | Adhesion (kN) | SD (±kN) |
|---|---|---|---|---|---|---|
| 1 | 200 | 4.0 | 120 | factorial (−1, −1, −1) | 8.8912 | 0.39 |
| 2 | 300 | 4.0 | 120 | factorial (+1, −1, −1) | 6.0890 | 0.27 |
| 3 | 200 | 6.0 | 120 | factorial (−1, +1, −1) | 7.6644 | 0.34 |
| 4 | 300 | 6.0 | 120 | factorial (+1, +1, −1) | 5.1202 | 0.23 |
| 5 | 200 | 4.0 | 180 | factorial (−1, −1, +1) | 6.2924 | 0.28 |
| 6 | 300 | 4.0 | 180 | factorial (+1, −1, +1) | 8.4822 | 0.37 |
| 7 | 200 | 6.0 | 180 | factorial (−1, +1, +1) | 13.4730 | 0.59 |
| 8 | 300 | 6.0 | 180 | factorial (+1, +1, +1) | 8.5306 | 0.37 |
| 9 | 186 | 5.0 | 150 | axial (−α, 0, 0) | 7.0800 | 0.31 |
| 10 | 314 | 5.0 | 150 | axial (+α, 0, 0) | 6.5996 | 0.31 |
| 11 | 250 | 4.0 | 150 | axial (0, −α, 0) | 9.4474 | 0.41 |
| 12 | 250 | 6.0 | 150 | axial (0, +α, 0) | 8.3622 | 0.37 |
| 13 | 250 | 5.0 | 106 | axial (0, 0, −α) | 4.9310 | 0.22 |
| 14 | 250 | 5.0 | 194 | axial (0, 0, +α) | 6.3776 | 0.28 |
| 15 | 250 | 5.0 | 150 | center point (0, 0, 0) | 5.1922 | 0.23 |
| 16 | 250 | 5.0 | 150 | center point (repeat) | 6.5488 | 0.29 |
| 17 | 250 | 5.0 | 150 | center point (repeat) | 5.9198 | 0.26 |
| № | Current (A) | Pressure (Bar) | Distance (mm) | Adhesion (kN) (SD) |
|---|---|---|---|---|
| 1 | 230 | 4.8 | 170 | 9.62 (±0.28) |
| 2 | 230 | 5.0 | 170 | 9.08 (±0.27) |
| 3 | 230 | 5.2 | 170 | 9.21 (±0.27) |
| 4 | 230 | 4.8 | 175 | 8.85 (±0.26) |
| 5 | 230 | 5.0 | 175 | 7.16 (±0.21) |
| 6 | 230 | 5.2 | 175 | 8.34 (±0.24) |
| 7 | 230 | 4.8 | 180 | 8.89 (±0.26) |
| 8 | 230 | 5.0 | 180 | 7.61 (±0.22) |
| 9 | 230 | 5.2 | 180 | 10.52 (±0.31) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magazov, N.; Rakhadilov, B.; Bayandinova, M. Two-Step Statistical and Physical–Mechanical Optimization of Electric Arc Spraying Parameters for Enhanced Coating Adhesion. Processes 2025, 13, 3349. https://doi.org/10.3390/pr13103349
Magazov N, Rakhadilov B, Bayandinova M. Two-Step Statistical and Physical–Mechanical Optimization of Electric Arc Spraying Parameters for Enhanced Coating Adhesion. Processes. 2025; 13(10):3349. https://doi.org/10.3390/pr13103349
Chicago/Turabian StyleMagazov, Nurtoleu, Bauyrzhan Rakhadilov, and Moldir Bayandinova. 2025. "Two-Step Statistical and Physical–Mechanical Optimization of Electric Arc Spraying Parameters for Enhanced Coating Adhesion" Processes 13, no. 10: 3349. https://doi.org/10.3390/pr13103349
APA StyleMagazov, N., Rakhadilov, B., & Bayandinova, M. (2025). Two-Step Statistical and Physical–Mechanical Optimization of Electric Arc Spraying Parameters for Enhanced Coating Adhesion. Processes, 13(10), 3349. https://doi.org/10.3390/pr13103349






