Study on the Thermodynamic Behavior of Large Volume Liquid Hydrogen Bottle Under the Coupling of Different Motion States and Operational Parameters
Abstract
1. Introduction
2. Numerical Theory Basis
2.1. Basic Conservation Equation
2.2. Turbulence Model
2.3. Evaporation–Condensation Model
2.4. Theoretical Basis of Heat Conduction
3. Structural Modeling of Large Volume Vehicle Liquid Hydrogen Bottle
3.1. Model Simplification
3.2. Mesh Generation and Boundary Conditions
3.2.1. Meshing
3.2.2. Boundary Conditions and Initial Conditions
3.3. Grid Independence Verification
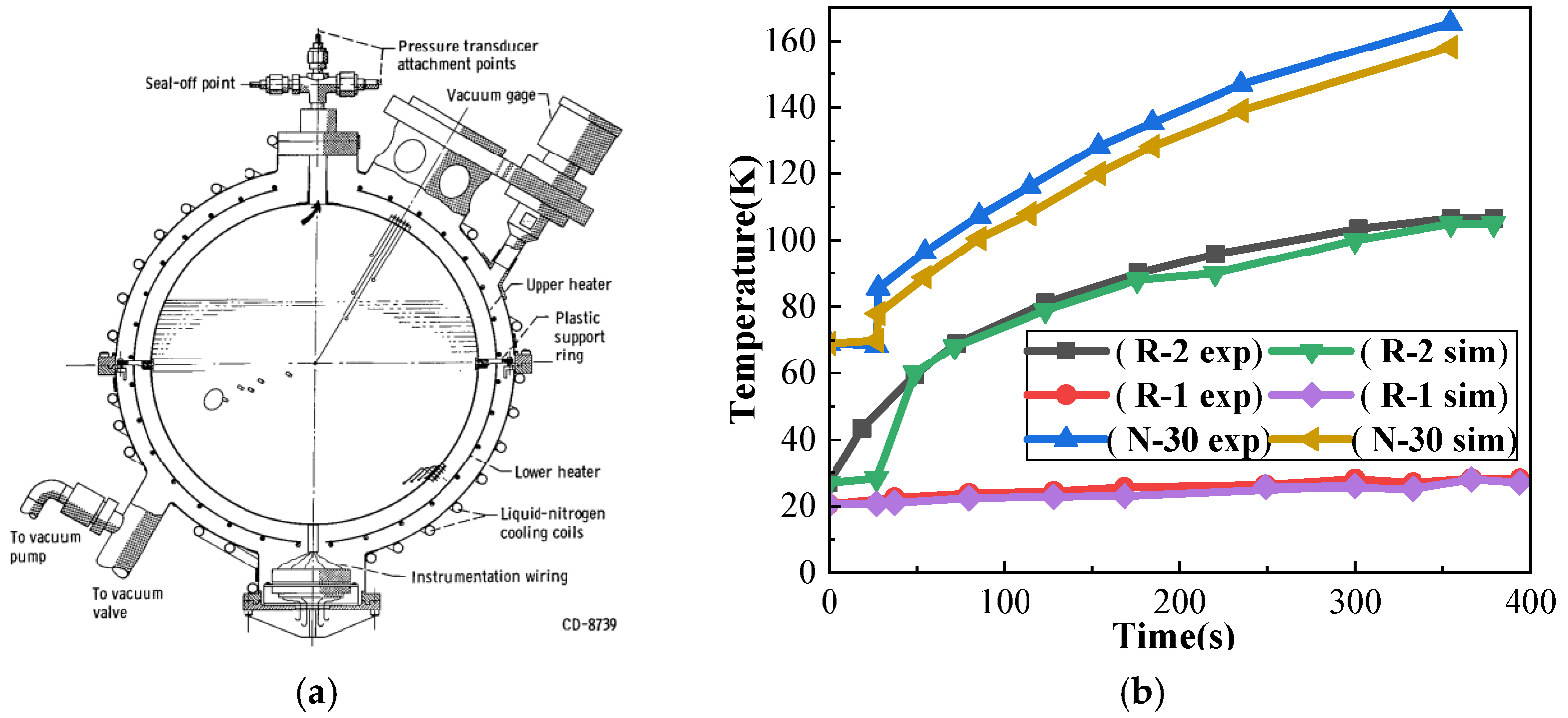
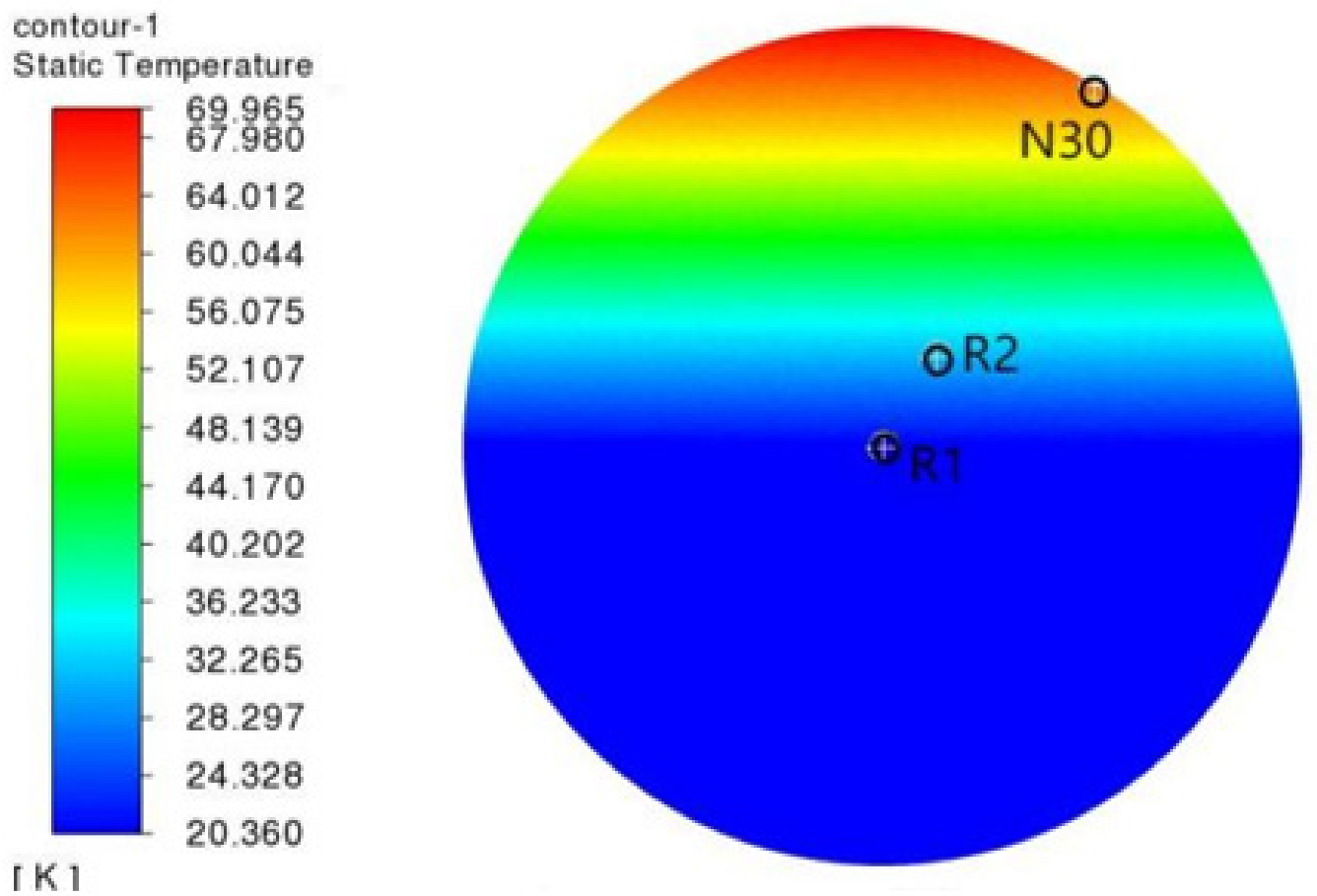
3.4. Validation of Model Accuracy
3.5. Simulation Conditions and Group Settings
4. Simulation Results and Analysis
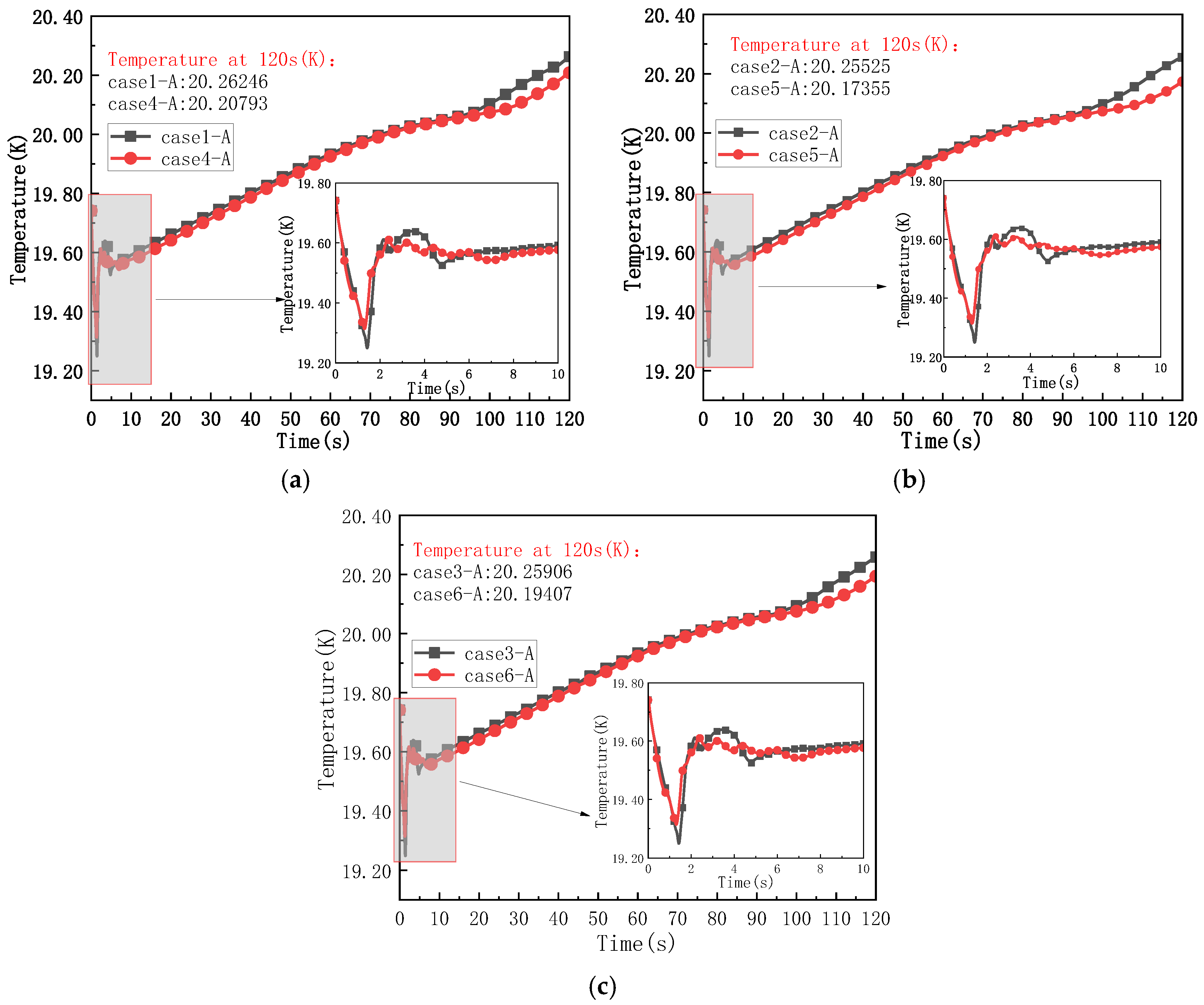
4.1. Thermodynamic Changes of Fluid in the Liquid Hydrogen Bottle Under Different Motion States
4.2. Thermodynamic Changes of the Fluid in the Liquid Hydrogen Bottle Under the Coupling of Different Operating Pressures and Motion States
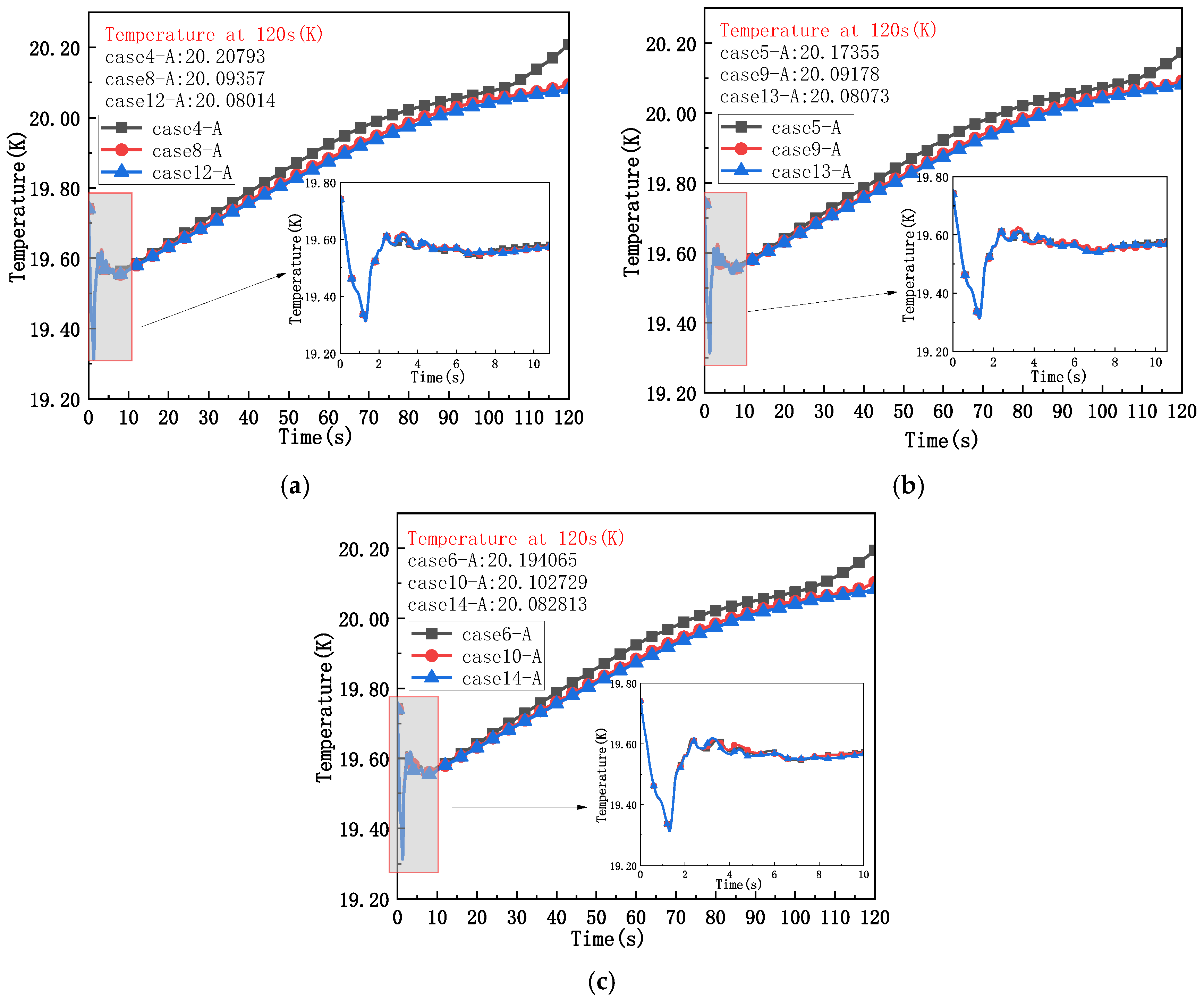
4.3. Change in the Thermodynamic Behavior of Fluid in the Liquid Hydrogen Bottle Under the Coupling of Different Insulation Thicknesses and Operating Pressures
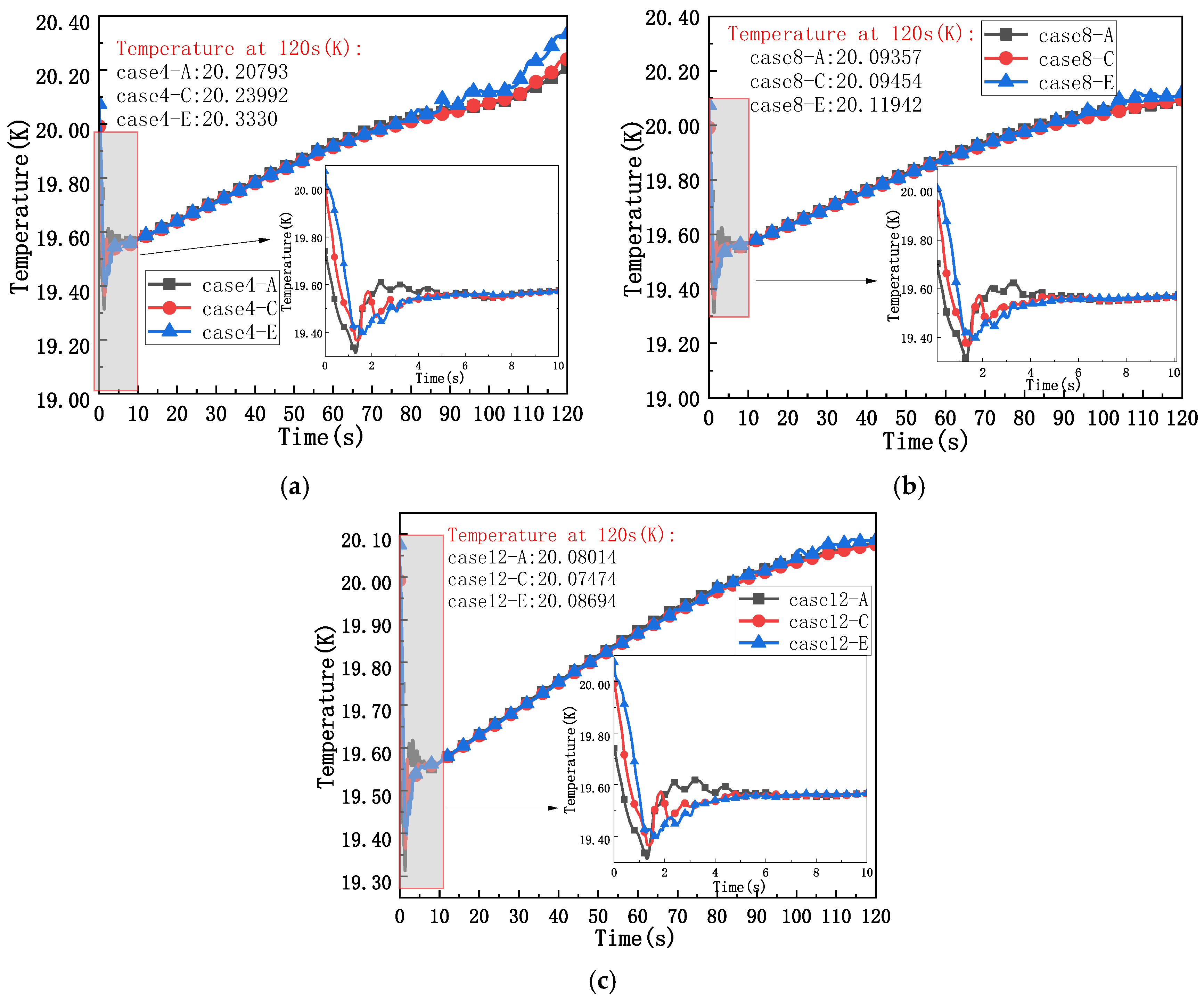
4.4. Thermodynamic Changes of Fluid in the Liquid Hydrogen Bottle with Different Insulation Thicknesses and Different Positions in the Liquid Hydrogen Bottle
5. Conclusions
- In comparison with the changes in the thermodynamic behavior of the fluid within the liquid hydrogen tank under static conditions, motion enhances the heat and mass transfer between the gas and liquid phases inside the tank. This results in a more uniform phase distribution within the liquid hydrogen tank than that observed under static conditions, along with an accelerated pressure drop rate and a lower temperature. The uniform acceleration (such as acceleration of 4.4 m/s2) during vehicle start-up is similar to the uniform deceleration state during braking. Both of them can promote the heat and mass transfer of gas–liquid two-phase, increase the uniformity of phase state in the liquid hydrogen bottle by about 3.8% (compared with stationary), and reduce the temperature by 0.044~0.055 K. In the case of the same absolute value of acceleration, the difference between the effects of acceleration and deceleration on thermodynamic behavior is less than 0.5%, which can be classified as the common effect of the ‘non-stationary motion state’.
- The changes in the operating pressure and motion state have an effect on the heating rate in the liquid hydrogen bottle. Compared with 1.2 MPa and 0.5 MPa, a moderate operating pressure (0.85 MPa) can slow down the heating rate in the liquid hydrogen bottle and prolong the dormancy period of liquid hydrogen to reduce the possible evaporation gas. Under the coupling of the operating pressure and motion state, the change in the motion state has a dominant influence on the temperature of the fluid domain in the liquid hydrogen bottle.
- The variation law of fluid temperature in a liquid hydrogen bottle under the coupling of insulation layer thickness and operating pressure is dominated by the operating pressure when the thickness of insulation layer is low, and when the thickness of the insulation layer increases to a certain value, it is dominated by the thickness of the insulation layer, and the heating rate in the liquid hydrogen bottle basically does not change.
- When the position in the liquid hydrogen bottle and the thickness of the insulation layer change, and when the thickness of the insulation layer is small, the temperature in the liquid hydrogen bottle changes, showing that the near-wall temperature growth rate is always higher than the far-wall temperature growth rate. As the thickness of the insulation layer increases, this phenomenon is mitigated, and the temperature rise rates at different locations inside the liquid hydrogen tank tend to converge.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, S.; Yang, X. Research progress of lossless and safe storage technology for cryogenic liquid tanks. Int. J. Green Energy 2022, 19, 1230–1251. [Google Scholar] [CrossRef]
- Birk, A.M.; Cunningham, M.H. Liquid temperature stratification and its effect on BLEVEs and their hazards. J. Hazard. Mater. 1996, 48, 219–237. [Google Scholar] [CrossRef]
- Zhu, Y.; Bu, Y.; Gao, W.; Xie, F.; Guo, W.; Li, Y. Numerical Study on Thermodynamic Coupling Characteristics of Fluid Sloshing in a Liquid Hydrogen Tank for Heavy-Duty Trucks. Energies 2023, 16, 1851. [Google Scholar] [CrossRef]
- Hou, C.; Yu, Y.; Liu, X.; Ding, J.; Cui, Z. Effects of longitudinal excitation on liquid hydrogen sloshing in spacecraft storage tanks under microgravity conditions. Int. J. Hydrogen Energy 2023, 51, 765–780. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, Y.; Lei, G.; Li, Y. Fluid sloshing dynamic performance in a liquid hydrogen tank. Int. J. Hydrogen Energy 2019, 44, 13885–13894. [Google Scholar] [CrossRef]
- Smith, J.R.; Gkantonas, S.; Mastorakos, E. Modelling of Boil-Off and Sloshing Relevant to Future Liquid Hydrogen Carriers. Energies 2022, 15, 2046. [Google Scholar] [CrossRef]
- Jeon, G.M.; Park, J.C.; Kim, J.W.; Lee, Y.B.; Kim, D.S.; Kang, D.E.; Lee, S.B.; Lee, S.W.; Ryu, M.C. Experimental and numerical investigation of change in boil-off gas and thermodynamic characteristics according to filling ratio in a C-type cryogenic liquid fuel tank. Energy 2022, 255, 124530. [Google Scholar] [CrossRef]
- Chung, S.-M.; Jeon, G.-M.; Park, J.-C. Numerical approach to analyze fluid flow in a type C tank for liquefied hydrogen carrier (part 1: Sloshing flow). Int. J. Hydrogen Energy 2022, 47, 5609–5626. [Google Scholar] [CrossRef]
- Ryu, M.-R.; Yun, S.; Kim, B.-K.; Kang, D.; Kim, G.; Lee, H. Numerical analysis of sloshing effects in cryogenic liquefied-hydrogen storage tanks for trains under various vibration conditions. Cryogenics 2024, 143, 103961. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, Y.; Lei, G.; Li, Y. Fluid thermal stratification in a non-isothermal liquid hydrogen tank under sloshing excitation. Int. J. Hydrogen Energy 2018, 43, 22622–22635. [Google Scholar] [CrossRef]
- Zheng, Z.; Xu, A.; Jiang, W.; Wang, B.; Sun, P.; Li, P.; Huang, Y. Simulation of sloshing and settling behavior of liquid hydrogen in an insulated tank during coastal period. Int. J. Hydrogen Energy 2025, 97, 117–129. [Google Scholar] [CrossRef]
- Lv, H.; Chen, L.; Zhang, Z.; Chen, S.; Hou, Y. Numerical study on thermodynamic characteristics of large-scale liquid hydrogen tank with baffles under sloshing conditions. Int. J. Hydrogen Energy 2024, 57, 562–574. [Google Scholar] [CrossRef]
- Kang, D.-H.; An, J.-H.; Lee, C.-J. Numerical modeling and optimization of thermal insulation for liquid hydrogen storage tanks. Energy 2024, 291, 130143. [Google Scholar] [CrossRef]
- Li, K.; Wen, J.; Xin, B.; Zhou, A.; Wang, S. Transient-state modeling and thermodynamic analysis of self-pressurization liquid hydrogen tank considering effect of vacuum multi-layer insulation coupled with vapor-cooled shield. Energy 2024, 286, 129450. [Google Scholar] [CrossRef]
- Jiang, W.; Sun, P.; Li, P.; Zuo, Z.; Huang, Y. Transient thermal behavior of multi-layer insulation coupled with vapor cooled shield used for liquid hydrogen storage bottle. Energy 2021, 231, 120859. [Google Scholar] [CrossRef]
- Wu, J.; Xie, R.; Yu, M.; Luo, C.; Wang, B.; Zhang, X.; Jiang, L. Techno-economic analysis on the performance of hydrogen adsorbents in the vacuum layer of cryogenic liquid storage bottle. Int. J. Hydrogen Energy 2024, 88, 132–141. [Google Scholar] [CrossRef]
- Li, K.; Wen, J.; Wang, S. Insulation and cost optimization of vapor-cooled shield coupled with para-to-ortho hydrogen conversion based on self-pressurization model of liquid hydrogen bottle and NSGA-II. J. Energy Storage 2024, 99, 113229. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, L.; Xu, X.; Guo, L.; Zhou, Y.; Wang, J. A novel insulation system based on active cooling without power input for liquid hydrogen storage. Energy 2019, 182, 1–10. [Google Scholar] [CrossRef]
- Joseph, J.; Agrawal, G.; Agarwal, D.K.; Pisharady, J.C.; Kumar, S.S. Effect of insulation thickness on pressure evolution and thermal stratification in a cryogenic bottle. Appl. Therm. Eng. 2017, 111, 1629–1639. [Google Scholar] [CrossRef]
- Wang, H.; Wang, B.; Pan, Q.; Wu, Y.; Jiang, L.; Wang, Z.; Gan, Z. Modeling and thermodynamic analysis of thermal performance in self-pressurized liquid hydrogen bottles. Int. J. Hydrogen Energy 2022, 47, 30530–30545. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, D.; Lv, H.; Zhang, C. Dispersion characteristics of large-scale liquid hydrogen spills in a real-world liquid hydrogen refueling station with various releasing and environmental conditions. Renew. Energy 2024, 236, 121327. [Google Scholar] [CrossRef]
- Zhu, S.; Fang, S.; Bao, S.; Zhi, X.; Wang, K.; Qiu, L. Efficient cooling strategies for liquid hydrogen pipelines: A comparative analysis. Renew. Energy 2024, 236, 121488. [Google Scholar] [CrossRef]
- Boryaev, A.; Chernyaev, I.; Yuqing, Z. Heat and mass transfer and hydrodynamics in cryogenic hydrogen fuel systems. Fuel 2022, 321, 124004. [Google Scholar] [CrossRef]
- Barnett, D.O. Liquid nitrogen stratification analysis and experiments in a partially filled, spherical container. Adv. Cryog. Eng. 1967, 13, 174–185. [Google Scholar]
- Zhu, H.Q.; Xie, L.H.; Cao, Y.B.; Zhang, X. Study on influence of pressure and filling level on mass flow of cryogenic insulated cylinder. Cryog. Supercond. 2022, 50, 97–102. [Google Scholar]
- Zhu, H.Q.; Feng, Y.K.; Cai, Y.B.; Zhang, X.; Wei, G.M.; Zhang, J.F. Study on temperature distribution in the gas phase of cryogenic vessels. China Sci. Pap. 2021, 16, 97–103. [Google Scholar]
- Bonab, S.A.; Yazdani-Asrami, M. Investigation on the heat transfer estimation of subcooled liquid hydrogen for transportation applications using intelligent technique. Int. J. Hydrogen Energy 2024, 84, 468–479. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, E.; Shi, J. Dynamic thermal performance of cryogenic liquid hydrogen heating from gas-liquid stratification to supercritical under a constant heat flux condition: A two-step simulation. Int. J. Hydrogen Energy 2024, 136, 1242–1250. [Google Scholar] [CrossRef]
- Wang, J.; Webley, P.A.; Hughes, T.J. Thermodynamic modelling of low fill levels in cryogenic storage bottles for application to liquid hydrogen maritime transport. Appl. Therm. Eng. 2024, 256, 124054. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, X.; Li, M.; Su, D.; Dang, C. Numerical simulation of heat transfer characteristics of falling-film evaporation of R32/R134a non-azeotropic refrigerant outside a horizontal tube. Int. Commun. Heat Mass Transf. 2023, 148, 107001. [Google Scholar] [CrossRef]
- Liu, Z.; Sunden, B.; Yuan, J. VOF modeling and analysis of filmwise condensation between vertical parallel plates. Heat Transf. Res. 2022, 43, 47–68. [Google Scholar] [CrossRef]
- Chen, G.B.; Bao, R.; Huang, Y.H. Low Temperature Engineering Technology: Data Volume; Chemical Industry Press: Beijing, China, 2006. [Google Scholar]
- Tao, W.Q. Heat Transfer: Fundamentals and Engineering Applications, 5th ed.; Higher Education Press: Beijing, China, 2019. [Google Scholar]
- Li, S.; Yan, Y.; Wei, W.; Wang, Z.; Ni, Z. Numerical simulation on the thermal dynamic behavior of liquid hydrogen in a storage bottle for trailers. Case Stud. Therm. Eng. 2022, 40, 102520. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, Y.; Li, F.; Shen, J.; Xing, Z.; Zhou, H. Simulation study on the influencing factors of thermal conductivity of large-volume vehicle-mounted liquid hydrogen bottles under different filling rates. Int. J. Hydrogen Energy 2024, 69, 804–816. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, L.; Wang, J.; Xi, X.; Zhou, H.; Zhou, Y.; Wang, J. Thermodynamic analysis and comparison of four insulation schemes for liquid hydrogen storage bottle. Energy Convers. Manag. 2019, 186, 526–534. [Google Scholar] [CrossRef]
- Qu, Q.X.; Huang, C.J.; Sun, W.T. Application and Analysis of Austenitic Stainless Steel in Cryogenic Propellant Tank of Launch Vehicle. In Proceedings of the China Materials Conference 2024, Guangzhou, China, 8–11 July 2024. [Google Scholar]
- Aydelott, J.C. Normal Gravity Self-Pressurization of 9-Inch-/23 cm/Diameter Spherical Liquid Hydrogen Tankage; Technical Report; NASA: Cleveland, OH, USA, 1967.


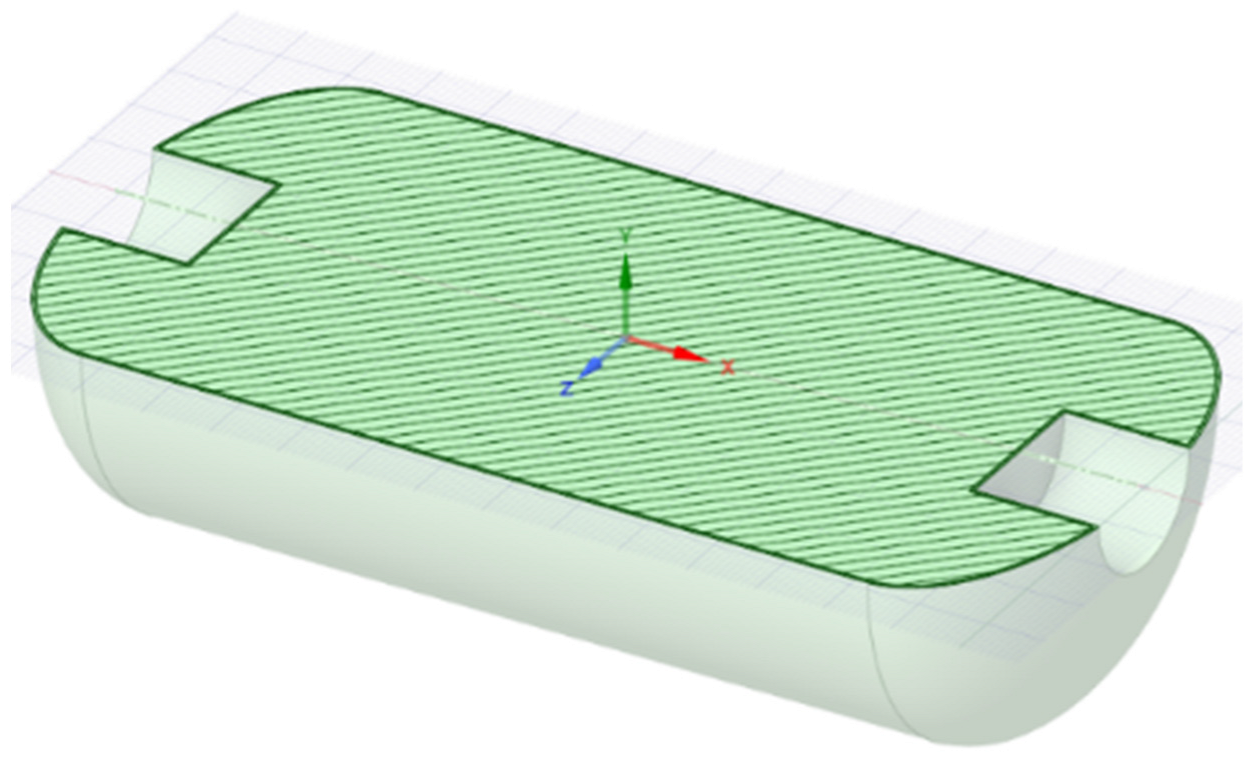




| Grid Size m | Grid Numbers | Point A K | Point B K | Point C K | Point D K | Point E K | Maximum Error% |
|---|---|---|---|---|---|---|---|
| 0.03 | 55,435 | 18.8912 | 18.8903 | 18.8906 | 18.8928 | 19.0024 | 5.1454 |
| 0.02 | 443,482 | 19.8650 | 19.8641 | 19.8649 | 19.8672 | 19.8718 | 0.2581 |
| 0.01 | 3,547,856 | 19.9147 | 19.9150 | 19.9153 | 19.9186 | 19.9223 | - |
| Detector Number | Position cm | Experimental Value K | Value of Simulation K | Error K |
|---|---|---|---|---|
| N30 | (11.499, 0, 5.7495) | 68.5 | 69.965 | 1.415 |
| R2 | (5.7495, 0, 2.8748) | 26.1 | 28.297 | 2.197 |
| R1 | (0, 0, 0) | 20.5 | 20.728 | 0.228 |
| Simulation Condition Number | Motion State | Operational Pressure MPa | Insulating Layer Thickness m |
|---|---|---|---|
| 1 | Static condition | 0.5 | 0.2 |
| 2 | Static condition | 0.85 | 0.2 |
| 3 | Static condition | 1.2 | 0.2 |
| 4 | Uniform deceleration linear motion | 0.5 | 0.2 |
| 5 | 0.85 | ||
| 6 | 1.2 | ||
| 7 | Static condition | 0.85 | 0.35 |
| 8 | Uniform deceleration linear motion | 0.5 | 0.35 |
| 9 | 0.85 | ||
| 10 | 1.2 | ||
| 11 | Static condition | 1.2 | 0.5 |
| 12 | Uniform deceleration linear motion | 0.5 | 0.5 |
| 13 | 0.85 | ||
| 14 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Liu, Y.; Hao, Y.; Li, F.; Zhou, H. Study on the Thermodynamic Behavior of Large Volume Liquid Hydrogen Bottle Under the Coupling of Different Motion States and Operational Parameters. Processes 2025, 13, 3340. https://doi.org/10.3390/pr13103340
Shen J, Liu Y, Hao Y, Li F, Zhou H. Study on the Thermodynamic Behavior of Large Volume Liquid Hydrogen Bottle Under the Coupling of Different Motion States and Operational Parameters. Processes. 2025; 13(10):3340. https://doi.org/10.3390/pr13103340
Chicago/Turabian StyleShen, Jun, Yuhang Liu, Yongmei Hao, Fei Li, and Hui Zhou. 2025. "Study on the Thermodynamic Behavior of Large Volume Liquid Hydrogen Bottle Under the Coupling of Different Motion States and Operational Parameters" Processes 13, no. 10: 3340. https://doi.org/10.3390/pr13103340
APA StyleShen, J., Liu, Y., Hao, Y., Li, F., & Zhou, H. (2025). Study on the Thermodynamic Behavior of Large Volume Liquid Hydrogen Bottle Under the Coupling of Different Motion States and Operational Parameters. Processes, 13(10), 3340. https://doi.org/10.3390/pr13103340





