Research on Stuck Pipe Prediction Based on Supervised and Unsupervised Ensemble Learning
Abstract
1. Introduction
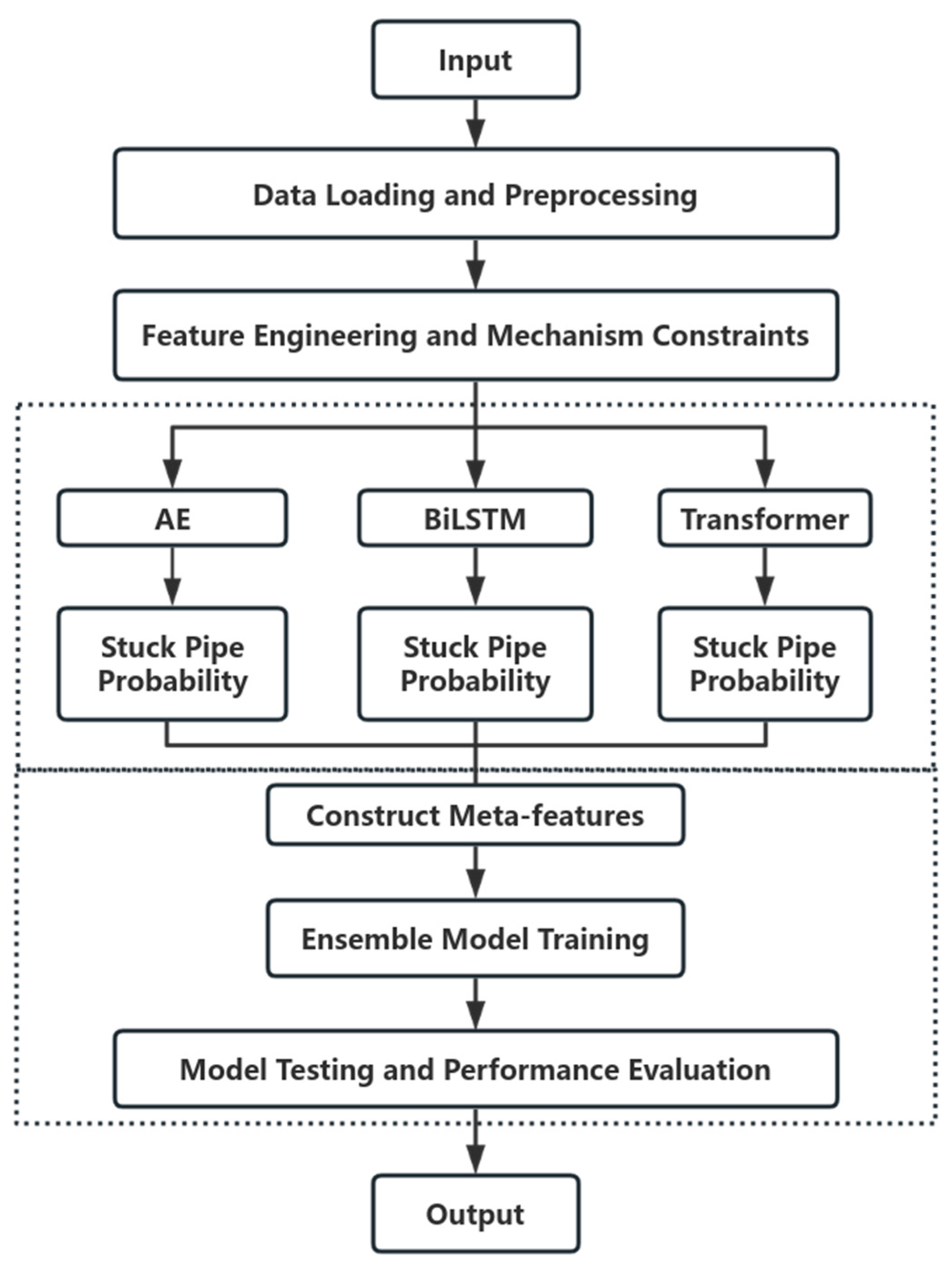
2. Research Methods
2.1. Data Preprocessing and Feature Engineering
2.2. Feature Engineering
2.3. Mechanism Constraints
- (1)
- Accurately identify and filter pseudo-stuck pipe samples. Based on the physical characteristics of drilling conditions, scenarios where parameters are abnormal but not stuck pipe are defined. For example, during drilling, due to operations such as setting and making a connection, the hook height will briefly exceed the range of 10–30 m and the hook load will rise or fall rapidly in a short time, but the load change conforms to the rules. Such samples are marked as invalid stuck pipe signals and excluded; on the contrary, for the characteristics of real stuck pipe events, such as static bit position, rotational speed approaching zero, but severe fluctuation of hook load, the weight of these samples in the training set is highlighted through mechanism constraints, making it easier for the model to capture real stuck pipe samples (Figure 2).
- (2)
- Systematically filter data noise in non-effective drilling stages. For non-drilling stages such as tripping in, tripping out, and setting, the invalid intervals are defined through multi-parameter joint criteria, and only samples in the normal drilling stage are retained for model training. This operation significantly reduces the interference of non-target working conditions on the model and improves the signal-to-noise ratio of effective signals in the training dataset.
- (3)
- Establishing working condition adaptive differentiated judgment rules. Based on the physical laws of different drilling stages, scenario-specific stuck pipe identification logic is designed: in the normal drilling stage, the torque fluctuation amplitude is taken as the core criterion; in the tripping stage, focus is placed on monitoring abnormal trends in hook load to determine tripping obstacles caused by stuck pipe, thereby improving the judgment stability of the model in diverse scenarios.
2.4. Intelligent Algorithm Design
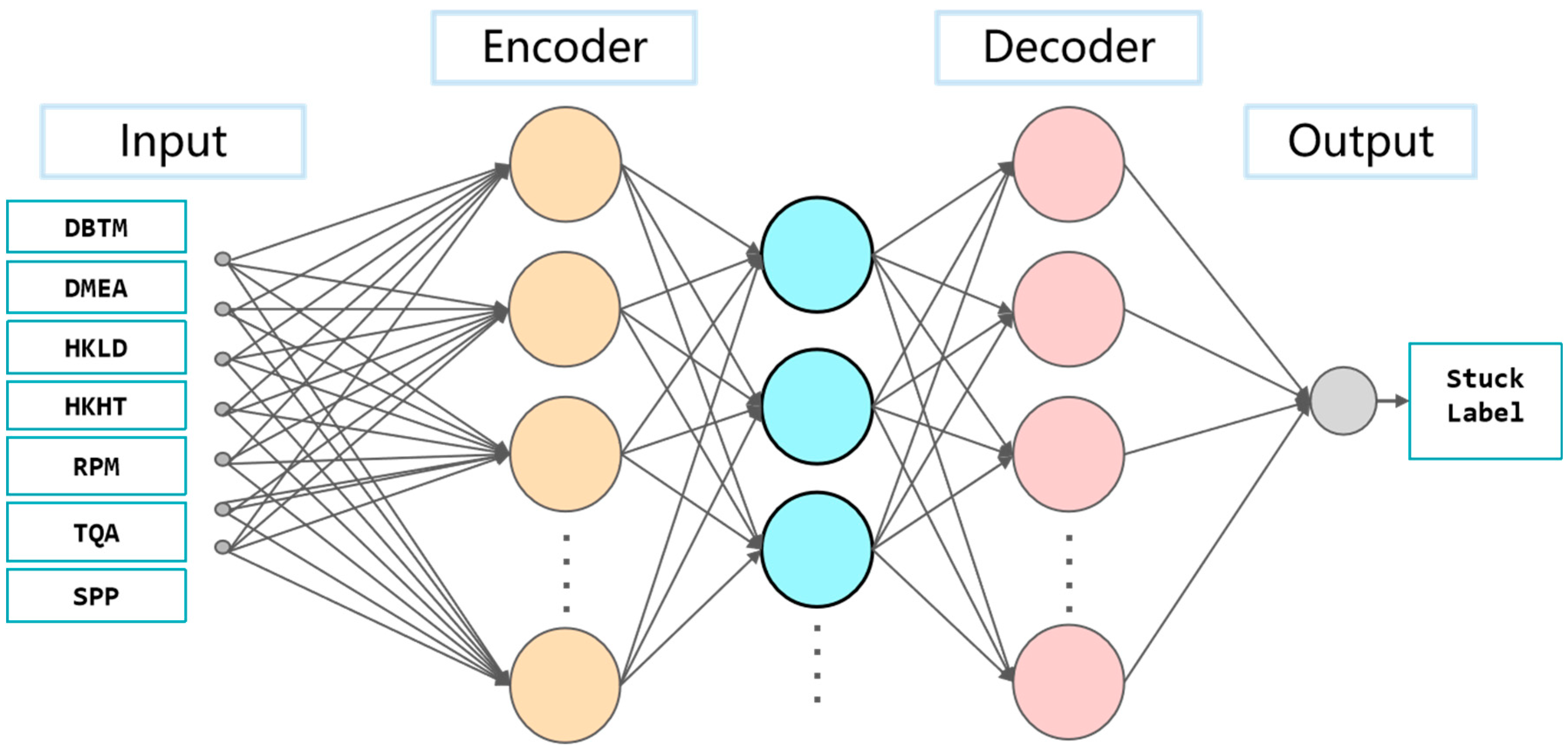
2.4.1. Autoencoder (AE)
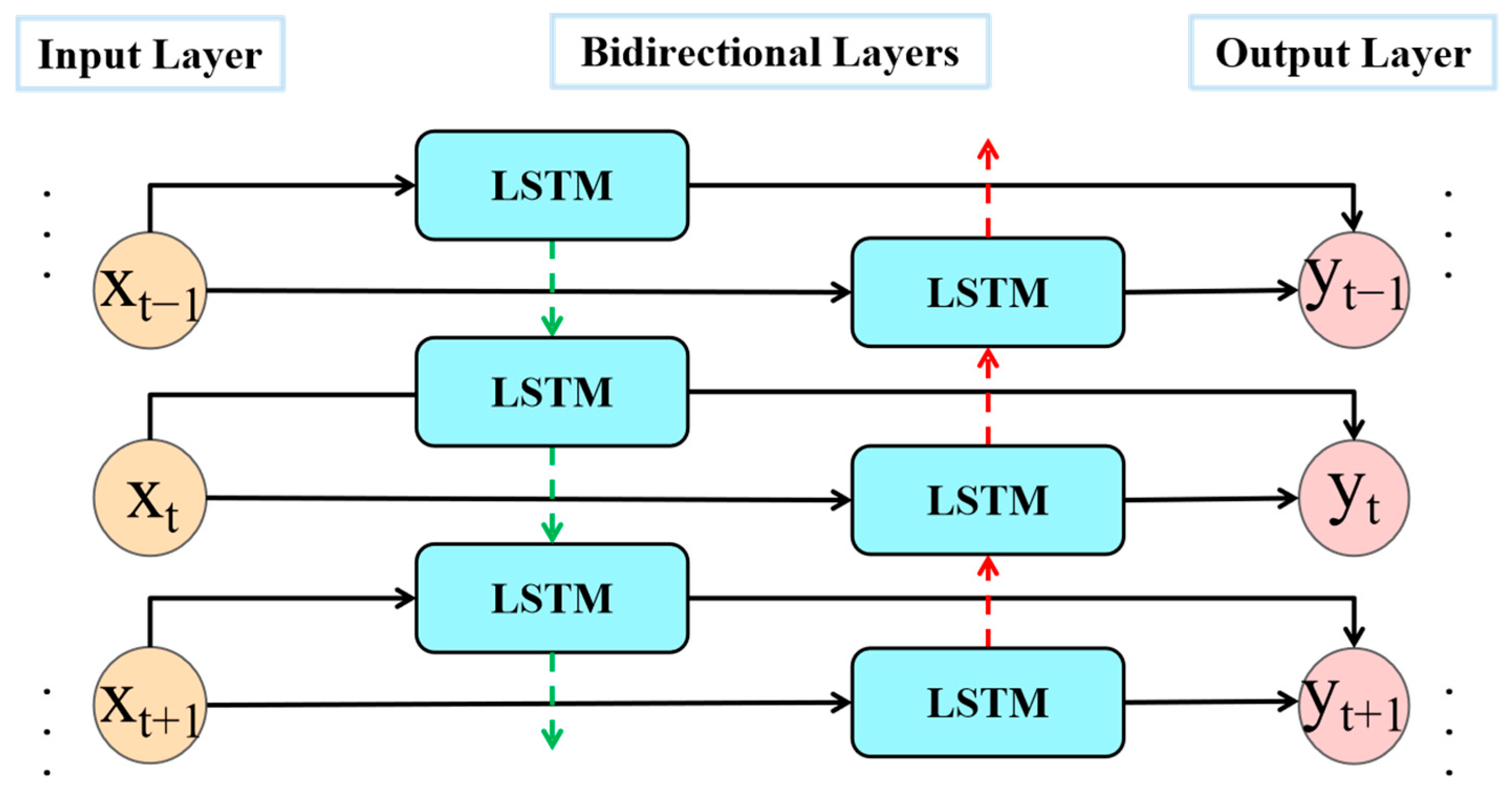
2.4.2. Bidirectional Long Short-Term Memory Network (BiLSTM)
2.4.3. Transformer Model
2.4.4. Ensemble Learning
3. Test Results and Analysis
3.1. Test Results
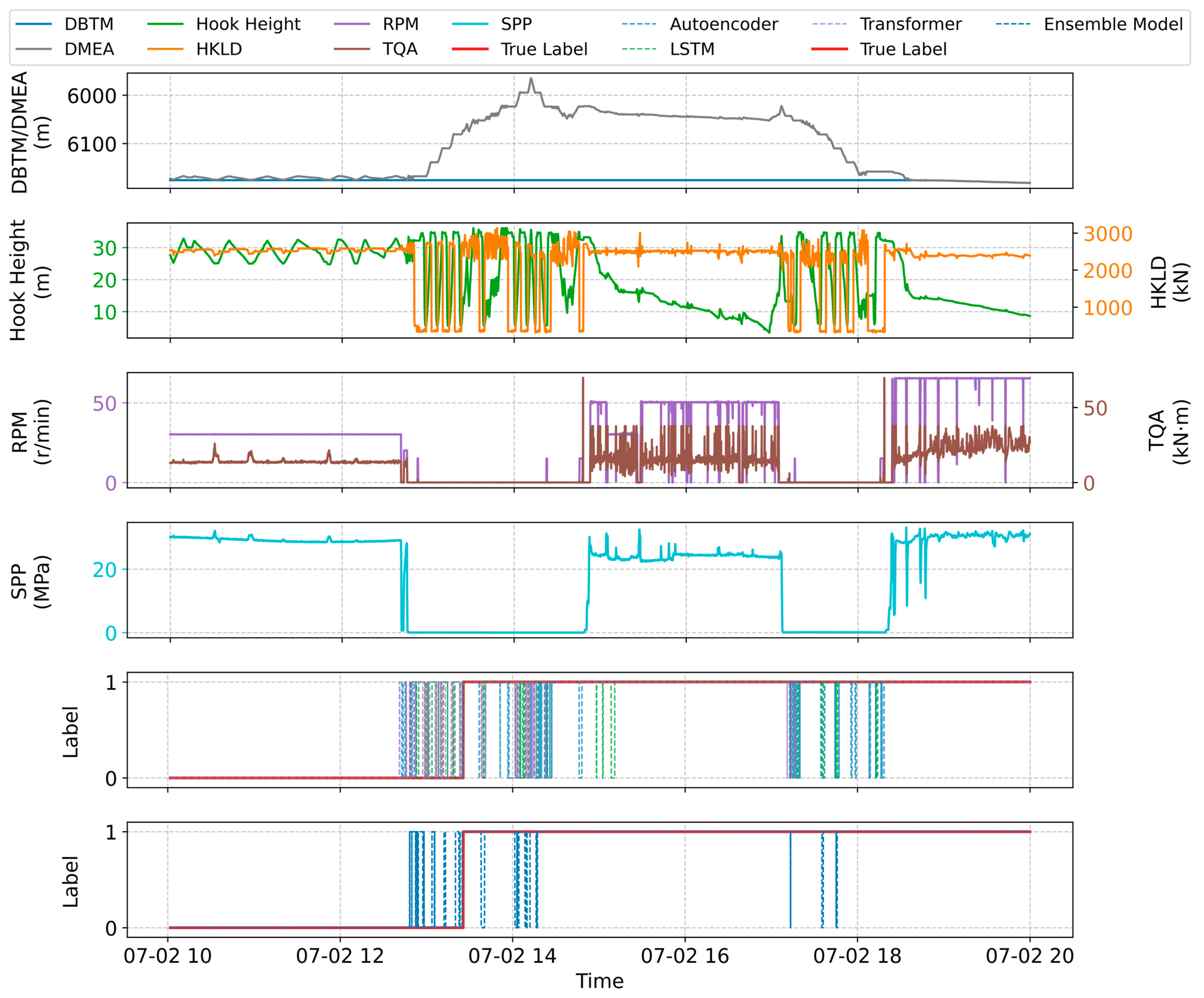
3.2. Analysis of Prediction Result Curves
3.3. Summary
- (1)
- The ensemble model proposed in this paper can capture different feature patterns in drilling data by integrating the advantages of Autoencoder, bidirectional BiLSTM, and Transformer. The Autoencoder provides compressed features of data, the bidirectional BiLSTM is good at capturing local time-series dependencies, and the Transformer can better capture long-distance dependencies, and their combination makes the ensemble model perform better in the stuck pipe prediction task.
- (2)
- The drilling mechanism knowledge constraint can effectively assist the model in identifying stuck pipe signs. After adding mechanism features, the accuracy of the model is increased by 10% on average, verifying the importance of domain knowledge in model construction.
4. Conclusions and Prospects
- (1)
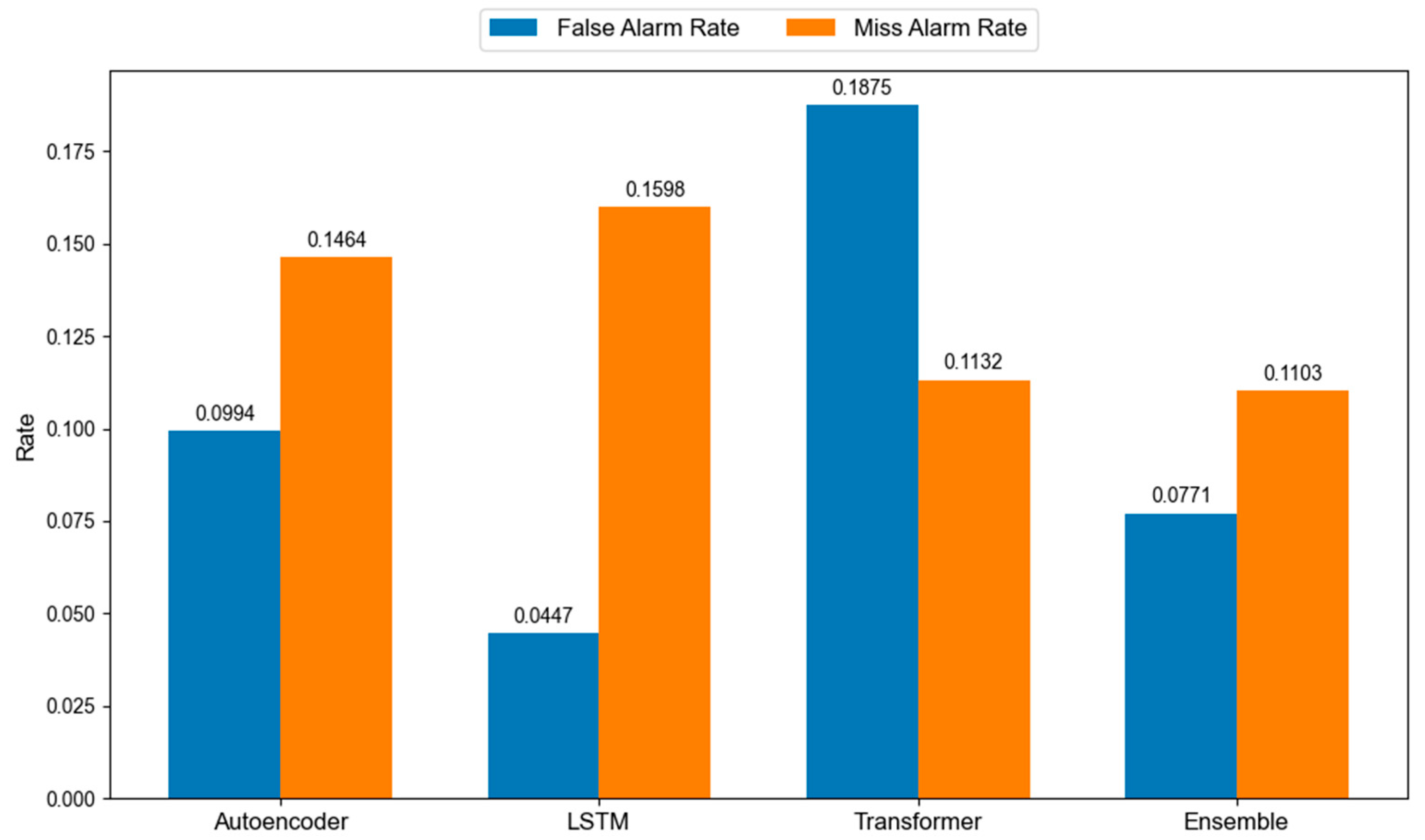
- This study proposed a stuck pipe prediction method based on a deep learning ensemble model, which realizes accurate prediction of stuck pipe risks through four stages: data preprocessing, feature engineering, mechanism constraints, and ensemble prediction. Experimental results showed that the accuracy of this method on the test set reached 90.1% and the precision reached 95.9%, with the optimal balance between false alarm rate and miss rate. By integrating mechanism constraints with the ensemble model, the prediction stability was significantly better than that of single models, which can provide effective risk early warning for drilling operations.
- (2)
- This study still has several limitations. For the mechanism constraint part of the model, manual threshold adjustment is required across different blocks or drilling platforms. The proposed ensemble learning model has certain time and computational cost limitations, making it currently difficult to integrate into drilling rig systems. The ensemble learning strategies among the various models lack a dynamic update mechanism, and the ensemble model has not yet established an automatic update process based on real-time data, which prevents the realization of real-time updates during the drilling process.
- (3)
- Future research can be carried out in the following aspects: investigating the automatic dynamic update of mechanism constraint thresholds, studying more effective model ensemble strategies, such as dynamic weighted fusion, to further improve the adaptive ability of the model, and combining real-time drilling data to develop an online learning mechanism, so that the model can adapt to different drilling environments and continuously optimize prediction performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Full Name | Abbreviation | Full Name | Abbreviation |
| Bit position | DBTM | False alarm rate | FAR |
| Hook height | HKHT | Miss rate | MR |
| Hook load | HKLD | Autoencoder | AE |
| Weight on bit | WOB | Bidirectional long short-term memory network | BiLSTM |
| Rotary speed | RPM | ||
| Torque | TQA | ||
| Standpipe pressure | SPP |
References
- Chen, T.; Zhang, Y.Z.; Xu, C. Research and Application of Intelligent Identification Algorithm for Drilling Conditions in Coal Mine Underground. Saf. Coal Mines 2025, 56, 242–249. [Google Scholar]
- Li, G.; Song, X.; Tian, S.; Zhu, Z. Intelligent Drilling and Completion: A Review. Engineering 2022, 18, 33–48. [Google Scholar] [CrossRef]
- Nautiyal, A.; Mishra, A.K. Machine learning approach for intelligent prediction of petroleum upstream stuck pipe challenge in oil and gas industry. Env. Dev. Sustain. 2022, 27, 24167–24193. [Google Scholar] [CrossRef]
- Salvatore, D.; Marta, P.; Matteo, M.; Piroddi, L.; Spelta, A.; Zausa, F. Stuck pipe prediction from rare events in oil drilling operations. Upstream Oil Gas Technol. 2023, 11, 100096. [Google Scholar] [CrossRef]
- Wu, H.L.; Wang, Z.B.; Si, L.; Zou, X.Y.; Gu, J.H.; Wei, D.; Tan, C. A sticking predictor construction and evaluation method for drill tools sticking prediction. Rev. Sci. Instrum. 2025, 96, 015116. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Xue, Y.; Meng, Z.; Sader, M.; Zhang, W.; Li, J. Drill Sticking Prediction Based on Modal Decomposition and Physical Constraint Model of Near-Bit Data. Processes 2025, 13, 1802. [Google Scholar] [CrossRef]
- Siruvuri, C.; Nagarakanti, S.; Samuel, R. Stuck pipe prediction and avoidance: A convolutional neural network approach. In Proceedings of the IADC/SPE Drilling Conference, SPE, Miami, FL, USA, 21–23 February 2006; p. SPE 98378-MS. [Google Scholar]
- Zhu, S.; Song, X.Z.; Li, G.S.; Zhu, Z.P.; Yao, X.Z. Intelligent Real-time Analysis of Drill String Friction & Torque and Stuck Pipe Trend Prediction. Oil Drill. Prod. Technol. 2021, 43, 428–435. [Google Scholar]
- Chamkalani, A.; Pordel Shahri, M.; Poordad, S. Support vector machine model: A new methodology for stuck pipe prediction. In Proceedings of the SPE Unconventional Gas Conference and Exhibition, Muscat, Oman, 28–30 January 2013; p. SPE 164003-MS. [Google Scholar]
- Yi, S.Q.; Wei, K. Random Forest Stuck Pipe Risk Assessment Method Based on SMOTE Undersampling. Pet. Geol. Eng. 2023, 37, 100–103. [Google Scholar]
- Ahmed, O.S.; Aman, B.M.; Zahrani, M.A.; Ajikobi, F.I. Stuck pipe early warning system utilizing moving window machine learning approach. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 11–14 November 2019; p. SPE 197674-MS. [Google Scholar]
- Zhang, W.X. Prevention of Coiled Tubing Downhole Complications Based on GAN-LSTM. Master’s Thesis, Yangtze University, Jingzhou, China, 2024. [Google Scholar]
- Al-Baiyat, I.; Heinze, L. Implementing artificial neural networks and support vector machines in stuck pipe prediction. In Proceedings of the SPE Kuwait International Petroleum Conference and Exhibition, Kuwait City, Kuwait, 10–12 December 2012; p. SPE 163370-MS. [Google Scholar]
- Abbas, A.K.; Almubarak, H.; Abbas, H.; Dawood, J. Application of machine learning approach for intelligent prediction of pipe sticking. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 11–14 November 2019; p. SPE 197396-MS. [Google Scholar]
- Liu, Z.H.; Song, X.Z.; Zhu, S.; Ye, S.L.; Zhang, C.K.; Ma, B.D.; Zhu, Z.P. Intelligent Stuck Pipe Prediction Method Based on VC-SVM and Particle Swarm Optimization. China Pet. Mach. 2024, 52, 1–11. [Google Scholar]
- Zhang, T.; Xia, P.; Li, J.; Wang, B.; Zhan, J.H. Study on SCNGO-SVM Stuck Pipe Warning Method Based on Downhole Parameters. China Pet. Mach. 2025, 53, 20–27, 36. [Google Scholar]
- Liu, M.C.; Song, X.Z.; Li, D.Y.; Zhu, S.; Fu, L.; Zhu, Z.P.; Zhang, C.K.; Pan, T. Intelligent Prediction Model and Interpretation of Drill String Friction. Coal Geol. Explor. 2023, 51, 89–99. [Google Scholar]
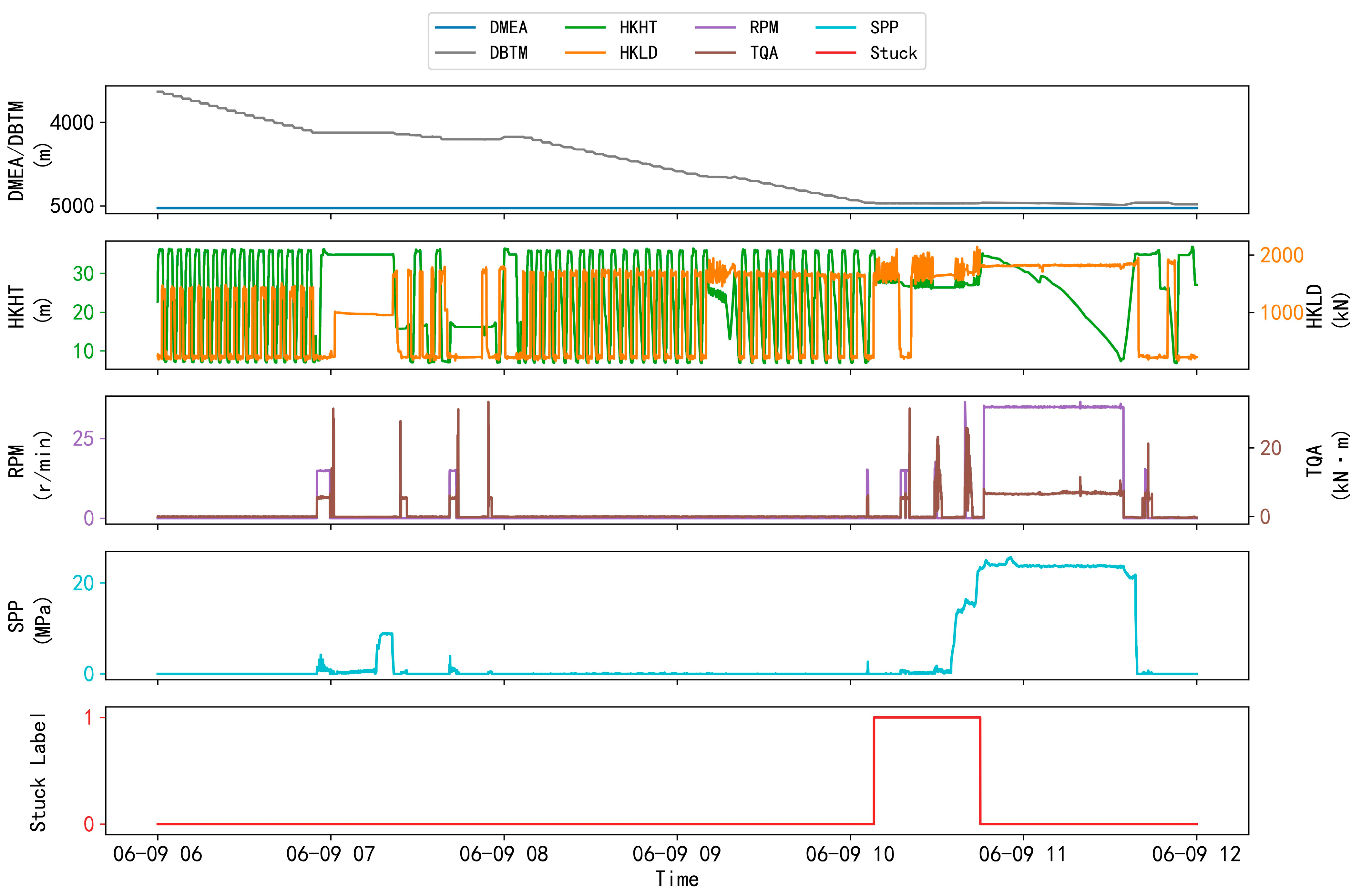
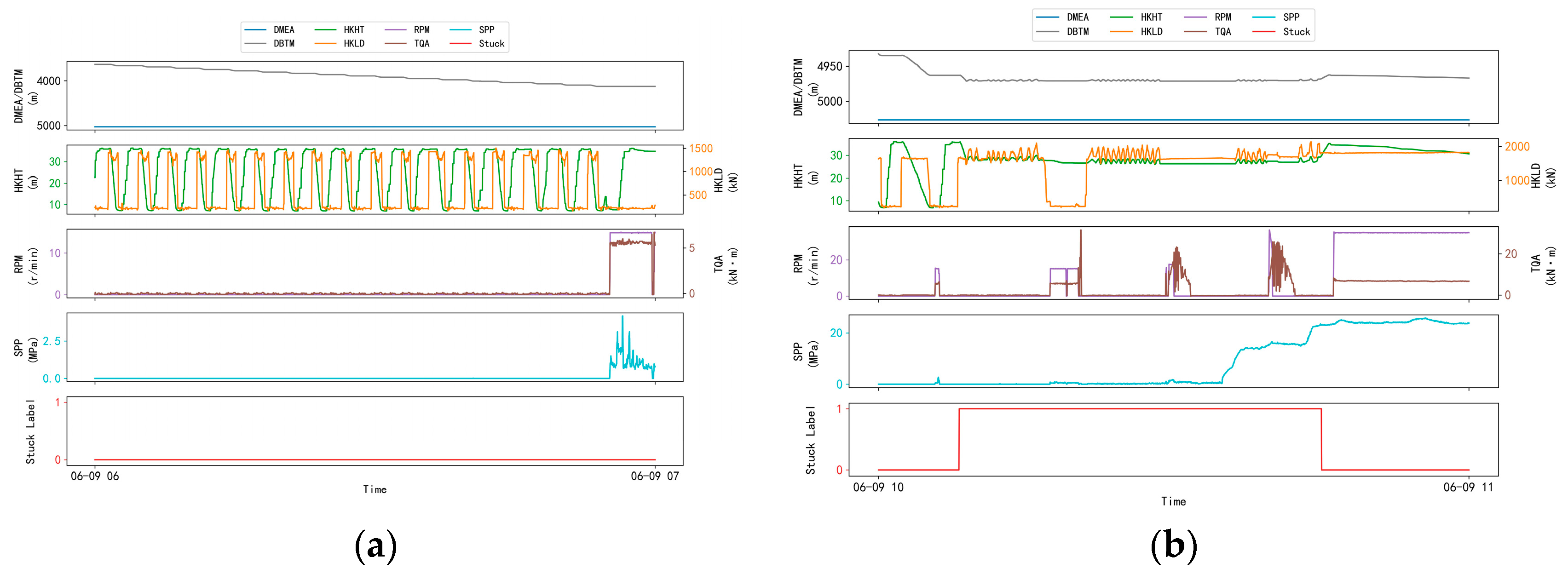
| Category of Constraint Condition | Specific Judgment Logic | Involved Drilling Parameters | Key Thresholds/Rules |
|---|---|---|---|
| Data Validity Filtering | Filter invalid data and only perform pipe sticking judgment on valid data | HKLD, HKHT | HKLD > 600; 5 ≤ HKHT ≤ 26; negative or abnormal parameters are set to 0 |
| Stuck Pipe Judgment | Determine suspected sticking if DBTM is stable, RPM table stops, and HKLD fluctuates sharply | DBTM, RPM, HKLD | DBTM fluctuation < 0.3; maximum RPM < 1; HKLD fluctuation (max–min) > 100 |
| Torque Anomaly Warning | Judge whether torque rises abnormally based on the sliding window of recent data | RPM, TQA | Mean RPM of the last 25 points < 2; mean TQA of the last 25 points > 10 |
| Model Type | Hyperparameter Category | Parameter Value | Model Type | Hyperparameter Category | Parameter Value |
|---|---|---|---|---|---|
| BiLSTM | Number of Hidden Layers | 2 layers | Transformer | Number of Encoder Layers | 2 layers |
| Learning Rate | 0.001 | Number of Attention Heads | 4 heads | ||
| Number of Neurons | 64 (1st layer), 32 (2nd layer) | Feature Dimension | 64 | ||
| Activation Function | Internal Gating: tanh + sigmoid; Classification Head: ReLU (hidden layer), Sigmoid (output layer) | Learning Rate | 0.001 | ||
| AE | Encoding Layer Dimension | Hidden Layers: 64 → 32; Bottleneck Layer: 16 | Ensemble model | Number of Hidden Layers | 2 layers |
| Learning Rate | 0.001 | Number of Neurons | 16 (1st layer), 8 (2nd layer) | ||
| Training Epochs | 50 | Activation Function | ReLU (hidden layer), Sigmoid (output layer) | ||
| Batch Size | 32 | Learning Rate | 0.001 |
| Model | Accuracy (Without Mechanism Constraints) | Accuracy (With Mechanism Constraints) | Precision | False Alarm Rate | Miss Rate |
|---|---|---|---|---|---|
| AE | 0.751 | 0.869 | 0.945 | 0.099 | 0.146 |
| BiLSTM | 0.787 | 0.879 | 0.974 | 0.045 | 0.160 |
| Transformer | 0.747 | 0.862 | 0.905 | 0.188 | 0.113 |
| Ensemble model | 0.826 | 0.901 | 0.959 | 0.077 | 0.110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, B.; Wang, Y.; Li, Q.; Song, X.; Zhu, Z.; Liu, M.; Yang, Y. Research on Stuck Pipe Prediction Based on Supervised and Unsupervised Ensemble Learning. Processes 2025, 13, 3309. https://doi.org/10.3390/pr13103309
Xia B, Wang Y, Li Q, Song X, Zhu Z, Liu M, Yang Y. Research on Stuck Pipe Prediction Based on Supervised and Unsupervised Ensemble Learning. Processes. 2025; 13(10):3309. https://doi.org/10.3390/pr13103309
Chicago/Turabian StyleXia, Boyi, Yiwei Wang, Qihao Li, Xianzhi Song, Zhaopeng Zhu, Muchen Liu, and Yanlong Yang. 2025. "Research on Stuck Pipe Prediction Based on Supervised and Unsupervised Ensemble Learning" Processes 13, no. 10: 3309. https://doi.org/10.3390/pr13103309
APA StyleXia, B., Wang, Y., Li, Q., Song, X., Zhu, Z., Liu, M., & Yang, Y. (2025). Research on Stuck Pipe Prediction Based on Supervised and Unsupervised Ensemble Learning. Processes, 13(10), 3309. https://doi.org/10.3390/pr13103309






