Are Soft Silicone Hydrogel Contact Lenses More Compliant in a Warm, Hydrated Environment?

Abstract

Soft contact lenses are usually characterised at room temperature, yet they function on the eye at body temperature, where their mechanics and optical performance can change. This study investigated whether soft silicone hydrogel lenses become more compliant in a physiological environment. Two silicone hydrogel materials (Definitive 74 and Unisil) were tested at 24 °C and 35 °C using uniaxial tensile and compression methods, with Ogden hyperelastic models fitted and finite element analysis performed on a realistic eye model. Both materials became more compliant at 35 °C, with Definitive 74 showing a larger modulus decrease (0.40 to 0.32 MPa) than Unisil (0.73 to 0.70 MPa). Finite element simulations indicated that these temperature-driven changes in compliance significantly affected refractive power, especially when the lens base curve exceeded the corneal radius by more than 5%. These findings demonstrate that soft silicone hydrogel lenses are indeed more compliant in a warm, hydrated environment, highlighting the need for physiologically relevant testing to inform design, fitting strategies, comfort, and vision outcomes.

1. Introduction

Contact lenses are transparent, thin, curved medical devices worn by over 150 million people worldwide [1]. They rest on the anterior eye surface, separated by the tear film that coats the anterior eye, and serve primarily to correct refractive errors, although cosmetic applications also exist. Soft contact lenses may be characterised by their mechanical compliance or stiffness, which governs how they respond to applied loads. Rigid lenses maintain their original geometry under regular physiological forces, whereas soft lenses readily deform under eyelid pressure or handling during insertion and cleaning.

Early contact lenses were rigid in nature and required precise alignment to the ocular surface, with negligible geometric distortion under physiological loads. The advent of soft lenses, formed from hydrated polymer networks, introduced a new complexity, as on-eye fit arises from stretching and draping, rather than a fixed geometry. Hence, lens fit cannot be determined solely from corneal topography but depends critically on the lens’s mechanical properties [2]. The flexibility of soft lenses permits accommodation of a range of corneal shapes with a limited set of base curves and diameters, which has underpinned their global adoption.

The dominant soft lens materials are hydrogels and silicone hydrogels, introduced in the mid to late 20th century [3]. In contrast to rigid lenses, whose shape remains effectively constant in situ, soft lenses undergo deformation in vivo, and their performance depends on how material properties evolve under ocular conditions [3,4].

Several studies have established that the mechanical behaviour of rigid and soft lens materials correlates with clinical performance [5,6,7,8,9], but measuring deformation in situ is difficult. Therefore, predictions hinge on three key inputs: the off-eye geometry, the applied physiological load, typical eyelid pressure, and the material’s mechanical response under realistic conditions of temperature and hydration.

A critical yet often underemphasised factor is the ocular environment, particularly the behaviour of the tear film and the effect of temperature. The tear film is structured into mucin, aqueous, and lipid layers, stabilising the interface and mediating evaporation, lubrication, and osmotic balance [10]. Contact lens placement essentially divides the tear film into a pre-lens and a post-lens layer, with the lens sandwiched in between, disrupting normal turnover, increasing evaporation, and altering osmolarity [11].

Importantly, the ocular surface is warmer than standard laboratory conditions, with corneal temperatures generally ranging between 33 °C and 35 °C in healthy eyes [12,13,14]. This means that lenses worn on the eye experience a consistently higher thermal load than when characterised at room temperature (≈20–24 °C). Recent studies demonstrate that physiological temperature and blinking behaviour influence lens dehydration dynamics, refractive index (RI), and compliance [13,15,16]. In particular, RI changes are strongly linked to hydration state [17,18,19], and hydrogels are known to soften and become more compliant as temperature rises [20]. Thus, temperature alters lens modulus and impacts fit, optical performance, and wearer comfort. Characterising lenses solely at room temperature risks underestimating their true behaviour on-eye.

Given these considerations, the present study investigates how the warm ocular environment affects the mechanical response and optical performance of two representative silicone hydrogel materials (Definitive 74 and Unisil). Combining laboratory testing at physiological temperature with finite element simulations provides insight into compliance and refractive outcomes under conditions that better approximate real-world wear.

2. Materials and Methods

A total of 10 Definitive 74 and 10 Unisil contact lens raw material discs were prepared per manufacturer guidelines (Contamac Ltd., Saffron Walden, Essex, UK). Each material required a distinct hydration protocol, tailored to its composition and physical properties, to ensure conditions as close as possible to physiological. The key material characteristics of Definitive 74 and Unisil, as reported by the manufacturer, are summarised in

Table 1. Material Characteristics of Definitive 74 and Unisil as reported by the manufacturer.

Property	Definitive 74	Unisil
Oxygen Permeability at 35 °C (Barrer)	60	50
Water Content at 20 °C by Weight (%)	74	62
Swell Factor at 20 °C	1.62	1.41
Hydrated RI at 20 °C	1.38	1.40
Dry RI at 20 °C	1.52	1.51
Modulus of Elasticity (MPa)	0.40	0.80
Tensile Strength (MPa)	0.75	0.88
Elongation to Break (%)	225	200

. These values highlight essential differences in oxygen permeability, water content, mechanical strength, and optical properties, all of which influence the lenses’ flexibility, durability, and ultimate on-eye performance.

Hydrated specimens were subjected to uniaxial tensile and compression testing to evaluate the mechanical performance of the two materials. These experiments allowed us to quantify elasticity, strength, and deformation behaviour at both room temperature (24 °C) and physiological temperature (35 °C). The resulting data provided the basis for developing material models, which were subsequently applied in finite element simulations of lens–eye interactions. This combined approach made it possible to link laboratory measurements to clinically relevant outcomes such as changes in refractive power.

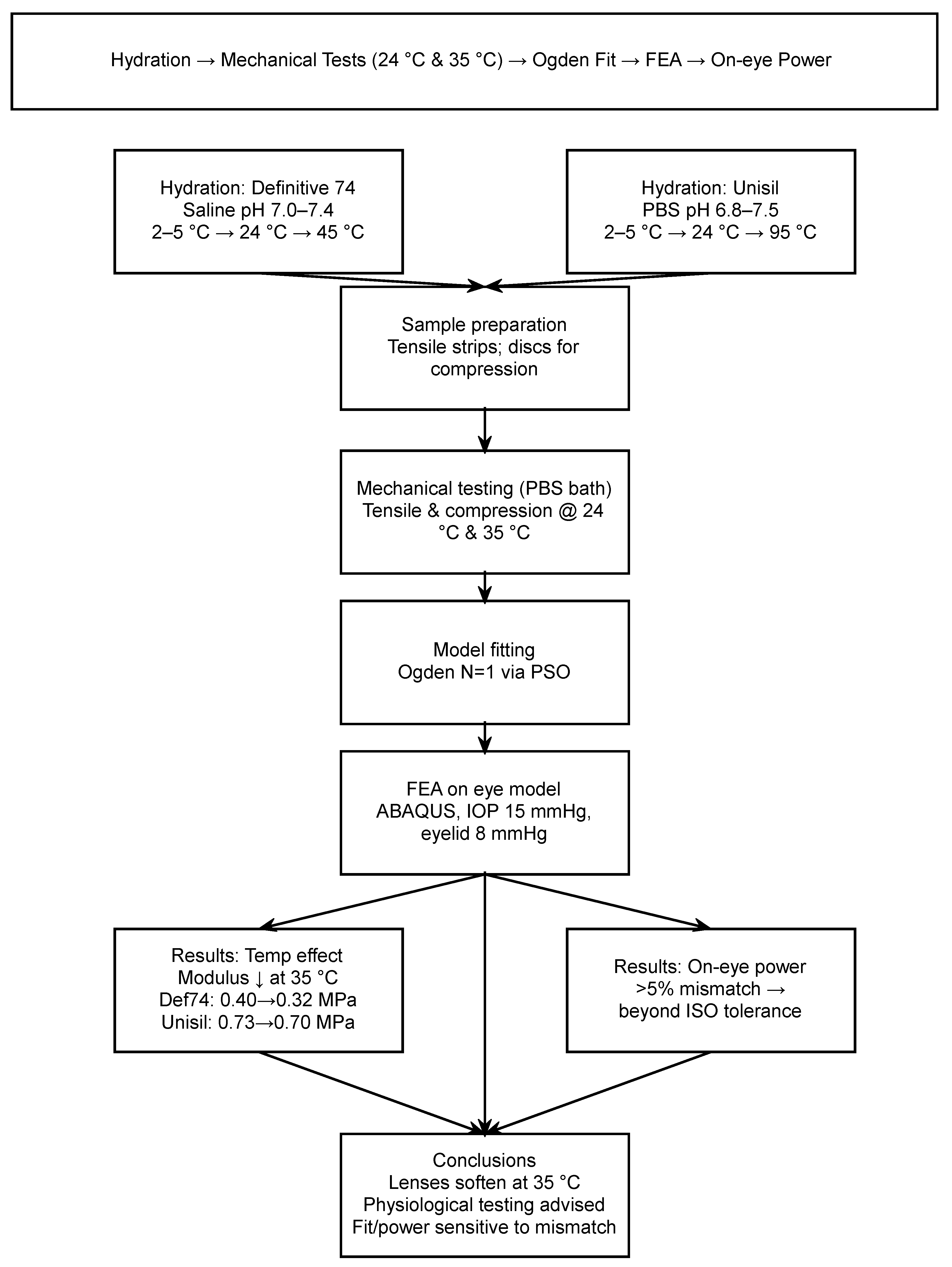
Since the experimental and simulation protocols involve several interdependent steps, a visual summary is provided in Figure 1. This workflow diagram outlines the sequence from material hydration through mechanical testing, model fitting using the Ogden hyperelastic formulation, and finite element analysis on a representative eye model, before arriving at the final interpretation of results.

2.1. Definitive 74 Hydration

Specimens made from Definitive 74, a silicone hydrogel material, were prepared using a controlled hydration process. A non-buffered saline solution, prepared for hydration purposes, was adjusted to a potential hydrogen (pH) range of 7.00 to 7.40. The pH was adjusted by adding analytical grade anhydrous sodium carbonate to the saline in small aliquots, with monitoring using a calibrated pH meter (Mettler Toledo, Leicester, UK) at room temperature.

For initial hydration, 7 mL of the saline solution was chilled to a temperature of 2 °C to 5 °C in glass vials. Definitive 74 discs were placed into the vials and allowed to hydrate for one hour, during which the saline gradually warmed to room temperature at 24 °C. The vials were then transferred to a water bath (Thermo-Fisher, Loughborough, Cheshire, UK) maintained at 45 ± 5 °C for 16 h to ensure complete hydration. After this incubation period, the vials were removed and allowed to cool to room temperature for two hours. The hydrated specimens were transferred into fresh saline and prepared for subsequent testing.

2.2. Unisil Hydration

Unisil specimens, composed of a silicone hydrogel material with inherent hydrophobicity, required an alternative hydration method involving higher temperatures and prolonged incubation. Specimens were hydrated using 7 mL of phosphate-buffered saline (PBS) (Sigma Aldrich, Gillingham, Dorset, UK) with a pH range of 6.8 to 7.5.

Initially, specimens were placed in chilled PBS (2 °C to 5 °C) to begin the hydration process. The vials were then kept at room temperature (24 °C) for one hour, allowing the specimens to equilibrate gradually. Subsequently, the vials were transferred to an isothermal oven (Fisherbrand, Loughborough, Leicestershire, UK) maintained at 95 °C for 16 h. During this period, the high temperature facilitated hydration by overcoming the hydrophobic resistance of the silicone component.

After the incubation period, vials were cooled to a temperature of 40 °C before being removed from the oven. Specimens were allowed to settle at room temperature for at least one hour, during which the buffered saline was replaced with fresh PBS to ensure the stability of hydrated parameters. Finally, specimens were prepared for testing and further processing.

2.3. RI Measurement

The RI was measured by Digital Abbe Refractometer DR-A1-Plus (ATAGO Co., Ltd., Minato-ku, Tokyo, Japan) with an RI measure range of 1.3 to 1.71, a measuring temperature range of 5 °C to 50 °C, a minimum indication value of 10⁻⁴, and an accuracy of ±2 × 10⁻⁴. As the used refractometer cannot measure the material blanks, two sets of contact lenses were cut from Definitive 74 and Unisil as raw materials. They were hydrated following the same protocol used in the current study, then measured at room and anterior eye physiological temperatures, before their RIs were measured.

2.4. Uniaxial Tensile Test

Tensile testing is considered a benchmark in material science as it is a straightforward test that provides a modulus of elasticity, which describes the material’s stiffness or resistance to a tensile load. In the contact lens industry, this tension-modulus relates to the handling and durability of the lens outside the eye and is a rough indication of material performance on the eye.

Small tensile modulus values, also called Young’s modulus, indicate that the material is more deformable on the eye and offers less resistance against the eyelid [21]. Conversely, a material with a high modulus is comparatively stiffer and easier for wearers to handle [22].

After being hydrated, the tested sample was cut into rectangular-shaped cross-section strips for tensile testing of soft materials. Each strip was fixed between two jaws, slowly moving at a pre-determined rate while the strip elongation was recorded. Material stress was calculated as the tensile force over the cross-sectional area, while the material strain was calculated as the ratio between the sample elongation and its original no-load length. The linear stress to the strain ratio was the tension modulus of elasticity of this material [23].

In the current study, specimens were prepared by excising a uniform strip from hydrated lens discs using a bespoke strip-cutting tool to a width of 4 mm and a length of 14 mm. Specimens conformed to a length-to-width ratio higher than 2.5 to avoid Saint-Venant-related issues during testing [24]. Three equidistant thickness measurements were taken using an ultrasound pachymeter (Pachmate 55; DGH Technologies, Exton, PA, USA) with ±5 µm accuracy along the effective length of the specimen, and the average value was used in the post-test analysis. The average and standard deviation values of width and thickness for tensile samples were 4.39 ± 0.13 mm and 1.48 ± 0.11 mm, respectively.

During the tensile testing, excised strips were mounted within spring-loaded sample grips with an exposed length of 10 mm between spring-loaded testing jaws before being subjected to a 10% per-minute strain rate that was selected to optimise data points captured within a sufficient rate window that did not allow specimens to display extreme viscoelastic behaviour [25]. A UniVert uniaxial testing machine (CellScale, Waterloo, ON, Canada) with a 1.0 N load cell at a 0.0001 N accuracy was employed (Figure 2). Lens strips were mounted between the tensile jaws and elongated at a strain rate of 10% per minute until failure.

2.5. Uniaxial Compression Test

Compression modulus is more related to the response to eyelid pressure on soft contact lenses while worn on the eye [9,26]. Silicone hydrogels partially recover during stretching under limited tension but recover to their original sizes under a limited compression load [27]. Unlike the uniaxial tensile test, the compression version of the test cannot use thin strips of the material, as the cross-section has to be big enough compared to the length of the sample to avoid buckling during the testing procedure. In these tests, the sample was set between two flat platens where the bottom one was fixed, and the upper one was slowly moved at a pre-determined rate towards the bottom platen, compressing the sample in between. While this setup better replicates pressure-related deformation, the presence of fluid in the test chamber may have introduced minor hydrostatic effects, potentially influencing the measured compression load [28,29].

In the current study, lens raw material discs were taken from the solution and measured with an electronic vernier calliper (D00352, Duratool, Taiwan) of 0.1 mm accuracy. For compressive samples, the average and standard deviation values for diameter and thickness were 17.95 ± 1.31 mm and 7.03 ± 0.33 mm.

A UniVert uniaxial testing machine with uniform circular compression platens and a 50 N load cell with 0.1 N accuracy was used for compression testing. Samples were compressed at a loading rate of 10% per minute until a load of 50 N was applied.

All tests were conducted at a sample collection rate of 5 Hz. Specimens were housed in a temperature-controlled testing chamber filled with PBS and maintained at either 24 °C or 35 °C to simulate room temperature and physiological on-eye temperature, respectively.

2.6. Stress–Strain Curves

Both tensile and compressive loading data were analysed to characterise the full-range mechanical response of the contact lens materials. Tensile stress was calculated by dividing the applied force by the initial rectangular cross-sectional area, with strain determined as the elongation ratio to the original gauge length. For compression, stress was derived from the applied force and the initial circular cross-sectional area. At the same time, strain was calculated based on the reduction in height relative to the original sample height.

Figure 3 combines the tensile and compressive stress–strain results for Definitive 74 and Unisil at 24 °C and 35 °C. Including both loading modes in a single plot highlights the materials’ nonlinear behaviour across the full strain spectrum and reveals how elevated temperature reduces stiffness. This comprehensive approach allowed for the accurate fitting of both linear elastic and Ogden hyperelastic models, capturing the mechanical characteristics relevant to on-eye performance.

2.7. Finite Element Modelling

A comprehensive material model for the contact lens was developed by integrating tensile and compression test data. The Particle Swarm Optimisation (PSO) algorithm [30,31], implemented via MATLAB R2025b’s Global Optimisation Toolbox, was employed to fit the experimental tensile data to the Ogden nonlinear material model. The optimisation parameters were configured with a swarm size of 50, an initial span of 2000, and a maximum of 100 iterations. A convergence criterion was established, setting a tolerance of 10⁻⁶ for changes in the objective function value per iteration, as determined from preliminary investigations [32]. The material parameters μ and α were constrained within the ranges of 10⁻³ to 10 and 0 to 50, respectively.

The error was minimised between the fitted stress–strain data and the experimentally measured data via the objective function ($\mathit{e}\mathit{r}\mathit{r}$), which was set to:

$$\mathit{m}\mathit{i}\mathit{n}\left(\mathit{e}\mathit{r}\mathit{r}={\displaystyle \frac{\mathit{1}}{\mathit{n}}}\sum _{\mathit{i}=\mathit{1}}^{\mathit{N}}{\left({\mathit{\sigma }}_{\mathit{e}\mathit{x}\mathit{p}}^{\mathit{i}}-{\mathit{\sigma }}_{\mathit{p}\mathit{r}\mathit{e}}^{\mathit{i}}\right)}^{\mathit{2}}\right)$$

(1)

where σ_exp is the experimental stress, σ_pre is the predicted Ogden stress, and n is the number of measured stress–strain data points. The constitutive Ogden strain energy equation can be articulated in terms of the three principal stretches as [33]

$$\mathit{U}=\sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\displaystyle \frac{\mathbf{2}{\mathit{\mu }}_{\mathit{i}}}{{\mathit{\alpha }}_{\mathit{i}}^{\mathbf{2}}}}\left({\overline{\mathit{\lambda }}}_{\mathbf{1}}^{{\mathit{\alpha }}_{\mathit{i}}}+{\overline{\mathit{\lambda }}}_{\mathbf{2}}^{{\mathit{\alpha }}_{\mathit{i}}}+{\overline{\mathit{\lambda }}}_{\mathbf{3}}^{{\mathit{\alpha }}_{\mathit{i}}}-\mathbf{3}\right)$$

(2)

where $\mathit{U}$ is the strain energy; ${\mathit{\mu }}_{\mathit{i}}$ and ${\mathit{\alpha }}_{\mathit{i}}$, are material parameters; ${\overline{\mathit{\lambda }}}_{\mathit{i}}$ are the deviatoric principal stretches (ratio between the deformed length ${\mathit{L}}_1$ and the initial length ${\mathit{L}}_0$) in principal directions. Since no lateral forces were applied during the tests, principal stretches can be simplified to ${\overline{\mathit{\lambda }}}_{\mathbf{2}}={\overline{\mathit{\lambda }}}_{\mathbf{3}}={{\overline{\mathit{\lambda }}}_{\mathbf{1}}}^{-{\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}}$, hence

$$\mathit{\sigma }={\displaystyle \frac{\partial \mathit{U}}{\partial {\overline{\mathit{\lambda }}}_{\mathbf{1}}}}=\sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\displaystyle \frac{\mathbf{2}{\mathit{\mu }}_{\mathit{i}}}{{\mathit{\alpha }}_{\mathit{i}}^{\mathbf{2}}}}\left({{\mathit{\alpha }}_{\mathit{i}}\overline{\mathit{\lambda }}}_{\mathbf{1}}^{{\mathit{\alpha }}_{\mathit{i}}}-{\mathit{\alpha }}_{\mathit{i}}{\overline{\mathit{\lambda }}}_{\mathbf{1}}^{-{\displaystyle \frac{{\mathit{\alpha }}_{\mathit{i}}}{\mathbf{2}}}-\mathbf{1}}\right)$$

(3)

$$\mathrm{where} {\overline{\mathit{\lambda }}}_{\mathbf{1}}=\mathbf{1}+\mathit{\epsilon }$$

(4)

Consequently, the stress–strain association can be defined in a uniaxial approach as [33,34]

$$\mathit{\sigma }=\sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\displaystyle \frac{\mathbf{2}{\mathit{\mu }}_{\mathit{i}}}{{\mathit{\alpha }}_{\mathit{i}}}}\left[{\left(\mathbf{1}+\mathit{\epsilon }\right)}^{{\mathit{\alpha }}_{\mathit{i}}-\mathbf{1}}-{\left(\mathbf{1}+\mathit{\epsilon }\right)}^{-\left({\displaystyle \frac{{\mathit{\alpha }}_{\mathit{i}}}{\mathbf{2}}}+\mathbf{1}\right)}\right]$$

(5)

To accurately represent the nonlinear behaviour of the contact lens material under various loading conditions, Ogden hyperelastic material models of orders 1 through 4 were evaluated in this study. It was observed that increasing the model order beyond the first (N = 1) did not significantly reduce the root mean squared error (RMSE), suggesting that higher-order models do not enhance the fit to the experimental data.

The contact lens geometry was defined using standard optical parameters: base curve, diameter, central thickness, and optical zone diameter. The front surface curvature was calculated via Lensmaker’s equation, using spherical refractive power ranging from −25 D to 25 D and wet refractive indices.

The lens profile was divided into three radial zones: the optical zone, a transition zone with geometric blending, and a peripheral zone. The two-dimensional (2D) meridional profile was constructed by joining three circular arcs with continuity and revolved around the optical axis to generate the full three-dimensional (3D) shape. Both front and back surfaces were modelled, and the final geometry was aligned to a patient-specific eye model mesh.

The final lens mesh was constructed using a structured hexahedral topology. A layered spherical coordinate system was used to interpolate front and back lens surfaces with controlled radial resolution. Lens models were generated with two through-thickness layers to ensure structural fidelity in subsequent Finite element analyses (FEAs). This computer-based simulation method breaks complex geometries into small elements to predict how they deform under loads.

FEAs were conducted using an averaged geometry model of the anterior human eye, where an element-specific eye model with material properties was built based on the eye collagen contents determined using x-ray scattering for the age of 40 [35]. Full details about the eye model were published in [36]. The eye model comprised 43,806 nodes in two layers containing 29,200 elements. The contact lens model was built with 54,129 nodes forming 35,760 elements in 2 layers. A hybrid element type C3D8H eight-node brick was used for the eye and contact lenses in the ABAQUS 6.14 (Dassault Systèmes, Vélizy-Villacoublay, France) FEA software package. The mesh convergence study of the FE model was conducted following the method described in the previous study [37], see Figure 4 and Appendix A for more details.

The eye was modelled under the effects of 15 mmHg IOP to mimic the aqueous and vitreous static pressure [5,38]. In contrast, the eyelid pressure of 8 mmHg [39] was modelled as a dynamic pressure representing the eye blink within 0.6 s time following Kwon’s high-speed camera characterisation of the blinking kinematics [6,40]. The tear film effect was approximated by applying a surface-tension load of 43.6 mPa [41] to the posterior surface of the contact lens and the anterior corneal surface, acting towards each other. During the ABAQUS simulation, the displacement of the eye’s equatorial nodes was constrained in the axial direction (Z-axis). The analysis began with calculating the stress-free eye’s geometry where IOP equal zero through an iterative process presented in [42]. The stress-free model was computed using the average IOP [43] and a maximal node position error of less than 10⁻⁴ mm, Figure 2.

The generated nodes and elements were merged with the host eye geometry. Special node sets were created to define the lens apex, front and back surfaces, and peripheral edges, to facilitate boundary condition assignment and lens–eye interaction modelling.

3. Results

When contact lens raw materials were tested in the current study, Definitive 74 and Unisil showed different behaviour from the room temperature of 24 °C to the physiological temperature of 35 °C. They also showed different load resistance responses to high temperatures.

On one side, Definitive 74 recorded a modulus of elasticity of E = 0.4 MPa when tested at 24 °C, then the modulus reduced when tested at 35 °C, recording E = 0.32 MPa. Conversely, Unisil’s modulus was E = 0.73 MPa at 24 °C and reduced to 0.7 MPa when tested at 35 °C, Figure 2.

As both materials showed some nonlinear behaviour through their stress–strain curves, linear material models were then switched to Ogden nonlinear material models with parameters µ = 0.11 MPa, α = 8.38 at 24 °C and µ = 0.1 MPa, α = 2.67 at 35 °C for Definitive 74. For Unisil, nonlinear Ogden material model parameters were µ = 0.24 MPa, α = 3.47 at 24 °C and µ = 0.23 MPa, α = 0.31 at 35 °C,

Table 2. Linear and nonlinear material model fitting parameters for the two soft contact lens materials.

	Definitive 74		Unisil
	24 °C	35 °C	24 °C	35 °C
E (Linear fit)	0.40	0.32	0.73	0.7
µ (Ogden nonlinear fit)	0.11	0.10	0.24	0.23
α (Ogden nonlinear fit)	8.38	2.67	3.47	0.31

.

Across the room and physiological temperatures, both materials showed a slight but consistent rise in RI. For Definitive 74, the mean RI increased from 1.3727 ± 0.0002 at room temperatures to 1.3738 ± 0.0002 at physiological temperature with a 0.08% increase. Unisil behaved similarly, rising from 1.3974 ± 0.0002 to 1.3987 ± 0.0004 with a 0.093% increase.

FEA revealed that the refractive power change depends on the lens base curve relative to the central corneal radius. Compared to the International Organisation for Standardisation (ISO) standard tolerance, both materials showed considerable refractive power change once the ratio between the lens base curve and the central corneal radius exceeded 5%. The effect is more observable when the base curve is bigger than the central corneal radius (ratio more prominent than 1.0).

Figure 5 presents three-dimensional maps showing how refractive power changes with variations in the ratio between the lens base curve and the central corneal radius. The results reveal that the induced change in refractive power becomes clinically significant once this ratio exceeds approximately 5%, mainly when the base curve is flatter than the cornea (ratio > 1.0). This effect was observed in both materials, though more pronounced in Unisil. These simulations demonstrate how even slight mismatches in curvature between the lens and cornea can lead to noticeable changes in visual performance. The data underline the importance of precise lens fitting, especially in borderline cases where the base curve may not align closely with the corneal profile.

Figure 6 illustrates the ratio of refractive power change at 24 °C compared to that at 35 °C for both Definitive 74 and Unisil. This comparison highlights how temperature influences the optical performance of each material. A ratio above one indicates that the lens experienced a greater power change at room temperature than at physiological temperature, suggesting higher stiffness at the lower temperature. Across the tested range, Definitive 74 displayed a relatively consistent ratio close to one, indicating stable optical behaviour regardless of temperature. In contrast, Unisil exhibited more variation, reflecting greater sensitivity to thermal changes. These findings suggest that Definitive 74 may offer more predictable on-eye performance, while Unisil’s behaviour depends more on the testing environment. This further supports the need to simulate physiological conditions when evaluating soft contact lenses.

Comparing the temperature effect showed that the refractive power change in the temperature of 35 °C is less than that of 24 °C in both materials; however, Definitive 74 showed more steady behaviour among the spherical power range −10 D to 0 D with ratios closer to one.

4. Discussion

According to the manufacturer, Definitive 74 and Unisil are two latheable silicone hydrogel materials for soft contact lens manufacturing. Both materials offer high oxygen permeability, supporting corneal health during extended wear. Definitive 74 stands out for its exceptionally high water content (74%) and low modulus (0.4 MPa), delivering enhanced comfort and flexibility without requiring surface treatment. In contrast, Unisil features a moderate water content (62%) and a higher modulus (0.8 MPa), allowing for more structurally complex lens designs with increased visual precision. While both materials exhibit good wettability, their differing mechanical and physical properties cater to distinct clinical and design needs. Yet, a meaningful gap remains in characterising these materials under physiologically relevant conditions. Most laboratory assessments are conducted at room temperature, which does not accurately represent the ocular surface temperature. This discrepancy may lead to misinterpretation of performance in vivo. Therefore, this study aimed to critically evaluate the thermal stability and accuracy of reported material parameters when subjected to elevated temperatures that better simulate the ocular environment.

Regarding mechanical behaviour and temperature effects, the results indicate that both Definitive 74 and Unisil exhibited temperature-dependent mechanical properties, with their respective elastic moduli decreasing at physiological temperature (35 °C) compared to room temperature (24 °C). This reduction suggests that the materials become more flexible at higher temperatures, aligning with previous studies that highlight the effect of temperature on hydrogel-based materials. The decrease in modulus, particularly for Definitive 74, suggests a greater sensitivity to temperature variations, which could influence the on-eye performance and comfort of the lens.

The slight increase in RI observed from room temperature to physiological temperature for both materials diverges from the recent in vitro findings of Schurig et al., who measured several hydrogel and silicone hydrogel lenses and reported a decrease in RI between room and physiological temperatures using an automatic refractometer [15]. Still, none of the Schurig’s tested materials were Contamac’s Definitive 74 or Unisil. Nevertheless, the direction of change seen in the current study is mechanistically plausible because RI in soft lenses tracks water content as lower water contents lead to higher RI, a relationship documented for both conventional and silicone hydrogels by González-Méijome et al. [17]. Consistent with that framing, the Unisil Contamac’s datasheet warns that partially hydrated lenses measure a higher RI than fully hydrated lenses and prescribes heat-assisted hydration, supporting the idea that subtle temperature-driven hydration shifts could yield a positive change in RI under specific protocols. Although contact lenses work at physiological temperature, the manufacturer reports the hydrated RI only at 20 °C and provides no temperature coefficient, making direct comparison with current measured values very challenging.

Regarding material selection and contact lens performance implications, a key observation from the FEA is that the ratio between the lens base curve and the central corneal radius significantly affects the refractive power change. When this ratio exceeds 5%, refractive power deviations surpass the ISO standard tolerance, making the choice of lens curvature a critical factor in lens design. Additionally, the Ogden nonlinear material model demonstrated that an increase in model order beyond one did not result in significant improvements in fit, confirming that a first-order Ogden model is sufficient for describing the material behaviour of these soft contact lenses.

The observed mechanical differences between Definitive 74 and Unisil further underscore the importance of material selection. While Unisil exhibited a higher modulus than Definitive 74, both materials followed a nonlinear stress–strain relationship. This suggests that traditional linear elasticity models may not adequately predict soft contact lens deformation on the eye. This supports the need for continued refinement of computational models to ensure accurate simulations of real-world usage conditions. Moreover, higher modulus lenses have been shown to cause greater corneal topographic changes over time [44], reinforcing the need for careful material selection in design.

In terms of practical considerations and from a clinical perspective, the temperature-dependent mechanical behaviour of contact lenses suggests that lens fitting, and power calculations performed at room temperature may not directly translate to the in-eye performance. For example, lenses with a lower modulus at physiological temperature might conform more closely to the corneal surface, potentially affecting refractive power and stability. This underscores the need for standardised testing protocols that replicate physiological conditions to improve the predictive accuracy of material performance.

Furthermore, the study highlights that the interaction between material stiffness and eyelid pressure must be carefully considered. Since the uniaxial compression test is more representative of eyelid pressure effects, incorporating compression behaviour into future lens design methodologies may improve comfort and stability assessments.

In theory, if the tensile modulus of elasticity is an accurate measure, materials with the same moduli should behave the same on the eye; however, in practice, soft materials with similar moduli may not behave similarly [4]. Therefore, investigating the full range of physical characteristics and their relationship would be useful to specialist practitioners [45,46], as a single mechanical test is quite limited.

The main challenge is determining the mechanical characteristics of soft contact lens materials, where the testing methods use different test protocols. A possible solution is to develop a standardised testing technique to measure soft contact lens material’s stiffness, as previous studies emphasised [4,47,48]. Such a test will result in comparable values if researchers follow its standard protocol in every test. Regrettably, some crucial aspects of material behaviour are not deemed essential in the current commercial designs of soft contact lenses [49].

Many studies describe the material behaviour of hydrogels and silicone hydrogels using tensile modulus of elasticity [8,20,21,48,49] based on uniaxial tensile testing. However, the eyelid pressure on contact lenses cannot be described as tensile stress. Eyelid pressure is linked to blinking, which causes the main cyclic load on the lens as the eye blinks 12 times per minute on average [40].

From a clinical standpoint, these results emphasise the need to evaluate lens behaviour under conditions as close as possible to the eye’s natural environment. The decrease in modulus at physiological temperature suggests that material flexibility and lens fit may be underestimated when tests are carried out only at room temperature. A good soft contact lens should provide comfort and stable vision to a high standard. While selecting a material with a lower modulus may appear attractive, very soft lenses can lose substantial stiffness on the eye, leading to excessive deformation, optical distortion, easier breakage during handling, and a shorter useful life. In contrast, a lens with a slightly higher modulus will still soften under physiological conditions but is more likely to retain its geometry, giving more consistent vision, greater durability during handling, and longer lifespan. As a practical rule of thumb, clinicians should remember that most soft lenses lose some stiffness on-eye [21,49], and the extent of this change depends on the specific material.

This study has some limitations that should be acknowledged. Only two silicone hydrogel materials were investigated, which limits the generalisability of the findings across the wide range of lenses available on the market. The experiments were performed under controlled hydration, whereas in actual wear, lenses gradually dehydrate in most cases. In addition, no in vivo testing was conducted, so the predictions made by the FEA remain to be validated directly on the eye, which is technically challenging. Lastly, while the simulation included realistic boundary conditions, aspects such as blink dynamics and tear film turnover were somehow simplified.

5. Conclusions

This study demonstrated that the mechanical behaviour of silicone hydrogel contact lenses is strongly influenced by temperature, with an apparent reduction in modulus observed at physiological conditions compared with room temperature. These changes directly affect how lenses fit, flex, and perform on the eye. They underline the importance of evaluating materials under warm, hydrated conditions that mimic the ocular environment.

Clinically, sensation comfort alone is insufficient; a lens must also maintain stable vision and withstand the demands of regular handling. Materials with a very low modulus may feel soft initially but risk excessive on-eye deformation, optical distortion, and reduced durability. In contrast, lenses with a slightly higher modulus soften appropriately on-eye while better preserving their geometry, providing more consistent vision and longer-lasting performance. These results highlight the need for researchers, designers, and clinicians to consider the balance between softness, stability, and durability when selecting and assessing soft contact lens materials.