A Comprehensive Approach to Identifying the Parameters of a Counterflow Heat Exchanger Model Based on Sensitivity Analysis and Regularization Methods

Abstract

The study presents a robust methodology for simultaneous state and parameter estimation in nonlinear thermal systems, demonstrated on a counter-current heat exchanger model operating with nitrogen under industrial conditions. To address challenges of ill-conditioning and parameter correlation, local sensitivity analysis is combined with regularization through optimal parameter subset selection using orthogonalization and D-optimal experimental design. The Unscented Kalman Filter (UKF) is employed to jointly estimate the augmented state vector in real time, leveraging high-fidelity dynamic simulations generated in Unisim Design with the Peng–Robinson equation of state. The proposed framework achieves high estimation accuracy and numerical stability, even under limited sensor availability and measurement noise. Monte Carlo simulations confirm robustness to ±2.5% uncertainty in initial conditions, while residual autocorrelation analysis validates estimator optimality. The approach provides a practical solution for real-time monitoring and model-based control in industrial heat exchangers and offers a generalizable strategy for building identifiable, noise-resilient models of complex nonlinear systems.

1. Introduction

Simultaneous state and parameter estimation in nonlinear thermal systems—particularly in counter-current heat exchangers—remains a cornerstone challenge in industrial process monitoring, control, and digital twin deployment. Heat exchangers, as critical components in power generation, petrochemical refining, and refrigeration systems, operate under strong nonlinearities (e.g., logarithmic mean temperature difference, Peng–Robinson equation of state), limited sensor availability, and persistent disturbances such as fouling or flow variability. These factors render conventional estimation techniques fragile, especially when model parameters are poorly identifiable or the estimator is ill-suited to handle high nonlinearity.

The recent literature reflects two dominant, yet often disjoint, research thrusts: (i) the development of advanced nonlinear filtering algorithms, and (ii) the application of identifiability-aware parameter selection. However, few studies integrate both into a unified, validated framework for industrial heat exchanger models.

Matajira-Rueda et al. (2021) [1] propose optimization-based strategies using metaheuristic algorithms to estimate thermal properties of heat transfer systems, rely on synthetic data and do not address real-time state estimation. Similarly, Loyola-Fuentes et al. (2019) [2] and the PDE-based study by Kazaku et al. (2023) [3] use gradient-based optimization for parameter fitting but require good initial guesses and offer no recursive filtering capability—limiting their utility in dynamic industrial environments.

On the filtering side, several works employ the Extended Kalman Filter (EKF). The study by Tassanbayev et al. (2023) [4] applies EKF to a high-fidelity Unisim Design heat exchanger model but reports significant pressure estimation errors (>5000 Pa under noise)—errors directly attributed to EKF’s first-order linearization failing under strong thermodynamic nonlinearities. A similar limitation is observed in Muenthong et al. (2020) [5], where EKF-based fouling detection suffers from steady-state offset under model mismatch.

In contrast, sigma-point filters like the Unscented Kalman Filter (UKF) avoid linearization and better capture higher-order statistical moments. UKF has been successfully applied in bioprocess monitoring [6,7], where nonlinear growth kinetics and thermal dynamics dominate. Kemmer et al. [6] demonstrate UKF’s value for adaptive feeding in bioreactors, while Yousefi-Darani et al. [7] combine UKF with sensitivity analysis for yeast cultivation—but both assume full parameter observability and do not rigorously address practical unidentifiability.

This gap is critical, as Liu et al. (2021) [8] and Krivorotko et al. (2020) [9] emphasize; even the most sophisticated filter fails when the underlying model includes practically unidentifiable parameters—those that are theoretically estimable but numerically indistinguishable due to ill-conditioned sensitivity matrices or high inter-parameter correlation. In heat exchanger models, parameters such as heat transfer coefficients, partition mass, and hydraulic conductivities often exhibit strong collinearity, leading to estimation variance inflation and divergence.

Recent works further underscore the necessity of this integration. Bo et al. (2020) [10] applied EKF, EnKF, and Moving Horizon Estimation (MHE) to a 1D infiltration model and found that even advanced filters like EnKF suffered from bias when all parameters were estimated simultaneously—highlighting that “parameter correlations remained a major source of estimation bias” despite algorithmic sophistication. Similarly, Obiri et al. (2023) [11] combined global sensitivity analysis with sensor selection for monoclonal antibody production but noted that “not all model parameters are practically identifiable,” necessitating careful subset selection before estimation.

Moreover, the presence of unknown inputs or unmodeled disturbances—common in real plants—further complicates estimation. Asgari et al. (2020) [12] proposed a robust EKF using an unknown-but-bounded (UBB) framework to handle unknown inputs in nonlinear systems. While effective for certain classes of disturbances, their method still relies on EKF linearization and does not address parameter identifiability. In thermal systems governed by Peng–Robinson EOS, such linearization introduces irreducible bias that UBB bounds cannot fully compensate for.

Crucially, Liu & McAuley (2024) [13] recently advanced the field by proposing a simultaneous parameter estimation and tuning (SPET) framework that jointly estimates model parameters and EKF tuning matrices (process and measurement noise covariances) in systems with nonstationary disturbances, multi-rate sampling, and measurement delays. Their approach significantly improves prediction accuracy in CSTR models. However, SPET still operates within the EKF paradigm, inheriting its vulnerability to strong nonlinearities. Furthermore, SPET does not incorporate formal identifiability analysis or optimal experimental design to guide parameter subset selection—relying instead on assumed model structures. Even in climate science, where box models are fitted to Earth system data, Proistosescu & Huybers (2020) [14] caution that “structural simplifications can mask slow modes of response,” leading to biased climate sensitivity estimates. Their Bayesian approach highlights the danger of overparameterization without identifiability constraints—a lesson directly transferable to engineering estimation.

Recent theoretical and applied studies further validate the dual necessity of nonlinear filtering and identifiability-aware design in complex estimation problems. Kamalapurkar (2017) [15] demonstrated that sigma-point Kalman filters—particularly the UKF—outperform EKF in second-order nonlinear mechanical systems by preserving higher-order statistics without linearization, a finding directly transferable to thermodynamic systems with strong nonlinearities such as those governed by the Peng–Robinson equation of state. Similarly, Stojanović et al. (2020) [16] showed that UKF maintains robustness under non-Gaussian noise and fault conditions, reinforcing its suitability for industrial environments where disturbances are rarely idealized.

The practical relevance of UKF has also been confirmed in thermal system applications beyond heat exchangers. Gonzólez-Cagigal et al. (2023) [17] applied UKF to estimate hotspot temperatures in power transformers under dynamic loading, achieving high accuracy despite limited sensor data—paralleling the challenges faced in heat exchanger monitoring. Likewise, Alexander et al. (2020) [18] reviewed UKF and other nonlinear estimators in bioprocesses and concluded that while UKF is effective for online monitoring, its performance is critically dependent on model structure and parameter observability—a caveat that underscores the need for pre-estimation identifiability analysis.

This brings us to a foundational methodological insight—filter choice alone is insufficient without structural model validation. Lund & Foss (2008) [19] pioneered the use of sensitivity vector orthogonalization to rank and select parameters in nonlinear dynamic models, showing that decorrelating sensitivity profiles drastically reduces estimation variance. Complementarily, Franceschini & Macchietto (2008) [20] established D-optimal experimental design as a rigorous framework for maximizing parameter precision by optimizing the Fisher Information Matrix—a principle now widely adopted in chemical engineering for model-based design of experiments.

These strategies have proven effective across domains: Latyshenko et al. (2017) [21] reported up to 70% variance reduction in biological inverse problems using orthogonalization, while Yao et al. (2003) [22] demonstrated significant improvements in kinetic parameter estimates in polymerization reactors through D-optimal design. Yet, in most of these works, parameter selection remains a preprocessing step, decoupled from the estimator itself.

In contrast, the current research integrates these tools into a unified estimation architecture: orthogonalization and D-optimal design are not merely used to prune parameters, but to construct an augmented state vector that is inherently well-conditioned and information-rich. This co-design ensures that the UKF operates on a model subspace where parameters are both practically identifiable and minimally correlated—a prerequisite for statistical reliability.

Finally, the validity of any estimator must be confirmed through residual diagnostics. Ramakrishnan et al. (2020) [23] emphasized that residual autocorrelation—“whitening” cost function, the Ljung–Box statistic, is introduced, which not only minimizes the error but also minimized the correlations between errors, ensuring that the whitening objective functions lead to much better extrapolation–a property very desirable for reliable control systems. Following this principle, our framework includes rigorous residual analysis, confirming that estimation errors behave as white noise, thereby validating the statistical soundness of the proposed approach.

Despite these advances, a significant methodological gap remains: while many studies focus either on developing advanced filtering algorithms or on performing sensitivity analysis for parameter selection, few offer a comprehensive, integrated framework that combines both within a single, validated methodology for industrial heat exchanger models. Moreover, there is a notable scarcity of studies that rigorously validate their approach using high-fidelity industrial simulators (such as Unisim Design R410) and statistical measures such as residual autocorrelation to confirm the “whiteness” of estimation errors—a gold standard for validating estimator optimality [7,10].

The research presented in this study bridges this gap by introducing a unified, end-to-end methodology for simultaneous state and parameter estimation in a counter-current heat exchanger. Unlike previous fragmented approaches, the proposed method co-designs the estimation strategy around the model’s inherent limitations:

–

Structural and practical identifiability are first diagnosed using local sensitivity analysis, revealing a severely ill-conditioned full-parameter set (condition number ≈ 1.2 × 10⁴, collinearity index γ ≈ 85).

–

Orthogonalization and D-optimal design are then applied—not as competing alternatives but as complementary tools—to select the parameter subset that maximizes information content while minimizing mutual correlation.

–

The Unscented Kalman Filter (UKF) is deployed for joint estimation on a high-fidelity Unisim Design model with nitrogen as the working fluid and Peng–Robinson thermodynamics—ensuring industrial relevance.

–

Statistical validation via residual autocorrelation confirms that estimation errors behave as “white noise,” verifying the absence of systematic bias and establishing estimator optimality.

The innovation of this work lies not in the invention of new algorithms but in their strategic integration and rigorous validation. Sensitivity analysis and regularization are no longer preprocessing steps—they are core components of a unified estimation architecture. This co-designed approach ensures numerical stability, minimizes mutual parameter correlation, and maximizes information extraction from sparse measurements—making it uniquely suited for deployment in real-world industrial environments where robustness and reliability are non-negotiable. Key practical outcomes demonstrate the transformative impact of strategic parameter selection: pressure estimation errors are reduced from >5000 Pa (naive full-parameter estimation) to just ±14 Pa—a 99.7% improvement in accuracy. Monte Carlo simulations confirm robustness to ±2.5% initial condition uncertainty and measurement noise, ensuring reliability under real-world industrial variability.

Thus, this paper delivers not only a methodological advancement, but also a practically deployable solution for high-accuracy, noise-resilient estimation in complex thermal systems—addressing a long-standing gap between theoretical estimation and industrial operational needs.

To guide the reader through the logical progression of this work, the remainder of the paper is structured as follows: In Section 2, we detail the mathematical formulation of the heat exchanger model, the construction of the extended state-space system, and the implementation of the Unscented Kalman Filter alongside the orthogonalization and D-optimal design algorithms for parameter subset selection. In Section 3, we present the simulation environment, the experimental setup, and the comparative performance evaluation of optimal and suboptimal parameter subsets, supported by Monte Carlo simulations and statistical validation of estimation residuals. Lastly, in Section 4, we summarize the key findings, emphasizing the critical role of strategic parameter selection in achieving robust, high-accuracy estimation under industrial constraints, and outline directions for future research.

2. Materials and Methods

The object of study is a counter-current heat exchanger modeled by a system of nonlinear ordinary differential equations (ODEs) that describe the dynamic heat transfer between two fluids flowing in opposite directions [4]. In practical operation, full measurement of all state variables and model parameters is often infeasible, necessitating simultaneous state and parameter estimation for accurate process monitoring and control. However, this joint estimation problem is inherently ill-conditioned due to weak observability and strong parameter-state coupling, leading to numerical instability and high sensitivity to measurement noise. To address this challenge, regularization through parameter subset selection is employed. In the study, a set of identifiable parameters is selected based on experimental data generated from simulations of the heat exchanger model in the Unisim Design R410 (Des Plaines, IL, USA) software environment. Orthogonalization and optimization techniques are applied to analyze the sensitivity matrix and identify the most influential and estimable parameters, ensuring improved conditioning of the inverse problem.

The effectiveness of the selected parameter subset is validated through Monte Carlo simulations using a sigma-point Kalman filtering algorithm, specifically the Unscented Kalman Filter (UKF) [24], which demonstrates enhanced convergence, accuracy, and robustness in the joint estimation process. For numerical implementation, the continuous-time ODE model is discretized using an implicit finite-difference scheme, resulting in a system of nonlinear difference equations that preserve the dynamic characteristics of the original system.

The continuous-time dynamics of the system are discretized and described by a system of nonlinear finite-difference equations:

$$\begin{array}{c}x\left(k+1\right)=f\left(x\left(k\right),\theta ,k\right),\hspace{1em}k\in \left(0,T\right),\hfill \\ x\left(0\right)=x_{0,}\hfill \\ y\left(k\right)=h\left(x\left(k\right),\theta ,k\right),\hfill \end{array}$$

(1)

where $x\left(k\right)\in R^{n_x}$—vector of state functions ($n_x)$—number of equations, $\theta \in R^{n_{\theta }}$—vector of parameters ($n_{\theta })$—number of parameters, $y\left(k\right)\in R^{n_y}$—vector of measurement functions, and $f\left(·\right)$ and $h\left(·\right)$—equations of state and measurement, generally nonlinear ($n_y\le n_x$), respectively.

2.1. Extended System

To estimate the state and parameters of system (1) simultaneously, the state vector is extended by including the parameter. This method is a standard approach for joint state and parameter estimation [25,26], leading to the following extended system:

$$x_{\theta }\left(k+1\right)=\left[\begin{array}{c}f\left(x\left(k\right),u\left(k\right),\theta \left(k\right)\right)\\ \theta \left(k\right)\end{array}\right]=F_{\theta }\left(x_{\theta }\left(k\right),u\left(k\right)\right)$$

(2a)

$$y\left(k\right)=H\left(x\left(k\right),\theta \left(k\right)\right)=H_{\theta }\left(x_{\theta }\left(k\right)\right)$$

(2b)

where $x_{\theta }\left(k\right)={\left[{x\left(k\right)}^T{\theta \left(k\right)}^T\right]}^T\in R^{n_x+n_{\theta }}$—extended vector of states and $F_{\theta }\left(·\right)$ and $H_{\theta }(·)$—extended state and output equations, respectively.

The goal of simultaneous state and parameter estimation is to estimate the extended state based on input and output information. First, it is necessary to determine whether the entire extended $x_{\theta }$ state vector is observable. As shown in [4,24,27], observability can be assessed by determining the rank of the sensitivity matrix computed along a typical trajectory within a sliding window of data from the extended system:

$$S_{\theta }\left(k\right)=\left[\begin{array}{c}{S}_{y,x_{\theta }(k-N)}\left(k-N\right)\\ S_{y,x_{\theta }(k-N)}\left(k-N+1\right)\\ \begin{array}{c}⋮\\ S_{y,x_{\theta }(k-N)}\left(k\right)\end{array}\end{array}\right]$$

(3)

where $N$—the data window size must be no less than $n_x+n_{\theta }$.

The input sensitivities of the measured output vector with respect to the extended state vector, as included in expression (3), based on the input and output data of the process, can be defined as [4,24,27,28]:

$$\begin{gathered} \begin{array}{c}{S}_{y,x_{\theta }\left(k-N\right)}\left(i\right)={\displaystyle \frac{\partial H_{\theta }}{\partial x_{\theta }}}(i){\displaystyle \frac{\partial F_{\theta }}{\partial x_{\theta }}}(i-1){\displaystyle \frac{\partial F_{\theta }}{\partial x_{\theta }}}(i-2)\cdots {\displaystyle \frac{\partial F_{\theta }}{\partial x_{\theta }}}(k-N), \\ \hfill \\ {\displaystyle \frac{\partial F_{\theta }}{\partial x_{\theta }}}\left(i\right)=\left[\begin{array}{cc}{\displaystyle \frac{\partial F_{\theta }}{\partial x}}(i)& {\displaystyle \frac{\partial F_{\theta }}{\partial \theta }}\\ 0& I_{n_{\theta } \times n_{\theta }}\end{array}\right],{\displaystyle \frac{\partial H_{\theta }}{\partial x_{\theta }}}\left(i\right)=\left[\begin{array}{cc}{\displaystyle \frac{\partial H}{\partial x}}(i)& {\displaystyle \frac{\partial H}{\partial \theta }}\end{array}\right].\hfill \end{array} \end{gathered}$$

(4)

The rank of the sensitivity matrix $S_{\theta }\left(k\right)$ is evaluated at each sampling instant to assess the local observability of the extended state vector. If the matrix is rank-deficient, not all components of the extended state can be uniquely estimated from the available input and output data. However, even a full-rank sensitivity matrix does not guarantee practical observability, particularly in complex nonlinear systems. Significant estimation challenges arise when the matrix is numerically close to rank deficiency-i.e., when it is poorly conditioned. In such cases, the estimation problem becomes highly sensitive to measurement noise, leading to large variances and significant deviations in the parameter estimates, which undermines the reliability and robustness of the solution.

While introducing additional output measurement channels can improve system observability and identifiability, such enhancements are often impractical or unjustified due to hardware constraints or increased system complexity. In such cases, regularization techniques offer a viable alternative to enhance estimation performance, including ridge regression [29,30], principal component analysis (PCA) [31], and parameter subset selection methods [4,24,27,30], all of which aim to improve the numerical conditioning of the estimation problem by reducing parameter correlations, filtering out insignificant modes, or selecting the most informative subset of estimable parameters.

2.2. Selecting Parameters for Estimation

The selection of parameters for estimation must account for two key factors: (1) the sensitivity of the output variables to small parameter variations and (2) the degree of correlation between the effects of different parameters on the outputs. If a parameter has only a negligible influence on the measurable outputs-below a defined significance threshold—it cannot be reliably estimated from the available data, as the signal-to-noise ratio becomes too low. Similarly, when changes in two or more parameters produce nearly identical responses in the output variables, their effects are said to be correlated, leading to practical unidentifiability. In such cases, the corresponding sensitivity vectors become linearly dependent or nearly so, making it impossible to distinguish the individual contributions of the parameters. Therefore, a well-posed estimation problem requires that the sensitivity vectors associated with the selected parameters be approximately linearly independent-i.e., no sensitivity vector should be expressible as a linear combination of the others.

A variety of parameter selection methods have been developed based on these principles, including the orthogonalization method [19,32], the collinearity index approach [33,34], principal component-based analysis [35,36], eigenvalue-based techniques [37,38], the relative gain array method [39], hierarchical parameter clustering [40], and hybrid strategies [41,42]. These methods simultaneously consider sensitivity magnitude and parameter interdependence but differ in the weighting assigned to each criterion and in the algorithmic approach to selecting parameter subsets. While all are computationally efficient and have demonstrated effectiveness in various applications, none can guarantee the identification of a globally optimal parameter set.

Parameter subset selection can be performed using either heuristic or optimization-based approaches. A parameter with minimal influence on the outputs should generally be excluded from estimation, as its inclusion increases problem ill-conditioning and amplifies the impact of measurement noise on the overall estimation accuracy.

Based on sensitivity analysis, the primary criteria governing parameter selection are as follows: (i) the norm of the sensitivity vector for a given parameter must be sufficiently large relative to those of other parameters, indicating strong observability and (ii) the sensitivity vectors of the selected parameters must exhibit low mutual correlation, ensuring numerical stability and identifiability in the joint estimation framework.

2.2.1. Orthogonal Algorithm

To address practical unidentifiability arising from parameter collinearity, an orthogonalization-based parameter subset selection strategy is employed. Two complementary implementations of this approach are used: Algorithm 1 (a sequential residual-based selection procedure) and Algorithm 2 (a perpendicular-projection-based variant), both adapted from established methodologies in the literature [9,21,28,32,37]. Since output data and parameters usually comprise different units of measurement, and there may be order differences in their numerical values, sensitivity vectors are often normalized:

$${\displaystyle \frac{{\overline{\theta }}_i}{{\sigma }_j}}·s_j,i=1,\cdots ,n_{\theta }; j=1,\cdots ,n_y,$$

(5)

where ${\overline{\theta }}_i$—nominal value of the i-th parameter; ${\sigma }_j$—root mean square deviation of the j-th output variable.

Sequence of the Algorithm 1 [9,28,32,37]:

• Calculate the sum of the squares of the elements of each column $S_{\theta }$.
• Select the parameter whose column in $S_{\theta }$ has the largest sum of squares of its elements as the first parameter to be estimated.
• Mark the corresponding column as $X_l$ (l $=$ 1 or the first iteration).
• Calculate ${\widehat{s}}_l$, the prediction of the full sensitivity matrix $S_{\theta }$, using a subset of the columns $X_l$:

  $${\widehat{s}}_l=X_l{\left(X_l^T{X}_l\right)}^{-1}{X}_l^T{S}_{\theta }.$$

  (6)
• Calculate the residual matrix $X_l:X_l=S_{\theta }-{\widehat{s}}_l$
• Calculate the sum of the squares of the residuals in each column of ${\mathrm{R}}_l$. The column with the largest sum corresponds to the next parameter to be estimated.
• Select the appropriate column in ${ S}_{\theta }$ and complete the matrix $X_l$, by including the new column. The extended matrix is denoted as $X_{l+1}$.
• Increment the iteration counter by one and repeat steps 4–7 until the sum of the squares of the elements of the largest column in the residual matrix is less than the specified threshold value.

Algorithm 2 of the orthogonal method [9,21,28,32,37]:

• Set the criterion δ₁, the array of numbers of identifiable parameters U $=\mathrm{\varnothing }$ and the array of numbers of unidentifiable parameters $I=\left\{1,\cdots ,n_{\theta }\right\}$. Construct the sensitivity matrix $S_{\theta }$ of the following form (3).
• Select from the sensitivity matrix $S_{\theta }$ the column l with the largest sum of squares of the elements, add it to the matrix E as the first column, and remove it from $S_{\theta }$. Add the element l to the array U and remove it from I.
• If U is blank, then stop the algorithm: for this model, all parameters are identifiable. Otherwise, go to step 4.
• For each column $S_m,m=1,...,n,$ of the matrix $S_{\theta }$, where $n$ is the number of remaining columns from $S_{\theta }$, calculate the perpendiculars:

  $$s_m^{⟂}=s_m-s_m^{proj}, s_m^{proj}={\sum }_{i=1}^{n_{\theta }-n}{\displaystyle \frac{\left(s_m,E_i\right)}{\left(E_i,E_i\right)}}{E}_i, E=\left(E_1,\cdots ,E_{n_{\theta }-n}\right),m=1,\cdots ,n$$

  (7)
• From the obtained matrix of perpendiculars $S^{⟂}$, select the column l with the largest sum of squares of the elements. If $‖S_l^{⟂}‖\le \delta$, then stop the algorithm. All parameters from U are identifiable, otherwise go to step 6.
• Add element l to U, remove it from U, remove the corresponding column from $S_{\theta }$, and add it to E; go to step 3.

The condition number of the full sensitivity matrix $S_{\theta }$, (prior to any parameter selection) has been calculated as the ratio of its largest to smallest singular value. For the heat exchanger model under the simulated operating conditions, this condition number has found to be ~1.2 × 10⁴, indicating severe ill-conditioning. The singular value spectrum showed a rapid decay, with the first two singular values capturing >95% of the total variance, confirming strong parameter correlations.

The collinearity index γ for the full parameter set {${\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5\}$ was computed as $\gamma =1/\sqrt{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(\mathrm{C}\right)}$, where ${\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}$ is the smallest eigenvalue of the correlation matrix C derived from $S_{\theta }^T{,S}_{\theta }$. The computed collinearity index was γ ≈ 85, which is well above the commonly accepted threshold of 20, signifying high practical unidentifiability for the full set.

The data window size N used for computing the sensitivity matrix in Equation (3) was set to N = 100 samples. This value was chosen as a balance between capturing sufficient transient dynamics and ensuring computational tractability for the Monte Carlo simulations. The stopping threshold δ for Algorithm 2 (Equation (7)) was set to $\delta =0.05$ meaning that the algorithm terminates when the norm of the largest perpendicular sensitivity vector falls below 5% of the norm of the first selected parameter’s sensitivity vector, ensuring that only parameters with significant, non-redundant information are included.

2.2.2. Optimization of the Identifiable Parameters’ Selection

Parameter selection methods [9,24,27,28] aim to address the challenge of identifying an estimable subset from the full set of model parameters. These methods must balance two key criteria: the magnitude of a parameter’s effect on the outputs (sensitivity) and the degree of correlation between the effects of different parameters. However, heuristic or rule-based approaches do not guarantee an optimal selection, as they may fail to fully account for the multivariate structure of the sensitivity space. A more systematic and rigorous approach involves formulating the parameter selection problem as an optimization task. The matrix $S_{\theta }^T{S}_{\theta }$ and the Fisher information matrix (FIM), which governs the Cramér–Rao lower bound on the covariance of unbiased parameter estimators, is directly determined by the sensitivity matrix. Specifically, the inverse of the FIM provides a theoretical lower bound on the parameter estimation covariance, with the measurement noise covariance acting only as a scaling factor. Therefore, by strategically selecting a subset of parameters—thereby shaping the structure of the sensitivity matrix—one can directly improve the precision of the resulting estimates. This principle underpins optimization-based experimental design, where the goal is to maximize information content and minimize estimation uncertainty through optimal parameter subset selection.

The parameter selection problem is formulated using the D-criterion for experimental design [20,43] as follows:

$$\begin{gathered} \begin{array}{c}J=\arg \underset{I}{\max } det\left(S_{\theta }^T{S}_{\theta }\right), \\ \hfill \\ I=\left\{1,\cdots ,n_{\theta }\right\}.\hfill \end{array} \end{gathered}$$

(8)

As noted in [28], a poorly conditioned sensitivity matrix—characterized by small vector norms or linear dependencies—reduces the value of criterion (8). In contrast, maximizing this criterion through optimal parameter selection improves the precision and robustness of the estimates.

3. Results

3.1. The Heat Exchanger Model

Heat exchangers are among the key pieces of technological equipment in thermal power and oil refining plants [4]. Due to the high thermal inertia of these systems, inlet temperature variations are typically slow compared to the residence time of the fluid within the heat exchanger and the thermal response time of the partition. As a result, most transient processes can be considered quasi-stationary. Under this assumption, the temperature distribution along the heat exchanger closely follows the steady-state profile corresponding to the current inlet and outlet conditions. The dynamic model developed in this study is based on this quasi-stationary approximation, combined with the assumption that the specific heat capacity of the working fluid varies insignificantly between the inlet and outlet, enabling the use of simplified heat transfer expressions.

Differential equations describing the weights of hot ($M_H$) and cold ($M_C$) substances in a heat exchanger (kg) depending on the flow rates of the input flows are presented below:

$${\displaystyle \frac{d{M}_H}{dt}}=F_H^{\left(0\right)}-F_H^{\left(1\right)},$$

(9)

$${\displaystyle \frac{d{M}_C}{dt}}=F_C^{\left(1\right)}-F_C^{\left(0\right)},$$

(10)

where $F_H^{\left(0\right)}$ and $F_C^{\left(1\right)}$—input flow rates—hot and cold, respectively, kg/s; $F_H^{\left(1\right)}$ and $F_C^{\left(0\right)}$—output flow rates—hot and cold, respectively, kg/s.

$${\displaystyle \frac{d{H}_H^{\left(1\right)}}{dt}}={\displaystyle \frac{F_H^{\left(0\right)}\left(H_H^{\left(0\right)}-H_H^{\left(1\right)}\right)-Q_H}{M_H}},$$

(11)

$${\displaystyle \frac{d{H}_C^{\left(0\right)}}{dt}}={\displaystyle \frac{F_C^{\left(1\right)}\left(H_C^{\left(1\right)}-H_C^{\left(0\right)}\right)+Q_C}{M_C}},$$

(12)

$H_H^{\left(1\right)}$ and $H_C^{\left(0\right)}$—specific enthalpies of hot and cold substances in a heat exchanger, J/kg.

The model calculates heat transfer based on the temperature differences across the partition, which is a standard and physically meaningful approach for heat exchanger modeling under the assumption of constant heat capacity $Q_H$ and $Q_C$—heat transfer rates from a hot substance to a partition and from a partition to a cold substance, W.

Due to the assumption that the heat capacities of the substance change little between the input and output, expressions for the logarithmic mean temperature difference can be used for the heat transfer rates:

$$\begin{array}{c}{Q}_H=U_H\mathrm{A}∆{\mathrm{T}}_{\mathrm{l}\mathrm{m},\mathrm{h}}\hfill \\ {\mathrm{T}}_{\mathrm{l}\mathrm{m},\mathrm{h}}={\displaystyle \frac{\left(T_H^{\left(0\right)}-T_B^{\left(0\right)}\right)-\left(T_H^{\left(1\right)}-T_B^{\left(1\right)}\right)}{ln\frac{T_H^{\left(0\right)}-T_B^{\left(0\right)}}{T_H^{\left(1\right)}-T_B^{\left(1\right)}}}}\hfill \end{array}$$

(13)

$$\begin{array}{c}{Q}_{\mathrm{C}}=U_{\mathrm{C}}\mathrm{A}∆{\mathrm{T}}_{\mathrm{l}\mathrm{m},\mathrm{c}}\hfill \\ {\mathrm{T}}_{\mathrm{l}\mathrm{m},\mathrm{c}}={\displaystyle \frac{\left(T_B^{\left(0\right)}-T_C^{\left(0\right)}\right)-\left(T_B^{\left(1\right)}-T_C^{\left(1\right)}\right)}{ln\frac{T_B^{\left(0\right)}-T_C^{\left(0\right)}}{T_B^{\left(1\right)}-T_C^{\left(1\right)}}}}\hfill \end{array}$$

(14)

${\mathrm{T}}_{\mathrm{l}\mathrm{m},\mathrm{h}}$ and ${\mathrm{T}}_{\mathrm{l}\mathrm{m},\mathrm{c}}$—logarithmic mean temperature differences for the hot and cold sides; $U_H$ and $U_{\mathrm{C}}$—heat transfer coefficients from a hot substance to a solid partition and from a solid partition to a cold substance, W/(m² · C⁰); A—heat exchange surface area, m²; $T_B^{\left(0\right)}$ and $T_B^{\left(1\right)}$—temperatures at the hot-side and cold-side ends of the solid partition, C⁰; $T_H^{\left(0\right)}$ and $T_C^{\left(1\right)}$—temperatures of hot and cold intput flows, C⁰; $T_H^{\left(1\right)}$ and $T_C^{\left(0\right)}$—temperatures of hot and cold output flows, C⁰.

Expressions for $T_B^{\left(0\right)}$ and $T_B^{\left(1\right)}$ have the following form:

$${\displaystyle \frac{d{T}_B^{\left(0\right)}}{dt}}={\displaystyle \frac{2}{M_B{C}_B}}\left[{\displaystyle \frac{\left(T_H^{\left(0\right)}-T_B^{\left(0\right)}\right)Q_H}{\left(T_H^{\left(0\right)}-T_B^{\left(0\right)}\right)+\left(T_H^{\left(1\right)}-T_B^{\left(1\right)}\right)}}-{\displaystyle \frac{\left(T_B^{\left(0\right)}-T_C^{\left(0\right)}\right)Q_C}{\left(T_B^{\left(0\right)}-T_C^{\left(0\right)}\right)+\left(T_B^{\left(1\right)}-T_C^{\left(1\right)}\right)}}\right],$$

(15)

$${\displaystyle \frac{d{T}_B^{\left(1\right)}}{dt}}={\displaystyle \frac{2}{M_B{C}_B}}\left[{\displaystyle \frac{\left(T_H^{\left(1\right)}-T_B^{\left(1\right)}\right)Q_H}{\left(T_H^{\left(0\right)}-T_B^{\left(0\right)}\right)+\left(T_H^{\left(1\right)}-T_B^{\left(1\right)}\right)}}-{\displaystyle \frac{\left(T_B^{\left(1\right)}-T_C^{\left(1\right)}\right)Q_C}{\left(T_B^{\left(0\right)}-T_C^{\left(0\right)}\right)+\left(T_B^{\left(1\right)}-T_C^{\left(1\right)}\right)}}\right],$$

where $M_B$—partition weight, kg; $C_B$—specific heat capacity of the partition material, J/(kg · C⁰).

The relationships for the densities of hot ${\rho }_H^{\left(1\right)}$ and cold ${\rho }_C^{\left(0\right)}$ substances in the heat exchanger are determined in the form:

$${\rho }_H^{\left(1\right)}={\displaystyle \frac{M_H}{V_H}},{\rho }_C^{\left(0\right)}={\displaystyle \frac{M_C}{V_C}},\mathrm{kg}/{\mathrm{m}}^3,$$

where $V_H$ and $V_C$—volumes of spaces with hot and cold substances, m³.

Input flow consumptions

$$F_H^{\left(0\right)}=K_H\sqrt{{\rho }_H^{\left(0\right)}\left(P_H^{\left(0\right)}-P_H^{\left(1\right)}\right)},\hspace{1em}{F}_C^{\left(1\right)}=K_C\sqrt{{\rho }_C^{\left(1\right)}\left(P_C^{\left(1\right)}-P_C^{\left(0\right)}\right)},$$

(16)

where $K_H$ and $K_{\mathrm{C}}$—coefficients of hydraulic conductivity of hot and cold spaces.

Relationships between thermodynamic parameters:

For input flow densities $\tilde{\rho }\left(T_C^{\left(1\right)},P_C^{\left(1\right)}\right)$, kg/m³;

For input flow pressures $P_H^{\left(1\right)}=\tilde{P}\left({\rho }_H^{\left(1\right)},H_H^{\left(1\right)}\right),P_C^{\left(0\right)}=\tilde{P}\left({\rho }_C^{\left(0\right)},H_C^{\left(0\right)}\right)$, Pa;

For specific enthalpies of hot $H_H^{\left(0\right)}=\tilde{H}\left(T_H^{\left(0\right)},P_H^{\left(0\right)}\right),$ and cold $H_C^{\left(1\right)}=\tilde{H}\left(T_C^{\left(1\right)},P_C^{\left(1\right)}\right)$ substances, J/kg;

For output flow temperatures $T_H^{\left(1\right)},T_C^{\left(0\right)}$.

Are determined from the equation of state of the substance or are given in tabular form:

$$\tilde{\rho }\left(T_C^{\left(1\right)},P_C^{\left(1\right)}\right), \tilde{P}\left({\rho }_H^{\left(1\right)},H_H^{\left(1\right)}\right),\tilde{H}\left(T_H^{\left(0\right)},P_H^{\left(0\right)}\right),\tilde{T}\left({\rho }_C^{\left(0\right)},H_C^{\left(0\right)}\right).$$

(17)

The state variables:

$x_1\left(k\right),x_2\left(k\right)$—specific enthalpies of hot and cold substances in a heat exchanger; $x_3\left(k\right),x_4\left(k\right)$—weights of hot and cold substances in the heat exchanger; $x_5\left(k\right),x_6\left(k\right)-$ temperatures of the ends of the partition.

Let us designate the parameters of the model to be estimated:

${\theta }_1\left(k\right),{\theta }_2\left(k\right)$—heat transfer coefficients from a hot substance to a partition and from a partition to a cold substance, W/(m² · C⁰);

${\theta }_3\left(k\right)$—partition weight, kg; ${\theta }_4\left(k\right),{\theta }_5\left(k\right)$—coefficients of hydraulic conductivity of hot and cold spaces, ${\displaystyle \frac{kg/s}{\sqrt{\frac{kg}{m^3}Pa}}}$.

Since the model parameters are largely insensitive to technological process variations, they are considered constant for the purpose of estimation:

$${\theta }_1\left(k\right)={\theta }_1\left(k+1\right)={\theta }_1,$$

$${\theta }_2\left(k\right)={\theta }_2\left(k+1\right)={\theta }_{2,}$$

$${\theta }_3\left(k\right)={\theta }_3\left(k+1\right)={\theta }_3,$$

$${\theta }_4\left(k\right)={\theta }_4\left(k+1\right)={\theta }_4,$$

$${\theta }_5\left(k\right)={\theta }_5\left(k+1\right)={\theta }_5,k=1,\cdots$$

The following variables are available for measurement:

$y_2\left(k\right),y_4\left(k\right)$—input and output flow temperatures, $T_H^{\left(1\right)}$—of hot and $T_C^{\left(0\right)}$—cold, C⁰; $y_1\left(k\right),y_3\left(k\right)$—pressure of input and output flows, $P_H^{\left(1\right)}$—of hot and $P_C^{\left(0\right)}$—cold, Pa.

The extended vector:

$$x_e\left(k\right)={\left(x_1\left(k\right)x_2\left(k\right)x_3\left(k\right)x_4\left(k\right)x_5\left(k\right)x_6\left(k\right){\theta }_1\left(k\right){\theta }_2\left(k\right){\theta }_3\left(k\right){\theta }_4\left(k\right){\theta }_5\left(k\right)\right)}^T,$$

(18)

The heat exchanger model in these terms:

$$x_e\left(k\right)=f\left(x\left(k\right),\theta \left(k\right)\right),\hspace{1em}k=0,\cdots$$

(19)

with initial conditions ${ x}_e\left(0\right)=x_e\left(x\left(0\right),\theta \left(0\right)\right).$ The function includes differential Equations (9)–(12) and (15) considering relations (13) and (14).

The measurement model takes the following form:

$$y\left(k\right)=h\left(x\left(k\right),\theta \left(k\right)\right),\hspace{1em}k=0,\cdots$$

(20)

The function h(∙) is defined based on the Peng–Robinson equation of state [35,36,37] and allows one to determine the values of temperatures and pressures of flows for the specific enthalpies of matter and masses of substances calculated using model (19).

Modeling Results

A dynamic model of a one-dimensional counter-current heat exchanger was developed using the Unisim Design R410 process simulation environment. Nitrogen was employed as the primary heat transfer fluid in the simulation. The technological configuration of the heat exchanger, together with the relevant process parameters, is summarized in

Table 1. Nominal design and operating parameters of the counter-current heat exchanger model used in Unisim Design simulations.

Technological Parameters of the Simulated Heat Exchanger
$\mathrm{Volume} \mathrm{of} \mathrm{heat} \mathrm{exchanger} \mathrm{space} \mathrm{with} \mathrm{hot} \mathrm{substance}, V_H$$, [{\mathrm{m}}^3$]	4.30
$\mathrm{Volume} \mathrm{of} \mathrm{space} \mathrm{of} \mathrm{heat} \mathrm{exchanger} \mathrm{with} \mathrm{cold} \mathrm{substance}, V_C$$, [{\mathrm{m}}^3$]	5.70
$\mathrm{Heat} \mathrm{exchange} \mathrm{surface} \mathrm{area}, \mathrm{A}, [{\mathrm{m}}^2$]	60.32
$\mathrm{Specific} \mathrm{heat} \mathrm{capacity} \mathrm{of} \mathrm{the} \mathrm{partition} \mathrm{material}, C_B$, J/(kg · C0)	473
Parameters of the technological process
Heat transfer coefficient from hot substance to partition, [W/(m2 · C0)]	298
Heat transfer coefficient from partition to cold substance, [W/(m2 · C0)]	265
Partition weight, [kg];	847
$\mathrm{Coefficient} \mathrm{of} \mathrm{hydraulic} \mathrm{conductivity} \mathrm{of} \mathrm{hot} \mathrm{space},$ $\left[{\displaystyle \frac{\mathrm{k}\mathrm{g}/\mathrm{s}}{\sqrt{{\mathrm{m}}^2·\mathrm{P}\mathrm{a}}}}\right]$	7.532 × 10−3
$\mathrm{Coefficient} \mathrm{of} \mathrm{hydraulic} \mathrm{conductivity} \mathrm{of} \mathrm{cold} \mathrm{space}, \left[{\displaystyle \frac{\mathrm{k}\mathrm{g}/\mathrm{s}}{\sqrt{{\mathrm{m}}^2·\mathrm{P}\mathrm{a}}}}\right]$	7.724 × 10−3

.

The experimental material represents the realizations of disturbances and output variables (

Table 2. Disturbances and output variables.

Disturbances		Output Variables
$T_H^{\left(0\right)},T_C^{\left(1\right)}$	$[\mathrm{C}$]	$T_H^{\left(1\right)},T_C^{\left(0\right)}$	$[\mathrm{C}$]
$P_H^{\left(0\right)},P_C^{\left(1\right)}$	$[\mathrm{P}\mathrm{a}$]	$P_H^{\left(1\right)},P_C^{\left(0\right)}$	$[\mathrm{P}\mathrm{a}$]
$F_H^{\left(1\right)},F_C^{\left(0\right)}$	$[\mathrm{k}\mathrm{g}/\mathrm{s}$]

) measured over 7200 s, with an interval of 1 s.

The task is to build a process model that includes six state variables and five parameters based on the results of the experiment in the Unisim Design environment, the conditions of its implementation (Table 1 and Table 2), in addition to a table of thermodynamic properties of the coolant. Concurrently, in conditions of the nonlinear nature of the interaction, the interdependence of technological factors, the presence of disturbances, and the impossibility of measuring a number of indicators, it is necessary to resolve issues related to the local identifiability of the model parameters.

Moreover, to quantitatively justify the validity of the quasi-stationary approximation and, by extension, the use of Logarithmic Mean Temperature Difference (LMTD) expressions within the dynamic model, comparison of relevant characteristic time scales of the system is performed.

Fluid residence time, representing time for a fluid particle to traverse the exchanger, is calculated as ${\tau }_{res}=V/\dot{m}.$ For the hot side (V = 4.30 m³) and representative nominal mass flow rate of ~0.5 kg/s (from Table 2), ${\tau }_{res}\approx 8.6 \mathrm{s}$. For the cold side (V = 5.70 m³), ${\tau }_{res},c\approx 11.4 \mathrm{s}$.

The thermal response time of the solid partition, estimated as τ_wall = (m_p · C_{p_p})/(U_avg · A), is approximately 119 s, using the parameters from Table 1 and the average heat transfer coefficient U_avg = (298 + 265)/2 W/(m² · C⁰)

In contrast, the characteristic time scale of applied disturbances (τ_dist), based on the step changes and ramps listed in Table 2 over the simulation, ranges from 500 to 3000 s.

Since τ_dist is at least 4–5 times longer than τ_wall and over 50 times longer than τ_res, disturbance evolves sufficiently slowly relative to the system’s internal dynamics. This significant separation of time scales confirms that the internal temperature profile has ample time to reach a quasi-equilibrium state corresponding to current boundary conditions before those conditions change appreciably, thereby validating the use of the quasi-steady-state LMTD formulation in the dynamic ODE framework.

3.2. Performance Evaluation of Parameter Subset Selection Strategies

A subset of estimable parameters is formed using the orthogonalization method. Based on the algorithm, the column of the matrix with the largest sum of squares of its elements will be determined, i.e., the first column, corresponding to the parameter ${\theta }_1$.

Thereafter, based on the norm of the projected sensitivity vector—which serves as an indicator of parameter influence—the next parameter, ${\theta }_2$, is selected in addition to the one already included. Similarly, the parameters are included in the following order ${\theta }_4,{\theta }_5,{\theta }_3$. Thus, a sequential selection of parameters is performed by trial and error.

The application of the parameter selection optimization method yields the following results: the optimal solution in terms of the D-optimal criterion yields a set that includes all parameters. Suboptimal options are located in the immediate vicinity of the solution found$-{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4$ and ${\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5$.

In order to determine the effect of the choice of estimated parameter set on the qualitative characteristics of the state vector estimation, including the previously defined variants—optimal and two suboptimal sets—an evaluation is performed using experimental data obtained from the heat exchanger model simulated in the Unisim Design software environment. To estimate the extended state vector, the Sigma-Point Kalman Filter (Unscented) filtering algorithm was used in [44]. Experimental–statistical modeling was conducted using the Monte Carlo method. The dependence on variable initial conditions of the extended state vector was analyzed. The initial condition vector was assumed to follow a normal distribution:

$$x_e^i\left(0\right)~N\left({\overline{x}}_e^i\left(0\right),{\sigma }_i^2\right),\hspace{1em}i=1,\cdots ,11,$$

where ${\overline{x}}_e^i\left(0\right)$ are equal to the corresponding parameters of the heat exchanger equipment for $i=1,\cdots ,6$ and the parameters of the technological process for $i=7,\cdots ,11$. The variances ${\sigma }_i^2$ are taken to be approximately 2.5% of ${\overline{x}}_e^i\left(0\right)$. The variance of the error of the Peng–Robinson equation in (20) is taken to be equal to 2.5% of the nominal.

For each variant, based on the generated initial conditions, an evaluation was performed using the sigma-point algorithm (Sigma-Point Kalman Filter (Unscented) filtering. The simulation results of 20 realizations of each investigated variant were averaged and are summarized in

Table 3. Average residual errors in estimating measured variables for a 7200 s sample for options for selecting a subset of parameters for identification.

Option for Selecting a Subset of Parameters for Identification	Variable	Mean Bias (Pa or C0)	RMSE (Pa or C0)	Normalized RMSE (% or Nominal)
$\left\{{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5\right\}$- optimal	Input flow pressure, [Pa]	−0.8 ± 2.1	13.5	0.07%
	Output flow pressure, [Pa]	+1.2 ± 1.8	14.0	0.07%
	Input flow temperature, [C]	−0.02 ± 0.05	0.43	0.14%
	Output flow temperature, [C]	−0.03 ± 0.08	1.60	0.53%
$\left\{{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4\right\}$	Input flow pressure, [Pa]	−5424.5 ± 357.2	362.1	1.81%
	Output flow pressure, [Pa]	−1424.7 ± 24.8	25.0	0.13%
	Input flow temperature, [C]	−2.75 ± 3.23	4.25	1.42%
	Output flow temperature, [C]	−4.75 ± 0.58	5.79	1.93%
$\left\{{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5\right\}$	Input flow pressure, [Pa]	−5978.5 ± 462.2	467.0	2.34%
	Output flow pressure, [Pa]	−1689.6 ± 31.4	32.0	0.16%
	Input flow temperature, [C]	−3.15 ± 3.49	4.70	1.57%
	Output flow temperature, [C]	−2.10 ± 0.62	6.22	2.07%

.

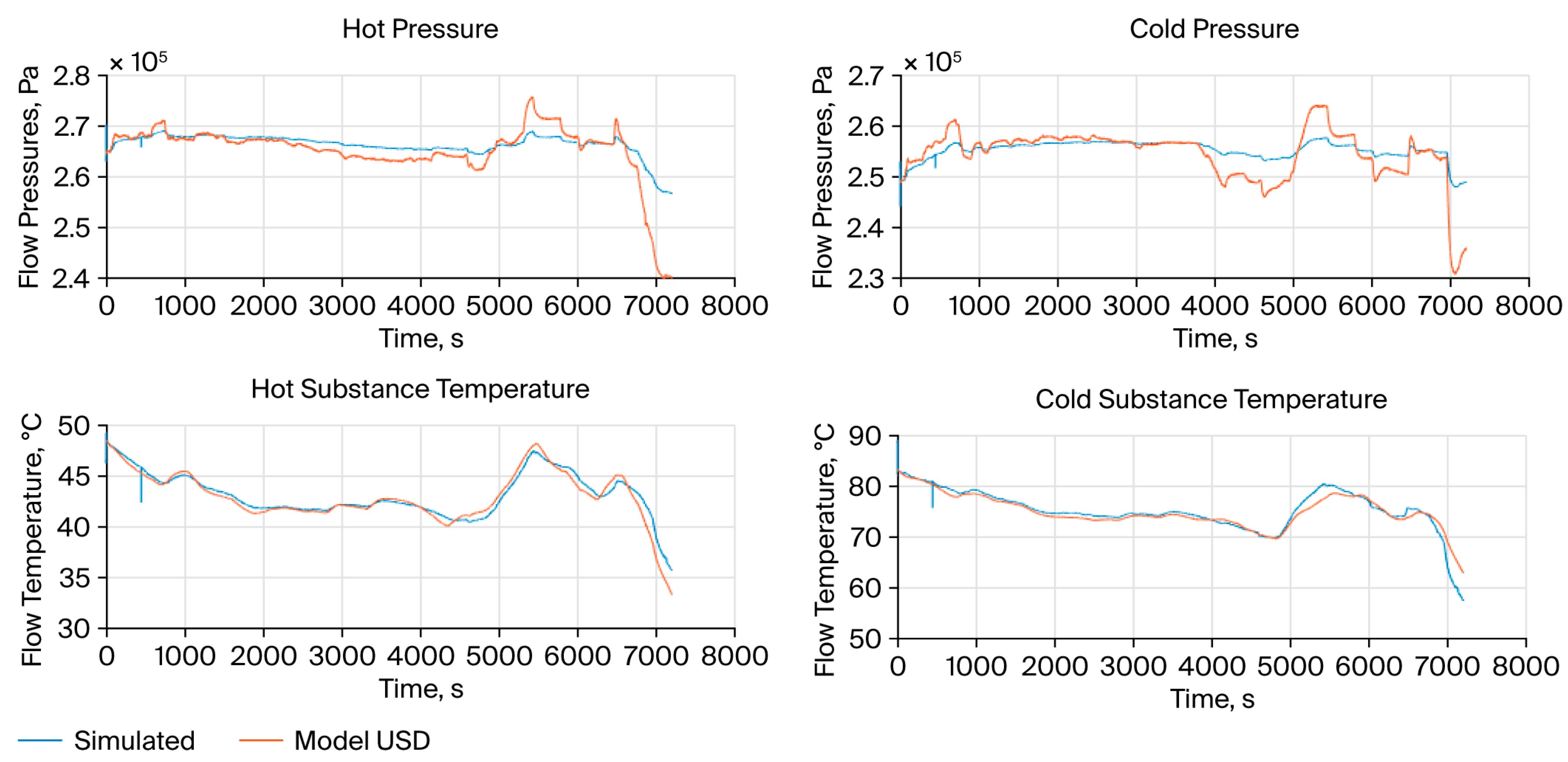
The results displayed in Figure 1 presents a direct, time-series comparison of the inlet and outlet pressure trajectories for both the hot and cold fluid streams. The “observed” trajectories are the ground-truth pressure values generated by the high-fidelity Unisim Design simulator, which serves as the virtual plant. The “estimated” trajectories are the real-time predictions produced by the Unscented Kalman Filter (UKF) using the optimal parameter subset $\left\{{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5\right\}$.

The near-perfect visual overlap of the estimated and observed curves is not merely qualitative; it is quantitatively supported by the extremely low residual errors (±13–14 Pa, as reported in Table 3). This result demonstrates that the UKF, when fed with the optimally selected parameters, can accurately reconstruct the true, unmeasured internal states and dynamics of the system. The fidelity is maintained even during significant transient events (e.g., step changes in inlet flow or temperature, as defined in Table 2), proving the estimator’s robustness to process disturbances. This level of accuracy validates the model’s suitability for real-time applications such as model-predictive control (MPC) or soft-sensing, where precise state knowledge is critical.

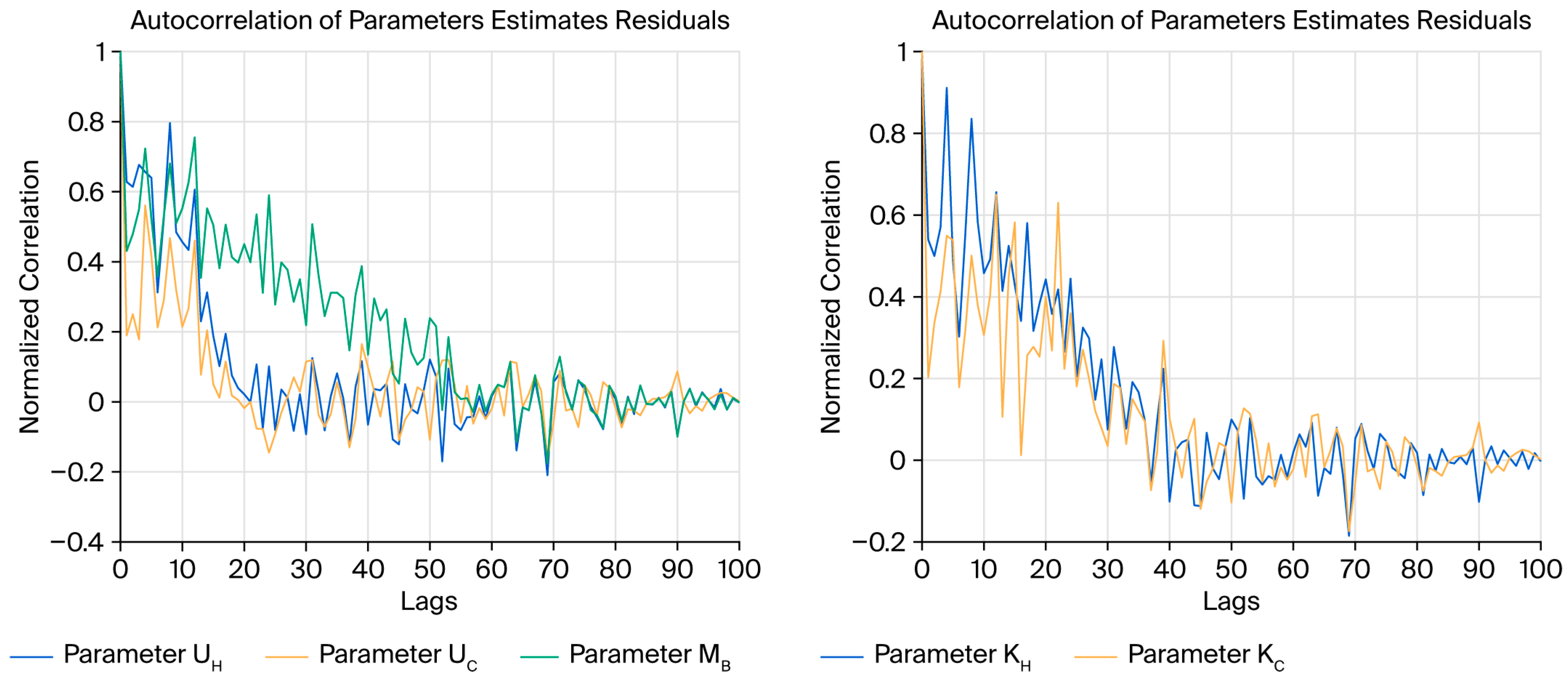
The results presented in Figure 2 display the autocorrelation function (ACF) for the residuals of the five estimated parameters over the 7200 s simulation window. The ACF is plotted for multiple lags (e.g., Lag 0 to Lag 50 or 100).

The key observation is that for all parameters, the ACF shows a sharp, significant peak at Lag 0 (which is inherent to any signal) and then rapidly decays to values that lie within the 95% confidence interval (at approximately ±1.96/√N, where N is the number of samples) for all subsequent lags (Lag 1, 2, 3, …).

This “whiteness” of the residuals is a fundamental statistical criterion for estimator optimality. It confirms that the UKF has fully captured the underlying system dynamics. There are no unmodeled dynamics or structural errors causing predictable patterns in the residuals. Moreover, estimation errors are random and uncorrelated over time, meaning that the filter is not “chasing” its own past errors, which is a sign of a well-tuned, stable estimator.

In addition, the estimated parameters are not just numerically close to their true values (as shown by the low RMSE in Table 3), but they are also statistically unbiased and their uncertainty is effectively characterized. This rigorous validation confirms that the dramatic accuracy improvement (from >5000 Pa to ±14 Pa) is not a coincidence but the direct result of the well-posed, co-designed estimation architecture.

Moreover, to rigorously assess the robustness of the proposed estimation framework, we conducted additional Monte Carlo simulations (

Table 4. Plants parameter perturbation scenario.

Parameter Perturbation Scenario	Variable	Mean Bias (Pa or C0)	RMSE (Pa or C0)	Normalized RMSE (% or Nominal)
Nominal model (no perturbation)	Input flow pressure, [Pa]	−0.8	13.5	0.07%
	Output flow pressure, [Pa]	+1.2	14.0	0.07%
	Input flow temperature, [C]	−0.02	0.43	0.14%
	Output flow temperature, [C]	−0.03	1.60	0.53%
$\left\{{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5\right\}$ perturbed randomly ±5%	Input flow pressure, [Pa]	−1.1	16.8	0.08%
	Output flow pressure, [Pa]	+1.5	17.2	0.09%
	Input flow temperature, [C]	−0.03	0.51	0.17%
	Output flow temperature, [C]	−0.04	1.85	0.61%
$\left\{{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5\right\}$$\mathrm{perturbed} \mathrm{randomly} \pm 10\%$	Input flow pressure, [Pa]	−1.9	21.3	0.11%
	Output flow pressure, [Pa]	+2.1	22.0	0.11%
	Input flow temperature, [C]	−0.05	0.62	0.21%
	Output flow temperature, [C]	−0.06	2.10	0.70%

) in which the true plant parameters were perturbed by ±5% and ±10% relative to their nominal values listed in Table 1. The UKF estimator was not re-tuned or re-identified—it used the same optimal parameter subset $\left\{{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5\right\}$ and filter gains derived under nominal conditions. Results, averaged over 20 Monte Carlo runs with ±2.5% uncertainty in initial conditions and measurement noise, demonstrate that even under a 10% model-plant mismatch, pressure RMSE remains below 22 Pa and temperature RMSE below 2.1 C⁰. Critically, residual autocorrelation functions continue to exhibit “white noise” behavior, confirming that the estimator remains unbiased and structurally sound.

These findings validate the practical deployability of the method in real industrial settings where exact model fidelity is rarely attainable.

4. Conclusions

In this paper, we investigate the problem of simultaneous estimation of state and parameters for classes of dynamic systems described using nonlinear ordinary differential equations, with application to a counterflow heat exchanger model constructed under conditions of limited measurement availability and stochastic disturbances. A theoretical and methodological analysis of the problems of parameter identifiability and observability of an extended dynamic system, including both state variables and unknown model parameters, is performed, which determines the relevance of using regularization methods and strategies for the optimal selection of identifiable parameters. Parameter selection algorithms based on the orthogonalization of sensitivity vectors were implemented, and a formalized approach to optimizing parameter configuration using the D-criterion of experimental design theory was developed. The effectiveness of the selection procedures was justified, ensuring numerically stable behavior of the sensitivity matrix, reducing the mutual correlation of parameter effects and, as a result, increasing the accuracy of estimation in conditions of noisy measurements and variability of initial conditions.

A numerical experiment implemented on the basis of a heat exchanger model in the Unisim Design software environment and including statistical modeling using the Monte Carlo method with the sigma-point Kalman filter algorithm confirmed the applicability of the proposed methods. It has been experimentally established that the use of preliminary parameter selection procedures provides significantly higher measurement informativeness and improves the numerical properties of the estimation problem compared to the naive full inclusion of all model parameters in the identification procedure.

The proposed approach thus demonstrates a high degree of versatility and practical significance in the tasks of constructing identifiable and observable mathematical models of complex technical systems.