Interpretable Machine Learning for Shale Gas Productivity Prediction: Western Chongqing Block Case Study
Abstract
1. Introduction
2. Data and Methods
2.1. Data Sources
- Initial identification of full parameter sets (including geological parameters) through a comprehensive well history review.
- Selection of high-integrity parameters via data quality evaluation. Prioritizing parameters with complete engineering monitoring records maintained dataset integrity and prevented interpolation bias.
2.2. Grey Correlation Analysis
2.3. Machine Learning Models
2.3.1. Support Vector Regression
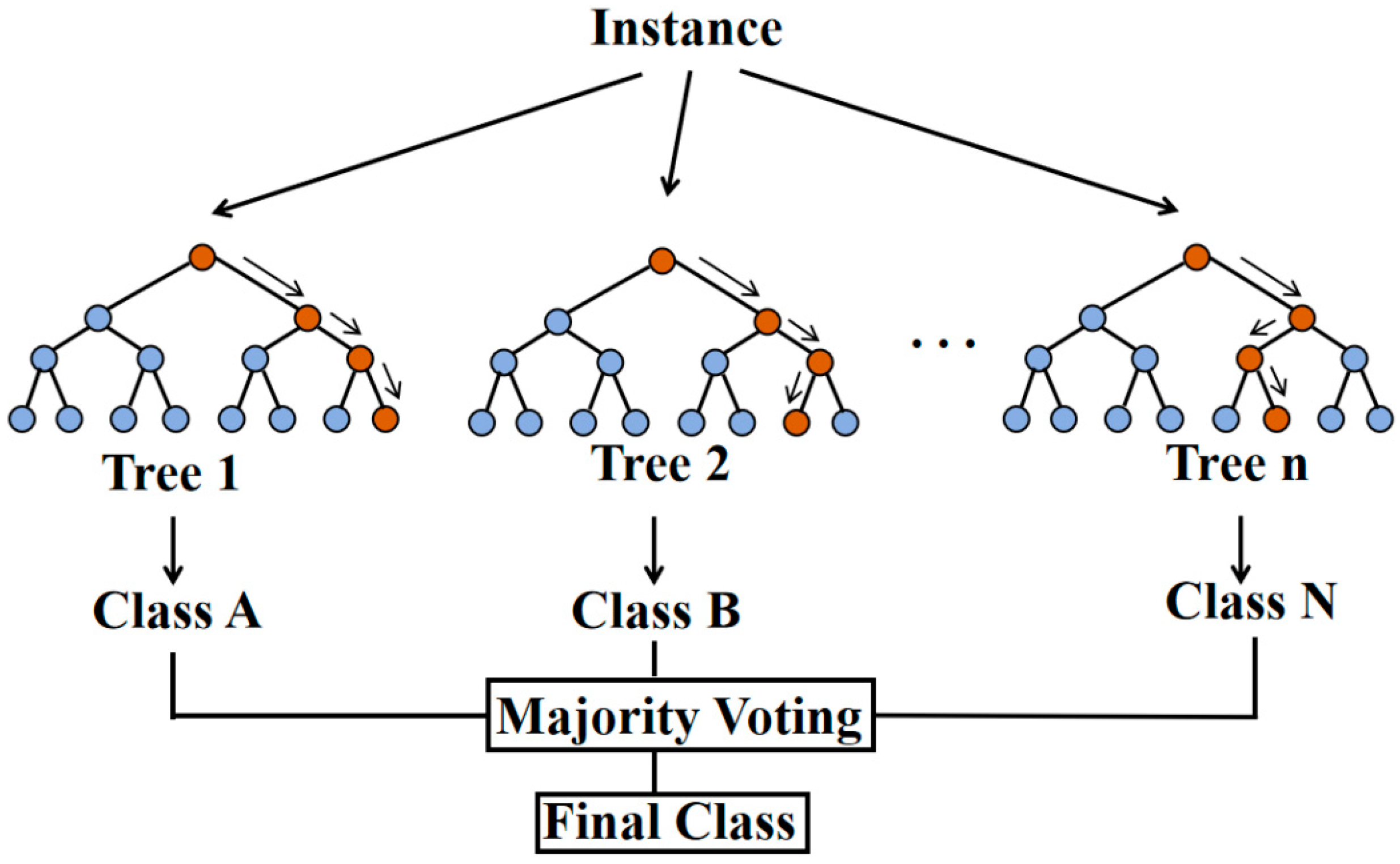
2.3.2. Random Forest Regression
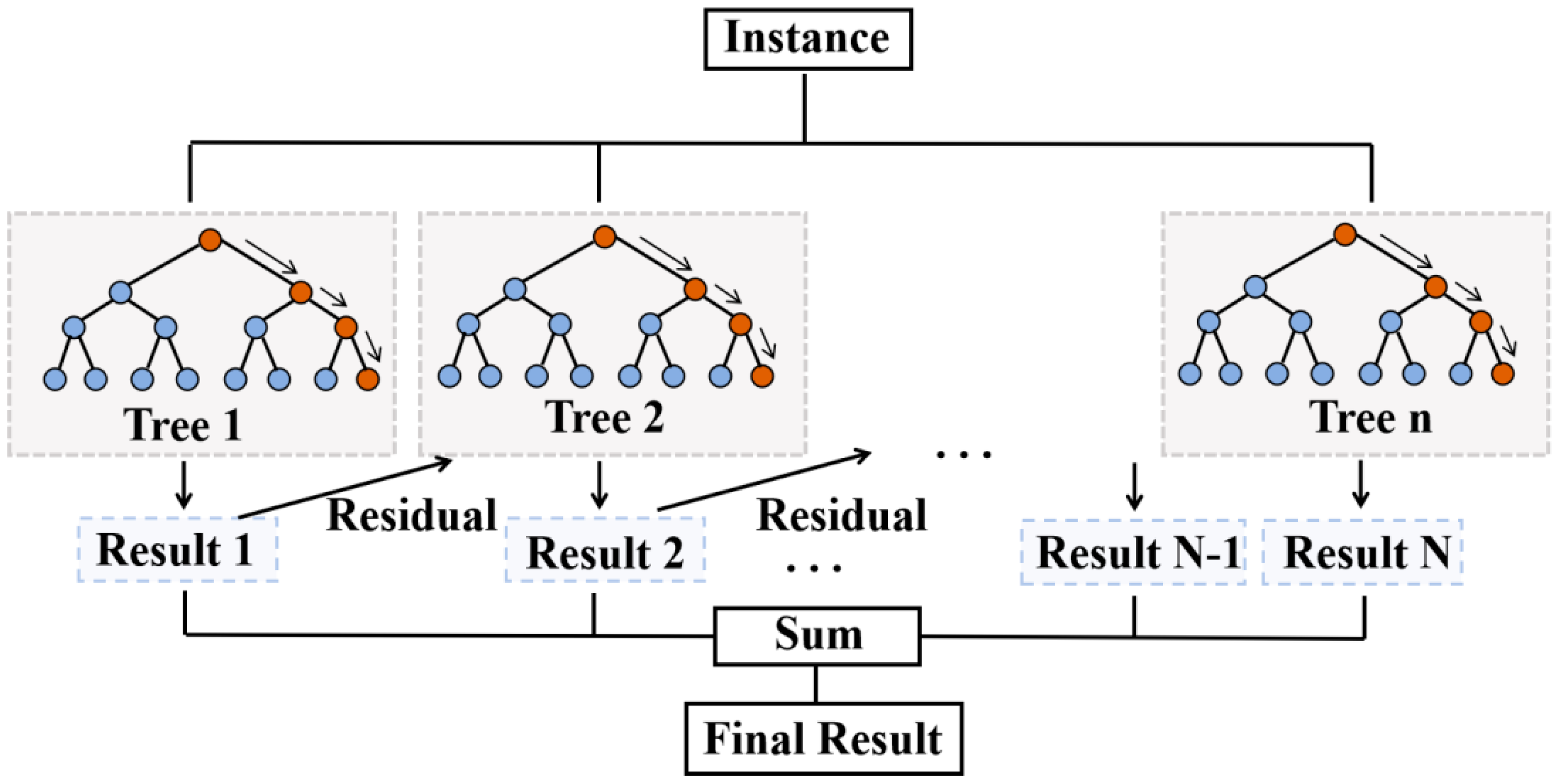
2.3.3. eXtreme Gradient Boosting
2.4. SHAP Interpretability Mechanisms
3. Experimental Results and Discussion
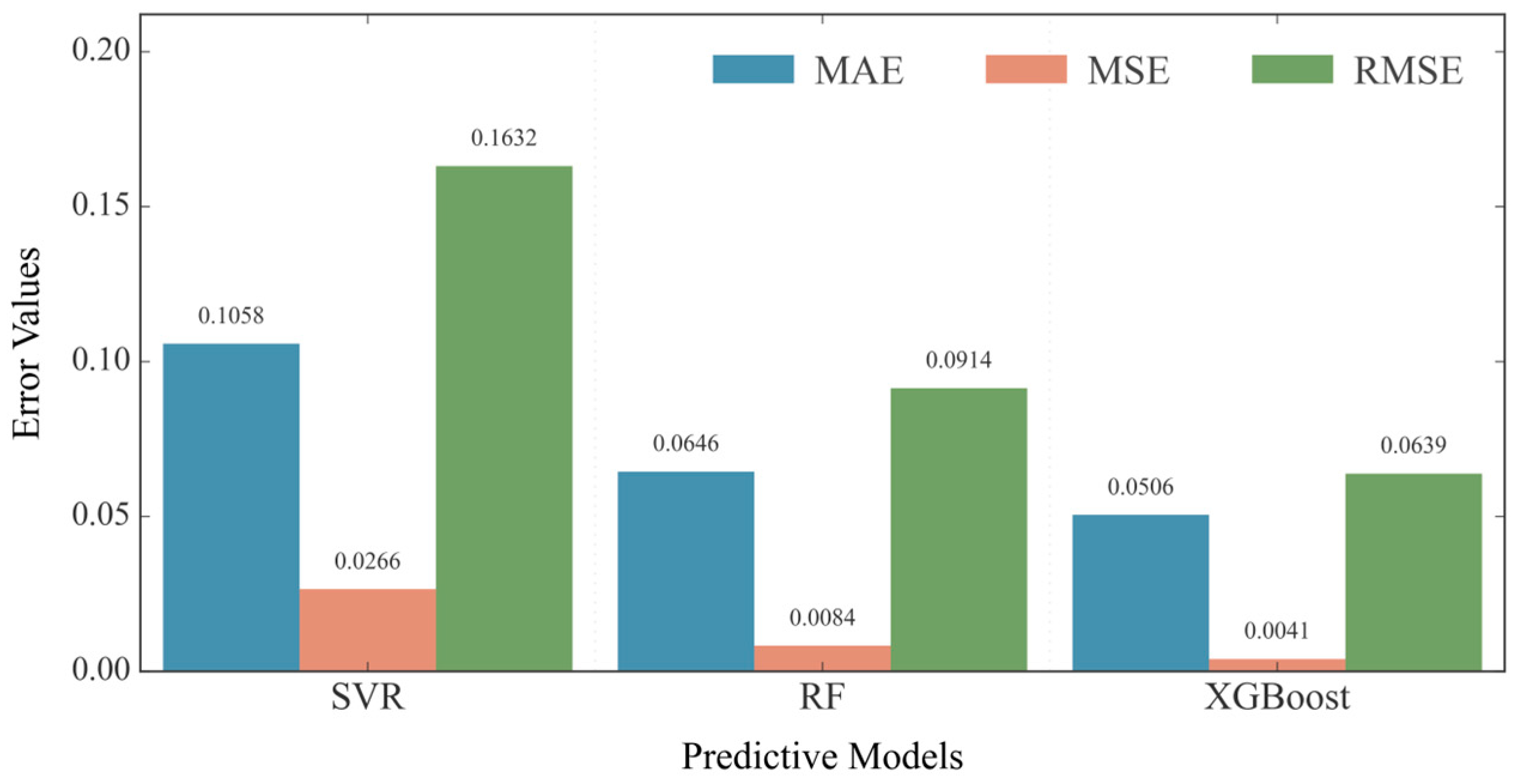
3.1. Model Performance Comparison and Optimization
3.2. Cross-Validation and Statistical Significance Analysis
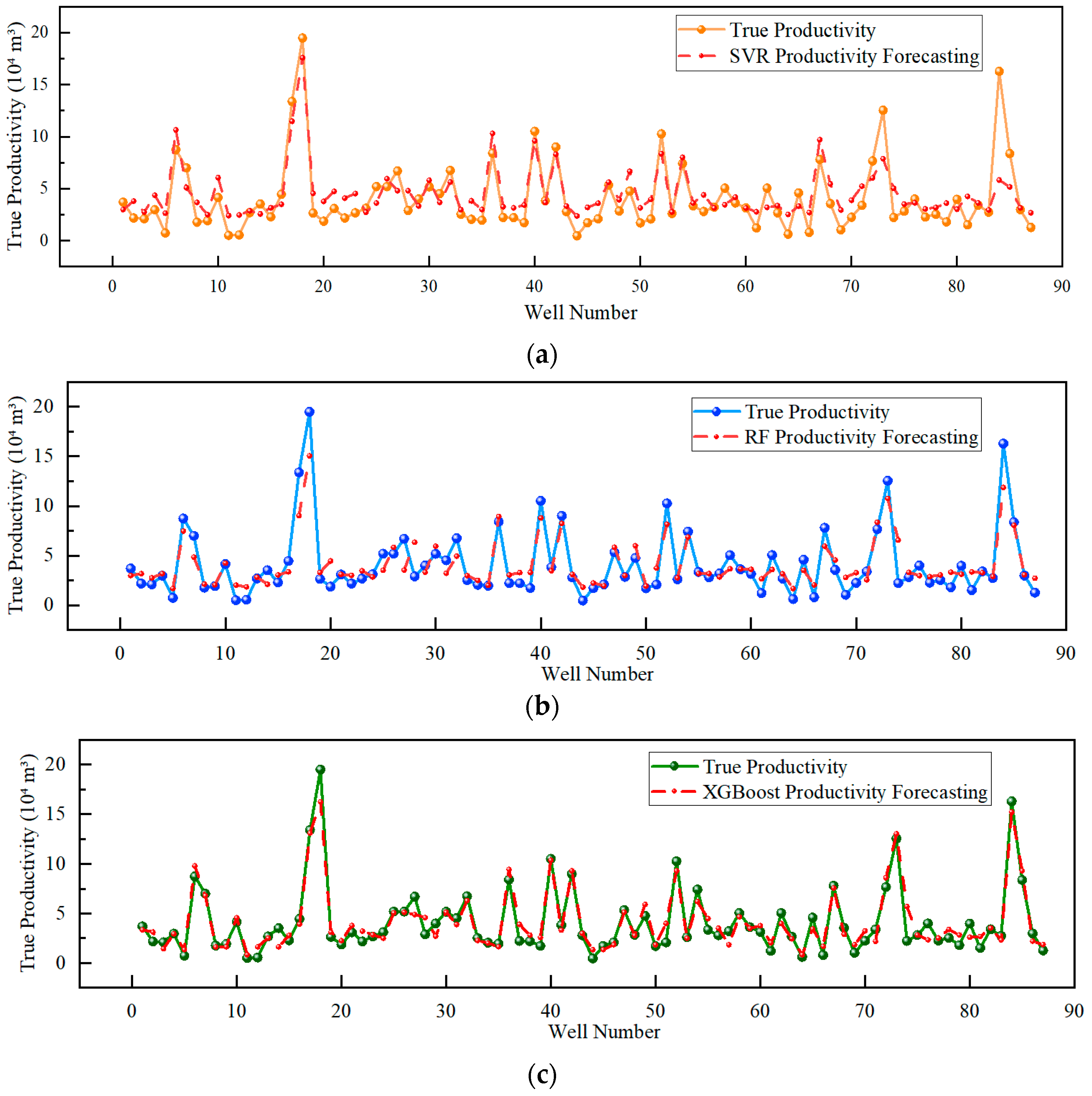
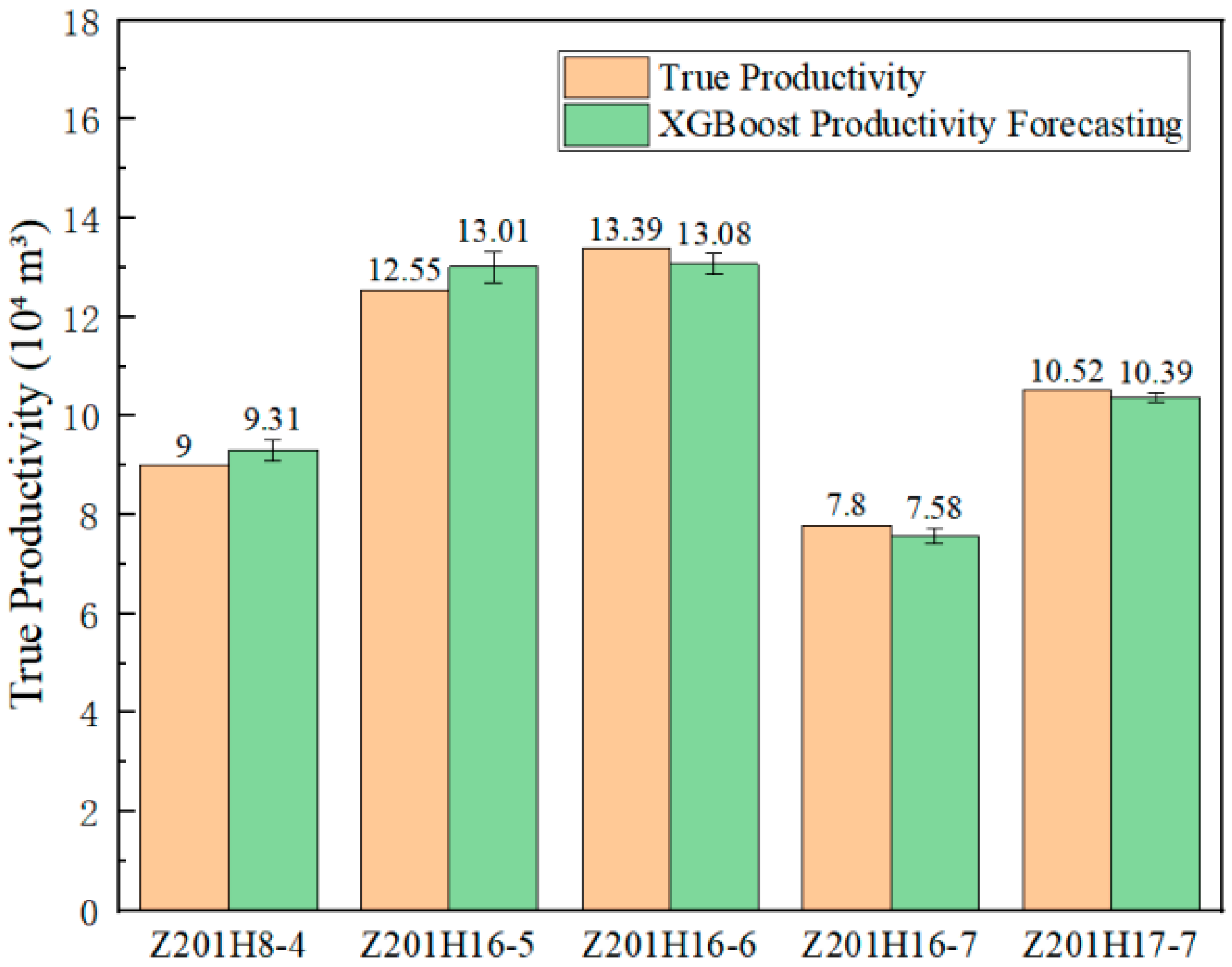
3.3. Model Validation in the Work Zone
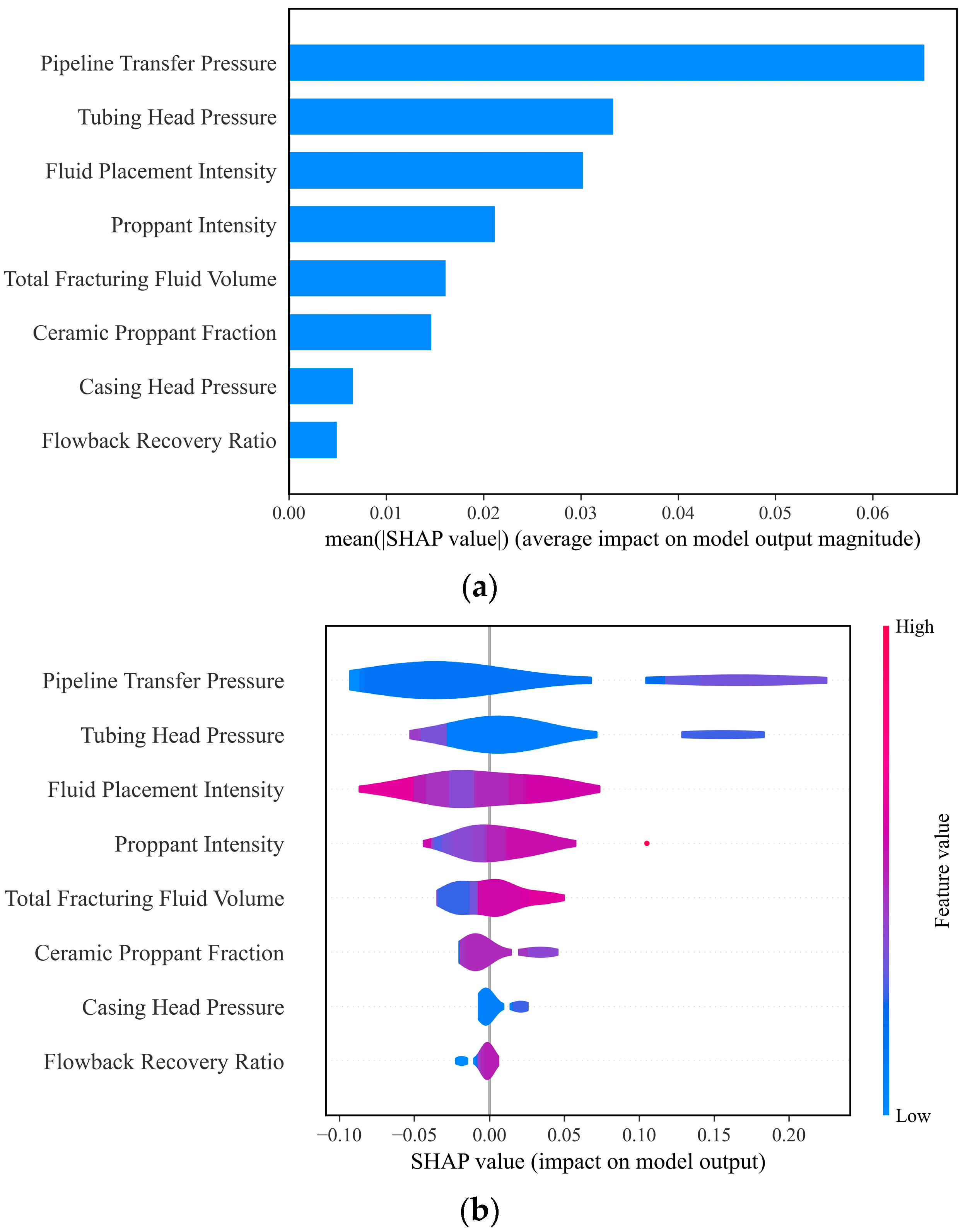
3.4. Analysis Results of the Main Control Factors
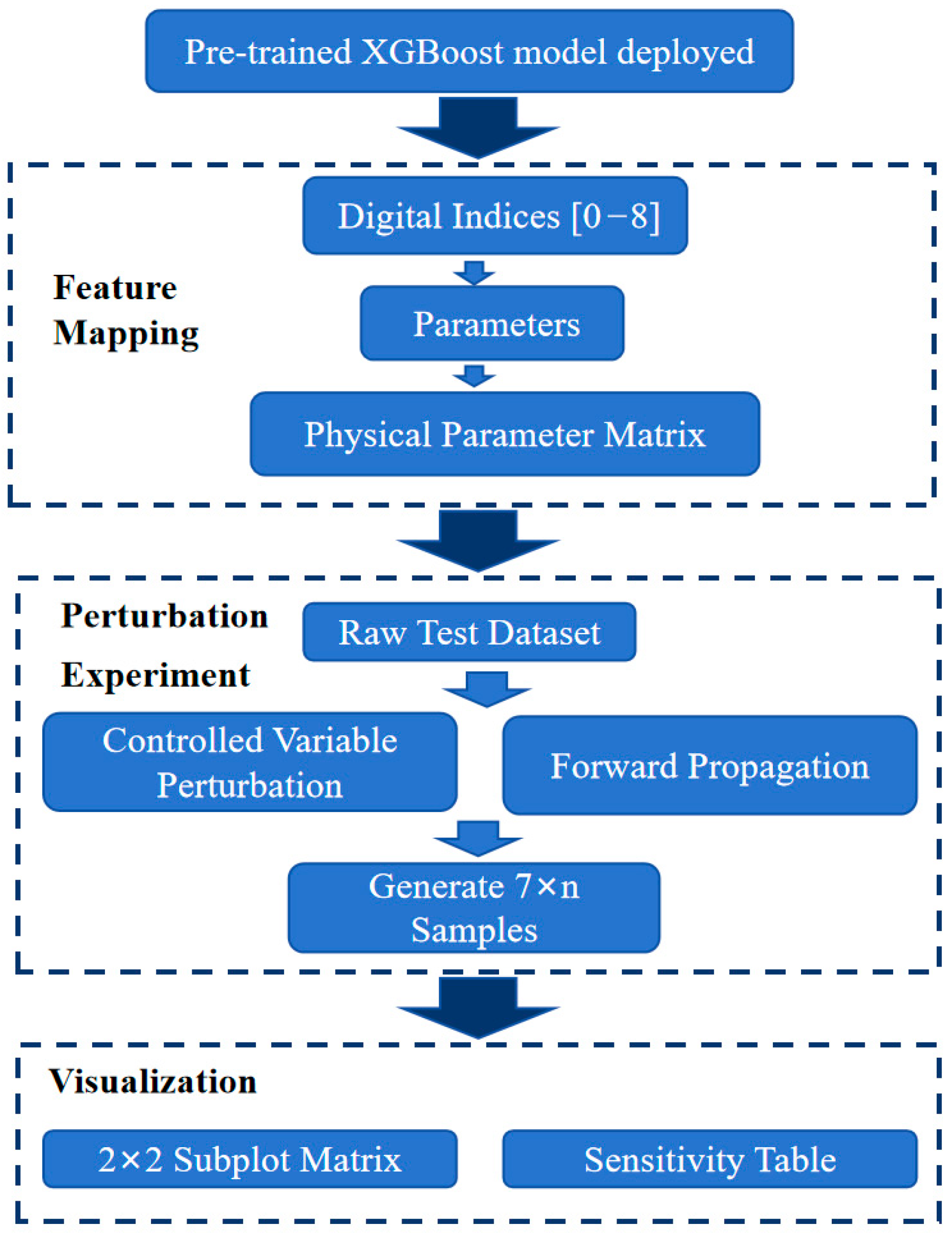
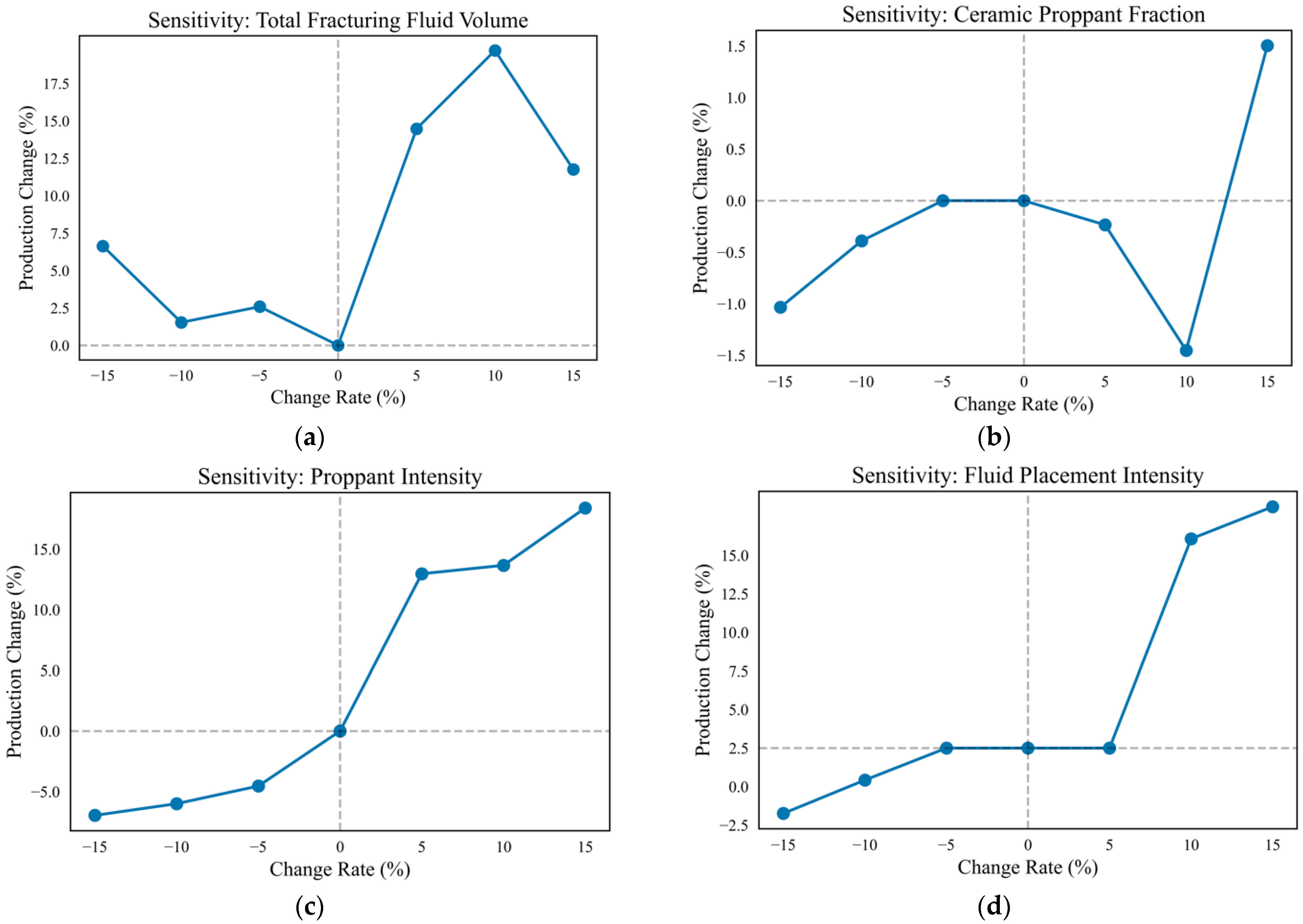
3.5. Parameter Sensitivity Analysis
4. Conclusions
- Through model training, parameter optimization, and cross-validation, this study confirmed XGBoost’s superior performance with a test set R2 of 0.907, representing 12.11% and 131.38% improvements over RF and SVR, respectively. The model achieved significantly lower error metrics: RMSE (0.06393) decreased by 30.1% vs. RF and 60.8% vs. SVR; MAE (0.05059) decreased by 21.7% and 52.2% compared to RF and SVR; and MSE (0.00409) decreased by 51.1% and 84.6% compared to RF and SVR, demonstrating comprehensive prediction accuracy advantages. The comparative analysis conclusively demonstrated that the XGBoost model significantly outperformed both the Random Forest and Support Vector Machine models, establishing it as the most effective tool for productivity prediction under the studied conditions. The field validation in the Western Chongqing Gas Field maintained productivity prediction errors consistently below 5%, fulfilling real-time engineering decision-making requirements.
- Gray relational analysis further confirmed the dominant influence of dynamic parameters like pipeline transfer pressure and average tubing head pressure on productivity. Global sensitivity analysis via SHAP interpretability revealed pressure parameters as primary drivers (|mean SHAP| ≈ 0.045), significantly outperforming ceramic proppant fraction (|mean SHAP| ≈ 0.025). Mechanistically, elevated ceramic proppant fraction moderately enhanced productivity but remained weaker than pressure effects; proppant intensity exhibited threshold behavior requiring avoidance of low-value negative-impact zones; and fluid placement intensity showed diminishing marginal returns at high values. Consequently, engineering optimization should prioritize pressure parameter adjustment, target optimal proppant intensity thresholds, and treat ceramic proppant fraction as a secondary adjustment parameter.
- Based on the test set well group sensitivity analysis, total fracturing fluid volume and proppant intensity were identified as strongly elastic parameters (|E| > 0.5), requiring priority optimization within the economic range (+5%~+10%). Weakly elastic parameters like ceramic proppant fraction (|E| < 0.3) should undergo narrow-window control (−3%~+2%) for cost efficiency. This establishes a tiered control strategy for deep shale gas development in the Western Chongqing Block: the primary focus should be on economically optimizing strongly elastic parameters, followed by the secondary stabilization of weakly elastic parameters. The model enables well-specific customization, allowing future sensitivity analyses and parameter optimization designs for individual wells in the block. It is important to note that the present sensitivity analysis evaluates the impact of varying one parameter while holding the others constant. Future work could employ more advanced global sensitivity analysis techniques (e.g., Sobol indices) to explore interaction effects between parameters and to identify the most influential parameter combinations under different geological and operational scenarios.
- This study establishes an interpretable ML framework that delivers robust predictions of key shale gas development indicators for the Western Chongqing Block. The model’s primary immediate application is in field-scale development planning, providing data-driven guidance on overall stimulation design and well spacing based on global sensitivity analysis. The practical guidelines outlined in Section 3.5 provide a clear pathway for deploying this methodology elsewhere, emphasizing the necessity of local calibration. A critical finding is that, while the current model offers block-level optimization advice, the transition to single-well customized optimization presents a compelling frontier. Our future research will therefore focus on adapting this framework to generate well-specific sensitivity analyses, ultimately moving towards a truly digital twin solution for shale gas development that can provide tailored engineering recommendations for every individual well.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, W.; Zhu, J.; Wang, H.; Kong, D. Transport Diffusion Behaviors and Mechanisms of CO2/CH4 in Shale Nanopores: Insights from Molecular Dynamics Simulations. Energy Fuels 2022, 36, 11903–11912. [Google Scholar] [CrossRef]
- Zhao, Y.-L.; Li, N.-Y.; Zhang, L.-H.; Zhang, R.-H. Productivity analysis of a fractured horizontal well in a shale gas reservoir based on discrete fracture network model. J. Hydrodyn. 2019, 31, 552–561. [Google Scholar] [CrossRef]
- Luo, G.; Tian, Y.; Bychina, M.; Ehlig-Economides, C. Production Optimization Using Machine Learning in Bakken Shale. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018; OnePetro: Houston, TX, USA, 2018; p. URTEC-2902505-MS. [Google Scholar]
- Wang, K.; Li, H.; Wang, J.; Jiang, B.; Bu, C.; Zhang, Q.; Luo, W. Predicting Production and Estimated Ultimate Recoveries for Shale Gas Wells: A New Methodology Approach. Appl. Energy 2017, 206, 1416–1431. [Google Scholar] [CrossRef]
- Fang, X.; Yue, X.; An, W.; Feng, X. Experimental Study of Gas Flow Characteristics in Micro-/Nano-Pores in Tight and Shale Reservoirs Using Microtubes under High Pressure and Low Pressure Gradients. Microfluid. Nanofluid. 2019, 23, 5. [Google Scholar] [CrossRef]
- Pang, W.; Du, J.; Zhang, T. Production Data Analysis of Shale Gas Wells with Abrupt Gas Rate or Pressure Changes. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 15–21 March 2019; p. D041S046R001. [Google Scholar]
- Zhou, Y.; Gu, Z.; He, C.; Yang, B.; Xiong, J. Analysis of Influencing Factors on Shale Gas Well Productivity based on Random Forest. Int. J. Energy 2025, 6, 37–46. [Google Scholar] [CrossRef]
- Wang, M.; He, J.; Liu, S.; Zeng, C.; Jia, S.; Nie, Z.; Zhang, C. Effect of sedimentary facies characteristics on deep shale gas desserts: A case from the Longmaxi Formation, South Sichuan Basin, China. Minerals 2023, 13, 476. [Google Scholar] [CrossRef]
- Li, J.; Zeng, X.; Lian, C.; Lin, H.; Liu, S.; Lei, F.; Wan, Y. Research on the comprehensive dessert evaluation method in shale oil reservoirs based on fractal characteristics of conventional logging curves. Sci. Rep. 2025, 15, 9318. [Google Scholar] [CrossRef]
- Jiang, M.; Peng, C.; Wu, J.; Wang, Z.; Liu, Y.; Zhao, B.; Zhang, Y. A New Approach to a Fracturing Sweet Spot Evaluation Method Based on Combined Weight Coefficient Method—A Case Study in the BZ Oilfield, China. Processes 2024, 12, 1830. [Google Scholar] [CrossRef]
- Liu, S.; Wang, M.; Cheng, Y.; Yu, X.; Duan, X.; Kang, Z.; Xiong, Y. Fractal insights into permeability control by pore structure in tight sandstone reservoirs, Heshui area, Ordos Basin. Open Geosci. 2025, 17, 20250791. [Google Scholar] [CrossRef]
- Stalgorova, E.; Mattar, L. Analytical Model for History Matching and Forecasting Production in Multifrac Composite Systems. In Proceedings of the SPE Canada Unconventional Resources Conference, Calgary, AL, Canada, 30 October–1 November 2012; p. SPE-162516-MS. [Google Scholar]
- Du, F.; Huang, J.; Chai, Z.; Killough, J. Effect of Vertical Heterogeneity and Nano-Confinement on the Recovery Performance of Oil-Rich Shale Reservoir. Fuel 2020, 267, 117199. [Google Scholar] [CrossRef]
- Huang, S.; Ding, G.; Wu, Y.; Huang, H.; Lan, X.; Zhang, J. A Semi-Analytical Model to Evaluate Productivity of Shale Gas Wells with Complex Fracture Networks. J. Nat. Gas Sci. Eng. 2018, 50, 374–383. [Google Scholar] [CrossRef]
- Lin, X.; Floudas, C.A. A Novel Continuous-Time Modeling and Optimization Framework for Well Platform Planning Problems. Optim. Eng. 2003, 4, 65–95. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Meng, M.; Zhao, C. Application of Support Vector Machines to a Small-Sample Prediction. Adv. Pet. Explor. Dev. 2015, 10, 72–75. [Google Scholar] [CrossRef]
- Hui, G.; Chen, S.; He, Y.; Wang, H.; Gu, F. Machine Learning-Based Production Forecast for Shale Gas in Unconventional Reservoirs via Integration of Geological and Operational Factors. J. Nat. Gas Sci. Eng. 2021, 94, 104045. [Google Scholar] [CrossRef]
- Song, L.; Wang, C.; Lu, C.; Yang, S.; Tan, C.; Zhang, X. Machine Learning Model of Oilfield Productivity Prediction and Performance Evaluation. J. Phys. Conf. Ser. 2023, 2468, 012084. [Google Scholar] [CrossRef]
- Rahmanifard, H.; Gates, I.D. Innovative integrated workflow for data-driven production forecasting and well completion optimization: A Montney Formation case study. Geoenergy Sci. Eng. 2024, 238, 212899. [Google Scholar] [CrossRef]
- Guan, W.; Peng, X.; Zhu, S.; Yang, C.; Peng, Z.; Ma, X. Research on productivity prediction method of infilling well based on improved LSTM neural network: A case study of the middle-deep shale gas in South Sichuan. Pet. Reserv. Eval. Dev. 2025, 15, 479–487. [Google Scholar] [CrossRef]
- Wang, S.; Chen, S. Insights to fracture stimulation design in unconventional reservoirs based on machine learning modeling. J. Pet. Sci. Eng. 2019, 174, 682–695. [Google Scholar] [CrossRef]
- Zhou, X.; Ran, Q. Production prediction based on ASGA-XGBoost in shale gas reservoir. Energy Explor. Exploit. 2024, 42, 462–475. [Google Scholar] [CrossRef]
- Guevara, J.; Zadrozny, B.; Buoro, A.; Tolle, J.; Limbeck, J.; Wu, M.; Hohl, D. An Interpretable Machine Learning Methodology for Well Data Integration and Sweet Spotting Identification; NIPS 2018 Workshop Book; HAL: Montreal, QC, Canada, 2018; p. Hal-02199055. [Google Scholar]
- Liu, H.-H.; Zhang, J.; Liang, F.; Temizel, C.; Basri, M.A.; Mesdour, R. Incorporation of physics into machine learning for production prediction from unconventional reservoirs: A brief review of the gray-box approach. SPE Reserv. Eval. Eng. 2021, 24, 847–858. [Google Scholar] [CrossRef]
- Castro, M.; Mendes Júnior, P.R.; Soriano-Vargas, A.; de Oliveira Werneck, R.; Gonçalves, M.M.; Filho, L.L.; Moura, R.; Zampieri, M.; Linares, O.; Ferreira, V.; et al. Time series causal relationships discovery through feature importance and ensemble models. Sci. Rep. 2023, 13, 11402. [Google Scholar] [CrossRef]
- Syed, F.I.; Alnaqbi, S.; Muther, T.; Dahaghi, A.K.; Negahban, S. Smart shale gas production performance analysis using machine learning applications. Pet. Res. 2022, 7, 21–31. [Google Scholar] [CrossRef]
- Dong, Y.; Qiu, L.; Lu, C.; Song, L.; Ding, Z.; Yu, Y.; Chen, G. A data-driven model for predicting initial productivity of offshore directional well based on the physical constrained eXtreme gradient boosting (XGBoost) trees. J. Pet. Sci. Eng. 2022, 211, 110176. [Google Scholar] [CrossRef]
- Ma, K.; Wu, C.; Huang, Y.; Mu, P.; Shi, P. Oil well productivity capacity prediction based on support vector machine optimized by improved whale algorithm. J. Pet. Explor. Prod. Technol. 2024, 14, 3251–3260. [Google Scholar] [CrossRef]
- Li, J.-H.; Ji, L. Productivity forecast for multi-stage fracturing in shale gas wells based on a random forest algorithm. Energy Sources Part A Recovery Util. Environ. Eff. 2025, 47, 2834–2843. [Google Scholar] [CrossRef]
- GB/T 41612-2022; Technical Specifications for Shale Gas Well Production Prediction. Standard Press of China: Beijing, China, 2022. (In Chinese)
- NB/T 14024-2017; Technical Specifications for Shale Gas Well Production Prediction. National Energy Administration: Beijing, China, 2017.
- Abbas, K.; Jiahua, C.; Shili, L. Feature selection in finite mixture of sparse normal linear models in high-dimensional feature space. Biostatistics 2011, 12, 156–172. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- King, G.E. Thirty Years of Gas Shale Fracturing: What Have We Learned? SPE Annual Technical Conference and Exhibition. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010; p. SPE-133456-MS. [Google Scholar]
- Wang, X.; Fang, H.; Fang, S. An integrated approach for exploitation block selection of shale gas—Based on cloud model and grey relational analysis. Resour. Policy 2020, 68, 101797. [Google Scholar] [CrossRef]
- Lozng, Z.L.; Wen, Z.T.; Li, H.; Zeng, X. An evaluation method of shale reservoir crushability based on grey correlation analysis. Reserv. Eval. Dev. 2020, 10, 37–42. [Google Scholar] [CrossRef]
- Aili, Q. Grey Relational Analysis on Elderly People’ Life Quality and Sports. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 63–69. [Google Scholar] [CrossRef]
- Xiao, H. Production evaluation method based on grey correlation analysis for shale gas horizontal wells in Weiyuan block. Well Test. 2018, 27, 73–78. [Google Scholar]
- Chen, D.; Tan, Z.; Wu, L.; Xia, L.; Li, H.; Zhao, Y. Method of low-permeability reservoir productivity evaluation while drilling based on grey correlation analysis of logging parameters. Mud Logging Eng. 2025, 36, 34–40+55. [Google Scholar]
- Buchanan, J.W.; Ali, H. Evaluation of Privacy-Preserving Support Vector Machine (SVM) Learning Using Homomorphic Encryption. Cryptography 2025, 9, 33. [Google Scholar] [CrossRef]
- Ignatenko, V.; Surkov, A.; Koltcov, S. Random forests with parametric entropy-based information gains for classification and regression problems. PeerJ. Comput. Sci. 2024, 10, e1775. [Google Scholar] [CrossRef]
- Mohammadian, E.; Kheirollahi, M.; Liu, B.; Ostadhassan, M.; Sabet, M. A case study of petrophysical rock typing and permeability prediction using machine learning in a heterogenous carbonate reservoir in Iran. Sci. Rep. 2022, 12, 4505. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Li, J.; Ma, D.; Wang, Z.; Zhang, J.; Yuan, C.; Feng, Y.; Li, H. Prediction for Rock Compressive Strength Based on Ensemble Learning and Bayesian Optimization. Earth Sci. 2023, 48, 1686–1695. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Oona, R.; Jarmo, T.; Riku, K. Evaluation metrics and statistical tests for machine learning. Sci. Rep. 2024, 14, 6086. [Google Scholar] [PubMed]
- Song, Y.; Zhu, Y.; Zeng, B. Efficient Identification Method of Interbeds Based on Neural Network Combined with Grey Relational Analysis—Taking the Lower Sub-Member of the Sangonghe Formation in Moxizhuang Oilfield as an Example. J. Geosci. Environ. Prot. 2025, 13, 51–68. [Google Scholar] [CrossRef]
- Raheem, O.; Morales, M.M.; Pan, W.; Torres-Verdín, C. Improved estimation of two-phase capillary pressure with nuclear magnetic resonance measurements via machine learning. Artif. Intell. Geosci. 2025, 6, 100144. [Google Scholar] [CrossRef]
- Zhang, T.; Peng, F.; Yan, R.; Tang, X.; Yuan, J.; Deng, R. An uncertainty quantification and accuracy enhancement method for deep regression prediction scenarios. Mech. Syst. Signal Process. 2025, 227, 112394. [Google Scholar] [CrossRef]
- Chen, R.; Liu, X.; Zhou, S.; Zhang, W.; Liu, H.; Yan, D.; Wang, H. Application of machine learning model in shale TOC content prediction based on well log data: Enhancing model interpretability by SHAP. Earth Sci. Inform. 2025, 18, 428. [Google Scholar] [CrossRef]
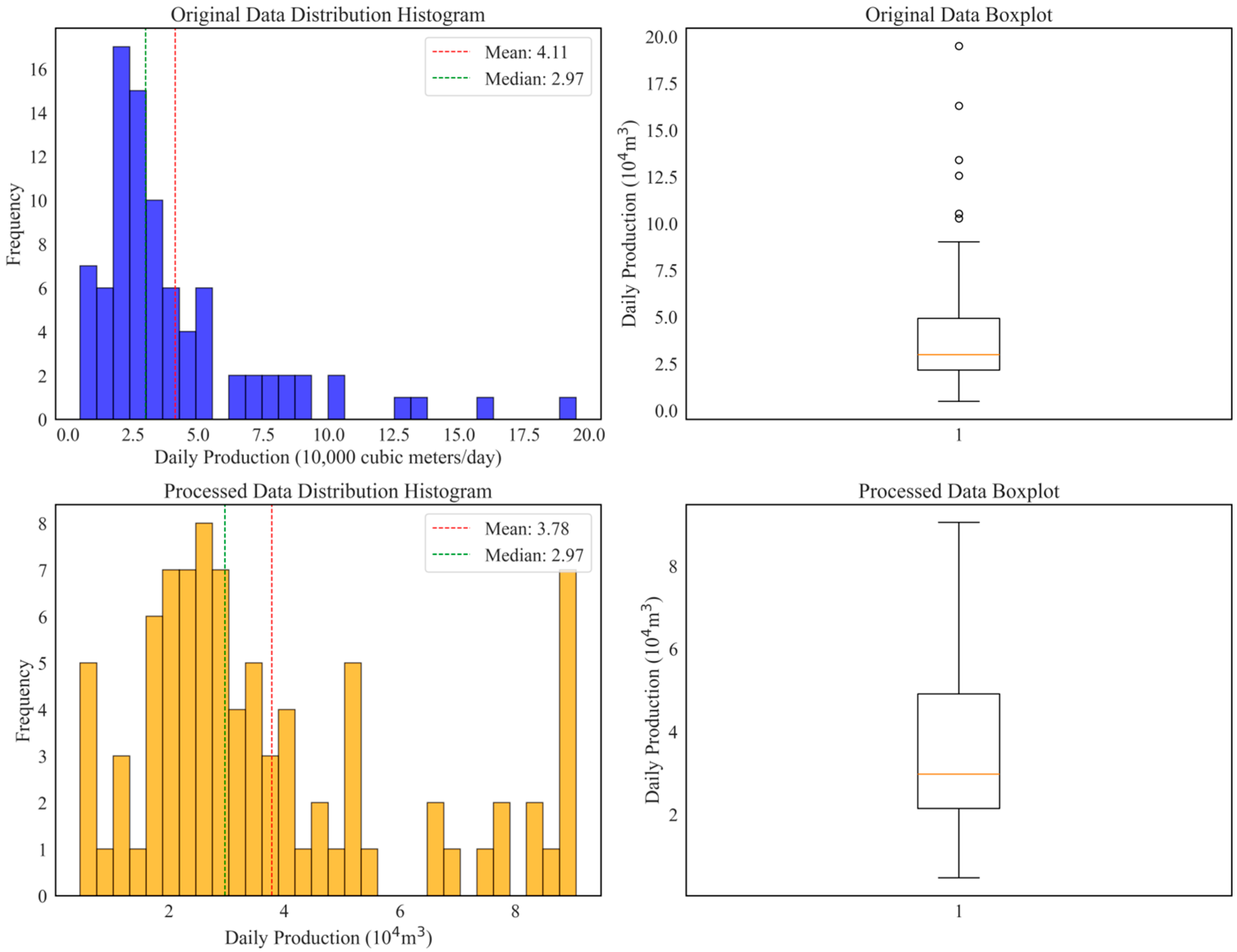
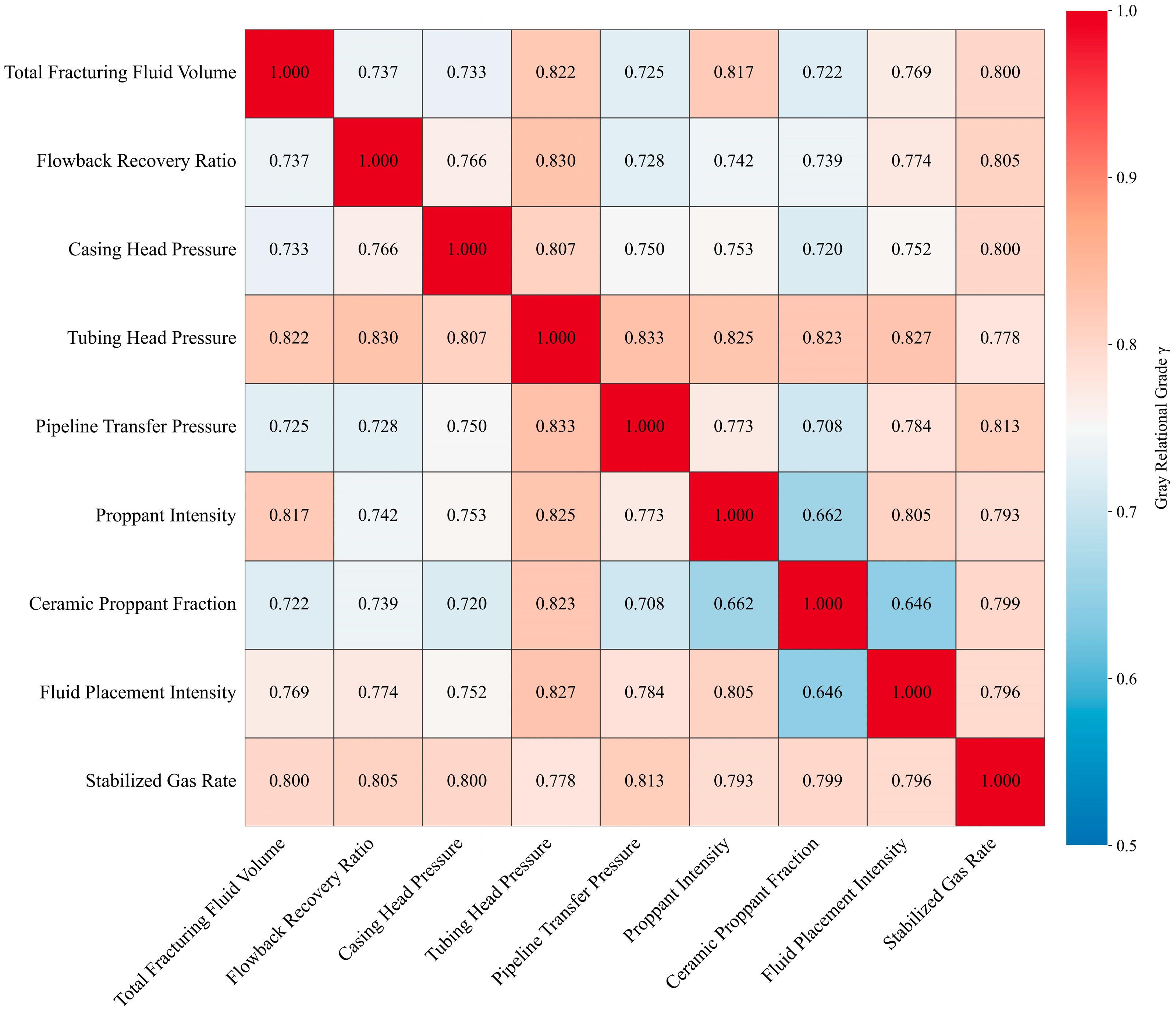
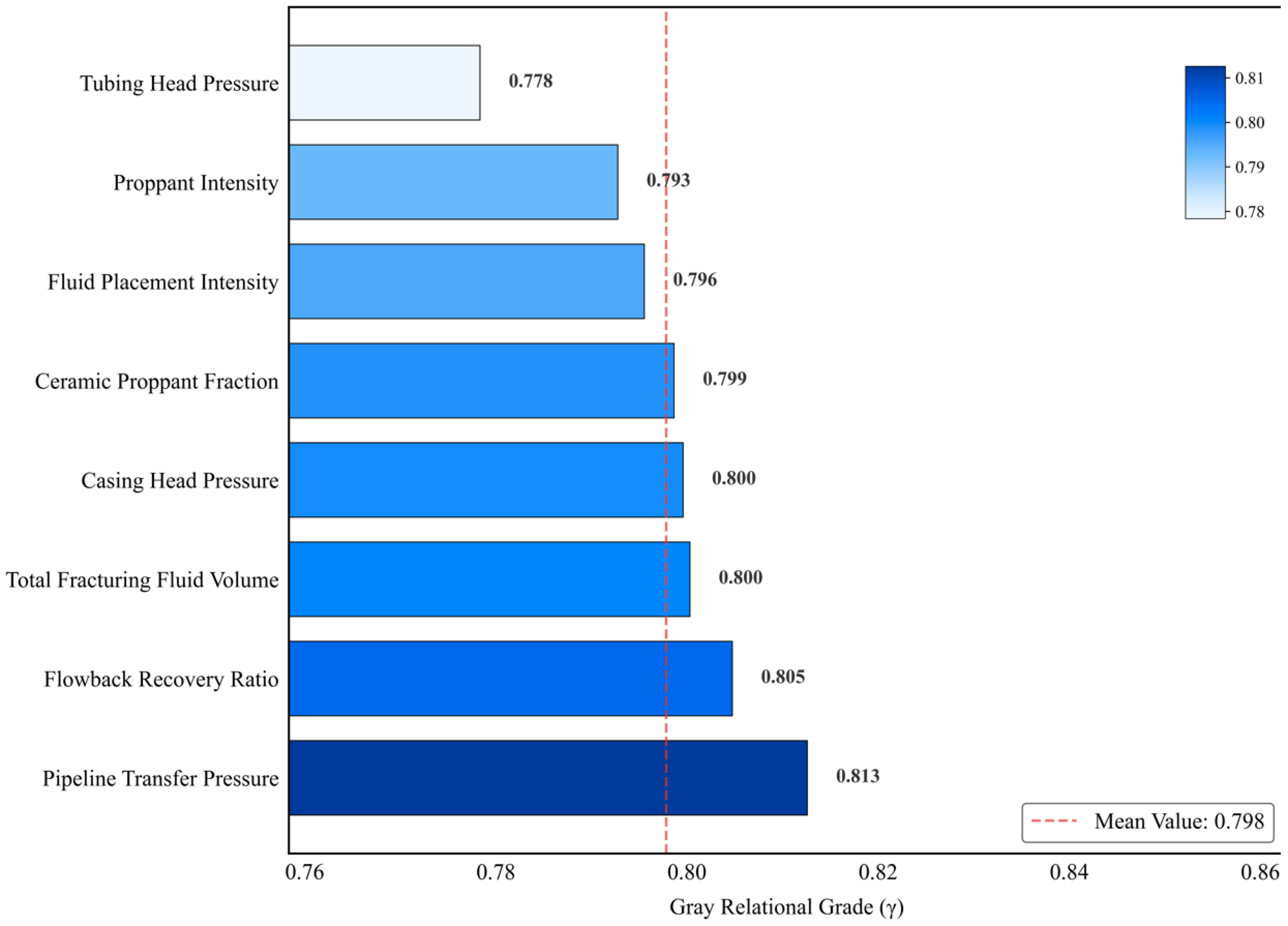





| Feature Name | Physical Significance | Unit |
|---|---|---|
| Proppant Intensity | Proppant injection per unit layer thickness | t/m |
| Ceramic Proppant Fraction | Mass fraction of ceramic sand in total proppant | % |
| Fluid Placement Intensity | Fracturing fluid injection volume per unit thickness of formation | m3/m |
| Total Fracturing Fluid Volume | Total injection volume of fracturing fluid in a single well | m3 |
| Flowback Recovery Ratio | Percentage of fracturing fluid returned to the wellhead | % |
| Casing Head Pressure | Production casing head pressure | MPa |
| Tubing Head Pressure | Tubing head pressure | MPa |
| Pipeline Transfer Pressure | Input pressure | MPa |
| Stabilized Gas Rate | Stabilized daily gas production | 104 m3/d |
| Selected Parameters | Average Missing Rate |
|---|---|
| Eight engineering production parameters | 4.5% |
| Porosity, brittleness index, total organic carbon, Poisson’s ratio | 26.7% |
| Model | Key Parameters | Values | Basis of Tuning Parameter |
|---|---|---|---|
| SVR | Kernel Type | “rbf” (Radial Basis Function) | Captures complex, nonlinear relationships between features and the target variable without the need for manual feature transformation. |
| Regularization Parameter (C) | 5 | Determines the trade-off between achieving a low error on the training data and minimizing the model’s complexity. A moderate value of 5 was chosen to prevent overfitting (which a very high C would cause) while still allowing the model to capture the underlying nonlinear trends (which a very low C would suppress). | |
| Kernel Coefficient (gamma) | 3 | Defines the influence range of a single training example. A relatively high value of 3 means the influence of each example is more localized, leading to a more complex, finer-grained decision boundary. This value was optimized to capture the intricate patterns in the shale gas productivity data without excessive smoothing. |
| Model | Key Parameters | Values | Basis of Tuning Parameter |
|---|---|---|---|
| RF | Number of trees (n_estimators) | 300 | Ensures model stability and predictive accuracy; beyond this point, performance plateaus (convergence) |
| Splitting criterion (criterion) | “squared_error” | Minimizes mean squared error (MSE), which is optimal for regression tasks and directly reduces prediction variance | |
| Maximum depth (max_depth) | 3 | Strongly regularizes the model by creating simple, interpretable trees and effectively prevents overfitting on limited data | |
| Minimum samples for split (min_samples_split) | 2 | Allows trees to grow to their maximum potential depth under the max_depth constraint, learning as much detail as the depth allows | |
| Minimum samples in leaf (min_samples_leaf) | 1 | Works in conjunction with max_depth to control overfitting; a value of 1 allows for fine-grained predictions within the depth limit | |
| Number of features for split (max_features) | “sqrt” | Introduces randomness in tree building using a subset of features (√(n_features)) for each split, improving model diversity and generalization | |
| Bootstrap sampling (bootstrap) | True | Trains each tree on a different random subset of the data (with replacement), significantly enhancing the ensemble’s robustness and stability |
| Model | Key Parameters | Values | Basis of Tuning Parameter |
|---|---|---|---|
| XGBoost | Number of Trees (n_estimators) | 1500 | Iterative saturation point of residuals. |
| Maximum Depth (max_depth) | 5 | Suppresses overfitting by limiting tree complexity for small sample sizes. | |
| Learning Rate | 0.8 | Balances convergence speed and final model accuracy. | |
| L2 Regularization (reg_lambda) | 1.6 | Constrains leaf node weights to improve generalization and prevent overfitting. | |
| L1 Regularization (reg_alpha) | 0.2 | Encourages sparsity and performs feature selection by shrinking less important feature weights to zero. | |
| Minimum Child Weight (min_child_weight) | 1 | Sets the minimum sum of instance weight needed in a child node, controlling tree growth in sparse data. | |
| Gamma | 0.005 | The minimum loss reduction required to make a further partition on a leaf node. A higher value makes the algorithm more conservative, preventing overfitting. | |
| Subsample Ratio (subsample) | 0.75 | The fraction of samples used for fitting individual trees. Introduces randomness to improve model robustness and generalization. | |
| Column Subsample Ratio (colsample_bytree) | 0.7 | The fraction of features used to build each tree. Enhances diversity among trees and helps prevent overfitting. | |
| Number of Trees (n_estimators) | 1500 | Iterative saturation points of residuals. | |
| Maximum Depth (max_depth) | 5 | Suppresses overfitting by limiting tree complexity for small sample sizes. | |
| Learning Rate | 0.8 | Balances convergence speed and final model accuracy. | |
| L2 Regularization (reg_lambda) | 1.6 | Constrains leaf node weights to improve generalization and prevent overfitting. |
| Evaluation Index | RF | SVR | XGBoost | |||
|---|---|---|---|---|---|---|
| Training Set | Testing Set | Training Set | Testing Set | Training Set | Testing Set | |
| RMSE | 0.07313 | 0.09143 | 0.07486 | 0.16316 | 0.04627 | 0.06393 |
| MAE | 0.05476 | 0.06456 | 0.06724 | 0.10579 | 0.03496 | 0.05059 |
| MSE | 0.00535 | 0.00836 | 0.0056 | 0.02662 | 0.00214 | 0.00409 |
| R2 | 0.811 | 0.809 | 0.802 | 0.392 | 0.924 | 0.907 |
| Statistical Metric | XGBoost | Random Forest | SVM |
|---|---|---|---|
| Sample Size (n) | 100 | 100 | 100 |
| Mean (Mean) | 0.5521 | 0.4559 | 0.3652 |
| Standard Deviation (SD) | 0.0779 | 0.1167 | 0.0696 |
| Median (Median) | 0.5543 | 0.4590 | 0.3619 |
| 95% Confidence Interval | [0.5368, 0.5674] | [0.4330, 0.4788] | [0.3515, 0.3789] |
| Parameter | Elasticity | Interpretation |
|---|---|---|
| Total Fracturing Fluid Volume | 0.73 | Highly Elastic |
| Ceramic Proppant Fraction | −0.05 | Inelastic |
| Proppant Intensity | 0.98 | Highly Elastic |
| Fluid Placement Intensity | 0.63 | Highly Elastic |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhao, Y.; Li, Y.; Sun, C.; Chen, W.; Zhang, D. Interpretable Machine Learning for Shale Gas Productivity Prediction: Western Chongqing Block Case Study. Processes 2025, 13, 3279. https://doi.org/10.3390/pr13103279
Zhang H, Zhao Y, Li Y, Sun C, Chen W, Zhang D. Interpretable Machine Learning for Shale Gas Productivity Prediction: Western Chongqing Block Case Study. Processes. 2025; 13(10):3279. https://doi.org/10.3390/pr13103279
Chicago/Turabian StyleZhang, Haijie, Ye Zhao, Yaqi Li, Chaoya Sun, Weiming Chen, and Dongxu Zhang. 2025. "Interpretable Machine Learning for Shale Gas Productivity Prediction: Western Chongqing Block Case Study" Processes 13, no. 10: 3279. https://doi.org/10.3390/pr13103279
APA StyleZhang, H., Zhao, Y., Li, Y., Sun, C., Chen, W., & Zhang, D. (2025). Interpretable Machine Learning for Shale Gas Productivity Prediction: Western Chongqing Block Case Study. Processes, 13(10), 3279. https://doi.org/10.3390/pr13103279






