Heat Extraction Performance Evaluation of Horizontal Wells in Hydrothermal Reservoirs and Multivariate Sensitivity Analysis Based on the XGBoost-SHAP Algorithm
Abstract
1. Introduction
2. Modeling
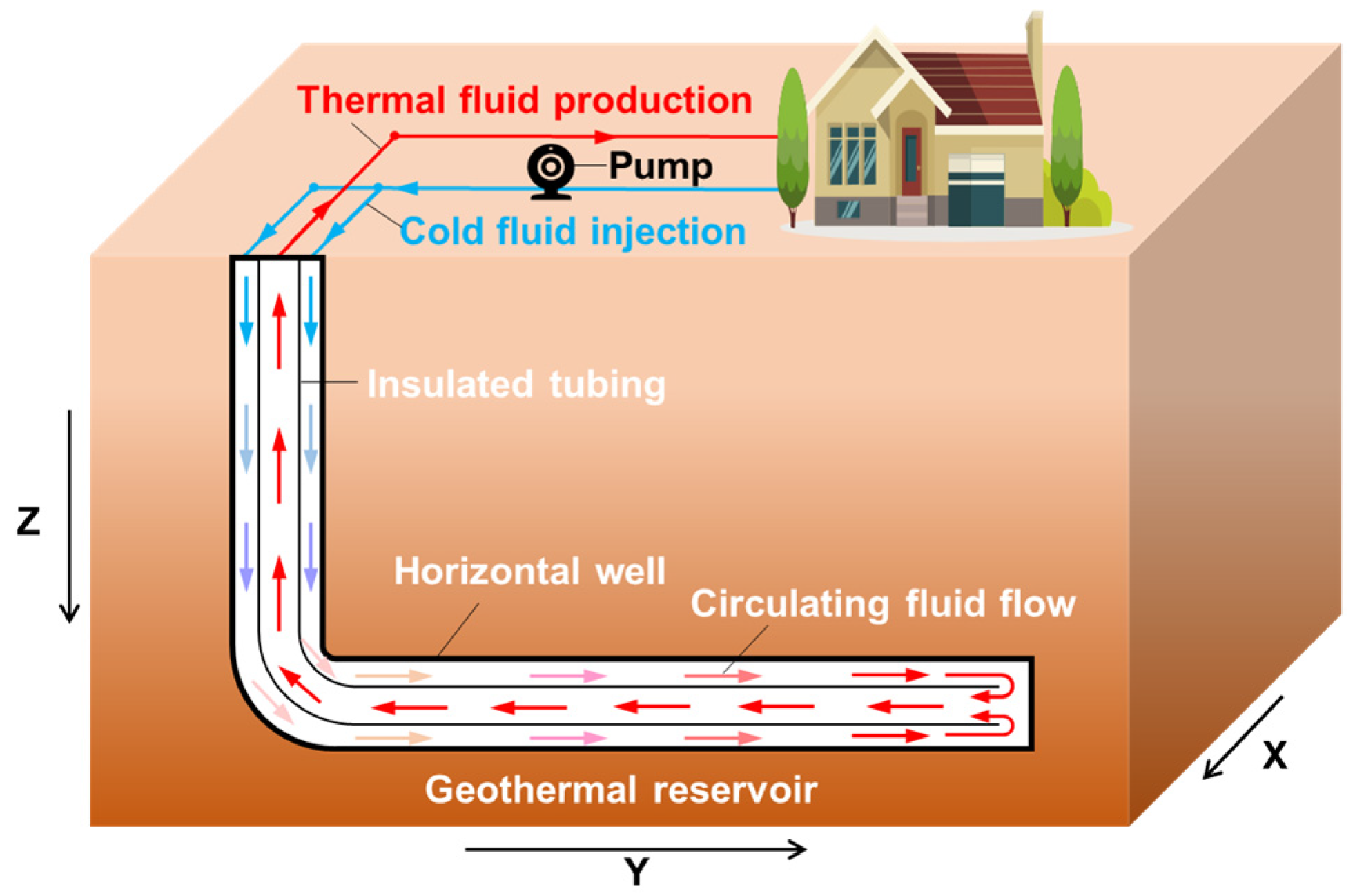
2.1. Conceptual Model
2.2. Mathematical Model
2.3. Numerical Code
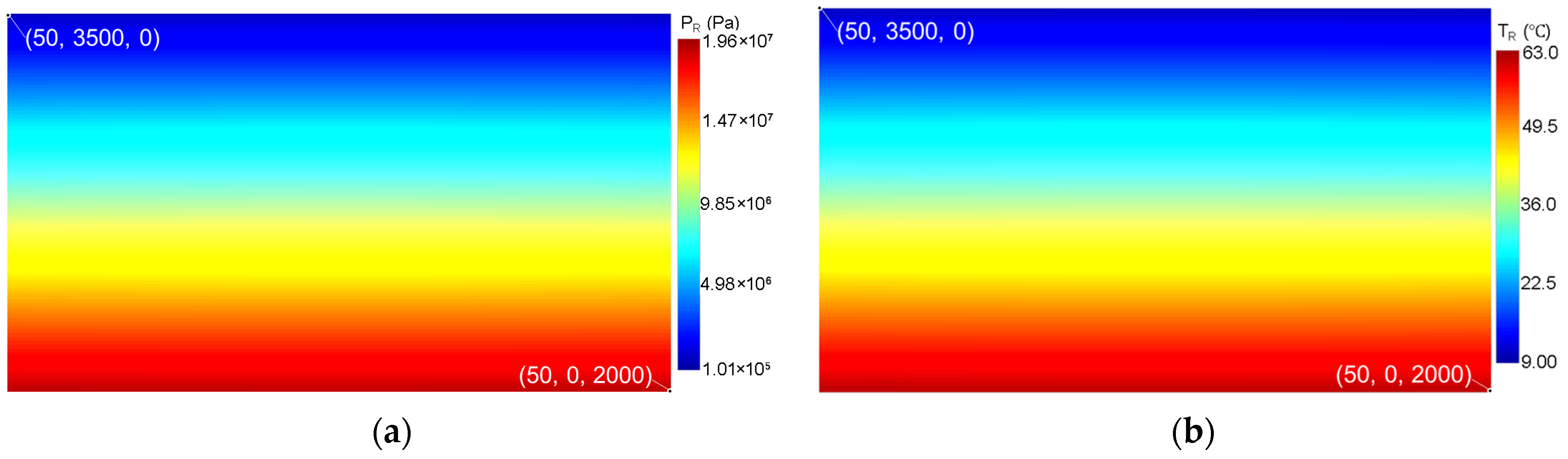
2.4. Initial and Boundary Conditions
2.5. Simulation Scheme
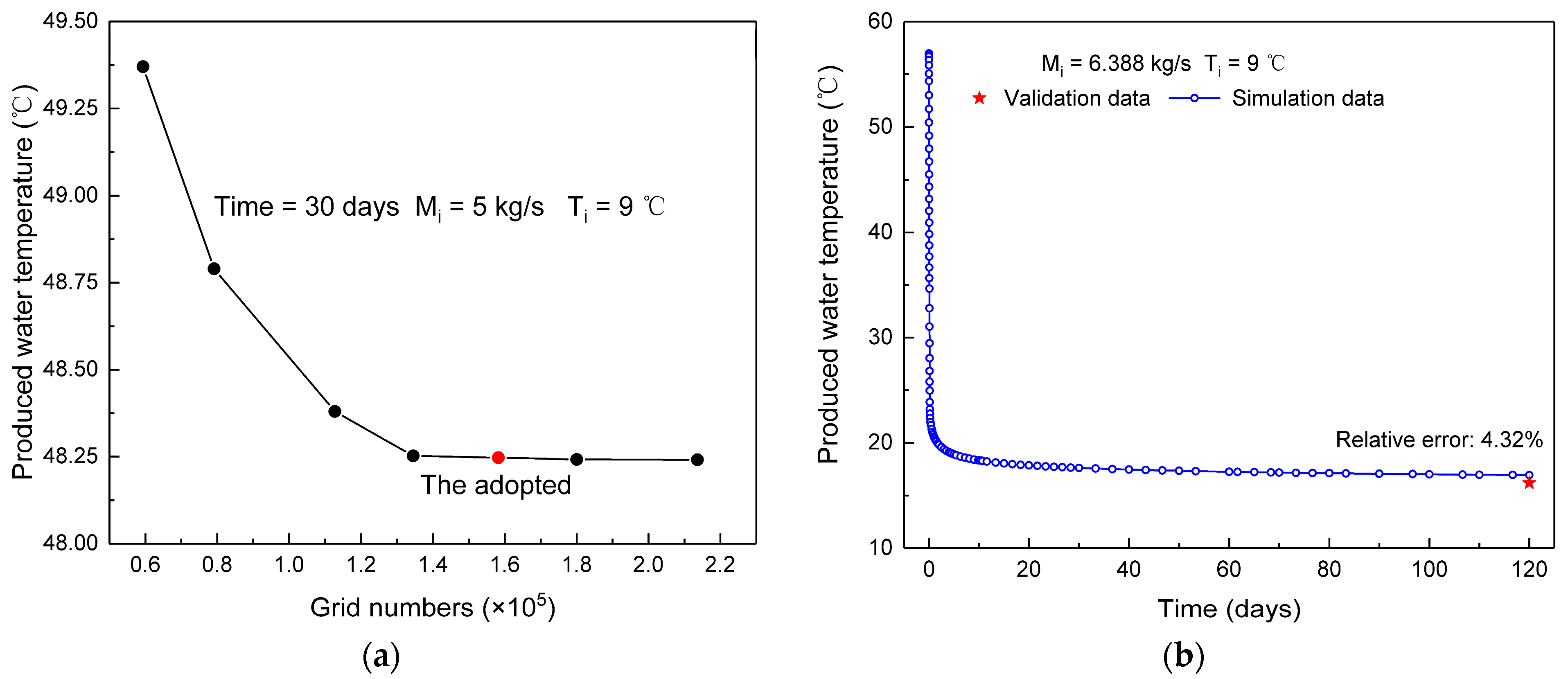
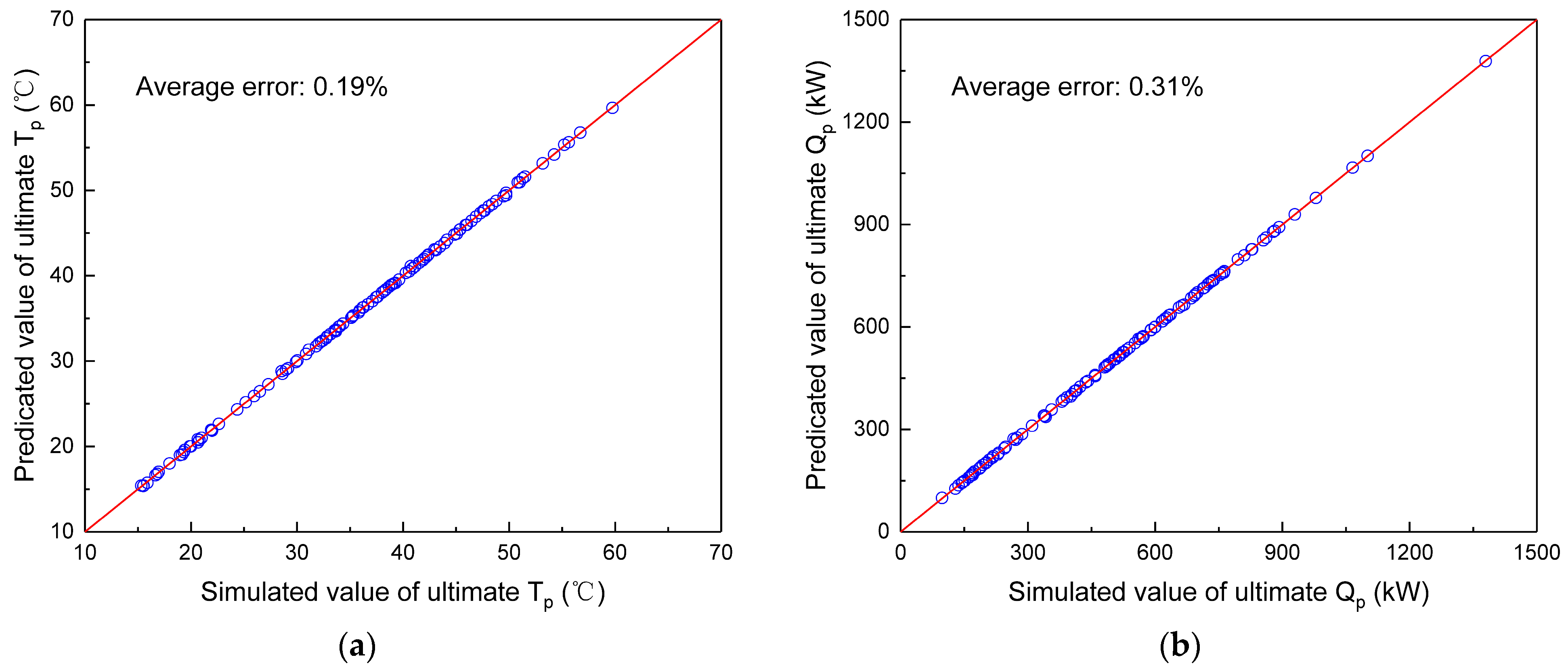
2.6. Mesh Sensitivity Analysis and Model Validation
3. Results
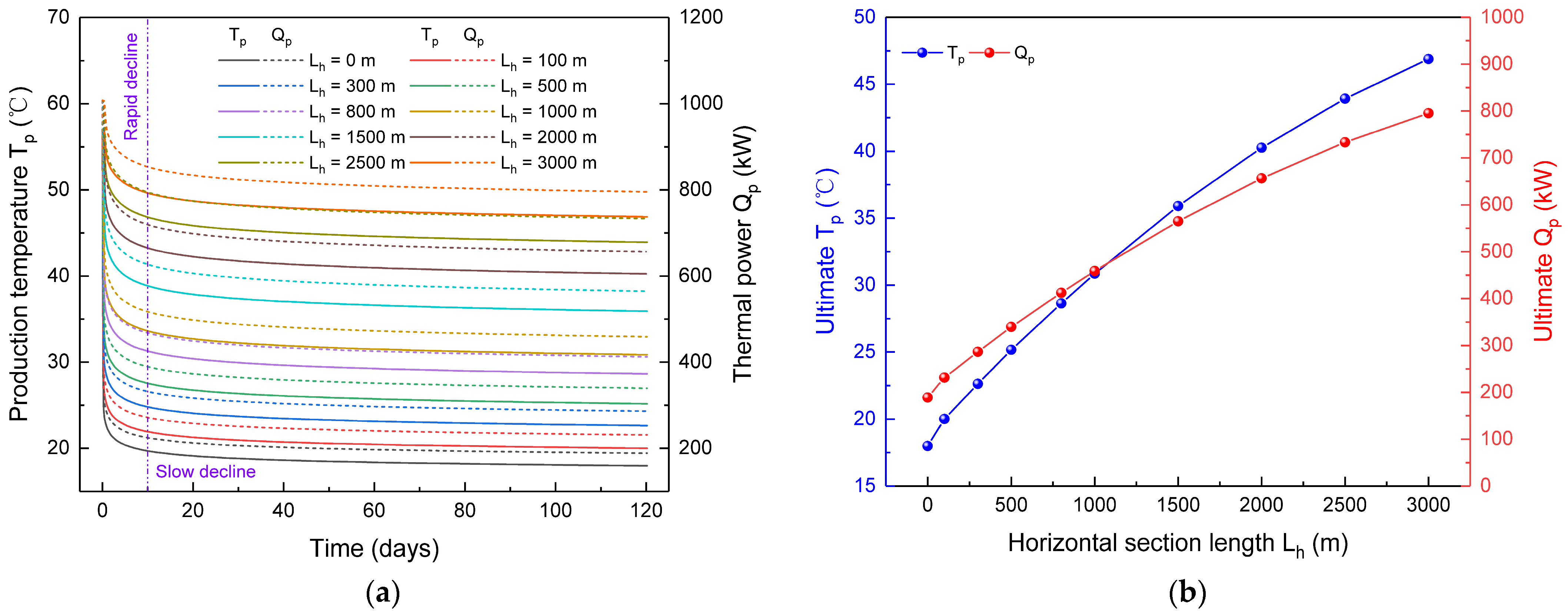
3.1. The Effect of Horizontal Section Length
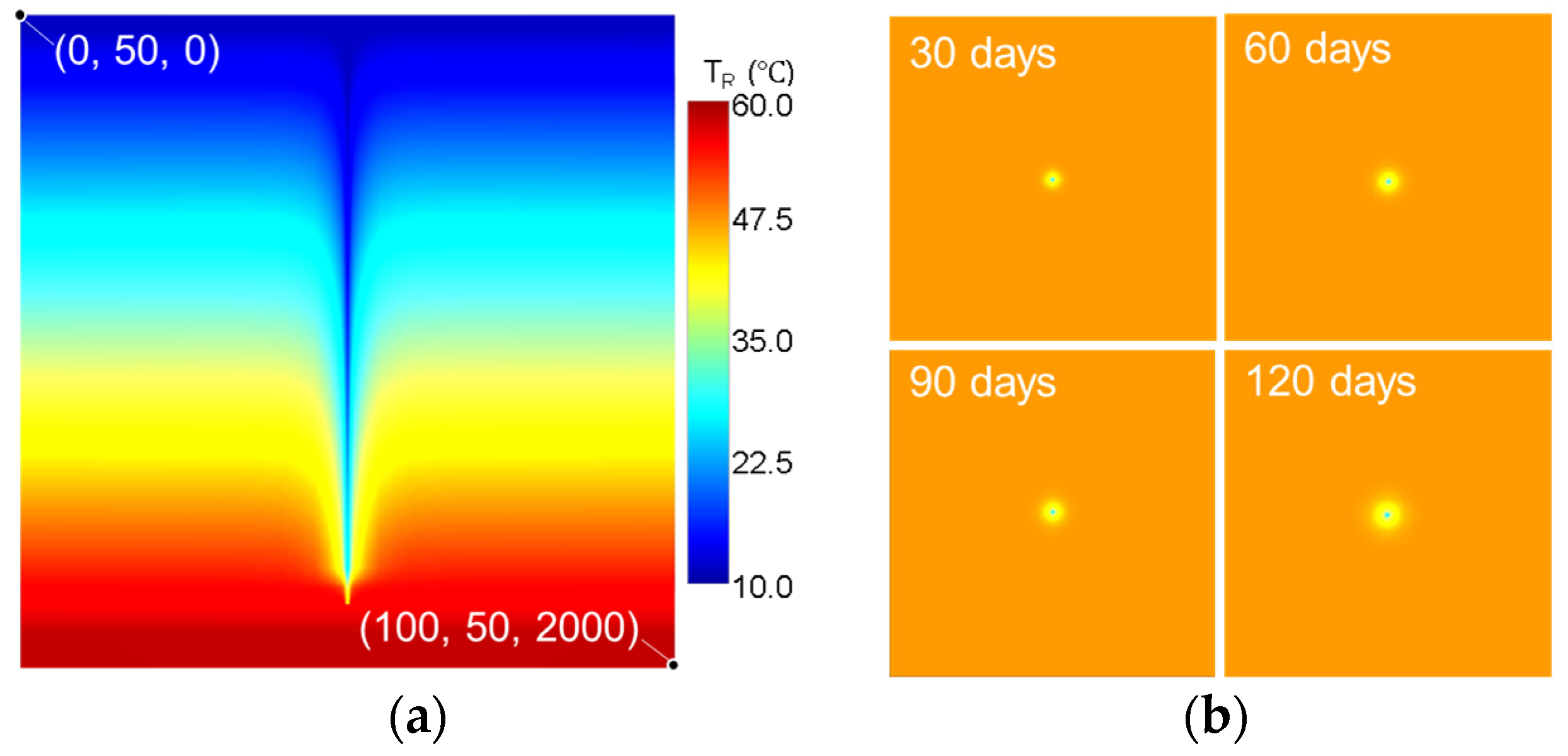
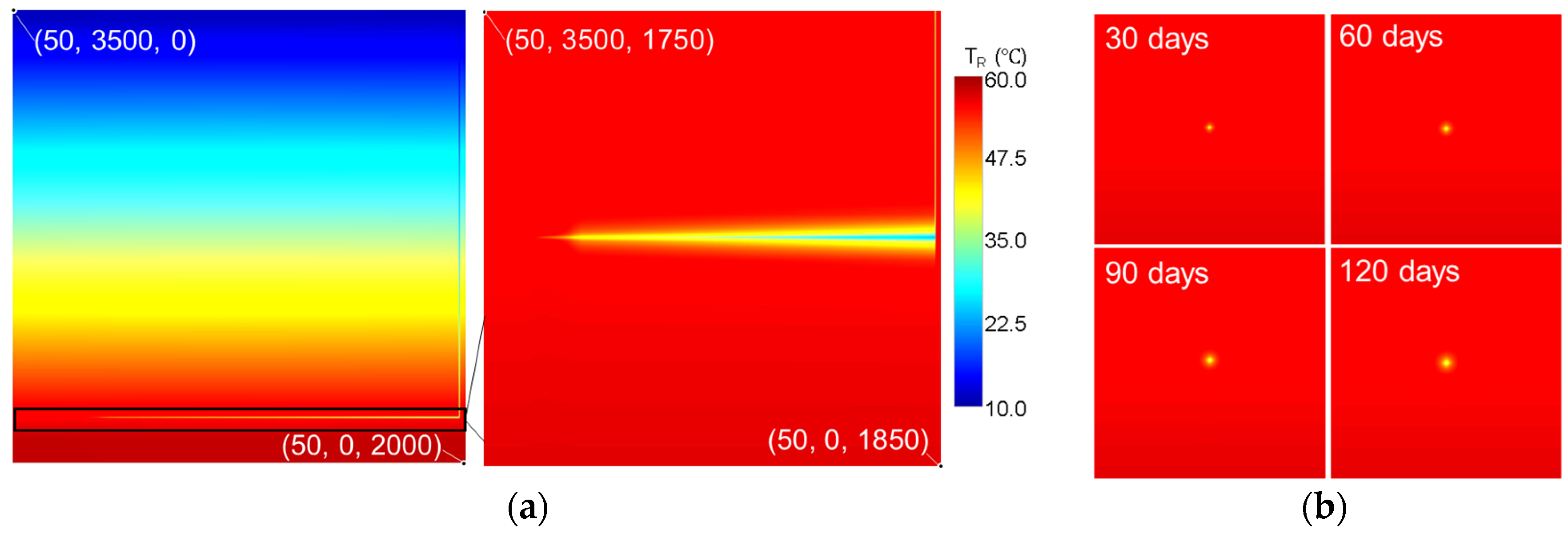
3.1.1. Temperature Field Evolution
3.1.2. Heat Extraction Performance
3.2. The Influence of Injection Rate
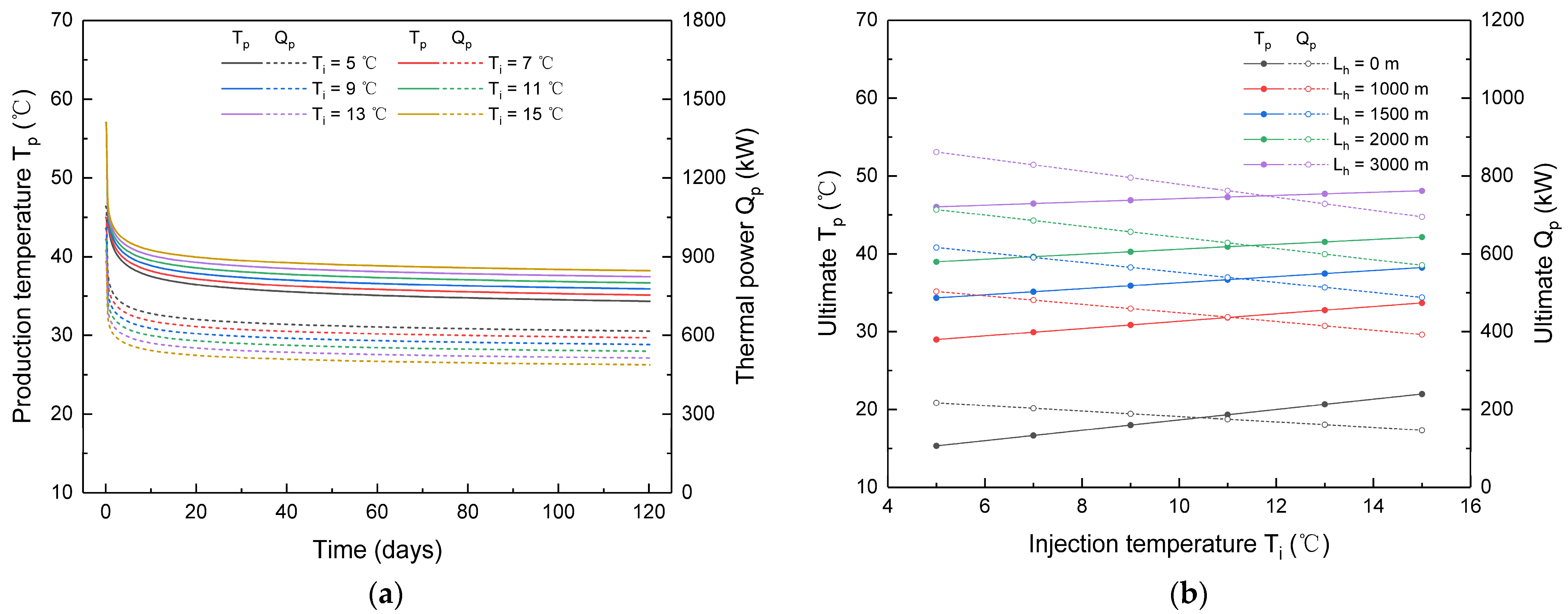
3.3. The Influence of Injection Water Temperature
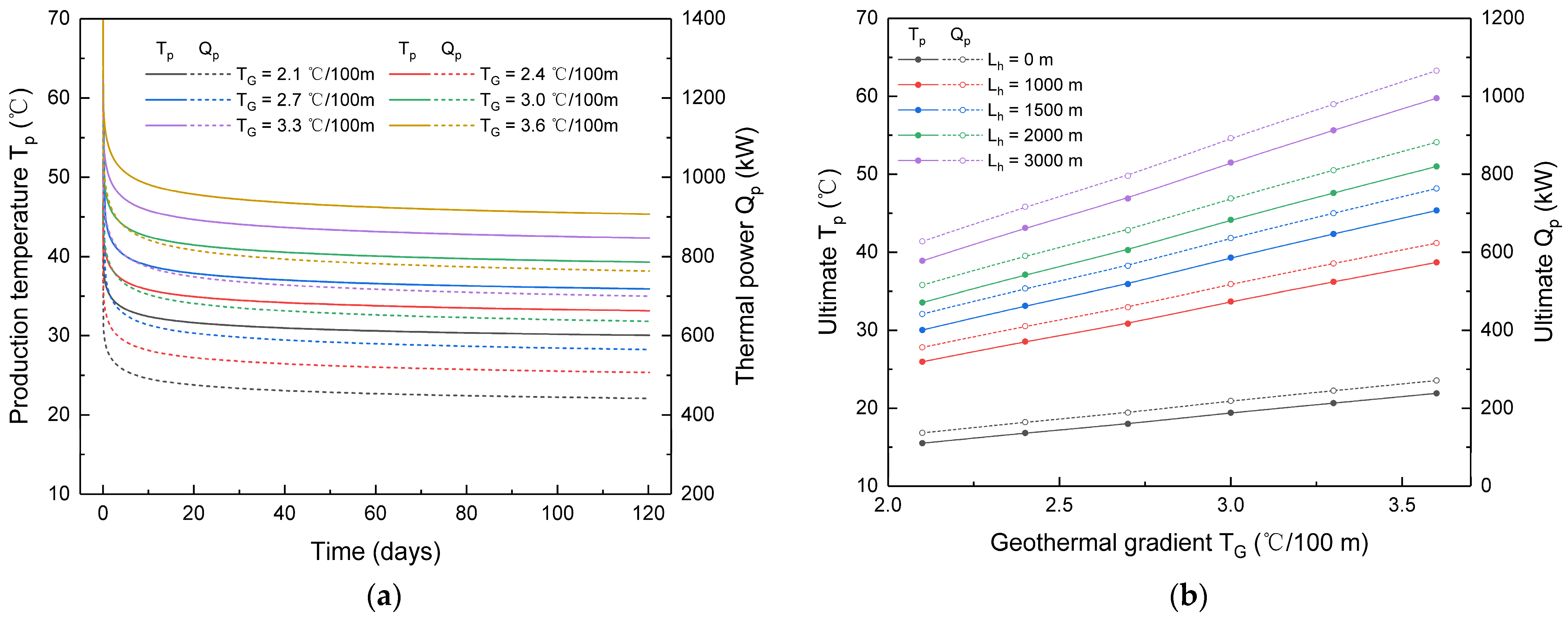
3.4. The Influence of Geothermal Gradient
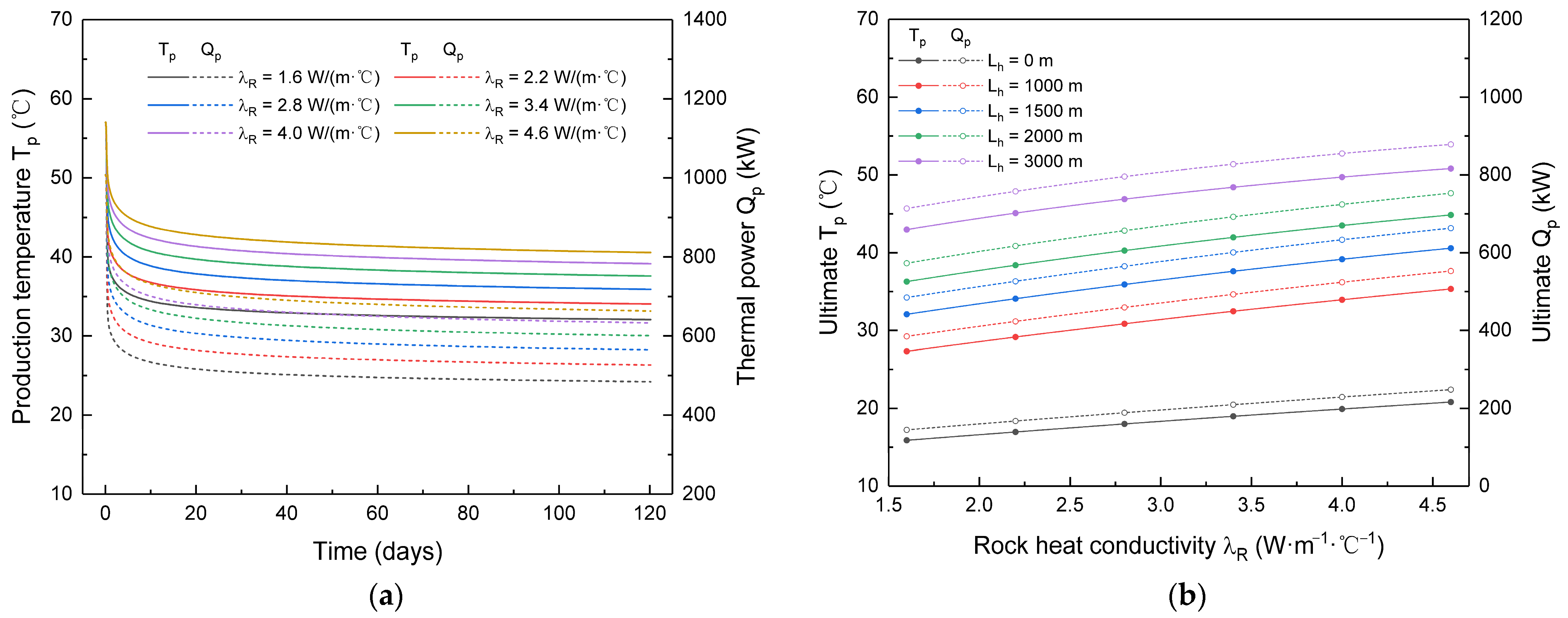
3.5. The Influence of Rock Heat Conductivity
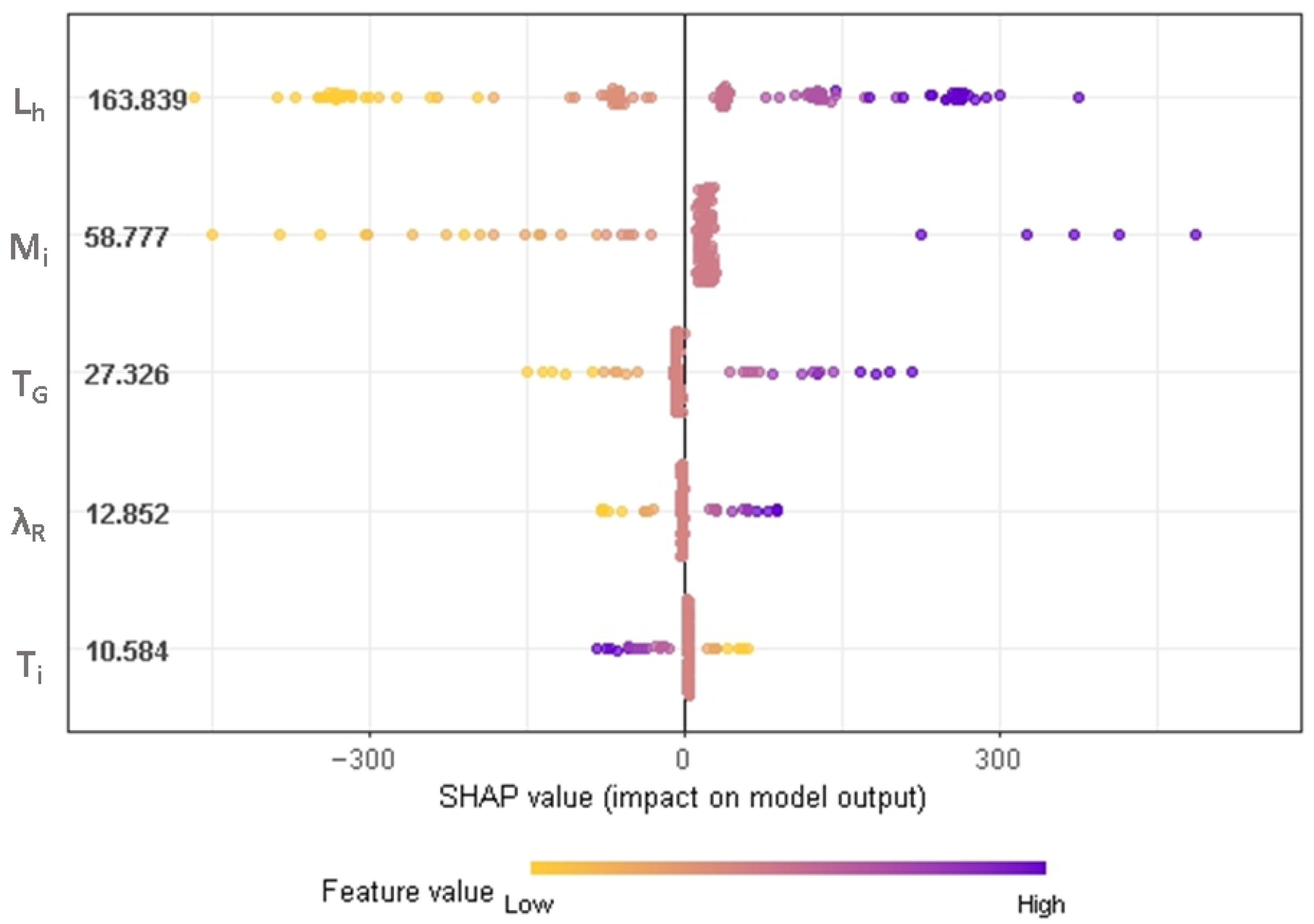
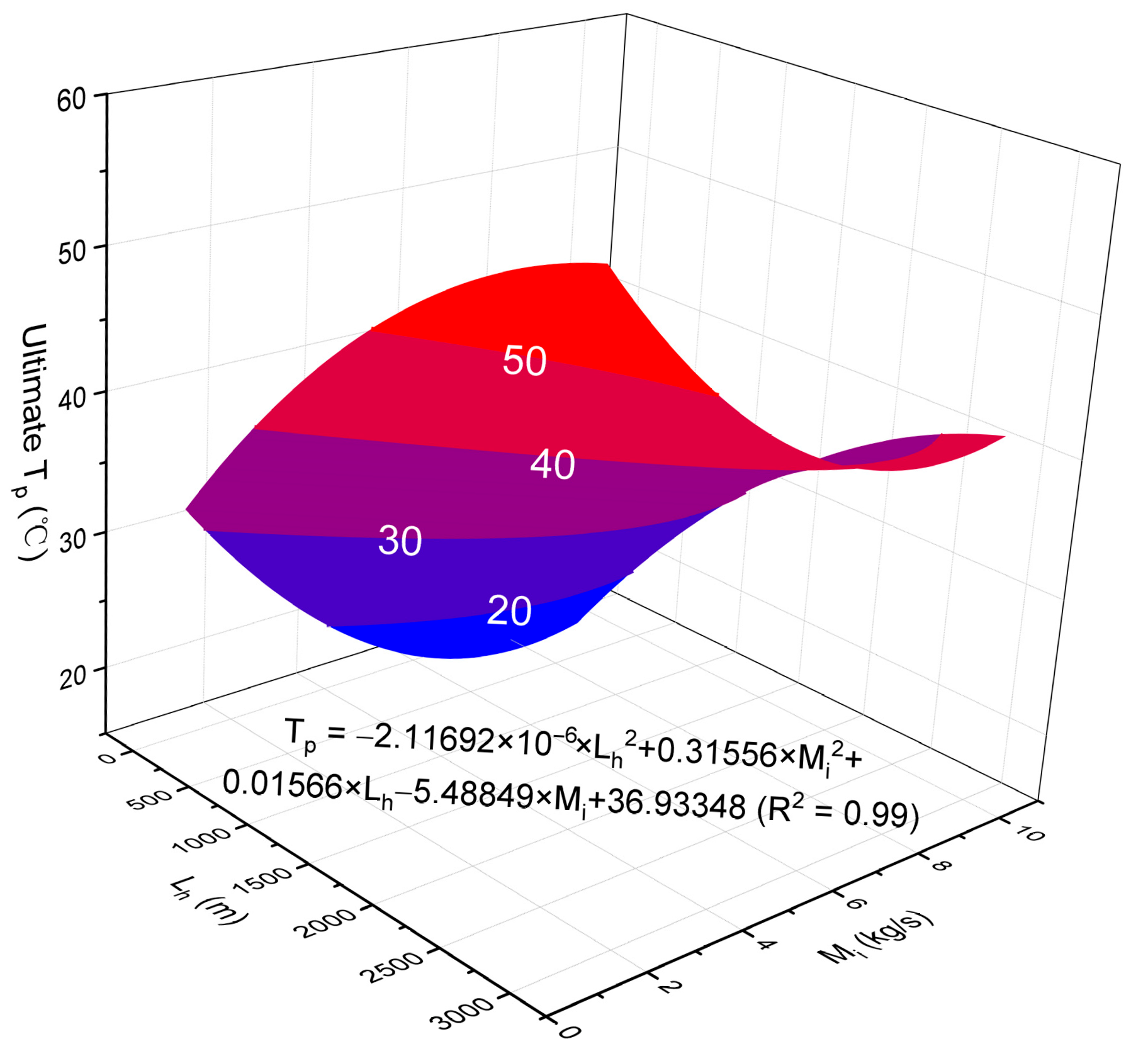
4. Multivariate Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hong, Y.; Cao, S.; Xu, P.; Pan, Z. Interpreting the effect of global economic risks on crude oil market: A supply-demand perspective. Int. Rev. Financ. Anal. 2024, 91, 103008. [Google Scholar] [CrossRef]
- Höök, M.; Tang, X. Depletion of fossil fuels and anthropogenic climate change—A review. Energy Policy 2013, 52, 797–809. [Google Scholar] [CrossRef]
- Zhang, T.; Guo, W.; Yang, L.; Li, J.; Tu, J.; Zhu, C. Effect of permeability and oil content on the autothermal pyrolysis in-situ conversion technology. Geoenergy Sci. Eng. 2025, 247, 213692. [Google Scholar] [CrossRef]
- Guo, W.; Pan, J.; Yang, Q.; Li, Q.; Deng, S.; Zhu, C. Study of the residual carbon oxidation trigger mechanism in fractured oil shale formation under real condition. Int. Commun. Heat Mass Transf. 2025, 160, 108369. [Google Scholar] [CrossRef]
- Afifa; Arshad, K.; Hussain, N.; Ashraf, M.H.; Saleem, M.Z. Air pollution and climate change as grand challenges to sustainability. Sci. Total Environ. 2024, 928, 172370. [Google Scholar] [CrossRef]
- Nkinyam, C.M.; Ujah, C.O.; Asadu, C.O.; Kallon, D.V.V. Exploring geothermal energy as a sustainable source of energy: A systemic review. Unconv. Resour. 2025, 6, 100149. [Google Scholar] [CrossRef]
- Huang, R.; Song, R.; Zhang, C.; Wang, Y.; Liu, G.; Li, T.; Wu, Y. Geothermal resources along the coast of Beibu Gulf and their utilization: An example from Hepu geothermal field. Nat. Gas Explor. Dev. 2022, 45, 141–149. [Google Scholar]
- Zhu, J.; Hu, K.; Lu, X.; Huang, X.; Liu, K.; Wu, X. A review of geothermal energy resources, development, and applications in China: Current status and prospects. Energy 2015, 93, 466–483. [Google Scholar] [CrossRef]
- Bao, Y.; Zhao, F.; Du, L.; Pang, Z.; Kong, Y.; Yang, F.; Yang, C.; Huang, J.; Ma, C.; Wu, M.; et al. Review on assessment methodology for hydrothermal resources based on renewable energy attributes. Energy Geosci. 2025, 6, 100397. [Google Scholar] [CrossRef]
- Lebbihiat, N.; Atia, A.; Arıcı, M.; Meneceur, N. Geothermal energy use in Algeria: A review on the current status compared to the worldwide, utilization opportunities and countermeasures. J. Clean. Prod. 2021, 302, 126950. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, C.; Yang, Y.; Song, R. Cascade utilization of geothermal resources in western Sichuan Province. Nat. Gas Explor. Dev. 2021, 44, 15. [Google Scholar]
- Kamila, Z.; Kaya, E.; Zarrouk, S.J. Reinjection in geothermal fields: An updated worldwide review 2020. Geothermics 2021, 89, 101970. [Google Scholar] [CrossRef]
- Bodvarsson, G.S.; Stefansson, V. Some theoretical and field aspects of reinjection in geothermal reservoirs. Water Resour. Res. 2010, 25, 1235–1248. [Google Scholar] [CrossRef]
- Stefansson, V.-đ. Geothermal reinjection experience. Geothermics 1997, 26, 99–139. [Google Scholar] [CrossRef]
- Zhang, L.; Chao, J.; Geng, S.; Zhao, Z.; Chen, H.; Luo, Y.; Qin, G. Particle migration and blockage in geothermal reservoirs during water reinjection: Laboratory experiment and reaction kinetic model. Energy 2020, 206, 118234. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Yan, G.; Liu, X.; Huang, Y.; Tian, S.; Xu, Q. Study on prevention and control measures of sandstone geothermal reinjection plugging. Water Sci. Technol. 2023, 87, 1571–1581. [Google Scholar] [CrossRef]
- Xia, J.; Tian, H.; Dou, B.; Xiao, P.; Zheng, J.; Lai, X. Experimental Review: Particle clogging in porous sandstone geothermal reservoirs during tail water reinjection. J. Hydrol. 2023, 625, 130066. [Google Scholar] [CrossRef]
- Li, C.; Guan, Y.; Yang, R.; Lu, X.; Xiong, W.; Long, A. Effect of inner pipe type on the heat transfer performance of deep-buried coaxial double-pipe heat exchangers. Renew. Energy 2020, 145, 1049–1060. [Google Scholar] [CrossRef]
- Li, C.; Jiang, C.; Guan, Y.; Tan, Z.; Zhao, Z.; Zhou, Y. Development and applicability of heat transfer analytical model for coaxial-type deep-buried pipes. Energy 2022, 255, 124533. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Song, R.; Wang, Y.; Sun, H.; Zheng, L. Adaptability of single-well downhole heat exchanger in developing mid-deep geothermal resources. Nat. Gas Explor. Dev. 2021, 44, 17. [Google Scholar]
- Spitler, J.D.; Gehlin, S.E.A. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Horne, R.N. Design considerations of a down-hole coaxial geothermal heat exchanger. Trans.-Geotherm. Resour. Counc. 1980, 4, CONF-800920-. [Google Scholar]
- Morita, K.; Sugimoto, S.; Yamada, Y.; Fujita, T.; Mukai, R.-I. Preliminary Considerations for Power Generation Using a Downhole Coaxial Heat Exchanger System (I). J. Geotherm. Res. Soc. Jpn. 1989, 11, 319–338. [Google Scholar] [CrossRef]
- Morita, K.; Mizogami, F.; Bollmeier, W.S. Analysis of the Results from the Proof of Concept Experiment in Hawaii Studies on the Downhole Coaxial Heat Exchanger. J. Geotherm. Res. Soc. Jpn. 1993, 15, 275–303. [Google Scholar] [CrossRef]
- Zanchini, E.; Lazzari, S.; Priarone, A. Improving the thermal performance of coaxial borehole heat exchangers. Energy 2010, 35, 657–666. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, C.; Li, G.; Guo, X.; Wang, G.; Shi, Y.; Peng, C.; Tan, Y. Performance analysis of a downhole coaxial heat exchanger geothermal system with various working fluids. Appl. Therm. Eng. 2019, 163, 114317. [Google Scholar] [CrossRef]
- Song, X.; Zheng, R.; Li, G.; Shi, Y.; Wang, G.; Li, J. Heat extraction performance of a downhole coaxial heat exchanger geothermal system by considering fluid flow in the reservoir. Geothermics 2018, 76, 190–200. [Google Scholar] [CrossRef]
- Liu, S.; Dahi Taleghani, A. Closed-loop geothermal systems: Critical review of technologies, performance enhancement, and emerging solutions. Renew. Sustain. Energy Rev. 2025, 225, 116177. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Xie, Y.; Zhang, Y.; Gao, X. Thermal performance analysis on the composition attributes of deep coaxial borehole heat exchanger for building heating. Energy Build. 2020, 221, 110019. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, F.; Liu, J.; Ma, Z.; Han, E.; Song, M. Field test and numerical investigation on the heat transfer characteristics and optimal design of the heat exchangers of a deep borehole ground source heat pump system. Energy Convers. Manag. 2017, 153, 603–615. [Google Scholar] [CrossRef]
- Xu, W.; Li, J.; Zhang, G.; Sun, Z.; Li, J. Research status and future development of the medium-deep geothermal heat pump heating system—A comprehensive review. Renew. Sustain. Energy Rev. 2025, 225, 116141. [Google Scholar] [CrossRef]
- Gu, F.; Li, Y.; Zhang, Y.; Gao, Y.; Yang, P.; Wang, A.; Cui, J. Convection-heat transfer coupling mechanism for closed-loop heat extraction from hydrothermal resources using horizontal wells. Coal Geol. Explor. 2024, 52, 121–130. [Google Scholar] [CrossRef]
- Wang, G.; Song, X.; Song, G.; Shi, Y.; Yu, C.; Xu, F.; Ji, J.; Song, Z. Analyzes of thermal characteristics of a hydrothermal coaxial closed-loop geothermal system in a horizontal well. Int. J. Heat Mass Transf. 2021, 180, 121755. [Google Scholar] [CrossRef]
- Hou, X.; Zhong, X.; Nie, S.; Wang, Y.; Tu, G.; Ma, Y.; Liu, K.; Chen, C. Study on the heat recovery behavior of horizontal well systems in the Qiabuqia geothermal area of the Gonghe Basin, China. Energy 2024, 286, 129424. [Google Scholar] [CrossRef]
- Liao, J.; Xie, Y.; Zhao, P.; Xia, K.; Xu, B.; Wang, H.; Li, C.; Li, C.; Liu, H. Probabilistic assessment of the thermal performance of low-enthalpy geothermal system under impact of spatially correlated heterogeneity by using XGBoost algorithms. Energy 2024, 313, 133947. [Google Scholar] [CrossRef]
- Liu, H.; Sun, W.; Zheng, J.; Dou, B. Adaptive Kriging-Based Heat Production Performance Optimization for a Two-Horizontal-Well Geothermal System. Appl. Sci. 2024, 14, 6415. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.M.; Moridis, G.J. TOUGH2 User’s Guide Version 2. 1999. Available online: https://scispace.com/pdf/tough2-user-s-guide-version-2-2qtqe8so9y.pdf (accessed on 3 June 2024).
- Moridis, G.; Pruess, K. Flow and Transport Simulations Using T2CG1, A Package of Conjugate Gradient Solvers for the TOUGH2 Family of Codes. 1995. Available online: https://scispace.com/pdf/flow-and-transport-simulations-using-t2cg1-a-package-of-3t38261q9r.pdf (accessed on 10 March 2024).
- Xu, T.; Hu, Z.; Feng, B.; Feng, G.; Li, F.; Jiang, Z. Numerical evaluation of building heating potential from a co-axial closed-loop geothermal system using wellbore–reservoir coupling numerical model. Energy Explor. Exploit. 2019, 38, 733–754. [Google Scholar] [CrossRef]
- Nie, S.; Li, J.; Liu, K.; Zhong, X.; Wang, Y. Numerical Evaluation of Commingled Production Potential of Marine Multilayered Gas Hydrate Reservoirs Using Fractured Horizontal Wells and Thermal Fluid Injection. J. Mar. Sci. Eng. 2024, 12, 365. [Google Scholar] [CrossRef]
- Song, X.; Zhang, Y.; Li, G.; Li, R.; Yu, C.; Li, J.; Guo, X. Performance Study of the Downhole Coaxial Closed-Loop Heat Exchange Technology in Xiong’an New Area. J. Tianjin Univ. Sci. Technol. 2021, 54, 972–980. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. Extreme Gradient Boosting. 2014. Available online: https://github.com/dmlc/xgboost (accessed on 13 July 2025).
- Saadallah, A. SHAP-Guided Regularization in Machine Learning Models. In Proceedings of the 3rd World Conference on eXplainable Artificial Intelligence, Istanbul, Turkey, 11 July 2025. [Google Scholar]
- Gu, M.; Kang, S.; Xu, Z.; Lin, L.; Zhang, Z. AE-XGBoost: A Novel Approach for Machine Tool Machining Size Prediction Combining XGBoost, AE and SHAP. Mathematics 2025, 13, 835. [Google Scholar] [CrossRef]



| Parameters | Value and Unit |
|---|---|
| Formation density | 2650 kg/m3 |
| Density of water | 1000 kg/m3 |
| Wellbore diameter | 0.2 m |
| Porosity of the reservoir | 0.20 |
| Reservoir permeability | 100 mD |
| Rock heat conductivity | 2.8 W/(m·°C) |
| Specific heat capacity of formation | 920 J/(kg·°C) |
| Specific heat capacity of water | 4200 J/(kg·°C) |
| Geothermal gradient | 0.027 °C/m |
| Surface temperature | 9 °C |
| Hydrostatic pressure gradient | 0.0098 MPa/m |
| Scenario No. | Lh, m | Mi, kg/s | Ti, °C | TG, °C/100 m | λR, W/(m·°C) | Simulation Objective |
|---|---|---|---|---|---|---|
| 1# | 0; 100; 300; 500; 800; 1000; 1500; 2000; 2500; 3000 | 5 | 9 | 2.7 | 2.8 | Impact of Lh (Section 3.1) |
| 2# | 0; 1000; 1500; 2000; 3000 | 1; 2; 3; 4; 5; 10 | 9 | 2.7 | 2.8 | Impact of Mi (Section 3.2) |
| 3# | 0; 1000; 1500; 2000; 3000 | 5 | 5; 7; 9; 11; 13; 15 | 2.7 | 2.8 | Impact of Ti (Section 3.3) |
| 4# | 0; 1000; 1500; 2000; 3000 | 5 | 9 | 2.1; 2.4; 2.7; 3.0; 3.3; 3.6 | 2.8 | Impact of TG (Section 3.4) |
| 5# | 0; 1000; 1500; 2000; 3000 | 5 | 9 | 2.7 | 1.6; 2.2; 2.8; 3.4; 4.0; 4.6 | Impact of λR (Section 3.5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, S.; Liu, K.; Yang, B.; Zhong, X.; Guo, H.; Li, J.; Xu, K. Heat Extraction Performance Evaluation of Horizontal Wells in Hydrothermal Reservoirs and Multivariate Sensitivity Analysis Based on the XGBoost-SHAP Algorithm. Processes 2025, 13, 3237. https://doi.org/10.3390/pr13103237
Nie S, Liu K, Yang B, Zhong X, Guo H, Li J, Xu K. Heat Extraction Performance Evaluation of Horizontal Wells in Hydrothermal Reservoirs and Multivariate Sensitivity Analysis Based on the XGBoost-SHAP Algorithm. Processes. 2025; 13(10):3237. https://doi.org/10.3390/pr13103237
Chicago/Turabian StyleNie, Shuaishuai, Ke Liu, Bo Yang, Xiuping Zhong, Hua Guo, Jiangfei Li, and Kangtai Xu. 2025. "Heat Extraction Performance Evaluation of Horizontal Wells in Hydrothermal Reservoirs and Multivariate Sensitivity Analysis Based on the XGBoost-SHAP Algorithm" Processes 13, no. 10: 3237. https://doi.org/10.3390/pr13103237
APA StyleNie, S., Liu, K., Yang, B., Zhong, X., Guo, H., Li, J., & Xu, K. (2025). Heat Extraction Performance Evaluation of Horizontal Wells in Hydrothermal Reservoirs and Multivariate Sensitivity Analysis Based on the XGBoost-SHAP Algorithm. Processes, 13(10), 3237. https://doi.org/10.3390/pr13103237






