Discrete-Time Linear Quadratic Optimal Tracking Control of Piezoelectric Actuators Based on Hammerstein Model
Abstract
1. Introduction
2. Model Identification with an Improved PSO Algorithm
2.1. Dual Strategy Improved PSO Algorithm
2.1.1. Principle of PSO Algorithm
2.1.2. Convergent Cross-Mutations

2.1.3. Adaptive Inertia Weights and Learning Factors
2.2. Benchmark Function Test Experiment
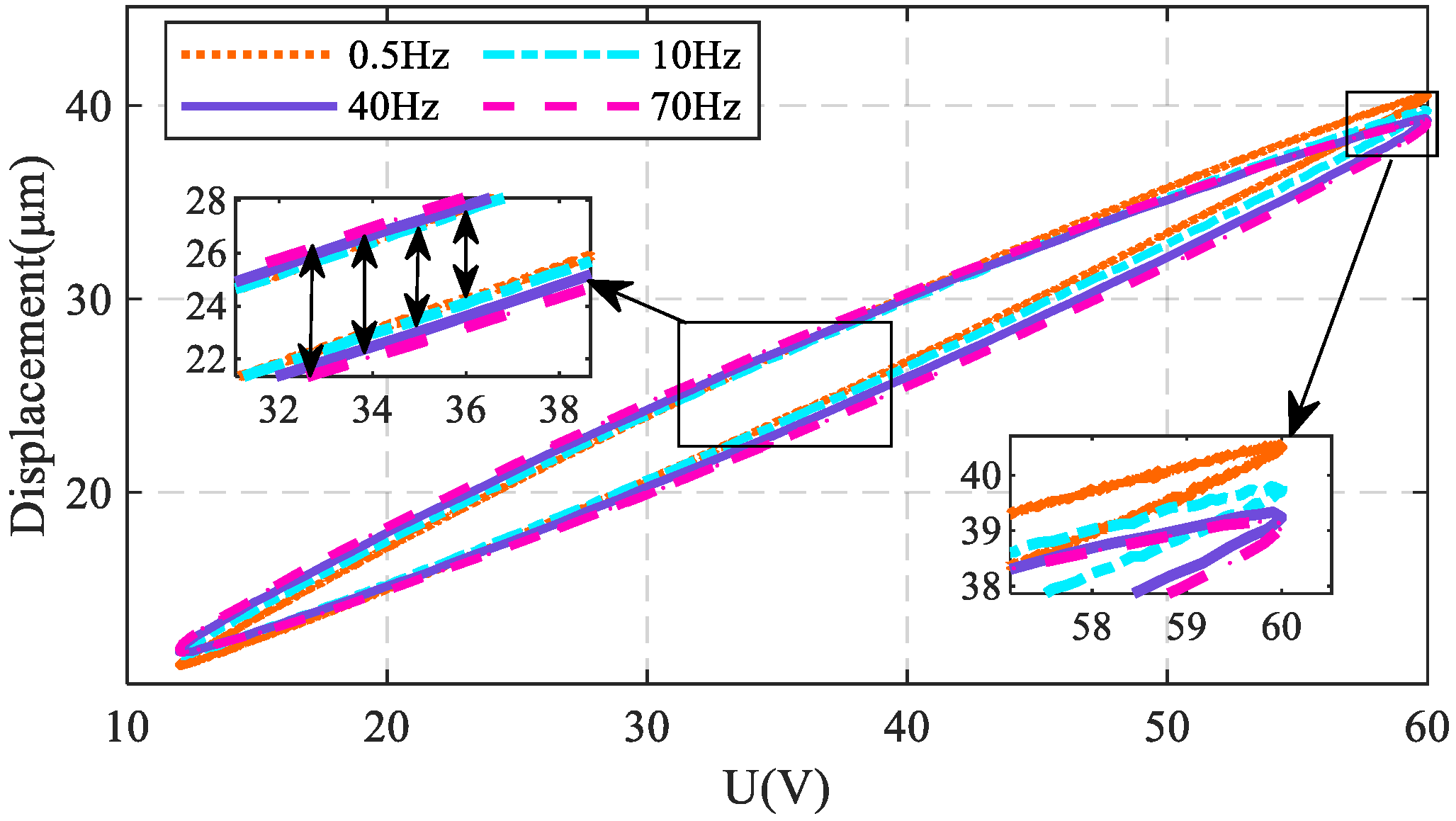
2.3. Piezoelectric Actuator Model Identification
2.3.1. Experimental Platform and Model
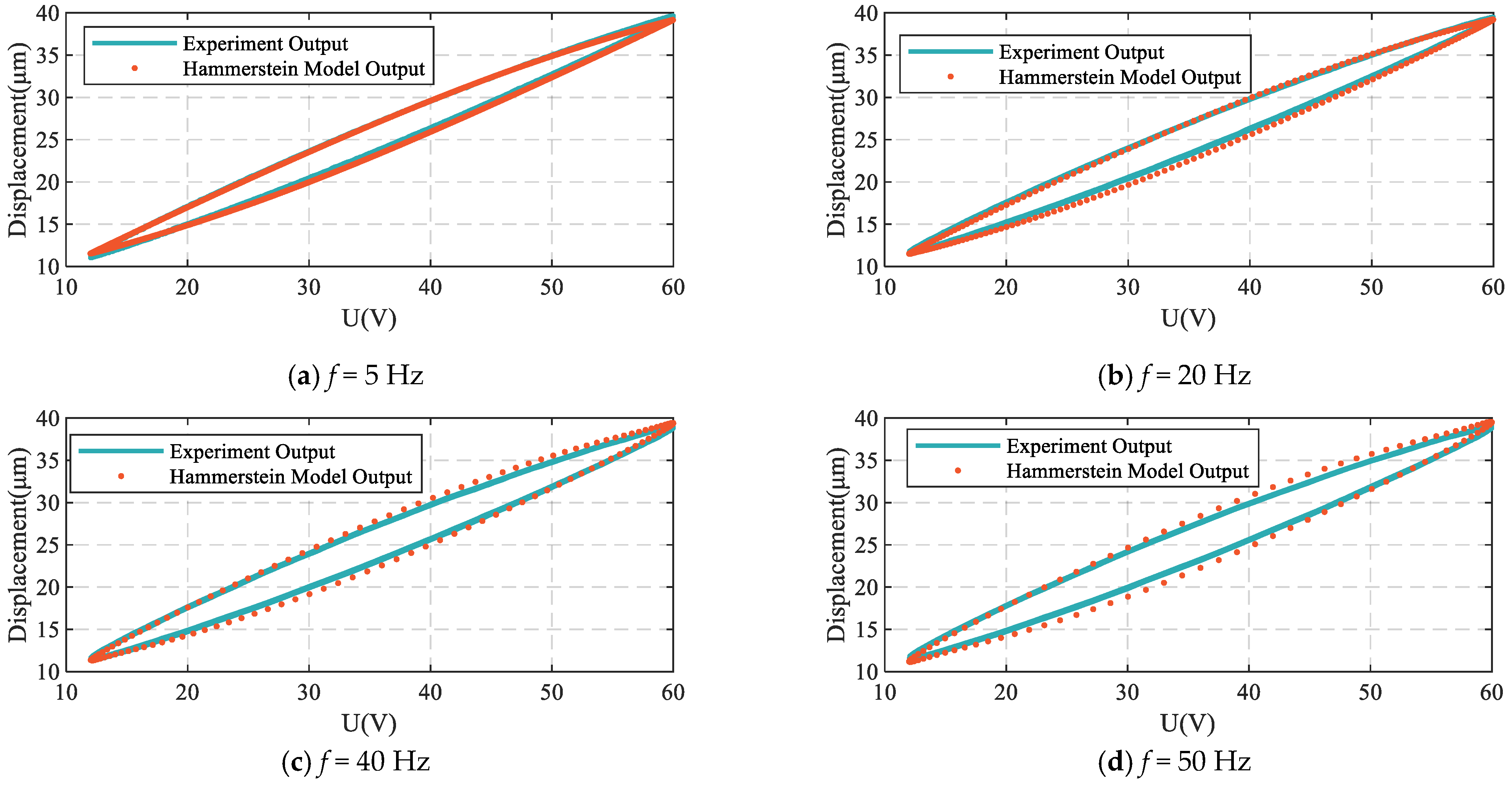
2.3.2. Model Identification and Validation
3. Tracking Controller Design
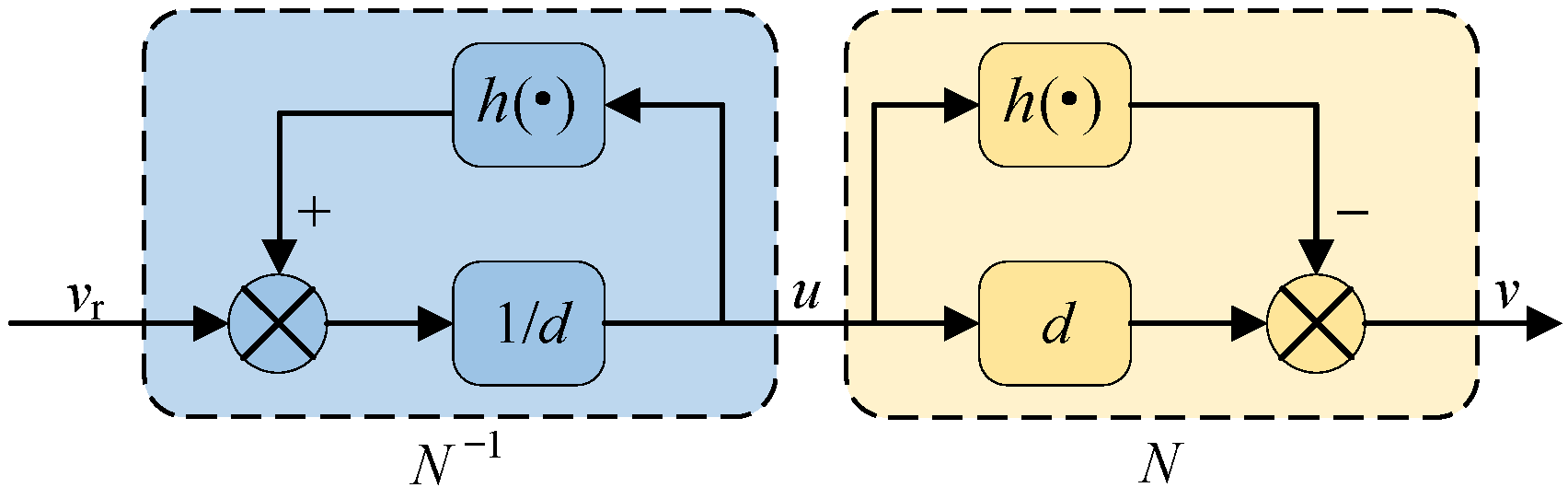
3.1. Hysteresis Compensator
3.2. DLQT Controller Based on Hysteresis Compensation
4. Hardware-in-the-Loop Tracking Control Experiment
4.1. Introduction to the Experiment
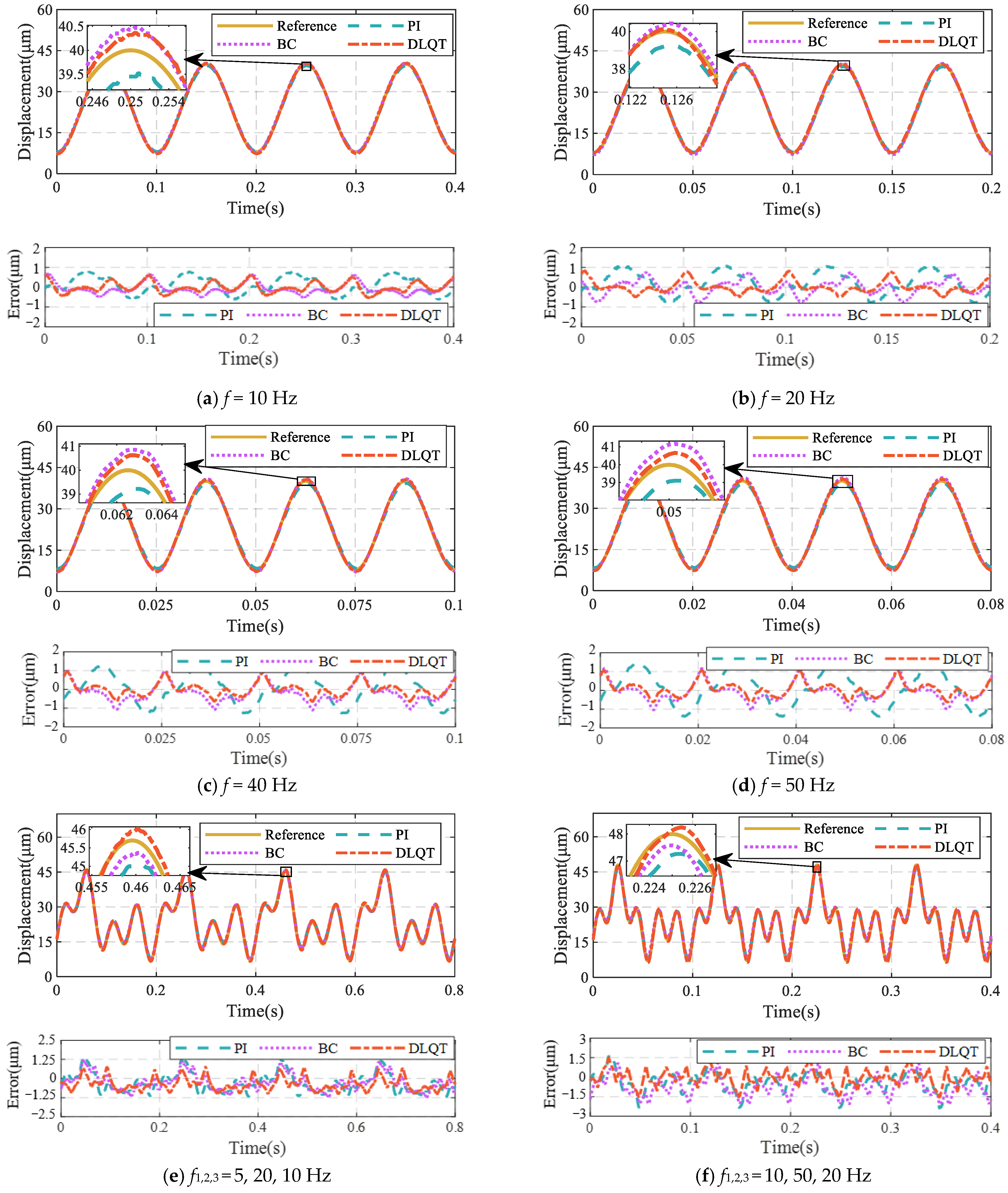
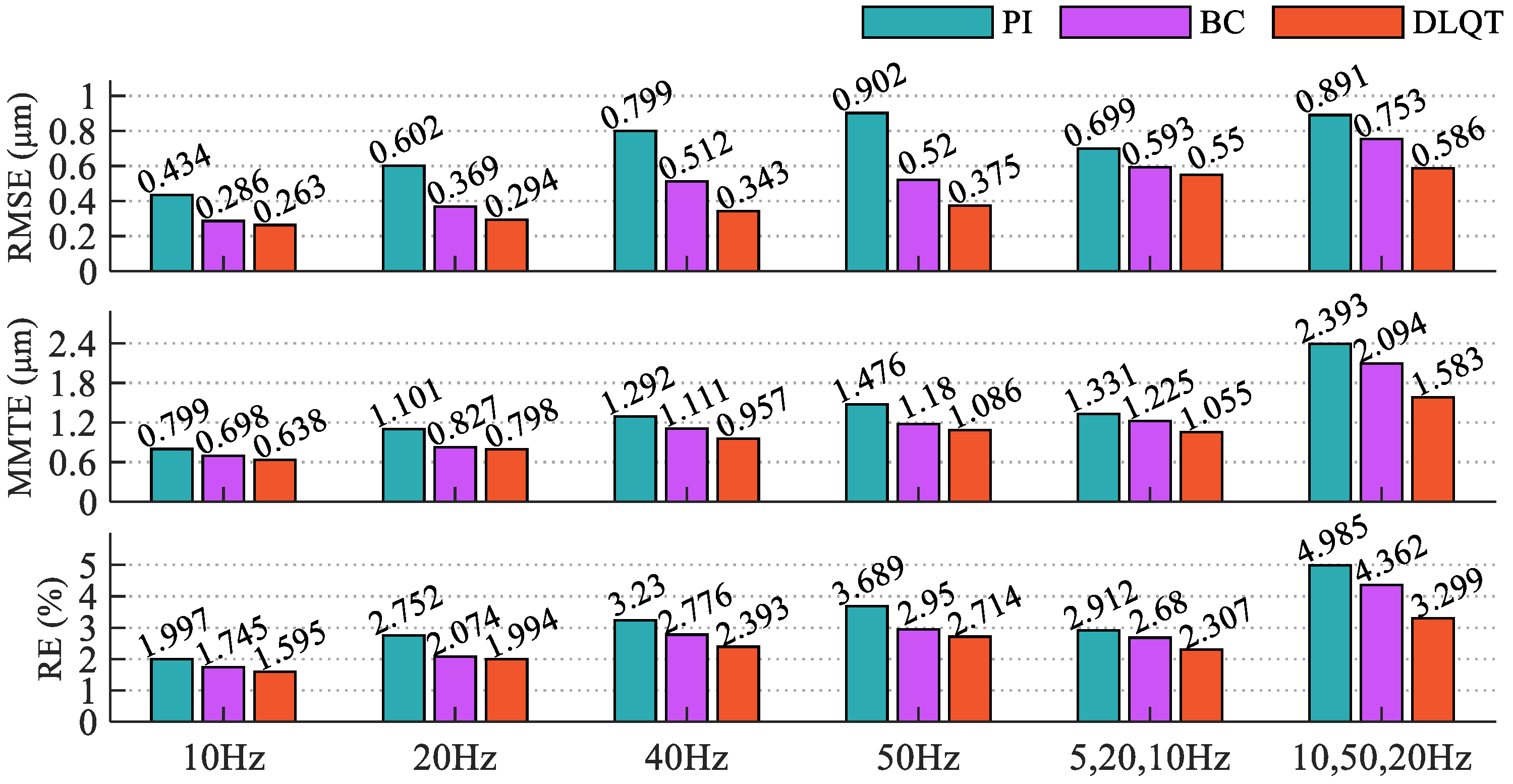
4.2. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, X.; Wu, S.; Wang, X.; Wang, Z.; Zhu, Q.; Sun, J.; Huang, P.; Wang, X.; Huang, W.; Lu, Q. Review on piezoelectric actuators: Materials, classifications, applications, and recent trends. Front. Mech. Eng. 2024, 19, 6. [Google Scholar] [CrossRef]
- Jin, H.; Gao, X.; Ren, K.; Liu, J.; Qiao, L.; Liu, M.; Chen, W.; He, Y.; Dong, S.; Xu, Z.; et al. Review on piezoelectric actuators based on high-performance piezoelectric materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 3057–3069. [Google Scholar] [CrossRef] [PubMed]
- Chang, Q.; Chen, W.; Zhang, S.; Deng, J.; Liu, Y. Review on Multiple-Degree-of-Freedom Cross-Scale Piezoelectric Actuation Technology. Adv. Intell. Syst. 2024, 6, 2300780. [Google Scholar] [CrossRef]
- Mei, T.; Huang, K.; Fang, H.; Fan, Q.; Xiao, H.; Xu, Q.; Dai, X.; Yang, Q.; Liu, C. High-precision and large-range deflection of light beams with fast steering mirrors. Opt. Lett. 2024, 49, 5427–5430. [Google Scholar] [CrossRef]
- Gao, C.; Zeng, Z.; Peng, S.; Shuai, C. Magnetostrictive alloys: Promising materials for biomedical applications. Bioact. Mater. 2022, 8, 177–195. [Google Scholar]
- Li, J.; Zhang, Y.; Yan, M.; Zhong, C.; Zhao, L.; Zhai, D.; Luo, H.; Yuan, X.; Zhang, D. 3D printing of flexible piezoelectric composite with integrated sensing and actuation applications. Adv. Powder Mater. 2024, 3, 100226. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.P.; Rogers, C.A. Dynamic output characteristics of piezoelectric actuators. Smart Struct. Mater. 1993, 1916, 341–352. [Google Scholar]
- Chang, F.; Luus, R. A noniterative method for identification using Hammerstein model. IEEE Trans. Autom. Control 2003, 16, 464–468. [Google Scholar] [CrossRef]
- Wills, A.; Schön, T.B.; Ljung, L.; Ninness, B. Identification of hammerstein–wiener models. Automatica 2013, 49, 70–81. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Dynamic Preisach models of hysteresis. IEEE Trans. Magn. 2002, 24, 2925–2927. [Google Scholar] [CrossRef]
- Oh, J.H.; Bernstein, D.S. Semilinear Duhem model for rate-independent and rate-dependent hysteresis. IEEE Trans. Autom. Control 2005, 50, 631–645. [Google Scholar]
- Kanchan, M.; Santhya, M.; Bhat, R.; Naik, N. Application of modeling and control approaches of piezoelectric actuators: A review. Technologies 2023, 11, 155. [Google Scholar] [CrossRef]
- Cai, J.; Dong, W.; Nagamune, R. A survey of Bouc-Wen hysteretic models applied to piezo-actuated mechanical systems: Modeling, identification, and control. J. Intell. Mater. Syst. Struct. 2023, 34, 1843–1863. [Google Scholar] [CrossRef]
- Zhang, Q. A tutorial on linear least square estimation. arXiv 2022, arXiv:2211.15347. [Google Scholar] [CrossRef]
- Chu, S.; Mao, Y.; Dong, Z.; Yang, X. Parameter identification of high-speed USV maneuvering response model based on maximum likelihood algorithm. Acta Armamentarii 2020, 41, 127. [Google Scholar]
- Beheshti, Z.; Shamsuddin, S.M.H. A review of population-based meta-heuristic algorithms. Int. J. Adv. Soft Comput. Appl. 2013, 5, 1–35. [Google Scholar]
- Alhijawi, B.; Awajan, A. Genetic algorithms: Theory, genetic operators, solutions, and applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Song, Y.; Cai, X.; Zhou, X.; Zhang, B.; Chen, H.; Li, Y.; Deng, W.; Deng, W. Dynamic hybrid mechanism-based differential evolution algorithm and its application. Expert Syst. Appl. 2023, 213, 118834. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; AI-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Awadallah, M.A.; Makhadmeh, S.N.; Al-Betar, M.A.; Dalbah, L.M.; Al-Redhaei, A.; Kouka, S.; Enshassi, O.S. Multi-objective ant colony optimization. Arch. Comput. Methods Eng. 2025, 32, 995–1037. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An overview of variants and advancements of PSO algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Brown, D.F.; Xie, S.Q. A Piecewise Particle Swarm Optimisation Modelling Method for Pneumatic Artificial Muscle Actuators. Actuators 2024, 13, 286. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, Y.; Liu, J. Research on structure optimization and motion characteristics of wearable medical robotics based on Improved Particle Swarm Optimization Algorithm. Future Gener. Comput. Syst. 2022, 129, 187–198. [Google Scholar] [CrossRef]
- Fang, S.; Wang, Y.; Wang, W.; Chen, Y.; Chen, Y. Design of permanent magnet synchronous motor servo system based on improved particle swarm optimization. IEEE Trans. Power Electron. 2021, 37, 5833–5846. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, X.; Yang, J. Modified particle swarm optimization with attention-based LSTM for wind power prediction. Energies 2022, 15, 4334. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, Z.; Terzi, S.; Anwer, N.; Eynard, B. Dynamic task allocations with Q-learning based particle swarm optimization for human-robot collaboration disassembly of electric vehicle battery recycling. Comput. Ind. Eng. 2025, 204, 111133. [Google Scholar] [CrossRef]
- Yu, S.Y.; Feng, Y.Y.; Yang, X.P. Extended state observer–based fractional order sliding-mode control of piezoelectric actuators. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2021, 235, 39–51. [Google Scholar] [CrossRef]
- Liu, H.T.; Zhang, G.L.; Zhou, K.M. Identification of low-damping resonance characteristics and the high-bandwidth control of a piezo-positioning stage. J. Vib. Shock 2024, 43, 287–296. [Google Scholar]
- Salah, M.; Saleem, A. Hysteresis compensation-based robust output feedback control for long-stroke piezoelectric actuators at high frequency. Sens. Actuators A Phys. 2021, 319, 112542. [Google Scholar] [CrossRef]
- FU, Y.; CHEN, W. Optimal tracking control method for discrete-time linear multivariable systems with decoupling performance. Acta Autom. Sin. 2022, 48, 1931–1939. [Google Scholar]
- Argentim, L.M.; Rezende, W.C.; Santos, P.E.; Aparecido Aguiar, R. PID, LQR and LQR-PID on a quadcopter platform. In Proceedings of the 2013 International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh, 17–18 May 2013; pp. 1–6. [Google Scholar]
- Cao, Y.; Ren, W. Optimal linear-consensus algorithms: An LQR perspective. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 40, 819–830. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks (ICNN’95), Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Ratnaweera, A. Particle swarm optimization with self-adaptive acceleration coefficients. In Proceedings of the 1st International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2002), Singapore, 18–22 November 2002; Volume 1, pp. 264–268. [Google Scholar]
- Srinivas, M.; Patnaik, L.M. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man. Cybern. 1994, 24, 656–667. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Liu, D.; Dong, J.; Guo, S.; Tan, L.; Yu, S. Parameter identification of model for piezoelectric actuators. Micromachines 2023, 14, 1050. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R.; Wang, H.N.; Xiong, T. The identification strategy of bouc-wen model based on improved particle swarm optimization algorithm. In Proceedings of the 33rd Chinese Control and Decision Conference (CCDC 2021), Kunming, China, 22–24 May 2021; pp. 6528–6532. [Google Scholar]
- Xu, X.; Rong, H.; Trovati, M.; Liptrott, M.; Bessis, N. CS-PSO: Chaotic particle swarm optimization algorithm for solving combinatorial optimization problems. Soft Comput. 2018, 22, 783–795. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; The University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Liu, Z.; Xu, X.; Guo, J.; He, Y.; Zhuang, Y.; Yu, S. Damping force tracking control of magnetorheological damper based on Koopman operators. Control Theory Appl. 2024, 1–11. Available online: https://link.cnki.net/urlid/44.1240.TP.20241010.1652.014 (accessed on 1 October 2025).
- Liu, B.; Tang, W. Modern Control Theory; China Machine Press: Beijing, China, 2006. [Google Scholar]
- Qiao, J.H. Backstepping Control Method and Implementation, 1st ed.; China Machine Press: Beijing, China, 2012; pp. 21–24. [Google Scholar]
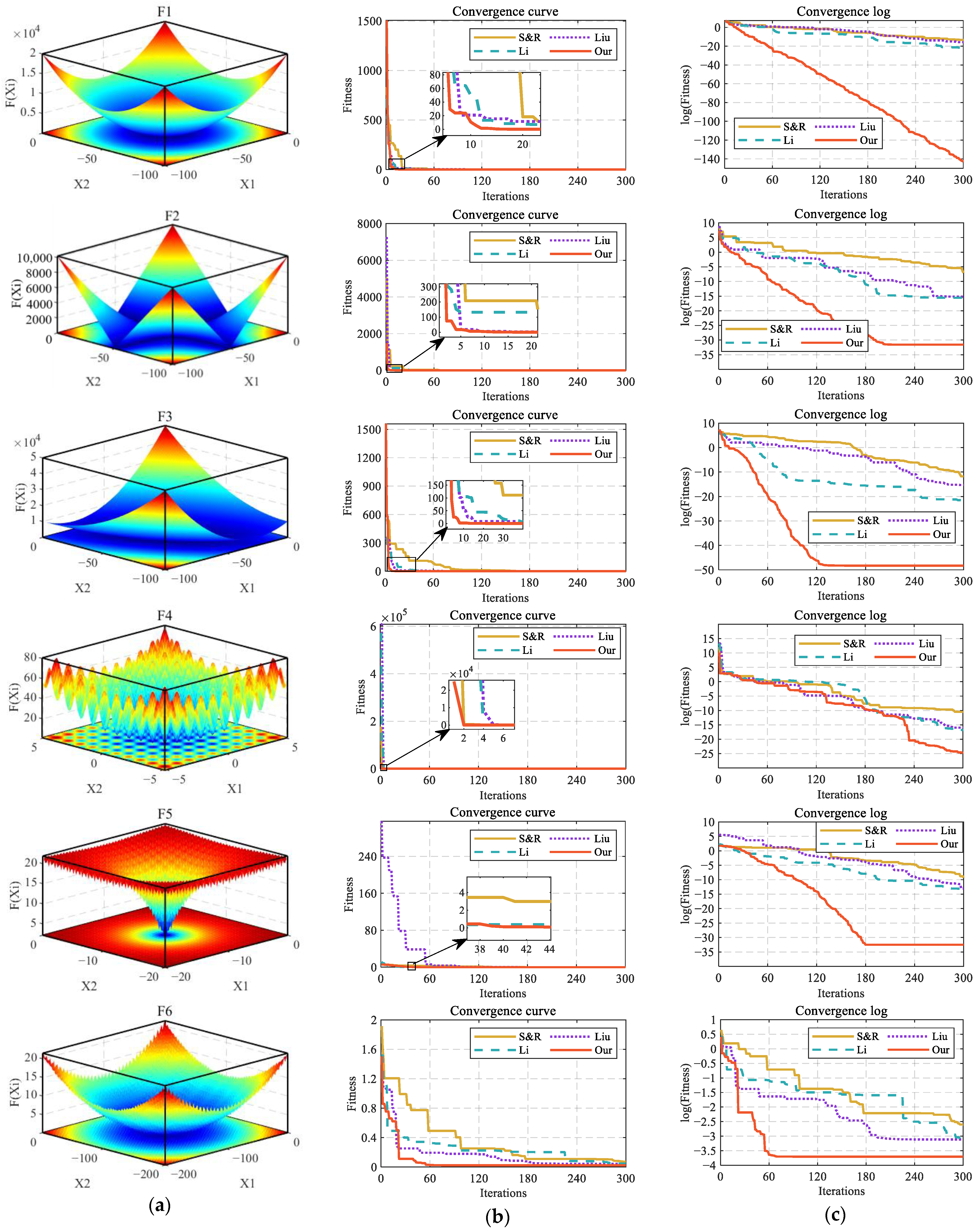








| Method | Parameter Settings |
|---|---|
| S&R | T = 300, S = 40, D = n = 5, |
| Liu | T = 300, S = 40, D = n = 5, |
| Li | T = 300, S = 40, D = n = 5, |
| Our | T = 300, S = 40, D = n = 5, , c1 and c2 are shown in Equation (8). |
| Function | S&R | Liu | Li | Our | |
|---|---|---|---|---|---|
| F1 | Best | 1.4337 × 10−6 | 1.3816 × 10−7 | 4.2809 × 10−10 | 1.1202 × 10−62 |
| Average | 3.4861 × 10−7 | 9.3276 × 10−7 | 3.9715 × 10−9 | 6.7365 × 10−59 | |
| Std | 4.5334 × 10−7 | 2.0364 × 10−7 | 8.7832 × 10−10 | 4.9113 × 10−60 | |
| F2 | Best | 8.9185 × 10−4 | 2.0018 × 10−7 | 1.7446 × 10−7 | 1.9621 × 10−14 |
| Average | 9.5461 × 10−4 | 3.9654 × 10−6 | 8.4981 × 10−6 | 3.7619 × 10−13 | |
| Std | 2.3782 × 10−5 | 8.9723 × 10−7 | 9.2365 × 10−7 | 2.9946 × 10−14 | |
| F3 | Best | 7.4398 × 10−6 | 2.1724 × 10−7 | 3.8459 × 10−10 | 1.0498 × 10−21 |
| Average | 9.3972 × 10−5 | 1.9527 × 10−6 | 6.6498 × 10−11 | 9.8951 × 10−19 | |
| Std | 2.7861 × 10−5 | 5.9434 × 10−7 | 6.5228 × 10−11 | 6.0572 × 10−20 | |
| F4 | Best | 2.8238 × 10−5 | 1.1436 × 10−7 | 4.5237 × 10−8 | 1.8025 × 10−11 |
| Average | 8.5928 × 10−5 | 3.8249 × 10−6 | 2.9746 × 10−6 | 8.3268 × 10−10 | |
| Std | 2.1733 × 10−5 | 1.2829 × 10−6 | 6.9835 × 10−7 | 1.1327 × 10−10 | |
| F5 | Best | 9.2254 × 10−5 | 2.0069 × 10−6 | 1.7834 × 10−6 | 7.5495 × 10−15 |
| Average | 6.3481 × 10−4 | 1.3256 × 10−5 | 6.7739 × 10−6 | 4.2289 × 10−14 | |
| Std | 1.7883 × 10−4 | 3.1394 × 10−6 | 1.2198 × 10−6 | 2.4026 × 10−15 | |
| F6 | Best | 7.4068 × 10−2 | 4.4367 × 10−2 | 6.6499 × 10−2 | 2.4644 × 10−2 |
| Average | 9.2329 × 10−2 | 6.6854 × 10−2 | 7.8826 × 10−2 | 3.9771 × 10−2 | |
| Std | 8.5073 × 10−3 | 6.4164 × 10−3 | 2.0182 × 10−3 | 1.0566 × 10−3 |
| Method | MMFE (μm) | RMSE (μm) | RE (%) |
|---|---|---|---|
| S&R | 0.8184 | 0.3075 | 2.01 |
| Liu | 0.8013 | 0.2964 | 2.00 |
| Li | 0.7978 | 0.2835 | 1.95 |
| Ours | 0.6669 | 0.2559 | 1.65 |
| Frequency | MMFE (μm) | RMSE (μm) | RE (%) |
|---|---|---|---|
| 5 Hz | 0.7035 | 0.2952 | 1.7587 |
| 20 Hz | 0.9069 | 0.4053 | 2.2649 |
| 40 Hz | 0.9428 | 0.4738 | 2.3918 |
| 50 Hz | 1.1834 | 0.6041 | 2.9916 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Zhao, X.; Li, X.; Wang, C.; Tan, L.; Li, X.; Yu, S. Discrete-Time Linear Quadratic Optimal Tracking Control of Piezoelectric Actuators Based on Hammerstein Model. Processes 2025, 13, 3212. https://doi.org/10.3390/pr13103212
Liu D, Zhao X, Li X, Wang C, Tan L, Li X, Yu S. Discrete-Time Linear Quadratic Optimal Tracking Control of Piezoelectric Actuators Based on Hammerstein Model. Processes. 2025; 13(10):3212. https://doi.org/10.3390/pr13103212
Chicago/Turabian StyleLiu, Dongmei, Xiguo Zhao, Xuan Li, Changchun Wang, Li Tan, Xuejun Li, and Shuyou Yu. 2025. "Discrete-Time Linear Quadratic Optimal Tracking Control of Piezoelectric Actuators Based on Hammerstein Model" Processes 13, no. 10: 3212. https://doi.org/10.3390/pr13103212
APA StyleLiu, D., Zhao, X., Li, X., Wang, C., Tan, L., Li, X., & Yu, S. (2025). Discrete-Time Linear Quadratic Optimal Tracking Control of Piezoelectric Actuators Based on Hammerstein Model. Processes, 13(10), 3212. https://doi.org/10.3390/pr13103212





