Abstract
The dynamic and time-sensitive nature of online food delivery, along with real-world factors like sudden changes in order volumes and the availability of couriers, distinguishes it from traditional vehicle routing scenarios. Apart from the many studies in the literature that handle this problem from specific angles, our solution proposes a new approach that provides real-time routing with the awareness of the expectations of multiple stakeholders in the ecosystem. For this purpose, we develop a Mixed Integer Programming (MIP) model that minimizes unmet demand and workforce requirements simultaneously to meet platform and courier expectations while maintaining the timeliness of the operation to meet restaurant and customer expectations. Since the model requires more time to provide good results for even small-size problems, we develop a multi-step algorithmic approach supported by strategies that hold or dissolve a part of the solutions to create opportunities for better results. A framework for agent-based simulation was created to implement the strategies and the algorithmic steps, accurately mimicking the operations and movements of couriers. The effectiveness of this solution was evaluated through experiments based on a real-world case study. The results indicate that our solution can generate high-quality results in a short time across various configurations, which are defined by different demand and supply patterns and varying problem sizes.
1. Introduction
The Online Food Delivery (OFD) ecosystem has experienced rapid growth and revolutionary transformation in recent years, driven by advances in communication and mobile device technologies and an increasing desire for faster service [1]. While being a form of Pick-up and Delivery Problem with Time Windows (PDPTW) in principle, OFD requires a more dynamic approach and problem-specific details to be included in careful consideration due to the complexity that comes with a huge number of stakeholders. The increased demand for food delivery services provided by restaurants has created a multi-billion-dollar industry by integrating the logistics services into the ecosystem. This expansion has led to the emergence of online restaurant marketplaces with integrated delivery networks, transforming the traditional restaurant-operated delivery model. As a result of this transformation, optimizing OFD logistics involves a complex interplay of various stakeholders, each with their distinct roles and expectations within this rapidly expanding ecosystem, such as:
Online Food Delivery Marketplace:
Role: These marketplace platforms, such as Grubhub, Uber Eats, Just Eat, and Meituan, serve as aggregators connecting customers to restaurants and often provide integrated delivery networks. They manage orders, assign couriers, and strive to optimize delivery operations.
Expectations: Marketplaces aim to achieve higher efficiency levels and provide a higher service quality at a lower cost. They seek to minimize total delivery cost and maximize profitability [2]. This involves optimizing order allocation and routing, ensuring the availability of reliable delivery capacity in time and at minimum cost, and adopting strategies like demand management to improve system performance [3]. They must balance conflicting objectives, as solely pursuing cost reduction can reduce overall delivery efficiency while focusing too much on efficiency can increase costs [4].
Restaurants
Role: Restaurants prepare foods and provide an expected ready time for orders. Partnering with online marketplaces allow them to offer food-delivery service to their customers and potentially scale up their operations.
Expectations: Restaurants desire to increase their opportunity to offer food delivery and grow their business. Implicitly, they expect timely pickup of orders by couriers to maintain food quality and customer satisfaction, since their reputation and profits are directly impacted by delivery service quality [4].
Couriers
Role: Couriers are typically contracting individuals in a crowdsourced delivery model, using their own transportation mode (e.g., car, motorbike, bike) to perform last-mile delivery tasks. Essentially, they pick up orders from restaurants and try to deliver them to customers in a timely manner.
Expectations: Couriers seek fair distribution of work and orders, as uneven allocation can lead to unbalanced earnings. They often desire a minimum guaranteed hourly payment if earnings from deliveries fall below a certain threshold. They also expect to avoid unpaid waiting time at restaurants (due to delayed food preparation) or delivery addresses [5]. Having a flexible number of couriers is advantageous in a market with high order-rate fluctuations.
Customers
Role: Customers place food orders online using a marketplace and expect to receive them at their specified drop-off location.
Expectations:
Fast Service/Delivery: This is a paramount expectation; an order is usually expected to be delivered as soon as possible (within an hour at most) and should not be wandering around after being ready. Customers are time-sensitive, with varying degrees of tolerance for delays [6].
On-time Readiness and Delivery: Customers expect their orders to be delivered within a promised time window. Delays can significantly decrease customer satisfaction and may incur penalty costs for platforms [4].
Food Quality/Freshness: Maintaining the temperature and integrity of foods is critical, especially for perishable items. Customers expect their food to arrive fresh and warm, influencing their overall satisfaction [6].
Cost Reduction: Customers exhibit resistance to delivery fees, and low delivery fees are often a significant factor in their choices [3].
Personalized Needs: For specific groups, like the elderly, personalized nutritional needs and dietary requirements may be a consideration [7].
The dynamic nature and stringent service-quality targets of OFD make it a challenging problem in last-mile logistics, requiring efficient dispatching technology and innovative solutions to meet the diverse expectations of these stakeholders.
As shown in Table 1, each stakeholder has different expectations and next to each one, the actions which would help to meet them. These are some of the main expectations that are formed by combining both observations from the author’s experience in the industry and the related studies in the literature. It might be impossible or impractical to meet all the expectations at the same time due to conflicts such as the fact that providing fairness to couriers might yield a lower utilization on average or providing on-time delivery might cause sub-optimal routes in some cases and consequently unmet demand. This issue can partially be overcome by finding sweet spots during the routing part of the problem, which is the focus of this study, by relaxing the boundaries of the problem to some extent and using an approach with custom solutions such as problem-specific algorithms. Meeting at least one expectation of each stakeholder is achievable since there are already similarities among them, such as timely conducted responsibilities and managing the demand as smoothly as possible.

Table 1.
The actions necessary to meet the stakeholder expectations.
The OFD problem naturally comes with many uncertainties. The arrival times of orders, the time they are ready, and the time it takes for couriers to complete their designated routes are elements that contain a certain amount of randomness. Managing this process by breaking it into smaller pieces will help to cope with the unknowns and make the process easier to manage. A multi-step algorithm, used within a rolling horizon framework, allows the system to plan for periods ahead, be prepared for upcoming events, and adapt decisions in real time based on the latest system information. This method encourages more flexible assignment strategies, eliminating the dependence on outdated information or fixed batching plans. An algorithmic framework is necessary in terms of evaluating trade-offs over time instead of committing to a single global optimum based on a narrow perspective. The multi-step algorithm facilitates this by breaking the decision-making process into a series of evolving sub-problems, each informed by the latest available information and previous computations. This allows for better alignment with the expectations of stakeholders in real time. Additionally, in operational settings, quick decisions are often necessary despite the available information being incomplete. By breaking down the optimization process into smaller, more manageable sub-problems, this method accounts for real-world limitations such as limited computing time and data availability while still allowing for effective optimization. Utilizing a simulation environment enables the algorithm to be evaluated in a realistic and controlled context that mimics the dynamics found in actual systems. Utilizing a rolling horizon approach with one-minute intervals ensures precise responsiveness, and event-triggered optimization helps to avoid unnecessary computations during periods of low activity.
For this purpose and meeting stakeholder expectations, we present a Mixed Integer Programming (MIP) model which aims to minimize the unmet demand and required number of couriers to provide higher utilization rate. The model also ensures the operation and specified tasks are performed in predetermined timeframes. Then, a simulation environment is created in a rolling horizon method approach to solve the problem with a custom-designed algorithm and test the algorithm performance. Unlike some common divide-and-conquer approaches, where a clustering method creates smaller groups of sub-problems to decrease the combinatorial complexity, we aim to create a different approach where each component of the algorithm deals with specific parts of the problem. This way, a robust system will be designed which does not require parameter tuning and analysis or major adjustments based on changing circumstances. Finally, a numerical analysis is performed, first by taking the MIP model results as benchmark solutions and comparing the performance of the exact solution and our proposed solution method on various instances, then by a comparison with the most relevant study from the literature, and lastly by analyzing the algorithm components and comparing their performances.
The structure of this paper for the remaining parts is as follows. A summary of the OFD-related literature and brief details about these studies are given in Section 2. Then, we define the OFD problem and the MIP formulation to solve the problem with given settings in Section 3, while Section 4 focuses on the created simulation environment, steps and strategies, and the optimization algorithm and its components in detail. The performance of our methodology, comparisons, and analysis are presented in Section 5, and finally, the conclusion of our study is presented in Section 6.
2. Literature Review
PDPTW has been extensively studied in the literature, and many application cases are still in the scope of researchers in different areas such as cold-chain transportation [1,2] and e-commerce last mile delivery operations [3,4], along with public transportation [5,6] and meal delivery routing [7,8]. In recent years, along with the effects of the global pandemic and remote-working, the OFD ecosystem has seen a meteoric rise in demand for meal delivery services. This has caught the attention of academia, resulting in an increase in the number of publications focusing on OFD problems by transforming the static PDPTW into OFD routing problem.
While OFD is dynamic by nature, some of studies handle the food delivery problem statically as well. Yildiz and Savelsbergh [9] develop an exact solution approach for the Meal Delivery Routing Problem (MDRP) by introducing a simultaneous column and row generation algorithm and a Selective Column Inclusion scheme for efficiency. They focus on providing insights into high-quality solution characteristics and assessment of the quality of OFD algorithms. Katiyar et al. [10] employ and compare artificial bee colony and cuckoo search algorithms to optimize meal deliveries. Their model focuses on minimizing distance traveled and transportation costs and ensuring timely delivery within specified time windows to maintain food quality. A two-stage solution that maximizes the satisfaction of time-sensitive customers as the objective for meal delivery routing problem is established by Wang and Jiang [11]. To increase the efficiency of a fast meal delivery service, they apply the Hierarchical Agglomerative Clustering (HAC) algorithm by hierarchically classifying a large number of meal orders and creating delivery batches based on the nearest pickup locations. Bi et al. [12] demonstrate that for the meal delivery service providers, Shared Logistics Services Mode (SLSM) can save logistics costs and meet customer needs better than Traditional Logistics Services Mode (TLSM). They propose a multi-objective routing problem which aims to minimize customer dissatisfaction and delivery costs, and then they develop an Improved Ant Lion Optimizer algorithm to solve the problem. Hong et al. [13] examine meal delivery routing for elderly using trucks and robots. A mixed integer programming model is proposed to address the problem, and then an improved adaptive large neighborhood search algorithm, incorporating simulated annealing and artificial bee colony algorithms, is utilized to enhance solution effectiveness and avoid local optimality. Kim and Chung [14] employ a mixed-integer linear programming model to optimize order assignment and routing. They utilize a tabu search algorithm to effectively solve medium-sized and large-sized meal delivery routing problems, enhancing efficiency for both single and multiple-order deliveries. Martínez-Sykora et al. [15] introduce a multi-objective approach for MDRP by employing an Integer Linear Programming (ILP) model for small-scale and a Variable Neighborhood Search (VNS) algorithm for large-scale problems. Their model holds a weighted objective function to derive the Pareto front and aims to equitably distribute orders among couriers and to minimize their total workload simultaneously.
Handling the problem dynamically, on the other hand, allows for capturing the uncertainties and responding to them from a more realistic standpoint. Simoni and Winkenbach [16] propose an Order Batching and Assignment (OBA) algorithm by utilizing a graph-based clustering approach to decompose the problem into sub-problems. As in our study, they create a simulation framework to model a realistic operation and to showcase the performance of advanced policies. Chen et al. [17] propose an optimization algorithm based on Graph Neural Network (GNN) for OFD order dispatching, combining machine learning and operational research methods to dispatch orders to couriers in real time in order to improve delivery efficiency and customer satisfaction. The solution consists of two attention mechanisms to learn the matching relationship between orders and couriers and greedy and regret value-based dispatching heuristics to ensure solution quality. A multi-objective model and an action consolidation–non-dominated sorting genetic algorithm is proposed by Shao et al. [18] to deal with the uncertain conditions of meal deliveries. They utilize a rolling scheduling framework for their selected delivery mode of automatic guide vehicles. Wang and Gao [19] propose a hybrid adaptive genetic algorithm (AGA) and adaptive large neighborhood search (ALNS) algorithm to solve the dynamic meal delivery routing problem, enhancing both global and local search capabilities for optimizing both customer satisfaction and minimizing costs simultaneously by integrating a waiting strategy. Xie et al. [20] employ a Receding Horizon Control (RHC) strategy to transform the dynamic meal delivery routing problem into a static one, utilizing a dynamic optimization model that accounts for time-varying speeds and road network subdivisions to minimize delivery costs. Xu et al. [21] proposes a two-stage optimization model utilizing an improved variable neighborhood search algorithm for initial distribution planning, followed by a periodic optimization strategy for dynamic adjustments to address the meal delivery routing problem while considering merchant priorities. The meal preparation times are especially focused in the route optimization undertaken by Wang et al. [22] using genetic algorithms and clustering ideas. They address dynamic demand and utilize a periodic optimization method for real-time path adjustment, considering preparation times as random variables.
As mentioned in the previous section, our approach considers multiple stakeholders and aims to meet their delivery-related expectations dynamically in real time. As far as our knowledge extends, this is the first study to focus on all the stakeholders in the OFD environment and try to optimize their needs simultaneously. As seen in Table 2, our approach stands out by this specialty and the high number of performance parameters to be optimized.

Table 2.
A summary of related studies.
3. Problem Definition
The assumptions and model definitions are based on the study of Yıldız and Savelsbergh [9], with minor changes. Essentially, customers put their food orders through the marketplace platform in an unpredictable fashion. The restaurants are immediately informed about the order and the order ready times are assumed to be constant and known beforehand based on the order contents. Couriers participate in the system according to their shift start and end times. As soon as they log in, the system includes them in routing processes and assigns them orders to be picked from designated restaurants and to be dropped off to the corresponding customers until they log out. An order is defined by two distinct actions: a pick-up and a drop-off task. A courier can execute multiple pick-up tasks consecutively and carry them at the same time as batches from the same or different restaurants. An order cannot be picked up until it is ready, and if a courier arrives at a restaurant before the food is ready, the courier waits idly during that time. Besides the traveling between tasks, a courier spends a pre-defined service duration when executing tasks. When their shift ends, couriers log out of the system, and for the sake of simplicity, courier overtime is not considered when assigning tasks. An order is not assigned to a courier if order delivery time exceeds the courier’s working hours due to routing calculations. The system runs until all orders are processed or all couriers have logged out and no new courier is planned to be logged-in.
The basic assumptions about the problem that are effective throughout this study are as follows:
- The cost of missing an order is assumed to be bigger than the highest courier hiring cost due to the fact that the indirect cost of a dissatisfied customer may cause the loss of customer loyalty, bad reviews, and negative word of mouth, eventually causing a greater and incalculable cost than the opportunity cost of the order itself.
- All couriers are crowdsourced, and a courier with no assigned order is assumed to not be employed and does not receive any payment.
- An order cannot be picked before its ready time; thus, a courier ends up waiting for the order to be ready in case of arriving early. Waiting times of couriers are included in their en-route statuses.
- A working courier is assumed to be idly waiting at their last visited location in-between en-route statuses.
As we mentioned in the problem assumptions, we anticipate the cost of lost sales or missing an order is assumed to be incalculable and bigger than the opportunity cost of the order itself. Also, since we model our solution to increase the number of possible batches, our objective function is not directly related to operational costs but to inform about the impact of decisions. Therefore, the cost or payment made to couriers for delivering a single order is disregarded since it does not affect the decision of prioritization of completing as much order as possible. The cost of hiring a courier is taken into account only to be less than the cost of not completing an order in any case. By doing so, the proposed solution will provide a practical solution that fulfills the maximum number of requests primarily with the least possible resources secondarily.
Mathematical Model
The main stakeholder expectations which can be fulfilled by operational efficiency are presented in Table 1, along with the actions to take in response. We designed our model to meet each of those expectations by incorporating the corresponding actions into the model objective and constraints. By minimizing the number of unassigned orders and the number of utilized couriers, we essentially try to complete the maximum number of orders and create a high number of batches in routes by utilizing the least number of couriers; thus, Actions 2, 3, 5, and 6 are taken by doing so. Actions 1 and 8 are directly related to the pick-up and drop-off time windows. While our postponement strategy aims to minimize courier waiting times at restaurants and is parallel with Action 4, the dissolving strategy aims to create more efficient routes by discarding less efficient ones and is connected to Action 7.
Let be the set of orders and be the set of couriers in the system. Each order has a checkout time of representing the time at which the order appears in the marketplace associated with a restaurant and a drop-off location. Let and be the sets of pick-up and drop-off tasks, respectively. Each order is associated with a pick-up, , and a drop-off task, (see Table 3). This type of indexing provides tractability and simplicity in terms of affiliating tasks and corresponding orders. A pick-up task cannot be performed before the time window lower bound , which can be associated directly with and preparation duration , . Similarly, a drop-off task cannot be performed after the time window upper bound , , which can be determined by the maximum allowed drop-off time by the service provider. The pick-up time window upper bound and drop-off time window lower bound can be determined arbitrarily according to service-level agreements between the marketplace platform and the restaurants.

Table 3.
Parameters and variables.
Shift start and end times of couriers, or log-in and log-out times, are represented by and , respectively, for each courier . An order and its associated pick-up and drop-off tasks can only be assigned to a courier between this time interval.
The objective here is to simultaneously minimize the number of unassigned orders and number of employed couriers. Info about employed couriers is controlled by Equation (2) by checking their order assignment statuses. Equation (3) prevents execution of the same task by the same, courier and Equation (4) helps subtour elimination. Route continuity is achieved by Equation (5) while if two tasks are performed consecutively by the same courier, Equation (6) forces the corresponding orders of those tasks to be assigned to the same courier as well. Equation (7) ensures that if an order is assigned to a courier, the corresponding pick-up task is either the first task of that courier or should be visited after another task by the same courier. Equations (8)–(10) restrict the orders and first pick-up tasks to be assigned to at most one courier and couriers to at most one pick-up tasks. Task beginning and ending times are associated with courier shifts by Equations (11) and (12). Equations (13) and (14) guarantees that there should be at least a total of traveling and service durations between two tasks which are assigned to the same courier. Equation (15) prevents the arrival time of unassigned tasks from taking arbitrary values and exhausting the solution process. Pick-up tasks should always be processed before the drop-off tasks, and this is guaranteed by Equation (16). Equations (17)–(19) ensures that the arrival times of assigned couriers to related tasks are limited with time windows. Non-negativity and binary constraints are provided with Equations (20) and (21).
4. Simulation Framework
A simulation environment was created to capture uncertainties such as the arrival of orders, delivery sequences, and the possibility of changes in routes. Therefore, orders and couriers are entered into the system according to the records in the data, and it is assumed that there is no information about upcoming orders beforehand. As seen in Figure 1, the simulation starts by preparing this data set. Then, the time counter starts and the system checks whether there is a new order or courier entering the system. In the advanced stages of the simulation, information such as assigned and unassigned orders transferred from previous iterations and couriers whose shifts are ongoing are also included in the current orders and couriers along with new orders and couriers. After the status and locations of the current orders and couriers are updated, information such as distance and duration matrices and updated time windows that will be required for routing are created. The compiled information is transferred to the routing algorithm, the obtained routes and the courier information to which those routes are assigned to are recorded, the transition to the next time point is made, and the process is repeated from the beginning. The simulation stops when all the orders are delivered and all the couriers have logged out.
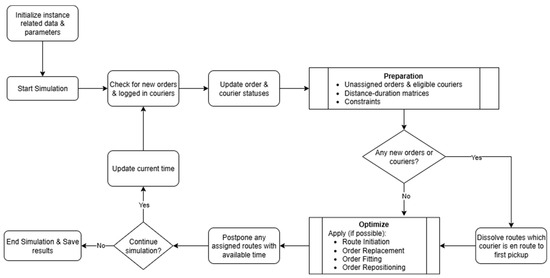
Figure 1.
Proposed simulation framework.
The simulation operates in distinct, fixed 1 min intervals (known as time-stepped simulation). During each step, the system looks for triggering events, such as new orders or courier availability. If any events are identified, the optimization module is activated. Otherwise, the simulation moves on to the next time frame. The algorithm considers the current state and optimizes system evolution over a 60 min planning horizon. Only the immediate decisions are fixed in the plan, while the rest are held in temporary status as time progresses and new events unfold. This structure allows for a time-stepped simulation complemented by event-triggered optimization.
The two key points other than the optimization step in this simulation flow are postponing and partially dissolving assigned routes.
4.1. Postponing Assignments
This method is used in response to the possibility that single-order routes, which are formed especially during the opening phase of the system and when orders start to arrive or when the average batch ratio is less than 2 for the active routes, may become more efficient. In the case of a single order assigned to a courier, the postponement decision is made according to the waiting duration (Tw) between order ready time (Tr) and courier arrival time (Ta), Tr − Ta = Tw. The assignment of the order is postponed if the assigned courier waits for the order to be ready when they arrive at the restaurant, or Tw > 0. At each simulation step, this available duration is checked, and postponement is repeated until Tw ≤ 0. For example, if Tw = 5 for a courier–order pair, this order can be postponed at most 5 times since each simulation step is 1 min. If a new route is created by combining it with a new order while Tw > 0, the previous recorded assignment is deleted and the new route is assigned. If no new route is created until Tw = 0, the recorded route is carried out. In this way, the courier is prevented from waiting for the food at the restaurant. If another more efficient route is assigned to the courier during this period, the delayed order will have to wait for a new courier.
4.2. Dissolving Routes
Similar to the assignment postponement method, the disruption of some existing routes is a method designed and used to evaluate more efficient route creation opportunities. Only routes consisting of at most 2 orders and where the courier assigned to the route is still en-route to receive the first order are determined as suitable for this method. There are actually two main reasons for this choice:
- The disruption of routes with more than 2 orders creates a risk of both delaying the orders which are on later steps of the route and extending the time to obtain results due to increased complexity in the optimization step,
- Preferring the situations when the courier is en-route creates an opportunity to catch the situations in which another order might be placed in the same restaurant with one of the assigned orders during this period.
In the event that a new order arrives in the current time period or a new courier enters the system, suitable routes are reconsidered to be dissolved. The most important point to note for this process is that the courier is en-route and is assumed to be unaware of the information about route change during the drive. In order not to disrupt the flow, the couriers whose routes are dissolved while en-route are assumed to reach their next task location on the estimated arrival time and ready to be assigned new orders from that point on.
4.3. Optimization Algorithm
The optimization step is a framework which consists of a number of algorithmic sub-steps and will be referred as the “Multi-step algorithm” from this point on. Each algorithm deals with a specific subset of the problem and is triggered only once at each optimization step in the given sequence: Route initiation (Algorithm 1) → Order replacement (Algorithm 2) → Order fitting (Algorithm 3) → Order repositioning (Algorithm 4). The details and triggering mechanisms of algorithms are explained in the following sections. In general, the multi-step algorithm is only triggered in specific iterations by following actions:
- When at least one new order is placed;
- When the status of at least one courier is changed from en-route to idle;
- When there is at least one unassigned order in the system.
| Algorithm 1: Route Initiation | |||||||||||
| 1 | |||||||||||
| 2 | |||||||||||
| 3 | |||||||||||
| 4 | |||||||||||
| 5 | |||||||||||
| 6 | |||||||||||
| 7 | |||||||||||
| 8 | |||||||||||
| 9 | |||||||||||
| 10 | |||||||||||
| 11 | |||||||||||
| 12 | |||||||||||
| 13 | |||||||||||
| 14 | |||||||||||
| 15 | |||||||||||
| 16 | |||||||||||
| 17 | |||||||||||
| 18 | |||||||||||
| 19 | |||||||||||
| 20 | |||||||||||
| 21 | |||||||||||
| 22 | |||||||||||
| 23 | |||||||||||
| 24 | |||||||||||
| 25 | |||||||||||
| 26 | |||||||||||
| 27 | |||||||||||
| 28 | |||||||||||
| 29 | |||||||||||
| 30 | |||||||||||
| 31 | |||||||||||
| Algorithm 2: Order Replacement for Route Duration Minimization | |||||||||
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 9 | |||||||||
| 10 | |||||||||
| 11 | |||||||||
| 12 | |||||||||
| 13 | |||||||||
| 14 | |||||||||
| 15 | |||||||||
| 16 | |||||||||
| 17 | |||||||||
| 18 | |||||||||
| 19 | then | ||||||||
| 20 | |||||||||
| 21 | |||||||||
| 22 | |||||||||
| 23 | |||||||||
| 24 | |||||||||
| 25 | |||||||||
| 26 | |||||||||
| 27 | |||||||||
| 28 | |||||||||
| Algorithm 3: Fit Unassigned Orders into Existing Routes | |||||||||
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 9 | |||||||||
| 10 | |||||||||
| 11 | |||||||||
| 12 | (k) | ||||||||
| 13 | |||||||||
| 14 | |||||||||
| 15 | |||||||||
| 16 | |||||||||
| 17 | |||||||||
| 18 | |||||||||
| 19 | |||||||||
| 20 | |||||||||
| 21 | |||||||||
| 22 | |||||||||
| Algorithm 4: Repositioning Orders for Optimal Sequencing | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | |||||
As a general rule in this methodology, no pick-up task should have greater ready time than the succeeding pick-up tasks. This rule is applied in all algorithmic steps as part of the feasibility conditions.
4.3.1. Route Initiation
Algorithm 1 starts by creating an initial feasible solution. First, unassigned orders currently in the system, , are listed in an ascending fashion based on their ready times. Starting from the first order n where orders are assigned to the closest idle courier k where , with a greedy approach. During this assignment, feasibility checks are also performed, ensuring that feasible routes are created at each step. While the orders are assigned to the couriers, the reference points for the couriers with no prior assignment are their current location. As for the couriers who already have at least one order assigned during this process, it becomes the point where the last assigned order will be picked up or delivered on their current route. When an order is up for assignment, reference location of couriers are evaluated by their closeness to the pick-up location of the candidate order. As seen in Figure 2, order 1 is already assigned to the courier during the process and now order 2 is up for assignment. If the closest point for restaurant pick-up task 2 (R2) of order 2 is the location of restaurant pick-up task 1 (R1) of order 1, order 2 is added to the route as R1-R2-C1-C2 in option 1. However, if the customer drop-off task 1 (C1) of order 1 is the closest, then the process continues as R1-C1-R2-C2 in option 2. In both options, customer drop-off task 2 (C2) of order 2 is added to the end of the route since it causes less delay due to prior orders in the route being placed earlier in all cases. The process continues until all unassigned orders are examined for feasible assignments. The route initiation algorithm is triggered by the following cases when there are the following:
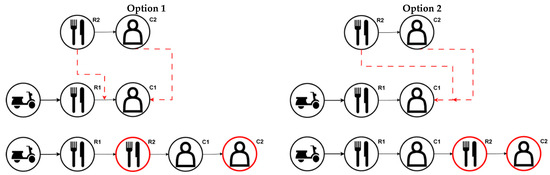
Figure 2.
Representation of the mid-process of initiating feasible routes.
- At least one courier with no assigned route;
- At least one unassigned order in the system.
In the rest of the steps, the objective is to improve the routes initiated in the previous step or in previous iterations and to obtain better routes while minimizing the number of unassigned orders. The following methods are applied to eligible orders and routes:
- Replacing an assigned but not started to be processed order in a route with an unassigned order or an order from another route with the same status;
- Fitting a new order on an existing route;
- Changing the sequence of destinations on a route.
4.3.2. Order Replacement
First, an assigned order n where , is selected to be replaced by considering the duration between the order placement and planned drop-off times. Starting from the highest duration, each assigned order is evaluated to be replaced. The candidate order is selected among the rest of the orders which are currently in the system and whose delivery process is yet to be started. The replacement occurs with no extra major change in the route; only the order to be replaced is taken out of the route and the replacement order is placed in the exact sequence in terms of the positions of its pick-up and drop-off tasks in the route. If the replacement order is not unassigned, two orders switch places in exact positions on their routes. As seen in Figure 3, order 1 (restaurant pick-up task 1 (R1) and customer drop-off task 1 (C1)) is selected to be replaced with candidate order 3 (restaurant pick-up task 3 (R3) and customer drop-off task 3 (C3)), in the exact task positions and under feasibility conditions. The previous route formation, R1-R2-C1-C2 temporarily becomes R3-R2-C3-C2 and the procedure continues as explained in Algorithm 2.
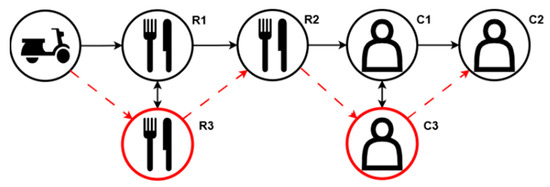
Figure 3.
Representation of replacing selected orders (R1→R3–C1→C3) in a route.
The criterion required for the replacement to take place here is whether there is reduction in the route completion duration of route r of the replaced order and of route r′ of the candidate order if is an assigned order. After each eligible order is controlled for replacement, the swap with the most positive impact is made and the process continues with the next order to be replaced. Order replacement algorithm is triggered by the following cases when there is one or more of the following:
- More than one couriers with assigned routes;
- At least one courier with assigned route and at least one unassigned order in the system.
4.3.3. Order Fitting
In the case of a high number of unassigned orders and insufficient number of couriers, Algorithm 3 takes place to minimize the number of unassigned orders. The assignment is carried out by placing unassigned orders on the optimum route and in the optimum position which causes minimum total delay, i.e., the total deviation in duration to execute steps assigned already plus the total duration to execute new steps. In Figure 4, order 3 is examined for fitting among orders 1 and 2. The optimum place to fit order 3 in the R1-R2-C1-C2 sequence is found by placing restaurant pick-up task 3 (R3) of order 3 right after customer drop-off task 1 (C1) of order 1 and customer drop-off task 3 (C3) of order 3 after customer drop-off task 2 (C2) of order 2, thus creating the new sequence of R1-R2-C1-R3-C2-C3. The order fitting algorithm is triggered by the following cases when there are the following:
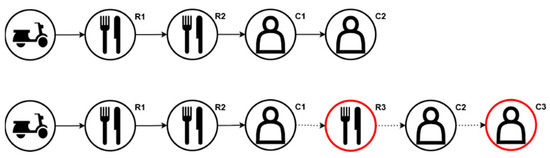
Figure 4.
Representation of fitting a new/unassigned order (R3–C3) in a route.
- At least one courier with assigned route;
- At least one unassigned order in the system.
4.3.4. Order Repositioning
Tasks on the route are reorganized in terms of positioning to find an optimal sequence. Finding the optimal sequence is fairly straightforward, since applying methods such as 2-opt and checking feasibility would result in the optimal sequence in a short time.
Optimal repositioning is completely objective-related; it can involve minimizing the total distance or minimizing the delay for pick-up or drop-off tasks, or for both of them. A basic local search method and limiting search space with feasibility conditions would work and does not take too much computational effort since a typical route has at most 4 orders. As seen in Figure 5, the original sequence of R1-R2-C1-R3-C2-C3 evolves into R1-R3-R2-C1-C3-C2 after repositioning orders and finding the sequence with minimum total route duration. The details of order repositioning is explained in Algorithm 4 and it is triggered by one case only, which is when there is at least one courier with assigned route.
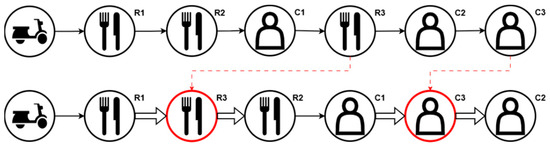
Figure 5.
Representation of repositioning order steps of a selected order (R3–C3) in a route.
5. Results and Analysis
Both the MIP model and the algorithm are tested in terms of performance using Grubhub MDRP test instances (https://github.com/grubhub/mdrplib, accessed on 17 April 2025) and the results are compared for solution quality. The preliminary tests show that solving the instances, even the smallest ones, in reasonable time via modeling is not possible; thus, smaller parts are sliced from the whole for each selected instance. Namely, the first 20 orders according to their placement time and 10 couriers according to their log-in times, both in an ascending order, are selected to create smaller fragments. Instance characteristics and details about encoding in instance names are given by Reyes et al. [23].
The testing environment for the mathematical model is created by using the pyomo package and Gurobi v11.0.3rc0 win64 on 11th Gen Intel® Core™ i7-11850H (manufactured by Intel Corporation in Santa Clara, CA, USA) with 2.50 GHz processor speed and 32 GB Ram memory. The algorithm is developed by using Java v19.0.2 in the same environment.
Among all Grubhub instances, the selected ones are the reduced sample instances (represented with “r” in the instance name right after the seed value) which are sampled from the original dataset and presented in an ascending order in terms of order placement and courier log-in times. A total of 80 instances are selected and run for benchmarking purposes in the previously mentioned setting. A time limit of 10 min is set for each instance and the ones which present an optimal solution in given time (20 instances in total) are selected for comparison and the results are displayed in Table 4. Then, the same 20 instances are run in the simulation environment using the algorithmic steps presented in the previous section with a time limit of 30 s at each optimization phase. The results are compared in terms of the number of incomplete or unassigned orders, the number of excess or unutilized couriers, the waiting time of food orders for courier to pick-up, the duration between checkout and delivery, and the optimality gap between the exact solutions and our proposed solutions.

Table 4.
Performance comparison between the exact solution and proposed solution (PS).
According to the results, our heuristics method provides optimal and near-optimal solutions in all instances with an average of 1,3% relative gap from the exact solution provided by the MIP model. The gap primarily depends on the difference between unassigned orders since the objective function is affected more by this due to the assumption made in the problem definition that the cost of an unassigned order should be greater that cost of hiring a courier in any case and secondarily by the difference between unutilized or excess number of couriers. Additionally, the duration performance parameters show that when the system completes fewer orders or utilizes more couriers compared to optimal levels, the pick-up and delivery durations naturally become shorter in some cases. This creates a trade-off decision that falls to the platform managers to obtain desired performance levels or create balance between specific parameters. Overall, the results demonstrate that our solution shows good performance with small problem instances.
The problem is NP-Hard by nature, and so an exact solution can only be obtained from a small instance in reasonable time [16]. Due to the sophisticated and time-consuming structure of the problem, full-size instance results are compared with past studies as seen in Table 5. The study conducted by the authors of [16] evaluates 16 instances in terms of “Average Batch Size” and “Courier Utilization Rate”, among other performance indicators which are outside of the focus of this study. As we run the same instances with the same parameters such as “at most 4 batches in each assignment” and “1 min time limit for optimization instead of 2”, the results comparison shows that our algorithm yields higher batch ratios in each instance, 14% greater batch ratios on average.

Table 5.
Performance comparison between the reference study and proposed solution.
As for the courier utilization, the rate is calculated in the same manner as the reference study. All activities such as driving, waiting for the order to be ready, and pick-up and drop-off services are determined as utilized time as opposed to idle time. Our method provides higher utilization rates in 11 out of 16 instances, 5.5% more utilization on average. This tells us that our method forces the system to meet the demand by creating more batches on each route and requiring a smaller number of couriers to carry out the operation.
For further analysis, we test the method performance by expanding the test instances to 104 samples in total. Then, we group the instances according to the number of orders placed as “small” with 48, “medium” with 40, and “large” with 16 instances. The number of orders ranges between 242 and 354 for small instances, 483 and 708 for medium instances, and 967 and 1185 for large instances. A time limit of 30 s is set for small and medium-size instances, which none of the instances have reached, and a 60 s limit is set for large-size instances. To see the performance of the multi-step algorithm and the effects of strategies employed, four main settings are established:
- I.
- Algorithm only;
- II.
- Algorithm + Postponing strategy;
- III.
- Algorithm + Dissolving strategy;
- IV.
- Algorithm + Both strategies.
Each instance group is run in a simulation framework for each setting, and the results are aggregated under seven different performance metrics, namely Average Missed Order Rate, Average Employed Courier Rate, Average Batch Size, Average Early Pickup Rate, Average Courier Waiting Duration, and Average Number of Orders Assigned to a Courier. These metrics are carefully selected to be in line with the objective of our methodology. In the following sections, individual and combined effects of our algorithm and applied strategies will be analyzed under these metrics.
5.1. Effects of Postponing Strategy
As mentioned in Section 4, postponing assignments strategy is employed with the idea of creating opportunities for more efficient routes by waiting for the last possible moment to take action. In this setting, the test results show that the sole effect of postponing assignments in batch sizes is very positive, ranging between 92% and 123%; more batching opportunities are definitely created, as seen in Figure 6. As for the workforce efficiency, 2.8% to 4.2% fewer couriers are needed to carry out the operations with the help of this strategy (see Figure 7). The rest of the metrics show that while this strategy alone can decrease the missed orders and better utilize couriers by assigning more orders to each, this approach should be carefully considered since it might overload the system and cause delays in the operational steps (see Table 5).
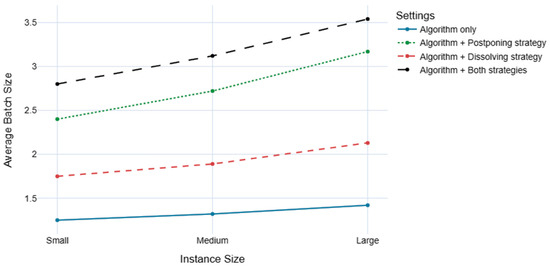
Figure 6.
Order batching performances of four different strategies.
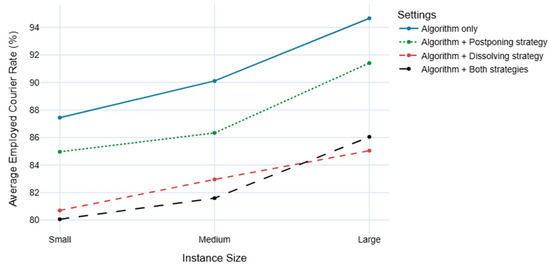
Figure 7.
Courier employment requirements of four different strategies.
5.2. Effects of Dissolving Strategy
Similar to the approach in postponing strategy, we aim to achieve better routes specifically for orders that are yet to be ready. As we expected, this setting dramatically decreases the workforce utilization or courier employment rate by 7.7% to 10.1% compared to the multi-step algorithm-only results (see Figure 7). The same effect can be observed in the waiting times of couriers at the restaurant for meals to be ready. The strategy provides a 38.1% to 44.8% improvement in the number of early pick-up orders and an 11.9% to 22.1% decrease in the courier waiting times at the restaurant. However, the strategy forces the system to process the orders in a timely manner by missing or rejecting some of the orders and relaxing the system load (see Table 5).
5.3. The Combined Effects of Both Strategies
After individually testing the performance of strategies, we combined them with the multi-step algorithm, expecting to see their strengths affect the end results and provide better performance than both of them in pairwise comparisons. In Figure 6, we can observe that this setting yields more batches than the rest of the settings, 123.9% to 149.3% more than the solo algorithm, 37.5% to 39.7% more than the dissolving strategy, and 10.4% to 14.2% more than the postponing strategy. We can see similar results in courier employment rates, with the combined strategies setting providing superior results overall, excluding the large instances where the dissolving strategy yields slightly better results (only 1.2% less) while not supplying the demand at the level of current strategy (see Figure 7). For the rest of the metrics, as shown in Table 6, we can easily say that the combined strength of both strategies supports the weak points of each other and, in the end, creates a robust system that provides satisfactory results for all the stakeholders in reasonable time.

Table 6.
Comparison between strategies on other performance metrics with different instance sizes.
The batch limit is set to 4 in all previous tests. To see the sensitivity of our solution to the business decisions on limiting the maximum batch number, we expand our tests with different batch limits, and the results are presented in Table 7. We compare the results with the same performance parameters, and although it might not seem particularly significant in numerical terms, we see the highest difference in average missed orders of 40% when we decrease the limit from 4 to 2 in large instances. Among all parameters, the highest differences are all in the same category, while the rest of the parameters remain below 10% difference in each case and instance. This shows us that our solution is resilient to drastic changes and still provides good results.

Table 7.
Testing the sensitivity of the combination of algorithm + both strategies with different batch sizes.
6. Conclusions
OFD problems represent the rapidly developing challenge at the intersection of operations research, real-time logistics, customer service, and technological advancements. Unlike traditional logistics problems, OFD reference is marked by high expectations for extreme time sensitivity and quality of service. This complexity has moved beyond the need to coordinate the interests of many stakeholders—including customers, courier, restaurants and platform providers—each with different priority and obstacles. In this study, we have highlighted the underlying complications of the OFD process and emphasize the need for rapid, adaptive and scalable routing solutions.
The scope of our approach to the OFD problem is shaped by the main expectations of the stakeholders in this ecosystem. In order to maintain the sustainability and continuity of this ecosystem, each stakeholder should receive the contentment of being a part of this system, and this can be achieved by creating an optimization strategy that considers their expectations. Our proposed solution employs an MIP formulation that considers the expectations of each stakeholder by minimizing the unmet demand and the required workforce to decrease employment costs while maintaining timely pick-up and delivery operations. The model falls short on solving bigger problems in terms of computation time, and to overcome that obstacle, we present a rolling horizon framework for our multi-step algorithm and strategies which provide highly promising results. To show the performance of our proposed solution, we create a simulation framework to mimic the real-time OFD operations and test our solution with publicly provided Grubhub instances. Our multi-step algorithm and proposed strategies show high performance in terms of order batching, courier employment rates, and all the other metrics defined in the previous section. The strategies, when applied individually, still present good results; however, their strengths differ in various metrics. These strategies, namely dissolving routes and postponing assignments, can be utilized in different scenarios both individually or combined. This decision, along with how aggressively or when they are utilized, falls to the user by considering the trade-off between supplying less demand to make pick-ups/deliveries more promptly and supplying more demand to create more efficient routes and extending time constraints. Overall, the multi-step algorithm and combined strategies provide a more balanced and rapid solution to the OFD problem.
Many insights and takeaways can be derived from the results of this study and determined as future directions. An important one is that clustering methods can be implemented not directly to the optimization sequence but in a parallel structure. In this way, another module, which can be activated by a system load threshold and tracks the orders currently in the system, continuously provides feasible clusters or routes to the optimization process while not causing any extra computational delay to the process.
Another important takeaway is considering order cancellations, as some of the customers may change their minds during the process and cancel their order. This can disrupt the delivery flow and can cause routes to be less efficient. Another strategy that considers sudden order cancellation and re-optimizes the current routes in the process would make the system more robust to unpredictability. The other side of that coin is the demand rejection strategy: the platform should decide which orders should be accepted or rejected when the system is overloaded due to not having a sufficient number of couriers. This can occur in many different scenarios such as orders coming at rush hours, traffic congestion, and harsh weather conditions causing delays or couriers being involved in road accidents. A workload control and a decision-making strategy that continuously checks the system load and decides which orders to accept or reject can be beneficial for all the stakeholders since any delay due to high numbers of orders and insufficient workforce would create dissatisfaction to everyone involved from different angles.
The proposed approach considers all stakeholder perspectives; however, the decision makers and the main practitioners here are logistics managers and platform operators. From a managerial perspective, a multi-step algorithm and assignment strategies provide an opportunity to handle the process with ease through trackability in each step and more precisely by tuning each part specifically to achieve desired outcomes. Data-driven and adaptive routing strategies such as our solution will yield more robustness and efficiency for real-time operational decisions and processes. The main advantages of our solution are being fast, flexible, and efficient in terms of meeting multiple stakeholder expectations simultaneously. There are limitations for this approach as well, such as scalability, which should be covered by clustering or similar divide-and-conquer methods as we mentioned earlier, and not being fully generalizable for every case. However, through continuous refinement and real-world validation, this framework could play a crucial role in shaping the design of advanced OFD platforms that successfully balance the varied and sometimes conflicting needs of all stakeholders involved.
For future directions, adding a stochastic aspect to food preparation times or courier travel durations would make the problem more realistic. Although our multi-step algorithm adapts to the changing circumstances, a proactive approach to uncertainty would turn the solution into a more resilient system that can yield efficient results and decrease the dependency on accurate data.
Another direction would be to intentionally include the fairness factor for couriers. Our solution has a positive and indirect effect on fairness by utilizing a minimum number of couriers and increasing their workloads to the limits. However, in a setting where all the couriers are utilized with guaranteed hourly payment, balancing the workload would play a more crucial role in terms of both fairness and resource utilization.
Finally, different delivery modes are already utilized in the OFD ecosystem, such as bikes, cars, or unmanned ground and aerial vehicles. Exploring and including those options would be a good starting point to make the solution more adaptive to transportational challenges such as urban conditions and new trends in delivery logistics.
Author Contributions
Conceptualization, S.Ü., G.T., and S.B.; methodology, S.Ü., G.T., and S.B.; software, S.Ü.; validation, S.Ü., G.T., and S.B.; formal analysis, S.Ü.; writing—original draft preparation, S.Ü.; writing—review and editing, G.T. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available in Meal Delivery Routing Problem Test Instances at https://github.com/grubhub/mdrplib (accessed on 17 April 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| OFD | Online Food Delivery |
| MDRP | Meal Delivery Routing Problem |
| PDPTW | Pickup and Delivery Problem with Time Windows |
| MIP | Mixed Integer Programming |
References
- Deng, F.; Qin, H.; Li, J.; Cheng, C. The Pickup and Delivery Problem with Time Windows and Incompatibility Constraints in Cold Chain Transportation. Transp. Sci. 2023, 57, 444–462. [Google Scholar] [CrossRef]
- Yang, S.; Xia, J.; Guo, S.; Fang, X.; Ni, C. A novel time-dependent electric vehicle pickup and delivery problem with time windows in cold supply chains. Expert Syst. Appl. 2025, 294, 128813. [Google Scholar] [CrossRef]
- Jiang, L.; Liang, C.; Dong, J.; Lu, W.; Mladenovic, M. A Disruption Recovery Problem with Time Windows Change in the Last Mile Delivery of Online Shopping. Math. Probl. Eng. 2018, 2018, 2096416. [Google Scholar] [CrossRef]
- Muñoz-Villamizar, A.; Velazquez-Martínez, J.C.; Caballero-Caballero, S. A large-scale last-mile consolidation model for e-commerce home delivery. Expert Syst. Appl. 2024, 235, 121200. [Google Scholar] [CrossRef]
- Posada, M.; Andersson, H.; Häll, C.H. The integrated dial-a-ride problem with timetabled fixed route service. Public Transp. 2017, 9, 217–241. [Google Scholar] [CrossRef]
- Bertsimas, D.; Jaillet, P.; Martin, S. Online Vehicle Routing: The Edge of Optimization in Large-Scale Applications. Oper. Res. 2019, 67, 143–162. [Google Scholar] [CrossRef]
- Kohar, A.; Jakhar, S.K. A capacitated multi pickup online food delivery problem with time windows: A branch-and-cut algorithm. Ann. Oper. Res. 2021. [Google Scholar] [CrossRef]
- Ulmer, M.W.; Thomas, B.W.; Campbell, A.M.; Woyak, N. The Restaurant Meal Delivery Problem: Dynamic Pickup and Delivery with Deadlines and Random Ready Times. Transp. Sci. 2021, 55, 75–100. [Google Scholar] [CrossRef]
- Yildiz, B.; Savelsbergh, M. Provably High-Quality Solutions for the Meal Delivery Routing Problem. Transp. Sci. 2019, 53, 1372–1388. [Google Scholar] [CrossRef]
- Katiyar, S.; Khan, R.; Kumar, S. Artificial Bee Colony Algorithm for Fresh Food Distribution without Quality Loss by Delivery Route Optimization. J. Food Qual. 2021, 2021, 4881289. [Google Scholar] [CrossRef]
- Wang, W.; Jiang, L. Two-Stage Solution for Meal Delivery Routing Optimization on Time-Sensitive Customer Satisfaction. J. Adv. Transp. 2022, 2022, 9711074. [Google Scholar] [CrossRef]
- Bi, H.; Zhu, X.; Lu, F.; Huang, M. The Meal Delivery Routing Problem in E-commerce Platforms under the Shared Logistics Mode. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 1799–1819. [Google Scholar] [CrossRef]
- Hong, W.; Yin, W.; Xu, S. Collaborative truck-robot routing problem with meal delivery for the elderly on the personalized needs. Int. J. Ind. Eng. Comput. 2024, 15, 615–626. [Google Scholar] [CrossRef]
- Kim, S.H.; Chung, B.D. Integrated food delivery problem considering both single-order and multiple order deliveries. Comput. Ind. Eng. 2024, 196, 110458. [Google Scholar] [CrossRef]
- Martínez-Sykora, A.; McLeod, F.; Cherrett, T.; Friday, A. Exploring fairness in food delivery routing and scheduling problems. Expert Syst. Appl. 2024, 240, 122488. [Google Scholar] [CrossRef]
- Simoni, M.D.; Winkenbach, M. Crowdsourced on-demand food delivery: An order batching and assignment algorithm. Transp. Res. Part C Emerg. Technol. 2023, 149, 104055. [Google Scholar] [CrossRef]
- Chen, J.-F.; Wang, L.; Liang, Y.; Yu, Y.; Feng, J.; Zhao, J.; Ding, X. Order Dispatching Via GNN-Based Optimization Algorithm for On-Demand Food Delivery. IEEE Trans. Intell. Transport. Syst. 2024, 25, 13147–13162. [Google Scholar] [CrossRef]
- Shao, Q.; Miao, J.; Liao, P.; Liu, T. Dynamic Scheduling Optimization of Automatic Guide Vehicle for Terminal Delivery under Uncertain Conditions. Appl. Sci. 2024, 14, 8101. [Google Scholar] [CrossRef]
- Wang, W.; Gao, S. Waiting Strategy for the Dynamic Meal Delivery Routing Problem with Time-Sensitive Customers Using a Hybrid Adaptive Genetic Algorithm and Adaptive Large Neighborhood Search Algorithm. Systems 2024, 12, 170. [Google Scholar] [CrossRef]
- Xie, F.; Chen, Z.; Zhang, Z. Research on Dynamic Takeout Delivery Vehicle Routing Problem under Time-Varying Subdivision Road Network. Mathematics 2024, 12, 962. [Google Scholar] [CrossRef]
- Xu, H.; Qian, W.; Guo, K.; Wang, X. Research on Takeaway Delivery Route Optimization Problem Considering Merchant Priority. Sustainability 2024, 16, 11127. [Google Scholar] [CrossRef]
- Wang, X.; Ji, C.; Xu, H.; Guo, K. Research on Dynamic Optimization of Takeout Delivery Routes Considering Food Preparation Time. Sustainability 2025, 17, 2771. [Google Scholar] [CrossRef]
- Reyes, D.; Erera, A.; Savelsbergh, M.W.P.; Sahasrabudhe, S.; O’Neil, R. The Meal Delivery Routing Problem. Optimization Online. 2018. Available online: https://optimization-online.org/wp-content/uploads/2018/04/6571.pdf (accessed on 2 February 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).