Research on Hydraulic Fracturing Crack Propagation Based on Global Cohesive Model
Abstract
1. Introduction
2. Cohesive Element Model
2.1. Element Constitutive Model
2.2. Crack Initiation and Propagation Criteria
2.3. Numerical Model
2.4. Test Supplement
3. Results and Discussion
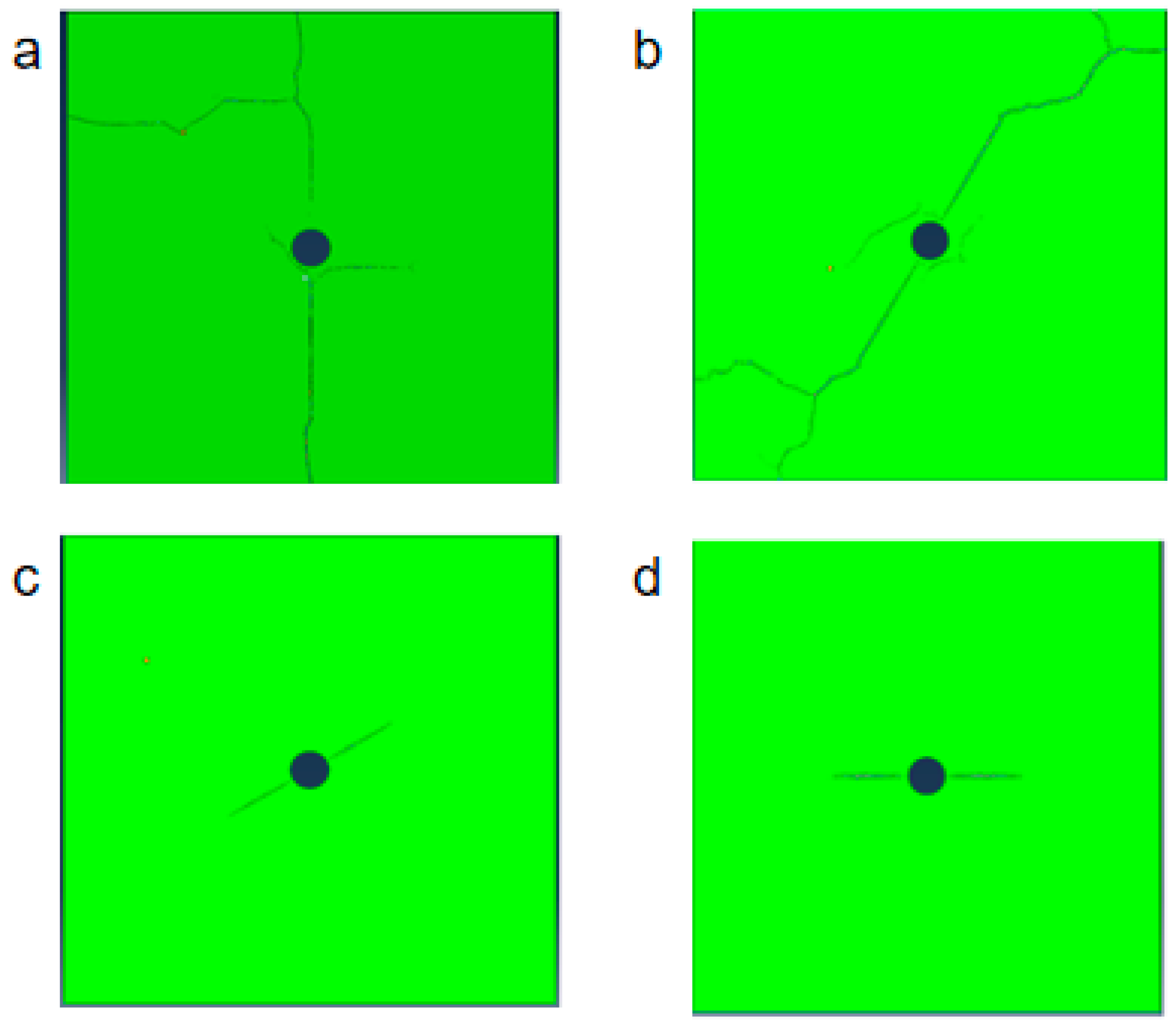
3.1. The Influence of Crack Inclination
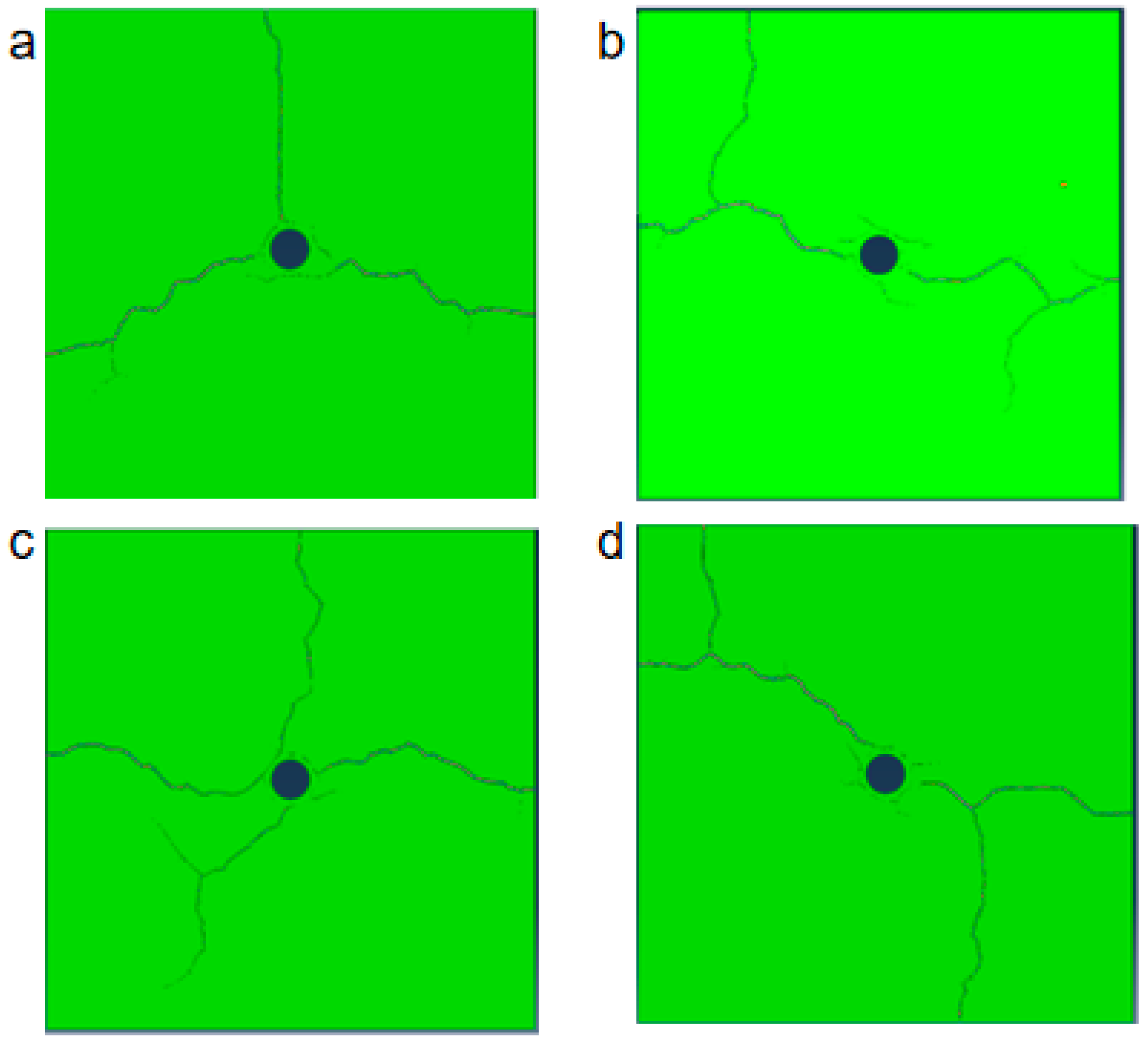
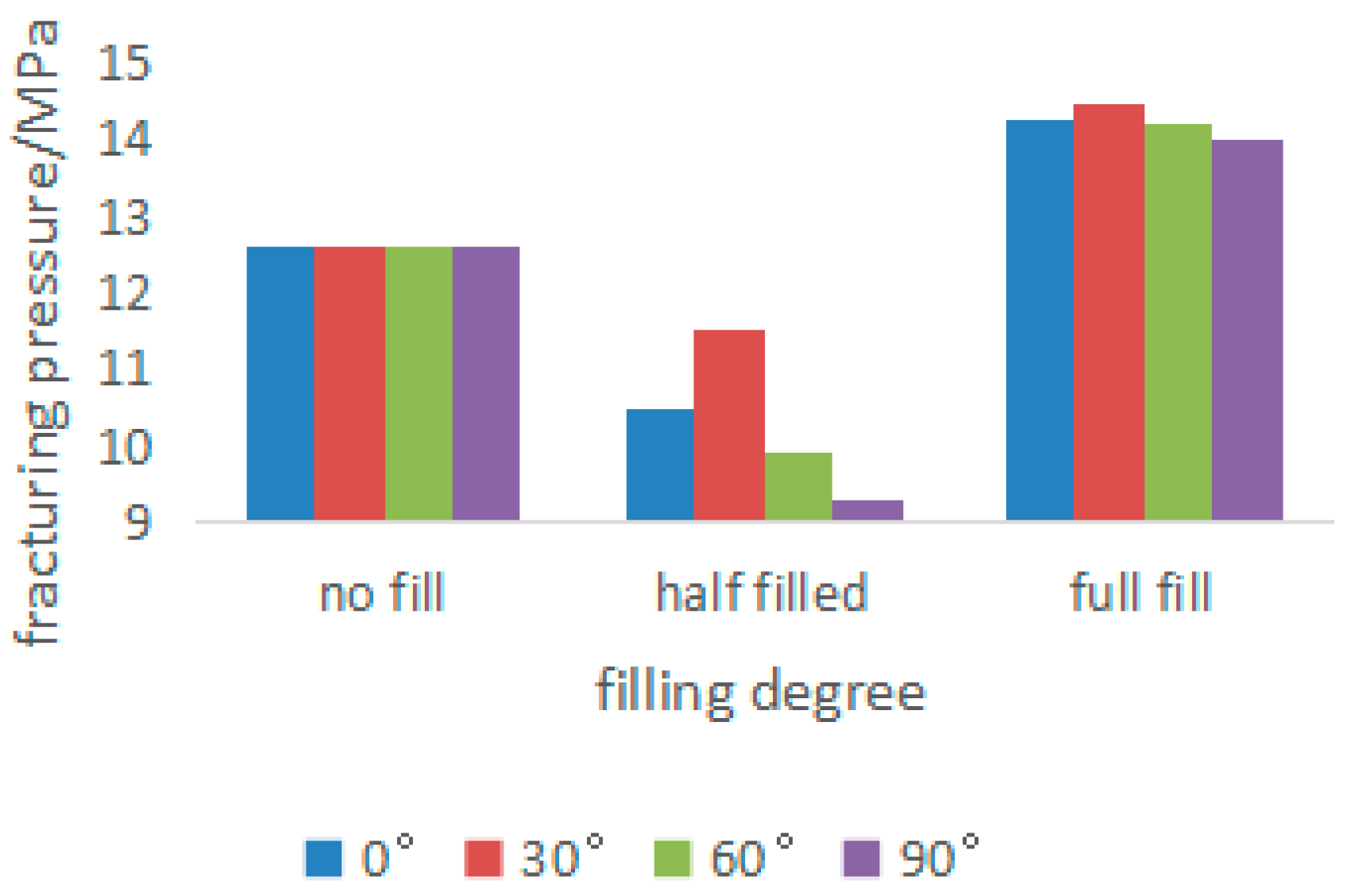
3.2. The Influence of Filling Degree
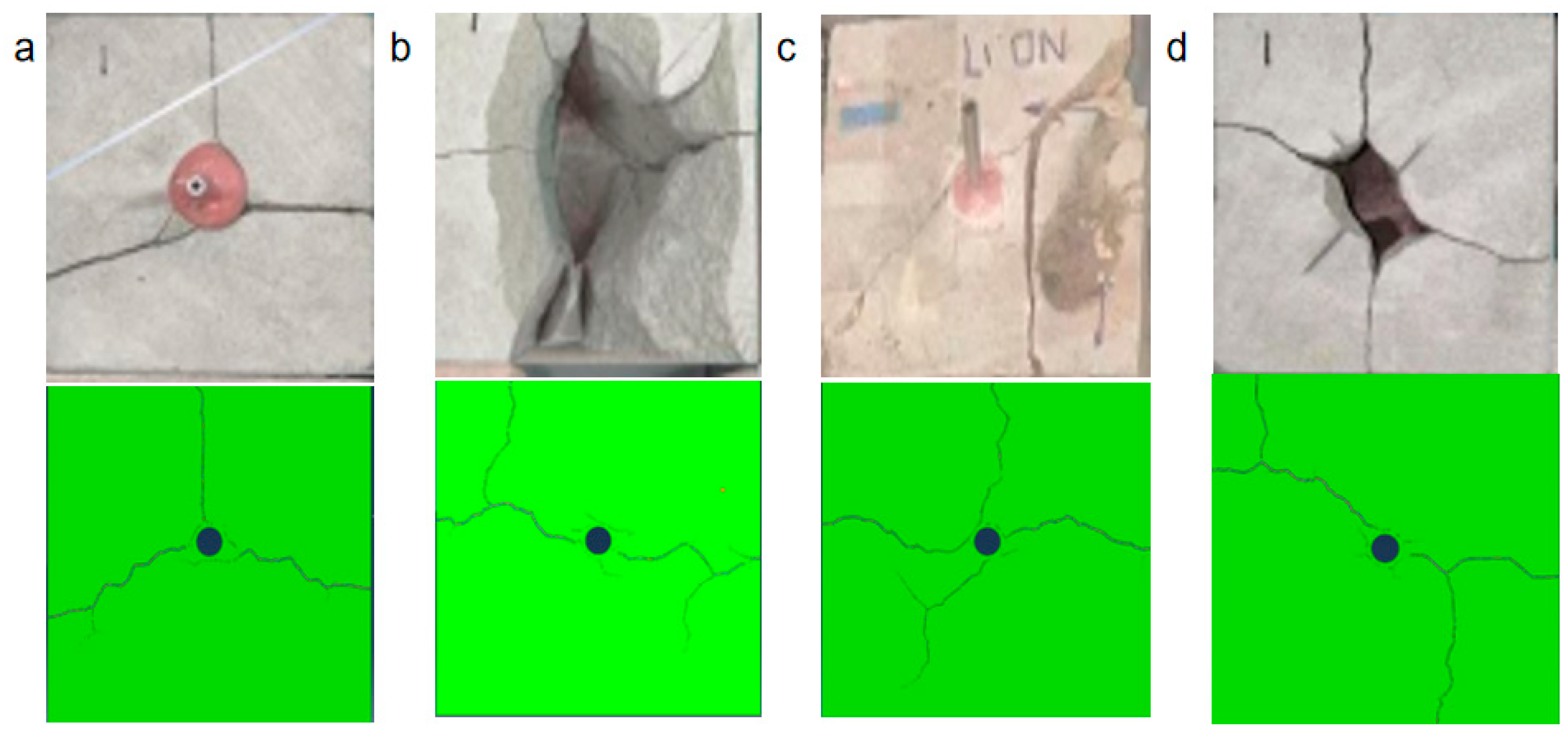
3.3. Experimental Verification
3.3.1. Fracturing Pressure
3.3.2. Crack Propagation
3.4. Discussion
4. Conclusions
- (1)
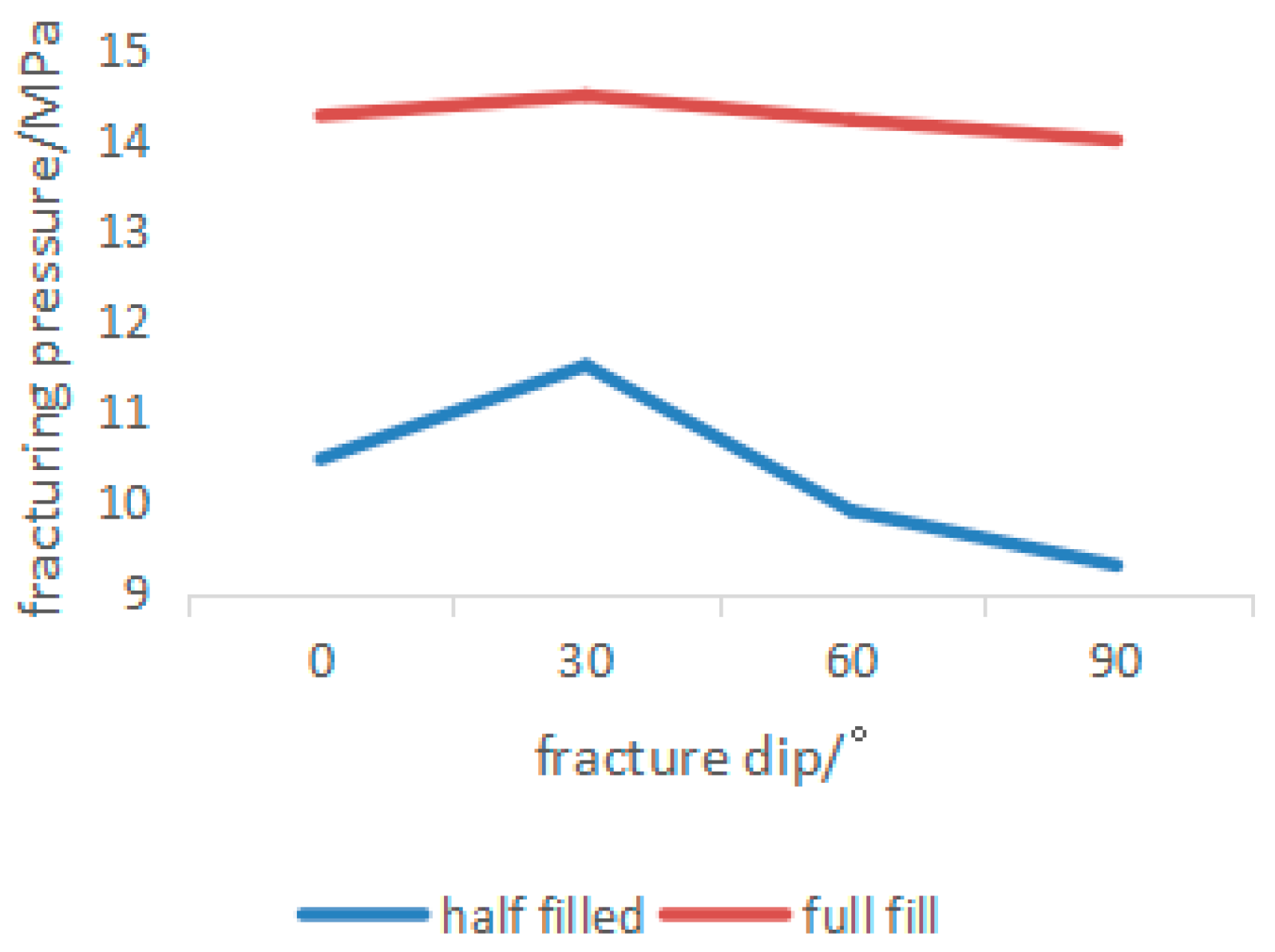
- The results show that the fracture pressure and crack propagation paths are significantly influenced by the filling level. At the same time, the fracture pressure and crack propagation paths are also affected by the crack inclination.
- (2)
- The fracture pressure always reaches its maximum value at the fully filled degree and reaches its minimum value at the semi-filled state. When considering the crack inclination, the fracture pressure always reaches its maximum value when the crack inclination is 30°. When the crack inclination is greater than 30°, the fracture pressure will gradually decrease.
- (3)
- In the semi-filled state, when the crack inclination is less than 30°, the crack will propagate along the natural crack and generate branch cracks near the end face. Small cracks will also form near the wellbore, forming a more complex crack network. When the crack inclination is greater than 30°, it can be clearly seen that, except for the main crack, no other obvious cracks are generated. The complexity of the cracks in the full-filling state significantly increases, especially when the crack inclination is 60° and 90°, as the cracks do not completely propagate along the natural cracks but will bend significantly and generate multiple branch cracks extending to the surface. When the crack inclination is 30°, the cracks extend and branch at an angle perpendicular to the natural crack, and multiple different angles of bending and branch cracks occur. When the crack inclination is 0°, three cracks will extend from the wellbore to the surface, and only one extends along the main crack.
- (4)
- Based on the true triaxial hydraulic fracturing test, the obtained fracture propagation pattern is consistent with the model. However, due to the presence of natural fractures and other factors, the fracture pressure is relatively low.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, X.; Huang, Z.; Long, T.; Li, G.; Tian, S.; Wang, H.; Yang, R.; Li, K.; Wang, Z. Radial Wellbore Cross-Layer Fracturing in Multi-Lithologic Superimposed Shale Oil Reservoirs: A Laboratory Study. Engineering 2025, 45, 188–211. [Google Scholar] [CrossRef]
- Qiu, G.; Chang, X.; Li, J.; Guo, Y.; Zhou, Z.; Wang, L.; Wan, Y.; Wang, X. Study on the interaction between hydraulic fracture and natural fracture under high stress. Theor. Appl. Fract. Mech. 2024, 130, 104259. [Google Scholar] [CrossRef]
- Deng, D.; Ren, Q.; Yang, Y.; Wang, J.; Zeng, C.; He, P.; Liu, J.; Liu, P.; Luo, Y. Investigation of Hydraulic Fracture Propagation Characteristics in the Shale Reservoir with Natural Fractures and Bedding Plane. Geofluids 2025, 2025, 9970558. [Google Scholar] [CrossRef]
- Wei, C.; Yu, L.; Geng, S.; Yuan, Z.; Wang, Y. Experimental and numerical studies on propagation behavior between hydraulic fractures and pre-existing fractures under prepulse combined hydraulic fracturing. J. Rock Mech. Geotech. Eng. 2025, 17, 2879–2892. [Google Scholar] [CrossRef]
- Qin, M.; Yang, D.; Jia, Y.; Zhou, Y. Peridynamics modeling of hydraulic fracture interaction with natural fractures in fractured rock mass. Eng. Fract. Mech. 2024, 307, 110299. [Google Scholar] [CrossRef]
- Barbosa, L.G.; Cleto, P.R.; Maedo, M.A.; Camargo, M.; Rodrigues, E.A.; Manzoli, O.L. Simulation of the natural fractures influence on hydraulic fractures propagation using high aspect ratio interface elements. Comput. Geotech. 2025, 179, 107026. [Google Scholar] [CrossRef]
- Zheng, Y.; He, R.; Huang, L.; Bai, Y.; Wang, C.; Chen, W.; Wang, W. Exploring the effect of engineering parameters on the penetration of hydraulic fractures through bedding planes in different propagation regimes. Comput. Geotech. 2022, 146, 104736. [Google Scholar] [CrossRef]
- Han, P.; Wang, K.; Pang, J.; Ji, X.; Zhang, C. Response properties of geometries of coal penetrating fracture on seepage behavior. Int. J. Min. Sci. Technol. 2025, 35, 191–211. [Google Scholar] [CrossRef]
- Zhong, C.; Chen, J.; Leung, J.Y. Analysis of downhole temperature-strain response in hydraulic fracturing—A coupled geomechanics-thermal-flow simulation approach. Geoenergy Sci. Eng. 2025, 247, 213710. [Google Scholar] [CrossRef]
- Tan, P.; Chen, Z.W.; Huang, L.K.; Zhao, Q.; Shao, S.R. Evaluation of the combined influence of geological layer property and in-situ stresses on fracture height growth for layered formations. Pet. Sci. 2024, 21, 3222–3236. [Google Scholar] [CrossRef]
- Cruz, F.; Roehl, D.; do Amaral Vargas, E., Jr. An XFEM implementation in Abaqus to model intersections between fractures in porous rocks. Comput. Geotech. 2019, 112, 135–146. [Google Scholar] [CrossRef]
- Kong, X.; Huang, H.; Xie, G.; Yan, R.; Xu, H.; Li, S. Experimental study on equilibrium initiation and extension of multiple clusters of fractures based on true triaxial physical simulation. J. Nat. Gas Geosci. 2023, 8, 349–362. [Google Scholar] [CrossRef]
- Huang, T.; Zhu, H.; Liu, Q.; Dai, X.; Tang, X.; Yi, X.; He, X.; She, C.; Zheng, M. Study on multi-cluster fracture interlaced competition propagation model of hydraulic fracturing in heterogeneous reservoir. Geoenergy Sci. Eng. 2025, 244, 213415. [Google Scholar] [CrossRef]
- Ouchi, H.; Foster, J.T.; Sharma, M.M. Effect of reservoir heterogeneity on the vertical migration of hydraulic fractures. J. Pet. Sci. Eng. 2017, 151, 384–408. [Google Scholar] [CrossRef]
- Nagaso, M.; Mikada, H.; Takekawa, J. The role of rock strength heterogeneities in complex hydraulic fracture formation–numerical simulation approach for the comparison to the effects of brittleness. J. Pet. Sci. Eng. 2018, 172, 572–587. [Google Scholar] [CrossRef]
- Parvizi, H.; Rezaei-Gomari, S.; Nabhani, F.; Turner, A. Evaluation of heterogeneity impact on hydraulic fracturing performance. J. Pet. Sci. Eng. 2017, 154, 344–353. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, J.; Hu, Y.; Zhang, S.; Huang, T.; Liu, X. Numerical simulation of multistage fracturing optimization and application in coalbed methane horizontal wells. Eng. Fract. Mech. 2020, 223, 106738. [Google Scholar] [CrossRef]
- Azarov, A.V.; Serdyukov, S.V. Stress Determination in Rock Mass by Fracture Propagation Pressure Nearby Cylindrical Opening. J. Min. Sci. 2025, 61, 13–28. [Google Scholar] [CrossRef]
- Li, X. Fracture reorientation mechanism during hydraulic fracturing based on XFEM simulation. Front. Earth Sci. 2024, 12, 1503934. [Google Scholar] [CrossRef]
- Zhong, Y.; Yu, H.; Wang, Q.; Chen, X.; Ke, X.; Huang, H.; Wu, H. Hydraulic fracturing in layered heterogeneous shale: The interaction between adjacent weak interfaces. Eng. Fract. Mech. 2024, 303, 110115. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, B.; Wang, D.; Jia, Z. Features of fracture height propagation in cross-layer fracturing of shale oil reservoirs. Pet. Explor. Dev. 2021, 48, 469–479. [Google Scholar] [CrossRef]
- Zou, Y.S.; Yang, C.; Zhang, S.C.; Ma, X.F.; Li, Y.C.; Zou, L.Q. Multi-fracture growth behavior during TPDF in a horizontal well of multi-clustered perforations: An experimental research. Pet. Sci. 2024, 21, 4230–4247. [Google Scholar] [CrossRef]
- He, L.; Eyre, M.; Coggan, J.; Holley, S.; Watkins, D. Investigating hydraulic anisotropy of fractured rock mass using three-dimensional numerical modelling and laser scanning: A case study at South Crofty mine in Cornwall, UK. J. Hydrol. Reg. Stud. 2025, 60, 102541. [Google Scholar] [CrossRef]
- Sarkar, P.; Yoon, S.; Kim, J.; Baek, S.; Sun, A.; Yoon, H. Surrogate models for development of unconventional shale reservoirs by an integrated numerical approach of hydraulic fracturing, flow and geomechanics, and machine learning. Geomech. Energy Environ. 2025, 43, 100691. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, Z.; Liu, Z.H.; Wu, L.; Wu, Y.; Guo, J. The impact of step sizes on pressure prediction in fracturing treatment via deep learning algorithms. Pet. Sci. Technol. 2025, 43, 2572–2588. [Google Scholar] [CrossRef]
- Konstantinou, C.; Papanastasiou, P. A data-driven and machine learning-assisted interpretation of hydraulic fracturing experiments in various formations. Geomech. Energy Environ. 2025, 43, 100707. [Google Scholar] [CrossRef]
- Liu, M.; Xie, H.; Pan, W.; Ding, S.; Li, G. Prediction of cutting force via machine learning: State of the art, challenges and potentials. J. Intell. Manuf. 2023, 36, 703–764. [Google Scholar] [CrossRef]
- Der, O.; Tasci, M.; Basar, G.; Ercetin, A. Intelligent modeling and prediction of CO2 laser cutting performance in FFF-printed thermoplastics using machine learning algorithms. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2025. [Google Scholar] [CrossRef]
- Swapnil, K.; Abhijit, C.; Avtar, S.; Siladitya, P. Phase field method to model hydraulic fracturing in saturated porous reservoir with natural fractures. Eng. Fract. Mech. 2023, 286, 109289. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, X.; Rabczuk, T. Phase field method for quasi-static hydro-fracture in porous media under stress boundary condition considering the effect of initial stress field. Theor. Appl. Fract. Mech. 2020, 107, 102523. [Google Scholar] [CrossRef]
- Navidtehrani, Y.; Betegón, C.; Vallejos, J.; Martínez-Pañeda, E. A phase field model for hydraulic fracture: Drucker–Prager driving force and a hybrid coupling strategy. Comput. Methods Appl. Mech. Eng. 2025, 444, 118155. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, J.; Yi, L.; Yi, D.; Li, X. A Cohesive Phase-Field Model for Dynamic Mixed-Mode Hydraulic Fractures. Rock Mech. Rock Eng. 2025, 1–23. [Google Scholar] [CrossRef]
- Wang, J. Hydraulic Fracturing Simulation of Concrete Face Slab Based on XFEM and Cohesive Model. China Water Power Electrif. 2025, 6, 11–17. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Xin, J.; Huang, H. Research on the effect mechanism of mesoscopic damage behavior of microencapsulated resin mineral composites based on cohesive elements. Comput. Part. Mech. 2025, 1–15. [Google Scholar] [CrossRef]
- ABAQUS Inc. ABAQUS Analysis User’s Manual; Dassault Systèmes: Providence, RI, USA, 2023. [Google Scholar]
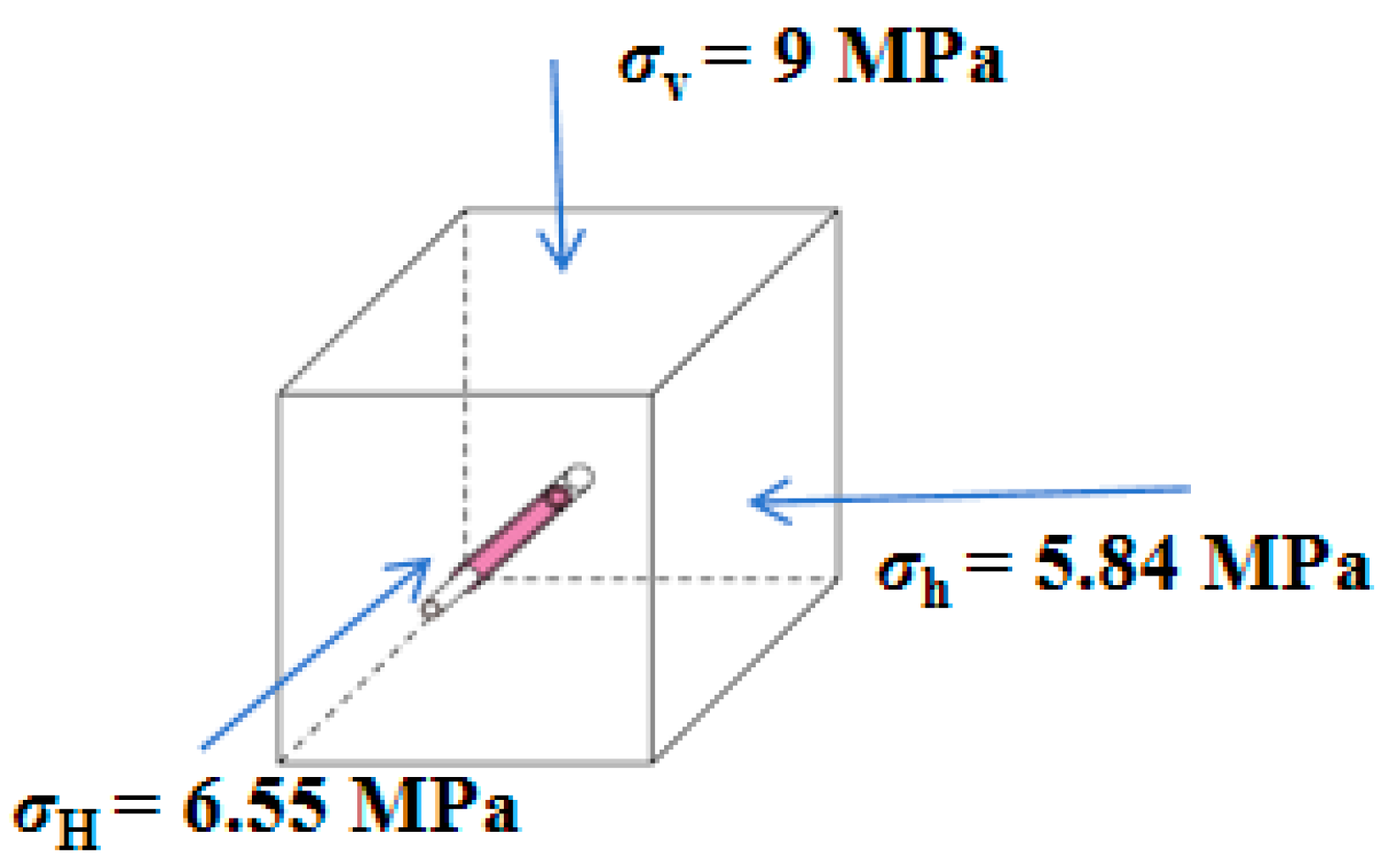





| Parameter | Value |
|---|---|
| Model dimension | 20 cm × 20 cm |
| Wellbore radius | 0.8 cm |
| Maximum horizontal stress | 9 MPa |
| Minimum horizontal stress | 5.84 MPa |
| Vertical stress | 6.55 MPa |
| Young’s modulus | 20 GPa |
| Poisson’s ratio | 0.1 |
| Void ratio | 0.1 |
| Top/Bottom coefficient | 1 × 10−14 |
| viscosity | 0.001 |
| Tensile strength | 7.42 MPa |
| Compressive strength | 67.8 MPa |
| Initial pore pressure | 0 |
| Experimental Group Number | Fill Status | Fracture Dip |
|---|---|---|
| 1 | No fill | / |
| 2 | Half filled | 0°/30°/60°/90° |
| 3 | Full fill | 0°/30°/60°/90° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Yang, W.; Li, Y. Research on Hydraulic Fracturing Crack Propagation Based on Global Cohesive Model. Processes 2025, 13, 3146. https://doi.org/10.3390/pr13103146
Xu S, Yang W, Li Y. Research on Hydraulic Fracturing Crack Propagation Based on Global Cohesive Model. Processes. 2025; 13(10):3146. https://doi.org/10.3390/pr13103146
Chicago/Turabian StyleXu, Shengxian, Wenwu Yang, and Yang Li. 2025. "Research on Hydraulic Fracturing Crack Propagation Based on Global Cohesive Model" Processes 13, no. 10: 3146. https://doi.org/10.3390/pr13103146
APA StyleXu, S., Yang, W., & Li, Y. (2025). Research on Hydraulic Fracturing Crack Propagation Based on Global Cohesive Model. Processes, 13(10), 3146. https://doi.org/10.3390/pr13103146






