Mitigating Salinity Effects: Thermal Performance Analysis of a Packing-Free Shower Cooling Tower for Seawater Application Using a Comprehensive Droplet-Based Model

Abstract

This study addresses the operational challenges of conventional packed cooling towers in seawater applications, where salt deposition and blockage significantly impair performance. A packing-free shower cooling tower (SCT) utilizing droplet-based heat and mass transfer is proposed as a robust alternative for high-salinity applications where conventional packed towers are prone to fouling and blockage. A comprehensive numerical model was developed and validated experimentally, showing a maximum error of less than 6% in predicting outlet water temperature. The analysis demonstrates that increasing salinity markedly reduces cooling efficiency—for instance, at threefold concentration (S ≈ 57.96 g/kg), efficiency decreased by 5.59% in summer and 4.91% in winter compared to freshwater, due to reduced vapor pressure and inhibited evaporation. However, elevating the inlet water temperature and air-to-water ratio partially counteracted these effects by enhancing evaporative and convective transfer. Larger droplet diameters also adversely affected performance, with cooling efficiency dropping from 75.87% (1 mm droplets) to 28.92% (3.5 mm droplets) in freshwater summer conditions. Notably, seasonal variations influenced the magnitude of salinity-related performance loss, with winter operations exhibiting less degradation. These findings provide critical insights and a reliable predictive tool for the design and optimization of high-salinity cooling systems.

1. Introduction

Seawater cooling towers have been widely adopted in coastal regions since the 1970s to reduce thermal pollution from industrial waste heat discharge into marine environments. By recirculating and cooling seawater, these systems help mitigate ecological damage, comply with stringent environmental regulations on thermal emissions, and conserve increasingly scarce freshwater resources [1]. As governments worldwide implement stricter policies on heated effluent discharge, seawater cooling technology—particularly integrated with cooling towers—has gained prominence as a sustainable alternative to once-through cooling systems.

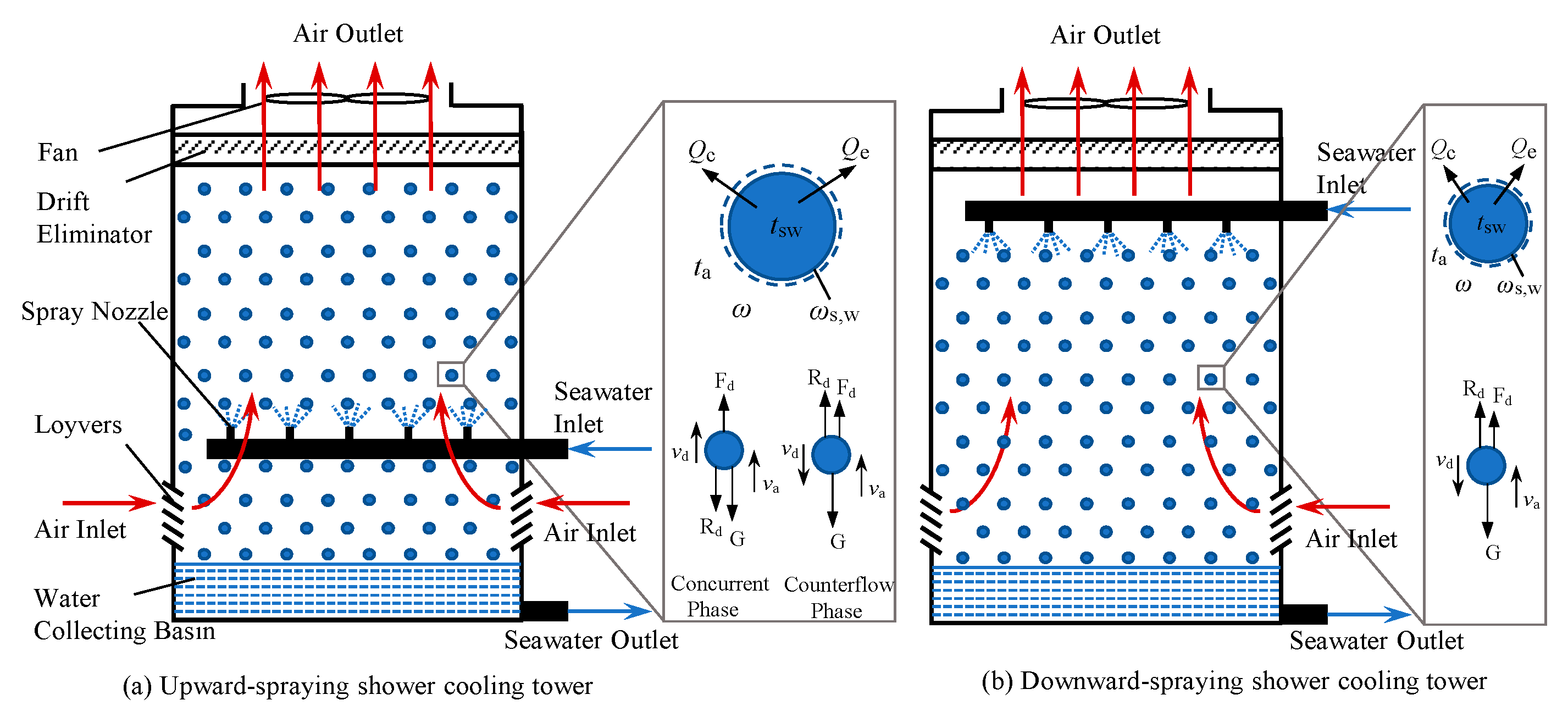
Conventional cooling towers (CCTs), shown schematically in Figure 1a, typically employ packed fill materials made of wood, plastic, or fiberglass to maximize contact area between water and air, thereby enhancing heat and mass transfer. While effective in freshwater settings, these packs are highly prone to fouling, scaling, and salt crystallization when operated with seawater [2]. Accumulated deposits not only diminish thermal efficiency by obstructing contact surfaces but also increase air-side pressure drop, leading to higher energy consumption for ventilation. Additional operational issues include frequent clogging, structural degradation due to corrosion [3], elevated noise levels, and costly maintenance or replacement cycles. These drawbacks underscore the critical need for alternative cooling tower architectures that sacrifice some thermal efficiency for vastly improved reliability when handling high-salinity water.

In response, the packing-free shower cooling tower (SCT) has been developed as an innovative alternative specifically for such challenging water qualities. It relies entirely on sprayed droplets rather than structured packing to facilitate heat and mass transfer, thereby eliminating the surfaces most prone to fouling at the cost of reduced contact area and residence time. As illustrated in Figure 1b, the SCT uses nozzle arrays to create a fine dispersion of water droplets, followed by a drenching zone that extends residence time. This design eliminates surfaces prone to fouling, making it particularly suitable for saline and impaired water quality conditions.

The significant evolution of seawater cooling technology since the mid-1950s has established cooling towers as a competitive alternative for closed-loop seawater recycling [2]. Over subsequent decades, countries including the United States, Japan, and Germany have made substantial advancements in natural draft and mechanical draft counterflow/parallel flow designs, with single-tower capacities now reaching 199,800 m³/h and heights exceeding 200 m to accommodate million-kilowatt-scale power units [2]. Critical to this progress has been addressing challenges related to concentration ratios (typically limited to 1.5–2.0 to prevent excessive scaling [4,5]), corrosion control, microbial growth, and salt drift management through specialized fill materials, drift eliminators, distribution systems, cement formulations, and anti-fouling chemical treatments [2].

Although SCT concepts have been explored since the 1990s—e.g., Givoni and colleagues [6] investigated SCT performance for building air-conditioning across various climates—most prior work remains experimental, with limited theoretical development or mechanistic modeling. In China, interest in SCTs is growing, yet comprehensive studies targeting seawater applications are still scarce [7]. By contrast, freshwater cooling towers have been extensively studied through both numerical and experimental approaches [8,9,10,11,12,13,14,15,16,17,18,19,20], leaving a significant gap in validated models and design guidelines dedicated to seawater operation [21,22]. Notably, the distinct thermophysical properties of seawater—including reduced specific heat, lower saturated vapor pressure, higher density, and altered viscosity compared to freshwater—fundamentally impact heat and mass transfer processes, leading to approximately 13% reduction in thermal performance according to experimental tower tests [7].

A principal challenge in seawater cooling is high salinity, which considerably alters thermophysical properties such as vapor pressure, specific heat, density, and viscosity [23]. These changes directly impact evaporation rates and heat transfer efficiency, necessitating specialized models that account for solute effects. Environmental concerns also pose significant constraints; drift emissions (0.002–0.2% of circulating water) can deposit salt onto surrounding structures and vegetation, potentially causing corrosion and ecological damage [2,3,24], while blowdown wastewater containing concentrated ions and treatment chemicals requires careful management to minimize marine pollution [4,5]. Consequently, understanding and mitigating these impacts through advanced drift reduction technologies (e.g., high-efficiency drift eliminators) and wastewater treatment strategies remains an active research focus [7,25].

Substantial research efforts have addressed these challenges through material innovations and system optimizations. China’s research initiatives, such as the “Seawater Recycling Cooling Technology Research and Engineering Demonstration” project, have achieved international advanced levels in critical parameters including carbon steel corrosion rates and drift loss rates (salt spray splash) [7,25]. This project developed comprehensive technological solutions including seawater corrosion inhibitors, scale inhibitors, biocides, and specialized cooling tower designs that systematically address corrosion, fouling, algal control, and salt deposition issues [7,25]. Numerical modeling approaches have also advanced, with studies employing three-dimensional simulations incorporating site meteorological data and tower design parameters to predict drift droplet diffusion patterns and salt deposition amounts [26]. Such models help evaluate environmental impacts under various operating conditions and inform the design of mitigation strategies.

It is therefore essential to develop a fundamental understanding of how dissolved salts influence droplet-level transport phenomena and overall tower performance, particularly for packing-free designs that operate on different principles than conventional packed towers.

In this study, we address this critical research gap by developing a comprehensive steady-state numerical model to simulate the thermal performance of a seawater SCT. The scientific novelty of this work lies in the development of a mechanistic, droplet-level model that explicitly incorporates the altered thermophysical properties of seawater (e.g., vapor pressure, specific heat capacity) and their impact on heat and mass transfer processes. While building upon the general droplet dynamics framework established by Kloppers [27,28], we significantly extend and adapt the methodology to address the unique challenges of packing-free SCTs operating under saline conditions. This includes modeling the effects of high salinity on evaporation driving forces and incorporating governing equations for supersaturated air regimes where condensation occurs. The model is rigorously validated against experimental data from a full-scale industrial tower, demonstrating a maximum error of less than 6% in predicting outlet water temperature. This validated model is then employed as a computational tool to perform a systematic analysis of performance across various salinities, air-to-water ratios, inlet temperatures, and droplet sizes, which provides insights that are difficult to obtain experimentally. The results offer novel, fundamental insights into the behavior of seawater SCTs and establish a robust theoretical basis for their design and optimization, thereby advancing the adoption of seawater as a sustainable cooling medium.

2. Thermophysical Properties of Seawater

The performance of cooling towers operating with seawater is fundamentally influenced by the distinct thermophysical properties of seawater, which differ markedly from those of fresh water due to the presence of dissolved salts and other constituents. In conventional packed cooling towers, these properties lead to operational challenges such as salt deposition, fouling, and eventually a significant reduction in thermal efficiency. The adoption of a packing-free shower cooling tower (SCT) design presents an effective countermeasure, particularly advantageous for handling high-salinity, high-turbidity, or high-temperature seawater where fouling and corrosion are prevalent.

Seawater is a multicomponent electrolyte solution comprising dissolved salts, organic matter, gases, and suspended solids. More than 80 elements have been identified in seawater, with dissolved inorganic salts making up approximately 3.5% by mass (35‰). These dissolved substances substantially alter properties such as density, specific heat, vapor pressure, and thermal conductivity—each playing a critical role in heat and mass transfer processes within cooling systems [29].

2.1. Seawater Salinity

Salinity is defined as the total mass of dissolved inorganic salts per unit mass of seawater, typically expressed in parts per thousand (‰). It is a master variable that governs many physical and thermodynamic properties of seawater. Major ions include chloride, sodium, sulfate, magnesium, and calcium, with chloride alone constituting nearly 55% of total dissolved solids. Natural seawater salinity generally ranges between 32‰ and 37.5‰, with an average of approximately 35‰.

In cooling tower applications, salinity increases over time due to evaporative concentration, a phenomenon that must be accounted for in design and operation. As salinity rises, properties such as vapor pressure, specific heat, and viscosity change, directly influencing thermal performance. For engineering purposes, seawater with a salinity of 34.5‰ is often designated as the baseline “1-concentration” condition, with higher concentrations (e.g., 2×, 3×) representing evaporatively concentrated states.

2.2. Seawater Density

The density of seawater, denoted as ρ (kg/m³), is a function of temperature (T, °C), salinity (S, g/kg), and pressure (P, Pa). The fundamental relationship is described by the internationally recognized equation of state for seawater [29]. For the operating conditions typical of cooling towers, the pressure dependence is often negligible, and density can be accurately correlated as a function of T and S only [29]. The density increases with decreasing temperature and increasing salinity. For example, at a constant temperature of 30 °C, the density of standard seawater (S ≈ 35 g/kg) is approximately 1022.2 kg/m³, which is about 2.3% higher than that of fresh water (995.65 kg/m³) [29]. For 2-concentration and 3-concentration seawater (S ≈ 70 and 105 g/kg, respectively), density increases to roughly 1048.1 kg/m³ (+5.3%) and 1076.7 kg/m³ (+8.1%), respectively. These changes influence pumping requirements, droplet dynamics, and convective heat transfer within the tower.

2.3. Specific Heat Capacity of Seawater

The specific heat capacity at constant pressure, c_p (kJ/kg·K), indicates the amount of energy required to raise the temperature of a unit mass of seawater by one degree Celsius. It is inversely related to salinity; higher salinity leads to a lower c_p. This relationship is well-established experimentally and can be described by empirical correlations. The correlation proposed by Sharqawy et al. [28] expresses c_p as a function of temperature and salinity and is accurate within 1.5% for practical cooling tower operating ranges. This means saline water requires less energy to heat up compared to fresh water. Compared to fresh water (c_p ≈ 4.18 kJ/kg·K at 30 °C), the c_p of seawater is reduced by approximately 3.9% at 1-concentration (S = 35 g/kg, c_p ≈ 4.02 kJ/kg·K), 7.2% at 2-concentrations (S = 70 g/kg), and 9.8% at 3-concentrations (S = 105 g/kg) [28]. This reduction affects the thermal load handling capacity and cooling rate in the system.

2.4. Saturated Vapor Pressure of Seawater

The saturated vapor pressure of seawater, Psw (kPa), is lower than that of pure water, Pw, due to the presence of dissolved salts, which reduce the activity of water molecules. The vapor pressure lowering effect is a critical factor inhibiting evaporation. While Raoult’s law provides a first-order estimate for ideal solutions, seawater exhibits significant non-ideal behavior. The accurate correlation developed by Sharqawy et al. [28], which is a function of salinity and temperature, is therefore employed in our model. This correlation shows that the relative reduction in vapor pressure, (Pw − Pw)/Pw, is largely independent of temperature within the 20–50 °C range and is primarily a function of salinity. For instance, at 30 °C, the saturated vapor pressure is reduced by approximately 1.8% at 1-concentration (S = 35 g/kg), 5.2% at 2-concentrations (S = 70 g/kg), and 7.8% at 3-concentrations (S = 105 g/kg) compared to fresh water. This suppression of vapor pressure must be carefully considered in mass transfer calculations, as it directly governs the driving force for evaporation.

2.5. Additional Properties: Thermal Conductivity and Viscosity

Beyond the properties discussed above, thermal conductivity (k, W/m·K) and dynamic viscosity (μ, Pa·s) also play vital roles in heat transfer and fluid dynamics within cooling systems. Seawater’s thermal conductivity is slightly lower than that of fresh water and decreases with increasing salinity. Similarly, viscosity increases with salinity, affecting droplet formation, air-water contact, and pumping power requirements. The correlations for these properties as functions of temperature and salinity are also well-documented by Sharqawy et al. [28]. These properties collectively determine the overall efficiency and energy consumption of seawater cooling towers.

3. Mathematical Modeling

The present model advances the state-of-the-art by synthesizing several mathematical approaches into a comprehensive framework specifically adapted for seawater SCTs. The core innovation lies in the integration of: (1) a droplet-scale mechanics model that tracks the motion and heat/mass transfer of individual saline water droplets; (2) a system-level model based on control volume analysis, typically used for packed towers, here applied to the entire spray zone; and (3) a dual-regime formulation that switches between governing equations for unsaturated and supersaturated air conditions to ensure physical fidelity across all operating scenarios.

While the general principles of the governing equations are universal, their application to seawater cooling is enabled by the critical implementation of salinity-dependent thermophysical properties derived in Section 2. This integration of fundamental seawater properties into a hybrid droplet-system model represents the novel computational methodology at the heart of this work.

3.1. Droplet-Level Mathematical Model

To investigate the thermal performance of the SCT as shown in Figure 2, it is helpful to study the heat and mass transfer process at the single water droplet level first. Some assumptions concerning the water droplet are made to describe the motion characteristics of water droplet in mathematical language: the water droplet is assumed to be spherical and its diameter is small enough so that the temperature of the water droplet can be assumed to be uniform; all water droplets have the uniform diameter; collision or scatteration of the water droplet are ignored; circumgyration, liberation and the non-uniformity of internal flow and temperature distribution in the water droplets are ignored.

To analyze the thermal performance of the shower cooling tower (SCT) depicted in Figure 2, it is essential to model the heat and mass transfer processes at the scale of an individual water droplet. The following assumptions are adopted to simplify the droplet dynamics and thermodynamics: Each water droplet is spherical and sufficiently small such that its temperature remains uniform; All droplets are of identical size; Droplet collisions, break-up, and coalescence are neglected; Internal circulation, rotation, oscillation, and non-uniform temperature distributions within the droplet are disregarded.

The total heat transfer from a water droplet comprises convective and evaporative components. The energy balance over a control volume enclosing the droplet can be expressed as:

$${\displaystyle \frac{d{U}_d}{dt}}=-(Q_{dc}+Q_{de})$$

(1)

where

$$U_d=m_d{c}_{pw}{T}_w$$

$$Q_{dc}=h_c{A}_d(T_w-T_a)$$

$$Q_{de}=h_d{A}_d(w_{sw}-w_a)i_{\nu }$$

(2)

The resultant expression derived from the above is:

$$\begin{array}{c}\frac{d{T}_w}{dt}=-{\displaystyle \frac{[h_c(T_w-T_a)+h_d(w_{sw}-w)i_{\nu }]A_d}{{\rho }_w{m}_d}}\hfill \\ =-{\displaystyle \frac{6h_d[l{e}_f(i_{masw}-i_{ma})+(1-l{e}_f)(w_{sw}-w)i_{\nu }]}{c_{pw}{\rho }_w{d}_d}}\hfill \end{array}$$

(3)

The rate of evaporation from the droplet surface is governed by the mass transfer equation:

$${\displaystyle \frac{d{m}_d}{dt}}=h_d(w_{sw}-w_a)A_d$$

(4)

where

$$h_c=N{u}_d\lambda /d_d$$

$${\mathrm{R}\mathrm{e}}_d=(u_d+u_a)d_d/\nu$$

$$\mathrm{P}\mathrm{r}=\mu c_{pa}/\lambda$$

$$Nu=2+0.6{\mathrm{R}\mathrm{e}}^{1/2} {\mathrm{P}\mathrm{r}}^{1/3}$$

(5)

$$\begin{array}{c}d{w}_a={\displaystyle \frac{d{m}_w}{m_a}}=N_d{\displaystyle \frac{d{m}_d}{m_{a}dt}}\hfill \\ =(\frac{m_w}{m_a}){\displaystyle \frac{h_d(w_{sw}-w_a)A_d}{m_d{u}_d}}dz\hfill \end{array}$$

(6)

Bosnjaković [21] provides a comprehensive analysis of the Lewis factor and its derivation.

3.2. Droplet Force Analysis

In our previous study [13], the forces acting on a single water droplet were analyzed in detail. In the present work, only the key results are employed. During the motion of a droplet ejected from a nozzle, the main forces include gravity G_d, buoyancy F_d, and air resistance R_d, which are expressed as follows:

• gravity

  $$G_d=m_{d}g=\pi d_d^3{\rho }_{w}g/6$$

  (7)
• buoyancy

  $$F_d=\pi d_d^3{\rho }_{a}g/6$$

  (8)
• resistance

  $$R_d=\pi C_d{\rho }_a{U}^2{d}_d^2/8$$

  (9)

The drag coefficient C_d, which depends on the flow regime, is given by [22]:

• transition flow:

  $$C_d=18.5/{\mathrm{R}\mathrm{e}}^{3/5} 1.9169\le \mathrm{R}\mathrm{e}<508.3917$$
• turbulence flow:

  $$C_d=0.44 \mathrm{R}\mathrm{e}\ge 508.3917$$

  (10)

From Newton’s second law, the equation of motion for the droplet is derived as:

$$u_d=dz/dt$$

$$a_d={\displaystyle \frac{d{u}_d}{dt}}=u_d{\displaystyle \frac{d{u}_d}{dz}}$$

(11)

Substituting the expressions of the forces leads to the kinetic equation:

$$\begin{array}{c}{\rho }_w{u}_d{\displaystyle \frac{d{u}_d}{dz}}\hfill \\ =({\rho }_w-{\rho }_a)g-3C_d{\rho }_a(u_d+u_a{)}^2/4d_d\hfill \end{array}$$

(12)

3.3. Energy Balance Equations for the Shower Cooling Tower [20]

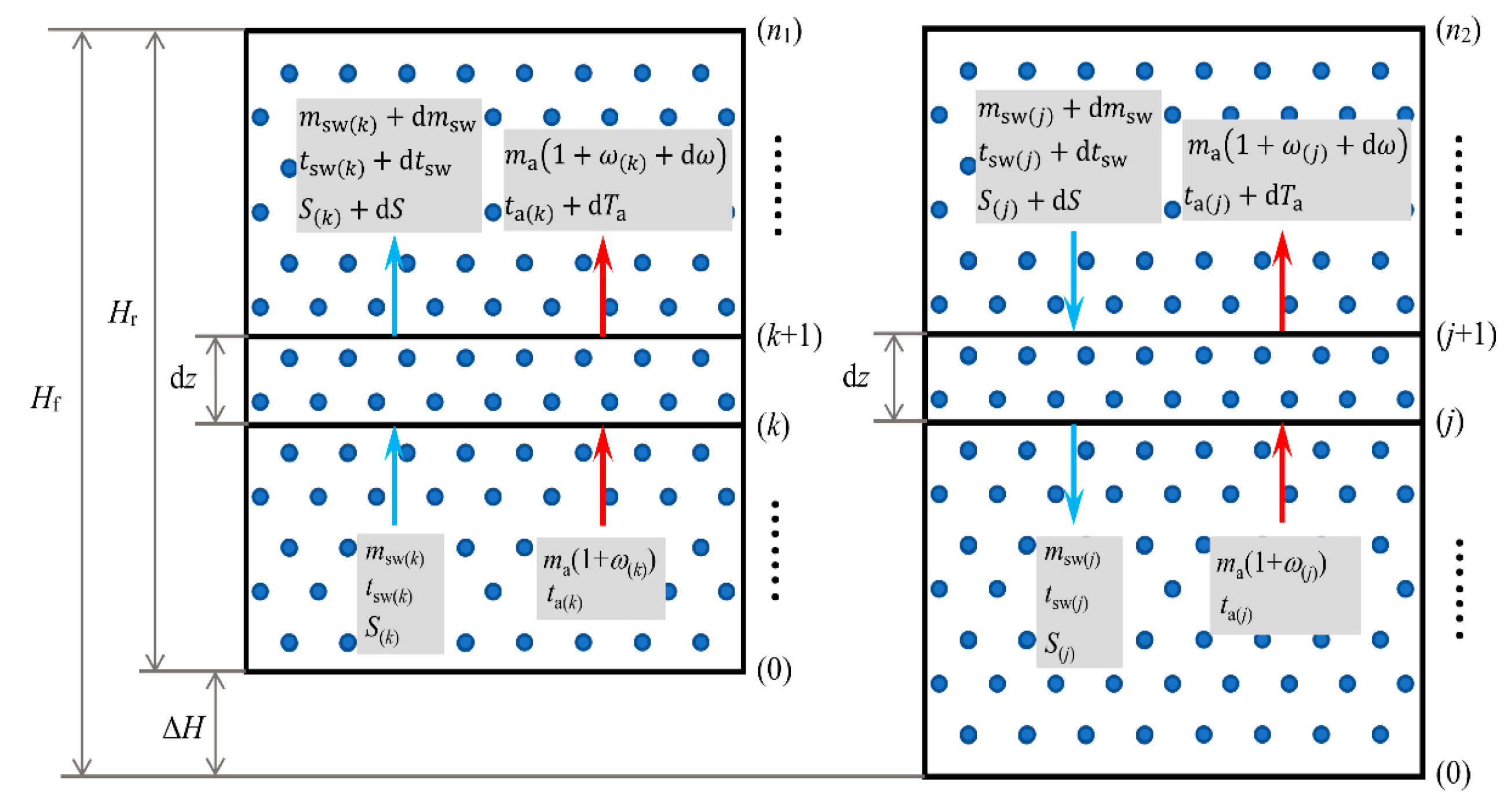
This section bridges the droplet-scale analysis from the previous sections with the macroscopic performance of the entire tower. It integrates the micro-scale droplet behavior into a system-level, control-volume model akin to those used for packed towers but adapted for the unique packing-free, droplet-driven environment of the SCT. This section extends the analysis to a one-dimensional model that accounts for variations in the vertical direction of a countercurrent shower cooling tower.

The tower of height H is divided into N control volumes of finite thickness dz. Water is distributed uniformly in the form of droplets with average diameter $d_d$. The positive direction is defined from the top to the bottom.

A mass balance over the control volume (Figure 3) gives:

$$d{m}_w=m_{a}dw$$

(13)

The energy balance is expressed as:

$$m_{a}d{i}_{ma}=m_{w}d{i}_w+i_{w}d{m}_w$$

(14)

Substituting the mass balance into the energy balance and rearranging yields:

$$d{T}_w={\displaystyle \frac{m_a}{m_w}}({\displaystyle \frac{d{i}_{ma}}{c_{pw}}}-T_{w}dw)$$

(15)

At the water-air interface, the energy balance is:

$$dQ=d{Q}_c+d{Q}_e$$

(16)

where dQ_c is the sensible heat transfer due to temperature difference:

$$d{Q}_c=h(T_w-T_a)dA$$

(17)

and dQ_c is the latent heat transfer due to vapor concentration difference:

$$d{Q}_e=i_v{h}_d(w_{sw}-w_a)dA$$

(18)

The enthalpy of the water vapor at the bulk water temperature, T_w, is:

$$i_{\nu }=i_{fgw0}+c_{p\nu }{T}_w$$

(19)

The term i_fgw0 represents the latent heat of vaporization (enthalpy of vaporization) of water, evaluated at the reference temperature of 0 °C (approximately 2501 kJ/kg).

The enthalpy of saturated air at water temperature is:

$$i_{masw}=c_{pa}{T}_w+w_{sw}(i_{fgw0}+c_{pv}{T}_w)$$

(20)

$$i_{masw}=c_{pa}{T}_w+w{i}_{\nu }+(w_{sw}-w)i_{\nu }$$

(21)

The enthalpy of the air-vapor mixture per unit mass of dry air is:

$$i_{ma}=c_{pa}{T}_a+w(i_{f\mathrm{g}\mathrm{w}0}+c_{p\nu }{T}_a)$$

(22)

Subtracting and simplifying yields:

$$T_w-T_a={\displaystyle \frac{(i_{masw}-i_{ma})-(w_{sw}-w)i_{\nu }}{c_{pma}}}$$

(23)

Substituting into the interface energy balance and rearranging gives:

$$dQ=[{\displaystyle \frac{h}{c_{pma}}}(i_{masw}-i_{ma})+(h_d-{\displaystyle \frac{h}{c_{pma}}})i_{\nu }(w_{sw}-w)]dA$$

(24)

Define the Lewis factor as:

$${\displaystyle \frac{h}{c_{\mathrm{p}\mathrm{m}\mathrm{a}}{h}_d}}=L{e}_f$$

For air-water systems, Bosnjakovic [22] proposed an empirical relation for Le_f:

$$L{e}_f={0.865}^{0.667}({\displaystyle \frac{w_{sw}+0.622}{w_a+0.622}}-1)/[\mathrm{l}\mathrm{n}({\displaystyle \frac{w_{sw}+0.622}{w_a+0.622}})]$$

(25)

The Merkel model assumes Le_f = 1 for simplicity, but actual evaporation rates depend on the true value of Le_f [20].

The Lewis factor relation proposed by Bosnjaković [22] is indeed derived for air-water systems. In the present model for seawater application, the critical influence of salinity is incorporated not through a modification of the Le_f value itself, but through its effect on the saturation vapor pressure at the droplet-air interface. Specifically, the saturation humidity ratio of the air immediately adjacent to the seawater droplet, w_sw, is calculated using the saturation vapor pressure of seawater (P_sw), which is a function of both temperature and salinity, as detailed in Section 2.4. This P_sw is lower than that of pure water at the same temperature. Consequently, the mass transfer driving force (w_sw − w_a) is reduced under saline conditions. The Le_f relation continues to describe the ratio of heat to mass transfer potential, while the absolute value of the mass transfer potential is governed by the thermophysical properties of seawater. This approach is consistent with the methodology adopted in foundational studies of saline cooling systems [30].

The enthalpy transfer to the air is:

$$d{i}_{ma}={\displaystyle \frac{dQ}{m_a}}={\displaystyle \frac{h_d}{m_a}}[L{e}_f(i_{mazw}-i_{ma})+(1-L{e}_f)i_{\nu }(w_{zw}-w)]dA$$

(26)

The number of droplets in a control volume of thickness dz is:

$$N_d={\displaystyle \frac{m_{w}dz}{m_d{u}_d}}$$

(27)

The corresponding interfacial area is:

$$dA={\displaystyle \frac{m_{w}dz}{m_d{u}_d}}\pi d_d^2={\displaystyle \frac{6m_{w}dz}{{\rho }_w{u}_d{d}_d}}$$

(28)

Substituting into the enthalpy transfer equation:

$$d{i}_{ma}={\displaystyle \frac{dQ}{m_a}}=({\displaystyle \frac{m_w}{m_a}}){\displaystyle \frac{6h_d}{{\rho }_w{u}_d{d}_d}}[L{e}_f(i_{masw}-i_{ma})+(1-L{e}_f)i_{\nu }(w_{sw}-w)]dz$$

$${\displaystyle \frac{d{i}_{ma}}{dz}}={\displaystyle \frac{dQ}{m_a}}=({\displaystyle \frac{m_w}{m_a}}){\displaystyle \frac{6h_d}{{\rho }_w{u}_d{d}_d}}[L{e}_f(i_{macw}-i_{ma})+(1-L{e}_f)i_{\nu }(w_{sw}-w)]$$

(29)

From the above, we obtain:

$$m_{a}d{w}_a=h_d(w_{sw}-w_a)dA$$

(30)

Rearranging gives:

$$d{w}_a=({\displaystyle \frac{m_w}{m_a}}){\displaystyle \frac{6h_d}{{\rho }_w{u}_d{d}_d}}(w_{sw}-w_a)dz$$

(31)

However, under conditions where the computed wet-bulb temperature exceeds the dry-bulb temperature, the air becomes supersaturated. This leads to condensation of excess vapor, forming mist, and invalidates the assumption of unsaturated air. Therefore, the model must be corrected to account for supersaturation effects.

To ensure the clarity and reproducibility of the model, the specific heat capacity values used in the calculations are provided herein. The specific heat capacity of dry air (c_pa) is taken as 1.006 kJ/(kg·°C), and the specific heat capacity of water vapor (c_pv) is 1.86 kJ/(kg·°C). These values are standard constants for the temperature ranges encountered in cooling tower operations [30]. The specific heat capacity of liquid water (c_pw) is not a constant in the model but is treated as a function of temperature and salinity, as detailed in Section 2.3. For freshwater calculations, a temperature-dependent correlation is used, while for seawater, the model incorporates the salinity-dependent reduction described by the equations governing seawater thermophysical properties.

3.4. Heat and Mass Transfer Governing Equations Under Supersaturated Conditions

To enhance the model’s realism and accuracy for high-load seawater cooling applications, the framework is extended to account for supersaturated air conditions, where the air’s moisture content exceeds saturation, leading to mist formation. This extension, adapting the approach of Poppe and Rögener [10], is a critical addition that allows the model to predict performance accurately across a wider range of operational states beyond the standard unsaturated assumption.

The control volume illustrated in Figure 3 remains applicable even under supersaturated air conditions. When the air becomes supersaturated, excess water vapor condenses into mist. The enthalpy of supersaturated air is thus expressed as:

$$i_{ss}=c_{pa}{T}_a+w_{sa}(i_{fgw0}+c_{pv}{T}_a)+(w_a-w_{sa})c_{pw}{T}_a$$

(32)

Following the approach of Poppe and Rögener [8], it is assumed that the heat and mass transfer coefficients for supersaturated air are identical to those for unsaturated air. The driving potential for mass transfer is the difference in humidity ratio between the saturated air at the water-air interface and the saturated free stream air:

$$d{m}_w=h_d(w_{sw}-w_{sa})dA$$

(33)

Following a derivation procedure analogous to that for unsaturated air, we obtain:

$$dQ=h(T_w-T_a)dA+i_v{h}_d(w_{sw}-w_{sa})dA$$

(34)

$$T_w-T_a={\displaystyle \frac{(i_{masw}-i_{ss})-(w_{sw}-w_{sa})i_v+(w_a-w_{sa})c_{pw}{T}_w}{c_{pa}+w_{sa}{c}_{pv}+(w-w_{sa})i_v}}$$

(35)

$$dQ=h_c{\displaystyle \frac{\left(i_{masw}-i_{ss}\right)-\left(w_{sw}-w_{sa}\right)i_v+\left(w_a-w_{sa}\right)c_{pw}{T}_w}{c_{pa}+w_{sa}{c}_{pw}+\left(w-w_{sa}\right)i_v}}dA+i_v{h}_d\left(w_{sw}-w_{sa}\right)dA$$

(36)

Substituting the expression for interfacial heat transfer yields:

$$\begin{gathered} d{i}_{ma}=({\displaystyle \frac{m_w}{m_a}}){\displaystyle \frac{6h_d}{{\rho }_w{u}_d{d}_d}}\{{\displaystyle \frac{h_c}{h_d{c}_{pwax}}}[(i_{max}-i_{zc})-(w_{sv}-w_{sa})i_v \\ +(w_a-w_{sa})c_{pv}{T}_w]+i_v(w_{sw}-w_{sa})]\}dz \end{gathered}$$

(37)

The specific heat of supersaturated air per unit mass and defined as:

$$c_{pmas}=c_{pa}+w_{sa}{c}_{p\nu }+\left(w-w_{sa}\right)i_{\nu }$$

and the Lewis factor for the supersaturated regime is given by Bosnjakovic’s empirical relation:

$$L{e}_f={0.865}^{0.667}\left({\displaystyle \frac{w_{sw}+0.622}{w_{sa}+0.622}}-1\right)/\left[\mathrm{l}\mathrm{n}\left({\displaystyle \frac{w_{sw}+0.622}{w_{sa}+0.622}}\right)\right]$$

(38)

By following an analogous procedure to the unsaturated case, the governing equations for supersaturated air are derived as:

$$\begin{gathered} d{T}_w={\displaystyle \frac{6h_d}{c_{pw},c_{w}s{\lambda }_d{d}_d^{\prime }}}\{L{e}_f\left[\left(i_{mssw}-i_{ss}\right)-\left(w_{sw}-w_{sz}\right)i_v+\left(w_{sz}-w_{sw}\right)c_{pw}{T}_w\right] \\ +i_v\left(w_{sw}-w_{sz}\right)]-\left(w_{sw}-w_{sz}\right)c_{sw}{T}_w)dz \end{gathered}$$

(39)

$$d{w}_a=\left({\displaystyle \frac{m_w}{m_a}}\right){\displaystyle \frac{6h_d}{{\rho }_w{u}_d{d}_d}}\left(w_{sw}-w_{sa}\right)dz$$

(40)

This completes the derivation of the governing equation system for shower cooling towers operating under supersaturated air conditions.

3.5. Numerical Solution Procedure

The system of differential equations for both unsaturated and supersaturated air conditions is solved using a fourth-order Runge–Kutta method [23,24]. The input parameters include the water-to-air flow rate ratio, air velocity, initial droplet velocity, droplet diameter, height of the spray zone, inlet water temperature, and inlet air dry-bulb and wet-bulb temperatures.

For unsaturated conditions, the governing equations consist of (3), (12), (29) and (31). For supersaturated conditions, the system comprises Equations (3), (37), (39) and (40), where the Lewis factor Le_f must be replaced by Le_f,sup. As the heat and mass transfer models are derived separately for these two regimes, the appropriate set of equations must be selected based on the saturation state of the air.

The velocity of water droplets changes both temporally and spatially along the tower height. To accurately compute the heat transfer and temperature variation of the droplets, the tower is discretized into n segments of thickness Δz. Each segment i is treated as a control volume where water enters at temperature T_w,i and exits at T_w,i+1, while air enters with enthalpy h_a,i and exits with h_a,i+1. An iterative numerical procedure is applied within each segment based on initial and boundary conditions. After solving all segments, the spatial distributions of water and air state parameters are obtained. The solution is considered reliable provided the step size Δz is sufficiently small to ensure numerical stability and convergence.

4. Experimental Apparatus and Procedure

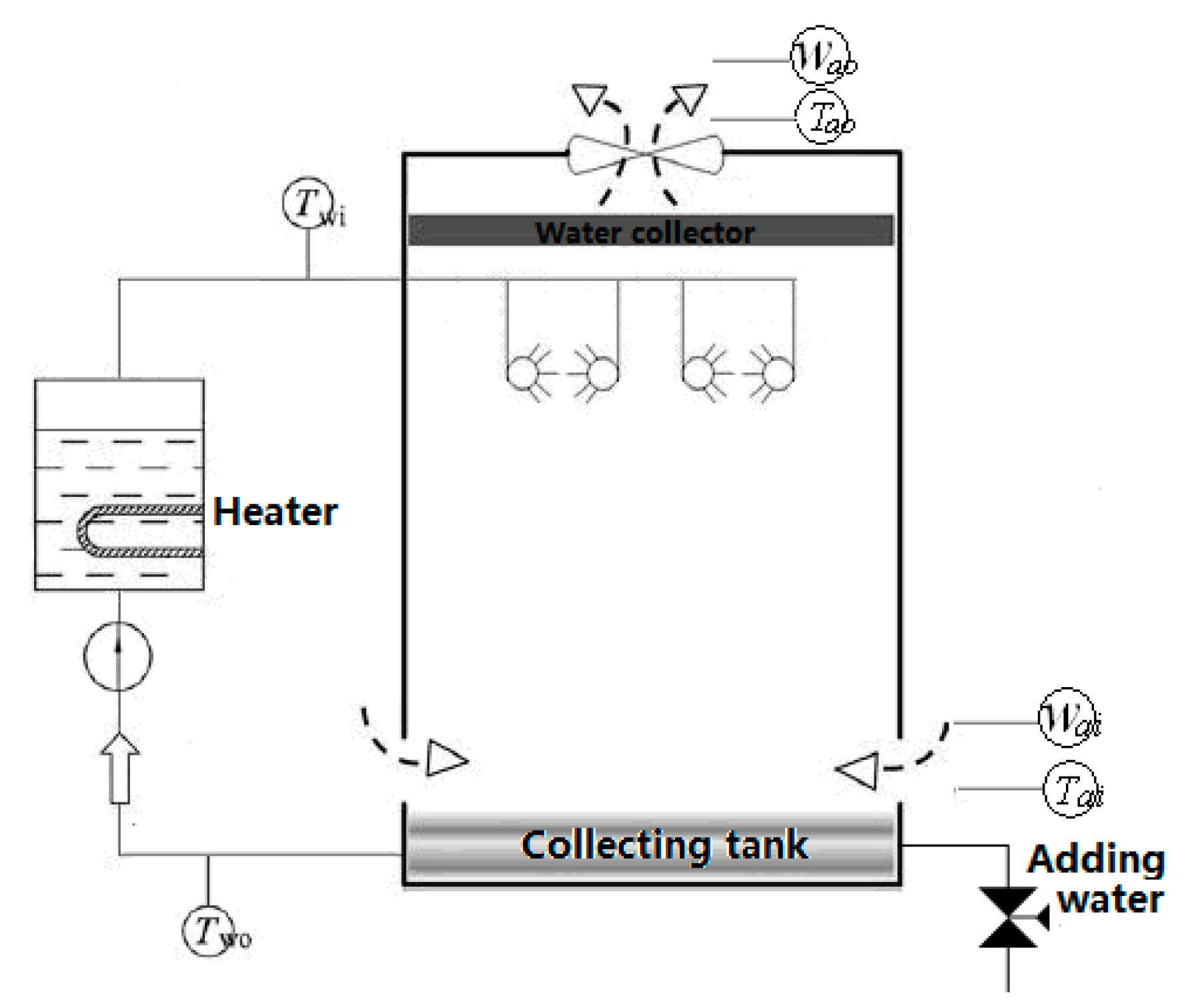
Existing experimental studies on cooling towers reported in the literature often differ significantly from the packing-free shower cooling tower (SCT) design under investigation. Therefore, experimental validation using a full-scale industrial tower under real operating conditions was deemed essential. The experiments were conducted on a dedicated SCT test rig located at Jiangsu Seagull Cooling Tower Co., Ltd., Changzhou, China. A schematic layout of the experimental setup is provided in Figure 4, and a photograph of the actual tower is shown in Figure 5.

The droplet size measurement was performed using a laser diffraction analyzer (see

Table 1. Instruments used in the experimental study.

Measurement	Instrument Type	Accuracy	Range
Water Temperature	PT100 RTD	±0.1 °C	0–100 °C
Air Temperature	Thermocouple	±0.2 °C	−40–120 °C
Water Flow Rate	Electromagnetic Flowmeter	±0.5%	0–200 m3/h
Air Flow Rate	Pilot Tube Anemometer	±2%	0–15 m/s
Droplet Size	Laser Diffraction Analyzer	±1 µm	0.5–2000 µm

). The instrument was positioned approximately 1.5 m directly below the nozzle array. This location was carefully selected to ensure that the droplets had fully developed beyond the initial breakup region near the nozzles, thus providing a representative measurement of the droplet size during the main heat and mass transfer process within the tower. Measurements were taken at multiple points across the cross-section to account for spatial variations. The droplet population was characterized by a distribution (e.g., Rosin-Rammler type), and the key parameter reported in

Table 2. Comparison of measured and numerically predicted outlet water temperatures under various operating conditions.

Parameters	Case 1	Case 2	Case 3	Case 4	Case 5	Case 6	Case 7
Nozzle height (m)	4.4	4.4	4.4	4.9	4.9	5.4	5.4
Water flow rate (m3/h)	48.45	87.80	105.4	97.72	58.86	103.4	61.7
Air flow rate (m3/h)	86,206	86,206	117,525	101,987	117,535	86,206	105,932
Droplet diameter (mm)	1.6	1.6	1.6	1.6	1.7	1.8	1.5
Atmospheric pressure (kPa)	102	101.6	103.1	102.1	101.7	102.3	102.3
Dry-bulb temperature of inlet air (℃)	25	28.6	19	28	28.5	26	23.8
Wet-bulb temperature of inlet air (℃)	20.6	21.6	14.2	21.7	19	21.3	17.4
Inlet water temperature (℃)	43.6	43.8	44.8	42.8	42.2	45.5	41.3
Experimental outlet water temperature (℃)	31.5	33.4	32	32.7	28.5	35.2	28.3
Computed water temperature (℃)	31.1	33.1	32.1	32.2	29.1	34.9	28.2
Relative error (%)	−3.4	−2.9	0.8	−4.76	5.13	−2.91	−0.77

is the Sauter Mean Diameter (D[3,2]). This diameter, which represents the surface-area-weighted mean, is the most relevant metric for modeling heat and mass transfer processes, as it accurately reflects the total interfacial area available for exchange.

The experimental tests were conducted using both freshwater and artificial seawater to validate the model under different salinity conditions. The freshwater cases (e.g., Cases 1–7 in Table 2) served as the baseline. For saline water tests, artificial seawater was prepared by dissolving commercial sea salt mixtures in tap water to achieve target salinities. The salinity of the circulating water was monitored in real-time using a calibrated conductivity meter and maintained within a narrow deviation (±2%) of the target value throughout each steady-state test.

The test rig was equipped with comprehensive instrumentation to measure all relevant thermal and flow parameters. Key measurements included inlet and outlet water temperatures, air dry-bulb and wet-bulb temperatures at the inlet and outlet, water flow rate, air flow rate, and droplet size distribution. To ensure measurement representativeness and account for spatial variations, multiple sensors were deployed for key parameters: water temperatures were measured using four PT100 sensors sourced from Omega Engineering (Norwalk, CT, USA) at both the inlet and outlet arranged in an annular configuration, while air temperatures were measured using arrays of three thermocouples at both the inlet and outlet ducts. A single, highly accurate electromagnetic flowmeter was used for water flow measurement, and air flow rate was determined by a Pitot tube traverse across the inlet duct according to standard practice.

The selection of these specific instruments is justified by their high accuracy, reliability, and established use in both industrial and academic settings for thermal-fluid experiments (as documented by their specifications in Table 1). Furthermore, all sensors were calibrated prior to the testing campaign against traceable standards in a certified calibration facility to ensure measurement validity.

The experiments were conducted using a steady-state method. The system was allowed to stabilize for approximately 30 min under fixed operating conditions before any measurements were recorded. Once stability was achieved (indicated by variations of less than ±0.3 °C in water temperature and ±2% in flow rates over a 10-min period), five consecutive sets of all parameters were recorded simultaneously at 3-min intervals. 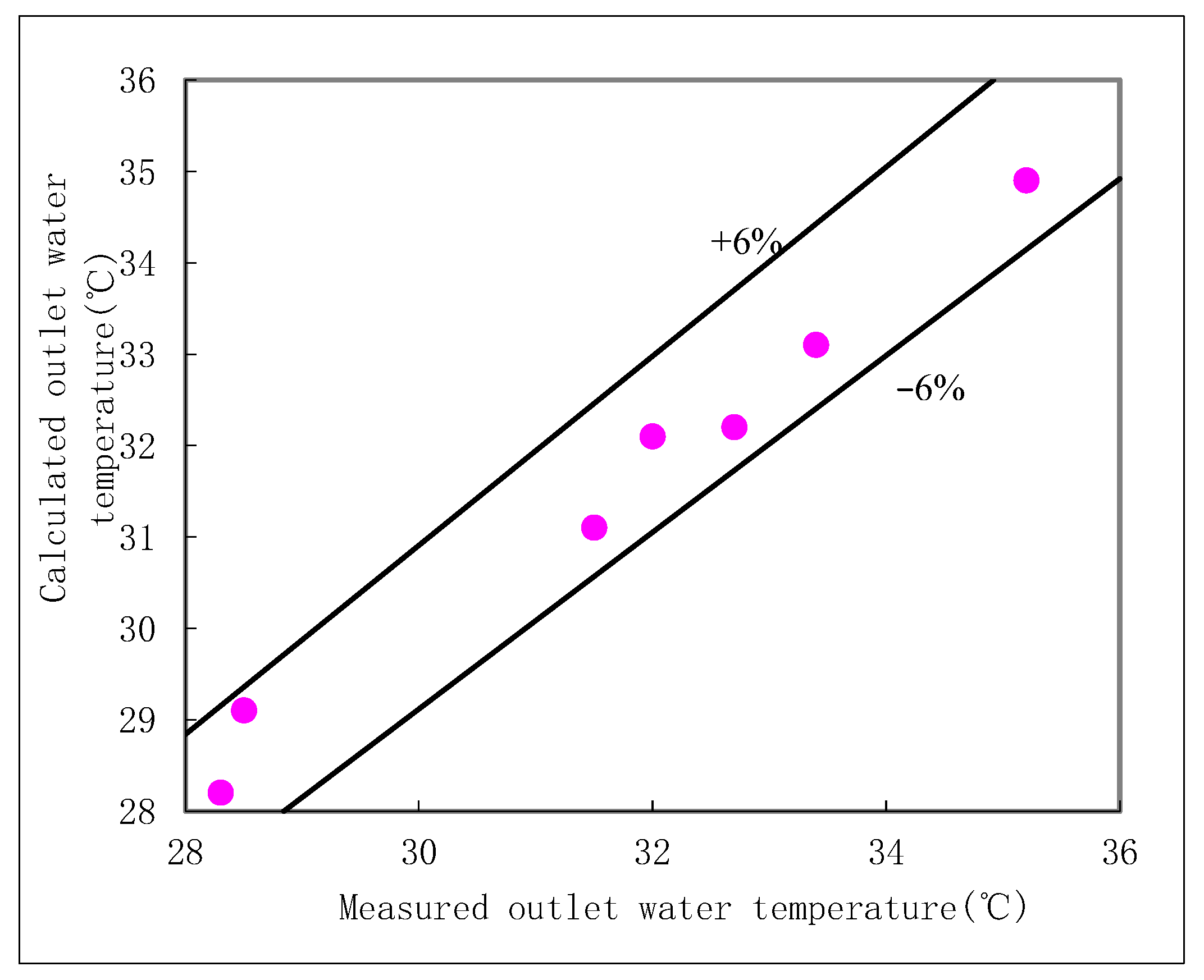This process was repeated for each operating condition listed in Table 2. The average values of these five measurements were used for subsequent analysis. A data set was considered valid only when the thermal balance error between the air and water streams was less than 5%. This stringent criterion, combined with multi-sensor averaging and repeated measurements, ensured the high reliability and reproducibility of the experimental data, as shown in Figure 6.

This close agreement, validated for both freshwater and seawater operation, indicates that the theoretical model is capable of estimating the thermal performance of real-world shower cooling towers with satisfactory accuracy. The successful validation presented in Table 2 justifies the use of this model for the comprehensive parametric investigation of seawater SCT performance under various operating conditions, which is presented in the following section.

5. Results and Discussion

5.1. Influence of Salinity on Outlet Water Temperature

Using the validated numerical model, a systematic parametric study was conducted to evaluate the performance of the seawater shower cooling tower (SCT). The analysis focused on the effects of salinity, droplet diameter, and seasonal conditions. The baseline operating parameters for this study are defined in

Table 3. Baseline parameters used in the parametric analysis of the seawater shower cooling tower performance.

Nozzle Height (m)	5	5
Dry-bulb temperature of inlet air (°C)	33.5	10.5
Wet-bulb temperature of inlet air (°C)	26.7	3.7
Atmospheric pressure (kPa)	102	102
Water flowrate(m3/h)	55.21	55.21
Air flowrate (m3/h)	86,206	86,206
Inlet water temperature (°C)	48	48

. The outlet water temperatures and cooling efficiency were predicted under both summer and winter conditions for four water types.

Salinity influences thermal performance through three primary mechanisms: it reduces the vapor pressure, decreases the specific heat capacity, and increases the density of the water. The first two effects tend to diminish thermal performance, while the third may partially compensate by promoting higher mass flow rates. However, the positive effect of increased density is insufficient to fully counteract the negative impacts of reduced vapor pressure and specific heat, resulting in an overall decline in cooling efficiency. This performance reduction becomes more significant at higher salt concentrations and under more demanding cooling conditions.

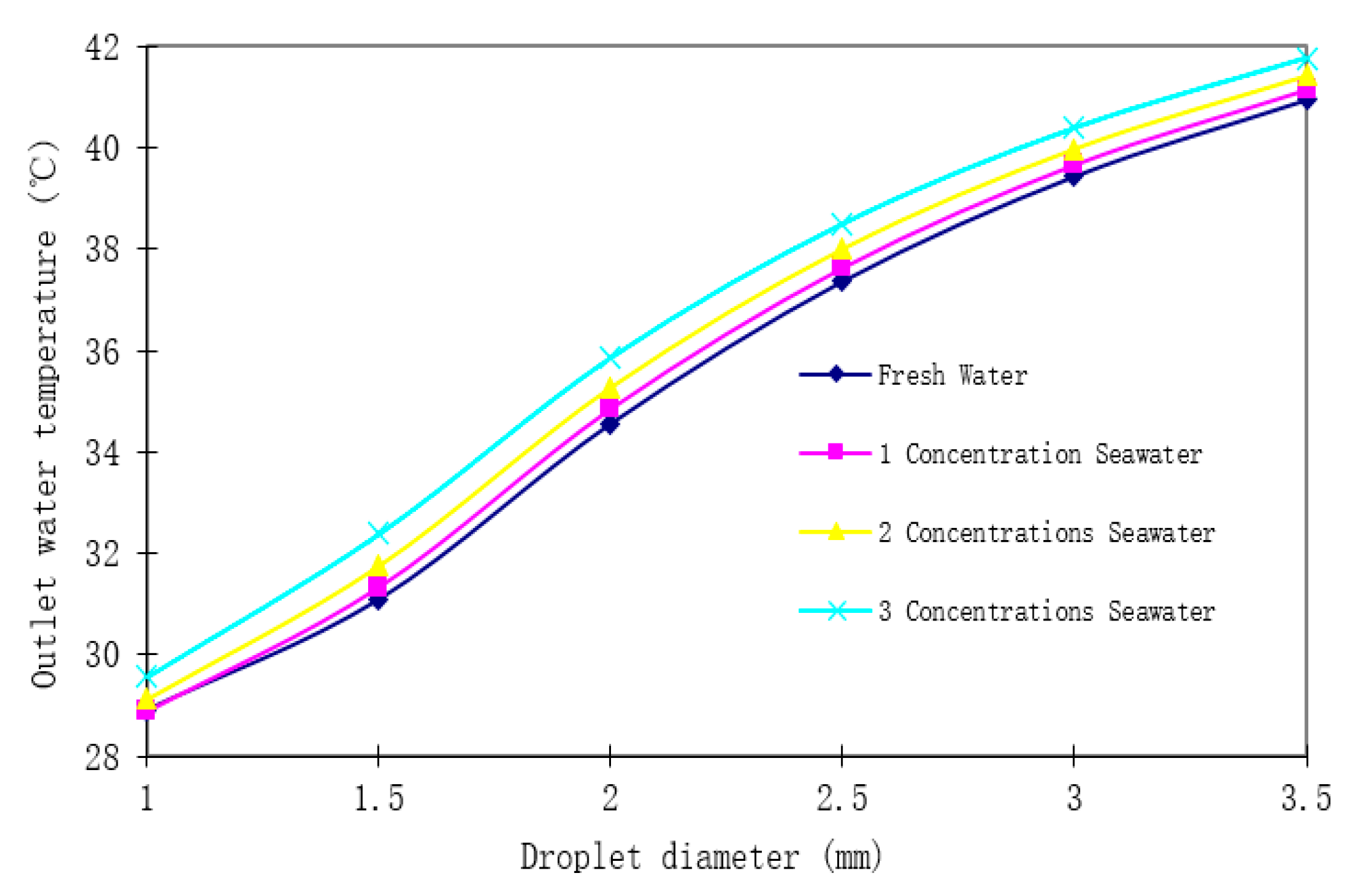
As illustrated in Figure 7 and

Table 4. Parametric study results (Summer): Cooling efficiency as a function of droplet diameter and seawater salinity.

Droplet Diameter (mm)	1	1.5	2
Fresh water cooling efficiency (%)	75.87	67.93	54.65
1 concentrations seawater cooling efficiency (%)	75.73	66.85	53.29
2 concentrations seawater cooling efficiency (%)	74.41	64.88	51.36
3 concentrations seawater cooling efficiency (%)	72.58	62.35	48.92
Droplet diameter (mm)	2.5	3	3.5
Fresh water cooling efficiency (%)	43.43	35.12	28.92
1 concentrations seawater cooling efficiency (%)	42.25	34.08	28.03
2 concentrations seawater cooling efficiency (%)	40.52	32.63	26.81
3 concentrations seawater cooling efficiency (%)	38.45	30.85	25.31

, the cooling performance in summer decreases with increasing droplet diameter and salinity. Compared to freshwater, the cooling efficiency reduction was 2.17% for 1-concentration seawater, 5.59% for 2-concentration seawater, and 9.86% for 3-concentration seawater. Furthermore, the detrimental effect of salinity was amplified with larger droplet diameters.

As shown in Figure 8 and

Table 5. Parametric study results (Winter): Cooling efficiency as a function of droplet diameter and seawater salinity.

Droplet Diameter (mm)	1	1.5	2
Fresh water cooling efficiency (%)	43.09	38.17	30.34
1 concentrations seawater cooling efficiency (%)	43.14	37.61	29.66
2 concentrations seawater cooling efficiency (%)	42.60	36.66	28.71
3 concentrations seawater cooling efficiency (%)	41.63	35.26	27.40
Droplet diameter (mm)	2.5	3	3.5
Fresh water cooling efficiency (%)	23.99	19.32	15.91
1 concentrations seawater cooling efficiency (%)	23.39	18.8	15.46
2 concentrations seawater cooling efficiency (%)	22.55	18.1	14.85
3 concentrations seawater cooling efficiency (%)	23.99	19.32	15.91

, during winter operation, the reduction in cooling performance was slightly less severe than in summer. Compared to freshwater, the efficiency decreased by 1.95% for 1-concentration seawater, 4.91% for 2-concentration seawater, and 9.01% for 3-concentration seawater.

The results demonstrate that salinity has a more pronounced effect on cooling performance during summer conditions, which can be attributed to the greater reliance on evaporative cooling mechanisms when ambient temperatures are higher. The interaction between droplet size and salinity effects highlights the importance of optimizing nozzle design for saline water applications.

The non-linear relationship between droplet diameter and cooling performance, evident in Figure 7 and Figure 8 reveals a fundamental aspect of droplet-based heat and mass transfer. The distinct change in curvature, which is from concave for diameters below approximately 2 mm to convex for larger diameters, can be explained by the shifting dominance between evaporative and sensible cooling mechanisms.

For small droplets (1–2 mm), the surface-area-to-volume ratio is large, maximizing the area available for mass transfer. In this regime, evaporative cooling is the dominant mechanism. Since the evaporation rate is highly sensitive to the available surface area, a small increase in diameter results in a disproportionate loss of cooling capacity, leading to the steep, concave decline in efficiency.

For larger droplets (>2 mm), the surface-area-to-volume ratio decreases significantly. Evaporation is substantially curtailed due to the reduced interfacial area, and sensible convective cooling becomes increasingly influential relative to latent heat transfer. As sensible heat transfer is a less efficient process and exhibits a different scaling relationship with diameter, the rate of performance degradation slows, resulting in the flattened, convex shape of the curve. The transition point represents the diameter where the dominant mode of heat transfer shifts from evaporative to sensible.

This phenomenon is observed in both freshwater and seawater operations. However, as previously discussed, the elevated salinity of seawater suppresses vapor pressure, further inhibiting the evaporative mechanism and exacerbating the performance penalty across all droplet sizes, particularly in the small-diameter, evaporation-dominant regime.

5.2. Variation of Cooling Water Temperature Difference with Seawater Salinity, Air-to-Water Ratio, and Inlet Water Temperature

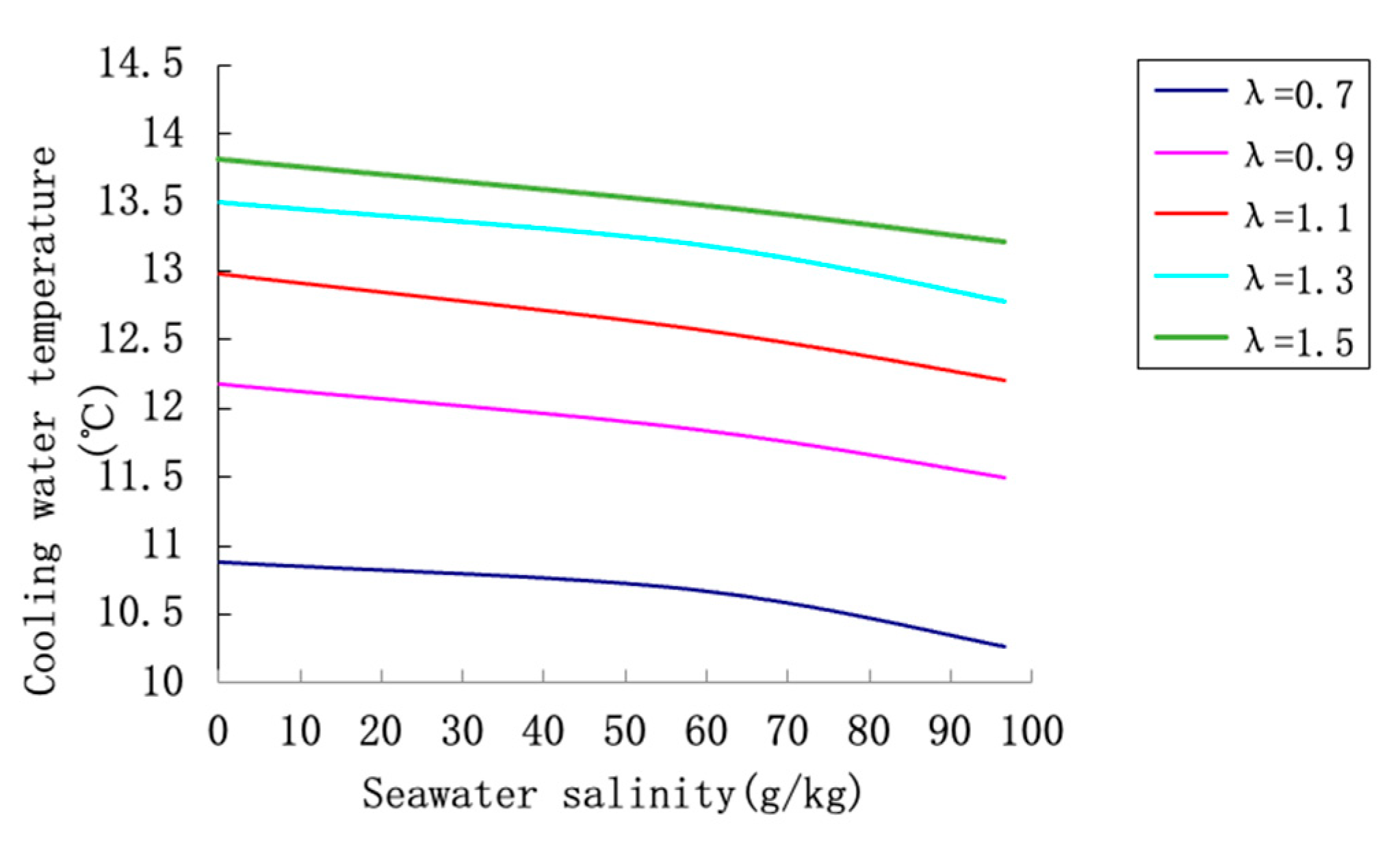
Three typical concentrations of circulating water were selected: freshwater (S = 0 g/kg), three-fold concentration (S = 57.96 g/kg), and five-fold concentration (S = 96.60 g/kg). When the inlet water temperature t₁ = 42 °C, the variation of the cooling water temperature difference with seawater salinity and air-to-water ratio is shown in Figure 9. When the air-to-water ratio λ = 0.7, the variation of the cooling water temperature difference with seawater salinity and inlet water temperature is illustrated in Figure 10. When the seawater salinity S = 57.96 g/kg, the variation of the cooling water temperature difference with inlet water temperature and air-to-water ratio is presented in Figure 11.

To systematically evaluate the thermal performance of the cooling tower under hypersaline conditions, three representative concentrations of circulating water were selected: freshwater (S = 0 g/kg), three-fold concentration (S = 57.96 g/kg), and five-fold concentration (S = 96.60 g/kg). The effects of key operating parameters—seawater salinity, air-to-water ratio, and inlet water temperature—on the cooling temperature difference (ΔT) were analyzed. The results are presented and interpreted in detail below.

Figure 9 depicts the combined effects of seawater salinity and air-to-water ratio on ΔT, with the inlet water temperature maintained at 42 °C. A clear declining trend in ΔT is observed as salinity increases across all air-to-water ratios. For example, when λ increases from 0.6 to 1.0, the ΔT for freshwater rises markedly, whereas the increase is less pronounced for high-salinity water. This suggests that higher salinity not only reduces the cooling efficiency but also weakens the enhancing effect of air-to-water ratio. The converging curves at high λ values imply that increasing air flow becomes less effective when salt content is elevated, highlighting a coupling effect between salinity and air-to-water ratio.

Figure 10 demonstrates how ΔT responds to variations in seawater salinity and inlet water temperature under a constant air-to-water ratio (λ = 0.7). Each curve represents a specific inlet temperature, illustrating that higher inlet temperatures consistently lead to greater ΔT, though the degree of improvement is modulated by salinity. At 45 °C, for instance, increasing salinity from 0 to 96.6 g/kg reduces ΔT by nearly 30%, underscoring the strong inhibitory role of salt. The parallel nature of the curves indicates that the influence of inlet temperature remains robust even under high-salinity conditions, reaffirming that thermal effects partially counteract salinity-induced performance degradation.

Figure 11 explores the interdependence of inlet water temperature and air-to-water ratio at a fixed salinity (S = 57.96 g/kg). The surface-like representation shows that ΔT improves with both higher temperature and greater air flow, though the marginal gain decreases at higher λ. For instance, at t₁ = 40 °C, increasing λ from 0.8 to 1.2 results in a ΔT increase of about 1.5 °C, which is smaller than the increase observed when λ changes from 0.4 to 0.8. This demonstrates the presence of a saturation effect wherein additional air supply yields limited cooling enhancement. Meanwhile, higher inlet temperatures amplify the overall cooling range, showing synergistic behavior between thermal and operational factors.

The analysis demonstrates that hypersaline conditions impair cooling tower performance by reducing vapor pressure and limiting evaporation rates. This effect is particularly strong at high salinity levels, where thermodynamic activity of water is substantially lowered.

Higher inlet water temperatures compensate to some extent by elevating vapor pressure and rejuvenating the evaporation potential. This is especially relevant in industrial settings where heat load or ambient conditions cause inlet temperature fluctuations.

Increasing the air-to-water ratio enhances cooling efficiency by improving the carrier capacity of the air; however, the law of diminishing returns applies at higher ratios. Optimizing λ is therefore crucial for balancing energy consumption (fan power) against cooling gain.

These insights are valuable for the design and operation of cooling systems using seawater or brine, particularly in power plants or refineries located in coastal or water-scarce regions. Future work could incorporate dynamic modeling or economic optimization to identify feasible operating windows under real-world constraints.

5.3. Variation of Cooling Tower Efficiency with Seawater Salinity, Air-to-Water Ratio, and Inlet Water Temperature

The wet-bulb temperature (τ) of the air represents the thermodynamic limit for cooling in wet cooling towers. The cooling efficiency is defined as the ratio of the actual temperature drop to the maximum possible temperature drop between the inlet water and the air wet-bulb temperature $\mathsf{\eta }={\displaystyle \frac{\Delta \mathrm{t}}{{\mathrm{t}}_1-\tau }}={\displaystyle \frac{{\mathrm{t}}_1-{\mathrm{t}}_2}{{\mathrm{t}}_1-\mathsf{\tau }}}$.

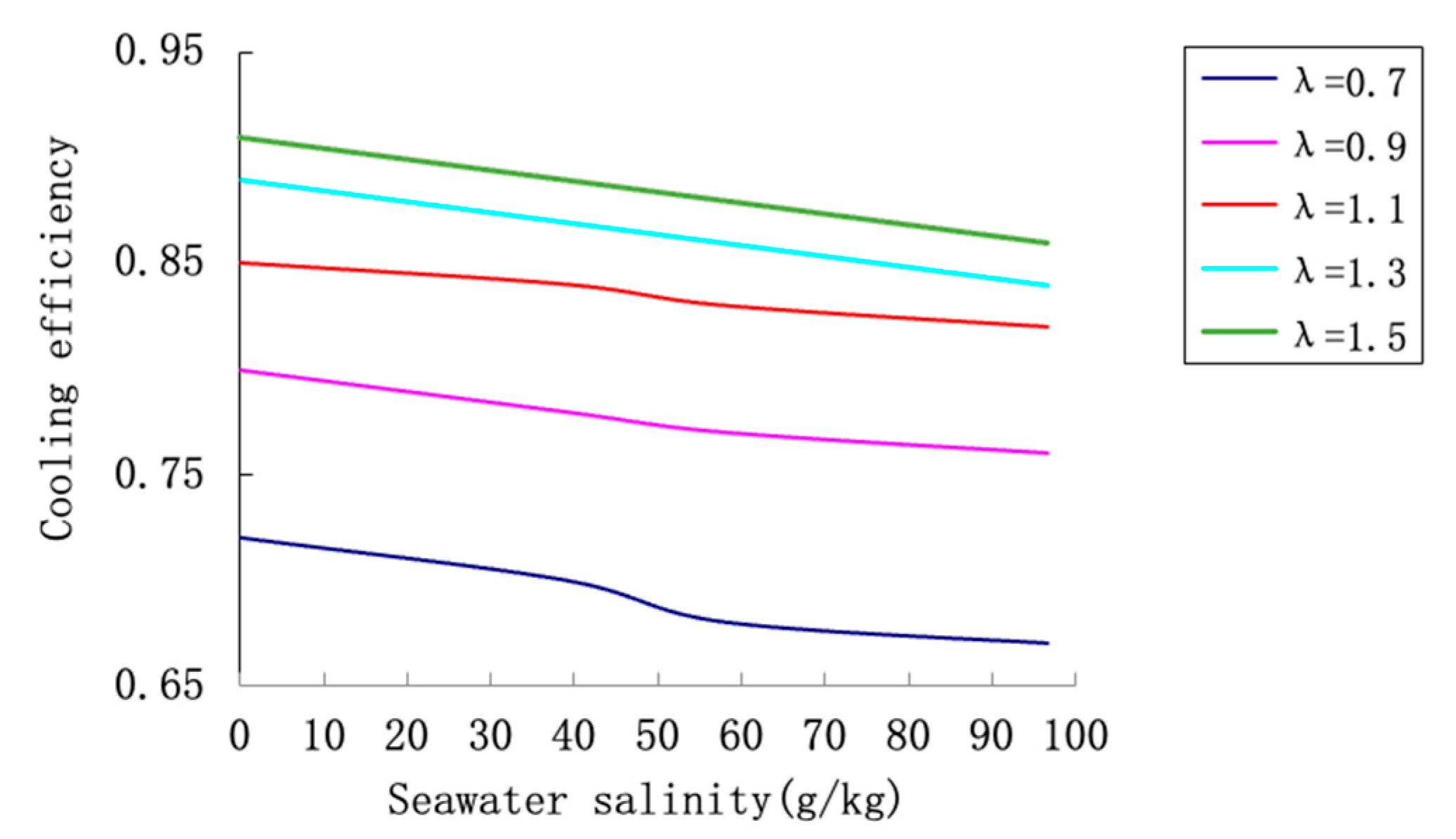
To comprehensively investigate this efficiency under hypersaline conditions, three representative salinity levels were selected: freshwater (S = 0 g/kg), three-fold concentration (S = 57.96 g/kg), and five-fold concentration (S = 96.60 g/kg). The analysis focuses on how efficiency responds to variations in three key parameters: seawater salinity, air-to-water ratio (λ), and inlet water temperature (t₁).

Figure 12 presents the combined effects of seawater salinity and air-to-water ratio on cooling efficiency at a fixed inlet water temperature of 42 °C. The results demonstrate that efficiency increases with higher air-to-water ratios but decreases substantially with increasing salinity. For instance, at λ = 1.0, the efficiency drops from approximately 78% for freshwater to about 62% for the five-fold concentration saline water. This represents a relative reduction of over 20%. The divergence between the curves at higher λ values indicates that increasing airflow cannot fully compensate for the performance degradation caused by high salinity. The underlying mechanism involves reduced vapor pressure and decreased evaporation rates in saline water, which impair both latent and sensible heat transfer processes.

Figure 13 illustrates the variation of cooling efficiency with seawater salinity and inlet water temperature at a constant air-to-water ratio (λ = 0.7). The results show that higher inlet temperatures consistently improve cooling efficiency across all salinity levels. For example, at S = 57.96 g/kg, increasing t₁ from 35 °C to 45 °C enhances efficiency from about 55% to nearly 70%. This improvement occurs because elevated water temperature increases the vapor pressure differential between the water surface and the air, thereby enhancing evaporation rates. However, the efficiency values for saline water remain consistently below those of freshwater at any given temperature, highlighting the persistent negative impact of salinity even at elevated temperatures.

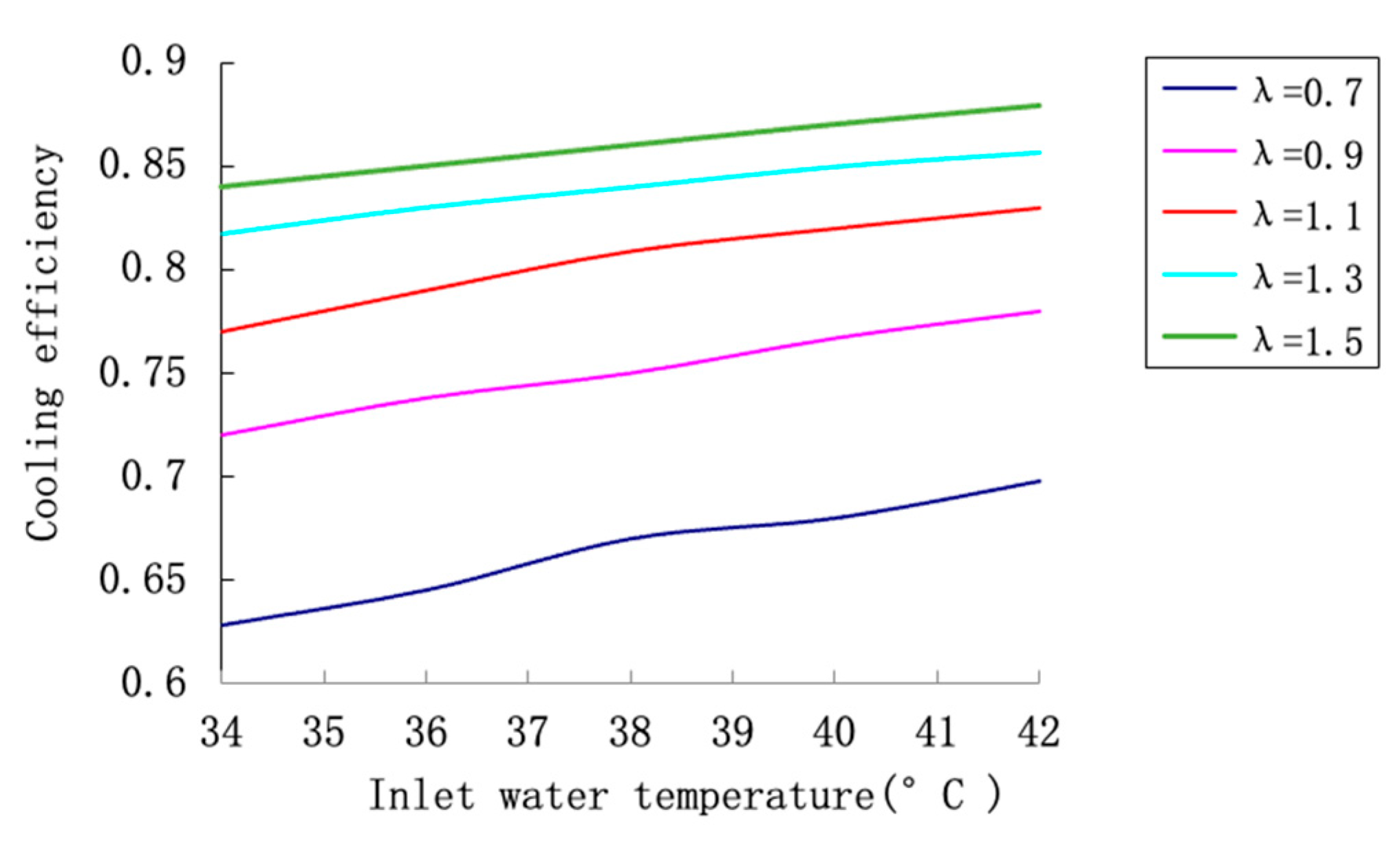
Figure 14 examines the combined effects of inlet water temperature and air-to-water ratio on cooling efficiency at a fixed salinity of 57.96 g/kg. The results reveal that efficiency improves with both increasing inlet temperature and higher air-to-water ratio, though the marginal gains diminish at higher values of λ. For instance, at t₁ = 40 °C, increasing λ from 0.6 to 1.0 improves efficiency by approximately 15 percentage points, while a further increase to 1.4 yields only an additional 5-point improvement. This saturation effect occurs because the air becomes increasingly saturated with moisture, reducing its capacity for further evaporation. The synergistic relationship between temperature and airflow is evident, as higher temperatures amplify the beneficial effects of increased airflow.

The reduction in cooling efficiency with increasing salinity is primarily attributed to thermodynamic suppression of vapor pressure and physical properties changes. Higher salt content lowers the activity of water molecules, reducing the driving force for evaporation. Additionally, increased salinity affects fluid properties such as surface tension and viscosity, which may influence droplet formation and heat transfer surfaces in actual tower operations.

The positive effect of higher inlet water temperature stems from enhanced thermal driving forces. While this improves efficiency, operators must balance this benefit against potential scaling concerns and increased pumping costs associated with higher temperatures.

The relationship with air-to-water ratio demonstrates classic mass transfer behavior. Initially, increased airflow provides substantial benefits by maintaining a steeper humidity gradient. However, the law of diminishing returns applies as the air approaches saturation. This has direct implications for energy optimization, as fan power consumption must be balanced against cooling performance.

These findings are particularly relevant for coastal power plants and industrial facilities using seawater cooling. The results suggest that operational strategies should be adapted based on seasonal variations in salinity and temperature. For high-salinity conditions, moderate increases in airflow combined with optimal inlet temperature control may provide the most energy-efficient solution.

Future research should focus on developing predictive models that incorporate these nonlinear relationships, enabling real-time optimization of cooling tower operations under varying salinity conditions. Additionally, economic analyses could help determine the cost-effectiveness of different mitigation strategies for salinity-induced efficiency reduction.

5.4. Mechanistic Analysis of the Performance Reduction in Seawater SCTs

The observed reduction in cooling performance for seawater, which intensifies with both increasing salinity and droplet size, can be fundamentally attributed to the interplay between the thermophysical properties of seawater and the governing mechanisms of heat and mass transfer. This section delves into the underlying physics to explain these phenomena.

The cooling process in an SCT is predominantly driven by two simultaneous mechanisms: (1) sensible heat transfer due to the temperature difference between the water droplet and the ambient air $\mathrm{Q}\mathrm{c}=\mathrm{h}\mathrm{c}\mathrm{A}(\mathrm{T}\mathrm{w}-\mathrm{T}\mathrm{a})$, and (2) latent heat transfer due to the evaporation of water, which is governed by the vapor pressure difference ($\mathrm{Q}\mathrm{e}=\mathrm{h}\mathrm{d}\mathrm{A}({\mathrm{w}}_{\mathrm{w}\mathrm{s}}-{\mathrm{w}}_{\mathrm{a}}){\mathrm{h}}_{\mathrm{f}\mathrm{g}}$). The presence of dissolved salts in seawater directly modifies the key properties that act as the driving forces for these mechanisms.

Reduction in Latent Heat Transfer (Dominant Effect): The primary factor for performance degradation is the suppression of evaporation. Dissolved salts lower the water activity at the droplet surface, which consequently lowers the saturated vapor pressure ${\mathrm{P}}_{\mathrm{s}\mathrm{w}}$ at the water-air interface compared to freshwater at the same temperature. This is quantified by Raoult’s law in ideal solutions. Since the mass transfer driving force is proportional to (${\mathrm{w}}_{\mathrm{s}\mathrm{w}}-{\mathrm{w}}_{\mathrm{a}}$), and ${\mathrm{w}}_{\mathrm{w}\mathrm{s}}$ is directly related to ${\mathrm{P}}_{\mathrm{s}\mathrm{w}}$, a reduction in vapor pressure leads to a smaller driving force for evaporation (Δw). This directly reduces the latent heat rejection rate ($\mathrm{Q}\mathrm{e}$), which is the most efficient cooling mechanism. This effect is exacerbated in larger droplets, which have a smaller surface-area-to-volume ratio, making it harder to dissipate heat and further amplifying the negative impact of reduced vapor pressure.

Alteration in Sensible Heat Transfer: Seawater has a lower specific heat capacity (${\mathrm{c}}_{\mathrm{p}}$) than freshwater. This means that for the same amount of heat rejected, the temperature of a seawater droplet will decrease more than that of a freshwater droplet. While this might seem beneficial, it creates a complex feedback loop. A faster droplet temperature drop reduces the sensible heat drive $(\mathrm{T}\mathrm{w}-\mathrm{T}\mathrm{a})$ and, more importantly, further reduces the interfacial vapor pressure ${\mathrm{P}}_{\mathrm{s}\mathrm{w}}$ (since ${\mathrm{P}}_{\mathrm{s}\mathrm{w}}$ is a strong function of temperature), thereby curbing the latent heat transfer rate sooner than in freshwater. Thus, the lower ${\mathrm{c}}_{\mathrm{p}}$ ultimately contributes to a less effective overall cooling process.

The Role of the Lewis Factor (${\mathrm{L}\mathrm{e}}_{\mathrm{f}}$): The Lewis factor, which relates the heat and mass transfer coefficients (${\mathrm{L}\mathrm{e}}_{\mathrm{f}}={\mathrm{h}}_{\mathrm{c}}/{\mathrm{h}}_{\mathrm{d}}{\mathrm{c}}_{\mathrm{p}\mathrm{a}}$), is also influenced by the properties of the solution. For seawater, the calculation of ${\mathrm{w}}_{\mathrm{s}\mathrm{w}}$ and the enthalpy of saturated air (${\mathrm{h}}_{\mathrm{s}\mathrm{w}}$) must account for salinity. The model shows that the effective ${\mathrm{L}\mathrm{e}}_{\mathrm{f}}$ for seawater deviates from that of freshwater, affecting the precise ratio of sensible to latent heat loss throughout the cooling process. This nuanced change in the heat and mass transfer analogy further differentiates the performance of seawater from freshwater.

In conclusion, the performance penalty is not due to a single factor but a synergistic effect. The reduction in saturated vapor pressure is the most significant culprit, directly hampering evaporation. This is compounded by a lower specific heat capacity, which accelerates the droplet’s cooling rate and prematurely weakens the driving forces for both sensible and latent heat transfer. The larger the droplet, the more pronounced these effects become due to reduced heat and mass transfer surface area. This mechanistic understanding confirms that the model is not just empirically accurate but is also capturing the correct underlying physics of seawater droplet cooling.

6. Conclusions

Comparison of Heat and Moisture Exchange Characteristics Between Upward-Spraying Tower and Downward-Spraying Shower Cooling Tower Under Different Salinity Conditions

This study has developed a comprehensive theoretical and numerical model to evaluate the thermal performance of packing-free shower cooling towers (SCTs) operating with seawater. The model integrates droplet-level heat and mass transfer mechanics with system-wide energy balances, accounting for the significant influences of seawater salinity on thermophysical properties and phase-change dynamics. The following key conclusions can be drawn:

The developed model accurately predicts the outlet water temperature of seawater SCTs, with a maximum error of less than 6% across a wide range of operating conditions when validated against experimental data from a full-scale industrial tower. This demonstrates its reliability as a tool for design and performance analysis.

Seawater salinity profoundly impacts cooling performance. Increasing salinity reduces the cooling temperature difference and efficiency due primarily to the suppression of vapor pressure, which inhibits evaporation—the dominant cooling mechanism. A reduction in specific heat capacity and an increase in density also play contributory roles. For instance, at a three-fold concentration (≈57.96 g/kg), cooling efficiency decreased by approximately 5.59% in summer and 4.91% in winter compared to freshwater.

The detrimental effect of salinity is exacerbated by larger droplet diameters. Larger droplets have a lower surface-area-to-volume ratio, which amplifies the negative impact of reduced vapor pressure by further limiting evaporative heat transfer.

Higher inlet water temperatures and increased air-to-water ratios can partially mitigate the performance loss caused by salinity. Elevated inlet temperature boosts the vapor pressure driving force, while a higher air-to-water ratio enhances the mass transfer capacity. However, both effects are subject to diminishing returns, particularly at higher salinity levels.

Operational performance varies seasonally. The cooling performance reduction was more pronounced in summer than in winter, attributed to a greater reliance on evaporative cooling under high ambient temperatures.

The model successfully captures the physics of supersaturated air conditions, where excess moisture condenses as mist, providing a more complete simulation framework for real-world operating regimes beyond the simple unsaturated assumption.

The insights and the validated model presented in this study provide a solid theoretical foundation for the design, optimization, and operation of packing-free seawater cooling towers. They are particularly valuable for industrial applications in coastal and water-scarce regions, supporting the broader adoption of seawater as a sustainable cooling resource. Future work should focus on integrating this model with economic optimization frameworks and dynamic control strategies to maximize energy and water savings in practical engineering applications.