Optimal Guidance Mechanism for EV Charging Behavior and Its Impact Assessment on Distribution Network Hosting Capacity

Abstract

With the rapid growth in the penetration of Electric Vehicles (EVs), their large-scale uncoordinated charging behavior presents significant challenges to the hosting capacity of traditional distribution networks (DNs). The novelty of this paper lies in its methodology, which integrates a Markov Chain Monte Carlo (MCMC) method for realistic load profiling with a bi-level optimization framework for Time-of-Use (TOU) pricing, whose effectiveness is then rigorously evaluated through an Optimal Power Flow (OPF)-based assessment of the grid’s hosting capacity. First, to compensate for the limitations of historical data, the MCMC method is employed to simulate the uncoordinated charging process of a large-scale EV fleet. Second, the bi-level optimization model is constructed to formulate a globally optimal TOU tariff that maximizes charging cost savings for EV users. At the same time, its lower-level simulates the optimal economic response of the EV user population. Finally, the change in the minimum daily hosting capacity is calculated based on the OPF. Case study simulations for IEEE 33-bus and IEEE 69-bus systems demonstrate that the proposed model effectively shifts charging loads to off-peak hours, achieving stable user cost savings of 20.95%. More importantly, the findings reveal substantial security benefits from this economic strategy, validated across diverse network topologies. In the 33-bus system, the minimum daily capacity enhancement ranged from 174.63% for the most vulnerable node to 2.44% for the strongest node. In the 69-bus system, vulnerable nodes still achieved a significant 78.62% improvement. This finding highlights the limitations of purely economic assessments and underscores the necessity of the proposed integrated framework for achieving precise, location-dependent security planning.

1. Introduction

Currently, while the global economy is in a flourishing stage of development, the over-dependence on and consumption of traditional energy have become issues of high concern to the international community. With the extensive use of fossil fuels, the problem of environmental degradation has become increasingly prominent. Against this backdrop, the low-carbon transformation process of the transportation sector is accelerating [1]. By utilizing clean energy, EVs can fundamentally avoid the tailpipe pollution problems of traditional fuel vehicles, achieving zero emissions and zero pollution. Consequently, EVs are experiencing explosive growth and are gradually becoming the core of the future transportation sector [2,3].

However, the large-scale integration of EVs fundamentally changes the characteristics of the load. Unlike traditional loads, the charging behavior of EVs exhibits high randomness and space-time uncertainty [4]. Without effective coordination and management, this uncoordinated charging will cause the peak EV charging load to superimpose on the peak of the base electricity demand, creating a “dual-peak” phenomenon. This will severely affect the stable operation of the power system and lead to a reduction in grid voltage levels, compromising the secure and stable operation of the grid [5,6]. Therefore, it is crucial to regulate EV charging behavior, transforming them from a potential burden on the grid into a dispatchable resource [7].

To address the issues above and achieve synergistic interaction between EVs and the grid, scholars worldwide have conducted in-depth research from multiple dimensions. Reference [8] used the Monte Carlo method combined with probabilistic distribution data of vehicle travel distance, arrival, and departure times to simulate the aggregated charging load profile of large-scale EVs under uncoordinated charging. Reference [9], based on Markov theory and extensive data, constructed a refined EV aggregation model that accurately describes user travel patterns. Reference [10] developed a time-inhomogeneous Markov model, setting different state transition probabilities for different times to more realistically and dynamically capture the all-day behavior of EVs. Reference [11] proposed a multi-objective charging scheduling model to combine peak shaving and valley filling with user economics. By categorizing charging demand into emergency and non-emergency, it optimizes the scheduling of flexible non-emergency demand to achieve a win-win situation for both the grid and users. Reference [12] constructed a bi-level optimization model for a Vehicle-to-Grid (V2G) enabled charging station based on TOU pricing. It utilizes the bidirectional interaction capability of V2G to find a pricing scheme that significantly reduces the overall peak load of the charging station. Reference [13] built a comprehensive framework for EV hosting capacity, from assessment to enhancement. Through a comprehensive evaluation system including security and economic resilience indicators, it identifies the key bottlenecks constraining hosting capacity. Reference [14] proposed a direct method for assessing EV hosting capacity. An iterative algorithm progressively increases the charging load in the grid and performs power flow calculations until the first constraint violation occurs.

Despite these valuable contributions, several limitations remain. Existing studies often focus on isolated aspects of the problem: complex behavioral models may lack integration with grid security analysis; advanced optimization strategies frequently rely on simplified economic metrics (such as peak-to-valley ratios) for evaluation, failing to capture network security indicators; and grid impact assessments often depend on non-optimized charging scenarios. Consequently, a unified framework remains elusive for quantitatively linking random user behavior, economic optimization, and their impact on grid security margins. This paper proposes and validates an integrated analytical framework that methodologically bridges these three domains, analyzing the physical security benefits derived from unified economically optimal coordination strategies.

The main innovative contributions of this paper can be summarized into the following three points:

(1)

Developing an integrated framework. By combining economic optimization models with OPF-based capacity assessments, this approach directly quantifies the impact of TOU optimization strategies on the physical security margin of distribution grids. This integrated methodology overcomes the shortcomings of traditional evaluation metrics (such as the peak-to-valley difference), which cannot directly reflect the grid’s security margin, thereby enabling a more comprehensive assessment.

(2)

To address the challenge of sparse historical EV data, an inhomogeneous MCMC method is adopted to generate large-scale, high-fidelity EV charging baseline loads from a small amount of data, providing a realistic basis for optimization and evaluation.

(3)

A price-signal-based bi-level optimization framework is designed to guide user charging behavior by formulating an optimal TOU tariff that maximizes the total economic benefits for the user group.

2. EV Random Charging Demand Modeling Based on MCMC

2.1. Markov Chain

The Markov Chain, proposed by the Soviet mathematician Markov at the beginning of the 20th century, is an analytical method that uses the current state of a variable to predict its future state. Studying the initial probabilities of different states and the transition probabilities between them determines the trend of state changes, thereby achieving the goal of future prediction [15].

A Markov Chain is a mathematical model used to describe a series of transitions between states. Its characteristic feature is that the transition to the next state depends only on the present state and is independent of all prior states. That is, for a given random process {X_t, t = 0, 1, 2, …}, knowing the past states X₀, X₁, X₂, X₃, …, X_t−2 and the present state X_t−1, the future state X_t depends only on the present state X_t−1 and is independent of the past states. This process {X_t, t = 0, 1, 2, 3, …} is said to have the “Markov property,” also known as “memorylessness”.

This fundamental characteristic is formalized in the mathematical definition of a Markov Chain. Let there be a random process {X_t, t = 0, 1, 2, 3, …}, with its state space being S = {s₀, s₁, …, s_i, s_j, …, s_n−1, s_n, …}. If for any t ≥ 0 and any state s₀, s₁, …, s_i, s_j, …, s_n−1, s_n, …, it holds that:

$$\begin{array}{c}\hfill P(X_t=s_n|X_{t-1}=s_{n-1},\cdots ,X_j=s_j,X_i=s_i,\cdots ,\hfill \\ \hfill \hspace{1em}\hspace{1em}{X}_1=s_1,X_0=s_0)=P(X_t=s_n|X_{t-1}=s_{n-1})\hfill \end{array}$$

(1)

Such a random process is called a Markov Chain. The state of X_t at time t, X_t = s_n, is only related to the state at time t−1, X_t−1 = s_n−1, and is independent of the states before time t−1.

Let there be a random process {X_t, t = 0, 1, 2, 3, ⋯}, with its state space being S = {s₀, s₁, ⋯, s_i, s_j, ⋯, s_n−1, s_n, ⋯}. Let f_ij denote the frequency of transitioning from state i to state j in one step within the state sequence, where i, j∈S. At the same time, let f_i be the total number of occurrences of state i in the state sequence. The one-step transition probability, denoted as p_ij, is then defined as the ratio of f_ij to f_i, where i, j∈S. That is:

$$p_{ij}={\displaystyle \frac{f_{ij}}{f_i}}$$

(2)

where ∑∞ j = 0 p_ij = 1, ∀ i, j∈S.

Representing all the one-step transition probabilities p_ij in matrix form yields the one-step transition probability matrix of the Markov Chain, denoted as P.

$$P=\left[\begin{array}{lllll}{P}_{11}& P_{12}& \cdots & P_{1j}& \cdots \\ P_{21}& P_{22}& \cdots & P_{2j}& \cdots \\ & & ⋮& & \\ P_{i1}& P_{i2}& \cdots & P_{ij}& \cdots \\ & & ⋮& & \end{array}\right]$$

(3)

Similarly, the k-step state transition probability p(k) ij and the k-step transition probability matrix of the Markov Chain, denoted as P^(k), can be obtained.

$$P^{\left(k\right)}=\left[\begin{array}{lllll}{P}_{11}^{\left(k\right)}& P_{12}^{\left(k\right)}& \cdots & P_{1j}^{\left(k\right)}& \cdots \\ P_{21}^{\left(k\right)}& P_{22}^{\left(k\right)}& \cdots & P_{2j}^{\left(k\right)}& \cdots \\ & & ⋮& & \\ P_{i1}^{\left(k\right)}& P_{i2}^{\left(k\right)}& \cdots & P_{ij}^{\left(k\right)}& \cdots \\ & & ⋮& & \end{array}\right]$$

(4)

The core feature of the aforementioned Markov Chain is that the one-step transition probability P (X_t = s_n∣X_t−1 = s_n−1) = p_ij does not depend on the time step t. Regardless of the stage of the random process, the probability of transitioning from state i to state j remains constant. This property is called time-homogeneity, and the corresponding Markov Chain is known as a time-homogeneous Markov Chain. Its transition characteristics are completely described by a fixed transition probability matrix P.

Since the state transition process of an EV within a day exhibits significant probabilistic and temporal characteristics, which the aforementioned Markov Chain cannot capture, this paper employs a time-inhomogeneous Markov Chain to model its behavior.

A time-inhomogeneous Markov Chain is an extension of the basic Markov Chain. Unlike a time-homogeneous Markov Chain, its state transition probabilities are not fixed but change over time. This feature allows it to more flexibly capture the dynamic transformations of a system [16].

Specifically, for a random process {X_t, t = 0, 1, 2, 3, ⋯}, its state space is S_t = {s₀, s₁, ⋯, s_i, s_j, ⋯, s_n−1, s_n, ⋯}, If for any t ≥ 0 and any state s₀(t), s₁(t), ⋯, s_i(t), s_j(t), ⋯, s_n−1(t), s_n(t), ⋯, it holds that:

$$\begin{array}{l}\hfill P\left(X_t=s_n\left(t\right)|X_{t-1}=s_{n-1}\left(t\right),\cdots ,X_j=s_j\left(t\right)\right.,\hfill \\ \hfill \hspace{1em}\hspace{1em} X_i=s_i\left(t\right),\cdots ,X_1=s_1\left(t\right),X_0=s_0\left(t\right))\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=P\left(X_t=s_n\left(t\right)|X_{t-1}=s_{n-1}\left(t\right)\right)\hfill \end{array}$$

(5)

Such a random process is called a time-inhomogeneous Markov Chain. Its one-step transition probability is p_ij(t), and its k-step state transition probability is p(k) ij(t).

The one-step transition probability matrix of the time-inhomogeneous Markov Chain is denoted as P(t).

$$P\left(t\right)=\left[\begin{array}{lllll}{P}_{11}\left(t\right)& P_{12}\left(t\right)& \cdots & P_{1j}\left(t\right)& \cdots \\ P_{21}\left(t\right)& P_{22}\left(t\right)& \cdots & P_{2j}\left(t\right)& \cdots \\ & & ⋮& & \\ P_{i1}\left(t\right)& P_{i2}\left(t\right)& \cdots & P_{ij}\left(t\right)& \cdots \\ & & ⋮& & \end{array}\right]$$

(6)

2.2. EV Behavior Modeling Based on Markov Chain

The state transition process of an EV within a day exhibits significant probabilistic and temporal characteristics. Its state at the next time step depends mainly on its current state and the transition probabilities between states. It is independent of its earlier historical states, exhibiting the “memorylessness” property. Therefore, a time-inhomogeneous Markov chain can be used to model the random driving and charging behaviors of EV users.

In this paper, the state space for the daily behavior of an EV is defined as S = {s_d, s_f, s_s}, where s_d, s_f, and s_s represent the non-charging state, fast-charging state, and slow-charging state, respectively. The state transitions of the EV’s daily behavior are shown in Figure 1.

Maximum likelihood estimation is used to estimate the time-inhomogeneous state transition probabilities of the EV’s daily behavior from real user travel history data.

$$P_{ij}(t)={\displaystyle \frac{N_{ij}(t)}{N_i(t)}}={\displaystyle \frac{N_{ij}(t)}{{\displaystyle \sum _{k\in S}{N}_{ik}}(t)}}$$

(7)

where N_ij(t) is the number of transitions from state i to state j during time period t, and N_i(t) is the total number of transitions from state i during time period t.

By calculating the state transition probabilities for the 24 time periods within a day, the state transition matrix for the EV’s daily behavior is constructed, as shown in the Equation (8).

$$P\left(t\right)=\left[\begin{array}{ccc}{P}_{11}\left(t\right)& P_{12}\left(t\right)& P_{13}\left(t\right)\\ P_{21}\left(t\right)& P_{22}\left(t\right)& P_{23}\left(t\right)\\ P_{31}\left(t\right)& P_{32}\left(t\right)& P_{33}\left(t\right)\end{array}\right]$$

(8)

The essence of the EV’s daily behavior at the energy level is the dynamic change in the battery’s State of Charge (SOC). The transitions between different states of the EV all correspond to changes in SOC. The fast-charging or slow-charging states correspond to the replenishment of SOC, while each non-charging state may correspond to either no change or a consumption of SOC.

Therefore, the Equation (9) is used to model the dynamic evolution process of the EV battery’s SOC [17].

$$SOC(t+1)=SOC(t)+({\eta }_{ch}\cdot P_{ch}(t)-{\displaystyle \frac{P_{dis}(t)}{{\eta }_{dis}}})$$

(9)

where P_ch(t) and η_ch are the charging power and efficiency of the EV battery, which include fast charging (P_qc(t), η_qc) and slow charging (P_sc(t), η_sc). Similarly, P_dis(t) and η_dis are the discharging power and efficiency, including driving discharge (P_disf(t), η_disf) and natural discharge (P_diss (t), η_diss). SOC is the state of charge of the EV battery, used to reflect the current remaining capacity of the battery, as defined in the Equation (10).

$$SOC(t)={\displaystyle \frac{E\left(t\right)}{E_{\max }}}\times 100\%$$

(10)

where E(t) and E_max are the current and maximum capacity of the battery, respectively.

In summary, by coupling the Markov state with the SOC dynamic evolution model, the key transition from behavior to energy is completed.

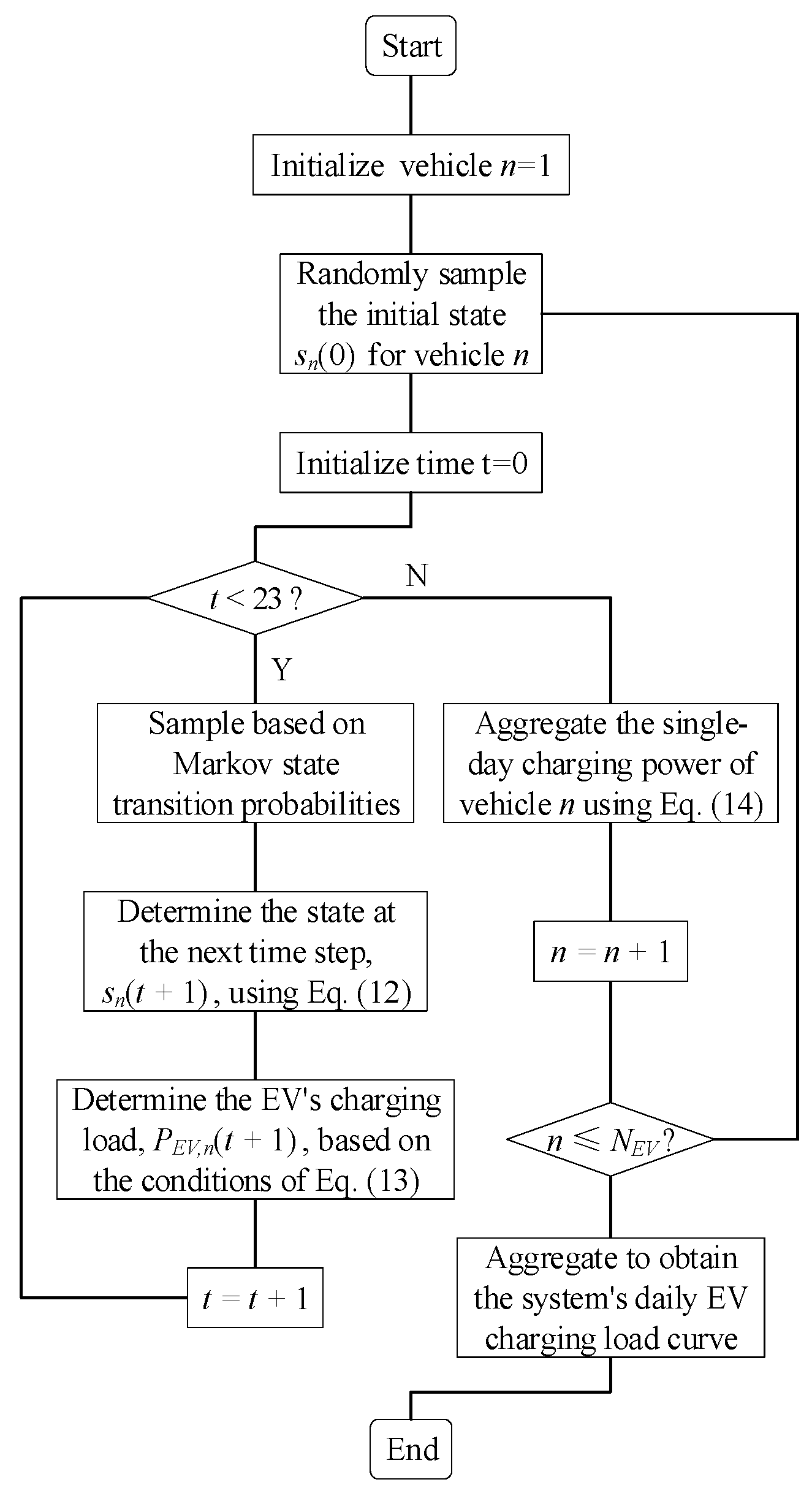
2.3. Charging Demand Scenario Generation Based on Monte Carlo Simulation

The previous section constructed a comprehensive model capable of accurately describing the daily random behavior and energy state of a single EV. However, the focus of grid planning and operation is on the system-level total load formed by the aggregation of a large number of EVs. Given the difficulty of collecting individual EV behavior data, this section employs the Monte Carlo simulation method to generate numerous system-level charging demand scenarios based on typical EV behavior patterns.

Monte Carlo simulation is a numerical method that uses extensive random sampling to study the statistical laws of random processes. Its essence is to simulate the behavior of a random system through repeated random sampling. In this paper, each sampling is based on the constructed time-inhomogeneous Markov chain.

A fundamental random event ω_n is defined as the complete 24 h behavior trajectory of the n-th typical EV, i.e.,

$${\omega }_n={\left\{\left(s_n\left(t\right)\right)\right\}}_{t=0}^{24}$$

(11)

where s_n(t) is the state of the n-th typical EV at time t.

As shown in Figure 2.

First, the initial state distribution of the EV, s_n(0), is generated by random sampling. Then, based on sampling from the transition probabilities in the Markov state matrix, the probability distribution of the EV’s state at the next time step is determined, and a state for the next time step is randomly sampled from the calculated probability distribution. This random sampling process is represented by the Equation (12).

$$s_n\left(t+1\right)=Sample\left\{\pi \left(s_n\left(t\right),t\right)\right\}$$

(12)

where the Sample(·) function performs a random draw according to the probability distribution vector π(s_n(t), t). This vector is the row in the time-inhomogeneous Markov transition matrix P(t) that corresponds to the EV’s current state, s_n(t).

Based on the state, the EV’s charging load is determined according to the conditions of the Equation (13).

$$\left\{\begin{array}{cc}{P}_{EV,n}\left(t\right)=P_{fc,n}(t)& if{s}_n\left(t\right)=s_f\\ P_{EV,n}\left(t\right)=P_{sc,n}(t)& if{s}_n\left(t\right)=s_s\\ P_{EV,n}\left(t\right)=0\hfill & if{s}_n\left(t\right)=s_d\end{array}\right.$$

(13)

Only when the EV is in a charging state does the system have a positive charging load, which is numerically equal to the EV’s charging power.

By simulating the 24 h behavior trajectories of a large number of individual EVs and aggregating their charging power over the time dimension, the system-level daily charging load curve can be generated.

$$L(t)={\displaystyle \sum _{n=1}^{N_{EV}}{P}_{EV,n}\left(t\right)}$$

(14)

where N_EV is the number of simulated EVs, and P_EV,n(t) is the charging load of the n-th EV, which satisfies the conditional Equation (14).

Through the process described above, the modeling dilemma caused by the difficulty in obtaining real user data can be effectively resolved. This method allows the generation of charging load samples whose statistical characteristics are consistent with actual conditions.

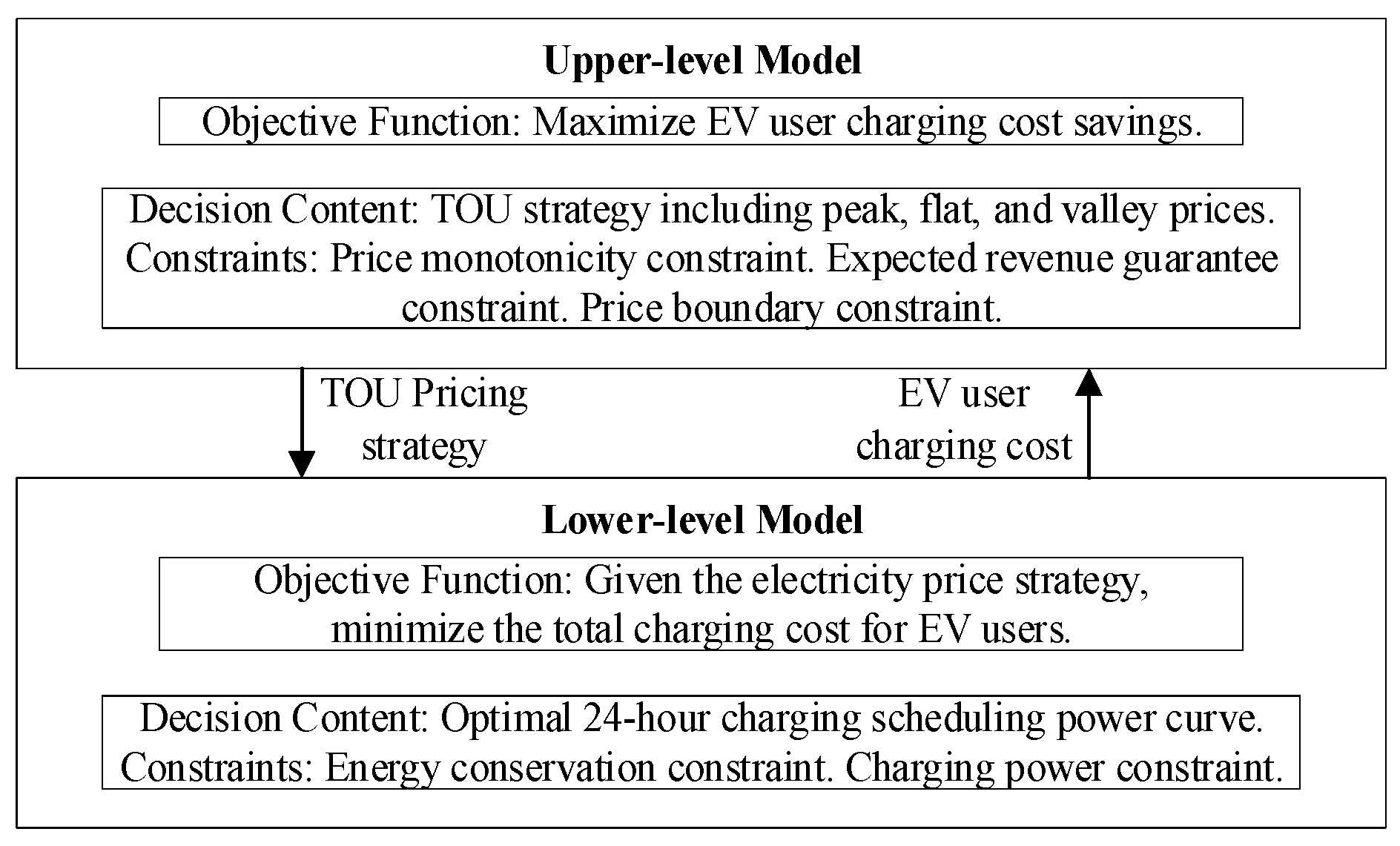
3. A Bi-Level Optimization Model of EV User Charging Behavior Based on TOU Guidance

The EV charging behavior simulated by the Markov and Monte Carlo methods is random and highly correlated with user behavior. This uncertain and uncoordinated charging behavior can lead to surges in grid load, increasing the operational risks of the power grid.

To find an optimal TOU pricing scheme that can effectively guide EV users to charge in an orderly manner while considering the interests of both the grid company and the users, this paper constructs a TOU-based bi-level optimization model, as shown in Figure 3.

The objective of the upper-level model is to formulate a globally optimal TOU tariff that maximizes the charging cost savings for EV users. The lower-level model simulates the optimal economic response of the EV user group to the tariff given by the upper level. The bi-level models iterate through price information and charging costs. The upper level sends the TOU tariff information to the lower level, and the lower level provides feedback on the EV users’ charging costs to the upper level.

3.1. Upper-Level Optimization: Optimal TOU Decision

The upper-level model, from the perspective of the benefits for both the grid company and users, seeks an optimal set of peak, flat, and valley electricity prices.

(1)

Objective Function:

To maximize the charging cost savings for EV users. Meanwhile, to handle complex operational constraints, this model adopts the penalty function method, transforming constraint violations into penalty terms in the objective function. Therefore, the final objective function for the upper-level model can be expressed as:

$$\begin{array}{cc}\hfill max F\left(x\right)=& \Delta C_{EV}-x_{penalty}\hfill \\ \hfill =& C_{EV}^{base}-C_{EV}^{TOU}\left(x\right)-x_{penalty}\hfill \\ \hfill =& {\displaystyle \sum _{t=1}^{24}{L}_{EV,t}^{base}\cdot x_{base}}-{\displaystyle \sum _{t=1}^{24}{L}_{EV,t}\left(x\right)\cdot x_t}\hfill \\ & \begin{array}{c}\end{array}-x_{penalty}\hfill \end{array}$$

(15)

where x = (x_peak, x_flat, x_valley) is the decision variable of the upper-level model, i.e., the vector of peak, flat, and valley prices. ΔC_EV represents the EV user’s charging cost savings; $C_{EV}^{base}$, $C_{EV\left(x\right),}^{TOU}$ and $L_{EV,t}^{base}$, L_EV,t(x) are the EV charging costs and charging loads under the flat tariff and TOU tariff, respectively; x_base is the flat tariff; x_penalty is the penalty term.

(2)

Constraints:

Price Rationality Constraint: To ensure the logical and economic rationality of the electricity prices, the prices must satisfy a monotonically decreasing characteristic, and the valley price must not be lower than the marginal generation cost, i.e.,

$$x_{peak}>x_{flat}>x_{valley}\ge C_{marg}$$

(16)

where x_peak, x_peak, x_peak, and x_marg are the peak, flat, valley, and marginal prices, respectively, in yuan/kWh.

Grid Company Revenue Guarantee Constraint: To maintain the sustainable operation of the grid company, it is required that its total revenue C_TOU after implementing the TOU tariff should not be lower than a certain proportion of the baseline revenue C_base. If this is violated, a penalty is triggered:

$$\begin{array}{l}{C}^{TOU}<\left(1-\delta \right)\cdot C^{base}\\ x_{penalty}=\lambda \cdot \left|\left(1-\delta \right)\cdot C^{base}-C^{TOU}\right|\end{array}$$

(17)

where δ is the revenue guarantee coefficient; λ is a significant penalty factor.

3.2. Lower-Level Optimization: EV Charging Behavior Guidance Based on Optimal TOU

The lower-level model, from the perspective of user charging benefits, reschedules the original charging plan to minimize its charging costs after receiving the TOU tariff x from the upper level.

(1)

Objective Function:

To minimize the total charging cost for EV users over 24 h:

$$min C_{EV}^{TOU}(x)=min {\displaystyle \sum _{t=1}^{24}{L}_{EV,t}\left(x\right)\cdot x_t}$$

(18)

(2)

Constraints:

To efficiently model the complex charging response of a large user group to price signals, this model employs a heuristic load allocation algorithm based on price response weights to efficiently simulate the collective behavior of users. The main constraints include:

Energy Conservation Constraint: The total amount of charged energy after scheduling must be strictly equal to the total daily charging demand of the users:

$${\displaystyle \sum _{t=1}^{24}{L}_{EV,t}}=D_{EV}^{total}$$

(19)

where $D_{EV}^{total}$ is the total daily charging demand of EV users.

Price-Responsive Load Allocation Mechanism Constraint: This is the core of the algorithm. It mainly quantifies the attractiveness of each time slot for charging load by constructing a weight w_t that is negatively correlated with the electricity price:

$$w_t={\displaystyle \frac{max\left(x\right)-x_t}{max\left(x\right)-min\left(x\right)}}+\epsilon$$

(20)

where ε is a small positive constant to ensure a base weight even during the highest price periods, avoiding extreme load shifting, the algorithm allocates the users’ flexible charging demand proportionally according to this weight.

Inelastic Demand and Power Constraints: Considering the inelastic demand of some users who do not participate in optimization or must charge immediately, the model allocates a γ proportion of the baseline load as a non-transferable base load.

$$L_{EV,t}^{fixed}=\gamma L_{EV,t}\left(t\right)$$

(21)

where $L_{EV,t}^{fixed}$ is the non-transferable base load.

Meanwhile, the charging power in each time slot cannot exceed the power limit for that slot.

$$L_{EV,t}\le P_{max,t}$$

(22)

where P_max,t is the upper limit of the EV charging power.

4. Distribution Network Capacity Assessment Model Based on OPF

4.1. Hosting Capacity Evaluation Model of DN

OPF aims to find a power flow solution that satisfies all physical and operational constraints while optimizing a predefined objective function, such as generation cost, network loss, or load supply [18]. Here, to calculate the hosting capacity of the EV connection points in the grid, the objective function is set to the total acceptable load at the EV connection points.

(1)

Objective Function: To maximize the average daily acceptable total load at the EV connection points.

$$max{\displaystyle \sum _{t=1}^{24}\frac{1}{24}\Delta P_{i,t}}$$

(23)

where ΔP_i,t is the active power increment at the target node at time t.

To ensure the power factor remains constant after adding the new load, the corresponding reactive power increment is set as:

$$\Delta Q_{i,t}=\Delta P_{i,t}\times \tan {\varphi }_i$$

(24)

where ϕ_i is the power factor angle of node i.

(2)

Constraints: These include distribution network operational constraints and security constraints.

The distribution network is modeled using the Distflow branch model [19], as shown in Figure 4.

According to the power balance at node i, the power flowing into node i is equal to the power flowing out of node i, which gives:

$$\left\{\begin{array}{l}{\displaystyle \sum _{ji\in {\Omega }_b}\left(P_{t,ji}-r_{ji}{I}_{t,ji}^2\right)}+P_{t,i}-\left(\Delta P_{i,t}\right)={\displaystyle \sum _{ik\in {\Omega }_b}{P}_{t,ik}}\\ {\displaystyle \sum _{ji\in {\Omega }_b}\left(Q_{t,ji}-x_{ji}{I}_{t,ji}^2\right)}+Q_{t,i}-\left(\Delta Q_{i,t}\right)={\displaystyle \sum _{ik\in {\Omega }_b}{Q}_{t,ik}}\end{array}\right.$$

(25)

where Ω_b is the set of branches; P_t,ji and Q_t,ji are the active and reactive power flowing into branch ji; r_ji and x_ji are the resistance and reactance of branch ji; I_t,ji is the current in branch ji; P_t,i and Q_t,i are the injected power at node i; P_t,ik and Q_t,ik are the power flowing out from node i.

The voltage drop Equation is:

$$\begin{array}{l}{U}_{i,t}=\sqrt{{\left(U_{j,t}-{\displaystyle \frac{P_{t,ji}{r}_{ji}+Q_{t,ji}{x}_{ji}}{U_{j,t}}}\right)}^2+{\left({\displaystyle \frac{P_{t,ji}{x}_{ji}-Q_{t,ji}{r}_{ji}}{U_{j,t}}}\right)}^2}\\ \Rightarrow U_{j,t}^2-U_{i,t}^2=2\left(P_{t,ji}{r}_{ji}+Q_{t,ji}{x}_{ji}\right)-\left(r_{ji}^2+x_{ji}^2\right)I_{t,ji}^2\end{array}$$

(26)

where U_i,t and U_j,t are the voltages at nodes i and j; I2 t,ji is determined by the Equation (27).

$$I_{t,ij}^2{U}_{i,t}^2=P_{t,ij}^2+Q_{t,ij}^2$$

(27)

Distribution network security constraints include limits on voltage and current, as well as limits on generator output.

$$\begin{array}{l}{\left(U_{min}\right)}^2\le U_{t,i}^2\le {\left(U_{max}\right)}^2\\ I_{t,ij}^2\le {\left(I_{max}\right)}^2\\ G_{min}\le G_{t,i}\le G_{max}\end{array}$$

(28)

where U_max and U_min are the upper and lower limits of the node voltage; I_max is the maximum current that the branch can carry; U_max and U_min are the upper and lower limits of the generator output.

4.2. SOCP Convex Relaxation of Hosting Capacity Model

Equations (25) and (26) involve squared terms of current and voltage, and the Equation (27) includes the product of squared terms of current I_t,ji and voltage U_t,j, all of which constitute non-convex constraints. The existence of such non-convex constraints makes the feasible region of the distribution network hosting capacity assessment problem, as described by the above model, a complex non-convex set, which is difficult for existing methods to solve efficiently.

In this section, a combination of variable substitution and second-order cone programming (SOCP) relaxation is used to handle this issue [20], transforming the original non-convex problem into a standard convex optimization problem to achieve fast and accurate computation.

First, the original model is linearized by removing the phase angles of current and voltage, retaining their magnitudes, and introducing the following auxiliary variables: v_t,i = $U_{t,i}^2$ and l_t,ji = $I_{t,ji}^2$. Thus, Equations (25) and (28) can be transformed into:

$$\left\{\begin{array}{l}{\displaystyle \sum _{ji\in {\Omega }_b}\left(P_{t,ji}-r_{ji}{l}_{t,ji}\right)}+P_{t,i}-\left(\Delta P_{i,t}\right)={\displaystyle \sum _{ik\in {\Omega }_b}{P}_{t,ik}}\\ {\displaystyle \sum _{ji\in {\Omega }_b}\left(Q_{t,ji}-x_{ji}{l}_{t,ji}\right)}+Q_{t,i}-\left(\Delta Q_{i,t}\right)={\displaystyle \sum _{ik\in {\Omega }_b}{Q}_{t,ik}}\end{array}\right.$$

(29)

$$v_{t,j}-v_{t,i}=2\left(P_{t,ji}{r}_{ji}+Q_{t,ji}{x}_{ji}\right)-\left(r_{ji}^2+x_{ji}^2\right)l_{t,ji}$$

(30)

$$l_{t,ji}={\displaystyle \frac{P_{t,ij}^2+Q_{t,ij}^2}{v_{t,i}}}$$

(31)

$$\begin{array}{l}{v}_{min}\le v_{t,i}\le v_{max}\\ l_{t,ij}\le l_{max}\\ G_{min}\le G_{t,i}\le G_{max}\end{array}$$

(32)

After the variable substitution, the original non-convex equality constraint (27) is transformed into the Equation (31), which is still a non-convex quadratic constraint. Therefore, it is relaxed to:

$$l_{t,ji}\ge {\displaystyle \frac{P_{t,ij}^2+Q_{t,ij}^2}{v_{t,i}}}$$

(33)

The effectiveness of this relaxation lies in the fact that for radial distribution networks, this relaxation is tight, meaning the inequality will automatically hold as an equality at the optimal point.

Through the transformations described above, the original nonlinear, non-convex model is successfully reformulated into a standard second-order cone programming model, which can be solved efficiently and reliably, ensuring the global optimality of the obtained solution.

5. Case Study

All simulations and algorithm implementations in this research were conducted in a Python (Version 3.11) environment. This paper adopts the standard IEEE 33-bus and IEEE 69-bus distribution network case study model, as shown in Figure 5 and Figure 6. The voltage level is 10 kV, and detailed parameters can be found in [21,22]. The EV charging station is placed at three representative nodes to analyze the impact of network location: node 3 (on the main feeder), node 29 (in the middle of a branch), and node 18 (at the end of a long feeder). This comparative analysis highlights the varying effects of the optimization strategy across different parts of the network.

The base load curve for node 18 is shown in Figure 7. It exhibits higher electricity consumption during the midday and evening hours, showing a dual-peak characteristic. The peak periods are 11:00 and 16:00–21:00; the flat periods are 07:00–10:00, 12:00–15:00, and 22:00–23:00; and the valley periods are 00:00–06:00.

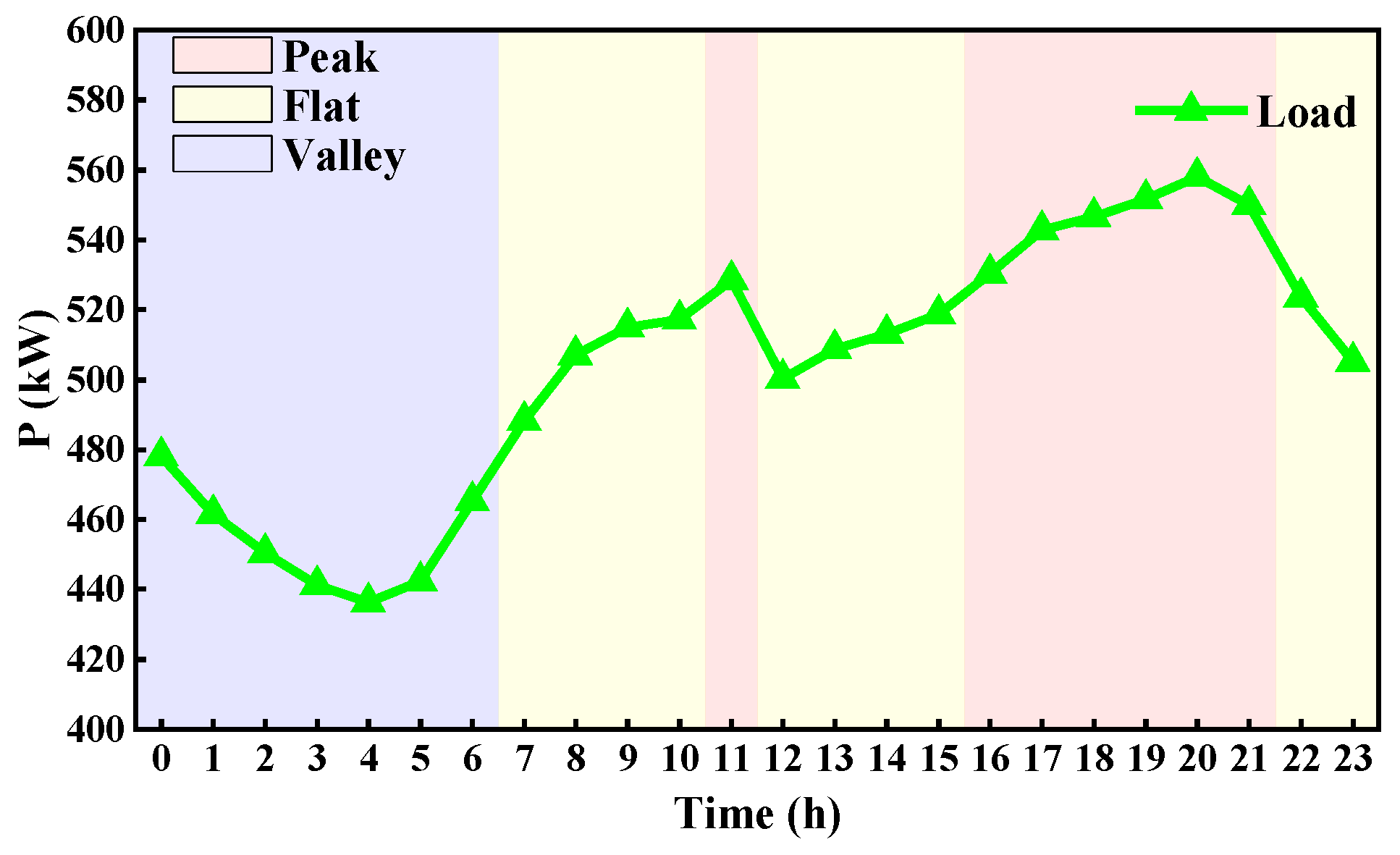
5.1. Simulating EV Charging Loads Using MCMC

The EV historical data contains one year of charging behavior data for 52 typical EVs in the same region. Due to the limitations of the data and the representativeness of typical EV charging behavior in the same area, the MCMC algorithm can be used to simulate these 52 typical EVs to obtain the charging behavior of 300 EVs in that region.

The EV charging behavior is divided into three states: non-charging, slow charging (<7 kW), and fast charging (≥7 kW). The number of state transitions for different EVs at different time periods is counted to calculate the state transition probabilities. Each of the 52 EVs has 24 time-inhomogeneous state transition matrices, resulting in a total of 1248 matrices, each with a size of 3 × 3.

Table 1. The transition probabilities of EV 2 and EV 28 at 0 h and 18 h.

	EV 2 at 0:00			EV 28 at 18:00
	sd	sf	ss	sd	sf	ss
sd	0	1	0	0	0.9873	0.0217
sf	0.0111	0.9889	0	0	0.9969	0.0031
ss	0.3333	0.3333	0.3333	0.3333	0.3333	0.3333

shows the state transition probabilities for EV 2 and EV 28 at 0:00 and 18:00, respectively.

Using the constructed Markov model, Monte Carlo sampling is performed according to the flowchart. The number of samples is set to 1000. The initial state is randomly sampled based on the probability values of the three states in each EV’s historical data. The state at the next time step is randomly sampled based on the transition probabilities of the Markov transition matrix. A total of 24 samples are taken to obtain one daily charging load curve for a single EV. This process is repeated 1000 times, and the average is taken to get the average daily charging load curve, which represents the daily charging behavior of that EV.

By randomly sampling 300 times from the 52 typical EVs, the daily charging load curves for 300 EVs are obtained, thus compensating for the limitations of the historical data from only 52 EVs. Figure 8 shows the aggregated charging power of the 300 EVs.

5.2. Optimization Results of EV Charging Behavior Based on TOU and Hosting Capacity Analysis

5.2.1. Optimal TOU Tariff and Coordinated Charging Behavior

The aggregated EV charging power curve generated in Section 5.1 serves as the baseline scenario for uncoordinated charging. The primary objective of our bi-level optimization model is to determine a globally optimal TOU for the entire EV user population. As shown in

Table 2. Economic Comparison Before and After TOU Optimization.

Indicator	Before Optimization	After Optimization	Cost Savings
Electricity price (yuan/kW)	0.65	Peak: 0.92 Flat: 0.65 Valley: 0.32
EV charging cost (yuan)	3881.91	3068.63	813.28 (20.95%)

, based on the system’s peak, flat, and valley periods, the model yields a single, optimal set of prices: 0.92 yuan/kWh for the peak period, 0.65 yuan/kWh for the flat period, and 0.32 yuan/kWh for the valley period. This tariff results in a total charging cost saving of 20.95% for the users. This demonstrates the effectiveness of the proposed bi-level optimization model in achieving its primary economic objective.

Figure 9 compares the EV charging load curves before and after this TOU-based optimization. As shown in the figure, under the guidance of the price signal, the peak load is successfully shifted. During the peak period, the optimized charging load peak is reduced to about 300 kW, a decrease of over 60%. During the valley period, a large amount of charging demand shifted from the peak period and was successfully guided to the valley period with the lowest electricity price. The optimized curve maintains a high charging level throughout the valley period, effectively utilizing the grid’s off-peak resources. This fully demonstrates that the lower-level model can effectively guide EV charging behavior.

5.2.2. Impact Analysis of Nodal Location on Hosting Capacity

To quantitatively assess the impact of the coordinated charging strategy on the grid’s physical security, this section analyzes the change in the distribution network’s hosting capacity. The proposed OPF-based hosting capacity calculation model is used to evaluate the grid’s condition before and after the coordinated charging is applied. In this analysis, we focus specifically on the minimum daily hosting capacity. This metric is selected as the primary indicator of grid security because it represents the system’s most vulnerable moment over 24 h, directly reflecting the grid’s bottleneck and its ability to withstand extreme load conditions.

To investigate the impact of network topology on the effectiveness of the proposed strategy, we conducted a comparative analysis by placing the EV charging station at three representative nodes within the IEEE 33-bus system: node 3 (on the main feeder, electrically strong), node 29 (in the middle of a branch, moderately strong), and node 18 (at the end of a long feeder, electrically vulnerable).

The results are summarized in

Table 3. Comparison before and after optimization.

Indicator	Node 3 (Strong)	Node 29 (Moderate)	Node 18 (Vulnerable)
Cost Savings (%)	20.95%	20.95%	20.95%
Min. Hosting Capacity (Before Opt.)	15,132.47 kW	1666.89 kW	200.02 kW
Min. Hosting Capacity (After Opt.)	15,502.04 kW	1984.48 kW	549.32 kW
Min. Hosting Capacity Improvement (%)	2.44%	19.05%	174.63%

. On the economic level, the outcome is consistent across all nodes. The bi-level optimization model yields the same optimal TOU tariff and achieves an identical charging cost reduction of 20.95% for the EV users. This is because the economic optimization is independent of the physical location of the load. It is solely dependent on the aggregated charging demand profile of the EV fleet and the predefined peak, flat, and valley time periods.

However, a starkly different picture emerges when assessing the impact on the grid’s physical security. As shown in Table 3, the improvement in minimum hosting capacity is highly dependent on the node’s initial vulnerability.

➢

For the most vulnerable node (node 18), which had a very low initial hosting capacity of 200.02 kW, the optimization yields a remarkable 174.63% increase. This demonstrates that load shifting provides immense relief to the most stressed parts of the network.

➢

For the moderately strong node (node 29), the improvement is significant but minor at 19.05%.

➢

For the strongest node (node 3), which already possessed a high initial hosting capacity of 15,132.47 kW, the same load shifting strategy results in only a modest 2.44% improvement.

Under identical TOU optimization strategies, hosting capacity varies significantly across different nodes. Research findings indicate that evaluating coordination strategies based solely on economic metrics is insufficient. The safety benefit of enhanced load-bearing capacity inversely correlates with a node’s initial strength, with the most pronounced improvement occurring at the network’s most vulnerable nodes. This discovery underscores the necessity of the comprehensive evaluation framework proposed herein, which precisely quantifies these location-dependent safety benefits, providing more refined insight for power grid planning and investment decisions.

5.2.3. Sensitivity Analysis

To further validate the robustness and logical consistency of the model, a sensitivity analysis was conducted on two key parameters: electric vehicle penetration rate and inelastic load ratio. This analysis used the most vulnerable node (Node 18) as the test case, with results summarized in

Table 4. Sensitivity Analysis Results at Node 18.

Analysis Type	Parameter Value	Min. Hosting Capacity (Before Opt.)	Min. Hosting Capacity (After Opt.)	Min. Hosting Capacity Improvement
EV Penetration	300 EVs	200.02 kW	549.32 kW	349.30 kW (174.63%)
	500 EVs	−191.06 kW	432.93 kW	623.99 kW *
Inelastic Ratio	10%	200.02 kW	607.71 kW	407.69 kW (203.82%)
	20%	200.02 kW	549.32 kW	349.30 kW (174.63%)
	30%	200.02 kW	497.74 kW	297.72 kW (148.85%)

* A percentage is not applicable as the baseline is negative.

.

First, a scenario with higher electric vehicle penetration was simulated by increasing the number of electric vehicles from 300 (baseline) to 500. As shown in Table 4, the load increase from 500 electric vehicles placed significantly greater stress on the grid. This is reflected in the initial minimum capacity plummeting from a positive value of 200.02 kW to a negative value of −191.06 kW, indicating that system security constraints were immediately violated even without additional load. Despite these severe initial conditions, the optimization model effectively redistributed the load, not only eliminating security violations but also generating a positive capacity of 432.93 kW. This test validated the model’s scalability and its critical role in enhancing electric vehicle adoption rates.

Subsequent analysis examined the impact of varying inelastic load proportions, testing three scenarios: 10% (more flexible), 20% (baseline), and 30% (more rigid). Table 4 results reveal a clear logical trend: optimization potential diminishes as the proportion of inflexible loads increases. The minimum load capacity improvement rate decreased from 203.82% at the 10% ratio to 148.85% at the 30% ratio. This occurs because smaller flexible loads constrain the model’s ability to execute load shifting. This analysis validates the model’s logical consistency and underscores that the effectiveness of price-based coordination mechanisms is intrinsically linked to the flexibility of user demand.

5.2.4. Portability Verification on IEEE 69-Bus System

To validate the applicability of this framework in larger-scale, more complex network topologies, key experiments were conducted on the IEEE 69-bus system. Node 65, identified as vulnerable within this network, was selected as the connection point for the charging load of 300 electric vehicles.

As shown in

Table 5. Portability Verification: Comparison of Results on Vulnerable Nodes.

Indicator	Min. Hosting Capacity (Before Opt.)	Min. Hosting Capacity (After Opt.)	Min. Hosting Capacity Improvement
IEEE 33 (Node 18)	200.02 kW	549.32 kW	349.30 kW (174.63%)
IEEE 69 (Node 65)	435.84 kW	778.48 kW	342.64 kW (78.62%)

, experimental results demonstrate the framework’s continued high effectiveness. The optimized charging strategy significantly enhanced grid security, increasing the minimum daily carrying capacity from 435.84 kW to 778.48 kW—a 78.62% improvement.

The successful application of this approach across diverse and more complex network topologies indicates that the proposed analytical framework is not only applicable to specific systems but also possesses broad potential for implementation across various distribution network environments.

6. Conclusions

The primary scientific contribution of this study lies in establishing a comprehensive analytical framework that innovatively integrates a time-heterogeneous Markov chain Monte Carlo model, a two-layer optimization model for EV user charging behavior guided by TOU pricing, and an OPF-based capacity assessment model. Unlike traditional methods relying on simplified metrics such as peak-to-valley difference reduction, this framework directly quantifies the substantive impact on physical security margins.

Through in-depth case studies of the IEEE 33-bus and IEEE 69-bus systems, this framework demonstrates significant effectiveness in both reducing charging costs and enhancing grid capacity. Guided by TOU pricing, a substantial portion of the charging load was successfully shifted to off-peak periods, resulting in a consistent, significant reduction in total charging costs from 3881.91 yuan to 3068.63 yuan—a decrease of 20.95%. Furthermore, under the optimal time-of-use pricing strategy, node capacity variations across different locations showed significant disparities. The most vulnerable nodes experienced a capacity increase of 174.63%, while the most resilient nodes saw only a 2.44% improvement. This finding was further validated on the IEEE 69-bus system, where a vulnerable node still saw a significant 78.62% improvement in hosting capacity. This finding highlights the limitations of purely economic assessments and underscores the necessity of this framework’s integrated approach.

Finally, the limitations of this study must be clarified, as they also point to directions for future research. Although our MCMC model captures partial user diversity by training 52 distinct user profiles, it does not explicitly model user archetypes with varying price sensitivities. Furthermore, this study intentionally focused on the more prevalent grid-to-vehicle charging paradigm but did not consider V2G. Future research will focus on integrating more granular behavioral models and expanding the framework to incorporate bidirectional V2G capabilities. Integrating bidirectional power flows will introduce new complexities such as battery degradation costs and market participation patterns, but will also unlock broader grid service potential.