Study on Main Controlling Factors of CO2 Enhanced Gas Recovery and Geological Storage in Tight Gas Reservoirs
Abstract
1. Introduction
2. Methods
2.1. PR-EOS
2.2. Henry’s Law Model
2.3. Geochemical Reaction Kinetics Model
2.4. Numerical Model Parameters
3. Results and Discussions
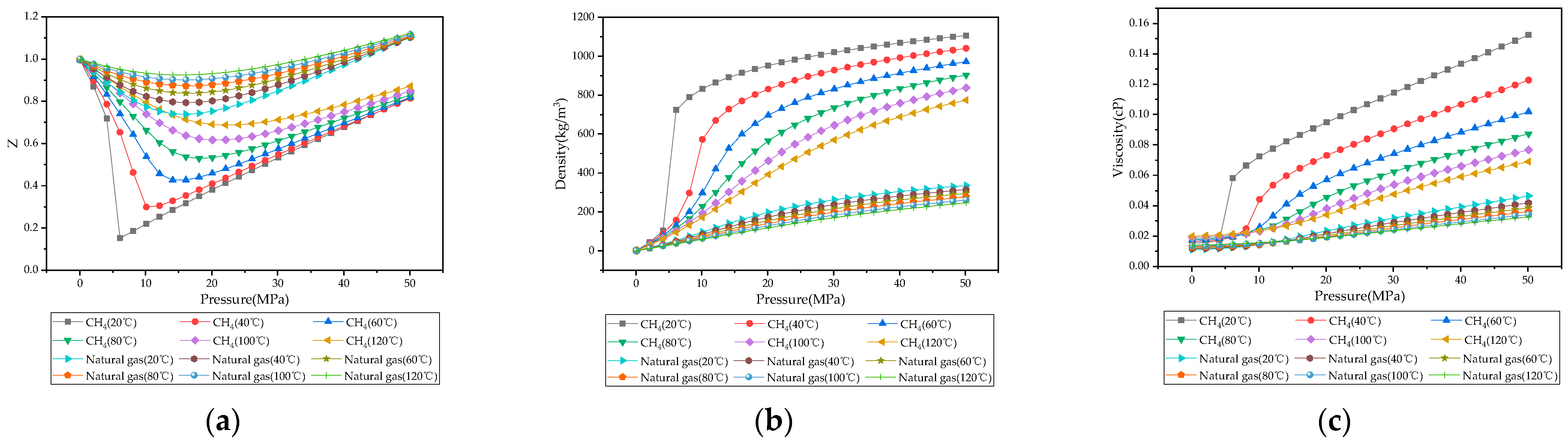
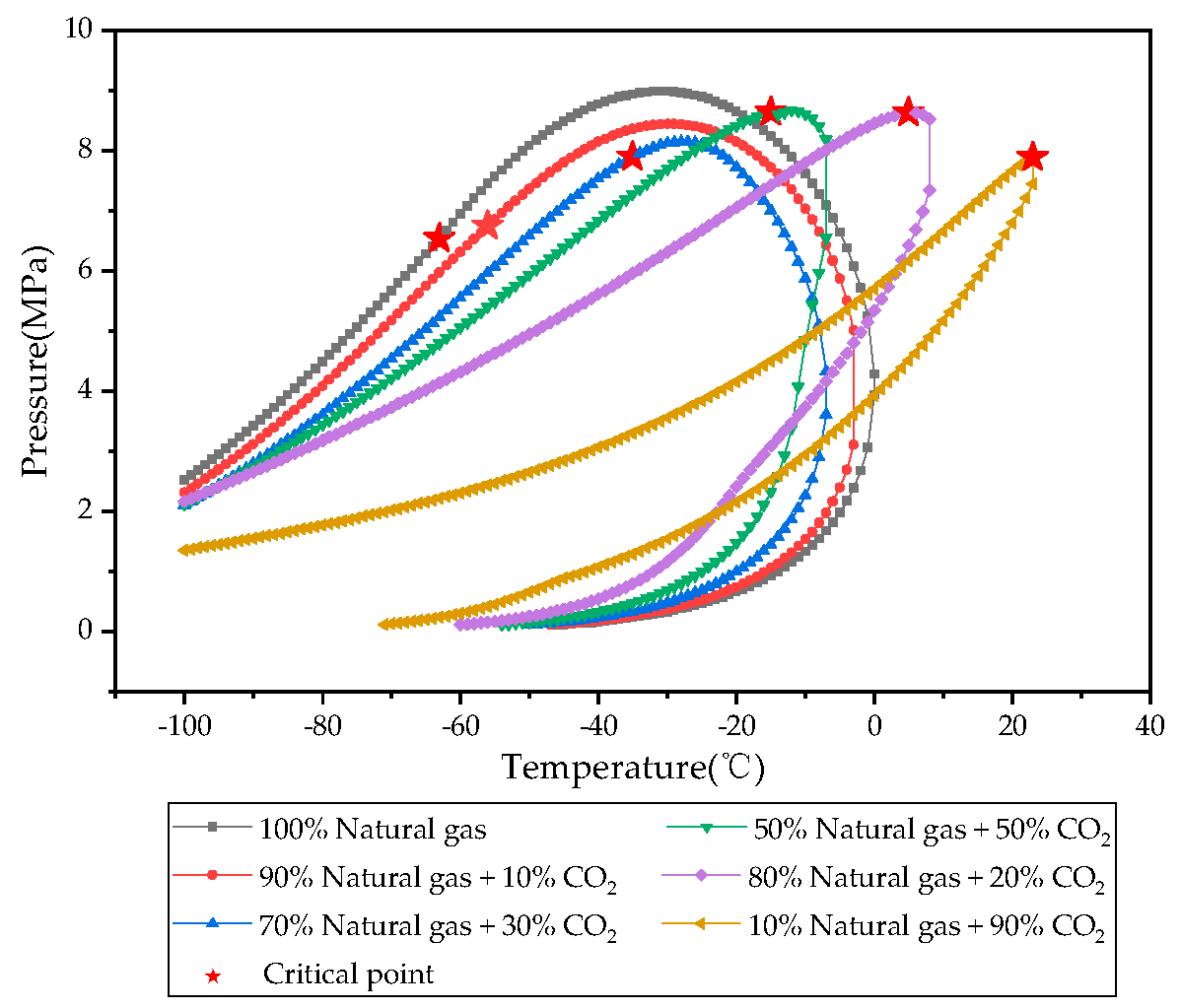
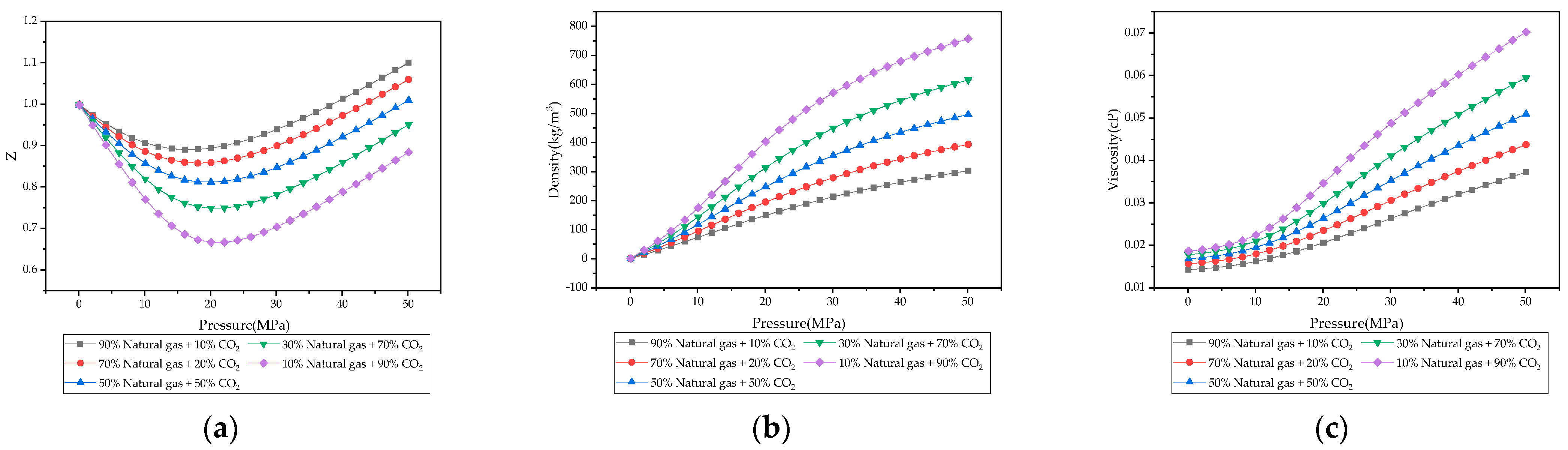
3.1. Physical Properties of CH4, CO2, Natural Gas, and CO2-Natural Gas Mixtures
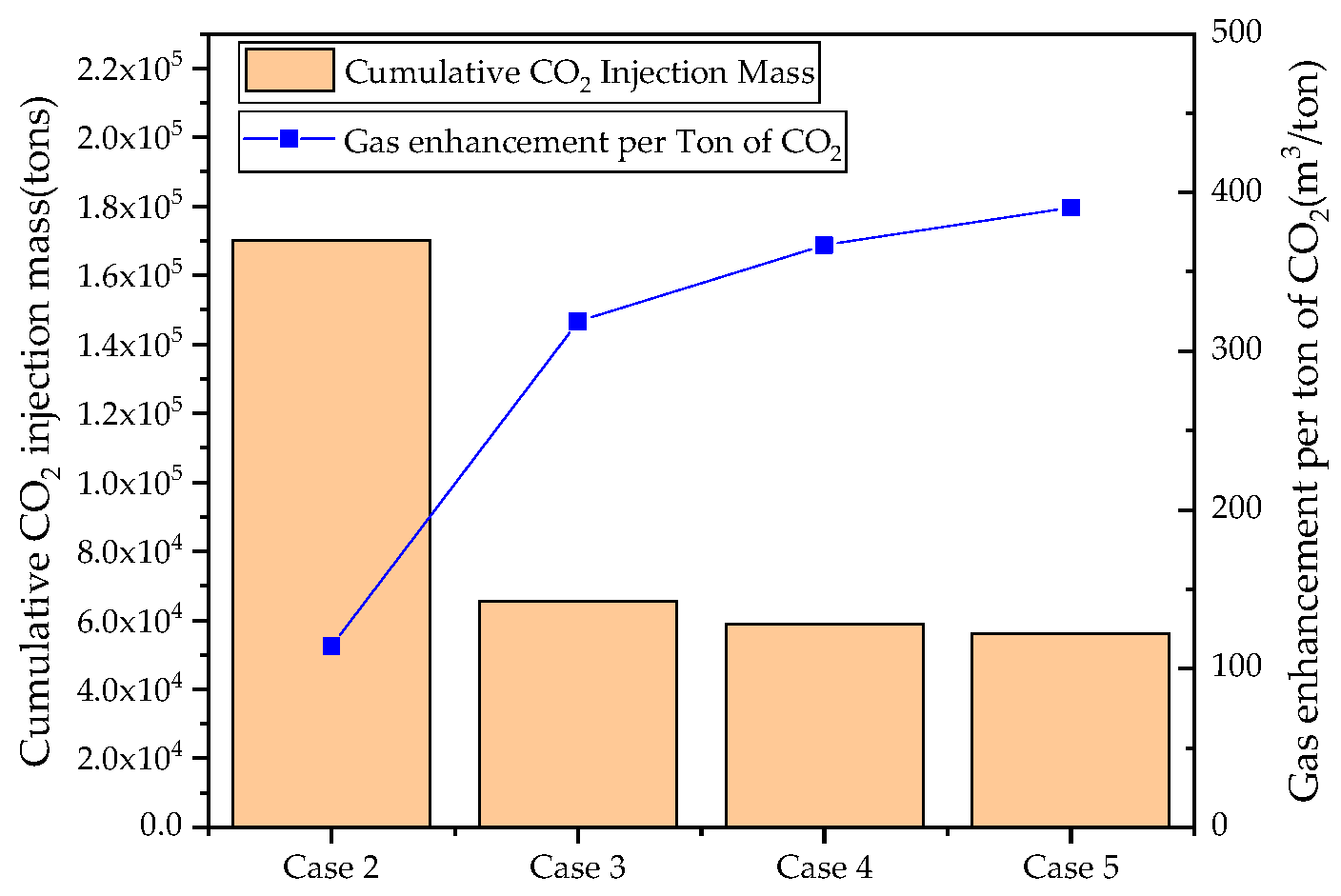
3.2. Effects of CO2 Injection Scheme on CSEGR
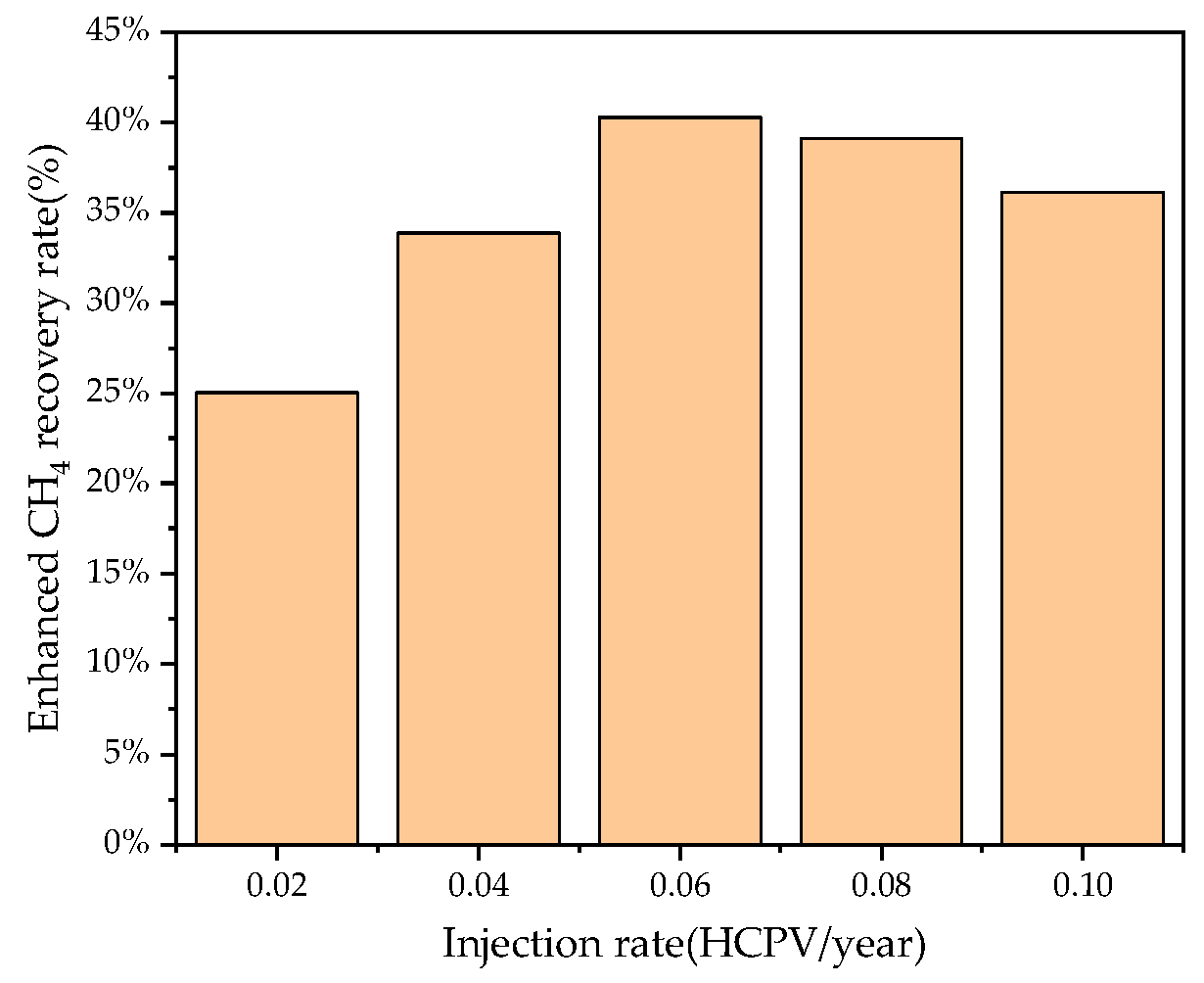
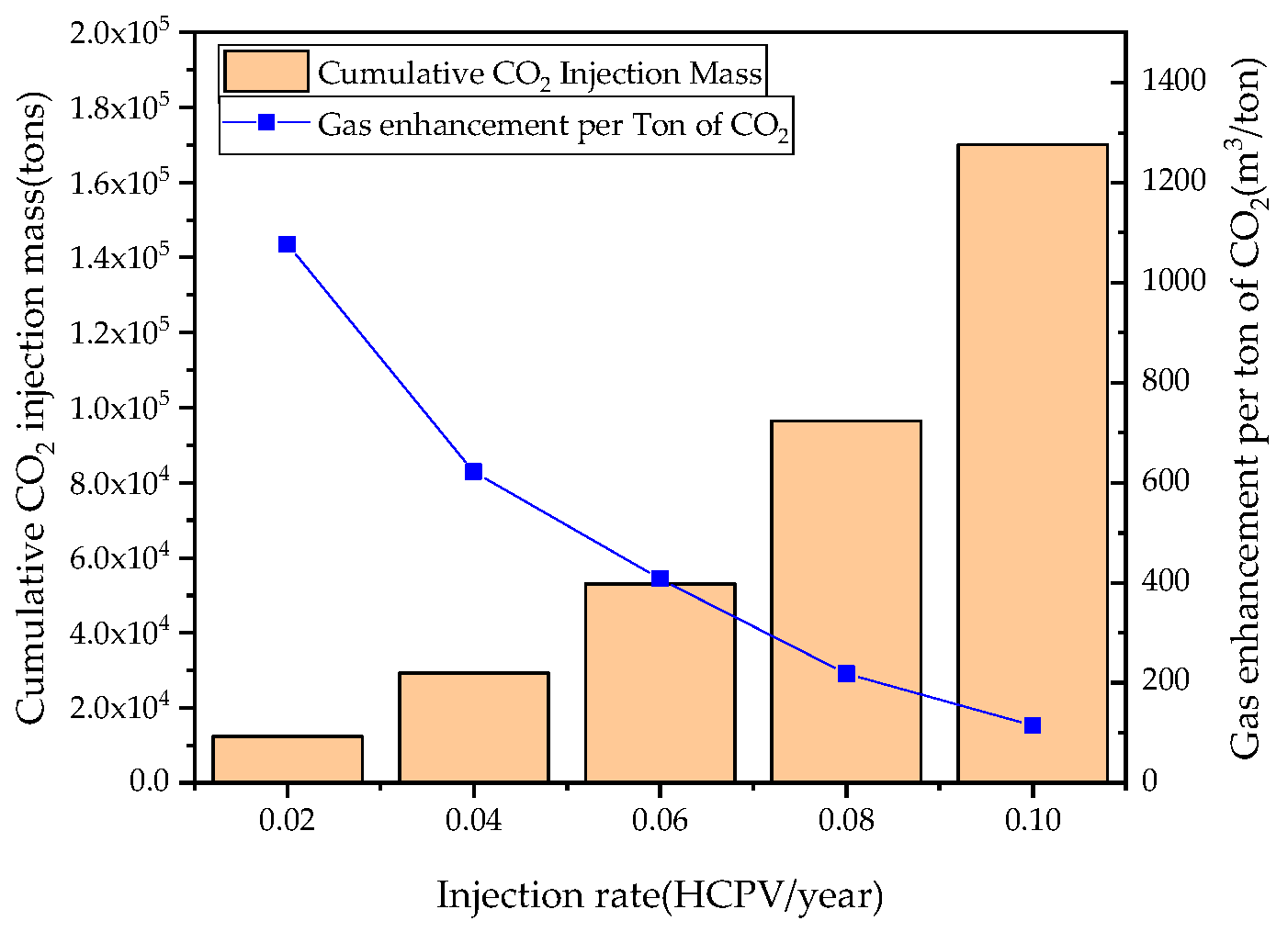
3.3. Effects of CO2 Injection Rate on CSEGR
3.4. Effects of Production Rate on CSEGR
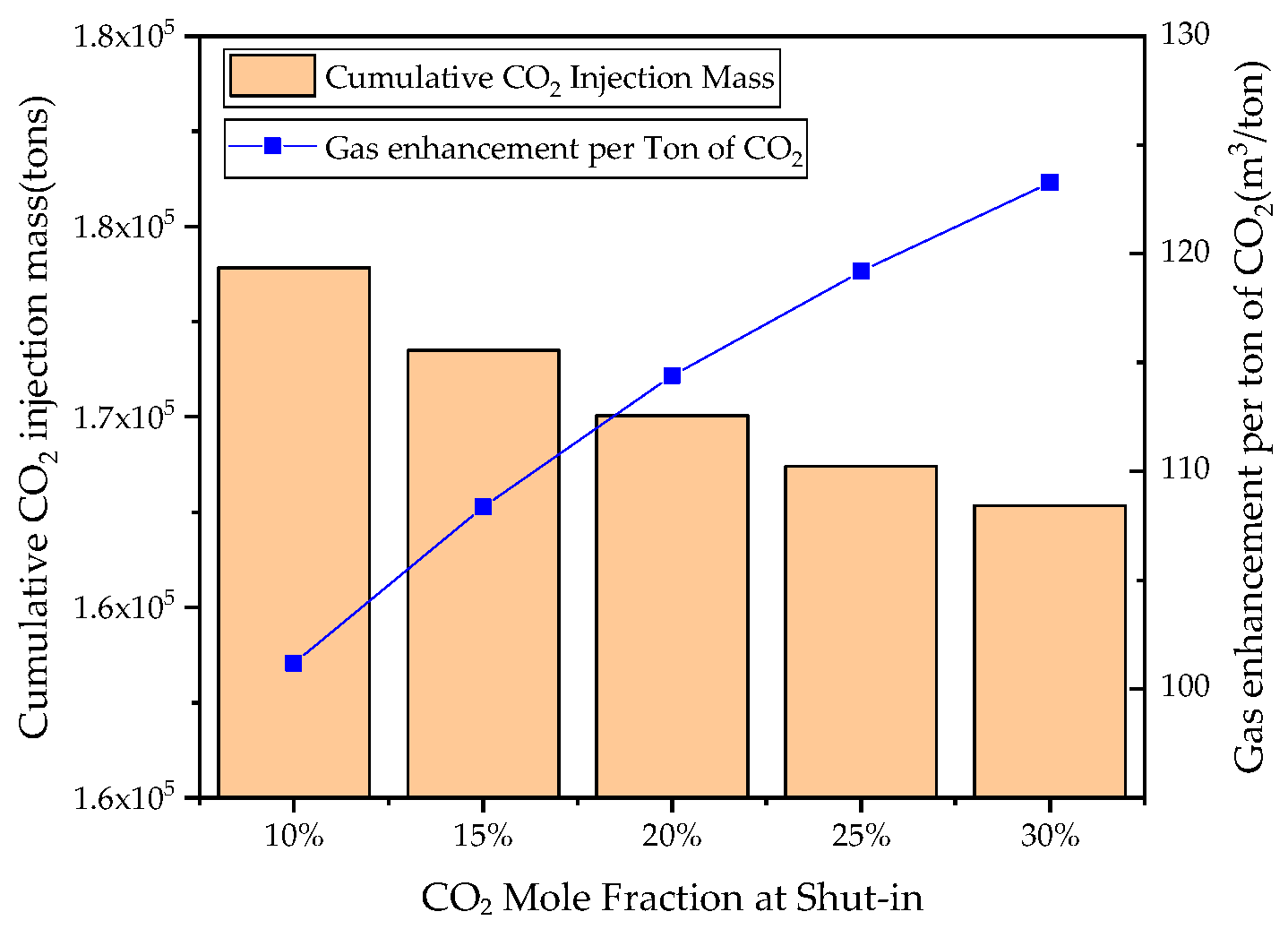
3.5. Effects of Shut-In Condition on CSEGR
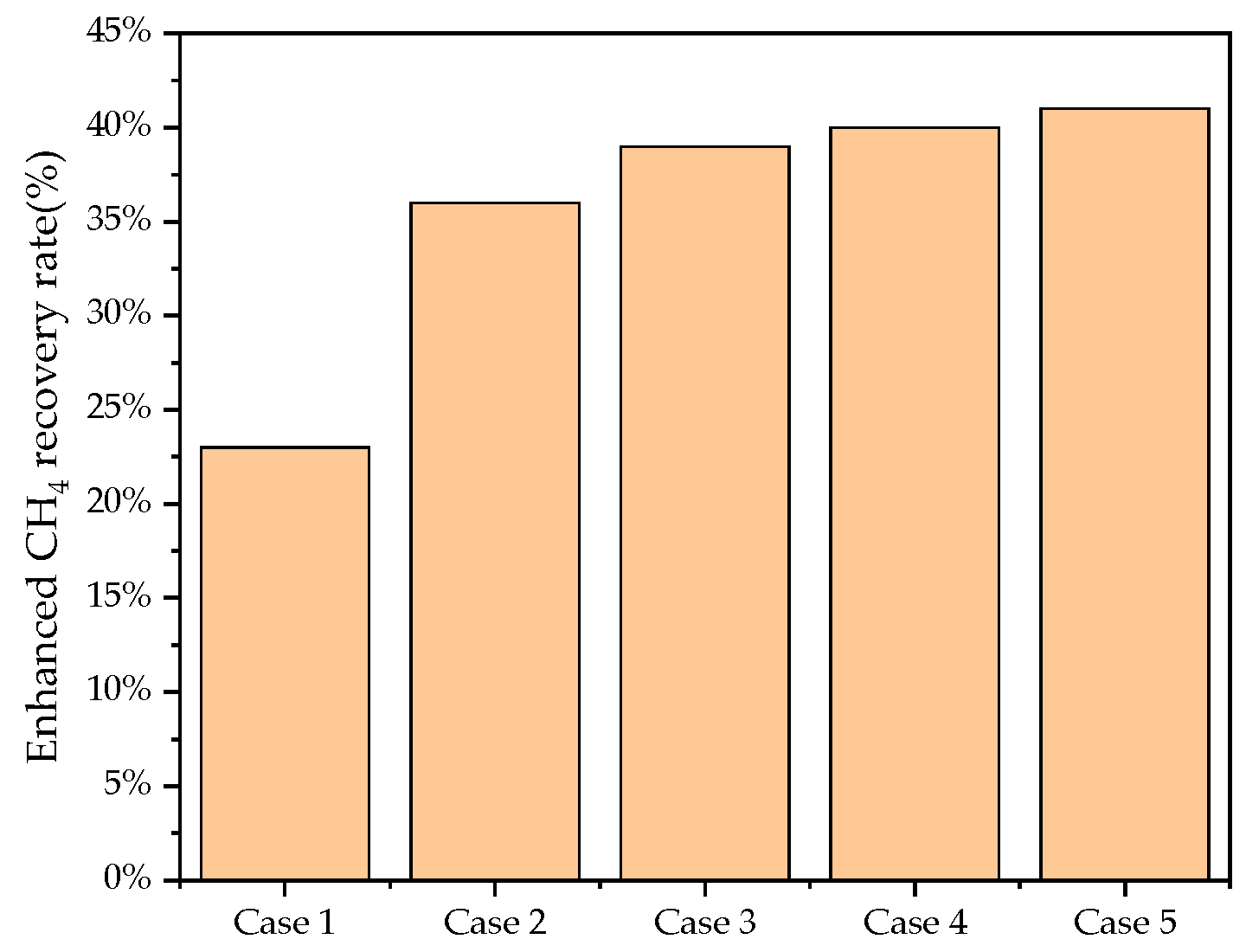
3.6. Main Controlling Factors for CCUS-EGR
4. Conclusions
- Under reservoir temperature and pressure conditions, CO2 exhibits significant differences in compressibility factor, density, and viscosity compared to natural gas. The higher density enables bottom injection to avoid large-scale mixing at the displacement front, while viscosity differences form favorable mobility ratios for piston-like displacement and improved front stability.
- Intermittent injection slightly outperforms continuous injection for recovery enhancement, with shut-in periods delaying CO2 breakthrough and improving utilization efficiency. However, continuous injection stores more CO2 mass during development. Injection rate affects energy replenishment and front advancement velocity, while production rates must balance recovery enhancement with formation energy constraints and corrosion prevention.
- For recovery enhancement effectiveness, factor significance ranking is injection rate > production rate > injection scheme > shut-in condition. For CO2 storage effectiveness, the ranking is: injection rate > injection scheme > production rate > shut-in condition. Injection rate directly determines energy replenishment and total CO2 mass injected, while injection scheme significantly affects total injection volume due to shut-in periods.
- During gas injection, supercritical, ionic, and dissolved CO2 continuously increase while mineral CO2 decreases. Storage mechanisms are dominated by structural and residual trapping, with supercritical CO2 dissolving into formation water. Mineral changes are characterized by calcite dissolution, anorthite dissolution, orthoclase precipitation followed by dissolution, and kaolinite/illite precipitation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSEGR | CO2 Storage with Enhanced Gas Recovery |
| HCPV | Hydrocarbon Pore Volume |
References
- Sun, L.; Zou, C.; Jia, A.; Wei, Y.; Zhu, R.; Wu, S.; Guo, Z. Development Characteristics and Orientation of Tight Oil and Gas in China. Pet. Explor. Dev. 2019, 46, 1073–1087. [Google Scholar] [CrossRef]
- Gao, H.; Li, H.A. Pore Structure Characterization, Permeability Evaluation and Enhanced Gas Recovery Techniques of Tight Gas Sandstones. J. Nat. Gas Sci. Eng. 2016, 28, 536–547. [Google Scholar] [CrossRef]
- Cheng, M.; Xue, W.; Guo, Z.; Hou, M.; Wang, C. Development of Large-Scale Tight Gas Sandstone Reservoirs and Recommendations for Stable Production-The Example of the Sulige Gas Field in the Ordos Basin. Sustainability 2023, 15, 9933. [Google Scholar] [CrossRef]
- Zou, C.; Zhu, R.; Liu, K.; Su, L.; Bai, B.; Zhang, X.; Yuan, X.; Wang, J. Tight Gas Sandstone Reservoirs in China: Characteristics and Recognition Criteria. J. Pet. Sci. Eng. 2012, 88–89, 82–91. [Google Scholar] [CrossRef]
- Lei, Q.; Xu, Y.; Cai, B.; Guan, B.; Wang, X.; Bi, G.; Li, H.; Li, S.; Ding, B.; Fu, H.; et al. Progress and Prospects of Horizontal Well Fracturing Technology for Shale Oil and Gas Reservoirs. Pet. Explor. Dev. 2022, 49, 191–199. [Google Scholar] [CrossRef]
- Zhou, F.; Su, H.; Liang, X.; Meng, L.; Yuan, L.; Li, X.; Liang, T. Integrated Hydraulic Fracturing Techniques to Enhance Oil Recovery from Tight Rocks. Pet. Explor. Dev. 2019, 46, 1065–1072. [Google Scholar] [CrossRef]
- Soliman, M.Y.; Hunt, J.L.; Azari, M. Fracturing Horizontal Wells In Gas Reservoirs. SPE Prod. Oper. 1999, 14, 277–283. [Google Scholar] [CrossRef]
- Jia, A.; Wei, Y.; Guo, Z.; Wang, G.; Meng, D.; Huang, S. Development Status and Prospect of Tight Sandstone Gas in China. Nat. Gas Ind. B 2022, 9, 467–476. [Google Scholar] [CrossRef]
- Stevens, S.H.; Kuuskraa, V.A.; Gale, J.; Beecy, D. CO2 Injection and Sequestration in Depleted Oil and Gas Fields and Deep Coal Seams: Worldwide Potential and Costs. Environ. Geosci. 2001, 8, 200–209. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, Z. Carbon Capture, Utilization and Storage. Appl. Energy 2019, 235, 1289–1299. [Google Scholar] [CrossRef]
- van der Burgt, M.J.; Cantle, J.; Boutkan, V.K. Carbon Dioxide Disposal from Coal-Based IGCC’s in Depleted Gas Fields. Energy Convers. Manag. 1992, 33, 603–610. [Google Scholar] [CrossRef]
- Oldenburg, C.M.; Pruess, K.; Benson, S.M. Process Modeling of CO2 Injection into Natural Gas Reservoirs for Carbon Sequestration and Enhanced Gas Recovery. Energy Fuels 2001, 15, 293–298. [Google Scholar] [CrossRef]
- Oldenburg, C. Carbon Sequestration In Natural Gas Reservoirs: Enhanced Gas Recovery and Natural Gas Storage; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2003. [Google Scholar]
- Zhao, E.; Jin, Z.; Li, G.; Hou, J.; Zeng, Y. Potential Assessment and Production Performance Analysis of CO2 Storage with Enhanced Gas Recovery from Tight Gas Reservoirs. Phys. Fluids 2025, 37, 063103. [Google Scholar] [CrossRef]
- Zhang, L.; Cao, C.; Wen, S.; Zhao, Y.; Peng, X.; Wu, J. Thoughts on the Development of CO2-EGR under the Background of Carbon Peak and Carbon Neutrality. Nat. Gas Ind. B 2023, 10, 383–392. [Google Scholar] [CrossRef]
- Hamza, A.; Hussein, I.A.; Al-Marri, M.J.; Mahmoud, M.; Shawabkeh, R.; Aparicio, S. CO2 Enhanced Gas Recovery and Sequestration in Depleted Gas Reservoirs: A Review. J. Pet. Sci. Eng. 2021, 196, 107685. [Google Scholar] [CrossRef]
- Wang, W.; Wen, J.; Wang, C.; Gomari, S.R.; Xu, X.; Zheng, S.; Su, Y.; Li, L.; Hao, Y.; Li, D. Current Status and Development Trends of CO2 Storage with Enhanced Natural Gas Recovery. Fuel 2023, 349, 128555. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Chen, M.; Xu, S. Experimental Study on Dispersion Characteristics and CH4 Recovery Efficiency of CO2, N2 and Their Mixtures for Enhancing Gas Recovery. J. Pet. Sci. Eng. 2022, 216, 110756. [Google Scholar] [CrossRef]
- Liu, S.-Y.; Ren, B.; Li, H.-Y.; Yang, Y.-Z.; Wang, Z.-Q.; Wang, B.; Xu, J.-C.; Agarwal, R. CO2 Storage with Enhanced Gas Recovery (CSEGR): A Review of Experimental and Numerical Studies. Pet. Sci. 2022, 19, 594–607. [Google Scholar] [CrossRef]
- Seo, J.G.; Mamora, D.D. Experimental and Simulation Studies of Sequestration of Supercritical Carbon Dioxide in Depleted Gas Reservoirs. J. Energy Resour. Technol. 2005, 127, 1–6. [Google Scholar] [CrossRef]
- Sidiq, H.; Amin, R. Impact of Pore-Pressure on the Recovery Efficiency from CO2-Methane Displacement Experiments. In Proceedings of the 2010 IEEE Workshop on Environmental Energy and Structural Monitoring Systems, Taranto, Italy, 9 September 2010; pp. 1–8. [Google Scholar]
- Vandeweijer, V.; van der Meer, B.; Hofstee, C.; Mulders, F.; D’Hoore, D.; Graven, H. Monitoring the CO2 Injection Site: K12-B. Energy Procedia 2011, 4, 5471–5478. [Google Scholar] [CrossRef]
- Hussen, C.; Amin, R.; Madden, G.; Evans, B. Reservoir Simulation for Enhanced Gas Recovery: An Economic Evaluation. J. Nat. Gas Sci. Eng. 2012, 5, 42–50. [Google Scholar] [CrossRef]
- Patel, M.J.; May, E.F.; Johns, M.L. High-Fidelity Reservoir Simulations of Enhanced Gas Recovery with Supercritical. Energy 2016, 111, 548–559. [Google Scholar] [CrossRef]
- Tileuberdi, N.; Gussenov, I. Review on Miscible, Immiscible, and Progressive Nitrogen Injection for Enhanced Oil Recovery. Energy Rep. 2024, 12, 360–367. [Google Scholar] [CrossRef]
- Shukla, R.; Ranjith, P.; Haque, A.; Choi, X. A Review of Studies on CO2 Sequestration and Caprock Integrity. Fuel 2010, 89, 2651–2664. [Google Scholar] [CrossRef]
- Massarweh, O.; Abushaikha, A.S. CO2 Sequestration in Subsurface Geological Formations: A Review of Trapping Mechanisms and Monitoring Techniques. Earth-Sci. Rev. 2024, 253, 104793. [Google Scholar] [CrossRef]
- Orivri, U.D.; Chanda, P.; Johnson, L.; Koehn, L.W.; Pollyea, R.M. Opportunities and Challenges for Geologic CO2 Sequestration in Carbonate Reservoirs: A Review. Int. J. Greenh. Gas Control 2025, 142, 104342. [Google Scholar] [CrossRef]
- Bertier, P.; Swennen, R.; Laenen, B.; Lagrou, D.; Dreesen, R. Experimental Identification of CO2–Water–Rock Interactions Caused by Sequestration of CO2 in Westphalian and Buntsandstein Sandstones of the Campine Basin (NE-Belgium). J. Geochem. Explor. 2006, 89, 10–14. [Google Scholar] [CrossRef]
- Shiraki, R.; Dunn, T.L. Experimental Study on Water–Rock Interactions during CO2 Flooding in the Tensleep Formation, Wyoming, USA. Appl. Geochem. 2000, 15, 265–279. [Google Scholar] [CrossRef]
- Oomole, O.; Osoba, J.S. Carbon Dioxide—Dolomite Rock Interaction During CO2 Flooding Process. In Proceedings of the Annual Technical Meeting; PETSOC: Banff, AB, Canada, 1983; p. PETSOC-83-34-17. [Google Scholar]
- Peng, D.-Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Li, Y.-K.; Nghiem, L.X. Phase Equilibria of Oil, Gas and Water/Brine Mixtures from a Cubic Equation of State and Henry’s Law. Can. J. Chem. Eng. 1986, 64, 486–496. [Google Scholar] [CrossRef]
- Cramer, S.D. Solubility of Methane in Brines from 0 to 300°. Ind. Eng. Chem. Process Des. Dev. 1984, 23, 533–538. [Google Scholar] [CrossRef]
- Arrhenius, S. Quantitative Relationship between the Rate a Reaction Proceed and Its Temperature. J. Phys. Chem. 1889, 4, 226–248. [Google Scholar]
- Kharaka, Y.K.; Gunter, W.D.; Aggarwal, P.K.; Perkins, E.H.; DeBraal, J.D. SOLMINEQ.88, A Computer Program for Geochemical Modeling of Water-Rock Interactions; U.S. Geological Survey: Reston, VA, USA, 1988. [Google Scholar]
- Chen, Z.; Li, R.; Du, Y.; Ma, S.; Zhang, X.; Shi, J. Effect of Confinement on the Vapor-Liquid-Liquid Three-Phase Equilibrium during CO2 Utilization and Sequestration in Shale Reservoirs. Adv. Geo-Energy Res. 2025, 16, 199–210. [Google Scholar] [CrossRef]
- Clemens, T.; Wit, K. CO2 Enhanced Gas Recovery Studied for an Example Gas Reservoir. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar]
- Jia, Y.; Shi, Y.; Yan, J. The Feasibility Appraisal for CO2 Enhanced Gas Recovery of Tight Gas Reservoir: Case Analysis and Economic Evaluation. In Proceedings of the International Petroleum Technology Conference, Virtual, 23 March–1 April 2021. [Google Scholar]









| Experimental Pressure (MPa) | CO2 Mole Fraction in Aqueous Phase (%) |
|---|---|
| 5 | 0.46139 |
| 15 | 0.98926 |
| 25 | 1.24225 |
| 35 | 1.40589 |
| 45 | 1.53514 |
| Reaction Classification | Reaction Equations |
|---|---|
| Phase Equilibrium Reaction | |
| Chemical Equilibrium Reactions | |
| Composition | Mole Fraction (%) |
|---|---|
| CO2 | 0.91 |
| N2 | 1.41 |
| C1 | 90.61 |
| C2 | 5.01 |
| C3 | 0.97 |
| iC4 | 0.25 |
| nC4 | 0.24 |
| iC5 | 0.13 |
| nC5 | 0.07 |
| C6 | 0.40 |
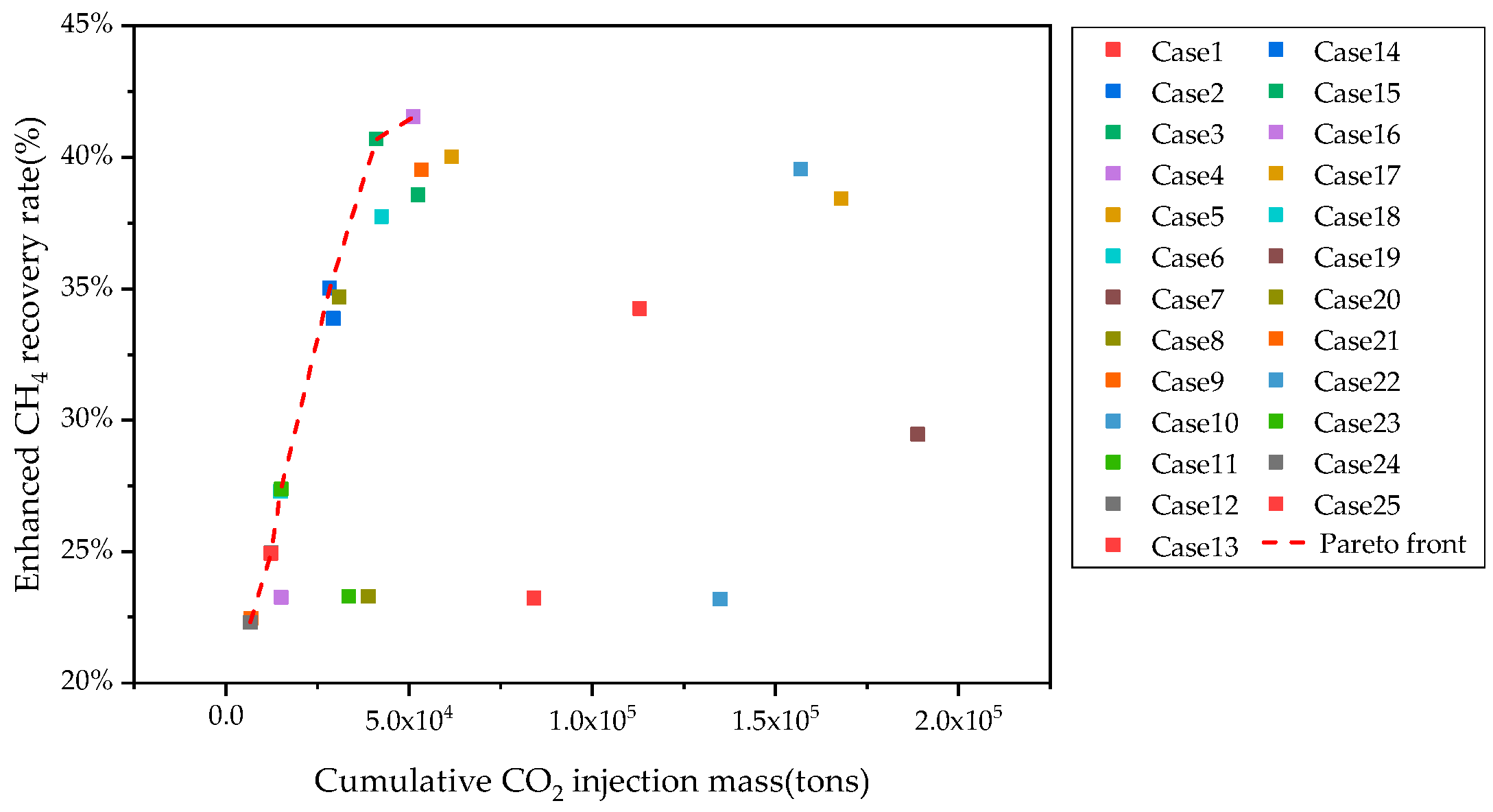
| Case ID | Injection Scheme | Injection Rate (HCPV/Year) | Production Rate (m3/day) | Shut-in Condition (%) | Gas Enhancement Per Ton of CO2 (m3/ton) | Enhanced CH4 Recovery Rate (%) | Cumulative CO2 Injection Mass (tons) |
|---|---|---|---|---|---|---|---|
| 1 | Intermittent | 1.0 | 1000 | 15 | 436.15 | 23.22% | 5.12 × 104 |
| 2 | Intermittent | 0.6 | 2000 | 20 | 533.04 | 35.01% | 4.11 × 104 |
| 3 | Continuous | 0.6 | 4000 | 10 | 349.62 | 38.56% | 6.16 × 104 |
| 4 | Continuous | 0.6 | 5000 | 30 | 135.51 | 41.53% | 1.57 × 105 |
| 5 | Continuous | 1.0 | 3000 | 30 | 398.31 | 38.42% | 5.34 × 104 |
| 6 | Intermittent | 0.4 | 5000 | 10 | 395.52 | 27.28% | 5.25 × 104 |
| 7 | Continuous | 0.8 | 1000 | 20 | 123.26 | 23.18% | 1.68 × 105 |
| 8 | Continuous | 0.4 | 2000 | 25 | 477.14 | 34.68% | 4.25 × 104 |
| 9 | Continuous | 0.6 | 3000 | 15 | 665.64 | 39.51% | 2.83 × 104 |
| 10 | Continuous | 0.8 | 5000 | 25 | 603.78 | 23.18% | 3.09 × 104 |
| 11 | Intermittent | 0.6 | 1000 | 25 | 162.83 | 23.30% | 1.13 × 105 |
| 12 | Continuous | 0.2 | 4000 | 20 | 621.97 | 24.95% | 2.93 × 104 |
| 13 | Continuous | 0.2 | 5000 | 15 | 83.87 | 24.92% | 1.89 × 105 |
| 14 | Continuous | 0.4 | 3000 | 20 | 978.14 | 33.87% | 1.51 × 104 |
| 15 | Intermittent | 0.8 | 4000 | 30 | 983.75 | 40.69% | 1.49 × 104 |
| 16 | Continuous | 0.2 | 1000 | 10 | 1085.95 | 23.26% | 1.24 × 104 |
| 17 | Intermittent | 1.0 | 5000 | 20 | 1089.74 | 40.01% | 1.23 × 104 |
| 18 | Intermittent | 0.8 | 3000 | 10 | 322.27 | 37.74% | 3.89 × 104 |
| 19 | Continuous | 1.0 | 2000 | 10 | 373.31 | 29.45% | 3.36 × 104 |
| 20 | Continuous | 0.4 | 1000 | 30 | 828.65 | 23.30% | 1.51 × 104 |
| 21 | Intermittent | 0.2 | 2000 | 30 | 148.37 | 22.46% | 8.42 × 104 |
| 22 | Continuous | 1.0 | 4000 | 25 | 92.46 | 39.54% | 1.35 × 105 |
| 23 | Intermittent | 0.4 | 4000 | 15 | 92.46 | 27.37% | 1.35 × 105 |
| 24 | Intermittent | 0.2 | 3000 | 25 | 1744.69 | 22.31% | 6.93 × 103 |
| 25 | Continuous | 0.8 | 2000 | 15 | 1798.75 | 34.25% | 6.67 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Li, J.; Liu, P.; Yang, Z.; Fu, B.; Liao, X. Study on Main Controlling Factors of CO2 Enhanced Gas Recovery and Geological Storage in Tight Gas Reservoirs. Processes 2025, 13, 3097. https://doi.org/10.3390/pr13103097
Liu L, Li J, Liu P, Yang Z, Fu B, Liao X. Study on Main Controlling Factors of CO2 Enhanced Gas Recovery and Geological Storage in Tight Gas Reservoirs. Processes. 2025; 13(10):3097. https://doi.org/10.3390/pr13103097
Chicago/Turabian StyleLiu, Lili, Jinbu Li, Pengcheng Liu, Zepeng Yang, Bin Fu, and Xinwei Liao. 2025. "Study on Main Controlling Factors of CO2 Enhanced Gas Recovery and Geological Storage in Tight Gas Reservoirs" Processes 13, no. 10: 3097. https://doi.org/10.3390/pr13103097
APA StyleLiu, L., Li, J., Liu, P., Yang, Z., Fu, B., & Liao, X. (2025). Study on Main Controlling Factors of CO2 Enhanced Gas Recovery and Geological Storage in Tight Gas Reservoirs. Processes, 13(10), 3097. https://doi.org/10.3390/pr13103097






