Abstract
Geothermal energy is a renewable and sustainable resource, but its efficient utilization is often constrained by operational inefficiencies and inadequate system management, highlighting the need for detailed energy assessments to improve performance and ensure long-term sustainability. This study aims for a comparative assessment of the performance of a binary geothermal power plant (GPP) considering air-cooled and evaporative cooling configurations using exergy analysis, based on real operating data. Exergetic parameters were applied to evaluate both overall system efficiency and the performance of individual components. The effect of geothermal fluid mass flow rate on turbine net power output was investigated. Additionally, a carbon emission analysis was conducted to assess environmental impact. Based on the energy content of the geothermal fluid entering the heat exchanger, the plant’s energy efficiency was calculated to be 7.5% for the air-cooled condenser configuration and 8.5% for the evaporative condenser configuration. On the basis of the heat input to the Rankine cycle, the overall energy efficiencies of the plant were found to be 39.76% and 43% for the air-cooled and evaporative condenser cases, respectively. The findings suggest that the overall exergy efficiency of the plant improves when employing the evaporative cooling system, reaching 53.57% compared to 48.38% for the air-cooled system. In the air-cooled configuration, Condenser I accounted for the highest exergy destruction at 27%, whereas in the evaporative system, Vaporizer II had the largest share at 25%. Furthermore, it was determined that the plant with an evaporative cooling system produced approximately 13% less carbon emissions compared to the air-cooled plant, which represents an advantage in terms of environmental sustainability.
1. Introduction
Increasing population density and rapid technological advancements have rendered energy one of the most essential needs both globally and for human life. The growing demand for energy continues to intensify this necessity over time. When current energy production methods in the global market are examined, the depletion risk of fossil fuel reserves and the environmental problems caused by these resources indicate that energy crises and severe environmental issues are likely to become inevitable in the near future [1]. Global warming is widely acknowledged as one of the most critical challenges, as it poses a severe threat to both the planet’s ecological stability and the well-being of future generations. The global shift toward renewable energy sources and the gradual decline in fossil fuel dependence reflect a growing commitment to establishing sustainable energy infrastructures. This transition is primarily driven by the urgent need to combat climate change, minimize environmental degradation, and secure a reliable and environmentally responsible energy future [2]. It is projected that renewable energy sources will surpass fossil fuels as the dominant source of energy by the year 2050, contributing approximately 63% to total global energy generation [3]. Unlike solar and wind energy, geothermal energy provides a stable and continuous source of electricity generation, as it is not affected by weather conditions. It represents a promising pathway toward addressing energy requirements, improving air quality, and advancing the decarbonization of the energy sector [4]. Turkey, currently ranked first in Europe and fourth globally in terms of geothermal energy capacity, demonstrates substantial potential in this field. Between 2015 and 2020, it achieved the highest increase in geothermal installed capacity among all nations [5].
Geothermal energy is utilized for both electricity generation and various direct applications, including space heating and cooling, industrial processing, and greenhouse climate control. High-enthalpy geothermal resources, typically exceeding 150 °C, are primarily employed in power generation. In contrast, medium-temperature resources (90–150 °C) and low-temperature resources (below 90 °C) are more suitable for direct-use applications [6]. Advancements in geothermal energy technologies and improvements in energy efficiency hold significant potential for promoting environmental sustainability. Geothermal energy has become a widely adopted and reliable source of electricity generation. As of today, geothermal power plants are operational in 21 countries, with a combined installed capacity exceeding 6000 MW [7]. Following the 1973 oil crisis, there was a global surge in the development of geothermal facilities, with the majority constructed during the 1970s and 1980s [8]. The urgent need to diversify energy sources and the virtually cost-free availability of geothermal resources often resulted in suboptimal plant designs during this period [6]. Currently, three primary types of geothermal power plants are in operation: dry steam, flash steam, and binary cycle systems. Among these, binary and hybrid flash/binary configurations are relatively recent technological developments, offering improved efficiency and adaptability across a wider range of geothermal resource conditions [9]. The increasing demand for electrical energy, coupled with the depletion of geothermal reservoir capacities, has highlighted the need for comprehensive analysis and optimization of geothermal power plants. Advances in design methodologies, pumping technologies, and cooling techniques have made it possible to significantly enhance the efficiency of these energy systems. Nevertheless, to implement targeted and effective improvements, it is essential to accurately identify the components responsible for performance losses. This requires comprehensive and methodologically sound analyses. Exergy analysis has become a well-established and powerful tool for evaluating energy systems, providing deeper insight than conventional energy analysis by accounting for the quality and usability of energy. It has proven to be particularly valuable in identifying inefficiencies and guiding optimization strategies when used in conjunction with other thermodynamic and engineering assessment methods [10,11]. By enabling a holistic evaluation of all system components and their individual contributions to overall irreversibility, exergy analysis facilitates the precise identification of energy loss locations, magnitudes, and root causes [12].
Numerous studies in the literature underscore the importance of exergy analysis as a critical diagnostic and design tool within the energy sector. Its application to geothermal power plants is especially emphasized, given their complex thermodynamic processes and the growing need to improve their efficiency and sustainability in the face of resource limitations. Başoğlu [13] carried out a comprehensive study on a binary geothermal power plant employing exergy-based analysis methodologies. The primary focus of the study was to assess the exergoenvironmental impacts of the system. The results indicated that approximately 0.6% of the total environmental impact is attributable to equipment, 1.9% to pollutant formation, and 97.5% to exergy destruction. Furthermore, it was reported that the pollutant gas emission levels of the plant exceed the European average. Turgut and Dincer [2] investigated an integrated binary geothermal system for the co-production of green methanol (0.019 kg/s), electricity, and freshwater. The system comprises a double-flash geothermal unit, an Organic Rankine Cycle (ORC), a multi-effect desalination (MED) system, an alkaline electrolyzer, and a methanol synthesis reactor. The overall energy and exergy efficiencies were calculated as 36.96% and 39.31%, respectively. Parametric studies were performed to examine the influence of flash pressure, geothermal well temperature, and electrolyzer performance on system output. Prasetyo et al. [14] conducted a study about the integration of an Organic Rankine Cycle (ORC) into the Ulumbu Geothermal Power Plant in Indonesia to enhance efficiency. By utilizing steam from backpressure turbines and optimizing the ORC design with vapor pressure and non-condensable gas (NCG) data, the system’s performance was improved. Among the two binary cycle models, Model 2 using R1233zd(E) increased thermal efficiency by 8.039% and added 2.006 kWe in output. A preliminary financial and GHG emission analysis confirmed the approach’s technical and environmental feasibility. Khanmohammadi et al. [15], conducted a study about an innovative poly-generation system utilizing geothermal energy to simultaneously produce electricity (684.3 kW), freshwater (864 m3/day), and hydrogen (371.86 kg/day). Comprehensive energy, exergy, exergoeconomic, and exergoenvironmental analyses were conducted, and system optimization was performed using the NSGA-III algorithm and the TOPSIS method. The reverse osmosis (RO) unit exhibited the highest exergy destruction rate at 204.8 kW. Increasing the reference temperature to 320 K improved energy efficiency from 39.78% to 55.43% and reduced total exergy destruction from 790.6 kW to 396.5 kW. Koroneos et al. [16] utilized exergy analysis as a fundamental methodological framework to evaluate the performance and efficiency of thermal systems, with a particular emphasis on geothermal energy conversion. Drawing on experimental data collected from a geothermal drilling site located on the island of Nisyros, Greece, the study estimates the maximum obtainable work and assesses the efficiency of a proposed geothermal power plant. The researchers apply various exergy estimation methods and efficiency indicators to conduct a comprehensive evaluation. The results indicate an exergetic efficiency of 41% and a thermal efficiency of 12.8%, thereby demonstrating the technical feasibility of the proposed system. Ramachandran et al. [3] evaluated the energy, exergy, and economic performance of a binary geothermal CHP plant in Puga Valley using an ORC with R123 and waste heat recovery for district heating. A multi-objective gray wolf optimizer, coupled with artificial neural networks, identifies optimal operating parameters based on exergy efficiency and cost rate. They reported that the plant achieves 1.08 MW net electricity, 4.19 MW thermal output, 36.8% exergy efficiency, and a cost rate of 33.84 USD/h. Compared to the base case, exergy destruction is reduced by 550 kW, and design requirements for a 5 MW plant are also addressed. Makhanlall et al. [17] conducted an exergy-topological analysis of a binary medium-grade geothermal power plant, demonstrating that high thermodynamic efficiency can be achieved without the use of expensive advanced working fluids. The boiler is identified as the component with the highest coefficient of influence, while pumps and the feed-water heater exhibit minimal impact. The condenser emerges as the primary source of exergy losses. Enhancing plant efficiency is shown to be feasible by reducing condenser pressure and extracting geothermal fluid at an appropriate pressure for feed-water preheating. Nasruddin et al. [18] compared an ORC using isopentane with a Kalina cycle using an ammonia-water mixture based on exergy, exergoeconomic and exergoenvironmental analysis for a site in Indonesia. Using MATLAB in conjunction with Engineering Equation Solver and a genetic algorithm, the study optimizes three objective functions. Results indicate that the ORC system achieves superior performance, with an exergy efficiency of 82.12%, an energy cost of 8.19 US cents/kWh, and a total environmental impact of 282.29 mPt/s. Kanoğlu et al. [6] conducted the exergy analysis of a binary geothermal power plant using actual operational data to evaluate overall system performance and identify key sources of exergy destruction. Major losses are observed in the brine reinjection process, heat exchanger, and condenser. Energy and exergy efficiencies are found to be 4.5% and 21.7% based on geothermal water input, and 10.2% and 33.5% for the binary Rankine cycle. The impact of varying turbine inlet pressure and temperature, as well as condenser pressure, on plant efficiencies, net power output, and brine reinjection temperature is also analyzed and discussed.
Extensive research has been conducted on geothermal energy systems, and exergy analysis is widely recognized as an effective tool in this field. However, to the best of the authors’ knowledge, no study has been carried out that comparatively evaluates the component-level performance of binary geothermal power plants under different cooling strategies. To address this gap, the present study has been conducted using real operational data. A comparative, detailed component-wise energy and exergy analysis of a binary geothermal power plant was performed under both evaporative and air-cooled conditions. The energy and exergy efficiencies of the entire plant as well as its individual components were calculated, and various exergetic parameters were employed. Furthermore, the influence of geothermal fluid mass flow rate on net power generation and the impact of different fuel types on carbon emissions were evaluated. The findings of this research are expected to provide valuable contributions to the optimization of geothermal power plant design and operation from both thermodynamic and environmental perspectives.
2. System Description
Binary cycle power plants utilize geothermal fluid (brine) extracted from liquid-dominated geothermal reservoirs. These systems employ a secondary (binary) working fluid such as isobutane, n-pentane, isopentane, or R-114 which is characterized by a relatively low boiling point. The binary fluid is fully vaporized and often superheated within a heat exchanger (vaporizer) using thermal energy from the geothermal brine. The resulting vapor is then expanded through a turbine to generate electricity. Following expansion, the vapor is condensed using either air-cooled or water-cooled condensers. The condensed fluid is subsequently pressurized and circulated back to the vaporizer, thereby completing the closed-loop Rankine cycle. This study focuses on the performance evaluation of the Mis-1 Binary Geothermal Power Plant (GPP), located in the Alaşehir region of Manisa Province, Turkey. Mis-1 GPP consists of 1 unit and has an installed capacity of 12.3 MW. The initial configuration of the power plant, referred to as Case 1, which is equipped with air-cooled condensers, is illustrated by the schematic flow diagram presented in Figure 1. Figure 2 presents the schematic flow diagram of Case 2, which has been revised to reflect the integration of an evaporative cooling system into the existing power cycle.
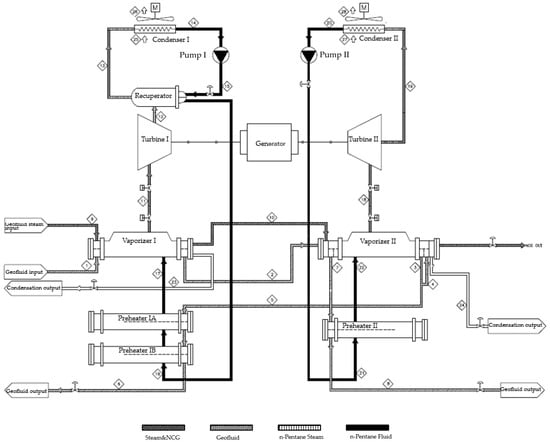
Figure 1.
Schematic flow diagram of the Mis-1 GPP equipped with air-cooled condensers.
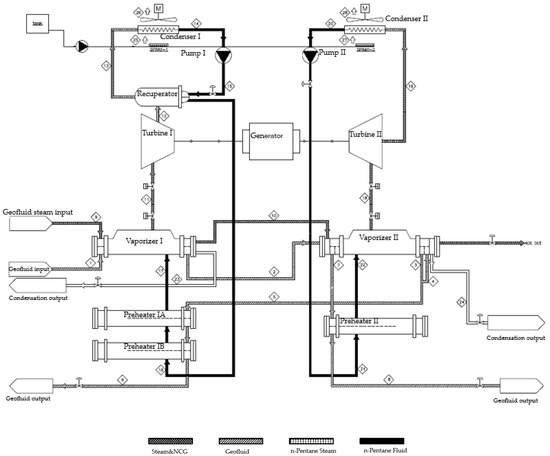
Figure 2.
Schematic flow diagram of the Mis-1 GPP equipped with evaporative cooling system.
In the first case, the Mis-1 Geothermal Power Plant (GPP) operates based on an air-cooled binary Organic Rankine Cycle. Mis-1 GPP was originally designed and installed exclusively with this configuration in 2008. As illustrated in Figure 1, the system comprises Vaporizer I, Vaporizer II, Preheater I-A, Preheater I-B, Preheater II, Recuperator, Turbine I, Turbine II, Condenser I, Condenser II, Pump I, Pump II and Generator distributed across the first and second operational levels. The heat is transferred to the system via geothermal fluids extracted from three artesian wells, each reaching a depth of approximately 2000 to 2500 m. These production wells operate within a temperature range of 155–160 °C, a pressure range of 7–9 bar, and a flow rate range of 750–800 tons per hour. At the top of each well, vertical separators are used to split the two-phase flow into steam and liquid brine. The production infrastructure including production wells, phase separators, control and safety automation systems, reinjection wells, and all associated piping and mechanical fittings fall outside the scope of this investigation. Once the geothermal fluid enters the power plant in both liquid and vapor phases, the ORC is activated and operates concurrently in high (Level I) and low pressure (Level II) loops. For the selected day, the temperature, pressure, mass flow rates, and thermophysical properties of the cycle, along with the corresponding calculated exergy flow rates, are tabulated in Table 1 in accordance with the state point numbering scheme illustrated in Figure 1.

Table 1.
Thermodynamic features and calculated exergy rates for real operating conditions in the Mis-1 air-cooled GPP (Case I) on 1 July 2022.
The geothermal fluid enters the Vaporizer I at a temperature of 154.9 °C, a pressure of 681 kPa, and a mass flow rate of 209.72 kg/s, where it transfers heat to the working fluid, n-pentane. Subsequently, the fluid flows into Vaporizer II located at Level II, continuing the heat exchange process with n-pentane. At this point, due to the reduced temperature and pressure of the geothermal fluid, an additional flow obtained from the separators is integrated into the system. Within Vaporizer II, both the geothermal liquid and the vapor phases pass through without mixing. Upon exiting Vaporizer II, non-condensable gases (NCGs) are vented to the atmosphere, while the condensed geothermal fluid is pressurized via reinjection pumps for subsurface reinjection. Thereafter, the geothermal fluid proceeds through Preheater I and Preheater II to facilitate further heat recovery. Geothermal fluid exiting the preheaters at 85.40 °C and 540 kPa is pumped, together with the condensed geothermal fluid, to the reinjection wells. As illustrated in Figure 1, n-pentane, after being heated in Vaporizer I on Level I, is delivered to Turbine I as superheated vapor at 131.8 °C and 1141 kPa (at point 11), where it is utilized to drive the turbine. The n-pentane leaving Turbine I at 84.8 °C and 187 kPa (point 12) is sent to the Recuperator, where its residual heat is used to preheat the fluid from Pump I. After exiting the recuperator, n-pentane enters the air-cooled condenser (Condenser I) at 69.8 °C (point 13), where it is condensed to a saturated liquid at 53.9 °C and 187 kPa (point 14). The liquid is then pressurized to 1370 kPa by Pump 1 and directed back to Recuperator (point 15), where it absorbs residual heat. This preheating improves the thermal efficiency of the downstream heat exchangers Preheater IA-IB and Vaporizer I. The fluid continues through Preheater IA-IB (point 16) and Vaporizer I (point 17), completing the Level I Organic Rankine Cycle (ORC). To enhance system performance, a second ORC operates on Level II. Here, n-pentane is heated in Vaporizer II to 101.9 °C and 626 kPa (point 18) and expands through Turbine II. The exhaust vapor is condensed in Condenser II at 71.7 °C (point 19) and pumped by Pump II to 171 kPa at 51.4 °C (point 20). The pressurized fluid then passes through Preheater II and Vaporizer II (point 21 and 22), completing the Level II cycle. Ultimately, the mechanical energy generated by Turbine I and Turbine II is converted into electrical energy via a shared generator, as shown in Figure 1. Both turbines are mounted on a common shaft and operate with n-pentane circulating in opposing directions to optimize energy extraction. In geothermal power plants, energy conversion efficiency is highly dependent on the performance of the condenser, which is a critical component in the Rankine cycle. Reducing condenser pressure allows the steam exiting the turbine to condense at a lower saturation pressure, thereby increasing the enthalpy drop between turbine exhaust and condensation conditions. This results in an enhancement of the network output and an overall improvement in cycle efficiency. To facilitate such performance gains, evaporative cooling systems are increasingly being integrated into condenser units. In these systems, spray nozzles atomize water into fine droplets that evaporate upon contact with ambient air, thereby reducing the local air temperature and enhancing heat transfer. This approach enables the condenser to maintain lower operational pressures, particularly under elevated ambient conditions, which is crucial for sustaining efficiency in geothermal power generation [19]. Case II focuses on quantifying the effect of integrating an evaporative cooling system into air-cooled condensers on overall system performance. The system operates using municipal water at 25 °C and 25 bar. Water consumption rates are recorded as 10.2 tonnes per hour for Condenser I and 7.8 tonnes per hour for Condenser II. Table 2 presents the thermodynamic properties measured at each node of Case II, which is equipped with an evaporative cooling system, under real operating conditions. Based on these measurements, the corresponding thermophysical parameters and exergy flow rates were calculated to evaluate the performance of the system in detail. The actual operational data of the geothermal power plant, including temperature, pressure, and flow rate values, were recorded by the control unit on 1 July and 30 August 2022, corresponding to the state points illustrated in Figure 1 and Figure 2. These data formed the basis for constructing the mass, energy, and exergy balance equations of the system. To perform the analyses, the thermophysical properties of the working fluids—brine, pentane, water, and air—were determined through the Engineering Equation Solver (EES) (https://fchartsoftware.com/ees/index.php/). Subsequently, the software was used to carry out detailed energy and exergy analyses of the plant.

Table 2.
Thermodynamic features and calculated exergy rates for real operating conditions in the Mis-1 GPP equipped with evaporative cooling system (Case II) on 30 August 2022.
3. Methodology
3.1. Energy and Exergy Analysis
The first law of thermodynamics focuses on the quantity of energy, stating it cannot be created or destroyed. In contrast, the second law deals with the quality of energy, addressing energy degradation, entropy, and irreversibilities during conversion processes. The second law of thermodynamics is an important tool for improving the performance of complex energy systems. Exergy analysis, based on this law, helps identify where energy is wasted and suggests ways to reduce energy use, lower environmental impact, and use resources more efficiently [20].
This study presents a comparative performance analysis of a binary geothermal power plant operating under air-cooled (Case I) and evaporative cooled (Case II) conditions, utilizing exergy analysis as the primary evaluation method. The thermodynamic performance evaluation was conducted by applying the mass, energy and exergy balance equations, which allowed for the determination of heat and work interactions and exergy destruction rates (representing system irreversibilities) could be expressed as follows:
(kg/s) refers to the mass flow rate, where ‘in’ and ‘out’ are used to identify the inlet and outlet conditions, respectively.
where and are the net heat and work inputs, h is the enthalpy, and is the rate of exergy destruction. The subscript 0 represents the dead state for the fluids. Also, is the net exergy transfer by heat at the specified temperature.
The specific exergy, neglecting kinetic and potential exergy contributions, can be defined as the difference in specific enthalpy and entropy relative to the environment:
The exergy rate of a fluid stream can be determined by multiplying its specific exergy by the mass flow rate
Exergy analysis is performed by applying exergy balance equations to each system component individually. At the component level, the product exergy rate () is the useful exergy output per unit time, while the fuel exergy rate () is the exergy input required to produce that output. The general expression for the exergy balance is given in the rate form as
The exergetic (or second-law) efficiency is generally defined as the quotient of total exergy output and total energy input, providing a measure of how effectively input energy is converted into useful work.
Table 3 presents the exergy balance equations and corresponding exergy efficiency formulations for the individual components of the geothermal power plant.

Table 3.
Exergy balance and exergy efficiency equations of the components of the GPP.
In the literature, several definitions are employed to determine the energy efficiency of binary geothermal power plants [19]. In the present study, multiple efficiency definitions have been applied for the analysis.
The energy efficiency of a geothermal power plant can be formulated as follows:
Here, the denominator represents the energy input to the geothermal power plant, defined as the product of the geothermal fluid mass flow rate and its enthalpy relative to the reference state. Based on the numbering system, the equation can be expressed as
A portion of the geothermal water is reinjected back into the ground at a temperature much higher than the environmental temperature. In this case, the thermal efficiency is expressed as
The efficiency equation can be formulated based on the above description as follows:
In exergy analysis, in order to comprehensively assess the impact of individual components on the overall system performance, several advanced exergy-based parameters—such as improvement potential rate (), exergetic factor (ƒ), fuel depletion ratio (y), relative irreversibility (RI), and sustainability index (SI)—are utilized in addition to conventional exergy efficiency. These indicators provide a deeper insight into system inefficiencies, optimization opportunities, and the environmental sustainability of energy conversion processes [21].
Depending on the purpose of the exergy analysis, the concept of improvement potential has been developed to identify the possible enhancements in the process or system under consideration, and it is expressed by Equation (12).
The exergetic factor, which indicates the share of the fuel consumed by the related component within the total fuel, is expressed by Equation (13), as follows:
The fuel depletion ratio, which represents the ratio of the exergy destruction of the related component to the total fuel input, is expressed by the following equation.
The relative irreversibility is defined as the ratio of the irreversibility of a given component to the total irreversibilities. It serves as an important tool for identifying inefficiencies within the system and is expressed by Equation (15).
The sustainability index (SI) is a performance indicator that relates the exergetic efficiency of a system to its environmental sustainability.
3.2. Carbon Emission Assessment
In recent years, climate change driven by greenhouse gas emissions particularly carbon dioxide (CO2) has emerged as a critical global environmental issue. In response, reducing carbon emissions has gained widespread international consensus as a necessary measure to mitigate atmospheric greenhouse gas concentrations and slow the progression of climate change [22]. In geothermal power plants, enhancing energy and exergy efficiencies constitutes a critical pathway toward improving overall system performance and reducing environmental impact. Energy and exergy analyses offer rigorous thermodynamic assessment tools to evaluate component-level and system-wide inefficiencies, particularly those arising from heat extraction, conversion, and reinjection processes [23]. By minimizing exergy destruction and optimizing the utilization of geothermal resources, these improvements can lead to significant reductions in specific energy consumption and associated CO2 emissions per unit of electricity generated. To evaluate the potential influence of energy demand reduction on carbon emissions, the Emission Factor Method outlined by the Intergovernmental Panel on Climate Change (IPCC) can be employed [24]. This widely accepted approach quantifies carbon emissions using the following calculation framework.
Here, CO2 emissions (E) are calculated by multiplying the activity-level data (AD) by the corresponding emission factor (EF) [22]. Activity-level data represent actions or processes that result in greenhouse gas emissions, such as residential electricity usage, the extent of green spaces, and similar indicators. The emission factor denotes the quantity of CO2 emitted per unit of activity. In practice, this means that emissions are estimated by applying the appropriate EF to the specific AD—for instance, the volume of electricity consumed. It is important to emphasize that emission factors vary depending on the type of fossil fuel utilized and the operational efficiency of the power plants involved in electricity generation.
4. Results and Discussion
In this study, a comparative thermodynamic performance analysis was conducted for a binary geothermal Organic Rankine Cycle (ORC) power plant operating with air-cooled and evaporative-cooled condenser systems. The same power plant was first operated using air-cooled condensers and later evaluated after the integration of an evaporative cooling system. To ensure a valid comparison, days with identical ambient air temperatures were selected for data collection, allowing consistent temperature and pressure measurements across system components. For the air-cooled configuration, data were recorded on 1 July 2022, when the ambient temperature was 33 °C. For the evaporative-cooled configuration, measurements were taken on 30 August 2022, under the same ambient temperature conditions. To evaluate the performance of the system, exergy analysis was employed. Furthermore, various exergetic parameters were utilized to obtain more comprehensive and analytically meaningful data. In addition to the exergy analysis, a carbon emission analysis was also conducted to assess both operational cases of the power plant (Case I and Case II). For this purpose, real operational data such as flow rate, pressure, and temperature values at the inlet and outlet lines of system components were collected from the control panel system of the existing geothermal power plant on the previously specified dates. Following the methodology outlined in the Section 3, the operational data corresponding to the state points indicated in Figure 1 and Figure 2 are compiled in Table 1 and Table 2. Utilizing these data and the relevant thermodynamic equations, the exergy analyses for both Case I and Case II were carried out. For both Case I and Case II, the exergetic product, fuel, and destruction values; fuel depletion ratios; relative irreversibility values; exergetic factors; improvement potential values; and sustainability indicators were listed for each component of the power plant as well as for the overall system in Table 4 and Table 5. For the Case I, among all components, Condenser I exhibited the highest exergy destruction, followed by Vaporizer I and Condenser II, indicating significant irreversibility within the heat rejection stages of the cycle. In Case II, where evaporative cooling is implemented, the component with the highest exergy destruction is Vaporizer II, followed by Condenser I and Preheater I. This indicates that the primary sources of irreversibility under evaporative cooling conditions are associated with the heat exchange and vaporization processes.

Table 4.
Results of exergy analysis and exergetic parameters for air-cooled GPP (Case I).

Table 5.
Results of exergy analysis and exergetic parameters equipped with evaporative cooling GPP (Case II).
As shown in Figure 3, the distribution of exergy destruction among system components under air-cooled conditions reveals that Condenser I accounts for the largest share (27%), followed closely by Vaporizer II (18%) and Condenser II (16%). Additionally, Turbine I and Preheater I each contribute 10%, Vaporizer I accounts for 8%, and both Turbine II and Preheater II contribute 5%, while Pump I and Pump II have the lowest impact, each at 1%. Under evaporative cooling conditions, the relative contributions to exergy destruction shift as shown in Figure 4. Vaporizer II remains the most dominant source with 25%, but Condenser I decreases to 21%, followed by Preheater I (11%), Condenser II (10%), Vaporizer I (9%), Turbine I (8%), Turbine II (5%), and again Pump I and Pump II at 1% each. These findings suggest that the implementation of evaporative cooling leads to a notable reduction in exergy destruction within Condenser I, highlighting an improvement in condenser thermodynamic performance. This can be attributed to the enhanced heat rejection efficiency achieved through the lowered condenser temperature in Case II. The exergetic efficiency of the plant was calculated to be 48.38% under air-cooled condenser conditions. In contrast, when evaporative cooling was applied to the condensers, the exergetic efficiency increased to 53.57%. This improvement highlights the thermodynamic advantage of evaporative cooling in reducing irreversibilities, particularly in the heat rejection process, thereby enhancing the overall performance of the power cycle. According to the literature, the exergetic efficiency of binary geothermal power plants is typically reported to be around 40% [2,6,13].
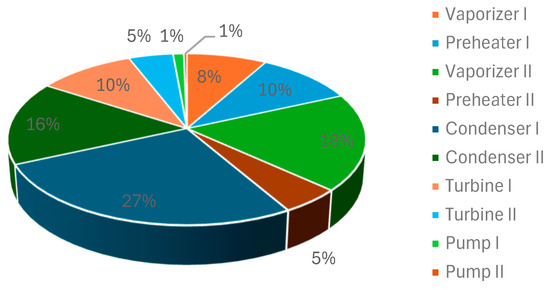
Figure 3.
Schematic representation of exergy destruction distribution among the components for the Case I.
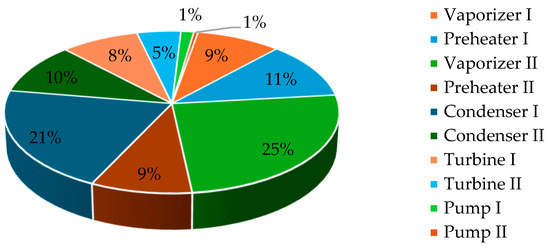
Figure 4.
Schematic representation of exergy destruction distribution among the components for Case II.
The exergetic efficiency values of all components of the GPP are presented in Figure 5 for both the air-cooled case (Case I) and the evaporative-cooled case (Case II). Regarding the heat exchangers, the exergetic efficiencies of Condenser I and II in the air-cooled system were calculated as 56.13% and 56.30%, respectively, whereas in the evaporative-cooled system, these values were determined as 69.35% and 72.93%, respectively. The exergetic efficiencies of Vaporizers I and II were found to be 94.69% and 79.33% in Case I, and 95.19% and 78.39% in Case II, respectively. The obtained exergetic efficiency values reflect a high level of performance, suggesting that the heat exchange system operates effectively. In binary geothermal power plants, heat exchangers play a vital role, and their individual efficiency has a considerable impact on the overall thermodynamic performance of the plant [6]. In the air-cooled configuration, the exergetic efficiencies of Turbine I and Turbine II were calculated to be 90.74% and 90.91%, respectively. With the implementation of evaporative cooling, these efficiencies increased to 94.15% and 93.19%, respectively. This improvement is primarily attributed to the reduction in turbine exhaust temperatures from 84.8 °C to 80.7 °C for Turbine I, and from 71.7 °C to 64.7 °C for Turbine II resulting in enhanced thermodynamic performance and reduced exergy destruction within the turbines. Exergy efficiencies of the components of the power plant with evaporative cooling were evaluated as shown in Figure 5. The Vaporizer I exhibits the maximum exergy efficiency. It has 95.19% exergy efficiency. It was followed by Turbine I with 94.15% and by Turbine II with 93.19%. On the other hand, Preheater II had a minimum exergy efficiency of 60.69%. When the exergy efficiency values of the components in the air-cooled system are examined, it is observed that the order of the components remains unchanged. Among these, Condenser I and Condenser II stand out as the components with the lowest exergy efficiencies, with values of 56.13% and 56.30%, respectively. These values are notably lower compared to those in Case II, indicating a decrease in performance under the current configuration.
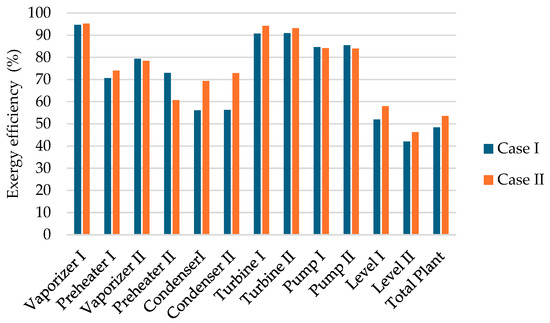
Figure 5.
A component-wise comparison of the exergetic efficiencies of the GPP for air-cooled and evaporative cooling conditions.
Moreover, several exergetic performance indicators were utilized to provide a more comprehensive assessment of the system. Improvement potential rate (IP) refers to the portion of exergy destruction that can be reduced, indicating where efficiency enhancements are most feasible within the system. Based on the IP values obtained for Case I, Condenser I exhibits the highest improvement potential with 739.37 kW, followed by Condenser II (433.75 kW) and Vaporizer II (239.09 kW). These findings indicate that targeted enhancements in these components, particularly within the air-cooled configuration, could significantly contribute to improving the overall exergy efficiency of the system. Conversely, Pump II (2.95 kW), Pump I (10.68 kW), Turbine II (25.73 kW), and Vaporizer I (27.32 kW) were found to have the lowest improvement potential. Due to their relatively minor contributions to overall exergy destruction, optimization efforts targeting these components are not expected to yield meaningful efficiency gains and may be deemed unnecessary within the scope of system enhancement.
In Case II, where evaporative cooling is applied, the highest improvement potentials were identified, respectively, in Condenser I (321.05 kW), Vaporizer II (276.28 kW), and Preheater II (178.49 kW). Notably, the improvement potentials of Condenser I and Condenser II were found to be approximately 50–60% lower compared to their counterparts under air-cooled conditions. This result clearly demonstrates the positive impact of evaporative cooling on the overall system performance. An analysis of the exergetic factor distributions among the system components for Case I reveals that the highest values are observed in Vaporizer I (52.07%), Turbine I (36.53%), and Vaporizer II (30.10%), respectively. The exergetic factor indicates the proportion of the total exergy fuel supplied to each component within the system, reflecting the component’s relative contribution to the overall exergy utilization process. Vaporizer I receives a substantial share of the system’s exergy fuel and demonstrates effective utilization, as evidenced by its high exergetic efficiency and comparatively low exergy destruction. In contrast, despite its high exergetic factor, Vaporizer II cannot be considered efficient in utilizing the supplied exergy fuel due to its significant exergy destruction rate (1156.48 kW). In Case II, a similar distribution trend is observed. Vaporizer I exhibits the highest exergetic factor, accounting for 50.83% of the total exergy fuel supplied to the system. It is followed by Turbine I with 38.58%, and Vaporizer II with 31.19%. On the other hand, the components with the lowest exergetic factor values are Preheater II (6.09%) and Condenser II (10.26%). Given their relatively minor share in the overall exergy fuel distribution, these components are not considered critical for further optimization studies.
In geothermal power plants, identifying components with the highest share of exergy destruction is essential for improving overall system efficiency. The Relative Irreversibility (RI) index is a valuable indicator in this context, as it quantifies the proportion of total exergy destruction attributable to each component. For the air-cooled configuration (Case I), the highest RI value was observed in Condenser I, accounting for 17.57% of the total system exergy destruction. This indicates that Condenser I contributes the most to thermodynamic irreversibilities in this case, suggesting that targeted improvements in this component could significantly enhance the system’s performance. To validate this result, the evaporatively cooled configuration (Case II) was analyzed. The RI value of Condenser I decreased to 11.89%, confirming the positive impact of evaporative cooling on both component-level and overall system performance. This comparison clearly demonstrates the potential of evaporative cooling to reduce irreversibilities and improve energy efficiency in geothermal power plants. In Case I, following Condenser I, the components with the next highest Relative Irreversibility (RI) values were Vaporizer II with 12.05%, Condenser II with 10.35%, and Preheater I with 6.66%. These results indicate that, in addition to Condenser I, these components also contribute significantly to the total exergy destruction and may represent potential targets for performance improvement. In Case II, the component with the highest RI value was Vaporizer II, accounting for 14.51% of the total exergy destruction. It was followed by Condenser I with 11.89%, and Preheater I with 6.64%. These findings further highlight how system configuration (specifically the implementation of evaporative cooling) affects the distribution of irreversibilities among system components.
It is evident that the sustainability index is closely linked to exergy efficiency, which serves as an indicator of the quality of resource conversion into useful output. A higher exergy efficiency corresponds to a greater sustainability index, reflecting improved conservation of exergy relative to exergy destruction. This index is also associated with the depletion of primary energy resources. A higher sustainability index signifies a more sustainable system, primarily due to reduced consumption and depletion of natural resources. In this context, for Case I, the components with the highest sustainability index values were calculated to be Vaporizer I (18.82), Turbine II (11.00), and Turbine I (10.80), respectively. For Case II, although the ranking remains similar, the implementation of evaporative cooling enhancement has led to an improvement in the sustainability of the components. Accordingly, the updated ranking is Vaporizer I (20.80), Turbine I (17.09), and Turbine II (14.69). The overall energy efficiency values of the plant are reported in Table 6. When the efficiency is evaluated on the basis of the energy content of the geothermal fluid entering the heat exchanger, the efficiencies are calculated as 7.5% for Case I and 8.5% for Case II. Alternatively, when the heat transfer to the binary Rankine cycle is considered as the reference, the corresponding energy efficiency values are determined to be 39.76% for Case I and 43% for Case II. These findings indicate that the choice of reference basis has a significant influence on the calculated efficiency values, and that Case II consistently exhibits superior performance compared to Case I.

Table 6.
Results of energy efficiency (first law) of the plant.
Figure 6 presents the influence of geothermal fluid mass flow rate on the power output of a GPP equipped with an air-cooled condenser. As the mass flow rate increases from 20 kg/s to 40 kg/s, the power generation of Turbine I rises from approximately 6400 kW to 9000 kW, whereas that of Turbine II increases from about 3700 kW to 5400 kW.
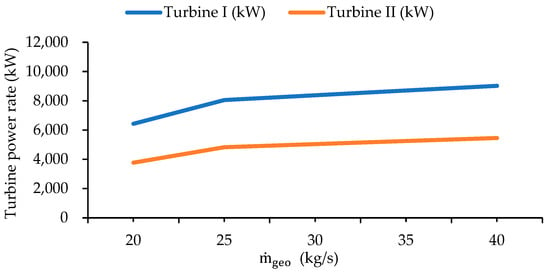
Figure 6.
The impact of geothermal fluid mass flow rate on turbine power generation rate for Case I.
Figure 7 illustrates the effect of geothermal fluid mass flow rate on turbine power generation for the GPP equipped with an evaporative-cooled condenser. When the mass flow rate is increased from 20 kg/s to 40 kg/s, the power output of Turbine I increases from approximately 8200 kW to 9600 kW, while that of Turbine II rises from around 4400 kW to 5500 kW.
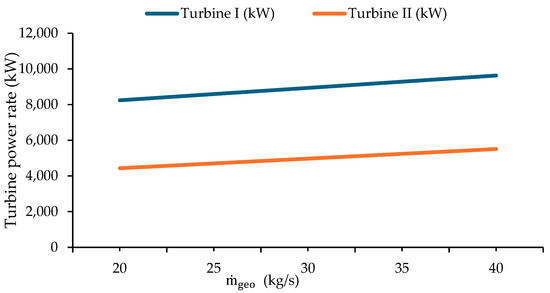
Figure 7.
The impact of geothermal fluid mass flow rate on turbine power generation rate for Case II.
The increase in the power load of the turbines indicates that the system operates on a larger energy scale as the geothermal mass flow rate rises. This is because a higher mass flow rate through the turbines results in greater power generation, as predicted by the thermodynamic equations [25]. These results clearly demonstrate the direct proportionality between the geothermal fluid supply and turbine performance, emphasizing the critical role of flow rate optimization in enhancing overall plant efficiency.
Table 7 provides a comparative assessment of carbon emissions associated with the binary geothermal power plant for different fuel types. Furthermore, the table demonstrates the potential for emission mitigation achieved through improvements in energy and exergy efficiencies, facilitated by the integration of an evaporative cooling system. In the case utilizing air-cooled condensers (Case I), the net power output of the binary geothermal power plant is calculated to be 8990 kW. However, when evaporative cooling is employed (Case II), the net power output increases to 10,160 kW. This improvement is primarily attributed to the enhancement in the system’s exergy efficiency.

Table 7.
Assessment of CO2 emissions of the GPP operating with different fuel sources.
In Table 7, the AD values were calculated based on a one-day operational interval. Accordingly, the net power outputs of 8990 kW and 10,160 kW correspond to 214,646.74 kWh/day and 242,518.90 kWh/day, respectively. The increase of 1170 kW in power generation, attributed to improved energy efficiency through evaporative cooling, results in an additional energy yield of 27,935.11 kWh per day. As shown in Table 7, the binary geothermal power plant utilizing evaporative cooling leads to lower carbon emissions for both fuel types compared to the air-cooled configuration. The greatest reduction in carbon emissions is observed for the industrial coal fuel type, with a decrease of 8942.87 kg CO2e. Figure 8 presents a comparative illustration of the carbon emission reductions achieved through evaporative versus air cooling for both coal and natural gas fuels.
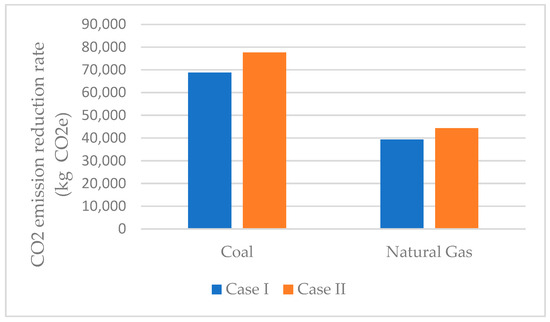
Figure 8.
Comparative CO2 emission reduction rate of the GPP for air-cooled and evaporative cooling conditions with different fuels.
5. Conclusions
This study presents a comprehensive exergetic performance analysis of a binary geothermal power plant (GPP) under two different cooling configurations: air-cooled (Case I) and evaporative-cooled (Case II). The findings clearly demonstrate that the integration of evaporative cooling significantly improves both component-level and overall system performance.
- The results demonstrated that implementing an evaporative-cooled condenser system significantly improves the thermodynamic performance of the power plant. Notably, the exergetic efficiency increased from 48.38% in the air-cooled system to 53.57% in the evaporative-cooled case. It is noteworthy that the integration of the evaporative-cooled condenser led to a significant improvement in the overall system energy efficiency, raising it from 39.76% to 43%. This improvement can be attributed to the reduced exergy destruction observed particularly in Condenser I, suggesting enhanced heat rejection capabilities due to lower condenser temperatures.
- The exergetic efficiencies of Condensers I and II increased notably from 56.13% and 56.30% in Case I to 69.35% and 72.93% in Case II, respectively, indicating a substantial reduction in exergy destruction due to enhanced heat rejection capacity. Similarly, Turbines I and II exhibited improved performance, with exergetic efficiencies rising from 90.74% and 90.91% to 94.15% and 93.19%, respectively. These enhancements are primarily attributed to lower turbine exhaust temperatures under evaporative cooling.
- The integration of the evaporative cooling system led to a reduction in the temperature of the air entering the condenser, which consequently lowered the condensation temperature on the condenser surface. This improvement resulted in a decrease in turbine exhaust pressure and, in turn, enhanced the net power output of the plant by approximately 13%.
- Among all components, Vaporizer I achieved the highest exergetic efficiency in both configurations, exceeding 94%, which reflects its critical role in effective heat transfer and minimal irreversibilities. The improvement potential (IP) rate identified Condenser I as the component with the highest optimization potential in both cases; however, the IP values were significantly lower in Case II, signifying that evaporative cooling effectively mitigates inefficiencies.
- The distribution of the exergetic factor highlighted the dominant role of Vaporizer I and Turbine I in the overall exergy utilization process. Despite its high exergy input, Vaporizer II was found to have substantial exergy destruction, particularly in the air-cooled case, suggesting the need for targeted design improvements.
- The relative irreversibility (RI) assessment further confirmed the positive impact of evaporative cooling. In Case I, Condenser I was responsible for the highest proportion of total exergy destruction (17.57%), whereas in Case II, this value decreased to 11.89%, with Vaporizer II becoming the primary source of irreversibility. This shift illustrates how cooling strategies influence thermodynamic losses across system components.
- Additionally, the sustainability index values improved across all major components in the evaporative-cooled configuration, reaffirming the correlation between higher exergy efficiency and improved sustainability performance. The integration of evaporative cooling led to an increase in net power output from 8990 kW to 10,160 kW, resulting in an additional daily energy yield of 27,935.11 kWh.
- Finally, the carbon emissions analysis demonstrated the environmental benefits of the improved system. The greatest reduction was observed for coal-based operation, with daily emissions decreasing by up to 8942.87 kg CO2e. These findings confirm that evaporative cooling not only enhances the thermodynamic performance of binary geothermal power plants but also contributes meaningfully to emission reduction and sustainable energy production.
Author Contributions
Conceptualization, A.G.C. and A.Ş.; methodology, A.G.C. and A.Ş.; software, A.G.C. and A.Ş.; validation, A.G.C. and A.Ş.; formal analysis, A.G.C. and A.Ş.; investigation, A.G.C. and A.Ş.; resources, A.Ş.; data curation, A.Ş. and A.G.C.; writing—original draft preparation, A.G.C. and A.Ş.; writing—review and editing, A.G.C. and A.Ş.; visualization, A.G.C. and A.Ş.; supervision, A.G.C.; project administration, A.G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the Mis Energy Company for technical assistance in conducting this research.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| AD | Activity-level data |
| CO2e | Carbon equivalent |
| ex | Specific exergy (kJ/kmol) |
| E | Energy (kJ) |
| EF | Emission factor |
| Exergy flow rate (kW) | |
| f | Exergetic factor (%) |
| Exergy rate of the fuel (kW) | |
| h | Enthalpy (kj/kg) |
| Improvement potential rate (kW) | |
| Mass flow rate (kg/s) | |
| P | Pressure (kPa) |
| Exergy rate of the product (kW) | |
| RI | Relative irreversibility (%) |
| Specific entropy (kJ/kg K) | |
| SI | Sustainability index (-) |
| T | Temperature (K or °C) |
| Work rate or power (kW) | |
| y | Fuel depletion ratio |
| Greek letters | |
| ηth | Energy (first law) efficiency (%) |
| ε | Exergy (second law) efficiency (%) |
| Subscripts and superscripts | |
| 0 | Dead (reference) state |
| a | Air |
| D | Destruction or destroyed |
| F | Fuel |
| g | Gas |
| geo | Geothermal fluid |
| i | Any (i) gas |
| in | Inflow |
| k | kth component |
| out | Outflow |
| P | Product |
| Over dot | Quantity per unit time |
References
- Alayi, R.; Ahmadi, M.H.; Visei, A.R.; Sharma, S.; Najaf, A. Technical and environmental analysis of photovoltaic and solar water heater cogeneration system: A case study of Saveh City. Int. J. Low-Carbon Technol. 2021, 16, 447–453. [Google Scholar]
- Turgut, H.S.A.; Dincer, I. Assessment of a new binary geothermal based methanol synthesis plant with power, hydrogen and freshwater. Energy Convers. Manag. 2023, 294, 117576. [Google Scholar] [CrossRef]
- Ramachandran, S.; Bhogilla, S.S.; Vijayan, P.K. Techno-Economic Analysis and Optimization of a Binary Geothermal Combined District Heat and Power Plant for Puga Valley, India. Renew. Energy 2024, 234, 121223. [Google Scholar] [CrossRef]
- Kubota, H.; Hondo, H.; Hienuki, S.; Kaieda, H. Determining Barriers to Developing Geothermal Power Generation in Japan: Societal Acceptance by Stakeholders Involved in Hot Springs. Energy Policy 2013, 61, 1079–1087. [Google Scholar] [CrossRef]
- Korucan, A.; Derin-Gure, P.; Celebi, B.; Baker, D.; Vander Velde, M. Opportunities and Challenges of Geothermal Energy in Türkiye. Energy Sustain. Dev. 2024, 79, 101417. [Google Scholar] [CrossRef]
- Kanoglu, M.; Bolatturk, A. Performance and Parametric Investigation of a Binary Geothermal Power Plant by Exergy. Renew. Energy 2008, 33, 2366–2374. [Google Scholar] [CrossRef]
- DiDippo, R. Geothermal energy electricity generation and environmental impact. Energy Policy 1991, 19, 798–807. [Google Scholar] [CrossRef]
- Kanoğlu, M. Exergy Analysis of a Dual-Level Binary Geothermal Power Plant. Geothermics 2002, 31, 709–724. [Google Scholar] [CrossRef]
- Phair, K.A. Getting the Most out of Geothermal Power. ASME Mech. Eng. 1994, 116, 76–80. [Google Scholar]
- Restrepo, Á.; Miyake, R.; Kleveston, F.; Bazzo, E. Exergetic and Environmental Analysis of a Pulverized Coal Power Plant. Energy 2012, 45, 205–217. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, L.; Dong, C.; Xu, G.; Morosuk, T.; Tsatsaronis, G. Comprehensive Exergy-Based Evaluation and Parametric Study of a Coal-Fired Ultra-Supercritical Power Plant. Appl. Energy 2013, 112, 1087–1099. [Google Scholar] [CrossRef]
- Ersayin, E.; Ozgener, L. Performance Analysis of Combined Cycle Power Plants: A Case Study. Renew. Sustain. Energy Rev. 2015, 43, 832–842. [Google Scholar] [CrossRef]
- Başoğlu, Y. Environmental Assessment of a Binary Geothermal Sourced Power Plant Accompanied by Exergy Analysis. Energy Convers. Manag. 2019, 195, 492–501. [Google Scholar] [CrossRef]
- Prasetyo, B.T.; Agustina, L.; Suyanto, S.; Guardi, A.; Sutriyanto, H.; Pujowidodo, H.; Harmadi, R.; Cahyadi, C.; Ifanda, I.; Anugia, Z.; et al. The Integrative Use of Binary Cycle Technology to Improve Thermal Efficiency and Efficiency in Geothermal Power Plants: A Case Study of Ulumbu Geothermal Power Plant in Indonesia. Energy Convers. Manag. 2024, 321, 119033. [Google Scholar] [CrossRef]
- Khanmohammadi, S.; Moradi, K.; Khanjani, S. Comprehensive Analysis of a Geothermal-Based Poly-Generation Plant to Achieve Optimal Exergy, Economic, and Environmental Performance. Energy 2025, 315, 134338. [Google Scholar] [CrossRef]
- Koroneos, C.; Polyzakis, A.; Xydis, G.; Stylos, N.; Nanaki, E. Exergy Analysis for a Proposed Binary Geothermal Power Plant in Nisyros Island, Greece. Geothermics 2017, 70, 38–46. [Google Scholar] [CrossRef]
- Makhanlall, D.; Zhang, F.; Xu, R.; Jiang, P. Exergy-Topological Analysis and Optimization of a Binary Power Plant Utilizing Medium-Grade Geothermal Energy. Appl. Therm. Eng. 2015, 88, 459–463. [Google Scholar] [CrossRef]
- Nasruddin, N.; Saputra, I.D.; Mentari, T.; Bardow, A.; Marcelina, O.; Berlin, S. Exergy, Exergoeconomic, and Exergoenvironmental Optimization of the Geothermal Binary Cycle Power Plant at Ampallas, West Sulawesi, Indonesia. Therm. Sci. Eng. Prog. 2020, 19, 100625. [Google Scholar] [CrossRef]
- DiPippo, R. Geothermal Power Plants: Principles, Applications, Case Studies and Environmental Impact, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- Çengel, Y.A.; Boles, M.A. Thermodynamics: An Engineering Approach, 3rd ed.; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Rosen, M.A.; Dincer, I.; Kanoglu, M. Role of Exergy in Increasing Efficiency and Sustainability and Reducing Environmental Impact. Energy Policy 2008, 36, 128–137. [Google Scholar] [CrossRef]
- Luo, X.; Ren, M.; Zhao, J.; Wang, Z.; Ge, J.; Gao, W. Life Cycle Assessment for Carbon Emission Impact Analysis for the Renovation of Old Residential Areas. J. Clean. Prod. 2022, 367, 132930. [Google Scholar] [CrossRef]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE). ASHRAE Handbook—Refrigeration; ASHRAE Inc.: Atlanta, GA, USA, 2010. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). IPCC Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies: Kanagawa, Japan, 2006; pp. 1–20. [Google Scholar]
- Yilmaz, F. A comprehensive energy, exergy, economic, and environmental (4E) assessment of a geothermal-driven polygeneration plant with energy storage using compressed hydrogen. J. Energy Storage 2025, 114, 115796. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).