Research on the Mechanical Properties and Failure Mechanism of Lignite Affected by the Strain Rate Under Static and Dynamic Loading Conditions
Abstract
1. Introduction
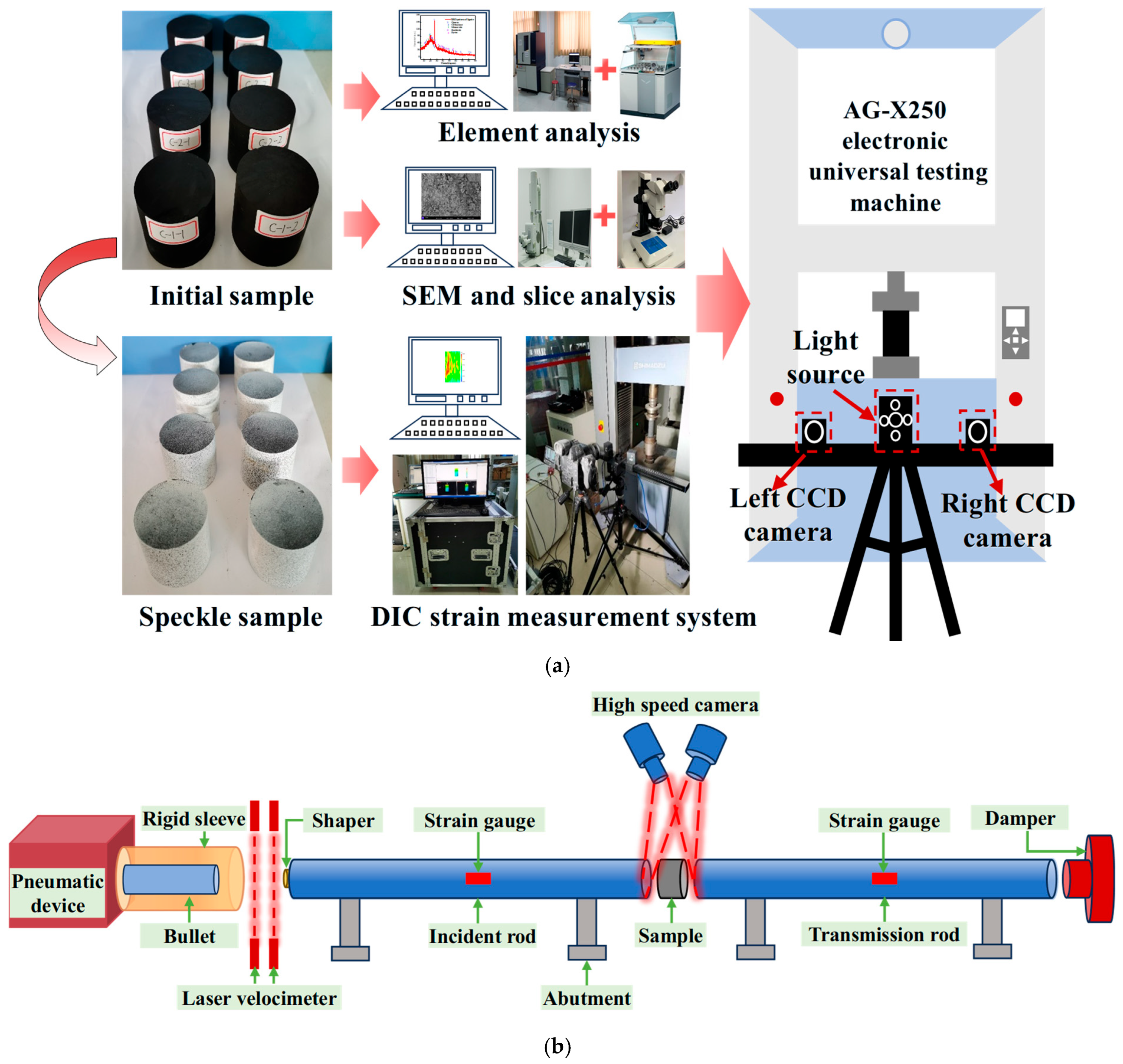
2. Methodology
2.1. Sample Preparation
2.2. Test System and Experimental Procedure
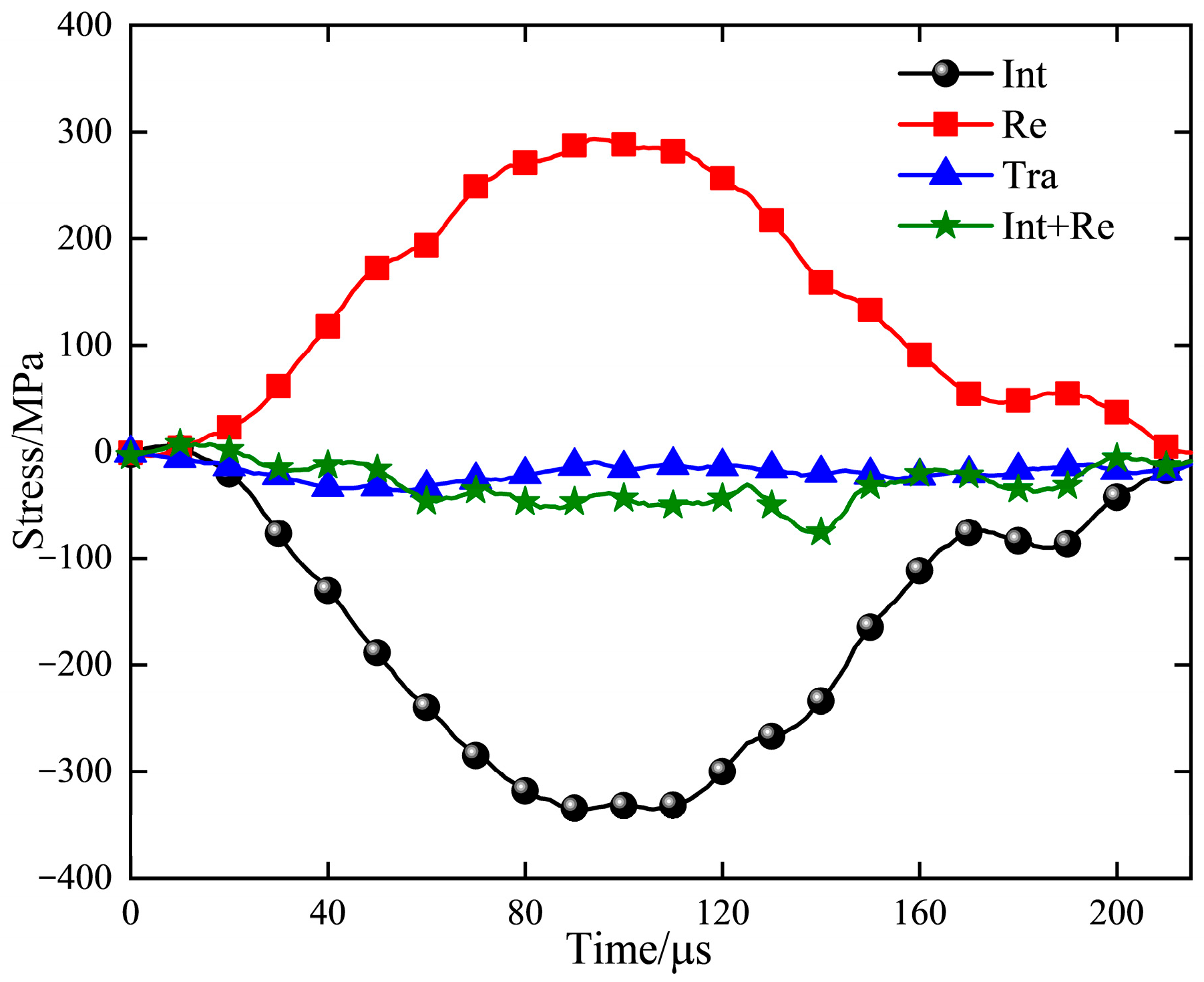
2.3. The Principle of the SHPB Test
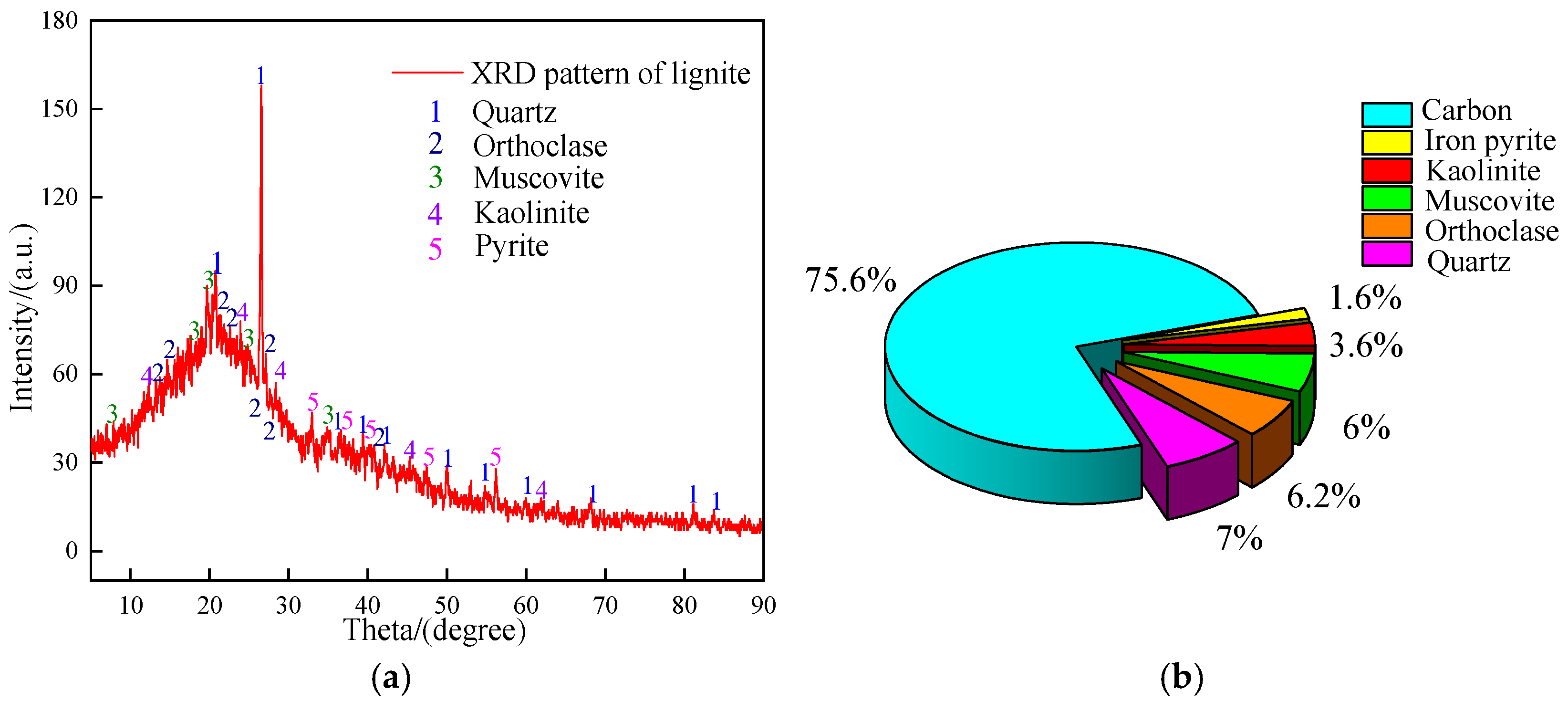
3. Composition and Mesoscopic Structure Analysis of Lignite
3.1. Mineral Composition
3.2. Micro-Morphology
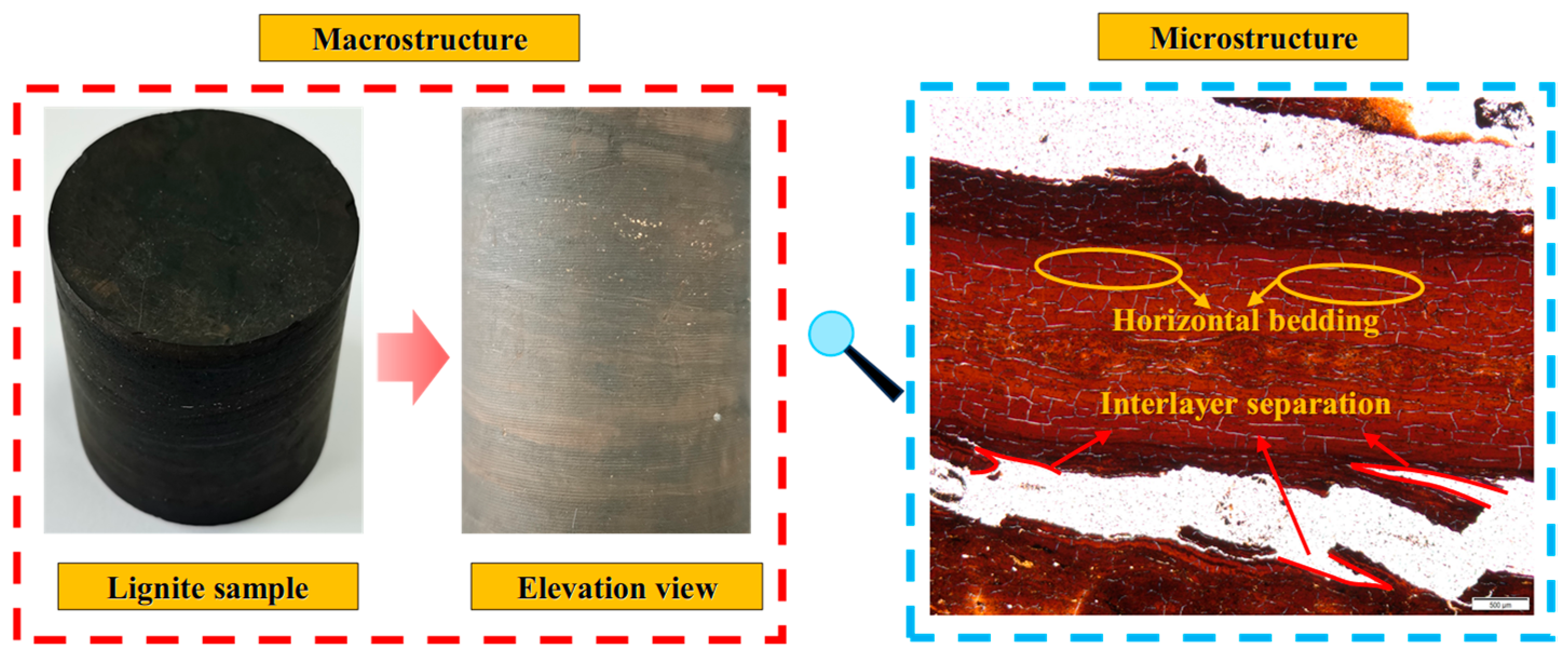
3.3. Meso-Structure Features
4. Mechanical Characteristics of Lignite Under Quasi-Static Loading and Dynamic Impact
4.1. Stress–Strain Curve
4.2. Macroscopic Failure
4.3. Energy Evolution
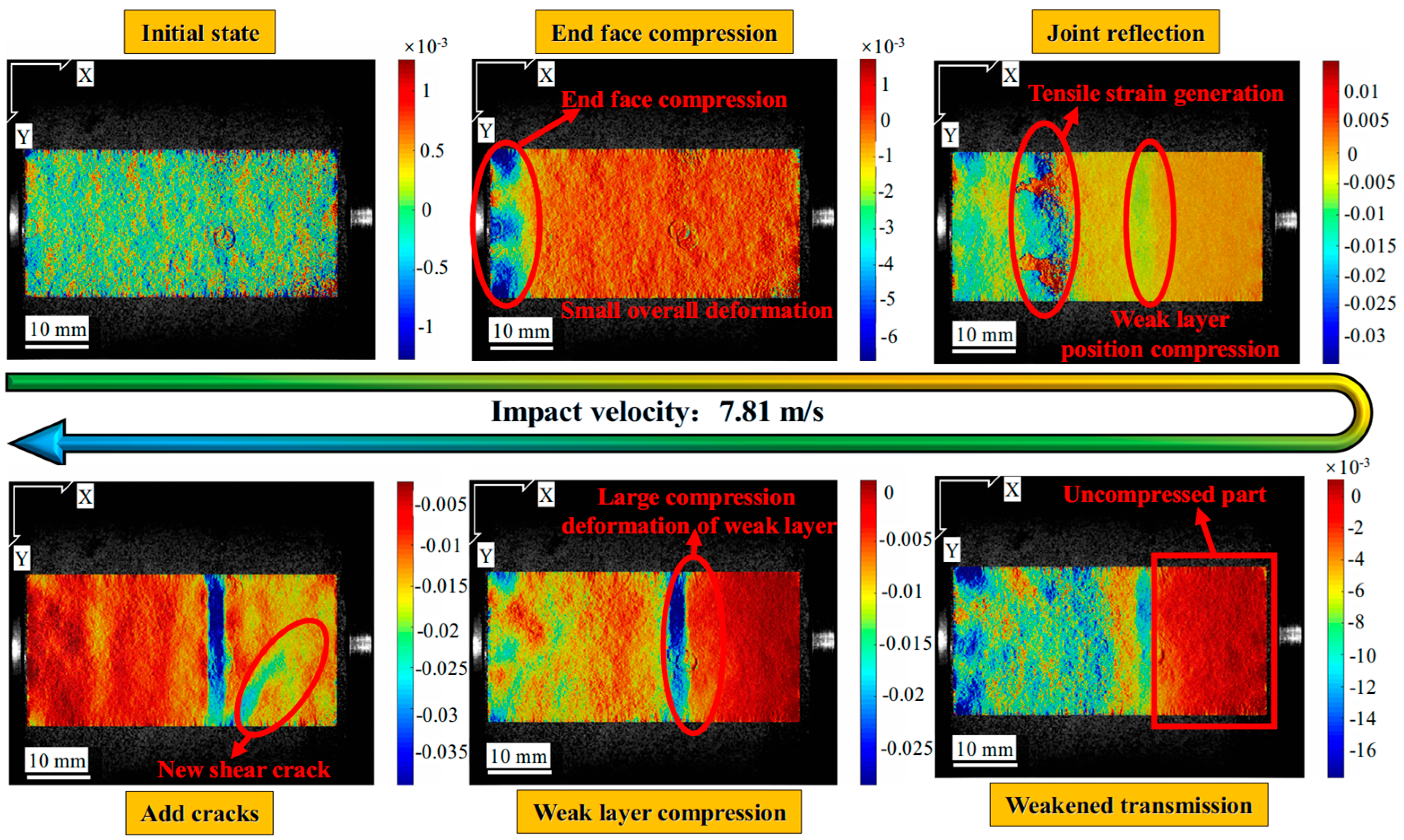
4.4. Strain Field Evolution
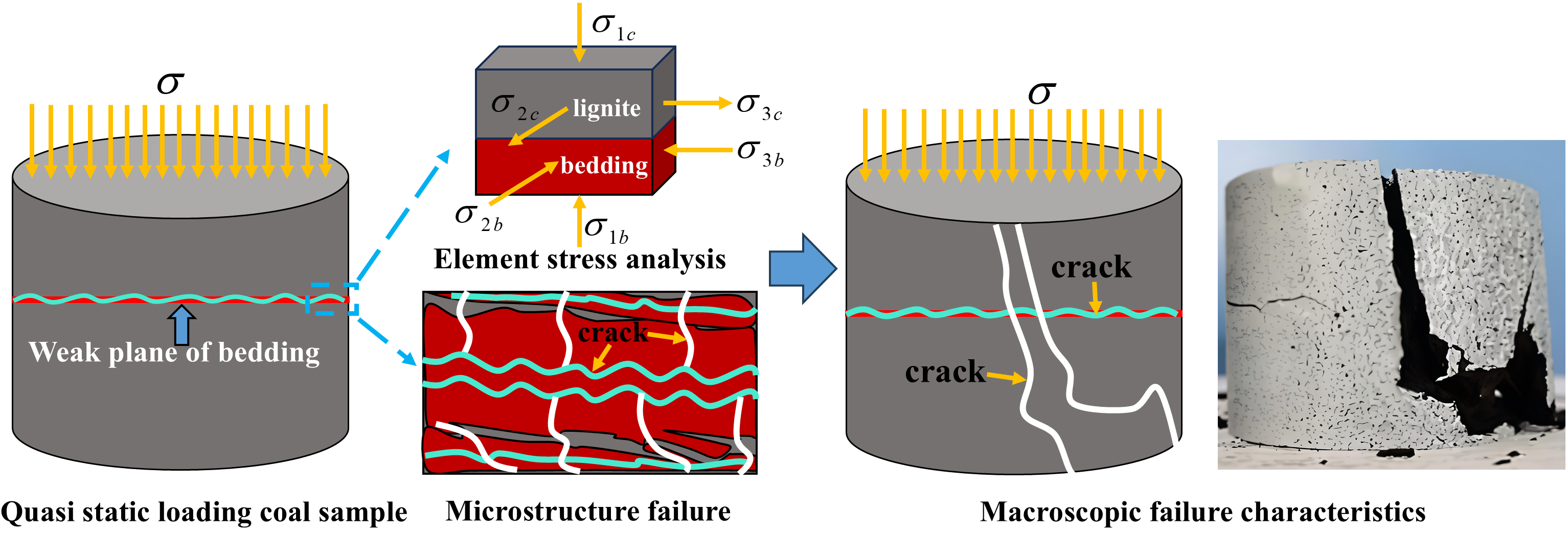
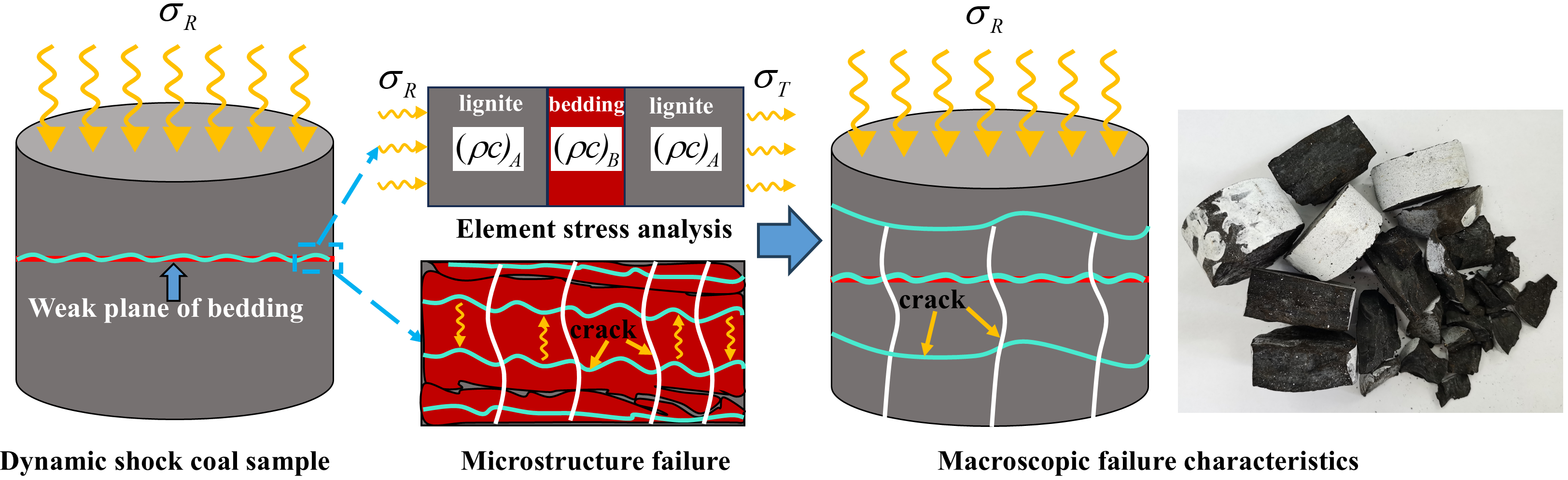
5. Failure Mechanism of Lignite Under Quasi-Static Loading and Dynamic Impact
6. Conclusions
- (1)
- The mineral composition analysis shows that the main minerals in lignite are quartz, orthoclase, muscovite, kaolinite, and pyrite. The lignite possesses a relatively intact microstructure with low porosity and fracture development, though localized small-sized pores are observed. Additionally, distinct horizontal bedding structures are identified within the lignite, with significant differences in strength characteristics among different bedding matrices.
- (2)
- In terms of mechanical behavior, lignite shows significant strain-rate sensitivity under dynamic loading, with strengthening effects escalating at higher rates, and the failure mode transitions from stratified fractures at low velocities to fine-grained fragmentation at high velocities. In contrast, quasi-static responses exhibit lower rate dependency, marked by tensile–shear delamination and slow crack propagation along bedding planes, generating large fragments.
- (3)
- Under the quasi-static loading, the surface of lignite is dominated by tensile strain and shows a significant trend of penetration with the increase in loading speed. Under the dynamic impact, the lignite forms a compressive–tensile composite strain field at the weak surface of the bedding, resulting in interlayer fracture failure of the lignite.
- (4)
- Under the quasi-static loading, the energy evolution analysis reveals that lignite exhibits progressive damage characteristics with the elastic energy dominating the energy allocation. The failure mode transitions from tensile–shear hybrid failure with multiple cracks to single-crack splitting failure. Under the dynamic impact conditions, the proportion of elastic energy progressively diminishes while the dissipative energy becomes predominant.
- (5)
- The horizontal bedding structure of lignite leads to different failure mechanisms under quasi-static loading and dynamic impact. Under the quasi-static loading, the interfacial friction arising from the different Poisson’s ratios between the bedding matrix and lignite constituents governing the progressive splitting failure dominated by bedding plane weakness. The layered failure of lignite under the dynamic impact is fundamentally attributed to the reflection phenomena of stress waves at bedding interfaces, which arise from the wave impedance disparity between the bedding matrix and coal constituents. Therefore, to ensure the stability of the lignite slope in the open-pit mine, the slope bedding should be specifically strengthened to prevent slope instability resulting from bedding plane failure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Z.H.; Chen, Z.H.; Wang, J.M.; Zhang, L.F.; Nian, G.Q. Catastrophe analysis of open-pit slope stability under blasting load. Chin. J. Rock. Soil. Mech. 2020, 41, 84857+868. [Google Scholar] [CrossRef]
- Tan, Y.L.; Ma, Q.; Liu, X.L.; Liu, X.S.; Elsworth, D.; Qian, R.P.; Shang, J.L. Study on the disaster caused by the linkage failure of the residual coal pillar and rock stratum during multiple coal seam mining: Mechanism of progressive and dynamic failure. Int. J. Coal Sci. Technol. 2023, 10, 14. [Google Scholar] [CrossRef]
- Ma, H.F.; Song, Y.Q.; Yang, J.K.; Zheng, J.J.; Shen, F.X.; Shao, Z.X. Experimental investigation on acoustic emission and damage characteristics of dehydrated lignite in uniaxial compression test. Bull. Eng. Geol. Environ. 2023, 82, 26. [Google Scholar] [CrossRef]
- Ma, Q.; Liu, X.L.; Tan, Y.L.; Wang, Y.R.; Wang, R.S.; Wang, E.Z.; Liu, X.S.; Zhao, Z.H.; Ren, D.R.; Xie, W.Q.; et al. Monitoring and evaluation of disaster risk caused by linkage failure and instability of residual coal pillar and rock strata in multi-coal seam mining. Geohazard Mech. 2023, 1, 297–307. [Google Scholar] [CrossRef]
- Liu, X.H.; Hao, Q.J.; Wu, S.Y.; Zhang, R.; Yu, J. Nonlinear mechanical properties of coal rock under quasi-static strain rate. J. China Coal Soc. 2019, 44, 1437–1445. [Google Scholar] [CrossRef]
- Liu, J.; Qiao, L.; Li, Y.; Li, Q.W.; Fan, D.J. Experimental study on the quasi-static loading rate dependency of mixed-mode I/II fractures for marble rocks. Theor. Appl. Fract. Mech. 2022, 121, 103431. [Google Scholar] [CrossRef]
- Yu, Y.Q.; Zhang, W.L.; Fan, L.D.; Gong, J.; Yang, M.; Sun, L. Strain rate effect and energy dissipation characteristics of sandstone in coal measures under impact loading. J. China Coal Soc. 2021, 46, 2281–2293. [Google Scholar] [CrossRef]
- Zhang, S.H.; Liu, L.S.; Zhong, Q.L.; Qiu, J.M.; Zhong, W. Energy distribution characteristics of blast seismic wave on open pit slope. Chin. J. Vib. Shock. 2019, 38, 224–232. [Google Scholar] [CrossRef]
- Zhang, J.C.; Lv, D.W.; Zhang, J.J.; Wang, F.; Yin, D.W.; Yu, H.Y. Dual-scale insights of two-phase flow in inter-cleats based on microfluidics: Interface jumps and energy dissipation. Int. J. Min. Sci. Technol. 2025, 35, 451–465. [Google Scholar] [CrossRef]
- Yang, J.K.; Ma, H.F.; Wang, F.; Shen, Y.Z.; Shi, L.F. Response of macro- and micromechanical characteristics of mudstone under dynamic impact based on FDM-DEM coupling. Geofluids 2025, 2025, 20. [Google Scholar] [CrossRef]
- Ma, Q.; Tan, Y.L.; Liu, X.S.; Gu, Q.H.; Li, X.B. Effect of coal thicknesses on energy evolution characteristics of roof rock-coal-floor rock sandwich composite structure and its damage constitutive model. Compos. Pt. B Eng. 2020, 198, 108086. [Google Scholar] [CrossRef]
- Chen, S.J.; Zhang, J.C.; Yin, D.W.; Li, F.X.; Lu, J.L.; Zhu, P.Y. Visualizing experimental investigation on gas–liquid replacements in a microcleat model using the reconstruction method. Deep. Undergr. Sci. Eng. 2023, 2, 295–303. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhao, J. A review of dynamic experimental techniques and mechanical behaviour of rock materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef]
- Jin, L.L.; Ma, H.F.; Yu, J.; Wang, F.; Yin, D.W.; Qu, X.; Yang, Y.S.; Tao, M.H. Correlation between macroscopic and microscopic mechanical behavior of tuff material under uniaxial compression. J. Mater. Res. Technol. 2025, 35, 764–776. [Google Scholar] [CrossRef]
- Zhang, J.C.; Lv, D.W.; Yin, D.; Zhang, X.Y.; Li, X.L.; Fan, K.K. Gas recovery and flowback in trans-coal-rock fracture: An in-situ wettability microscale visualization insight. Gas Sci. Eng. 2025, 142, 205707. [Google Scholar] [CrossRef]
- Ma, H.F.; Chen, S.J.; Song, Y.Q.; Yin, D.W.; Li, X.S.; Li, X.L. Experimental investigation into the effects of composition and microstructure on the tensile properties and failure characteristics of different gypsum rocks. Sci. Rep. 2021, 11, 14517. [Google Scholar] [CrossRef]
- Li, D.Y.; Han, Z.Y.; Sun, X.L.; Zhou, T.; Li, X.B. Dynamic mechanical properties and fracturing behavior of marble specimens containing single and double flaws in SHPB tests. Rock. Mech. Rock. Eng. 2019, 52, 1623–1643. [Google Scholar] [CrossRef]
- Zhang, M.T.; Wang, W.; Wang, Q.Z.; Zhang, S.Y. Dynamic failure process and strain-damage evolution law of sandstone based on SHPB experiments. Chin. J. Explos. Shock. Waves. 2021, 41, 40–53. [Google Scholar] [CrossRef]
- Han, Z.Y.; Li, D.Y.; Li, X.B. Dynamic mechanical properties and wave propagation of composite rock-mortar specimens based on SHPB tests. Int. J. Min. Sci. Technol. 2022, 32, 793–806. [Google Scholar] [CrossRef]
- Long, X.; Mao, M.H.; Su, Y.T.; Tian, M.K. Machine learning method to predict dynamic compressive response of concrete-like material at high strain rates. Def. Technol. 2023, 23, 100–111. [Google Scholar] [CrossRef]
- Wang, C.Q.; Guo, J.; Cao, L.Y.; Zhang, Y.C.; Li, C.X.; Ma, Z.M. Mechanical behavior and fiber reinforcing mechanism of high-toughness recycled aggregate concrete under high strain-rate impact loads. Constr. Build. Mater. 2024, 437, 136960. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Liang, B.; Wang, D.; Luan, H.J.; Zhang, G.C.; Dong, L.; Chen, L.G. Experimental study on failure mechanical properties and acoustic emission characteristics of soft rock-coal combination under dynamic disturbance. Eng. Fail. Anal. 2024, 158, 108016. [Google Scholar] [CrossRef]
- Gao, M.Z.; Zhang, J.G.; Li, S.W.; Wang, M.; Wang, Y.W.; Cui, P.F. Calculating changes in fractal dimension of surface cracks to quantify how the dynamic loading rate affects rock failure in deep mining. J. Cent. South. Univ. 2020, 27, 3013–3024. [Google Scholar] [CrossRef]
- Zheng, Y.; Shi, H.R.; Liu, X.H.; Zhang, W.J. Failure characteristics and constitutive model of coal rock at different strain rates. Chin. J. Explos. Shock. Waves 2021, 41, 45–57. [Google Scholar] [CrossRef]
- Li, X.B. Rock Dynamics Fundamentals and Applications; Science Press: Beijing, China, 2014; Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=2ae55e67893ab490e347ee2dd3c7b6ff (accessed on 20 July 2025).
- Gong, H.L.; Luo, Y.; Zhou, J.R.; Zhao, C.C.; Li, X.P. Fracture behaviors and damage evolution anisotropy of granite under coupling of multiaxial confinement and dynamic loading. Rock. Mech. Rock. Eng. 2023, 56, 2515–2534. [Google Scholar] [CrossRef]
- Liang, Y.P.; Kong, F.J.; Zou, Q.L.; Zhang, B.C. Effect of strain rate on mechanical response and failure characteristics of horizontal bedded coal under quasi-static loading. Geomech. Geophys. Geo-Energy Geo Resour. 2023, 9, 15. [Google Scholar] [CrossRef]
- Munoz, H.; Taheri, A.; Chanda, E.K. Pre-Peak and post-peak rock strain characteristics during uniaxial compression by 3D digital image correlation. Rock Mech. Rock Eng. 2016, 49, 2541–2554. [Google Scholar] [CrossRef]
- Pan, C.; Zhao, G.M.; Meng, X.R.; Dong, C.L.; Gao, P.F. Numerical investigation of the influence of mineral meso-structure on quasi-static compressive behaviors of granite using a breakable grain-based model. Front. Ecol. Evol. 2023, 11, 1288870. [Google Scholar] [CrossRef]
- Li, X.B.; Gong, Q. Research progress and prospect of deep mining rock mechanics based on coupled static-dynamic loading testing. J. China Coal Soc. 2021, 46, 846–866. [Google Scholar] [CrossRef]
- Li, X.B.; Gong, F.Q.; Wang, S.F.; Li, D.Y.; Tao, M.; Zhou, J.; Huang, L.Q.; Ma, C.D.; Du, K. Coupled static-dynamic loading mechanical mechanism and dynamic criterion of rock burst in deep hard rock mines. Chin. J. Rock. Mech. Eng. 2019, 38, 708–723. [Google Scholar] [CrossRef]
- Li, X.B.; Gong, F.Q.; Tao, M.; Dong, L.J.; Du, K.; Ma, C.D.; Zhou, Z.L.; Yin, T.B. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review. J. Rock Mech. Geotech. Eng. 2017, 9, 767–782. [Google Scholar] [CrossRef]
- Du, C.C.; Wen, S.; Kong, Q.M. Tests for dynamic mechanical properties of composite rock sample sunder 1-D dynamic-static combined loading. Chin. J. Vib. Shock. 2021, 40, 168–178+206. [Google Scholar] [CrossRef]
- Jing, S.L.; Wen, Z.J.; Jiang, Y.J.; Wen, J.H.; Du, W.J. Mechanical behaviors and failure characteristics of coal-rock combination under quasi-static and dynamic disturbance loading: A case based on a new equipment. Geomech. Geophys. Geo Energy Geo Resour. 2024, 10, 16. [Google Scholar] [CrossRef]
- Liu, S.H.; Qin, Z.H.; Lou, J.F. Experimental study of dynamic failure characteristics of coal-rock compound under one-dimensional static and dynamic loads. Chin. J. Rock. Mech. Eng. 2014, 33, 2064–2075. [Google Scholar] [CrossRef]
- Dai, B.; Zhao, G.F.; Zhang, L.; Liu, Y.; Zhang, Z.J.; Luo, X.Y.; Chen, Y. Energy dissipation of rock with different parallel flaw inclinations under dynamic and static combined loading. Mathematics 2022, 10, 4082. [Google Scholar] [CrossRef]
- Wang, W.; Liang, X.Y.; Zhang, M.T.; Jia, Z.Y.; Zhang, S.Y.; Wang, Q.Z. Experimental study on failure mechanism and crack density of sandstone under combined dynamic and static loading. Chin. J. Rock. Soil. Mech. 2021, 42, 2647–2658. [Google Scholar] [CrossRef]
- Zhou, Y.X.; Xia, K.; Li, X.B.; Li, H.B.; Ma, G.W.; Zhao, J.; Zhou, Z.L.; Dai, F. Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials. Int. J. Rock. Mech. Min. Sci. 2012, 49, 105–112. [Google Scholar] [CrossRef]
- Zhao, X.J.; Lu, F.Y.; Wang, W.; Li, Y.H.; Lin, Y.L. The Experimental and theoretical study on the incident pulse shaping technique. Chin. J. High. Press. Phys. 2004, 18, 231–236. Available online: https://www.gywlxb.cn/cn/article/pdf/preview/10.11858/gywlxb.2004.03.007.pdf (accessed on 30 July 2025).
- Zhang, J.S.; Guo, S.F.; Zhang, X.S.; Wang, L.; Cao, Y.X.; Liu, G.F. Dynamic damage constitutive model of plastic hardening-softening process of coal under impacting load. J. China Coal Soc. 2021, 46, 759–769. [Google Scholar] [CrossRef]
- Yang, L.; Wang, B.W.; Liu, C.Y.; Gan, S.; Yu, H. Energy dissipation characteristics and constitutive model of structural backfill under uniaxial compression. Chin. J. Nonferrous Met. 2024, 34, 3532–3546. [Google Scholar] [CrossRef]
- Liang, C.Y.; Wu, S.R.; Li, X.; Xin, P. Effects of strain rate on fracture characteristics and mesoscopic failure mechanisms of granite. Int. J. Rock. Mech. Min. Sci. 2015, 76, 146–154. [Google Scholar] [CrossRef]
- Chen, S.J.; Yin, D.W.; Zhang, B.L.; Ma, H.F.; Liu, X.Q. Mechanical characteristics and progressive failure mechanism of roof-coal pillar structure. Chin. J. Rock. Mech. Eng. 2017, 36, 1588–1598. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Wang, W.M.; Dai, C.Q.; Yan, J.X. Failure characteristics of three-body model composed of rock and coal with different strength and stiffness. Trans. Nonferrous Met. Soc. China 2014, 24, 1538–1546. [Google Scholar] [CrossRef]
- Yang, R.S.; Li, W.Y.; Fang, S.Z.; Zhu, Y.; Li, Y.L. Experimental study on impact dynamic characteristics of layered composite rocks. Chin. J. Rock. Mech. Eng. 2019, 38, 1747–1757. [Google Scholar] [CrossRef]
- Zhao, A.P.; Feng, C.; Guo, R.K.; Li, S.H.; Jia, J.J. Effect of joints on blasting and stress wave propagation. Chin. J. Rock. Mech. Eng. 2018, 37, 2027–2036. [Google Scholar] [CrossRef]

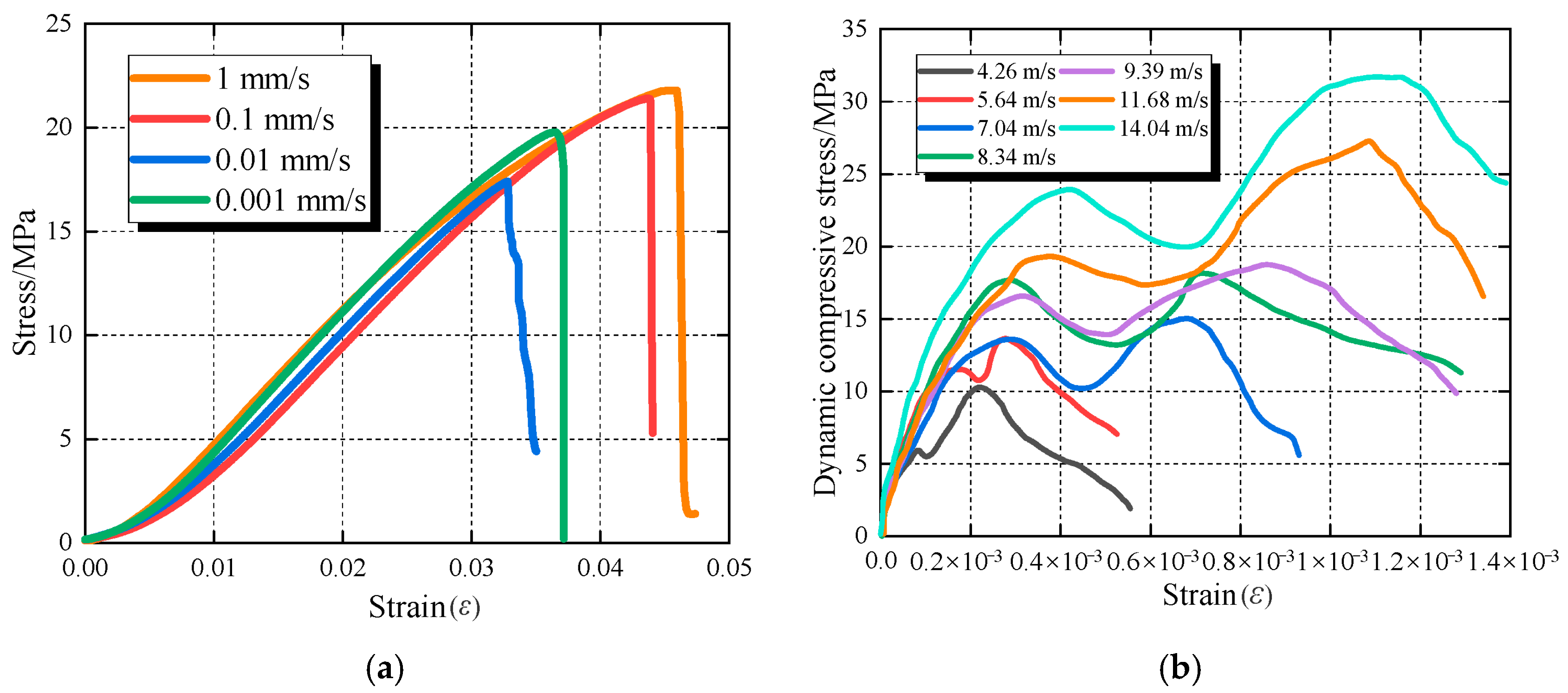
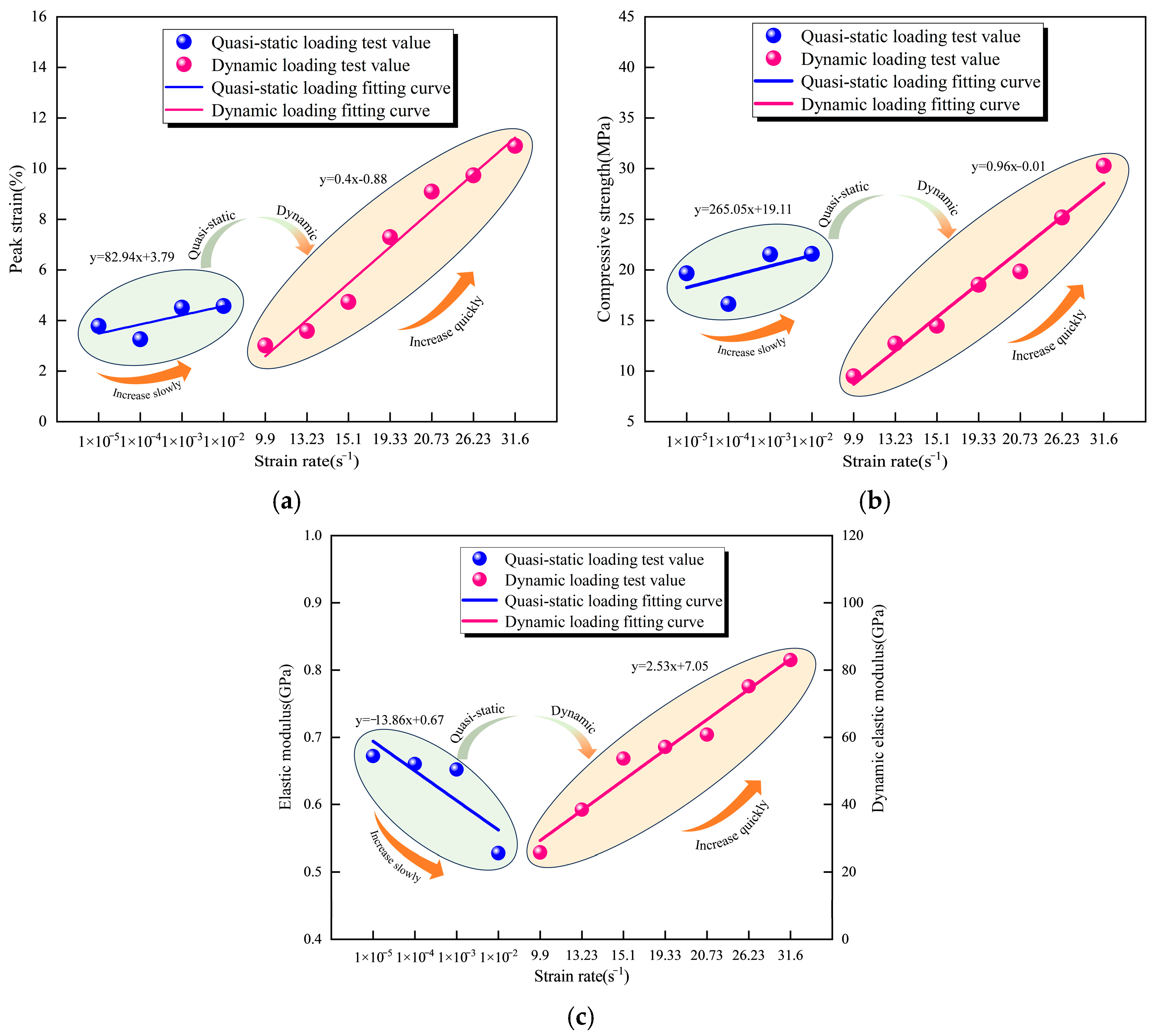

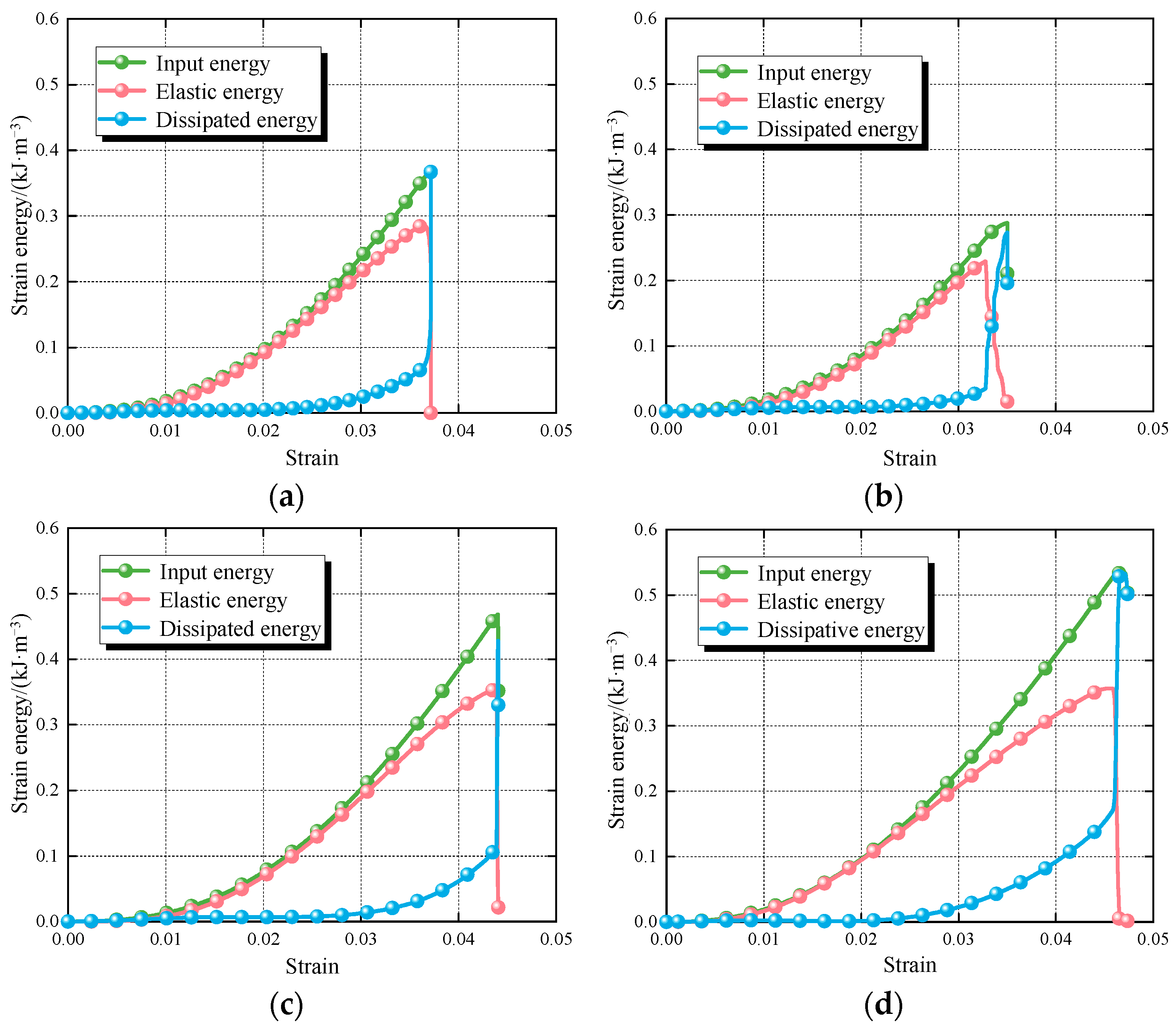


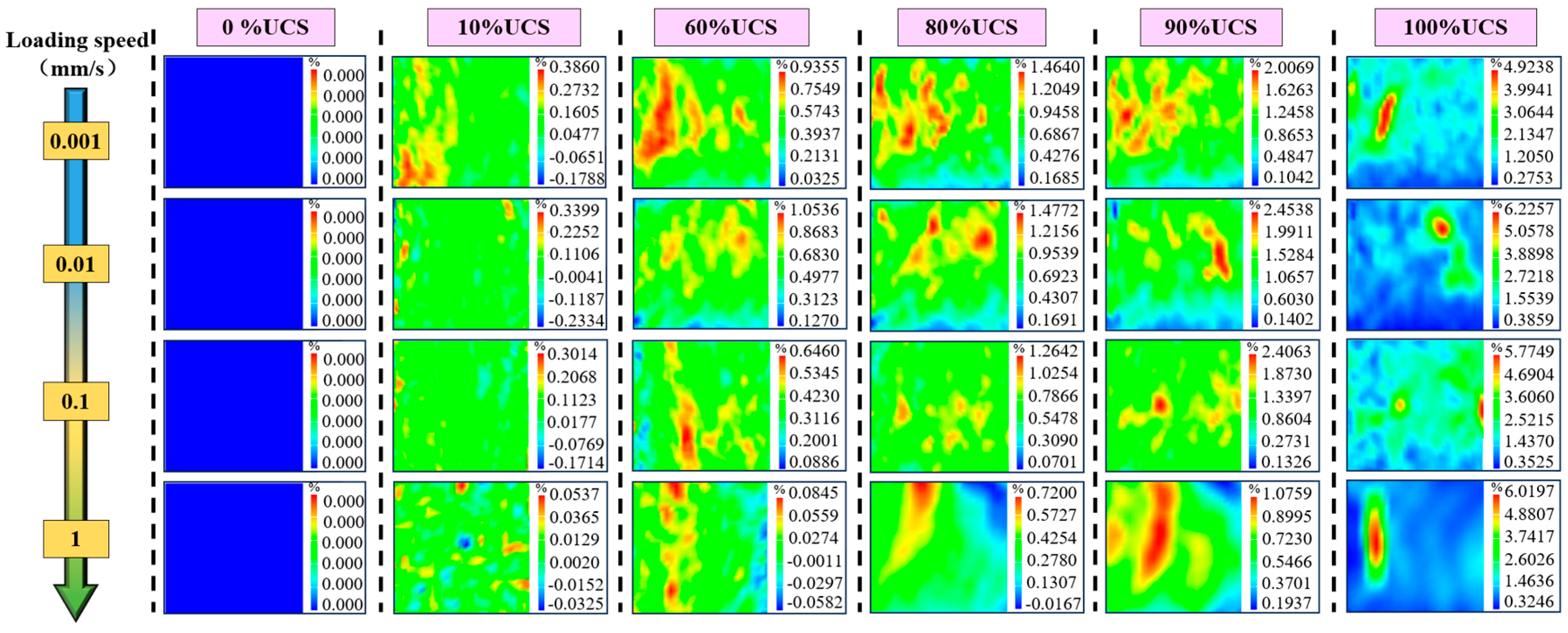
| Number | Loading Rate/Impact Velocity /(m/s) | Strain Rate /s−1 | Uniaxial/Dynamic Compressive Strength /MPa | Elastic Modulus /GPa | Peak Strain /% |
|---|---|---|---|---|---|
| C-1 | 1 × 10−6 | 1 × 10−5 | 18.49~20.25 | 0.652~0.687 | 3.65~3.93 |
| 19.65 | 0.672 | 3.78 | |||
| C-2 | 1 × 10−5 | 1 × 10−4 | 15.66~17.20 | 0.613~0.687 | 3.01~3.51 |
| 16.63 | 0.660 | 3.26 | |||
| C-3 | 1 × 10−4 | 1 × 10−3 | 21.40~21.67 | 0.641~0.665 | 4.10~4.71 |
| 21.54 | 0.652 | 4.50 | |||
| C-4 | 1 × 10−3 | 1 × 10−2 | 20.66~22.48 | 0.523~0.532 | 4.38~4.67 |
| 21.57 | 0.528 | 4.57 | |||
| D-1 | 4.33 | 9.90 | 9.47 | 25.78 | 3.01 × 10−2 |
| D-2 | 5.73 | 13.23 | 12.70 | 38.47 | 3.58 × 10−2 |
| D-3 | 7.03 | 15.10 | 14.47 | 53.67 | 4.73 × 10−2 |
| D-4 | 8.32 | 19.33 | 18.53 | 57.11 | 7.29 × 10−2 |
| D-5 | 9.38 | 20.73 | 19.83 | 60.80 | 9.09 × 10−2 |
| D-6 | 11.69 | 26.23 | 25.17 | 75.13 | 9.73 × 10−2 |
| D-7 | 13.95 | 31.60 | 30.27 | 82.94 | 10.90 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Ma, H.; Jin, L.; Wang, F.; Yin, D.; Qu, X.; Han, C.; Zhang, J.; Feng, F. Research on the Mechanical Properties and Failure Mechanism of Lignite Affected by the Strain Rate Under Static and Dynamic Loading Conditions. Processes 2025, 13, 3054. https://doi.org/10.3390/pr13103054
Yu J, Ma H, Jin L, Wang F, Yin D, Qu X, Han C, Zhang J, Feng F. Research on the Mechanical Properties and Failure Mechanism of Lignite Affected by the Strain Rate Under Static and Dynamic Loading Conditions. Processes. 2025; 13(10):3054. https://doi.org/10.3390/pr13103054
Chicago/Turabian StyleYu, Jiang, Hongfa Ma, Linlin Jin, Feng Wang, Dawei Yin, Xiao Qu, Chenghao Han, Jicheng Zhang, and Fan Feng. 2025. "Research on the Mechanical Properties and Failure Mechanism of Lignite Affected by the Strain Rate Under Static and Dynamic Loading Conditions" Processes 13, no. 10: 3054. https://doi.org/10.3390/pr13103054
APA StyleYu, J., Ma, H., Jin, L., Wang, F., Yin, D., Qu, X., Han, C., Zhang, J., & Feng, F. (2025). Research on the Mechanical Properties and Failure Mechanism of Lignite Affected by the Strain Rate Under Static and Dynamic Loading Conditions. Processes, 13(10), 3054. https://doi.org/10.3390/pr13103054







