A Star-Connected STATCOM Soft Open Point for Power Flow Control and Voltage Violation Mitigation
Abstract
1. Introduction
- (1)
- The SCS-SOP employs a low-voltage (LV) BTB-VSC to achieve partial-power regulation between MV feeders. By integrating STATCOM and BTB-VSC into a single device, the SCS-SOP significantly reduces the cost and volume compared to these full-power SOP topologies.
- (2)
- The operating principle of the SCS-SOP is described in detail. In this topology, the STATCOM regulates reactive power within feeders and the BTB-VSC controls active power between feeders, which eliminates the need for complex power decoupling control and enables straightforward control strategies.
- (3)
- The SCS-SOP can simultaneously regulate the active power between feeders and the reactive power within feeders, which is beneficial for mitigating voltage violations and enhancing power quality.
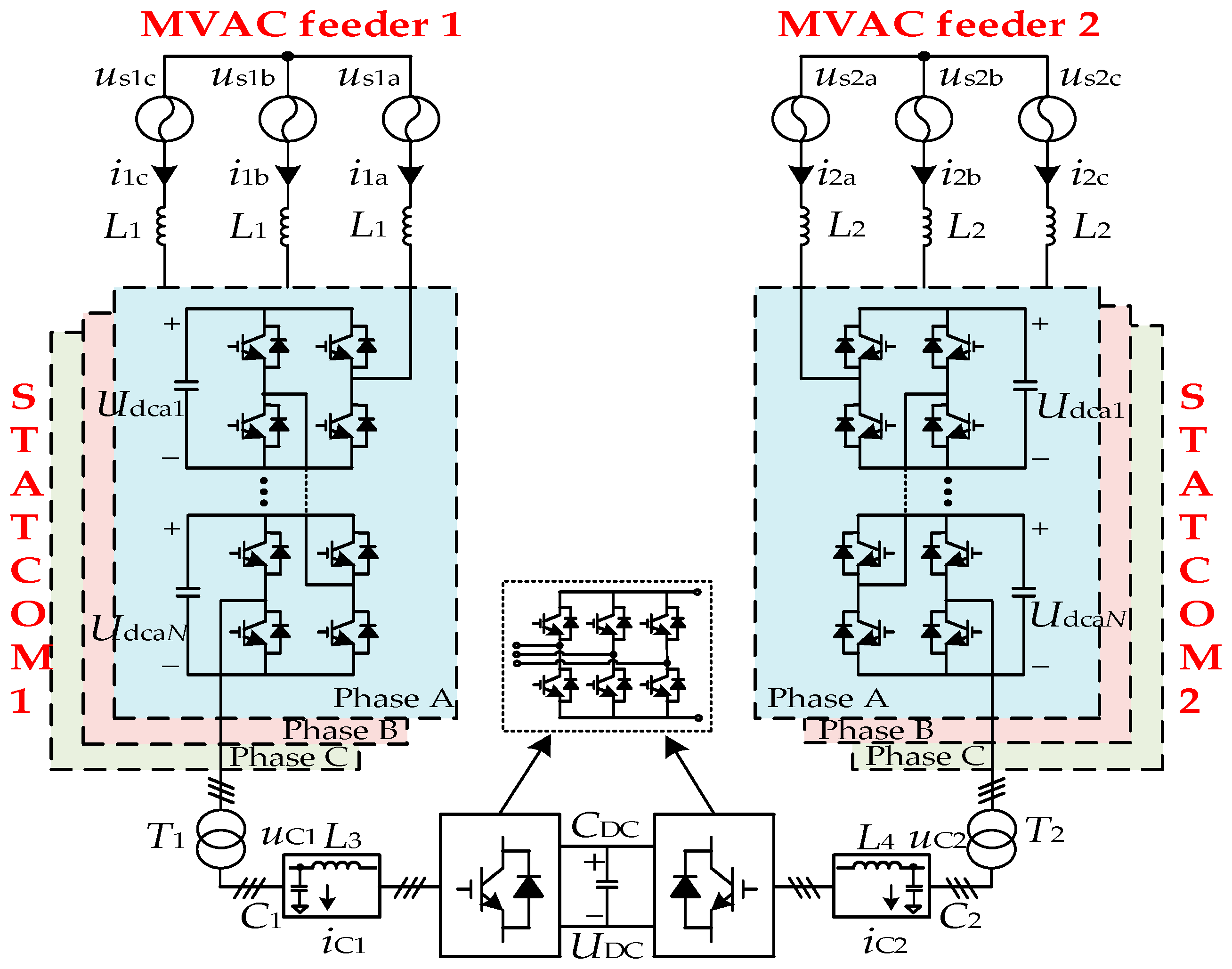
2. Topology of SCS-SOP
2.1. Topology Derivation of SCS-SOP
2.2. Topology Configuration of SCS-SOP
3. Operating Principle of SCS-SOP
3.1. Power Flow Regulation of SCS-SOP
3.2. Power Regulation Range of SCS-SOP
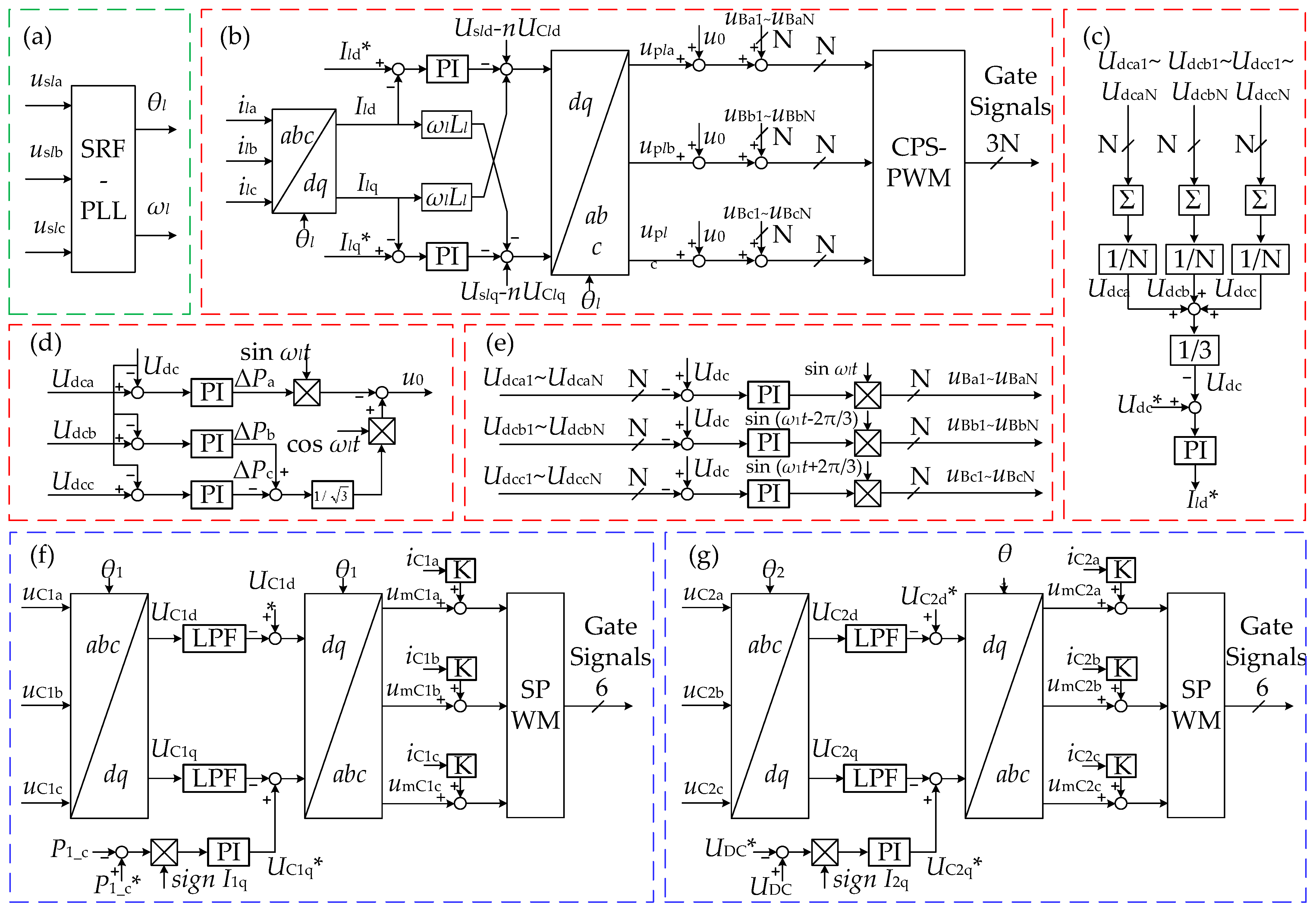
4. Control Strategies of SCS-SOP
4.1. Current Control Strategy of STATCOM
4.2. DC Voltage Control Strategy of STATCOM
4.3. Control Strategy of BTB-VSC
5. Comparison of Topologies
5.1. Comparison of Number of Active Components
5.2. Comparison of Capacitance Requirements
5.3. Comparison of Semiconductor Die Size
5.4. Comparison of Applicable Scenarios
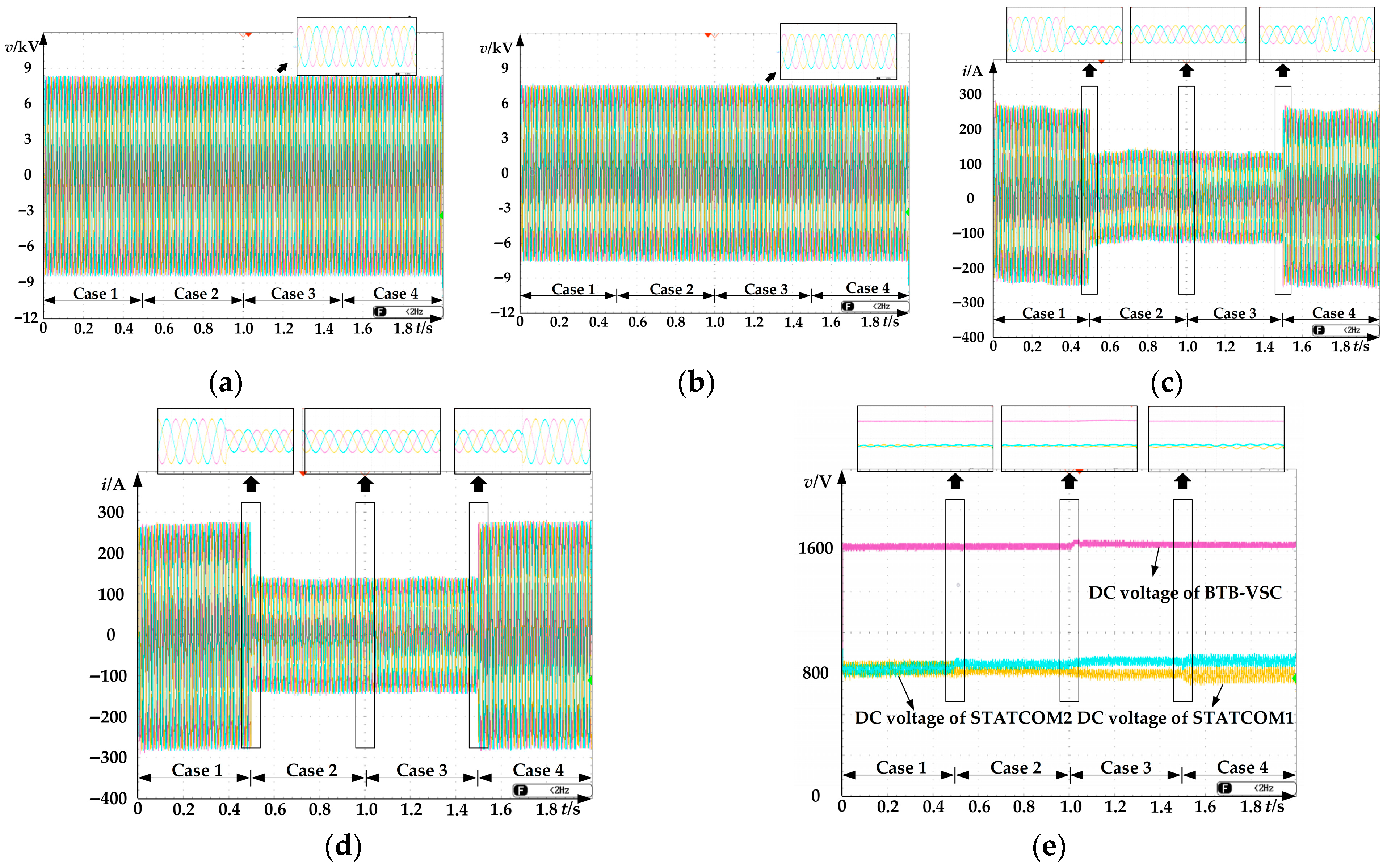
6. Simulation and Experimental Verification
6.1. Simulation Verification of SCS-SOP
- (1)
- Case 1 (0–0.5 s): The reactive power Q1 of STATCOM1 and the active power P1_c of BTB-VSC are set to 1 p.u. The reactive power Q2 of STATCOM2 and the active power P2_c of BTB-VSC are set to −1 p.u.
- (2)
- Case 2 (0.5–1 s): Q1 and P1_c are reduced to 0.5 p.u. Meanwhile, Q2 and P2_c are increased to −0.5 p.u.
- (3)
- Case 3 (1–1.5 s): Q1 remains at 0.5 p.u. P1_c is reversed to −0.5 p.u. Q2 remains at −0.5 p.u. And P2_c is reversed to 0.5 p.u.
- (4)
- Case 4 (1.5–2 s): Q1 is increased to 1 p.u. P1_c and Q2 are decreased to −1 p.u. And P2_c is increased to 1 p.u.
6.2. Experimental Verification of SCS-SOP
7. Conclusions
- (1)
- By incorporating the BTB-VSC, the STATCOM is innovatively utilized as SOP. Integrating the STATCOM and BTB-VSC into a single device significantly reduces the cost and volume of the components.
- (2)
- The STATCOM regulates reactive power within feeders, while the BTB-VSC regulates active power between feeders. As a result, the SCS-SOP eliminates the need for complex power decoupling control and features a relatively simple control strategy.
- (3)
- The SCS-SOP is capable of coordinating active power flow among feeders while managing reactive power inside feeders, thereby helping to mitigate voltage violations and improve power quality.
- (4)
- Compared to the full-power MMC BTB-VSC, the proposed partial-power SCS-SOP offers advantages in terms of the number of active components, capacitance requirements, and semiconductor die size.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gutiérrez, J.S.E.; Téllez, A.A. Optimal Placement of a Unified Power Quality Conditioner (UPQC) in Distribution Systems Using Exhaustive Search to Improve Voltage Profiles and Harmonic Distortion. Energies 2025, 18, 4499. [Google Scholar] [CrossRef]
- Lefeng, C.; Pan, P.; Pengrong, H.; Mengya, Z.; Xiaobo, M.; Wentian, L. Leveraging evolutionary game theory for cleaner production: Strategic insights for sustainable energy markets, electric vehicles, and carbon trading. J. Clean. Prod. 2025, 512, 145682. [Google Scholar] [CrossRef]
- Gan, D.; Ling, H.; Mao, Z.; Gu, R.; Zhou, K.; Lin, K. A Network Partition-Based Optimal Reactive Power Allocation and Sizing Method in Active Distribution Network. Processes 2025, 13, 2524. [Google Scholar] [CrossRef]
- Tang, C.-Y.; Lin, J.-T. Bidirectional Power Flow Control of a Multi Input Converter for Energy Storage System. Energies 2019, 12, 3756. [Google Scholar] [CrossRef]
- Chang, W.-N.; Chang, C.-M.; Yen, S.-K. Improvements in Bidirectional Power-Flow Balancing and Electric Power Quality of a Microgrid with Unbalanced Distributed Generators and Loads by Using Shunt Compensators. Energies 2018, 11, 3305. [Google Scholar] [CrossRef]
- Janiga, K.; Miller, P.; Małkowski, R.; Izdebski, M. An ANN-Based Method for On-Load Tap Changer Control in LV Networks with a Large Share of Photovoltaics—Comparative Analysis. Energies 2024, 17, 5749. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, W. A Shared Resonance Damping Scheme for Multiple Switchable Capacitors. IEEE Trans. Power Del. 2018, 33, 1973–1980. [Google Scholar] [CrossRef]
- He, L.; Tan, Z.; Li, Y.; Cao, Y.; Chen, C. A Coordinated Consensus Control Strategy for Distributed Battery Energy Storages Considering Different Frequency Control Demands. IEEE Trans. Sustain. Energy 2024, 15, 304–315. [Google Scholar] [CrossRef]
- Alanazi, M. Optimal Integration of Distributed Generators and Soft Open Points in Radial Distribution Networks: A Hybrid WCA-PSO Approach. Processes 2025, 13, 1775. [Google Scholar] [CrossRef]
- Lai, Z.; Yi, H.; Wang, Z.; Zhuo, F.; Zhuang, H. Transient Analysis and Overcurrent Limited Strategy for Supply Restoration-Oriented Hybrid Soft Open Point. IEEE Trans. Power Electron. 2024, 39, 2660–2676. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, L. A Robust Strategy for Leveraging Soft Open Points to Mitigate Load Altering Attacks. IEEE Trans. Smart Grid 2022, 13, 1555–1569. [Google Scholar] [CrossRef]
- Huo, Y.; Li, P.; Ji, H.; Yan, J.; Song, G.; Wu, J.; Wang, C. Data-Driven Adaptive Operation of Soft Open Points in Active Distribution Networks. IEEE Trans. Ind. Inf. 2021, 17, 8230–8242. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.; Wang, C.; Zhao, J.; Song, G.; Ding, F.; Wu, J. Optimal Operation of Soft Open Points in Active Distribution Networks Under Three-Phase Unbalanced Conditions. IEEE Trans. Smart Grid 2019, 10, 380–391. [Google Scholar] [CrossRef]
- Ding, T.; Wang, Z.; Jia, W.; Chen, B.; Chen, C.; Shahidehpour, M. Multiperiod Distribution System Restoration With Routing Repair Crews, Mobile Electric Vehicles, and Soft-Open-Point Networked Microgrids. IEEE Trans. Smart Grid 2020, 11, 4795–4808. [Google Scholar] [CrossRef]
- Yang, X.; Xu, C.; Zhang, Y.; Yao, W.; Wen, J.; Cheng, S. Real-Time Coordinated Scheduling for ADNs With Soft Open Points and Charging Stations. IEEE Trans. Power Syst. 2021, 36, 5486–5499. [Google Scholar] [CrossRef]
- Song, S.; Kim, J.; Lee, J.; Jang, G. AC Transmission Emulation Control Strategies for the BTB VSC HVDC System in the Metropolitan Area of Seoul. Energies 2017, 10, 1143. [Google Scholar] [CrossRef]
- Wang, X.; Chen, W.; Zhao, H.; Lan, J.; Chen, Y.; Hao, Z.; Jiang, W.; Mou, X.; Gong, X. A Seamless Integrated Control Method for SNOP Based on BTB-VSC. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 3577–3591. [Google Scholar] [CrossRef]
- Portillo, R.; Prats, M.; Leon, J.; Sanchez, J.; Carrasco, J.; Galvan, E.; Franquelo, L. Modeling Strategy for Back-to-Back Three-Level Converters Applied to High-Power Wind Turbines. IEEE Trans. Ind. Electron. 2006, 53, 1483–1491. [Google Scholar] [CrossRef]
- Akagi, H.; Kitada, R. Control and Design of a Modular Multilevel Cascade BTB System Using Bidirectional Isolated DC/DC Converters. IEEE Trans. Power Electron. 2011, 26, 2457–2464. [Google Scholar] [CrossRef]
- Li, M.; Yang, H.; Zhao, R.; Zheng, T.; Si, C.; Lu, Y.; Yang, Y. Comparative Study on the Operating Area of M3C and B2B MMC for Soft Open Point Application. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019-ECCE Asia), Busan, Republic of Korea, 27–31 May 2019; pp. 1205–1212. [Google Scholar]
- Ma, D.; Chen, W.; Shu, L.; Qu, X.; Gao, S.; Hou, K. A Multiport AC–AC–DC Converter for Soft Normally Open Point. IEEE Trans. Circuit and Syst. II Exp. Briefs 2022, 69, 2146–2150. [Google Scholar] [CrossRef]
- Ma, D.; Chen, W.; Shu, L.; Qu, X.; Zhan, X.; Liu, Z. A Multiport Power Electronic Transformer Based on Modular Multilevel Converter and Mixed-Frequency Modulation. IEEE Trans. Circuit Syst. II Exp. Briefs 2020, 67, 1284–1288. [Google Scholar] [CrossRef]
- Briz, F.; Lopez, M.; Rodriguez, A.; Zapico, A.; Arias, M.; Diaz-Reigosa, D. MMC based SST. In Proceedings of the 2015 IEEE 13th International Conference on Industrial Informatics (INDIN), Cambridge, UK, 22–24 July 2015; pp. 1591–1598. [Google Scholar]
- Yan, Y.; Sun, Y.; Guo, W.; Ji, Z.; Li, D.; Zhao, J. A Novel Modular Multilevel Converter Based Power Electronic Transformer With Integrated Switching Pairs. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–8. [Google Scholar]
- Zhang, J.; Feng, X.; Zhou, J.; Zang, J.; Wang, J.; Shi, G.; Cai, X.; Li, Y. Series–Shunt Multiport Soft Normally Open Points. IEEE Trans. Ind. Electron. 2023, 70, 10811–10821. [Google Scholar] [CrossRef]
- Lu, D.; Zhu, J.; Wang, J.; Yao, J.; Wang, S.; Hu, H. A Simple Zero-Sequence-Voltage-Based Cluster Voltage Balancing Control and the Negative Sequence Current Compensation Region Identification for Star-Connected Cascaded H-Bridge STATCOM. IEEE Trans. Power Electron. 2018, 33, 8376–8387. [Google Scholar]
- Lu, D.; Wang, S.; Yao, J.; Yang, T.; Hu, H. Cluster Voltage Regulation Strategy to Eliminate Negative-Sequence Currents Under Unbalanced Grid for Star-Connected Cascaded H-Bridge STATCOM. IEEE Trans. Power Electron. 2019, 34, 2193–2205. [Google Scholar] [CrossRef]
- Marzoughi, A.; Burgos, R.; Boroyevich, D.; Xue, Y. Design and Comparison of Cascaded H-Bridge, Modular Multilevel Converter, and 5-L Active Neutral Point Clamped Topologies for Motor Drive Applications. IEEE Trans. Ind. Appl. 2018, 54, 1404–1413. [Google Scholar] [CrossRef]



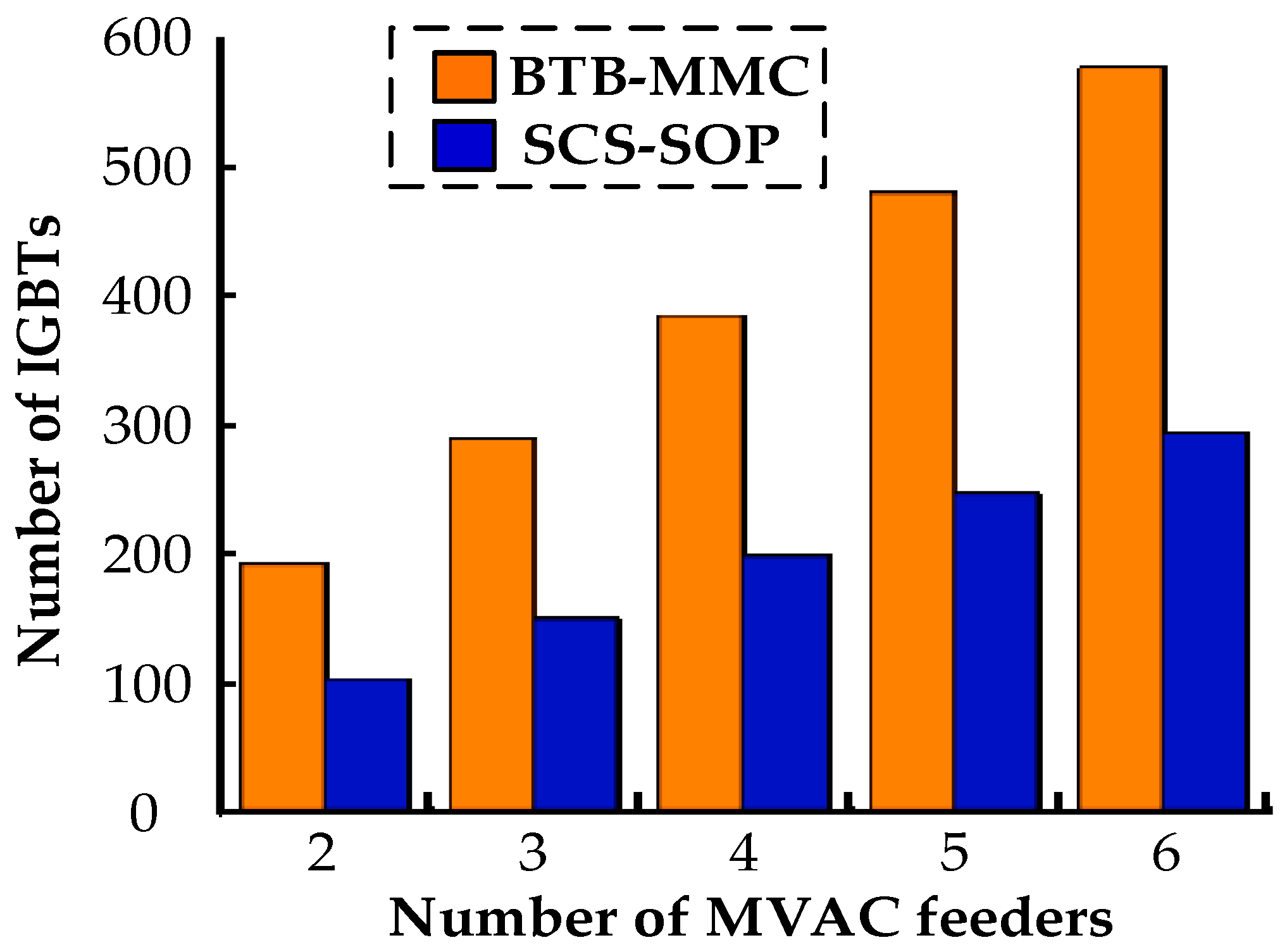

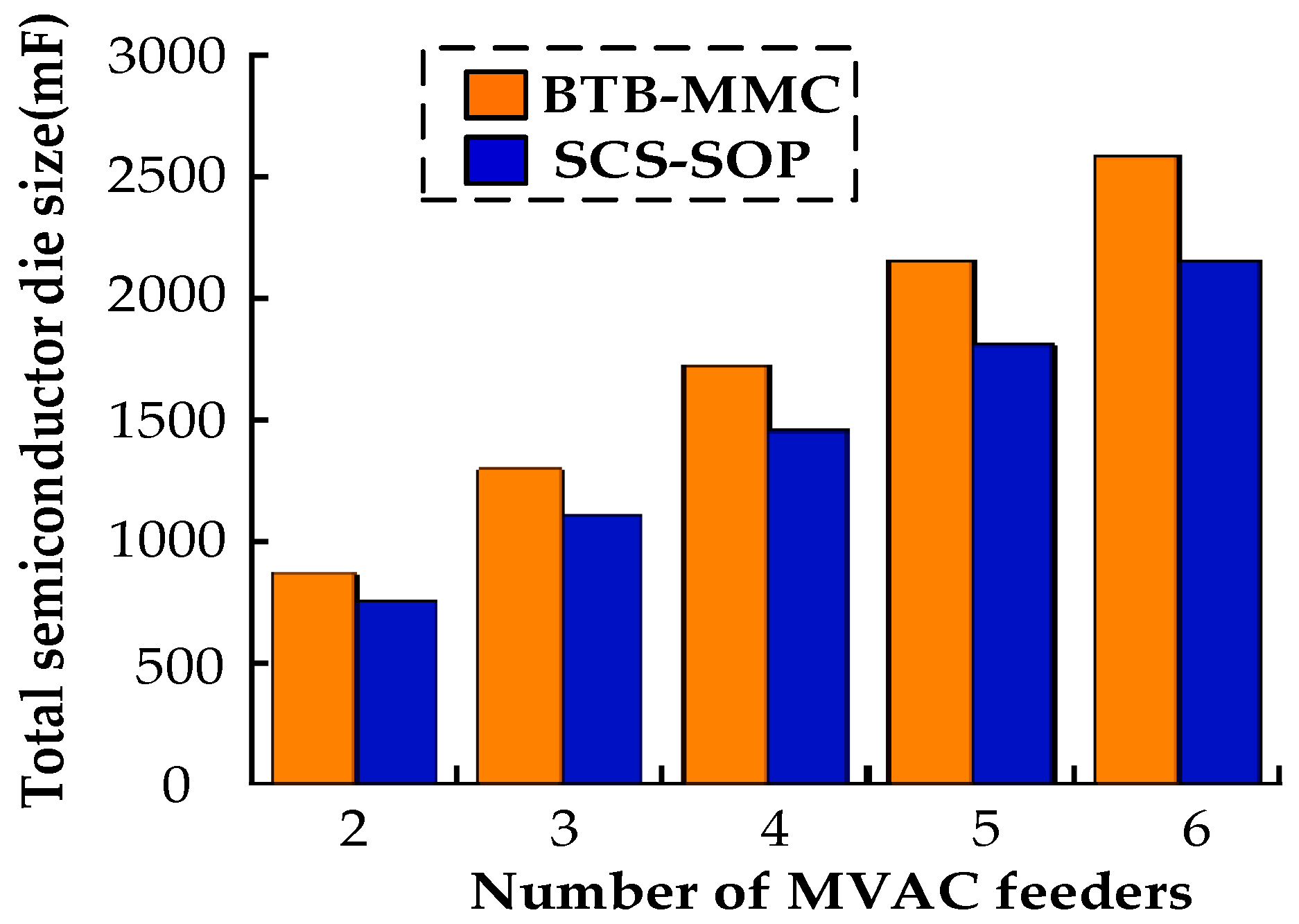


| Scheme | Number of HBSMs | Number of FBSMs | Number of IGBTs | Number of Capacitors |
|---|---|---|---|---|
| BTB-MMC [17] | 48l | 0 | 96l | 48l |
| SCS-SOP | 3 | 12l | 51l | 12l + 1 |
| Categories | BTB-MMC | SCS-SOP |
|---|---|---|
| Number of components | More | Fewer |
| Capacitance requirements | More | Less |
| Semiconductor die size | More | Less |
| Power transmission capability | Stronger | Weaker |
| Control complexity | Relatively complex | Relatively simple |
| Scalability | Feasible | Feasible |
| Volume and Cost | Higher | Lower |
| Applicable Scenarios | More flexible | Relatively limited |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Nominal voltage of feeder 1/2 | 10/9 kV | Rated capacity of transformer T1/T2 | 500 kW |
| Frequency of feeder 1/2 | 50 Hz | Ratio of transformer | 1:1 |
| Initial phase of feeder 1/2 | 3°/0° | Filter capacitor C1/C2 | 10 µF |
| Connect reactor L1/L2 | 20 mH | Filter inductor L3/L4 | 1 mH |
| Rated capacity of STATCOM Q1/Q2 | 3 Mvar | DC voltage of the BTB-VSC | 1600 V |
| No. of FBSMs in the CHB per phase (N) | 12 | DC capacitor of the BTB-VSC | 9.5 mF |
| DC voltage of the FBSMs | 800 V | Switch frequency of the BTB-VSC | 12.8 kHz |
| DC capacitor of the FBSMs | 5.6 mF | Rated capacity of BTB-VSC P1_c/P2_c | 300 kW |
| Switch frequency of the FBSMs | 500 Hz | Active damping factor K | −1 |
| Case | Q1/p.u. | P1_c/p.u. | Q2/p.u. | P2_c/p.u. |
|---|---|---|---|---|
| 1 | 1 | 1 | −1 | −1 |
| 2 | 0.5 | 0.5 | −0.5 | −0.5 |
| 3 | 0.5 | −0.5 | −0.5 | 0.5 |
| 4 | 1 | −1 | −1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, T.; Liu, Y.; Huang, F.; Xie, G. A Star-Connected STATCOM Soft Open Point for Power Flow Control and Voltage Violation Mitigation. Processes 2025, 13, 3030. https://doi.org/10.3390/pr13103030
Luo T, Liu Y, Huang F, Xie G. A Star-Connected STATCOM Soft Open Point for Power Flow Control and Voltage Violation Mitigation. Processes. 2025; 13(10):3030. https://doi.org/10.3390/pr13103030
Chicago/Turabian StyleLuo, Tianlu, Yanyang Liu, Feipeng Huang, and Guobo Xie. 2025. "A Star-Connected STATCOM Soft Open Point for Power Flow Control and Voltage Violation Mitigation" Processes 13, no. 10: 3030. https://doi.org/10.3390/pr13103030
APA StyleLuo, T., Liu, Y., Huang, F., & Xie, G. (2025). A Star-Connected STATCOM Soft Open Point for Power Flow Control and Voltage Violation Mitigation. Processes, 13(10), 3030. https://doi.org/10.3390/pr13103030






