Numerical Simulation of Salmon Freezing Using Pulsating Airflow in a Model Tunnel
Abstract
Highlights
- CFD conjugate model for improved salmon freezing in a tunnel with a pulsed airflow
- Pulsating airflow freezing allowed important energy savings compared to steady flow
- Higher Nusselt number in food and faster freezing achieved by pulsed inlet airflow
- Fast numerical predictions and third-order accuracy calculation of transient terms
- High-quality freezing of solid food in mixed convective heat refrigeration tunnel
Abstract
1. Introduction
2. Material and Methods
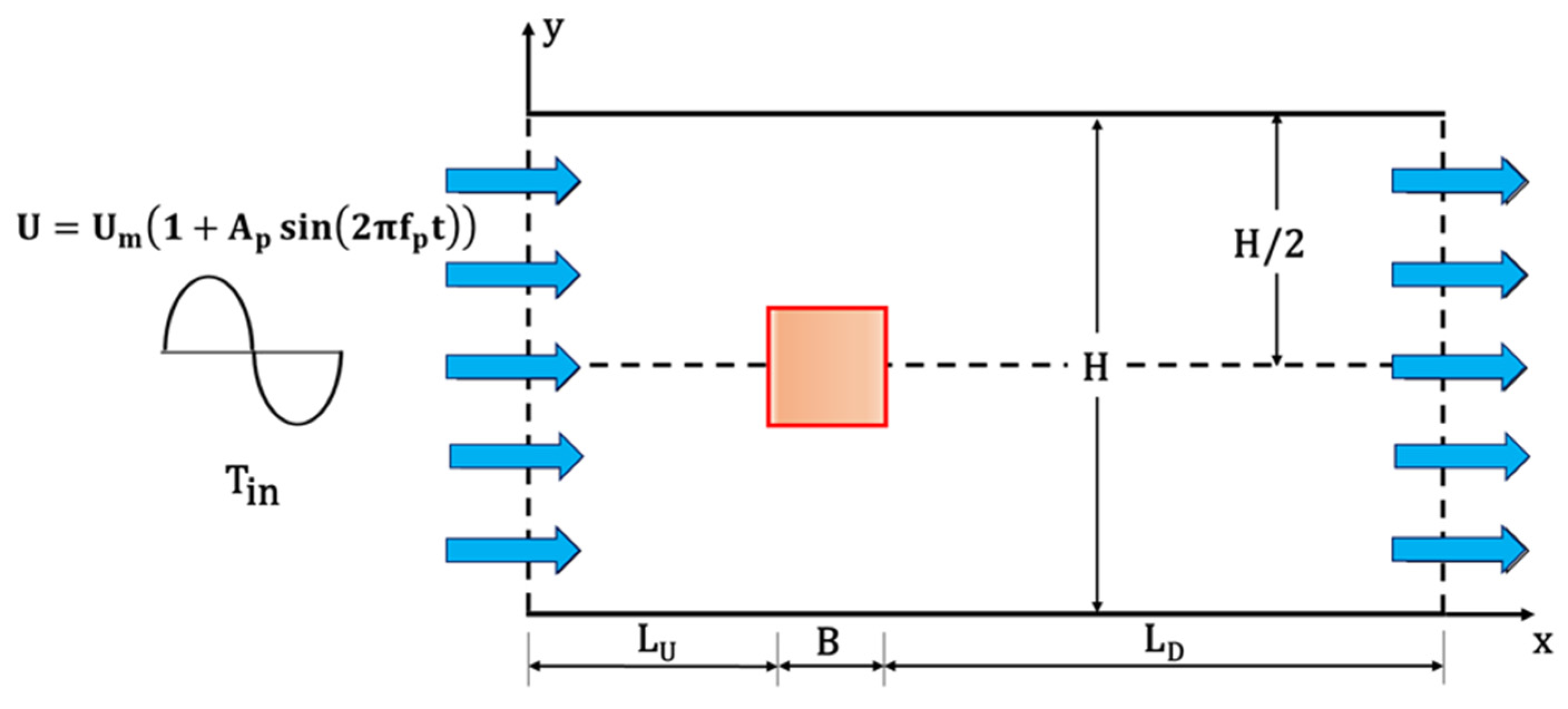
2.1. Freezing Tunnel Model
2.2. Mathematical Model Equations
2.3. Initial and Boundary Conditions
2.4. Thermophysical Properties
2.5. Calculation of Dimensionless Numbers and Energy Consumption
2.6. Computational Implementation
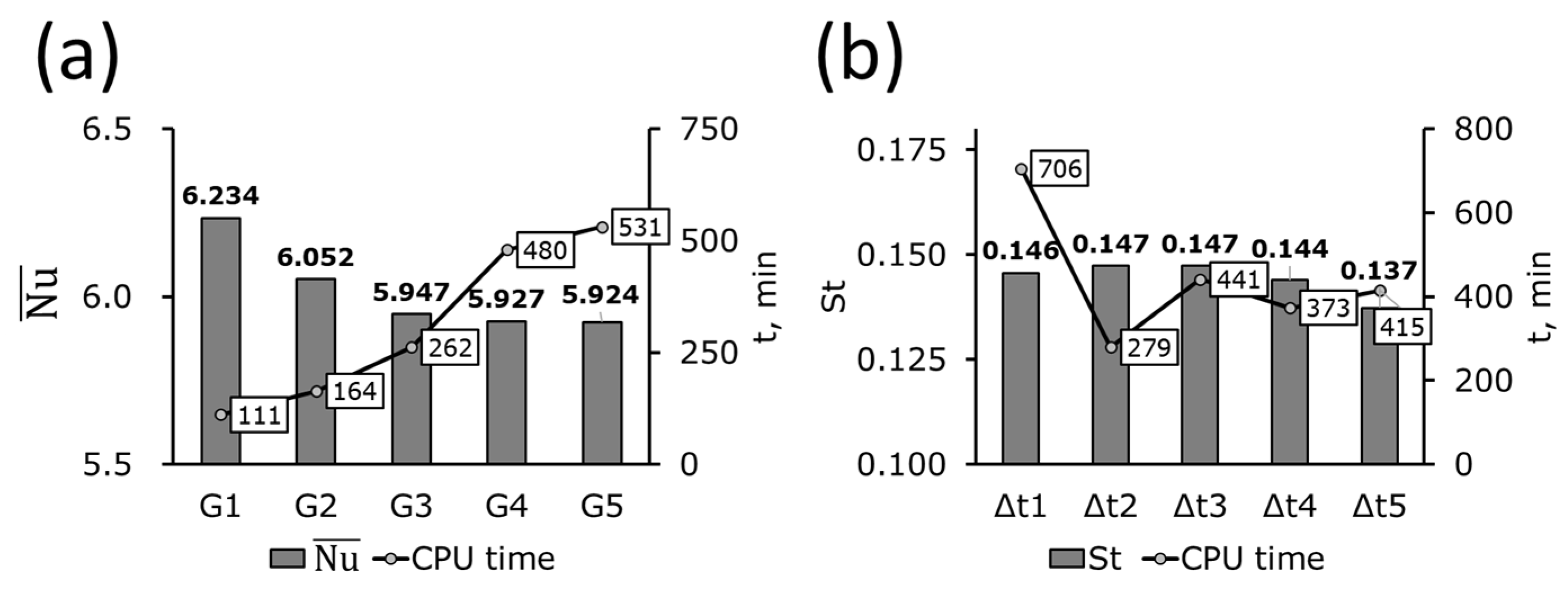
2.6.1. Time and Grid Analysis
2.6.2. Computational Model Validation
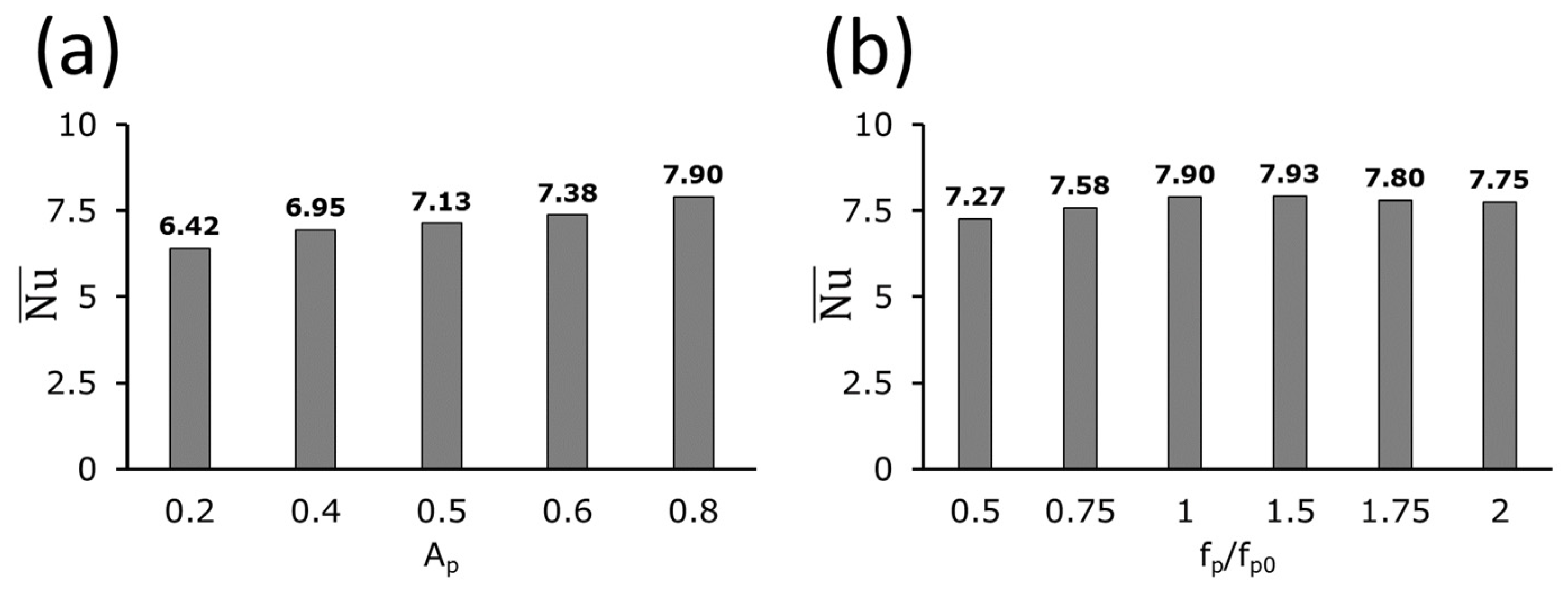
2.6.3. Effects of Pulsating Frequency and Amplitude over Dimensionless Heat Flux
3. Results and Discussion
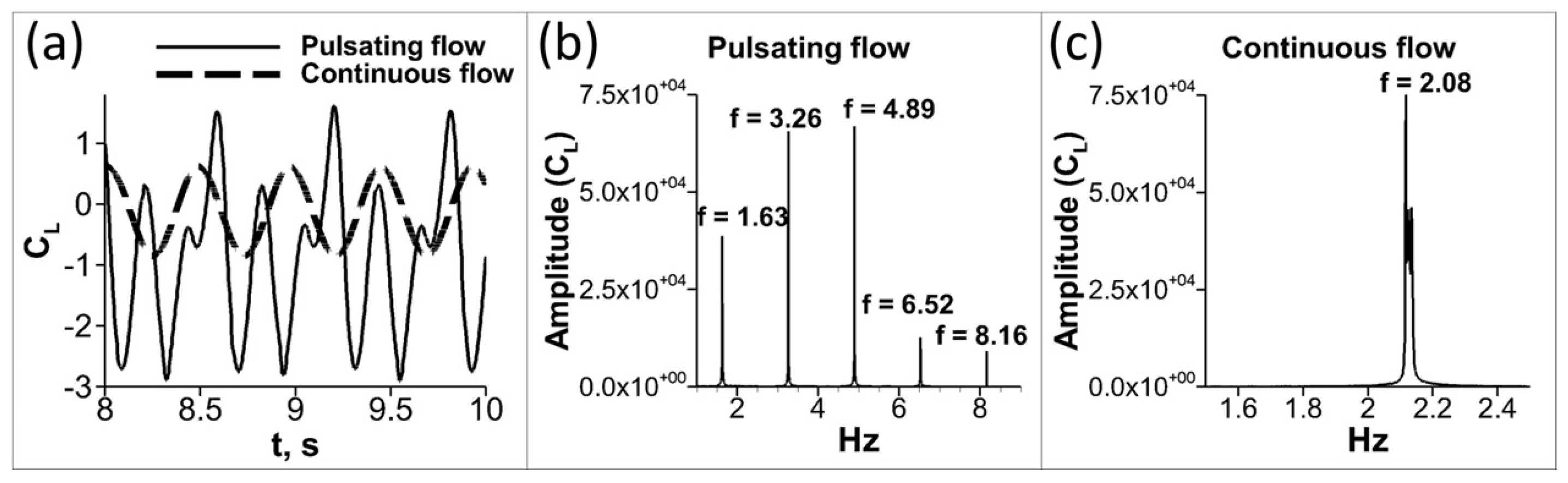
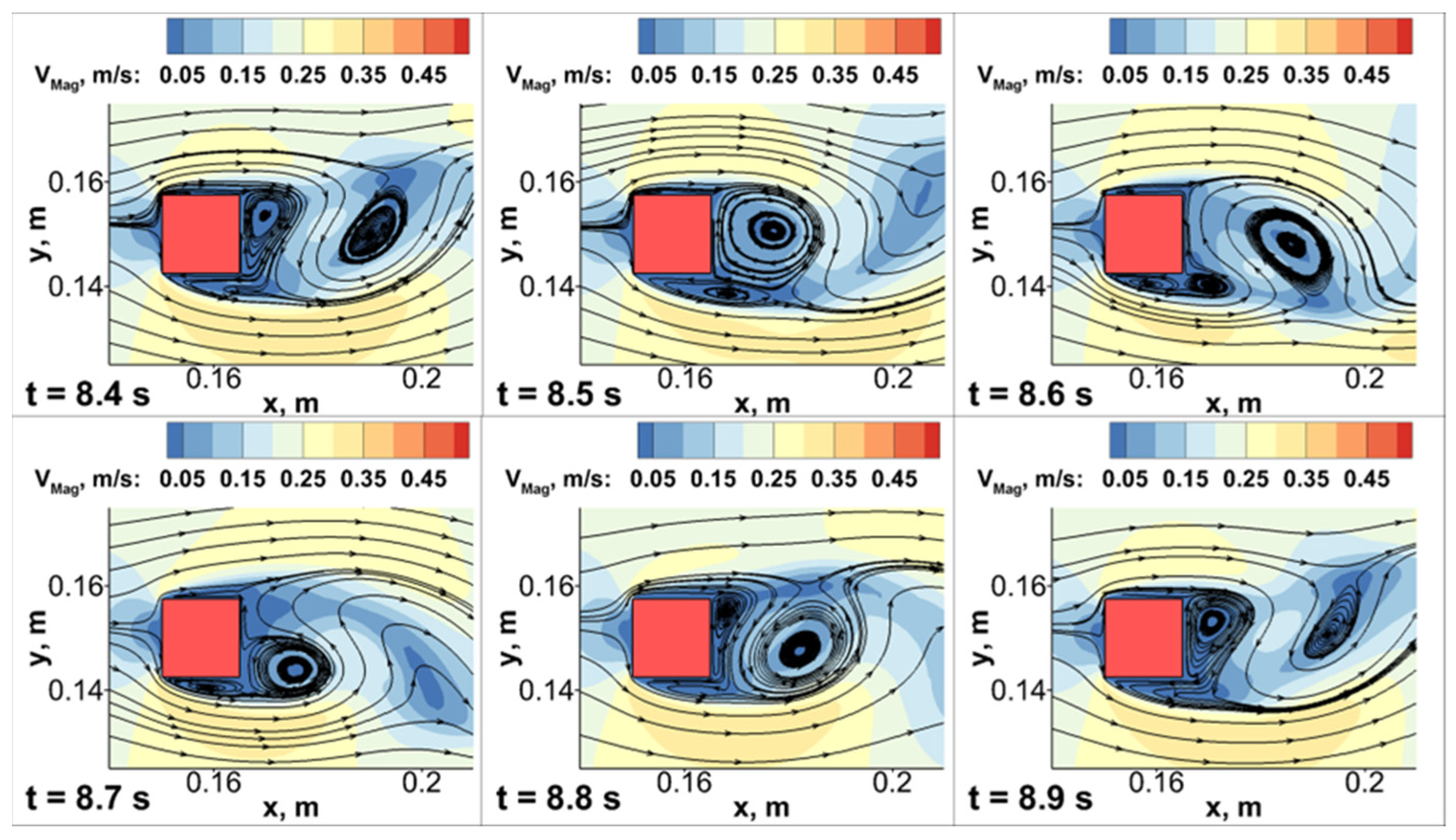
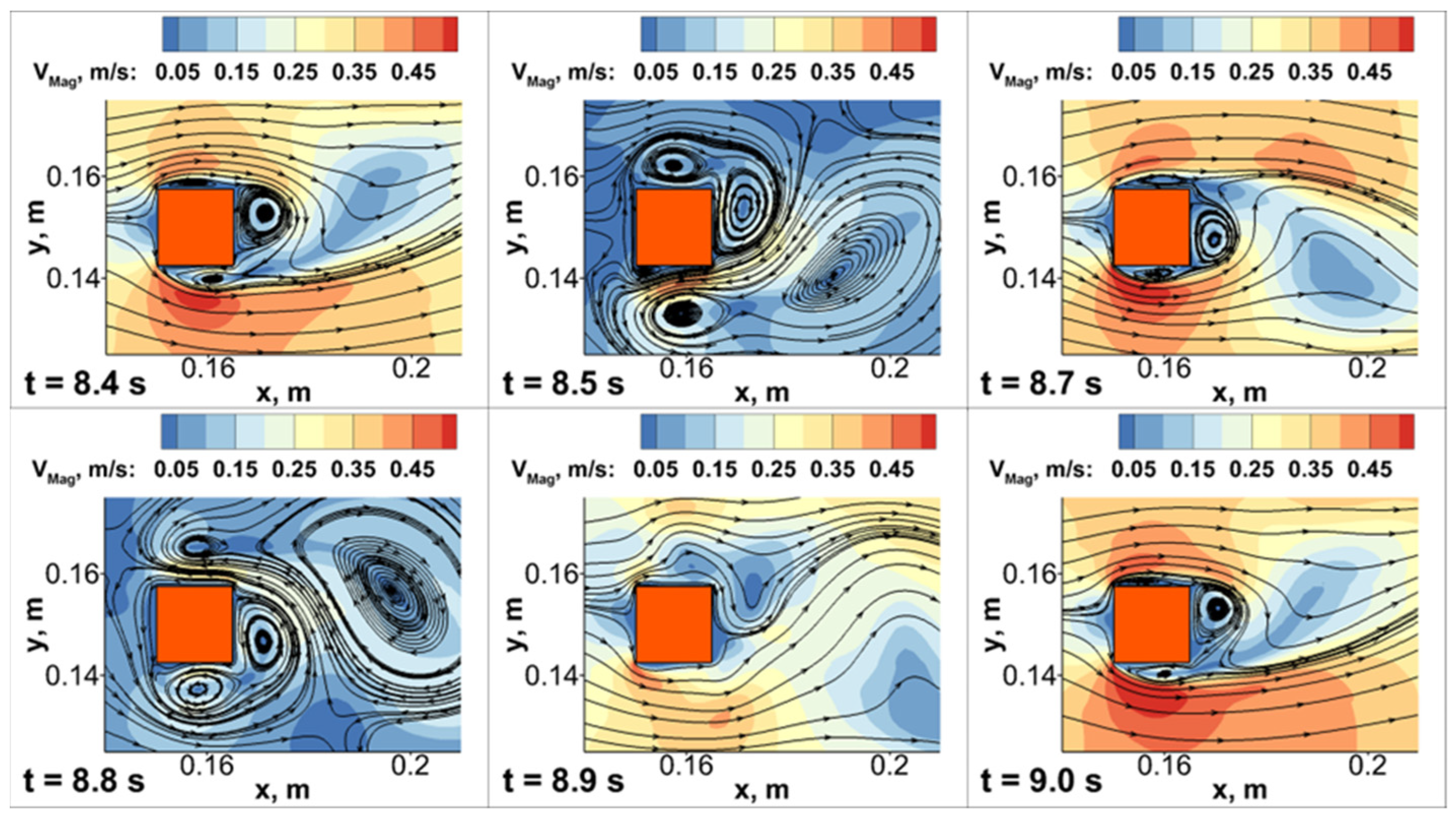
3.1. Effect of Inlet Pulsating Airflow on Fluid Mechanics
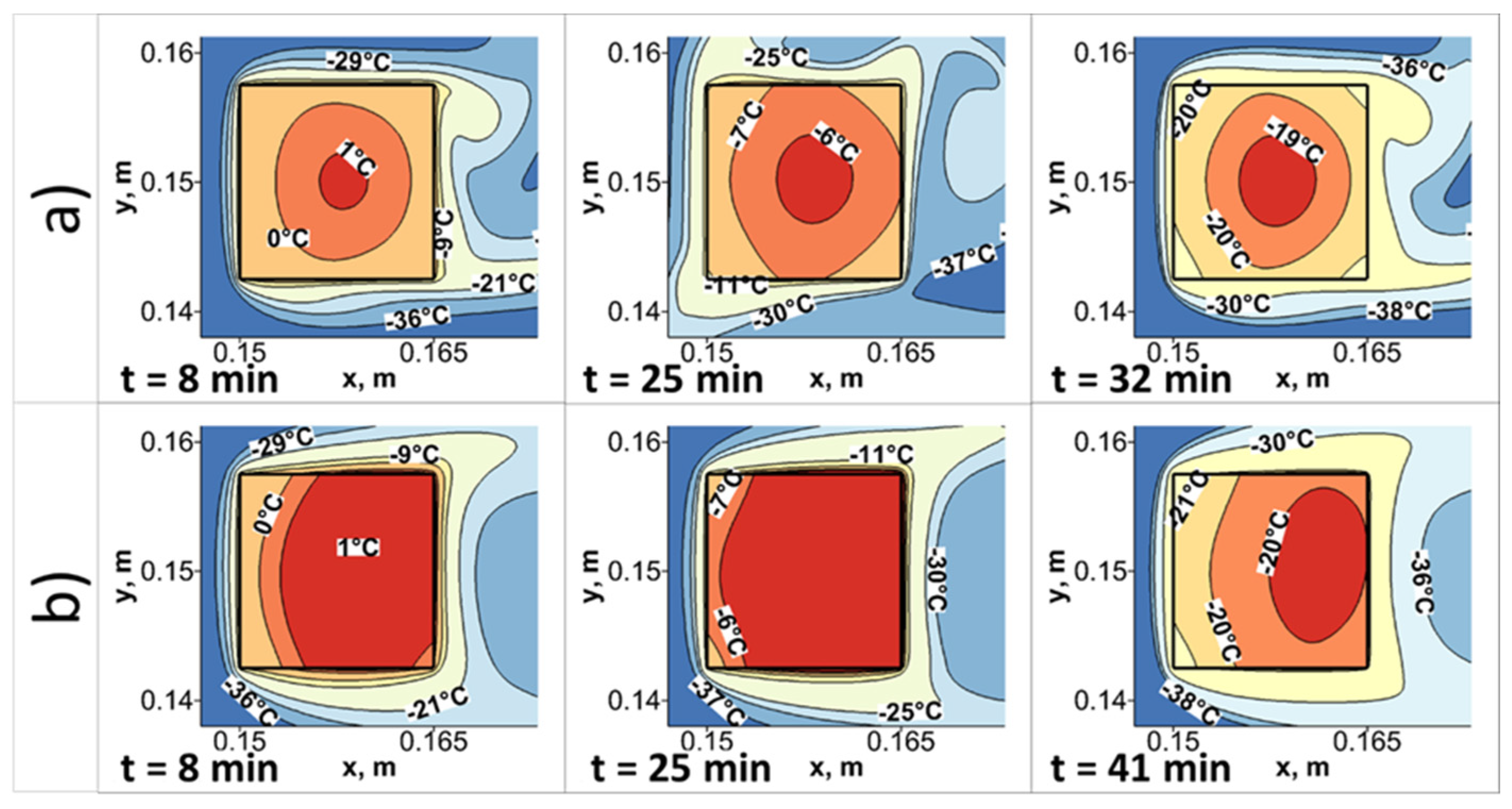
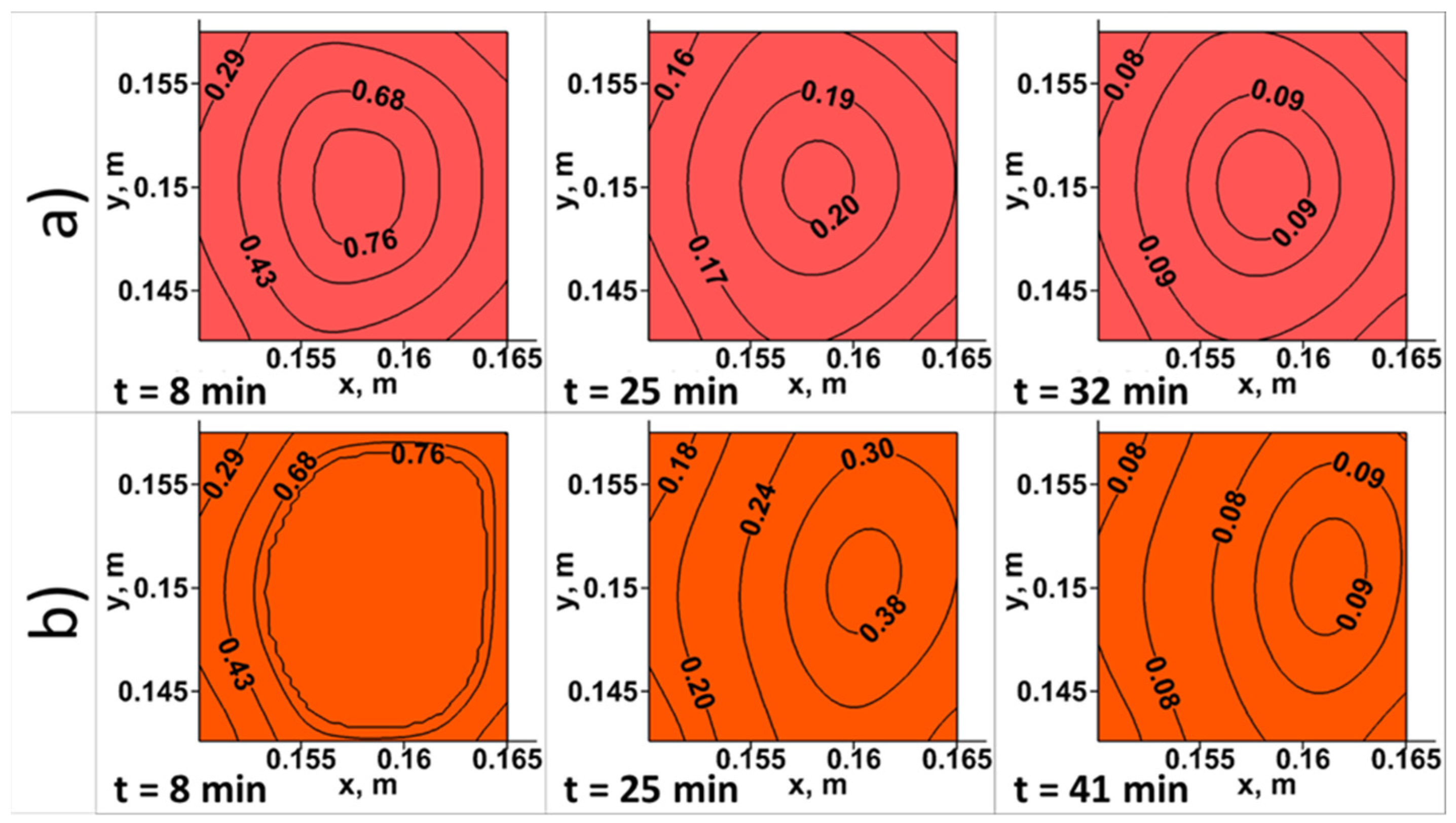
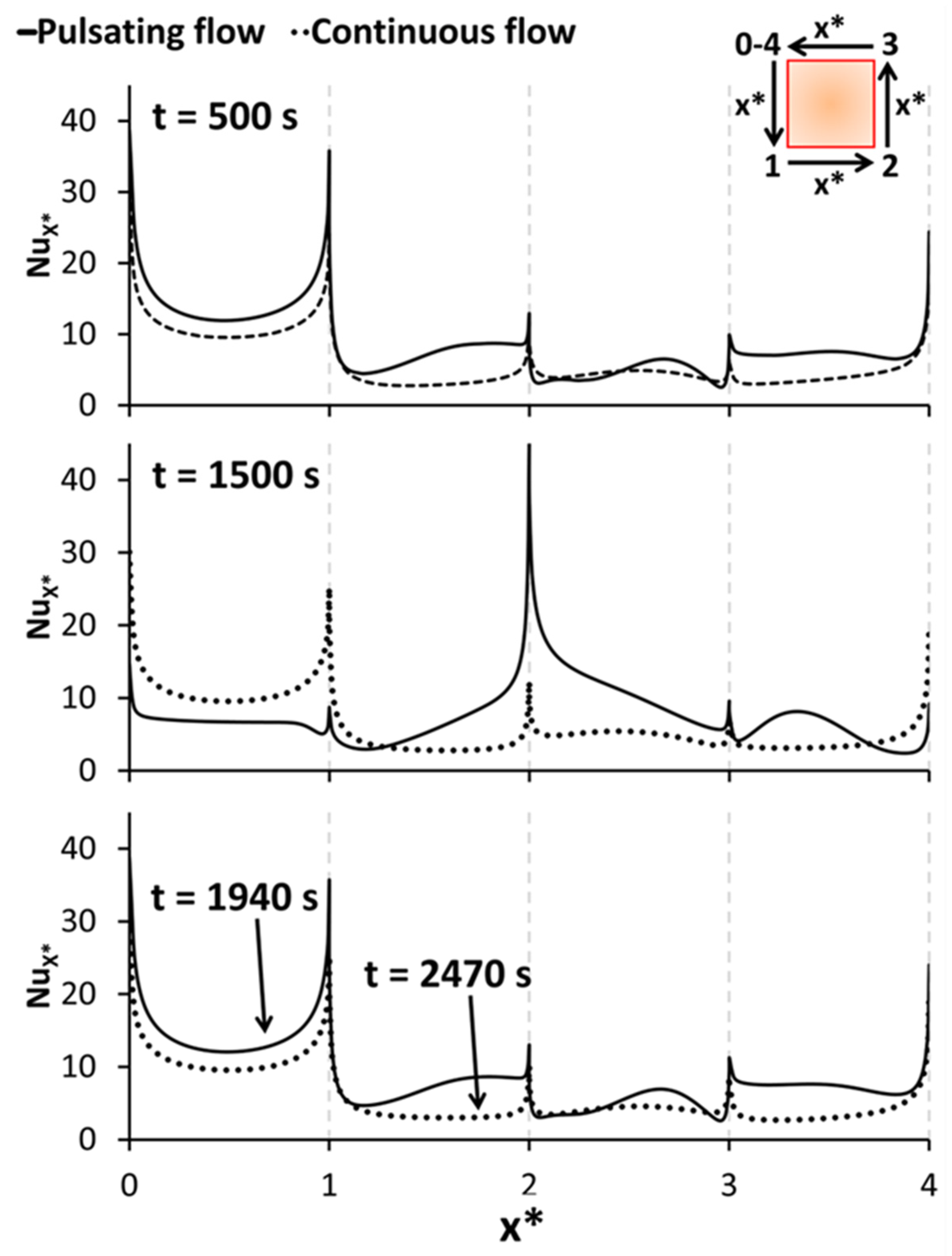
3.2. Effect of Pulsating Inlet Airflow on Heat Transfer
3.3. Dimensionless Heat Flux Analysis and Energy Saving
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Amplitude | Dimensionless |
| B | Characteristic length; square side | m |
| CL | Lift coefficient | Dimensionless |
| CLV, CLP | Lift coefficients due to viscous and pressure forces | Dimensionless |
| CD | Drag coefficient | Dimensionless |
| CDV, CDP | Drag coefficients due to viscous and pressure forces | Dimensionless |
| cp | Specific heat at constant pressure | J kg−1 K−1 |
| Cf | Continuous flow | Dimensionless |
| f | Frequency | Hz |
| Gr | Grashoff number | Dimensionless |
| g | Gravity constant | m s−2 |
| H | Height of tunnel | m |
| k | Thermal conductivity | W m−1K−1 |
| Water Latent heat of fusion = 333.55 | kJ kg−1 | |
| LD | Distance from the channel outlet to the downstream face of food | m |
| LU | Distance from the channel inlet to upstream face of food | m |
| Mass of food | kg | |
| Nu | Nusselt number | Dimensionless |
| p | Pressure | Pa |
| Pf | Pulsating flow | Dimensionless |
| Pr | Prandtl number | Dimensionless |
| Re | Reynolds number | Dimensionless |
| Ri | Richardson number | Dimensionless |
| St | Strouhal number | Dimensionless |
| t | Time | s |
| Process time | s | |
| T | Temperature | °C, K |
| u | Velocity components | m s−1 |
| U | Inlet velocity | m s−1 |
| Vmag | Velocity magnitude | m s−1 |
| x | Position component | m |
| x* | Dimensionless coordinate around square food | Dimensionless |
| X | Fraction | Dimensionless |
| Greek letters | ||
| Sub-relaxation | Dimensionless | |
| β | Thermal expansion coefficient | K−1 |
| Convergence criteria | Dimensionless | |
| Dynamic viscosity | Pa s | |
| density | kg m−3 | |
| Generalized dependent variable | ||
| Subscripts | ||
| ∞ | Free stream | |
| av | Average | |
| ap | Apparent | |
| b | Bottom | |
| bw | Bond water | |
| cf | Change phase | |
| f | Front | |
| fin | Final | |
| flu | Fluid | |
| fro | Frozen | |
| i | Horizontal direction index; i-th term formula | |
| ice | Quantity of ice | |
| in | Inlet | |
| ini | Initial | |
| int | Interface | |
| j | Vertical direction index | |
| m | Mean value | |
| p | Pulsating | |
| p0 | Natural frequency | |
| r | Rear | |
| ref | Reference value | |
| s | Quantity of solids | |
| sol | Solid | |
| t | Top | |
| tc | Thermal center | |
| u | Unfrozen | |
| uw | Unfrozen water | |
| w | Liquid water | |
| wo | Initial quantity of water | |
| Superscript | ||
| k | k-th term formula | |
| Specific volume |
References
- Liu, Z.; Lu, D.; Shen, T.; Guo, H.; Bai, Y.; Wang, L.; Gong, M. New configurations of absorption heat transformer and refrigeration combined system for low-temperature cooling driven by low-grade heat. Appl. Therm. Eng. 2023, 228, 120567. [Google Scholar] [CrossRef]
- Daghooghi-Mobarakeh, H.; Subramanian, V.; Phelan, P.E. Experimental study of water freezing process improvement using ultrasound. Appl. Therm. Eng. 2022, 202, 117827. [Google Scholar] [CrossRef]
- Sharif, Z.; Mustapha, F.; Jai, J.; Yusof, N.M.; Zaki, N. Review on methods for preservation and natural preservatives for extending the food longevity. Chem. Eng. Res. Bull. 2017, 19, 145. [Google Scholar] [CrossRef]
- Liu, Z.; Lou, F.; Qi, X.; Wang, Q.; Zhao, B.; Yan, J.; Shen, Y. Experimental study on cold storage phase-change materials and quick-freezing plate in household refrigerators. J. Food Process. Eng. 2019, 42, e13279. [Google Scholar] [CrossRef]
- Svendsen, E.S.; Widell, K.N.; Tveit, G.M.; Nordtvedt, T.S.; Uglem, S.; Standal, I.; Greiff, K. Industrial methods of freezing, thawing and subsequent chilled storage of whitefish. J. Food Eng. 2022, 315, 110803. [Google Scholar] [CrossRef]
- Yang, D.; Xie, J.; Tang, W.; Wang, J.; Shu, Z. Air-impingement freezing of peeled shrimp: Analysis of flow field, heat transfer, and freezing time. Adv. Mech. Eng. 2019, 11, 1687814019835040. [Google Scholar] [CrossRef]
- Alam, T.; Kim, M.H. A comprehensive review on single phase heat transfer enhancement techniques in heat exchanger applications. Renew. Sustain. Energy Rev. 2018, 81, 813–839. [Google Scholar] [CrossRef]
- Tabilo, E.J.; Moraga, N.O. Improved water freezing with baffles attached to a freezing tunnel: Mathematical modeling and numerical simulation by a conjugate finite volume model. Int. J. Refrig. 2021, 128, 177–185. [Google Scholar] [CrossRef]
- Kurtulmuş, N.; Sahin, B. Experimental investigation of pulsating flow structures and heat transfer characteristics in sinusoidal channels. Int. J. Mech. Sci. 2020, 167, 105268. [Google Scholar] [CrossRef]
- Ye, Q.; Zhang, Y.; Wei, J. A comprehensive review of pulsating flow on heat transfer enhancement. Appl. Therm. Eng. 2021, 196, 117275. [Google Scholar] [CrossRef]
- Blythman, R.; Persoons, T.; Jeffers, N.; Murray, D.B. Heat transfer of laminar pulsating flow in a rectangular channel. Int. J. Heat Mass Transf. 2019, 128, 279–289. [Google Scholar] [CrossRef]
- Akdag, U.; Akcay, S.; Demiral, D. Heat transfer enhancement with nanofluids under laminar pulsating flow in a trapezoidal-corrugated channel. Prog. Comput. Fluid Dyn. 2017, 17, 302–312. [Google Scholar] [CrossRef]
- Mikheev, N.I.; Molochnikov, V.M.; Mikheev, A.N.; Dushina, O.A. Hydrodynamics and heat transfer of pulsating flow around a cylinder. Int. J. Heat Mass Transf. 2017, 109, 254–265. [Google Scholar] [CrossRef]
- Saxena, A.; Ng, E.Y.K. Steady and pulsating flow past a heated rectangular cylinder(s) in a channel. J. Thermophys. Heat Trans. 2018, 32, 401–413. [Google Scholar] [CrossRef]
- Bhalla, N.; Dhiman, A.K. Pulsating flow and heat transfer analysis around a heated semi-circular cylinder at low and moderate Reynolds numbers. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 3019–3037. [Google Scholar] [CrossRef]
- Bayomy, A.M.; Saghir, M.Z. Heat development and comparison between the steady and pulsating flows through aluminum foam heat sink. J. Therm. Sci. Eng. Appl. 2017, 9, 031006. [Google Scholar] [CrossRef]
- Esfe, M.H.; Bahiraei, M.; Torabi, A.; Valadkhani, M. A critical review on pulsating flow in conventional fluids and nanofluids: Thermo-hydraulic characteristics. Int. Commun. Heat Mass Transf. 2021, 120, 104859. [Google Scholar] [CrossRef]
- Yang, B.; Gao, T.; Gong, J.; Li, J. Numerical investigation on flow and heat transfer of pulsating flow in various ribbed channels. Appl. Therm. Eng. 2018, 145, 576–589. [Google Scholar] [CrossRef]
- Hayakawa, S.; Fukue, T.; Sugimoto, Y.; Hiratsuka, W.; Shirakawa, H.; Koito, Y. Effect of rib height on heat transfer enhancement by combination of a rib and pulsating Flow. Front. Heat Mass Transf. 2022, 18, 1–9. [Google Scholar] [CrossRef]
- Moraga, N.O.; Rivera, D.R. Advantages in predicting conjugate freezing of meat in a domestic freezer by CFD with turbulence k-ɛ 3D model and a local exergy destruction analysis. Int. J. Refrig. 2021, 126, 76–87. [Google Scholar] [CrossRef]
- González, N.P.; Moraga, N.O. Energy and exergy analysis of conjugate 3D unsteady heat conduction with solidification of water by turbulent buoyancy-driven freezing of solid food in air. Therm. Sci. Eng. Prog. 2023, 37, 101566. [Google Scholar] [CrossRef]
- Hoang, D.K.; Lovatt, S.J.; Olatunji, J.R.; Carson, J.K. Validated numerical model of heat transfer in the forced air freezing of bulk packed whole chickens. Int. J. Refrig. 2020, 118, 93–103. [Google Scholar] [CrossRef]
- Huo, Y.; Yang, D.; Xie, J.; Yang, Z. Simulation Analysis and Experimental Verification of Freezing Time of Tuna under Freezing Conditions. Fishes 2023, 8, 470. [Google Scholar] [CrossRef]
- Rivera, D.R.; Moraga, N.O. Turbulent mixed convection of air in a cavity with a heat-conducting inner solid: Effect of surface radiation and thermal diffusivity on heat transfer and exergy destruction. Int. J. Mech. Sci. 2022, 218, 107035. [Google Scholar] [CrossRef]
- Tabilo, E.J.; Moraga, N.O. Unsteady conjugate model of fluid mechanics and mass transfer for butanol pervaporation process by non-porous membrane. Int. Commun. Heat Mass Transf. 2021, 127, 105539. [Google Scholar] [CrossRef]
- Rodríguez-Ramos, F.; Tabilo, E.J.; Moraga, N.O. Modeling inactivation of Clostridium botulinum and vitamin destruction of non-Newtonian liquid-solid food mixtures by convective sterilization in cans. Innov. Food Sci. Emerg. Technol. 2021, 73, 102762. [Google Scholar] [CrossRef]
- Rodríguez-Núñez, K.; Tabilo, E.; Moraga, N.O. Conjugate unsteady natural heat convection of air and non-Newtonian fluid in thick-walled cylindrical enclosure partially filled with a porous media. Int. Commun. Heat Mass Transf. 2019, 108, 104304. [Google Scholar] [CrossRef]
- González, N.P.; Rivera, D.R.; Moraga, N.O. Conjugate turbulent natural heat convection and solid food freezing modelling: Effects of position and number of pieces of salmon on the cooling rate. Therm. Sci. Eng. Prog. 2021, 26, 101101. [Google Scholar] [CrossRef]
- Buceta, J.P.; Passot, S.; Scutellà, B.; Bourlés, E.; Fonseca, F.; Trelea, I.C. Use of 3D mathematical modelling to understand the heat transfer mechanisms during freeze-drying using high-throughput vials. Appl. Therm. Eng. 2022, 207, 118099. [Google Scholar] [CrossRef]
- Cui, P.; He, L.; Mo, X. Flow and heat transfer analysis of a domestic refrigerator with complex wall conditions. Appl. Therm. Eng. 2022, 209, 118306. [Google Scholar] [CrossRef]
- Gulati, T.; Datta, A.K. Enabling computer-aided food process engineering: Property estimation equations for transport phenomena-based models. J. Food Eng. 2013, 116, 483–504. [Google Scholar] [CrossRef]
- Rao, M.; Rizvi, S.; Datta, A.; Ahmed, J. Engineering Properties of Foods, 4th ed.; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2014. [Google Scholar]
- de Lima, W.C.P.B.; Nascimento, L.P.C.; Dantas, R.L.; Tresena, N.L.; Júnior, J.B.S.; de Lima, G.S.; de Lima, A.G.B. Heat Transfer in the Cooling, Freezing and Post-Freezing of Liquid Food: Modeling and Simulation. Diffus. Found. 2020, 25, 37–53. [Google Scholar] [CrossRef]
- Hoang, D.K.; Lovatt, S.J.; Olatunji, J.R.; Carson, J.K. Improved prediction of thermal properties of refrigerated foods. J. Food Eng. 2021, 297, 110485. [Google Scholar] [CrossRef]
- Yu, J.Y.; Lin, W.; Zheng, X.T. Effect on the flow and heat transfer characteristics for sinusoidal pulsating laminar flow in a heated square cylinder. Heat Mass Transf./Waerme Stoffuebertragung 2014, 50, 849–864. [Google Scholar] [CrossRef]
- Kiani, H.; Sun, D.W. Numerical simulation of heat transfer and phase change during freezing of potatoes with different shapes at the presence or absence of ultrasound irradiation. Heat Mass Transf. 2018, 54, 885–894. [Google Scholar] [CrossRef]
- Wang, W.; Li, W.; Bu, Y.; Li, X.; Zhu, W. Nano freezing–thawing of Atlantic salmon fillets: Impact on thermodynamic and quality characteristics. Foods 2023, 12, 2887. [Google Scholar] [CrossRef] [PubMed]
- Rivera, D.R.; Moraga, N.O. Energy analysis of convective freezer cabinet with PCMs and salmon-fillet during charging, discharging and normal operation processes by CFD modeling. J. Energy Storage 2024, 83, 110558. [Google Scholar] [CrossRef]
- ASHRAE. 2014 ASHRAE Handbook: Refrigeration; ASHRAE: Atlanta, GA, USA, 2014. [Google Scholar]
- Çengel, Y.A. Heat and Mass Transfer: A Practical Approach, 3rd ed.; McGraw-Hill Science/Engineering/Math: University Park, PA, USA, 2007; Available online: https://books.google.cl/books?id=WgZaAAAAYAAJ (accessed on 22 July 2011).
- Choi, Y.; Okos, M.R. Effects of temperature and composition on the thermal properties of foods. J. Food Process. Appl. 1986, 1, 93–101. [Google Scholar]
- Moraga, N.O.; Jaime, J.I.; Cabrales, R.C. An approach to accelerate the convergence of SIMPLER algorithm for convection-diffusion problems of fluid flow with heat transfer and phase change. Int. Commun. Heat Mass Transf. 2021, 129, 105715. [Google Scholar] [CrossRef]
- Li, Z.Y.; Tao, W.Q. A new stability-guaranteed second-order difference scheme. Numer. Heat Transf. Part B Fundam. 2002, 42, 349–365. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow, 6th ed.; Hemisphere Publishing Corporation: Washington, DC, USA, 1980. [Google Scholar]
- Curtiss, C.F.; Hirschfelder, J.O. Integration of stiff equations. Proc. Natl. Acad. Sci. USA 1952, 38, 235–243. [Google Scholar] [CrossRef]
- Okajima A, Strouhal number of rectangular cylinders. J. Fluid Mech. 1982, 123, 379–398. [CrossRef]
- Fowler, T.S.; Witherden, F.D.; Girimaji, S.S. Pulsating flow past a square cylinder: Analysis of force coefficient spectra and vortex structure development. J. Fluids Eng. Trans. ASME 2020, 142, 121106. [Google Scholar] [CrossRef]
- Mahir, N.; Altaç, Z. Numerical investigation of flow and combined natural-forced convection from an isothermal square cylinder in cross flow. Int. J. Heat Fluid Flow 2019, 75, 103–121. [Google Scholar] [CrossRef]
- Luo, S.C.; Tong, X.H.; Khoo, B.C. Transition phenomena in the wake of a square cylinder. J. Fluids Struct. 2007, 23, 227–248. [Google Scholar] [CrossRef]
- Sharma, A.; Eswaran, V. Heat and fluid flow across a square cylinder in the two-dimensional laminar flow regime. Numer. Heat Transf. Part A Appl. 2004, 45, 247–269. [Google Scholar] [CrossRef]
- Saha, A.K.; Biswas, G.; Muralidhar, K. Three-dimensional study of flow past a square cylinder at low Reynolds numbers. Int. J. Heat Fluid Flow 2003, 24, 54–66. [Google Scholar] [CrossRef]
- Robichaux, J.; Balachandar, S.; Vanka, S.P. Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 1999, 11, 560–578. [Google Scholar] [CrossRef]
- Sohankar, A.; Norberg, C.; Davidson, L. Numerical simulation of unsteady low-Reynolds number flow around rectangular cylinders at incidence. J. Wind Eng. 1997, 69–71, 189–201. [Google Scholar] [CrossRef]
- Sen, S.; Mittal, S.; Biswas, G. Flow past a square cylinder at low Reynolds numbers. Int. J. Numer. Methods Fluids 2011, 67, 1160–1174. [Google Scholar] [CrossRef]
- Moschandreou, T.; Zamir, M. Heat transfer in a tube with pulsating flow and constant heat flux. Int. J. Heat Mass Transf. 1997, 40, 2461–2466. [Google Scholar] [CrossRef]
- Ji, T.H.; Kim, S.Y.; Hyun, J.M. Experiments on heat transfer enhancement from a heated square cylinder in a pulsating channel flow. Int. J. Heat Mass Transf. 2008, 51, 1130–1138. [Google Scholar] [CrossRef]
- Kono, S.; Kon, M.; Araki, T.; Sagara, Y. Effects of relationships among freezing rate, ice crystal size and color on surface color of frozen salmon fillet. J. Food Eng. 2017, 214, 158–165. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Z.; Sun, D.W. Effects of freezing on cell structure of fresh cellular food materials: A review. Trends Food Sci. Technol. 2018, 75, 46–55. [Google Scholar] [CrossRef]


| Profiles | Δumax | Δvmax | ||||||
|---|---|---|---|---|---|---|---|---|
| G5-G1 | G5-G2 | G5-G3 | G5-G4 | G5-G1 | G5-G2 | G5-G3 | G5-G4 | |
| Horizontal y = 10B | 1.3 × 10−1 | 4.0 × 10−2 | 1.1 × 10−1 | 1.0 × 10−1 | 2.3 × 10−1 | 4.4 × 10−2 | 3.4 × 10−1 | 3.5 × 10−1 |
| Vertical x = 10.5B | 6.4 × 10−2 | 6.2 × 10−2 | 6.4 × 10−2 | 5.5 × 10−2 | 2.2 × 10−2 | 1.3 × 10−2 | 1.4 × 10−2 | 1.3 × 10−2 |
| Forced Convection | Mix. Conv. | ||||||
|---|---|---|---|---|---|---|---|
| Reynolds Number | 100 | 120 | 140 | 160 | 200 | 250 | (Ri = 0.65) |
| Strouhal number | |||||||
| Present | 0.152 | 0.155 | 0.157 | 0.155 | 0.155 | 0.147 | 0.151 |
| Mahir and Altaç 3D, 2019 [48] | 0.152 | 0.158 | 0.158 | 0.164 | 0.152 | 0.152 | — |
| Okajima, 1982 (exp.) [46] | 0.142 | — | 0.145 | — | 0.144 | 0.143 | — |
| Luo et al., 2007 (exp.) [49] | — | — | 0.145 | 0.152 | 0.159 | 0.159 | — |
| Sharma and Eswaran, 2004 [50] | 0.152 | 0.159 | 0.163 | 0.164 | — | — | — |
| Saha et al., 2003 [51] | 0.152 | 0.159 | 0.163 | 0.159 | 0.16 | 0.164 | — |
| Fowler et al., 2020 [47] | — | — | — | — | 0.153 | — | — |
| Mean CD | |||||||
| Present | 1.471 | 1.407 | 1.402 | 1.404 | 1.394 | 1.344 | 1.53 |
| Mahir and Altaç 3D, 2019 [48] | 1.433 | 1.443 | 1.461 | 1.483 | 1.491 | 1.554 | — |
| Okajima, 1982 (exp.) [46] | 1.593 | — | 1.476 | — | — | 1.479 | — |
| Robichaux et al., 1999 [52] | 1.533 | 1.541 | 1.561 | 1.583 | 1.636 | 1.671 | — |
| Saha et al., 2003 [51] | 1.496 | 1.507 | 1.558 | 1.525 | 1.595 | 1.682 | — |
| Fowler et al., 2020 [47] | — | — | — | — | 1.484 | — | — |
| RMS CL | |||||||
| Present | 0.133 | 0.200 | 0.242 | 0.283 | 0.370 | 0.473 | 0.660 |
| Mahir and Altaç 3D, 2019 [48] | 0.176 | 0.226 | 0.270 | 0.318 | 0.303 | 0.313 | — |
| Sharma and Eswaran, 2004 [50] | 0.192 | 0.230 | 0.270 | 0.317 | — | — | — |
| Sohankar et al., 1997 [53] | 0.153 | — | — | — | 0.367 | — | — |
| Sen et al., 2011 [54] | 0.191 | 0.243 | 0.276 | — | — | — | — |
| Fowler et al., 2020 [47] | — | — | — | — | 0.433 | — | — |
| Mean Nu | |||||||
| Present | 4.057 | 4.399 | 4.708 | 4.983 | 5.451 | 5.947 | 6.453 |
| Mahir and Altaç 3D, 2019 [48] | 4.032 | 4.355 | 4.662 | 4.942 | 5.272 | 5.618 | — |
| Mahir and Altaç 2D, 2019 [48] | 4.020 | 4.356 | 4.657 | 4.932 | 5.435 | 6.02 | — |
| Sharma and Eswaran, 2004 [50] | 4.010 | 4.375 | 4.69 | 4.983 | — | — | — |
| Yu et al., 2014 [35] | 4.420 | — | — | — | — | — | — |
| Mean Nu | t = 8 min | t = 25 min | t = 32 min/41 min | |||
|---|---|---|---|---|---|---|
| Pulsating | Continuous | Pulsating | Continuous | Pulsating | Continuous | |
| Front | 16.7 | 12.7 | 7.0 | 12.7 | 16.8 | 12.7 |
| Bottom | 7.8 | 4.6 | 8.3 | 4.6 | 7.8 | 4.6 |
| Rear | 4.5 | 4.4 | 12.0 | 5.0 | 4.6 | 4.3 |
| Top | 8.0 | 5.0 | 5.2 | 4.7 | 8.0 | 4.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabilo, E.J.; Lemus-Mondaca, R.; Puente, L.; Moraga, N.O. Numerical Simulation of Salmon Freezing Using Pulsating Airflow in a Model Tunnel. Processes 2024, 12, 1852. https://doi.org/10.3390/pr12091852
Tabilo EJ, Lemus-Mondaca R, Puente L, Moraga NO. Numerical Simulation of Salmon Freezing Using Pulsating Airflow in a Model Tunnel. Processes. 2024; 12(9):1852. https://doi.org/10.3390/pr12091852
Chicago/Turabian StyleTabilo, Edgardo J., Roberto Lemus-Mondaca, Luis Puente, and Nelson O. Moraga. 2024. "Numerical Simulation of Salmon Freezing Using Pulsating Airflow in a Model Tunnel" Processes 12, no. 9: 1852. https://doi.org/10.3390/pr12091852
APA StyleTabilo, E. J., Lemus-Mondaca, R., Puente, L., & Moraga, N. O. (2024). Numerical Simulation of Salmon Freezing Using Pulsating Airflow in a Model Tunnel. Processes, 12(9), 1852. https://doi.org/10.3390/pr12091852








