An Improved Porosity Calculation Algorithm for Particle Flow Code
Abstract
1. Introduction
2. Methodology
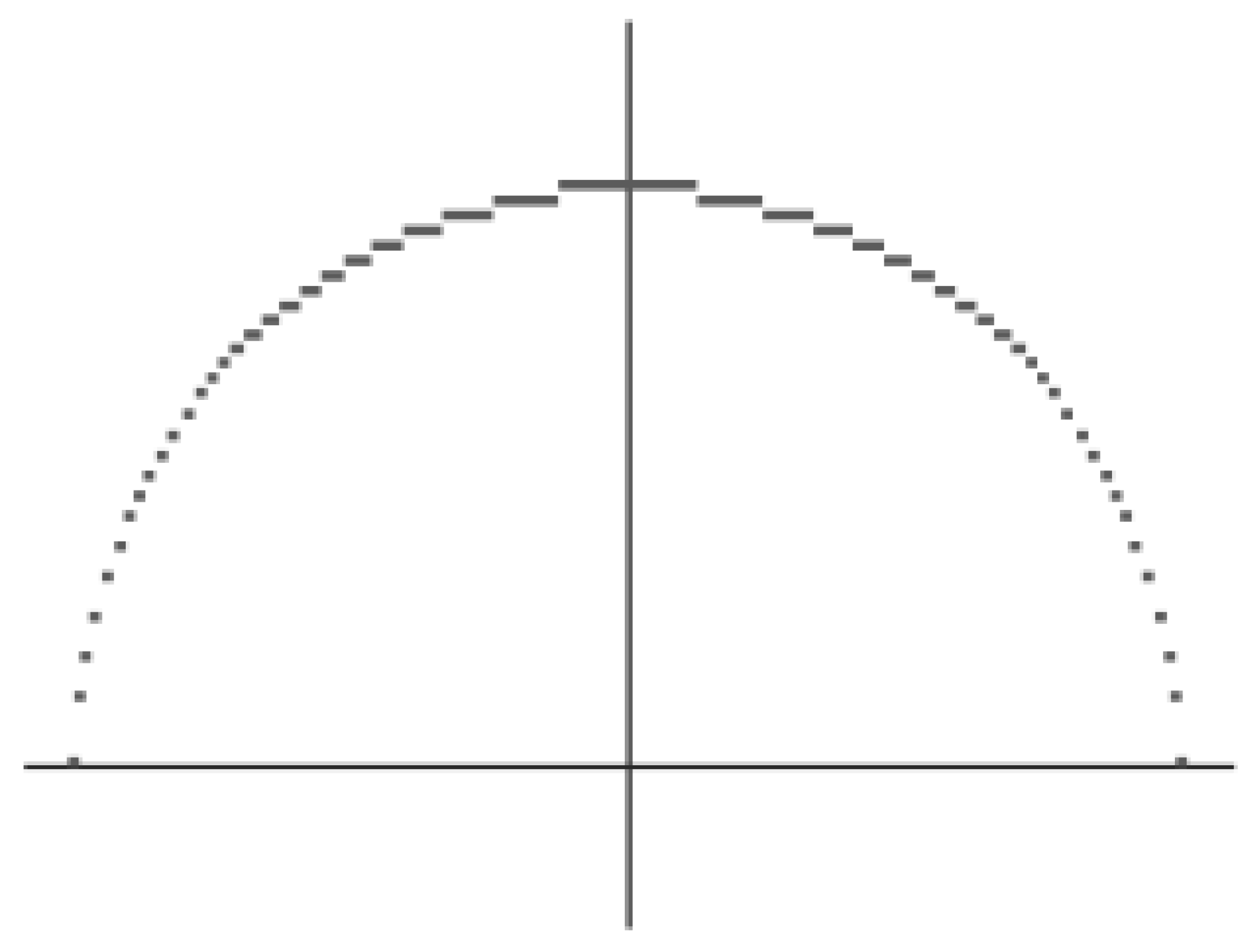
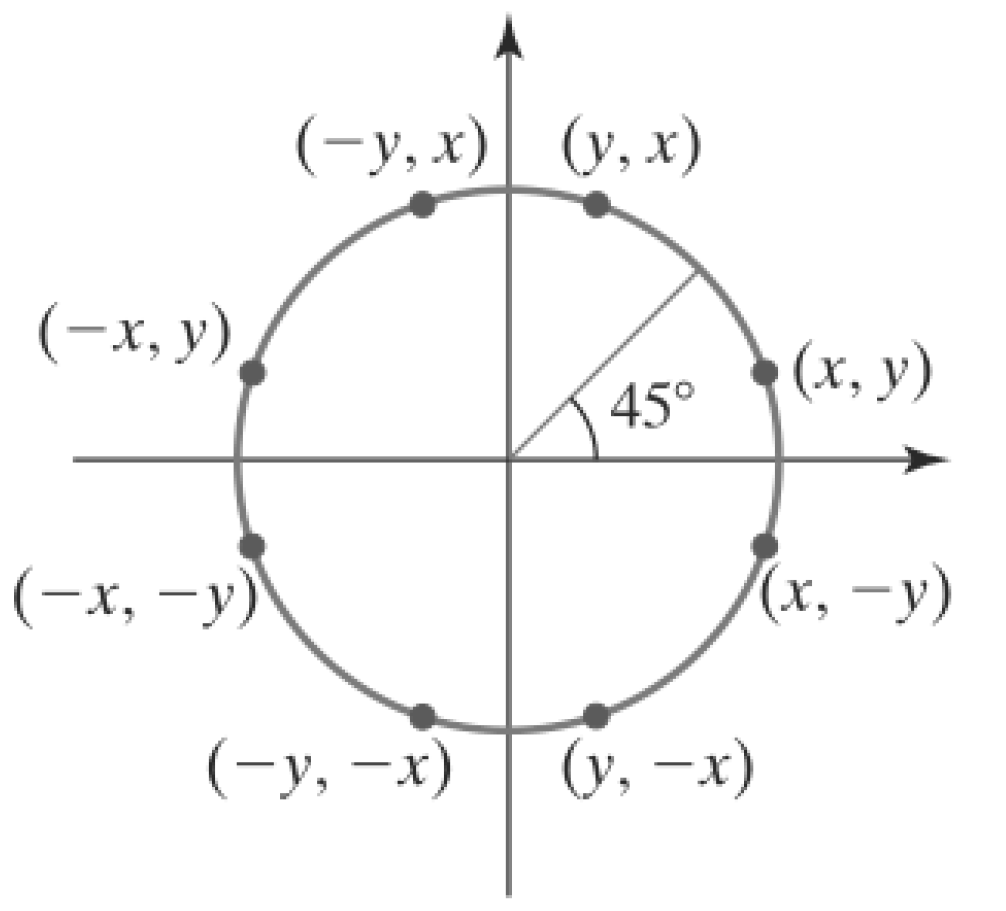
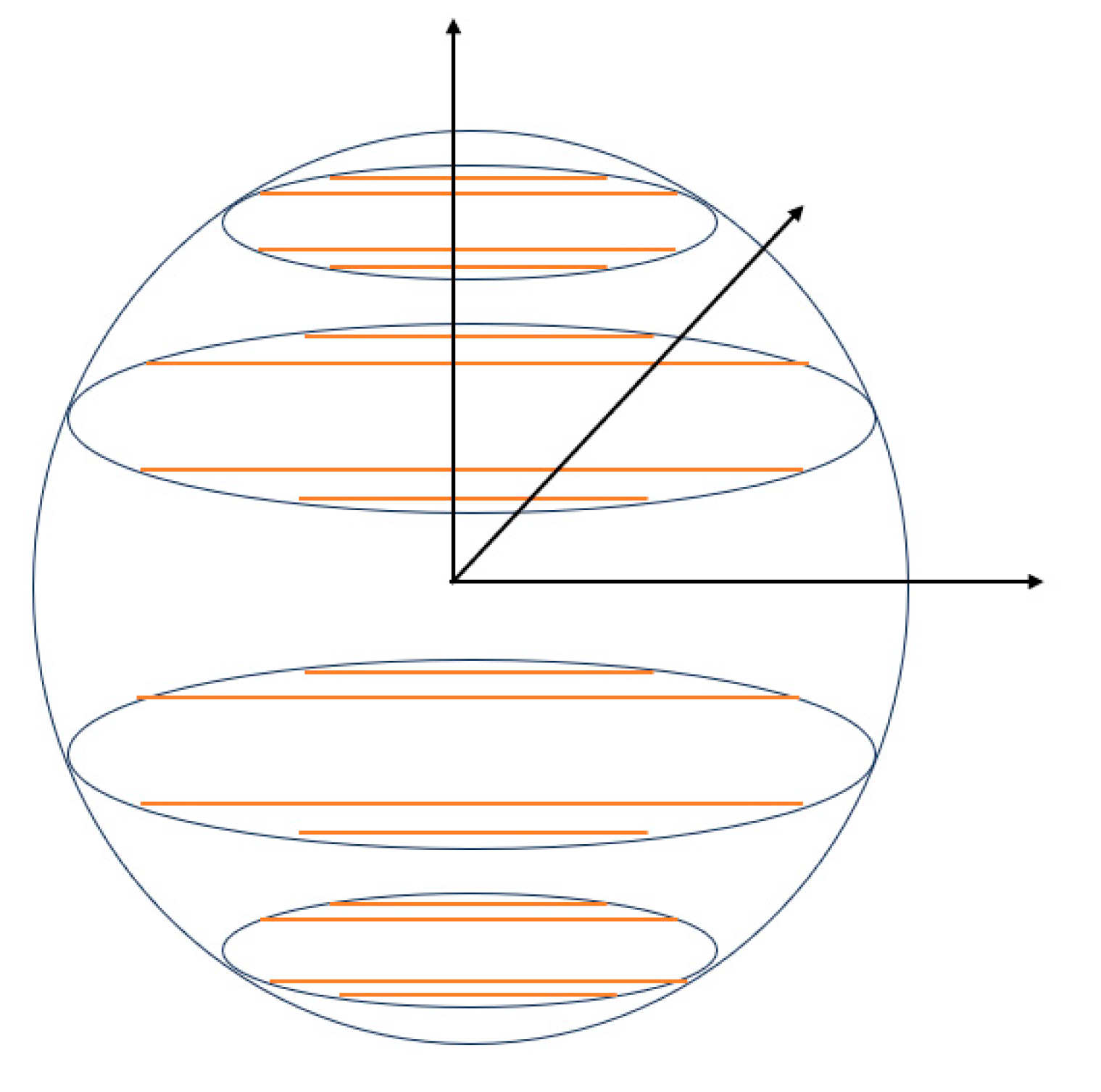
2.1. Traversal Sphere Algorithm
| Algorithm 1: Traversal sphere algorithm. | |
| 1: | #cells is the matrix of the mesh |
| 2: | def line(x,y,z,cells,ball): |
| 3: | for i in range(x): |
| 4: | cells[i+ball.x][y+ball.y][z+ball.z]=True |
| 5: | cells[−i+ball.x][y+ball.y][z+ball.z]=True |
| 6: | def disk(ball,celss,r,z): |
| 7: | # x is the x-coordinate of the axis in this loop |
| 8: | x=0 |
| 9: | yr=r |
| 10: | # Calculate the initial value of the decision parameter, P is decision parameter |
| 11: | p = 5/4 |
| 12: | # Inner loop |
| 13: | while(yr>=x): |
| 14: | #Northern Hemisphere |
| 15: | line(x,yr,z,cells,ball) |
| 16: | line(yr,x,z,cells,ball) |
| 17: | line(x,−yr,z,cells,ball) |
| 18: | line(yr,−x,z,cells,ball) |
| 19: | #Southern Hemisphere |
| 20: | line(x,yr,−z,cells,ball) |
| 21: | line(yr,x,−z,cells,ball) |
| 22: | line(x,−yr,−z,cells,ball) |
| 23: | line(yr,−x,−z,cells,ball) |
| 24: | if(p<0): |
| 25: | p = p+2*x+3 |
| 26: | else: |
| 27: | p=p+2*(x−yr)+5 |
| 28: | yr−=1 |
| 29: | x+=1 |
| 30: | def circle(ball,cells): |
| 31: | # Execute the midpoint circle algorithm first, get, x and z |
| 32: | #r is radius of ball |
| 33: | r=ball.r |
| 34: | # z is the z-coordinate of the axis in this loop |
| 35: | z=0 |
| 36: | yr=r |
| 37: | # Calculate the initial value of the decision parameter, P is decision parameter |
| 38: | P = 5/4 |
| 39: | # Outer loop |
| 40: | while(yr>=x): |
| 41: | # Execute the disc algorithm twice with x and z |
| 42: | disk(ball,cells,z,yr) |
| 43: | disk(ball,cells,yr,z) |
| 44: | if(p<0): |
| 45: | p = p +2*z+3 |
| 46: | else: |
| 47: | p = p +2*(z−yr)+5 |
| 48: | yr-=1 |
| 49: | z+=1 |
| 50: | def main():: |
| 51: | # i is the one of the ball |
| 52: | for i in balls: |
| 53: | circle(i,cells) |
2.2. Traversal of Small-Grid Algorithm
| Algorithm 2: Traversal of small-grid algorithm. | |
| 1: | # Calculate the distance between two points |
| 2: | def distance(i,j,k,x,y,z,r): |
| 3: | return (i−x)*(i−x)+(j−y)(j−y)+(k−z)(k−z)−r*r |
| 4: | # i+r |
| 5: | # Inner loop |
| 6: | def small_cube(i,j,k,cells,cells_ball): |
| 7: | for x,y,z,r in range(i−r, i+r, j−r, j+r, k−r, k+r): |
| 8: | # The decision function is called only if the center of the circle is inside the small cube |
| 9: | if(cells_ball[x][y][z]==True): |
| 10: | #Call the distance function |
| 11: | display=distance(i,j,k,x,y,z,r) |
| 12: | # If the ball is with |
| 13: | if(d<0): |
| 14: | cells[i][j][k]=True |
| 15: | return |
| 16: | def main(): |
| 17: | # Traverse the grid in the R range |
| 18: | # Mark with the coordinates of the center of the sphere |
| 19: | for ball in balls: |
| 20: | cells_ball[ball.x][ball.y][ball.z]=True |
| 21: | #Outer loop, which traverses small grids |
| 22: | for i,j,k in range(cells): |
| 23: | small_cube(i,j,k,cells,cells_ball) |
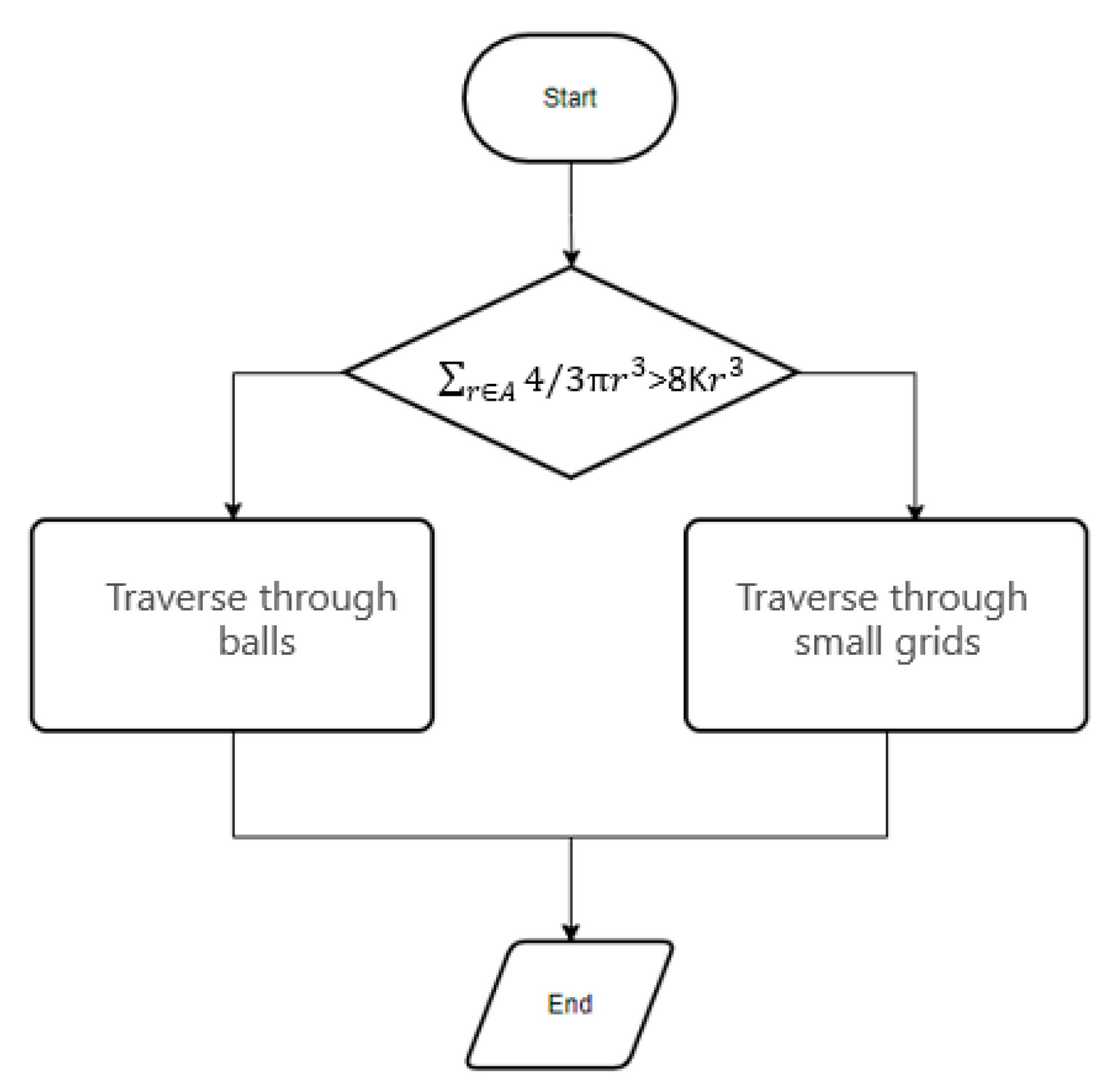
2.3. Algorithm Flowchart
3. Results and Discussion
3.1. Verification of the Sphere Algorithm
3.2. Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cundall, P.A. A computer model for simulating progressive, large-scale movement in blocky rock system. Proc. Int. Symp. Rock Mech. 1971, 8, 129–136. [Google Scholar]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Wang, C.; Tannant, D.D.; Lilly, P.A. Numerical analysis of the stability of heavily jointed rock slopes using PFC2D. Int. J. Rock Mech. Min. Sci. 2003, 40, 415–424. [Google Scholar] [CrossRef]
- Gao, W.; Yang, H.; Hu, R. Soil–rock mixture slope stability analysis by microtremor survey and discrete element method. Bull. Eng. Geol. Environ. 2022, 81, 121. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Xu, P.; Lou, J.; Shan, B.; Wang, F.; Cao, C.; Chen, X.; Que, J. Stability evaluation and potential failure process of rock slopes characterized by non-persistent fractures. Nat. Hazards Earth Syst. Sci. 2020, 20, 2921–2935. [Google Scholar] [CrossRef]
- Fattahi, H.; Sadeghi, M.; Ghaedi, H. Analysis of Rock Fall Phenomenon in Steep Wall Using Modeling by Rocfall Mass-Lump Method and PFC 3D Discrete Element Method-Case Study. Ferdowsi Civ. Eng. 2021, 34, 95–115. [Google Scholar]
- Rafiee, R.; Ataei, M.; KhalooKakaie, R.; Jalali, S.E.; Sereshki, F.; Noroozi, M. Numerical modeling of influence parameters in cavabililty of rock mass in block caving mines. Int. J. Rock Mech. Min. Sci. 2018, 105, 22–27. [Google Scholar] [CrossRef]
- Svartsjaern, M. A prognosis methodology for underground infrastructure damage in sublevel cave mining. Rock Mech. Rock Eng. 2019, 52, 247–263. [Google Scholar] [CrossRef]
- Sjöberg, J. Solving rock mechanics issues through modelling: Then, now, and in the future? In Underground Mining Technology 2020: Proceedings of the Second International Conference on Underground Mining Technology, 3–4 November 2020; Wesseloo, J., Ed.; Australian Centre for Geomechanics: Perth, Australia, 2020. [Google Scholar]
- Wang, K.; Zhang, G.; Wang, Y.; Zhang, X.; Li, K.; Guo, W.; Du, F. A numerical investigation of hydraulic fracturing on coal seam permeability based on PFC-COMSOL coupling method. Int. J. Coal Sci. Technol. 2022, 9, 10. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, W.; Chen, J.; Xiao, X.; Li, Y.; Zhao, X. Simulation of hydraulic fracturing using particle flow method and application in a coal mine. Int. J. Coal Geol. 2014, 121, 1–13. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, L.; Pan, Z.; Han, Z. Numerical investigation of fluid-driven near-borehole fracture propagation in laminated reservoir rock using PFC2D. J. Nat. Gas Sci. Eng. 2016, 36, 719–733. [Google Scholar] [CrossRef]
- Wang, G.; Al-Ostaz, A.; Cheng, A.D.; Mantena, P.R. Hybrid lattice particle modeling of wave propagation induced fracture of solids. Comput. Methods Appl. Mech. Eng. 2009, 199, 197–209. [Google Scholar] [CrossRef]
- Jia, L.; Chen, M.; Zhang, W.; Xu, T.; Zhou, Y.; Hou, B.; Jin, Y. Experimental study and numerical modeling of brittle fracture of carbonate rock under uniaxial compression. Mech. Res. Commun. 2013, 50, 58–62. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Ge, S.; Reza, M.; Li, Z. Investigation on the influence mechanism of rock brittleness on rock fragmentation and cutting performance by discrete element method. Measurement 2018, 113, 120–130. [Google Scholar]
- Ferellec, J.F.; Mochizuki, C.; Hirata, A. DEM simulation of bulk material flow in a feeding system of blast furnace. In Numerical Modeling in Micromechanics via Particle Methods-2004, Proceedings of the 2nd International PFC Symposium, Kyoto, Japan, 28–29 October 2004; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Shimizu, Y.; Cundall, P.A. Three-dimensional DEM simulations of bulk handling by screw conveyors. J. Eng. Mech. 2001, 127, 864–872. [Google Scholar] [CrossRef]
- Peng, Z.; Doroodchi, E.; Luo, C.; Moghtaderi, B. Influence of void fraction calculation on fidelity of CFD-DEM simulation of gas-solid bubbling fluidized beds. AIChE J. 2014, 60, 2000–2018. [Google Scholar] [CrossRef]
- Xiao, H.; Sun, J. Algorithms in a robust hybrid CFD-DEM solver for particle-laden flows. Commun. Comput. Phys. 2011, 9, 297–323. [Google Scholar] [CrossRef]
- Babic, M. Average balance equations for granular materials. Int. J. Eng. Sci. 1997, 35, 523–548. [Google Scholar] [CrossRef]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Donald, H. Computer Graphics with OpenGL; Pearson Education: Chennai, India, 2004. [Google Scholar]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media; Springer Science & Business Media: Singapore, 2012; Volume 1. [Google Scholar]
- Furtney, J.; Zhang, F.; Han, Y. Review of methods and applications for incorporating fluid flow in the discrete element method. In Proceedings of the 3rd International FLAC/DEM Symposium, Hangzhou, China, 22–24 October 2013. [Google Scholar]
- Guyer, J.E.; Wheeler, D.; Warren, J.A. FiPy: Partial differential equations with Python. Comput. Sci. Eng. 2009, 11, 6–15. [Google Scholar] [CrossRef]







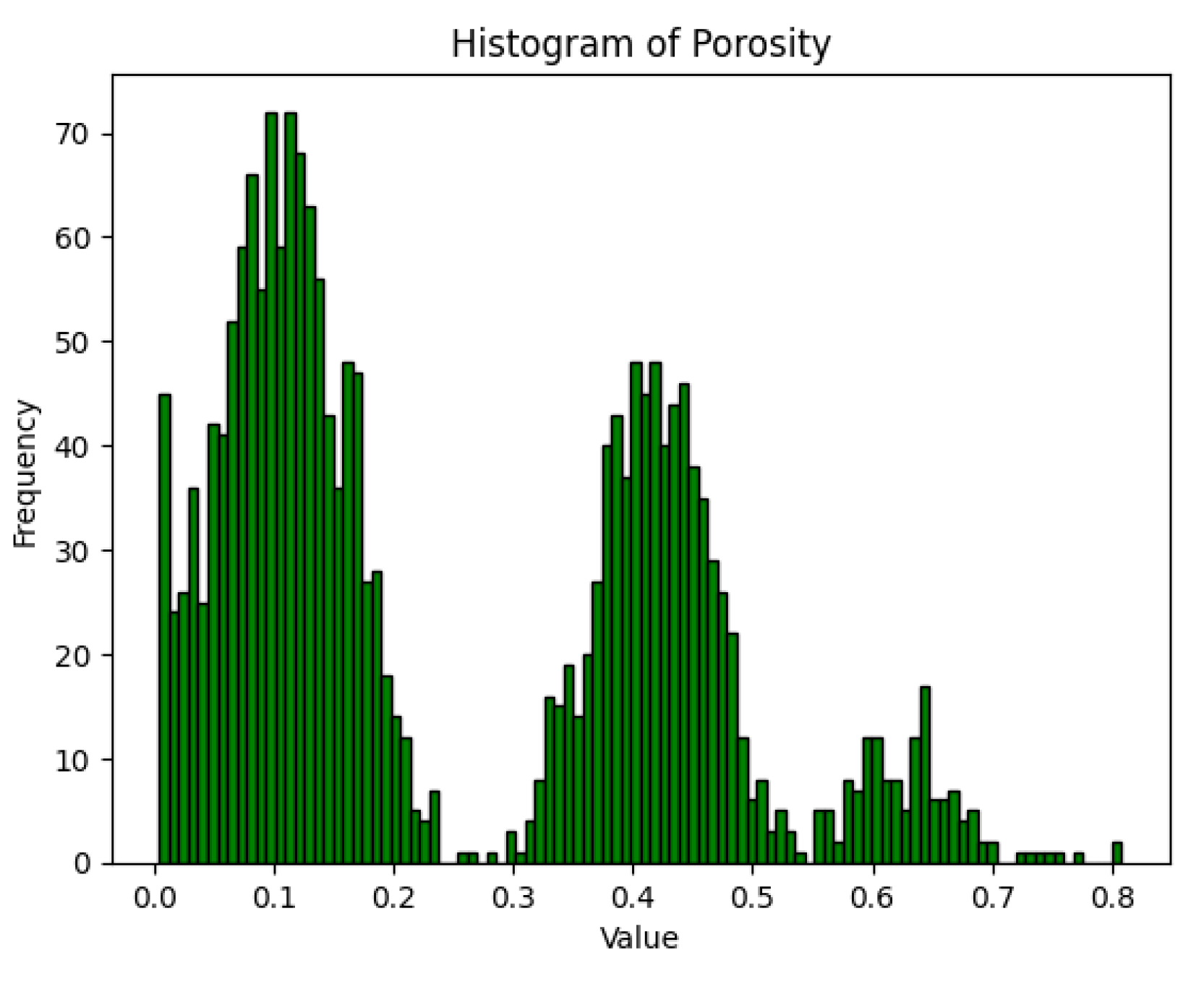
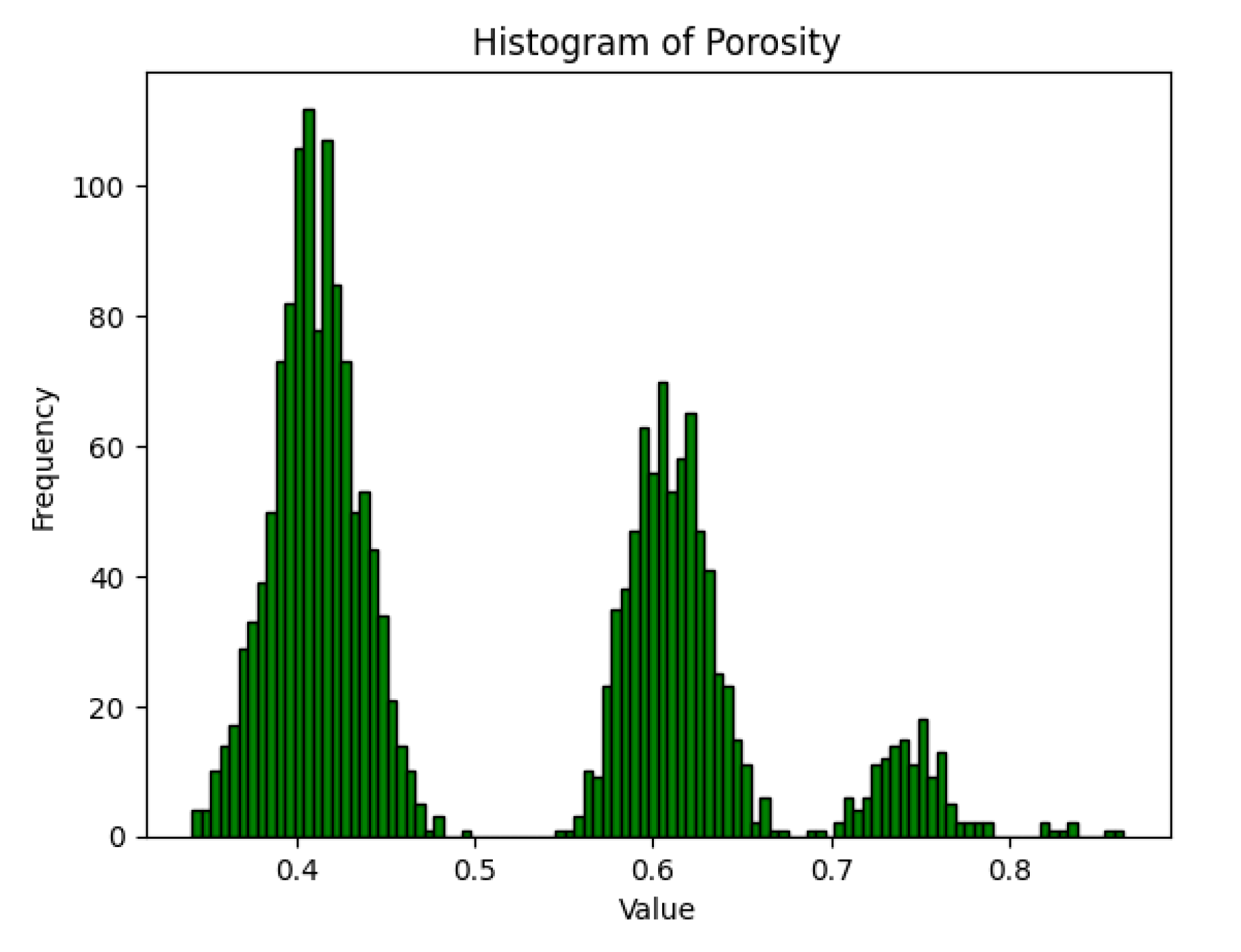
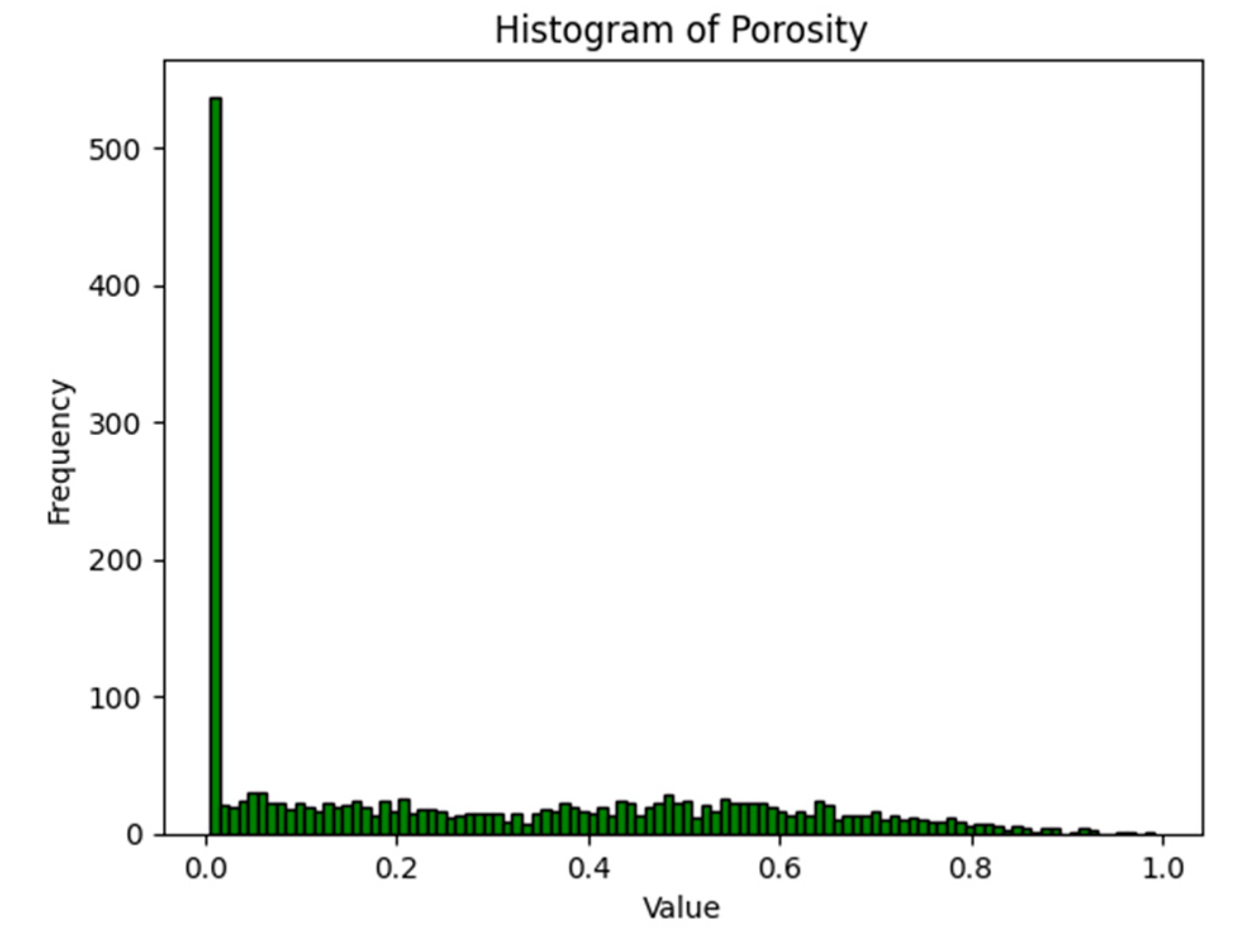

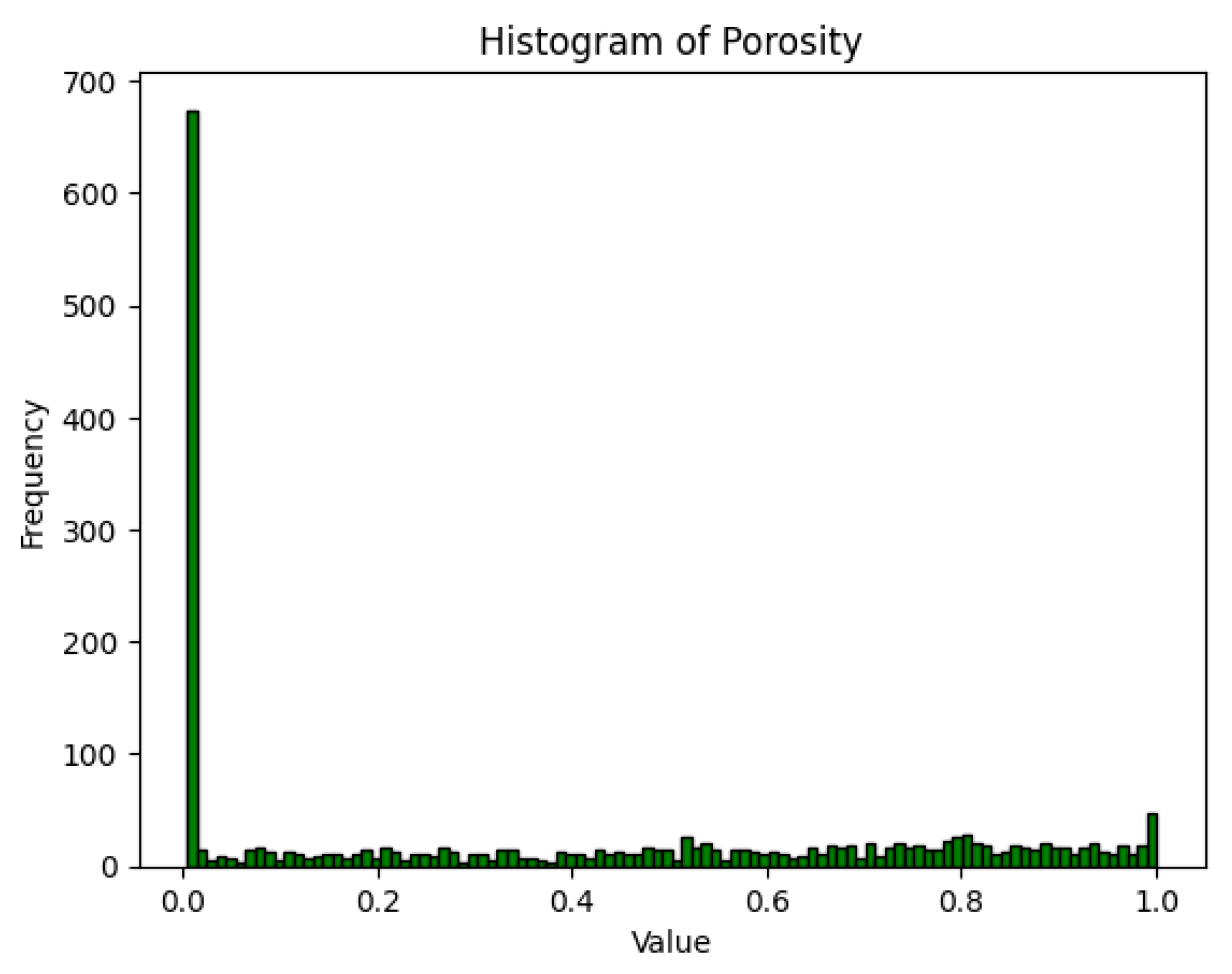


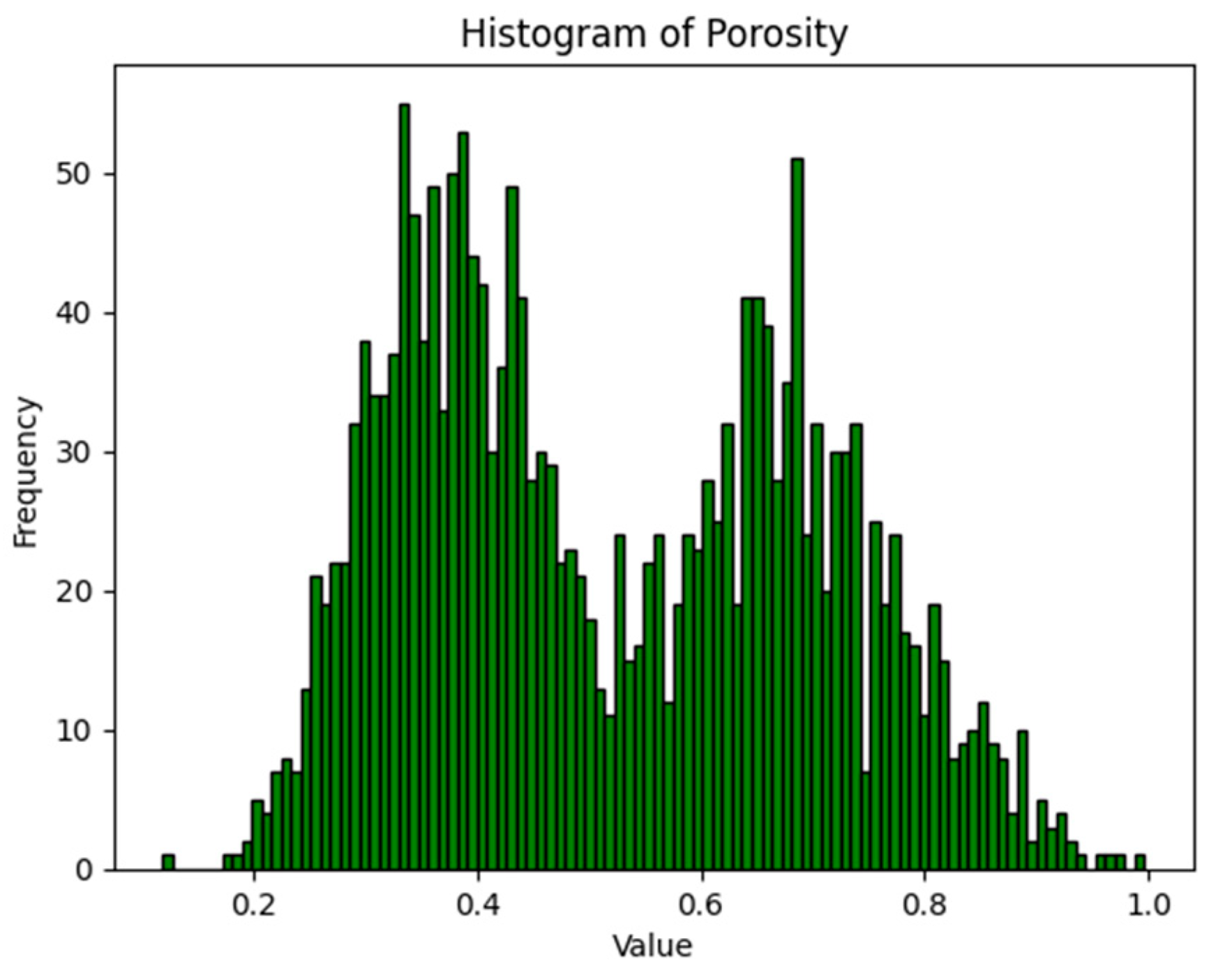
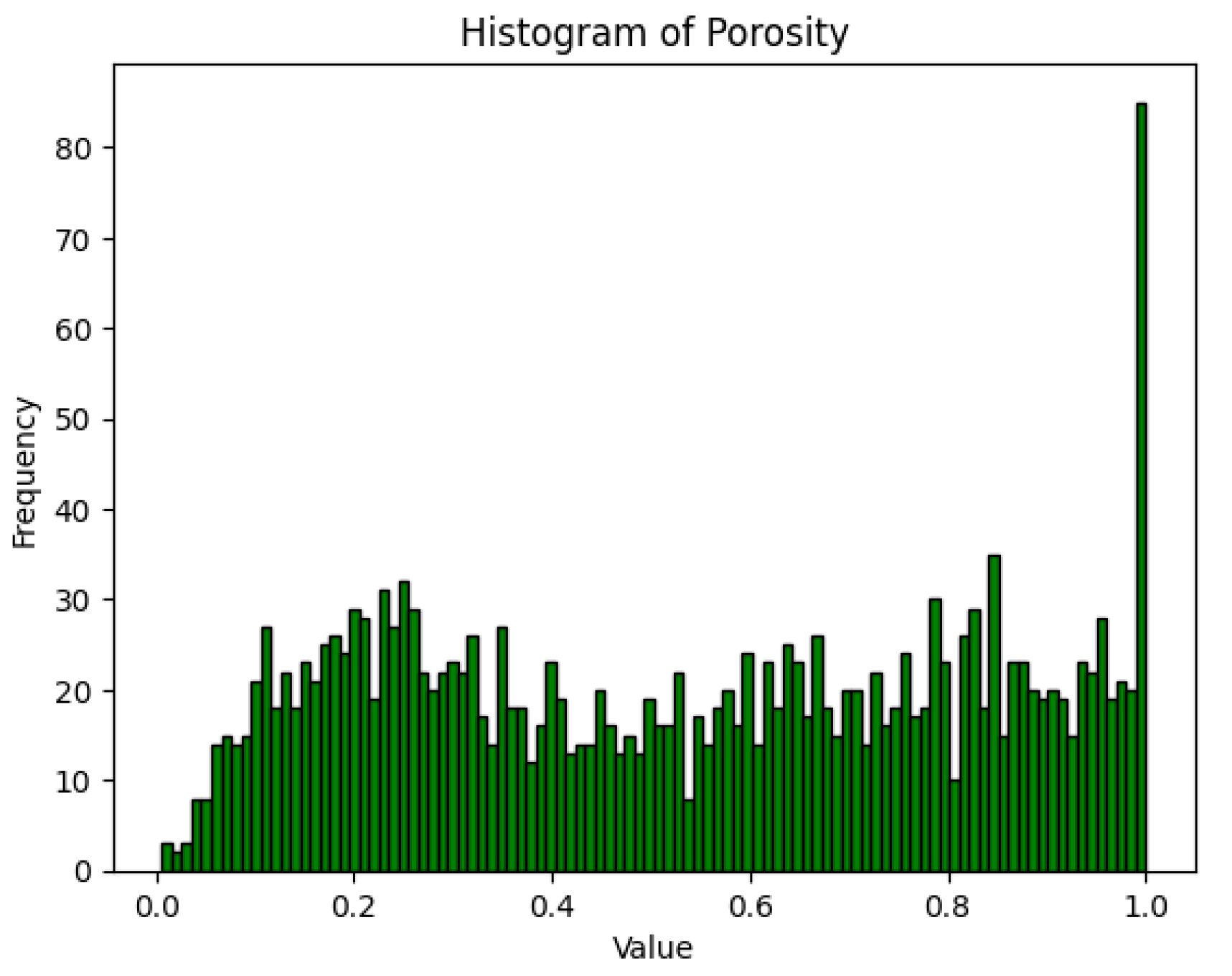
| Theoretical Value | Calculated in This Paper | Error | Radius |
|---|---|---|---|
| 4.2 | 1 | 76.1% | 1 |
| 33.5 | 35 | −4.4% | 2 |
| 113.1 | 93 | 17.8% | 3 |
| 268.1 | 223 | 16.8% | 4 |
| 523.6 | 529 | −1.0% | 5 |
| 904.8 | 819 | 9.5% | 6 |
| 1436.8 | 1405 | 2.2% | 7 |
| 2144.7 | 1987 | 7.4% | 8 |
| 3053.6 | 2845 | 6.8% | 9 |
| 4188.8 | 4175 | 0.3% | 10 |
| 5575.3 | 5425 | 2.7% | 11 |
| 7238.2 | 7111 | 1.8% | 12 |
| 9202.8 | 8985 | 2.4% | 13 |
| 11,494.0 | 11,267 | 2.0% | 14 |
| 14,137.2 | 13,793 | 2.4% | 15 |
| 17,157.3 | 16,595 | 3.3% | 16 |
| 20,579.5 | 20,165 | 2.0% | 17 |
| 24,429.0 | 24,115 | 1.3% | 18 |
| 28,730.9 | 28,461 | 0.9% | 19 |
| 33,510.3 | 32,943 | 1.7% | 20 |
| 38,792.4 | 37,969 | 2.1% | 21 |
| 44,602.2 | 43,823 | 1.7% | 22 |
| 50,965.0 | 50,537 | 0.8% | 23 |
| 57,905.8 | 57,115 | 1.4% | 24 |
| 65,449.8 | 64,025 | 2.2% | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Xin, X.; Cui, Y.; Yu, G. An Improved Porosity Calculation Algorithm for Particle Flow Code. Processes 2024, 12, 1410. https://doi.org/10.3390/pr12071410
Zhang S, Xin X, Cui Y, Yu G. An Improved Porosity Calculation Algorithm for Particle Flow Code. Processes. 2024; 12(7):1410. https://doi.org/10.3390/pr12071410
Chicago/Turabian StyleZhang, Siyu, Xiankang Xin, Yongzheng Cui, and Gaoming Yu. 2024. "An Improved Porosity Calculation Algorithm for Particle Flow Code" Processes 12, no. 7: 1410. https://doi.org/10.3390/pr12071410
APA StyleZhang, S., Xin, X., Cui, Y., & Yu, G. (2024). An Improved Porosity Calculation Algorithm for Particle Flow Code. Processes, 12(7), 1410. https://doi.org/10.3390/pr12071410






