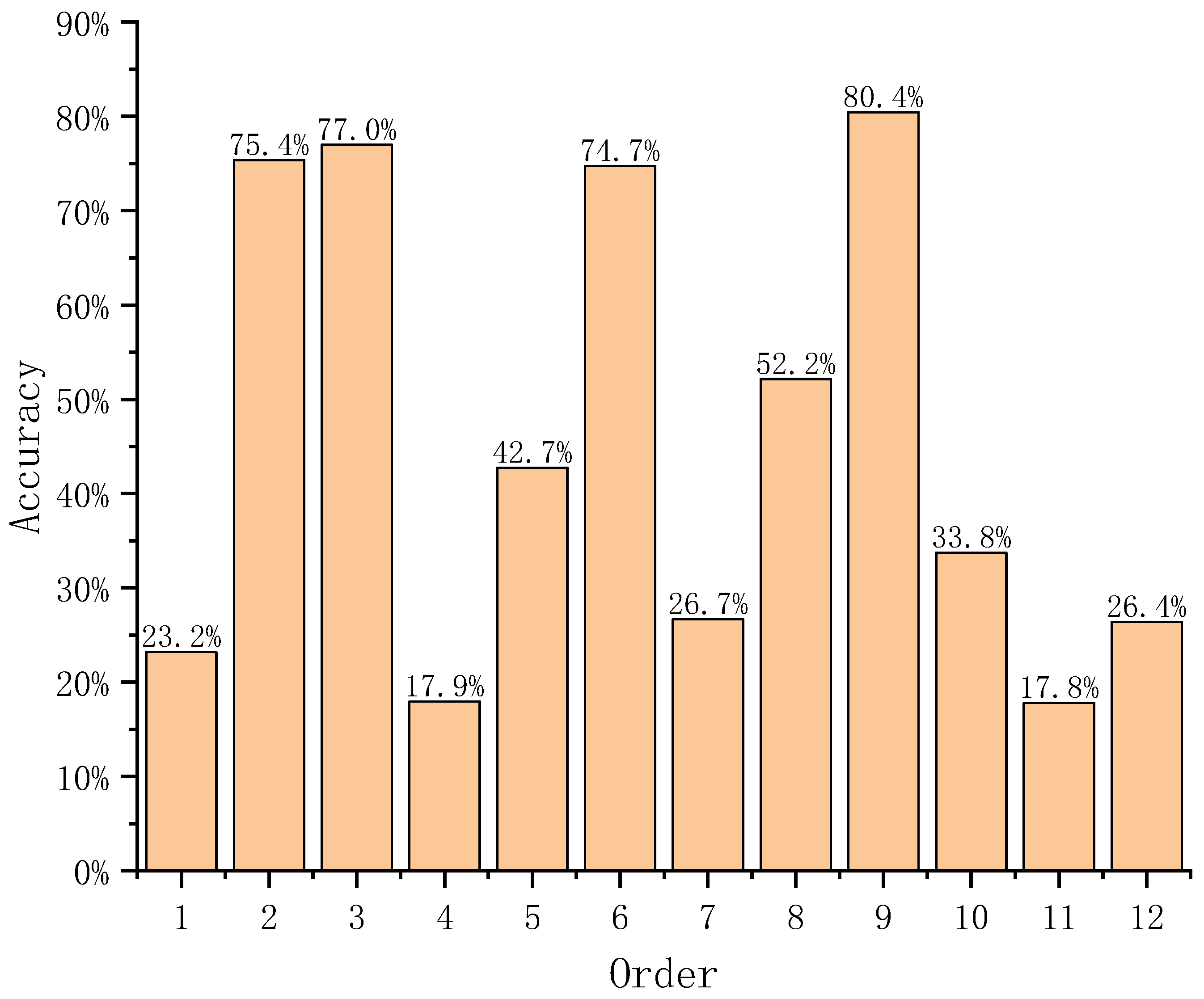Enhancing Damage Localization in GFRP Composite Plates: A Novel Approach Using Feedback Optimization and Multi-Label Classification

Abstract

Damage localization in GFRP (glass-fiber-reinforced polymer) composite plates is a crucial research area in marine engineering. This study introduces a feedback-based damage index (DI) combined with multi-label classification to enhance the accuracy of damage localization and address scenarios involving multiple damages. The research begins with the creation of a modal database for yachts’ GFRP composite plates using finite element modeling (FEM). A method for deriving a feedback-weighted matrix, based on the accuracy of the DI, is then developed. Sensitivity analysis reveals that the feedback DI is 50% more sensitive than the traditional DI, reducing false positives and missed detections. The associated feedback-weighted matrix depends solely on the structural shape, ensuring its transferability. To address the challenge for localizing multiple damages, a multi-label classification approach is proposed. The synergy between the feedback optimization and multi-label classification enables the rapid and precise localization of multiple damages in GFRP composite plates. Modal testing on damaged GFRP plates confirms the enhanced accuracy for combining the feedback DI with multi-label classification for pinpointing damage locations. Compared with traditional methods, this feedback DI method improves sensitivity, while multi-label classification effectively handles multiple damage scenarios, enhancing the overall efficiency of the damage diagnosis. The effectiveness of the proposed methods is validated through experimentation, offering robust theoretical support for composite plate damage diagnostics.

1. Introduction

Compared with traditional metals, GFRP exhibits higher specific strength and stiffness, excellent corrosion resistance, and superior fatigue performance [1,2]. Consequently, GFRP is increasingly replacing traditional metals in structural applications and has had widespread use in marine structures. During operation, these materials may sustain damage due to factors such as fatigue loads, impacts from external objects, and environmental conditions (e.g., humidity and temperature). Notably, even low-speed impacts can inflict internal damage on GFRP structures, leading to matrix cracking, delamination, fiber fracture, and other forms of damage. If such damage is not promptly detected, it could result in catastrophic failure [3,4]. Therefore, the early detection of damage in GFRP structures using non-destructive testing (NDT) methods is of paramount importance.

Traditional NDT techniques, such as ultrasonics [5,6], acoustic emission [7,8], and thermal imaging [9], primarily focus on detecting material discontinuities, like cracks and defects, to determine the presence of damage within or on the surface of structures. However, these methods have notable limitations, including stringent requirements for the testing environment, restrictions on the size of the structure that can be tested, and high operational costs, rendering them less suitable for marine engineering applications [10]. In contrast, vibration-based non-destructive diagnostic techniques offer significant benefits, such as the capability to globally assess large structures at a lower cost. Recent advancements in control technology, signal processing, and algorithm development have further enhanced the efficacy of vibration-based non-destructive diagnostic methods [11,12].

The technology of vibration-based non-destructive diagnosis primarily explores the relationship between modal parameters and structural damage. The diagnostic theory utilizing natural frequencies is relatively mature, as these frequencies are easily obtainable and have been commonly researched from earlier studies. Cawley et al. [13] introduced a diagnostic method based on the variation ratios of natural frequencies, demonstrating through matrix perturbation theory that the ratio of the natural frequency changes in any two orders before and after the damage is solely a function of the damage location. Hearn [14] proposed using the natural frequency square variation ratio for diagnosing structural damage locations. Wu et al. [15] investigated damage diagnosis in a cantilever beam using natural frequencies and modal shapes. Despite being an overall indicator of structural stiffness, natural frequencies exhibit low sensitivity, limiting their use for damage diagnosis primarily to the localization of single damages in simple structures. The diagnosis of multi-damaged structures using natural frequencies often leads to errors. The diagnostic method based on modal shapes, typically combined with perturbation theory, faces challenges when the area or degree of structural damage is minimal, resulting in insignificant changes in modal shapes. Thus, modal shapes are generally used only to confirm the presence of damage [16]. Modal strain energy (MSE) proves to be effective for diagnosing structural damage using low-order incomplete modes. Seyedpoor [17] and Lale Arefi [18] discussed a two-step MSE diagnosis approach for structural damage. Fu et al. [19] applied the modal strain energy change ratio (MSECR) for identifying damage locations in plate structures and proposed a method to mitigate the nearby effect, reducing mislocalization. Wei et al. [20] optimized the damage-degree diagnosis using finite element models and the strain energy method based on the response’s sensitivity. Although MSE is highly practical, calculating a structure’s modal strain energy requires computing the element stiffness matrix, which can impose a significant computational burden.

Compared to modal shapes and natural frequencies, modal curvature offers higher sensitivity and requires fewer computations than MSE, presenting a wide scope for application in structural damage diagnosis. Pandey [21] was the first to suggest the use of modal curvature for damage diagnosis by calculating the modal curvature of a simply supported beam from modal shapes and verifying the method’s accuracy. Abdel Wahab and De Roeck [22] introduced a one-dimensional modal-curvature-based DI that could enhance the accuracy of damage diagnosis, demonstrating its effectiveness with numerical data from beam models. Long Viet Ho [23] expanded this approach to two-dimensional models and defined the DI for plate structures. In conclusion, for large-scale structures, like ships, NDT methods grounded in modal parameters are the most apt. Among these, the modal-curvature-based technique stands out for its ability to diagnose multiple damages and its minimal computational demand.

In recent years, machine-learning technology has emerged as a significant research direction in the field of damage diagnosis [24]. Notably, multi-label classification technology, with its capability to process complex data patterns, has demonstrated considerable promise across various domains, including image recognition, text classification, and medical diagnosis [25]. The adoption of this technology in damage diagnosis, particularly for addressing complex damage patterns and interactions between damages, offers an effective approach.

Recent research highlights that deep-learning technologies, such as convolutional neural networks (CNNs) [26] and recurrent neural networks (RNNs) [27], excel in tackling multi-label classification challenges. Their capacity to accurately capture and classify complex data patterns positions them as particularly effective in multi-label classification applications, thereby enhancing their utility and efficiency in the field of damage diagnosis.

For composite plates featuring multiple damage locations, traditional methods of damage localization exhibit a lack of sensitivity, complicating the precise identification of damage sites. In response, this paper introduces a method termed “feedback optimization”. This approach enhances sensitivity and accuracy in damage localization by analyzing changes in modal parameters and integrating them with optimization algorithms. The incorporation of a weighting mechanism within feedback optimization facilitates the adaptive adjustment of the DI calculation method, catering to diverse damage characteristics. This significantly boosts the sensitivity and precision of damage localization in multi-damage scenarios. Additionally, this paper investigates the integration of the feedback optimization method with multi-label classification technology. This synergistic approach capitalizes on the robust data processing capabilities of multi-label classification to concurrently detect and pinpoint multiple damage sites within a structure. By combining these two methods, not only the accuracy for identifying multiple damage points can be improved but also the interactions between damages can be handled, thus providing a more comprehensive and efficient solution for assessing the integrity of composite plates.

The paper is organized as follows: Section 2 establishes the connection between the stiffness of the composite plate structures and damage through the failure criteria of composite plates, laying the foundation for the creation of a damaged-composite-plate database. Section 3 introduces the feedback DI and studies its accuracy, sensitivity, and transferability. Section 4 proposes a scheme for diagnosing multiple damages using multi-label classification and explores the advantages for combining multi-label classification with the feedback DI. The experimental results and discussion are provided in Section 5. Finally, the conclusions are drawn in Section 6.

2. Failure Analysis of GFRP

To explore diagnostic methods for damage in GFRP, an analysis of GFRP failure is essential. This analysis, grounded in the fatigue damage mechanism of laminated composites, entails making failure judgments for predominant fatigue failure modes, such as matrix cracking, matrix yielding, matrix-fiber shearing, fiber breakage, fiber yielding, and delamination. The fatigue failure criteria adopted in this study are outlined in

Table 1. Fatigue failure criteria.

Failure Mode	Failure Criterion
$\mathrm{Matrix}\mathrm{tensile}\mathrm{cracking}\mathrm{for}({\sigma }_{yy}>0$)	${\left(\frac{{\sigma }_{yy}}{X_T}\right)}^2+{\left(\frac{{\sigma }_{xy}}{S_{xy}}\right)}^2+{\left(\frac{{\sigma }_{yz}}{S_{yz}}\right)}^2\ge 1$
$\mathrm{Matrix}\mathrm{compressive}\mathrm{cracking}\mathrm{for}({\sigma }_{yy}<0$)	${\left(\frac{{\sigma }_{yy}}{Y_T}\right)}^2+{\left(\frac{{\sigma }_{xy}}{S_{xy}}\right)}^2+{\left(\frac{{\sigma }_{xz}}{S_{xz}}\right)}^2\ge 1$
$\mathrm{Fiber}\mathrm{tensile}\mathrm{failure}\mathrm{for}({\sigma }_{xx}>0$)	$\frac{{\sigma }_{xx}}{X_T}\ge 1$
$\mathrm{Fiber}\mathrm{compressive}\mathrm{failure}\mathrm{for}({\sigma }_{xx}<0$)	$\frac{{\sigma }_{xx}}{X_C}\ge 1$
$\mathrm{Fiber}\text{-}\mathrm{matrix}\mathrm{shear}\mathrm{out}\mathrm{for}({\sigma }_{xx}<0$)	${\left(\frac{{\sigma }_{xx}}{X_C}\right)}^2+{\left(\frac{{\sigma }_{xy}}{S_{xy}}\right)}^2+{\left(\frac{{\sigma }_{xz}}{S_{xz}}\right)}^2\ge 1$
$\mathrm{Delamination}\mathrm{in}\mathrm{tension}\mathrm{for}({\sigma }_{zz}>0$)	${\left(\frac{{\sigma }_{zz}}{Z_T}\right)}^2+{\left(\frac{{\sigma }_{xz}}{S_{xz}}\right)}^2+{\left(\frac{{\sigma }_{yz}}{S_{yz}}\right)}^2\ge 1$
$\mathrm{Delamination}\mathrm{in}\mathrm{compression}\mathrm{for}({\sigma }_{zz}<0$)	${\left(\frac{{\sigma }_{zz}}{Z_C}\right)}^2+{\left(\frac{{\sigma }_{xz}}{S_{xz}}\right)}^2+{\left(\frac{{\sigma }_{yz}}{S_{yz}}\right)}^2\ge 1$

[28].

${\sigma }_{ij}$ represents the stress components in the principal material direction of each element, while $X_T$ and $X_C$ denote the tensile and compressive strengths in the fiber direction, respectively. $Y_T$ and $Y_C$ correspond to the transverse tensile and compressive strengths, respectively. $Z_T$ refers to the tensile strength in the thickness direction. $S_{xy}$ is the shear strength between the fiber and the transverse surface, $S_{yz}$ is the shear strength between the transverse and thickness directions, and $S_{xz}$ is the shear strength between the fiber and the thickness direction. $S_f$ represents the shear strength considering the fiber’s failure, $S_{myz}$ is the shear strength for matrix cracking in the transverse and thickness directions, and $S_{lyz}$ is the shear strength for delamination in the transverse and thickness directions. Once failure occurs in an element, the material properties of that element change, and the distribution of stress among the elements is consequently altered.

The damage process of GFRP can be categorized into two distinct phases: the gradual degradation of the material properties, followed by an abrupt decline as follows:

(a)

Gradual Degradation Model: For GFRP subjected to fatigue loads, the number of cycles incrementally inflicts progressive damage on the constituents of the GFRP. This sequential damage culminates in a gradual degradation in the material properties. The following stiffness degradation model utilized in this investigation is detailed in [29]:

$$E(n,\sigma ,k)={\left[1-{\left(\frac{\lg n-\lg 0.25}{\lg N_f-\lg 0.25}\right)}^{\lambda }\right]}^{1/\gamma }\left(E_0-\frac{\sigma }{{\epsilon }_f}\right)+\frac{\sigma }{{\epsilon }_f}$$

(1)

In the formula, $E_0$ represents the initial stiffness, while $\lambda$ and $\gamma$ are curve-fitting coefficients, which are independent of the stress. ${\epsilon }_f$ denotes the average strain at failure, as determined through fatigue testing. The fatigue life, $N_f$, under the maximum fatigue stress, $\sigma$, and stress ratio, $k$, can be calculated using the following equation [30]:

$$\frac{\ln \left(a/f\right)}{\ln \left[(1-m)(c+m)\right]}=A+B\lg N_f\left(a=\frac{{\sigma }_a}{{\sigma }_t},m=\frac{{\sigma }_m}{{\sigma }_t},c=\frac{{\sigma }_c}{{\sigma }_t}\right)$$

(2)

${\sigma }_t$ and ${\sigma }_c$ represent the tensile and compressive strengths, respectively. ${\sigma }_a$ is the amplitude of the fatigue load, and ${\sigma }_m$ is the mean stress of the fatigue load. The coefficients $f$, $A$, and $B$ are fitting parameters obtained through fatigue testing.

(b)

Abrupt Decline Model: Once damage accumulates beyond a certain threshold, the material properties of the compromised elements exhibit an abrupt decline, mirroring their diminished load-bearing capacity.

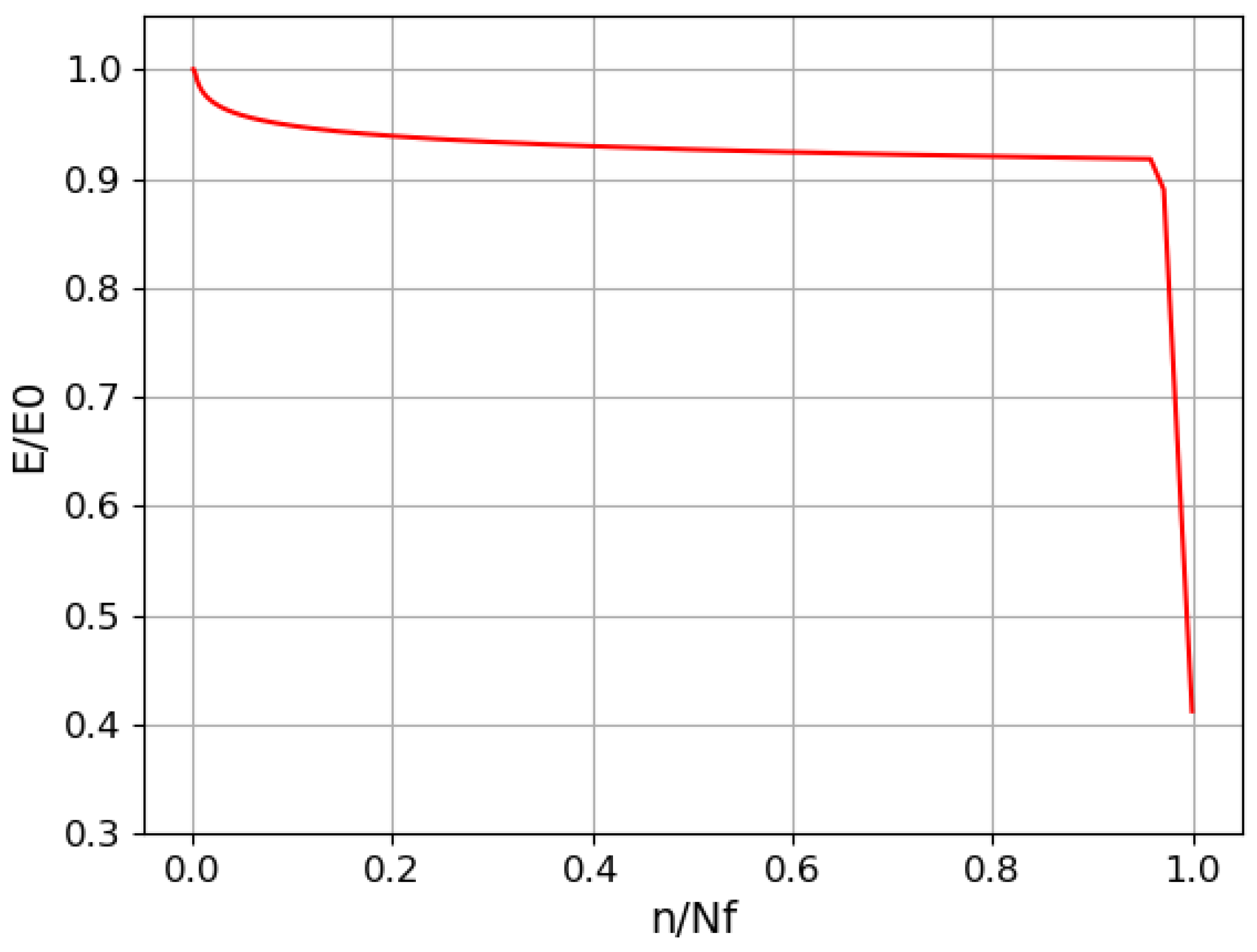
This phenomenon of stiffness reduction in GFRP is illustrated in Figure 1.

Notably, n/Nf represents the normalized fatigue life of the GFRP, and E/E0 represents the normalized stiffness of the GFRP.

As depicted in Figure 1, the variations in the GFRP stiffness effectively mirror the different stages of the damage that the GFRP undergoes. Assessing the stiffness of the GFRP serves as an efficient non-destructive diagnostic technique for evaluating the GFRP’s condition.

3. Damage Localization Based on the Feedback DI

The theory of the damage diagnosis based on the modal curvature [23] is as follows:

For a plate structure, the deflection field of the plate is given by $w(x,y)$, where $(x,y)$ represents the two-dimensional position of the plate, and $D(x,y)$ represents the flexural stiffness of the plate. The modal curvature, which is the second derivative of the deflection field, is expressed as follows:

$$C(x,y)={\mathsf{\nabla }}^{2}w(x,y)$$

(3)

${\mathsf{\nabla }}^2$ represents the Laplace operator, which denotes the second derivative of the deflection field in two-dimensional space.

Damage can cause local stiffness variations in the structure; if the flexural stiffness at $(x_0,y_0)$ changes to $D^{\prime }(x_0,y_0)$ then the deflection field, $w^{\prime }(x,y)$, at that location can be expressed as follows:

$$w^{\prime }(x,y)=w(x,y)+\Delta w(x,y)$$

(4)

$\Delta w(x,y)$ represents the deflection variation caused by the stiffness change.

The modal curvature after the deflection variation can be expressed as follows:

$$\begin{gathered} C^{\prime }(x,y)={\mathsf{\nabla }}^2\left(w\right(x,y)+\Delta w(x,y\left)\right) \\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}={\mathsf{\nabla }}^{2}w(x,y)+{\mathsf{\nabla }}^2\Delta w(x,y) \\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=C(x,y)+{\mathsf{\nabla }}^2\Delta w(x,y) \end{gathered}$$

(5)

The curvature is inversely proportional to the stiffness; the structural damage will reduce the local stiffness and increase the local curvature.

The modal curvature’s DI can be obtained using the above theory. To identify the modal slopes and modal curvatures, the first and second derivatives of the modal shapes are computed, respectively. The slope is denoted as ${\phi }^{\prime }$, and the curvature is denoted as ${\phi }^{″}$; they are determined using the central finite difference method. This involves using the displacement values of the modal shape in both the x-direction and y-direction for each mode.

In the x-direction:

$$\left\{\begin{array}{c}{\phi }_x^{\prime }\left(i,j\right)=\frac{\phi \left(i+1,j\right)-\phi \left(i-1,j\right)}{2\times l_x}\\ {\phi }_x^{″}\left(i,j\right)=\frac{\phi \left(i+1,j\right)+\phi \left(i-1,j\right)-2\times \phi \left(i,j\right)}{l_x^2}\end{array}\right.$$

(6)

In the y-direction:

$$\left\{\begin{array}{c}{\phi }_y^{\prime }\left(i,j\right)=\frac{\phi \left(i,j+1\right)-\phi \left(i,j-1\right)}{2\times l_y}\\ {\phi }_y^{″}\left(i,j\right)=\frac{\phi \left(i,j+1\right)+\phi \left(i,j-1\right)-2\times \phi \left(i,j\right)}{l_y^2}\end{array}\right.$$

(7)

where $l_x$ is the distance between two successive points in the x-direction, $l_y$ is the distance between two successive points in the y-direction, and $\phi \left(i,j\right)$ represents the displacement value of modal shape at the ith point in the x-direction and the jth point in the y-direction.

The slope and curvature of the modal shape of the pristine plate and damaged plate can be calculated as follows:

$$\left\{\begin{array}{c}{\theta }_H\left(i,j\right)=\sqrt{{{\phi }^{\prime }}_{x\_H}^2\left(i,j\right)+{{\phi }^{\prime }}_{y\_H}^2\left(i,j\right)}\\ {\kappa }_H\left(i,j\right)=\sqrt{{{\phi }^{″}}_{x\_H}^2\left(i,j\right)+{{\phi }^{″}}_{y\_H}^2\left(i,j\right)}\\ {\theta }_D\left(i,j\right)=\sqrt{{{\phi }^{\prime }}_{x\_D}^2\left(i,j\right)+{{\phi }^{\prime }}_{y\_D}^2\left(i,j\right)}\\ {\kappa }_D\left(i,j\right)=\sqrt{{{\phi }^{″}}_{x\_D}^2\left(i,j\right)+{{\phi }^{″}}_{y\_D}^2\left(i,j\right)}\end{array}\right.$$

(8)

where $\theta$ and $\kappa$ imply the slope and curvature of modal shape of the whole plate, respectively; subscript $H$ denotes the pristine plate; and subscript $D$ denotes the damaged plate.

Then, the differences between the modal shapes, $\Delta \phi$, and derivatives, $\Delta \theta$ and $\Delta \kappa$, of the pristine and damaged plates are calculated as follows:

$$\left\{\begin{array}{c}\Delta \theta \left(i,j\right)=\left|{\theta }_D\left(i,j\right)\right|-\left|{\theta }_H\left(i,j\right)\right|\\ \Delta \kappa \left(i,j\right)={\kappa }_D\left(i,j\right)-{\kappa }_H\left(i,j\right)\\ \Delta \phi \left(i,j\right)={\phi }_D\left(i,j\right)-{\phi }_H\left(i,j\right)\\ \Delta {\phi }^2\left(i,j\right)={\phi }_D^2\left(i,j\right)-{\phi }_H^2\left(i,j\right)\end{array}\right.$$

(9)

The parameters in Formula (7) are used to calculate the DI at all the nodes on the plate as follows:

$$DI=\left|\left(\left|\Delta \kappa \right|\times \Delta {\phi }^2\right)-\left(\Delta {\theta }^2\times \Delta \phi \right)\right|\times \Delta \kappa$$

(10)

The normalized form of the DI is calculated based on the mean and standard deviation for all the nodes on the plate as follows:

$$DI=\left\{\begin{array}{c}0,DI\le 0\hfill \\ \frac{DI-mean\left(DI\right)}{std\left(DI\right)},DI>0\end{array}\right.$$

(11)

Each mode can obtain a DI, and the DI can be obtained by linearly adding all the DIs as follows:

$$TotalDI=\sum _{mode=1}^n{DI}_{mode}$$

(12)

The DI is a matrix that represents the rate of change in the structural modal curvature, with each element corresponding to the rate of change in the modal curvature at the location of the structure’s modal shape. When the individual elements in the DI matrix increase, it indicates a significant change in the modal curvature at the corresponding location of the structure. According to Equations (3)–(5), damage is likely to have occurred at that location.

3.1. Research on the Accuracy of DI Based on Statistical Methods

Most studies on damage diagnosis rely on a restricted set of simulations and experiments to validate their algorithms. To investigate the accuracy of the DI, a comprehensive structural damage database for composite plates was developed using the finite element method.

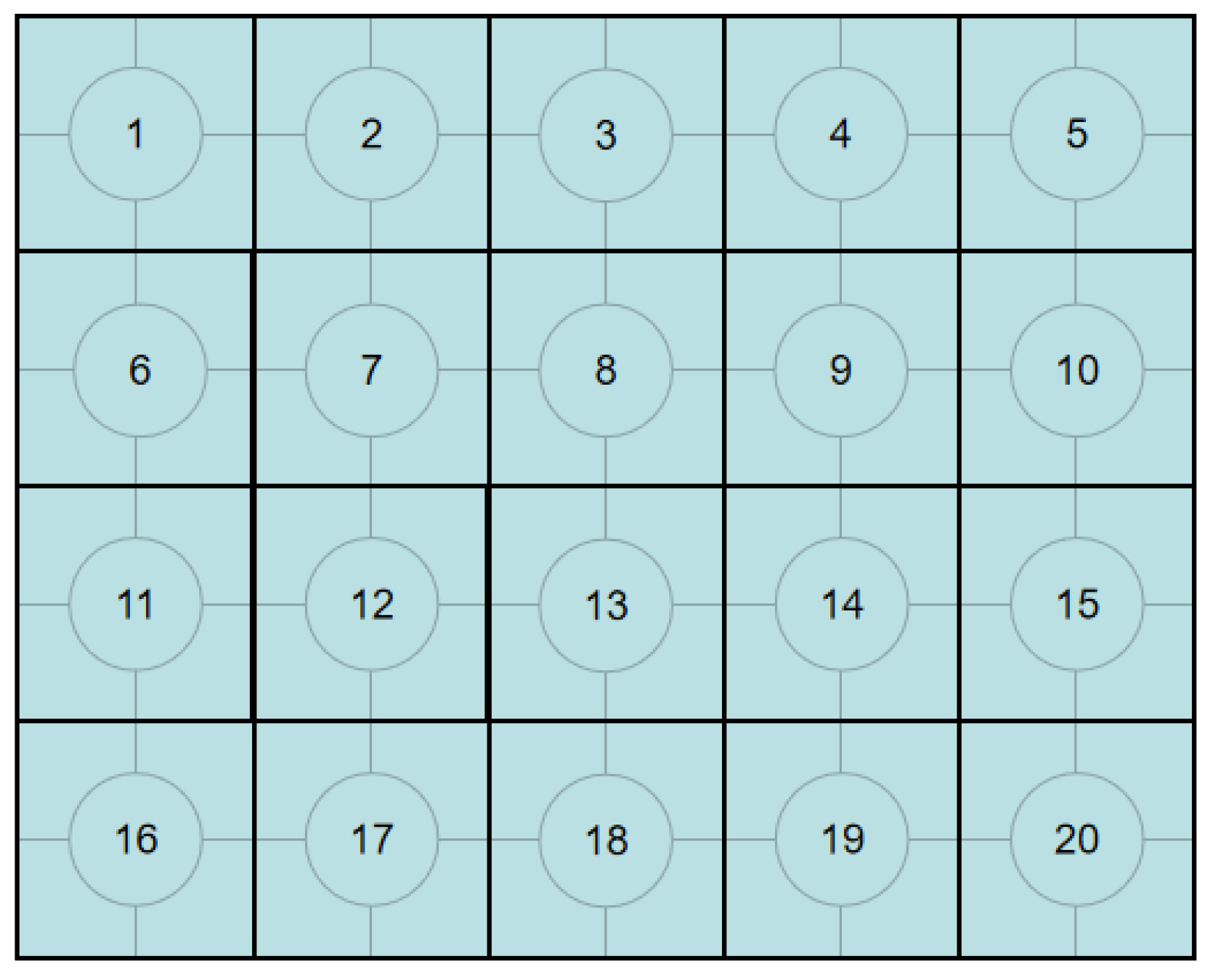
The geometric configuration of the composite plate is rectangular, measuring 0.5 m in length and 0.4 m in width. The plate is constructed from ply materials, including PVC foam and epoxy e-glass wet, with its ply design detailed in

Table 2. Ply design of GFRP composite plate.

Layer	Material	Angle	Thickness	Density	Poisson’s Ratio	Young’s Modulus	Shear Modulus
1	PVC Foam (80 kg/m3)	0°	12 mm	80 kg/m3	0.3	0.1 GPa	0.04 GPa
2	Epoxy E-Glass Wet	±45°	1.2 mm	1850 kg/m3	0.28	35 GPa	4.7 GPa
					0.28	9 GPa	4.7 GPa
					0.4	9 GPa	3.5 GPa

. As depicted in Figure 2, the plate is segmented into 20 square sections, each with a dimension of 0.1 m on a side, which are further subdivided into four quadrants for the purpose of the curvature analysis. The plate is subjected to free-boundary conditions. The database comprises 12,600 damage models, formulated based on fatigue failure criteria. These models encapsulate various stages of damage in GFRP, including 5400 models for single-layer damage, 5400 for double-layer damage, and 1800 models representing complete damage.

For the finite element model, S4R shell elements were used with a mesh size of 0.05 m × 0.05 m rectangles. This modeling approach was determined based on two key considerations: (1) Modal analysis does not require an overly detailed mesh division, and (2) a significant number of finite element model calculations must be performed. Balancing these factors enabled us to efficiently conduct our analyses while maintaining the integrity of our results.

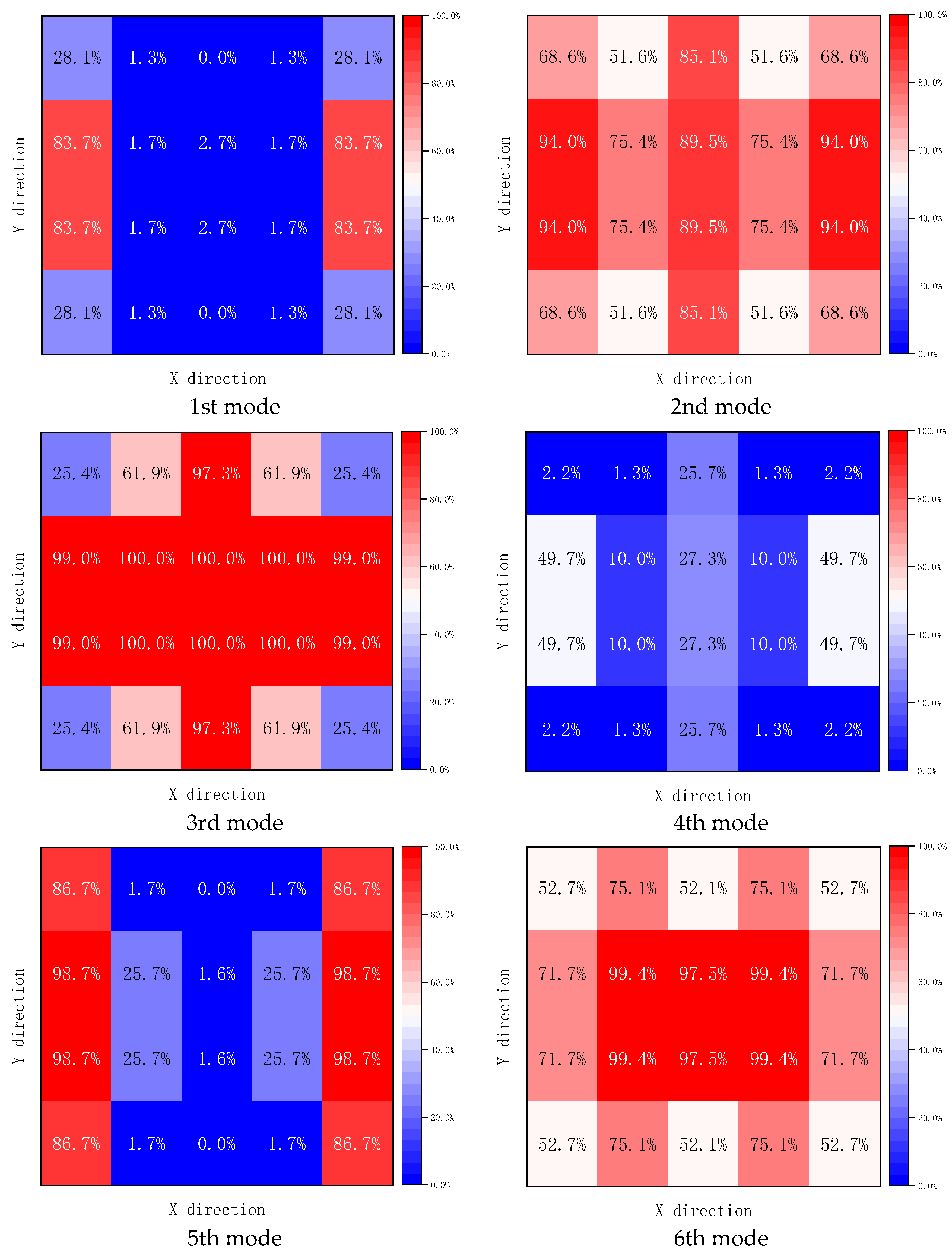
The modal shapes for all the models within the database are determined using the FEM. Any rigid body modal shapes are excluded from consideration. The 12 modal shapes of the pristine composite plate are depicted in Figure 3.

The DIs for all the damaged composite plates in the database are calculated using Formulas (6)–(12). The DI is deemed as being accurate for the damage localization of the given damaged modal shape when the maximum value of the DI coincides with the damaged part. By statistically analyzing the damage localization results from all the models in the database, the accuracy of the DI is presented in

Table 3. The accuracy of the DI.

	Correct	Accuracy
DI	9126	72.43%

.

A DI indicative of incorrect damage localization is illustrated in Figure 4. In the figure, the red square represents the predetermined damage location, whereas the peak of the DI, marking the identified damage location, is situated adjacent to the red area, potentially resulting in a misdiagnosis. This scenario serves as a typical example and could be addressed by augmenting the number of nodes; however, this adjustment would excessively complicate the damage localization process.

3.2. Feedback Optimization Method for the Modal Curvature’s DI

To enhance the precision of the damage localization in composite plates via the DI, each order of the DI was analyzed individually. The accuracy of the damage localization was determined for each order of the DI across all the models. The localization accuracy for the composite plates at each order is depicted in Figure 5.

Figure 5 illustrates that certain orders of the DI have a minimal impact on the accuracy of the damage localization, leading to a reduction in the overall accuracy. Notably, the highest accuracy attained through the application of the 9th order of the DI is merely 80.4%. Consequently, additional research is warranted to explore how the position of the damage influences the accuracy of the damage localization.

The distribution of the accuracy across each order is depicted in Figure 6. It is evident that the location of the damage significantly affects the efficacy of the damage localization. This variation in effectiveness is attributed to the presence of different boundary conditions in various regions of a structure, as illustrated in Figure 7. Such disparate boundary conditions result in distinct dynamic responses in different areas.

The analysis of the results presented in Figure 6 reveals that various orders of the DI possess differing levels of accuracy at different damage locations. For instance, the 3rd order DI demonstrates high accuracy for damage located in the middle of the composite plate but performs suboptimally for damage situated at the corners. In contrast, the 5th order DI achieves greater accuracy for corner damages. Adhering to this pattern, employing a reasoned weighted calculation for the DI can markedly enhance the DIs precision.

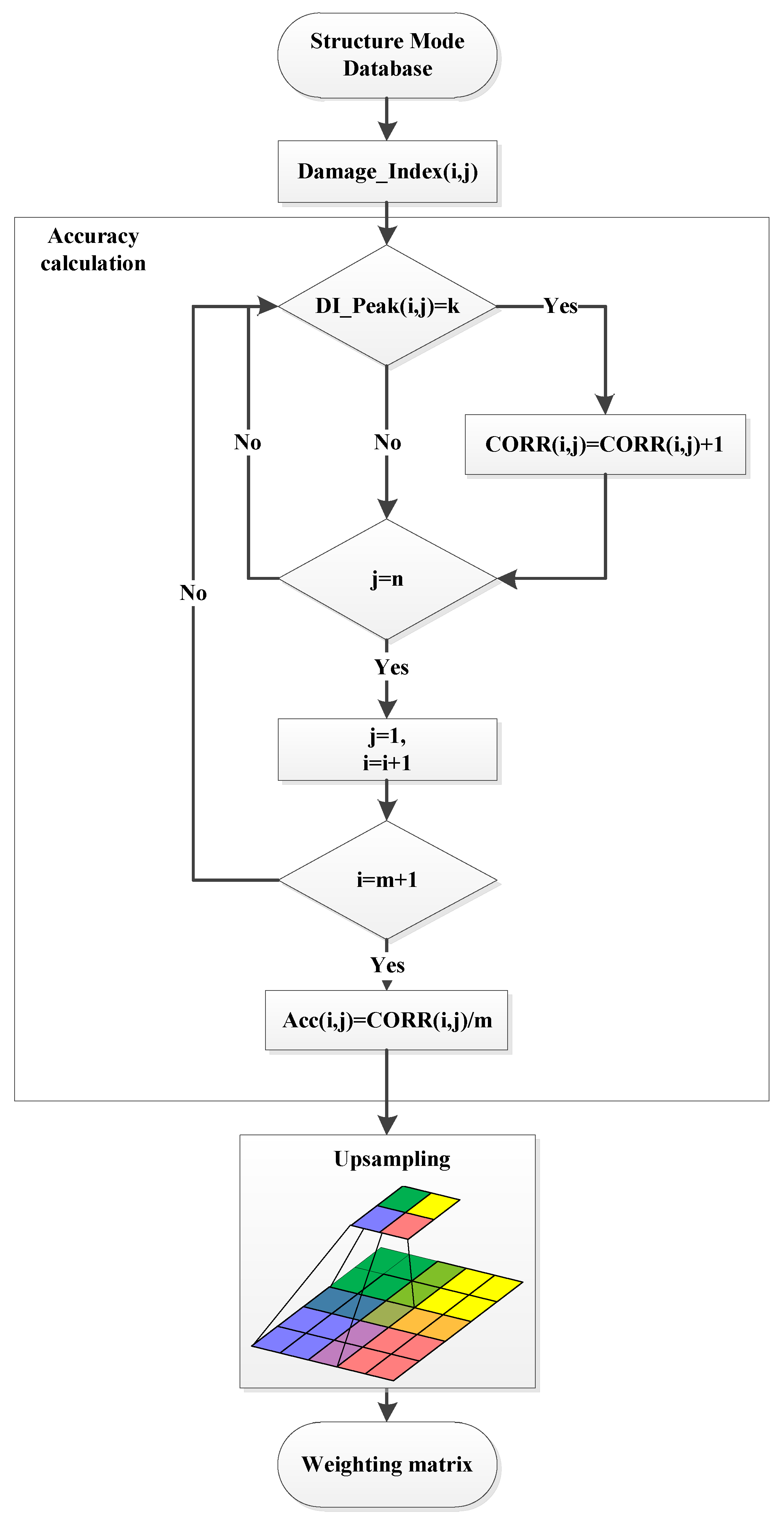
Figure 6 illustrates the accuracy of the DI at various damage locations across different orders. Given that the accuracy of the damage localization correlates with the weight of the DI, the weight assigned to the DI can be determined based on the accuracy of the damage localization. Figure 8 presents the flowchart for computing the feedback-weighted matrix for the DI. In Figure 8, i is the modal order, j is the model number, k is the number of damage locations, m is the highest modal order of the model, n is the number of models, DI_peak is the number of elements where the maximum value of the DI is located, CORR is the number of correct diagnoses, and ACC is the diagnostic accuracy. The principle for calculating the feedback-weighted matrix is as follows: Based on the damaged-composite-plate database, the accuracy of the DI for all the damage locations in the composite plate’s structure is statistically analyzed. The accuracy is then used as a weight to alter the distribution of the DI, achieving the purpose of the feedback optimization.

To upsample the accuracy matrix into a feedback-weighted matrix using a transpose convolution, a three-dimensional transpose convolutional kernel is defined as follows:

$$K=\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$$

(13)

Then, the accuracy matrix is upsampled into the feedback-weighted matrix as follows:

$$Weight(i,j)=\sum _m\sum _{n}K(m,n)\ast Acc(i+m,j+n)$$

(14)

$$FeedbackDI=Weight·DI$$

(15)

where m and n represent the row and column indices of the transpose convolutional kernel, respectively. The center of the transpose convolutional kernel is aligned with the corresponding position in the accuracy matrix.

The process of the feedback optimization was applied to the DI, resulting in an enhanced version known as the feedback DI. The models contained within the composite-plate database underwent damage localization using this feedback DI, with the outcomes detailed in

Table 4. The accuracy of the feedback DI.

	Correct	Accuracy
Feedback DI	11,662	92.56%

. When compared to the data presented in Table 3, the accuracy of the damage localization in the composite plate significantly increased from 72.43% to 92.56% following the implementation of the feedback optimization.

3.3. Sensitivity Analysis of the DI

Sensitivity, as defined by Formula (16), primarily gauges the distinctiveness of the DI at the site of the damage within the overall DI matrix. A higher DI value at the location of the damage indicates a greater sensitivity of the DI, which, in turn, enhances the effectiveness of the damage localization. Sensitivity serves as a metric to assess the capability of a technique to accurately identify structural damage. Low sensitivity in a damage diagnosis technique may lead to errors during the diagnostic process. Missed detections could compromise the safety and reliability of the structure, posing a significant risk. Conversely, false positives can result in unnecessary expenditures. Subsequently, the sensitivity of both the DI and feedback DI in the damage diagnosis performance will be compared.

$$Sensitivity=\sum _{i=1}^n\frac{\mathit{max}\left({DI}_i\right)/sum\left({DI}_i\right)}{n}$$

(16)

The subscript $i$ represents the model number, $n$ represents the total number of models, $max$ represents the maximum value in the matrix, and $sum$ represents the total of the matrix elements. The models in the composite-plate database are used to compare the sensitivity between the DI and the feedback DI, as shown in

Table 5. The sensitivity of the DI.

	DI	Feedback DI
Sensitivity	0.1973	0.3055

.

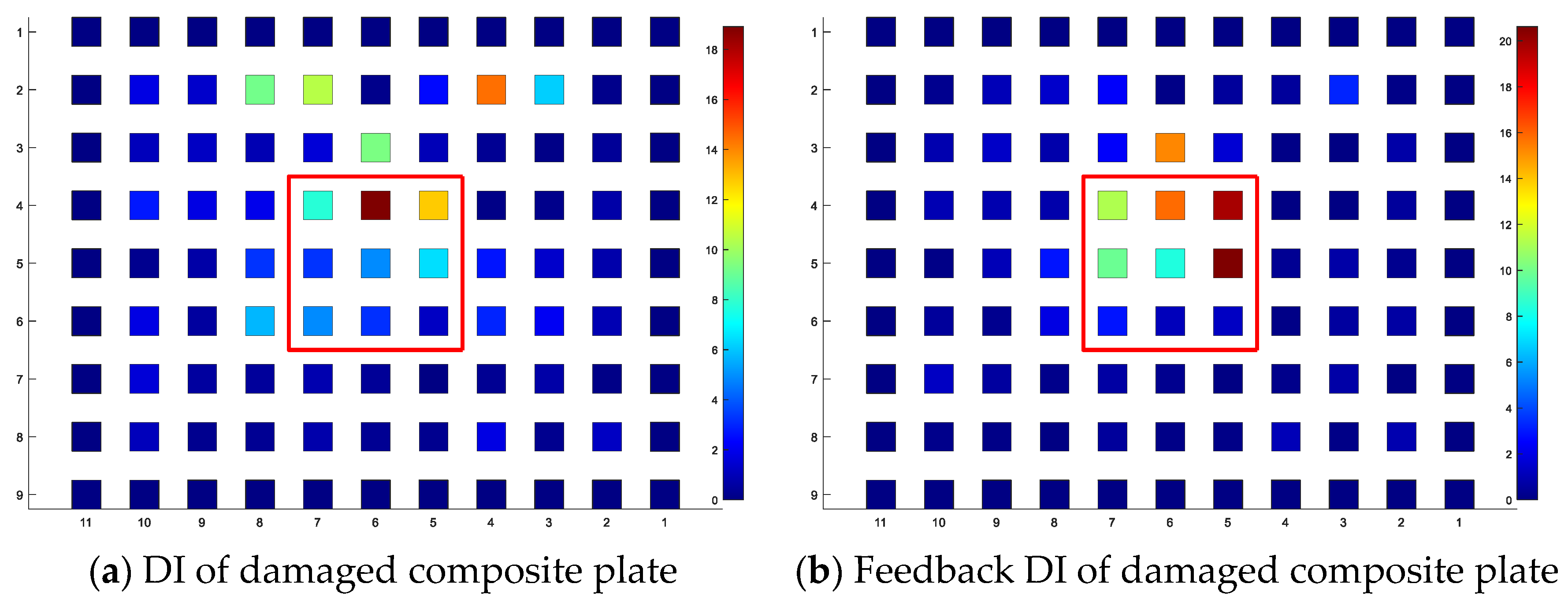
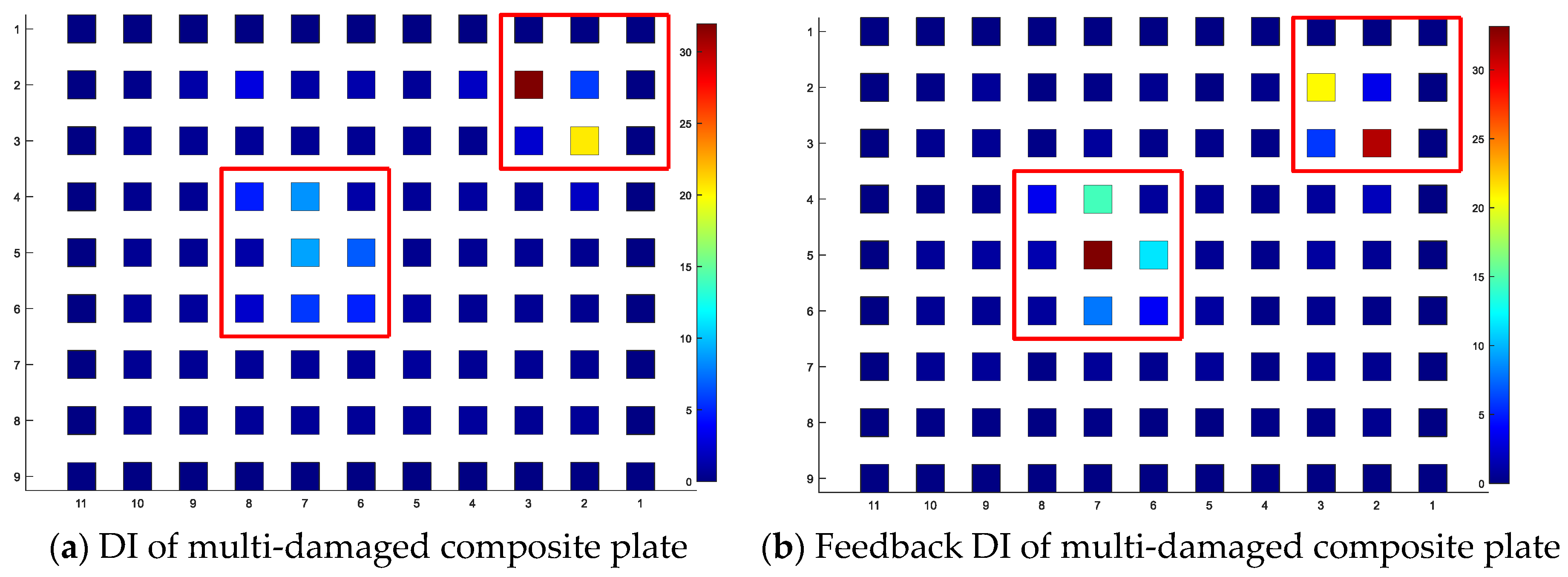
The sensitivity of the feedback DI is observed to be 50% higher than that of the traditional DI. To further dissect the distinctions between the two methodologies, a damage model was selected for a detailed analysis. The results for both the DI and the feedback DI were plotted and are presented in Figure 9, offering a visual comparison to highlight the enhanced sensitivity and diagnostic capability of the feedback DI approach.

In Figure 9, the regions enclosed by the red squares denote the damaged areas. Figure 9a displays the DI, while Figure 9b showcases the feedback DI. In comparison with the peak of the DI, that of the feedback DI more accurately aligns with the damaged area. This attribute significantly reduces the risk for misdiagnosing damage and offers substantial benefits in the assessment of structures with multiple damages. Figure 10 further illustrates the DI and feedback DI for a model featuring multiple damages, providing insights into their comparative diagnostic capabilities.

The model depicted in Figure 10 represents a scenario with dual damage sites, the regions enclosed by the red squares denote the damaged areas, both of equal severity. Figure 10a illustrates the DI, and Figure 10b presents the feedback DI. In Figure 10a, the disproportionate amplitude of the DI could result in one damage site being overlooked. Conversely, in Figure 10b, the feedback DI successfully identifies the locations of both damage sites, demonstrating its superior diagnostic accuracy and effectiveness in detecting multiple damages within a structure.

These research findings indicate that the feedback DI, compared with the traditional DI, exhibits enhanced sensitivity. This increased sensitivity translates to improved performance, notably in minimizing instances of missed detections and false positives, thereby offering a more reliable approach to damage diagnosis in structures.

3.4. Transferability of the Feedback DI

The calculation of the feedback DI necessitates the computation of the feedback-weighted matrix, which relies on a structural damage database. However, creating a comprehensive structural damage database may not always be feasible. To tackle this challenge, forthcoming research will explore the transferability of the feedback-weighted matrix.

The DI is derived from the structural modal shapes, typically dimensionless parameters that are normalized. Consequently, modal shapes are predominantly influenced by the structure’s geometry and boundary conditions. Thus, the feedback-weighted matrix can be utilized for structures that share similar geometric and boundary conditions, indicating that the feedback-weighted matrix possesses transferability regarding both structural dimensions and material properties. This enables broader applicability across different structural assessments without necessitating individualized calibrations for each unique case.

The transferability of the feedback-weighted matrix across different structural sizes is set to be demonstrated. A new database for a GFRP composite plate is created using the FEM, maintaining consistency in the material and layer design with the original database, as detailed in Table 1, but with the dimensions increased tenfold to result in a rectangle measuring 5 m in length and 4 m in width. This database comprises 5400 variations of single-layer damage models. The feedback-weighted matrix derived from the small-scale plate is applied to calculate the feedback DI for the large-scale plate’s database, with its accuracy presented in

Table 6. The accuracy of the large-scale plate’s damage location.

	Correct	Accuracy
DI	3626	67.15%
Feedback DI	5164	95.63%

. Despite the substantial alteration in the structural dimensions, the feedback-weighted matrix remains applicable, showcasing its potential for use in diverse structural assessments without the need for recalibration to accommodate size variations.

The applicability of the feedback-weighted matrix to structures with varying material properties will also be explored. A database for a carbon-fiber-composite plate was developed using the FEM, featuring the ply design outlined in

Table 7. Ply design of carbon-fiber-composite plate.

Layer	Material	Angle	Thickness
1	Carbon fiber	±45°	1.2 mm
2		±45°	1.2 mm

and dimensions of 0.5 m in length and 0.4 m in width. This database includes 5400 damage models. Utilizing the feedback-weighted matrix derived from the GFRP composite plate, the feedback DI for the carbon-fiber-composite plate’s database was computed, with its accuracy detailed in

Table 8. Accuracy of carbon-fiber-composite plate’s damage location.

	Correct	Accuracy
DI	3386	62.70%
Feedback DI	5198	96.26%

. Despite the alteration in the material’s properties, the feedback-weighted matrix proved to be adaptable, illustrating its versatility across different composite materials without the necessity for adjustments based on material characteristics.

These research findings highlight the feedback-weighted matrix’s transferability across structures with fundamentally similar shapes. Consequently, the complexity associated with employing the feedback DI can be mitigated by creating a database encompassing shapes that are commonly utilized and computing their corresponding weighted matrices. This approach streamlines the application of the feedback DI across various structural assessments, enhancing its practicality and ease of use in the field of damage diagnosis.

4. Multi-Damage Localization Based on Multi-Label Classification

Typically, it cannot be guaranteed that there is only a single point of damage in a GFRP composite plate. Single-label classification algorithms are not capable for addressing the problem of damage localization for multiple damages. Therefore, this paper adopts the INSDIF algorithm [31], transforming the damage localization of the GFRP composite plate to a multi-label classification problem. This enables the localization of multiple damages in a GFRP composite plate.

$X={ℝ}^d$ denotes an input space, and $Y=\left\{1,2,\cdots ,Q\right\}$ denotes a finite set of possible labels. Given a multi-label training set, $S=\left\{\left({\mathrm{x}}_1,y_1\right),\left({\mathrm{x}}_2,y_2\right),\cdots ,\left({\mathrm{x}}_N,y_N\right)\right\}$, where $x_i\in X$ is a single instance, and $y_i\subseteq Y$ is the label set associated with $x_i$, the goal of multi-label learning is to learn a function, $h:X\to 2^Y$, from S, which predicts a set of labels for an unseen example.

First, for each class, $C_l$, the k nearest neighbors of instances $x_i$ that belong to this class are determined using the KNN algorithm. Typically, the KNN method employs the traditional Euclidean distance formula for calculating distances, which inherently assigns an equal weight to each attribute. However, this can result in neighbor distances being dominated by a large number of irrelevant attributes. This paper introduces attribute weighting to the distance calculation. A matrix, $W$, is defined to describe the similarity between an instance and its neighbors as follows:

$$W_i(z)=\left\{\begin{array}{l}\frac{1}{Z_i}\exp \left(-\frac{{‖x_i-x_z‖}^2}{2{\sigma }^2}\right),z\in N_i\\ 0,otherwise\end{array}\right.$$

(17)

$$Z_i={\displaystyle \sum _{z\in N_i}\exp \left(-\frac{{‖x_i-x_z‖}^2}{2{\sigma }^2}\right)},{\displaystyle \sum _z{W}_i(z)=1}$$

(18)

$N_i$ are the k nearest neighbors of instances $x_i$, $‖\cdot ‖$ is the Euclidean distance operator, and $\sigma$ is used to estimate the average distance between instances.

The average vector, $v_{il}$, is calculated as follows by taking the average of the k nearest neighbors of instance $x_i$ belonging to class $C_l$:

$$v_{il}=\raisebox{1ex}{$\left({\displaystyle \sum _{x_i\in N_{il}}{w}_i(z)x_i}\right)$}\!\left/ \!\raisebox{-1ex}{$\left|N_{il}\right|$}\right.$$

(19)

where $v_{il}$ can be regarded as a profile-style vector approximating the common characteristics of class $C_l$. Actually, this kind of prototype vector has already shown its effectiveness in solving text categorization problems. After acquiring the prototype vectors, each example, $x_i$, is re-represented by a bag of instances, $B_i$, where each instance in $B_i$ is just the difference between xi and one prototype vector as follows:

$$B_i=\left\{x_i-v_{il}\left|l\in Y\right.\right\}$$

(20)

In this way, each example is transformed to a bag for which the size equals the number of possible classes.

The n instance bags transformed through the category-weighting method are taken as input, yielding Q values as output. For each output, $y_l$, there exists $y\in l$. The first layer utilizes the KNN algorithm to divide the training set into M mutually exclusive subsets. The second layer corresponds to the weight matrix, $W={\left[w_{jl}\right]}_{M\times T}$, where $w_{jl}$ is the weight connecting $C_j$ to the output, $y_l$.

To assess the efficacy for employing multi-label classification for damage localization in GFRP composite plates, three distinct damage databases were developed using the FEM. These databases pertain to composite plates measuring 0.5 m in length and 0.4 m in width, adhering to the ply configurations detailed in

Table 9. Ply design of composite plate.

Layer	Material	Angle	Scope	Resin Content	Thickness
1	E-glass Warp-Knitted Fabric	±45°	Overall	60%	1.2 mm
2	M80-12 mm PVC Foam	±45°	Overall		12 mm
3	E-glass Warp-Knitted Fabric	±45°	Overall	60%	1.2 mm
4	E-glass Warp-Knitted Fabric	±45°	Overall	60%	1.2 mm

. This setup facilitates a comprehensive analysis of multi-label classification’s potential in pinpointing damage across various scenarios within GFRP composite structures.

The three databases include a single-damage database, a double-damage database, and a triple-damage database, containing 3240, 10,260, and 6840 models, respectively. For multi-label classification, 70% of the models from each database are designated as the training set, while the remaining models serve as the test set. Inputs for the classification process comprise the modal shapes, DI, and feedback DI of the models, with the damage locations acting as labels for both training and validation purposes. The outcomes of this classification process are illustrated in Figure 11, showcasing the effectiveness for using these parameters for accurately identifying and localizing damage within GFRP composite plates.

Modal shapes serve as the foundational data of the model, with the DI representing a damage characteristic derived from these modal shapes, and the feedback DI acting as an enhanced version of this characteristic through optimization. Figure 11 demonstrates that as the number of damage locations increases, the accuracy of the damage localization tends to decrease. Nonetheless, data pre-processing can markedly enhance the accuracy for localizing damage. Among the methods that were tested, the feedback DI achieves the highest accuracy in the multi-label classification, indicating its effectiveness in refining the processes of damage identification and localization in composite plates.

5. Experiment

This section aims to validate the proposed method for damage localization in GFRP composite plates via experimental testing. The test specimen is a GFRP composite plate, custom-manufactured by a yacht factory and measuring 0.5 m in length and 0.4 m in width. The ply configuration of the specimen adheres to the specifications detailed in Table 9, ensuring consistency with the theoretical and computational aspects of the research for a comprehensive assessment of the method’s practical applicability and effectiveness.

The experiment was conducted using a Simcenter Testlab, and the modal testing process is shown in Figure 12. The test equipment is outlined in

Table 10. Test equipment.

Apparatus	Version	Producer	Sensitivity
Single-Axis Accelerometer	333B30	PCB	10 mV/(m/s2)
PC	Notebook Workstation	DELL	-
DAQ System	LMS SCADAS	SIEMENS	-
Hammer	INV9311	Coinv	2.8 N/pc

.

The experimental method was impact testing with free-boundary conditions, the test method was the moving hammer method, the bandwidth was 1000 Hz, and the resolution was 0.5 Hz. Four PCB accelerometers were used to ensure that no mode was hidden during the testing process. The experimental setup photograph is shown in Figure 13. The test samples included a pristine composite plate and a composite plate damaged during the manufacturing process. The damaged area and damage design are shown in Figure 14.

The visible damages in red circles depicted in Figure 14 were intentionally introduced during the lamination process of the composite plates. By strategically leaving bubbles at specific locations, voids were created within the laminate structure as the resin cured. These voids subsequently led to delamination, serving as the specific type of defect studied in our experiments. The modal shapes of the pristine and damaged plates can be obtained through experiments and are shown in

Table 11. Modal shapes of the pristine and damaged plates.

Mode	Pristine	Damaged
1st
2nd
3rd
4th
5th
6th
7th
8th
9th
10th
11th
12th

.

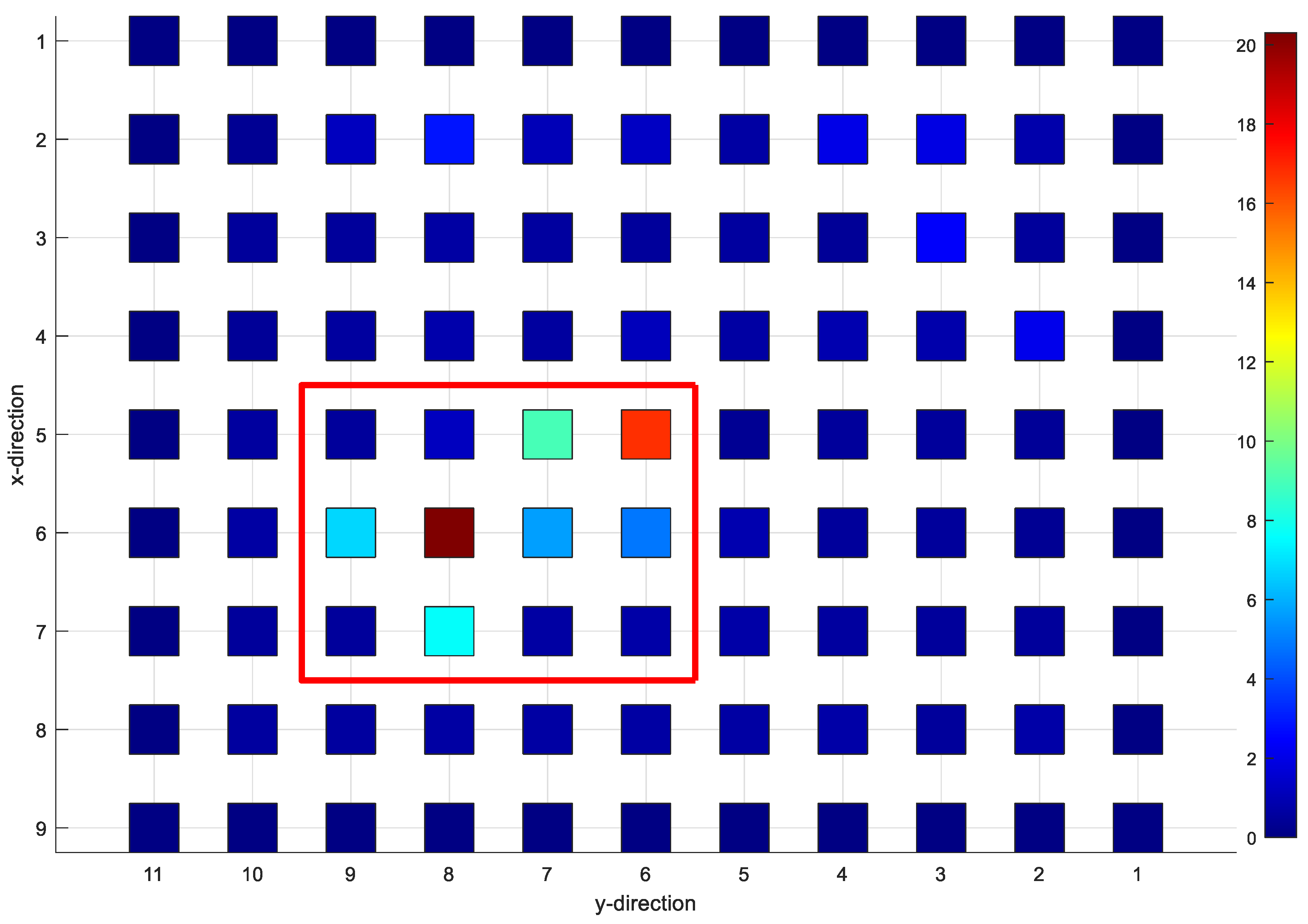
The DI for the damaged plate is determined from the modal shapes of both the undamaged (pristine) and damaged plates. This DI undergoes optimization through the application of the feedback-weighted matrix, resulting in the feedback DI. The optimized feedback DI, showcasing the enhanced ability to pinpoint and quantify damage, is illustrated in Figure 15, providing a visual representation of the damage localization improvements achieved through this feedback optimization process. The regions enclosed by the red squares denote the damaged areas, feedback DI accurately indicates the area of damage.

The feedback DI is input to the multi-label classification model trained by the finite element model’s dataset, resulting in a damage location vector. This damage location vector is then converted back to the following matrix:

$$\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]$$

(21)

Each element in the matrix represents different positions on the GFRP composite plate. In the matrix, 1 indicates a damaged location, while 0 represents a pristine location. In reference to Figure 13, it can be observed that the matrix accurately accomplishes the damage localization of the tested damaged GFRP composite plate.

6. Conclusions

In response to the current challenge for rapidly and accurately localizing multiple damages in GFRP composite plates, a damage localization method combining feedback optimization with multi-label classification was proposed. Compared with traditional modal methods and machine-learning approaches, feedback optimization significantly enhances the sensitivity of the damage localization, while multi-label classification resolves the issue for diagnosing damage at multiple locations. Through theoretical analysis and experimental verification, the following conclusions have been drawn:

(1)

A single-damage database for GFRP composite plates was established based on the fatigue failure criteria, and the accuracy of the DI was studied using the database. The study showed that the damage localization accuracy of the DI was only 72.43%. Feedback optimization was proposed, and the accuracy of the feedback DI reached 92.56%, which significantly improved the accuracy compared with that of the DI. A sensitivity index was proposed. Compared with the DI, the feedback DI exhibited lower probabilities of false detections and missed detections; additionally, the feedback DI is transferable. The feedback-weighted matrix is only related to the structural shape and is not affected by structural dimensions or material parameters. This characteristic facilitates the use of the feedback DI;

(2)

A method for using multi-label classification was proposed to solve the problem of the multi-damage localization. The INSDIF algorithm was applied to the damage localization of the GFRP composite plates. A multi-damage database for GFRP composite plates was established to validate this method. The results showed that the combination of the feedback optimization and the multi-label classification method can rapidly and accurately accomplish the multi-damage localization of GFRP composite plates;

(3)

The effectiveness of the feedback DI and multi-label classification was verified through experiments using a GFRP composite plate customized by a yacht factory. The experimental results showed that the feedback DI and multi-label classification can effectively locate damage in GFRP composite plates.