Abstract
This article is devoted to the further development of a viable technology for low-temperature cryopreservation of reproductive cells of sturgeon fish using acoustic–mechanical fields and intelligent control of the freezing process. Before vitrification begins, the piezoactuator acts on a mixture of cryoprotectant and reproductive cells. This promotes intensive mixing of the cryoprotector and its diffusion through the cell membrane. When vitrification is carried out directly, a phase transition phenomenon is observed, accompanied by crystal formation. This article presents a new mathematical model describing this process as developed by the authors. The corresponding boundary conditions are formulated. Numerical experiments were carried out using the finite element method. It has been established that during vitrification without the use of a cryoprotectant, a sharp temperature jump is observed at the front of the crystalline formation boundary. The use of a cryoprotectant leads to a slowdown in the process of crystal formation, that is, to a weakening of the effect of one of the most important cryoprotective factors. The comparison with full-scale experiments showed qualitative agreement with the experimental results, which indicates the adequacy of the proposed model. The results obtained can be used in the future during the vitrification process and the evaluation of the quality of cryofreezing. The application of a new methodological approach to methods of long-term preservation at low temperatures of the genetic and reproductive material of hydrobionts using acoustic and mechanical effects and an intelligent control module opens up great opportunities for the creation of new cost-effective biotechnologies that make it possible to make the transition to a new type of aquatic farms, increase the stability of aquaculture, in general, to make environmental protection measures to save rare and endangered species more effective.
1. Introduction
One of the most important problems facing humanity and urgently requiring an indispensable solution is food shortage and the fight against hunger. Governments of different countries and many public organizations, including the world’s largest humanitarian organization, the United Nations and its “UN World Food Program” (WFP), are concerned about this global challenge to humanity [1,2,3,4]. In this regard, the introduction of cryopreservation technology into the processes of artificial reproduction of commercial fish species can significantly increase the productivity of fish farms, and significantly reduce food shortages in a timely manner.
Another urgent task of our time in the context of mankind’s technogenic impact on the natural environment is the preservation of the biological and genetic diversity of the animal world. At the same time, it is necessary to take care of the preservation of both the genetic resources of rare, endangered fish species [5,6,7] and the commercial stock of valuable fish species (genetic improvement programs, broodstock management, assistance to species with reproductive problems) [8,9,10]. An effective non-invasive and non-lethal approach to solving this problem is the creation of cryobanks [6,11,12,13,14]. Such cryobanks are capable of ensuring the safety of cryopreserved germ cell samples without loss of their reproductive qualities for decades, as well as developing selection and breeding direction in marine and freshwater aquaculture farms: sperm saving; simplification of broodstock management; transportation of gametes from different fish farms; and storage of germplasm for genetic selection programs or species conservation.
In the case of fish reproductive cells, the process of low-temperature cryopreservation results in a significant decrease in cell temperature [15,16,17]. Particular attention is paid to salmon and sturgeon fish [18,19,20,21,22], of which the decline in population has reached alarming levels and threatens the complete extinction of these species.
The temperature change is made from a temperature of plus 4 °C to a deep freezing temperature in liquid nitrogen of minus 195.75 °C. This process can be carried out in two main ways:
- -
- Slow freezing (less than 10 K/min) [23];
- -
- Vitrification (fast freezing, more than 10 K/min).
The vitrification process [13,24] has a significant drawback: as a result of placing the frozen material (reproductive cells) in liquid nitrogen, a sharp temperature jump and formation of intracellular ice occurs. This phenomenon causes an increase in the membrane structures of the cell and its destruction. In order to prevent this phenomenon, a cryoprotectant should be used [25,26].
In this regard, it is important to develop and improve cryopreservation protocols: determining the optimal equilibration time; chemical composition of the cryoprotectant; percentage of components, et cetera [27,28,29,30,31,32]. All these efforts are aimed at making cryopreservation technology viable and cost effective.
Another direction for optimizing cryopreservation protocols is additional external influence on the suspension, for example, by external acoustic fields [33,34,35,36]. Cryopreservation with simultaneous exposure to germ cells by acoustic–mechanical fields contributes to a more uniform distribution of the cryoprotectant among fish cells and a uniform freezing process. This will contribute to improving the quality of the cryopreservation process by reducing the uneven temperature distribution in the frozen suspension and increasing cell survival.
The purpose of this work is as follows:
- -
- Construction of a continuous mathematical model of the crystallization process [37] taking into account the phase transition, but without identification of the phase boundary;
- -
- It is subsequent discretization based on the finite element method and carrying out the numerical experiments.
2. Materials and Methods
2.1. Materials (Cryoprotector Substance)
In this research, the cryoprotectant substance was used, which protects fish cells from acoustic–mechanical and low-temperature influences. The cryoprotectants used for cryopreservation contained the following substances: NaCl; KCl; CaCl2; NaHCO3; HCl; sucrose; mannitol; egg yolk—10%; dimethyl sulfoxide—10%.
2.2. Semen Scoring and Freezing Procedure
For freezing, sperm of 4 points (the number of motile sperm from 50 to <75%) and 5 points (the number of motile sperm from 75 to 100%) were used [38].
The cryofreezing procedure was as follows: the sperm was mixed with a cryoprotective medium. The acoustic–mechanical effect is carried out by a piezoactuator. The mixture of sperm and medium is placed in tubes for freezing. The tubes are placed in a cryopreservation freezer.
All scientific studies were carried out on the reproductive cells of male sturgeon fish species, including rare and endangered ones, such as Huso huso (Linnaeus, 1758) and Acipenser ruthenus (Linnaeus, 1758). The studies also used sperm from Acipenser gueldenstaedtii (Brant et Ratzeburg, 1833) and Acipenser baerii (Brandt, 1869), and hybrids of Russian and Lena sturgeon and sterlet with beluga were also used in the research.
Many species of fish, including sturgeon, are currently on the verge of extinction. The Azov beluga—Huso huso (Linnaeus, 1758) is listed in the Red Book of the International National Union for Conservation of Nature and Natural Resources (IUCN) [39], the European Red List (see Appendix 2, CITES (Convention on International Trade in Endangered Species of Wild Fauna and Flora)) [40]. Since 1956, it has been reproduced at sturgeon hatcheries in the Rostov Region and Krasnodar Territory (Russian Federation); currently, almost its entire stock consists of fish of hatchery origin. The sterlet is listed in the Red Book of the International Union for Conservation of Nature and Natural Resources (IUCN), and the Don population is listed in the Red Book of the Russian Federation (2001) [41] as endangered. The particularly tense situation has developed with sterlet stocks in the Lower Don basin.
2.3. Mathematical Model for Crystallization
The quality of biological material during cryopreservation on crystal formation and freezing temperature regime.
The first problem is solved by using a cryoprotectant, and a mathematical model of its penetration using acoustic influence was considered earlier in [42].
To solve the second problem, the freezing temperature regime, it is necessary to build a crystallization model taking into account the temperature jump. This work is devoted to the study of this problem. A mathematical model of crystallization is constructed based on the thermal conductivity equation, taking into account the release of heat during the transition from the liquid to the solid phase. Numerical implementation of the constructed model using the finite element method allows us to study the temperature change inside the vessel. From experimental works [33,35], it is known that, depending on the freezing protocol, there may be a temperature jump, which affects the quality of the frozen material. Using the constructed mathematical model and its numerical implementation, modes and areas of occurrence of temperature jumps can be identified; therefore, it is possible to optimize both the cryopreservation protocol itself and the geometry of the vessel.
Such fields of specially selected power and frequency can be created, for example, by a piezoactuator. The working element of the piezoactuator is a round piezoceramic plate with preliminary polarization in thickness. The front surfaces of the plate are electrodes and an electrical voltage is applied to them. The plate is glued to the bottom of the vessel with the suspension from the outside. The piezoactuator oscillates due to the inverse piezoelectric effect.
The works of the authors [42,43,44] are devoted to mathematical modeling of the acoustic effect on a suspension (reproductive cells placed in a cryoprotectant) during equilibration. In these works, within the framework of continuum mechanics, a mathematical model of the effect of the piezoactuator on the reproductive cells of fish during cryopreservation was constructed. For this purpose, the equations of continuum mechanics are used as follows:
- -
- Linear theory of elasticity;
- -
- Linear theory of electroelasticity;
- -
- Equations of motion of liquid and gaseous media (in the acoustic approximation).
Appropriate boundary conditions for mechanical and electric fields are added to these equations.
The constructed model is an initial boundary value problem and, in general, its solution can be obtained only numerically using finite element analysis software packages. The conducted series of numerical experiments (to build a geometric model, generate a finite element mesh, and carry out calculations, the free software package for finite element analysis ACELAN was used) made it possible to perform modal analysis, find resonant frequencies, and determine the electromechanical coupling coefficient, depending on the radius of the piezoelectric element. Analysis of the results obtained indicates the presence of sections with positive and negative components of the vertical and horizontal speed in the first bending mode. This phenomenon in the frequency range acceptable for biological objects should cause intensive mixing of the cryoprotectant inside the occupied volume. A series of full-scale experiments carried out showed the adequacy of the theoretical model.
The constructed model should be supplemented with a model of cryoprotectant diffusion through the cell membrane. This model is based on the equation of mass transfer through the membrane, which describes the multiphase diffusion of several impurities interacting with each other. A feature of the mathematical modeling of the diffusion of the cryoagent component through the cell membrane is that, according to modern concepts, quite a lot of different models of intracellular transfer of substances are used for applied problems.
In order to improve the quality of freezing and control this process, it is necessary to study in more depth the transition of suspension from the liquid phase to the solid phase. The thermodynamic process under study can be described by a mathematical model called the Stefan heat problem.
In contrast to [45,46], the mathematical model is constructed in an axisymmetric formulation based on a non-stationary heat equation in which the thermophysical properties of the suspension depend on temperature. It is accepted that the heat capacity at the front of the free boundary (phase transition boundary) changes according to a law that takes into account the blurring of this boundary. In addition, the changes in thermal conductivity and heat capacity in the solid and liquid phases were taken into account. We consider that the thermophysical properties on the surface of the frozen material during crystallization change abruptly during the transition from the zone with a higher temperature to the zone with a lower temperature. A temperature source is set on a surface, which corresponds to the heat released during the crystallization process. In the numerical implementation of the model, this source is replaced by a volumetric one with a narrow Gaussian distribution. The work uses the FlexPDE program for scenario models for solving differential equations using the finite element method.
The mathematical model of crystallization is based on the non-stationary heat-transfer equation for a homogeneous medium, which has two states—liquid and solid phase:
where
The following notations are used in Formulas (1)–(4): T—temperature; —heat capacity of liquid and solid phases; —thermal conductivity of liquid and solid phases; —crystallization temperature; and —an internal heat source associated with the crystallization process in the vicinity of the surface with a temperature of .
Boundary conditions can be of different types, namely: (5) constant temperature; (6) the condition of thermal insulation, meaning, the absence of heat flow; and (7) the condition of heat exchange with the environment, where is the heat transfer coefficient.
Specifically, the boundary Condition (5) corresponds to a constant temperature. The boundary Condition (6) is a condition of thermal insulation; that is, it indicates the absence of heat flow. The boundary Condition (7) is a condition indicating the presence of heat exchange with the environment (here, h is the heat transfer coefficient).
It should be noted that in the case of heat exchange with the environment (Condition (7)), the heat transfer coefficient also depends on the phase of the substance. If the vessel walls are thin enough and the coefficient is large enough, then at such a boundary, it makes sense to use Condition (5), which corresponds to a fast freezing process. Further in the calculations, this condition will be specified on the cylindrical surface and the lower end.
2.4. Finite Element Modeling
For a numerical experiment, let us consider the non-stationary problem of crystallization of a suspension (reproductive cells placed in a cryoprotectant) in a circular cylindrical region.
An axisymmetric cylindrical container has thin walls. The top cover is made of heat-insulating material. The material to be frozen (fish reproductive cells) at room temperature is placed in the container. Next, the container with the contents is frozen with liquid nitrogen at a temperature of minus 195.75 °C. Thus, the boundary conditions are as follows:
- -
- Condition (5) is set at the lower end; that is, a constant temperature of minus 195.75 °C is set;
- -
- Condition (5) is also set on the lateral cylindrical boundary; that is, a constant temperature of minus 195.75 °C is set;
- -
- The upper end of the container is thermally insulated (Figure 1), which is described by Condition (6).
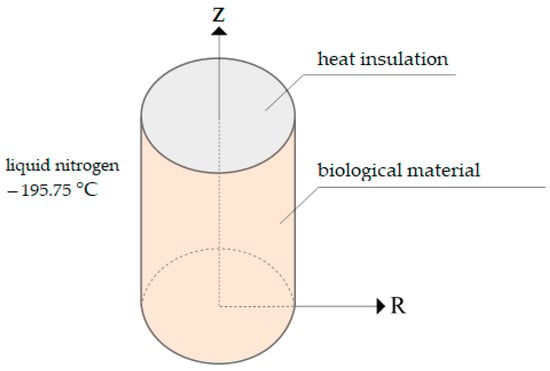 Figure 1. Setting the boundary conditions for a frozen cylindrical cryovial sample model.
Figure 1. Setting the boundary conditions for a frozen cylindrical cryovial sample model.
The finite element method was chosen for solving the initial boundary value problem. In the program of scenario models for solving differential equations by the FlexPDE finite element method, a solution script has been developed (a geometric model has been created, and a finite element grid has been generated). The resulting finite element mesh is shown in Figure 2 and contains 2780 cubic triangular finite elements with 1471 nodes.
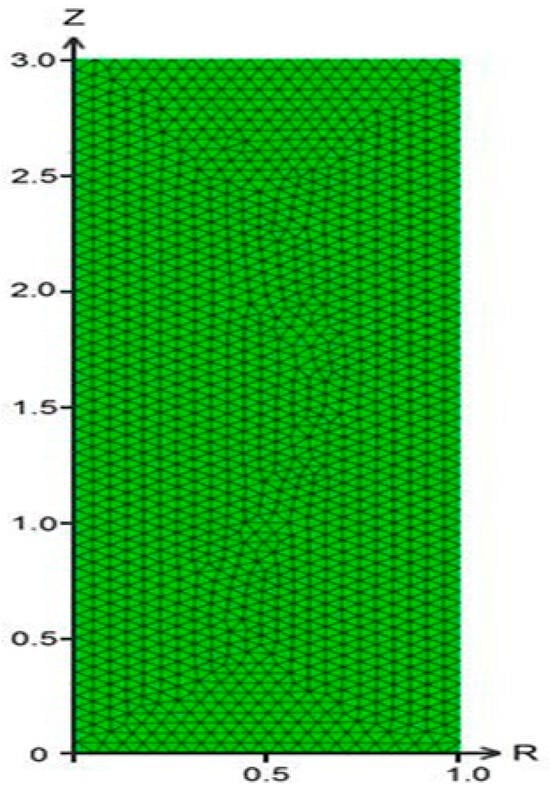
Figure 2.
Finite element mesh: z—designation of the vertical axis (along the axis of the cylinder from bottom to top); R—designation of the horizontal axis (along the radius of the cylinder from the center to the outside); 0—(the origin of the coordinate system) in the lower left corner.
3. Results
Over time, the non-stationary turns into a stationary mode: the entire volume of the liquid goes into the solid phase since a constant temperature and thermal insulation are set at the container boundary (Condition (5)). The interphase boundary begins to move from the boundaries at which a constant temperature is set into the interior of the region under consideration. Thus, Figure 3 shows a heat map of the temperature distribution by volume (depending on depth and radius). The distribution is shown specifically at the beginning of the process (a), in the presence of two phases (b), and when the entire volume is already in the solid phase (c).
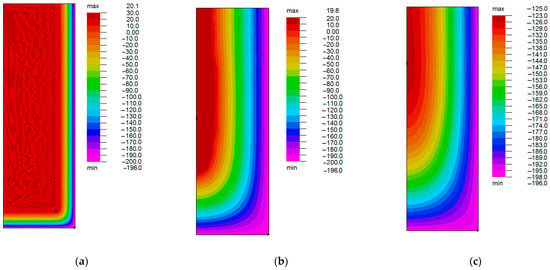
Figure 3.
Temperature distribution of the suspension during crystallization: (a) the beginning of the process, (b) the presence of two phases, (c) the entire volume in the solid phase.
The temperature distribution over the radius in the middle section for different time points is shown in Figure 3 (natural convection (x,y), simplified). It is possible to notice a well-defined temperature jump at the beginning of the process in the region of the phase front (Figure 3a). Further, in the presence of two phases, at the front of the temperature distribution, there are features in the form of an inflection point in the graph.
In this work, the temperature distribution is numerically studied, as a function of time for points lying in the direction from the cylinder walls to points lying on the axis. These distributions are shown in Figure 4, Figure 5, Figure 6 and Figure 7. Their analysis shows that in the region of the phase boundary, there are some features that arise due to the temperature jump. Figure 4 shows the dependence of temperature on time, depending on the location of points along the radius (with respect to the second vertical coordinate, these points are located in the middle of the region). These graphs show horizontal sections corresponding to the temperature jump and phase transition. In Figure 4, Figure 5, Figure 6 and Figure 7, the colors of the lines correspond to the points in the cryotube (the points are indicated in Figure 4, Figure 5, Figure 6 and Figure 7 in the rectangle on the right).

Figure 4.
Suspension temperature distribution along the radius: (a) at the beginning of the process; (b) in the presence of two phases.
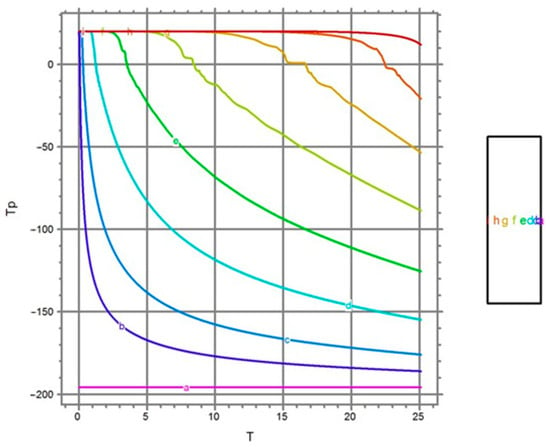
Figure 5.
Temperature distribution at selected points along the radius, depending on time.
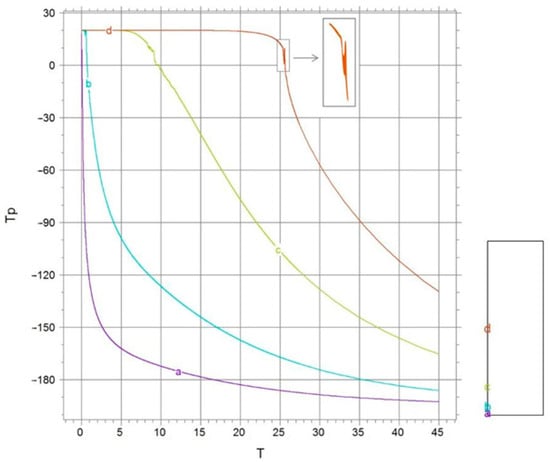
Figure 6.
Temperature distribution at points on the symmetry axis, depending on time (the temperature jump is highlighted in red and orange colors).
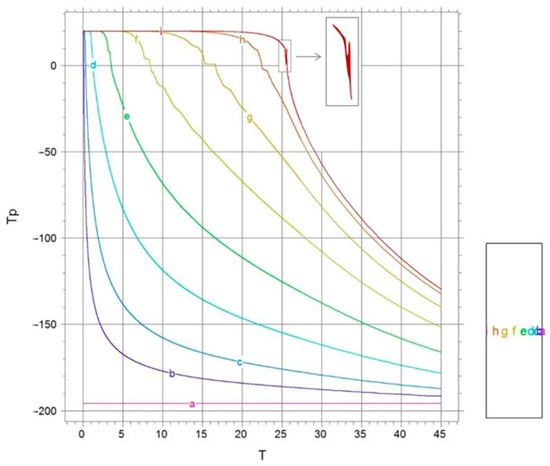
Figure 7.
Temperature distribution at points on the symmetry axis, depending on time.
Figure 6 and Figure 7 clearly show temperature jumps in the region of crystallization temperature—orange and red curves. Figure 6 shows the dependence of temperature on time for a point located in the center of the region in height at r = 0. Similarly, Figure 7 shows the dependence of temperature on time for a point located in the center of the region in height at r = 0.5 R (where R is the radius of the region under consideration). The magnitude of such a jump is about 10 degrees.
The results obtained can be used in the vitrification process to assess the quality of reproductive cells freezing.
4. Discussion
Cryopreservation is one of the most attractive and rapidly developing areas of the conservation of rare endangered species. Currently, in world research practice, work on cryopreservation and the use of frozen fish sperm is carried out quite widely. Over the past few decades, scientific knowledge about the specifics of cryopreservation procedures for fish sperm has increased significantly. In fish, unlike warm-blooded animals, sperm is most suitable for cryopreservation according to its cytological and cryobiological characteristics, but methods suitable for mammals could not be used.
In Russian aquaculture, cryopreserved sperm is currently underused, while the practice of fish farming dictates the need for widespread use of cryosperm to solve the problems of producing high-quality fish seeding material and material for selection and breeding work. At the moment, to date, the effectiveness of defrosted sperm does not yet meet high fish farming requirements due to the diversity of morphophysiological specificity of fish germ cells, which is most relevant for further improvement of cryopreservation technologies, not only to preserve the gene pool, but also for widespread use in commercial aquaculture when growing economically valuable fish. In this case, it is necessary to solve a number of extremely important issues on the scientific foundations of cryotechnology for low-temperature freezing of male germ cells, taking into account their species characteristics and criteria of potential significance (quality). When forming cryobanks of male reproductive cells, it is important to store high-quality material.
In previous studies [33,35,47], a mathematical model of the effect of acoustic fields on reproductive cells during cryopreservation was constructed. This applies to all stages of cryopreservation (mixing with a cryoprotectant, diffusion, and temperature jump). This technology has received several patents in the Russian Federation [33,47]. In previous studies [35,48], experimental confirmation of the constructed mathematical theory of acoustic–mechanical action was given.
In this work, the mathematical model of the crystallization process was constructed and the program for its numerical implementation was developed. An axisymmetric case is considered: the temperature of liquid nitrogen is set on the side surface and the base of a circular cylinder; the upper end is thermally insulated. Calculations of the non-stationary problem were carried out, and spatial distributions of temperature at different time points and its time dependences for different sets of points were obtained and analyzed. The results of the numerical analysis show the presence of some significant features in the spatial and temporal temperature distributions in the vicinity of the crystallization front. Specifically, as the front moves, time intervals appear at which the temperature is constant, and then temperature jumps appear.
Figure 8 shows the temperature dependences in the experiment carried out in [47]. There is a temperature jump in the suspension when the cryoprotectant is not used (dotted curve), and no temperature jump when the cryoprotectant is used (solid line). The completed series of full-scale experiments showed a qualitative match with the calculation results presented in Figure 4, Figure 5, Figure 6 and Figure 7. This indicates the adequacy of the proposed model.
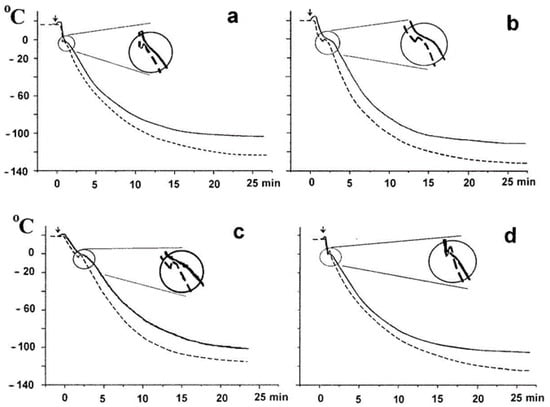
Figure 8.
Temperature jump—full-scale experiment. (a)—distilled water: control version, not treated with ultrasound (---); ultrasound-treated solution (---). ultrasonically treated (---); ultrasonically treated solution (-), (b)—sturgeon base solution: control version, not treated with ultrasonicated (---); ultrasonicated solution (-), (c)—base solution for sturgeon: control version, not treated with ultrasound (---); ultrasonicated solution (-), (c)—+10% dimethyl sulphoxide base solution: control version, not treated with ultrasonicated solution (---); ultrasonicated solution (-), (d)—base solution +10% dimethyl sulfoxide: control version, not treated (---); ultrasonicated solution (-), (d)—base solution +10% dimethyl sulfoxide +10% egg yolk: control variant, not ultrasonically treated (---); ultrasonically treated solution (-).
The studies carried out using a cylindrical vessel and instantly placing it in liquid nitrogen showed qualitative agreement with the experimental results [33,35]. It was found that, at the beginning of the process, there are time intervals with a relatively constant temperature. However, as the phase transition front moves toward the cylinder axis, a region appears in which a temperature jump occurs, which was observed in the above experiments. This confirms the adequacy of the proposed model.
5. Conclusions
As a result of the research, a mathematical model was obtained, which describes the process of freezing a liquid (suspension), taking into account the temperature jump that occurs at the boundary of solid and liquid phases. The boundary between the solid and liquid phases is determined by the crystallization temperature. The mathematical model takes into account their thermophysical properties. The initial boundary value problem of thermal conductivity is considered, in which the heat capacity and thermal conductivity change abruptly at the phase boundary. At the phase boundary, internal heat sources are taken into account, characterizing its release during crystallization. The proposed model is implemented in the FlexPDE finite element analysis software package. In computer implementation, the surface heat source is replaced by a narrow volumetric Gaussian distribution. In a numerical experiment, a non-stationary axisymmetric problem is considered for a circular cylinder at the lower end and side boundary, of which a constant temperature of liquid nitrogen is set to minus 195.75 °C, and the upper end is thermally insulated. The spatial distributions of temperature at different time points and its time dependences at different points of the internal volume of the cylinder were constructed. The results of the numerical analysis show the presence of some features in these temperature distributions in the vicinity of the crystallization front. As the front moves, time intervals appear in which the temperature is constant, and then temperature jumps appear. The data of this temperature behavior can be used when carrying out the vitrification procedure and the assessment of the quality of freezing of biological cells, since the temperature in these areas, having dropped to the crystallization temperature, rises sharply by almost ten degrees.
The application of a new methodological approach to methods of long-term preservation at low temperatures of genetic and reproductive material of hydrobionts using acoustic and mechanical effects and an intelligent control module opens up great opportunities for the creation of new cost-effective biotechnologies that will make the transition to a new type of aquaculture, increase the stability of aquaculture, and increase the effectiveness of environmental protection measures to save rare and endangered species.
Author Contributions
Conceptualization, A.M., A.S. and D.R.; methodology, E.P., B.M. and A.O.; literature search, I.S. and D.N.; formal analysis, O.P. and T.M.; investigation, A.M., E.P., B.M. and A.O.; resources, D.N., O.P. and A.M.; writing—review and editing, D.R., T.M. and A.O.; supervision, A.S., A.M., E.P., B.M. and I.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out at the Don State Technical University with the support of the RNF grant No. 21-16-00118.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The research was conducted under the Strategic Academic Leadership Programme of Don State Technical University (‘Priority 2030’).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Available online. Available online: https://www.wfp.org/ (accessed on 10 November 2023).
- Global Report on Food Crises. Joint Analysis for Better Decisions, 2023. WFP, 2023. Available online: https://www.fsinplat-form.org/sites/default/files/resources/files/GRFC2023-hi-res.pdf/ (accessed on 10 November 2023).
- Brander, K.M. Global fish production and climate change. Proc. Natl. Acad. Sci. USA 2007, 104, 19709–19714. [Google Scholar] [CrossRef]
- Froehlich, H.E.; Koehn, J.Z.; Holsman, K.K.; Halpern, B.S. Emerging trends in science and news of climate change threats to and adaptation of aquaculture. Aquaculture 2021, 549, 737812. [Google Scholar] [CrossRef]
- Di Iorio, M.; Rusco, G.; Esposito, S.; D’andrea, M.; Roncarati, A.; Iaffaldano, N. The role of semen cryobanks for protecting endangered native salmonids. Front. Mar. Sci. 2022, 9, 1075498. [Google Scholar] [CrossRef]
- Martínez-Páramo, S.; Horváth; Labbé, C.; Zhang, T.; Robles, V.; Herráez, P.; Suquet, M.; Adams, S.; Viveiros, A.; Tiersch, T.R.; et al. Cryobanking of aquatic species. Aquaculture 2016, 472, 156–177. [Google Scholar] [CrossRef] [PubMed]
- Comizzoli, P.; Holt, W.V. Recent advances and prospects in germplasm preservation of rare and endangered species. Adv. Exp. Med. Biol. 2014, 753, 331–356. [Google Scholar] [CrossRef] [PubMed]
- Mayer, I. The Role of Reproductive Sciences in the Preservation and Breeding of Commercial and Threatened Teleost Fishes. In Reproductive Sciences in Animal Conservation. Advances in Experimental Medicine and Biology; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Judycka, S.; Nynca, J.; Ciereszko, A. Opportunities and challenges related to the implementation of sperm cryopreservation into breeding of salmonid fishes. Theriogenology 2019, 132, 12–21. [Google Scholar] [CrossRef] [PubMed]
- Asturiano, J.F.; Cabrita, E.; Horváth, A. Progress, challenges and perspectives on fish gamete cryopreservation: A mini-review. Gen. Comp. Endocrinol. 2017, 245, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T. Importance of cryobanking in aquatic species conservation and aquaculture. Cryobiology 2018, 80, 169. [Google Scholar] [CrossRef]
- Diwan, A.D.; Harke, S.N.; Gopalkrishna; Panche, A.N. Cryobanking of Fish and Shellfish Egg, Embryos and Larvae: An Overview. Front. Mar. Sci. 2020, 7, 00251. [Google Scholar] [CrossRef]
- Hrytsyniak, I.; Shvets, T. Cryopreservation of fish germ cells. Thematic bibliography. Ribogospodarsʹka nauka Ukraïni. 2018, 4, 79–101. [Google Scholar] [CrossRef]
- Kilbride, P.; Meneghel, J.; Manilal Chawda, M.; Ross, S.; Crompton, T. Scaling up Cryopreservation from Cell Suspensions to Tissues: Challenges and Successes. Biomed. Eng. IntechOpen 2023, 84457. [Google Scholar] [CrossRef]
- Jaiswal, A.N.; Vagga, A. Cryopreservation: A Review Article. Cureus 2022, 14, e31564. [Google Scholar] [CrossRef]
- Assylbekova, A.; Barinova, G.; Aubakirova, G.; Makhanbetova, A.; Kuanchaleyev, Z.; Mussin, S.; Mussina, A. Cryopreservation of Reproductive Cells of Male Russian Sturgeon. Exp. Biol. 2022, 92, 132–138. [Google Scholar] [CrossRef]
- de Siqueira-Silva, D.H.; Saito, T.; dos Santos-Silva, A.P.; Costa, R.d.S.; Psenicka, M.; Yasui, G.S. Biotechnology applied to fish reproduction: Tools for conservation. Fish Physiol. Biochem. 2018, 44, 1469–1485. [Google Scholar] [CrossRef] [PubMed]
- Hunt, C.J. Cryopreservation: Vitrification and Controlled Rate Cooling. Methods Mol Biol. 2017, 1590, 41–77. [Google Scholar] [CrossRef]
- Lujić, J.; Marinović, Z.; Bajec, S.S.; Djurdjevič, I.; Kása, E.; Urbányi, B.; Horváth. First successful vitrification of salmonid ovarian tissue. Cryobiology 2017, 76, 154–157. [Google Scholar] [CrossRef] [PubMed]
- Pšenička, M.; Saito, T.; Rodina, M.; Dzyuba, B. Cryopreservation of early stage Siberian sturgeon Acipenser baerii germ cells, comparison of whole tissue and dissociated cells. Cryobiology 2016, 72, 119–122. [Google Scholar] [CrossRef] [PubMed]
- Igna, V.; Telea, A.; Florea, T.; Popp, R.; Grozea, A. Evaluation of Russian sturgeon (Acipenser gueldenstaedtii) Semen Quality and Semen Cryopreservation. Animals 2022, 12, 2153. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhang, T.; Zhao, F.; Feng, G.; Liu, J.; Yang, G.; Zhang, L.; Zhuang, P. Effects of cryopreservation on acrosin activity and DNA damage of Russian sturgeon (Acipenser guelden-staedtii) semen. Cryoletters 2021, 42, 129–136. [Google Scholar] [PubMed]
- Marques, L.S.; Fossati, A.A.N.; Rodrigues, R.B.; Da Rosa, H.T.; Izaguirry, A.P.; Ramalho, J.B.; Moreira, J.C.F.; Santos, F.W.; Zhang, T.; Streit, D.P. Slow freezing versus vitrification for the cryopreservation of zebrafish (Danio rerio) ovarian tissue. Sci. Rep. 2019, 9, 15353. [Google Scholar] [CrossRef] [PubMed]
- Magnotti, C.; Cerqueira, V.; Lee-Estevez, M.; Farias, J.G.; Valdebenito, I.; Figueroa, E. Cryopreservation and vitrification of fish semen: A review with special emphasis on marine species. Rev. Aquac. 2016, 10, 15–25. [Google Scholar] [CrossRef]
- Rajan, R.; Matsumura, K. Development and application of cryoprotectants. In Survival Strategies in Extreme Cold and Desiccation: Adaptation Mechanisms and Their Applications; Springer Nature Singapore Pte Ltd. Springer: Singapore, 2018; pp. 339–354. [Google Scholar] [CrossRef]
- Bhattacharya, M.S. A review on cryoprotectant and its modern implication in cryonics. Asian J. Pharm. 2016, 10, 154–159. [Google Scholar] [CrossRef]
- Niu, J.; Wang, X.; Liu, P.; Liu, H.; Li, R.; Li, Z.; He, Y.; Qi, J. Effects of Cryopreservation on Sperm with Cryodiluent in Viviparous Black Rockfish (Sebastes schlegelii). Int. J. Mol. Sci. 2022, 23, 3392. [Google Scholar] [CrossRef] [PubMed]
- Xin, M.; Siddique, M.A.M.; Dzyuba, B.; Cuevas-Uribe, R.; Shaliutina-Kolešová, A.; Linhart, O. Progress and challenges of fish sperm vitrification: A mini review. Theriogenology 2017, 98, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Kása, E.; Bernáth, G.; Kollár, T.; Żarski, D.; Lujić, J.; Marinović, Z.; Bokor, Z.; Hegyi; Urbányi, B.; Vílchez, M.C.; et al. Development of sperm vitrification protocols for freshwater fish (Eurasian perch, Perca fluviatilis) and marine fish (European eel, Anguilla anguilla). Gen. Comp. Endocrinol. 2016, 245, 102–107. [Google Scholar] [CrossRef] [PubMed]
- Rusco, G.; Di Iorio, M.; Gibertoni, P.P.; Esposito, S.; Penserini, M.; Roncarati, A.; Cerolini, S.; Iaffaldano, N. Optimization of Sperm Cryopreservation Protocol for Mediterranean Brown Trout: A Comparative Study of Non-Permeating Cryoprotectants and Thawing Rates In Vitro and In Vivo. Animals 2019, 9, 304. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.H.; Park, J.Y.; Lee, I.Y.; Zidni, I.; Lim, H.K. Effects of cryoprotective agents and treatment methods on sperm cryopreservation of stone flounder, Kareius bicoloratus. Aquaculture 2020, 531, 735969. [Google Scholar] [CrossRef]
- Hu, E.; Daniels, H.; Gill, A.O.; Tiersch, T.R.; Cuevas-Uribe, R. Vitrification as an Alternative Approach for Sperm Cryopreservation in Marine Fishes. North Am. J. Aquac. 2017, 79, 187–196. [Google Scholar] [CrossRef]
- Ren, S.; Shu, Z.; Pan, J.; Peng, J.; Wang, J.; Zhao, C.; Gao, D. Development of a Novel Electromagnetic Rewarming Technology for the Cryopreservation of Stem Cells with Large Volume. In Novel Perspectives of Stem Cell Manufacturing and Therapies; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Rahman, S.M.; Strüssmann, C.A.; Suzuki, T.; Majhi, S.K.; Hattori, R.S.; Alam, A. Effects of ultrasound on permeation of cryoprotectants into Japanese whiting Sillago japonica embryos. Cryobiology 2017, 77, 19–24. [Google Scholar] [CrossRef]
- Ponomareva, E.; Firsova, A.; Krasilnikova, A.; Kovalenko, M.; Rudoy, D. Acoustic-mechanical effect on the sperm of sturgeon fish using piezoactuators. E3S Web Conf. 2022, 363, 03020. [Google Scholar] [CrossRef]
- Alcalá, E.; Encabo, L.; Barroso, F.; Puentes, A.; Risco, I.; Risco, R. Sound waves for solving the problem of recrystallization in cryopreservation. Sci. Rep. 2023, 13, 7603. [Google Scholar] [CrossRef] [PubMed]
- Blagin, A.V.; Blagina, L.V.; Knyazev, S.Y.; Shcherbakova, E.E.; Nefyodova, N.A. Crystallization Processes in Gradient Fields; DSTU: Rostov-on-Don, Russia, 2021; 196p. (In Russian) [Google Scholar]
- Agarwal, N.K. Cryopreservation of Fish Semen. In Himalayan Aquatic Biodiversity Conservation & New Tools in Biotechnology Edition, 1st ed.; Chapter 8; Transmedia Publication: Srinagar (Garhawal) Uttarakhand, India, 2011. [Google Scholar] [CrossRef]
- Union for Conservation of Nature and Natural Resources. Available online: https://iucn.org/ (accessed on 10 November 2023).
- Convention on International Trade in Endangered Species of Wild Fauna and Flora. Available online: https://www.fisheries.noaa.gov/national/international-affairs/convention-international-trade-endangered-species-wild-fauna-and (accessed on 10 November 2023).
- Red Book of the Russian Federation. Available online: https://www.mnr.gov.ru/activity/red_book/krasnaya-kniga-rossiyskoy-federatsii/?ysclid=ls4q0e9eui253200674 (accessed on 10 November 2023).
- Ponomareva, E.N.; Soloviev, A.N.; Matrosov, A.A.; Chebanenko, V.A.; Nizhnik, D.A.; Egorova, A.A.; Krasilnikova, A.A. Mathematical Simulation of the Acoustic Effect on a Cryoprotectant with Fish Sperm at Equilibration. Biophysics 2022, 67, 549–558. [Google Scholar] [CrossRef]
- Matrosov, A.A.; Nizhnik, D.A.; Ponomareva, E.N.; Soloviev, A.N. Modeling the Impact of Piezoactuator on Fish Reproductive Cells in the Cryoprotective Environment; DSTU: Rostov-on-Don, Russia, 2022; pp. 266–269. (In Russian) [Google Scholar]
- Matrosov, A.A.; Nizhnik, D.A.; Pakhomov, V.I.; Soloviev, A.N. Diffusion of Cryoprotectant Through the Membrane of Re-productive Cells During Equilibration. In Physics and Mechanics of New Materials and Their Applications (PHENMA); Springer: Berlin/Heidelberg, Germany, 2023; pp. 508–514. [Google Scholar] [CrossRef]
- Krishna, R. Modelling of Cell Suspention During Cryopreservation. National Institute of Technology, Rourkela, 2013. 53p. Available online: http://ethesis.nitrkl.ac.in/5341/1/211BM2008.pdf (accessed on 10 November 2023).
- Cincotti, A.; Fadda, S. Modelling the Cryopreservation Process of a Suspension of Cells: The Effect of a Size-Distributed Cell Population//Computational Modeling in Tissue Engineering. In Studies in Mechanobiology, Tissue Engineering and Biomaterials; Springer: Berlin/Heidelberg, Germany, 2012; pp. 145–182. [Google Scholar] [CrossRef]
- Andreev, A.A.; Sadikova, D.G.; Ponomareva, E.N.; Krasilnikova, A.A.; Belaya, M. Method of Reduction of Low-Temperature Jump of Cryoprotectant. Solutions. Patent RU 2540598 C2, 10 February 2015. [Google Scholar]
- Ponomareva, E.; Matrosov, A.; Kovalenko, M.; Rudoy, D.; Pakhomov, V. Low-temperature preservation of sterlet reproductive cells (Acipenser ruthenus Linnaeus, 1758) by the acoustic-mechanical influence method. E3S Web Conf. 2023, 462, 03058. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).