Abstract
Optimization algorithms play a crucial role in a wide range of fields, from designing complex systems to solving mathematical and engineering problems. However, these algorithms frequently face major challenges, such as convergence to local optima, which limits their ability to find global, optimal solutions. To overcome these challenges, it has become imperative to explore more efficient approaches by incorporating chaotic maps within these original algorithms. Incorporating chaotic variables into the search process offers notable advantages, including the ability to avoid local minima, diversify the search, and accelerate convergence toward optimal solutions. In this study, we propose an improved Archimedean optimization algorithm called Chaotic_AO (CAO), based on the use of ten distinct chaotic maps to replace pseudorandom sequences in the three essential components of the classical Archimedean optimization algorithm: initialization, density and volume update, and position update. This improvement aims to achieve a more appropriate balance between the exploitation and exploration phases, offering a greater likelihood of discovering global solutions. CAO performance was extensively validated through the exploration of three distinct groups of problems. The first group, made up of twenty-three benchmark functions, served as an initial reference. Group 2 comprises three crucial engineering problems: the design of a welded beam, the modeling of a spring subjected to tension/compression stresses, and the planning of pressurized tanks. Finally, the third group of problems is dedicated to evaluating the efficiency of the CAO algorithm in the field of signal reconstruction, as well as 2D and 3D medical images. The results obtained from these in-depth tests revealed the efficiency and reliability of the CAO algorithm in terms of convergence speeds, and outstanding solution quality in most of the cases studied.
1. Introduction
The exploration of problems characterized by high nonlinearities and multiplicities of local optima is a major concern in the fields of computer science, artificial intelligence, and machine learning. Traditional methods often face insurmountable challenges in regard to solving complex, multimodal problems. In such cases, nature-inspired approaches stand out by exploiting their ability to combine diversification and stochastic intensification to achieve optimal solutions in these complex contexts [1,2]. In recent decades, a considerable range of metaheuristic optimization algorithms has emerged as valuable alternatives for tackling these problems. These approaches have proven their effectiveness in finding solutions to demanding computational challenges, and they continue to gain in importance as the practical applications of artificial intelligence and machine learning multiply [3,4].
Two key features of metaheuristic methods are intensification and diversification, which play a crucial role in the search for optimal solutions [5]. Intensification targets the currently most promising solutions and selects the best-performing candidates, while diversification enables the optimizer to explore the search space more efficiently, largely through the use of randomization.
The ongoing evolution of the field of global optimization has seen the emergence of several new metaheuristic algorithms, each bringing its own innovations for improving computational efficiency, solving large-scale problems, and implementing robust optimization codes. Among these newcomers, ABC (Artificial Bee Colony) has adopted an approach that simulates the behavior of bees in their search for nectar [6]. Cuckoo search (CS) was inspired by the brooding behavior of certain birds to explore the search space [7]. HS (Harmony Search) introduced a notion of harmonious search inspired by music [8]. The BA (Bat Algorithm) exploits bat behavior to optimize functions [9]. Other algorithms, such as Genetic Algorithm (GA) [10,11,12], Chicken Swarm Optimization (CSO), Gray Wolf Optimizer (GWO), Firefly Algorithm (FA), Whale Optimization Algorithm (WOA), and Antlion Optimizer (ALO), also saw the light of day, each bringing their own perspective to solving complex problems [13,14,15,16,17,18].
This diversity of approaches testifies to the richness and adaptability of metaheuristic algorithms in the search for solutions to a variety of domains and problems. It also reflects the scientific community’s ongoing commitment to exploring new avenues for pushing back the boundaries of optimization.
Recently, a new population-based metaheuristic optimization algorithm called Archimedes’ Optimization Algorithm (AO) was proposed [19], inspired by Archimedes’ Law from the field of physics. The operating principle of Archimedes’ optimization algorithm (AO) is inspired by Archimedes’ famous law governing the buoyancy of bodies immersed in a fluid. This fundamental law establishes a balance between the buoyant force exerted by the fluid on an immersed object and the weight of that object. When we apply this principle to AOA, the entities in the population are analogous to objects immersed in the fluid. Each of these entities is characterized by a series of parameters, including acceleration, density, and volume, which are key elements in determining whether an entity will float or sink in the algorithm’s search space. The upward force, in the context of AO, represents the ability of an entity to emerge as an optimal solution. It is equivalent to the buoyancy of the entity, which is determined by the relationship between the weight of the object (representing the quality of the solution) and the weight of the displaced fluid (which can be interpreted as the potential of the solution). If the fluid displaced (the potential of the solution) is less than the weight of the object (the quality of the solution), the entity (the solution) will tend to ‘sink’, in the sense that it will not be retained as the optimal solution. On the other hand, when the weight of the object (the quality of the solution) is equal to the weight of the fluid displaced (the potential of the solution), the floating entity (solution) is in equilibrium. Herein lies the central conception of AO: finding the equilibrium point where a retained solution is in equilibrium, and where the net force of the fluid is zero. Although the AO algorithm is effective for solving complex problems, it cannot always overcome the pitfalls of the local optimum.
The phenomenon of chaos, characterized by its extreme sensitivity to initial conditions, has long intrigued researchers and become a key component in the field of optimization. Chaotic functions, often described as complex and unpredictable, vary irregularly over time, and are particularly sensitive to these initial conditions [20,21,22,23]. This sensitivity to initial values is an essential indicator of chaotic functions, as even a small, seemingly insignificant change in these conditions can lead to significant variations that cannot be neglected. It is in this context that metaheuristic algorithms have explored the potential offered by chaotic functions to improve their performance. Chaotic functions have proven particularly effective in the search for solutions to problems of local or premature convergence. Chaotic optimization methods have thus been adopted in many recent studies to break the vicious cycle of optimization. In addition, these chaotic functions have added value to global optimization algorithms by diversifying the search space. Chaotic theory has significant potential for improving the performance of metaheuristic algorithms.
The integration of chaos-based enhancement within various global optimization algorithms offers significant advantages. Consider, for example, its application within PSO, where it has the potential to deliver substantial improvements. In the context of PSO, chaos-based enhancement offers advantages in terms of increased diversification and exploration of the search space [24]. The chaotic properties of this approach play an essential role in preventing premature convergence to local optima. By promoting particle diversity, it enables a more exhaustive and dynamic exploration of the optimization landscape. Similarly, the introduction of chaos-based improvement within Genetic Algorithms (GA) opens up promising prospects [25]. It offers an opportunity to enhance genetic diversity within populations, thus promoting more efficient exploration of the search space. This diversification contributes to faster convergence towards optimal solutions by widening the field of exploration of potential solutions. The application of chaos in ACO (Ant Colony Optimization) mechanisms can significantly enhance the ability of ants to discover optimal paths [26]. By introducing chaotic exploration, this approach stimulates the search for alternative solutions, thus optimizing convergence towards quality solutions within the ant network. In the case of Artificial Bee Algorithms (ABC), the use of chaos-based enhancement can promote a more dynamic exploration of the search space [27]. This dynamic approach overcomes the limitations of traditional methods, stimulating further diversification of the solutions explored by the artificial bee colony.
This encouraged us to use chaotic maps to further optimize the Archimedean Optimization Algorithm (AO). In this study, we introduce a new chaos-enhanced Archimedean optimization algorithm (CAO). Our approach consists of using chaotic map functions to influence the generation of the random parameters of the AO algorithm. This integration allows us to scan the search space more dynamically and to refine various aspects of the algorithm. Thanks to this synergy, we have been able to achieve optimal fitness function values with increased success. To achieve this, we incorporated ten distinct chaotic maps to replace pseudorandom sequences in three AO components.
To evaluate the performance of the chaos-enhanced Archimedes optimization (CAO) algorithm, we have undertaken exhaustive testing using three distinct problem groups, each representing a set of specific challenges. The aim of this rigorous evaluation is to demonstrate the robustness and effectiveness of the CAO algorithm. The first group of problems consists of twenty-three benchmark functions (unimodal, multimodal, and multimodal with fixed dimension). Group 2 comprises three engineering problems, namely, the design of a welded beam, the design of a spring subjected to tension/compression stresses, and the design of a pressure vessel. These practical problems test the CAO algorithm’s ability to solve complex engineering optimization challenges. This evaluation will determine the applicability of the CAO algorithm to real-world problems. The third group of problems is dedicated to validating the CAO algorithm in the field of 2D and 3D medical image and signal reconstruction. We use discrete orthogonal Meixner moments (MMs) for this purpose. The aim of this series of tests is to demonstrate the CAO algorithm’s ability to solve image and signal processing problems, with an emphasis on accuracy and efficiency. To establish a meaningful comparison, we compare the performance of the CAO algorithm with that of other optimization algorithms in the literature.
The main contributions of this work are summarized as follows:
- (a)
- With the aim of achieving an optimal balance between exploitation and exploration for the Archimedean optimization (AO) algorithm, we introduce a new Archimedean optimization algorithm enhanced by chaotic maps (CAO).
- (b)
- To assess the effectiveness of the CAO method, we conducted extensive experiments using a set of twenty-three well-known numerical reference functions. In addition, the method was successfully applied to three real-world engineering problems, confirming its relevance in real-world contexts.
- (c)
- As an innovative application, CAO is used to optimize the selection of Meixner polynomial parameters, contributing to optimal reconstruction of medical signals and images. This application demonstrates the versatility of the CAO method for solving a variety of problems, from numerical optimization to medical image reconstruction.
The structure of the rest of this article is as follows: Section 3 looks at the presentation of the mathematical models underlying the standard Archimedes optimization algorithm. Section 4 is devoted to an examination of chaotic maps, while Section 5 explains in detail the Archimedes chaotic algorithm we have developed. Section 6 is dedicated to evaluating the performance of the proposed algorithm through a series of in-depth tests. Section 7 concludes our study.
2. Problem Formulation
In optimization problems, the task is often to find optimal solutions in a defined decision space. This formulation of the problem encompasses the effort to minimize a specific objective function over a set of admissible solutions, where the limits of each coordinate are precisely specified. Such a structured approach enables systematic exploration of the decision space, ensuring that the solutions sought respect the prescribed constraints.
- Objective function
- Decision variables
- Bounds for each coordinatewhere and are the specified lower and upper bounds for each coordinate , and n is the number of variables.
This complete formulation encapsulates the optimization problem, clearly defining the objective, decision variables, coordinate constraints, and decision space. It thus establishes a formal basis for analyzing and solving the optimization problem.
3. The Standard Archimedes Optimization Algorithm
The Archimedean Optimization Algorithm (AO) is a physics-inspired metaheuristic optimization algorithm that has emerged recently, and its operating principle is inspired by Archimedes’ law of physics [28]. AO is a population-based algorithm where the individuals in the population are immersed objectives. AO starts a review process using an initial population of individuals endowed with random accelerations, densities, and volumes. The evaluation process begins with the suitability of this preliminary population and then continues through iterations until the end condition is reached. During each iteration, the density and volume of everyone are updated. Based on its interaction with other neighboring individuals, the acceleration of everyone is revised. The updated volume, density, and acceleration values determine the new position of everyone. AO has the distinct advantage of achieving a harmonious balance between exploration and exploitation, making it well suited to engineering optimization problems [29,30].
The main steps of the Archimedean Optimization (AO) algorithm are described below:
Step 1: Initialize the positions (), volume (), density (), and acceleration () of all objects.
where and are the lower and upper bounds of the search-space, respectively.
Step 2: Update the densities () and volumes () of an object using the following equation:
where and are the best volume and best density, respectively, thus far.
Step 3: Calculation of the density factor and transfer operator.
When two objects first collide, they attempt to attain a stable state after some time has passed, and is used in the AO to do this. The shift from exploration to exploitation in the search process is accomplished by utilizing the following formula:
Similarly, the density factor decreases over time, allowing one to concentrate in a favorable area.
where represents the iteration number and denotes the maximum iterations.
Step 4: Exploration phase
If TF ≤ 0.5 (objects are colliding), for , the update of the object’s acceleration is performed using Equation (8).
where and denote the density and volume of the random material, respectively.
Step 5: Exploitation phase
If TF > 0.5 (objects are not colliding), for , the update of the object’s acceleration is performed using Equation (9).
Step 6: Normalize the acceleration.
The normalized acceleration is calculated using:
where and are the normalization ranges, and is the minimum acceleration value while is the maximum acceleration value.
Step 7: Update the position.
The calculation of the object’s position is determined by the following equation:
T increases with time and is directly proportional to the transfer operator defined by:
F is the flag used to change the direction of movement using Equation (13).
where .
Step 8: Evaluation
Select the object’s position that exhibits the best fitness value upon evaluating each object.
The global optimization algorithms use random variables to explore the search space, commonly in the form of a uniform distribution (rand). However, this use of random variables frequently leads to local optima, thus limiting search efficiency. This is why we suggest using sequences generated by chaotic maps to determine the values of parameters, which, in the AO algorithm, were of a random nature. The integration of chaotic variables into the search process represents a significant advance over an entirely random approach. The advantages inherent in this approach are substantial, and chaotic maps, which we will detail in the next section, play a key role in the search for optimal solutions.
4. Chaotic Maps
In recent years, chaos theory has made significant advances and has been successfully exploited in a variety of scientific fields. Promising applications include image and signal encryption, feature selection, and parameter optimization. Chaotic maps, in particular, have proven highly useful, possessing three fundamental characteristics: sensitivity to initial conditions, randomness, and dynamics. These unique properties have enabled chaotic maps to be incorporated into several renowned optimization algorithms, including moth flame optimization (MFO), firefly algorithm (FA), artificial bee colony (ABC), biogeography-based optimization (BBO), particle swarm optimization (PSO), and gray wolf optimizer (GWO). This fusion of chaos theory with optimization algorithms has paved the way for more efficient solutions and better performance, both in solving complex problems and in improving engineering processes [31,32,33]. Chaotic maps have added an extra dimension to the search for solutions by introducing an element of dynamics and unpredictability, which has proved beneficial in escaping local minima and improving the quality of the solutions found.
In this subsection, we outline ten one-dimensional chaotic maps of particular relevance to optimization algorithms used to generate chaotic sequences, as detailed in Table 1 and illustrated in Figure 1. It is important to note that the initial point can be chosen arbitrarily, in the range 0 to 1 (or according to the specific scope of the chaotic map in question). The use of these dynamic values is of paramount importance, as it contributes significantly to improving the search capability of the AO.

Table 1.
Chaotic maps.
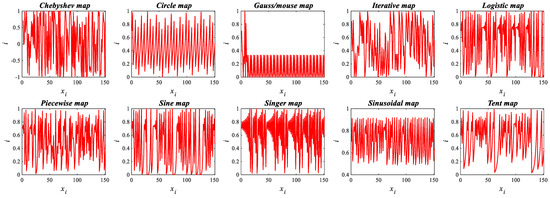
Figure 1.
Chaotic map values.
The idea behind this method is based on three key principles: (i) Introduction of a chaotic state into the optimization variables using a similar support approach. (ii) Extension of the range of chaotic movements to encompass the interval of optimization variables. (iii) Use of chaotic sequences to enhance the efficiency of the search process.
By combining these principles, it becomes possible to inject an element of controlled chaos into the optimization variables, explore a wider range of potential solutions, and thus improve search efficiency in a well-controlled way. This innovative approach offers promising prospects for the optimization of complex problems, in particular by widening the range of solutions explored and enabling a more diversified and efficient search.
5. Proposed Chaotic-Archimede Optimization Algorithm (CAO)
In the classic configuration of the Archimedean optimization algorithm, an initial set of random solutions originates in the extent of the search space. This set of solutions is then subjected to a series of updating equations, each contributing to the distinct exploration and exploitation of the search space. The exploration equations are responsible for guiding the solutions to various regions of the search space, seeking to exhaustively explore the different possibilities. In contrast, exploitation equations steer solutions towards the best solution identified so far, while probing the surroundings of this optimal solution. However, it is crucial to note that these equations have a random component, meaning that solutions mutate at random intervals and in random directions This random nature of the equations underlines the sensitivity to random parameters, which exert a substantial influence on the quality of the solutions obtained and, by extension, on the final results of the algorithm. A judicious modification of these random parameters could therefore play a decisive role in optimizing the overall process, potentially leading to more robust and accurate solutions.
Although not yet mathematically proven, various studies converge towards the conclusion that the integration of chaotic maps significantly improves the performance of metaheuristic optimization algorithms, as developed by many researchers [34,35]. For example, Wang et al. in [34] demonstrated the performance improvement of the Remora optimization algorithm (ROA) based solely on chaotic tent mapping. Similarly, Wang et al. in [35] introduced the Levy operator to help the crystal structure algorithm (CryStAl) to effectively free itself from the attraction of the local optimal value.
However, in the context of this study, our aim is to take advantage of ten chaotic maps, thus opening up several perspectives for improving the performance of our proposed algorithm, specifically in terms of avoiding local optimum, rather than being limited to the use of a single chaotic map or operator.
This study presents the development of a new algorithm called the Chaos-Enhanced Archimedean Optimization (CAO) algorithm. The introduction of chaotic variables into the AO search process confers significant advantages over a purely random approach. More specifically, the ergodic properties of chaotic maps are exploited to increase search efficiency by bypassing local minima.
In the CAO, chaotic sequences are generated by ten distinct types of chaotic maps, namely Chebyshev, circular, Gaussian, iterative, logistic, patchy, sinusoidal, Singer, sinusoidal, and tent, as illustrated in Table 1. These sequences replace the random sequences of the original AO in three crucial components of the optimization algorithm, namely initialization, density and volume updating, and position updating. This integration enhances the AO algorithm’s ability to bypass local optima, thus increasing the probability of converging to the global optimum in a limited number of iterations.
Each chaotic map is tested independently in each of these components. The pseudocode of the CAO algorithm is shown in Algorithm 1, while Figure 2 illustrates the CAO flowchart. In this algorithm, represents a chaotic sequence generated by a specific chaotic map. The results obtained in this study show that chaotic maps increase the performance of optimization methods.
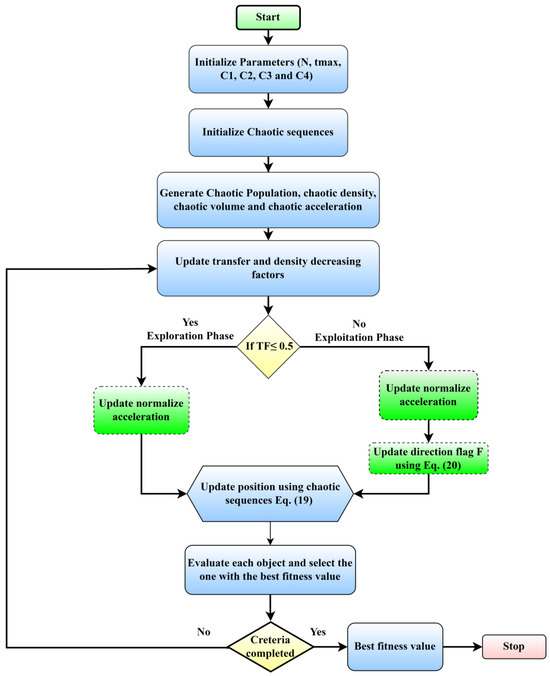
Figure 2.
CAO algorithm flowchart.
| Algorithm 1. pseudo code of CAO |
| 1 Initialization (N, tmax, C1, C2, C3 and C4). 2 Initialize chaotic value . 3 for i = 1:n 4 for j = 1: n 5 ; 6 ; 7 ; 8 ; 9 ; 10 end 11 end 12 Evaluate the initial population and select the one with the best fitness value. 13 t (iteration counter) = 1 14 While t < tmax do 15 for each object i do 16 for j = 1: n 17 //Update density and volume of each object. 18 ; 19 ; 20 end 21 //Update transfer and density decreasing factors TF and . 22 ; ; 23 if TF ≤ 0.5 then ---//Exploration phase 24 //Update acceleration and normalize acceleration. 25 ; 26 for i = 1:n 27 ; 28 ; 29 end 30 else ---//Exploitation phase 31 //Update acceleration and normalize acceleration. 32 ; 33 for i = 1:n 34 ; 35 ; 36 ; 37 end 38 end 39 end while 40 Evaluate each object and select the one with the best fitness value. 41 t = t + 1 42 Return |
- (a)
- Utilization of chaotic maps in initializing the population
Since AO adopts the traditional initialization method, the randomness and diversity of the initial population cannot be guaranteed. In contrast to traditional initialization methods, the use of chaotic for initialization significantly preserves population diversity.
However, in our chaotic optimization algorithm (CAO), we make an innovative choice by using chaotic sequences instead of simple random generation rand (0, 1). These chaotic sequences are used to initialize the position, volume, density, and acceleration of all objects, according to the following formulas:
In order to verify the rationality of this method, we compared the initial value generated by the chaotic map with that generated by traditional initialization, and the results are shown in Figure 3. As this figure shows, the initial value generated by the chaotic map is more extensive than that generated by the uniform random distribution, and it is not difficult to observe that the initial positions obtained on the basis of initialization by chaotic mapping are more uniformly distributed in the search space. Consequently, the former can improve the ergodicity of the initial value and accelerate the convergence speed of the algorithm.
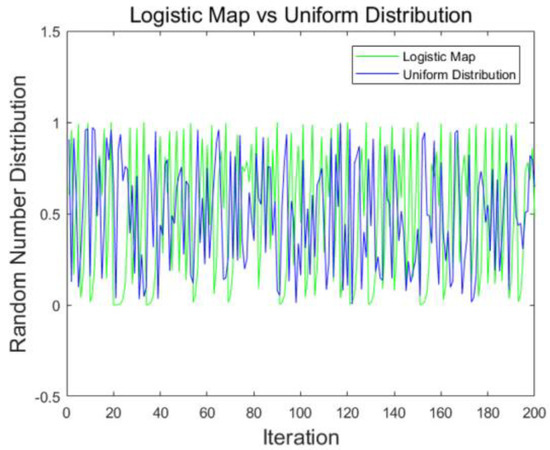
Figure 3.
Initial value by utilizing both a chaotic map and a uniform random distribution.
- (b)
- Chaotic maps applied to update density and volume
The density and volume of object i are updated at iteration t + 1 according to Equation (5). In this equation, the parameters rand1 and rand2 are essential to the AO algorithm, and their values are usually randomly generated from the interval [0, 1]. However, a significant innovation in our approach is the use of chaotic maps to generate these parameters. Instead of using random values at each iteration to determine the optimal points, we adopt a more sophisticated method using chaotic maps to assign values to rand1 and rand2. This innovative approach promises substantial improvements in the search for optimal solutions. The density and volume of object i for iteration t + 1 are updated using the following equation:
- (c)
- Chaotic maps applied to update position
In the standard optimization algorithm (AO), the position of objects i is updated in accordance with Equation (11). It is important to note that the values rand3 and rand4, needed in this equation, are usually randomly generated in the interval [0, 1]. However, in our chaotic optimization algorithm (CAO), we introduce a crucial innovation: instead of relying on random values at each iteration, we use chaotic maps to determine these parameters. This innovative approach promises to open up new perspectives in improving algorithm efficiency and finding optimal solutions. The calculation of the new position of object i is determined by the following equation:
The variable in expression represents a random position associated with a random number generation process. This variable can take on different values at random.
F is the flag used to change the direction of movement using (Equation (20)).
The following observations reinforce the demonstration of the theoretical effectiveness of the proposed chaotic algorithms:
As a first significant improvement, the chaos-enhanced Archimedean optimization algorithm determines the positions, volumes, densities, and accelerations of all objects by choosing the best solution from among those randomly generated.
Chaotic map integration supports CAO by orchestrating chaotic updates of density, volume, and position, substantially improving the exploration process.
When it comes to probing a promising area in the search space, these chaotic parameters play an essential role in fostering chaotic neighborhood exploitation.
6. Simulation Results
To evaluate the effectiveness of the proposed Chaos-Archimede Optimization Algorithm (CAO), we undertook tests on three distinct problem sets. The first group, comprising twenty-three benchmark functions (unimodal, multimodal, and multimodal with fixed dimension) identified in Table 2, served as the basis for our evaluation. The second group consists of three significant engineering problems: the design problem for a welded beam, the design problem for a tension/compression spring, and the design problem for a pressure vessel. These engineering problems enable us to test the effectiveness of our algorithms in practical contexts. Finally, the third group of tests highlights the versatility of the CAO approach. It is devoted to validating our CAO algorithm for signal reconstruction, as well as 2D and 3D medical images. In this series of tests, we used discrete orthogonal Meixner moments (MMs) as a key tool. These experiments cover a diverse range of application domains and demonstrate the adaptability and efficiency of our CAO algorithm in a variety of contexts.

Table 2.
Unimodal, multimodal, and multimodal with fixed dimensions test functions.
For the first group, made up of 23 test functions in Table 2, the aim is to determine the value of x that minimizes the function f(x) in each specific case. This solution search is formulated under the constraint minf(x). It is important to note that the search range, the possible values for the components of x, varies according to the specific nature of each function. Each function may have distinct range requirements for the different variables, and this variability must be considered when searching for the optimal solution for each test function.
In the second group, the aim is to find optimal values for x that minimize the cost functions associated with the welded beam, tension/compression spring, and pressure vessel design problems. The search scope is adjusted accordingly to meet the specifics of each engineering problem [36].
In the third problem, we seek to optimize the polynomial Meixner parameters (β, u) by minimizing the objective function MSE (Mean Square Error), with the aim of obtaining optimal parameters that enable 1D, 2D, and 3D signals to be reconstructed with excellent quality. The dimension of this problem is equal to 2, as we are looking for optimal values of β and u. The search range for the parameters is defined as follows: The search range for β extends from 0 to N (the size of the signal), while the search range for u varies from 0 to 1. This choice of range reflects the specific conditions of the problem, and is intended to guarantee an exhaustive exploration of the possible values of β and u with the aim of obtaining optimal parameters for the reconstruction of multidimensional signals.
Chaos-Archimede Optimization Algorithms (CAO) take advantage of ten types of chaotic maps, as illustrated in Table 1. This diversity of chaotic maps has enabled us to sequentially develop ten variations of Chaos-Archimede optimization algorithms, which we have designated as follows: CAO1 (Chebyshev-AO), CAO2 (Circular-AO), CAO3 (Gauss-AO), CAO4 (Iterative-AO), CAO5 (Logistic-AO), CAO6 (Piecewise-AO), CAO7 (Sine-AO), CAO8 (Singer-AO), CAO9 (Sinusoidal-AO), and CAO10 (Tent-AO). The performance of these ten new algorithms was evaluated by comparing them with the standard AO algorithm. Notably, the comparative analysis shows that CAO10 stands out with the most remarkable performance of the set.
Continuing our exploration, we extended the comparison by including CAO10 in a set of original optimization algorithms, such as the whale optimization algorithm [36], the gray wolf optimizer [37], salp swarm algorithm [38], multiverse optimizer [39], gravitational search algorithm [40], sine cosine algorithm [41], particle swarm optimization [42], and moth-flame optimization [43]. The results obtained highlight the efficiency of CAO10, which competes with these original algorithms in a promising way, opening new perspectives for diverse optimization applications.
6.1. Reference Function Validation
- (a)
- Extensibility test
To evaluate the performance of the Chaos-Archimede Optimization (CAO) algorithm, this section carries out an in-depth comparison between the results obtained by CAO and those of the original AO algorithm. Tests are specifically carried out on twenty-three benchmark functions (F1–F23), involving rigorous evaluations of the scalability of both algorithms.
The aim of scalability tests is to analyze the impact of dimensions on the efficiency of stochastic optimizers. They enable us to understand how problem dimensions affect the quality of the solutions generated, as well as the efficiency of the CAO when the dimension is dynamically increased. Three different dimensions are therefore examined in this study: 20, 30, and 50. To assess the performance of the algorithms, several performance measures are used. These include: (1) the mean and standard deviation of the final solutions obtained for each function. (2) Analysis of the convergence of the functions obtained to assess the speed with which the algorithms converge toward optimal solutions. (3) Ranking to identify the chaotic map that performs best among all available chaotic maps.
All optimization algorithms are subjected to the same experimental conditions, including an identical population size and a predefined maximum value set at 500. This rigorous methodological approach ensures a fair comparison of CAO versus AO performance, highlighting the potential advantages of using chaotic maps in the context of stochastic optimization.
- (1)
- In statistics, the standard deviation is a fundamental measure used to quantify the amplitude of variation and dispersion within a data set. A standard deviation close to zero indicates that optimal solutions tend to be very close to the mean, reflecting a high concentration of results. On the other hand, a high standard deviation reflects a greater dispersion of optimal solutions over a wide range of values, suggesting greater variability. Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11 show the mean error and standard deviation of solutions obtained from experiments with the ten CAO optimization algorithms and the standard AO for dimensions of 20, 30, and 50, respectively. Analysis of these results reveals that CAO optimization algorithms outperform AO in all functions (F1-F23), regardless of the number of dimensions. Moreover, these CAO algorithms systematically display a clear superiority in the higher dimensions, underlining their ability to handle complex problems. Notably, the CAO10 algorithm stands out as offering exceptional accuracy compared to other CAO variants, reinforcing its status as the preferred choice for optimizing varied, multidimensional problems. These results demonstrate that integrating chaotic maps into CAO optimization algorithms can significantly improve their efficiency, paving the way for more accurate solutions and greater convergence in complex optimization contexts.
 Table 3. Results on unimodal benchmark functions (F1 to F7) with Dim = 20.
Table 3. Results on unimodal benchmark functions (F1 to F7) with Dim = 20. Table 4. Results on multimodal benchmark functions (F8 to F13) with Dim = 20.
Table 4. Results on multimodal benchmark functions (F8 to F13) with Dim = 20. Table 5. Results on multimodal with fixed dimension benchmark functions (F14 to F23) with Dim = 20.
Table 5. Results on multimodal with fixed dimension benchmark functions (F14 to F23) with Dim = 20. Table 6. Results on unimodal benchmark functions (F1 to F7) with Dim = 30.
Table 6. Results on unimodal benchmark functions (F1 to F7) with Dim = 30. Table 7. Results on multimodal benchmark functions (F8 to F13) with Dim = 30.
Table 7. Results on multimodal benchmark functions (F8 to F13) with Dim = 30. Table 8. Results on multimodal with fixed dimension benchmark functions (F14 to F23) with Dim = 30.
Table 8. Results on multimodal with fixed dimension benchmark functions (F14 to F23) with Dim = 30. Table 9. Results on unimodal benchmark functions (F1 to F7) with Dim = 50.
Table 9. Results on unimodal benchmark functions (F1 to F7) with Dim = 50. Table 10. Results on multimodal benchmark functions (F8 to F13) with Dim = 50.
Table 10. Results on multimodal benchmark functions (F8 to F13) with Dim = 50. Table 11. Results on multimodal with fixed dimension benchmark functions (F14 to F23) with Dim = 50.
Table 11. Results on multimodal with fixed dimension benchmark functions (F14 to F23) with Dim = 50. - (2)
- The convergence test represents an essential criterion for assessing the performance of algorithms in achieving the global optimum. Figure 4, Figure 5 and Figure 6 illustrate the convergence curves of test functions using CAO optimization algorithms and standard AO for dimensions of 20, 30, and 50, respectively. As these figures show, all CAO algorithms demonstrate a remarkable ability to find optimal solutions to reference functions in all functions (F1–F23). These algorithms demonstrate reliability and stability, standing out for their ability to explore search spaces more thoroughly than the standard AO algorithm. Moreover, they converge on optimal solutions considerably faster than the standard algorithm. These observations show that the use of chaotic maps in optimization significantly improves algorithm performance, contributing to greater efficiency and a significant reduction in the time needed to reach optimal solutions.
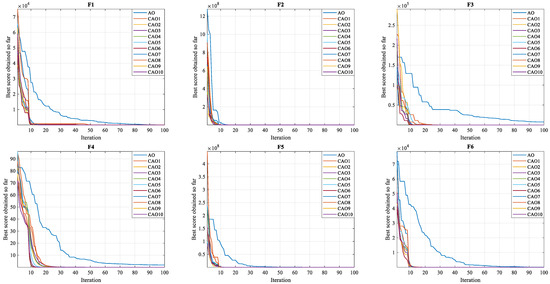
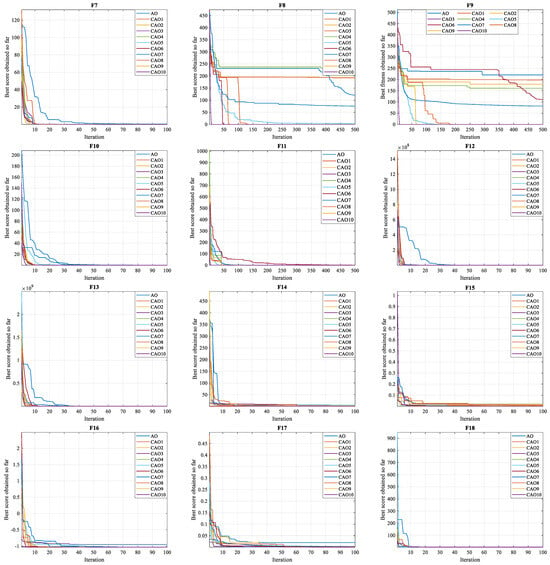
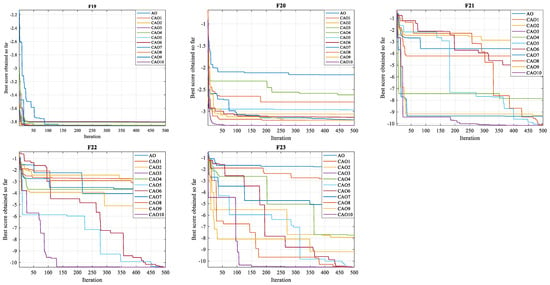 Figure 4. 20D Convergence graphs.
Figure 4. 20D Convergence graphs.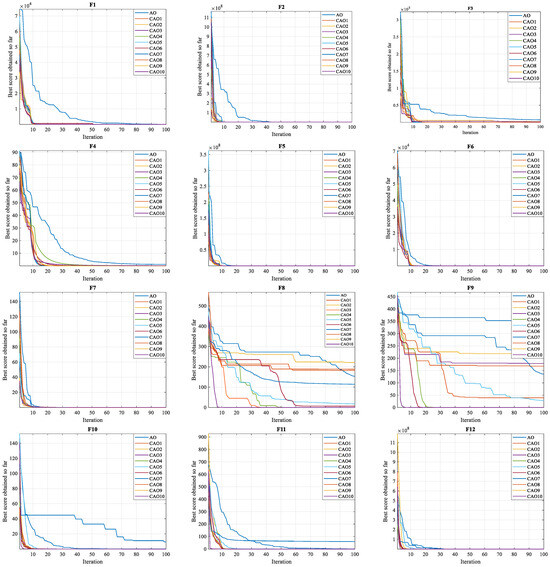
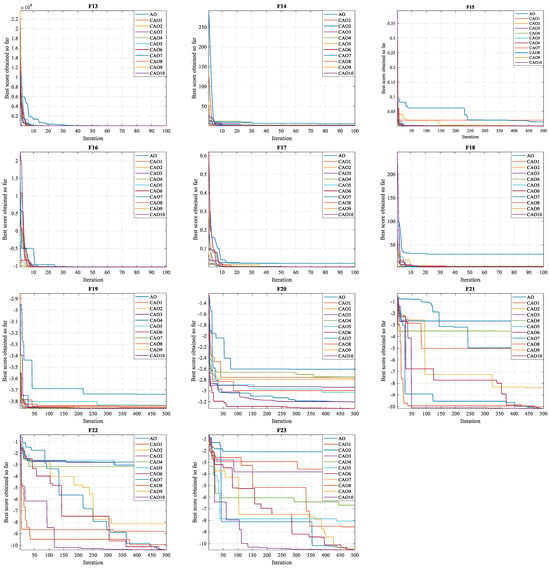 Figure 5. 30D Convergence graphs.
Figure 5. 30D Convergence graphs.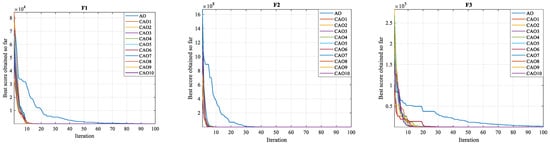
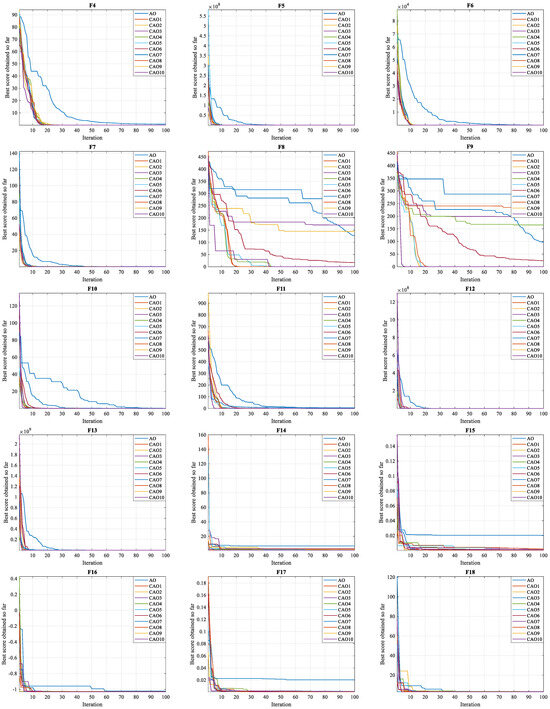
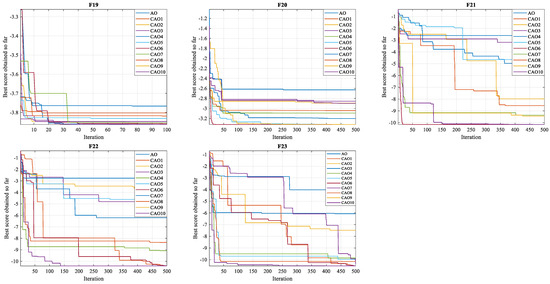 Figure 6. 50D Convergence graphs.
Figure 6. 50D Convergence graphs. - (3)
- In ranking-based analysis, algorithms are evaluated and ranked according to their average performance. For this purpose, a standard ranking system is used to establish the competition between algorithms. Figure 7 show the ranking of algorithms according to their performance in 20, 30, and 50 dimensions. In this ranking system, the ranking value 1 indicates the best performance, while the ranking value 11 reflects the least favorable performance. Clearly, the ten chaotic maps outperform the original AO algorithm. In addition, the CAO10 algorithm stands out by achieving significantly higher rankings than the other CAO variants.
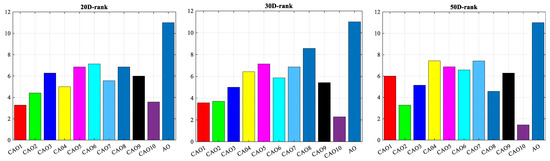 Figure 7. 20D, 30D, and 50D Rank bar graph.
Figure 7. 20D, 30D, and 50D Rank bar graph.
These results convincingly demonstrate that introducing chaotic maps into the optimization process confers a significant performance advantage over the standard Archimedean optimization algorithm. In particular, the CAO10 algorithm stands out as the preeminent choice, highlighting its exceptional efficiency and ability to obtain optimal solutions in multidimensional spaces. This ranking analysis underlines the importance of integrating chaotic variables into optimization for improved performance and a better ability to solve a variety of problems.
- (b)
- Comparison test with other optimization algorithms
To verify the effectiveness of the proposed algorithm, CAO10 was compared with ten well-known algorithms: Whale Optimization Algorithm, Gray Wolf Optimizer, Salp Swarm Algorithm, Multiverse Optimizer, Gravitational Search Algorithm, Sine Cosine Algorithm, Particle Swarm Optimization, and Moth-Flame Optimization. The parameter values for the above algorithms have been set in accordance with their original papers. Table 12 shows the parameter values for each algorithm. In all experiments, the population size and maximum number of iterations were set to 30 and 500, respectively.

Table 12.
Parameter values for all algorithms.
The mean results (Mean) and standard deviations (Std) obtained by the different algorithms when solving problems F1–F23 are presented in Table 13, Table 14 and Table 15. The evaluation of the convergence behavior of the algorithms in solving the set of problems is also shown in Figure 8. Moreover, Table 13, Table 14 and Table 15 show conclusively that the CAO10 algorithm outperforms all other algorithms in all cases (F1–F23).

Table 13.
Comparison results on unimodal benchmark functions (F1 to F7).

Table 14.
Comparison results on multimodal benchmark functions (F8 to F13).

Table 15.
Comparison results on multimodal with fixed dimension benchmark functions (F14 to F23).
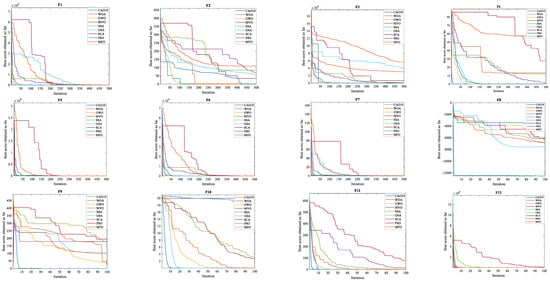
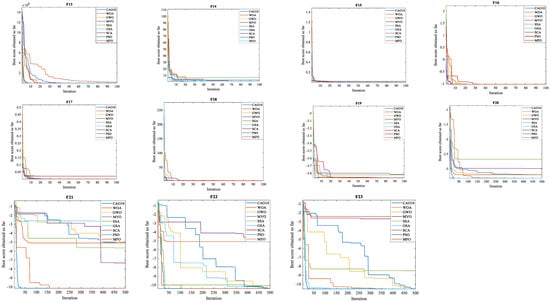
Figure 8.
Convergence curves for CAO10 and other original algorithms.
The convergence curves shown in Figure 8 highlight the exceptional convergence speed of CAO10 compared with other algorithms in all situations. Indeed, CAO10 shows remarkable convergence from the very first stages of the search, whereas other algorithms struggle to improve the quality of solutions, even after a greater number of exploratory stages.
These results highlight the strengths of the CAO10 algorithm, which manages to significantly speed up the early stages of the search due to its chaotic initialization strategy. In addition, CAO10 significantly improves its chances of avoiding local optima, thus favoring the discovery of optimal solutions.
In short, these findings attest to the undeniable effectiveness of the CAO10 algorithm, demonstrating its ability to solve a wide range of problems quickly and accurately. This combination of rapid convergence and high performance makes it a preferred choice for optimization in complex contexts.
6.2. Comparative Study on Two Real-World Applications
In this subsection, we use the CAO10 algorithm to solve three crucial engineering mathematical modeling problems, namely: (a) the design of welded beams; (b) the design of tension/compression springs; and (c) the design of pressure vessels. The results obtained are compared with those of numerous algorithms, including WOA, GWO, SSA, MVO, GSA, SCA, PSO, and MFO.
- (a)
- The welded beam design problem (WBDP)
The objective of this test is to optimize the values of the supplied variables (l, h, t, and b) to minimize the manufacturing cost for the WBD problem (Figure 9). To meet this challenge, we used the CAO10 algorithm proposed for solving the WBD problem, which we compared with various other optimization algorithms to determine its degree of superiority.
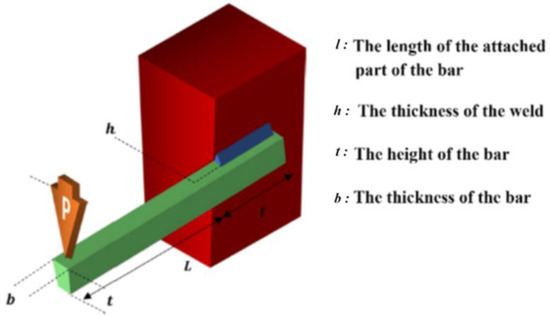
Figure 9.
WBD problem [36].
The results of this comparison are shown in Table 16. They remarkably reveal that the performance of the CAO10 algorithm exceeds that of all the other algorithms considered, a significant finding. As a result, it can be concluded that the CAO10 algorithm succeeds in identifying the best solution for the WBD problem in pursuit of the best possible solution.

Table 16.
Comparison results for WBDP.
- (b)
- The problem of tension/compression springs (TCSP)
In the TCSP problem, our aim is to minimize the minimum weight of this spring by optimizing three essential design variables (d, D, and the number of active coils, N), as illustrated in Figure 10. To solve this complex problem, we used the CAO10 algorithm, which was specifically designed for this task. We then compared the performance of the CAO10 algorithm with that of various competing optimization techniques.
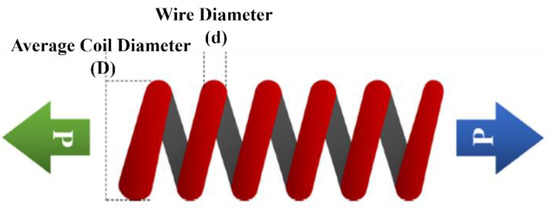
Figure 10.
TCS problem [36].
The results of this comparison, summarized in Table 17, convincingly demonstrating the performance of the CAO10 algorithm. The CAO10 algorithm generates a greater number of optimal solutions than the other approaches examined.

Table 17.
Comparison results for TCSP.
- (c)
- Pressure vessel design problem (PVDP)
In the context of the PVDP, the main objective is to determine the total cost of the cylindrical pressure vessel, as shown in Figure 11. To satisfy the four constraints (Th, Ts, R, and L), optimization operations must take into account four design factors. Using the CAO10 algorithm to solve this problem, the simulation results obtained are compared with those obtained by several different optimization algorithms, as shown in Table 18. On the basis of these data, we can conclude that the suggested CAO10 algorithm has a better cost value than all other comparative algorithms, with the exception of the shortest path method.
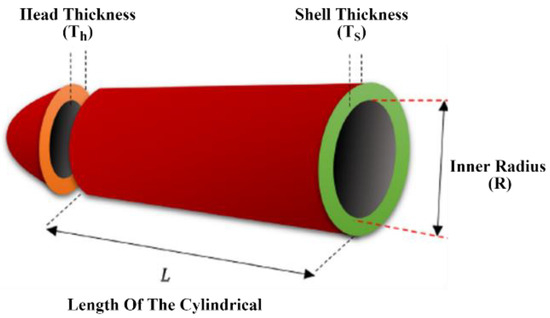
Figure 11.
PVD problem [36].

Table 18.
Comparison results for PVD.
These results underline the exceptional effectiveness of the CAO10 algorithm in solving complex problems such as WBDP, TCSP, and PVDP, demonstrating its ability to achieve optimal solutions and outperform other optimization approaches. This breakthrough offers promising prospects for the application of the CAO10 algorithm in industrial optimization and engineering contexts, where the search for optimal solutions is of crucial importance.
6.3. Reconstruction of 2D and 3D Signals and Images Using Meixner Moments and the Chaos-Archimède Algorithm (CAO)
Discrete orthogonal moments [44] play a prominent role in signal and image analysis, and their usefulness extends to a multitude of varied applications. They have been successful in areas such as classification, reconstruction, watermarking, encryption, and compression [45,46,47,48,49]. They are a versatile tool for representing and processing complex data. In the context of signal and image reconstruction, the use of discrete orthogonal Meixner moments (MMs) is complemented by the calculation of polynomial Meixner values (MPs). These polynomials depend on local parameters, noted as (β, u). To achieve optimum reconstruction quality, it is imperative to adjust these parameters appropriately. This is where the Optimized Chaos-Archimede (CAO) algorithm comes in, proposing an innovative solution. The CAO10 algorithm is used to determine optimal values for (β, u), thus guaranteeing superior quality in image reconstruction. Figure 12 summarizes the key steps in implementing the CAO algorithm for signal and image reconstruction.
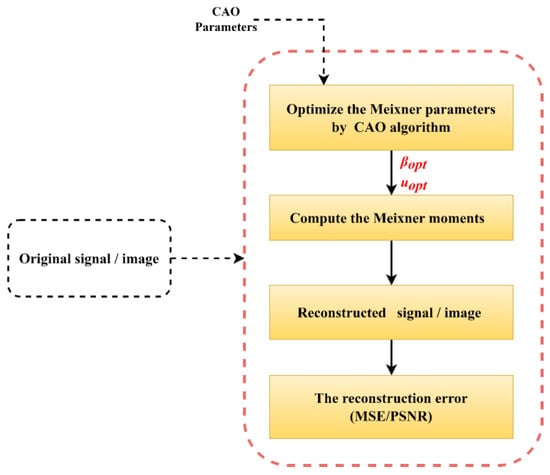
Figure 12.
Reconstruction method using MMs and CAO.
In this subsection, we validate the CAO10 algorithm’s ability to reconstruct large medical signals and images using MMs. This validation process comprises three distinct tests. The first test aims to evaluate the performance of the proposed method for bio signals. The second test looks at the reconstruction of medical color images. Its aim is to demonstrate the ability of the CAO10 algorithm, in combination with MMs, to render color images accurately. Finally, the third test tackles an even more complex challenge, namely, the reconstruction of 3D images. We use the reconstruction method based on the CAO10 algorithm to achieve optimum results in the context of these three-dimensional images.
To assess the similarity between the original signal or image and those reconstructed, we use the criteria of mean square error (MSE) and peak signal-to-noise ratio (PSNR) in decibels (dB). These metrics enable us to objectively measure the quality of the reconstruction by quantifying the difference between the original signal or image and its reconstructed version, thus providing an accurate assessment of the CAO10 algorithm’s performance in each test scenario.
- (a)
- Optimal bio signal reconstruction using MMs and the CAO algorithm
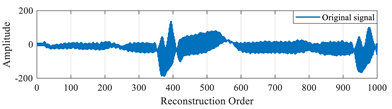
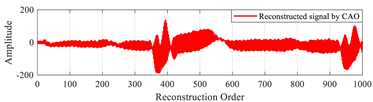
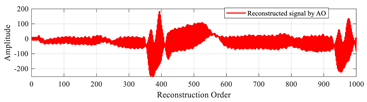
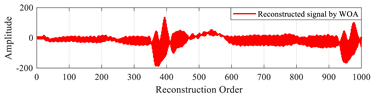
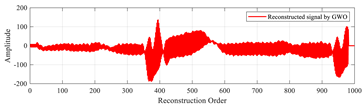
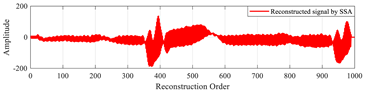
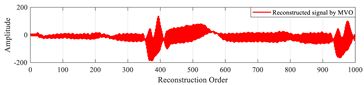
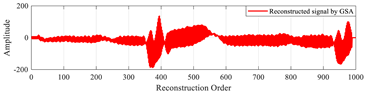
In this test, we verify the efficiency of the CAO10 algorithm for reconstructing large signals. To do this, we choose to reconstruct a specific ECG signal, named “MIT-BIH record 124”, of size 1000 taken from the MIT-BIH database [50]. The CAO10 algorithm was employed to optimize the local parameters (β, u) of the MPs used in the reconstruction of this signal. The results obtained with the CAO10 algorithm were compared with those generated by various other optimization algorithms, such as WOA, GWO, SSA, MVO, GSA, SCA, PSO, and MFO.
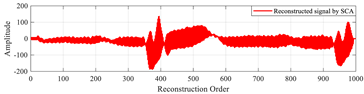
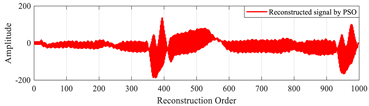
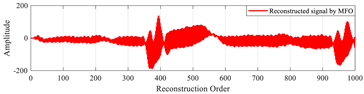
Table 19 illustrates the original signal, as well as a set of signals reconstructed using the different optimization methods. This figure also highlights the reconstruction errors, measured in terms of MSE and PSNR, as well as the optimal values of the local parameters (β, u) of the MPs. In addition, Figure 13 shows the PSNR values of signals reconstructed using various algorithms.

Table 19.
“MIT-BIH record 111” signals reconstructed by MMs using the proposed method based on the CAO algorithm method, compared with other algorithms.
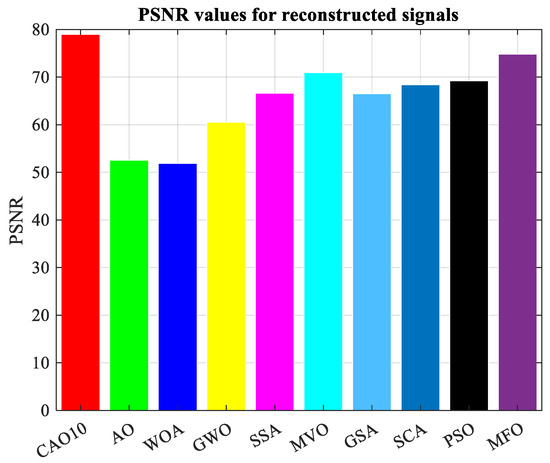
Figure 13.
PSNR values for reconstructed signals.
The results of this test demonstrate that the method based on the CAO10 algorithm enables optimal determination of the parameters (β, u), leading to excellent signal reconstruction quality, characterized by low MSE and high PSNR compared with other optimization algorithms. These findings clearly underline the superiority and robustness of the CAO10 algorithm in the context of biological signal reconstruction, opening up new prospects for improving complex signal analysis in medicine and elsewhere.
- (b)
- Optimal reconstruction of 2D medical images using CAO-optimized MMs
In this test, we evaluate the ability of the MM-based reconstruction method and CAO10 algorithm to reconstruct color medical images. We used 2D images of size 1024 from the database to carry out these experiments.
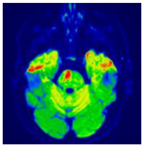
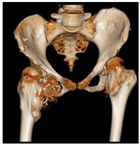
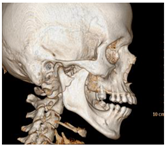
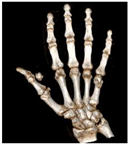
The CAO10 algorithm was used to optimize MMs parameters and perform medical image reconstruction. The results obtained by the CAO10 algorithm were compared with those generated by several other commonly used optimization algorithms, including WOA, GWO, SSA, MVO, GSA, SCA, PSO, and MFO. The reconstructed images, including those with the names “Brain”, “multiple-osteochondromas”, “mandible-fracture”, and “soft-tissue-chondroma-thumb”, were evaluated in terms of reconstruction quality. Table 20 shows the results of this evaluation, including reconstructed images, optimized MMs parameter values, and reconstruction errors, while Figure 14 shows the MSE and PSNR curves of the “brain” image reconstructed using various algorithms.

Table 20.
Simulation results for medical image reconstruction of size 1024.
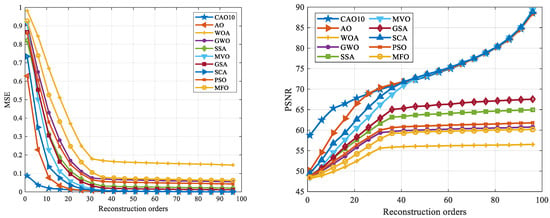
Figure 14.
MSE and PSNR plot of reconstructed ‘Brain’ image.
The results obtained attest to the ability of the CAO10 algorithm to determine optimal values of the parameters (β, u) enabling the reconstruction of all images with a considerably low MSE (high PSNR), thus outperforming the other algorithms evaluated. These findings eloquently demonstrate the superiority of the CAO10 algorithm in the field of medical image reconstruction.
- (c)
- Optimal reconstruction of 3D images by MMs and the CAO algorithm
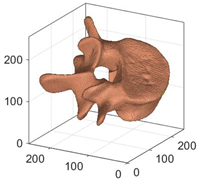
In this subsection, we evaluate the effectiveness of the proposed 3D reconstruction method based on MMs and the CAO10 algorithm. We used the “Verterba” 3D image of voxel size 256 downloaded from the [49] database. Table 21 shows the results of the reconstruction of this image using the CAO10 algorithm compared with other optimization algorithms. The values of the optimized parameters (β, u) and the error measures MSE and PSNR are also displayed.

Table 21.
The comparison results of the 3D image of the “corona” with size .
The results of this test show that the MMs values optimized by the CAO10 algorithm lead to better reconstruction quality, characterized by very low MSE and high PSNR, compared with other methods. These results demonstrate the effectiveness of our approach to polynomial parameter selection and 3D image reconstruction.
7. Conclusions
In conclusion, this study presents a significant advance in the field of optimization thanks to the introduction of the improved Archimedes optimization algorithm, Chaotic_AO (CAO). This algorithm is based on the use of ten distinct chaotic maps to replace pseudorandom sequences in the essential components of AO, namely, initialization, density and volume updating, and position updating. This enhancement has succeeded in striking a more appropriate balance between mining and exploration, offering an increased probability of discovering global solutions.
Evaluation of CAO’s performance across three distinct groups of problems highlighted its efficiency and reliability. The results of these tests clearly revealed that the CAO algorithm is not only efficient but also reliable. It demonstrated remarkable convergence speeds and exceptional solution quality in most of the cases studied. These observations confirm the real potential of the CAO algorithm for solving varied and complex problems. Overall, CAO offers exciting new prospects for improving optimization techniques, paving the way for wide-ranging applications in fields from engineering to medicine.
Following on from our current research, we plan to extend the application of the CAO algorithm to other areas of optimization, with particular emphasis on complex problems, such as multi-criteria optimization with conflicting objectives. This focus on more complex scenarios is intended to assess the robustness and versatility of the algorithm in the face of a variety of challenges.
Author Contributions
Conceptualization, Formal analysis, Writing original draft, Software: A.B. and M.A.T. Investigation, Visualization, Data curation: H.K. Validation, Methodology, Project administration, Supervision: M.S., H.Q., Y.E.A. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare that we have no competing interests in the submission of this manuscript.
References
- Ayyarao, T.S.L.V.; Ramakrishna, N.S.S.; Elavarasan, R.M.; Polumahanthi, N.; Rambabu, M.; Saini, G.; Khan, B.; Alatas, B. War Strategy Optimization Algorithm: A New Effective Metaheuristic Algorithm for Global Optimization. IEEE Access 2022, 10, 25073–25105. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Khodadadi, N.; Mirjalili, S. Mountain Gazelle Optimizer: A new Nature-inspired Metaheuristic Algorithm for Global Optimization Problems. Adv. Eng. Softw. 2022, 174, 103282. [Google Scholar] [CrossRef]
- Hajizadeh, Y.; Christie, M.; Demyanov, V. Ant colony optimization for history matching and uncertainty quantification of reservoir models. J. Pet. Sci. Eng. 2011, 77, 78–92. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Kumar, B.S.; Sowmya, R.; Alhelou, H.H.; Abualigah, L.; Yildiz, A.R.; Mirjalili, S. A New Arithmetic Optimization Algorithm for Solving Real-World Multiobjective CEC-2021 Constrained Optimization Problems: Diversity Analysis and Validations. IEEE Access 2021, 9, 84263–84295. [Google Scholar] [CrossRef]
- Azizi, M.; Talatahari, S.; Gandomi, A.H. Fire Hawk Optimizer: A novel metaheuristic algorithm. Artif. Intell. Rev. 2023, 56, 287–363. [Google Scholar] [CrossRef]
- Bencherqui, A.; Karmouni, H.; Daoui, A.; Alfidi, M.; Qjidaa, H.; Sayyouri, M. Optimization of Jacobi Moments Parameters using Artificial Bee Colony Algorithm for 3D Image Analysis. In Proceedings of the 2020 Fourth International Conference on Intelligent Computing in Data Sciences (ICDS), Fez, Morocco, 21–23 October 2020; pp. 1–7. [Google Scholar]
- Mareli, M.; Twala, B. An adaptive Cuckoo search algorithm for optimisation. Appl. Comput. Inform. 2018, 14, 107–115. [Google Scholar] [CrossRef]
- Alia, O.M.; Mandava, R. The variants of the harmony search algorithm: An overview. Artif. Intell. Rev. 2011, 36, 49–68. [Google Scholar] [CrossRef]
- Alsalibi, B.; Abualigah, L.; Khader, A.T. A novel bat algorithm with dynamic membrane structure for optimization problems. Appl. Intell. 2021, 51, 1992–2017. [Google Scholar] [CrossRef]
- Majak, J.; Pohlak, M.; Eerme, M.; Velsker, T. Design of car frontal protection system using neural network and genetic algorithm. Mechanika 2012, 18, 453–460. [Google Scholar] [CrossRef]
- Kers, J.; Majak, J.; Goljandin, D.; Gregor, A.; Malmstein, M.; Vilsaar, K. Extremes of apparent and tap densities of recovered GFRP filler materials. Compos. Struct. 2010, 92, 2097–2101. [Google Scholar] [CrossRef]
- Kers, J.; Majak, J. Modelling a new composite from a recycled GFRP. Mech. Compos. Mater. 2008, 44, 623–632. [Google Scholar] [CrossRef]
- Abdelhamid, A.A.; Towfek, S.K.; Khodadadi, N.; Alhussan, A.A.; Khafaga, D.S.; Eid, M.M.; Ibrahim, A. Waterwheel Plant Algorithm: A Novel Metaheuristic Optimization Method. Processes 2023, 11, 1502. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E. Initialisation Approaches for Population-Based Metaheuristic Algorithms: A Comprehensive Review. Appl. Sci. 2022, 12, 896. [Google Scholar] [CrossRef]
- Louzazni, M.; Khouya, A.; Amechnoue, K.; Gandelli, A.; Mussetta, M.; Crăciunescu, A. Metaheuristic Algorithm for Photovoltaic Parameters: Comparative Study and Prediction with a Firefly Algorithm. Appl. Sci. 2018, 8, 339. [Google Scholar] [CrossRef]
- Rahman, A.; Sokkalingam, R.; Othman, M.; Biswas, K.; Abdullah, L.; Kadir, E.A. Nature-Inspired Metaheuristic Techniques for Combinatorial Optimization Problems: Overview and Recent Advances. Mathematics 2021, 9, 2633. [Google Scholar] [CrossRef]
- Kisi, O. Machine Learning with Metaheuristic Algorithms for Sustainable Water Resources Management. Sustainability 2021, 13, 8596. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Almutari, M.S.; Ezugwu, A.E. K-Means-Based Nature-Inspired Metaheuristic Algorithms for Automatic Data Clustering Problems: Recent Advances and Future Directions. Appl. Sci. 2021, 11, 11246. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2020, 51, 1531–1551. [Google Scholar] [CrossRef]
- Qayyum, A.; Ahmad, J.; Boulila, W.; Rubaiee, S.; Arshad; Masood, F.; Khan, F.; Buchanan, W.J. Chaos-Based Confusion and Diffusion of Image Pixels Using Dynamic Substitution. IEEE Access 2020, 8, 140876–140895. [Google Scholar] [CrossRef]
- Hu, T. Discrete Chaos in Fractional Henon Map. Appl. Math. 2014, 5, 2243–2248. [Google Scholar] [CrossRef]
- Setoudeh, F.; Dezhdar, M.M.; Najafi, M. Nonlinear analysis and chaos synchronization of a memristive-based chaotic system using adaptive control technique in noisy environments. Chaos Solitons Fractals 2022, 164, 112710. [Google Scholar] [CrossRef]
- Thounaojam, U.S. Stochastic chaos in chemical Lorenz system: Interplay of intrinsic noise and nonlinearity. Chaos Solitons Fractals 2022, 165, 112763. [Google Scholar] [CrossRef]
- Chuang, L.-Y.; Hsiao, C.-J.; Yang, C.-H. Chaotic particle swarm optimization for data clustering. Expert Syst. Appl. 2011, 38, 14555–14563. [Google Scholar] [CrossRef]
- Tahir, M.; Tubaishat, A.; Al-Obeidat, F.; Shah, B.; Halim, Z.; Waqas, M. A novel binary chaotic genetic algorithm for feature selection and its utility in affective computing and healthcare. Neural Comput. Appl. 2020, 34, 11453–11474. [Google Scholar] [CrossRef]
- Yang, L.; Li, K.; Zhang, W.; Ke, Z.; Xiao, K.; Du, Z. An improved chaotic ACO clustering algorithm. In Proceedings of the 2018 IEEE 20th International Conference on High Performance Computing and Communications; IEEE 16th International Conference on Smart City; IEEE 4th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Exeter, UK, 28–30 June 2018; pp. 1642–1649. [Google Scholar]
- Masdari, M.; Barshande, S.; Ozdemir, S. CDABC: Chaotic discrete artificial bee colony algorithm for multi-level clustering in large-scale WSNs. J. Supercomput. 2019, 75, 7174–7208. [Google Scholar] [CrossRef]
- Kharrich, M.; Selim, A.; Kamel, S.; Kim, J. An effective design of hybrid renewable energy system using an improved Archimedes Optimization Algorithm: A case study of Farafra, Egypt. Energy Convers. Manag. 2023, 283, 116907. [Google Scholar] [CrossRef]
- Akdag, O. A Improved Archimedes Optimization Algorithm for multi/single-objective Optimal Power Flow. Electr. Power Syst. Res. 2022, 206, 107796. [Google Scholar] [CrossRef]
- Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Metaheuristic-Based Algorithms for Optimizing Fractional-Order Controllers—A Recent, Systematic, and Comprehensive Review. Fractal Fract. 2023, 7, 553. [Google Scholar] [CrossRef]
- Chu, H.; Yi, J.; Yang, F. Chaos Particle Swarm Optimization Enhancement Algorithm for UAV Safe Path Planning. Appl. Sci. 2022, 12, 8977. [Google Scholar] [CrossRef]
- Valencia-Ponce, M.A.; González-Zapata, A.M.; de la Fraga, L.G.; Sanchez-Lopez, C.; Tlelo-Cuautle, E. Integrated Circuit Design of Fractional-Order Chaotic Systems Optimized by Metaheuristics. Electronics 2023, 12, 413. [Google Scholar] [CrossRef]
- Adeyemi, V.-A.; Tlelo-Cuautle, E.; Perez-Pinal, F.-J.; Nuñez-Perez, J.-C. Optimizing the Maximum Lyapunov Exponent of Fractional Order Chaotic Spherical System by Evolutionary Algorithms. Fractal Fract. 2022, 6, 448. [Google Scholar] [CrossRef]
- Wang, S.; Rao, H.; Wen, C.; Jia, H.; Wu, D.; Liu, Q.; Abualigah, L. Improved Remora Optimization Algorithm with Mutualistic Strategy for Solving Constrained Engineering Optimization Problems. Processes 2022, 10, 2606. [Google Scholar] [CrossRef]
- Wang, W.; Tian, J.; Wu, D. An Improved Crystal Structure Algorithm for Engineering Optimization Problems. Electronics 2022, 11, 4109. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Li, Y.; Lin, X.; Liu, J. An Improved Gray Wolf Optimization Algorithm to Solve Engineering Problems. Sustainability 2021, 13, 3208. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Fu, Y.; Zhou, M.; Guo, X.; Qi, L.; Sedraoui, K. Multiverse Optimization Algorithm for Stochastic Biobjective Disassembly Sequence Planning Subject to Operation Failures. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1041–1051. [Google Scholar] [CrossRef]
- Duman, S.; Güvenç, U.; Sönmez, Y.; Yörükeren, N. Optimal power flow using gravitational search algorithm. Energy Convers. Manag. 2012, 59, 86–95. [Google Scholar] [CrossRef]
- Sindhu, R.; Ngadiran, R.; Yacob, Y.M.; Zahri, N.A.H.; Hariharan, M. Sine–cosine algorithm for feature selection with elitism strategy and new updating mechanism. Neural Comput. Appl. 2017, 28, 2947–2958. [Google Scholar] [CrossRef]
- Cui, Y.; Meng, X.; Qiao, J. A multi-objective particle swarm optimization algorithm based on two-archive mechanism. Appl. Soft Comput. 2022, 119, 108532. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, X.; Liu, J. An Improved Moth-Flame Optimization Algorithm for Engineering Problems. Symmetry 2020, 12, 1234. [Google Scholar] [CrossRef]
- Bencherqui, A.; Daoui, A.; Karmouni, H.; Qjidaa, H.; Alfidi, M.; Sayyouri, M. Optimal reconstruction and compression of signals and images by Hahn moments and artificial bee Colony (ABC) algorithm. Multimed. Tools Appl. 2022, 81, 29753–29783. [Google Scholar] [CrossRef]
- Tahiri, M.A.; Bencherqui, A.; Karmouni, H.; Jamil, M.O.; Sayyouri, M.; Qjidaa, H. Optimal 3D object reconstruction and classification by separable moments via the Firefly algorithm. In Proceedings of the 2022 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 18–20 May 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Tahiri, M.A.; Karmouni, H.; Azzayani, A.; Sayyouri, M.; Qjidaa, H. Fast 3D Image Reconstruction by Separable Moments based on Hahn and Krawtchouk Polynomials. In Proceedings of the 2020 Fourth International Conference on Intelligent Computing in Data Sciences (ICDS), Fez, Morocco, 21–23 October 2020. [Google Scholar]
- Tahiri, M.A.; Karmouni, H.; Bencherqui, A.; Daoui, A.; Sayyouri, M.; Qjidaa, H.; Hosny, K.M. New color image encryption using hybrid optimization algorithm and Krawtchouk fractional transformations. Vis. Comput. 2022, 39, 6395–6420. [Google Scholar] [CrossRef]
- Rabab, O.; Tahiri, M.A.; Bencherqui, A.; Amakdouf, H.; Jamil, M.O.; Qjidaa, H. Efficient Localization and Reconstruction Of 3D Objects Using The New Hybrid Squire Moment. In Proceedings of the 2022 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 18–20 May 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Tahiri, M.A.; Karmouni, H.; Sayyouri, M.; Qjidaa, H. 2D and 3D image localization, compression and reconstruction using new hybrid moments. Multidimens. Syst. Signal Process. 2022, 33, 769–806. [Google Scholar] [CrossRef]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).