Abstract
The waterflooding effect evaluation of carbonate fractured–vuggy reservoirs constitutes a comprehensive multiple-information decision-making process involving quantitative unascertained measure theory. This paper establishes a novel comprehensive methodology to evaluate the waterflooding effects of carbonate fractured–vuggy reservoirs for the first time. A new evaluation grading criteria is proposed using the Mahalanobis distance method based on the multi-index comprehensive unascertained measure theory derived from a modified five-scale analytical hierarchy process–entropy weight method. The actual field data from the carbonate fractured–vuggy reservoirs and the nine evaluation indices are specifically applied to demonstrate the calculation process for the construction of the grading system model on the waterflooding effects and to verify the accuracy of the Mahalanobis distance method by comparing the calculation results with the Minkowski and Euclidean distance methods. The proposed methodology facilitates the effective evaluation of the waterflooding strategies implemented in carbonate fractured–vuggy reservoirs with three categories; the ones with outstanding performance usually demonstrated favorable index characteristics, with substantial contributions to the enhanced oil recovery, manifesting with complete well patterns, a balance in the injection–production dynamics, excellent waterflooding utilization, and control competence. In contrast, fractured–vuggy units with fair waterflooding performance revealed limitations in the enhanced oil recovery. It can also be inferred that the mediocre waterflooding performance of the fractured–vuggy units is associated with incomplete well patterns, an imbalance in the injection–production dynamics, low waterflooding utilization, and a negligible waterflooding effect. The results in this study show that this newly proposed integrated model can effectively assess the waterflooding effects quantitatively and provide a more precise scientific basis for evaluating the waterflooding effects in carbonate fractured–vuggy reservoirs, with potential applicability in other fields.
1. Introduction
Carbonate reservoirs, categorized as porous, fractured–porous, and fractured–vuggy types [1,2], have served a significant role in global oil and gas resources with their colossal reserves, globally accounting for around 70%, 52%, and 60% of the oil and gas resources, the proven oil and gas reserves, and the total oil and gas production [3]. With the stratigraphic concentration in the Ordovician, Carboniferous, Paleogene, and Neogene, carbonate reservoirs are extensively distributed worldwide. They are discovered in regions such as the porous carbonates of the Persian Gulf Basin in the Middle East, the Pre-Caspian Basin in Central Asia, the Sirte Basin in North Africa, the Gulf of Mexico and the Permian Basin in the United States, and additionally in the Sichuan Basin in China. Furthermore, there are the fractured–porous carbonates of pre-Tertiary faulted sediments and the fractured–vuggy carbonates of the Ordos and Tarim Basins in China [3,4]. Waterflooding is currently the most prevailing secondary oil recovery technique for carbonate reservoirs, especially with a notable boost in crude oil recovery rates during the development of carbonate fractured–vuggy reservoirs. Thus, more in-depth studies are still needed to elaborately and accurately assess the waterflooding efficiency of carbonate fractured–vuggy reservoirs. The T Oilfield, located in the Tarim Basin of China, exemplifies a typical carbonate fractured–vuggy reservoir. It has development primary layers ranging from the Ordovician Yijianfang to the Yingshan formations, with a proven reserve exceeding 1.5 billion tons [5]; a large-scale oilfield with an annual production of 7 million tons was developed after the exploration of the exposed denudation area in the east and the shallow buried area of the T Oilfield in the west, as well as the deeply buried area of the S oilfield [6]. The T Oilfield has been undergoing waterflooding development schemes since 2005, which is currently progressing to the middle–late developmental stages [7]. The establishment of evaluation methods for waterflooding on carbonate fractured–vuggy reservoirs is crucial for accurately assessing the impact of waterflooding, elucidating the exploitation of the utilization efficiency of waterflooding, and determining the necessity for pilot experiments for tertiary oil recovery in carbonate fractured–vuggy fields.
This paper aims to develop a comprehensive and robust model for the waterflooding development effect evaluation of carbonate fractured–vuggy reservoirs from publicly available data, with the potential to provide a more precise scientific comprehension for peer industries, and with the accuracy validated by the waterflooding effect evaluation data from 26 carbonate fractured–vuggy units. Based on the unascertained measure theory, this proposed model innovates by applying the five-scale AHP entropy–unascertained measure theory to determine the comprehensive weights of the evaluation indices and by introducing the Mahalanobis distance method to enhance the judgmental criteria for the evaluation results. This methodology is employed to seek out the potential applications in the comprehensive decision-making process, providing multiple informational aspects for numerous fields, and offering an exemplary case in the waterflooding effect evaluation of carbonate fractured–vuggy reservoirs.
2. Literature Review
The evaluation methods on the waterflooding development effect can be traced back to the 1950s, when Guthrie and Greenberger [8] employed multiple correlation analysis methods to obtain the waterflooding recovery by using Craze and Buckley’s recovery data [9]. Various evaluation methods, combined with diverse mathematical theories, have been employed over the following decades [10], which include the system analysis method (SAM) [11], the gray correlation method (GCM) [12], and the fuzzy comprehensive evaluation method (FCEM) [13,14]. Based on large-scale systems, an integral system was applied as the reservoir with the SAM to study the correlation between injection and production wells for the evaluation of the waterflooding effects and the oil recovery of the entire reservoir system. The GCM regards the influencing factors and evaluation results of the waterflooding development effect as a gray process containing known and unknown information, in which each evaluation standard and indicator in the gray information system can be determined by studying the relevant parameters, and then whitening the gray system by using these parameters, indicators, and the characteristic values. Furthermore, originating from fuzzy mathematics, the evaluations can be transferred qualitatively to quantitatively via the FCEM by using the theory of membership degrees. The FCEM first identifies the influencing factors and evaluation grades of the reservoir waterflooding development effect, then it determines the weight of the influencing factors and the membership degree vectors to obtain the evaluation matrix; the evaluation matrix and the weight vector of the influencing factors are fuzzy-calculated and normalized to obtain the comprehensive evaluation results of the reservoir waterflooding development effect in the final step [15]. In addition, based on the reservoir numerical model, and incorporated with the interwell tracer technology, Guo et al. [16] evaluated the balanced displacement effect during the reservoir waterflooding development process, according to the interwell areal sweep efficiency estimated by the tracer types and their monitoring amounts in the injection wells, and enabled the rapid assessment of the offshore reservoir waterflooding development effect. Makhotin et al. [17] assessed the practicability of machine-learning techniques in the evaluation of the reservoir waterflooding development effects. Scale precipitation can have a detrimental influence on the development effect during waterflooding, which can be inhibited via the response surface methodology [18]. Linear regression models, neural networks, and gradient boosting on decision trees were evaluated for their evaluation of the waterflooding development effects, with the results showing that the machine-learning models could reduce the computational complexity and evaluate the waterflooding effects effectively. Analogous to the signal processing techniques, capacity resistance networks have been applied to the subsurface flow for porous media since 1943 [19,20]. With the combination of nonlinear multivariate regression techniques and multiple material balance equations, an extensively acknowledged semianalytical modeling methodology called the capacitance resistance model (CRM) was first introduced by Yousef et al. [21,22] to offer the possibility of promptly calibrating the waterflooding performance, providing more accessible data regarding the injection and production rates and pressure [23,24], which was further developed by Sayarpour et al. [23] with three semianalytical models (the CRMP, CRMT, and CRMIP) to deal with the various control volumes for versatile conditions.
Evaluating the reservoir waterflooding development effect is a decision-making process involving diverse uncertainties, which makes the unascertained measure (UM) more suitable and applicable to a broad application in diverse fields. The unascertained measure is a qualitative and quantitative combined evaluation method based on fuzzy theory which can quantitively provide measurements for the degree of a specific property. Taking the safety engineering field as an instance, Yang et al. [25] proposed an improved UM–SPA coupling for a landslide-susceptibility evaluation model based on the unascertained measure theory and set pair analysis theory, and the comparable results indicated that this proposed improved UM–SPA model outperformed the traditional analytic hierarchy process (AHP) and entropy–AHP models. The UM theory has also been coupled with various methodologies for comprehensive evaluation methods in other scenarios, such as the ones developed by Zhang et al. [26] with variable weight theory for the evaluation of the risk of coal and gas outbursts in underground coal mines; by Ma et al. [27] for the evaluation of blast casting results combined with the intuitionistic fuzzy set to evaluate the blast casting results of the Heidaigou open-pit mine; by Sheng et al. [28] for the evaluation of the risk assessments of urban gas pipelines. Moreover, by applying the UM theory, Zhou et al. [29] established a 100% accurate and comprehensive optimal unascertained combination model, the P-CW-CIP, for the estimation of coal burst hazards with the parabolic function, synthetic weights, and the credible identification principle. Other valuable resources [30,31,32,33,34,35] are worth being referred to for a deeper understanding of the application in other industries based on the UM theory. One noticeable application in carbon capture utilization and storage (CCUS) for the oil and gas industry is from Zhan et al. [36], who proposed a novel CO2 geological sequestration suitability evaluation model with the aid of the UM theory, which was validated by evaluating tectonic units in the Songliao Basin, China, with about an 83% consistency compared with previous studies.
In summary, due to the distinctive geological structure of carbonate fractured–vuggy reservoirs, their development and theoretical research present specific challenges, and many individuals have undertaken various efforts in this regard [37,38,39,40,41,42,43]. Currently, the primary methods for evaluating waterflooding development effects in carbonate fractured–vuggy reservoirs include system analysis, gray correlation, and fuzzy comprehensive evaluation methods. However, the development approach of carbonate fractured–vuggy reservoirs is unique, which focuses on the fractured–vuggy units as the basic development unit and employs nonfixed injection wells with the point injection development method. Due to this uniqueness, the system analysis and gray correlation methods cannot accurately assess the correlation between the injection wells and the production wells. Although the fuzzy comprehensive evaluation method is capable of effectively addressing the above issue, using the maximum membership principle in fuzzy comprehensive evaluation can lead to inaccurate evaluation results when there are overlaps in the value ranges of multiple indices. Therefore, new methodologies are urgently needed to accurately evaluate the waterflooding development effects in carbonate fractured–vuggy reservoirs.
3. Model Development Procedures
The purpose of this section is to demonstrate the procedures for developing the integrated evaluation model based on the modified multi-index comprehensive unascertained measure theory and the Mahalanobis distance method. The idea of the unascertained measure theory was first proposed by Wang [44] in 1990, with four components, including the single-index unascertained measure matrix, the index weight, the multi-index comprehensive measure evaluation vector, and grade evaluation [45]. The standardized steps derived from the unascertained measure theory involve first employing the single-index unascertained function to build its UM matrix, followed by the multiplication of the weights of the evaluation indices with the single-index UM matrix to derive the multi-index comprehensive UM. On the contrary, the modified UM theory originated using the modified five-scale AHP–entropy weight method to obtain more accurate comprehensive weights before the multiplication prepared for the grade evaluation in the final step using the Mahalanobis distance method, as Figure 1 shows. The conventional unascertained measure theory employs confidence criteria for the grade evaluation, where selecting confidence values is a subjective process and can markedly impact the evaluation results. The advantage of the unascertained measure–Mahalanobis distance methodology proposed in this paper lies in quantitatively conducting a grade evaluation by calculating the Mahalanobis distance between the multi-index comprehensive unascertained measure and the unascertained measures of the evaluation results. This approach can substantially mitigate the subjectivity in the grade evaluation process.
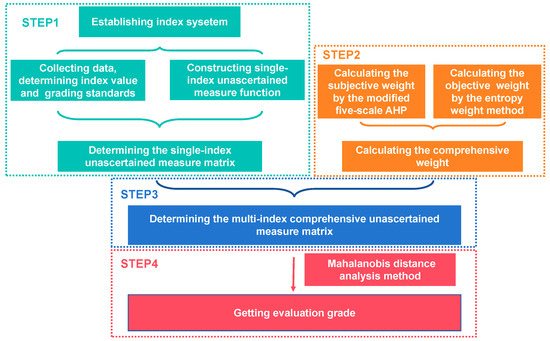
Figure 1.
Model development procedures.
3.1. Single-Index Unascertained Measure Definition
In order to effectively construct a UM model, the evaluation object set and evaluation index set should be assumed, where and denote the i-th () evaluation object and the j-th () evaluation index, and can be further expressed as an m-dimensional vector . Here, is defined as the measured value of with respect to . If contains evaluation grades, the evaluation grade set can be expressed as , with as the k-th () evaluation grade, and where indicates that is superior to . It should be noted that any random index in the evaluation grade set should be independent and without any intersections.
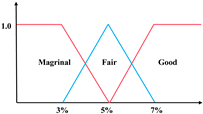
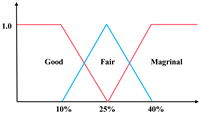
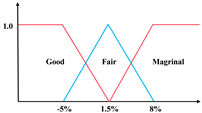
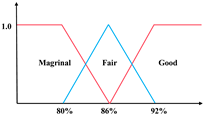
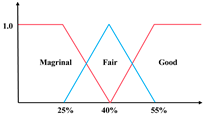
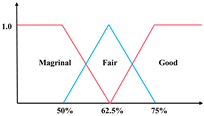
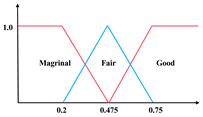
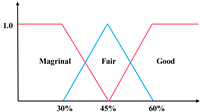
The single-index UM is denoted as to represent the j-th evaluation index of the evaluation object , with the measured value belonging to the evaluation grade , which needs to satisfy the non-negativity, normalization, and additivity conditions. The conditions can be generally expressed into: (1) , (2) , (3) , where . As Figure 2 shows, the single-index UM is typically determined by its UM functions, and the rules are: (1) when , and others equal 0; (2) when , and others equal 0; (3) when , , , and others equal to 0. According to the above rules, the single-index UM matrix is expressed as
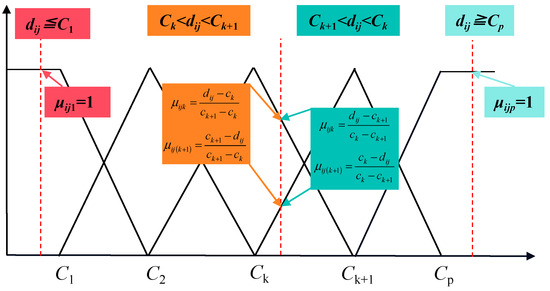
Figure 2.
Unascertained measurement function of the single index.
3.2. Comprehensive Index Weight Determination
The analytic hierarchy process (AHP) method was innovated by Saaty in the 1970s, which is the most favorable for calculating the weights of indices in the application of complicated multicriteria decision-making formatted under a hierarchical structure [46,47,48]. However, since the AHP is a subjective methodology that mimics the human brain to make more qualitative rather than quantitative decisions, potential subjective selection errors may be caused in the weight calculation process. The entropy weight method is then employed as an objectively comprehensive index weight evaluation approach to mitigate this subjective effect, which can be further used to estimate the multi-index comprehensive UM based on the single-index UM. Introduced by Clausius in the 1850s, entropy is a thermodynamic concept for the characterization of the degree of systematic disorder, which is also used to estimate the uncertainty in information technology for the amount of information provided by an individual in a set. A lower entropy value indicates that the index with a more significant weight can provide more information and cause more systematic influence when it changes, and vice versa. Therefore, the weight of each index can be estimated via the entropy by evaluating the individual variation degree.
In this paper, a modified five-scale AHP is employed to calculate the subjective weight () of the evaluation index [49,50,51]. Compared to the conventional AHP, which determines the weights of the evaluation indices through single-level hierarchical ranking and consistency checking, this modified AHP method has several advantages. It first reduces system errors through the analytical realization of subjective fuzzy factors. Additionally, it significantly decreases the iteration number and improves the convergence speed without the need for consistency checking. This is achieved through the optimal transfer matrix, which possesses consistency satisfaction generated from the comparison matrix. The first step to model the five-scale AHP is to establish the hierarchical structure model of the evaluation indices and to determine the comparison matrix () of the evaluation indices based on the five-scale value-assignment principles, as shown in Table 1. According to Equations (2)–(5), the eigenvectors of the optimal transfer matrix () can be obtained using the square root method; following this, the subjective weight () for the waterflooding development effect evaluation can be calculated. The subjective weights of the evaluation criteria are further adjusted using the entropy weight method, and the judgment matrix () is normalized using the extreme value method to obtain the entropy weight standardized matrix (). The objective weights () of the evaluation indices can further be calculated by Equation (8) to finally estimate the comprehensive weight () of the evaluation indices with Equation (9). The calculation workflow of the comprehensive weight () is shown in Figure 3.
where is the element (the i-th row and j-th column) in the comparison matrix, is the summation of the values in the i-th row, is the summation of the values in the j-th row, is the maximum value within the values of and , is the minimum value within the values of and , is the element (the i-th row and j-th column) in the judgment matrix, is the element (the i-th row and j-th column) in the antisymmetric matrix (similar notations for and ), is the element (the i-th row and j-th column) in the optimal transfer matrix, is the calculated entropy value of each evaluation index based on the judgment matrix, and is the element in the entropy weight standardized matrix .

Table 1.
The value-assignment principles of the comparison matrix for the five-scale AHP [51].
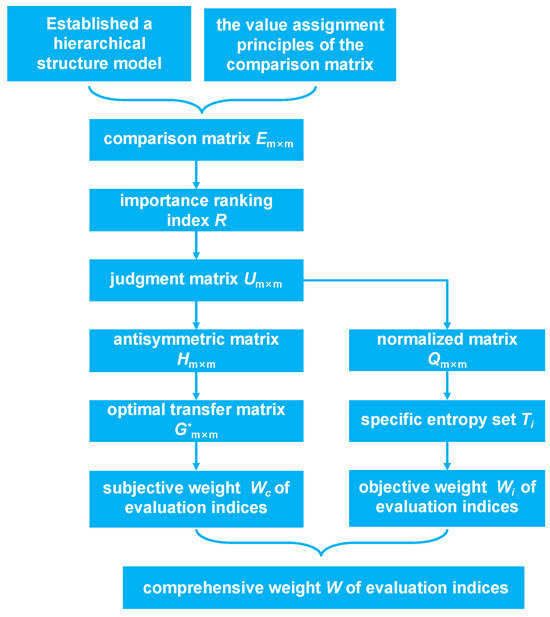
Figure 3.
The calculation workflow of the comprehensive weight.
3.3. Multi-index Comprehensive Unascertained Measure Calculation
With reference to the single-index UM and the comprehensive weight introduced in the previous sections, the multi-index comprehensive UM can then be evaluated. Here, , expressed in Equation (10), denotes the degree to which the i-th evaluation objective belongs to the k-th evaluation grade ; , expressed in Equation (11), is the i-th row vector denoting the comprehensive UM vector . As the equations below show, stands for an element in the single-index UM matrix and is used for the expression of an element in the multi-index comprehensive UM matrix.
3.4. Grade Evaluation with the Mahalanobis Distance Method
The credible degree recognition criterion is applied to determine the evaluation grade in the current UM theory, which considers the evaluation grade space as an assorted set. When the accumulative measure value of any row vector in the multi-index comprehensive UM exceeds the credible degree, the corresponding should be the evaluation result. The choice of credible degree values is an intensely subjective process and can be significantly impacted by different individuals, and its value range is between 0.5 and 1.0, with a typical value of 0.6 or 0.7 [31]. The terminology of Mahalanobis distance discrimination [52] is applied for the grade evaluation to eliminate the subjectivity of the value choice for the credible degree, and it is intuitively based on the distance between the sample and the calculated centroid of various classified data in a distribution to assign the sample to the class with the closest distance. The evaluation results and the measured value can be categorized into grades (), and the sample means of each class are similarly defined as the classification centroids of the grades, where the UM for the evaluation grades can be denoted as . The Mahalanobis distance () between the multi-index comprehensive UM matrix and the UM of the evaluation grades () can be calculated as follows:
4. Waterflooding Development Effect Evaluation of the Fractured–Vuggy Carbonate Reservoir
The T Oilfield, dominating from the Ordovician Yijianfang to Yingshan formations, constitutes a substantial nonconformity and ancient karst-induced trap for oil and gas, characterized by the extensive areal coverage of the reservoir and a strong heterogeneity in the oil and gas distribution. The predominant storage spaces include vugs, karst vugs, and fractures in the matrix without storage and permeability capacities. Classified by different distribution patterns and storage scales, the reservoirs of the T Oilfield fall into three types: fractured, fractured–porous, and fractured–vuggy. The fractured-type reservoir has a maximum porosity of 2% and a permeability limit of 0.01 × 10−3 μm2. In the fractured–porous-type reservoir, the average porosity values are 3.69% for the fractures, 2.67% for the pores, and 2.17% for the matrix. The fractured–vuggy-type reservoir, mainly composed of limestone, exhibits an extremely low matrix porosity and permeability, with vugs and pores contributing 68% to the storage capacity, which stands as the predominant reservoir in the T Oilfield, as depicted in Figure 4. Currently, the majority of the T Oilfield reservoirs continue to implement waterflooding strategies, with specific blocks applied with field experiments involving nitrogen injection to enhance the oil recovery [53,54,55].
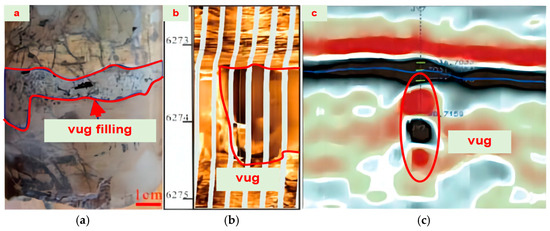
Figure 4.
The core image (a), FMI logging (b), and seismic reflection (c) of the fractured–vuggy carbonate reservoir spaces [56].
Following the steps for the construction of the innovative evaluation model in the previous section, a waterflooding development effect evaluation system for carbonate fractured–vuggy reservoirs is established, with the calculation details as a case study to show the implementation of the proposed methodology. The evaluation indices selected for the construction of the index system are based on industry standards and conventions. The model development procedures of the waterflooding development effect evaluation in carbonate fractured–vuggy reservoirs are shown in Figure 5.
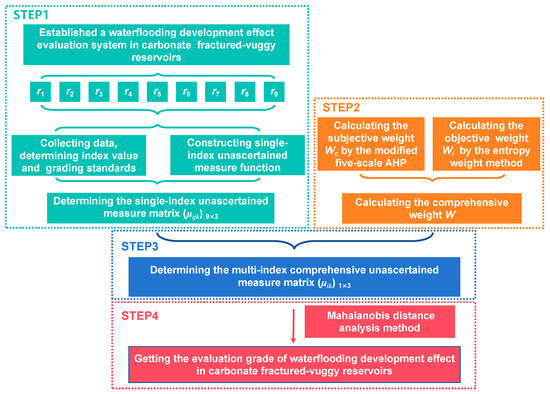
Figure 5.
Model development procedures of waterflooding development effect evaluation in carbonate fractured–vuggy reservoirs.
4.1. Establishment of the Waterflooding Development Effect Evaluation System
In 1996, the earliest industry standard for classifying the oilfield development degree was issued in China, which proposed a 10-index, 3-level classification criterion for carbonate fractured–vuggy reservoirs [57]. In 2009, an eight-indicator, three-level classification criterion specifically for clastic reservoirs waterflooding development was introduced by the CNPC based on the previous industry standard. Unlike the fractured–porous carbonate and clastic reservoirs, fractured–vuggy reservoirs are unique in their matrix, with a particular permeability and storage capacity, where the fractured–vuggy units are typically treated as the primary development units and the “point-like waterflooding and irregular well pattern” as the waterflooding development scheme. Thus, a waterflooding development effect evaluation system and grading criteria specified for fractured–vuggy reservoirs proposed by Lei are adopted in this paper [58]. Four evaluation aspects, namely, the degrees of the well-pattern completeness, the injection–production balance, the injected-water utilization, and the waterflooding effect characteristics, are covered in this paper. Several indices are prioritized accordingly for the various waterflooding evaluation aspects of the carbonate fractured–vuggy reservoirs. These aspects encompass the utilization of waterflooding reserve control and the degrees of utilization to assess the effectiveness of waterflooding for enhancing the control within fractured–vuggy units. Additionally, the evaluation involves considerations of the energy-retention degree and the injection–withdrawal ratio to determine if the internal pressure is adequately maintained. The water storage rate is analyzed to gauge the effective utilization of the injection water. Furthermore, scrutiny is applied to ascertain whether the oil-stabilization and water-controlling objectives are achieved. This involves examining the parameters, such as the rate of decline in production, the water-cut increasing rate, the enhanced oil recovery, and the square water–oil exchange rate. The physical meanings and calculation methods of each index are summarized in Table 2, with their scaling criteria shown in Table 3.

Table 2.
Waterflooding development effect evaluation system of fractured–vuggy reservoirs.

Table 3.
Waterflooding development effect grading criteria for the evaluation indices of fractured–vuggy reservoirs.
4.2. Waterflooding Development Effect Evaluation Based on the Unascertained Measure
4.2.1. Single-Index Unascertained Measure Calculation
After the waterflooding schemes of the twenty fractured–vuggy units collected from the T Oilfield, the oilfield data were chosen to build the evaluation model of the waterflooding development effect. As Table 4 shows, the evaluation objective, evaluation index, and evaluation grade spaces of this specific case are expressed in , {enhanced oil recovery, production decline rate, water-cut increasing rate, energy-retention degree, waterflooding reserve utilization degree, waterflooding reserves control degree, injection–withdrawal ratio, water storage rate, square water–oil exchange rate}, , and {excellent, fair, moderate},. According to the rules shown in Figure 1, the unascertained measure functions have been derived and are summarized in Table 5, and the single-index UM matrix based on the data from the 26 fractured–vuggy T units has also been established, as shown in Table 6.

Table 4.
Evaluation indices of the waterflooding development effect for fractured–vuggy units.

Table 5.
Unascertained measure functions of each evaluation index.

Table 6.
Unascertained measure matrices of each evaluation index.
4.2.2. Comprehensive Index Weight Calculation
In this section, the five-scale method is applied to calculate the subjective weight () of the evaluation indices. First, a hierarchical structure model for the waterflooding development effect evaluation needs to be established, where the model target layer is the evaluation model for the waterflooding development effects of the carbonate fractured–vuggy reservoirs with the project layer as the relevant indices, as shown in Figure 6. Based on the prebuilt hierarchical structure model and the value-assignment principles of the comparison matrix for the five-scale AHP, the comparison matrix can be derived, as shown in Table 7, combined with the actual field development situations. The accuracy of the comparison matrix has been validated by the consistency check via the conventional AHP, and the calculated result (CR = 0.019 < 0.1) indicates that the chosen value of the comparison matrix is reasonable for the subsequent calculations. The parameters of the evaluation indices can be further calculated, such as the importance ranking index R () by Equation (2), the judgment matrix (Table 8) by Equation (3), the antisymmetric matrix (Table 9) by Equation (4), and the optimal transfer matrix (Table 10) by Equation (5). The square root method is applied for the eigenvector calculations to obtain the evaluation index subjective weight , which needs to be corrected by the entropy weight method. Using the extreme value method, the judgment matrix can be standardized to acquire the normalized matrix with the entropy weight satisfaction, as shown in Table 11. The specific entropy set = {0.9878, 0.9054, 0.9149, 0.9405, 0.9254, 0.9108, 0.9198, 0.9684, 0.9639}, calculated via Equations (6) and (7), needs further normalization for the entropy weight method. The comprehensive and objective evaluation weight of the waterflooding development effect is finally determined by Equation (8).
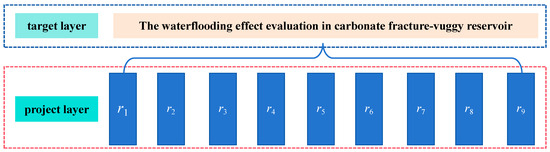
Figure 6.
The analytic hierarchy process model with the evaluation indices of the waterflooding development effect evaluation.

Table 7.
The comparison matrix for the evaluation indices.

Table 8.
The judgment matrix for the evaluation indices.

Table 9.
The antisymmetric matrix for the evaluation indices.

Table 10.
The optimal transfer matrix for the evaluation indices.

Table 11.
The normalized matrix by the entropy weight method for the evaluation indices.
The weight calculation results of different types for the nine evaluation indices are presented separately in Table 12 and Figure 7, which indicate that the subjective weight () is of high dispersion between 0.0349 and 0.2328, while the objective weight () shows lower dispersion, with a range from 0.0349 to 0.2328. It can also be concluded that the evaluation indices with a higher comprehensive weight have a more significant impact on the waterflooding effect evaluation, which are the enhanced oil recovery (0.2427), the square water–oil exchange rate (0.1996), the energy-retention degree (0.1503), and the waterflooding reserve utilization degree (0.1203). In contrast, the remaining evaluation indices with comprehensive weight values less than 0.1 have relatively less impact. These results suggest that a larger size of newly increased recoverable reserves with waterflooding schemes will result in a smaller volume requirement for a water injection per ton of oil produced, a better maintenance of the reservoir pressure, a larger recoverable reserve volume with waterflooding under current injection–production well-pattern conditions, and the better waterflooding development performance of the carbonate fractured–vuggy reservoirs, and vice versa.

Table 12.
The index weight calculation for the evaluation indices.
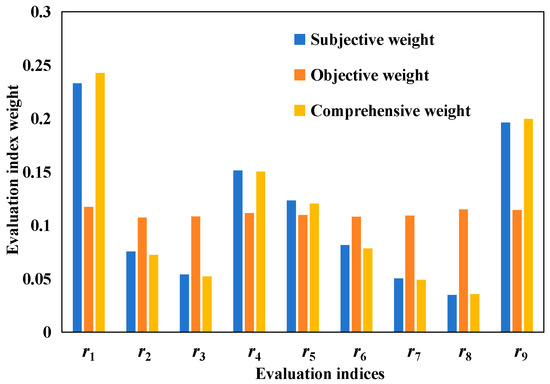
Figure 7.
The calculation comparisons between subjective, objective, and comprehensive index weight calculations of each evaluation index for waterflooding development effect.
4.2.3. Multi-Index Comprehensive Unascertained Measure Calculation
According to the single-index measure matrix and the comprehensive index weight of the waterflooding effect evaluation system for carbonate fractured–vuggy units, the multi-index comprehensive unascertained measure for this specific case can be calculated by Equation (10), as shown in Table 13.

Table 13.
Multi-index comprehensive UM matrix calculation results.
4.2.4. Model Calculation Results with Validations
Comprehensive evaluation scores for the waterflooding development effect evaluation of each carbonate fractured–vuggy unit in the work from Lei [58] can be obtained by numericizing the weighted average of the evaluation vectors, which is capable of ranking the waterflooding development effect evaluations of the fractured–vuggy units, but cannot explicitly determine their grade level. Therefore, based on the multi-index comprehensive UM matrix , the Mahalanobis distance analysis method is employed to determine the evaluation grade level of the waterflooding development effect of the fractured–vuggy units. According to the evaluation grade spaces {excellent, fair, moderate}, the evaluation grade results for the waterflooding development effect of the fractured–vuggy units can be categorized into three classes (i.e., f1, f2, and f3), and the relevant , denoted as the measured value of the evaluation objective for the evaluation index , is also classified into three categories. The sample averages of each category are determined as the classification center for three classification modes (f1, f2, and f3), with the unascertained measure of the evaluation results being f1 = {1, 0, 0}, f2 = {0, 1, 0} and f3 = {0, 0, 1}. The Mahalanobis distance analysis method is applied to calculate the distances between the multi-index comprehensive UM matrix and the UM of the evaluation results f1, f2, and f3, and the minimum among the three distance calculation sets is chosen as the grade level for the waterflooding development effect evaluation of the fractured–vuggy carbonates. Based on Equations (12) and (13), the calculation process of the Mahalanobis distance method is demonstrated using the example of the first fractured–vuggy unit. The Mahalanobis distances (d1, d2, and d3) are computed separately by combining the multi-index comprehensive UM matrix of the first fracture–vuggy unit with the unascertained measures (f1, f2, and f3) of the evaluation results. The minimum distance, , is selected for the grade evaluation. The calculated results are shown below, with the values of d1 = 0.383, d2 = 2.743, d3 = 2.816, and = 0.383. Therefore, the waterflooding development effect grade for the first fractured–vuggy unit is determined to be excellent.
The values for the 26 fractured–vuggy units were calculated using the aforementioned method, and Table 14 shows the summarized evaluation results of the waterflooding development effect for the 26 fractured–vuggy carbonate units, where the Minkowski distance [31] and Euclidean distance [59] methods are also used for validation comparisons, showing the high consistency compared with Mahalanobis distance for testing its calculation accuracy in this case study. The evaluation results show that 16 fractured–vuggy units have ideal performance in the waterflooding development, featured by the favorable evaluation indices results after waterflooding, with a high enhanced oil recovery, good reservoir pressure maintenance by the injected water inside the fractured–vuggy units, fair degrees of reserve utilization and control, a low production decline rate, and a high square water–oil exchange rate. The fractured–vuggy units in this category generally exhibit excellent performance characteristics for the completeness of the well patterns, the injection–withdrawal balance, the waterflooding utilization, and the waterflooding development effect. On the other hand, three fractured–vuggy units have fair performance, with seven fractured–vuggy units showing moderate waterflooding development effects.

Table 14.
The comparison calculations of various approaches.
5. Conclusions
The waterflooding development evaluation of carbonate fractured–vuggy reservoirs can provide crucial theoretical support to determine the degree of implementation necessity for enhanced oil recovery as the next step. Due to the middle–late development stage of most carbonate fractured–vuggy reservoirs in China, it is essential to evaluate the waterflooding efficiency to develop future strategies. In this study, the procedures for the construction of the innovative evaluation model were put forward first. The model was derived starting from the definitions of the single-index unascertained measure matrix, then highlighted by the modified five-scale analytical hierarchy process to obtain the comprehensive entropy weight for each index. The multi-index comprehensive unascertained measure matrix was calculated by multiplying the single-index unascertained measure matrix with the comprehensive weights, which was used to calculate the Mahalanobis distance for the grade evaluation. The Mahalanobis distance theory was applied to establish a novel evaluation grading methodology with the capacity to eliminate the subjectivity of the credible degree criterion to increase the accuracy of the evaluation grades, and its accuracy was validated with a high consistency by the comparisons with the Minkowski distance method and the Euclidean distance method.
The carbonate fractured–vuggy reservoirs were chosen for a statistically comprehensive waterflooding evaluation as a case study for the model application, with the methodology verified by field data from 26 fractured–vuggy reservoirs. The evaluation indices to construct a modified multi-index comprehensive unascertained measure included nine aspects: the waterflooding reserve utilization degree, the waterflooding reserve control degree, the energy-retention degree, the injection–withdrawal ratio, the water storage rate, the rate of decline in production, the water-cut increasing rate, the enhanced oil recovery, and the square water–oil exchange rate. The waterflooding development effect evaluations were categorized into three grades. The fractured–vuggy units with excellent waterflooding performances typically exhibited favorable effects on the enhanced oil recovery, a high maintenance capability with the inside pressure of the fractured–vuggy units, an excellent waterflooding utilization and control capacity, a low production decline rate after the waterflooding, and a high square water–oil exchange rate. The fractured–vuggy units with fair waterflooding performances demonstrated a weaker capacity in the enhanced oil recovery, the energy-retention degree, and the rate of decline in production. It can also be concluded that the moderate performance of the fractured–vuggy units behaved with incomplete well patterns, a poor injection–production balance, a low waterflooding utilization, and an insignificant waterflooding effect.
Author Contributions
Conceptualization, Z.S. and T.L.; methodology, Z.S., S.G. and Z.L.; validation, Z.S.; investigation, N.K.; data curation, N.K.; writing—original draft preparation, Z.S., S.G. and Z.L.; writing—review and editing, Z.S., S.G. and Z.L.; supervision, T.L.; project administration, Z.S. and T.L.; funding acquisition, T.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52074223.
Data Availability Statement
The data are contained within the article and references.
Conflicts of Interest
Shihui Gao was employed by the PetroChina Changqing Oilfield Company. Nan Kang was employed by the China Petroleum Pipeline Engineering Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Li, Y. The Theory and Method for Development of Carbonate Fractured-Cavity Reservoirs in T Oilfield. Acta Pet. Sin. 2013, 34, 115–121. [Google Scholar]
- Wang, D.; Sun, J. Oil Recovery for Fractured-Vuggy Carbonate Reservoirs by Cyclic Water Huff and Puff: Performance Analysis and Prediction. Sci. Rep. 2019, 9, 15231. [Google Scholar] [CrossRef]
- Li, Y.; Kang, Z.; Xue, Z.; Zheng, S. Theories and Practices of Carbonate Reservoirs Development in China. Pet. Explor. Dev. 2018, 45, 669–678. [Google Scholar] [CrossRef]
- Bois, C.; Bouche, P.; Pelet, R. Global Geologic History and Distribution of Hydrocarbon Reserves. AAPG Bull. 1982, 66, 1248–1270. [Google Scholar] [CrossRef]
- Lu, G.; Zhang, L.; Liu, Q.; Xu, Q.; Zhao, Y.; Li, X.; Deng, G.; Wang, Y. Experiment Analysis of Remaining Oil Distribution and Potential Tapping for Fractured-Vuggy Reservoir. J. Pet. Sci. Eng. 2022, 208, 109544. [Google Scholar] [CrossRef]
- Ji, B.; Zheng, S.; Gu, H. On the Development Technology of Fractured-Vuggy Carbonate Reservoirs: A Case Study on T Oilfield and Shunbei Oil and Gas Field. Oil Gas Geol. 2022, 43, 1459–1465. [Google Scholar]
- Luo, J.; Lu, X.; Wu, B.; He, X.; Li, X.; Wang, L. A Water Breakthrough Warning System of High-Yield Wells in Fractured-Vuggy Reservoirs in T Oilfield. Pet. Explor. Dev. 2013, 40, 501–506. [Google Scholar] [CrossRef]
- Guthrie, R.; Greenberger, M. The Use of Multiple Correlation Analyses for Interpreting Petroleum-Engineering Data. In Drilling and Production Practice; American Petroleum Institute: Washington, DC, USA, 1955; pp. 135–137. [Google Scholar]
- Rogers, J.B.; Terry, R.E. Applied Petroleum Reservoir Engineering, 3rd ed.; Pearson Education: Beijing, China, 2015. [Google Scholar]
- Zhang, J. Evaluation Methods of Development Effect for Water Drive Oilfield and Development Trend. Lithol. Reserv. 2012, 24, 118–122. [Google Scholar]
- Zhi, L. Using System Analysis Method to Evaluate Waterflooding Effect of Waterflooding Oilfield. In Proceedings of the International Conference on Frontier Computing, Singapore, 10–13 July 2020. [Google Scholar]
- Zhang, J.; Wang, M.; Gong, P.; Yang, Z.; Liu, X. Study on Water Injection Formula by Grey Correlation Method for Offshore Water Flooding Reservoir. J. Geosci. Environ. Prot. 2018, 6, 1–11. [Google Scholar] [CrossRef][Green Version]
- Jia, H.; Li, P.; Lv, W.; Ren, J.; Cheng, C.; Zhang, R.; Zhou, Z.; Liang, Y. Application of Fuzzy Comprehensive Evaluation Method to Assess Effect of Conformance Control Treatments on Water-Injection Wells. Petroleum, 2022; in press. [Google Scholar] [CrossRef]
- Zhang, P.; Feng, G. Application of Fuzzy Comprehensive Evaluation to Evaluate the Effect of Water Flooding Development. J. Pet. Explor. Prod. Technol. 2018, 8, 1455–1463. [Google Scholar] [CrossRef]
- Chen, L.; Li, C.; Li, Z.; Shi, Y.; Wan, L.; Wang, J.; Wang, Z.; Zhao, A. Quantitative Evaluation Method for Development of Water Flooding in Reservoir, Involves Establishing Evaluation Degree of Membership Degree Matrix to Evaluate Development Effect of Water Flooding in Infiltration Complex Block Reservoir. China Patent CN107038516-A, 11 August 2017. [Google Scholar]
- Guo, M.; Jiang, S.; Li, J.; Liu, L.; Liu, M.; Peng, D.; Shi, D.; Tang, X.; Tian, T.; Zhai, L.; et al. Tracer Technology Based Offshore Reservoir Water Injection Development Result Quantitatively Evaluating Method, Involves Adding Tracers in Water Wells, and Evaluating Balanced Displacement of Waterflood Development Process. China Patent CN106285647-A, 4 January 2017. [Google Scholar]
- Makhotin, I.; Orlov, D.; Koroteev, D. Machine Learning to Rate and Predict the Efficiency of Waterflooding for Oil Production. Energies 2022, 15, 1199. [Google Scholar] [CrossRef]
- Khormali, A.; Ahmadi, S. Prediction of Barium Sulfate Precipitation in Dynamic Tube Blocking Tests and Its Inhibition for Waterflooding Application Using Response Surface Methodology. J. Pet. Explor. Prod. Technol. 2023, 13, 2267–2281. [Google Scholar] [CrossRef]
- Bruce, W.A. An Electrical Device for Analyzing Oil-Reservoir Behavior. Trans. AIME 1943, 151, 112–124. [Google Scholar] [CrossRef]
- Holanda, R.; Gildin, E.; Jensen, J.; Lake, L.; Kabir, C. A State-of-the-Art Literature Review on Capacitance Resistance Models for Reservoir Characterization and Performance Forecasting. Energies 2018, 11, 3368. [Google Scholar] [CrossRef]
- Yousef, A.; Lake, L.; Jensen, J. Analysis and Interpretation of Interwell Connectivity from Production and Injection Rate Fluctuations Using a Capacitance Model. In Proceedings of the SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK, USA, 22 April 2006. [Google Scholar]
- Yousef, A.; Gentil, P.; Jensen, J.; Lake, L. A Capacitance Model to Infer Interwell Connectivity from Production and Injection Rate Fluctuations. SPE Reserv. Eval. Eng. 2006, 9, 630–646. [Google Scholar] [CrossRef]
- Sayarpour, M.; Zuluaga, E.; Kabir, C.; Lake, L. The Use of Capacitance–Resistance Models for Rapid Estimation of Waterflood Performance and Optimization. J. Pet. Sci. Eng. 2009, 69, 227–238. [Google Scholar] [CrossRef]
- Liang, X.; Weber, D.; Edgar, T.; Lake, L.; Sayarpour, M.; Al-Yousef, A. Optimization of Oil Production Based on A Capacitance Model of Production and Injection Rates. In Proceedings of the Hydrocarbon Economics and Evaluation Symposium, Dallas, TX, USA, 1 April 2007. [Google Scholar]
- Yang, X.; Hao, Z.; Liu, K.; Tao, Z.; Shi, G. An Improved Unascertained Measure-Set Pair Analysis Model Based on Fuzzy AHP and Entropy for Landslide Susceptibility Zonation Mapping. Sustainability 2023, 15, 6205. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, E.; Zhang, C.; Li, Z.; Wang, D. A Comprehensive Risk Assessment Method for Coal and Gas Outburst in Underground Coal Mines Based on Variable Weight Theory and Uncertainty Analysis. Process Saf. Environ. Prot. 2022, 167, 97–111. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, J.; Xu, C.; Lai, X.; Luo, Q.; Liu, C.; Li, K. Comprehensive Evaluation of Blast Casting Results Based on Unascertained Measurement and Intuitionistic Fuzzy Set. Shock Vib. 2021, 2021, 8864618. [Google Scholar] [CrossRef]
- Sheng, K.; Lai, X.; Chen, Y.; Jiang, J.; Zhou, L. Risk Assessment of Urban Gas Pipeline Based on Different Unknown Measure Functions. Teh. Vjesn. Tech. Gaz. 2021, 28, 1605–1614. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, C.; Wang, M.; Khandelwal, M. Proposing a Novel Comprehensive Evaluation Model for the Coal Burst Liability in Underground Coal Mines Considering Uncertainty Factors. Int. J. Min. Sci. Technol. 2021, 31, 799–812. [Google Scholar] [CrossRef]
- Dong, L.; Zhou, Y.; Deng, S.; Wang, M.; Sun, D. Evaluation Methods of Man-Machine-Environment System for Clean and Safe Production in Phosphorus Mines: A Case Study. J. Cent. South Univ. 2021, 28, 3856–3870. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, J.; Zhao, Y.; Yang, S. A Novel Method for Predicting Rockburst Intensity Based on an Improved Unascertained Measurement and an Improved Game Theory. Mathematics 2023, 11, 1862. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, C.; Khandelwal, M.; Tao, M.; Li, C. Novel Approach to Evaluate Rock Mass Fragmentation in Block Caving Using Unascertained Measurement Model and Information Entropy with Flexible Credible Identification Criterion. Eng. Comput. 2022, 38, 3789–3809. [Google Scholar] [CrossRef]
- Li, Q.; Yu, Y. Durability Evaluation of Concrete Bridges Based on the Theory of Matter Element Extension—Entropy Weight Method—Unascertained Measure. Math. Probl. Eng. 2021, 2021, 2646723. [Google Scholar] [CrossRef]
- Qu, X.; Shi, L.; Han, J. Spatial Evaluation of Groundwater Quality Based on Toxicological Indexes and Their Effects on Ecology and Human Health. J. Clean. Prod. 2022, 377, 134255. [Google Scholar] [CrossRef]
- Zhong, Y.; Liang, X. A Hybrid Evaluation of Information Entropy Meta-Heuristic Model and Unascertained Measurement Theory for Tennis Motion Tracking. Adv. Nano Res. 2022, 12, 263–279. [Google Scholar]
- Zhan, J.; Su, Z.; Fan, C.; Li, X.; Ma, X. Suitability Evaluation of CO2 Geological Sequestration Based on Unascertained Measurement. Arab. J. Sci. Eng. 2022, 47, 11453–11467. [Google Scholar] [CrossRef]
- Arbogast, T.; Lehr, H.L. Homogenization of a Darcy–Stokes System Modeling Vuggy Porous Media. Comput. Geosci. 2006, 10, 291–302. [Google Scholar] [CrossRef]
- Popov, P.; Qin, G.; Bi, L.; Efendiev, Y.; Ewing, R.; Kang, Z.; Li, J. Multiscale Methods for Modeling Fluid Flow Through Naturally Fractured Carbonate Karst Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Anaheim, CA, USA, 11 November 2007. [Google Scholar]
- Arbogast, T.; Brunson, D.S. A Computational Method for Approximating a Darcy–Stokes System Governing a Vuggy Porous Medium. Comput. Geosci. 2007, 11, 207–218. [Google Scholar] [CrossRef]
- Pal, M. A Unified Approach to Simulation and Upscaling of Single-phase Flow through Vuggy Carbonates. Int. J. Numer. Methods Fluids 2012, 69, 1096–1123. [Google Scholar] [CrossRef]
- Pal, M.; Jadhav, S. An Efficient Workflow for Meshing Large Scale Discrete Fracture Networks for Solving Subsurface Flow Problems. Pet. Sci. Technol. 2022, 40, 1945–1978. [Google Scholar] [CrossRef]
- Ding, L.; Jouenne, S.; Gharbi, O.; Pal, M.; Bertin, H.; Rahman, M.A.; Economou, I.G.; Romero, C.; Guérillot, D. An Experimental Investigation of the Foam Enhanced Oil Recovery Process for a Dual Porosity and Heterogeneous Carbonate Reservoir under Strongly Oil-Wet Condition. Fuel 2022, 313, 122684. [Google Scholar] [CrossRef]
- Pal, M. A Microscale Simulation Methodology for Subsurface Heterogeneity Quantification Using Petrographic Image Analysis with Multiscale Mixed Finite Element Method. Pet. Sci. Technol. 2021, 39, 582–611. [Google Scholar] [CrossRef]
- Wang, G. Unascertained Information and Its Mathematical Treatment. Harbin Archit. Civ. Eng. Inst. 1990, 23, 1–8. [Google Scholar]
- Li, W.; Li, Q.; Liu, Y.; Li, H.; Pei, X. Construction Safety Risk Assessment for Existing Building Renovation Project Based on Entropy-Unascertained Measure Theory. Appl. Sci. 2020, 10, 2893. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with the Analytic Hierarchy Process. Int. J. Serv. Sci. 2008, 1, 83. [Google Scholar] [CrossRef]
- Saaty, T.L. How to Make a Decision: The Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Karahalios, H. The Application of the AHP-TOPSIS for Evaluating Ballast Water Treatment Systems by Ship Operators. Transp. Res. Part D Transp. Environ. 2017, 52, 172–184. [Google Scholar] [CrossRef]
- Okada, H.; Styles, S.W.; Grismer, M.E. Application of the Analytic Hierarchy Process to Irrigation Project Improvement. Agric. Water Manag. 2008, 95, 205–210. [Google Scholar] [CrossRef]
- Wang, X.; Duan, Q. A Method for Calculating the Weight of Oil and Gas Pipeline Risk Factor Based on Improved Analytic Hierarchy Process. Oil Gas Storage Transp. 2019, 38, 1227–1231. [Google Scholar]
- Yeager, M.; Gregory, B.; Key, C.; Todd, M. On Using Robust Mahalanobis Distance Estimations for Feature Discrimination in a Damage Detection Scenario. Struct. Health Monit. 2019, 18, 245–253. [Google Scholar] [CrossRef]
- Su, Z. The Study of Interwell Connectivity in Fracture-Vuggy Carbonate Reservoirs by Dynamic Data. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2018. [Google Scholar]
- Zhong, J.; Mao, C.; Li, Y.; Yuan, X.; Wang, S.; Niu, Y. The Characteristics of Ordovician Carbonate Reservoir Storage Space in the Tarim Basin; Petroleum Industry Press: Beijing, China, 2014. [Google Scholar]
- Hou, J.; Hu, X.; Li, Y.; Li, Y. Geological Modeling of Paleokarst Carbonate Reservoirs; China University of Petroleum Press: Beijing, China, 2017. [Google Scholar]
- Wang, X.; You, L.; Zhu, B.; Tang, H.; Qu, H.; Feng, Y.; Zhong, Z. Numerical Simulation of Bridging Ball Plugging Mechanism in Fractured-Vuggy Carbonate Reservoirs. Energies 2022, 15, 7361. [Google Scholar] [CrossRef]
- SY/T 6219-1996; Oilfield Development Grading. China National Petroleum Corporation (CNPC): Beijing, China, 1996.
- Lei, Y. Comprehensive Evaluation of Water Injection Effect of the Fracture-Cavern Reservoirs in the 4 District of T Oil Field. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2017. [Google Scholar]
- Wang, J.; Hu, B.; Li, J.; Chang, J.; Cui, A.; Cui, K. Slope Stability Evaluation and Application of Open-Pit Mine Based on Uncertainty Measurement Theory. Chin. J. Nonferrous Met. 2021, 31, 1388–1394. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).