Impact of Temperature on Cement Displacement Efficiency: Analysis of Velocity, Centralization, and Density Differences
Abstract
:1. Introduction
2. Materials and Methods
2.1. Rheology Measurement Experiment
2.1.1. Rheological Testing of Drilling Fluid at Different Temperatures
2.1.2. Rheological Testing of Cement Slurry at Different Temperatures
2.2. Geometric Model and Mesh Generation
2.3. Numerical Simulation of Control Equations
3. Results and Discussions
3.1. Model and Experimental Validation
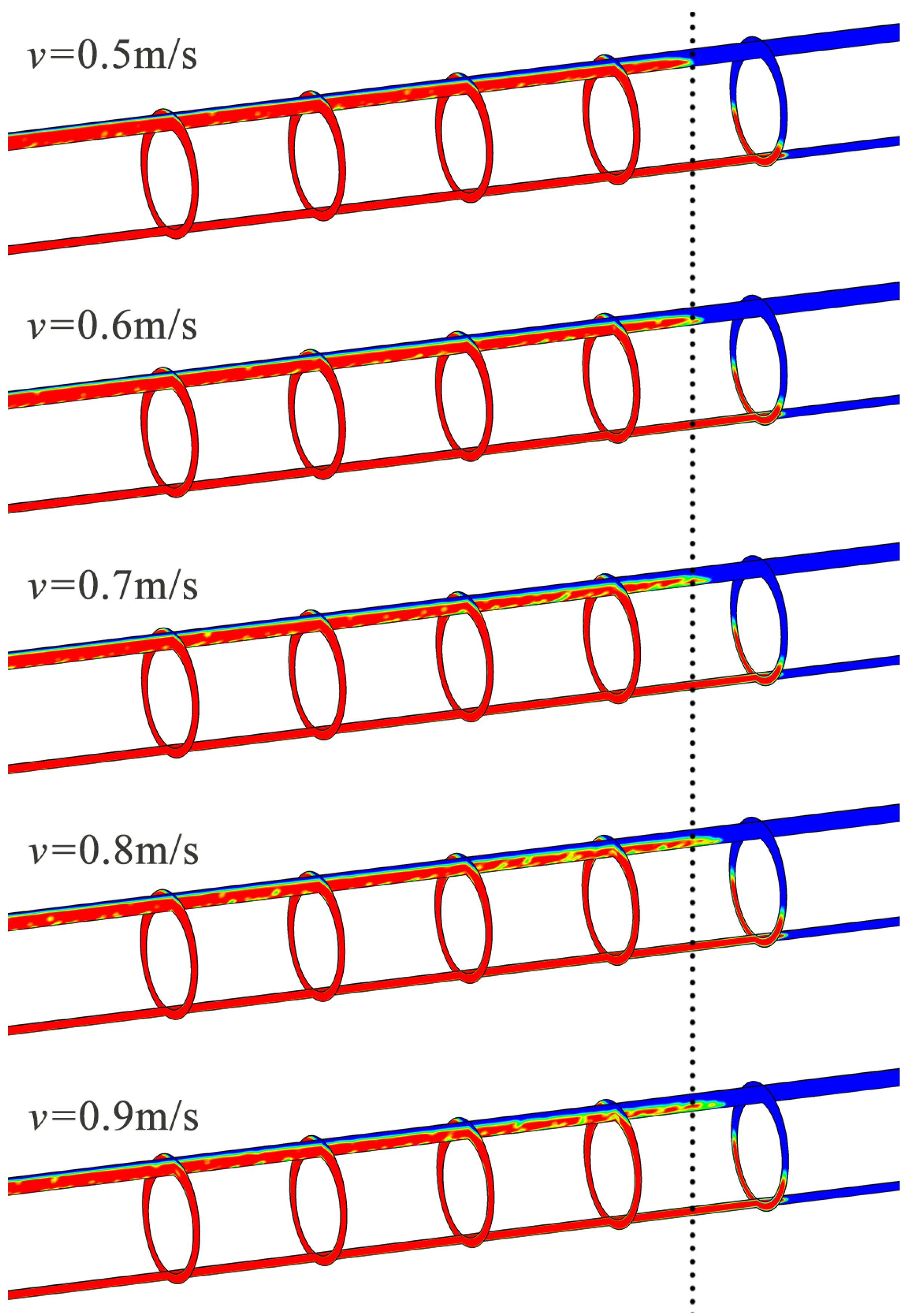
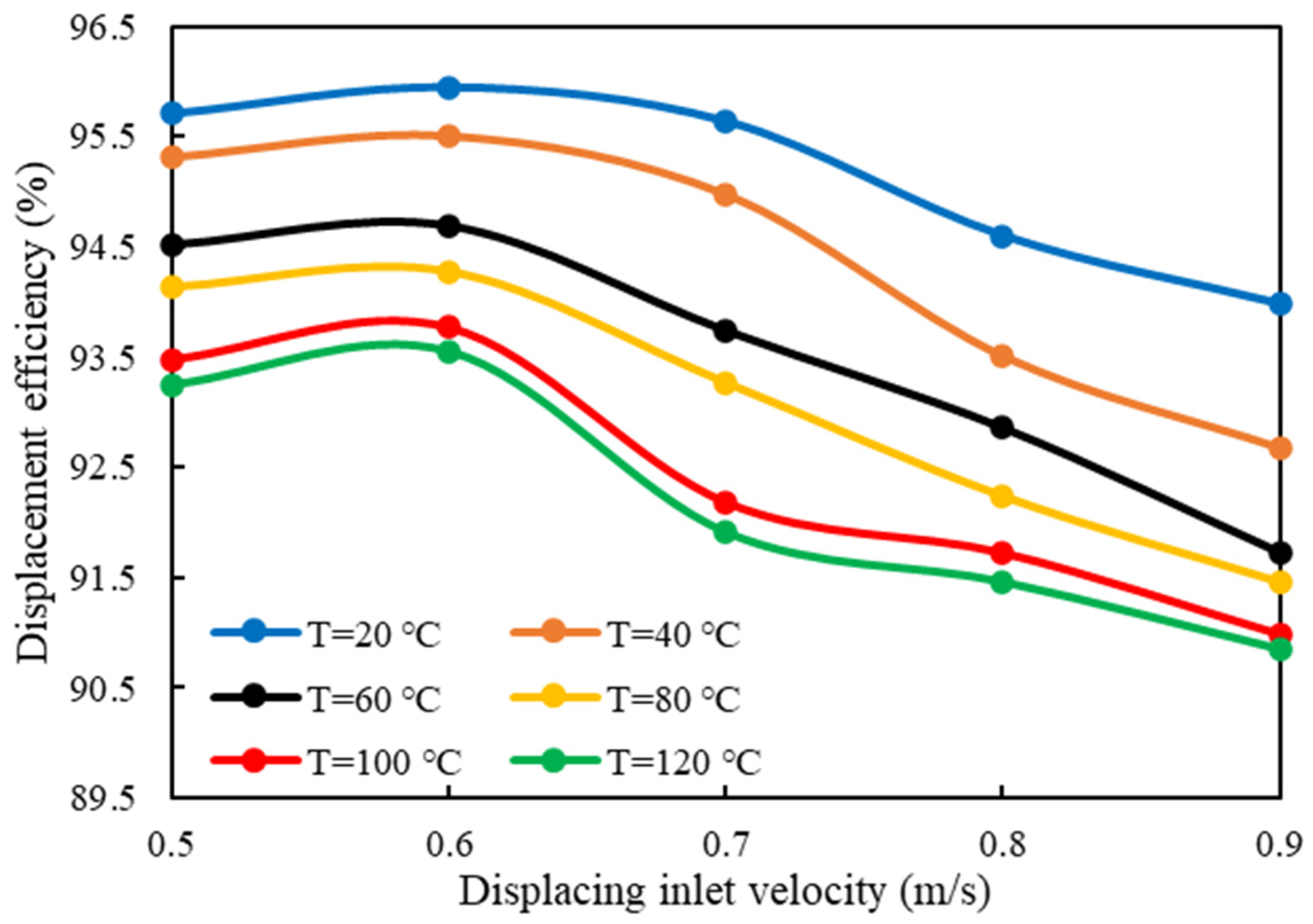
3.2. Displacement Inlet Velocity
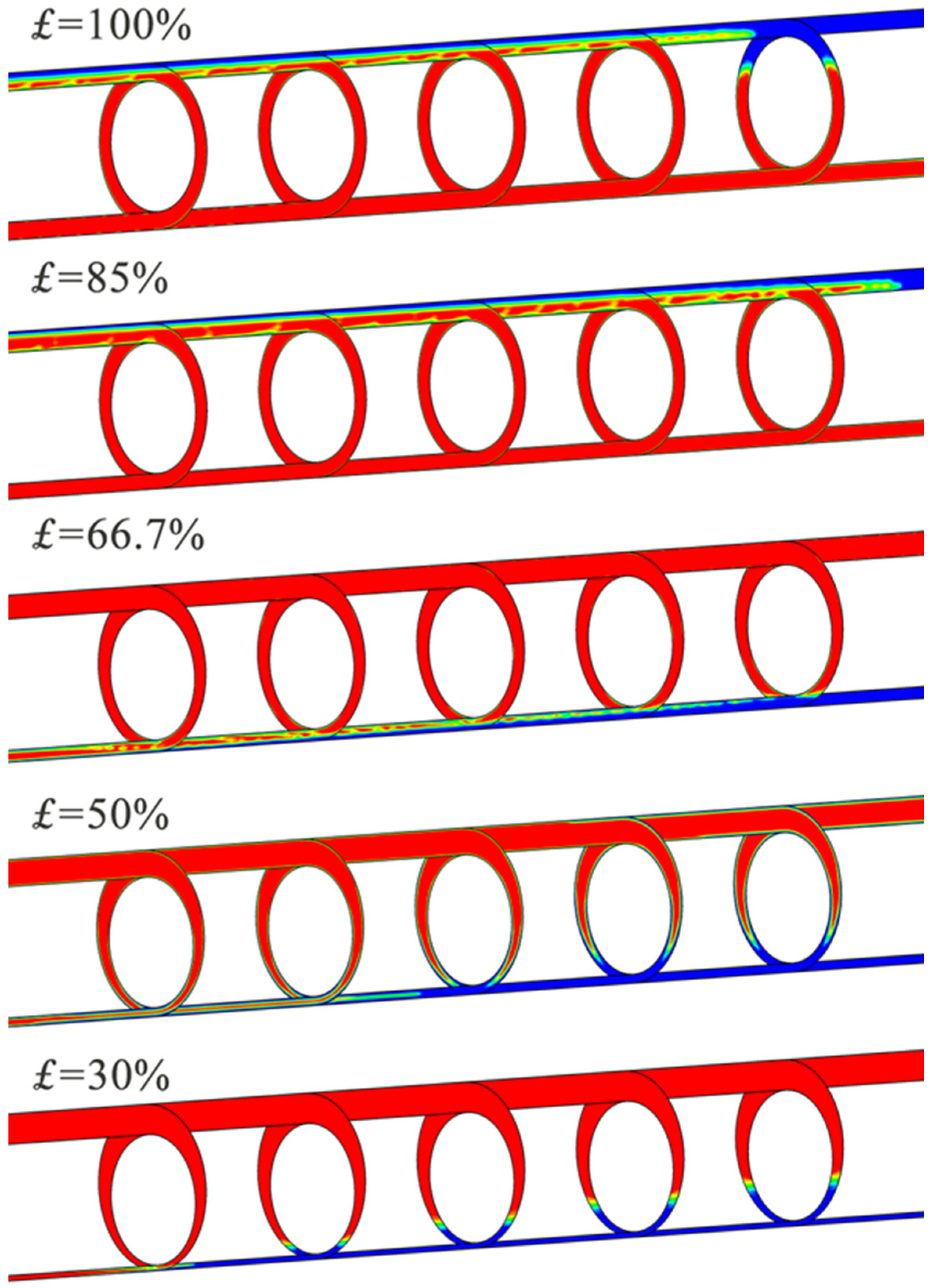
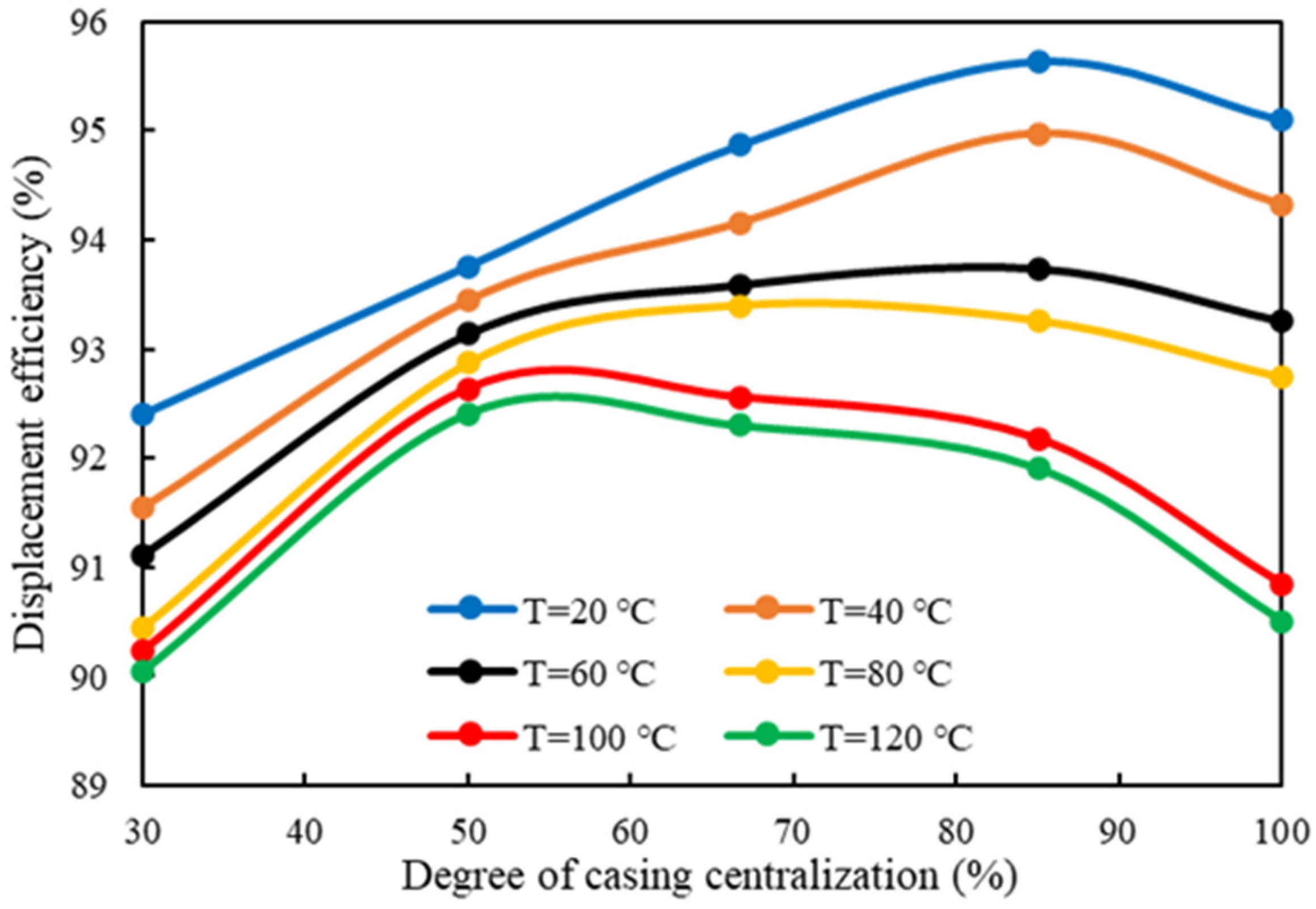
3.3. Degree of Casing Centralization
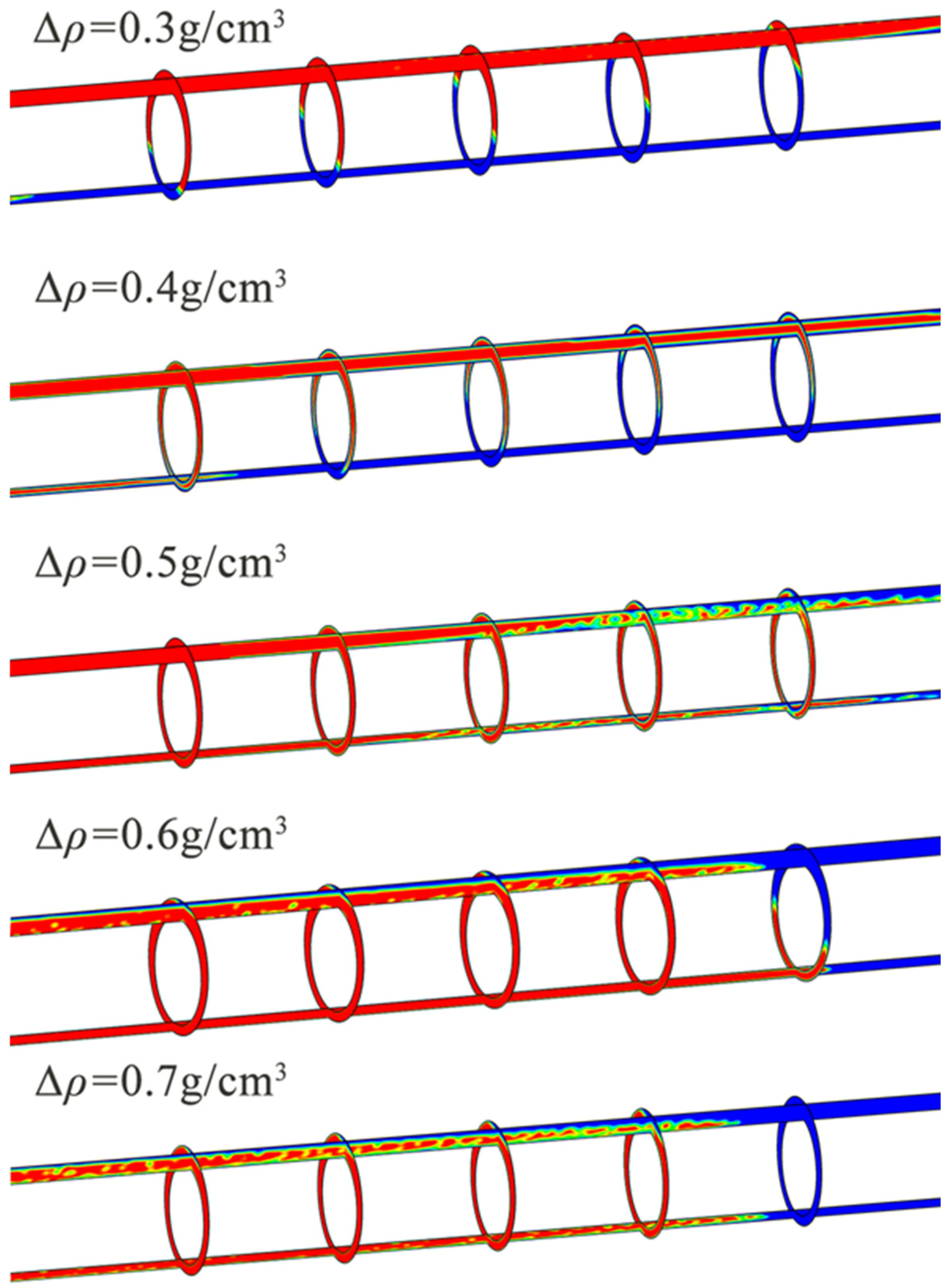
3.4. Density Difference
4. Conclusions
- (1)
- Temperature Effects on Rheology: The study confirms that temperature significantly affects the rheological properties of both cement slurry and drilling fluid. As temperature increases, reductions in shear stress and viscosity alter fluid behavior, impacting the displacement process.
- (2)
- Displacement Speed: Proper control of displacement speed is essential at varying temperatures. Increased speeds can enhance efficiency but may cause interface instability and fluid mixing, particularly at higher temperatures.
- (3)
- Casing Centralization: Optimal casing centralization is crucial for maintaining displacement efficiency. Results indicate that an intermediate level of centralization can counteract gravitational and resistance effects in the annulus, especially under non-ideal temperature conditions.
- (4)
- Density Difference: An optimal range of density difference between cement slurry and drilling fluid must be maintained. While a higher density difference can increase buoyancy and promote displacement, excessive differences may lead to instability and layering. For high-temperature environments, operators should consider reducing the density difference to avoid efficiency loss due to fluid instability.
- (5)
- Shortcomings and Prospects: In order to facilitate their use, the results need to be adjusted. This can be considered based on the field data research and analysis to derive the impact weight of each factor, according to the weight assigned to derive the optimization equation, through iterative calculations to derive the optimal values of cementing parameters under a given working condition in practice.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Epelle, E.I.; Gerogiorgis, D.I. A review of technological advances and open challenges for oil and gas drilling systems engineering. AIChE J. 2020, 66, e16842. [Google Scholar] [CrossRef]
- Wang, H.; Huang, H.; Bi, W.; Ji, G.; Zhou, B.; Zhuo, L. Deep and Ultra-Deep Oil and Gas Well Drilling Technologies: Progress and Prospect. Nat. Gas Ind. B 2022, 9, 141–157. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, Z.; Zhao, Y.; Xue, Y.; Wang, C.; Xiong, C.; Chen, S. Theoretical and Experimental Study on Cementing Displacement Interface for Highly Deviated Wells. Energies 2023, 16, 733. [Google Scholar] [CrossRef]
- Zeng, B.; Zhou, X.; Cao, J.; Zhou, F.; Wang, Y.; Wang, Y.; Song, Y.; Hu, J.; Du, Y. A Casing Deformation Prediction Model Considering the Properties of Cement. Processes 2023, 11, 695. [Google Scholar] [CrossRef]
- Stryczek, S.; Wiśniowski, R.; Gonet, A.; Złotkowski, A. The Influence of Time of Rheological Parameters of Fresh Cement Slurries. AGH Drill. Oil Gas 2014, 31, 123–133. [Google Scholar] [CrossRef]
- Lund, B.; Ytrehus, J.D.; Taghipour, A.; Divyankar, S.; Saasen, A. Fluid-Fluid Displacement for Primary Cementing in Deviated Washout Sections. In Proceedings of the ASME 2018 37th International Conference on Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018; Volume 8, pp. 1–9. [Google Scholar] [CrossRef]
- Renteria, A.; Sarmadi, P.; Frigaard, I. Cementing Irregular Horizontal Wellbores. In Proceedings of the ASME 2021 40th International Conference on Ocean, Offshore and Arctic Engineering, Online, 21–30 June 2021; Volume 10, pp. 1–10. [Google Scholar] [CrossRef]
- Wang, J.; Xiong, Y.; Lu, Z.; Zhang, W.; Wu, J.; Wei, R.; Li, X. Research on Key Technologies to Improve Cementing Displacement Efficiency. ACS Omega 2022, 7, 37039–37049. [Google Scholar] [CrossRef]
- McLean, R.H.; Manry, C.W.; Whitaker, W.W. Displacement Mechanics in Primary Cementing. J. Pet. Technol. 1967, 19, 251–260. [Google Scholar] [CrossRef]
- Zulqarnain, M.; Tyagi, M. Development of Simulations Based Correlations to Predict the Cement Volume Fraction in Annular Geometries after Fluid Displacements during Primary Cementing. J. Pet. Sci. Eng. 2016, 145, 1–10. [Google Scholar] [CrossRef]
- Mohamed, A.; Salehi, S.; Ahmed, R. Significance and Complications of Drilling Fluid Rheology in Geothermal Drilling: A Review. Geothermics 2021, 93, 102066. [Google Scholar] [CrossRef]
- Bu, Y.; Tian, L.; Li, Z.; Zhang, R.; Wang, C.; Yang, X. Effect of Casing Rotation on Displacement Efficiency of Cement Slurry in Highly Deviated Wells. J. Nat. Gas Sci. Eng. 2018, 52, 317–324. [Google Scholar] [CrossRef]
- Kiran, R.; Teodoriu, C.; Dadmohammadi, Y.; Nygaard, R.; Wood, D.; Mokhtari, M.; Salehi, S. Identification and Evaluation of Well Integrity and Causes of Failure of Well Integrity Barriers (A Review). J. Nat. Gas Sci. Eng. 2017, 45, 511–526. [Google Scholar] [CrossRef]
- Sun, B.; Wang, X.; Wang, Z.; Gao, Y. Transient Temperature Calculation Method for Deep-Water Cementing Based on Hydration Kinetics Model. Appl. Therm. Eng. 2018, 129, 1426–1434. [Google Scholar] [CrossRef]
- Hemphill, T. Prediction of Rheological Behavior of Ester-Based Drilling Fluids under Downhole Conditions. In Proceedings of the SPE International Oil Conference and Exhibition in Mexico, Villahermosa, Mexico, 5–7 March 1996; pp. 243–253. [Google Scholar] [CrossRef]
- Fakoya, M.F.; Ahmed, R.M. A Generalized Model for Apparent Viscosity of Oil-Based Muds. J. Pet. Sci. Eng. 2018, 165, 777–785. [Google Scholar] [CrossRef]
- Politte, M.D. Invert Oil Mud Rheology As a Function of Temperature and Pressure. In Proceedings of the SPE/IADC Drilling Conference, New Orleans, LA, USA, 6–8 March 1985; pp. 305–322. [Google Scholar] [CrossRef]
- Sherif, T.; Ahmed, R.; Shah, S.; Amani, M. Rheological Behavior of Oil-Based Drilling Foams. J. Nat. Gas Sci. Eng. 2015, 26, 873–882. [Google Scholar] [CrossRef]
- Wang, F.; Tan, X.; Wang, R.; Sun, M.; Wang, L.; Liu, J. High Temperature and High Pressure Rheological Properties of High-Density Water-Based Drilling Fluids for Deep Wells. Pet. Sci. 2012, 9, 354–362. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Y.; Tyagi, M.; Chen, Y.; Kam, S.I. Multi-Dimensional CFD Analysis for the Prediction of Transient Wellbore Circulating Temperature Profile to Guide Offshore Cementing Job. J. Korean Soc. Miner. Energy Resour. Eng. 2019, 56, 344–358. [Google Scholar] [CrossRef]
- Yuan, B.; Yang, S.; Xu, B.; Zeng, S.; Li, P. Novel Evaluation Method for Flushing Efficiency Based on the Principle of Wall Shear Rate Equality under High Temperature and High Pressure. ACS Omega 2022, 7, 38796–38810. [Google Scholar] [CrossRef]
- Shatskyi, I.; Velychkovych, A.; Vytvytskyi, I.; Senyushkovych, M. Modeling of Nonlinear Properties of Casing Centralizers Equipped with Axial Thrust. In IOP Conference Series: Materials Science and Engineering, Proceedings of the 11th International Conference on Advanced Manufacturing Technologies (ICAMaT 2020), Bucharest, Romania, 29–30 October 2020; IOP Publishing: Bristol, UK, 2021; Volume 1018, p. 012003. [Google Scholar] [CrossRef]
- Shatskyi, I.; Vytvytskyi, I.; Senyushkovych, M.; Velychkovych, A. Modelling and Improvement of the Design of Hinged Centralizer for Casing. In IOP Conference Series: Materials Science and Engineering, Proceedings of the Innovative Manufacturing Engineering and Energy (IManEE 2019)—“50 Years of Higher Technical Education at the University of Pitesti”—The 23rd Edition of IManEE 2019 International Conference, Pitesti, Romania, 22–24 May 2019; IOP Publishing: Bristol, UK, 2019; Volume 564, p. 012073. [Google Scholar] [CrossRef]
- Shatskyi, I.; Velychkovych, A.; Vytvytskyi, I.; Seniushkovych, M. Analytical Models of Contact Interaction of Casing Centralizers with Well Wall. Eng. Solid Mech. 2019, 7, 355–366. [Google Scholar] [CrossRef]
- Hazra, A.; Raigar, R.K.; Lal, K.; Negi, H.S.; Kumar, P. Importance of Controlling Fluid Loss & Settling Behaviour of Weighted Spacers in HPHT Conditions. In Proceedings of the 2nd Indian Oil & Gas Chemistry, Chemicals & Additives Conference & Exhibition (IOGCA 2019), Ahmedabad, India, 16–17 September 2019; pp. 1–12. [Google Scholar]
- Lichinga, K.N.; Maagi, M.T.; Wang, Q.; Hao, H.; Gu, J. Experimental Study on Oil Based Mudcake Removal and Enhancement of Shear Bond Strength at Cement-Formation Interface. J. Pet. Sci. Eng. 2019, 176, 754–761. [Google Scholar] [CrossRef]
- Ikpeka, P.; Benedict, U.; Utojiuba, D.; Odo, J.; Uzuegbu, G. Effects of Additive Concentrations on Cement Rheology at Differenttemperature Conditions. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Virtual, 11–13 August 2020. [Google Scholar] [CrossRef]
- Memon, K.R.; Shuker, M.T.; Tunio, S.Q.; Lashari, A.A.; Abbass, G. Investigating Rheological Properties of High Performance Cement System for Oil Wells. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 3865–3870. [Google Scholar] [CrossRef]
- Gao, H.; Ai, Z.; Zhang, J.; Zhou, B.; Chen, F.; Wang, W.; Liu, Z.; Deng, Q.; Shi, Y.; Wang, Z. Numerical Simulation of Improving Cementing Displacement Efficiency under Narrow Safety Density Window. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Bali, Indonesia, 29–31 October 2019. [Google Scholar] [CrossRef]
- Mohammed, M.H.; Pusch, R.; Knutsson, S.; Hellström, G. Rheological Properties of Cement-Based Grouts Determined by Different Techniques. Engineering 2014, 6, 217–229. [Google Scholar] [CrossRef]
- Pernites, R.; Padilla, F.; Clark, J.; Gonzalez, A.; Fu, D. Novel and High Performing Wellbore Cleaning Fluids with Surprisingly Flat Viscosity over Time and Different Temperatures. In Proceedings of the SPE Western Regional Meeting, Garden Grove, CA, USA, 22–26 April 2018. [Google Scholar] [CrossRef]
- Durmaz, S.; Karbasforoushan, H.; Ozbayoglu, E.M.; Miska, S.Z.; Yu, M.; Takach, N. Mixing of Cement Slurries during Cement Plug Setting. In Proceedings of the SPE Deepwater Drilling and Completions Conference, Galveston, TX, USA, 14–15 September 2016. [Google Scholar] [CrossRef]
- Funkhouser, G.P.; Leotaud, L.; Bratcher, J. Delayed-Release Suspending Aid Provides Cement-Slurry Stability in High-Temperature, Horizontal Wells. In Proceedings of the SPE International Symposium on Oilfield Chemistry, The Woodlands, TX, USA, 9–10 April 2015; Volume 1, pp. 221–230. [Google Scholar] [CrossRef]
- Shadravan, A.; Narvaez, G.; Alegria, A.; Carman, P.; Perez, C.; Erger, R. Engineering the Mud-Spacer-Cement Rheological Hierarchy Improves Wellbore Integrity. In Proceedings of the SPE E&P Health, Safety, Security and Environmental Conference-Americas, Denver, CO, USA, 16–18 March 2015; pp. 374–387. [Google Scholar] [CrossRef]
- An, J.; Li, J.; Huang, H.; Liu, G.; Yang, H.; Zhang, G.; Li, W. Mud Loss Behavior in Fractured Formation with High Temperature and Pressure. Energy Rep. 2023, 9, 2638–2652. [Google Scholar] [CrossRef]
- Wu, Y.; Salehi, S.; Khalifeh, M. Characterization of the Mud Displacement in an Enlarged Wellbore: An Integrated Rock-Fluid Model. J. Nat. Gas Sci. Eng. 2022, 100, 104471. [Google Scholar] [CrossRef]
- Renteria, A.; Sarmadi, P.; Thompson, C.; Frigaard, I.A. Effects of Wellbore Irregularity on Primary Cementing of Horizontal Wells, Part 1: Large Scale Effects. J. Pet. Sci. Eng. 2022, 208, 109581. [Google Scholar] [CrossRef]
- Balogh, M.; Parente, A.; Benocci, C. RANS Simulation of ABL Flow over Complex Terrains Applying an Enhanced K-ε Model and Wall Function Formulation: Implementation and Comparison for Fluent and OpenFOAM. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 360–368. [Google Scholar] [CrossRef]
- Vefring, E.H.; Bjorkevoll, K.S.; Hansen, S.A.; Sterri, N.; Saevareid, O.; Aas, B.; Merlo, A. Optimization of displacement efficiency during primary cementing. In Proceedings of the Latin American and Caribbean Petroleum Engineering Conference, Rio de Janeiro, Brazil, 30 August–3 September 1997. [Google Scholar] [CrossRef]
- Foroushan, H.K.; Ozbayoglu, E.; Gomes, P.J.; Miska, S.; Yu, M. Mud-Cement Displacement in Eccentric Annuli: Analytical Solution, Instability Analysis, and Computational Fluid Dynamics Simulations. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, Fort Worth, TX, USA, 6–8 March 2018. [Google Scholar] [CrossRef]
- Foroushan, H.K.; Lund, B.; Ytrehus, J.D.; Saasen, A. Cement Placement: An Overview of Fluid Displacement Techniques and Modelling. Energies 2021, 14, 573. [Google Scholar] [CrossRef]
- Nasiri Khalaji, M.; Koca, A.; Kotcioğlu, İ. Investigation of Numerical Analysis Velocity Contours K-ε Model of RNG, Standard and Realizable Turbulence for Different Geometries. Int. J. Innov. Res. Rev. 2019, 3, 29–34. [Google Scholar]
- Xu, B.; Zhou, S.; He, F.; Wang, F.; Guo, J. Using Particle Image Velocimetry to Evaluate the Displacement Efficiency of Drilling Mud in Horizontal Well Cementing. J. Pet. Sci. Eng. 2020, 195, 107647. [Google Scholar] [CrossRef]


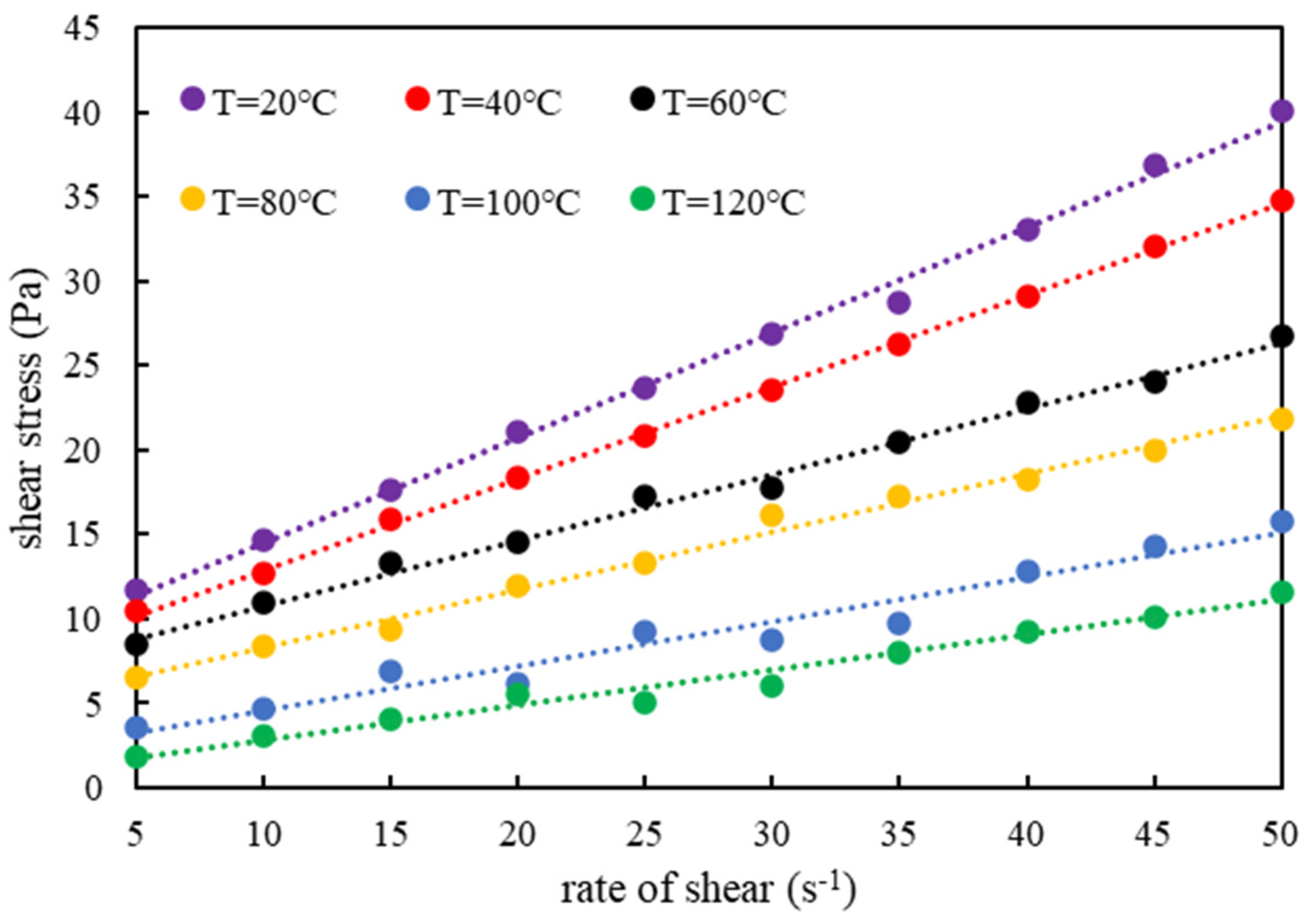
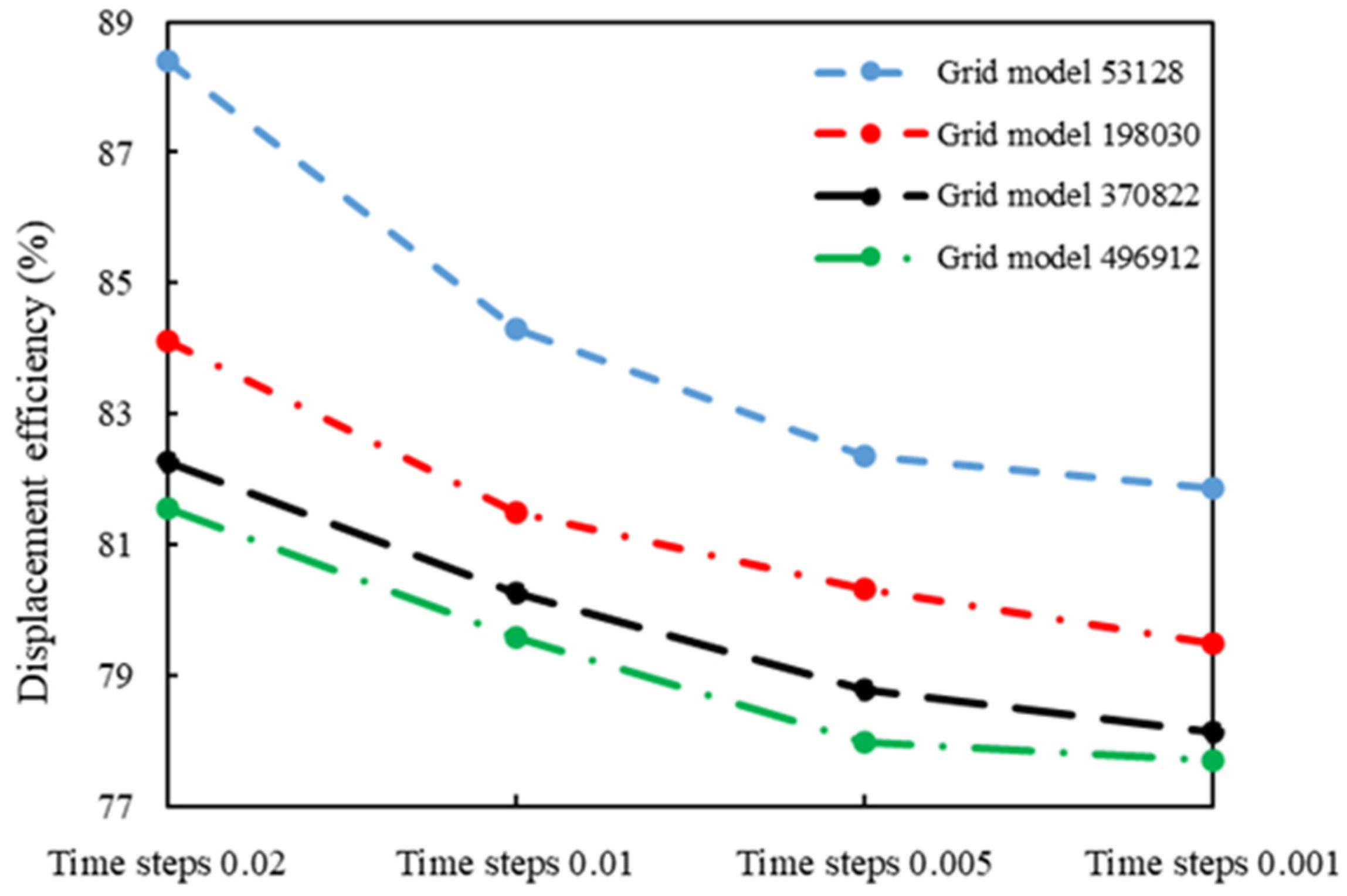
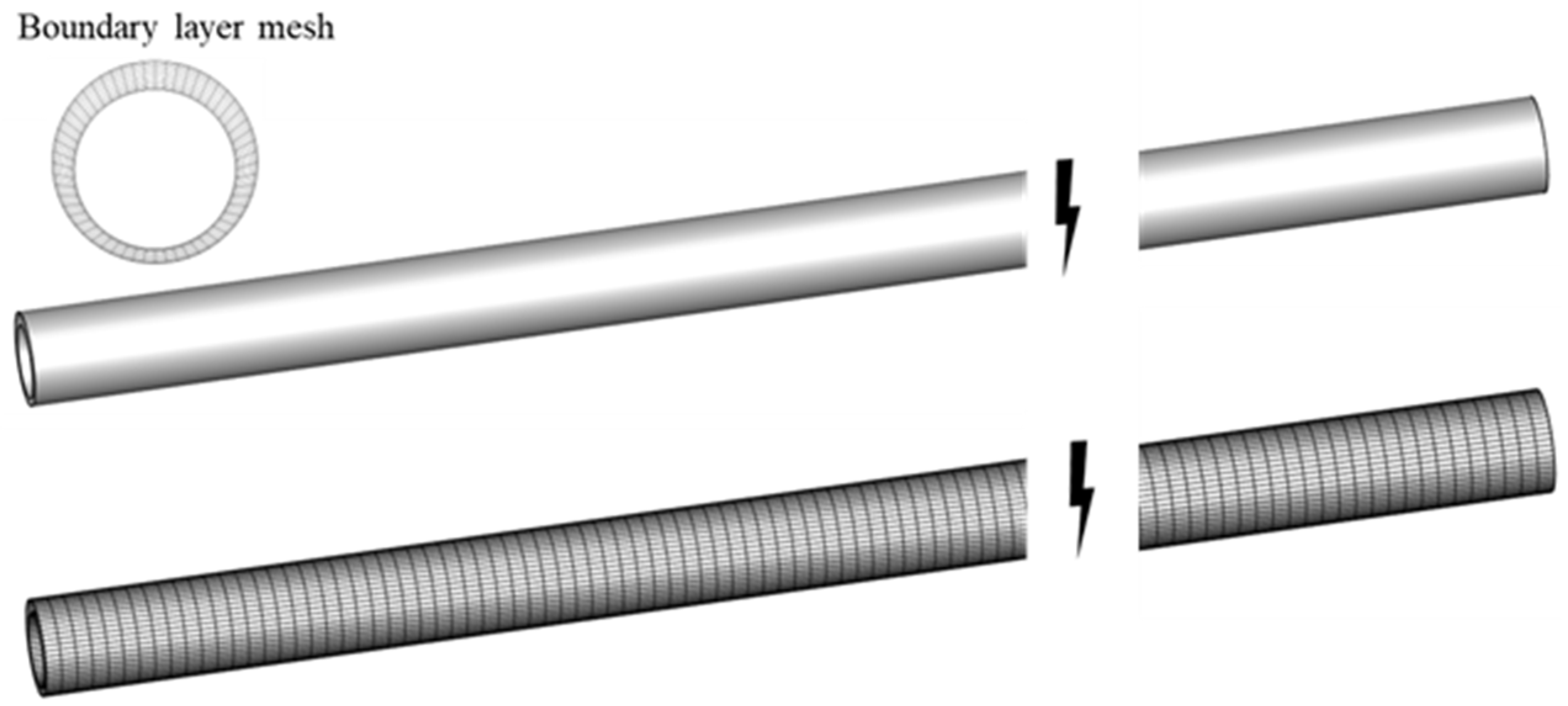
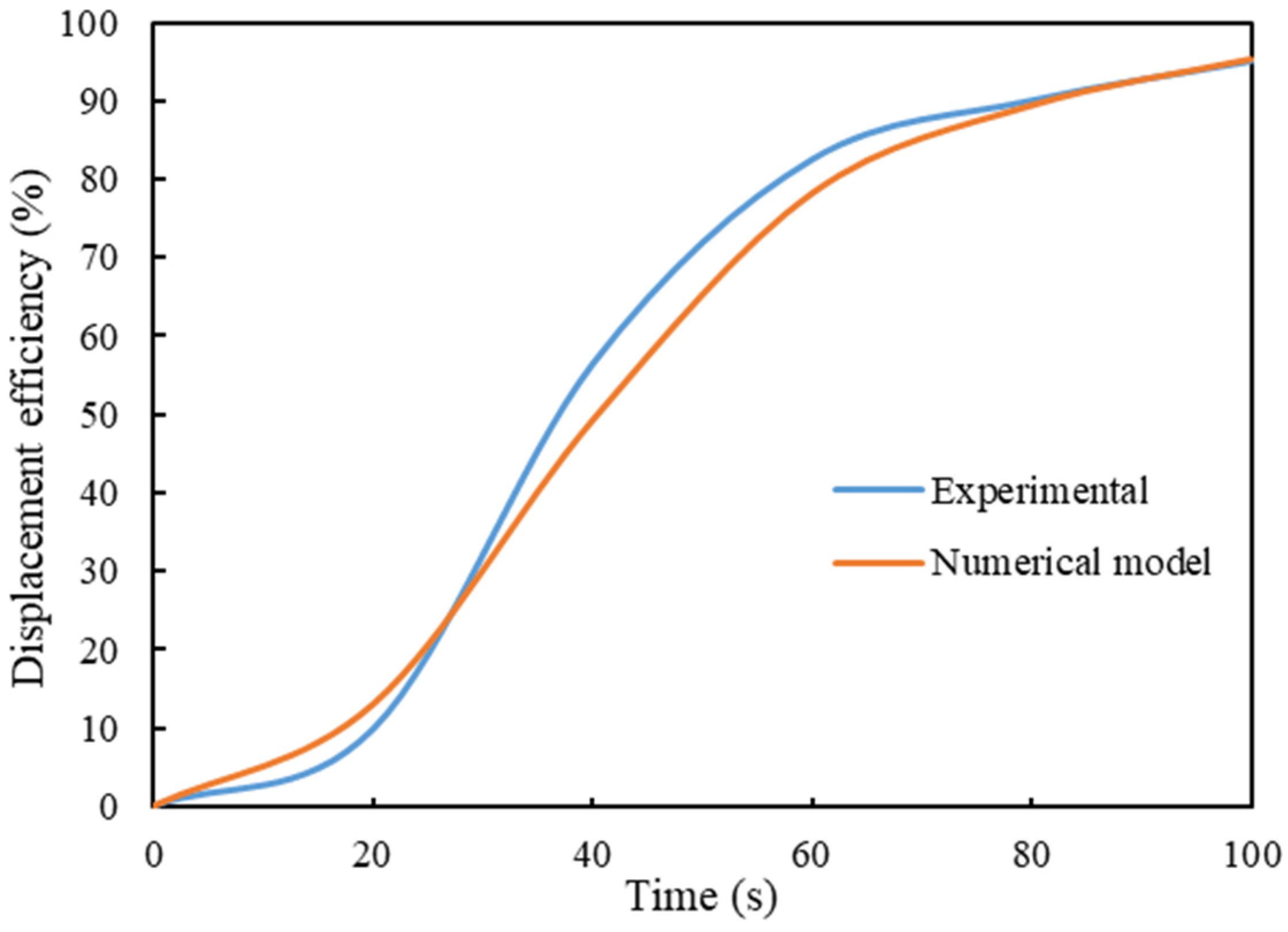

| Temperature/°C | τ0/Pa | Standard Error | K/Pa∙sn | Standard Error | n |
|---|---|---|---|---|---|
| 20 | 6.410 | 0.088 | 0.497 | 0.005 | 0.858 |
| 40 | 14.011 | 1.109 | 0.419 | 0.060 | 0.870 |
| 60 | 20.186 | 1.759 | 0.430 | 0.105 | 0.851 |
| 80 | 29.376 | 1.533 | 0.372 | 0.092 | 0.851 |
| 100 | 35.219 | 1.636 | 0.340 | 0.098 | 0.850 |
| 120 | 40.058 | 1.889 | 0.251 | 0.093 | 0.886 |
| Temperature/°C | τ0/Pa | Standard Error | μ/Pa∙s | Standard Error | R2 |
|---|---|---|---|---|---|
| 20 | 8.342 | 0.419 | 0.622 | 0.014 | 0.995 |
| 40 | 7.470 | 0.157 | 0.543 | 0.005 | 0.999 |
| 60 | 6.926 | 0.331 | 0.389 | 0.011 | 0.993 |
| 80 | 4.885 | 0.321 | 0.342 | 0.010 | 0.992 |
| 100 | 1.950 | 0.617 | 0.263 | 0.020 | 0.951 |
| 120 | 0.737 | 0.375 | 0.208 | 0.012 | 0.970 |
| Variables | Values |
|---|---|
| Annulus Length, L (m) | 10 |
| Casing Pipe diameter, D0 (mm) | 244.5 |
| Hole diameter, D1 (mm) | 311.1 |
| Angle of inclination, θ1 (deg) | 90 |
| Displacing inlet velocity, v (m/s) | 0.5, 0.6, 0.7, 0.8, 0.9 |
| Degree of casing centralization, £ (%) | 30, 50, 66.7, 85, 100 |
| Density difference, ∆ρ (g/cm3) | 0.3, 0.4, 0.5, 0.6, 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Zhang, J.; Liu, D.; Ju, G.; Sun, X. Impact of Temperature on Cement Displacement Efficiency: Analysis of Velocity, Centralization, and Density Differences. Processes 2024, 12, 2923. https://doi.org/10.3390/pr12122923
Tang X, Zhang J, Liu D, Ju G, Sun X. Impact of Temperature on Cement Displacement Efficiency: Analysis of Velocity, Centralization, and Density Differences. Processes. 2024; 12(12):2923. https://doi.org/10.3390/pr12122923
Chicago/Turabian StyleTang, Xiaowei, Jian Zhang, Dewei Liu, Guoshuai Ju, and Xiaofeng Sun. 2024. "Impact of Temperature on Cement Displacement Efficiency: Analysis of Velocity, Centralization, and Density Differences" Processes 12, no. 12: 2923. https://doi.org/10.3390/pr12122923
APA StyleTang, X., Zhang, J., Liu, D., Ju, G., & Sun, X. (2024). Impact of Temperature on Cement Displacement Efficiency: Analysis of Velocity, Centralization, and Density Differences. Processes, 12(12), 2923. https://doi.org/10.3390/pr12122923






