Deep Reinforcement Learning-Based Robotic Puncturing Path Planning of Flexible Needle

Abstract

The path planning of flexible needles in robotic puncturing presents challenges such as limited model accuracy and poor real-time performance, which affect both efficiency and accuracy in complex medical scenarios. To address these issues, this paper proposes a deep reinforcement learning-based path planning method for flexible needles in robotic puncturing. Firstly, we introduce a unicycle model to describe needle motion and design a hierarchical model to simulate layered tissue interactions with the needle. The forces exerted by tissues at different positions on the flexible needle are considered, achieving a combination of kinematic and mechanical models. Secondly, a deep reinforcement learning framework is built, integrating obstacle avoidance and target attraction to optimize path planning. The design of state features, the action space, and the reward function is tailored to enhance the model’s decision-making capabilities. Moreover, we incorporate a retraction mechanism to bolster the system’s adaptability and robustness in the dynamic context of surgical procedures. Finally, laparotomy simulation results validate the proposed method’s effectiveness and generalizability, demonstrating its superiority over current state-of-the-art techniques in robotic puncturing.

1. Introduction

In minimally invasive surgery, puncture needles are essential tools for sampling and injection therapies, primarily available in two types, namely rigid and flexible. Flexible needles, which can navigate around obstacles such as nerves, blood vessels, and bones, offer significant clinical benefits by reducing trauma and allowing for adaptable insertion paths. As a result, they have garnered considerable attention in medical engineering research [1]. Traditional path planning relies heavily on a physician’s expertise, which introduces variability. An automated and precise approach to path planning can reduce the physician’s workload, minimize surgical risks, and improve both the success and efficiency of procedures. This need becomes even more pressing with the integration of robotic systems in the operating room, as these systems must execute punctures with high precision and autonomy in real time under complex and dynamic conditions. Robust path planning is crucial for ensuring safe needle insertion while avoiding damage to sensitive anatomical structures, making accurate and adaptive planning vital for the success of such procedures.

The path planning of flexible needles includes rule-based, mathematical optimization, and simulation methods. Rule-based methods are simple to implement but struggle to handle complex situations [2]. Mathematical optimization methods can find the global optimum in complex environments but require accurate models and a large number of computations, and they are not suitable for real-time computation. Simulation methods are used for algorithm training and validation, but they may differ from the actual surgical environment, affecting accuracy. With the development of artificial intelligence (AI) algorithms, reinforcement learning (RL) methods have been proposed for path planning. However, they face the problems of the curse of dimensionality, poor convergence, and poor generalization, although no data need to be provided in advance [3].

This paper presents an unicycle model [4] as the kinematic basis for the flexible needle, designs a hierarchical model for human tissue representation, combines the kinematic and mechanical models, and finally proposes a deep reinforcement learning-based flexible needle path planning method in robotic puncturing. By setting the obstacle repulsion and endpoint gravitational model, the reinforcement learning model is designed. The state features, action space, and reward function are defined. The retraction action is designed to improve the efficiency of path planning and the adaptability and robustness in a complex environment. The DQN algorithm is designed for agent training. The effectiveness and generalization of the method are verified by parameter sensitivity analysis and simulation experiments.

2. Related Work

There are various path planning methods for flexible needle puncturing, among which the rapidly exploring random tree (RRT) and its improved versions have been widely studied. Zhao et al. [5] proposed the Reachability and Greedy Heuristic-Guided RRT algorithm (RGHG-RRT), which improves the computational speed and searching capability. Xiong et al. [6] presented an improved RRT algorithm (I-RRT), which solves the path continuity and physical constraint issues. Hon et al. [7] introduced the RRT algorithm to simulate the real puncture environment by considering anatomical hindrances and 3D scenes. Zhang et al. [8] further improved the RRT algorithm to optimize the path planning by 3D coordinate transformation and artificial potential field cost.

Cai et al. [9] proposed a simplified particle swarm optimization (PSO) algorithm for the path planning of flexible needle puncturing. This approach adjusts the center angle of the arc and the needle’s rotation angle to make the path conform to a circular arc kinematic model. It easily adapts to changes in boundary conditions, allowing for simple and efficient path planning, with errors controlled to the millimeter level. Tan et al. [10] proposed an improved PSO algorithm with an adaptive parameter adjustment mechanism to establish a needle motion model and a three-dimensional space puncture path transformation model through a multi-objective function to optimize the path length and collision detection. The needle motion model and the transformation model of the 3D spatial puncture path were established. The path length, error, and collision detection were optimized by a multi-objective function to achieve a faster planning speed and higher accuracy. Tan et al. [11] further proposed a bee foraging learning-based PSO algorithm (BFL-PSO) and a 3D needle retraction strategy. This approach shortens the puncture distance, improves accuracy, and significantly reduces both paths and errors, demonstrating good adaptability to multi-objective path planning.

With the rapid development of AI algorithms, Tan et al. [12], Lee et al. [13], and Hu et al. [14] proposed path planning methods based on the Markov decision process (MDP), deep Q-network (DQN), and double deep Q-network (DDQN), respectively. These approaches aim to improve penetration path planning for flexible needles in 2D and 3D environments while enhancing path optimization, safety, and robustness.

Compared with traditional path planning methods, deep reinforcement learning methods have the following metrics:

• Dealing with high-dimensional state and action spaces;
• Automatically extracting features;
• Learning complex policies;
• Improving environment perception and decision-making capabilities;
• Better interpretability.

However, there are several challenges with this approach, such as enhancing goal planning and exploration capabilities.

3. Path Planning of Flexible Needle in Robotic Puncturing

This section describes and transforms the flexible needle path planning in robotic puncturing, including corresponding kinematic and mathematical models.

3.1. Definition of the Internal Human Environment

The surgical environment definition describes the physical parameters and constraints in path planning within the internal human environment. In laparotomy, the surgical environment definition mainly includes the human body space scale size, obstacle situation, lesion target location, and tissue layering model.

The length, width, and height of the abdomen of an adult is about 55–75 cm, 20–30 cm, and 15–25 cm, respectively. However, the exact values of surgery vary according to individual height and body size [15]. The size of the organs involved in abdominal puncture is usually 10~15 cm. The length of the space can be appropriately reduced when setting the space to improve the learning efficiency of the agent, while the width and height of the space can be appropriately increased so that the agent can fully utilize its exploration ability.

3.1.1. Obstacle Situation

Obstacle situations refer to potential obstacles that may be encountered in the puncture path, such as other organs, blood vessels, and similar structures. These obstacles may block or interfere with the puncture path and affect the smooth operation. Therefore, the location, distribution, and shape of the obstacles need to be considered when defining the environment, as irregularly shaped obstacles, such as curved blood vessels or non-uniform tissue structures, can complicate the boundaries and increase the difficulty of path planning. Meanwhile, a reasonable reward function needs to be designed to encourage the agent to avoid these obstacles and find the optimal path, taking into account the complexity introduced by their shapes.

3.1.2. Lesion Target Location

The lesion target location pinpoints the precise coordinates, dimensions, and contours of the lesion area within the abdominal region, with its precise definition being pivotal to the agent’s decision-making process. Consequently, the establishment of a well-calibrated reward function is essential to direct the agent towards the target area effectively.

In this paper, to facilitate a comprehensive exploration of the internal anatomy of the human body, the lesion target is delineated as a spherical point situated at the base of the abdominal cavity. Furthermore, the surrounding region is also designated as part of the lesion target location. This strategic configuration enables the agent to execute puncturing or sampling procedures with enhanced efficacy, ensuring that the agent’s actions are not only targeted but also optimally positioned for maximum impact.

3.1.3. Hierarchical Model of the Human Body

To achieve a higher fidelity in simulating real-world scenarios, this paper introduces a streamlined layered model of the human body, encompassing the skin, subcutaneous tissue and muscle, and nerve tissue layers. Each stratum is designed to represent tissues of analogous density, thereby capturing the fundamental characteristics of tissue interaction during the flexible needle puncture procedure.

Given the variance in density across these layers, the flexible needle’s trajectory will exhibit distinct motion radii as it navigates through each stratum. This nuanced approach allows for a more realistic portrayal of needle behavior, accounting for the physiological nuances of the human body’s layered structure.

3.2. Modeling of the Flexible Needle Puncture Problem

In laparotomy, the prime goal is to ensure that the puncture needle reaches the target location accurately. This requires precise positioning of the patient, precise control of the procedure, and protection of the surrounding tissues [16]. An algorithm that computes an optimal path for the puncture needle should be designed to reach the target location safely and accurately, given the structure of the patient’s abdomen and the target location.

3.2.1. Kinematic Modeling

During the puncture process, the motion trajectory produced by the flexible needle is influenced by the force interaction between the needle and the tissue. Currently, related kinematic models have been proposed, including the unicycle model [4], bicycle model [17], cantilever beam model [18], and spring–beam–damper model [19]. To accurately describe the flexible needle deflection with fewer parameters to reduce the decision variables in the reinforcement learning model and thus improve the learning efficiency [20], this paper introduces the unicycle model to describe the trajectory of the flexible needle.

In this unicycle model, it is defined that the flexible needle is rigidly attached in the axial direction and that the tissue to be punctured is isotropic, homogeneous, and non-deforming. As shown in Figure 1, after the tip of the needle is inserted into human tissue, the tip is subjected to pressure perpendicular to the beveled surface of the needle tip due to the compression of the tissue. The asymmetric forces on the beveled surface and the back of the needle tip change the trajectory of the needle. Meanwhile, the radius of the needle’s trajectory remains constant, and the insertion speed has little effect on the curvature of the flexible needle.

In a three-dimensional human body space, the trajectory of the needle is shown in Figure 2. Assume that the forward speed of the needle is denoted as ν and the rotational speed of the needle in the axial direction is denoted as ω. The local coordinate system of the needle tip is denoted as ${\mathsf{\Phi }}_{\mathrm{p}}$ and the world coordinate system is denoted as ${\Phi }_w$. The position and state of the needle tip in the world coordinate system are represented as

$$\begin{array}{c}{L}_w={\left[x,y,z,\alpha ,\beta ,\gamma \right]}^T\end{array}$$

(1)

where α, β, and γ are the rotation angles around the x, y, and z axes of the world coordinate system so that the velocity of the needle in the world coordinate system can be expressed as

$$\begin{array}{c}{V}_w=L_w^{\prime }\end{array}$$

(2)

The trajectory of a flexible needle with a slanted tip has a constant radius in three dimensions. The velocity of the tip in the local coordinate system ${\Phi }_p$ is formulated as

$$\begin{array}{c}{V}_p=v\cdot {\left[0,0,1,k,0,0\right]}^T+w\cdot {\left[0,0,0,0,0,1\right]}^T\end{array}$$

(3)

The relationship between the local coordinate system of the needle tip and the world coordinate system can be expressed by a velocity transformation equation.

$$\begin{array}{c}{V}_p=Q{V}_w\end{array}$$

(4)

where Q is the transformation matrix between the local coordinate system of the needle tip and the world coordinate system. According to this velocity transformation equation, the kinematic model of the needle can be obtained as

$$\begin{array}{c}\dot{L}=\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\\ \dot{\alpha }\\ \dot{\beta }\\ \dot{\gamma }\end{array}\right]=\left[\begin{array}{cc}\mathrm{s}\mathrm{i}\mathrm{n}\beta & 0\\ -\mathrm{c}\mathrm{o}\mathrm{s}\beta \mathrm{s}\mathrm{i}\mathrm{n}\alpha & 0\\ \mathrm{c}\mathrm{o}\mathrm{s}\beta \mathrm{c}\mathrm{o}\mathrm{s}\alpha & 0\\ k\mathrm{c}\mathrm{o}\mathrm{s}\gamma \mathrm{s}\mathrm{e}\mathrm{c}\beta & 0\\ k\mathrm{s}\mathrm{i}\mathrm{n}\gamma & 0\\ -k\mathrm{c}\mathrm{o}\mathrm{s}\gamma \mathrm{t}\mathrm{a}\mathrm{n}\beta & 1\end{array}\right]·\left[\begin{array}{c}v\\ w\end{array}\right]\end{array}$$

(5)

Since the puncture trajectory of the flexible needle is independent of the puncture speed and rotation angle, the time variable can be separated from the control variables and the system model can be transformed into

$$\begin{array}{c}\dot{L}=\left[\begin{array}{cc}\mathrm{s}\mathrm{i}\mathrm{n}\beta & 0\\ -\mathrm{c}\mathrm{o}\mathrm{s}\beta \mathrm{s}\mathrm{i}\mathrm{n}\alpha & 0\\ \mathrm{c}\mathrm{o}\mathrm{s}\beta \mathrm{c}\mathrm{o}\mathrm{s}\alpha & 0\\ k\mathrm{c}\mathrm{o}\mathrm{s}\gamma \mathrm{s}\mathrm{e}\mathrm{c}\beta & 0\\ k\mathrm{s}\mathrm{i}\mathrm{n}\gamma & 0\\ -k\mathrm{c}\mathrm{o}\mathrm{s}\gamma \mathrm{t}\mathrm{a}\mathrm{n}\beta & 1\end{array}\right]·\left[\begin{array}{c}s\\ \theta \end{array}\right]\end{array}$$

(6)

In Equation (6), the tip advancement distance s and the rotation angle θ can be used as the control variables of the tip movement. With the stop-and-go strategy, the puncture trajectory consists of n segments of paths in $\left\{\left[s_1, {\theta }_1\right]\cdot \left[s_2, {\theta }_2\right], \dots , \left[s_n, {\theta }_n\right]\right\}$, where $\left[s_1, {\theta }_1\right]$ denotes the advancement distance of the first segment of the puncture path and the rotation angle.

3.2.2. Mathematical Path Planning Model

To evaluate the planned path and find the optimal solution, a mathematical model is established based on this planning process.

Table 1. Notations and implications in path planning model.

Notations		Implications
Path Information	$n$	Number of path planning
	$P=\left\{P_1,P_2,\dots ,P_n\right\}$	Pathway set
	$P_i$	$i$th path
	$L_i$	$\mathrm{Length} \mathrm{of} \mathrm{path} P_i$
	$T_i$	$\mathrm{Elapsed} \mathrm{time} \mathrm{for} \mathrm{path} P_i$
	$l_i$	$\mathrm{Number} \mathrm{of} \mathrm{arc} \mathrm{segments} \mathrm{of} \mathrm{path} P_i$
	$D_i$	$\mathrm{Distance} \mathrm{of} \mathrm{endpoint} \mathrm{of} \mathrm{path} P_i$ from target point
	$R_i$	$\mathrm{Total} \mathrm{reward} \mathrm{for} \mathrm{path} P_i$
Obstacle Information	$m$	Number of obstacles
	$O=(O_1,O_2,\cdots ,O_m)$	Obstacle course
	$O_j$	$j$th obstacle
	$R_j$	$\mathrm{Radius} \mathrm{of} \mathrm{obstacle} O_j$
	$d_{i,j}$	$\mathrm{Distance} \mathrm{of} \mathrm{path} P_i$$\mathrm{from} \mathrm{obstacle} O_j$
	$J_{i,j}=\{0,1\}$	$\mathrm{Whether} \mathrm{path} P_i$$\mathrm{collides} \mathrm{with} \mathrm{obstacle} O_j$
Other Information	α	Precision factor
	β	Length factor
	γ	Obstacle avoidance factor
	λ	Time factor

provides an overview of the parameters, which define path information, obstacle information, and other related information.

The objective function is two-fold. The first aspect is defined to consider the path length, the deviation between the target point and the endpoint of the path, the collision obstacle indication, and the planning time. The optimal path is obtained based on computing the sum by multiplying it with the product of the length coefficient, the accuracy coefficient, the obstacle avoidance coefficient, and the time coefficient. The first objective function is formulated as

$$\begin{array}{c}\begin{array}{c}\left.F=\mathrm{m}\mathrm{i}\mathrm{n}\left\{f\right(P_1),f(P_2),\cdots ,f(P_n)\right\}\\ which f\left(P_i\right)=\alpha D_i+\beta L_i+\gamma {\displaystyle \frac{1}{d_{i,j}}}+\lambda T_i\end{array}\end{array}$$

(7)

The second aspect of the objective function is to directly find the path that minimizes the punishment (i.e., maximizes the reward) based on the results of reinforcement learning with a reasonable reward function setting, and the second objective function is formulated as

$$\begin{array}{c}\left.R=\mathrm{m}\mathrm{a}\mathrm{x}\{R_1,R_2,\cdots ,R_n\right\}\end{array}$$

(8)

$$s.t.:R_i=\left\{\begin{array}{c}0\\ R_i\end{array}\right.\begin{array}{c}{J}_{i,j}=1\\ J_{i,j}=0\end{array},\forall i,j$$

(9)

$$\begin{array}{c}{D}_i<d, \forall i\end{array}$$

(10)

$$l_i\le x,\forall i$$

(11)

$$\alpha +\beta +\gamma +\lambda =1$$

(12)

Constraint (9) indicates whether the flexible needle collides with obstacles. And if no collision occurs, then the normal calculation is rewarded. Constraint (10) indicates that the end position of the path is considered to have reached the endpoint when the distance from the target point position is d. Constraint (11) indicates that the number of arc segments of the path should not be more than x. It restricts the number of rotations of the flexible needle and filters out the excessively long paths that are not in line with the optimal characteristics to improve search efficiency.

4. Deep Reinforcement Learning-Based Path Planning

This section describes the overall solution of deep reinforcement learning-based flexible needle path planning in robotic puncturing. The implementation framework, key technologies, and training processes are involved.

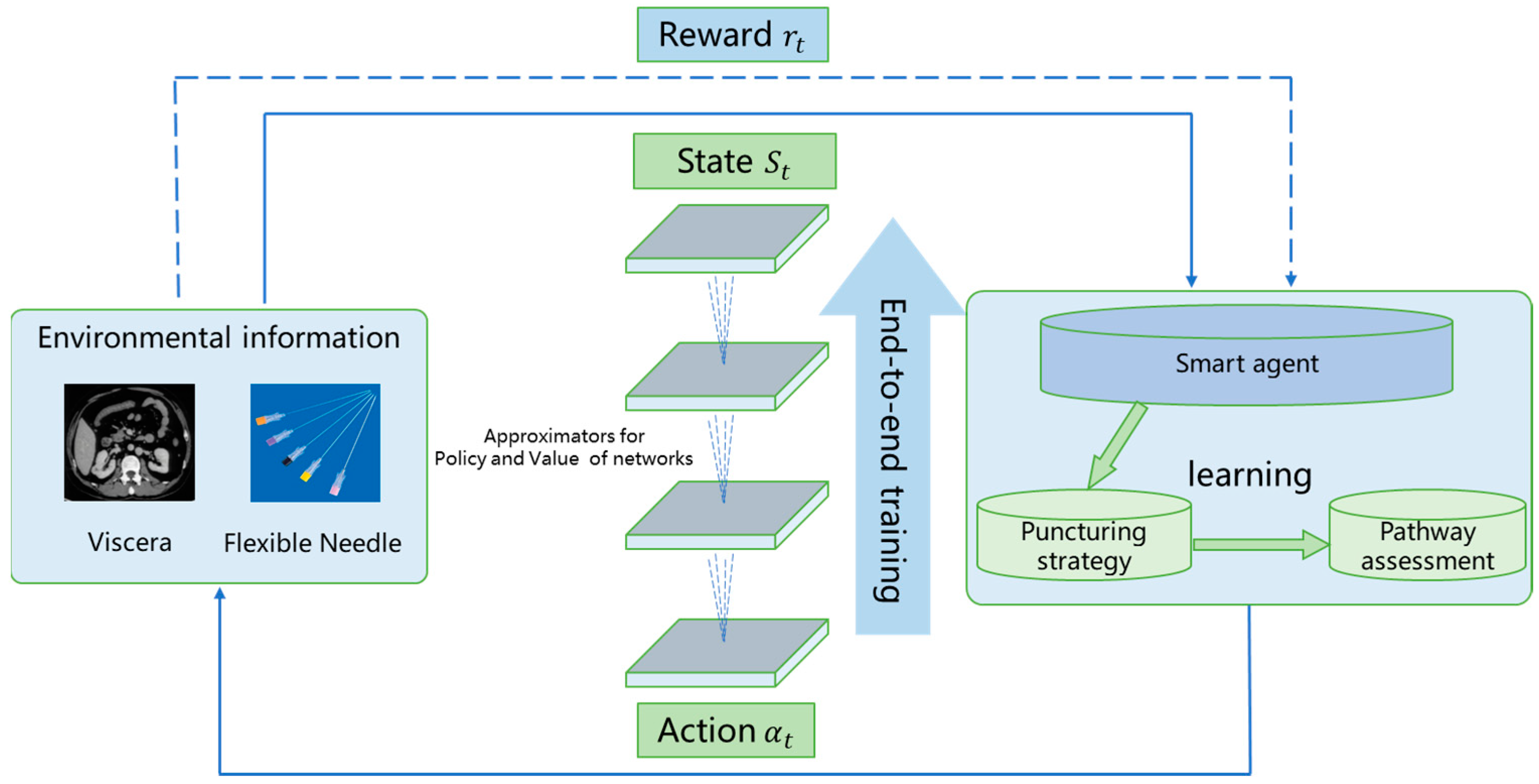
4.1. Framework of DRL-Based Path Planning

Figure 3 shows an end-to-end deep reinforcement learning-based robotic puncturing path planning of a flexible needle [21], which mainly includes the steps of environment perception, state representation, action space definition, reinforcement learning modeling, agent–environment interaction, path planning and execution, and result evaluation and feedback.

Firstly, sensors are used to obtain relevant information in the surgical environment, including tissue structure and the position of the flexible needle. These data are used to construct the environment state for the agent to make decisions. The environmental data are converted into states that can be understood by the deep reinforcement learning model, including the position, angle, speed, and obstacle information of the needle tip, and defines the space of actions that can be performed by the agent, such as the movement and rotation of the needle.

Secondly, a neural network is used to construct the reinforcement learning model, including the policy network and value network [22]. The policy network generates the action strategy, and the value network estimates the state value and gives the action value. The agent selects the action according to the current state and policy, interacts with the simulated or actual surgical environment, obtains new state and reward information, and updates the model parameters. Through continuous training and optimization, the agent gradually learns how to select the optimal action and find a safe, accurate, and effective path.

Finally, the path generated by the agent is evaluated to determine if it meets the preset metrics for safety and efficiency. If the path does not meet the requirements, feedback is provided to the reinforcement learning model for further training and optimization to improve the accuracy and reliability of path planning.

4.2. Reinforcement Learning Modeling

After defining the human body environment, the next step is to establish the reinforcement learning model for the flexible needle path planning, which includes state features, the action space, and the reward function.

4.2.1. State Features

State features are crucial to perceive the environment in reinforcement learning, which directly impacts learning efficiency and performance. In the path planning of flexible needle puncturing (PPFNP), state features are primarily defined based on the following aspects:

• Position information: this includes the absolute and relative position of the needle tip and the degree of bending of the needle to ensure that the needle can accurately reach the target position;
• Tissue information: this includes the density and hardness information of the surrounding tissues to ensure that no important tissues are damaged during the puncture process;
• Obstacle information: this identifies the location and size of obstacles (e.g., other organs, blood vessels) in the path to avoid collision.

The following principles need to be followed when designing state features:

• Able to describe the features and variations in the puncture environment, including global and local features;
• Applicable to puncture problems in different environments, contained within the state space;
• Provides a numerical representation of the information about the agent to enable the description of different problems in a uniform manner through formalization.

The puncturing path planning process requires a comprehensive consideration of state features such as needle position, posture, and the number of agent decisions, as shown in

Table 2. State variables and features.

Notations	Implications
$x$	$\mathrm{Needle} \mathrm{coordinates} \mathrm{in} x$-axis direction
y	$\mathrm{Needle} \mathrm{coordinates} \mathrm{in} y$-axis direction
$z$	$\mathrm{Needle} \mathrm{coordinates} \mathrm{in} z$-axis direction
$\mathrm{d}x=x_2-x$	$\mathrm{Projection} \mathrm{of} \mathrm{the} \mathrm{straight}-\mathrm{line} \mathrm{distance} \mathrm{of} \mathrm{the} \mathrm{needle} \mathrm{from} \mathrm{the} \mathrm{target} \mathrm{point} \mathrm{in} \mathrm{the} x$-axis direction
$\mathrm{d}y=y_2-y$	$\mathrm{Projection} \mathrm{of} \mathrm{the} \mathrm{straight}-\mathrm{line} \mathrm{distance} \mathrm{of} \mathrm{the} \mathrm{needle} \mathrm{from} \mathrm{the} \mathrm{target} \mathrm{point} \mathrm{in} \mathrm{the} y$-axis direction
$\mathrm{d}z=z_2-z$	$\mathrm{Projection} \mathrm{of} \mathrm{the} \mathrm{straight}-\mathrm{line} \mathrm{distance} \mathrm{of} \mathrm{the} \mathrm{needle} \mathrm{from} \mathrm{the} \mathrm{target} \mathrm{point} \mathrm{in} \mathrm{the} z$-axis direction
$d_{-}cto=\left|\mathrm{x}-x_0\right|+\left|y-y_0\right|+|z-z_0|$	Manhattan distance between the current position of the needle and its initial position
$d_{-}ctt=\left|\mathrm{x}-x_2\right|+\left|y-y_2\right|+|z-z_2|$	Manhattan distance between the current state of the needle and the target point
$d_{-}ott=\left|x_2-x_0\right|+\left|y_2-y_0\right|+|z_2-z_0|$	Manhattan distance of the initial point from the target point
$d_{-}cts=\left|\mathrm{x}-x_1\right|+\left|y-y_1\right|+|z-z_1|$	Manhattan distance of the needle from the obstacle
$n$	Number of needle rotations

.

In Table 2, $\left(x_0, y_0, z_0\right),\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)$ represent the position coordinates of the initial point, obstacle, and target point in the 3D space, respectively. Therefore, a total of 12 state variables are used in this paper to represent the state features of the PPFNP problem.

$$\begin{array}{c}S=\left\{x, y, z, dx, dy, dz, d_{c}to, d_{c}tt, d_{o}tt, d_{c}ts, n, step\right\}\end{array}$$

(13)

Agents can make action decisions by sensing these features during interaction with the environment.

4.2.2. Action Space

The action space delineates the comprehensive array of actions that an intelligent agent is capable of executing within its operational environment. In the context of flexible needle path planning, the action space is meticulously crafted around two pivotal dimensions.

Feed action: This aspect pertains to the depth of needle insertion. By meticulously adjusting the feed length, the agent can effectively alter the needle tip’s position without necessitating a change in the needle’s base position. This capability is crucial for navigating through the intricacies of the tissue with precision.

Rotation action: Given the complexity of tissue structures and the imperative to circumvent obstacles, the agent must possess the agility to manipulate the needle’s rotation. This is adeptly managed by defining both the rotation angle and the axis of rotation, thereby enabling the agent to navigate around obstacles and adapt to the tissue’s contours.

Consequently, this paper establishes the action space for the flexible needle as a strategic amalgamation of these two critical actions, providing the agent with the requisite flexibility and control to effectively plan and execute needle paths. It can be formulated as follows:

$$\begin{array}{c}A=\left\{s, \theta \right\}\end{array}$$

(14)

4.2.3. Reward Function

Rewards in our system are meticulously divided into two distinct categories, the single-step reward and multiple rewards. Single-step rewards are promptly dispensed following each individual action, serving as an immediate reflection of the quality of the action taken. Conversely, multiple rewards are allocated upon the task’s completion, reflecting an assessment of the overall task execution. In addressing the PPFNP challenge, the design of the reward function demands a thorough consideration of both the task’s objectives and its constraints. This paper introduces an innovative composite reward structure, prioritizing single-step rewards to drive immediate quality action while incorporating multiple rewards to provide a holistic evaluation and to ensure that the agent strategically plans the optimal path.

The single-step reward structure encompasses the following three key components:

• Tissue damage: negative rewards are imposed for any tissue damage incurred during needle insertions or rotations, thereby discouraging harmful maneuvers.
• Proximity to target: positive rewards are awarded as the needle draws nearer to the target, incentivizing accurate navigation.
• Distance from obstacles: negative rewards are imposed when the agent ventures too near an obstacle, promoting obstacle avoidance.

The round rewards, on the other hand, consist of the following:

• Success rate: positive rewards are granted for successfully reaching the target location, reinforcing successful completion of the task.
• Obstacle avoidance: negative rewards are applied for any collisions with obstacles or boundary infringements within the exploration space, emphasizing the importance of safe navigation.
• Path efficiency: negative rewards are given for reaching the target via a convoluted path, encouraging the adoption of more direct routes.

By judiciously combining single-step and round rewards, the agent receives clear feedback after each action and at the end of each round. This feedback loop facilitates the gradual refinement of path planning behaviors, leading to the mastery of a more efficient, stable, and robust path planning strategy. To effectively tackle the PPFNP problem, this paper has meticulously defined specific reward functions, as detailed in

Table 3. Composite reward functions for the PPFNP problem.

Classes	Reward Functions	Implications
Single-step reward	$r_{-}s$	Negative reward for damage to normal tissue per step
	$r_{-}c$	Negative reward per needle rotation
	${r_{-}n}_{-}o=\left\{\begin{array}{c}0 , { d}_{-}cto>d_{-}o\\ {\displaystyle \frac{d_{-}o}{d_{-}cto}} , { d}_{-}cto<d_{-}o\end{array}\right.$	Negative reward for approaching an obstacle
	${r_{-}n}_{-}t=\left\{\begin{array}{c}{\displaystyle \frac{d_{-}ott}{d_{-}ctt}}\cdot d_{-}j , { d}_{-}ctt>d_{-}t\\ d_{-}c\mathrm{to}\cdot d_{-}j , { d}_{-}ctt<d_{-}t\end{array}\right.$	Positive rewards for approaching the target position
Multiple reward	$r_{-}o$	Negative reward for collision with obstacles
	$r_{-}b$	Negative reward to reach space boundaries
	$r_{-}w$	Negative reward for exceeding the worst step
	$r_{-}t$	Positive rewards for reaching the target location

.

The composite reward functions for the PPFNP contain a total of two kinds of positive rewards and six kinds of negative rewards. Regarding ${r_{-}n}_{-}o$ and ${r_{-}n}_{-}t$, this paper also designs an obstacle repulsion model and an endpoint gravitational model, which are shown in Figure 4, respectively.

As depicted in Figure 4, the vicinity of the obstacle is demarcated into two distinct regions, a no-repulsion zone and a repulsion zone. The no-repulsion zone signifies an area where the agent remains unaffected by the obstacle’s repulsive force. Conversely, within the repulsion zone, the agent is subjected to a forceful repulsion emanating from the obstacle as it ventures into this space. The agent’s movement trajectory, as delineated in the figure, is influenced by a dual force dynamic, namely the repulsive force exerted by the obstacle and the gravitational pull of the target point, particularly when the agent is within the repulsion zone. Furthermore, the intensity of the repulsive force is not uniform throughout the repulsion zone; it escalates as the agent approaches closer to the obstacle. The direction of this force is consistently radially outward from the obstacle’s center, directed towards the agent.

As depicted in Figure 4, the vicinity of the target point is demarcated into two distinct zones, the weak gravity region and the strong gravity region. The strong gravity region, which is in closer proximity to the target point, exerts a more potent gravitational pull on the agent, effectively encouraging a swift and direct approach towards the target. Conversely, the weak gravity region, situated at a greater distance from the target point, applies a less intense gravitational force. This subtler influence fosters a more comprehensive exploration of the surrounding environment.

In both regions, the gravitational force escalates as the agent progresses along a direct path towards the target point, thereby discouraging aimless wandering. The gravitational force is consistently oriented from the agent towards the target point, ensuring that the agent’s trajectory is both goal-oriented and efficient. This strategic distribution of gravitational forces facilitates a balance between rapid target acquisition and thorough environmental scanning.

In order to reduce the useless exploration of the flexible needle agent and make it reach the target position as soon as possible, this paper adds $d_{-}j$ in ${r_{-}n}_{-}t$, which indicates whether the current action is close to the target position or not, and $d_{-}j$ is formulated as

$$\begin{array}{c}{d}_{-}j=d_{-}ctt-\left(\left|x-x_2\right|+\left|y-y_2\right|+\left|z-z_2\right|\right)\end{array}$$

(15)

When the result of $d_{-}j$ is greater than 0, it means that the current action of the agent is close to the target position and should be rewarded positively. When the result of $d_{-}j$ is less than 0, it means that the current action of the agent is far from the target position and should be rewarded negatively.

Once the single-step and multiple rewards have been meticulously established, it becomes imperative to categorize the planned path and compute the cumulative reward. This cumulative reward is a reflection of the total reward amassed by the agent throughout the learning journey. Given the medical surgical context of this problem, the path classification should prioritize precision and take into account several critical factors.

Endpoint deviation: the classification must ascertain whether the discrepancy between the path’s endpoint and the target point adheres to the stipulated accuracy standards.

Obstacle collision: it is essential to evaluate whether the path intersects with any critical obstacles, such as vital organs or blood vessels, which could compromise patient safety.

Path length: the classification should also consider whether the path’s length falls within an acceptable range, ensuring that it does not surpass the maximum permissible length.

Model space adherence: lastly, it is crucial to verify that the agent remains within the designated model space during the path planning process, maintaining procedural integrity.

By meticulously considering these factors, the path classification system can effectively gauge the quality of the agent’s learning outcomes, ensuring that the planned paths are not only accurate but also safe and efficient within the constraints of medical surgery. Based on these criteria, this paper defines the cumulative reward obtained at the end of path planning as follows:

Among the five types of rewards outlined in

Table 4. Cumulative rewards for the PPFNP problem.

Cumulative Reward	Implications
$R_{-}n=r_{-}s+r_{-}c+{r_{-}n}_{-}o+{r_{-}n}_{-}t$	Normal puncture procedure
$R_{-}o=R_{-}n+r_{-}o$	Collision with obstacles
$R_{-}b=R_{-}n+r_{-}b$	Outside the model boundary
$R_{-}t=R_{-}n+r_{-}t$	Reach target position
$R_{-}w=R_{-}n+r_{-}t+r_{-}w$	Exceeding the worst possible step size

, all except the normal puncture process are designed to trigger the termination of path planning. However, positive reward feedback is exclusively granted when the agent successfully navigates to the target location. The agent’s learning is contingent upon the diverse reward feedback it encounters, which guides its behavior towards planning paths that yield higher cumulative rewards.

Through this feedback-driven learning process, the agent gradually refines its path planning strategies, prioritizing those that not only meet the necessary criteria but also maximize the total reward. This approach ensures that the agent’s learning is both goal-oriented and reward-driven, ultimately leading to the selection of optimal paths that align with the desired outcomes.

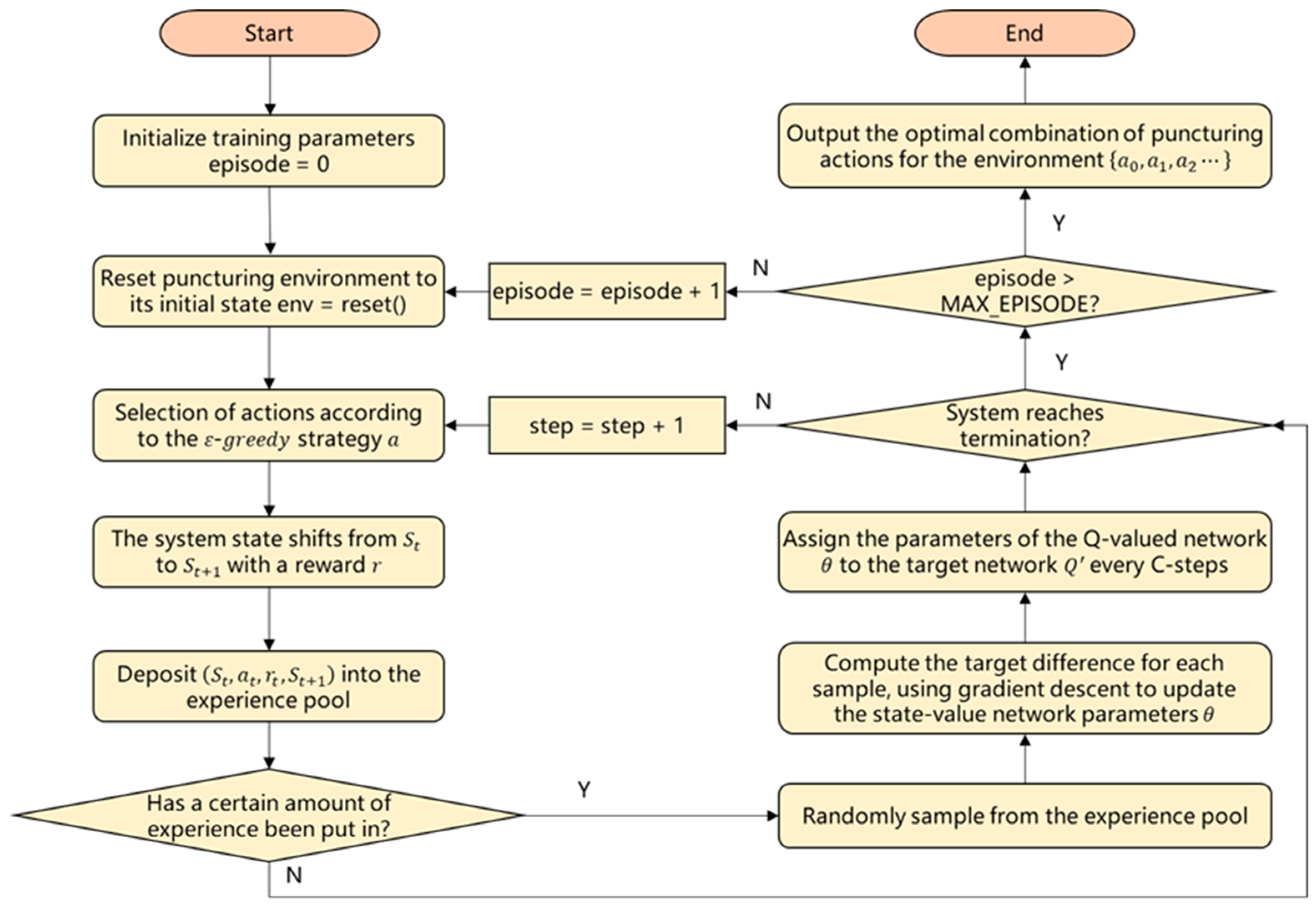
4.3. Algorithms for Agent Training

Having established the exploration environment and formulated the reinforcement learning model, the choice of an apt reinforcement learning algorithm becomes a pivotal decision. In the realm of flexible needle puncture, the agent navigates within a three-dimensional space and encounters a multitude of intricate states, rendering conventional Q-learning methods infeasible due to their complexity.

The deep Q-network (DQN) emerges as an ideal candidate for tackling problems with discrete action spaces. Given that the flexible needle’s maneuverability is confined to two primary actions—feeding and rotating—these actions align seamlessly with the strengths of a DQN. This alignment enables the agent to effectively leverage DQN’s capabilities to navigate the complex state space and optimize its path planning, ensuring that the learning process is both efficient and effective.

4.3.1. DQN Algorithm

Upon initializing the network, the flexible needle agent employs an ε-greedy strategy to select a puncture action. This strategy adeptly marries a greedy approach with random exploration, ensuring that the agent balances the exploitation of known optimal actions with the discovery of new, potentially more effective strategies.

Upon executing the chosen action, the agent garners state and reward data, which serve as the foundation for learning. A time-differentiated objective function is meticulously computed to refine the Q-value function, while a loss function is concurrently calculated to fine-tune the Q-network’s parameters. This process nudges the parameters closer to their true values, enhancing the network’s predictive accuracy.

Every C training steps, the value network’s weights are meticulously copied to the target network, facilitating a systematic update process. This iterative cycle continues until the network achieves convergence or the pre-established number of training rounds is reached, ensuring that the learning process is both thorough and exhaustive.

The pseudocode encapsulating the DQN algorithm’s operational framework is presented in Algorithm 1, offering a clear, step-by-step guide to the agent’s learning journey.

Algorithm 1. DQN Algorithm
	Hyper-Parameter: experience pool capacity $N$, reward discount factor $\gamma$, delay step for target state-action value function update $C,\epsilon$ in the $\epsilon -greedy$
	Input: empty experience pool $D$, Initialize the state-action value function Q function with parameters θ
	Initialize the target state-action value function $\widehat{Q}$ using the parameter $\widehat{\theta }\leftarrow \theta$
1:	for episode = 0, 1, 2, …… do
2:	Initialize the environment and acquire observations $O_0$
3:	Initialization sequence $S_0=\left\{O_0\right\}$ and preprocess the sequence ${\varphi }_0=\varphi \left(S_0\right)$
4:	for t = 0, 1, 2, …… do
5:	Select a random action $A_t$ by probability $\epsilon$, otherwise select the action: $\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{A}_t=arg{max}_{a}Q(\varphi \left(S_t\right), a;\theta )$
6:	Perform action $A_t$ and obtain observation data $O_{t+1}$ and reward data $R_t$
7:	Set $D_t=1$ if the council is over, otherwise $D_t=0$
8:	Set $S_{t+1}=\{S_t, A_t, O_{t+1}\}$ and pre-processing ${\varphi }_{t+1}=\varphi \left(S_{t+1}\right)$
9:	Store the state transfer data $({\varphi }_t, A_t, R_t, D_t, {\varphi }_{t+1})$ into D
10:	Random sampling of small batches of state transfer data from D $({\varphi }_i, A_i, R_i, D_i, {\varphi }_i^{\prime })$
11:	If $D_i=0$, set $Y_i=R_i+\gamma {\mathrm{m}\mathrm{a}\mathrm{x}}_{a^{\prime }}\widehat{Q}({\varphi }_i^{\prime },a^{\prime };\widehat{\theta })$, otherwise, set $Y_i=R_i$
12:	Perform a gradient descent step on ${\left(Y_i-Q\left({\varphi }_i, A_i;\theta \right)\right)}^2$ for θ
13:	Synchronize the target network $\widehat{Q}$ every C steps
14:	Jump out of the loop if the segment ends
15:	end for
16:	end for

4.3.2. Training Process

As shown in Figure 5, a flowchart of the DQN algorithm is shown, and the specific steps for training a flexible needle intelligence with this algorithm are as follows:

First, to train the flexible needle agent, start by setting the following essential parameters:

• MEMORY_SIZE: the capacity of the experience pool, storing more data as the size increases.
• BATCH_SIZE: the number of experiences sampled for gradient computation.
• MAX_EPISODES: the limit on the episodes per training cycle, with each episode consisting of a series of actions.
• LEARNING_RATE: the step size for weight updates during learning.
• Q_UPDATE_FREQ: the frequency at which the target network’s parameters are updated from the prediction network.
• INITIAL_PARAMETERS: initialize the Q network’s parameters (θ), the target network’s parameters (θ^), and the reward discount factor (γ).

The agent performs the following processes in each puncture action decision stage:

Step 1: initialize the puncture environment to the original state, including the starting puncture point information, lesion target information, organ obstacle information, and flexible needle movement information.

Step 2: observe the current state features of the environment and the agent.

Step 3: use ε-greedy strategy to randomly select the puncture action a.

Step 4: The environment updates the state and feeds back rewards according to the action of the flexible needle agent. When a = 0, it indicates that the agent makes a needle-piercing movement and advances a distance along the current movement direction. When a = 1, it means that the agent performs a rotational movement, rotating a certain angle along the axial direction of the needle body to change the current movement direction of the needle.

Step 5: record the experience data $\left(s_t, a_t, r_t, s_{t+1}\right)$ and save them to the experience pool D.

Step 6: Randomly select BATCH_SIZE bars of empirical data in the experience pool D. Use the target network $\widehat{Q}$ to calculate the target value ${\widehat{y}}_i$.

$$\begin{array}{c}{\widehat{y}}_i=\left\{\begin{array}{c}{r}_i, s_{i+1} \mathrm{end} \mathrm{state}\\ r_i+\gamma \widehat{Q}\left(s_{i+1}, arg\underset{a}{\mathrm{m}\mathrm{a}\mathrm{x}}\widehat{Q}\left(s_{i+1}, a;\widehat{\theta }\right);\widehat{\theta }\right), \mathrm{Other} \mathrm{statuses}\end{array}\right.\end{array}$$

(16)

Step 7: use the value network to calculate the predicted value $y_i$.

$$\begin{array}{c}{y}_i=Q\left(s_i,a_i;\theta \right)\end{array}$$

(17)

Step 8: the Q network parameters θ are updated using ${\left({\widehat{y}}_i-y_i\right)}^2$ as the loss function, and gradient descent is performed on θ.

Step 9: the parameter θ of the Q network is assigned to the target network $\widehat{Q}$ every C steps.

Step 10: Determine whether the current turn is over or not using judgment criteria according to the reward function path planning termination condition judgment. If the termination condition is not reached, return to Step 2.

Step 11: determine whether the maximum number of cycles MAX_EPISODE has been reached—if not, return to Step 1 and continue to execute the next steps; otherwise, the cycle ends.

5. Simulation Experiment Results

The above tests for training algorithms were written based on Python 3.9.7. The hardware conditions for the experiments were a host computer with an Intel(R) Core(TM) i5-10400F CPU at 2.90 GHz and a personal computer with NVIDIA GeForce GTX 1650 4 GB. The parameter settings for constructing the experimental environment are detailed in

Table 5. Surgical environment and agent parameters.

Parameters	Settings
Spatial extent	50 × 50 × 50
Obstacle radius	3
Flexible needle curvature	0.0069
Number of intelligences per turn	1
Initial point position	[25, 25, 0]
Location of the target	[25, 25, 50]
Maximum number of steps	50
Maximum number of revolutions	5

. Based on these settings, the agent puncture environment was constructed. After setting up the experimental environment, the flexible needle agent underwent training, with training parameters specified in

Table 6. Flexible needle agent training parameters.

Parameters	Settings
Neural network layers	3
Number of neurons in the hidden layer	20
Number of neural networks	2
Hidden layer activation function	ReLU
Output layer activation function	linear function
Gradient descent optimizer	RMSProp
Discovery strategy	ε-greedy
Experience pool size	5000
Learning rate	[0.001, 0.005, 0.01, 0.05, 0.1]
Discount factor	[0.80, 0.85, 0.90, 0.95, 0.99]
Batch size	[16, 32, 64, 128, 256]
Q-target update frequency	[10, 20, 30, 40, 50]
Number of training iterations	8000

. Once the experimental environment was established and the training parameters were set, a sensitivity analysis of the relevant parameters was initiated.

5.1. Sensitivity Analysis

To identify the relevant parameters that can optimize the performance of the algorithm, this paper first conducts a parameter sensitivity analysis of the algorithm and compares and tests the key parameters that will affect the performance of the deep reinforcement learning algorithm, such as the learning rate [23], the discount factor [24], the batch size [25], and the target Q-network updating frequency [26]. The relevant parameters involved in the parameter sensitivity comparison experiment are shown below.

(1)

Learning rate

Experiments varying the learning rate to optimize reward convergence are detailed in Figure 6a. A rate of 0.05 offers stable but lower rewards, possibly indicating a local optimum. At 0.001, rewards are higher but more volatile. Analysis suggests a learning rate of 0.005 strikes a balance, providing stable, higher rewards with less fluctuation, making it the optimal choice.

(2)

Discount factor

This study assesses reward convergence across different discount factors to balance immediate and long-term rewards, as shown in Figure 6b. A discount factor of 0.9 starts with fluctuating rewards but eventually stabilizes at a high level, indicating that the agent initially struggles to learn the optimal puncture strategy but improves over time. Thus, a discount factor of 0.9 is found to be suitable for achieving stable total rewards.

(3)

Batch size

The batch size impacts the agent’s learning efficiency. Experiments, as seen in Figure 6c, show that small batch sizes lead to unstable reward curves with high volatility, while large ones lead to lower rewards due to suboptimal learning. Batch sizes of 64 and 128 provide stable, high-reward curves, indicating superior agent performance. Other sizes result in erratic curves and variable strategy effectiveness.

(4)

Update frequency of the target Q-network

A balanced update frequency is key to algorithm stability. This study examines reward acquisition across different frequencies, as shown in Figure 6d. Low frequencies lead to slow convergence, while high frequencies cause volatility. Findings indicate that an update frequency of 40 for the target Q-network stabilizes the reward curve, suggesting it is optimal for the agent to find effective puncture strategies.

5.2. DQN-Based Simulation Experiments for the PPFNP Problem

Once the reinforcement learning algorithm’s parameters were set, we executed targeted experiments for the PPFNP problem. In this setup, the human body’s internal environment is static, featuring a single target and obstacles to be circumvented during the 3D puncture from the starting point. The needle pauses and re-plans its path upon encountering boundaries or obstacles, persisting until it successfully hits the target.

To address this challenge, we simulated the human body’s interior, mapped obstacles and lesion targets, and developed a reinforcement learning model incorporating states, actions, and rewards. The DQN algorithm was selected to train the agent, with the results shown in Figure 7. By integrating digital twin technology, we created a virtual replica of the patient’s anatomy that updates in real time, allowing for dynamic simulations of the puncture process. This digital twin model enhances path planning accuracy by continuously reflecting the patient’s internal changes and providing real-time feedback for optimal decision-making.

Figure 7 illustrates the escalating reward trend in the flexible needle agent with increasing training rounds, signifying the agent’s improving performance and its ability to discover more rewarding puncture paths. Figure 7 offers a 3D view of the agent’s trajectory, where the red dot is the target, the larger spheres are obstacles, and the blue dots trace the agent’s planned path, with each dot representing a step in the agent’s decision-making process. The figure demonstrates the agent’s adept navigation around obstacles to reach the target. By integrating digital twin technology into this process, the system gains the ability to simulate complex, real-time scenarios more accurately, ensuring that the agent’s path is continuously optimized to account for patient-specific anatomical variations and dynamic changes.

To assess the DQN-based method’s efficacy and versatility in flexible needle puncture path planning, we performed experiments in simulated environments, comparing various methods across different scenarios. Our focus was on two primary scenarios.

5.2.1. Different Space Dimensions

Variations in individual characteristics, such as age and body shape, lead to variations in the size of abdominal space environments. To demonstrate the algorithm’s adaptability across these varying conditions, it is essential to evaluate its performance under different environmental space sizes. To this end, we conducted experiments with three distinct space dimensions, namely (30, 30, 30), (50, 50, 50), and (70, 70, 70), which represent smaller, medium, and larger abdominal space ranges, respectively (with values scaled up to ensure complete coverage of the actual space sizes). The outcomes of these experiments are depicted in Figure 7, showcasing the algorithm’s effectiveness across a spectrum of environmental conditions.

Figure 8 shows the algorithm’s consistent performance across varying abdominal space sizes. As space size grows, the algorithm’s execution remains smooth, with clear reward convergence. Despite facing challenges in smaller spaces, stability and convergence are maintained, with rewards being lower but stable. In larger spaces, higher rewards are achieved due to increased operational freedom. This trend confirms the algorithm’s adaptability and expected performance across different environments.

5.2.2. Number of Different Intelligences

In prior tests, the algorithm was found to have unused computational capacity. To optimize the computer’s performance, we raised the number of flexible needle agents per training round. This increase not only speeds up training but also bolsters learning stability, as agents learn autonomously without one’s failure affecting others. We thus experimented with setups involving one, three, and five agents, with results depicted in Figure 9.

Figure 9 presents three curves, each representing training with one, three, or five agents, and all exhibit similar upward trajectories. This indicates that the core learning pattern of the algorithm remains consistent regardless of the number of agents involved. The improvement in performance over time is uniform across setups, suggesting that the computational resources are effectively harnessed and learning efficiency is comparable. The curves, though subject to minor oscillations, demonstrate a commendable level of stability, highlighting the algorithm’s resilience and consistent performance across varying agent configurations.

5.2.3. Model Comparison

In the comparative experiment, we designed four control groups and conducted detailed performance evaluations for different models. The main objective of these control groups is to test the performance of each model in path planning experiments. We focused on calculating the average score, highest score, and lowest score of each model in the experiment to comprehensively evaluate the superiority and inferiority of the model.

Table 7. Scores in path planning experiments with different models.

	Category	Original DRL				Improved DRL
Goals		Learning Rate	Discount Factor	Batch Size	Update Frequency
Average		45	−4	134	3	246
Max		161	212	186	43	332
Min		−6	−64	64	−51	197

shows the scores of each model on these indicators. By analyzing the data in the table, it is evident that the improved DRL model outperforms the original DQN model significantly in all indicators.

The improved model performs well on the average score, significantly higher than the traditional DQN, indicating that in most cases, the improved model can more effectively find paths and obtain higher returns. And the improved model also showed a significant improvement in the highest score of each round, indicating its superior performance in extreme situations and a better ability to handle complex path planning tasks. Finally, at the lowest score, the performance of the improved model is more robust, with a significantly higher minimum score than the traditional DQN, indicating that the improved model can maintain ideal performance even under the most unfavorable conditions rather than the possibility of extremely low scores or failures like the original DQN.

5.3. Discussion

This paper encapsulates the merits of employing deep reinforcement learning in the context of flexible needle puncture path planning, which are as follows:

• Managing high-dimensional spaces: deep reinforcement learning autonomously distills essential features from raw data, adeptly handling complex, nonlinear interactions and alleviating the feature engineering burden.
• Crafting sophisticated strategies: it surpasses conventional approaches by crafting more nuanced strategies, thereby boosting performance and efficiency.
• Enhancing environmental awareness: it bolsters the agent’s environmental perception, aiding in collision avoidance and optimal path identification.
• Adaptive strategy optimization: the dynamic strategy adjustment in response to performance feedback facilitates an ongoing refinement of goal-oriented planning and exploration.
• Behavioral clarity: the agent’s behavior, shaped by environmental interactions, becomes more transparent and understandable, fostering usability and trust.

Looking ahead, future research directions are poised to include the following:

• Addressing practical application challenges: Integrating path planning algorithms with medical equipment for precise navigation while ensuring needle stability, safety, and ease of use, presents significant challenges. Cross-disciplinary collaboration is crucial to merge these algorithms with practical applications, advancing flexible needle path planning in digital healthcare.
• Incorporating dynamic needle characteristics: The kinematic model of a unicycle, which assumes quasi-static needle motion and neglects external forces, often deviates from reality due to factors like needle deformation and tissue friction. Future research could address these biases by integrating the needle’s dynamic properties into the model. Combining mechanical analysis with real-time feedback control—using force sensors, visual feedback, or other intelligent perception techniques—can improve path accuracy and system robustness. This fusion of data-driven and physical models holds promise for enhancing practical performance.
• Integrating medical imaging: Existing medical imaging technologies, such as MRI, CT, and ultrasound, offer detailed anatomical insights that can be leveraged to guide needle path planning. Future work may focus on the seamless integration of these imaging modalities with real-time navigation systems, allowing for more accurate needle placement and adaptive path adjustments based on real-time visual feedback. This combination of imaging and path planning is key to advancing minimally invasive procedures and improving patient outcomes.
• Insights from recent research: Recent studies on needle path planning have provided valuable insights into the optimization of puncture trajectories. One study highlights the use of machine learning to predict tissue properties and improve the adaptability of needle insertion paths. Another explores biomechanical modeling to simulate tissue deformation, helping refine path planning under different operational conditions [27,28,29]. These advancements suggest that combining predictive models with real-time sensor feedback could enhance the precision and reliability of needle navigation in complex medical scenarios.

6. Conclusions

This paper delves into the realm of flexible needle path planning, leveraging deep reinforcement learning to optimize puncture strategies. The needle is treated as an intelligent agent navigating a virtual human abdominal environment, aiming to refine its actions through reward-based feedback to ascertain the most effective sequence. The study commences by establishing a virtual environment that mimics the human body, detailing the spatial dimensions, positioning of obstacles, and the precise location of lesion targets. A tiered model is crafted to depict the trajectory radii of various needle segments. Following this, a reinforcement learning framework is formulated, encompassing 12 distinct states, two possible actions, and a comprehensive reward system consisting of eight single-step and five cumulative rewards to gauge the performance of the path. The deep Q-network (DQN) algorithm is then selected to train the agent, with a sensitivity analysis of parameters to identify the most favorable configuration. Experiments in path planning are conducted using these optimized parameters, evaluating the method’s efficacy and its ability to generalize across scenarios. The outcomes are encapsulated in three-dimensional path simulation diagrams, which vividly illustrate the approach’s success in addressing the static single-target flexible needle puncture path planning challenge.